विडलर विद्युत धारा स्रोत: Difference between revisions
No edit summary |
No edit summary |
||
| (13 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Electronic circuit}} | {{short description|Electronic circuit}} | ||
[[File:Widlar Patent.PNG|thumb|350px|विडलर से आरेख | [[File:Widlar Patent.PNG|thumb|350px|विडलर से आरेख देखे मूल पेटेंट]]'''विडलर विद्युत धारा स्रोत''' मूल दो-[[अवरोध]] [[वर्तमान दर्पण]] का संशोधन है जो केवल उत्पादन अर्धचालक के लिए उत्सर्जक अध:पतन रोकनेवाला को सम्मिलित करता है, जो वर्तमान स्रोत को केवल मध्यम प्रतिरोधक मानों का उपयोग करके कम धाराओं को उत्पन्न करने में सक्षम बनाता है।<ref name=Gray>{{cite book |title=एनालॉग इंटीग्रेटेड सर्किट का विश्लेषण और डिजाइन|author=PR Gray, PJ Hurst, SH Lewis & RG Meyer |year=2001 |edition=4th|publisher=John Wiley and Sons |isbn=0-471-32168-0 |url=http://www.worldcat.org/search?q=0471321680&qt=owc_search |pages= §4.4.1.1 pp. 299–303}}</ref><ref name=Sedra>{{cite book |title=माइक्रोइलेक्ट्रॉनिक सर्किट|author1=AS Sedra |author2=KC Smith |name-list-style=amp |edition=5th |isbn=0-19-514251-9 |year=2004 |publisher=Oxford University Press |url=http://www.worldcat.org/search?q=0195142519&qt=owc_search |no-pp=true |pages=Example 6.14, pp. 654–655 }}</ref><ref name=Rashid>{{cite book |title=Microelectronic circuits: analysis and design |author=MH Rashid |year=1999 |publisher=PWS Publishing Co. |isbn=0-534-95174-0 |url=http://www.worldcat.org/search?q=0534951740&qt=owc_search |pages=661–665}}</ref> | ||
विडलर परिपथ का उपयोग [[द्विध्रुवी ट्रांजिस्टर|द्विध्रु]]<ref name="journal">See, for example, Figure 2 in [https://www.utdallas.edu/~hellums/docs/JournalPapers/WidlarBandgap.pdf ''IC voltage regulators''].</ref>[[द्विध्रुवी ट्रांजिस्टर| | विडलर परिपथ का उपयोग [[द्विध्रुवी ट्रांजिस्टर|द्विध्रु]]<ref name="journal">See, for example, Figure 2 in [https://www.utdallas.edu/~hellums/docs/JournalPapers/WidlarBandgap.pdf ''IC voltage regulators''].</ref> [[द्विध्रुवी ट्रांजिस्टर|V ट्रांजिस्टर]], एमओएसएफईटी और यहां तक कि [[ वेक्यूम - ट्यूब | शून्यक-नलिका]] के साथ भी किया जा सकता है। उदाहरण अनुप्रयोग 741-प्रकार के ऑप एम्प का परिचालन प्रवर्धकआंतरिक परिपथ है,<ref name=Sedra2>{{cite book |title=§9.4.2, p. 899 |author1=AS Sedra |author2=KC Smith |name-list-style=amp |edition=5th |isbn=0-19-514251-9 |year=2004 |url=http://www.worldcat.org/search?q=0195142519&qt=owc_search }}</ref> और विडलर ने परिपथ को कई बनावट में हिस्से के रूप में इस्तेमाल किया जाता है। | ||
इस परिपथ का नाम इसके आविष्कारक [[बॉब विडलर]] के नाम पर रखा गया है और 1967 में इसका | इस परिपथ का नाम इसके आविष्कारक [[बॉब विडलर]] के नाम पर रखा गया है और 1967 में इसका एकस्व अधिकार-पत्र कराया गया था।<ref name="patent">RJ Widlar: US Patent Number 03320439; Filed May 26, 1965; Granted May 16, 1967: [http://patimg1.uspto.gov/.piw?Docid=03320439&homeurl=http%3A%2F%2Fpatft.uspto.gov%2Fnetacgi%2Fnph-Parser%3FSect1%3DPTO2%2526Sect2%3DHITOFF%2526p%3D1%2526u%3D%25252Fnetahtml%25252FPTO%25252Fsearch-bool.html%2526r%3D16%2526f%3DG%2526l%3D50%2526co1%3DAND%2526d%3DPALL%2526s1%3DWidlar.INNM.%2526OS%3DIN%2FWidlar%2526RS%3DIN%2FWidlar&PageNum=&Rtype=&SectionNum=&idkey=NONE&Input=View+first+page '' Low-value current source for integrated circuits'']</ref><ref name="Linear">See Widlar: [https://scholar.google.com/scholar?as_q=&num=10&btnG=Search+Scholar&as_epq=emitter+degeneration+resistor+&as_oq=&as_eq=&as_occt=any&as_sauthors=Widlar&as_publication=&as_ylo=1965&as_yhi=1975&as_allsubj=all&hl=en&lr= ''Some circuit design techniques for linear integrated circuits''] and [http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=1049994 ''Design techniques for monolithic operational amplifiers'']</ref> | ||
== डीसी विश्लेषण == | == डीसी विश्लेषण == | ||
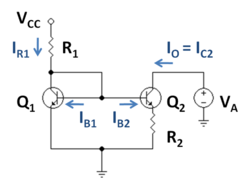
[[File:Widlar Current Source.PNG|thumb|250px|चित्र 1: बाइपोलर ट्रांजिस्टर का उपयोग करते हुए विडलर करंट स्रोत का एक संस्करण।]]चित्रा 1 द्विध्रुवी | [[File:Widlar Current Source.PNG|thumb|250px|चित्र 1: बाइपोलर ट्रांजिस्टर का उपयोग करते हुए विडलर करंट स्रोत का एक संस्करण।]]चित्रा 1 द्विध्रुवी अर्धचालक का उपयोग करते हुए विडलर वर्तमान स्रोत का उदाहरण है, जहां उत्सर्जक रोकनेवाला R<sub>2</sub> आउटपुट अर्धचालक Q<sub>2</sub> जुड़ा है, और Q<sub>2</sub> में वर्तमान को कम करने का प्रभाव है Q<sub>1</sub> के सापेक्ष. इस परिपथ की कुंजी यह है कि प्रतिरोधक R<sub>2</sub> के पार वोल्टेज गिरता है अर्धचालक Q<sub>2</sub> के आधारित उत्सर्जन वोल्टेज से घटाता है, जिससे इस अर्धचालक को अर्धचालक Q<sub>1</sub> की तुलना में समाप्त कर दिया जाता है. यह अवलोकन चित्र 1 में परिपथ के दोनों ओर पाए जाने वाले आधार वोल्टेज अभिव्यक्ति की बराबरी करके व्यक्त किया गया है: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 14: | Line 14: | ||
\Rightarrow {} &\frac{1}{R_2}\left(V_{BE1} - V_{BE2}\right) = (\beta_2 + 1)I_{B2}\ , | \Rightarrow {} &\frac{1}{R_2}\left(V_{BE1} - V_{BE2}\right) = (\beta_2 + 1)I_{B2}\ , | ||
\end{align}</math> | \end{align}</math> | ||
जहां | जहां β<sub>2</sub> उत्पादन अर्धचालक का बीटा-मान है, जो इनपुट अर्धचालक के समान नहीं है, आंशिक रूप से क्योंकि दो अर्धचालक में धाराएं बहुत भिन्न हैं।<ref name=Gray2>{{cite book |title=Figure 2.38, p. 115 |author=PR Gray, PJ Hurst, SH Lewis & RG Meyer |year=2001 |isbn=0-471-32168-0 |url=http://www.worldcat.org/search?q=0471321680&qt=owc_search }}</ref> चर /<sub>B2</sub> उत्पादन अर्धचालक, V<sub>BE</sub> का आधार वर्तमान है | आधारित उत्सर्जन वोल्टेज को संदर्भित करता है। इस समीकरण का अर्थ है (शॉकली द्विधुवी समीकरण का उपयोग करके): | ||
समीकरण 1 | |||
:<math>\begin{align} | :<math>\begin{align} | ||
(\beta_2 + 1)I_{B2} &= \left(1 + \frac{1}{\beta_2} \right) I_{C2} = \frac{1}{R_2} \left(V_{BE1} - V_{BE2}\right) \\ | (\beta_2 + 1)I_{B2} &= \left(1 + \frac{1}{\beta_2} \right) I_{C2} = \frac{1}{R_2} \left(V_{BE1} - V_{BE2}\right) \\ | ||
&= \frac{V_\text{T}}{R_2} \left[ \ln\left(I_{C1}/I_{S1}\right) - \ln\left(I_{C2}/I_{S2}\right) \right] = \frac{V_\text{T}}{R_2} \ln \left(\frac{I_{C1}I_{S2}}{I_{C2}I_{S1}}\right)\ , | &= \frac{V_\text{T}}{R_2} \left[ \ln\left(I_{C1}/I_{S1}\right) - \ln\left(I_{C2}/I_{S2}\right) \right] = \frac{V_\text{T}}{R_2} \ln \left(\frac{I_{C1}I_{S2}}{I_{C2}I_{S1}}\right)\ , | ||
\end{align}</math> | \end{align}</math> | ||
जहां | जहां V<sub>T</sub> बोल्ट्जमान स्थिरांक है | अर्धचालक भौतिकी में भूमिका: उष्मीय वोल्टेज है। | ||
यह समीकरण सन्निकटन करता है कि धाराएँ स्केल धाराओं, | यह समीकरण सन्निकटन करता है कि धाराएँ स्केल धाराओं, की तुलना में बहुत बड़ी हैं /<sub>S1</sub> और मैं /<sub>S2</sub>; द्विध्रुवी रेलमार्गसंयोग अर्धचालक संचालन के क्षेत्रों के निकट वर्तमान स्तरों को छोड़कर सन्निकटन मान्य है। निम्नलिखित में, स्केल धाराओं को समान माना जाता है; व्यवहार में, इसे विशेष रूप से व्यवस्थित करने की आवश्यकता है। | ||
== निर्दिष्ट धाराओं के साथ डिजाइन प्रक्रिया == | == निर्दिष्ट धाराओं के साथ डिजाइन प्रक्रिया == | ||
दर्पण को | दर्पण को बनाने करने के लिए, उत्पादन वर्तमान को दो प्रतिरोधक मान R<sub>1</sub>से संबंधित होना चाहिए और R<sub>2</sub>. बुनियादी अवलोकन यह है कि उत्पादक अर्धचालक बाइपोलर रेलमार्गसंयोग अर्धचालक संचालन के क्षेत्रों में केवल तभी तक होता है जब तक इसका संग्रहकर्ता आधारित वोल्टेज गैर-शून्य होता है। इस प्रकार, दर्पण के बनाने के लिए सबसे सरल पूर्वाग्रह स्थिति लागू वोल्टेज V<sub>A</sub> संग्रह करती है बेस वोल्टेज V<sub>B</sub> के बराबर करने के लिए. V<sub>A</sub> का यह न्यूनतम उपयोगी मूल्य वर्तमान दर्पण वर्तमान स्रोत का अनुपालन वोल्टेज कहा जाता है। उस पूर्वाग्रह की स्थिति के साथ, [[प्रारंभिक प्रभाव]] बनावट में कोई भूमिका नहीं निभाता है।<ref name=note1>Of course, one might imagine a design where the output resistance of the mirror is a major consideration. Then a different approach is necessary.</ref> | ||
ये विचार निम्नलिखित डिजाइन प्रक्रिया का सुझाव देते हैं: | ये विचार निम्नलिखित डिजाइन प्रक्रिया का सुझाव देते हैं: | ||
* वांछित | * वांछित उत्पादन परिपथ का चयन करें, I<sub>O</sub> = /<sub>C2</sub> | ||
* संदर्भ वर्तमान का चयन करें, | *संदर्भ वर्तमान का चयन करें, /<sub>R1</sub>, उत्पादन परिपथ से बड़ा माना जाता है, शायद काफी बड़ा (यही परिपथ का उद्देश्य है)। | ||
* | * Q<sub>1</sub> के उत्पादक सामग्री संग्रहकर्ता वर्तमान का निर्धारण करें, /<sub>C1</sub>: | ||
::<math>I_{C1} = \frac{\beta_1}{\beta_1+1} \left( I_{R1} - \frac{I_{C2}}{\beta_2} \right)\ . </math> | ::<math>I_{C1} = \frac{\beta_1}{\beta_1+1} \left( I_{R1} - \frac{I_{C2}}{\beta_2} \right)\ . </math> | ||
* | * आधार वोल्टेज निर्धारित करें V<sub>BE1</sub> द्विधुर्वी प्रतिमान शॉकली द्विधुवी प्रतिमान का उपयोग करना था | | ||
::<math> V_{BE1} = V_\text{T} \ln \left(\frac{I_{C1}} {I_S} \right) = V_A\ . </math> | ::<math> V_{BE1} = V_\text{T} \ln \left(\frac{I_{C1}} {I_S} \right) = V_A\ . </math> | ||
:जहां | :जहां /<sub>S</sub> उपकरण प्राचल है जिसे कभी-कभी स्केल वाहक कहा जाता है। | ||
: | :आधारित वोल्टेज का मान भी अनुपालन वोल्टेज संग्रह करता है V<sub>A</sub> = V<sub>BE1</sub>. यह वोल्टेज सबसे कम वोल्टेज है जिसके लिए दर्पण ठीक से काम करता है। | ||
* | * R<sub>1</sub> निर्धारित करें: | ||
::<math> R_1 = \frac {V_{CC} - V_A}{I_{R1}}\ . </math> | ::<math> R_1 = \frac {V_{CC} - V_A}{I_{R1}}\ . </math> | ||
* | * उत्सर्जक लेग प्रतिरोध R<sub>2</sub> ज्ञात कीजिए Q<sub>1</sub> का उपयोग करना था। (अव्यवस्था को कम करने के लिए, पैमाने की धाराओं को बराबर चुना जाता है): | ||
::<math>R_2 = \frac{V_\text{T}}{\left(1 + \frac{1}{\beta_2} \right) I_{C2}} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math> | ::<math>R_2 = \frac{V_\text{T}}{\left(1 + \frac{1}{\beta_2} \right) I_{C2}} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math> | ||
== दिए गए प्रतिरोधक मानों के साथ करंट का पता लगाना == | == दिए गए प्रतिरोधक मानों के साथ करंट का पता लगाना == | ||
बनावट की समस्या का व्युत्क्रम वर्तमान का पता लगाना है जब प्रतिरोधक मान ज्ञात होते हैं। आगे पुनरावृत्त विधि का वर्णन किया गया है। मान लें कि वर्तमान स्रोत पक्षपाती है इसलिए उत्पादक अर्धचालक Q<sub>2</sub> का संग्रहकर्ता-आधारित वोल्टेज शून्य है। R<sub>1</sub> के माध्यम से वर्तमान इनपुट या संदर्भ वर्तमान के रूप में दिया गया है, | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 50: | Line 49: | ||
&= \frac{1}{R_1} \left(V_{CC} - V_{BE1}\right) | &= \frac{1}{R_1} \left(V_{CC} - V_{BE1}\right) | ||
\end{align}</math> | \end{align}</math> | ||
पुनर्व्यवस्थित, | पुनर्व्यवस्थित, /<sub>C1</sub> के रूप में पाया जाता है: | ||
समीकरण। 2 | |||
:<math>I_{C1} = \frac{\beta_1}{\beta_1 + 1} \left( \frac{V_{CC} - V_{BE1}}{R_1} - \frac{I_{C2}}{\beta_2} \right) </math> | :<math>I_{C1} = \frac{\beta_1}{\beta_1 + 1} \left( \frac{V_{CC} - V_{BE1}}{R_1} - \frac{I_{C2}}{\beta_2} \right) </math> | ||
द्विधुवी समीकरण प्रदान करता है: | |||
समीकरण। 3 | |||
:<math>V_{BE1} = V_\text{T} \ln \left( \frac{I_{C1}}{I_{S1}}\right) \ . </math> | :<math>V_{BE1} = V_\text{T} \ln \left( \frac{I_{C1}}{I_{S1}}\right) \ . </math> | ||
:Eq.1 प्रदान करता है: | |||
:<math>I_{C2} = \frac{V_\text{T}}{\left(1 + \frac{1}{\beta_2} \right) R_2} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math> | :<math>I_{C2} = \frac{V_\text{T}}{\left(1 + \frac{1}{\beta_2} \right) R_2} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math> | ||
ये तीन संबंध धाराओं के लिए एक गैर-रैखिक, निहित निर्धारण हैं जिन्हें पुनरावृति द्वारा हल किया जा सकता है। | ये तीन संबंध धाराओं के लिए एक गैर-रैखिक, निहित निर्धारण हैं जिन्हें पुनरावृति द्वारा हल किया जा सकता है। | ||
* हम | * हम के लिए प्रराम्भित मानों का अनुमान लगाते हैं /<sub>C1</sub> और /<sub>C2</sub>. | ||
* हम | * हम V<sub>BE1</sub> के लिए एक मान पाते हैं: | ||
*: <math>V_{BE1} = V_\text{T} \ln \left( \frac{I_{C1}}{I_{S1}}\right) \ . </math> | *: <math>V_{BE1} = V_\text{T} \ln \left( \frac{I_{C1}}{I_{S1}}\right) \ . </math> | ||
* हम | * हम के लिए एक नया मान पाते हैं /<sub>C1</sub>: | ||
*: <math>I_{C1} = \frac{\beta_1}{\beta_1 + 1} \left( \frac {V_{CC} - V_{BE1}}{R_1} - \frac{I_{C2}}{\beta_2} \right) </math> | *: <math>I_{C1} = \frac{\beta_1}{\beta_1 + 1} \left( \frac {V_{CC} - V_{BE1}}{R_1} - \frac{I_{C2}}{\beta_2} \right) </math> | ||
* हम | * हम के लिए एक नया मान पाते हैं /<sub>C2</sub>: | ||
*: <math>I_{C2} = \frac{V_\text{T}}{\left(1 + \frac{1}{\beta_2} \right) R_2} \ln \left(\frac{I_{C1}}{I_{C2}}\right)\ . </math> | *: <math>I_{C2} = \frac{V_\text{T}}{\left(1 + \frac{1}{\beta_2} \right) R_2} \ln \left(\frac{I_{C1}}{I_{C2}}\right)\ . </math> | ||
यह प्रक्रिया अभिसरण के लिए दोहराई जाती है, और | यह प्रक्रिया अभिसरण के लिए दोहराई जाती है, और स्प्रेडशीट में आसानी से स्थापित की जाती है। लघु क्रम में समाधान प्राप्त करने के लिए प्रारंभिक मानों को धारण करने वाली स्प्रेडशीट कोशिकाओं में नए मानों को कॉपी करने के लिए बस स्थूल का उपयोग करता है। | ||
ध्यान दें कि दिखाए गए | ध्यान दें कि दिखाए गए परिपथ के साथ, यदि V<sub>CC</sub> परिवर्तन,उत्पादन वाहक बदल जाता था। इसलिए, V<sub>CC</sub> में उतार-चढ़ाव के बावजूद उत्पादन वाहक को स्थिर रखने के लिए, प्रतिरोध R<sub>1</sub> का उपयोग करने के बजाय परिपथ को [[वर्तमान स्रोत]] द्वारा संचालित किया जाना चाहिए था. | ||
=== सटीक समाधान === | === सटीक समाधान === | ||
उपर्युक्त | उपर्युक्त अतीन्द्रिय समीकरणों को ठीक [[लैम्बर्ट डब्ल्यू समारोह|लैम्बर्ट W फलन]] के संदर्भ में हल किया जा सकता है। | ||
== आउटपुट प्रतिबाधा == | == आउटपुट प्रतिबाधा == | ||
[[File:Widlar small-signal.PNG|thumb|350px |चित्रा 2: चित्रा 1 में दिखाए गए विडलर स्रोत के आउटपुट प्रतिरोध को खोजने के लिए लघु-संकेत | [[File:Widlar small-signal.PNG|thumb|350px |चित्रा 2: चित्रा 1 में दिखाए गए विडलर स्रोत के आउटपुट प्रतिरोध को खोजने के लिए लघु-संकेत परिपथ। एक परीक्षण वर्तमान ''I''<sub>x</sub> आउटपुट पर लगाया जाता है, और आउटपुट प्रतिरोध तब R<sub>O</sub> होता है = V<sub>x</sub> //<sub>x</sub>.]]वर्तमान स्रोत की महत्वपूर्ण संपत्ति इसका छोटा संकेत वृद्धिशील उत्पादक प्रतिबाधा है, जो आदर्श रूप से अनंत होना चाहिए। विडलर परिपथ ट्रांके लिस्थानीजिस्टर वर्तमान प्रतिपुस्टि पेश करता है <math>\scriptstyle Q_{2}</math>. Q<sub>2</sub> में वर्तमान में कोई वृद्धि R<sub>2</sub>भर में वोल्टेज ड्रॉप बढ़ाता है, V<sub>BE</sub> को कम करना Q<sub>2</sub> के लिए, जिससे वर्तमान में वृद्धि का मुकाबला होता है | | ||
परिपथ के लिए एक छोटे-संकेत प्रतिमान का उपयोग करके उत्पादक प्रतिरोध पाया जार Q<sub>1</sub> इसके छोटे-संकेत उत्सर्जक प्रतिरोध r<sub>E</sub> द्वारा प्रतिस्थापित किया जाता है क्योंकि यह द्विधुवी जुड़ा हुआ है।<ref name=diode>In a ''diode-connected transistor'' the collector is short-circuited to the base, so the transistor collector-base junction has no time-varying voltage across it. As a result, the transistor behaves like the base-emitter diode, which at low frequencies has a small-signal circuit that is simply the resistor ''r''<sub>E</sub> = ''V''<sub>T</sub> / ''I''<sub>E</sub>, with ''I''<sub>E</sub> the DC [[Q-point]] emitter current. See [[Diode modelling#Small-signal modeling|diode small-signal circuit]].</ref> अर्धचालक Q<sub>2</sub> किया जा सकता है। इस प्रतिक्रिया का मतलब है कि परिपथ का उत्पादक प्रतिबाधा बढ़ गया है, क्योंकि प्रतिक्रिया में R सम्मिलित है किसी दिए गए वर्तमान को चलाने के लिए एक बड़े वोल्टेज का उपयोग करने के लिए विवश करता है। चित्र 2 में दिखाया गया है। अर्धचालक इसके [[ हाइब्रिड-पाई मॉडल | हाइब्रिड-पाई प्रतिमान]] के साथ बदल दिया गया है। एक परीक्षण वर्तमान है /<sub>x</sub> उत्पादक पर संलग्न है। | |||
आकृति का उपयोग करते हुए, किरचॉफ के नियमों का उपयोग करके | आकृति का उपयोग करते हुए, किरचॉफ के नियमों का उपयोग करके उत्पादक प्रतिरोध निर्धारित किया जाता है। किरचॉफ के वोल्टेज कानून का उपयोग जमीन से बाईं ओर R<sub>2</sub> के जमीन कनेक्शन के लिए: | ||
:<math>I_b \left[ ( R_1 \parallel r_E ) + r_\pi \right] + [I_x + I_b] R_2 = 0 \ . </math> | :<math>I_b \left[ ( R_1 \parallel r_E ) + r_\pi \right] + [I_x + I_b] R_2 = 0 \ . </math> | ||
पुनर्व्यवस्थित: | पुनर्व्यवस्थित: | ||
:<math>I_b = -I_x \frac{R_2}{( R_1 \parallel r_E ) + r_\pi + R_2} \ . </math> | :<math>I_b = -I_x \frac{R_2}{( R_1 \parallel r_E ) + r_\pi + R_2} \ . </math> | ||
R<sub>2</sub> के मूल सम्पर्क से किरचॉफ के वोल्टेज कानून का उपयोग करना परीक्षण वर्तमान के आधार पर: | |||
:<math>V_x = I_x (R_2 + r_O) + I_b (R_2 - \beta r_O)\ , </math> | :<math>V_x = I_x (R_2 + r_O) + I_b (R_2 - \beta r_O)\ , </math> | ||
या, | या, /<sub>b</sub> के लिए प्रतिस्थापन: | ||
समीकरण। 4 | |||
:<math>R_O = \frac{V_x}{I_x} = r_O \left[ 1 + \frac{\beta R_2}{( R_1 \parallel r_E ) + r_\pi + R_2} \right] </math> <math>+ \ R_2 \left[ \frac{( R_1 \parallel r_E ) + r_\pi}{( R_1 \parallel r_E ) + r_\pi + R_2} \right] \ . </math> | :<math>R_O = \frac{V_x}{I_x} = r_O \left[ 1 + \frac{\beta R_2}{( R_1 \parallel r_E ) + r_\pi + R_2} \right] </math> <math>+ \ R_2 \left[ \frac{( R_1 \parallel r_E ) + r_\pi}{( R_1 \parallel r_E ) + r_\pi + R_2} \right] \ . </math> | ||
# | #समीकरण। 4 के अनुसार, विडलर वर्तमान स्रोत का उत्पादक रोकनेवाला उत्पादक अर्धचालक के ही ऊपर बढ़ जाता है (जो कि r<sub>O</sub> है) जब तक R<sub>2</sub> की तुलना में काफी बड़ा है r<sub>π</sub> उत्पादक अर्धचालक (बड़े प्रतिरोध R<sub>2</sub> कारक गुणा R<sub>O</sub> बनाओ मूल्य (β + 1) तक पहुंचें)। उत्पादक अर्धचालक में कम वर्तमान होता है, जिससे r<sub>π</sub> बनता है बड़ा, और R<sub>2</sub> में वृद्धि इस धारा को और कम करता है, जिससे r<sub>π</sub> में सहसंबद्ध वृद्धि होती हैl इसलिए, R<sub>2</sub> का एक लक्ष्य ≫ r<sub>π</sub> अवास्तविक हो सकता है, और आगे की चर्चा प्रदान की जाती है उत्पादक प्रतिरोध की वर्तमान निर्भरता प्रतिरोध R<sub>1</sub>∥r<sub>E</sub> सामान्यतौर पर छोटा होता है क्योंकि उत्सर्जक प्रतिरोध r<sub>E</sub> सामान्यतौर पर केवल कुछ ओम होते हैं। | ||
=== आउटपुट प्रतिरोध की वर्तमान निर्भरता === | === आउटपुट प्रतिरोध की वर्तमान निर्भरता === | ||
[[File:Widlar Resistance Plot.PNG|thumb| | [[File:Widlar Resistance Plot.PNG|thumb|340x340px|डिज़ाइन सूत्र का उपयोग करके। केंद्र पैनल: प्रतिरोध R<sub>O2</sub> आउटपुट ट्रांजिस्टर एमिटर लेग ''I<sub>c2</sub>''; | ||
निचला पैनल: आउटपुट प्रतिरोध में योगदान देने वाला प्रतिपुष्टि कारक होता है। संदर्भ ट्रांजिस्टर Q<sub>1</sub> में वर्तमान स्थिर रखा जाता है, जिससे अनुपालन वोल्टेज तय होता है। भूखंड I मानते हैं ''I''<sub>C1</sub> = 10 mA, ''V''<sub>A</sub> = 50 ''V'', ''V''<sub>CC</sub> = 5 V, ''I''<sub>S</sub> = 10 fA, β<sub>1, 2</sub> = 100 धारा से स्वतंत्र।]]प्रतिरोधों की वर्तमान निर्भरता r<sub>π</sub> और r<sub>O</sub> लेख हाइब्रिड-पीआई प्रतिरूप में चर्चा की गई है। प्रतिरोधक मानों की वर्तमान निर्भरता है: | |||
:<math>r_\pi = \frac{v_{be}}{i_b}\Bigg|_{v_{ce} = 0} = \frac{V_\text{T}}{I_\text{B2}} = \beta_2\frac{V_\text{T}}{I_\text{C2}}\ ,</math> | :<math>r_\pi = \frac{v_{be}}{i_b}\Bigg|_{v_{ce} = 0} = \frac{V_\text{T}}{I_\text{B2}} = \beta_2\frac{V_\text{T}}{I_\text{C2}}\ ,</math> | ||
और | और | ||
:<math>r_O = \frac{v_{ce}}{i_c}\Bigg|_{v_{be} = 0} = \frac {V_A}{I_{C2}}</math> | :<math>r_O = \frac{v_{ce}}{i_c}\Bigg|_{v_{be} = 0} = \frac {V_A}{I_{C2}}</math> | ||
प्रारंभिक प्रभाव के कारण | प्रारंभिक प्रभाव के कारण उत्पादक प्रतिरोध है जब V<sub>CB</sub> = 0 V (उपकरण पैरामीटर V<sub>A</sub> प्रारंभिक वोल्टेज है)। | ||
इस लेख में | इस लेख में R<sub>2</sub> से (सुविधा के लिए स्केल धाराओं को बराबर समुच्चय करना): | ||
{{anchor|Eq5}समीकरण। 5 | |||
<nowiki>{{anchor|Eq5}समीकरण। 5</nowiki> | |||
:<math>R_2 = \frac{V_\text{T}}{\left(1 + \frac{1}{\beta_2} \right) I_{C2}} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math> | :<math>R_2 = \frac{V_\text{T}}{\left(1 + \frac{1}{\beta_2} \right) I_{C2}} \ln \left(\frac {I_{C1}}{I_{C2}}\right)\ . </math> | ||
नतीजतन, छोटे | नतीजतन, छोटे r<sub>E</sub> के सामान्य मामले के लिए, और R<sub>O</sub>में दूसरे कार्यकाल की उपेक्षा करना इस अपेक्षा के साथ कि अग्रणी शब्द जिसमें सम्मिलित है r<sub>O</sub> बहुत बड़ा है: | ||
{{Anchor|Eq6}समीकरण। 6 | |||
<nowiki>{{Anchor|Eq6}समीकरण। 6</nowiki> | |||
:<math>\begin{align} | :<math>\begin{align} | ||
R_O &\approx r_O \left( 1 + \frac{\beta_2 R_2}{r_\pi + R_2} \right) \\ | R_O &\approx r_O \left( 1 + \frac{\beta_2 R_2}{r_\pi + R_2} \right) \\ | ||
&= r_O \left( 1 + \frac{\beta_2 \ln \left(\frac{I_{C1}}{I_{C2}}\right)}{\beta_2 + 1 + \ln \left(\frac {I_{C1}}{I_{C2}}\right)} \right) | &= r_O \left( 1 + \frac{\beta_2 \ln \left(\frac{I_{C1}}{I_{C2}}\right)}{\beta_2 + 1 + \ln \left(\frac {I_{C1}}{I_{C2}}\right)} \right) | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ | : | ||
जहाँ समीकरण।5 को प्रतिस्थापित करके अंतिम रूप प्राप्त होता है R<sub>2</sub> l समीकरण 6 से पता चलता है कि उत्पादक प्रतिरोध का मान r<sub>O</sub> से बहुत बड़ा है केवल बनावट के लिए उत्पादक अर्धचालक परिणाम /<sub>C1</sub> >> /<sub>C2</sub>. चित्रा 3 दिखाता है कि परिपथ उत्पादक प्रतिरोध R<sub>O</sub> प्रतिपुष्टि द्वारा इतना अधिक निर्धारित नहीं किया जाता है जितना कि प्रतिरोध r<sub>O</sub> की वर्तमान निर्भरता द्वारा उत्पादक अर्धचालक का (चित्र 3 में उत्पादक प्रतिरोध परिमाण के चार क्रमों में भिन्न होता है, चूँकि प्रतिक्रिया कारक केवल परिमाण के क्रम से भिन्न होता है)। | |||
/<sub>c1</sub> की वृद्धि प्रतिक्रिया कारक को बढ़ाने के लिए भी अनुपालन वोल्टेज में वृद्धि हुई है, अच्छी बात नहीं है क्योंकि इसका मतलब है कि वर्तमान स्रोत अत्यधिक प्रतिबंधित वोल्टेज श्रेणी पर काम करता है। इसलिए, उदाहरण के लिए, अनुपालन वोल्टेज समुच्चय के लक्ष्य के साथ, /<sub>c1</sub> पर ऊपरी सीमा रखकर,और उत्पादक प्रतिरोध को पूरा करने के लक्ष्य के साथ, उत्पादक वर्तमान का अधिकतम मान /<sub>C2</sub> सीमित है। | |||
चित्र 3 में केंद्र | चित्र 3 में केंद्र भाग उत्सर्जक लेग प्रतिरोधक और उत्पादक वर्तमान के बीच बनावट ट्रेड-ऑफ दिखाता है: कम उत्पादक वर्तमान के लिए बड़े लेग रोकनेवाला की आवश्यकता होती है, और इसलिए बनावट के लिए एक बड़ा क्षेत्र था| क्षेत्र पर ऊपरी सीमा इसलिए उत्पादक वर्तमान पर एक निचली सीमा और परिपथ उत्पादक प्रतिरोध पर एक ऊपरी सीमा निर्धारित करती है। | ||
# | #समीकरण।6 R<sub>O</sub> के लिए R<sub>2</sub> के मान के चयन पर निर्भर करता हैl समीकरण।5 के अनुसार। इसका मतलब समीकरण।6 एक परिपथ व्यवहार सूत्र नहीं है, बल्कि बनावट मान समीकरण है। R<sub>2</sub> समीकरण।5 का उपयोग करके किसी विशेष डिज़ाइन उद्देश्य के लिए चयन किया जाता है। उसके बाद इसका मूल्य तय हो गया है। यदि परिपथ संचालन के कारण वर्तमान, वोल्टेज या तापमान डिज़ाइन किए गए मानों से विचलित हो जाते हैं; फिर R<sub>O</sub> में परिवर्तन की भविष्यवाणी करने के लिए ऐसे विचलन के कारण, समीकरण।4 का उपयोग किया जाना चाहिए, समीकरण।6 का नहीं था |. | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 127: | Line 129: | ||
==संदर्भ== | ==संदर्भ== | ||
<references /> | <references /> | ||
==अग्रिम पठन== | ==अग्रिम पठन== | ||
* {{cite book |title=Current Sources and Voltage References: A Design Reference for Electronics Engineers|author=Linden T. Harrison |publisher= Elsevier-Newnes |year=2005 |isbn= 0-7506-7752-X |url=https://books.google.com/books?id=03JmxpE39N4C}} | * {{cite book |title=Current Sources and Voltage References: A Design Reference for Electronics Engineers|author=Linden T. Harrison |publisher= Elsevier-Newnes |year=2005 |isbn= 0-7506-7752-X |url=https://books.google.com/books?id=03JmxpE39N4C}} | ||
| Line 134: | Line 134: | ||
|isbn=0-07-059096-6 |publisher=Tata McGraw-Hill |year=2005 }} | |isbn=0-07-059096-6 |publisher=Tata McGraw-Hill |year=2005 }} | ||
* [http://sync.cn.nctu.edu.tw/mhcheng/analog-ic/Chap6.pdf Current mirrors and active loads: Mu-Huo Cheng] | * [http://sync.cn.nctu.edu.tw/mhcheng/analog-ic/Chap6.pdf Current mirrors and active loads: Mu-Huo Cheng] | ||
[[de:Stromspiegel#Beispiele]] | [[de:Stromspiegel#Beispiele]] | ||
[[Category:CS1 maint]] | |||
[[Category: | |||
[[Category:Created On 19/06/2023]] | [[Category:Created On 19/06/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:इलेक्ट्रॉनिक डिजाइन]] | |||
[[Category:एनालॉग सर्किट]] | |||
Latest revision as of 15:49, 30 August 2023
विडलर विद्युत धारा स्रोत मूल दो-अवरोध वर्तमान दर्पण का संशोधन है जो केवल उत्पादन अर्धचालक के लिए उत्सर्जक अध:पतन रोकनेवाला को सम्मिलित करता है, जो वर्तमान स्रोत को केवल मध्यम प्रतिरोधक मानों का उपयोग करके कम धाराओं को उत्पन्न करने में सक्षम बनाता है।[1][2][3]
विडलर परिपथ का उपयोग द्विध्रु[4] V ट्रांजिस्टर, एमओएसएफईटी और यहां तक कि शून्यक-नलिका के साथ भी किया जा सकता है। उदाहरण अनुप्रयोग 741-प्रकार के ऑप एम्प का परिचालन प्रवर्धकआंतरिक परिपथ है,[5] और विडलर ने परिपथ को कई बनावट में हिस्से के रूप में इस्तेमाल किया जाता है।
इस परिपथ का नाम इसके आविष्कारक बॉब विडलर के नाम पर रखा गया है और 1967 में इसका एकस्व अधिकार-पत्र कराया गया था।[6][7]
डीसी विश्लेषण
चित्रा 1 द्विध्रुवी अर्धचालक का उपयोग करते हुए विडलर वर्तमान स्रोत का उदाहरण है, जहां उत्सर्जक रोकनेवाला R2 आउटपुट अर्धचालक Q2 जुड़ा है, और Q2 में वर्तमान को कम करने का प्रभाव है Q1 के सापेक्ष. इस परिपथ की कुंजी यह है कि प्रतिरोधक R2 के पार वोल्टेज गिरता है अर्धचालक Q2 के आधारित उत्सर्जन वोल्टेज से घटाता है, जिससे इस अर्धचालक को अर्धचालक Q1 की तुलना में समाप्त कर दिया जाता है. यह अवलोकन चित्र 1 में परिपथ के दोनों ओर पाए जाने वाले आधार वोल्टेज अभिव्यक्ति की बराबरी करके व्यक्त किया गया है:
जहां β2 उत्पादन अर्धचालक का बीटा-मान है, जो इनपुट अर्धचालक के समान नहीं है, आंशिक रूप से क्योंकि दो अर्धचालक में धाराएं बहुत भिन्न हैं।[8] चर /B2 उत्पादन अर्धचालक, VBE का आधार वर्तमान है | आधारित उत्सर्जन वोल्टेज को संदर्भित करता है। इस समीकरण का अर्थ है (शॉकली द्विधुवी समीकरण का उपयोग करके):
समीकरण 1
जहां VT बोल्ट्जमान स्थिरांक है | अर्धचालक भौतिकी में भूमिका: उष्मीय वोल्टेज है।
यह समीकरण सन्निकटन करता है कि धाराएँ स्केल धाराओं, की तुलना में बहुत बड़ी हैं /S1 और मैं /S2; द्विध्रुवी रेलमार्गसंयोग अर्धचालक संचालन के क्षेत्रों के निकट वर्तमान स्तरों को छोड़कर सन्निकटन मान्य है। निम्नलिखित में, स्केल धाराओं को समान माना जाता है; व्यवहार में, इसे विशेष रूप से व्यवस्थित करने की आवश्यकता है।
निर्दिष्ट धाराओं के साथ डिजाइन प्रक्रिया
दर्पण को बनाने करने के लिए, उत्पादन वर्तमान को दो प्रतिरोधक मान R1से संबंधित होना चाहिए और R2. बुनियादी अवलोकन यह है कि उत्पादक अर्धचालक बाइपोलर रेलमार्गसंयोग अर्धचालक संचालन के क्षेत्रों में केवल तभी तक होता है जब तक इसका संग्रहकर्ता आधारित वोल्टेज गैर-शून्य होता है। इस प्रकार, दर्पण के बनाने के लिए सबसे सरल पूर्वाग्रह स्थिति लागू वोल्टेज VA संग्रह करती है बेस वोल्टेज VB के बराबर करने के लिए. VA का यह न्यूनतम उपयोगी मूल्य वर्तमान दर्पण वर्तमान स्रोत का अनुपालन वोल्टेज कहा जाता है। उस पूर्वाग्रह की स्थिति के साथ, प्रारंभिक प्रभाव बनावट में कोई भूमिका नहीं निभाता है।[9]
ये विचार निम्नलिखित डिजाइन प्रक्रिया का सुझाव देते हैं:
- वांछित उत्पादन परिपथ का चयन करें, IO = /C2
- संदर्भ वर्तमान का चयन करें, /R1, उत्पादन परिपथ से बड़ा माना जाता है, शायद काफी बड़ा (यही परिपथ का उद्देश्य है)।
- Q1 के उत्पादक सामग्री संग्रहकर्ता वर्तमान का निर्धारण करें, /C1:
- आधार वोल्टेज निर्धारित करें VBE1 द्विधुर्वी प्रतिमान शॉकली द्विधुवी प्रतिमान का उपयोग करना था |
- जहां /S उपकरण प्राचल है जिसे कभी-कभी स्केल वाहक कहा जाता है।
- आधारित वोल्टेज का मान भी अनुपालन वोल्टेज संग्रह करता है VA = VBE1. यह वोल्टेज सबसे कम वोल्टेज है जिसके लिए दर्पण ठीक से काम करता है।
- R1 निर्धारित करें:
- उत्सर्जक लेग प्रतिरोध R2 ज्ञात कीजिए Q1 का उपयोग करना था। (अव्यवस्था को कम करने के लिए, पैमाने की धाराओं को बराबर चुना जाता है):
दिए गए प्रतिरोधक मानों के साथ करंट का पता लगाना
बनावट की समस्या का व्युत्क्रम वर्तमान का पता लगाना है जब प्रतिरोधक मान ज्ञात होते हैं। आगे पुनरावृत्त विधि का वर्णन किया गया है। मान लें कि वर्तमान स्रोत पक्षपाती है इसलिए उत्पादक अर्धचालक Q2 का संग्रहकर्ता-आधारित वोल्टेज शून्य है। R1 के माध्यम से वर्तमान इनपुट या संदर्भ वर्तमान के रूप में दिया गया है,
पुनर्व्यवस्थित, /C1 के रूप में पाया जाता है:
समीकरण। 2
द्विधुवी समीकरण प्रदान करता है:
समीकरण। 3
- Eq.1 प्रदान करता है:
ये तीन संबंध धाराओं के लिए एक गैर-रैखिक, निहित निर्धारण हैं जिन्हें पुनरावृति द्वारा हल किया जा सकता है।
- हम के लिए प्रराम्भित मानों का अनुमान लगाते हैं /C1 और /C2.
- हम VBE1 के लिए एक मान पाते हैं:
- हम के लिए एक नया मान पाते हैं /C1:
- हम के लिए एक नया मान पाते हैं /C2:
यह प्रक्रिया अभिसरण के लिए दोहराई जाती है, और स्प्रेडशीट में आसानी से स्थापित की जाती है। लघु क्रम में समाधान प्राप्त करने के लिए प्रारंभिक मानों को धारण करने वाली स्प्रेडशीट कोशिकाओं में नए मानों को कॉपी करने के लिए बस स्थूल का उपयोग करता है।
ध्यान दें कि दिखाए गए परिपथ के साथ, यदि VCC परिवर्तन,उत्पादन वाहक बदल जाता था। इसलिए, VCC में उतार-चढ़ाव के बावजूद उत्पादन वाहक को स्थिर रखने के लिए, प्रतिरोध R1 का उपयोग करने के बजाय परिपथ को वर्तमान स्रोत द्वारा संचालित किया जाना चाहिए था.
सटीक समाधान
उपर्युक्त अतीन्द्रिय समीकरणों को ठीक लैम्बर्ट W फलन के संदर्भ में हल किया जा सकता है।
आउटपुट प्रतिबाधा
वर्तमान स्रोत की महत्वपूर्ण संपत्ति इसका छोटा संकेत वृद्धिशील उत्पादक प्रतिबाधा है, जो आदर्श रूप से अनंत होना चाहिए। विडलर परिपथ ट्रांके लिस्थानीजिस्टर वर्तमान प्रतिपुस्टि पेश करता है . Q2 में वर्तमान में कोई वृद्धि R2भर में वोल्टेज ड्रॉप बढ़ाता है, VBE को कम करना Q2 के लिए, जिससे वर्तमान में वृद्धि का मुकाबला होता है |
परिपथ के लिए एक छोटे-संकेत प्रतिमान का उपयोग करके उत्पादक प्रतिरोध पाया जार Q1 इसके छोटे-संकेत उत्सर्जक प्रतिरोध rE द्वारा प्रतिस्थापित किया जाता है क्योंकि यह द्विधुवी जुड़ा हुआ है।[10] अर्धचालक Q2 किया जा सकता है। इस प्रतिक्रिया का मतलब है कि परिपथ का उत्पादक प्रतिबाधा बढ़ गया है, क्योंकि प्रतिक्रिया में R सम्मिलित है किसी दिए गए वर्तमान को चलाने के लिए एक बड़े वोल्टेज का उपयोग करने के लिए विवश करता है। चित्र 2 में दिखाया गया है। अर्धचालक इसके हाइब्रिड-पाई प्रतिमान के साथ बदल दिया गया है। एक परीक्षण वर्तमान है /x उत्पादक पर संलग्न है।
आकृति का उपयोग करते हुए, किरचॉफ के नियमों का उपयोग करके उत्पादक प्रतिरोध निर्धारित किया जाता है। किरचॉफ के वोल्टेज कानून का उपयोग जमीन से बाईं ओर R2 के जमीन कनेक्शन के लिए:
पुनर्व्यवस्थित:
R2 के मूल सम्पर्क से किरचॉफ के वोल्टेज कानून का उपयोग करना परीक्षण वर्तमान के आधार पर:
या, /b के लिए प्रतिस्थापन:
समीकरण। 4
- समीकरण। 4 के अनुसार, विडलर वर्तमान स्रोत का उत्पादक रोकनेवाला उत्पादक अर्धचालक के ही ऊपर बढ़ जाता है (जो कि rO है) जब तक R2 की तुलना में काफी बड़ा है rπ उत्पादक अर्धचालक (बड़े प्रतिरोध R2 कारक गुणा RO बनाओ मूल्य (β + 1) तक पहुंचें)। उत्पादक अर्धचालक में कम वर्तमान होता है, जिससे rπ बनता है बड़ा, और R2 में वृद्धि इस धारा को और कम करता है, जिससे rπ में सहसंबद्ध वृद्धि होती हैl इसलिए, R2 का एक लक्ष्य ≫ rπ अवास्तविक हो सकता है, और आगे की चर्चा प्रदान की जाती है उत्पादक प्रतिरोध की वर्तमान निर्भरता प्रतिरोध R1∥rE सामान्यतौर पर छोटा होता है क्योंकि उत्सर्जक प्रतिरोध rE सामान्यतौर पर केवल कुछ ओम होते हैं।
आउटपुट प्रतिरोध की वर्तमान निर्भरता

प्रतिरोधों की वर्तमान निर्भरता rπ और rO लेख हाइब्रिड-पीआई प्रतिरूप में चर्चा की गई है। प्रतिरोधक मानों की वर्तमान निर्भरता है:
और
प्रारंभिक प्रभाव के कारण उत्पादक प्रतिरोध है जब VCB = 0 V (उपकरण पैरामीटर VA प्रारंभिक वोल्टेज है)।
इस लेख में R2 से (सुविधा के लिए स्केल धाराओं को बराबर समुच्चय करना):
{{anchor|Eq5}समीकरण। 5
नतीजतन, छोटे rE के सामान्य मामले के लिए, और ROमें दूसरे कार्यकाल की उपेक्षा करना इस अपेक्षा के साथ कि अग्रणी शब्द जिसमें सम्मिलित है rO बहुत बड़ा है:
{{Anchor|Eq6}समीकरण। 6
जहाँ समीकरण।5 को प्रतिस्थापित करके अंतिम रूप प्राप्त होता है R2 l समीकरण 6 से पता चलता है कि उत्पादक प्रतिरोध का मान rO से बहुत बड़ा है केवल बनावट के लिए उत्पादक अर्धचालक परिणाम /C1 >> /C2. चित्रा 3 दिखाता है कि परिपथ उत्पादक प्रतिरोध RO प्रतिपुष्टि द्वारा इतना अधिक निर्धारित नहीं किया जाता है जितना कि प्रतिरोध rO की वर्तमान निर्भरता द्वारा उत्पादक अर्धचालक का (चित्र 3 में उत्पादक प्रतिरोध परिमाण के चार क्रमों में भिन्न होता है, चूँकि प्रतिक्रिया कारक केवल परिमाण के क्रम से भिन्न होता है)।
/c1 की वृद्धि प्रतिक्रिया कारक को बढ़ाने के लिए भी अनुपालन वोल्टेज में वृद्धि हुई है, अच्छी बात नहीं है क्योंकि इसका मतलब है कि वर्तमान स्रोत अत्यधिक प्रतिबंधित वोल्टेज श्रेणी पर काम करता है। इसलिए, उदाहरण के लिए, अनुपालन वोल्टेज समुच्चय के लक्ष्य के साथ, /c1 पर ऊपरी सीमा रखकर,और उत्पादक प्रतिरोध को पूरा करने के लक्ष्य के साथ, उत्पादक वर्तमान का अधिकतम मान /C2 सीमित है।
चित्र 3 में केंद्र भाग उत्सर्जक लेग प्रतिरोधक और उत्पादक वर्तमान के बीच बनावट ट्रेड-ऑफ दिखाता है: कम उत्पादक वर्तमान के लिए बड़े लेग रोकनेवाला की आवश्यकता होती है, और इसलिए बनावट के लिए एक बड़ा क्षेत्र था| क्षेत्र पर ऊपरी सीमा इसलिए उत्पादक वर्तमान पर एक निचली सीमा और परिपथ उत्पादक प्रतिरोध पर एक ऊपरी सीमा निर्धारित करती है।
- समीकरण।6 RO के लिए R2 के मान के चयन पर निर्भर करता हैl समीकरण।5 के अनुसार। इसका मतलब समीकरण।6 एक परिपथ व्यवहार सूत्र नहीं है, बल्कि बनावट मान समीकरण है। R2 समीकरण।5 का उपयोग करके किसी विशेष डिज़ाइन उद्देश्य के लिए चयन किया जाता है। उसके बाद इसका मूल्य तय हो गया है। यदि परिपथ संचालन के कारण वर्तमान, वोल्टेज या तापमान डिज़ाइन किए गए मानों से विचलित हो जाते हैं; फिर RO में परिवर्तन की भविष्यवाणी करने के लिए ऐसे विचलन के कारण, समीकरण।4 का उपयोग किया जाना चाहिए, समीकरण।6 का नहीं था |.
यह भी देखें
- वर्तमान स्रोत
- वर्तमान दर्पण
- विल्सन वर्तमान स्रोत
संदर्भ
- ↑ PR Gray, PJ Hurst, SH Lewis & RG Meyer (2001). एनालॉग इंटीग्रेटेड सर्किट का विश्लेषण और डिजाइन (4th ed.). John Wiley and Sons. pp. §4.4.1.1 pp. 299–303. ISBN 0-471-32168-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ AS Sedra & KC Smith (2004). माइक्रोइलेक्ट्रॉनिक सर्किट (5th ed.). Oxford University Press. Example 6.14, pp. 654–655. ISBN 0-19-514251-9.
- ↑ MH Rashid (1999). Microelectronic circuits: analysis and design. PWS Publishing Co. pp. 661–665. ISBN 0-534-95174-0.
- ↑ See, for example, Figure 2 in IC voltage regulators.
- ↑ AS Sedra & KC Smith (2004). §9.4.2, p. 899 (5th ed.). ISBN 0-19-514251-9.
- ↑ RJ Widlar: US Patent Number 03320439; Filed May 26, 1965; Granted May 16, 1967: Low-value current source for integrated circuits
- ↑ See Widlar: Some circuit design techniques for linear integrated circuits and Design techniques for monolithic operational amplifiers
- ↑ PR Gray, PJ Hurst, SH Lewis & RG Meyer (2001). Figure 2.38, p. 115. ISBN 0-471-32168-0.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ Of course, one might imagine a design where the output resistance of the mirror is a major consideration. Then a different approach is necessary.
- ↑ In a diode-connected transistor the collector is short-circuited to the base, so the transistor collector-base junction has no time-varying voltage across it. As a result, the transistor behaves like the base-emitter diode, which at low frequencies has a small-signal circuit that is simply the resistor rE = VT / IE, with IE the DC Q-point emitter current. See diode small-signal circuit.
अग्रिम पठन
- Linden T. Harrison (2005). Current Sources and Voltage References: A Design Reference for Electronics Engineers. Elsevier-Newnes. ISBN 0-7506-7752-X.
- Sundaram Natarajan (2005). Microelectronics: Analysis and Design. Tata McGraw-Hill. p. 319. ISBN 0-07-059096-6.
- Current mirrors and active loads: Mu-Huo Cheng