तलीय लैमिना: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
गणित में, '''तलीय लैमिना''' (प्लानर लैमिना) या समतल पटल एक आकृति है जो ठोस की पतली परत, सामान्यतः एकसमान समतल परत का प्रतिनिधित्व करती है। यह समाकलन में एक ठोस सतह के तलीय अनुप्रस्थ काट के आदर्श मॉडल के रूप में भी कार्य करती है।<ref>{{citation| first1=Tony|last1=Atkins| first2=Marcel|last2=Escudier| title=A Dictionary of Mechanical Engineering (1 ed.)| chapter=Plane lamina| chapter-url=https://www.oxfordreference.com/view/10.1093/acref/9780199587438.001.0001/acref-9780199587438-e-4614| date=2013| publisher=[[Oxford University Press]]| isbn=9780199587438| doi=10.1093/acref/9780199587438.001.0001| access-date=2021-06-08}}</ref> | |||
गणित में, '''तलीय लैमिना''' (या समतल पटल | |||
जड़त्व के क्षणों या समतल आकृतियों के द्रव्यमान के केंद्र को निर्धारित करने के साथ-साथ 3डी निकायों के लिए संबंधित गणनाओं में सहायता के लिए तलीय लैमिना का उपयोग किया जा सकता है। | जड़त्व के क्षणों या समतल आकृतियों के द्रव्यमान के केंद्र को निर्धारित करने के साथ-साथ 3डी निकायों के लिए संबंधित गणनाओं में सहायता के लिए तलीय लैमिना का उपयोग किया जा सकता है। | ||
| Line 63: | Line 58: | ||
& = \left.\left(-\frac{x^4}{2}+\frac{4x^3}{3}-20x^2+80x\right)\right|_{x=0}^2 \\ | & = \left.\left(-\frac{x^4}{2}+\frac{4x^3}{3}-20x^2+80x\right)\right|_{x=0}^2 \\ | ||
& = \frac{248}{3} \end{align}</math> | & = \frac{248}{3} \end{align}</math> | ||
अंततः द्रव्यमान का केंद्र है: | |||
:<math>\left( \frac{M_y}m, \frac{M_x}m \right) = | :<math>\left( \frac{M_y}m, \frac{M_x}m \right) = | ||
| Line 73: | Line 68: | ||
<ref name=MathWorld>{{MathWorld |id=Lamina |title=Lamina |author= |access-date=2021-03-09 |ref= }}</ref> | <ref name=MathWorld>{{MathWorld |id=Lamina |title=Lamina |author= |access-date=2021-03-09 |ref= }}</ref> | ||
}} | }} | ||
[[Category: | [[Category:All articles needing additional references]] | ||
[[Category:All articles that are too technical]] | |||
[[Category:Articles needing additional references from October 2021]] | |||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:Articles with multiple maintenance issues]] | |||
[[Category:Created On 18/05/2023]] | [[Category:Created On 18/05/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Wikipedia articles that are too technical from October 2015]] | |||
[[Category:माप सिद्धांत]] | |||
Latest revision as of 16:12, 30 August 2023
गणित में, तलीय लैमिना (प्लानर लैमिना) या समतल पटल एक आकृति है जो ठोस की पतली परत, सामान्यतः एकसमान समतल परत का प्रतिनिधित्व करती है। यह समाकलन में एक ठोस सतह के तलीय अनुप्रस्थ काट के आदर्श मॉडल के रूप में भी कार्य करती है।[1]
जड़त्व के क्षणों या समतल आकृतियों के द्रव्यमान के केंद्र को निर्धारित करने के साथ-साथ 3डी निकायों के लिए संबंधित गणनाओं में सहायता के लिए तलीय लैमिना का उपयोग किया जा सकता है।
परिभाषा
मूल रूप से एक तलीय लैमिना को समतल में परिमित क्षेत्र के एक आंकड़े (सवृत समुच्चय) D के रूप में परिभाषित किया जाता है, जिसमें कुछ द्रव्यमान m होता है।[2]
यह स्थिर घनत्व के लिए जड़त्व या द्रव्यमान के केंद्र के क्षणों की गणना करने में उपयोगी है क्योंकि एक पटल का द्रव्यमान उसके क्षेत्रफल के समानुपाती होता है। एक चर घनत्व की स्थिति मे कुछ (गैर-ऋणात्मक) सतह घनत्व फलन द्वारा दिए गए तलीय लैमिना D का द्रव्यमान m आकृति के ऊपर ρ का तलीय समाकलन है:[3]
गुण
तलीय लैमिना के द्रव्यमान के केंद्र बिंदु हैं:
जहाँ y-अक्ष में संपूर्ण पटल का क्षण है और x-अक्ष के संपूर्ण पटल का क्षण है:
समतलीय डोमेन पर लिए गए योग और समाकलन के साथ बिन्दु है।
उदाहरण
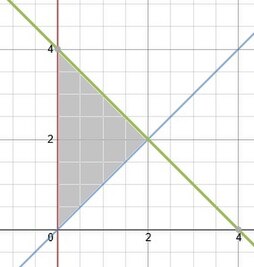
रेखाओ और द्वारा दिए गए शीर्षों के साथ एक लैमिना के द्रव्यमान का केंद्र खोजें जहां घनत्व के रूप में दिया गया है।
इसके लिए द्रव्यमान और आघूर्ण और का पता लगाना आवश्यक है।
जहां द्रव्यमान है जिसे समान रूप से पुनरावृत्त समाकल के रूप में व्यक्त किया जा सकता है:
आंतरिक समाकल है:
इसे बाहरी समाकल परिणामों के रूप में प्रयुक्त किया जा सकता है:
इसी प्रकार दोनों क्षणों की गणना की जाती है:
आंतरिक समाकल के साथ:
और
अंततः द्रव्यमान का केंद्र है:
संदर्भ
- ↑ Atkins, Tony; Escudier, Marcel (2013), "Plane lamina", A Dictionary of Mechanical Engineering (1 ed.), Oxford University Press, doi:10.1093/acref/9780199587438.001.0001, ISBN 9780199587438, retrieved 2021-06-08
- ↑ "Planar Laminae", WolframAlpha, retrieved 2021-03-09
- ↑ "Lamina". MathWorld. Retrieved 2021-03-09.