नमूनाकरण (सांख्यिकी): Difference between revisions
(नमूनाकरण) |
m (Neeraja moved page नमूनाकरण to नमूनाकरण (सांख्यिकी) without leaving a redirect) |
||
| (34 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Selection of data points in statistics.}} | {{Short description|Selection of data points in statistics.}} | ||
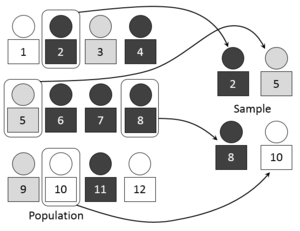
[[File:Simple random sampling.PNG|thumb|300px|नमूनाकरण प्रक्रिया का एक दृश्य प्रतिनिधित्व]] | [[File:Simple random sampling.PNG|thumb|300px|नमूनाकरण प्रक्रिया का एक दृश्य प्रतिनिधित्व]] | ||
सांख्यिकी, गुणवत्ता आश्वासन, और सर्वेक्षण पद्धति में, नमूना एक सांख्यिकीय जनसंख्या के बीच में से व्यक्तियों के एक सबसेट (एक सांख्यिकीय नमूने) का चयन है, जो पूरी जनसंख्या की विशेषताओं का अनुमान लगाता है।सांख्यिकीविद् ऐसे नमूने एकत्र करने का प्रयास करते हैं,जो विचाराधीन जनसंख्या के प्रतिनिधि हैं।नमूनाकरण(सैंपलिंग) में पूरी जनसंख्या को मापने की तुलना में कम लागत और तेजी से डेटा संग्रह होता है,और उन मामलों में अंतर्दृष्टि प्रदान कर सकता है, जहां यह पूरी जनसंख्या को मापना असंभव है। | [[सांख्यिकी]], गुणवत्ता आश्वासन, और सर्वेक्षण पद्धति में, नमूना एक [[सांख्यिकीय जनसंख्या]] के बीच में से व्यक्तियों के एक सबसेट (एक सांख्यिकीय नमूने) का चयन है, जो पूरी जनसंख्या की विशेषताओं का अनुमान लगाता है।सांख्यिकीविद् ऐसे नमूने एकत्र करने का प्रयास करते हैं,जो विचाराधीन जनसंख्या के प्रतिनिधि हैं।नमूनाकरण(सैंपलिंग) में पूरी जनसंख्या को मापने की तुलना में कम लागत और तेजी से डेटा संग्रह होता है,और उन मामलों में अंतर्दृष्टि प्रदान कर सकता है, जहां यह पूरी जनसंख्या को मापना असंभव है। | ||
प्रत्येक अवलोकन स्वतंत्र वस्तुओं या व्यक्तियों के एक या अधिक गुणों (जैसे वजन, स्थान, रंग) को मापता है।सर्वेक्षण के नमूने में,प्रतिदर्श अभिकल्प (नमूना डिजाइन)को समायोजित करने के लिए जानकारी(डेटा) तैयार करना है, विशेष रूप से स्तरीकृत नमूनाकरण में।<ref>{{Cite book|url=https://www.measureevaluation.org/resources/publications/ms-16-112|title=Sampling and Evaluation |author=Lance, P. |author2=Hattori, A.|publisher=MEASURE Evaluation|year=2016|location=Web|pages=6–8, 62–64}}</ref>संभावना सिद्धांत और सांख्यिकीय सिद्धांत से परिणाम अभ्यास को निर्देशित या मार्गदर्शन करने के लिए नियोजित हैं।व्यवसाय और चिकित्सा अनुसंधान में, जनसंख्या के बारे में जानकारी इकट्ठा करने के लिए नमूना व्यापक रूप से उपयोग किया जाता है।<ref>सालेंट, प्रिसिला, आई। डिलमैन, और ए। डॉन।अपना खुद का सर्वेक्षण कैसे करें।नंबर 300.723 S3।1994।</ref>स्वीकृति नमूनाकरण का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या सामग्री का उत्पादन शासित विनिर्देशों को पूरा करता है। | प्रत्येक अवलोकन स्वतंत्र वस्तुओं या व्यक्तियों के एक या अधिक गुणों (जैसे वजन, स्थान, रंग) को मापता है।सर्वेक्षण के नमूने में,प्रतिदर्श अभिकल्प (नमूना डिजाइन)को समायोजित करने के लिए जानकारी(डेटा) तैयार करना है, विशेष रूप से स्तरीकृत नमूनाकरण में।<ref>{{Cite book|url=https://www.measureevaluation.org/resources/publications/ms-16-112|title=Sampling and Evaluation |author=Lance, P. |author2=Hattori, A.|publisher=MEASURE Evaluation|year=2016|location=Web|pages=6–8, 62–64}}</ref>[[संभावना सिद्धांत]] और [[सांख्यिकीय सिद्धांत]] से परिणाम अभ्यास को निर्देशित या मार्गदर्शन करने के लिए नियोजित हैं।व्यवसाय और चिकित्सा अनुसंधान में, जनसंख्या के बारे में जानकारी इकट्ठा करने के लिए नमूना व्यापक रूप से उपयोग किया जाता है।<ref>सालेंट, प्रिसिला, आई। डिलमैन, और ए। डॉन।अपना खुद का सर्वेक्षण कैसे करें।नंबर 300.723 S3।1994।</ref>[[स्वीकृति नमूनाकरण]] का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या सामग्री का उत्पादन शासित विनिर्देशों को पूरा करता है। | ||
== जनसंख्या परिभाषा == | == जनसंख्या परिभाषा == | ||
| Line 12: | Line 12: | ||
यद्यपि जनसंख्या की रुचि में अक्सर भौतिक वस्तुएं होती हैं, कभी -कभी समय, स्थान, या इन आयामों के कुछ संयोजन के साथ नमूना लेना आवश्यक होता है। उदाहरण के लिए, सुपर बाजार(सुपरमार्केट)स्टाफिंग की एक जांच विभिन्न समय पर नियंत्रण पंक्ति (चेकआउट लाइन) की लंबाई की जांच कर सकती है, या लुप्तप्राय पेंगुइन पर एक अध्ययन का उद्देश्य समय के साथ विभिन्न शिकार के मैदानों के उनके उपयोग को समझना हो सकता है। लंबी अवधि के लिए,ध्यान संकेन्द्रण या महत्वपूर्ण अवसर पर हो सकता है। | यद्यपि जनसंख्या की रुचि में अक्सर भौतिक वस्तुएं होती हैं, कभी -कभी समय, स्थान, या इन आयामों के कुछ संयोजन के साथ नमूना लेना आवश्यक होता है। उदाहरण के लिए, सुपर बाजार(सुपरमार्केट)स्टाफिंग की एक जांच विभिन्न समय पर नियंत्रण पंक्ति (चेकआउट लाइन) की लंबाई की जांच कर सकती है, या लुप्तप्राय पेंगुइन पर एक अध्ययन का उद्देश्य समय के साथ विभिन्न शिकार के मैदानों के उनके उपयोग को समझना हो सकता है। लंबी अवधि के लिए,ध्यान संकेन्द्रण या महत्वपूर्ण अवसर पर हो सकता है। | ||
अन्य मामलों में, जांच की गई 'जनसंख्या' और भी कम मूर्त हो सकती है। उदाहरण के लिए, जोसेफ जैगर ने मोंटे कार्लो में एक कैसीनो में रूले पहियों के व्यवहार का अध्ययन किया, और एक पक्षपाती पहिया की पहचान करने के लिए इसका उपयोग किया। इस मामले में, 'जनसंख्या' जैगर जांच करना चाहता था (यानी असीम रूप से कई परीक्षणों पर इसके परिणामों की संभावना वितरण), जबकि उसका 'नमूना' उस पहिया से देखे गए परिणामों से बना था। जैसे कि तांबे की विद्युत चालकता कुछ भौतिक विशेषता के बार -बार माप लेते हैं,इसी तरह के विचार तब उत्पन्न होते हैं , | अन्य मामलों में, जांच की गई 'जनसंख्या' और भी कम मूर्त हो सकती है। उदाहरण के लिए, जोसेफ जैगर ने मोंटे कार्लो में एक कैसीनो में रूले पहियों के व्यवहार का अध्ययन किया, और एक पक्षपाती पहिया की पहचान करने के लिए इसका उपयोग किया। इस मामले में, 'जनसंख्या' जैगर जांच करना चाहता था (यानी असीम रूप से कई परीक्षणों पर इसके परिणामों की [https://en.wikipedia.org/wiki/Probability_distribution'''संभावना वितरण''']), जबकि उसका 'नमूना' उस पहिया से देखे गए परिणामों से बना था। जैसे कि तांबे की [https://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity'''विद्युत चालकता'''] कुछ भौतिक विशेषता के बार -बार माप लेते हैं,इसी तरह के विचार तब उत्पन्न होते हैं , | ||
यह स्थिति अक्सर उस कारण प्रणाली के बारे में ज्ञान की तलाश से उत्पन्न होती है, जिसका परिणाम जनसंख्या का अवलोकन है। ऐसे मामलों में,नमूना सिद्धांत प्रेक्षित जनसंख्या को एक बड़े अतिजनसंख्या ('सुपरपॉपुलेशन') से एक नमूने के रूप में मान सकता है। उदाहरण के लिए,एक शोधकर्ता 100 रोगियों के एक परीक्षण समूह पर एक नए 'धूम्रपान छोड़ो'( 'क्विट स्मोकिंग') की सफलता दर का अध्ययन कर सकता है, ताकि कार्यक्रम के प्रभावों की भविष्यवाणी को देशव्यापी उपलब्ध कराया जा सके। जिस यह उपचार देश की अतिजनसंख्या(सुपरपॉपुलेशन) तक पहुंच पाए- एक समूह जो अभी तक अस्तित्व में नहीं है, क्योंकि कार्यक्रम अभी तक सभी के लिए उपलब्ध नहीं है। | यह स्थिति अक्सर उस कारण प्रणाली के बारे में ज्ञान की तलाश से उत्पन्न होती है, जिसका परिणाम जनसंख्या का अवलोकन है। ऐसे मामलों में,नमूना सिद्धांत प्रेक्षित जनसंख्या को एक बड़े अतिजनसंख्या ('सुपरपॉपुलेशन') से एक नमूने के रूप में मान सकता है। उदाहरण के लिए,एक शोधकर्ता 100 रोगियों के एक परीक्षण समूह पर एक नए 'धूम्रपान छोड़ो'( 'क्विट स्मोकिंग') की सफलता दर का अध्ययन कर सकता है, ताकि कार्यक्रम के प्रभावों की भविष्यवाणी को देशव्यापी उपलब्ध कराया जा सके। जिस यह उपचार देश की अतिजनसंख्या(सुपरपॉपुलेशन) तक पहुंच पाए- एक समूह जो अभी तक अस्तित्व में नहीं है, क्योंकि कार्यक्रम अभी तक सभी के लिए उपलब्ध नहीं है। | ||
| Line 36: | Line 36: | ||
|title= Elementary survey sampling |year= 2006 |url= https://archive.org/details/elementarysurvey00sche_0 | |title= Elementary survey sampling |year= 2006 |url= https://archive.org/details/elementarysurvey00sche_0 | ||
|url-access= registration | |url-access= registration | ||
}}</ref>ढांचा(फ्रेम )का सबसे सीधा प्रकार उपयुक्त संपर्क जानकारी के साथ जनसंख्या के तत्वों (अधिमानतः पूरी आबादी) की एक सूची है। उदाहरण के लिए, एक जनमत सर्वेक्षण में, संभावित नमूने ढांचा(फ्रेम) में एक चुनावी रजिस्टर और एक टेलीफोन निर्देशिका शामिल हैं। | }}</ref>ढांचा(फ्रेम )का सबसे सीधा प्रकार उपयुक्त संपर्क जानकारी के साथ जनसंख्या के तत्वों (अधिमानतः पूरी आबादी) की एक सूची है। उदाहरण के लिए, एक जनमत सर्वेक्षण में, संभावित नमूने ढांचा(फ्रेम) में एक चुनावी रजिस्टर और एक [[:en:Telephone_directory|'''टेलीफोन निर्देशिका''']] शामिल हैं। | ||
एक संभावना नमूना वह नमूना है जिसमें आबादी में प्रत्येक इकाई के पास नमूने में चयनित होने का एक मौका (शून्य से अधिक) होता है, और यह संभावना सटीक रूप से निर्धारित की जा सकती है। इन लक्षणों का संयोजन चयन की संभावना के अनुसार नमूना इकाइयों को भारित करके, जनसंख्या योग के निष्पक्ष अनुमानों का उत्पादन करना संभव बनाता है। | एक संभावना नमूना वह नमूना है जिसमें आबादी में प्रत्येक इकाई के पास नमूने में चयनित होने का एक मौका (शून्य से अधिक) होता है, और यह संभावना सटीक रूप से निर्धारित की जा सकती है। इन लक्षणों का संयोजन चयन की संभावना के अनुसार नमूना इकाइयों को भारित करके, जनसंख्या योग के निष्पक्ष अनुमानों का उत्पादन करना संभव बनाता है। | ||
| Line 53: | Line 53: | ||
=== गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग) === | === गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग) === | ||
गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग)वह नमूनाकरण विधि है, जहां आबादी के कुछ तत्वों के पास चयन का ''कोई'' मौका नहीं होता है (इन्हें कभी -कभी "बीमाकृत राशि (कवरेज)से बाहर अनाच्छादित (अंडरकवर्ड)" 'के रूप में संदर्भित किया जाता है), या जहां चयन की संभावना सटीक रूप से निर्धारित नहीं हो सकती है । इसमें जनसंख्या के हित के बारे में मान्यताओं के आधार पर तत्वों का चयन शामिल है, जो चयन के लिए मानदंड बनाता है। इसलिए, क्योंकि तत्वों का चयन गैर-यादृच्छिक है, गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग )नमूने की त्रुटियों के अनुमान की अनुमति नहीं देता है। ये स्थितियां बहिष्करण पूर्वाग्रह को जन्म देती हैं, इस बात पर सीमाएँ लगाती हैं कि एक नमूना आबादी के बारे में कितनी जानकारी प्रदान कर सकता है। नमूना और जनसंख्या के बीच संबंध के बारे में जानकारी सीमित है, जिससे नमूना से आबादी में अनुमान(एक्सट्रपलेशन) करना मुश्किल हो जाता है। | |||
नॉनप्रोबैबिलिटी सैंपलिंग | |||
<blockquote> | <blockquote> | ||
| Line 60: | Line 59: | ||
</blockquote> | </blockquote> | ||
नॉनप्रोबैबिलिटी सैंपलिंग विधियों में सुविधा नमूनाकरण, कोटा नमूनाकरण और उद्देश्यपूर्ण नमूना शामिल हैं। इसके अलावा, गैर - | गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग) विधियों में सुविधा नमूनाकरण, कोटा नमूनाकरण और उद्देश्यपूर्ण नमूना शामिल हैं। इसके अलावा, गैर - गैर-प्रतिक्रिया प्रभाव किसी भी ''संभाव्यता अभिकल्पना (डिजाइन) को एक गैर -लाभकारी अभिकल्पना(डिजाइन) में बदल सकते हैं, यदि गैर -जिम्मेदारियों की विशेषताओं को अच्छी तरह से समझा नहीं जाता है, क्योंकि गैर -जिम्मेदारियों को प्रभावी ढंग से प्रत्येक तत्व की संभावना को नमूना होने की संभावना को संशोधित किया जाता है।'' | ||
== नमूनाकरण विधियाँ == | == नमूनाकरण विधियाँ == | ||
ऊपर पहचाने गए किसी भी प्रकार के फ्रेम के भीतर, विभिन्न प्रकार के नमूने विधियों को व्यक्तिगत रूप से या संयोजन में नियोजित किया जा सकता है।आमतौर पर इन डिजाइनों के बीच विकल्प को प्रभावित करने वाले कारकों में शामिल हैं: | ऊपर पहचाने गए किसी भी प्रकार के ढांचे (फ्रेम) के भीतर, विभिन्न प्रकार के नमूने विधियों को व्यक्तिगत रूप से या संयोजन में नियोजित किया जा सकता है।आमतौर पर इन ''अभिकल्पना (''डिजाइनों) के बीच विकल्प को प्रभावित करने वाले कारकों में शामिल हैं: | ||
* फ्रेम की प्रकृति और गुणवत्ता | * ढांचे(फ्रेम) की प्रकृति और गुणवत्ता | ||
* फ्रेम पर इकाइयों के बारे में सहायक जानकारी की उपलब्धता | * ढांचे(फ्रेम) पर इकाइयों के बारे में सहायक जानकारी की उपलब्धता | ||
* सटीकता की आवश्यकताएं, और सटीकता को मापने की आवश्यकता | * सटीकता की आवश्यकताएं, और सटीकता को मापने की आवश्यकता | ||
* क्या नमूने का विस्तृत विश्लेषण अपेक्षित है | * क्या नमूने का विस्तृत विश्लेषण अपेक्षित है | ||
* लागत/परिचालन चिंताएं | * लागत/परिचालन चिंताएं | ||
=== | === सामान्य उद्देश्यरहित नमूना === | ||
[[File:Simple random sampling.PNG|thumb|300px|एक साधारण यादृच्छिक नमूने का चयन करने का एक दृश्य प्रतिनिधित्व]] | [[File:Simple random sampling.PNG|thumb|300px|एक साधारण यादृच्छिक नमूने का चयन करने का एक दृश्य प्रतिनिधित्व]] | ||
किसी दिए गए आकार के एक साधारण यादृच्छिक नमूने (SRS) में, एक नमूना फ्रेम के सभी सबसेट में चयनित होने की समान संभावना है। इस प्रकार फ्रेम के प्रत्येक तत्व में चयन की समान संभावना होती है: फ्रेम को विभाजित या विभाजन नहीं किया जाता है। इसके अलावा, किसी भी दिए गए तत्वों के पास किसी भी अन्य जोड़ी | किसी दिए गए आकार के एक साधारण यादृच्छिक नमूने सॉफ्टवेयर रिक्वायरमेंट स्पेसिफिकेशन (SRS) में, एक नमूना ढांचे ( फ्रेम) के सभी प्रतिनिधि नमूना (सबसेट) में चयनित होने की समान संभावना है। इस प्रकार ढांचे(फ्रेम) के प्रत्येक तत्व में चयन की समान संभावना होती है: ढांचे (फ्रेम को विभाजित या विभाजन नहीं किया जाता है। इसके अलावा, किसी भी दिए गए तत्वों के जोड़ी के पास किसी भी अन्य जोड़ी(और इसी तरह ट्रिपल के लिए, और इसी तरह) के रूप में चयन का एक ही मौका है। यह पूर्वाग्रह को कम करता है और परिणामों के विश्लेषण को सरल बनाता है। विशेष रूप से, नमूने के अंदर व्यक्तिगत परिणामों के बीच फेरबदल का सूचक समग्र आबादी में फेरबदल का एक अच्छा संकेतक है, जो परिणामों की सटीकता का अनुमान लगाना अपेक्षाकृत आसान हो जाता है। | ||
सरल यादृच्छिक नमूनाकरण नमूने की त्रुटि के लिए | सरल यादृच्छिक नमूनाकरण नमूने की त्रुटि के लिए आलोचनीय हो सकता है क्योंकि चयन की यादृच्छिकता के परिणामस्वरूप एक नमूना हो सकता है जो आबादी को पूरा करना (मेकअप) प्रतिबिंबित नहीं करता है। उदाहरण के लिए, किसी दिए गए देश के दस लोगों का एक साधारण यादृच्छिक नमूना औसतन पांच पुरुषों और पांच महिलाओं की रचना करेगा, लेकिन किसी भी परीक्षण में एक लिंग(सेक्स) का प्रतिनिधित्व करने और दूसरे को कम करने की संभावना है। व्यवस्थित और स्तरीकृत तकनीक एक अधिक प्रतिनिधि नमूने चुनने के लिए आबादी के बारे में जानकारी का उपयोग करके इस समस्या को दूर करने का प्रयास करती है। | ||
इसके अलावा, एक बड़ी | इसके अलावा, एक बड़ी लक्षित आबादी से सरल यादृच्छिक नमूना लेना बोझिल और थकाऊ हो सकता है। कुछ मामलों में, जांचकर्ता आबादी के उपसमूहों के लिए विशिष्ट शोध प्रश्नों में रुचि रखते हैं। उदाहरण के लिए, शोधकर्ताओं को यह जांचने में रुचि हो सकती है कि क्या नौकरी के प्रदर्शन के भविष्यवक्ता के रूप में संज्ञानात्मक क्षमता नस्लीय समूहों में समान रूप से लागू होती है। सरल यादृच्छिक नमूना इस स्थिति में शोधकर्ताओं की जरूरतों को समायोजित नहीं कर सकता है, क्योंकि यह आबादी के उप -समूह प्रदान नहीं करता है, और अन्य नमूनाकरण रणनीतियों, जैसे कि स्तरीकृत नमूनाकरण, इसके बजाय उपयोग किया जा सकता है। | ||
=== व्यवस्थित नमूनाकरण === | === व्यवस्थित नमूनाकरण === | ||
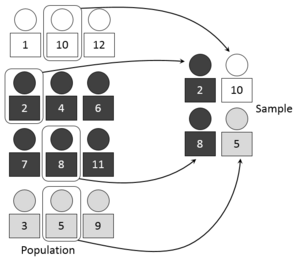
[[File:Systematic sampling.PNG|thumb|350px|व्यवस्थित नमूनाकरण तकनीक का उपयोग करके एक यादृच्छिक नमूने का चयन करने का एक दृश्य प्रतिनिधित्व]] | [[File:Systematic sampling.PNG|thumb|350px|व्यवस्थित नमूनाकरण तकनीक का उपयोग करके एक यादृच्छिक नमूने का चयन करने का एक दृश्य प्रतिनिधित्व]] | ||
व्यवस्थित नमूनाकरण (जिसे अंतराल नमूनाकरण के रूप में भी जाना जाता है) कुछ | व्यवस्थित नमूनाकरण (जिसे अंतराल नमूनाकरण के रूप में भी जाना जाता है) कुछ क्रम योजना के अनुसार आबादी की व्यवस्था के अध्ययन पर निर्भर करता है, और फिर उस आदेशित सूची के माध्यम से नियमित अंतराल पर तत्वों का चयन करता है। व्यवस्थित नमूने में एक यादृच्छिक शुरुआत शामिल होती है और फिर तब से प्रत्येक केटीएच ( kth)तत्व के चयन के साथ आगे बढ़ती है। इस मामले में, k = (जनसंख्या आकार/नमूना आकार)। यह महत्वपूर्ण है कि प्रारंभिक बिंदु स्वचालित रूप से सूची में पहला नहीं है,बल्कि सूची में पहले से केटीएच ( kth) तत्व तक यादृच्छिक रूप से चुना गया है। एक सरल उदाहरण टेलीफोन निर्देशिका से प्रत्येक 10 वें नाम का चयन करना होगा (एक 'प्रत्येक 10 वां' नमूना, जिसे '10 के छूट( स्किप) के साथ नमूनाकरण' के रूप में भी जाना जाता है)। | ||
जब | जब प्रारंभिक बिंदु यादृच्छिक होता है, तब तक व्यवस्थित नमूनाकरण एक प्रकार संभावना का नमूना है। इसे लागू करना आसान है और प्रेरित स्तरीकरण इसे कुशल बना सकता है, यदि परिवर्तनीय सूची द्वारा का आदेश दिया जाता है, वह परिवर्तनीय ब्याज के साथ सहसंबद्ध है। आंकड़ाकोष(डेटाबेस) से कुशल नमूनाकरण के लिए 'हर 10 वीं' नमूनाकरण8 विशेष रूप से उपयोगी है। | ||
उदाहरण के लिए, मान लीजिए कि हम एक लंबी सड़क के लोगों का नमूना लेना चाहते हैं जो एक गरीब क्षेत्र ( | उदाहरण के लिए, मान लीजिए कि हम एक लंबी सड़क के लोगों का नमूना लेना चाहते हैं जो एक गरीब क्षेत्र (घर संख्या- 1) में शुरू होता है और एक महंगे जिले के (घर संख्या- 1000) में समाप्त होता है। इस गली के पतों का एक सरल यादृच्छिक चयन उच्च अंत से बहुत अधिक और निम्न अंत से बहुत कम के साथ समाप्त होता है।जिससे एक गैर-प्रतिनिधि नमूना होता है। सड़क के साथ प्रत्येक 10 वीं स्ट्रीट नंबर का चयन करना (जैसे) यह सुनिश्चित करता है कि इन सभी जिलों का प्रतिनिधित्व करते हुए, नमूना सड़क की लंबाई के साथ समान रूप से फैला हुआ है। (ध्यान दें कि यदि हम हमेशा #1 पर शुरू करते हैं और #991 पर समाप्त होते हैं, तो नमूना कम अंत की ओर थोड़ा पक्षपाती है; #1 और #10 के बीच की शुरुआत को यादृच्छिक रूप से चुनकर, यह पूर्वाग्रह समाप्त हो जाता है।) | ||
हालांकि, व्यवस्थित नमूना विशेष रूप से सूची में आवधिकता के लिए कमजोर है। यदि आवधिकता मौजूद है और अवधि का उपयोग किए गए अंतराल का एक बहु या कारक है, तो नमूना विशेष रूप से समग्र आबादी के लिए अप्रभावी होने की संभावना है, जिससे योजना सरल यादृच्छिक नमूने की तुलना में कम सटीक हो जाती है। | हालांकि, व्यवस्थित नमूना विशेष रूप से सूची में आवधिकता के लिए कमजोर है। यदि आवधिकता मौजूद है और अवधि का उपयोग किए गए अंतराल का एक बहु या कारक है, तो नमूना विशेष रूप से समग्र आबादी के लिए अप्रभावी होने की संभावना है, जिससे योजना सरल यादृच्छिक नमूने की तुलना में कम सटीक हो जाती है। | ||
उदाहरण के लिए, एक ऐसी सड़क पर विचार करें जहां विषम संख्या वाले घर | उदाहरण के लिए, एक ऐसी सड़क पर विचार करें जहां उत्तर की ओर सड़क के विषम संख्या वाले घर (महंगे) हैं, और दक्षिण तरफ सम-संख्या वाले सभी घर (सस्ते) हैं। ऊपर दी गई नमूना योजना के तहत, एक प्रतिनिधि नमूना प्राप्त करना असंभव है;विषम संख्या वाले सभी घरों में किए गए नमूना (सैंपल) या तो महंगे पक्ष से होंगे, या वे सभी समान-संख्या वाले सस्ते पक्ष से होंगे, जब तक कि शोधकर्ता को इस पूर्वाग्रह का पूर्व ज्ञान नहीं है और एक छूट(स्किप) का उपयोग करके इसे बचता है जो दोनों पक्षों (किसी भी विषम संख्या वाले स्किप) के बीच छूटना सुनिश्चित करता है । | ||
व्यवस्थित नमूने का एक और दोष यह है कि परिदृश्यों में भी जहां यह एसआरएस की तुलना में अधिक सटीक है, इसके सैद्धांतिक गुणों को उस सटीकता को निर्धारित करना मुश्किल | व्यवस्थित नमूने का एक और दोष यह है कि परिदृश्यों में भी जहां यह एसआरएस की तुलना में अधिक सटीक है, इसके सैद्धांतिक गुणों को उस सटीकता को निर्धारित करना मुश्किल बनाते है। (ऊपर दिए गए व्यवस्थित नमूने के दो उदाहरणों में, संभावित नमूनाकरण त्रुटि का अधिकांश हिस्सा पड़ोसी घरों के बीच भिन्नता के कारण है - लेकिन क्योंकि यह विधि कभी भी दो पड़ोसी घरों का चयन नहीं करती है, नमूना हमें उस भिन्नता के बारे में कोई जानकारी नहीं देगा।) | ||
जैसा कि ऊपर वर्णित है, व्यवस्थित नमूनाकरण एक ईपीएस विधि है, क्योंकि सभी तत्वों में चयन की समान | जैसा कि ऊपर वर्णित है, व्यवस्थित नमूनाकरण एक ईपीएस विधि है, क्योंकि सभी तत्वों में चयन की संभावना समान है (दिए गए उदाहरण में दस में से एक)। यह 'सरल यादृच्छिक नमूना' नहीं है क्योंकि एक ही आकार के अलग -अलग प्रतिनिधि नमूना (सबसेट) में अलग -अलग चयन संभावनाएं हैं - उदा। सेट {4,14,24, ..., 994} में चयन की एक-दस संभावना है, लेकिन सेट {4,13,24,34, ...} में चयन की शून्य संभावना है। | ||
व्यवस्थित नमूने को गैर-ईपीएस दृष्टिकोण के लिए भी अनुकूलित किया जा सकता है; एक उदाहरण के लिए, नीचे पीपीएस नमूनों की चर्चा देखें। | व्यवस्थित नमूने को गैर-ईपीएस दृष्टिकोण के लिए भी अनुकूलित किया जा सकता है; एक उदाहरण के लिए, नीचे पीपीएस नमूनों की चर्चा देखें। | ||
=== स्तरीकृत नमूनाकरण === | === स्तरीकृत नमूनाकरण === | ||
[[File:Stratified sampling.PNG|thumb|300px|स्तरीकृत नमूनाकरण तकनीक का उपयोग करके एक यादृच्छिक नमूने का चयन करने का एक दृश्य प्रतिनिधित्व]] | [[File:Stratified sampling.PNG|thumb|300px|स्तरीकृत नमूनाकरण तकनीक का उपयोग करके एक यादृच्छिक नमूने का चयन करने का एक दृश्य प्रतिनिधित्व]] | ||
जब आबादी | जब आबादी अलग -अलग श्रेणियों को अपनाती है, तो इन श्रेणियों द्वारा ढांचे( फ्रेम) को अलग -अलग स्तरों में व्यवस्थित किया जा सकता है।प्रत्येक स्तरों (स्ट्रैटम) को एक स्वतंत्र उप-जनसंख्या के रूप में नमूना लिया जाता है, जिसमें से व्यक्तिगत तत्वों को यादृच्छिक रूप से चुना जा सकता है।<ref name="Robert M. Groves, et al"/>जनसंख्या के आकार के लिए इस यादृच्छिक चयन (या नमूने) का आकार जनसंख्या के अनुपात को एक नमूना अंश कहा जाता है।<ref name=sampling-minimax/> स्तरीकृत नमूने के लिए कई संभावित लाभ हैं।<ref name=sampling-minimax/> | ||
सबसे पहले, आबादी को अलग -अलग, स्वतंत्र स्तर में विभाजित करने से शोधकर्ताओं को विशिष्ट उपसमूहों के बारे में निष्कर्ष निकालने में सक्षम हो सकता है जो अधिक सामान्यीकृत यादृच्छिक नमूने में खो सकते हैं। | सबसे पहले, आबादी को अलग -अलग, स्वतंत्र स्तर में विभाजित करने से शोधकर्ताओं को विशिष्ट उपसमूहों के बारे में निष्कर्ष निकालने में सक्षम हो सकता है जो अधिक सामान्यीकृत यादृच्छिक नमूने में खो सकते हैं। | ||
दूसरा, एक स्तरीकृत नमूनाकरण विधि का उपयोग करने से अधिक कुशल सांख्यिकीय अनुमान हो सकते हैं (बशर्ते कि स्ट्रेटा को नमूने की उपलब्धता के बजाय प्रश्न में मानदंड के लिए प्रासंगिकता के आधार पर चुना जाता है)। यहां तक कि अगर एक स्तरीकृत नमूनाकरण दृष्टिकोण सांख्यिकीय दक्षता में वृद्धि नहीं करता है, तो इस तरह की रणनीति के परिणामस्वरूप | दूसरा, एक स्तरीकृत नमूनाकरण विधि का उपयोग करने से अधिक कुशल सांख्यिकीय अनुमान हो सकते हैं (बशर्ते कि स्तर( स्ट्रेटा) को नमूने की उपलब्धता के बजाय प्रश्न में मानदंड के लिए प्रासंगिकता के आधार पर चुना जाता है)। यहां तक कि अगर एक स्तरीकृत नमूनाकरण दृष्टिकोण सांख्यिकीय दक्षता में वृद्धि नहीं करता है, तो इस तरह की रणनीति के परिणामस्वरूप साधारण यादृच्छिक नमूने की तुलना में कम दक्षता नहीं होगी, बशर्ते कि प्रत्येक स्तर(स्ट्रैटम)आबादी में समूह के आकार के लिए आनुपातिक हो। | ||
तीसरा, | तीसरा, कभी-कभी ऐसा होता है कि समग्र आबादी की तुलना में आबादी के भीतर व्यक्तिगत, पूर्व-मौजूदा स्तर(स्ट्रैट) के लिए जानकारी (डेटा)अधिक आसानी से उपलब्ध होता है; ऐसे मामलों में, एक स्तरीकृत नमूनाकरण दृष्टिकोण का उपयोग करना समूहों में जानकारी (डेटा) एकत्र करने की तुलना में अधिक सुविधाजनक हो सकता है (हालांकि यह संभावित रूप से मानदंड-प्रासंगिक स्तर( स्ट्रैट) का उपयोग करने के पहले से नोट किए गए महत्व के साथ बाधाओं पर हो सकता है)। | ||
अंत में, चूंकि प्रत्येक स्ट्रैटम को एक स्वतंत्र आबादी के रूप में माना जाता है, इसलिए अलग-अलग | अंत में, चूंकि प्रत्येक स्तर(स्ट्रैटम) को एक स्वतंत्र आबादी के रूप में माना जाता है, इसलिए अलग-अलग स्तर(स्ट्रैट)के नमूनाकरण को अलग-अलग दृष्टिकोण लागू किए जा सकता है, संभावित रूप से शोधकर्ताओं को जनसंख्या के अंदर प्रत्येक पहचाने गए उपसमूह के लिए सर्वोत्तम अनुकूल (या सबसे अधिक लागत प्रभावी) का उपयोग करने के लिए सक्षम किया जाता है। | ||
हालांकि, स्तरीकृत नमूने का उपयोग करने के लिए कुछ संभावित कमियां हैं। सबसे पहले, स्ट्रेटा की पहचान करना और इस तरह के दृष्टिकोण को लागू करना नमूना चयन की लागत और जटिलता को बढ़ा सकता है, साथ ही जनसंख्या अनुमानों की बढ़ती जटिलता के लिए अग्रणी हो सकता है। दूसरा, कई मानदंडों की जांच करते समय, स्तरीकरण चर | हालांकि, स्तरीकृत नमूने का उपयोग करने के लिए कुछ संभावित कमियां हैं। सबसे पहले,स्तर( स्ट्रेटा) की पहचान करना और इस तरह के दृष्टिकोण को लागू करना नमूना चयन की लागत और जटिलता को बढ़ा सकता है, साथ ही जनसंख्या अनुमानों की बढ़ती जटिलता के लिए अग्रणी हो सकता है। दूसरा, कई मानदंडों की जांच करते समय, स्तरीकरण कुछ परिवर्तनशील (चर)से संबंधित हो सकते हैं, लेकिन दूसरों के लिए नहीं, आगे अभिकल्प(डिजाइन) को जटिल कर सकते हैं, और संभावित रूप से स्तर(स्ट्रैटा) की उपयोगिता को कम कर सकते हैं। अंत में, कुछ मामलों में (जैसे कि बड़ी संख्या में स्तर( स्ट्रैटा)के साथअभिकल्प(डिजाइन, या प्रति समूह एक निर्दिष्ट न्यूनतम नमूना आकार के साथ), स्तरीकृत नमूने को संभावित रूप से अन्य तरीकों की तुलना में एक बड़े नमूने की आवश्यकता हो सकती है (हालांकि ज्यादातर मामलों में, आवश्यक नमूना आकार सरल यादृच्छिक नमूने के लिए आवश्यक से बड़ा नहीं होगा)। | ||
; एक स्तरीकृत नमूनाकरण दृष्टिकोण सबसे प्रभावी है जब तीन स्थितियों को पूरा किया जाता है: | ; एक स्तरीकृत नमूनाकरण दृष्टिकोण सबसे प्रभावी है जब तीन स्थितियों को पूरा किया जाता है: | ||
# स्ट्रेटा के भीतर परिवर्तनशीलता कम से कम है | # स्तर(स्ट्रेटा)के भीतर परिवर्तनशीलता कम से कम है | ||
# स्ट्रैट के बीच परिवर्तनशीलता अधिकतम होती है | # स्तर(स्ट्रैट) के बीच परिवर्तनशीलता अधिकतम होती है | ||
# जिन चर पर आबादी को स्तरीकृत किया जाता है, वे वांछित आश्रित चर के साथ दृढ़ता से सहसंबद्ध हैं। | # जिन चर पर आबादी को स्तरीकृत किया जाता है, वे वांछित आश्रित परिवर्तनशील (चर)के साथ दृढ़ता से सहसंबद्ध हैं। | ||
; अन्य नमूने विधियों पर लाभ | ; अन्य नमूने विधियों पर लाभ | ||
| Line 122: | Line 118: | ||
# विभिन्न उप -योगों के लिए विभिन्न नमूनाकरण तकनीकों का उपयोग करने की अनुमति देता है। | # विभिन्न उप -योगों के लिए विभिन्न नमूनाकरण तकनीकों का उपयोग करने की अनुमति देता है। | ||
# अनुमान की सटीकता/दक्षता में सुधार करता है। | # अनुमान की सटीकता/दक्षता में सुधार करता है। | ||
# आकार में व्यापक रूप से भिन्न होने वाले स्ट्रैट से समान संख्याओं का नमूना करके स्ट्रैट के बीच अंतर के परीक्षणों की सांख्यिकीय शक्ति के अधिक संतुलन की अनुमति देता है। | # आकार में व्यापक रूप से भिन्न होने वाले स्तर(स्ट्रैट) से समान संख्याओं का नमूना करके स्तर (स्ट्रैट)के बीच अंतर के परीक्षणों की सांख्यिकीय शक्ति के अधिक संतुलन की अनुमति देता है। | ||
; नुकसान | ; नुकसान | ||
# प्रासंगिक स्तरीकरण चर के चयन की आवश्यकता है जो मुश्किल हो सकता है। | # प्रासंगिक स्तरीकरण परिवर्तनशील(चर)के चयन की आवश्यकता है जो मुश्किल हो सकता है। | ||
# तब उपयोगी नहीं है जब कोई सजातीय उपसमूह नहीं हैं। | # तब उपयोगी नहीं है जब कोई सजातीय उपसमूह नहीं हैं। | ||
# लागू करने के लिए महंगा हो सकता है। | # लागू करने के लिए महंगा हो सकता है। | ||
; पोस्टस्ट्रैटिफिकेशन | ; पश्च स्तरीकरण( पोस्टस्ट्रैटिफिकेशन) | ||
स्तरीकरण को कभी -कभी पोस्टस्ट्रैटिफिकेशन नामक एक प्रक्रिया में नमूनाकरण चरण के बाद पेश किया जाता है।<ref name="Robert M. Groves, et al"/>यह दृष्टिकोण आम तौर पर एक उपयुक्त स्तरीकरण | स्तरीकरण को कभी -कभी पश्च स्तरीकरण(पोस्टस्ट्रैटिफिकेशन) नामक एक प्रक्रिया में नमूनाकरण चरण के बाद पेश किया जाता है।<ref name="Robert M. Groves, et al"/>यह दृष्टिकोण आम तौर पर एक उपयुक्त स्तरीकरण परिवर्तनशीलता( चर0 के पूर्व ज्ञान की कमी के कारण लागू किया जाता है या जब प्रयोगकर्ता के पास नमूनाकरण चरण के दौरान एक परिवर्तनशील स्तरीकरण बनाने के लिए आवश्यक जानकारी का अभाव होता है।यद्यपि यह विधि पूर्व (पोस्ट)हॉक दृष्टिकोणों के नुकसान के लिए अतिसंवेदनशील है, यह सही स्थिति में कई लाभ प्रदान कर सकता है।कार्यान्वयन आमतौर पर एक साधारण यादृच्छिक नमूने का अनुसरण करता है।एक सहायक परिवर्तनशील (चर) स्तरीकरण के लिए अनुमति देने के अलावा,पश्च स्तरीकरण( पोस्टस्ट्रैटिफिकेशन) का उपयोग भारोत्तोलन(वेटिंग) को लागू करने के लिए किया जा सकता है, जो एक नमूने के अनुमानों की सटीकता में सुधार कर सकता है।<ref name="Robert M. Groves, et al"/> | ||
; | ;अधिप्रतिचयन( ओवरसाम्पलिंग ) | ||
चॉइस-आधारित सैंपलिंग स्तरीकृत नमूनाकरण रणनीतियों में से एक है।पसंद-आधारित नमूने में,<ref>{{cite journal|last1=Scott|first1=A.J.|last2=Wild|first2=C.J.|year=1986|title=Fitting logistic models under case-control or choice-based sampling|journal=[[Journal of the Royal Statistical Society, Series B]]|volume=48|issue=2|pages=170–182|jstor=2345712}}</ref>डेटा को लक्ष्य पर स्तरीकृत किया जाता है और प्रत्येक स्ट्रैटम से एक नमूना लिया जाता है ताकि नमूने में दुर्लभ लक्ष्य वर्ग का अधिक प्रतिनिधित्व किया | चयन(चॉइस)-आधारित नमूनाकरण (सैंपलिंग)स्तरीकृत नमूनाकरण रणनीतियों में से एक है।पसंद-आधारित नमूने में,<ref>{{cite journal|last1=Scott|first1=A.J.|last2=Wild|first2=C.J.|year=1986|title=Fitting logistic models under case-control or choice-based sampling|journal=[[Journal of the Royal Statistical Society, Series B]]|volume=48|issue=2|pages=170–182|jstor=2345712}}</ref> जानकारी (डेटा) को लक्ष्य पर स्तरीकृत किया जाता है और प्रत्येक स्तर(स्ट्रैटम) से एक नमूना लिया जाता है ताकि नमूने में दुर्लभ लक्ष्य वर्ग का अधिक प्रतिनिधित्व किया जाए।प्रतिरूप(मॉडल) इस पक्षपाती नमूने पर बनाया गया है।लक्ष्य पर निविष्ट परिवर्तनशील (इनपुट चर) प्रभावों को अक्सर पसंद-आधारित नमूने के साथ अधिक सटीकता के साथ अनुमानित किया जाता है, तब भी जब एक यादृच्छिक नमूने की तुलना में एक छोटा समग्र नमूना आकार लिया जाता है।परिणामों को आमतौर पर अधिप्रतिचयन(ओवरसाम्पलिंग) को लिए सही करने के लिए समायोजित किया जाना चाहिए। | ||
=== संभाव्यता- | === संभाव्यता-आनुपातिक-से-आकार नमूनाकरण ('पीपीएस') === | ||
कुछ मामलों में नमूना डिजाइनर के पास एक सहायक परिवर्तनशील(चर) या"आकार माप" के उपाय तक पहुंच होती है, जिसे आबादी में प्रत्येक तत्व के हित के लिए परिवर्तनशीलता( चर) से संबंधित माना जाता है। इन आंकड़ों का उपयोग नमूना अभिकल्प( डिजाइन) सटीकता में सुधार करने के लिए किया जा सकता है। जैसा कि ऊपर चर्चा की गई है, एक विकल्प स्तरीकरण के आधार के रूप में सहायक परिवर्तनशीलता(चर) का उपयोग करना है। | |||
एक अन्य विकल्प आकार ('पीपीएस') नमूने के लिए संभाव्यता आनुपातिक है, अधिकतम 1. तक,जिसमें प्रत्येक तत्व के चयन के लिए संभावना इसके आकार के उपाय के लिए आनुपातिक है, । एक साधारण संभाव्यता-आनुपातिक-से-आकार नमूनाकरण (पीपीएस डिजाइन)में ये चयन संभावनाएं तब कर सकती हैं जब पॉइसन नमूनाकरण(सैंपलिंग) को आधार के रूप में उपयोग किया जाए। हालांकि, इसमें परिवर्तनशील(चर) नमूना आकार की खामी है, और जनसंख्या के विभिन्न हिस्से अभी भी चयन में मौका भिन्नता के कारण खत्म हो सकते हैं या कम प्रतिनिधित्व कर सकते हैं। | |||
व्यवस्थित नमूनाकरण सिद्धांत का उपयोग आकार के नमूने के लिए एक संभावना आनुपातिक बनाने के लिए किया जा सकता है। यह एक एकल नमूना इकाई के रूप में आकार परिवर्तनशीलता(चर) के भीतर प्रत्येक गणना का इलाज करके किया जाता है। नमूनों को तब परिवर्तनशील आकार के भीतर इन गणनाओं के बीच भी अंतराल का चयन करके पहचाना जाता है। इस विधि को कभी-कभी अंकेक्षण(ऑडिट) या फोरेंसिक नमूनाकरण (सैंपलिंग) के मामले इस पद्धति को कभी-कभी पीपीएस-अनुक्रमिक या मौद्रिक इकाई के नमूने कहा जाता है। | |||
व्यवस्थित नमूनाकरण सिद्धांत का उपयोग आकार के नमूने के लिए एक संभावना आनुपातिक बनाने के लिए किया जा सकता है। यह एक एकल नमूना इकाई के रूप में आकार चर के भीतर प्रत्येक गणना का इलाज करके किया जाता है। नमूनों को तब आकार | |||
<blockquote> | <blockquote> | ||
उदाहरण: मान लीजिए कि हमारे पास 150, 180, 200, 220, 220, 260, और | उदाहरण: मान लीजिए कि हमारे पास 150, 180, 200, 220, 220, 260, और क्रमशः 490 छात्रों (कुल 1500 छात्रों) की आबादी वाले छह स्कूल हैं, और हम छात्र की आबादी को आकार तीन के पीपीएस नमूने के आधार के रूप में उपयोग करना चाहते हैं। ऐसा करने के लिए, हम पहले स्कूल नंबरों को 1 to 150, दूसरा स्कूल 151 से 330 ( 150+180) आवंटित कर सकते हैं (1011 से 1500)। हम तब 1 और 500 (1500/3 के बराबर) के बीच एक यादृच्छिक शुरुआत उत्पन्न करते हैं और 500 के गुणकों द्वारा स्कूल की आबादी के माध्यम से गिनती करते हैं। यदि हमारी यादृच्छिक शुरुआत 137 थी, तो हम उन स्कूलों का चयन करेंगे जिन्हें 137, 637 की संख्या आवंटित की गई है, 637, 637, 637, 637, 637, 637 और 1137, यानी पहला, चौथा और छठा स्कूल। | ||
</blockquote> | </blockquote> | ||
पीपीएस दृष्टिकोण बड़े तत्वों पर नमूना केंद्रित करके किसी दिए गए नमूने के आकार | पीपीएस दृष्टिकोण बड़े तत्वों पर नमूना केंद्रित करके किसी दिए गए नमूने के आकार की सटीकता में सुधार कर सकता है जो जनसंख्या के अनुमानों पर सबसे अधिक प्रभाव डालता है। पीपीएस नमूनाकरण(सैंपलिंग) का उपयोग आमतौर पर व्यवसायों के सर्वेक्षणों के लिए किया जाता है, जहां तत्व का आकार बहुत भिन्न होता है और सहायक जानकारी अक्सर उपलब्ध होती है उदाहरण के लिए, होटलों में खर्च किए गए अतिथि-रातों की संख्या को मापने का प्रयास करने वाला एक सर्वेक्षण प्रत्येक होटल के कमरों की संख्या का उपयोग सहायक के रूप में कर सकता है। कुछ मामलों में, अधिक वर्तमान अनुमानों का उत्पादन करने का प्रयास करते समय हित की परिवर्तनशीलता के एक पुराने माप को सहायक परिवर्तनशीलता (चर) के रूप में उपयोग किया जा सकता है।<ref name="MySwedeLohr">* {{cite book|author=Lohr, Sharon L.|title=Sampling: Design and Analysis}} | ||
* {{cite book|author=Särndal, Carl-Erik |author2=Swensson, Bengt |author3=Wretman, Jan|title=Model Assisted Survey Sampling}}</ref> | * {{cite book|author=Särndal, Carl-Erik |author2=Swensson, Bengt |author3=Wretman, Jan|title=Model Assisted Survey Sampling}}</ref> | ||
=== क्लस्टर नमूनाकरण === | === गुच्छ प्रतिचयन(क्लस्टर) नमूनाकरण === | ||
[[File:Cluster sampling.PNG|thumb|300px|क्लस्टर सैंपलिंग तकनीक का उपयोग करके एक यादृच्छिक नमूने का चयन करने का एक दृश्य प्रतिनिधित्व]] | [[File:Cluster sampling.PNG|thumb|300px|क्लस्टर सैंपलिंग तकनीक का उपयोग करके एक यादृच्छिक नमूने का चयन करने का एक दृश्य प्रतिनिधित्व]] | ||
कभी-कभी समूहों ('क्लस्टर') में उत्तरदाताओं का चयन करना अधिक प्रभावी होता है।नमूनाकरण अक्सर भूगोल, या समय अवधिके अनुसार समूहित किया जाता है।(लगभग सभी नमूने समय में कुछ अर्थों में गुच्छ प्रतिचयन ('क्लस्टर') होते हैं - हालांकि यह शायद ही कभी इसे विश्लेषण में ध्यान में रखा जाता है।) उदाहरण के लिए, यदि किसी शहर के भीतर घरों का सर्वेक्षण करते हैं,तो हम 100 शहर चयनित ब्लॉकों का चयन करना चुन सकते हैं और फिर प्रत्येक परिवार का साक्षात्कार कर सकते हैं। | |||
कभी-कभी समूहों ('क्लस्टर') में उत्तरदाताओं का चयन करना अधिक | |||
क्लस्टरिंग यात्रा और प्रशासनिक लागतों को कम कर सकती है। ऊपर दिए गए उदाहरण में, एक साक्षात्कारकर्ता प्रत्येक घर के लिए एक अलग ब्लॉक में ड्राइव करने के बजाय एक ब्लॉक में कई घरों में जाने के लिए एक एकल यात्रा कर सकता है। | गुच्छ प्रतिचयन(क्लस्टरिंग) यात्रा और प्रशासनिक लागतों को कम कर सकती है। ऊपर दिए गए उदाहरण में, एक साक्षात्कारकर्ता प्रत्येक घर के लिए एक अलग ब्लॉक में अभियान (ड्राइव) करने के बजाय एक ब्लॉक में कई घरों में जाने के लिए एक एकल यात्रा कर सकता है। | ||
इसका | इसका अर्थ यह भी है कि किसी को लक्षित जनसंख्या में सभी तत्वों को सूचीबद्ध करने के लिए एक नमूना ढांचे (फ्रेम) की आवश्यकता नहीं है। इसके बजाय,गुच्छ प्रतिचयन( क्लस्टर) को गुच्छ प्रतिचयन-स्तरीय ढांचे (फ्रेम) से चुना जा सकता है, जिसमें केवल चयनित गुच्छ प्रतिचयन (क्लस्टर) के लिए बनाया गया तत्व-स्तरीय ढांचे( फ्रेम) होता है। ऊपर दिए गए उदाहरण में, नमूने को केवल प्रारंभिक चयन के लिए एक ब्लॉक-स्तरीय शहर के नक्शे की आवश्यकता होती है, और फिर पूरे शहर के घरेलू स्तर के नक्शे के बजाय 100 चयनित ब्लॉकों के एक घरेलू स्तरीय मानचित्र की आवश्यकता होती है। | ||
गुच्छ प्रतिचयन नमूनाकरण(जिसे क्लस्टर सैंपलिंग के रूप में भी जाना जाता है) आम तौर पर सरल यादृच्छिक नमूने के ऊपर नमूनाकरण अनुमानों की परिवर्तनशीलता को बढ़ाता है, यह इस बात पर निर्भर करता है कि गुच्छ प्रतिचयन(क्लस्टर) के भीतर गुच्छ प्रतिचयन (क्लस्टर) भिन्नता की तुलना में एक दूसरे के बीच कैसे भिन्न होते हैं। इस कारण से,गुच्छ प्रतिचयन नमूनाकरण( क्लस्टर सैंपलिंग) को सटीकता के समान स्तर को प्राप्त करने के लिए एसआरएस की तुलना में एक बड़े नमूने की आवश्यकता होती है - लेकिन गुच्छ प्रतिचयन (क्लस्टरिंग) से लागत बचत अभी भी इसे एक सस्ता विकल्प बना सकती है। | |||
क्लस्टर सैंपलिंग को आमतौर पर मल्टीस्टेज सैंपलिंग के रूप में लागू किया जाता है। यह क्लस्टर सैंपलिंग का एक जटिल रूप है जिसमें दो या दो से अधिक स्तरों की इकाइयाँ | गुच्छ प्रतिचयन नमूनाकरण(क्लस्टर सैंपलिंग) को आमतौर पर बहुचरणी नमूनाकरण (मल्टीस्टेज सैंपलिंग)के रूप में लागू किया जाता है। यह गुच्छ प्रतिचयन नमूनाकरण (क्लस्टर सैंपलिंग) का एक जटिल रूप है जिसमें दो या दो से अधिक स्तरों की इकाइयाँ को एक में अंतर्निहित (एम्बेडेड) करती हैं। पहले चरण में उन समूहों का निर्माण होता है जिनका उपयोग नमूना लेने के लिए किया जाएगा। दूसरे चरण में, प्रत्येक क्लस्टर से प्राथमिक इकाइयों का नमूना यादृच्छिक रूप से चुना जाता है। (बजाय सभी चयनित समूहों में निहित सभी इकाइयों का उपयोग करने के) । निम्नलिखित चरणों में, उन चयनित समूहों में से प्रत्येक में, इकाइयों के अतिरिक्त नमूने चुने जाते हैं, और इसी तरह इस प्रक्रिया के अंतिम चरण में चयनित सभी अंतिम इकाइयों (उदाहरण के लिए व्यक्ति ) का सर्वेक्षण किया जाता है। इस प्रकार, यह तकनीक,अनिवार्य रूप से पूर्ववर्ती यादृच्छिक नमूनों के यादृच्छिक उपसमूह लेने की प्रक्रिया है। | ||
मल्टीस्टेज सैंपलिंग नमूने की लागत को काफी हद तक कम कर सकती है, जहां पूर्ण जनसंख्या सूची का निर्माण करने की आवश्यकता होगी (इससे पहले कि अन्य नमूनाकरण विधियों को लागू किया जा सके)। चयनित नहीं होने वाले समूहों का वर्णन करने में शामिल काम को समाप्त करके, मल्टीस्टेज नमूनाकरण पारंपरिक क्लस्टर नमूने से जुड़ी बड़ी लागतों को कम कर सकता है।<ref name="MySwedeLohr"/>हालांकि, प्रत्येक नमूना पूरी आबादी का पूर्ण प्रतिनिधि नहीं हो सकता है। | बहुचरणी नमूनाकरण (मल्टीस्टेज सैंपलिंग) नमूने की लागत को काफी हद तक कम कर सकती है, जहां पूर्ण जनसंख्या सूची का निर्माण करने की आवश्यकता होगी (इससे पहले कि अन्य नमूनाकरण विधियों को लागू किया जा सके)। चयनित नहीं होने वाले समूहों का वर्णन करने में शामिल काम को समाप्त करके,बहुचरणी नमूनाकरण( मल्टीस्टेज नमूनाकरण) पारंपरिक गुच्छ प्रतिचयन (क्लस्टर) नमूने से जुड़ी बड़ी लागतों को कम कर सकता है।<ref name="MySwedeLohr"/>हालांकि, प्रत्येक नमूना पूरी आबादी का पूर्ण प्रतिनिधि नहीं हो सकता है। | ||
=== कोटा नमूना === | === कोटा नमूना === | ||
कोटा नमूनाकरण में, जनसंख्या को पहले पारस्परिक रूप से अनन्य उप-समूहों में विभाजित किया जाता है, जैसे कि स्तरीकृत नमूनाकरण में।तब निर्णय का उपयोग एक निर्दिष्ट अनुपात के आधार पर प्रत्येक खंड से विषयों या इकाइयों का चयन करने के लिए किया जाता है।उदाहरण के लिए, एक साक्षात्कारकर्ता को 45 से 60 वर्ष की आयु के बीच 200 महिलाओं और 300 पुरुषों का नमूना लेने के लिए कहा जा सकता है। | |||
कोटा | |||
यह यह दूसरा कदम है जो तकनीक को गैर-प्रतिकृति नमूने में से एक बनाता है।कोटा नमूने | यह यह दूसरा कदम है जो तकनीक को गैर-प्रतिकृति नमूने में से एक बनाता है।कोटा नमूनाकरण में नमूने का चयन गैर-यादृच्छिक है।उदाहरण के लिए, साक्षात्कारकर्ताओं को उन लोगों का साक्षात्कार करने के लिए लुभाया जा सकता है जो सबसे अधिक सहायक दिखते हैं।समस्या यह है कि ये नमूने पक्षपाती हो सकते हैं क्योंकि सभी को चयन का मौका नहीं मिलता है।यह यादृच्छिक तत्व इसकी सबसे बड़ी कमजोरी है और कोटा बनाम संभावना कई वर्षों से विवाद का विषय रहा है। | ||
=== मिनिमैक्स सैंपलिंग === | === अल्पमहिष्ठ नमूनाकरण (मिनिमैक्स सैंपलिंग) === | ||
असंतुलित डेटासेट में, जहां नमूना अनुपात | असंतुलित डेटासेट में, जहां जनसंख्या नमूना अनुपात के आंकड़ों का पालन नहीं करता है, कोई भी डेटासेट को एक रूढ़िवादी तरीके से मिनीमैक्स सैंपलिंग नामक कर सकता है।मिनिमैक्स सैंपलिंग का मूल एंडरसन मिनिमैक्स अनुपात में है जिसका मूल्य 0.5 साबित होता है: एक बाइनरी वर्गीकरण में, वर्ग-नमूना आकारों को समान रूप से चुना जाना चाहिए।यह अनुपात केवल गौसियन वितरण के साथ एलडीए क्लासिफायरर की धारणा के तहत मिनिमैक्स अनुपात साबित किया जा सकता है।मिनिमैक्स सैंपलिंग की धारणा हाल ही में वर्गीकरण नियमों के एक सामान्य वर्ग के लिए विकसित की गई है, जिसे क्लास-वार स्मार्ट क्लासिफायर कहा जाता है।इस मामले में, कक्षाओं के नमूने अनुपात का चयन किया जाता है ताकि वर्ग पूर्व संभावनाओं के लिए सभी संभावित जनसंख्या आँकड़ों पर सबसे खराब केस क्लासिफायर त्रुटि, सबसे अच्छा होगा।<ref name=sampling-minimax/> | ||
=== आकस्मिक नमूना === | === आकस्मिक नमूना === | ||
| Line 204: | Line 196: | ||
=== सैद्धांतिक नमूना === | === सैद्धांतिक नमूना === | ||
सैद्धांतिक नमूनाकरण<ref name=": 0>{{Cite web|url = http://www.fao.org/ag/humannutrition/32428-0613f516cb07eade922c8c19b4d0452c0.pdf|title = Examples of sampling methods}}</ref>तब होता है जब नमूनों को क्षेत्र की गहरी समझ विकसित करने या सिद्धांतों को विकसित करने के लक्ष्य के साथ अब तक एकत्र किए गए डेटा के परिणामों के आधार पर चुना जाता है।चरम या बहुत विशिष्ट मामलों का चयन किया जा सकता है ताकि संभावना को अधिकतम किया जा सके कि एक घटना वास्तव में अवलोकन योग्य होगी। | सैद्धांतिक नमूनाकरण<ref name=": 0>{{Cite web|url = http://www.fao.org/ag/humannutrition/32428-0613f516cb07eade922c8c19b4d0452c0.pdf|title = Examples of sampling methods}}</ref>तब होता है जब नमूनों को क्षेत्र की गहरी समझ विकसित करने या सिद्धांतों को विकसित करने के लक्ष्य के साथ अब तक एकत्र किए गए डेटा के परिणामों के आधार पर चुना जाता है।चरम या बहुत विशिष्ट मामलों का चयन किया जा सकता है ताकि संभावना को अधिकतम किया जा सके कि एक घटना वास्तव में अवलोकन योग्य होगी। | ||
== चयनित इकाइयों का प्रतिस्थापन == | == चयनित इकाइयों का प्रतिस्थापन == | ||
नमूनाकरण योजनाएं प्रतिस्थापन के बिना हो सकती हैं ('वॉर' | नमूनाकरण योजनाएं प्रतिस्थापन के बिना हो सकती हैं ('वॉर' - किसी भी तत्व को एक ही नमूने में एक से अधिक बार नहीं चुना जा सकता है) या प्रतिस्थापन के साथ ('wr' एक तत्व एक नमूने में कई बार दिखाई दे सकता है)।उदाहरण के लिए, यदि हम मछली पकड़ते हैं, उन्हें मापते हैं, और नमूने के साथ जारी रखने से पहले तुरंत उन्हें पानी में वापस कर देते हैं, तो यह एक डब्ल्यूआर डिजाइन है, क्योंकि हम एक ही मछली को एक से अधिक बार पकड़ने और मापने को समाप्त कर सकते हैं।हालांकि, अगर हम मछली को पानी या टैग पर नहीं लौटाते हैं और इसे पकड़ने के बाद प्रत्येक मछली को छोड़ते हैं, तो यह एक खराब डिजाइन बन जाता है। | ||
== नमूना आकार निर्धारण == | == नमूना आकार निर्धारण == | ||
| Line 216: | Line 207: | ||
=== नमूना आकार तालिकाओं का उपयोग करने के लिए चरण === | === नमूना आकार तालिकाओं का उपयोग करने के लिए चरण === | ||
# ब्याज के प्रभाव आकार, α, और β को पोस्ट करें। | # ब्याज के प्रभाव आकार, α, और β को पोस्ट करें। | ||
# नमूना आकार तालिका की जाँच करें<ref>कोहेन, 1988</ref> | # नमूना आकार तालिका की जाँच करें<ref>कोहेन, 1988</ref> चयनित α के अनुरूप तालिका का चयन करें | ||
## वांछित शक्ति के अनुरूप पंक्ति का पता लगाएं | ## वांछित शक्ति के अनुरूप पंक्ति का पता लगाएं | ||
## अनुमानित प्रभाव आकार के अनुरूप कॉलम का पता लगाएं। | ## अनुमानित प्रभाव आकार के अनुरूप कॉलम का पता लगाएं। | ||
| Line 277: | Line 268: | ||
== सर्वेक्षण वजन == | == सर्वेक्षण वजन == | ||
कई स्थितियों में | नमूना अंश कई स्थितियों में स्तर( स्ट्रैटम) द्वारा भिन्न हो सकता है और जनसंख्या का सही प्रतिनिधित्व करने के लिए आधार-सामग्री (डेटा) का वर्णन करना होगा। इस प्रकार उदाहरण के लिए, यूनाइटेड किंगडम में व्यक्तियों का एक साधारण यादृच्छिक नमूने में कुछ दूरस्थ स्कॉटिश द्वीपों में शामिल नहीं हो सकते है जो नमूने के लिए महंगे होंगे। एक सस्ती विधि शहरी और ग्रामीण स्तर के साथ एक स्तरीकृत नमूने का उपयोग करने के लिए होगी। ग्रामीण नमूने को नमूने में कम प्रतिनिधित्व दिया जा सकता है, लेकिन क्षतिपूर्ति विश्लेषण के लिए में उचित रूप से भारित किया जा सकता है। | ||
अधिक आम तौर पर, डेटा को आमतौर पर भारित किया जाना चाहिए यदि नमूना डिजाइन प्रत्येक व्यक्ति को चयनित होने का एक समान मौका नहीं देता है। उदाहरण के लिए, जब परिवारों के पास समान चयन संभावनाएं होती हैं, लेकिन एक व्यक्ति को प्रत्येक घर के भीतर से साक्षात्कार दिया जाता है, तो यह बड़े घरों के लोगों को साक्षात्कार के लिए एक छोटा मौका देता है। यह सर्वेक्षण भार का उपयोग करने के लिए जिम्मेदार हो सकता है। इसी तरह, एक से अधिक टेलीफोन लाइन वाले घरों में एक यादृच्छिक अंकों डायलिंग नमूने में चुने जाने की अधिक संभावना है, और वेट इसके लिए समायोजित कर सकते हैं। | अधिक आम तौर पर, डेटा को आमतौर पर भारित किया जाना चाहिए यदि नमूना डिजाइन प्रत्येक व्यक्ति को चयनित होने का एक समान मौका नहीं देता है। उदाहरण के लिए, जब परिवारों के पास समान चयन संभावनाएं होती हैं, लेकिन एक व्यक्ति को प्रत्येक घर के भीतर से साक्षात्कार दिया जाता है, तो यह बड़े घरों के लोगों को साक्षात्कार के लिए एक छोटा मौका देता है। यह सर्वेक्षण भार का उपयोग करने के लिए जिम्मेदार हो सकता है। इसी तरह, एक से अधिक टेलीफोन लाइन वाले घरों में एक यादृच्छिक अंकों डायलिंग नमूने में चुने जाने की अधिक संभावना है, और वेट इसके लिए समायोजित कर सकते हैं। | ||
| Line 289: | Line 280: | ||
== इतिहास == | == इतिहास == | ||
बहुत सारे का उपयोग | यादृच्छिक नमूना बहुत सारे पुराना विचार का एक उपयोग है, जिसका उल्लेख बाइबिल में कई बार किया गया है।1786 में पियरे साइमन लाप्लास ने अनुपात अनुमानक के साथ नमूने का उपयोग करके फ्रांस की आबादी का अनुमान लगाया।उन्होंने त्रुटि के संभाव्य अनुमानों की भी गणना की।इन्हें आधुनिक आत्मविश्वास अंतराल के रूप में नहीं बल्कि नमूना आकार के रूप में व्यक्त किया गया था ,जो कि संभावना 1000/1001 के साथ नमूना त्रुटि पर एक विशेष ऊपरी सीमा को प्राप्त करने के लिए आवश्यक होगा।उनके अनुमानों ने बेयस के प्रमेय को एक समान पूर्व संभावना के साथ इस्तेमाल किया और यह माना कि उनका नमूना यादृच्छिक था।अलेक्जेंडर इवानोविच चुप्रोव ने 1870 के दशक में शाही(इंपीरियल) रूस का नमूना सर्वेक्षण की शुरुआत की।अमेरिकी 1936 के राष्ट्रपति चुनाव में रिपब्लिकन जीत की लिटरेरी डाइजेस्ट की भविष्यवाणी गंभीर पूर्वाग्रह के कारण बुरी तरह से गड़बड़ा गई थी '''[https://www.wsj.com/articles/SB1159743222279370]'''।मैगज़ीन सदस्यता सूचियों (सब्सक्रिप्शन लिस्ट) और टेलीफोन निर्देशिकाओं के माध्यम से प्राप्त उनके नामों के साथ दो मिलियन से अधिक लोगों ने अध्ययन का जवाब दिया।यह सराहना नहीं की गई थी कि ये सूचियाँ रिपब्लिकन के प्रति भारी पक्षपाती थीं और परिणामी नमूना, यद्यपि बहुत बड़ा था, गहराई से त्रुटिपूर्ण था।<ref>डेविड एस। मूर और जॉर्ज पी। मैककेबे।सांख्यिकी के अभ्यास का परिचय।</ref><ref>{{Cite book |last1 = Freedman |first1=David |author-link1=David Freedman (statistician)| last2 = Pisani | first2 = Robert | last3 = Purves | first3 = Roger |title=Statistics | url=http://www.wwnorton.com/college/titles/math/stat4/comment.htm%7C <!-- place = [[New York City|New York]] |publisher = [[W. W. Norton & Company|Norton]] | year = 2007 | edition = 4th | isbn = 0-393-92972-8 -->}}</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 469: | Line 459: | ||
{{Authority control}} | {{Authority control}} | ||
{{DEFAULTSORT:Sampling (Statistics)}}[[Category: | {{DEFAULTSORT:Sampling (Statistics)}} | ||
[[Category: | [[Category:Machine Translated Page]] | ||
[[Category: | |||
[[Category: | [[Category:AC with 0 elements|Sampling (Statistics)]] | ||
[[Category: | [[Category:All articles lacking reliable references|Sampling (Statistics)]] | ||
[[Category:All articles with unsourced statements|Sampling (Statistics)]] | |||
[[Category:Articles lacking reliable references from December 2018|Sampling (Statistics)]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page|Sampling (Statistics)]] | |||
[[Category:Articles with invalid date parameter in template|Sampling (Statistics)]] | |||
[[Category:Articles with short description|Sampling (Statistics)]] | |||
[[Category:Articles with specifically marked weasel-worded phrases from July 2019|Sampling (Statistics)]] | |||
[[Category:Articles with unsourced statements from January 2017|Sampling (Statistics)]] | |||
[[Category:CS1|Sampling (Statistics)]] | |||
[[Category:CS1 maint|Sampling (Statistics)]] | |||
[[Category:Commons category link is locally defined|Sampling (Statistics)]] | |||
[[Category:Commons category link is the pagename|Sampling (Statistics)]] | |||
[[Category:Exclude in print|Sampling (Statistics)]] | |||
[[Category:Interwiki category linking templates|Sampling (Statistics)]] | |||
[[Category:Interwiki link templates|Sampling (Statistics)]] | |||
[[Category:Pages with empty portal template|Sampling (Statistics)]] | |||
[[Category:Pages with missing ISBNs|Sampling (Statistics)]] | |||
[[Category:Pages with script errors|Sampling (Statistics)]] | |||
[[Category:Portal-inline template with redlinked portals|Sampling (Statistics)]] | |||
[[Category:Portal templates with redlinked portals|Sampling (Statistics)]] | |||
[[Category:Short description with empty Wikidata description|Sampling (Statistics)]] | |||
[[Category:Templates that add a tracking category|Sampling (Statistics)]] | |||
[[Category:Templates using TemplateData|Sampling (Statistics)]] | |||
[[Category:Wikimedia Commons templates|Sampling (Statistics)]] | |||
[[Category:Wikipedia articles needing factual verification from July 2019|Sampling (Statistics)]] | |||
Latest revision as of 17:17, 30 August 2023
सांख्यिकी, गुणवत्ता आश्वासन, और सर्वेक्षण पद्धति में, नमूना एक सांख्यिकीय जनसंख्या के बीच में से व्यक्तियों के एक सबसेट (एक सांख्यिकीय नमूने) का चयन है, जो पूरी जनसंख्या की विशेषताओं का अनुमान लगाता है।सांख्यिकीविद् ऐसे नमूने एकत्र करने का प्रयास करते हैं,जो विचाराधीन जनसंख्या के प्रतिनिधि हैं।नमूनाकरण(सैंपलिंग) में पूरी जनसंख्या को मापने की तुलना में कम लागत और तेजी से डेटा संग्रह होता है,और उन मामलों में अंतर्दृष्टि प्रदान कर सकता है, जहां यह पूरी जनसंख्या को मापना असंभव है।
प्रत्येक अवलोकन स्वतंत्र वस्तुओं या व्यक्तियों के एक या अधिक गुणों (जैसे वजन, स्थान, रंग) को मापता है।सर्वेक्षण के नमूने में,प्रतिदर्श अभिकल्प (नमूना डिजाइन)को समायोजित करने के लिए जानकारी(डेटा) तैयार करना है, विशेष रूप से स्तरीकृत नमूनाकरण में।[1]संभावना सिद्धांत और सांख्यिकीय सिद्धांत से परिणाम अभ्यास को निर्देशित या मार्गदर्शन करने के लिए नियोजित हैं।व्यवसाय और चिकित्सा अनुसंधान में, जनसंख्या के बारे में जानकारी इकट्ठा करने के लिए नमूना व्यापक रूप से उपयोग किया जाता है।[2]स्वीकृति नमूनाकरण का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या सामग्री का उत्पादन शासित विनिर्देशों को पूरा करता है।
जनसंख्या परिभाषा
सफल सांख्यिकीय अभ्यास केंद्रित समस्या की परिभाषा पर आधारित है। नमूने में, उस जनसंख्या को परिभाषित करना शामिल है जिसमें से हमारा नमूना खींचा गया है। जनसंख्या में सभी लोगों या वस्तुओं को शामिल करने के रूप में परिभाषित किया जा सकता है, जो समझने की इच्छा रखते हैं। क्योंकि सभी से जानकारी इकट्ठा करने के लिए बहुत कम ही समय और पैसा होता है,और उसका लक्ष्य उस जनसंख्या का एक प्रतिनिधि नमूना (या सबसेट) खोजना हो जाता है।
कभी -कभी जो जनसंख्या को परिभाषित करता है वह स्पष्ट है। उदाहरण के लिए, एक निर्माता को यह तय करने की आवश्यकता होती है कि उत्पादन से सामग्री का एक बैच ग्राहक को जारी करने के लिए उच्च गुणवत्ता का है, या खराब गुणवत्ता के कारण रद्दी माल( स्क्रैप) या फिर से काम( रीवर्क) के लिए सजा सुनाई जानी चाहिए। इस मामले में बैच जनसंख्या है।
यद्यपि जनसंख्या की रुचि में अक्सर भौतिक वस्तुएं होती हैं, कभी -कभी समय, स्थान, या इन आयामों के कुछ संयोजन के साथ नमूना लेना आवश्यक होता है। उदाहरण के लिए, सुपर बाजार(सुपरमार्केट)स्टाफिंग की एक जांच विभिन्न समय पर नियंत्रण पंक्ति (चेकआउट लाइन) की लंबाई की जांच कर सकती है, या लुप्तप्राय पेंगुइन पर एक अध्ययन का उद्देश्य समय के साथ विभिन्न शिकार के मैदानों के उनके उपयोग को समझना हो सकता है। लंबी अवधि के लिए,ध्यान संकेन्द्रण या महत्वपूर्ण अवसर पर हो सकता है।
अन्य मामलों में, जांच की गई 'जनसंख्या' और भी कम मूर्त हो सकती है। उदाहरण के लिए, जोसेफ जैगर ने मोंटे कार्लो में एक कैसीनो में रूले पहियों के व्यवहार का अध्ययन किया, और एक पक्षपाती पहिया की पहचान करने के लिए इसका उपयोग किया। इस मामले में, 'जनसंख्या' जैगर जांच करना चाहता था (यानी असीम रूप से कई परीक्षणों पर इसके परिणामों की संभावना वितरण), जबकि उसका 'नमूना' उस पहिया से देखे गए परिणामों से बना था। जैसे कि तांबे की विद्युत चालकता कुछ भौतिक विशेषता के बार -बार माप लेते हैं,इसी तरह के विचार तब उत्पन्न होते हैं ,
यह स्थिति अक्सर उस कारण प्रणाली के बारे में ज्ञान की तलाश से उत्पन्न होती है, जिसका परिणाम जनसंख्या का अवलोकन है। ऐसे मामलों में,नमूना सिद्धांत प्रेक्षित जनसंख्या को एक बड़े अतिजनसंख्या ('सुपरपॉपुलेशन') से एक नमूने के रूप में मान सकता है। उदाहरण के लिए,एक शोधकर्ता 100 रोगियों के एक परीक्षण समूह पर एक नए 'धूम्रपान छोड़ो'( 'क्विट स्मोकिंग') की सफलता दर का अध्ययन कर सकता है, ताकि कार्यक्रम के प्रभावों की भविष्यवाणी को देशव्यापी उपलब्ध कराया जा सके। जिस यह उपचार देश की अतिजनसंख्या(सुपरपॉपुलेशन) तक पहुंच पाए- एक समूह जो अभी तक अस्तित्व में नहीं है, क्योंकि कार्यक्रम अभी तक सभी के लिए उपलब्ध नहीं है।
जिस जनसंख्या से नमूना लिया जाता है, वह उस जनसंख्या के समान नहीं हो सकती है, जिसके बारे में जानकारी वांछित है। अक्सर विचाराधीन मुद्दों के कारण इन दो समूहों के बीच बड़ा लेकिन पूरा अतिव्यापन(ओवरलैप) नहीं होता है। कभी -कभी वे पूरी तरह से अलग हो सकते हैं - उदाहरण के लिए, कोई व्यक्ति मानव स्वास्थ्य की बेहतर समझ प्राप्त करने के लिए चूहों का अध्ययन कर सकता है,या कोई 2008 में पैदा हुए लोगों से अभिलेख(रिकॉर्ड)का अध्ययन कर सकता है ताकि 2009 में पैदा हुए लोगों के बारे में भविष्यवाणियां की जा सकें।
सटीक जनसंख्या और जनसंख्या के प्रयोजन को सटीक बनाने में बिताया गया समय अक्सर अच्छी तरह से खर्च किया जाता है, क्योंकि यह कई अस्पष्टताओं के मुद्दों के प्रति प्रश्नों को उठाता है जो अन्यथा इस स्तर पर अनदेखी की जाती हैं।
नमूना फ्रेम
सबसे सरल मामले में, जैसे कि उत्पादन से सामग्री के एक बैच का नमूना (बहुत से स्वीकृति नमूनाकरण), जनसंख्या में हर एक वस्तु को पहचानने और मापने और उनमें से किसी एक को हमारे नमूने में शामिल करने के लिए सबसे अधिक वांछनीय होगा। सामान्यतय, अधिक सामान्य मामले में यह आमतौर पर संभव या व्यावहारिक नहीं है। चूहों के झुंड में सभी चूहों की पहचान करने का कोई तरीका नहीं है।जहां मतदान अनिवार्य नहीं है, वहां यह पहचानने का कोई तरीका नहीं है कि कौन से लोग आगामी चुनाव में (चुनाव से पहले) में वोट देंगे।ये अनिश्चित जनसंख्या से नीचे दिए गए किसी भी तरीके से नमूने के लिए उत्तरदायी नहीं हैं और जिस पर हम सांख्यिकीय सिद्धांत को लागू कर सकते हैं।
एक उपाय के रूप में, हम एक नमूना ढांचा(फ्रेम) की तलाश करते हैं जिसमें यह गुण हो कि हम हर एक तत्व की पहचान कर सकते हैं और हमारे नमूने में किसी भी शामिल हैं।[3][4][5][6]ढांचा(फ्रेम )का सबसे सीधा प्रकार उपयुक्त संपर्क जानकारी के साथ जनसंख्या के तत्वों (अधिमानतः पूरी आबादी) की एक सूची है। उदाहरण के लिए, एक जनमत सर्वेक्षण में, संभावित नमूने ढांचा(फ्रेम) में एक चुनावी रजिस्टर और एक टेलीफोन निर्देशिका शामिल हैं।
एक संभावना नमूना वह नमूना है जिसमें आबादी में प्रत्येक इकाई के पास नमूने में चयनित होने का एक मौका (शून्य से अधिक) होता है, और यह संभावना सटीक रूप से निर्धारित की जा सकती है। इन लक्षणों का संयोजन चयन की संभावना के अनुसार नमूना इकाइयों को भारित करके, जनसंख्या योग के निष्पक्ष अनुमानों का उत्पादन करना संभव बनाता है।
उदाहरण: हम किसी दिए गए गली में रहने वाले वयस्कों की कुल आय का अनुमान लगाना चाहते हैं। हम उस सड़क के प्रत्येक घर का दौरा करते हैं, वहां रहने वाले सभी वयस्कों की पहचान करते हैं, और प्रत्येक घर से एक वयस्क का बेतरतीब ढंग से चयन करते हैं। (उदाहरण के लिए, हम प्रत्येक व्यक्ति को एक यादृच्छिक संख्या आवंटित कर सकते हैं, जो 0 और 1 के बीच एक समान वितरण से उत्पन्न होता है, और प्रत्येक घर में उच्चतम संख्या वाले व्यक्ति का चयन कर सकता है)। हम तब चयनित व्यक्ति का साक्षात्कार करते हैं और उनकी आय पाते हैं।
अपने दम पर रहने वाले लोगों को चुना जाना निश्चित है, इसलिए हम बस अपनी आय को कुल के अपने अनुमान में जोड़ते हैं। लेकिन दो वयस्कों के घर में रहने वाले व्यक्ति के पास चयन का केवल एक-दो मौका है। इसे प्रतिबिंबित करने के लिए, जब हम इस तरह के घर में आते हैं, तो हम चयनित व्यक्ति की आय को दो बार कुल की ओर गिनेंगे। (जिस व्यक्ति को 'उस घर से चुना गया है, को शिथिल रूप से देखा जा सकता है, साथ ही उस व्यक्ति का प्रतिनिधित्व किया जा सकता है, जो' 'चयनित नहीं है।)'
उपरोक्त उदाहरण में, हर किसी के पास चयन की समान संभावना नहीं है;तो क्या तथ्य इसे एक संभावना नमूना बनाता है जबकि प्रत्येक व्यक्ति की संभावना ज्ञात है। जब जनसंख्या में प्रत्येक तत्व के चयन की समान संभावना होती है, इसेचयन की समान संभावना '(ईपीएस) प्रारूप(डिजाइन) के रूप में जाना जाता है। इस तरह केप्रारूप(डिजाइनों) को 'सेल्फ-वेटिंग' भी कहा जाता है क्योंकि सभी नमूना इकाइयाँ(सैंपल यूनिट्स) को एक ही वजन दिया जाता है।
संभाव्यता नमूनाकरण में शामिल हैं: सरल यादृच्छिक नमूनाकरण, व्यवस्थित नमूनाकरण, स्तरीकृत नमूनाकरण, आकार के नमूने के लिए संभावना आनुपातिक, और क्लस्टर या मल्टीस्टेज नमूनाकरण। संभावना नमूने के इन विभिन्न तरीकों में दो चीजें समान हैं:
- प्रत्येक तत्व में एक ज्ञात गैर-शून्य(नॉनजेरो) संभावना है।
- कुछ बिंदु पर यादृच्छिक चयन शामिल है।
गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग)
गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग)वह नमूनाकरण विधि है, जहां आबादी के कुछ तत्वों के पास चयन का कोई मौका नहीं होता है (इन्हें कभी -कभी "बीमाकृत राशि (कवरेज)से बाहर अनाच्छादित (अंडरकवर्ड)" 'के रूप में संदर्भित किया जाता है), या जहां चयन की संभावना सटीक रूप से निर्धारित नहीं हो सकती है । इसमें जनसंख्या के हित के बारे में मान्यताओं के आधार पर तत्वों का चयन शामिल है, जो चयन के लिए मानदंड बनाता है। इसलिए, क्योंकि तत्वों का चयन गैर-यादृच्छिक है, गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग )नमूने की त्रुटियों के अनुमान की अनुमति नहीं देता है। ये स्थितियां बहिष्करण पूर्वाग्रह को जन्म देती हैं, इस बात पर सीमाएँ लगाती हैं कि एक नमूना आबादी के बारे में कितनी जानकारी प्रदान कर सकता है। नमूना और जनसंख्या के बीच संबंध के बारे में जानकारी सीमित है, जिससे नमूना से आबादी में अनुमान(एक्सट्रपलेशन) करना मुश्किल हो जाता है।
उदाहरण: हम किसी दिए गए गली में हर घर का दौरा करते हैं, और दरवाजे का जवाब देने के लिए पहले व्यक्ति का साक्षात्कार करते हैं। एक से अधिक रहने वाले के साथ किसी भी घर में, यह एक गैर -लाभकारी नमूना है, क्योंकि कुछ लोगों को दरवाजे का जवाब देने की अधिक संभावना है (जैसे कि एक बेरोजगार व्यक्ति जो घर पर अपना अधिकांश समय बिताता है, एक नियोजित गृहिणी की तुलना में जवाब देने की अधिक संभावना है जो हो सकता है काम पर जब साक्षात्कारकर्ता कॉल करता है) और इन संभावनाओं की गणना करना व्यावहारिक नहीं है।
गैर संभावित नमूनाकरण (नॉनप्रोबैबिलिटी सैंपलिंग) विधियों में सुविधा नमूनाकरण, कोटा नमूनाकरण और उद्देश्यपूर्ण नमूना शामिल हैं। इसके अलावा, गैर - गैर-प्रतिक्रिया प्रभाव किसी भी संभाव्यता अभिकल्पना (डिजाइन) को एक गैर -लाभकारी अभिकल्पना(डिजाइन) में बदल सकते हैं, यदि गैर -जिम्मेदारियों की विशेषताओं को अच्छी तरह से समझा नहीं जाता है, क्योंकि गैर -जिम्मेदारियों को प्रभावी ढंग से प्रत्येक तत्व की संभावना को नमूना होने की संभावना को संशोधित किया जाता है।
नमूनाकरण विधियाँ
ऊपर पहचाने गए किसी भी प्रकार के ढांचे (फ्रेम) के भीतर, विभिन्न प्रकार के नमूने विधियों को व्यक्तिगत रूप से या संयोजन में नियोजित किया जा सकता है।आमतौर पर इन अभिकल्पना (डिजाइनों) के बीच विकल्प को प्रभावित करने वाले कारकों में शामिल हैं:
- ढांचे(फ्रेम) की प्रकृति और गुणवत्ता
- ढांचे(फ्रेम) पर इकाइयों के बारे में सहायक जानकारी की उपलब्धता
- सटीकता की आवश्यकताएं, और सटीकता को मापने की आवश्यकता
- क्या नमूने का विस्तृत विश्लेषण अपेक्षित है
- लागत/परिचालन चिंताएं
सामान्य उद्देश्यरहित नमूना
किसी दिए गए आकार के एक साधारण यादृच्छिक नमूने सॉफ्टवेयर रिक्वायरमेंट स्पेसिफिकेशन (SRS) में, एक नमूना ढांचे ( फ्रेम) के सभी प्रतिनिधि नमूना (सबसेट) में चयनित होने की समान संभावना है। इस प्रकार ढांचे(फ्रेम) के प्रत्येक तत्व में चयन की समान संभावना होती है: ढांचे (फ्रेम को विभाजित या विभाजन नहीं किया जाता है। इसके अलावा, किसी भी दिए गए तत्वों के जोड़ी के पास किसी भी अन्य जोड़ी(और इसी तरह ट्रिपल के लिए, और इसी तरह) के रूप में चयन का एक ही मौका है। यह पूर्वाग्रह को कम करता है और परिणामों के विश्लेषण को सरल बनाता है। विशेष रूप से, नमूने के अंदर व्यक्तिगत परिणामों के बीच फेरबदल का सूचक समग्र आबादी में फेरबदल का एक अच्छा संकेतक है, जो परिणामों की सटीकता का अनुमान लगाना अपेक्षाकृत आसान हो जाता है।
सरल यादृच्छिक नमूनाकरण नमूने की त्रुटि के लिए आलोचनीय हो सकता है क्योंकि चयन की यादृच्छिकता के परिणामस्वरूप एक नमूना हो सकता है जो आबादी को पूरा करना (मेकअप) प्रतिबिंबित नहीं करता है। उदाहरण के लिए, किसी दिए गए देश के दस लोगों का एक साधारण यादृच्छिक नमूना औसतन पांच पुरुषों और पांच महिलाओं की रचना करेगा, लेकिन किसी भी परीक्षण में एक लिंग(सेक्स) का प्रतिनिधित्व करने और दूसरे को कम करने की संभावना है। व्यवस्थित और स्तरीकृत तकनीक एक अधिक प्रतिनिधि नमूने चुनने के लिए आबादी के बारे में जानकारी का उपयोग करके इस समस्या को दूर करने का प्रयास करती है।
इसके अलावा, एक बड़ी लक्षित आबादी से सरल यादृच्छिक नमूना लेना बोझिल और थकाऊ हो सकता है। कुछ मामलों में, जांचकर्ता आबादी के उपसमूहों के लिए विशिष्ट शोध प्रश्नों में रुचि रखते हैं। उदाहरण के लिए, शोधकर्ताओं को यह जांचने में रुचि हो सकती है कि क्या नौकरी के प्रदर्शन के भविष्यवक्ता के रूप में संज्ञानात्मक क्षमता नस्लीय समूहों में समान रूप से लागू होती है। सरल यादृच्छिक नमूना इस स्थिति में शोधकर्ताओं की जरूरतों को समायोजित नहीं कर सकता है, क्योंकि यह आबादी के उप -समूह प्रदान नहीं करता है, और अन्य नमूनाकरण रणनीतियों, जैसे कि स्तरीकृत नमूनाकरण, इसके बजाय उपयोग किया जा सकता है।
व्यवस्थित नमूनाकरण
व्यवस्थित नमूनाकरण (जिसे अंतराल नमूनाकरण के रूप में भी जाना जाता है) कुछ क्रम योजना के अनुसार आबादी की व्यवस्था के अध्ययन पर निर्भर करता है, और फिर उस आदेशित सूची के माध्यम से नियमित अंतराल पर तत्वों का चयन करता है। व्यवस्थित नमूने में एक यादृच्छिक शुरुआत शामिल होती है और फिर तब से प्रत्येक केटीएच ( kth)तत्व के चयन के साथ आगे बढ़ती है। इस मामले में, k = (जनसंख्या आकार/नमूना आकार)। यह महत्वपूर्ण है कि प्रारंभिक बिंदु स्वचालित रूप से सूची में पहला नहीं है,बल्कि सूची में पहले से केटीएच ( kth) तत्व तक यादृच्छिक रूप से चुना गया है। एक सरल उदाहरण टेलीफोन निर्देशिका से प्रत्येक 10 वें नाम का चयन करना होगा (एक 'प्रत्येक 10 वां' नमूना, जिसे '10 के छूट( स्किप) के साथ नमूनाकरण' के रूप में भी जाना जाता है)।
जब प्रारंभिक बिंदु यादृच्छिक होता है, तब तक व्यवस्थित नमूनाकरण एक प्रकार संभावना का नमूना है। इसे लागू करना आसान है और प्रेरित स्तरीकरण इसे कुशल बना सकता है, यदि परिवर्तनीय सूची द्वारा का आदेश दिया जाता है, वह परिवर्तनीय ब्याज के साथ सहसंबद्ध है। आंकड़ाकोष(डेटाबेस) से कुशल नमूनाकरण के लिए 'हर 10 वीं' नमूनाकरण8 विशेष रूप से उपयोगी है।
उदाहरण के लिए, मान लीजिए कि हम एक लंबी सड़क के लोगों का नमूना लेना चाहते हैं जो एक गरीब क्षेत्र (घर संख्या- 1) में शुरू होता है और एक महंगे जिले के (घर संख्या- 1000) में समाप्त होता है। इस गली के पतों का एक सरल यादृच्छिक चयन उच्च अंत से बहुत अधिक और निम्न अंत से बहुत कम के साथ समाप्त होता है।जिससे एक गैर-प्रतिनिधि नमूना होता है। सड़क के साथ प्रत्येक 10 वीं स्ट्रीट नंबर का चयन करना (जैसे) यह सुनिश्चित करता है कि इन सभी जिलों का प्रतिनिधित्व करते हुए, नमूना सड़क की लंबाई के साथ समान रूप से फैला हुआ है। (ध्यान दें कि यदि हम हमेशा #1 पर शुरू करते हैं और #991 पर समाप्त होते हैं, तो नमूना कम अंत की ओर थोड़ा पक्षपाती है; #1 और #10 के बीच की शुरुआत को यादृच्छिक रूप से चुनकर, यह पूर्वाग्रह समाप्त हो जाता है।)
हालांकि, व्यवस्थित नमूना विशेष रूप से सूची में आवधिकता के लिए कमजोर है। यदि आवधिकता मौजूद है और अवधि का उपयोग किए गए अंतराल का एक बहु या कारक है, तो नमूना विशेष रूप से समग्र आबादी के लिए अप्रभावी होने की संभावना है, जिससे योजना सरल यादृच्छिक नमूने की तुलना में कम सटीक हो जाती है।
उदाहरण के लिए, एक ऐसी सड़क पर विचार करें जहां उत्तर की ओर सड़क के विषम संख्या वाले घर (महंगे) हैं, और दक्षिण तरफ सम-संख्या वाले सभी घर (सस्ते) हैं। ऊपर दी गई नमूना योजना के तहत, एक प्रतिनिधि नमूना प्राप्त करना असंभव है;विषम संख्या वाले सभी घरों में किए गए नमूना (सैंपल) या तो महंगे पक्ष से होंगे, या वे सभी समान-संख्या वाले सस्ते पक्ष से होंगे, जब तक कि शोधकर्ता को इस पूर्वाग्रह का पूर्व ज्ञान नहीं है और एक छूट(स्किप) का उपयोग करके इसे बचता है जो दोनों पक्षों (किसी भी विषम संख्या वाले स्किप) के बीच छूटना सुनिश्चित करता है ।
व्यवस्थित नमूने का एक और दोष यह है कि परिदृश्यों में भी जहां यह एसआरएस की तुलना में अधिक सटीक है, इसके सैद्धांतिक गुणों को उस सटीकता को निर्धारित करना मुश्किल बनाते है। (ऊपर दिए गए व्यवस्थित नमूने के दो उदाहरणों में, संभावित नमूनाकरण त्रुटि का अधिकांश हिस्सा पड़ोसी घरों के बीच भिन्नता के कारण है - लेकिन क्योंकि यह विधि कभी भी दो पड़ोसी घरों का चयन नहीं करती है, नमूना हमें उस भिन्नता के बारे में कोई जानकारी नहीं देगा।)
जैसा कि ऊपर वर्णित है, व्यवस्थित नमूनाकरण एक ईपीएस विधि है, क्योंकि सभी तत्वों में चयन की संभावना समान है (दिए गए उदाहरण में दस में से एक)। यह 'सरल यादृच्छिक नमूना' नहीं है क्योंकि एक ही आकार के अलग -अलग प्रतिनिधि नमूना (सबसेट) में अलग -अलग चयन संभावनाएं हैं - उदा। सेट {4,14,24, ..., 994} में चयन की एक-दस संभावना है, लेकिन सेट {4,13,24,34, ...} में चयन की शून्य संभावना है।
व्यवस्थित नमूने को गैर-ईपीएस दृष्टिकोण के लिए भी अनुकूलित किया जा सकता है; एक उदाहरण के लिए, नीचे पीपीएस नमूनों की चर्चा देखें।
स्तरीकृत नमूनाकरण
जब आबादी अलग -अलग श्रेणियों को अपनाती है, तो इन श्रेणियों द्वारा ढांचे( फ्रेम) को अलग -अलग स्तरों में व्यवस्थित किया जा सकता है।प्रत्येक स्तरों (स्ट्रैटम) को एक स्वतंत्र उप-जनसंख्या के रूप में नमूना लिया जाता है, जिसमें से व्यक्तिगत तत्वों को यादृच्छिक रूप से चुना जा सकता है।[3]जनसंख्या के आकार के लिए इस यादृच्छिक चयन (या नमूने) का आकार जनसंख्या के अनुपात को एक नमूना अंश कहा जाता है।[7] स्तरीकृत नमूने के लिए कई संभावित लाभ हैं।[7]
सबसे पहले, आबादी को अलग -अलग, स्वतंत्र स्तर में विभाजित करने से शोधकर्ताओं को विशिष्ट उपसमूहों के बारे में निष्कर्ष निकालने में सक्षम हो सकता है जो अधिक सामान्यीकृत यादृच्छिक नमूने में खो सकते हैं।
दूसरा, एक स्तरीकृत नमूनाकरण विधि का उपयोग करने से अधिक कुशल सांख्यिकीय अनुमान हो सकते हैं (बशर्ते कि स्तर( स्ट्रेटा) को नमूने की उपलब्धता के बजाय प्रश्न में मानदंड के लिए प्रासंगिकता के आधार पर चुना जाता है)। यहां तक कि अगर एक स्तरीकृत नमूनाकरण दृष्टिकोण सांख्यिकीय दक्षता में वृद्धि नहीं करता है, तो इस तरह की रणनीति के परिणामस्वरूप साधारण यादृच्छिक नमूने की तुलना में कम दक्षता नहीं होगी, बशर्ते कि प्रत्येक स्तर(स्ट्रैटम)आबादी में समूह के आकार के लिए आनुपातिक हो।
तीसरा, कभी-कभी ऐसा होता है कि समग्र आबादी की तुलना में आबादी के भीतर व्यक्तिगत, पूर्व-मौजूदा स्तर(स्ट्रैट) के लिए जानकारी (डेटा)अधिक आसानी से उपलब्ध होता है; ऐसे मामलों में, एक स्तरीकृत नमूनाकरण दृष्टिकोण का उपयोग करना समूहों में जानकारी (डेटा) एकत्र करने की तुलना में अधिक सुविधाजनक हो सकता है (हालांकि यह संभावित रूप से मानदंड-प्रासंगिक स्तर( स्ट्रैट) का उपयोग करने के पहले से नोट किए गए महत्व के साथ बाधाओं पर हो सकता है)।
अंत में, चूंकि प्रत्येक स्तर(स्ट्रैटम) को एक स्वतंत्र आबादी के रूप में माना जाता है, इसलिए अलग-अलग स्तर(स्ट्रैट)के नमूनाकरण को अलग-अलग दृष्टिकोण लागू किए जा सकता है, संभावित रूप से शोधकर्ताओं को जनसंख्या के अंदर प्रत्येक पहचाने गए उपसमूह के लिए सर्वोत्तम अनुकूल (या सबसे अधिक लागत प्रभावी) का उपयोग करने के लिए सक्षम किया जाता है।
हालांकि, स्तरीकृत नमूने का उपयोग करने के लिए कुछ संभावित कमियां हैं। सबसे पहले,स्तर( स्ट्रेटा) की पहचान करना और इस तरह के दृष्टिकोण को लागू करना नमूना चयन की लागत और जटिलता को बढ़ा सकता है, साथ ही जनसंख्या अनुमानों की बढ़ती जटिलता के लिए अग्रणी हो सकता है। दूसरा, कई मानदंडों की जांच करते समय, स्तरीकरण कुछ परिवर्तनशील (चर)से संबंधित हो सकते हैं, लेकिन दूसरों के लिए नहीं, आगे अभिकल्प(डिजाइन) को जटिल कर सकते हैं, और संभावित रूप से स्तर(स्ट्रैटा) की उपयोगिता को कम कर सकते हैं। अंत में, कुछ मामलों में (जैसे कि बड़ी संख्या में स्तर( स्ट्रैटा)के साथअभिकल्प(डिजाइन, या प्रति समूह एक निर्दिष्ट न्यूनतम नमूना आकार के साथ), स्तरीकृत नमूने को संभावित रूप से अन्य तरीकों की तुलना में एक बड़े नमूने की आवश्यकता हो सकती है (हालांकि ज्यादातर मामलों में, आवश्यक नमूना आकार सरल यादृच्छिक नमूने के लिए आवश्यक से बड़ा नहीं होगा)।
- एक स्तरीकृत नमूनाकरण दृष्टिकोण सबसे प्रभावी है जब तीन स्थितियों को पूरा किया जाता है
- स्तर(स्ट्रेटा)के भीतर परिवर्तनशीलता कम से कम है
- स्तर(स्ट्रैट) के बीच परिवर्तनशीलता अधिकतम होती है
- जिन चर पर आबादी को स्तरीकृत किया जाता है, वे वांछित आश्रित परिवर्तनशील (चर)के साथ दृढ़ता से सहसंबद्ध हैं।
- अन्य नमूने विधियों पर लाभ
- महत्वपूर्ण उप -योगों पर ध्यान केंद्रित करता है और अप्रासंगिक लोगों को अनदेखा करता है।
- विभिन्न उप -योगों के लिए विभिन्न नमूनाकरण तकनीकों का उपयोग करने की अनुमति देता है।
- अनुमान की सटीकता/दक्षता में सुधार करता है।
- आकार में व्यापक रूप से भिन्न होने वाले स्तर(स्ट्रैट) से समान संख्याओं का नमूना करके स्तर (स्ट्रैट)के बीच अंतर के परीक्षणों की सांख्यिकीय शक्ति के अधिक संतुलन की अनुमति देता है।
- नुकसान
- प्रासंगिक स्तरीकरण परिवर्तनशील(चर)के चयन की आवश्यकता है जो मुश्किल हो सकता है।
- तब उपयोगी नहीं है जब कोई सजातीय उपसमूह नहीं हैं।
- लागू करने के लिए महंगा हो सकता है।
- पश्च स्तरीकरण( पोस्टस्ट्रैटिफिकेशन)
स्तरीकरण को कभी -कभी पश्च स्तरीकरण(पोस्टस्ट्रैटिफिकेशन) नामक एक प्रक्रिया में नमूनाकरण चरण के बाद पेश किया जाता है।[3]यह दृष्टिकोण आम तौर पर एक उपयुक्त स्तरीकरण परिवर्तनशीलता( चर0 के पूर्व ज्ञान की कमी के कारण लागू किया जाता है या जब प्रयोगकर्ता के पास नमूनाकरण चरण के दौरान एक परिवर्तनशील स्तरीकरण बनाने के लिए आवश्यक जानकारी का अभाव होता है।यद्यपि यह विधि पूर्व (पोस्ट)हॉक दृष्टिकोणों के नुकसान के लिए अतिसंवेदनशील है, यह सही स्थिति में कई लाभ प्रदान कर सकता है।कार्यान्वयन आमतौर पर एक साधारण यादृच्छिक नमूने का अनुसरण करता है।एक सहायक परिवर्तनशील (चर) स्तरीकरण के लिए अनुमति देने के अलावा,पश्च स्तरीकरण( पोस्टस्ट्रैटिफिकेशन) का उपयोग भारोत्तोलन(वेटिंग) को लागू करने के लिए किया जा सकता है, जो एक नमूने के अनुमानों की सटीकता में सुधार कर सकता है।[3]
- अधिप्रतिचयन( ओवरसाम्पलिंग )
चयन(चॉइस)-आधारित नमूनाकरण (सैंपलिंग)स्तरीकृत नमूनाकरण रणनीतियों में से एक है।पसंद-आधारित नमूने में,[8] जानकारी (डेटा) को लक्ष्य पर स्तरीकृत किया जाता है और प्रत्येक स्तर(स्ट्रैटम) से एक नमूना लिया जाता है ताकि नमूने में दुर्लभ लक्ष्य वर्ग का अधिक प्रतिनिधित्व किया जाए।प्रतिरूप(मॉडल) इस पक्षपाती नमूने पर बनाया गया है।लक्ष्य पर निविष्ट परिवर्तनशील (इनपुट चर) प्रभावों को अक्सर पसंद-आधारित नमूने के साथ अधिक सटीकता के साथ अनुमानित किया जाता है, तब भी जब एक यादृच्छिक नमूने की तुलना में एक छोटा समग्र नमूना आकार लिया जाता है।परिणामों को आमतौर पर अधिप्रतिचयन(ओवरसाम्पलिंग) को लिए सही करने के लिए समायोजित किया जाना चाहिए।
संभाव्यता-आनुपातिक-से-आकार नमूनाकरण ('पीपीएस')
कुछ मामलों में नमूना डिजाइनर के पास एक सहायक परिवर्तनशील(चर) या"आकार माप" के उपाय तक पहुंच होती है, जिसे आबादी में प्रत्येक तत्व के हित के लिए परिवर्तनशीलता( चर) से संबंधित माना जाता है। इन आंकड़ों का उपयोग नमूना अभिकल्प( डिजाइन) सटीकता में सुधार करने के लिए किया जा सकता है। जैसा कि ऊपर चर्चा की गई है, एक विकल्प स्तरीकरण के आधार के रूप में सहायक परिवर्तनशीलता(चर) का उपयोग करना है।
एक अन्य विकल्प आकार ('पीपीएस') नमूने के लिए संभाव्यता आनुपातिक है, अधिकतम 1. तक,जिसमें प्रत्येक तत्व के चयन के लिए संभावना इसके आकार के उपाय के लिए आनुपातिक है, । एक साधारण संभाव्यता-आनुपातिक-से-आकार नमूनाकरण (पीपीएस डिजाइन)में ये चयन संभावनाएं तब कर सकती हैं जब पॉइसन नमूनाकरण(सैंपलिंग) को आधार के रूप में उपयोग किया जाए। हालांकि, इसमें परिवर्तनशील(चर) नमूना आकार की खामी है, और जनसंख्या के विभिन्न हिस्से अभी भी चयन में मौका भिन्नता के कारण खत्म हो सकते हैं या कम प्रतिनिधित्व कर सकते हैं।
व्यवस्थित नमूनाकरण सिद्धांत का उपयोग आकार के नमूने के लिए एक संभावना आनुपातिक बनाने के लिए किया जा सकता है। यह एक एकल नमूना इकाई के रूप में आकार परिवर्तनशीलता(चर) के भीतर प्रत्येक गणना का इलाज करके किया जाता है। नमूनों को तब परिवर्तनशील आकार के भीतर इन गणनाओं के बीच भी अंतराल का चयन करके पहचाना जाता है। इस विधि को कभी-कभी अंकेक्षण(ऑडिट) या फोरेंसिक नमूनाकरण (सैंपलिंग) के मामले इस पद्धति को कभी-कभी पीपीएस-अनुक्रमिक या मौद्रिक इकाई के नमूने कहा जाता है।
उदाहरण: मान लीजिए कि हमारे पास 150, 180, 200, 220, 220, 260, और क्रमशः 490 छात्रों (कुल 1500 छात्रों) की आबादी वाले छह स्कूल हैं, और हम छात्र की आबादी को आकार तीन के पीपीएस नमूने के आधार के रूप में उपयोग करना चाहते हैं। ऐसा करने के लिए, हम पहले स्कूल नंबरों को 1 to 150, दूसरा स्कूल 151 से 330 ( 150+180) आवंटित कर सकते हैं (1011 से 1500)। हम तब 1 और 500 (1500/3 के बराबर) के बीच एक यादृच्छिक शुरुआत उत्पन्न करते हैं और 500 के गुणकों द्वारा स्कूल की आबादी के माध्यम से गिनती करते हैं। यदि हमारी यादृच्छिक शुरुआत 137 थी, तो हम उन स्कूलों का चयन करेंगे जिन्हें 137, 637 की संख्या आवंटित की गई है, 637, 637, 637, 637, 637, 637 और 1137, यानी पहला, चौथा और छठा स्कूल।
पीपीएस दृष्टिकोण बड़े तत्वों पर नमूना केंद्रित करके किसी दिए गए नमूने के आकार की सटीकता में सुधार कर सकता है जो जनसंख्या के अनुमानों पर सबसे अधिक प्रभाव डालता है। पीपीएस नमूनाकरण(सैंपलिंग) का उपयोग आमतौर पर व्यवसायों के सर्वेक्षणों के लिए किया जाता है, जहां तत्व का आकार बहुत भिन्न होता है और सहायक जानकारी अक्सर उपलब्ध होती है उदाहरण के लिए, होटलों में खर्च किए गए अतिथि-रातों की संख्या को मापने का प्रयास करने वाला एक सर्वेक्षण प्रत्येक होटल के कमरों की संख्या का उपयोग सहायक के रूप में कर सकता है। कुछ मामलों में, अधिक वर्तमान अनुमानों का उत्पादन करने का प्रयास करते समय हित की परिवर्तनशीलता के एक पुराने माप को सहायक परिवर्तनशीलता (चर) के रूप में उपयोग किया जा सकता है।[9]
गुच्छ प्रतिचयन(क्लस्टर) नमूनाकरण
कभी-कभी समूहों ('क्लस्टर') में उत्तरदाताओं का चयन करना अधिक प्रभावी होता है।नमूनाकरण अक्सर भूगोल, या समय अवधिके अनुसार समूहित किया जाता है।(लगभग सभी नमूने समय में कुछ अर्थों में गुच्छ प्रतिचयन ('क्लस्टर') होते हैं - हालांकि यह शायद ही कभी इसे विश्लेषण में ध्यान में रखा जाता है।) उदाहरण के लिए, यदि किसी शहर के भीतर घरों का सर्वेक्षण करते हैं,तो हम 100 शहर चयनित ब्लॉकों का चयन करना चुन सकते हैं और फिर प्रत्येक परिवार का साक्षात्कार कर सकते हैं।
गुच्छ प्रतिचयन(क्लस्टरिंग) यात्रा और प्रशासनिक लागतों को कम कर सकती है। ऊपर दिए गए उदाहरण में, एक साक्षात्कारकर्ता प्रत्येक घर के लिए एक अलग ब्लॉक में अभियान (ड्राइव) करने के बजाय एक ब्लॉक में कई घरों में जाने के लिए एक एकल यात्रा कर सकता है।
इसका अर्थ यह भी है कि किसी को लक्षित जनसंख्या में सभी तत्वों को सूचीबद्ध करने के लिए एक नमूना ढांचे (फ्रेम) की आवश्यकता नहीं है। इसके बजाय,गुच्छ प्रतिचयन( क्लस्टर) को गुच्छ प्रतिचयन-स्तरीय ढांचे (फ्रेम) से चुना जा सकता है, जिसमें केवल चयनित गुच्छ प्रतिचयन (क्लस्टर) के लिए बनाया गया तत्व-स्तरीय ढांचे( फ्रेम) होता है। ऊपर दिए गए उदाहरण में, नमूने को केवल प्रारंभिक चयन के लिए एक ब्लॉक-स्तरीय शहर के नक्शे की आवश्यकता होती है, और फिर पूरे शहर के घरेलू स्तर के नक्शे के बजाय 100 चयनित ब्लॉकों के एक घरेलू स्तरीय मानचित्र की आवश्यकता होती है।
गुच्छ प्रतिचयन नमूनाकरण(जिसे क्लस्टर सैंपलिंग के रूप में भी जाना जाता है) आम तौर पर सरल यादृच्छिक नमूने के ऊपर नमूनाकरण अनुमानों की परिवर्तनशीलता को बढ़ाता है, यह इस बात पर निर्भर करता है कि गुच्छ प्रतिचयन(क्लस्टर) के भीतर गुच्छ प्रतिचयन (क्लस्टर) भिन्नता की तुलना में एक दूसरे के बीच कैसे भिन्न होते हैं। इस कारण से,गुच्छ प्रतिचयन नमूनाकरण( क्लस्टर सैंपलिंग) को सटीकता के समान स्तर को प्राप्त करने के लिए एसआरएस की तुलना में एक बड़े नमूने की आवश्यकता होती है - लेकिन गुच्छ प्रतिचयन (क्लस्टरिंग) से लागत बचत अभी भी इसे एक सस्ता विकल्प बना सकती है।
गुच्छ प्रतिचयन नमूनाकरण(क्लस्टर सैंपलिंग) को आमतौर पर बहुचरणी नमूनाकरण (मल्टीस्टेज सैंपलिंग)के रूप में लागू किया जाता है। यह गुच्छ प्रतिचयन नमूनाकरण (क्लस्टर सैंपलिंग) का एक जटिल रूप है जिसमें दो या दो से अधिक स्तरों की इकाइयाँ को एक में अंतर्निहित (एम्बेडेड) करती हैं। पहले चरण में उन समूहों का निर्माण होता है जिनका उपयोग नमूना लेने के लिए किया जाएगा। दूसरे चरण में, प्रत्येक क्लस्टर से प्राथमिक इकाइयों का नमूना यादृच्छिक रूप से चुना जाता है। (बजाय सभी चयनित समूहों में निहित सभी इकाइयों का उपयोग करने के) । निम्नलिखित चरणों में, उन चयनित समूहों में से प्रत्येक में, इकाइयों के अतिरिक्त नमूने चुने जाते हैं, और इसी तरह इस प्रक्रिया के अंतिम चरण में चयनित सभी अंतिम इकाइयों (उदाहरण के लिए व्यक्ति ) का सर्वेक्षण किया जाता है। इस प्रकार, यह तकनीक,अनिवार्य रूप से पूर्ववर्ती यादृच्छिक नमूनों के यादृच्छिक उपसमूह लेने की प्रक्रिया है।
बहुचरणी नमूनाकरण (मल्टीस्टेज सैंपलिंग) नमूने की लागत को काफी हद तक कम कर सकती है, जहां पूर्ण जनसंख्या सूची का निर्माण करने की आवश्यकता होगी (इससे पहले कि अन्य नमूनाकरण विधियों को लागू किया जा सके)। चयनित नहीं होने वाले समूहों का वर्णन करने में शामिल काम को समाप्त करके,बहुचरणी नमूनाकरण( मल्टीस्टेज नमूनाकरण) पारंपरिक गुच्छ प्रतिचयन (क्लस्टर) नमूने से जुड़ी बड़ी लागतों को कम कर सकता है।[9]हालांकि, प्रत्येक नमूना पूरी आबादी का पूर्ण प्रतिनिधि नहीं हो सकता है।
कोटा नमूना
कोटा नमूनाकरण में, जनसंख्या को पहले पारस्परिक रूप से अनन्य उप-समूहों में विभाजित किया जाता है, जैसे कि स्तरीकृत नमूनाकरण में।तब निर्णय का उपयोग एक निर्दिष्ट अनुपात के आधार पर प्रत्येक खंड से विषयों या इकाइयों का चयन करने के लिए किया जाता है।उदाहरण के लिए, एक साक्षात्कारकर्ता को 45 से 60 वर्ष की आयु के बीच 200 महिलाओं और 300 पुरुषों का नमूना लेने के लिए कहा जा सकता है।
यह यह दूसरा कदम है जो तकनीक को गैर-प्रतिकृति नमूने में से एक बनाता है।कोटा नमूनाकरण में नमूने का चयन गैर-यादृच्छिक है।उदाहरण के लिए, साक्षात्कारकर्ताओं को उन लोगों का साक्षात्कार करने के लिए लुभाया जा सकता है जो सबसे अधिक सहायक दिखते हैं।समस्या यह है कि ये नमूने पक्षपाती हो सकते हैं क्योंकि सभी को चयन का मौका नहीं मिलता है।यह यादृच्छिक तत्व इसकी सबसे बड़ी कमजोरी है और कोटा बनाम संभावना कई वर्षों से विवाद का विषय रहा है।
अल्पमहिष्ठ नमूनाकरण (मिनिमैक्स सैंपलिंग)
असंतुलित डेटासेट में, जहां जनसंख्या नमूना अनुपात के आंकड़ों का पालन नहीं करता है, कोई भी डेटासेट को एक रूढ़िवादी तरीके से मिनीमैक्स सैंपलिंग नामक कर सकता है।मिनिमैक्स सैंपलिंग का मूल एंडरसन मिनिमैक्स अनुपात में है जिसका मूल्य 0.5 साबित होता है: एक बाइनरी वर्गीकरण में, वर्ग-नमूना आकारों को समान रूप से चुना जाना चाहिए।यह अनुपात केवल गौसियन वितरण के साथ एलडीए क्लासिफायरर की धारणा के तहत मिनिमैक्स अनुपात साबित किया जा सकता है।मिनिमैक्स सैंपलिंग की धारणा हाल ही में वर्गीकरण नियमों के एक सामान्य वर्ग के लिए विकसित की गई है, जिसे क्लास-वार स्मार्ट क्लासिफायर कहा जाता है।इस मामले में, कक्षाओं के नमूने अनुपात का चयन किया जाता है ताकि वर्ग पूर्व संभावनाओं के लिए सभी संभावित जनसंख्या आँकड़ों पर सबसे खराब केस क्लासिफायर त्रुटि, सबसे अच्छा होगा।[7]
आकस्मिक नमूना
आकस्मिक नमूनाकरण (कभी -कभी हड़पने, सुविधा या अवसर के नमूने के रूप में जाना जाता है) एक प्रकार का गैर -अप्रोचता नमूनाकरण होता है जिसमें आबादी के उस हिस्से से निकाला जा रहा नमूना शामिल होता है जो हाथ के करीब होता है। अर्थात्, एक आबादी का चयन किया जाता है क्योंकि यह आसानी से उपलब्ध और सुविधाजनक है। यह व्यक्ति से मिलने या नमूने में किसी व्यक्ति को शामिल करने के माध्यम से हो सकता है जब कोई उनसे मिलता है या उन्हें तकनीकी साधनों जैसे कि इंटरनेट या फोन के माध्यम से खोजकर चुना जाता है। इस तरह के नमूने का उपयोग करने वाले शोधकर्ता इस नमूने से कुल आबादी के बारे में वैज्ञानिक रूप से सामान्यीकरण नहीं कर सकते हैं क्योंकि यह पर्याप्त प्रतिनिधि नहीं होगा। जैसे ऐसे क्षेत्र में समाज के अन्य सदस्य, यदि सर्वेक्षण को दिन के अलग -अलग समय और प्रति सप्ताह कई बार आयोजित किया जाना था। इस प्रकार का नमूना पायलट परीक्षण के लिए सबसे उपयोगी है। सुविधा नमूनों का उपयोग करने वाले शोधकर्ताओं के लिए कई महत्वपूर्ण विचारों में शामिल हैं:
- क्या अनुसंधान डिजाइन या प्रयोग के भीतर नियंत्रण हैं जो एक गैर-यादृच्छिक सुविधा नमूने के प्रभाव को कम करने के लिए काम कर सकते हैं, जिससे परिणाम यह सुनिश्चित करते हैं कि परिणाम जनसंख्या का अधिक प्रतिनिधि होंगे?
- क्या यह मानने का अच्छा कारण है कि एक विशेष सुविधा का नमूना एक ही आबादी से यादृच्छिक नमूने की तुलना में अलग -अलग प्रतिक्रिया या व्यवहार करना चाहिए?
- क्या शोध द्वारा पूछा जा रहा है कि एक सुविधा नमूने का उपयोग करके पर्याप्त रूप से उत्तर दिया जा सकता है?
सामाजिक विज्ञान अनुसंधान में, स्नोबॉल नमूना एक समान तकनीक है, जहां मौजूदा अध्ययन विषयों का उपयोग नमूने में अधिक विषयों को भर्ती करने के लिए किया जाता है। स्नोबॉल के नमूने के कुछ वेरिएंट, जैसे कि प्रतिवादी संचालित नमूनाकरण, चयन संभावनाओं की गणना की अनुमति देते हैं और कुछ शर्तों के तहत संभाव्यता नमूनाकरण तरीके हैं।
स्वैच्छिक नमूनाकरण
स्वैच्छिक नमूनाकरण विधि एक प्रकार का गैर-प्रक्रिया नमूना है।स्वयंसेवक एक सर्वेक्षण पूरा करने के लिए चुनते हैं।
सोशल मीडिया में विज्ञापनों के माध्यम से स्वयंसेवकों को आमंत्रित किया जा सकता है।[10]विज्ञापनों के लिए लक्ष्य आबादी को सामाजिक माध्यम द्वारा प्रदान किए गए उपकरणों का उपयोग करके स्थान, आयु, लिंग, आय, व्यवसाय, शिक्षा, या हितों जैसी विशेषताओं द्वारा चुना जा सकता है।विज्ञापन में अनुसंधान और एक सर्वेक्षण के लिंक के बारे में एक संदेश शामिल हो सकता है।लिंक का पालन करने और सर्वेक्षण पूरा करने के बाद, स्वयंसेवक नमूना आबादी में शामिल किए जाने वाले डेटा को प्रस्तुत करता है।यह विधि एक वैश्विक आबादी तक पहुंच सकती है लेकिन अभियान बजट तक सीमित है।आमंत्रित आबादी के बाहर स्वयंसेवकों को भी नमूने में शामिल किया जा सकता है।
इस नमूने से सामान्यीकरण करना मुश्किल है क्योंकि यह कुल आबादी का प्रतिनिधित्व नहीं कर सकता है।अक्सर, स्वयंसेवकों की सर्वेक्षण के मुख्य विषय में एक मजबूत रुचि होती है।
लाइन-इंटरसेप्ट सैंपलिंग
लाइन-इंटरसेप्ट सैंपलिंग एक ऐसे क्षेत्र में नमूनाकरण तत्वों की एक विधि है, जिसके द्वारा एक तत्व का नमूना लिया जाता है यदि एक चुना लाइन सेगमेंट, जिसे ट्रांसएक्ट कहा जाता है, तत्व को इंटरसेक्ट करता है।
पैनल सैंपलिंग
पैनल सैंपलिंग पहले एक यादृच्छिक नमूनाकरण विधि के माध्यम से प्रतिभागियों के एक समूह का चयन करने की विधि है और फिर उस समूह के लिए (संभावित रूप से समान) जानकारी के लिए कई बार कई बार पूछ रहा है।इसलिए, प्रत्येक प्रतिभागी का साक्षात्कार दो या अधिक समय बिंदुओं पर किया जाता है;डेटा संग्रह की प्रत्येक अवधि को एक लहर कहा जाता है।यह विधि 1938 में समाजशास्त्री पॉल लज़र्सफेल्ड द्वारा राजनीतिक अभियानों का अध्ययन करने के साधन के रूप में विकसित की गई थी।[11]यह अनुदैर्ध्य नमूनाकरण-विधि आबादी में परिवर्तन के अनुमानों की अनुमति देता है, उदाहरण के लिए, साप्ताहिक खाद्य व्यय के लिए नौकरी के तनाव के लिए पुरानी बीमारी के संबंध में।पैनल सैंपलिंग का उपयोग शोधकर्ताओं को उम्र के कारण व्यक्ति के स्वास्थ्य परिवर्तनों के बारे में सूचित करने के लिए भी किया जा सकता है या निरंतर निर्भर चर जैसे स्पूसल इंटरैक्शन में परिवर्तन को समझाने में मदद करने के लिए।[12]पैनल डेटा का विश्लेषण करने के कई प्रस्तावित तरीके हैं, जिनमें मनोवा, ग्रोथ कर्व्स और पिछड़ प्रभावों के साथ संरचनात्मक समीकरण मॉडलिंग शामिल हैं।
स्नोबॉल सैंपलिंग
स्नोबॉल के नमूने में प्रारंभिक उत्तरदाताओं का एक छोटा समूह ढूंढना और अधिक उत्तरदाताओं की भर्ती के लिए उनका उपयोग करना शामिल है।यह उन मामलों में विशेष रूप से उपयोगी है जहां आबादी छिपी हुई है या उनकी गणना करना मुश्किल है।
सैद्धांतिक नमूना
सैद्धांतिक नमूनाकरण[13]तब होता है जब नमूनों को क्षेत्र की गहरी समझ विकसित करने या सिद्धांतों को विकसित करने के लक्ष्य के साथ अब तक एकत्र किए गए डेटा के परिणामों के आधार पर चुना जाता है।चरम या बहुत विशिष्ट मामलों का चयन किया जा सकता है ताकि संभावना को अधिकतम किया जा सके कि एक घटना वास्तव में अवलोकन योग्य होगी।
चयनित इकाइयों का प्रतिस्थापन
नमूनाकरण योजनाएं प्रतिस्थापन के बिना हो सकती हैं ('वॉर' - किसी भी तत्व को एक ही नमूने में एक से अधिक बार नहीं चुना जा सकता है) या प्रतिस्थापन के साथ ('wr' एक तत्व एक नमूने में कई बार दिखाई दे सकता है)।उदाहरण के लिए, यदि हम मछली पकड़ते हैं, उन्हें मापते हैं, और नमूने के साथ जारी रखने से पहले तुरंत उन्हें पानी में वापस कर देते हैं, तो यह एक डब्ल्यूआर डिजाइन है, क्योंकि हम एक ही मछली को एक से अधिक बार पकड़ने और मापने को समाप्त कर सकते हैं।हालांकि, अगर हम मछली को पानी या टैग पर नहीं लौटाते हैं और इसे पकड़ने के बाद प्रत्येक मछली को छोड़ते हैं, तो यह एक खराब डिजाइन बन जाता है।
नमूना आकार निर्धारण
नमूना आकार निर्धारित करने के लिए सूत्र, टेबल और पावर फ़ंक्शन चार्ट अच्छी तरह से ज्ञात दृष्टिकोण हैं।
नमूना आकार तालिकाओं का उपयोग करने के लिए चरण
- ब्याज के प्रभाव आकार, α, और β को पोस्ट करें।
- नमूना आकार तालिका की जाँच करें[14] चयनित α के अनुरूप तालिका का चयन करें
- वांछित शक्ति के अनुरूप पंक्ति का पता लगाएं
- अनुमानित प्रभाव आकार के अनुरूप कॉलम का पता लगाएं।
- कॉलम और पंक्ति का चौराहा न्यूनतम नमूना आकार की आवश्यकता है।
नमूना और डेटा संग्रह
अच्छे डेटा संग्रह में शामिल हैं:
- परिभाषित नमूनाकरण प्रक्रिया के बाद
- डेटा को समय क्रम में रखना
- टिप्पणियों और अन्य प्रासंगिक घटनाओं पर ध्यान देना
- गैर-प्रतिक्रियाओं को रिकॉर्ड करना
नमूने के अनुप्रयोग
नमूनाकरण पूरी आबादी की विशेषताओं का अनुमान लगाने के लिए बड़े डेटा सेट के भीतर से सही डेटा बिंदुओं के चयन को सक्षम करता है।उदाहरण के लिए, हर दिन लगभग 600 मिलियन ट्वीट उत्पादित होते हैं।दिन के दौरान चर्चा किए गए विषयों को निर्धारित करने के लिए उन सभी को देखना आवश्यक नहीं है, और न ही प्रत्येक विषय पर भावना को निर्धारित करने के लिए सभी ट्वीट्स को देखना आवश्यक है।ट्विटर डेटा के नमूने के लिए एक सैद्धांतिक सूत्रीकरण विकसित किया गया है।[15]
विभिन्न प्रकार के संवेदी डेटा के निर्माण में जैसे ध्वनिकी, कंपन, दबाव, वर्तमान, वोल्टेज और नियंत्रक डेटा कम समय के अंतराल पर उपलब्ध हैं।डाउन-टाइम की भविष्यवाणी करने के लिए सभी डेटा को देखना आवश्यक नहीं हो सकता है लेकिन एक नमूना पर्याप्त हो सकता है।
नमूना सर्वेक्षण में त्रुटियां
सर्वेक्षण के परिणाम आमतौर पर कुछ त्रुटि के अधीन होते हैं।कुल त्रुटियों को नमूने की त्रुटियों और गैर-नमूनाकरण त्रुटियों में वर्गीकृत किया जा सकता है।यहां त्रुटि में व्यवस्थित पूर्वाग्रह के साथ -साथ यादृच्छिक त्रुटियां भी शामिल हैं।
नमूना लेना त्रुटियां और पूर्वाग्रह
नमूना लेना और पूर्वाग्रह नमूना डिजाइन से प्रेरित हैं।वे सम्मिलित करते हैं:
- चयन पूर्वाग्रह: जब वास्तविक चयन संभावनाएं परिणामों की गणना करने में ग्रहण किए गए लोगों से भिन्न होती हैं।
- यादृच्छिक नमूनाकरण त्रुटि: यादृच्छिक रूप से चयनित नमूने में तत्वों के कारण परिणामों में यादृच्छिक भिन्नता।
नॉन-सैंपलिंग त्रुटि
गैर-सैंपलिंग त्रुटियां अन्य त्रुटियां हैं जो डेटा संग्रह, प्रसंस्करण या नमूना डिजाइन में समस्याओं के कारण अंतिम सर्वेक्षण अनुमानों को प्रभावित कर सकती हैं।ऐसी त्रुटियों में शामिल हो सकते हैं:
- ओवर-कवरेज: जनसंख्या के बाहर से डेटा को शामिल करना
- अंडर-कवरेज: सैंपलिंग फ्रेम में आबादी में तत्व शामिल नहीं हैं।
- माप त्रुटि: उदा।जब उत्तरदाताओं ने एक प्रश्न को गलत समझा, या जवाब देना मुश्किल पाया
- प्रसंस्करण त्रुटि: डेटा कोडिंग में गलतियाँ
- गैर-प्रतिक्रिया या भागीदारी पूर्वाग्रह: सभी चयनित व्यक्तियों से पूर्ण डेटा प्राप्त करने में विफलता
नमूने के बाद, एक समीक्षा आयोजित की जानी चाहिए[by whom?] नमूने के बाद सटीक प्रक्रिया का पालन किया गया था, बजाय इसके कि किसी भी प्रभाव का अध्ययन करने के लिए, किसी भी विचलन के बाद के विश्लेषण पर हो सकता है।
एक विशेष समस्या में गैर-प्रतिक्रिया शामिल है।गैर-प्रतिक्रिया के दो प्रमुख प्रकार मौजूद हैं:[16][17]* यूनिट नॉनसेप्स (सर्वेक्षण के किसी भी हिस्से के पूरा होने की कमी)
- आइटम गैर-प्रतिक्रिया (सर्वेक्षण में प्रस्तुत या भागीदारी लेकिन सर्वेक्षण के एक या अधिक घटकों/प्रश्नों को पूरा करने में विफल)
सर्वेक्षण के नमूने में, नमूने के हिस्से के रूप में पहचाने गए कई व्यक्तियों में भाग लेने के लिए अनिच्छुक हो सकते हैं, भाग लेने का समय नहीं है (अवसर लागत),[18]या सर्वेक्षण प्रशासक उनसे संपर्क करने में सक्षम नहीं हो सकते हैं।इस मामले में, उत्तरदाताओं और गैर -जिम्मेदारियों के बीच अंतर का खतरा है, जिससे जनसंख्या मापदंडों के पक्षपाती अनुमान हैं।यह अक्सर सर्वेक्षण डिजाइन में सुधार, प्रोत्साहन की पेशकश, और अनुवर्ती अध्ययनों का संचालन करके संबोधित किया जाता है जो अनुत्तरदायी से संपर्क करने और बाकी फ्रेम के साथ उनकी समानता और अंतर को चिह्नित करने के लिए एक बार-बार प्रयास करते हैं।[19]प्रभाव को डेटा को भारित करके भी कम किया जा सकता है (जब जनसंख्या बेंचमार्क उपलब्ध हो) या अन्य प्रश्नों के उत्तर के आधार पर डेटा लगाकर।इंटरनेट के नमूने में विशेष रूप से एक समस्या है।इस समस्या के कारणों में अनुचित रूप से डिज़ाइन किए गए सर्वेक्षण शामिल हो सकते हैं,[17]ओवर-सर्वाइविंग (या सर्वेक्षण थकान),[12][20][need quotation to verify] और तथ्य यह है कि संभावित प्रतिभागियों के पास कई ई-मेल पते हो सकते हैं, जिनका वे अब और उपयोग नहीं करते हैं या नियमित रूप से जांच नहीं करते हैं।
सर्वेक्षण वजन
नमूना अंश कई स्थितियों में स्तर( स्ट्रैटम) द्वारा भिन्न हो सकता है और जनसंख्या का सही प्रतिनिधित्व करने के लिए आधार-सामग्री (डेटा) का वर्णन करना होगा। इस प्रकार उदाहरण के लिए, यूनाइटेड किंगडम में व्यक्तियों का एक साधारण यादृच्छिक नमूने में कुछ दूरस्थ स्कॉटिश द्वीपों में शामिल नहीं हो सकते है जो नमूने के लिए महंगे होंगे। एक सस्ती विधि शहरी और ग्रामीण स्तर के साथ एक स्तरीकृत नमूने का उपयोग करने के लिए होगी। ग्रामीण नमूने को नमूने में कम प्रतिनिधित्व दिया जा सकता है, लेकिन क्षतिपूर्ति विश्लेषण के लिए में उचित रूप से भारित किया जा सकता है।
अधिक आम तौर पर, डेटा को आमतौर पर भारित किया जाना चाहिए यदि नमूना डिजाइन प्रत्येक व्यक्ति को चयनित होने का एक समान मौका नहीं देता है। उदाहरण के लिए, जब परिवारों के पास समान चयन संभावनाएं होती हैं, लेकिन एक व्यक्ति को प्रत्येक घर के भीतर से साक्षात्कार दिया जाता है, तो यह बड़े घरों के लोगों को साक्षात्कार के लिए एक छोटा मौका देता है। यह सर्वेक्षण भार का उपयोग करने के लिए जिम्मेदार हो सकता है। इसी तरह, एक से अधिक टेलीफोन लाइन वाले घरों में एक यादृच्छिक अंकों डायलिंग नमूने में चुने जाने की अधिक संभावना है, और वेट इसके लिए समायोजित कर सकते हैं।
वेट अन्य उद्देश्यों को भी पूरा कर सकते हैं, जैसे कि गैर-प्रतिक्रिया के लिए सही करने में मदद करना।
यादृच्छिक नमूने के उत्पादन के तरीके
- यादृच्छिक संख्या तालिका
- छद्म यादृच्छिक संख्या जनरेटर के लिए गणितीय एल्गोरिदम
- फिजिकल रैंडमाइजेशन डिवाइस जैसे सिक्के, प्लेइंग कार्ड या परिष्कृत डिवाइस जैसे कि एर्नी
इतिहास
यादृच्छिक नमूना बहुत सारे पुराना विचार का एक उपयोग है, जिसका उल्लेख बाइबिल में कई बार किया गया है।1786 में पियरे साइमन लाप्लास ने अनुपात अनुमानक के साथ नमूने का उपयोग करके फ्रांस की आबादी का अनुमान लगाया।उन्होंने त्रुटि के संभाव्य अनुमानों की भी गणना की।इन्हें आधुनिक आत्मविश्वास अंतराल के रूप में नहीं बल्कि नमूना आकार के रूप में व्यक्त किया गया था ,जो कि संभावना 1000/1001 के साथ नमूना त्रुटि पर एक विशेष ऊपरी सीमा को प्राप्त करने के लिए आवश्यक होगा।उनके अनुमानों ने बेयस के प्रमेय को एक समान पूर्व संभावना के साथ इस्तेमाल किया और यह माना कि उनका नमूना यादृच्छिक था।अलेक्जेंडर इवानोविच चुप्रोव ने 1870 के दशक में शाही(इंपीरियल) रूस का नमूना सर्वेक्षण की शुरुआत की।अमेरिकी 1936 के राष्ट्रपति चुनाव में रिपब्लिकन जीत की लिटरेरी डाइजेस्ट की भविष्यवाणी गंभीर पूर्वाग्रह के कारण बुरी तरह से गड़बड़ा गई थी [1]।मैगज़ीन सदस्यता सूचियों (सब्सक्रिप्शन लिस्ट) और टेलीफोन निर्देशिकाओं के माध्यम से प्राप्त उनके नामों के साथ दो मिलियन से अधिक लोगों ने अध्ययन का जवाब दिया।यह सराहना नहीं की गई थी कि ये सूचियाँ रिपब्लिकन के प्रति भारी पक्षपाती थीं और परिणामी नमूना, यद्यपि बहुत बड़ा था, गहराई से त्रुटिपूर्ण था।[21][22]
यह भी देखें
- आंकड़ा संग्रहण
- अनुमान सिद्धांत
- Gy का नमूना सिद्धांत
- जर्मन टैंक समस्या
- होर्विट्ज़ -थॉम्पसन अनुमानक
- आधिकारिक आंकड़े
- अनुपात अनुमानक
- प्रतिकृति (सांख्यिकी)
- यादृच्छिक-नमूनाकरण तंत्र
- Resampling (सांख्यिकी)
- स्यूडो-रैंडम नंबर सैंपलिंग
- नमूना आकार निर्धारण
- नमूना (केस स्टडी)
- आंकड़ों की अशुद्धि
- नमूने का वितरण
- नमूनाकरण त्रुटि
- क्रमबद्धता
- सर्वेक्षण नमूनाकरण
- डिजाइन प्रभाव
टिप्पणियाँ
The textbook by Groves et alia provides an overview of survey methodology, including recent literature on questionnaire development (informed by cognitive psychology) :
- Robert Groves, et alia. Survey methodology (2010 2nd ed. [2004]) ISBN 0-471-48348-6.
The other books focus on the statistical theory of survey sampling and require some knowledge of basic statistics, as discussed in the following textbooks:
- David S. Moore and George P. McCabe (February 2005). "Introduction to the practice of statistics" (5th edition). W.H. Freeman & Company. ISBN 0-7167-6282-X.
- Freedman, David; Pisani, Robert; Purves, Roger (2007). Statistics (4th ed.). New York: Norton. ISBN 978-0-393-92972-0.
The elementary book by Scheaffer et alia uses quadratic equations from high-school algebra:
- Scheaffer, Richard L., William Mendenhal and R. Lyman Ott. Elementary survey sampling, Fifth Edition. Belmont: Duxbury Press, 1996.
More mathematical statistics is required for Lohr, for Särndal et alia, and for Cochran (classic[citation needed]):
- Cochran, William G. (1977). Sampling techniques (Third ed.). Wiley. ISBN 978-0-471-16240-7.
- Lohr, Sharon L. (1999). Sampling: Design and analysis. Duxbury. ISBN 978-0-534-35361-2.
- Särndal, Carl-Erik; Swensson, Bengt; Wretman, Jan (1992). Model assisted survey sampling. Springer-Verlag. ISBN 978-0-387-40620-6.
The historically important books by Deming and Kish remain valuable for insights for social scientists (particularly about the U.S. census and the Institute for Social Research at the University of Michigan):
- Deming, W. Edwards (1966). Some Theory of Sampling. Dover Publications. ISBN 978-0-486-64684-8. OCLC 166526.
- Kish, Leslie (1995) Survey Sampling, Wiley, ISBN 0-471-10949-5
संदर्भ
- ↑ Lance, P.; Hattori, A. (2016). Sampling and Evaluation. Web: MEASURE Evaluation. pp. 6–8, 62–64.
- ↑ सालेंट, प्रिसिला, आई। डिलमैन, और ए। डॉन।अपना खुद का सर्वेक्षण कैसे करें।नंबर 300.723 S3।1994।
- ↑ 3.0 3.1 3.2 3.3 Robert M. Groves; et al. (2009). Survey methodology. ISBN 978-0470465462.
- ↑ Lohr, Sharon L. Sampling: Design and analysis.
- ↑ Särndal, Carl-Erik; Swensson, Bengt; Wretman, Jan. Model Assisted Survey Sampling.
- ↑ Scheaffer, Richard L.; William Mendenhal; R. Lyman Ott. (2006). Elementary survey sampling.
- ↑ 7.0 7.1 7.2 Shahrokh Esfahani, Mohammad; Dougherty, Edward (2014). "Effect of separate sampling on classification accuracy". Bioinformatics. 30 (2): 242–250. doi:10.1093/bioinformatics/btt662. PMID 24257187.
- ↑ Scott, A.J.; Wild, C.J. (1986). "Fitting logistic models under case-control or choice-based sampling". Journal of the Royal Statistical Society, Series B. 48 (2): 170–182. JSTOR 2345712.
- ↑ 9.0 9.1 * Lohr, Sharon L. Sampling: Design and Analysis.
- Särndal, Carl-Erik; Swensson, Bengt; Wretman, Jan. Model Assisted Survey Sampling.
- ↑ Ariyaratne, Buddhika (30 July 2017). "Voluntary Sampling Method combined with Social Media advertising". heal-info.blogspot.com. Health Informatics. Retrieved 18 December 2018.[unreliable source?]
- ↑ Lazarsfeld, P., & Fiske, M. (1938)।राय को मापने के लिए एक नए उपकरण के रूप में पैनल।जनमत त्रैमासिक, 2 (4), 596–612।
- ↑ 12.0 12.1 ग्रोव्स, एट आलिया।सर्वेक्षण कार्यप्रणाली
- ↑ "Examples of sampling methods" (PDF).
- ↑ कोहेन, 1988
- ↑ Deepan Palguna; Vikas Joshi; Venkatesan Chakaravarthy; Ravi Kothari; L. V. Subramaniam (2015). Analysis of Sampling Algorithms for Twitter. International Joint Conference on Artificial Intelligence.
- ↑ बेरिंस्की, ए। जे। (2008)।गैर-प्रतिक्रिया का सर्वेक्षण करें।में: डब्ल्यू। डोन्सबैक और एम। डब्ल्यू। ट्रगोट (सं।), द सेज हैंडबुक ऑफ़ पब्लिक ओपिनियन रिसर्च (पीपी। 309–321)।हजार ओक्स, सीए: ऋषि प्रकाशन।
- ↑ 17.0 17.1 डिलमैन, डी। ए।, एल्टिंग, जे। एल।, ग्रोव्स, आर। एम।, और लिटिल, आर। जे। ए। (2002)।डिजाइन, डेटा संग्रह और विश्लेषण में गैर -सर्वेक्षण।में: आर। एम। ग्रोव्स, डी। ए। डिलमैन, जे। एल। एल्टिंग, और आर। जे। ए। लिटिल (एड्स), सर्वे नॉनस्पेसिस (पीपी। 3–26)।न्यूयॉर्क: जॉन विली एंड संस।
- ↑ डिलमैन, डी.ए., स्मिथ, जे.डी., और क्रिश्चियन, एल। एम। (2009)।इंटरनेट, मेल, और मिश्रित-मोड सर्वेक्षण: सिलवाया डिजाइन विधि।सैन फ्रांसिस्को: जोसी-बास।
- ↑ वाहनवर, वी।, बैटगेलज, जेड।, मैनफ्रेडा, के.एल., और ज़ालेटेल, एम। (2002)।वेब सर्वेक्षणों में गैर -जिम्मेदार।में: आर। एम। ग्रोव्स, डी। ए। डिलमैन, जे। एल। एल्टिंग, और आर। जे। ए। लिटिल (एड्स), सर्वे नॉनस्पेसिस (पीपी। 229–242)।न्यूयॉर्क: जॉन विली एंड संस।
- ↑ Porter; Whitcomb; Weitzer (2004). "Multiple surveys of students and survey fatigue". In Porter, Stephen R (ed.). Overcoming survey research problems. New directions for institutional research. San Francisco: Jossey-Bass. pp. 63–74. ISBN 9780787974770. Retrieved 15 July 2019.
- ↑ डेविड एस। मूर और जॉर्ज पी। मैककेबे।सांख्यिकी के अभ्यास का परिचय।
- ↑ Freedman, David; Pisani, Robert; Purves, Roger. Statistics.
अग्रिम पठन
- Singh, G N, Jaiswal, A. K., and Pandey A. K. (2021), Improved Imputation Methods for Missing Data in Two-Occasion Successive Sampling, Communications in Statistics: Theory and Methods. DOI:10.1080/03610926.2021.1944211
- Chambers, R L, and Skinner, C J (editors) (2003), Analysis of Survey Data, Wiley, ISBN 0-471-89987-9
- Deming, W. Edwards (1975) On probability as a basis for action, The American Statistician, 29(4), pp. 146–152.
- Gy, P (2012) Sampling of Heterogeneous and Dynamic Material Systems: Theories of Heterogeneity, Sampling and Homogenizing, Elsevier Science, ISBN 978-0444556066
- Korn, E.L., and Graubard, B.I. (1999) Analysis of Health Surveys, Wiley, ISBN 0-471-13773-1
- Lucas, Samuel R. (2012). doi:10.1007%2Fs11135-012-9775-3 "Beyond the Existence Proof: Ontological Conditions, Epistemological Implications, and In-Depth Interview Research."], Quality & Quantity, doi:10.1007/s11135-012-9775-3.
- Stuart, Alan (1962) Basic Ideas of Scientific Sampling, Hafner Publishing Company, New York[ISBN missing]
- Smith, T. M. F. (1984). "Present Position and Potential Developments: Some Personal Views: Sample surveys". Journal of the Royal Statistical Society, Series A. 147 (The 150th Anniversary of the Royal Statistical Society, number 2): 208–221. doi:10.2307/2981677. JSTOR 2981677.
- Smith, T. M. F. (1993). "Populations and Selection: Limitations of Statistics (Presidential address)". Journal of the Royal Statistical Society, Series A. 156 (2): 144–166. doi:10.2307/2982726. JSTOR 2982726. (Portrait of T. M. F. Smith on page 144)
- Smith, T. M. F. (2001). "Centenary: Sample surveys". Biometrika. 88 (1): 167–243. doi:10.1093/biomet/88.1.167.
- Smith, T. M. F. (2001). "Biometrika centenary: Sample surveys". In D. M. Titterington and D. R. Cox (ed.). Biometrika: One Hundred Years. Oxford University Press. pp. 165–194. ISBN 978-0-19-850993-6.
- Whittle, P. (May 1954). "Optimum preventative sampling". Journal of the Operations Research Society of America. 2 (2): 197–203. doi:10.1287/opre.2.2.197. JSTOR 166605.
मानक
आईएसओ
- आईएसओ 2859 श्रृंखला
- आईएसओ 3951 श्रृंखला
ASTM
- ASTM E105 सामग्री की संभावना नमूने के लिए मानक अभ्यास
- एएसटीएम E122 मानक अभ्यास नमूना आकार की गणना के लिए अनुमान लगाने के लिए, एक निर्दिष्ट सहनीय त्रुटि के साथ, बहुत या प्रक्रिया की विशेषता के लिए औसत
- ASTM E141 संभावना नमूनाकरण के परिणामों के आधार पर साक्ष्य की स्वीकृति के लिए मानक अभ्यास
- एएसटीएम E1402 मानक शब्दावली नमूनाकरण से संबंधित
- ASTM E1994 प्रक्रिया उन्मुख AOQL और LTPD नमूना योजनाओं के उपयोग के लिए मानक अभ्यास
- ASTM E2234 AQL द्वारा अनुक्रमित विशेषताओं द्वारा उत्पाद की एक धारा के नमूने के लिए मानक अभ्यास
ANXI, ASYA
- एनेसी/अस्या Z1.H
अमेरिकी संघीय और सैन्य मानक
- MIL-STD-105
- MIL-STD-1916
बाहरी संबंध
 Media related to नमूनाकरण (सांख्यिकी) at Wikimedia Commons
Media related to नमूनाकरण (सांख्यिकी) at Wikimedia Commons