अंकीय शोधन (डिजिटल फ़िल्टर): Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
{{Short description|Filter used on discretely-sampled signals in signal processing}} | {{Short description|Filter used on discretely-sampled signals in signal processing}} | ||
[[File:FIR Filter General.svg|thumb|250px|एन चरणों के साथ एक सामान्य परिमित आवेग प्रतिक्रिया फ़िल्टर, प्रत्येक एक स्वतंत्र देरी के साथ, डी<sub>i</sub>, and amplification gain, a<sub>i</sub>।]] | [[File:FIR Filter General.svg|thumb|250px|एन चरणों के साथ एक सामान्य परिमित आवेग प्रतिक्रिया फ़िल्टर, प्रत्येक एक स्वतंत्र देरी के साथ, डी<sub>i</sub>, and amplification gain, a<sub>i</sub>।]] | ||
अंकीय शोधन (डिजिटल फ़िल्टर), सिग्नल प्रोसेसिंग में एक ऐसी प्रणाली है जिसका उपयोग सिग्नल के आयामों को कम करने या बढ़ाने के लिए करती है, जो असतत समय सिग्नल पर गणितीय संचालन करती है। यह अन्य प्रमुख प्रकार के इलेक्ट्रॉनिक फ़िल्टर के विपरीत है, एनालॉग फ़िल्टर, आमतौर पर एक इलेक्ट्रॉनिक सर्किट है जो निरंतर समय एनालॉग सिग्नल पर काम कर रहा है। | '''अंकीय शोधन (डिजिटल फ़िल्टर)''', सिग्नल प्रोसेसिंग में एक ऐसी प्रणाली है जिसका उपयोग सिग्नल के आयामों को कम करने या बढ़ाने के लिए करती है, जो असतत समय सिग्नल पर गणितीय संचालन करती है। यह अन्य प्रमुख प्रकार के इलेक्ट्रॉनिक फ़िल्टर के विपरीत है, एनालॉग फ़िल्टर, आमतौर पर एक इलेक्ट्रॉनिक सर्किट है जो निरंतर समय एनालॉग सिग्नल पर काम कर रहा है। | ||
एक डिजिटल फ़िल्टर सिस्टम में आमतौर पर इनपुट सिग्नल का नमूना लेने के लिए एक एनालॉग-टू-डिजिटल कनवर्टर (एडीसी) होता है, इसके बाद एक माइक्रोप्रोसेसर और कुछ परिधीय घटक जैसे कि मेमोरी टू स्टोर डेटा और फ़िल्टर गुणांक आदि, सभी प्रोग्राम निर्देश (सॉफ्टवेयर) पर चल रहे हैं। माइक्रोप्रोसेसर पर चलने वाले प्रोग्राम निर्देश (सॉफ्टवेयर) एडीसी (ADC) से प्राप्त नंबरों पर आवश्यक गणितीय प्रबंध करके डिजिटल फिल्टर को लागू करते हैं। कुछ उच्च प्रदर्शन अनुप्रयोगों में, एक सामान्य प्रयोजन माइक्रोप्रोसेसर के बजाय एक [[:hi:एफपीजीए|FPGA]] या [[:hi:एसिक|ASIC]] का उपयोग किया जाता है, या फ़िल्टरिंग जैसे कार्यों में तेजी लाने के लिए विशिष्ट समानांतर वास्तुकला के साथ एक विशेष [[:hi:डिजिटल सिग्नल प्रोसेसर|डिजिटल सिग्नल प्रोसेसर]] (DSP) का उपयोग किया जाता है।<ref>{{Cite journal|last1=Lyakhov|first1=Pavel|last2=Valueva|first2=Maria|last3=Valuev|first3=Georgii|last4=Nagornov|first4=Nikolai|date=2020|title=High-Performance Digital Filtering on Truncated Multiply-Accumulate Units in the Residue Number System|journal=IEEE Access|volume=8|pages=209181–209190|doi=10.1109/ACCESS.2020.3038496|issn=2169-3536|doi-access=free}}</ref><ref>{{Cite journal|last1=Priya|first1=P|last2=Ashok|first2=S|date=April 2018|title=IIR Digital Filter Design Using Xilinx System Generator for FPGA Implementation|url=https://ieeexplore.ieee.org/document/8524520|journal=2018 International Conference on Communication and Signal Processing (ICCSP)|pages=0054–0057|doi=10.1109/ICCSP.2018.8524520|isbn=978-1-5386-3521-6|s2cid=53284942}}</ref> | एक डिजिटल फ़िल्टर सिस्टम में आमतौर पर इनपुट सिग्नल का नमूना लेने के लिए एक एनालॉग-टू-डिजिटल कनवर्टर (एडीसी) होता है, इसके बाद एक माइक्रोप्रोसेसर और कुछ परिधीय घटक जैसे कि मेमोरी टू स्टोर डेटा और फ़िल्टर गुणांक आदि, सभी प्रोग्राम निर्देश (सॉफ्टवेयर) पर चल रहे हैं। माइक्रोप्रोसेसर पर चलने वाले प्रोग्राम निर्देश (सॉफ्टवेयर) एडीसी (ADC) से प्राप्त नंबरों पर आवश्यक गणितीय प्रबंध करके डिजिटल फिल्टर को लागू करते हैं। कुछ उच्च प्रदर्शन अनुप्रयोगों में, एक सामान्य प्रयोजन माइक्रोप्रोसेसर के बजाय एक [[:hi:एफपीजीए|FPGA]] या [[:hi:एसिक|ASIC]] का उपयोग किया जाता है, या फ़िल्टरिंग जैसे कार्यों में तेजी लाने के लिए विशिष्ट समानांतर वास्तुकला के साथ एक विशेष [[:hi:डिजिटल सिग्नल प्रोसेसर|डिजिटल सिग्नल प्रोसेसर]] (DSP) का उपयोग किया जाता है।<ref>{{Cite journal|last1=Lyakhov|first1=Pavel|last2=Valueva|first2=Maria|last3=Valuev|first3=Georgii|last4=Nagornov|first4=Nikolai|date=2020|title=High-Performance Digital Filtering on Truncated Multiply-Accumulate Units in the Residue Number System|journal=IEEE Access|volume=8|pages=209181–209190|doi=10.1109/ACCESS.2020.3038496|issn=2169-3536|doi-access=free}}</ref><ref>{{Cite journal|last1=Priya|first1=P|last2=Ashok|first2=S|date=April 2018|title=IIR Digital Filter Design Using Xilinx System Generator for FPGA Implementation|url=https://ieeexplore.ieee.org/document/8524520|journal=2018 International Conference on Communication and Signal Processing (ICCSP)|pages=0054–0057|doi=10.1109/ICCSP.2018.8524520|isbn=978-1-5386-3521-6|s2cid=53284942}}</ref> | ||
| Line 24: | Line 23: | ||
किसी दिए गए डिजिटल फिल्टर के व्यवहार का विश्लेषण करने के लिए विभिन्न प्रकार की गणितीय तकनीकों को नियोजित किया जा सकता है। इन विश्लेषण तकनीकों में से कई को डिजाइन में भी नियोजित किया जा सकता है, और प्रायः एक फ़िल्टर विनिर्देश का आधार बनता है। | किसी दिए गए डिजिटल फिल्टर के व्यवहार का विश्लेषण करने के लिए विभिन्न प्रकार की गणितीय तकनीकों को नियोजित किया जा सकता है। इन विश्लेषण तकनीकों में से कई को डिजाइन में भी नियोजित किया जा सकता है, और प्रायः एक फ़िल्टर विनिर्देश का आधार बनता है। | ||
आमतौर पर, कोई फ़िल्टर की विशेषता यह गणना करके से होती है कि वे एक साधारण इनपुट जैसे आवेग का जवाब कैसे देंगे। अधिक जटिल संकेतों के लिए फ़िल्टर की प्रतिक्रिया की गणना करने के लिए इस जानकारी का विस्तार किया जा | आमतौर पर, कोई फ़िल्टर की विशेषता यह गणना करके से होती है कि वे एक साधारण इनपुट जैसे आवेग का जवाब कैसे देंगे। अधिक जटिल संकेतों के लिए फ़िल्टर की प्रतिक्रिया की गणना करने के लिए इस जानकारी का विस्तार किया जा सकता है। | ||
=== आवेग प्रतिक्रिया === | === आवेग प्रतिक्रिया === | ||
आवेग प्रतिक्रिया, प्रायः निरूपित की जाती है <math>h[k]</math> या <math>h_k</math>, इसका माप है कि एक फ़िल्टर क्रोनकर डेल्टा फ़ंक्शन का जवाब कैसे देगा। <ref>{{cite web |title=Lab.4&5. Introduction to FIR Filters |url=http://www.just.edu.jo/~hazem-ot/Lab.4&5.%20FIR%20Filters.pdf |publisher=Jordan University of Science and Technology-Faculty of Engineering |access-date=13 July 2020}}</ref>उदाहरण के लिए, एक अंतर समीकरण को देखते हुए, एक सेट होगा <math>x_0 = 1</math> तथा <math>x_k = 0</math> के लिये <math>k \ne 0</math> और मूल्यांकन | आवेग प्रतिक्रिया, प्रायः निरूपित की जाती है <math>h[k]</math> या <math>h_k</math>, इसका माप है कि एक फ़िल्टर क्रोनकर डेल्टा फ़ंक्शन का जवाब कैसे देगा। <ref>{{cite web |title=Lab.4&5. Introduction to FIR Filters |url=http://www.just.edu.jo/~hazem-ot/Lab.4&5.%20FIR%20Filters.pdf |publisher=Jordan University of Science and Technology-Faculty of Engineering |access-date=13 July 2020}}</ref> उदाहरण के लिए, एक अंतर समीकरण को देखते हुए, एक सेट होगा <math>x_0 = 1</math> तथा <math>x_k = 0</math> के लिये <math>k \ne 0</math> और मूल्यांकन करें। आवेग प्रतिक्रिया फ़िल्टर के व्यवहार का एक लक्षण वर्णन है।डिजिटल फिल्टर को आमतौर पर दो श्रेणियों में माना जाता है: अनंत आवेग प्रतिक्रिया (IIR) और परिमित आवेग प्रतिक्रिया (एफआईआर)। | ||
रैखिक समय-अपरिवर्तनीय एफआईआर फिल्टर के मामले में, आवेग प्रतिक्रिया फिल्टर गुणांक के अनुक्रम के बराबर है, और इस प्रकार: | रैखिक समय-अपरिवर्तनीय एफआईआर फिल्टर के मामले में, आवेग प्रतिक्रिया फिल्टर गुणांक के अनुक्रम के बराबर है, और इस प्रकार: | ||
| Line 34: | Line 33: | ||
दूसरी ओर IIR फ़िल्टर पुनरावर्ती हैं, आउटपुट के साथ वर्तमान और पिछले इनपुट दोनों के साथ -साथ पिछले आउटपुट के आधार पर।IIR फ़िल्टर का सामान्य रूप इस प्रकार है: | दूसरी ओर IIR फ़िल्टर पुनरावर्ती हैं, आउटपुट के साथ वर्तमान और पिछले इनपुट दोनों के साथ -साथ पिछले आउटपुट के आधार पर।IIR फ़िल्टर का सामान्य रूप इस प्रकार है: | ||
:<math>\ \sum_{m=0}^{M} a_{m}y_{n-m} = \sum_{k=0}^{N} b_{k} x_{n-k}</math> | :<math>\ \sum_{m=0}^{M} a_{m}y_{n-m} = \sum_{k=0}^{N} b_{k} x_{n-k}</math> | ||
आवेग प्रतिक्रिया की साजिश रचने से पता चलता है कि एक फ़िल्टर अचानक, क्षणिक गड़बड़ी का | आवेग प्रतिक्रिया की साजिश रचने से पता चलता है कि एक फ़िल्टर अचानक, क्षणिक गड़बड़ी का उत्तर कैसे देता है। IIR फ़िल्टर सदैव पुनरावर्ती होता है। जबकि एक पुनरावर्ती फ़िल्टर के लिए एक परिमित आवेग प्रतिक्रिया के लिए संभव है, एक गैर-पुनरावर्ती फिल्टर में सदैव एक परिमित आवेग प्रतिक्रिया होती है। उदाहरण: मूविंग एवरेज (MA) फ़िल्टर है, जिसे पुनरावर्ती दोनों को लागू किया जा सकता है{{cn|date=May 2019}} और गैर -पुनरावर्ती। | ||
==== अंतर समीकरण ===== | ==== अंतर समीकरण ===== | ||
असतत-समय प्रणालियों में, डिजिटल फ़िल्टर को अक्सर | [[:hi:खास समय|असतत-समय]] प्रणालियों में, डिजिटल फ़िल्टर को अक्सर [[:hi:जेड रूपान्तर|Z-ट्रांसफ़ॉर्म]] के माध्यम से [[:hi:अंतरण प्रकार्य|स्थानांतरण फ़ंक्शन]] को [[:hi:जेड रूपान्तर|रैखिक स्थिर-गुणांक अंतर समीकरण]] (LCCD) में परिवर्तित करके कार्यान्वित किया जाता है। असतत [[:hi:आवृत्ति डोमेन|आवृत्ति-डोमेन]] स्थानांतरण फ़ंक्शन को दो बहुपदों के अनुपात के रूप में लिखा जाता है। उदाहरण के लिए: | ||
:<math>H(z) = \frac{(z+1)^2} {(z-\frac{1}{2}) (z+\frac{3}{4})}</math> | :<math>H(z) = \frac{(z+1)^2} {(z-\frac{1}{2}) (z+\frac{3}{4})}</math> | ||
| Line 48: | Line 46: | ||
H(z) = \frac{1 + 2z^{-1} +z^{-2}} {1 +\frac{1}{4} z^{-1} - \frac{3}{8} z^{-2}} = \frac{Y(z)}{X(z)} | H(z) = \frac{1 + 2z^{-1} +z^{-2}} {1 +\frac{1}{4} z^{-1} - \frac{3}{8} z^{-2}} = \frac{Y(z)}{X(z)} | ||
</math> | </math> | ||
हर के गुणांक,<math>a_{k}</math>, 'फ़ीड-बैकवर्ड' गुणांक हैं और अंश के गुणांक 'फ़ीड-फॉरवर्ड' गुणांक हैं, <math>b_{k}</math> | हर के गुणांक,<math>a_{k}</math>, 'फ़ीड-बैकवर्ड' गुणांक हैं और अंश के गुणांक 'फ़ीड-फॉरवर्ड' गुणांक हैं, <math>b_{k}</math>। | ||
परिणामी रैखिक अंतर समीकरण है: | |||
:<math> | :<math> | ||
y[n] = -\sum_{k=1}^{M} a_{k} y[n-k] + \sum_{k=0}^{N} b_{k} x[n-k] | y[n] = -\sum_{k=1}^{M} a_{k} y[n-k] + \sum_{k=0}^{N} b_{k} x[n-k] | ||
| Line 74: | Line 74: | ||
यह समीकरण दिखाता है कि अगले आउटपुट नमूने की गणना कैसे करें, <math>y[n]</math>, पिछले आउटपुट के संदर्भ में, <math>y[n-p]</math>, वर्तमान इनपुट, <math>x[n]</math>, और पिछले इनपुट, <math>x[n-p]</math>।इस रूप में किसी इनपुट पर फ़िल्टर को लागू करना एक प्रत्यक्ष रूप I या II (नीचे देखें) प्राप्ति के बराबर है, जो मूल्यांकन के सटीक क्रम के आधार पर है। | यह समीकरण दिखाता है कि अगले आउटपुट नमूने की गणना कैसे करें, <math>y[n]</math>, पिछले आउटपुट के संदर्भ में, <math>y[n-p]</math>, वर्तमान इनपुट, <math>x[n]</math>, और पिछले इनपुट, <math>x[n-p]</math>।इस रूप में किसी इनपुट पर फ़िल्टर को लागू करना एक प्रत्यक्ष रूप I या II (नीचे देखें) प्राप्ति के बराबर है, जो मूल्यांकन के सटीक क्रम के आधार पर है। | ||
उदाहरण के लिए, जैसा कि कंप्यूटर प्रोग्रामर द्वारा कोड में उपरोक्त समीकरण को लागू करने वाले द्वारा उपयोग किया जाता है, इसे निम्नानुसार वर्णित किया जा सकता है: | |||
<math>y</math> = आउटपुट, या फ़िल्टर्ड मान <br> | <math>y</math> = आउटपुट, या फ़िल्टर्ड मान <br> | ||
| Line 90: | Line 90: | ||
== फ़िल्टर डिजाइन == | == फ़िल्टर डिजाइन == | ||
यद्यपि फ़िल्टर को सरलता से समझा और उसकी गणना की जाती है, लेकिन उनके डिजाइन और कार्यान्वयन की व्यावहारिक चुनौतियां महत्वपूर्ण हैं और बहुत उन्नत शोध का विषय हैं। | |||
यद्यपि फ़िल्टर को | |||
== फ़िल्टर | डिजिटल फ़िल्टर की दो श्रेणियां हैं: पुनरावर्ती फ़िल्टर और गैर -फ़िल्टर। इन्हें प्रायः अनंत आवेग प्रतिक्रिया (IIR) फिल्टर और परिमित आवेग प्रतिक्रिया (FIR) फ़िल्टर के रूप में संदर्भित किया जाता है।<ref>A. Antoniou, ''Digital Filters: Analysis, Design, and Applications'', New York, NY: McGraw-Hill, 1993., chapter 1</ref> | ||
== फ़िल्टर प्रत्यक्षीकरण == | |||
एक फ़िल्टर डिज़ाइन किए जाने के बाद, इसे एक सिग्नल फ्लो आरेख विकसित करके महसूस किया जाना चाहिए जो नमूना अनुक्रमों पर संचालन के संदर्भ में फ़िल्टर का वर्णन करता है। | एक फ़िल्टर डिज़ाइन किए जाने के बाद, इसे एक सिग्नल फ्लो आरेख विकसित करके महसूस किया जाना चाहिए जो नमूना अनुक्रमों पर संचालन के संदर्भ में फ़िल्टर का वर्णन करता है। | ||
| Line 104: | Line 101: | ||
=== प्रत्यक्ष रूप I === | === प्रत्यक्ष रूप I === | ||
IIR फ़िल्टर | IIR फ़िल्टर प्राप्ति के लिए एक सीधा दृष्टिकोण [[:hi:डिजिटल बाइकैड फ़िल्टर|प्रत्यक्ष रूप I]] है, जहां अंतर समीकरण का सीधे मूल्यांकन किया जाता है। यह फॉर्म छोटे फिल्टर के लिए व्यावहारिक है, लेकिन जटिल डिजाइनों के लिए अक्षम और अव्यवहारिक (संख्यात्मक रूप से अस्थिर) हो सकता है। <ref>J. O. Smith III, [http://ccrma.stanford.edu/~jos/filters/Direct_Form_I.html Direct Form I]</ref> सामान्य तौर पर, इस फॉर्म को ऑर्डर एन के फ़िल्टर के लिए 2N विलंब तत्वों (इनपुट और आउटपुट सिग्नल दोनों के लिए) की आवश्यकता होती है। | ||
[[File:Biquad filter DF-I.svg|400px]] | [[File:Biquad filter DF-I.svg|400px]] | ||
=== प्रत्यक्ष रूप II | === प्रत्यक्ष रूप II=== | ||
वैकल्पिक डिजिटल | वैकल्पिक [[:hi:डिजिटल बाइकैड फ़िल्टर|प्रत्यक्ष रूप II]] को केवल ''N'' विलंब इकाइयों की आवश्यकता होती है, जहां ''N'' फ़िल्टर का क्रम है - संभावित रूप से प्रत्यक्ष रूप I से आधा। यह संरचना प्रत्यक्ष प्रपत्र I के अंश और हर वर्गों के क्रम को उलट कर प्राप्त की जाती है, क्योंकि वे वास्तव में दो रेखीय प्रणालियाँ हैं, और क्रमपरिवर्तन गुण लागू होता है। फिर, कोई यह नोटिस करेगा कि विलंब के दो स्तंभ हैं ( <math>z^{-1}</math> ) जो केंद्र के जाल को टैप करते हैं, और इन्हें जोड़ा जा सकता है क्योंकि वे बेमानी हैं, जैसा कि नीचे दिखाया गया है। | ||
प्रतिकूल परिस्थिति यह है कि प्रत्यक्ष रूप II उच्च ''Q'' या अनुनाद के फिल्टर के लिए अंकगणितीय अतिप्रवाह की संभावना को बढ़ाता है। <ref>J. O. Smith III, [http://ccrma.stanford.edu/~jos/filters/Direct_Form_II.html Direct Form II]</ref> यह दिखाया गया है कि जैसे-जैसे ''क्यू'' बढ़ता है, दोनों प्रत्यक्ष रूप टोपोलॉजी का राउंड-ऑफ शोर बिना सीमा के बढ़ता है। <ref>L. B. Jackson, "On the Interaction of Roundoff Noise and Dynamic Range in Digital Filters," ''Bell Sys. Tech. J.'', vol. 49 (1970 Feb.), reprinted in ''Digital Signal Process'', L. R. Rabiner and C. M. Rader, Eds. (IEEE Press, New York, 1972).</ref> इसका कारण यह है कि, अवधारणात्मक रूप से, सिग्नल को पहले एक ऑल-पोल फिल्टर (जो सामान्य रूप से गुंजयमान आवृत्तियों पर लाभ बढ़ाता है) के माध्यम से पारित किया जाता है, उसके परिणाम संतृप्त होने से पहले, फिर एक ऑल-जीरो फिल्टर से गुजरता है (जो अक्सर बहुत कुछ को क्षीण करता है ऑल-पोल आधा बढ़ता है)। | |||
[[File:Biquad filter DF-II.svg|400px]] | [[File:Biquad filter DF-II.svg|400px]] | ||
=== कैस्केड | === कैस्केड दूसरे क्रम के खंड === | ||
एक सामान्य रणनीति | एक सामान्य रणनीति यह है कि उच्च-क्रम (2 से अधिक) डिजिटल फ़िल्टर को दूसरे क्रम के "बायक्वाड्राट्रिक" (या "बिक्वाड") सेक्शन <ref>J. O. Smith III, [http://ccrma.stanford.edu/~jos/filters/Series_Second_Order_Sections.html Series Second Order Sections]</ref> ( [[:hi:डिजिटल बाइकैड फ़िल्टर|डिजिटल बाईक्वाड फ़िल्टर]] देखें) की एक कैस्केड श्रृंखला के रूप में महसूस किया जाए। इस रणनीति का लाभ यह है कि गुणांक सीमा सीमित है। कैस्केडिंग डायरेक्ट फॉर्म II सेक्शन के परिणामस्वरूप ऑर्डर ''एन'' के फिल्टर के लिए ''एन'' विलंब तत्व होते हैं। कैस्केडिंग डायरेक्ट फॉर्म I सेक्शन का परिणाम ''N'' + 2 विलंब तत्वों में होता है, क्योंकि किसी भी सेक्शन के इनपुट के विलंब तत्व (पहले सेक्शन को छोड़कर) पिछले सेक्शन के आउटपुट के विलंब तत्वों के साथ निरर्थक हैं। | ||
=== अन्य रूप === | === अन्य रूप === | ||
अन्य रूपों में सम्मिलित हैं: | |||
अन्य रूपों में | |||
* प्रत्यक्ष रूप I और II ट्रांसपोज़ | * प्रत्यक्ष रूप I और II ट्रांसपोज़ | ||
* श्रृंखला/कैस्केड लोअर (विशिष्ट दूसरा) ऑर्डर सब्सक्रिप्शन | * श्रृंखला/कैस्केड लोअर (विशिष्ट दूसरा) ऑर्डर सब्सक्रिप्शन | ||
| Line 148: | Line 143: | ||
== एनालॉग और डिजिटल फिल्टर की तुलना == | == एनालॉग और डिजिटल फिल्टर की तुलना == | ||
डिजिटल फिल्टर घटक गैर- | डिजिटल फिल्टर घटक गैर-रैखिकताओं के अधीन नहीं हैं जो एनालॉग फिल्टर के डिजाइन को बहुत जटिल करते हैं। एनालॉग फिल्टर में अपूर्ण इलेक्ट्रॉनिक घटक होते हैं, जिनके मान एक सीमा सहनशीलता के लिए निर्दिष्ट होते हैं (उदाहरण के लिए प्रतिरोधी मूल्यों में अक्सर ± 5% की सहनशीलता होती है) और जो समय के साथ तापमान और बहाव के साथ भी बदल सकते हैं। जैसे-जैसे एनालॉग फिल्टर का क्रम बढ़ता है, और इस प्रकार इसकी घटक संख्या बढ़ती है, चर घटक त्रुटियों का प्रभाव बहुत बढ़ जाता है। डिजिटल फिल्टर में, गुणांक मान कंप्यूटर मेमोरी में संग्रहीत होते हैं, जिससे वे अधिक स्थिर और अनुमानित हो जाते हैं। <ref name="dspguide2">{{Cite web|url=http://www.dspguide.com/ch21/1.htm|title=Match #1: Analog vs. Digital Filters}}</ref> | ||
डिजिटल फिल्टर | क्योंकि डिजिटल फिल्टर के गुणांक निश्चित हैं, उनका उपयोग अधिक जटिल और चयनात्मक डिजाइन प्राप्त करने के लिए किया जा सकता है – विशेष रूप से डिजिटल फिल्टर के साथ, कोई कम पासबैंड रिपल, तेज संक्रमण, और उच्च स्टॉपबैंड क्षीणन प्राप्त कर सकता है, जो एनालॉग फिल्टर के साथ व्यावहारिक है। यहां तक कि अगर डिजाइन एनालॉग फिल्टर का उपयोग करके प्राप्त किया जा सकता है, तो समकक्ष डिजिटल फिल्टर को डिजाइन करने की इंजीनियरिंग लागत बहुत कम होगी। इसके अलावा, एक [[:hi:अनुकूली फिल्टर|अनुकूली फ़िल्टर]] या उपयोगकर्ता-नियंत्रित पैरामीट्रिक फ़िल्टर बनाने के लिए कोई भी डिजिटल फ़िल्टर के गुणांक को आसानी से संशोधित कर सकता है। हालांकि ये तकनीक एक एनालॉग फिल्टर में संभव हैं, फिर भी वे काफी अधिक कठिन हैं। | ||
डिजिटल फिल्टर | हालांकि, डिजिटल फिल्टर का उपयोग परिमित आवेग प्रतिक्रिया फिल्टर के डिजाइन में किया जा सकता है। समतुल्य एनालॉग फिल्टर अक्सर अधिक जटिल होते हैं, क्योंकि इनमें विलंब तत्वों की आवश्यकता होती है। | ||
डिजिटल फिल्टर एनालॉग सर्किटरी पर कम भरोसा करते हैं, संभावित रूप से बेहतर [[:hi:सिगनल-रव अनुपात|सिग्नल-टू-शोर अनुपात की]] अनुमति देते हैं। एक डिजिटल फ़िल्टर एनालॉग कम पास फ़िल्टरिंग, डिजिटल रूपांतरण के अनुरूप, डिजिटल से एनालॉग रूपांतरण के दौरान सिग्नल में शोर पेश करेगा और क्वांटिज़ेशन के कारण डिजिटल शोर पेश कर सकता है। एनालॉग फिल्टर के साथ, प्रत्येक घटक थर्मल शोर (जैसे [[:hi:जॉनसन शोर|जॉनसन शोर]] ) का स्रोत है, इसलिए जैसे-जैसे फ़िल्टर जटिलता बढ़ती है, वैसे ही रव (नॉइज़0 भी होता है। | |||
हालांकि, डिजिटल फिल्टर सिस्टम में उच्च मौलिक विलंबता का परिचय देते हैं। एनालॉग फ़िल्टर में, विलंबता अक्सर नगण्य होती है; कड़ाई से बोलते हुए यह एक विद्युत संकेत के लिए फिल्टर सर्किट के माध्यम से प्रचारित करने का समय है। डिजिटल सिस्टम में, विलंबता को डिजिटल सिग्नल पथ में विलंब तत्वों द्वारा, और [[:hi:अनुरूप से अंकीय परिवर्तक|एनालॉग-टू-डिजिटल]] और [[:hi:अंकीय-अनुरूप रूपांतरण|डिजिटल-से-एनालॉग कन्वर्टर्स]] द्वारा पेश किया जाता है जो सिस्टम को एनालॉग सिग्नल को संसाधित करने में सक्षम बनाता है। | |||
एनालॉग | बहुत ही साधारण मामलों में, एनालॉग फ़िल्टर का उपयोग करना अधिक लागत प्रभावी होता है। डिजिटल फ़िल्टर को पेश करने के लिए काफी ओवरहेड सर्किटरी की आवश्यकता होती है, जैसा कि पहले चर्चा की गई थी, जिसमें दो लो पास एनालॉग फिल्टर सम्मिलित हैं। | ||
पीसीबी पर | एनालॉग फिल्टर के लिए एक और तर्क कम बिजली की खपत है। एनालॉग फिल्टर के लिए काफी कम शक्ति की आवश्यकता होती है और इसलिए बिजली की आवश्यकता होने पर एकमात्र समाधान होता है। | ||
[[:hi:प्रिन्टेड सर्किट बोर्ड|पीसीबी (PCB)]] पर विद्युत सर्किट बनाते समय डिजिटल समाधान का उपयोग करना आम तौर पर आसान होता है, क्योंकि प्रसंस्करण इकाइयां वर्षों से अत्यधिक अनुकूलित होती हैं। एनालॉग घटकों के साथ समान सर्किट बनाने से [[:hi:इलेक्ट्रानिक परिपथ|असतत घटकों]] का उपयोग करते समय बहुत अधिक स्थान लगेगा। दो विकल्प [[:hi:फील्ड-प्रोग्रामेबल एनालॉग ऐरे|FPAAs]] <ref name="FPAA2">{{Cite journal|last=Bains|first=Sunny|title=Analog's answer to FPGA opens field to masses|journal=EETimes|date=July 2008|url=http://www.eetimes.com/document.asp?doc_id=1167814}}</ref> और [[:hi:एसिक|ASICs]] हैं, लेकिन वे कम मात्रा में महंगे हैं। | |||
== डिजिटल फिल्टर के प्रकार == | == डिजिटल फिल्टर के प्रकार == | ||
फिल्टर को चिह्नित करने के विभिन्न तरीके हैं; उदाहरण के लिए: | फिल्टर को चिह्नित करने के विभिन्न तरीके हैं; उदाहरण के लिए: | ||
एक फ़िल्टर को एक | * एक ''रैखिक'' फ़िल्टर इनपुट नमूनों का एक [[:hi:रैखिक परिवर्तन|रैखिक परिवर्तन]] है; अन्य फिल्टर ''[[:hi:अरेखीय तंत्र|अरेखीय]]'' हैं। रैखिक फिल्टर [[:hi:अध्यारोपण सिद्धान्त|सुपरपोजिशन सिद्धांत]] को संतुष्ट करते हैं, अर्थात यदि कोई इनपुट विभिन्न संकेतों का भारित रैखिक संयोजन है, तो आउटपुट संबंधित आउटपुट संकेतों का समान रूप से भारित रैखिक संयोजन है। | ||
* एक ''कारण'' फ़िल्टर इनपुट या आउटपुट संकेतों के केवल पिछले नमूनों का उपयोग करता है; जबकि एक ''गैर-कारण'' फ़िल्टर भविष्य के इनपुट नमूनों का उपयोग करता है। एक गैर-कारण फ़िल्टर को आमतौर पर इसमें देरी जोड़कर एक कारण फ़िल्टर में बदला जा सकता है। | |||
* ''समय-अपरिवर्तनीय'' फ़िल्टर में समय के साथ निरंतर गुण होते हैं; अन्य फ़िल्टर जैसे [[:hi:अनुकूली फिल्टर|अनुकूली फ़िल्टर]] समय के साथ बदलते हैं। | |||
* एक ''स्थिर'' फ़िल्टर एक आउटपुट उत्पन्न करता है जो समय के साथ स्थिर मान में परिवर्तित हो जाता है, या एक सीमित अंतराल के भीतर सीमित रहता है। एक ''अस्थिर'' फ़िल्टर एक आउटपुट उत्पन्न कर सकता है जो बिना सीमा के, बाउंडेड या शून्य इनपुट के साथ बढ़ता है। | |||
* एक [[:hi:परिमित आवेग प्रतिक्रिया|परिमित आवेग प्रतिक्रिया]] (एफआईआर) फ़िल्टर केवल इनपुट सिग्नल का उपयोग करता है, जबकि एक [[:hi:अनंत आवेग प्रतिक्रिया|अनंत आवेग प्रतिक्रिया]] (आईआईआर) फ़िल्टर इनपुट सिग्नल और आउटपुट सिग्नल के पिछले नमूने दोनों का उपयोग करता है। एफआईआर फिल्टर हमेशा स्थिर होते हैं, जबकि आईआईआर फिल्टर अस्थिर हो सकते हैं। | |||
एक फिल्टर को एक [[:hi:ब्लॉक आरेख|ब्लॉक आरेख]] द्वारा दर्शाया जा सकता है, जिसका उपयोग तब हार्डवेयर निर्देशों के साथ फिल्टर को लागू करने के लिए एक नमूना प्रसंस्करण [[:hi:अल्गोरिद्म|एल्गोरिथ्म]] प्राप्त करने के लिए किया जा सकता है। एक फिल्टर को [[:hi:पुनरावृत्ति संबंध|अंतर समीकरण]], [[:hi:शून्य और ध्रुव|शून्य और ध्रुवों]] का संग्रह या एक [[:hi:आवेग प्रतिक्रिया|आवेग प्रतिक्रिया]] या [[:hi:कदम की प्रतिक्रिया|चरण प्रतिक्रिया]] के रूप में भी वर्णित किया जा सकता है। | |||
डिजिटल | कुछ डिजिटल फिल्टर [[:hi:त्वरित फुरिअर रूपान्तर|तेजी से फूरियर ट्रांसफॉर्म]] पर आधारित होते हैं, एक गणितीय एल्गोरिदम जो एक सिग्नल के [[:hi:आवृत्ति स्पेक्ट्रम|आवृत्ति स्पेक्ट्रम]] को जल्दी से निकालता है, जिससे संशोधित स्पेक्ट्रम को वापस परिवर्तित करने से पहले स्पेक्ट्रम में हेरफेर किया जा सकता है (जैसे कि बहुत उच्च ऑर्डर बैंड-पास फिल्टर बनाना)। एक उलटा एफएफटी ऑपरेशन के साथ एक समय-श्रृंखला संकेत। ये फ़िल्टर O(n log n) कम्प्यूटेशनल लागत देते हैं जबकि पारंपरिक डिजिटल फ़िल्टर O(n <sup>2</sup> ) होते हैं। | ||
पारंपरिक रैखिक फिल्टर आमतौर पर क्षीणन पर आधारित होते | डिजिटल फिल्टर का दूसरा रूप [[:hi:अवस्था-समष्टि|राज्य-अंतरिक्ष (स्टेट स्पेस)]] मॉडल का है। एक अच्छी तरह से इस्तेमाल किया जाने वाला राज्य-अंतरिक्ष फ़िल्टर 1960 में [[:hi:रुदाल्फ एमिल कालमान|रुडोल्फ]] [[:hi:कालमान फिल्टर|कलमैन द्वारा प्रकाशित कलमन फ़िल्टर]] है। | ||
पारंपरिक रैखिक फिल्टर आमतौर पर क्षीणन पर आधारित होते हैं। वैकल्पिक रूप से नॉनलाइनियर फिल्टर को ऊर्जा हस्तांतरण फिल्टर सहित डिजाइन किया जा सकता है, <ref name="SAB12">Billings S.A. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains". Wiley, 2013</ref> जो उपयोगकर्ता को एक डिजाइन तरीके से ऊर्जा को स्थानांतरित करने की अनुमति देता है ताकि अवांछित शोर या प्रभाव को नए आवृत्ति बैंड में या तो कम या उच्च आवृत्ति में स्थानांतरित किया जा सके, जो एक सीमा में फैला हो आवृत्तियों, विभाजन, या केंद्रित। एनर्जी ट्रांसफर फिल्टर पारंपरिक फिल्टर डिजाइनों के पूरक हैं और फिल्टर डिजाइन में स्वतंत्रता के कई और डिग्री पेश करते हैं। डिजिटल ऊर्जा हस्तांतरण फिल्टर डिजाइन करने और गैर-रेखीय गतिशीलता को लागू करने और शोषण करने के लिए अपेक्षाकृत आसान हैं। | |||
== यह भी देखें == | == यह भी देखें == | ||
* बेसेल | |||
* बिलिनियर ट्रांसफॉर्म | * [[:hi:बेसेल फिल्टर|बेसेल फिल्टर]] | ||
* बटरवर्थ फ़िल्टर | * [[:hi:बिलिनियर ट्रांसफॉर्म|बिलिनियर ट्रांसफॉर्म]] | ||
* | * [[:hi:बटरवर्थ फ़िल्टर|बटरवर्थ फ़िल्टर]] | ||
* इलेक्ट्रॉनिक | * [[:hi:चेबिशेव फिल्टर|चेबीशेव फ़िल्टर]] | ||
* अण्डाकार फ़िल्टर ( | * [[:hi:इलेक्ट्रॉनिक फिल्टर|इलेक्ट्रॉनिक फिल्टर]] | ||
* फ़िल्टर | * [[:hi:अण्डाकार फिल्टर|अण्डाकार फ़िल्टर (कौअर फ़िल्टर)]] | ||
* उच्च-पास | * [[:hi:फ़िल्टर डिज़ाइन|फ़िल्टर डिज़ाइन]] | ||
* अनंत आवेग प्रतिक्रिया, परिमित आवेग प्रतिक्रिया | * [[:hi:उच्च पारक फिल्टर|हाई-पास फिल्टर]], [[:hi:लो पास फिल्टर|लो-पास फिल्टर]] | ||
* | * [[:hi:अनंत आवेग प्रतिक्रिया|अनंत आवेग प्रतिक्रिया]], [[:hi:परिमित आवेग प्रतिक्रिया|परिमित आवेग प्रतिक्रिया]] | ||
* मिलान फ़िल्टर | * [[:hi:लिंकविट्ज़-रिले फ़िल्टर|लिंकविट्ज़-रिले फ़िल्टर]] | ||
* नमूना (संकेत) | * [[:hi:मिलान फ़िल्टर|मिलान फ़िल्टर]] | ||
* | * [[:hi:नमूना (संकेत)|नमूना (संकेत)]] | ||
* द्वि-आयामी फ़िल्टर | * [[:hi:सविट्ज़की-गोले फ़िल्टर|सविट्ज़की-गोले फ़िल्टर]] | ||
* [[:hi:द्वि-आयामी फ़िल्टर|द्वि-आयामी फ़िल्टर]] | |||
==संदर्भ== | ==संदर्भ== | ||
Revision as of 18:24, 20 July 2022
अंकीय शोधन (डिजिटल फ़िल्टर), सिग्नल प्रोसेसिंग में एक ऐसी प्रणाली है जिसका उपयोग सिग्नल के आयामों को कम करने या बढ़ाने के लिए करती है, जो असतत समय सिग्नल पर गणितीय संचालन करती है। यह अन्य प्रमुख प्रकार के इलेक्ट्रॉनिक फ़िल्टर के विपरीत है, एनालॉग फ़िल्टर, आमतौर पर एक इलेक्ट्रॉनिक सर्किट है जो निरंतर समय एनालॉग सिग्नल पर काम कर रहा है।
एक डिजिटल फ़िल्टर सिस्टम में आमतौर पर इनपुट सिग्नल का नमूना लेने के लिए एक एनालॉग-टू-डिजिटल कनवर्टर (एडीसी) होता है, इसके बाद एक माइक्रोप्रोसेसर और कुछ परिधीय घटक जैसे कि मेमोरी टू स्टोर डेटा और फ़िल्टर गुणांक आदि, सभी प्रोग्राम निर्देश (सॉफ्टवेयर) पर चल रहे हैं। माइक्रोप्रोसेसर पर चलने वाले प्रोग्राम निर्देश (सॉफ्टवेयर) एडीसी (ADC) से प्राप्त नंबरों पर आवश्यक गणितीय प्रबंध करके डिजिटल फिल्टर को लागू करते हैं। कुछ उच्च प्रदर्शन अनुप्रयोगों में, एक सामान्य प्रयोजन माइक्रोप्रोसेसर के बजाय एक FPGA या ASIC का उपयोग किया जाता है, या फ़िल्टरिंग जैसे कार्यों में तेजी लाने के लिए विशिष्ट समानांतर वास्तुकला के साथ एक विशेष डिजिटल सिग्नल प्रोसेसर (DSP) का उपयोग किया जाता है।[1][2]
डिजिटल फिल्टर अपनी जटिलता के कारण समकक्ष एनालॉग फिल्टर की तुलना में अधिक महंगे हो सकते हैं, लेकिन वे विभिन्न प्रकार की व्यावहारिक डिजाइन बनाते हैं जो कि एनालॉग फिल्टर द्वारा अव्यावहारिक या असंभव हैं। डिजिटल फिल्टर अक्सर बहुत उच्च क्रम में बनाए जा सकते हैं, और वे परिमित आवेग प्रतिक्रिया फिल्टर होते हैं, एवं रैखिक चरण प्रतिक्रिया की अनुमति देता है। जब रीयल-टाइम एनालॉग सिस्टम के संदर्भ में उपयोग किया जाता है, तो संबंधित एनालॉग-टू-डिजिटल और डिजिटल-टू-एनालॉग रूपांतरणों और एंटी-अलियासिंग के कारण डिजिटल फिल्टर में कभी-कभी समस्याग्रस्त विलंबता (इनपुट और प्रतिक्रिया के बीच का अंतर) होता है। ) हो जाती है। फ़िल्टर, या उनके कार्यान्वयन में अन्य देरी के कारण हो सकते हैं
डिजिटल फिल्टर आम हैं और रेडियो, सेल फोन और एवी रिसीवर जैसे इलेक्ट्रॉनिक्स अब दिनचर्या का एक अनिवार्य तत्व हैं।
लक्षण वर्णन
एक अंकीय शोधन (डिजिटल फ़िल्टर) को ट्रांसफर फ़ंक्शन, या समकक्ष, इसके अंतर समीकरण द्वारा वर्णित किया जाता है। एक स्थानांतरण फ़ंक्शन का गणितीय विश्लेषण यह वर्णन कर सकता है कि यह किसी भी संख्या में इनपुट पर कैसे प्रतिक्रिया देगा। जैसे, एक फिल्टर को डिजाइन करने में शामिल समस्या में उपयुक्त विनिर्देश विकसित करना शामिल है, उदाहरण के लिए, एक विशिष्ट इंटरप्टिंग फ़्रीक्वेंसी (कट-ऑफ फ़्रीक्वेंसी) के साथ एक दूसरे क्रम का लो पास फ़िल्टर, और फिर एक ट्रांसफर आउटपुट फ़ंक्शन जो विनिर्देशों को लौटाता एवं पूरा करता है।
एक रैखिक, समय-अपरिवर्तनीय, अंकीय शोधन (डिजिटल फ़िल्टर) के लिए स्थानांतरण फ़ंक्शन को Z-डोमेन में स्थानांतरण फ़ंक्शन के रूप में व्यक्त किया जा सकता है; यदि यह कारण है, तो इसका रूप जो होगा वह निचे दर्शाया गया है:[3]
जहां फ़िल्टर का क्रम N या M से बड़ा है। इस स्थानांतरण फ़ंक्शन की आगे की चर्चा के लिए Z -transform का LCDD समीकरण देखें।
यह पुनरावर्ती फिल्टर का एक रूप है, जो आमतौर पर एक अनंत आवेग प्रतिक्रिया (IIR) व्यवहार की ओर जाता है, लेकिन सभी भाजक को एकरूपता के समान बना दिया जाता है, अर्थात् यदि कोई प्रतिक्रिया नहीं होती है, तो यह एक सीमित आवेग प्रतिक्रिया (FIR) फिल्टर बन जाता है।
विश्लेषण तकनीक
किसी दिए गए डिजिटल फिल्टर के व्यवहार का विश्लेषण करने के लिए विभिन्न प्रकार की गणितीय तकनीकों को नियोजित किया जा सकता है। इन विश्लेषण तकनीकों में से कई को डिजाइन में भी नियोजित किया जा सकता है, और प्रायः एक फ़िल्टर विनिर्देश का आधार बनता है।
आमतौर पर, कोई फ़िल्टर की विशेषता यह गणना करके से होती है कि वे एक साधारण इनपुट जैसे आवेग का जवाब कैसे देंगे। अधिक जटिल संकेतों के लिए फ़िल्टर की प्रतिक्रिया की गणना करने के लिए इस जानकारी का विस्तार किया जा सकता है।
आवेग प्रतिक्रिया
आवेग प्रतिक्रिया, प्रायः निरूपित की जाती है या , इसका माप है कि एक फ़िल्टर क्रोनकर डेल्टा फ़ंक्शन का जवाब कैसे देगा। [4] उदाहरण के लिए, एक अंतर समीकरण को देखते हुए, एक सेट होगा तथा के लिये और मूल्यांकन करें। आवेग प्रतिक्रिया फ़िल्टर के व्यवहार का एक लक्षण वर्णन है।डिजिटल फिल्टर को आमतौर पर दो श्रेणियों में माना जाता है: अनंत आवेग प्रतिक्रिया (IIR) और परिमित आवेग प्रतिक्रिया (एफआईआर)। रैखिक समय-अपरिवर्तनीय एफआईआर फिल्टर के मामले में, आवेग प्रतिक्रिया फिल्टर गुणांक के अनुक्रम के बराबर है, और इस प्रकार:
दूसरी ओर IIR फ़िल्टर पुनरावर्ती हैं, आउटपुट के साथ वर्तमान और पिछले इनपुट दोनों के साथ -साथ पिछले आउटपुट के आधार पर।IIR फ़िल्टर का सामान्य रूप इस प्रकार है:
आवेग प्रतिक्रिया की साजिश रचने से पता चलता है कि एक फ़िल्टर अचानक, क्षणिक गड़बड़ी का उत्तर कैसे देता है। IIR फ़िल्टर सदैव पुनरावर्ती होता है। जबकि एक पुनरावर्ती फ़िल्टर के लिए एक परिमित आवेग प्रतिक्रिया के लिए संभव है, एक गैर-पुनरावर्ती फिल्टर में सदैव एक परिमित आवेग प्रतिक्रिया होती है। उदाहरण: मूविंग एवरेज (MA) फ़िल्टर है, जिसे पुनरावर्ती दोनों को लागू किया जा सकता है[citation needed] और गैर -पुनरावर्ती।
अंतर समीकरण =
असतत-समय प्रणालियों में, डिजिटल फ़िल्टर को अक्सर Z-ट्रांसफ़ॉर्म के माध्यम से स्थानांतरण फ़ंक्शन को रैखिक स्थिर-गुणांक अंतर समीकरण (LCCD) में परिवर्तित करके कार्यान्वित किया जाता है। असतत आवृत्ति-डोमेन स्थानांतरण फ़ंक्शन को दो बहुपदों के अनुपात के रूप में लिखा जाता है। उदाहरण के लिए:
यह विस्तारित है:
और इसी फ़िल्टर कारण बनाने के लिए, अंश और भाजक को उच्चतम क्रम से विभाजित किया जाता है :
हर के गुणांक,, 'फ़ीड-बैकवर्ड' गुणांक हैं और अंश के गुणांक 'फ़ीड-फॉरवर्ड' गुणांक हैं, ।
परिणामी रैखिक अंतर समीकरण है:
या, ऊपर उदाहरण के लिए:
पुनर्व्यवस्थित शब्द:
फिर उलटा Z- ट्रांसफ़ॉर्म लेने से:
और अंत में, के लिए हल करके :
यह समीकरण दिखाता है कि अगले आउटपुट नमूने की गणना कैसे करें, , पिछले आउटपुट के संदर्भ में, , वर्तमान इनपुट, , और पिछले इनपुट, ।इस रूप में किसी इनपुट पर फ़िल्टर को लागू करना एक प्रत्यक्ष रूप I या II (नीचे देखें) प्राप्ति के बराबर है, जो मूल्यांकन के सटीक क्रम के आधार पर है।
उदाहरण के लिए, जैसा कि कंप्यूटर प्रोग्रामर द्वारा कोड में उपरोक्त समीकरण को लागू करने वाले द्वारा उपयोग किया जाता है, इसे निम्नानुसार वर्णित किया जा सकता है:
= आउटपुट, या फ़िल्टर्ड मान
= इनपुट, या आने वाले कच्चे मूल्य
= नमूना संख्या, पुनरावृत्ति संख्या, या समय अवधि संख्या
और इसीलिए:
= वर्तमान फ़िल्टर्ड (आउटपुट) मान
= अंतिम फ़िल्टर्ड (आउटपुट) मान
= 2-टू-लास्ट फ़िल्टर्ड (आउटपुट) मान
= वर्तमान कच्चा इनपुट मूल्य
= अंतिम कच्चा इनपुट मूल्य
= 2-टू-लेस्ट कच्चे इनपुट मूल्य
फ़िल्टर डिजाइन
यद्यपि फ़िल्टर को सरलता से समझा और उसकी गणना की जाती है, लेकिन उनके डिजाइन और कार्यान्वयन की व्यावहारिक चुनौतियां महत्वपूर्ण हैं और बहुत उन्नत शोध का विषय हैं।
डिजिटल फ़िल्टर की दो श्रेणियां हैं: पुनरावर्ती फ़िल्टर और गैर -फ़िल्टर। इन्हें प्रायः अनंत आवेग प्रतिक्रिया (IIR) फिल्टर और परिमित आवेग प्रतिक्रिया (FIR) फ़िल्टर के रूप में संदर्भित किया जाता है।[5]
फ़िल्टर प्रत्यक्षीकरण
एक फ़िल्टर डिज़ाइन किए जाने के बाद, इसे एक सिग्नल फ्लो आरेख विकसित करके महसूस किया जाना चाहिए जो नमूना अनुक्रमों पर संचालन के संदर्भ में फ़िल्टर का वर्णन करता है।
किसी दिए गए ट्रांसफर फ़ंक्शन को कई तरीकों से महसूस किया जा सकता है।विचार करें कि कैसे एक साधारण अभिव्यक्ति जैसे मूल्यांकन किया जा सकता है & ndash;एक भी समकक्ष की गणना कर सकता है ।उसी तरह, सभी अहसासों को एक ही हस्तांतरण फ़ंक्शन के कारक के रूप में देखा जा सकता है, लेकिन अलग -अलग अहसासों में अलग -अलग संख्यात्मक गुण होंगे।विशेष रूप से, कुछ अहसास उनके कार्यान्वयन के लिए आवश्यक संचालन या भंडारण तत्वों की संख्या के संदर्भ में अधिक कुशल हैं, और अन्य लोग बेहतर संख्यात्मक स्थिरता और कम राउंड-ऑफ त्रुटि जैसे लाभ प्रदान करते हैं।कुछ संरचनाएं निश्चित-बिंदु अंकगणित के लिए बेहतर हैं और अन्य फ़्लोटिंग-पॉइंट अंकगणित के लिए बेहतर हो सकते हैं।
प्रत्यक्ष रूप I
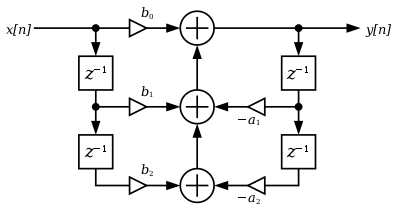
IIR फ़िल्टर प्राप्ति के लिए एक सीधा दृष्टिकोण प्रत्यक्ष रूप I है, जहां अंतर समीकरण का सीधे मूल्यांकन किया जाता है। यह फॉर्म छोटे फिल्टर के लिए व्यावहारिक है, लेकिन जटिल डिजाइनों के लिए अक्षम और अव्यवहारिक (संख्यात्मक रूप से अस्थिर) हो सकता है। [6] सामान्य तौर पर, इस फॉर्म को ऑर्डर एन के फ़िल्टर के लिए 2N विलंब तत्वों (इनपुट और आउटपुट सिग्नल दोनों के लिए) की आवश्यकता होती है।
प्रत्यक्ष रूप II
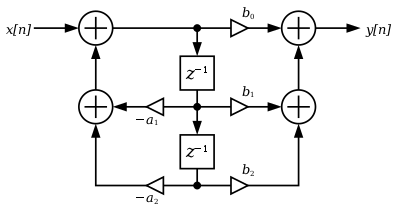
वैकल्पिक प्रत्यक्ष रूप II को केवल N विलंब इकाइयों की आवश्यकता होती है, जहां N फ़िल्टर का क्रम है - संभावित रूप से प्रत्यक्ष रूप I से आधा। यह संरचना प्रत्यक्ष प्रपत्र I के अंश और हर वर्गों के क्रम को उलट कर प्राप्त की जाती है, क्योंकि वे वास्तव में दो रेखीय प्रणालियाँ हैं, और क्रमपरिवर्तन गुण लागू होता है। फिर, कोई यह नोटिस करेगा कि विलंब के दो स्तंभ हैं ( ) जो केंद्र के जाल को टैप करते हैं, और इन्हें जोड़ा जा सकता है क्योंकि वे बेमानी हैं, जैसा कि नीचे दिखाया गया है।
प्रतिकूल परिस्थिति यह है कि प्रत्यक्ष रूप II उच्च Q या अनुनाद के फिल्टर के लिए अंकगणितीय अतिप्रवाह की संभावना को बढ़ाता है। [7] यह दिखाया गया है कि जैसे-जैसे क्यू बढ़ता है, दोनों प्रत्यक्ष रूप टोपोलॉजी का राउंड-ऑफ शोर बिना सीमा के बढ़ता है। [8] इसका कारण यह है कि, अवधारणात्मक रूप से, सिग्नल को पहले एक ऑल-पोल फिल्टर (जो सामान्य रूप से गुंजयमान आवृत्तियों पर लाभ बढ़ाता है) के माध्यम से पारित किया जाता है, उसके परिणाम संतृप्त होने से पहले, फिर एक ऑल-जीरो फिल्टर से गुजरता है (जो अक्सर बहुत कुछ को क्षीण करता है ऑल-पोल आधा बढ़ता है)।
कैस्केड दूसरे क्रम के खंड
एक सामान्य रणनीति यह है कि उच्च-क्रम (2 से अधिक) डिजिटल फ़िल्टर को दूसरे क्रम के "बायक्वाड्राट्रिक" (या "बिक्वाड") सेक्शन [9] ( डिजिटल बाईक्वाड फ़िल्टर देखें) की एक कैस्केड श्रृंखला के रूप में महसूस किया जाए। इस रणनीति का लाभ यह है कि गुणांक सीमा सीमित है। कैस्केडिंग डायरेक्ट फॉर्म II सेक्शन के परिणामस्वरूप ऑर्डर एन के फिल्टर के लिए एन विलंब तत्व होते हैं। कैस्केडिंग डायरेक्ट फॉर्म I सेक्शन का परिणाम N + 2 विलंब तत्वों में होता है, क्योंकि किसी भी सेक्शन के इनपुट के विलंब तत्व (पहले सेक्शन को छोड़कर) पिछले सेक्शन के आउटपुट के विलंब तत्वों के साथ निरर्थक हैं।
अन्य रूप
अन्य रूपों में सम्मिलित हैं:
- प्रत्यक्ष रूप I और II ट्रांसपोज़
- श्रृंखला/कैस्केड लोअर (विशिष्ट दूसरा) ऑर्डर सब्सक्रिप्शन
- समानांतर निचला (विशिष्ट दूसरा) ऑर्डर उपधारा
- निरंतर अंश विस्तार
- जाली और सीढ़ी
- एक, दो और तीन-मल्टीप्ली जाली रूप
- तीन और चार-मल्टीप्ली सामान्यीकृत सीढ़ी रूप
- अरमा संरचनाएं
- राज्य-स्थान संरचनाएं:
- इष्टतम (न्यूनतम शोर अर्थ में): मापदंडों
- ब्लॉक-इष्टतम और खंड-इष्टतम: मापदंडों
- गिवेंस रोटेशन के साथ इनपुट संतुलित: मापदंडों[10]
- युग्मित रूप: गोल्ड रड्रर (सामान्य), राज्य चर (चेम्बरलिन), किंग्सबरी, संशोधित राज्य चर, ज़ोज़र, संशोधित ज़ोल्ज़र
- वेव डिजिटल फिल्टर (WDF)[11]
- अग्रवाल -कैरेस (1AB और 2AB)
- हैरिस -ब्रोकिंग
- एनडी-टीडीएल
- मल्टीवेडबैक
- एनालॉग-प्रेरित रूप जैसे कि सलेन-की और स्टेट वेरिएबल फिल्टर
- सिस्टोलिक सरणियाँ
एनालॉग और डिजिटल फिल्टर की तुलना
डिजिटल फिल्टर घटक गैर-रैखिकताओं के अधीन नहीं हैं जो एनालॉग फिल्टर के डिजाइन को बहुत जटिल करते हैं। एनालॉग फिल्टर में अपूर्ण इलेक्ट्रॉनिक घटक होते हैं, जिनके मान एक सीमा सहनशीलता के लिए निर्दिष्ट होते हैं (उदाहरण के लिए प्रतिरोधी मूल्यों में अक्सर ± 5% की सहनशीलता होती है) और जो समय के साथ तापमान और बहाव के साथ भी बदल सकते हैं। जैसे-जैसे एनालॉग फिल्टर का क्रम बढ़ता है, और इस प्रकार इसकी घटक संख्या बढ़ती है, चर घटक त्रुटियों का प्रभाव बहुत बढ़ जाता है। डिजिटल फिल्टर में, गुणांक मान कंप्यूटर मेमोरी में संग्रहीत होते हैं, जिससे वे अधिक स्थिर और अनुमानित हो जाते हैं। [12]
क्योंकि डिजिटल फिल्टर के गुणांक निश्चित हैं, उनका उपयोग अधिक जटिल और चयनात्मक डिजाइन प्राप्त करने के लिए किया जा सकता है – विशेष रूप से डिजिटल फिल्टर के साथ, कोई कम पासबैंड रिपल, तेज संक्रमण, और उच्च स्टॉपबैंड क्षीणन प्राप्त कर सकता है, जो एनालॉग फिल्टर के साथ व्यावहारिक है। यहां तक कि अगर डिजाइन एनालॉग फिल्टर का उपयोग करके प्राप्त किया जा सकता है, तो समकक्ष डिजिटल फिल्टर को डिजाइन करने की इंजीनियरिंग लागत बहुत कम होगी। इसके अलावा, एक अनुकूली फ़िल्टर या उपयोगकर्ता-नियंत्रित पैरामीट्रिक फ़िल्टर बनाने के लिए कोई भी डिजिटल फ़िल्टर के गुणांक को आसानी से संशोधित कर सकता है। हालांकि ये तकनीक एक एनालॉग फिल्टर में संभव हैं, फिर भी वे काफी अधिक कठिन हैं।
हालांकि, डिजिटल फिल्टर का उपयोग परिमित आवेग प्रतिक्रिया फिल्टर के डिजाइन में किया जा सकता है। समतुल्य एनालॉग फिल्टर अक्सर अधिक जटिल होते हैं, क्योंकि इनमें विलंब तत्वों की आवश्यकता होती है।
डिजिटल फिल्टर एनालॉग सर्किटरी पर कम भरोसा करते हैं, संभावित रूप से बेहतर सिग्नल-टू-शोर अनुपात की अनुमति देते हैं। एक डिजिटल फ़िल्टर एनालॉग कम पास फ़िल्टरिंग, डिजिटल रूपांतरण के अनुरूप, डिजिटल से एनालॉग रूपांतरण के दौरान सिग्नल में शोर पेश करेगा और क्वांटिज़ेशन के कारण डिजिटल शोर पेश कर सकता है। एनालॉग फिल्टर के साथ, प्रत्येक घटक थर्मल शोर (जैसे जॉनसन शोर ) का स्रोत है, इसलिए जैसे-जैसे फ़िल्टर जटिलता बढ़ती है, वैसे ही रव (नॉइज़0 भी होता है।
हालांकि, डिजिटल फिल्टर सिस्टम में उच्च मौलिक विलंबता का परिचय देते हैं। एनालॉग फ़िल्टर में, विलंबता अक्सर नगण्य होती है; कड़ाई से बोलते हुए यह एक विद्युत संकेत के लिए फिल्टर सर्किट के माध्यम से प्रचारित करने का समय है। डिजिटल सिस्टम में, विलंबता को डिजिटल सिग्नल पथ में विलंब तत्वों द्वारा, और एनालॉग-टू-डिजिटल और डिजिटल-से-एनालॉग कन्वर्टर्स द्वारा पेश किया जाता है जो सिस्टम को एनालॉग सिग्नल को संसाधित करने में सक्षम बनाता है।
बहुत ही साधारण मामलों में, एनालॉग फ़िल्टर का उपयोग करना अधिक लागत प्रभावी होता है। डिजिटल फ़िल्टर को पेश करने के लिए काफी ओवरहेड सर्किटरी की आवश्यकता होती है, जैसा कि पहले चर्चा की गई थी, जिसमें दो लो पास एनालॉग फिल्टर सम्मिलित हैं।
एनालॉग फिल्टर के लिए एक और तर्क कम बिजली की खपत है। एनालॉग फिल्टर के लिए काफी कम शक्ति की आवश्यकता होती है और इसलिए बिजली की आवश्यकता होने पर एकमात्र समाधान होता है।
पीसीबी (PCB) पर विद्युत सर्किट बनाते समय डिजिटल समाधान का उपयोग करना आम तौर पर आसान होता है, क्योंकि प्रसंस्करण इकाइयां वर्षों से अत्यधिक अनुकूलित होती हैं। एनालॉग घटकों के साथ समान सर्किट बनाने से असतत घटकों का उपयोग करते समय बहुत अधिक स्थान लगेगा। दो विकल्प FPAAs [13] और ASICs हैं, लेकिन वे कम मात्रा में महंगे हैं।
डिजिटल फिल्टर के प्रकार
फिल्टर को चिह्नित करने के विभिन्न तरीके हैं; उदाहरण के लिए:
- एक रैखिक फ़िल्टर इनपुट नमूनों का एक रैखिक परिवर्तन है; अन्य फिल्टर अरेखीय हैं। रैखिक फिल्टर सुपरपोजिशन सिद्धांत को संतुष्ट करते हैं, अर्थात यदि कोई इनपुट विभिन्न संकेतों का भारित रैखिक संयोजन है, तो आउटपुट संबंधित आउटपुट संकेतों का समान रूप से भारित रैखिक संयोजन है।
- एक कारण फ़िल्टर इनपुट या आउटपुट संकेतों के केवल पिछले नमूनों का उपयोग करता है; जबकि एक गैर-कारण फ़िल्टर भविष्य के इनपुट नमूनों का उपयोग करता है। एक गैर-कारण फ़िल्टर को आमतौर पर इसमें देरी जोड़कर एक कारण फ़िल्टर में बदला जा सकता है।
- समय-अपरिवर्तनीय फ़िल्टर में समय के साथ निरंतर गुण होते हैं; अन्य फ़िल्टर जैसे अनुकूली फ़िल्टर समय के साथ बदलते हैं।
- एक स्थिर फ़िल्टर एक आउटपुट उत्पन्न करता है जो समय के साथ स्थिर मान में परिवर्तित हो जाता है, या एक सीमित अंतराल के भीतर सीमित रहता है। एक अस्थिर फ़िल्टर एक आउटपुट उत्पन्न कर सकता है जो बिना सीमा के, बाउंडेड या शून्य इनपुट के साथ बढ़ता है।
- एक परिमित आवेग प्रतिक्रिया (एफआईआर) फ़िल्टर केवल इनपुट सिग्नल का उपयोग करता है, जबकि एक अनंत आवेग प्रतिक्रिया (आईआईआर) फ़िल्टर इनपुट सिग्नल और आउटपुट सिग्नल के पिछले नमूने दोनों का उपयोग करता है। एफआईआर फिल्टर हमेशा स्थिर होते हैं, जबकि आईआईआर फिल्टर अस्थिर हो सकते हैं।
एक फिल्टर को एक ब्लॉक आरेख द्वारा दर्शाया जा सकता है, जिसका उपयोग तब हार्डवेयर निर्देशों के साथ फिल्टर को लागू करने के लिए एक नमूना प्रसंस्करण एल्गोरिथ्म प्राप्त करने के लिए किया जा सकता है। एक फिल्टर को अंतर समीकरण, शून्य और ध्रुवों का संग्रह या एक आवेग प्रतिक्रिया या चरण प्रतिक्रिया के रूप में भी वर्णित किया जा सकता है।
कुछ डिजिटल फिल्टर तेजी से फूरियर ट्रांसफॉर्म पर आधारित होते हैं, एक गणितीय एल्गोरिदम जो एक सिग्नल के आवृत्ति स्पेक्ट्रम को जल्दी से निकालता है, जिससे संशोधित स्पेक्ट्रम को वापस परिवर्तित करने से पहले स्पेक्ट्रम में हेरफेर किया जा सकता है (जैसे कि बहुत उच्च ऑर्डर बैंड-पास फिल्टर बनाना)। एक उलटा एफएफटी ऑपरेशन के साथ एक समय-श्रृंखला संकेत। ये फ़िल्टर O(n log n) कम्प्यूटेशनल लागत देते हैं जबकि पारंपरिक डिजिटल फ़िल्टर O(n 2 ) होते हैं।
डिजिटल फिल्टर का दूसरा रूप राज्य-अंतरिक्ष (स्टेट स्पेस) मॉडल का है। एक अच्छी तरह से इस्तेमाल किया जाने वाला राज्य-अंतरिक्ष फ़िल्टर 1960 में रुडोल्फ कलमैन द्वारा प्रकाशित कलमन फ़िल्टर है।
पारंपरिक रैखिक फिल्टर आमतौर पर क्षीणन पर आधारित होते हैं। वैकल्पिक रूप से नॉनलाइनियर फिल्टर को ऊर्जा हस्तांतरण फिल्टर सहित डिजाइन किया जा सकता है, [14] जो उपयोगकर्ता को एक डिजाइन तरीके से ऊर्जा को स्थानांतरित करने की अनुमति देता है ताकि अवांछित शोर या प्रभाव को नए आवृत्ति बैंड में या तो कम या उच्च आवृत्ति में स्थानांतरित किया जा सके, जो एक सीमा में फैला हो आवृत्तियों, विभाजन, या केंद्रित। एनर्जी ट्रांसफर फिल्टर पारंपरिक फिल्टर डिजाइनों के पूरक हैं और फिल्टर डिजाइन में स्वतंत्रता के कई और डिग्री पेश करते हैं। डिजिटल ऊर्जा हस्तांतरण फिल्टर डिजाइन करने और गैर-रेखीय गतिशीलता को लागू करने और शोषण करने के लिए अपेक्षाकृत आसान हैं।
यह भी देखें
- बेसेल फिल्टर
- बिलिनियर ट्रांसफॉर्म
- बटरवर्थ फ़िल्टर
- चेबीशेव फ़िल्टर
- इलेक्ट्रॉनिक फिल्टर
- अण्डाकार फ़िल्टर (कौअर फ़िल्टर)
- फ़िल्टर डिज़ाइन
- हाई-पास फिल्टर, लो-पास फिल्टर
- अनंत आवेग प्रतिक्रिया, परिमित आवेग प्रतिक्रिया
- लिंकविट्ज़-रिले फ़िल्टर
- मिलान फ़िल्टर
- नमूना (संकेत)
- सविट्ज़की-गोले फ़िल्टर
- द्वि-आयामी फ़िल्टर
संदर्भ
- ↑ Lyakhov, Pavel; Valueva, Maria; Valuev, Georgii; Nagornov, Nikolai (2020). "High-Performance Digital Filtering on Truncated Multiply-Accumulate Units in the Residue Number System". IEEE Access. 8: 209181–209190. doi:10.1109/ACCESS.2020.3038496. ISSN 2169-3536.
- ↑ Priya, P; Ashok, S (April 2018). "IIR Digital Filter Design Using Xilinx System Generator for FPGA Implementation". 2018 International Conference on Communication and Signal Processing (ICCSP): 0054–0057. doi:10.1109/ICCSP.2018.8524520. ISBN 978-1-5386-3521-6. S2CID 53284942.
- ↑ Smith, Julius O. "Introduction to digital filters". DSPRelated.com. The Related Media Group. Retrieved 13 July 2020.
- ↑ "Lab.4&5. Introduction to FIR Filters" (PDF). Jordan University of Science and Technology-Faculty of Engineering. Retrieved 13 July 2020.
- ↑ A. Antoniou, Digital Filters: Analysis, Design, and Applications, New York, NY: McGraw-Hill, 1993., chapter 1
- ↑ J. O. Smith III, Direct Form I
- ↑ J. O. Smith III, Direct Form II
- ↑ L. B. Jackson, "On the Interaction of Roundoff Noise and Dynamic Range in Digital Filters," Bell Sys. Tech. J., vol. 49 (1970 Feb.), reprinted in Digital Signal Process, L. R. Rabiner and C. M. Rader, Eds. (IEEE Press, New York, 1972).
- ↑ J. O. Smith III, Series Second Order Sections
- ↑ Li, Gang; Limin Meng; Zhijiang Xu; Jingyu Hua (July 2010). "A novel digital filter structure with minimum roundoff noise". Digital Signal Processing. 20 (4): 1000–1009. doi:10.1016/j.dsp.2009.10.018.
- ↑ Fettweis, Alfred (Feb 1986). "Wave digital filters: Theory and practice". Proceedings of the IEEE. 74 (2): 270–327. doi:10.1109/proc.1986.13458. S2CID 46094699.
- ↑ "Match #1: Analog vs. Digital Filters".
- ↑ Bains, Sunny (July 2008). "Analog's answer to FPGA opens field to masses". EETimes.
- ↑ Billings S.A. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains". Wiley, 2013
अग्रिम पठन
- J. O. Smith III, Introduction to Digital Filters with Audio Applications, Center for Computer Research in Music and Acoustics (CCRMA), Stanford University, September 2007 Edition.
- Mitra, S. K. (1998). Digital Signal Processing: A Computer-Based Approach. New York, NY: McGraw-Hill.
- Oppenheim, A. V.; Schafer, R. W. (1999). Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall. ISBN 9780137549207.
- Kaiser, J .F. (1974). Nonrecursive Digital Filter Design Using the Io-sinh Window Function. Proc. 1974 IEEE Int. Symp. Circuit Theory. pp. 20–23.
- Bergen, S. W. A.; Antoniou, A. (2005). "Design of Nonrecursive Digital Filters Using the Ultraspherical Window Function". EURASIP Journal on Applied Signal Processing. 2005 (12): 1910–1922. Bibcode:2005EJASP2005...44B. doi:10.1155/ASP.2005.1910.
- Parks, T. W.; McClellan, J. H. (March 1972). "Chebyshev Approximation for Nonrecursive Digital Filters with Linear Phase". IEEE Trans. Circuit Theory. CT-19 (2): 189–194. doi:10.1109/TCT.1972.1083419.
- Rabiner, L. R.; McClellan, J. H.; Parks, T. W. (April 1975). "FIR Digital Filter Design Techniques Using Weighted Chebyshev Approximation". Proc. IEEE. 63 (4): 595–610. Bibcode:1975IEEEP..63..595R. doi:10.1109/PROC.1975.9794. S2CID 12579115.
- Deczky, A. G. (October 1972). "Synthesis of Recursive Digital Filters Using the Minimum p-Error Criterion". IEEE Trans. Audio Electroacoustics. AU-20 (4): 257–263. doi:10.1109/TAU.1972.1162392.
]
[[Category: सिग्नल प्रोसेसिंग फ़िल्टर |*]