लाप्लासियन आव्यूह: Difference between revisions
No edit summary |
(→संदर्भ) |
||
| (5 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Matrix representation of a graph}} | {{Short description|Matrix representation of a graph}} | ||
[[ग्राफ सिद्धांत|आरेख सिद्धांत]] के गणित क्षेत्र में, '''[[लाप्लासियन]] आव्यूह''', जिसे विविक्त लाप्लेस संक्रियक '''आरेख लाप्लासियन, [[प्रवेश मैट्रिक्स|प्रवेश आव्यूह]]''', '''किरचॉफ आव्यूह''' या विविक्त लाप्लास संक्रियक भी कहा जाता है, '''आरेख (असतत गणित) का [[मैट्रिक्स (गणित)|आव्यूह (गणित)]]''' प्रतिनिधित्व है। [[पियरे-साइमन लाप्लास]] के नाम पर, आरेख लाप्लासियन आव्यूह को [[परिमित अंतर विधि]] द्वारा प्राप्त ऋणात्मक निरंतर लाप्लासियन का अनुमान लगाने वाले आरेख पर ऋणात्मक [[असतत लाप्लास ऑपरेटर|असतत लाप्लास संक्रियक]] के आव्यूह रूप के रूप में देखा जा सकता है। | [[ग्राफ सिद्धांत|आरेख सिद्धांत]] के गणित क्षेत्र में, '''[[लाप्लासियन]] आव्यूह''', जिसे विविक्त लाप्लेस संक्रियक '''आरेख लाप्लासियन, [[प्रवेश मैट्रिक्स|प्रवेश आव्यूह]]''', '''किरचॉफ आव्यूह''' या विविक्त लाप्लास संक्रियक भी कहा जाता है, '''आरेख (असतत गणित) का [[मैट्रिक्स (गणित)|आव्यूह (गणित)]]''' प्रतिनिधित्व है। [[पियरे-साइमन लाप्लास]] के नाम पर, आरेख लाप्लासियन आव्यूह को [[परिमित अंतर विधि]] द्वारा प्राप्त ऋणात्मक निरंतर लाप्लासियन का अनुमान लगाने वाले आरेख पर ऋणात्मक [[असतत लाप्लास ऑपरेटर|असतत लाप्लास संक्रियक]] के आव्यूह रूप के रूप में देखा जा सकता है। | ||
लाप्लासियन आव्यूह आरेख़ के कई उपयोगी गुणों से संबंधित है। किरचॉफ के प्रमेय के साथ, इसका उपयोग किसी दिए गए आरेख़ के लिए विस्तरित ट्री (गणित) की संख्या की गणना करने के लिए किया जा सकता है। आरेख़ के कट (आरेख़ सिद्धांत) सबसे कम कट का अनुमान [[फिडलर वेक्टर|फिडलर सदिश]] के माध्यम से लगाया जा सकता है - आरेख़ लाप्लासियन के दूसरे सबसे छोटे आइगेनमान के अनुरूप आइगेनसदिश - जैसा कि चीगर स्थिरांक (आरेख़ सिद्धांत) चीगर असमानताओं द्वारा स्थापित किया गया है। लाप्लासियन आव्यूह के एक आव्यूह का आइगेन अपघटन अरैखिक | इस प्रकार से लाप्लासियन आव्यूह आरेख़ के कई उपयोगी गुणों से संबंधित है। किरचॉफ के प्रमेय के साथ, इसका उपयोग किसी दिए गए आरेख़ के लिए विस्तरित ट्री (गणित) की संख्या की गणना करने के लिए किया जा सकता है। आरेख़ के कट (आरेख़ सिद्धांत) सबसे कम कट का अनुमान [[फिडलर वेक्टर|फिडलर सदिश]] के माध्यम से लगाया जा सकता है - आरेख़ लाप्लासियन के दूसरे सबसे छोटे आइगेनमान के अनुरूप आइगेनसदिश - जैसा कि चीगर स्थिरांक (आरेख़ सिद्धांत) चीगर असमानताओं द्वारा स्थापित किया गया है। लाप्लासियन आव्यूह के एक आव्यूह का आइगेन अपघटन अरैखिक विमीयता में अपघटन लाप्लासियन आइगेन प्रतिचित्र का निर्माण करने की अनुमति देता है जो कई [[ यंत्र अधिगम |यंत्र अधिगम]] अनुप्रयोगों में दिखाई देते हैं और [[ग्राफ ड्राइंग|आरेख रेखाचित्र]] में [[वर्णक्रमीय लेआउट|वर्णक्रमीय लेबाह्य]] निर्धारित करते हैं। इस प्रकार से आरेख-आधारित [[ संकेत आगे बढ़ाना |संकेत प्रक्रम]] [[असतत फूरियर रूपांतरण]] पर आधारित है जो संकेत के अनुरूप आरेख के लाप्लासियन आव्यूह के आइगेनसदिशों के लिए [[जटिल संख्या|मिश्रित संख्या]] ज्या तरंगों के मानक आधार को प्रतिस्थापित करके पारंपरिक असतत फूरियर परिवर्तन का विस्तार करता है। | ||
लाप्लासियन आव्यूह साधारण आरेख के लिए परिभाषित करना सबसे सरल है, परन्तु ग्लोसरी ऑफ आरेख सिद्धांत वेटेड आरेख के लिए अनुप्रयोगों में अधिक सामान्य है, अर्थात, इसके किनारों पर भार के साथ - आरेख आसन्न आव्यूह की प्रविष्टियां। [[वर्णक्रमीय ग्राफ सिद्धांत|वर्णक्रमीय आरेख सिद्धांत]] आरेख के गुणों को वर्णक्रम से जोड़ता है, अर्थात, आइगेनमान, और आरेख से जुड़े आव्यूह के आइगेनसदिश, जैसे कि इसकी आसन्न आव्यूह या लाप्लासियन आव्यूह है। असंतुलित भार आव्यूह वर्णक्रम को अवांछित रूप से प्रभावित कर सकता है, जिससे सामान्यीकरण की आवश्यकता होती है - आव्यूह प्रविष्टियों का स्तम्भ/पंक्ति सोपानी - जिसके परिणामस्वरूप सामान्यीकृत आसन्नता और लाप्लासियन आव्यूह होते हैं। | लाप्लासियन आव्यूह साधारण आरेख के लिए परिभाषित करना सबसे सरल है, परन्तु ग्लोसरी ऑफ आरेख सिद्धांत वेटेड आरेख के लिए अनुप्रयोगों में अधिक सामान्य है, अर्थात, इसके किनारों पर भार के साथ - आरेख आसन्न आव्यूह की प्रविष्टियां। अतः [[वर्णक्रमीय ग्राफ सिद्धांत|वर्णक्रमीय आरेख सिद्धांत]] आरेख के गुणों को वर्णक्रम से जोड़ता है, अर्थात, आइगेनमान, और आरेख से जुड़े आव्यूह के आइगेनसदिश, जैसे कि इसकी आसन्न आव्यूह या लाप्लासियन आव्यूह है। असंतुलित भार आव्यूह वर्णक्रम को अवांछित रूप से प्रभावित कर सकता है, जिससे सामान्यीकरण की आवश्यकता होती है - आव्यूह प्रविष्टियों का स्तम्भ/पंक्ति सोपानी - जिसके परिणामस्वरूप सामान्यीकृत आसन्नता और लाप्लासियन आव्यूह होते हैं। | ||
==सरल आरेख़ के लिए परिभाषाएँ== | ==सरल आरेख़ के लिए परिभाषाएँ== | ||
=== लाप्लासियन आव्यूह === | === लाप्लासियन आव्यूह === | ||
<math>n</math> शीर्ष <math>v_1, \ldots, v_n</math> के साथ एक सरल आरेख <math>G</math> को देखते हुए, इसके लाप्लासियन आव्यूह <math display="inline">L_{n \times n}</math> को अवयव-वार<ref name="Fan Chung">{{cite book | इस प्रकार से <math>n</math> शीर्ष <math>v_1, \ldots, v_n</math> के साथ एक सरल आरेख <math>G</math> को देखते हुए, इसके लाप्लासियन आव्यूह <math display="inline">L_{n \times n}</math> को अवयव-वार<ref name="Fan Chung">{{cite book | ||
| last = Chung | | last = Chung | ||
| first = Fan | | first = Fan | ||
| Line 30: | Line 29: | ||
द्वारा समकक्ष रूप से परिभाषित किया गया है, जहां D [[डिग्री मैट्रिक्स|घात आव्यूह]] है और A आरेख़ का आसन्न आव्यूह है। चूँकि <math display="inline">G</math> सरल आरेख है, <math display="inline">A</math> में मात्र 1s या 0s हैं और इसके विकर्ण अवयव सभी 0s हैं। | द्वारा समकक्ष रूप से परिभाषित किया गया है, जहां D [[डिग्री मैट्रिक्स|घात आव्यूह]] है और A आरेख़ का आसन्न आव्यूह है। चूँकि <math display="inline">G</math> सरल आरेख है, <math display="inline">A</math> में मात्र 1s या 0s हैं और इसके विकर्ण अवयव सभी 0s हैं। | ||
यहां लेबल, अप्रत्यक्ष आरेख़ और उसके लाप्लासियन आव्यूह का सरल उदाहरण दिया गया है। | इस प्रकार से यहां लेबल, अप्रत्यक्ष आरेख़ और उसके लाप्लासियन आव्यूह का सरल उदाहरण दिया गया है। | ||
{|class="wikitable" | {|class="wikitable" | ||
| Line 66: | Line 65: | ||
हम अप्रत्यक्ष आरेख़ के लिए देखते हैं कि आसन्न आव्यूह और लाप्लासियन आव्यूह दोनों सममित हैं, और लाप्लासियन आव्यूह की पंक्ति और स्तंभ-योग सभी शून्य हैं। | हम अप्रत्यक्ष आरेख़ के लिए देखते हैं कि आसन्न आव्यूह और लाप्लासियन आव्यूह दोनों सममित हैं, और लाप्लासियन आव्यूह की पंक्ति और स्तंभ-योग सभी शून्य हैं। | ||
[[निर्देशित ग्राफ|निर्देशित आरेख]]के लिए, या तो घात (आरेख़ सिद्धांत) का उपयोग किया जा सकता है, जो कि अनुप्रयोग पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरण में है: | इस प्रकार से [[निर्देशित ग्राफ|निर्देशित आरेख]]के लिए, या तो घात (आरेख़ सिद्धांत) का उपयोग किया जा सकता है, जो कि अनुप्रयोग पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरण में है: | ||
{|class="wikitable" | {|class="wikitable" | ||
!लेबल आव्यूह | !लेबल आव्यूह | ||
| Line 105: | Line 104: | ||
=== घटना आव्यूह के माध्यम से सममित लाप्लासियन === | === घटना आव्यूह के माध्यम से सममित लाप्लासियन === | ||
शीर्ष v और किनारे e के लिए अवयव B<sub>''ve''</sub> के साथ <math display="inline">|v| \times |e|</math> [[घटना मैट्रिक्स|घटना आव्यूह]] B (शीर्ष <math display="inline">v_i</math> और <math display="inline">v_j</math> को , i > j से जोड़ता है) को | इस प्रकार से शीर्ष v और किनारे e के लिए अवयव B<sub>''ve''</sub> के साथ <math display="inline">|v| \times |e|</math> [[घटना मैट्रिक्स|घटना आव्यूह]] B (शीर्ष <math display="inline">v_i</math> और <math display="inline">v_j</math> को, i > j से जोड़ता है) को | ||
:<math>B_{ve} = \left\{\begin{array}{rl} | :<math>B_{ve} = \left\{\begin{array}{rl} | ||
1, & \text{if } v = v_i\\ | 1, & \text{if } v = v_i\\ | ||
| Line 134: | Line 133: | ||
\end{array}\right)</math> | \end{array}\right)</math> | ||
|} | |} | ||
एक वैकल्पिक गुणनफल <math>B^\textsf{T}B</math> तथाकथित <math display="inline">|e| \times |e|</math> शीर्ष-आधारित लाप्लासियन को परिभाषित करता है , जो मूल रूप से उपयोग किए जाने वाले शीर्ष-आधारित लाप्लासियन आव्यूह L के विपरीत है। | एक वैकल्पिक गुणनफल <math>B^\textsf{T}B</math> तथाकथित <math display="inline">|e| \times |e|</math> शीर्ष-आधारित लाप्लासियन को परिभाषित करता है, जो मूल रूप से उपयोग किए जाने वाले शीर्ष-आधारित लाप्लासियन आव्यूह L के विपरीत है। | ||
===निर्देशित आरेख़ के लिए सममित लाप्लासियन=== | ===निर्देशित आरेख़ के लिए सममित लाप्लासियन=== | ||
एक निर्देशित आरेख का लाप्लासियन आव्यूह परिभाषा के अनुसार सामान्यतः गैर-सममित होता है, जबकि, उदाहरण के लिए, पारंपरिक [[वर्णक्रमीय क्लस्टरिंग]] मुख्य रूप से सममित आसन्नता और लाप्लासियन आव्यूह के साथ अप्रत्यक्ष आरेख के लिए विकसित की जाती है। समरूपता की आवश्यकता वाली तकनीकों को लागू करने के लिए तुच्छ दृष्टिकोण मूल निर्देशित आरेख को अप्रत्यक्ष आरेख में बदलना और बाद के लिए लाप्लासियन आव्यूह का निर्माण करना है। | इस प्रकार से एक निर्देशित आरेख का लाप्लासियन आव्यूह परिभाषा के अनुसार सामान्यतः गैर-सममित होता है, जबकि, इस प्रकार से उदाहरण के लिए, पारंपरिक [[वर्णक्रमीय क्लस्टरिंग]] मुख्य रूप से सममित आसन्नता और लाप्लासियन आव्यूह के साथ अप्रत्यक्ष आरेख के लिए विकसित की जाती है। अतः समरूपता की आवश्यकता वाली तकनीकों को लागू करने के लिए तुच्छ दृष्टिकोण मूल निर्देशित आरेख को अप्रत्यक्ष आरेख में बदलना और बाद के लिए लाप्लासियन आव्यूह का निर्माण करना है। | ||
आव्यूह संकेतन में, अप्रत्यक्ष आरेख़ के आसन्न आव्यूह को, उदाहरण के लिए, मूल निर्देशित आरेख़ के आसन्न आव्यूह <math>A</math> के OR गेट के रूप में परिभाषित किया जा सकता है और इसका आव्यूह <math>A^T</math> का परिवर्त है, जहां <math>A</math> की शून्य और एक प्रविष्टियाँ हैं मानों को संख्यात्मक के अतिरिक्त तार्किक माना जाए, जैसा कि निम्नलिखित उदाहरण में है: | आव्यूह संकेतन में, अप्रत्यक्ष आरेख़ के आसन्न आव्यूह को, इस प्रकार से उदाहरण के लिए, मूल निर्देशित आरेख़ के आसन्न आव्यूह <math>A</math> के OR गेट के रूप में परिभाषित किया जा सकता है और इसका आव्यूह <math>A^T</math> का परिवर्त है, जहां <math>A</math> की शून्य और एक प्रविष्टियाँ हैं मानों को संख्यात्मक के अतिरिक्त तार्किक माना जाए, जैसा कि निम्नलिखित उदाहरण में है: | ||
{| class="wikitable" | {| class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 163: | Line 162: | ||
=== लाप्लासियन आव्यूह सामान्यीकरण === | === लाप्लासियन आव्यूह सामान्यीकरण === | ||
बड़ी घात वाला शीर्ष, जिसे भारी नोड भी कहा जाता है, के परिणामस्वरूप आव्यूह गुणों पर प्रभावी होने वाले लाप्लासियन आव्यूह में बडे विकर्ण की प्रविष्टि होती है। सामान्यीकरण का उद्देश्य लाप्लासियन आव्यूह की प्रविष्टियों को शीर्ष घात द्वारा विभाजित करके ऐसे शीर्षों के प्रभाव को अन्य शीर्षों के प्रभाव के बराबर बनाना है। शून्य से विभाजन से बचने के लिए, शून्य घात वाले पृथक शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है। | बड़ी घात वाला शीर्ष, जिसे भारी नोड भी कहा जाता है, के परिणामस्वरूप आव्यूह गुणों पर प्रभावी होने वाले लाप्लासियन आव्यूह में बडे विकर्ण की प्रविष्टि होती है। इस प्रकार से सामान्यीकरण का उद्देश्य लाप्लासियन आव्यूह की प्रविष्टियों को शीर्ष घात द्वारा विभाजित करके ऐसे शीर्षों के प्रभाव को अन्य शीर्षों के प्रभाव के बराबर बनाना है। शून्य से विभाजन से बचने के लिए, शून्य घात वाले पृथक शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है। | ||
==== सममित रूप से सामान्यीकृत लाप्लासियन ==== | ==== सममित रूप से सामान्यीकृत लाप्लासियन ==== | ||
सममित रूप से सामान्यीकृत लाप्लासियन आव्यूह को इस प्रकार परिभाषित किया गया है:<ref name="Fan Chung" /> | इस प्रकार से सममित रूप से सामान्यीकृत लाप्लासियन आव्यूह को इस प्रकार परिभाषित किया गया है:<ref name="Fan Chung" /> | ||
: <math>L^\text{sym} := (D^+)^{1/2} L (D^+)^{1/2} = I - (D^+)^{1/2} A (D^+)^{1/2},</math> | : <math>L^\text{sym} := (D^+)^{1/2} L (D^+)^{1/2} = I - (D^+)^{1/2} A (D^+)^{1/2},</math> | ||
| Line 179: | Line 178: | ||
0 & \mbox{otherwise} | 0 & \mbox{otherwise} | ||
\end{cases}</math> द्वारा दिए गए हैं। | \end{cases}</math> द्वारा दिए गए हैं। | ||
सममित रूप से सामान्यीकृत लाप्लासियन आव्यूह सममित है यदि और मात्र यदि आसन्न आव्यूह सममित है। | अतः सममित रूप से सामान्यीकृत लाप्लासियन आव्यूह सममित है यदि और मात्र यदि आसन्न आव्यूह सममित है। | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 201: | Line 200: | ||
\end{array}\right)</math> | \end{array}\right)</math> | ||
|} | |} | ||
निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी भी घात (आरेख़ सिद्धांत) का उपयोग सामान्यीकरण के लिए किया जा सकता है: | इस प्रकार से निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी भी घात (आरेख़ सिद्धांत) का उपयोग सामान्यीकरण के लिए किया जा सकता है: | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 238: | Line 237: | ||
==== बाएँ (यादृच्छिक-चाल) और दाएँ सामान्यीकृत लाप्लासियन ==== | ==== बाएँ (यादृच्छिक-चाल) और दाएँ सामान्यीकृत लाप्लासियन ==== | ||
बाएं (यादृच्छिक-चाल) सामान्यीकृत लाप्लासियन आव्यूह को इस प्रकार परिभाषित किया गया है: | इस प्रकार से बाएं (यादृच्छिक-चाल) सामान्यीकृत लाप्लासियन आव्यूह को इस प्रकार परिभाषित किया गया है: | ||
: <math>L^\text{rw} := D^+L = I - D^+A,</math> | : <math>L^\text{rw} := D^+L = I - D^+A,</math> | ||
जहाँ <math>D^+</math> मूर-पेनरोज़ व्युत्क्रम है। <math display="inline">L^\text{rw}</math> के अवयव | जहाँ <math>D^+</math> मूर-पेनरोज़ व्युत्क्रम है। <math display="inline">L^\text{rw}</math> के अवयव | ||
| Line 246: | Line 245: | ||
0 & \mbox{otherwise} | 0 & \mbox{otherwise} | ||
\end{cases}</math> द्वारा दिये गये हैं। | \end{cases}</math> द्वारा दिये गये हैं। | ||
इसी प्रकार, दाएं सामान्यीकृत लाप्लासियन आव्यूह को | अतः इसी प्रकार, दाएं सामान्यीकृत लाप्लासियन आव्यूह को | ||
: <math>L D^+ = I - A D^+</math> के रूप में परिभाषित किया गया है। | : <math>L D^+ = I - A D^+</math> के रूप में परिभाषित किया गया है। | ||
यदि सभी पृथक शीर्षों के तुच्छ स्थितियों को छोड़कर, आसन्न आव्यूह सममित है, तो बाएँ या दाएँ सामान्यीकृत लाप्लासियन आव्यूह सममित नहीं है। उदाहरण के लिए, | यदि सभी पृथक शीर्षों के तुच्छ स्थितियों को छोड़कर, आसन्न आव्यूह सममित है, तो बाएँ या दाएँ सामान्यीकृत लाप्लासियन आव्यूह सममित नहीं है। इस प्रकार से उदाहरण के लिए, | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 279: | Line 278: | ||
उदाहरण यह भी दर्शाता है कि यदि <math>G</math> में कोई पृथक शीर्ष नहीं है, तो <math>D^+A</math> दाएं [[स्टोकेस्टिक मैट्रिक्स|प्रसंभाव्य आव्यूह]] और इसलिए यह एक यादृच्छिक चाल का आव्यूह है, ताकि बाएं सामान्यीकृत लाप्लासियन <math>L^\text{rw} := D^+L = I - D^+A</math> में प्रत्येक पंक्ति का योग शून्य हो। इस प्रकार हम कभी-कभी वैकल्पिक रूप से <math>L^\text{rw}</math> को यादृच्छिक-चाल सामान्यीकृत लाप्लासियन कहते हैं। कम असामान्य रूप से उपयोग किए जाने वाले दाएं सामान्यीकृत लाप्लासियन <math>L D^+ = I - A D^+</math> में प्रत्येक स्तम्भ का योग शून्य होता है क्योंकि <math>A D^+</math> को प्रसंभाव्य छोड़ दिया जाता है। | उदाहरण यह भी दर्शाता है कि यदि <math>G</math> में कोई पृथक शीर्ष नहीं है, तो <math>D^+A</math> दाएं [[स्टोकेस्टिक मैट्रिक्स|प्रसंभाव्य आव्यूह]] और इसलिए यह एक यादृच्छिक चाल का आव्यूह है, ताकि बाएं सामान्यीकृत लाप्लासियन <math>L^\text{rw} := D^+L = I - D^+A</math> में प्रत्येक पंक्ति का योग शून्य हो। इस प्रकार हम कभी-कभी वैकल्पिक रूप से <math>L^\text{rw}</math> को यादृच्छिक-चाल सामान्यीकृत लाप्लासियन कहते हैं। कम असामान्य रूप से उपयोग किए जाने वाले दाएं सामान्यीकृत लाप्लासियन <math>L D^+ = I - A D^+</math> में प्रत्येक स्तम्भ का योग शून्य होता है क्योंकि <math>A D^+</math> को प्रसंभाव्य छोड़ दिया जाता है। | ||
निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी को सामान्यीकरण के लिए घात (आरेख़ सिद्धांत) चुनने की भी आवश्यकता होती है: | इस प्रकार से निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी को सामान्यीकरण के लिए घात (आरेख़ सिद्धांत) चुनने की भी आवश्यकता होती है: | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 313: | Line 312: | ||
\end{array}\right)</math> | \end{array}\right)</math> | ||
|} | |} | ||
पंक्ति-योग सभी 0 के साथ बाएं बाह्य-घात सामान्यीकृत लाप्लासियन दाएं प्रसंभाव्य आव्यूह <math>D_{\text{out}}^+A</math> से संबंधित है, जबकि स्तम्भ-योग सभी 0 के साथ दाएं आंतरिक-घात सामान्यीकृत लाप्लासियन में बाएं प्रसंभाव्य आव्यूह <math>AD_{\text{in}}^+</math> सम्मिलित | पंक्ति-योग सभी 0 के साथ बाएं बाह्य-घात सामान्यीकृत लाप्लासियन दाएं प्रसंभाव्य आव्यूह <math>D_{\text{out}}^+A</math> से संबंधित है, जबकि स्तम्भ-योग सभी 0 के साथ दाएं आंतरिक-घात सामान्यीकृत लाप्लासियन में बाएं प्रसंभाव्य आव्यूह <math>AD_{\text{in}}^+</math> सम्मिलित है। | ||
== भारित किनारों वाले आरेख़ के लिए परिभाषाएँ == | == भारित किनारों वाले आरेख़ के लिए परिभाषाएँ == | ||
अनुप्रयोगों में सामान्य भारित किनारों वाले आरेख़ को सरलता से उनके आसन्न आव्यूह द्वारा परिभाषित किया जाता है जहां प्रविष्टियों के मान संख्यात्मक होते हैं और अब शून्य और तक सीमित नहीं होते हैं। वर्णक्रमीय क्लस्टरिंग और आरेख़-आधारित संकेत प्रोसेसिंग में, जहां आरेख़ शीर्ष डेटा बिंदुओं का प्रतिनिधित्व करते हैं, किनारे के भार की गणना की जा सकती है, उदाहरण के लिए, डेटा बिंदुओं के युग्म के बीच दूरी आव्यूह के व्युत्क्रमानुपाती के रूप में, जिसके परिणामस्वरूप सभी भार अनौपचारिक रूप से बड़े मानों के साथ गैर-ऋणात्मक होते हैं डेटा बिंदुओं के अधिक समान युग्म के अनुरूप हैं। डेटा बिंदुओं के बीच सहसंबंध और विरोधी सहसंबंध का उपयोग करने से स्वाभाविक रूप से धनात्मक और ऋणात्मक दोनों प्रकार के भार उत्पन्न होते हैं। सरल आरेख़ की अधिकांश परिभाषाएँ गैर-ऋणात्मक भार के मानक स्थितियों तक तुच्छ रूप से विस्तारित हैं, जबकि ऋणात्मक भार पर अधिक ध्यान देने की आवश्यकता होती है, विशेषकर सामान्यीकरण में। | अनुप्रयोगों में सामान्य भारित किनारों वाले आरेख़ को सरलता से उनके आसन्न आव्यूह द्वारा परिभाषित किया जाता है जहां प्रविष्टियों के मान संख्यात्मक होते हैं और अब शून्य और तक सीमित नहीं होते हैं। अतः वर्णक्रमीय क्लस्टरिंग और आरेख़-आधारित संकेत प्रोसेसिंग में, जहां आरेख़ शीर्ष डेटा बिंदुओं का प्रतिनिधित्व करते हैं, किनारे के भार की गणना की जा सकती है, इस प्रकार से उदाहरण के लिए, डेटा बिंदुओं के युग्म के बीच दूरी आव्यूह के व्युत्क्रमानुपाती के रूप में, जिसके परिणामस्वरूप सभी भार अनौपचारिक रूप से बड़े मानों के साथ गैर-ऋणात्मक होते हैं डेटा बिंदुओं के अधिक समान युग्म के अनुरूप हैं। डेटा बिंदुओं के बीच सहसंबंध और विरोधी सहसंबंध का उपयोग करने से स्वाभाविक रूप से धनात्मक और ऋणात्मक दोनों प्रकार के भार उत्पन्न होते हैं। सरल आरेख़ की अधिकांश परिभाषाएँ गैर-ऋणात्मक भार के मानक स्थितियों तक तुच्छ रूप से विस्तारित हैं, जबकि ऋणात्मक भार पर अधिक ध्यान देने की आवश्यकता होती है, विशेषकर सामान्यीकरण में। | ||
=== लाप्लासियन आव्यूह === | === लाप्लासियन आव्यूह === | ||
लाप्लासियन आव्यूह को | इस प्रकार से लाप्लासियन आव्यूह को | ||
: <math>L = D - A </math> | : <math>L = D - A </math> | ||
द्वारा परिभाषित किया गया है, जहां D घात आव्यूह है और A आरेख़ का आसन्न आव्यूह है। | द्वारा परिभाषित किया गया है, जहां D घात आव्यूह है और A आरेख़ का आसन्न आव्यूह है। | ||
निर्देशित आरेख़ के लिए, या तो घात (आरेख़ सिद्धांत) का उपयोग किया जा सकता है, जो कि अनुप्रयोग पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरण में है: | इस प्रकार से निर्देशित आरेख़ के लिए, या तो घात (आरेख़ सिद्धांत) का उपयोग किया जा सकता है, जो कि अनुप्रयोग पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरण में है: | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 360: | Line 359: | ||
=== घटना आव्यूह के माध्यम से सममित लाप्लासियन === | === घटना आव्यूह के माध्यम से सममित लाप्लासियन === | ||
[[Image:elastic network model.png|thumb|एक 2- | [[Image:elastic network model.png|thumb|एक 2-विमीय स्प्रिंग प्रणाली।]]भारित किनारों वाले आरेख़ के लिए कोई भारित घटना आव्यूह B को परिभाषित कर सकता है और इसका उपयोग <math>L = B B^\textsf{T}</math> के रूप में संबंधित सममित लाप्लासियन के निर्माण के लिए कर सकता है। यहां वर्णित वैकल्पिक स्पष्ट दृष्टिकोण, भार को संपर्क से अलग करना है: नियमित आरेख़ के लिए घटना आव्यूह का उपयोग करना जारी रखें और मात्र भार के मान रखने वाले आव्यूह को प्रस्तुत करें। [[ वसंत प्रणाली |स्प्रिंग प्रणाली]] इस मॉडल का उदाहरण है जिसका उपयोग [[यांत्रिकी]] में दी गई संदृढ़ता और इकाई लंबाई के स्प्रिंग की प्रणाली का वर्णन करने के लिए किया जाता है, जहां संदृढ़ता के मान आरेख किनारों के भार की भूमिका निभाते हैं। | ||
इस प्रकार हम शीर्ष v के लिए B<sub>''ve''</sub> और | इस प्रकार हम शीर्ष v के लिए B<sub>''ve''</sub> और | ||
| Line 372: | Line 371: | ||
के रूप में परिभाषित किया गया है जहाँ <math display="inline">B^\textsf{T}</math> B का परिवर्त है। | के रूप में परिभाषित किया गया है जहाँ <math display="inline">B^\textsf{T}</math> B का परिवर्त है। | ||
निर्माण को निम्नलिखित उदाहरण में दर्शाया गया है, जहां प्रत्येक किनारे <math display="inline">e_i</math> को <math display="inline">i=1, 2, 3, 4</math> के साथ भार मान i दिया गया है। | इस प्रकार से निर्माण को निम्नलिखित उदाहरण में दर्शाया गया है, जहां प्रत्येक किनारे <math display="inline">e_i</math> को <math display="inline">i=1, 2, 3, 4</math> के साथ भार मान i दिया गया है। | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Undirected graph|अप्रत्यक्ष आरेख]] | ! [[Undirected graph|अप्रत्यक्ष आरेख]] | ||
| Line 401: | Line 400: | ||
===निर्देशित आरेख़ के लिए सममित लाप्लासियन=== | ===निर्देशित आरेख़ के लिए सममित लाप्लासियन=== | ||
साधारण आरेख़ के जैसे, निर्देशित भारित आरेख़ का लाप्लासियन आव्यूह परिभाषा के अनुसार सामान्यतः गैर-सममित होता है। लाप्लासियन के निर्माण से पहले मूल निर्देशित आरेख को अप्रत्यक्ष आरेख में बदलकर समरूपता लागू की जा सकती है। अप्रत्यक्ष आरेख़ के आसन्न आव्यूह को, उदाहरण के लिए, मूल निर्देशित आरेख़ के आसन्न आव्यूह <math>A</math> के योग के रूप में परिभाषित किया जा सकता है और इसका आव्यूह निम्नलिखित उदाहरण के अनुसार <math>A^T</math> का परिवर्त है: | साधारण आरेख़ के जैसे, निर्देशित भारित आरेख़ का लाप्लासियन आव्यूह परिभाषा के अनुसार सामान्यतः गैर-सममित होता है। लाप्लासियन के निर्माण से पहले मूल निर्देशित आरेख को अप्रत्यक्ष आरेख में बदलकर समरूपता लागू की जा सकती है। अप्रत्यक्ष आरेख़ के आसन्न आव्यूह को, इस प्रकार से उदाहरण के लिए, मूल निर्देशित आरेख़ के आसन्न आव्यूह <math>A</math> के योग के रूप में परिभाषित किया जा सकता है और इसका आव्यूह निम्नलिखित उदाहरण के अनुसार <math>A^T</math> का परिवर्त है: | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 423: | Line 422: | ||
\end{array}\right)</math> | \end{array}\right)</math> | ||
|} | |} | ||
जहाँ <math>A</math> की शून्य और एक प्रविष्टियाँ को सरल आरेख, मानों के लिए तार्किक के अतिरिक्त संख्यात्मक माना जाता है, जो परिणामों में अंतर को समझाते हैं - सरल आरेख के लिए, सममित आरेख को अभी भी सरल होने की आवश्यकता है, इसके सममित आसन्न आव्यूह में मात्र तार्किक होना चाहिए , संख्यात्मक मान नहीं, उदाहरण के लिए, तार्किक योग '''1 v 1 = 1''' है, जबकि संख्यात्मक योग '''1 + 1 = 2''' है। | जहाँ <math>A</math> की शून्य और एक प्रविष्टियाँ को सरल आरेख, मानों के लिए तार्किक के अतिरिक्त संख्यात्मक माना जाता है, जो परिणामों में अंतर को समझाते हैं - सरल आरेख के लिए, सममित आरेख को अभी भी सरल होने की आवश्यकता है, इसके सममित आसन्न आव्यूह में मात्र तार्किक होना चाहिए, संख्यात्मक मान नहीं, इस प्रकार से उदाहरण के लिए, तार्किक योग '''1 v 1 = 1''' है, जबकि संख्यात्मक योग '''1 + 1 = 2''' है। | ||
वैकल्पिक रूप से, सममित लाप्लासियन आव्यूह की गणना घात (आरेख सिद्धांत) का उपयोग करके दो लाप्लासियन से की जा सकती है, जैसा कि निम्नलिखित उदाहरण में है: | इस प्रकार से वैकल्पिक रूप से, सममित लाप्लासियन आव्यूह की गणना घात (आरेख सिद्धांत) का उपयोग करके दो लाप्लासियन से की जा सकती है, जैसा कि निम्नलिखित उदाहरण में है: | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 459: | Line 458: | ||
\end{array}\right)</math> | \end{array}\right)</math> | ||
|} | |} | ||
बाह्य-घात लाप्लासियन परिवर्त और आंतरिक-घात लाप्लासियन का योग सममित लाप्लासियन आव्यूह के बराबर होता है। | अतः इस प्रकार से बाह्य-घात लाप्लासियन परिवर्त और आंतरिक-घात लाप्लासियन का योग सममित लाप्लासियन आव्यूह के बराबर होता है। | ||
===लाप्लासियन आव्यूह सामान्यीकरण=== | ===लाप्लासियन आव्यूह सामान्यीकरण=== | ||
सामान्यीकरण का लक्ष्य, सरल आरेख़ के जैसे, लाप्लासियन आव्यूह की विकर्ण प्रविष्टियों को सभी इकाई बनाना है, साथ ही ऑफ-विकर्ण प्रविष्टियों को तदनुसार सोपानी करना है। ग्लोसरी ऑफ आरेख सिद्धांत वेटेड आरेख में, शीर्ष में जुड़े हुए किनारों की छोटी संख्या के कारण बड़ी घात हो सकती है, परन्तु बड़े भार के साथ-साथ इकाई भार के साथ बड़ी संख्या में जुड़े किनारों के कारण भी है। | सामान्यीकरण का लक्ष्य, सरल आरेख़ के जैसे, लाप्लासियन आव्यूह की विकर्ण प्रविष्टियों को सभी इकाई बनाना है, साथ ही ऑफ-विकर्ण प्रविष्टियों को तदनुसार सोपानी करना है। ग्लोसरी ऑफ आरेख सिद्धांत वेटेड आरेख में, शीर्ष में जुड़े हुए किनारों की छोटी संख्या के कारण बड़ी घात हो सकती है, परन्तु बड़े भार के साथ-साथ इकाई भार के साथ बड़ी संख्या में जुड़े किनारों के कारण भी है। | ||
आरेख़ स्वयं-पाश, अर्थात, आसन्न आव्यूह के मुख्य विकर्ण पर गैर-शून्य प्रविष्टियाँ, आरेख़ लाप्लासियन मानों को प्रभावित नहीं करती हैं, परन्तु सामान्यीकरण कारकों की गणना के लिए गणना करने की आवश्यकता हो सकती है। | इस प्रकार से आरेख़ स्वयं-पाश, अर्थात, आसन्न आव्यूह के मुख्य विकर्ण पर गैर-शून्य प्रविष्टियाँ, आरेख़ लाप्लासियन मानों को प्रभावित नहीं करती हैं, परन्तु सामान्यीकरण कारकों की गणना के लिए गणना करने की आवश्यकता हो सकती है। | ||
==== सममित रूप से सामान्यीकृत लाप्लासियन ==== | ==== सममित रूप से सामान्यीकृत लाप्लासियन ==== | ||
| Line 470: | Line 469: | ||
सममित रूप से सामान्यीकृत लाप्लासियन को | सममित रूप से सामान्यीकृत लाप्लासियन को | ||
: <math>L^\text{sym} := (D^+)^{1/2} L (D^+)^{1/2} = I - (D^+)^{1/2} A (D^+)^{1/2}</math> | : <math>L^\text{sym} := (D^+)^{1/2} L (D^+)^{1/2} = I - (D^+)^{1/2} A (D^+)^{1/2}</math> | ||
के रूप में परिभाषित किया गया है, जहां L असामान्य लाप्लासियन है, A आसन्न आव्यूह है, D घात आव्यूह है, और <math>D^+</math> मूर-पेनरोज़ व्युत्क्रम है। चूँकि घात आव्यूह D विकर्ण है, इसका व्युत्क्रम वर्गमूल <math display="inline">(D^+)^{1/2}</math> मात्र विकर्ण आव्यूह है जिसकी विकर्ण प्रविष्टियाँ D की विकर्ण प्रविष्टियों के वर्गमूल के व्युत्क्रम हैं। यदि सभी किनारे के भार गैर-ऋणात्मक हैं तो सभी घात मान स्वचालित रूप से भी गैर-ऋणात्मक हैं और इसलिए प्रत्येक घात मान का अद्वितीय धनात्मक वर्गमूल होता है। शून्य से विभाजन से बचने के लिए, शून्य घात वाले शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है, जैसा कि निम्नलिखित उदाहरण में है: | के रूप में परिभाषित किया गया है, जहां L असामान्य लाप्लासियन है, A आसन्न आव्यूह है, D घात आव्यूह है, और <math>D^+</math> मूर-पेनरोज़ व्युत्क्रम है। चूँकि घात आव्यूह D विकर्ण है, इसका व्युत्क्रम वर्गमूल <math display="inline">(D^+)^{1/2}</math> मात्र विकर्ण आव्यूह है जिसकी विकर्ण प्रविष्टियाँ D की विकर्ण प्रविष्टियों के वर्गमूल के व्युत्क्रम हैं। यदि सभी किनारे के भार गैर-ऋणात्मक हैं तो सभी घात मान स्वचालित रूप से भी गैर-ऋणात्मक हैं और इसलिए प्रत्येक घात मान का अद्वितीय धनात्मक वर्गमूल होता है। इस प्रकार से शून्य से विभाजन से बचने के लिए, शून्य घात वाले शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है, जैसा कि निम्नलिखित उदाहरण में है: | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 505: | Line 504: | ||
सममित रूप से सामान्यीकृत लाप्लासियन सममित आव्यूह है यदि और मात्र यदि आसन्न आव्यूह A सममित है और D की विकर्ण प्रविष्टियाँ गैर-ऋणात्मक हैं, तो उस स्थिति में हम 'सममित सामान्यीकृत लाप्लासियन' शब्द का उपयोग कर सकते हैं। | सममित रूप से सामान्यीकृत लाप्लासियन सममित आव्यूह है यदि और मात्र यदि आसन्न आव्यूह A सममित है और D की विकर्ण प्रविष्टियाँ गैर-ऋणात्मक हैं, तो उस स्थिति में हम 'सममित सामान्यीकृत लाप्लासियन' शब्द का उपयोग कर सकते हैं। | ||
सममित सामान्यीकृत लाप्लासियन आव्यूह को भार रहित <math display="inline">|v| \times |e|</math> घटना आव्यूह B और विकर्ण <math display="inline">|e| \times |e|</math> आव्यूह W का उपयोग करके | इस प्रकार से सममित सामान्यीकृत लाप्लासियन आव्यूह को भार रहित <math display="inline">|v| \times |e|</math> घटना आव्यूह B और विकर्ण <math display="inline">|e| \times |e|</math> आव्यूह W का उपयोग करके | ||
: <math>L^\text{sym} := (D^+)^{1/2} L (D^+)^{1/2} = (D^+)^{1/2}B W B^\textsf{T} (D^+)^{1/2} = S S^T</math> | : <math>L^\text{sym} := (D^+)^{1/2} L (D^+)^{1/2} = (D^+)^{1/2}B W B^\textsf{T} (D^+)^{1/2} = S S^T</math> | ||
के रूप में भी लिखा जा सकता है, जिसमें किनारे का भार होता है और नवीन <math display="inline">|v| \times |e|</math> भारित घटना आव्यूह <math display="inline">S=(D^+)^{1/2}B W^{{1}/{2}}</math> को परिभाषित करता है, जिनकी पंक्तियों को शीर्षों द्वारा अनुक्रमित किया जाता है और जिनके स्तंभों को G के किनारों द्वारा अनुक्रमित किया जाता है, जैसे कि किनारे '''e = {u, v}''' के अनुरूप प्रत्येक स्तंभ में u के अनुरूप पंक्ति में एक प्रविष्टि <math display="inline">\frac{1}{\sqrt{d_u}}</math> होती है, v के अनुरूप पंक्ति में एक प्रविष्टि <math display="inline">-\frac{1}{\sqrt{d_v}}</math> होती है, और अन्यत्र 0 प्रविष्टियाँ होती हैं। | के रूप में भी लिखा जा सकता है, जिसमें किनारे का भार होता है और नवीन <math display="inline">|v| \times |e|</math> भारित घटना आव्यूह <math display="inline">S=(D^+)^{1/2}B W^{{1}/{2}}</math> को परिभाषित करता है, जिनकी पंक्तियों को शीर्षों द्वारा अनुक्रमित किया जाता है और जिनके स्तंभों को G के किनारों द्वारा अनुक्रमित किया जाता है, जैसे कि किनारे '''e = {u, v}''' के अनुरूप प्रत्येक स्तंभ में u के अनुरूप पंक्ति में एक प्रविष्टि <math display="inline">\frac{1}{\sqrt{d_u}}</math> होती है, v के अनुरूप पंक्ति में एक प्रविष्टि <math display="inline">-\frac{1}{\sqrt{d_v}}</math> होती है, और अन्यत्र 0 प्रविष्टियाँ होती हैं। | ||
| Line 511: | Line 510: | ||
==== यादृच्छिक चाल सामान्यीकृत लाप्लासियन ==== | ==== यादृच्छिक चाल सामान्यीकृत लाप्लासियन ==== | ||
यादृच्छिक चाल सामान्यीकृत लाप्लासियन को | इस प्रकार से यादृच्छिक चाल सामान्यीकृत लाप्लासियन को | ||
: <math>L^\text{rw} := D^+ L = I - D^+ A</math> | : <math>L^\text{rw} := D^+ L = I - D^+ A</math> | ||
के रूप में परिभाषित किया गया है जहां D घात आव्यूह है। चूँकि घात आव्यूह D विकर्ण है, इसके व्युत्क्रम <math display="inline">D^+</math> को मात्र विकर्ण आव्यूह के रूप में परिभाषित किया गया है, जिसमें विकर्ण प्रविष्टियाँ हैं जो D की संगत विकर्ण प्रविष्टियों के व्युत्क्रम हैं। पृथक शीर्षों (घात 0 वाले) के लिए, एक सामान्य विकल्प संबंधित अवयव <math display="inline">L^\text{rw}_{i,i}</math> को 0 पर समूहित करना है। <math display="inline">L^\text{rw}</math> के आव्यूह अवयव | के रूप में परिभाषित किया गया है जहां D घात आव्यूह है। चूँकि घात आव्यूह D विकर्ण है, इसके व्युत्क्रम <math display="inline">D^+</math> को मात्र विकर्ण आव्यूह के रूप में परिभाषित किया गया है, जिसमें विकर्ण प्रविष्टियाँ हैं जो D की संगत विकर्ण प्रविष्टियों के व्युत्क्रम हैं। पृथक शीर्षों (घात 0 वाले) के लिए, एक सामान्य विकल्प संबंधित अवयव <math display="inline">L^\text{rw}_{i,i}</math> को 0 पर समूहित करना है। <math display="inline">L^\text{rw}</math> के आव्यूह अवयव | ||
| Line 519: | Line 518: | ||
0 & \mbox{otherwise} | 0 & \mbox{otherwise} | ||
\end{cases}</math> द्वारा दिए गए हैं। | \end{cases}</math> द्वारा दिए गए हैं। | ||
यादृच्छिक-चाल सामान्यीकृत लाप्लासियन का नाम इस तथ्य से आता है कि यह आव्यूह <math display="inline">L^\text{rw} = I - P</math> है, जहां <math display="inline">P = D^+A</math> गैर-ऋणात्मक भार मानते हुए, आरेख़ पर यादृच्छिक चालक का संक्रमण आव्यूह है। उदाहरण के लिए, मान लीजिए कि <math display="inline"> e_i </math> i-वें [[मानक आधार]] सदिश को दर्शाता है। फिर <math display="inline">x = e_i P </math> एक [[संभाव्यता वेक्टर|प्रायिकता सदिश]] है जो शीर्ष <math display="inline">i</math> से चरण उठाने के बाद यादृच्छिक चालक के स्थानों के वितरण का प्रतिनिधित्व करता है; अर्थात <math display="inline">x_j = \mathbb{P}\left(v_i \to v_j\right)</math>। अधिक सामान्यतः, यदि सदिश <math display="inline"> x </math> आरेख़ के शीर्षों पर यादृच्छिक चालक के स्थान का प्रायिकता वितरण है, तो <math display="inline">x' = x P^t</math> <math display="inline">t</math> चरणों के बाद चालक का प्रायिकता वितरण है। | अतः यादृच्छिक-चाल सामान्यीकृत लाप्लासियन का नाम इस तथ्य से आता है कि यह आव्यूह <math display="inline">L^\text{rw} = I - P</math> है, जहां <math display="inline">P = D^+A</math> गैर-ऋणात्मक भार मानते हुए, आरेख़ पर यादृच्छिक चालक का संक्रमण आव्यूह है। इस प्रकार से उदाहरण के लिए, मान लीजिए कि <math display="inline"> e_i </math> i-वें [[मानक आधार]] सदिश को दर्शाता है। फिर <math display="inline">x = e_i P </math> एक [[संभाव्यता वेक्टर|प्रायिकता सदिश]] है जो शीर्ष <math display="inline">i</math> से चरण उठाने के बाद यादृच्छिक चालक के स्थानों के वितरण का प्रतिनिधित्व करता है; अर्थात <math display="inline">x_j = \mathbb{P}\left(v_i \to v_j\right)</math>। अधिक सामान्यतः, यदि सदिश <math display="inline"> x </math> आरेख़ के शीर्षों पर यादृच्छिक चालक के स्थान का प्रायिकता वितरण है, तो <math display="inline">x' = x P^t</math> <math display="inline">t</math> चरणों के बाद चालक का प्रायिकता वितरण है। | ||
यादृच्छिक चाल सामान्यीकृत लाप्लासियन को बाएं सामान्यीकृत लाप्लासियन <math>L^\text{rw} := D^+L</math> भी कहा जा सकता है क्योंकि सामान्यीकरण बाईं ओर सामान्यीकरण आव्यूह <math>D^+</math> द्वारा लाप्लासियन को गुणा करके किया जाता है। इसमें प्रत्येक पंक्ति का योग शून्य है क्योंकि <math>P = D^+A</math> दायाँ प्रसंभाव्य है, यह मानते हुए कि सभी भार गैर-ऋणात्मक हैं। | यादृच्छिक चाल सामान्यीकृत लाप्लासियन को बाएं सामान्यीकृत लाप्लासियन <math>L^\text{rw} := D^+L</math> भी कहा जा सकता है क्योंकि सामान्यीकरण बाईं ओर सामान्यीकरण आव्यूह <math>D^+</math> द्वारा लाप्लासियन को गुणा करके किया जाता है। इसमें प्रत्येक पंक्ति का योग शून्य है क्योंकि <math>P = D^+A</math> दायाँ प्रसंभाव्य है, यह मानते हुए कि सभी भार गैर-ऋणात्मक हैं। | ||
कम असामान्य रूप से उपयोग किए जाने वाले दाएं सामान्यीकृत लाप्लासियन <math>L D^+ = I - A D^+</math> में प्रत्येक स्तम्भ का योग शून्य होता है क्योंकि <math>A D^+</math> बायां प्रसंभाव्य है। | अतः कम असामान्य रूप से उपयोग किए जाने वाले दाएं सामान्यीकृत लाप्लासियन <math>L D^+ = I - A D^+</math> में प्रत्येक स्तम्भ का योग शून्य होता है क्योंकि <math>A D^+</math> बायां प्रसंभाव्य है। | ||
निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी को सामान्यीकरण के लिए घात (आरेख़ सिद्धांत) चुनने की भी आवश्यकता होती है: | इस प्रकार से निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी को सामान्यीकरण के लिए घात (आरेख़ सिद्धांत) चुनने की भी आवश्यकता होती है: | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 559: | Line 558: | ||
\end{array}\right)</math> | \end{array}\right)</math> | ||
|} | |} | ||
पंक्ति-योग सभी 0 के साथ बाएं बाह्य-घात सामान्यीकृत लाप्लासियन दाएँ प्रसंभाव्य आव्यूह <math>D_{\text{out}}^+A</math> से संबंधित है, जबकि सभी 0 के साथ दाएँ आंतरिक-घात सामान्यीकृत लाप्लासियन में बाएं प्रसंभाव्य आव्यूह <math>AD_{\text{in}}^+</math> सम्मिलित है। | अतः पंक्ति-योग सभी 0 के साथ बाएं बाह्य-घात सामान्यीकृत लाप्लासियन दाएँ प्रसंभाव्य आव्यूह <math>D_{\text{out}}^+A</math> से संबंधित है, जबकि सभी 0 के साथ दाएँ आंतरिक-घात सामान्यीकृत लाप्लासियन में बाएं प्रसंभाव्य आव्यूह <math>AD_{\text{in}}^+</math> सम्मिलित है। | ||
====ऋणात्मक भार==== | ====ऋणात्मक भार==== | ||
ऋणात्मक भार सामान्यीकरण के लिए कई आक्षेप प्रस्तुत करते हैं: | इस प्रकार से ऋणात्मक भार सामान्यीकरण के लिए कई आक्षेप प्रस्तुत करते हैं: | ||
* ऋणात्मक भार की उपस्थिति के परिणामस्वरूप गैर-पृथक शीर्षों के लिए स्वाभाविक रूप से शून्य पंक्ति- और/या स्तंभ-योग हो सकता है। धनात्मक भारों की बड़ी पंक्ति-योग और समान रूप से ऋणात्मक भारों की समान रूप से बड़ी पंक्ति-योग वाला शीर्ष, जिसका योग शून्य है, को भारी नोड माना जा सकता है और दोनों बड़े मानों को सोपानी किया जा सकता है, जबकि विकर्ण प्रविष्टि शून्य रहती है, जैसे कि पृथक शीर्ष आदि। | * ऋणात्मक भार की उपस्थिति के परिणामस्वरूप गैर-पृथक शीर्षों के लिए स्वाभाविक रूप से शून्य पंक्ति- और/या स्तंभ-योग हो सकता है। धनात्मक भारों की बड़ी पंक्ति-योग और समान रूप से ऋणात्मक भारों की समान रूप से बड़ी पंक्ति-योग वाला शीर्ष, जिसका योग शून्य है, को भारी नोड माना जा सकता है और दोनों बड़े मानों को सोपानी किया जा सकता है, जबकि विकर्ण प्रविष्टि शून्य रहती है, जैसे कि पृथक शीर्ष आदि। | ||
* ऋणात्मक भार ऋणात्मक पंक्ति- और/या स्तंभ-योग भी दे सकते हैं, जिससे कि गैर-सामान्यीकृत लाप्लासियन आव्यूह में संबंधित विकर्ण प्रविष्टि ऋणात्मक होगी और सममित सामान्यीकरण के लिए आवश्यक धनात्मक वर्गमूल स्थित नहीं होगा। | * ऋणात्मक भार ऋणात्मक पंक्ति- और/या स्तंभ-योग भी दे सकते हैं, जिससे कि गैर-सामान्यीकृत लाप्लासियन आव्यूह में संबंधित विकर्ण प्रविष्टि ऋणात्मक होगी और सममित सामान्यीकरण के लिए आवश्यक धनात्मक वर्गमूल स्थित नहीं होगा। | ||
| Line 568: | Line 567: | ||
== गुण == | == गुण == | ||
एक (अप्रत्यक्ष) आरेख़ G और उसके लाप्लासियन आव्यूह L के लिए [[eigenvalues|आइगेनमान]] <math display="inline">\lambda_0 \le \lambda_1 \le \cdots \le \lambda_{n-1}</math> के साथ: | इस प्रकार से एक (अप्रत्यक्ष) आरेख़ G और उसके लाप्लासियन आव्यूह L के लिए [[eigenvalues|आइगेनमान]] <math display="inline">\lambda_0 \le \lambda_1 \le \cdots \le \lambda_{n-1}</math> के साथ: | ||
* L [[सममित मैट्रिक्स|सममित आव्यूह]] है। | * L [[सममित मैट्रिक्स|सममित आव्यूह]] है। | ||
* L [[सकारात्मक-निश्चित मैट्रिक्स|धनात्मक-निश्चित आव्यूह]] (अर्थात सभी <math display="inline">i</math> के लिए <math display="inline">\lambda_i \ge 0</math> है) | * L [[सकारात्मक-निश्चित मैट्रिक्स|धनात्मक-निश्चित आव्यूह]] (अर्थात सभी <math display="inline">i</math> के लिए <math display="inline">\lambda_i \ge 0</math> है) है। इसे इस तथ्य से देखा जा सकता है कि लाप्लासियन सममित और विकर्ण रूप से प्रभावशाली आव्यूह अनुप्रयोग और गुण है। | ||
* L [[एम-मैट्रिक्स|एम-आव्यूह]] है (इसकी संवृत-विकर्ण प्रविष्टियाँ गैर-धनात्मक हैं, फिर भी इसके आइगेन मानों के वास्तविक भाग गैर-ऋणात्मक हैं)। | * L [[एम-मैट्रिक्स|एम-आव्यूह]] है (इसकी संवृत-विकर्ण प्रविष्टियाँ गैर-धनात्मक हैं, फिर भी इसके आइगेन मानों के वास्तविक भाग गैर-ऋणात्मक हैं)। | ||
* L की प्रत्येक पंक्ति और स्तंभ का योग शून्य है। वस्तुतः, योग में, शीर्ष की घात को प्रत्येक निकटवर्ती के लिए -1 के साथ जोड़ा जाता है। | * L की प्रत्येक पंक्ति और स्तंभ का योग शून्य है। वस्तुतः, योग में, शीर्ष की घात को प्रत्येक निकटवर्ती के लिए -1 के साथ जोड़ा जाता है। | ||
* परिणामस्वरूप, <math display="inline">\lambda_0 = 0</math>, क्योंकि सदिश <math display="inline">\mathbf{v}_0 = (1, 1, \dots, 1)</math> , <math display="inline">L \mathbf{v}_0 = \mathbf{0} </math> को संतुष्ट करता है। इसका तात्पर्य यह भी है कि लाप्लासियन आव्यूह एकवचन है। | * परिणामस्वरूप, <math display="inline">\lambda_0 = 0</math>, क्योंकि सदिश <math display="inline">\mathbf{v}_0 = (1, 1, \dots, 1)</math>, <math display="inline">L \mathbf{v}_0 = \mathbf{0} </math> को संतुष्ट करता है। इसका तात्पर्य यह भी है कि लाप्लासियन आव्यूह एकवचन है। | ||
* आरेख़ में सम्बद्ध अवयव (आरेख सिद्धांत) की संख्या लाप्लासियन के [[कर्नेल (रैखिक बीजगणित)]] का आयाम है और 0 आइगेनमान के आइगेनमान और आइगेनसदिश बीजगणितीय बहुलता है। | * आरेख़ में सम्बद्ध अवयव (आरेख सिद्धांत) की संख्या लाप्लासियन के [[कर्नेल (रैखिक बीजगणित)]] का आयाम है और 0 आइगेनमान के आइगेनमान और आइगेनसदिश बीजगणितीय बहुलता है। | ||
* L के सबसे छोटे गैर-शून्य आइगेनमान को [[वर्णक्रमीय अंतराल]] कहा जाता है। | * L के सबसे छोटे गैर-शून्य आइगेनमान को [[वर्णक्रमीय अंतराल]] कहा जाता है। | ||
* L का दूसरा सबसे छोटा आइगेनमान (शून्य हो सकता है) G की बीजगणितीय संपर्क (या फ़िडलर मान) है और आरेख़ के कट (आरेख सिद्धांत) सबसे विरल कट का अनुमान लगाता है। | * L का दूसरा सबसे छोटा आइगेनमान (शून्य हो सकता है) G की बीजगणितीय संपर्क (या फ़िडलर मान) है और आरेख़ के कट (आरेख सिद्धांत) सबसे विरल कट का अनुमान लगाता है। | ||
* लाप्लासियन फलन <math display="inline">f : V \to \mathbb{R}</math> के एन-विमीय सदिश समष्टि पर संक्रियक है , जहाँ <math display="inline">V</math> G और <math display="inline">n = |V|</math> का शीर्ष समुच्चय है। | * लाप्लासियन फलन <math display="inline">f : V \to \mathbb{R}</math> के एन-विमीय सदिश समष्टि पर संक्रियक है, जहाँ <math display="inline">V</math> G और <math display="inline">n = |V|</math> का शीर्ष समुच्चय है। | ||
* जब G, [[के-नियमित ग्राफ|के-नियमित आरेख]] होता है, तो सामान्यीकृत लाप्लासियन होता है: <math display="inline">\mathcal{L} = \tfrac{1}{k} L = I - \tfrac{1}{k} A</math>, जहां A आसन्नता आव्यूह है और I तत्समक आव्यूह है। | * जब G, [[के-नियमित ग्राफ|के-नियमित आरेख]] होता है, तो सामान्यीकृत लाप्लासियन होता है: <math display="inline">\mathcal{L} = \tfrac{1}{k} L = I - \tfrac{1}{k} A</math>, जहां A आसन्नता आव्यूह है और I तत्समक आव्यूह है। | ||
* एकाधिक सम्बद्ध घटक (आरेख़ सिद्धांत) वाले आरेख़ के लिए, L कक्ष आव्यूह कक्ष विकर्ण आव्यूह आव्यूह है, जहां प्रत्येक कक्ष प्रत्येक घटक के लिए संबंधित लाप्लासियन आव्यूह है, संभवतः शीर्षों को पुन: व्यवस्थित करने के बाद है (अर्थात L कक्ष विकर्ण आव्यूह के समान क्रमपरिवर्तन है)। | * एकाधिक सम्बद्ध घटक (आरेख़ सिद्धांत) वाले आरेख़ के लिए, L कक्ष आव्यूह कक्ष विकर्ण आव्यूह आव्यूह है, जहां प्रत्येक कक्ष प्रत्येक घटक के लिए संबंधित लाप्लासियन आव्यूह है, संभवतः शीर्षों को पुन: व्यवस्थित करने के बाद है (अर्थात L कक्ष विकर्ण आव्यूह के समान क्रमपरिवर्तन है)। | ||
| Line 594: | Line 593: | ||
: <math>L^\text{rw} = I-D^{-\frac{1}{2}}\left(I - L^\text{sym}\right) D^\frac{1}{2}</math>, | : <math>L^\text{rw} = I-D^{-\frac{1}{2}}\left(I - L^\text{sym}\right) D^\frac{1}{2}</math>, | ||
अर्थात, <math display="inline">L^\text{rw}</math> सामान्यीकृत लाप्लासियन <math display="inline">L^\text{sym}</math> के समान है। इस कारण से, यद्यपि <math display="inline">L^\text{rw}</math> सामान्य रूप से सममित नहीं है, इसके वास्तविक आइगेन मान हैं - निश्चित सामान्यीकृत सममित लाप्लासियन <math display="inline">L^\text{sym}</math> के आइगेन मान के समान है। | अर्थात, <math display="inline">L^\text{rw}</math> सामान्यीकृत लाप्लासियन <math display="inline">L^\text{sym}</math> के समान है। अतः इस कारण से, यद्यपि <math display="inline">L^\text{rw}</math> सामान्य रूप से सममित नहीं है, इसके वास्तविक आइगेन मान हैं - निश्चित सामान्यीकृत सममित लाप्लासियन <math display="inline">L^\text{sym}</math> के आइगेन मान के समान है। | ||
== निरंतर लाप्लासियन का अनुमान लगाने वाले असतत लाप्लास संक्रियक के रूप में व्याख्या == | == निरंतर लाप्लासियन का अनुमान लगाने वाले असतत लाप्लास संक्रियक के रूप में व्याख्या == | ||
| Line 610: | Line 609: | ||
| isbn = 978-3-540-40720-1 | | isbn = 978-3-540-40720-1 | ||
| citeseerx = 10.1.1.3.7020 | | citeseerx = 10.1.1.3.7020 | ||
}}.</ref> इस व्याख्या में, प्रत्येक आरेख शीर्ष को ग्रिड बिंदु के रूप में माना जाता है; शीर्ष की स्थानीय संपर्क इस ग्रिड बिंदु पर परिमित अंतर सन्निकटन स्टेंसिल (संख्यात्मक विश्लेषण) निर्धारित करती है, ग्रिड का आकार सदैव प्रत्येक किनारे के लिए होता है, और किसी भी ग्रिड बिंदु पर कोई बाधा नहीं होती है, जो सजातीय न्यूमैन के स्थितियों से मेल खाती है सीमा की स्थिति, अर्थात, मुक्त सीमा। इस प्रकार की व्याख्या किसी को अनुमति देती है, उदाहरण के लिए, अनंत संख्या में शीर्षों और किनारों वाले आरेख़ के स्थितियों में लाप्लासियन आव्यूह को सामान्यीकृत करना, जिससे अनंत आकार का लाप्लासियन आव्यूह बनता है। | }}.</ref> इस व्याख्या में, प्रत्येक आरेख शीर्ष को ग्रिड बिंदु के रूप में माना जाता है; शीर्ष की स्थानीय संपर्क इस ग्रिड बिंदु पर परिमित अंतर सन्निकटन स्टेंसिल (संख्यात्मक विश्लेषण) निर्धारित करती है, ग्रिड का आकार सदैव प्रत्येक किनारे के लिए होता है, और किसी भी ग्रिड बिंदु पर कोई बाधा नहीं होती है, जो सजातीय न्यूमैन के स्थितियों से मेल खाती है सीमा की स्थिति, अर्थात, मुक्त सीमा। इस प्रकार की व्याख्या किसी को अनुमति देती है, इस प्रकार से उदाहरण के लिए, अनंत संख्या में शीर्षों और किनारों वाले आरेख़ के स्थितियों में लाप्लासियन आव्यूह को सामान्यीकृत करना, जिससे अनंत आकार का लाप्लासियन आव्यूह बनता है। | ||
== लाप्लासियन आव्यूह का सामान्यीकरण और विस्तार == | == लाप्लासियन आव्यूह का सामान्यीकरण और विस्तार == | ||
=== सामान्यीकृत लाप्लासियन === | === सामान्यीकृत लाप्लासियन === | ||
सामान्यीकृत लाप्लासियन <math>Q</math> को इस प्रकार परिभाषित किया गया है:<ref>{{cite book |last1= Godsil |first1=C. |last2= Royle |first2=G. |date=2001 |title=बीजगणितीय ग्राफ सिद्धांत, गणित में स्नातक ग्रंथ|publisher= Springer-Verlag}}</ref> | इस प्रकार से सामान्यीकृत लाप्लासियन <math>Q</math> को इस प्रकार परिभाषित किया गया है:<ref>{{cite book |last1= Godsil |first1=C. |last2= Royle |first2=G. |date=2001 |title=बीजगणितीय ग्राफ सिद्धांत, गणित में स्नातक ग्रंथ|publisher= Springer-Verlag}}</ref> | ||
: <math>\begin{cases} | : <math>\begin{cases} | ||
Q_{i,j} < 0 & \mbox{if } i \neq j \mbox{ and } v_i \mbox{ is adjacent to } v_j\\ | Q_{i,j} < 0 & \mbox{if } i \neq j \mbox{ and } v_i \mbox{ is adjacent to } v_j\\ | ||
| Line 624: | Line 623: | ||
=== चुंबकीय लाप्लासियन === | === चुंबकीय लाप्लासियन === | ||
आसन्न आव्यूह की प्रविष्टियाँ मिश्रित-मानित हो सकती हैं, जिस स्थिति में आव्यूह समरूपता की धारणा को [[हर्मिटियन मैट्रिक्स|हर्मिटियन आव्यूह]] के साथ प्रतिस्थापित करने की आवश्यकता होती है। वास्तविक भार <math>w_{ij}</math> के साथ निर्देशित आरेख़ के लिए चुंबकीय लाप्लासियन का निर्माण मिश्रित प्रविष्टियों | आसन्न आव्यूह की प्रविष्टियाँ मिश्रित-मानित हो सकती हैं, जिस स्थिति में आव्यूह समरूपता की धारणा को [[हर्मिटियन मैट्रिक्स|हर्मिटियन आव्यूह]] के साथ प्रतिस्थापित करने की आवश्यकता होती है। अतः वास्तविक भार <math>w_{ij}</math> के साथ निर्देशित आरेख़ के लिए चुंबकीय लाप्लासियन का निर्माण मिश्रित प्रविष्टियों | ||
:<math>\gamma_q(i, j) = e^{i2 \pi q(w_{ij}-w_{ji})}</math> | :<math>\gamma_q(i, j) = e^{i2 \pi q(w_{ij}-w_{ji})}</math> | ||
के साथ सममित लाप्लासियन और हर्मिटियन चरण आव्यूह के वास्तविक सममित आव्यूह के [[हैडामर्ड उत्पाद (मैट्रिसेस)|हैडामर्ड गुणनफल (आव्यूह )]] के रूप में किया गया है जो जटिल तल में चरण में किनारे की दिशा को एन्कोड करता है। क्वांटम भौतिकी के संदर्भ में, चुंबकीय लाप्लासियन की व्याख्या उस संक्रियक के रूप में की जा सकती है जो आरेख पर मुक्त आवेशित कण की घटना विज्ञान का वर्णन करता है, जो एक चुंबकीय क्षेत्र की क्रिया के अधीन है और पैरामीटर <math>q</math> को विद्युत आवेश कहा जाता है।<ref>{{cite conference|title=हर्मिटियन लाप्लासियन पर आधारित निर्देशित ग्राफ़ के लिए ग्राफ़ सिग्नल प्रोसेसिंग| conference=ECML PKDD 2019: Machine Learning and Knowledge Discovery in Databases |pages=447–463 |year=2020|doi= 10.1007/978-3-030-46150-8_27|url=https://ecmlpkdd2019.org/downloads/paper/499.pdf |author1=Satoshi Furutani |author2=Toshiki Shibahara|author3= Mitsuaki Akiyama|author4= Kunio Hato|author5=Masaki Aida }}</ref> निम्नलिखित उदाहरण में <math>q=1/4</math>: | के साथ सममित लाप्लासियन और हर्मिटियन चरण आव्यूह के वास्तविक सममित आव्यूह के [[हैडामर्ड उत्पाद (मैट्रिसेस)|हैडामर्ड गुणनफल (आव्यूह)]] के रूप में किया गया है जो जटिल तल में चरण में किनारे की दिशा को एन्कोड करता है। क्वांटम भौतिकी के संदर्भ में, चुंबकीय लाप्लासियन की व्याख्या उस संक्रियक के रूप में की जा सकती है जो आरेख पर मुक्त आवेशित कण की घटना विज्ञान का वर्णन करता है, जो एक चुंबकीय क्षेत्र की क्रिया के अधीन है और पैरामीटर <math>q</math> को विद्युत आवेश कहा जाता है।<ref>{{cite conference|title=हर्मिटियन लाप्लासियन पर आधारित निर्देशित ग्राफ़ के लिए ग्राफ़ सिग्नल प्रोसेसिंग| conference=ECML PKDD 2019: Machine Learning and Knowledge Discovery in Databases |pages=447–463 |year=2020|doi= 10.1007/978-3-030-46150-8_27|url=https://ecmlpkdd2019.org/downloads/paper/499.pdf |author1=Satoshi Furutani |author2=Toshiki Shibahara|author3= Mitsuaki Akiyama|author4= Kunio Hato|author5=Masaki Aida }}</ref> निम्नलिखित उदाहरण में <math>q=1/4</math>: | ||
{|class="wikitable" | {|class="wikitable" | ||
! [[Adjacency matrix|संलग्नता आव्यूह]] | ! [[Adjacency matrix|संलग्नता आव्यूह]] | ||
| Line 661: | Line 660: | ||
=== विकृत लाप्लासियन === | === विकृत लाप्लासियन === | ||
विकृत लाप्लासियन को सामान्यतः | इस प्रकार से विकृत लाप्लासियन को सामान्यतः | ||
:<math>\Delta(s) = I - sA + s^2(D - I)</math> | :<math>\Delta(s) = I - sA + s^2(D - I)</math> | ||
| Line 667: | Line 666: | ||
=== चिह्नहीन लाप्लासियन === | === चिह्नहीन लाप्लासियन === | ||
चिह्नहीन लाप्लासियन को | अतः इस प्रकार से चिह्नहीन लाप्लासियन को | ||
:<math>Q = D + A</math> | :<math>Q = D + A</math> | ||
के रूप में परिभाषित किया जाता है, जहाँ <math>D</math> घात आव्यूह है, और <math>A</math> आसन्नता आव्यूह है।<ref>{{Cite journal|last1=Cvetković|first1=Dragoš|last2=Simić|first2=Slobodan K.|date=2010|journal=Applicable Analysis and Discrete Mathematics|volume=4|issue=1|pages=156–166|issn=1452-8630|jstor=43671298|title=साइनलेस लाप्लासियन पर आधारित ग्राफ़ के एक वर्णक्रमीय सिद्धांत की ओर, III|doi=10.2298/AADM1000001C}}</ref> हस्ताक्षरित लाप्लासियन <math>L</math> के जैसे , चिह्नहीन लाप्लासियन <math>Q</math> भी धनात्मक अर्ध-निश्चित है क्योंकि इसे | के रूप में परिभाषित किया जाता है, जहाँ <math>D</math> घात आव्यूह है, और <math>A</math> आसन्नता आव्यूह है।<ref>{{Cite journal|last1=Cvetković|first1=Dragoš|last2=Simić|first2=Slobodan K.|date=2010|journal=Applicable Analysis and Discrete Mathematics|volume=4|issue=1|pages=156–166|issn=1452-8630|jstor=43671298|title=साइनलेस लाप्लासियन पर आधारित ग्राफ़ के एक वर्णक्रमीय सिद्धांत की ओर, III|doi=10.2298/AADM1000001C}}</ref> हस्ताक्षरित लाप्लासियन <math>L</math> के जैसे, चिह्नहीन लाप्लासियन <math>Q</math> भी धनात्मक अर्ध-निश्चित है क्योंकि इसे | ||
:<math>Q = RR^\textsf{T}</math> | :<math>Q = RR^\textsf{T}</math> | ||
के रूप में गुणनखंडित किया जा सकता है, जहाँ <math display="inline">R</math> घटना आव्यूह है। <math>Q</math> के निकट 0-आइगेनसदिश है यदि और मात्र तभी जब इसमें पृथक शीर्षों के अतिरिक्त कोई द्विसमूह जुड़ा घटक हो। इसे | के रूप में गुणनखंडित किया जा सकता है, जहाँ <math display="inline">R</math> घटना आव्यूह है। <math>Q</math> के निकट 0-आइगेनसदिश है यदि और मात्र तभी जब इसमें पृथक शीर्षों के अतिरिक्त कोई द्विसमूह जुड़ा घटक हो। इसे | ||
| Line 675: | Line 674: | ||
<math>\mathbf{x}^\textsf{T} Q \mathbf{x} = \mathbf{x}^\textsf{T} R R^\textsf{T} \mathbf{x} \implies R^\textsf{T} \mathbf{x} = \mathbf{0}</math> के रूप में दिखाया जा सकता है। | <math>\mathbf{x}^\textsf{T} Q \mathbf{x} = \mathbf{x}^\textsf{T} R R^\textsf{T} \mathbf{x} \implies R^\textsf{T} \mathbf{x} = \mathbf{0}</math> के रूप में दिखाया जा सकता है। | ||
इसका एक हल है जहाँ <math>\mathbf{x} \neq \mathbf{0}</math> यदि और मात्र यदि आरेख़ में द्विदलीय जुड़ा हुआ घटक है। | इस प्रकार से इसका एक हल है जहाँ <math>\mathbf{x} \neq \mathbf{0}</math> यदि और मात्र यदि आरेख़ में द्विदलीय जुड़ा हुआ घटक है। | ||
=== निर्देशित बहुआरेख === | === निर्देशित बहुआरेख === | ||
निर्देशित बहुआरेख के लिए लाप्लासियन आव्यूह का एनालॉग परिभाषित किया जा सकता है।<ref name="Chaiken1978">{{cite journal | इस प्रकार से निर्देशित बहुआरेख के लिए लाप्लासियन आव्यूह का एनालॉग परिभाषित किया जा सकता है।<ref name="Chaiken1978">{{cite journal | ||
| title = Matrix Tree Theorems | | title = Matrix Tree Theorems | ||
| author1=Chaiken, S. | author2=Kleitman, D. | author-link2=Daniel Kleitman | | author1=Chaiken, S. | author2=Kleitman, D. | author-link2=Daniel Kleitman | ||
| Line 714: | Line 713: | ||
== संदर्भ == | == संदर्भ == | ||
{{reflist}} | {{reflist}} | ||
[[Category: | [[Category:Collapse templates]] | ||
[[Category:Created On 09/07/2023]] | [[Category:Created On 09/07/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with empty portal template]] | |||
[[Category:Pages with maths render errors]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Portal-inline template with redlinked portals]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:बीजगणितीय ग्राफ सिद्धांत]] | |||
[[Category:मैट्रिसेस]] | |||
[[Category:संख्यात्मक अंतर समीकरण]] | |||
Latest revision as of 15:40, 4 September 2023
आरेख सिद्धांत के गणित क्षेत्र में, लाप्लासियन आव्यूह, जिसे विविक्त लाप्लेस संक्रियक आरेख लाप्लासियन, प्रवेश आव्यूह, किरचॉफ आव्यूह या विविक्त लाप्लास संक्रियक भी कहा जाता है, आरेख (असतत गणित) का आव्यूह (गणित) प्रतिनिधित्व है। पियरे-साइमन लाप्लास के नाम पर, आरेख लाप्लासियन आव्यूह को परिमित अंतर विधि द्वारा प्राप्त ऋणात्मक निरंतर लाप्लासियन का अनुमान लगाने वाले आरेख पर ऋणात्मक असतत लाप्लास संक्रियक के आव्यूह रूप के रूप में देखा जा सकता है।
इस प्रकार से लाप्लासियन आव्यूह आरेख़ के कई उपयोगी गुणों से संबंधित है। किरचॉफ के प्रमेय के साथ, इसका उपयोग किसी दिए गए आरेख़ के लिए विस्तरित ट्री (गणित) की संख्या की गणना करने के लिए किया जा सकता है। आरेख़ के कट (आरेख़ सिद्धांत) सबसे कम कट का अनुमान फिडलर सदिश के माध्यम से लगाया जा सकता है - आरेख़ लाप्लासियन के दूसरे सबसे छोटे आइगेनमान के अनुरूप आइगेनसदिश - जैसा कि चीगर स्थिरांक (आरेख़ सिद्धांत) चीगर असमानताओं द्वारा स्थापित किया गया है। लाप्लासियन आव्यूह के एक आव्यूह का आइगेन अपघटन अरैखिक विमीयता में अपघटन लाप्लासियन आइगेन प्रतिचित्र का निर्माण करने की अनुमति देता है जो कई यंत्र अधिगम अनुप्रयोगों में दिखाई देते हैं और आरेख रेखाचित्र में वर्णक्रमीय लेबाह्य निर्धारित करते हैं। इस प्रकार से आरेख-आधारित संकेत प्रक्रम असतत फूरियर रूपांतरण पर आधारित है जो संकेत के अनुरूप आरेख के लाप्लासियन आव्यूह के आइगेनसदिशों के लिए मिश्रित संख्या ज्या तरंगों के मानक आधार को प्रतिस्थापित करके पारंपरिक असतत फूरियर परिवर्तन का विस्तार करता है।
लाप्लासियन आव्यूह साधारण आरेख के लिए परिभाषित करना सबसे सरल है, परन्तु ग्लोसरी ऑफ आरेख सिद्धांत वेटेड आरेख के लिए अनुप्रयोगों में अधिक सामान्य है, अर्थात, इसके किनारों पर भार के साथ - आरेख आसन्न आव्यूह की प्रविष्टियां। अतः वर्णक्रमीय आरेख सिद्धांत आरेख के गुणों को वर्णक्रम से जोड़ता है, अर्थात, आइगेनमान, और आरेख से जुड़े आव्यूह के आइगेनसदिश, जैसे कि इसकी आसन्न आव्यूह या लाप्लासियन आव्यूह है। असंतुलित भार आव्यूह वर्णक्रम को अवांछित रूप से प्रभावित कर सकता है, जिससे सामान्यीकरण की आवश्यकता होती है - आव्यूह प्रविष्टियों का स्तम्भ/पंक्ति सोपानी - जिसके परिणामस्वरूप सामान्यीकृत आसन्नता और लाप्लासियन आव्यूह होते हैं।
सरल आरेख़ के लिए परिभाषाएँ
लाप्लासियन आव्यूह
इस प्रकार से शीर्ष के साथ एक सरल आरेख को देखते हुए, इसके लाप्लासियन आव्यूह को अवयव-वार[1]
के रूप में या आव्यूह
द्वारा समकक्ष रूप से परिभाषित किया गया है, जहां D घात आव्यूह है और A आरेख़ का आसन्न आव्यूह है। चूँकि सरल आरेख है, में मात्र 1s या 0s हैं और इसके विकर्ण अवयव सभी 0s हैं।
इस प्रकार से यहां लेबल, अप्रत्यक्ष आरेख़ और उसके लाप्लासियन आव्यूह का सरल उदाहरण दिया गया है।
| लेबल आव्यूह | घात आव्यूह | संलग्नता आव्यूह | लाप्लासियन आव्यूह |
|---|---|---|---|
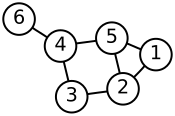
|
हम अप्रत्यक्ष आरेख़ के लिए देखते हैं कि आसन्न आव्यूह और लाप्लासियन आव्यूह दोनों सममित हैं, और लाप्लासियन आव्यूह की पंक्ति और स्तंभ-योग सभी शून्य हैं।
इस प्रकार से निर्देशित आरेखके लिए, या तो घात (आरेख़ सिद्धांत) का उपयोग किया जा सकता है, जो कि अनुप्रयोग पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरण में है:
| लेबल आव्यूह | संलग्नता आव्यूह | बाह्य-घात आव्यूह | बाह्य-घात लाप्लासियन | आंतरिक-घात आव्यूह | आंतरिक-घात लाप्लासियन |
|---|---|---|---|---|---|
निर्देशित आरेख़ में, आसन्न आव्यूह और लाप्लासियन आव्यूह दोनों असममित हैं। इसके लाप्लासियन आव्यूह में, स्तम्भ-योग या पंक्ति-योग शून्य हैं, यह इस बात पर निर्भर करता है कि घात (आरेख़ सिद्धांत) का उपयोग किया गया है या नहीं।
घटना आव्यूह के माध्यम से सममित लाप्लासियन
इस प्रकार से शीर्ष v और किनारे e के लिए अवयव Bve के साथ घटना आव्यूह B (शीर्ष और को, i > j से जोड़ता है) को
- द्वारा परिभाषित किया गया है।
यद्यपि इस परिभाषा में किनारों को तकनीकी रूप से निर्देशित किया गया है, उनकी दिशाएँ यादृच्छिक रूप से हो सकती हैं, फिर भी परिणाम समान सममित लाप्लासियन आव्यूह L को
के रूप में परिभाषित किया गया है जहां B का परिवर्त आव्यूह है।
| अप्रत्यक्ष आरेख | घटना आव्यूह | लाप्लासियन आव्यूह |
|---|---|---|
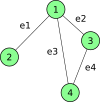
|
एक वैकल्पिक गुणनफल तथाकथित शीर्ष-आधारित लाप्लासियन को परिभाषित करता है, जो मूल रूप से उपयोग किए जाने वाले शीर्ष-आधारित लाप्लासियन आव्यूह L के विपरीत है।
निर्देशित आरेख़ के लिए सममित लाप्लासियन
इस प्रकार से एक निर्देशित आरेख का लाप्लासियन आव्यूह परिभाषा के अनुसार सामान्यतः गैर-सममित होता है, जबकि, इस प्रकार से उदाहरण के लिए, पारंपरिक वर्णक्रमीय क्लस्टरिंग मुख्य रूप से सममित आसन्नता और लाप्लासियन आव्यूह के साथ अप्रत्यक्ष आरेख के लिए विकसित की जाती है। अतः समरूपता की आवश्यकता वाली तकनीकों को लागू करने के लिए तुच्छ दृष्टिकोण मूल निर्देशित आरेख को अप्रत्यक्ष आरेख में बदलना और बाद के लिए लाप्लासियन आव्यूह का निर्माण करना है।
आव्यूह संकेतन में, अप्रत्यक्ष आरेख़ के आसन्न आव्यूह को, इस प्रकार से उदाहरण के लिए, मूल निर्देशित आरेख़ के आसन्न आव्यूह के OR गेट के रूप में परिभाषित किया जा सकता है और इसका आव्यूह का परिवर्त है, जहां की शून्य और एक प्रविष्टियाँ हैं मानों को संख्यात्मक के अतिरिक्त तार्किक माना जाए, जैसा कि निम्नलिखित उदाहरण में है:
| संलग्नता आव्यूह | सममित आसन्नता | सममित लाप्लासियन आव्यूह |
|---|---|---|
लाप्लासियन आव्यूह सामान्यीकरण
बड़ी घात वाला शीर्ष, जिसे भारी नोड भी कहा जाता है, के परिणामस्वरूप आव्यूह गुणों पर प्रभावी होने वाले लाप्लासियन आव्यूह में बडे विकर्ण की प्रविष्टि होती है। इस प्रकार से सामान्यीकरण का उद्देश्य लाप्लासियन आव्यूह की प्रविष्टियों को शीर्ष घात द्वारा विभाजित करके ऐसे शीर्षों के प्रभाव को अन्य शीर्षों के प्रभाव के बराबर बनाना है। शून्य से विभाजन से बचने के लिए, शून्य घात वाले पृथक शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है।
सममित रूप से सामान्यीकृत लाप्लासियन
इस प्रकार से सममित रूप से सामान्यीकृत लाप्लासियन आव्यूह को इस प्रकार परिभाषित किया गया है:[1]
जहाँ मूर-पेनरोज़ व्युत्क्रम है।
के अवयव इस प्रकार
- द्वारा दिए गए हैं।
अतः सममित रूप से सामान्यीकृत लाप्लासियन आव्यूह सममित है यदि और मात्र यदि आसन्न आव्यूह सममित है।
| संलग्नता आव्यूह | घात आव्यूह | सामान्यीकृत लाप्लासियन |
|---|---|---|
इस प्रकार से निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी भी घात (आरेख़ सिद्धांत) का उपयोग सामान्यीकरण के लिए किया जा सकता है:
| संलग्नता आव्यूह | बाह्य-घात आव्यूह | बाह्य-घात सामान्यीकृत लाप्लासियन | आंतरिक-घात आव्यूह | आंतरिक-घात सामान्यीकृत लाप्लासियन |
|---|---|---|---|---|
बाएँ (यादृच्छिक-चाल) और दाएँ सामान्यीकृत लाप्लासियन
इस प्रकार से बाएं (यादृच्छिक-चाल) सामान्यीकृत लाप्लासियन आव्यूह को इस प्रकार परिभाषित किया गया है:
जहाँ मूर-पेनरोज़ व्युत्क्रम है। के अवयव
- द्वारा दिये गये हैं।
अतः इसी प्रकार, दाएं सामान्यीकृत लाप्लासियन आव्यूह को
- के रूप में परिभाषित किया गया है।
यदि सभी पृथक शीर्षों के तुच्छ स्थितियों को छोड़कर, आसन्न आव्यूह सममित है, तो बाएँ या दाएँ सामान्यीकृत लाप्लासियन आव्यूह सममित नहीं है। इस प्रकार से उदाहरण के लिए,
| संलग्नता आव्यूह | घात आव्यूह | बाएं सामान्यीकृत लाप्लासियन | दाएँ सामान्यीकृत लाप्लासियन |
|---|---|---|---|
उदाहरण यह भी दर्शाता है कि यदि में कोई पृथक शीर्ष नहीं है, तो दाएं प्रसंभाव्य आव्यूह और इसलिए यह एक यादृच्छिक चाल का आव्यूह है, ताकि बाएं सामान्यीकृत लाप्लासियन में प्रत्येक पंक्ति का योग शून्य हो। इस प्रकार हम कभी-कभी वैकल्पिक रूप से को यादृच्छिक-चाल सामान्यीकृत लाप्लासियन कहते हैं। कम असामान्य रूप से उपयोग किए जाने वाले दाएं सामान्यीकृत लाप्लासियन में प्रत्येक स्तम्भ का योग शून्य होता है क्योंकि को प्रसंभाव्य छोड़ दिया जाता है।
इस प्रकार से निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी को सामान्यीकरण के लिए घात (आरेख़ सिद्धांत) चुनने की भी आवश्यकता होती है:
| संलग्नता आव्यूह | बाह्य-घात आव्यूह | बाह्य-घात बाएं सामान्यीकृत लाप्लासियन | आंतरिक-घात आव्यूह | आंतरिक-घात दाएँ सामान्यीकृत लाप्लासियन |
|---|---|---|---|---|
पंक्ति-योग सभी 0 के साथ बाएं बाह्य-घात सामान्यीकृत लाप्लासियन दाएं प्रसंभाव्य आव्यूह से संबंधित है, जबकि स्तम्भ-योग सभी 0 के साथ दाएं आंतरिक-घात सामान्यीकृत लाप्लासियन में बाएं प्रसंभाव्य आव्यूह सम्मिलित है।
भारित किनारों वाले आरेख़ के लिए परिभाषाएँ
अनुप्रयोगों में सामान्य भारित किनारों वाले आरेख़ को सरलता से उनके आसन्न आव्यूह द्वारा परिभाषित किया जाता है जहां प्रविष्टियों के मान संख्यात्मक होते हैं और अब शून्य और तक सीमित नहीं होते हैं। अतः वर्णक्रमीय क्लस्टरिंग और आरेख़-आधारित संकेत प्रोसेसिंग में, जहां आरेख़ शीर्ष डेटा बिंदुओं का प्रतिनिधित्व करते हैं, किनारे के भार की गणना की जा सकती है, इस प्रकार से उदाहरण के लिए, डेटा बिंदुओं के युग्म के बीच दूरी आव्यूह के व्युत्क्रमानुपाती के रूप में, जिसके परिणामस्वरूप सभी भार अनौपचारिक रूप से बड़े मानों के साथ गैर-ऋणात्मक होते हैं डेटा बिंदुओं के अधिक समान युग्म के अनुरूप हैं। डेटा बिंदुओं के बीच सहसंबंध और विरोधी सहसंबंध का उपयोग करने से स्वाभाविक रूप से धनात्मक और ऋणात्मक दोनों प्रकार के भार उत्पन्न होते हैं। सरल आरेख़ की अधिकांश परिभाषाएँ गैर-ऋणात्मक भार के मानक स्थितियों तक तुच्छ रूप से विस्तारित हैं, जबकि ऋणात्मक भार पर अधिक ध्यान देने की आवश्यकता होती है, विशेषकर सामान्यीकरण में।
लाप्लासियन आव्यूह
इस प्रकार से लाप्लासियन आव्यूह को
द्वारा परिभाषित किया गया है, जहां D घात आव्यूह है और A आरेख़ का आसन्न आव्यूह है।
इस प्रकार से निर्देशित आरेख़ के लिए, या तो घात (आरेख़ सिद्धांत) का उपयोग किया जा सकता है, जो कि अनुप्रयोग पर निर्भर करता है, जैसा कि निम्नलिखित उदाहरण में है:
| संलग्नता आव्यूह | आंतरिक-घात आव्यूह | आंतरिक-घात लाप्लासियन | बाह्य-घात आव्यूह | बाह्य-घात लाप्लासियन |
|---|---|---|---|---|
आरेख़ स्वयं-पाश, जो आसन्न आव्यूह के मुख्य विकर्ण पर गैर-शून्य प्रविष्टियों द्वारा स्वयं को प्रकट करते हैं, इसकी अनुमति है परन्तु आरेख़ लाप्लासियन मानों को प्रभावित नहीं करते हैं।
घटना आव्यूह के माध्यम से सममित लाप्लासियन
भारित किनारों वाले आरेख़ के लिए कोई भारित घटना आव्यूह B को परिभाषित कर सकता है और इसका उपयोग के रूप में संबंधित सममित लाप्लासियन के निर्माण के लिए कर सकता है। यहां वर्णित वैकल्पिक स्पष्ट दृष्टिकोण, भार को संपर्क से अलग करना है: नियमित आरेख़ के लिए घटना आव्यूह का उपयोग करना जारी रखें और मात्र भार के मान रखने वाले आव्यूह को प्रस्तुत करें। स्प्रिंग प्रणाली इस मॉडल का उदाहरण है जिसका उपयोग यांत्रिकी में दी गई संदृढ़ता और इकाई लंबाई के स्प्रिंग की प्रणाली का वर्णन करने के लिए किया जाता है, जहां संदृढ़ता के मान आरेख किनारों के भार की भूमिका निभाते हैं।
इस प्रकार हम शीर्ष v के लिए Bve और
- द्वारा परिभाषित किनारे e के साथ भारहीन घटना आव्यूह B की परिभाषा का पुन: उपयोग करते हैं।
अब हम विकर्ण आव्यूह W को भी परिभाषित करते हैं जिसमें किनारे का भार होता है। यद्यपि B की परिभाषा में किनारों को तकनीकी रूप से निर्देशित किया गया है, उनकी दिशाएं यादृच्छिक रूप से हो सकती हैं, फिर भी समान सममित लाप्लासियन आव्यूह L को
के रूप में परिभाषित किया गया है जहाँ B का परिवर्त है।
इस प्रकार से निर्माण को निम्नलिखित उदाहरण में दर्शाया गया है, जहां प्रत्येक किनारे को के साथ भार मान i दिया गया है।
| अप्रत्यक्ष आरेख | घटना आव्यूह | किनारे भार | लाप्लासियन आव्यूह |
|---|---|---|---|

|
निर्देशित आरेख़ के लिए सममित लाप्लासियन
साधारण आरेख़ के जैसे, निर्देशित भारित आरेख़ का लाप्लासियन आव्यूह परिभाषा के अनुसार सामान्यतः गैर-सममित होता है। लाप्लासियन के निर्माण से पहले मूल निर्देशित आरेख को अप्रत्यक्ष आरेख में बदलकर समरूपता लागू की जा सकती है। अप्रत्यक्ष आरेख़ के आसन्न आव्यूह को, इस प्रकार से उदाहरण के लिए, मूल निर्देशित आरेख़ के आसन्न आव्यूह के योग के रूप में परिभाषित किया जा सकता है और इसका आव्यूह निम्नलिखित उदाहरण के अनुसार का परिवर्त है:
| संलग्नता आव्यूह | सममित संलग्नता आव्यूह | सममित लाप्लासियन आव्यूह |
|---|---|---|
जहाँ की शून्य और एक प्रविष्टियाँ को सरल आरेख, मानों के लिए तार्किक के अतिरिक्त संख्यात्मक माना जाता है, जो परिणामों में अंतर को समझाते हैं - सरल आरेख के लिए, सममित आरेख को अभी भी सरल होने की आवश्यकता है, इसके सममित आसन्न आव्यूह में मात्र तार्किक होना चाहिए, संख्यात्मक मान नहीं, इस प्रकार से उदाहरण के लिए, तार्किक योग 1 v 1 = 1 है, जबकि संख्यात्मक योग 1 + 1 = 2 है।
इस प्रकार से वैकल्पिक रूप से, सममित लाप्लासियन आव्यूह की गणना घात (आरेख सिद्धांत) का उपयोग करके दो लाप्लासियन से की जा सकती है, जैसा कि निम्नलिखित उदाहरण में है:
| संलग्नता आव्यूह | बाह्य-घात आव्यूह | बाह्य-घात लाप्लासियन | आंतरिक-घात आव्यूह | आंतरिक-घात लाप्लासियन |
|---|---|---|---|---|
अतः इस प्रकार से बाह्य-घात लाप्लासियन परिवर्त और आंतरिक-घात लाप्लासियन का योग सममित लाप्लासियन आव्यूह के बराबर होता है।
लाप्लासियन आव्यूह सामान्यीकरण
सामान्यीकरण का लक्ष्य, सरल आरेख़ के जैसे, लाप्लासियन आव्यूह की विकर्ण प्रविष्टियों को सभी इकाई बनाना है, साथ ही ऑफ-विकर्ण प्रविष्टियों को तदनुसार सोपानी करना है। ग्लोसरी ऑफ आरेख सिद्धांत वेटेड आरेख में, शीर्ष में जुड़े हुए किनारों की छोटी संख्या के कारण बड़ी घात हो सकती है, परन्तु बड़े भार के साथ-साथ इकाई भार के साथ बड़ी संख्या में जुड़े किनारों के कारण भी है।
इस प्रकार से आरेख़ स्वयं-पाश, अर्थात, आसन्न आव्यूह के मुख्य विकर्ण पर गैर-शून्य प्रविष्टियाँ, आरेख़ लाप्लासियन मानों को प्रभावित नहीं करती हैं, परन्तु सामान्यीकरण कारकों की गणना के लिए गणना करने की आवश्यकता हो सकती है।
सममित रूप से सामान्यीकृत लाप्लासियन
सममित रूप से सामान्यीकृत लाप्लासियन को
के रूप में परिभाषित किया गया है, जहां L असामान्य लाप्लासियन है, A आसन्न आव्यूह है, D घात आव्यूह है, और मूर-पेनरोज़ व्युत्क्रम है। चूँकि घात आव्यूह D विकर्ण है, इसका व्युत्क्रम वर्गमूल मात्र विकर्ण आव्यूह है जिसकी विकर्ण प्रविष्टियाँ D की विकर्ण प्रविष्टियों के वर्गमूल के व्युत्क्रम हैं। यदि सभी किनारे के भार गैर-ऋणात्मक हैं तो सभी घात मान स्वचालित रूप से भी गैर-ऋणात्मक हैं और इसलिए प्रत्येक घात मान का अद्वितीय धनात्मक वर्गमूल होता है। इस प्रकार से शून्य से विभाजन से बचने के लिए, शून्य घात वाले शीर्षों को सामान्यीकरण की प्रक्रिया से बाहर रखा गया है, जैसा कि निम्नलिखित उदाहरण में है:
| संलग्नता आव्यूह | आंतरिक-घात आव्यूह | आंतरिक-घात सामान्यीकृत लाप्लासियन | बाह्य-घात आव्यूह | बाह्य-घात सामान्यीकृत लाप्लासियन |
|---|---|---|---|---|
सममित रूप से सामान्यीकृत लाप्लासियन सममित आव्यूह है यदि और मात्र यदि आसन्न आव्यूह A सममित है और D की विकर्ण प्रविष्टियाँ गैर-ऋणात्मक हैं, तो उस स्थिति में हम 'सममित सामान्यीकृत लाप्लासियन' शब्द का उपयोग कर सकते हैं।
इस प्रकार से सममित सामान्यीकृत लाप्लासियन आव्यूह को भार रहित घटना आव्यूह B और विकर्ण आव्यूह W का उपयोग करके
के रूप में भी लिखा जा सकता है, जिसमें किनारे का भार होता है और नवीन भारित घटना आव्यूह को परिभाषित करता है, जिनकी पंक्तियों को शीर्षों द्वारा अनुक्रमित किया जाता है और जिनके स्तंभों को G के किनारों द्वारा अनुक्रमित किया जाता है, जैसे कि किनारे e = {u, v} के अनुरूप प्रत्येक स्तंभ में u के अनुरूप पंक्ति में एक प्रविष्टि होती है, v के अनुरूप पंक्ति में एक प्रविष्टि होती है, और अन्यत्र 0 प्रविष्टियाँ होती हैं।
यादृच्छिक चाल सामान्यीकृत लाप्लासियन
इस प्रकार से यादृच्छिक चाल सामान्यीकृत लाप्लासियन को
के रूप में परिभाषित किया गया है जहां D घात आव्यूह है। चूँकि घात आव्यूह D विकर्ण है, इसके व्युत्क्रम को मात्र विकर्ण आव्यूह के रूप में परिभाषित किया गया है, जिसमें विकर्ण प्रविष्टियाँ हैं जो D की संगत विकर्ण प्रविष्टियों के व्युत्क्रम हैं। पृथक शीर्षों (घात 0 वाले) के लिए, एक सामान्य विकल्प संबंधित अवयव को 0 पर समूहित करना है। के आव्यूह अवयव
- द्वारा दिए गए हैं।
अतः यादृच्छिक-चाल सामान्यीकृत लाप्लासियन का नाम इस तथ्य से आता है कि यह आव्यूह है, जहां गैर-ऋणात्मक भार मानते हुए, आरेख़ पर यादृच्छिक चालक का संक्रमण आव्यूह है। इस प्रकार से उदाहरण के लिए, मान लीजिए कि i-वें मानक आधार सदिश को दर्शाता है। फिर एक प्रायिकता सदिश है जो शीर्ष से चरण उठाने के बाद यादृच्छिक चालक के स्थानों के वितरण का प्रतिनिधित्व करता है; अर्थात । अधिक सामान्यतः, यदि सदिश आरेख़ के शीर्षों पर यादृच्छिक चालक के स्थान का प्रायिकता वितरण है, तो चरणों के बाद चालक का प्रायिकता वितरण है।
यादृच्छिक चाल सामान्यीकृत लाप्लासियन को बाएं सामान्यीकृत लाप्लासियन भी कहा जा सकता है क्योंकि सामान्यीकरण बाईं ओर सामान्यीकरण आव्यूह द्वारा लाप्लासियन को गुणा करके किया जाता है। इसमें प्रत्येक पंक्ति का योग शून्य है क्योंकि दायाँ प्रसंभाव्य है, यह मानते हुए कि सभी भार गैर-ऋणात्मक हैं।
अतः कम असामान्य रूप से उपयोग किए जाने वाले दाएं सामान्यीकृत लाप्लासियन में प्रत्येक स्तम्भ का योग शून्य होता है क्योंकि बायां प्रसंभाव्य है।
इस प्रकार से निर्देशित आरेख़ के गैर-सममित आसन्न आव्यूह के लिए, किसी को सामान्यीकरण के लिए घात (आरेख़ सिद्धांत) चुनने की भी आवश्यकता होती है:
| संलग्नता आव्यूह | बाह्य-घात आव्यूह | बाह्य-घात बाएं सामान्यीकृत लाप्लासियन | आंतरिक-घात आव्यूह | आंतरिक-घात दाएँ सामान्यीकृत लाप्लासियन |
|---|---|---|---|---|
अतः पंक्ति-योग सभी 0 के साथ बाएं बाह्य-घात सामान्यीकृत लाप्लासियन दाएँ प्रसंभाव्य आव्यूह से संबंधित है, जबकि सभी 0 के साथ दाएँ आंतरिक-घात सामान्यीकृत लाप्लासियन में बाएं प्रसंभाव्य आव्यूह सम्मिलित है।
ऋणात्मक भार
इस प्रकार से ऋणात्मक भार सामान्यीकरण के लिए कई आक्षेप प्रस्तुत करते हैं:
- ऋणात्मक भार की उपस्थिति के परिणामस्वरूप गैर-पृथक शीर्षों के लिए स्वाभाविक रूप से शून्य पंक्ति- और/या स्तंभ-योग हो सकता है। धनात्मक भारों की बड़ी पंक्ति-योग और समान रूप से ऋणात्मक भारों की समान रूप से बड़ी पंक्ति-योग वाला शीर्ष, जिसका योग शून्य है, को भारी नोड माना जा सकता है और दोनों बड़े मानों को सोपानी किया जा सकता है, जबकि विकर्ण प्रविष्टि शून्य रहती है, जैसे कि पृथक शीर्ष आदि।
- ऋणात्मक भार ऋणात्मक पंक्ति- और/या स्तंभ-योग भी दे सकते हैं, जिससे कि गैर-सामान्यीकृत लाप्लासियन आव्यूह में संबंधित विकर्ण प्रविष्टि ऋणात्मक होगी और सममित सामान्यीकरण के लिए आवश्यक धनात्मक वर्गमूल स्थित नहीं होगा।
- सामान्यीकरण के प्रयोजन के लिए पंक्ति- और/या स्तंभ-योग का पूर्ण मान लेने के लिए तर्क दिए जा सकते हैं, इस प्रकार संभावित मान -1 को सामान्यीकृत लाप्लासियन आव्यूह के मुख्य विकर्ण की वैध इकाई प्रविष्टि के रूप में माना जा सकता है।
गुण
इस प्रकार से एक (अप्रत्यक्ष) आरेख़ G और उसके लाप्लासियन आव्यूह L के लिए आइगेनमान के साथ:
- L सममित आव्यूह है।
- L धनात्मक-निश्चित आव्यूह (अर्थात सभी के लिए है) है। इसे इस तथ्य से देखा जा सकता है कि लाप्लासियन सममित और विकर्ण रूप से प्रभावशाली आव्यूह अनुप्रयोग और गुण है।
- L एम-आव्यूह है (इसकी संवृत-विकर्ण प्रविष्टियाँ गैर-धनात्मक हैं, फिर भी इसके आइगेन मानों के वास्तविक भाग गैर-ऋणात्मक हैं)।
- L की प्रत्येक पंक्ति और स्तंभ का योग शून्य है। वस्तुतः, योग में, शीर्ष की घात को प्रत्येक निकटवर्ती के लिए -1 के साथ जोड़ा जाता है।
- परिणामस्वरूप, , क्योंकि सदिश , को संतुष्ट करता है। इसका तात्पर्य यह भी है कि लाप्लासियन आव्यूह एकवचन है।
- आरेख़ में सम्बद्ध अवयव (आरेख सिद्धांत) की संख्या लाप्लासियन के कर्नेल (रैखिक बीजगणित) का आयाम है और 0 आइगेनमान के आइगेनमान और आइगेनसदिश बीजगणितीय बहुलता है।
- L के सबसे छोटे गैर-शून्य आइगेनमान को वर्णक्रमीय अंतराल कहा जाता है।
- L का दूसरा सबसे छोटा आइगेनमान (शून्य हो सकता है) G की बीजगणितीय संपर्क (या फ़िडलर मान) है और आरेख़ के कट (आरेख सिद्धांत) सबसे विरल कट का अनुमान लगाता है।
- लाप्लासियन फलन के एन-विमीय सदिश समष्टि पर संक्रियक है, जहाँ G और का शीर्ष समुच्चय है।
- जब G, के-नियमित आरेख होता है, तो सामान्यीकृत लाप्लासियन होता है: , जहां A आसन्नता आव्यूह है और I तत्समक आव्यूह है।
- एकाधिक सम्बद्ध घटक (आरेख़ सिद्धांत) वाले आरेख़ के लिए, L कक्ष आव्यूह कक्ष विकर्ण आव्यूह आव्यूह है, जहां प्रत्येक कक्ष प्रत्येक घटक के लिए संबंधित लाप्लासियन आव्यूह है, संभवतः शीर्षों को पुन: व्यवस्थित करने के बाद है (अर्थात L कक्ष विकर्ण आव्यूह के समान क्रमपरिवर्तन है)।
- लाप्लासियन आव्यूह L का ट्रेस के बराबर है जहां विचारित आरेख़ के किनारों की संख्या है।
- अब इकाई-मानक आइगेन मान और संबंधित :
- के साथ , के आइगेन अपघटन पर विचार करें।
क्योंकि को स्वयं सदिश के आंतरिक गुणनफल के रूप में लिखा जा सकता है इससे ज्ञात होता है कि और इसलिए के आइगेनमान सभी गैर-ऋणात्मक हैं।
- सामान्यीकृत सममित लाप्लासियन के सभी आइगेनमान 0 = μ0 ≤ … ≤ μn−1 ≤ 2 को संतुष्ट करते हैं। ये आइगेनमान (सामान्यीकृत लाप्लासियन के वर्णक्रम के रूप में जाना जाता है) सामान्य आरेख़ के लिए अन्य आरेख़ अपरिवर्तनीयों से अच्छी तरह से संबंधित हैं।[1]
- कोई इसकी जाँच कर सकता है:
- ,
अर्थात, सामान्यीकृत लाप्लासियन के समान है। अतः इस कारण से, यद्यपि सामान्य रूप से सममित नहीं है, इसके वास्तविक आइगेन मान हैं - निश्चित सामान्यीकृत सममित लाप्लासियन के आइगेन मान के समान है।
निरंतर लाप्लासियन का अनुमान लगाने वाले असतत लाप्लास संक्रियक के रूप में व्याख्या
आरेख़ लाप्लासियन आव्यूह को परिमित अंतर विधि द्वारा प्राप्त ऋणात्मक निरंतर लाप्लासियन संक्रियक का अनुमान लगाने वाले आरेख़ पर ऋणात्मक असतत लाप्लास संक्रियक के आव्यूह रूप के रूप में देखा जा सकता है। (असतत पॉइसन समीकरण देखें)[2] इस व्याख्या में, प्रत्येक आरेख शीर्ष को ग्रिड बिंदु के रूप में माना जाता है; शीर्ष की स्थानीय संपर्क इस ग्रिड बिंदु पर परिमित अंतर सन्निकटन स्टेंसिल (संख्यात्मक विश्लेषण) निर्धारित करती है, ग्रिड का आकार सदैव प्रत्येक किनारे के लिए होता है, और किसी भी ग्रिड बिंदु पर कोई बाधा नहीं होती है, जो सजातीय न्यूमैन के स्थितियों से मेल खाती है सीमा की स्थिति, अर्थात, मुक्त सीमा। इस प्रकार की व्याख्या किसी को अनुमति देती है, इस प्रकार से उदाहरण के लिए, अनंत संख्या में शीर्षों और किनारों वाले आरेख़ के स्थितियों में लाप्लासियन आव्यूह को सामान्यीकृत करना, जिससे अनंत आकार का लाप्लासियन आव्यूह बनता है।
लाप्लासियन आव्यूह का सामान्यीकरण और विस्तार
सामान्यीकृत लाप्लासियन
इस प्रकार से सामान्यीकृत लाप्लासियन को इस प्रकार परिभाषित किया गया है:[3]
ध्यान दें कि साधारण लाप्लासियन सामान्यीकृत लाप्लासियन है।
चुंबकीय लाप्लासियन
आसन्न आव्यूह की प्रविष्टियाँ मिश्रित-मानित हो सकती हैं, जिस स्थिति में आव्यूह समरूपता की धारणा को हर्मिटियन आव्यूह के साथ प्रतिस्थापित करने की आवश्यकता होती है। अतः वास्तविक भार के साथ निर्देशित आरेख़ के लिए चुंबकीय लाप्लासियन का निर्माण मिश्रित प्रविष्टियों
के साथ सममित लाप्लासियन और हर्मिटियन चरण आव्यूह के वास्तविक सममित आव्यूह के हैडामर्ड गुणनफल (आव्यूह) के रूप में किया गया है जो जटिल तल में चरण में किनारे की दिशा को एन्कोड करता है। क्वांटम भौतिकी के संदर्भ में, चुंबकीय लाप्लासियन की व्याख्या उस संक्रियक के रूप में की जा सकती है जो आरेख पर मुक्त आवेशित कण की घटना विज्ञान का वर्णन करता है, जो एक चुंबकीय क्षेत्र की क्रिया के अधीन है और पैरामीटर को विद्युत आवेश कहा जाता है।[4] निम्नलिखित उदाहरण में :
| संलग्नता आव्यूह | सममित Laplacian | Phase matrix | Magnetic Laplacian |
|---|---|---|---|
विकृत लाप्लासियन
इस प्रकार से विकृत लाप्लासियन को सामान्यतः
के रूप में परिभाषित किया जाता है जहां I तत्समक आव्यूह है, A आसन्न आव्यूह है, D घात आव्यूह है, और s (मिश्रित-मानित) संख्या है। [5]
मानक लाप्लासियन मात्र और है जो चिन्ह रहित लाप्लासियन है।
चिह्नहीन लाप्लासियन
अतः इस प्रकार से चिह्नहीन लाप्लासियन को
के रूप में परिभाषित किया जाता है, जहाँ घात आव्यूह है, और आसन्नता आव्यूह है।[6] हस्ताक्षरित लाप्लासियन के जैसे, चिह्नहीन लाप्लासियन भी धनात्मक अर्ध-निश्चित है क्योंकि इसे
के रूप में गुणनखंडित किया जा सकता है, जहाँ घटना आव्यूह है। के निकट 0-आइगेनसदिश है यदि और मात्र तभी जब इसमें पृथक शीर्षों के अतिरिक्त कोई द्विसमूह जुड़ा घटक हो। इसे
के रूप में दिखाया जा सकता है।
इस प्रकार से इसका एक हल है जहाँ यदि और मात्र यदि आरेख़ में द्विदलीय जुड़ा हुआ घटक है।
निर्देशित बहुआरेख
इस प्रकार से निर्देशित बहुआरेख के लिए लाप्लासियन आव्यूह का एनालॉग परिभाषित किया जा सकता है।[7] इस स्थितियों में लाप्लासियन आव्यूह L को
के रूप में परिभाषित किया गया है, जहां D एक विकर्ण आव्यूह है, जिसमें Di,i शीर्ष i की बाह्यघात के बराबर है और A एक आव्यूह है जिसमें Ai,j i से j तक किनारों की संख्या के बराबर है (पाश सहित)।
ओपन सोर्स सॉफ़्टवेयर कार्यान्वयन
एप्लीकेशन सॉफ्टवेयर
- स्किकिट-लर्न स्पेक्ट्रल क्लस्टरिंग[10]
- पाईजीएसपी: पायथन में आरेख़ संकेत प्रोसेसिंग[11]
- मेगामैन: लाखों अंकों के लिए मैनिफोल्ड लर्निंग[12]
- स्मूथजी[13]
- डायनामिक आरेख़ के लिए लाप्लासियन परिवर्तन बिंदु संसूचन (केडीडी 2020)[14]
- लाप्लासियनऑप्ट (लाप्लासियन के भारित आरेख़ के दूसरे आइगेनमान को अधिकतम करने के लिए जूलिया पैकेज) [15]
- LigMG (बड़ा अनियमित आरेख़ बहुग्रिड)[16]
- लाप्लासियंस.जेएल[17]
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 1.2 Chung, Fan (1997) [1992]. Spectral Graph Theory. American Mathematical Society. ISBN 978-0821803158.
- ↑ Smola, Alexander J.; Kondor, Risi (2003), "Kernels and regularization on graphs", Learning Theory and Kernel Machines: 16th Annual Conference on Learning Theory and 7th Kernel Workshop, COLT/Kernel 2003, Washington, DC, USA, August 24–27, 2003, Proceedings, Lecture Notes in Computer Science, vol. 2777, Springer, pp. 144–158, CiteSeerX 10.1.1.3.7020, doi:10.1007/978-3-540-45167-9_12, ISBN 978-3-540-40720-1.
- ↑ Godsil, C.; Royle, G. (2001). बीजगणितीय ग्राफ सिद्धांत, गणित में स्नातक ग्रंथ. Springer-Verlag.
- ↑ Satoshi Furutani; Toshiki Shibahara; Mitsuaki Akiyama; Kunio Hato; Masaki Aida (2020). हर्मिटियन लाप्लासियन पर आधारित निर्देशित ग्राफ़ के लिए ग्राफ़ सिग्नल प्रोसेसिंग (PDF). ECML PKDD 2019: Machine Learning and Knowledge Discovery in Databases. pp. 447–463. doi:10.1007/978-3-030-46150-8_27.
- ↑ Morbidi, F. (2013). "विकृत आम सहमति प्रोटोकॉल" (PDF). Automatica. 49 (10): 3049–3055. doi:10.1016/j.automatica.2013.07.006. S2CID 205767404.
- ↑ Cvetković, Dragoš; Simić, Slobodan K. (2010). "साइनलेस लाप्लासियन पर आधारित ग्राफ़ के एक वर्णक्रमीय सिद्धांत की ओर, III". Applicable Analysis and Discrete Mathematics. 4 (1): 156–166. doi:10.2298/AADM1000001C. ISSN 1452-8630. JSTOR 43671298.
- ↑ Chaiken, S.; Kleitman, D. (1978). "Matrix Tree Theorems". Journal of Combinatorial Theory, Series A. 24 (3): 377–381. doi:10.1016/0097-3165(78)90067-5. ISSN 0097-3165.
- ↑ "SciPy". GitHub. 24 March 2022.
- ↑ "नेटवर्कएक्स". GitHub. 24 March 2022.
- ↑ "2.3. Clustering".
- ↑ "PyGSP: Graph Signal Processing in Python". GitHub. 23 March 2022.
- ↑ "Megaman: Manifold Learning for Millions of Points". GitHub. 14 March 2022.
- ↑ "स्मूथजी". GitHub. 17 September 2020.
- ↑ "Announcing Our Paper at KDD 2020".
- ↑ "Harshangrjn/LaplacianOpt.jl". GitHub. 2 February 2022.
- ↑ "LigMG (बड़ा अनियमित ग्राफ़ मल्टीग्रिड) - बड़े अनियमित ग्राफ़ के लिए एक वितरित मेमोरी ग्राफ़ लाप्लासियन सॉल्वर". GitHub. 5 January 2022.
- ↑ "लाप्लासियंस.जे.एल". GitHub. 11 March 2022.

