संवृत ग्राफ प्रमेय: Difference between revisions
mNo edit summary |
No edit summary |
||
| (12 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Theorem relating continuity to graphs}} | {{Short description|Theorem relating continuity to graphs}} | ||
{{multiple image | {{multiple image | ||
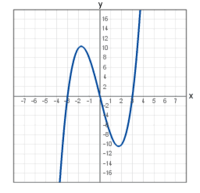
| footer = अंतराल <math>[-4, 4]</math> पर [[ | | footer = अंतराल <math>[-4, 4]</math> पर [[क्यूबिक फंक्शन]] <math>f(x) = x^3 - 9x</math> का ग्राफ़ बंद है क्योंकि फ़ंक्शन [[कंटीन्यूअस फंक्शन |कंटीन्यूअस]] है। <math>[-2, 2]</math> [[हैविसिडे फंक्शन ]] का ग्राफ़ बंद नहीं है, क्योंकि फ़ंक्शन निरंतर नहीं है। | ||
| width = 200 | | width = 200 | ||
| image1 = cubicpoly.png | | image1 = cubicpoly.png | ||
| Line 9: | Line 8: | ||
| alt2 = The Heaviside function | | alt2 = The Heaviside function | ||
}} | }} | ||
गणित में, | गणित में, '''संवृत ग्राफ़ प्रमेय''' कई आधारस्वरूप परिणामों में से एक को संदर्भित कर सकता है जो उनके ग्राफ़ के संदर्भ में निरंतर कार्यों को दर्शाता है। प्रत्येक स्थिति में [[बंद ग्राफ|संवृत ग्राफ]] वाले कार्य आवश्यक रूप से निरंतर होते हैं। | ||
== संवृत रेखांकन वाले रेखांकन और आरेख == | |||
यदि <math>f : X \to Y</math> [[टोपोलॉजिकल स्पेस|टोपोलॉजिकल]] स्थान के बीच एक आरेख है, फिर <math>f</math> ग्राफ सेट है <math>\operatorname{Gr} f := \{ (x, f(x)) : x \in X \}</math> या समकक्ष, | यदि <math>f : X \to Y</math> [[टोपोलॉजिकल स्पेस|टोपोलॉजिकल]] स्थान के बीच एक आरेख है, फिर <math>f</math> ग्राफ सेट है <math>\operatorname{Gr} f := \{ (x, f(x)) : x \in X \}</math> या समकक्ष, | ||
<math display=block>\operatorname{Gr} f := \{ (x, y) \in X \times Y : y = f(x) \}</math> | <math display=block>\operatorname{Gr} f := \{ (x, y) \in X \times Y : y = f(x) \}</math> | ||
कहा जाता है कि ग्राफ <math>f</math> | कहा जाता है कि ग्राफ <math>f</math> संवृत है यदि <math>\operatorname{Gr} f</math> <math>X \times Y</math> का एक [[बंद सेट|संवृत सेट]] है ([[उत्पाद टोपोलॉजी]] के साथ)। | ||
किसी भी निरंतर कार्य का एक | किसी भी निरंतर कार्य का एक संवृत ग्राफ हॉसडॉर्फ अंतरिक्ष स्थान होता है। | ||
कोई रैखिक आरेख, <math>L : X \to Y,</math> दो टोपोलॉजिकल वेक्टर स्थान के बीच जिनकी टोपोलॉजी (कॉची) ट्रांसलेशन इनवेरिएंट मेट्रिक्स के संबंध में पूर्ण हैं, और यदि अतिरिक्त (1a) <math>L</math> उत्पाद टोपोलॉजीके अर्थ में क्रमिक रूप से निरंतर है, फिर आरेख L निरंतर है और इसका ग्राफ, Gr L अनिवार्य रूप से | कोई रैखिक आरेख, <math>L : X \to Y,</math> दो टोपोलॉजिकल वेक्टर स्थान के बीच जिनकी टोपोलॉजी (कॉची) ट्रांसलेशन इनवेरिएंट मेट्रिक्स के संबंध में पूर्ण हैं, और यदि अतिरिक्त (1a) <math>L</math> उत्पाद टोपोलॉजीके अर्थ में क्रमिक रूप से निरंतर है, फिर आरेख L निरंतर है और इसका ग्राफ, Gr <math>L</math> अनिवार्य रूप से संवृत है।। इसके विपरीत यदि <math>L</math> (1a) के स्थान पर एक ऐसा रेखीय आरेख है, जिसका ग्राफ <math>L</math> (1b) है <math>X \times Y</math> कार्टेशियन उत्पाद स्थान में संवृत होने के लिए जाना जाता है , तब <math>L</math> निरंतर और आवश्यक रूप से क्रमिक निरंतर है।{{sfn|Rudin|1991|p=51-52}} | ||
=== निरंतर आरेख के उदाहरण जिनमें | === निरंतर आरेख के उदाहरण जिनमें संवृत ग्राफ नहीं है === | ||
यदि <math>X</math> कोई स्थान है तो पहचान आरेख <math>\operatorname{Id} : X \to X</math> निरंतर है लेकिन इसका ग्राफ <math>\operatorname{Gr} \operatorname{Id} := \{ (x, x) : x \in X \},</math>जो विकर्ण है, <math>X \times X</math> में | यदि <math>X</math> कोई स्थान है तो पहचान आरेख <math>\operatorname{Id} : X \to X</math> निरंतर है लेकिन इसका ग्राफ <math>\operatorname{Gr} \operatorname{Id} := \{ (x, x) : x \in X \},</math>जो विकर्ण है, <math>X \times X</math> में संवृत है यदि और केवल यदि <math>X</math> हॉसडॉर्फ है।{{sfn|Rudin|1991|p=50}} विशेष रूप से, यदि <math>X</math> हौसडॉर्फ नहीं है तब <math>\operatorname{Id} : X \to X</math> निरंतर है लेकिन इसका संवृत ग्राफ़ नहीं है। | ||
माना की <math>X</math> वास्तविक संख्याओं <math>\R</math> सामान्य [[यूक्लिडियन टोपोलॉजी]] के साथ को निरूपित करता है और <math>Y</math> अविवेकपूर्ण टोपोलॉजी के साथ <math>\R</math> को निरूपित करता है (जहां ध्यान दें कि <math>Y</math> हॉसडॉर्फनहीं है और यह कि Y में मान का प्रत्येक फलन सतत है)। माना की <math>f : X \to Y</math> द्वारा <math>f(0) = 1</math> और <math>f(x) = 0</math> सभी के लिए <math>x \neq 0</math>. परिभाषित किया जाना चाहिए फिर <math>f : X \to Y</math> निरंतर है लेकिन इसका ग्राफ<math>X \times X</math> में | माना की <math>X</math> वास्तविक संख्याओं <math>\R</math> सामान्य [[यूक्लिडियन टोपोलॉजी]] के साथ को निरूपित करता है और <math>Y</math> अविवेकपूर्ण टोपोलॉजी के साथ <math>\R</math> को निरूपित करता है (जहां ध्यान दें कि <math>Y</math> हॉसडॉर्फनहीं है और यह कि Y में मान का प्रत्येक फलन सतत है)। माना की <math>f : X \to Y</math> द्वारा <math>f(0) = 1</math> और <math>f(x) = 0</math> सभी के लिए <math>x \neq 0</math>. परिभाषित किया जाना चाहिए फिर <math>f : X \to Y</math> निरंतर है लेकिन इसका ग्राफ<math>X \times X</math> में संवृत नहीं है .{{sfn|Narici|Beckenstein|2011|pp=459-483}} | ||
== पॉइंट-सेट टोपोलॉजी में | == पॉइंट-सेट टोपोलॉजी में संवृत ग्राफ प्रमेय == | ||
[[बिंदु-सेट टोपोलॉजी]] में, | [[बिंदु-सेट टोपोलॉजी]] में, संवृत ग्राफ प्रमेय निम्नलिखित बताता है: | ||
{{Math theorem | {{Math theorem | ||
| name = बंद ग्राफ प्रमेय{{sfn|Munkres|2000|pp=163–172}} | | name = बंद ग्राफ प्रमेय{{sfn|Munkres|2000|pp=163–172}} | ||
| math_statement = यदि <math>f : X \to Y</math> एक [[ | | math_statement = यदि <math>f : X \to Y</math> एक [[टोपोलॉजी स्पेस ]] <math>X</math> से एक [[हौसड्राफ़ स्पेस ]] <math>Y,</math> में एक मैप है,तो <math>f</math> ग्राफ बंद हो जाता है यदि <math>f : X \to Y</math> is [[Continuous function (topology)|कंटीन्यूअस ]]. इसका विलोम तब सत्य होता है जब <math>Y</math> [[Compact space|कॉम्पैक्ट]] है. (ध्यान दें कि सघनता और हौसडॉर्फनेस एक-दूसरे से संबंधित नहीं हैं।) | ||
}} | }} | ||
| Line 43: | Line 40: | ||
दूसरा भाग | दूसरा भाग | ||
किसी भी खुले <math>V\subset Y</math> के लिए, हम | किसी भी खुले <math>V\subset Y</math> के लिए, हम परीक्षण करते हैं कि <math>f^{-1}(V)</math> खुला है तो कोई <math>x\in f^{-1}(V)</math> लें, हम <math>x</math> के कुछ खुले निकटता <math>U</math> का निर्माण करते हैं, जैसे कि <math >f(U)\subset V</math> । | ||
चूँकि <math>f</math> का ग्राफ़ बंद है, प्रत्येक बिंदु <math>(x, y')</math> के लिए "x पर लंबवत रेखा" पर, <math>y'\neq f( x)</math> , <math>f</math> के ग्राफ़ से एक खुला आयत <math>U_{y'}\times V_{y'}</math> अलग करें। ये खुले आयत, जब y-अक्ष पर प्रक्षेपित होते हैं, <math>f(x)</math> को छोड़कर y-अक्ष को कवर करते हैं, इसलिए एक और सेट <math>V</math> जोड़ें। | चूँकि <math>f</math> का ग्राफ़ बंद है, प्रत्येक बिंदु <math>(x, y')</math> के लिए "x पर लंबवत रेखा" पर, <math>y'\neq f( x)</math> , <math>f</math> के ग्राफ़ से एक खुला आयत <math>U_{y'}\times V_{y'}</math> अलग करें। ये खुले आयत, जब y-अक्ष पर प्रक्षेपित होते हैं, <math>f(x)</math> को छोड़कर y-अक्ष को कवर करते हैं, इसलिए एक और सेट <math>V</math> जोड़ें। | ||
सरलता से <math>U:= \bigcap_{y'\neq f(x)} U_{y'}</math> लेने का प्रयास <math>x</math> युक्त एक सेट का निर्माण करेगा, लेकिन इसकी | सरलता से <math>U:= \bigcap_{y'\neq f(x)} U_{y'}</math> लेने का प्रयास <math>x</math> युक्त एक सेट का निर्माण करेगा, लेकिन इसकी आश्वासन नहीं है खुले रहने के लिए, इसलिए हम यहाँ कॉम्पैक्टनेस का उपयोग करते हैं। | ||
चूँकि <math>Y</math> कॉम्पैक्ट है, हम <math>Y</math> का एक परिमित खुला आवरण ले सकते हैं जैसे <math>\{V, V_{y'_1}, ..., V_{y '_n}\}</math>. | चूँकि <math>Y</math> कॉम्पैक्ट है, हम <math>Y</math> का एक परिमित खुला आवरण ले सकते हैं जैसे <math>\{V, V_{y'_1}, ..., V_{y '_n}\}</math>. | ||
अब <math>U:= \bigcap_{i=1}^n U_{y'_i}</math> लें। यह <math>x</math> का एक खुला | अब <math>U:= \bigcap_{i=1}^n U_{y'_i}</math> लें। यह <math>x</math> का एक खुला निकटता है, क्योंकि यह केवल एक परिमित चौराहा है। हम दावा करते हैं कि यह <math>U</math> का खुला निकटता है जो हम चाहते हैं। | ||
मान | मान की नहीं, तो कुछ अनियंत्रित <math>x'\in U</math> ऐसा है कि <math>f(x') \not\in V</math> , तो इसका अर्थ होगा <math>f(x) ')\in V_{y'_i}</math> कुछ <math>i</math> के लिए ओपन कवरिंग द्वारा, लेकिन फिर <math>(x', f(x'))\in U\times V_{ y'_i} \subset U_{y'_i}\times V_{y'_i}</math> , एक विरोधाभास क्योंकि इसे <math>f</math> के ग्राफ़ से अलग होना माना जाता है। | ||
}}अ-हॉउसडॉर्फ स्थान बहुत कम देखे जाते हैं, लेकिन अ-सघन स्थान सामान्य हैं। अ-कॉम्पैक्ट का एक उदाहरण <math>Y</math> वास्तविक रेखा है, जो | }}अ-हॉउसडॉर्फ स्थान बहुत कम देखे जाते हैं, लेकिन अ-सघन स्थान सामान्य हैं। अ-कॉम्पैक्ट का एक उदाहरण <math>Y</math> वास्तविक रेखा है, जो संवृत ग्राफ के साथ असंतुलित कार्य की अनुमति देती है <math>f(x) = \begin{cases} | ||
\frac 1 x \text{ if }x\neq 0,\\ | \frac 1 x \text{ if }x\neq 0,\\ | ||
0\text{ else} | 0\text{ else} | ||
| Line 63: | Line 60: | ||
{{Math theorem | {{Math theorem | ||
| name = सेट-वैल्यूड फ़ंक्शंस के लिए बंद ग्राफ प्रमेय{{sfn|Munkres|2000|pp=163–172}} | | name = सेट-वैल्यूड फ़ंक्शंस के लिए बंद ग्राफ प्रमेय{{sfn|Munkres|2000|pp=163–172}} | ||
| math_statement = कॉम्पैक्ट रेंज स्पेस Y के लिए , एक सेट-वैल्यू फ़ंक्शन | | math_statement = कॉम्पैक्ट रेंज स्पेस Y के लिए , एक सेट-वैल्यू फ़ंक्शन <math>f : X \to 2^Y</math> का एक बंद ग्राफ़ है यदि और केवल यदि यह ऊपरी हेमीकंटिन्यूअस है 𝑓(x) सभी <math>x\in X</math> के लिए एक बंद सेट है | ||
}} | }} | ||
== कार्यात्मक विश्लेषण में == | == कार्यात्मक विश्लेषण में == | ||
यदि <math>T : X \to Y</math> [[टोपोलॉजिकल वेक्टर स्पेस|टोपोलॉजिकल वेक्टर स्थान]] (टीवीएस) के बीच एक रैखिक ऑपरेटर है तो हम कहते हैं कि <math>T</math> एक [[बंद रैखिक ऑपरेटर]] है यदि ग्राफ <math>T</math> ,<math>X \times Y</math> में | यदि <math>T : X \to Y</math> [[टोपोलॉजिकल वेक्टर स्पेस|टोपोलॉजिकल वेक्टर स्थान]] (टीवीएस) के बीच एक रैखिक ऑपरेटर है तो हम कहते हैं कि <math>T</math> एक [[बंद रैखिक ऑपरेटर|संवृत रैखिक ऑपरेटर]] है यदि ग्राफ <math>T</math> ,<math>X \times Y</math> में संवृत है जब <math>X \times Y</math> उत्पाद टोपोलॉजी से संपन्न है। | ||
संवृत ग्राफ़ प्रमेय कार्यात्मक विश्लेषण में एक महत्वपूर्ण परिणाम है जो गारंटी देता है कि कुछ प्रतिबंध के तहत एक संवृत रैखिक ऑपरेटर निरंतर है। | |||
मूल परिणाम को कई बार सामान्यीकृत किया गया है। | मूल परिणाम को कई बार सामान्यीकृत किया गया है। संवृत ग्राफ प्रमेयों का एक प्रसिद्ध संस्करण निम्नलिखित है। | ||
{{Math theorem|name= | {{Math theorem|name=प्रमेय{{sfn|Schaefer|Wolff|1999|p=78}}<ref>{{harvtxt|Trèves|2006}}, p. 173</ref>|math_statement= | ||
दो [[F- स्पेसेस]] (जैसे [[बंच स्पेसेस ]]s) के बीच एक रेखीय नक्शा निरंतर होता है अगर और केवल अगर इसका ग्राफ बंद हो। | |||
}} | }} | ||
== यह भी देखें == | == यह भी देखें == | ||
* | * | ||
* लगभग विवृत रेखीय मानचित्र | |||
* बैरल स्थान | |||
* संवृत ग्राफ़ | |||
* संवृत रैखिक ऑपरेटर | |||
* असंतत रेखीय मानचित्र | |||
* काकुतानी निश्चित-बिंदु प्रमेय | |||
* ओपन मैपिंग प्रमेय (कार्यात्मक विश्लेषण) | |||
* उर्सेस्कु प्रमेय | |||
* जालयुक्त स्थान | |||
* ज़ारिस्की का मुख्य प्रमेय | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 25/05/2023]] | |||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:कार्यात्मक विश्लेषण में प्रमेय]] | |||
== संदर्भ == | == संदर्भ == | ||
| Line 116: | Line 131: | ||
* {{planetmath reference|urlname=ProofOfClosedGraphTheorem|title=Proof of closed graph theorem }} | * {{planetmath reference|urlname=ProofOfClosedGraphTheorem|title=Proof of closed graph theorem }} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Collapse templates]] | |||
[[Category: | |||
[[Category: | |||
[[Category:Created On 25/05/2023]] | [[Category:Created On 25/05/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:कार्यात्मक विश्लेषण में प्रमेय]] | |||
Latest revision as of 12:10, 12 September 2023
गणित में, संवृत ग्राफ़ प्रमेय कई आधारस्वरूप परिणामों में से एक को संदर्भित कर सकता है जो उनके ग्राफ़ के संदर्भ में निरंतर कार्यों को दर्शाता है। प्रत्येक स्थिति में संवृत ग्राफ वाले कार्य आवश्यक रूप से निरंतर होते हैं।
संवृत रेखांकन वाले रेखांकन और आरेख
यदि टोपोलॉजिकल स्थान के बीच एक आरेख है, फिर ग्राफ सेट है या समकक्ष,
किसी भी निरंतर कार्य का एक संवृत ग्राफ हॉसडॉर्फ अंतरिक्ष स्थान होता है।
कोई रैखिक आरेख, दो टोपोलॉजिकल वेक्टर स्थान के बीच जिनकी टोपोलॉजी (कॉची) ट्रांसलेशन इनवेरिएंट मेट्रिक्स के संबंध में पूर्ण हैं, और यदि अतिरिक्त (1a) उत्पाद टोपोलॉजीके अर्थ में क्रमिक रूप से निरंतर है, फिर आरेख L निरंतर है और इसका ग्राफ, Gr अनिवार्य रूप से संवृत है।। इसके विपरीत यदि (1a) के स्थान पर एक ऐसा रेखीय आरेख है, जिसका ग्राफ (1b) है कार्टेशियन उत्पाद स्थान में संवृत होने के लिए जाना जाता है , तब निरंतर और आवश्यक रूप से क्रमिक निरंतर है।[1]
निरंतर आरेख के उदाहरण जिनमें संवृत ग्राफ नहीं है
यदि कोई स्थान है तो पहचान आरेख निरंतर है लेकिन इसका ग्राफ जो विकर्ण है, में संवृत है यदि और केवल यदि हॉसडॉर्फ है।[2] विशेष रूप से, यदि हौसडॉर्फ नहीं है तब निरंतर है लेकिन इसका संवृत ग्राफ़ नहीं है।
माना की वास्तविक संख्याओं सामान्य यूक्लिडियन टोपोलॉजी के साथ को निरूपित करता है और अविवेकपूर्ण टोपोलॉजी के साथ को निरूपित करता है (जहां ध्यान दें कि हॉसडॉर्फनहीं है और यह कि Y में मान का प्रत्येक फलन सतत है)। माना की द्वारा और सभी के लिए . परिभाषित किया जाना चाहिए फिर निरंतर है लेकिन इसका ग्राफ में संवृत नहीं है .[3]
पॉइंट-सेट टोपोलॉजी में संवृत ग्राफ प्रमेय
बिंदु-सेट टोपोलॉजी में, संवृत ग्राफ प्रमेय निम्नलिखित बताता है:
बंद ग्राफ प्रमेय[4] — यदि एक टोपोलॉजी स्पेस से एक हौसड्राफ़ स्पेस में एक मैप है,तो ग्राफ बंद हो जाता है यदि is कंटीन्यूअस . इसका विलोम तब सत्य होता है जब कॉम्पैक्ट है. (ध्यान दें कि सघनता और हौसडॉर्फनेस एक-दूसरे से संबंधित नहीं हैं।)
पहला भाग अनिवार्य रूप से परिभाषा के अनुसार है।
दूसरा भाग
किसी भी खुले के लिए, हम परीक्षण करते हैं कि खुला है तो कोई लें, हम के कुछ खुले निकटता का निर्माण करते हैं, जैसे कि ।
चूँकि का ग्राफ़ बंद है, प्रत्येक बिंदु के लिए "x पर लंबवत रेखा" पर, , के ग्राफ़ से एक खुला आयत अलग करें। ये खुले आयत, जब y-अक्ष पर प्रक्षेपित होते हैं, को छोड़कर y-अक्ष को कवर करते हैं, इसलिए एक और सेट जोड़ें।
सरलता से लेने का प्रयास युक्त एक सेट का निर्माण करेगा, लेकिन इसकी आश्वासन नहीं है खुले रहने के लिए, इसलिए हम यहाँ कॉम्पैक्टनेस का उपयोग करते हैं।
चूँकि कॉम्पैक्ट है, हम का एक परिमित खुला आवरण ले सकते हैं जैसे .
अब लें। यह का एक खुला निकटता है, क्योंकि यह केवल एक परिमित चौराहा है। हम दावा करते हैं कि यह का खुला निकटता है जो हम चाहते हैं।
मान की नहीं, तो कुछ अनियंत्रित ऐसा है कि , तो इसका अर्थ होगा कुछ के लिए ओपन कवरिंग द्वारा, लेकिन फिर , एक विरोधाभास क्योंकि इसे के ग्राफ़ से अलग होना माना जाता है।
अ-हॉउसडॉर्फ स्थान बहुत कम देखे जाते हैं, लेकिन अ-सघन स्थान सामान्य हैं। अ-कॉम्पैक्ट का एक उदाहरण वास्तविक रेखा है, जो संवृत ग्राफ के साथ असंतुलित कार्य की अनुमति देती है .
सेट-वैल्यू फ़ंक्शंस के लिए
सेट-वैल्यूड फ़ंक्शंस के लिए बंद ग्राफ प्रमेय[4] — कॉम्पैक्ट रेंज स्पेस Y के लिए , एक सेट-वैल्यू फ़ंक्शन का एक बंद ग्राफ़ है यदि और केवल यदि यह ऊपरी हेमीकंटिन्यूअस है 𝑓(x) सभी के लिए एक बंद सेट है
कार्यात्मक विश्लेषण में
यदि टोपोलॉजिकल वेक्टर स्थान (टीवीएस) के बीच एक रैखिक ऑपरेटर है तो हम कहते हैं कि एक संवृत रैखिक ऑपरेटर है यदि ग्राफ , में संवृत है जब उत्पाद टोपोलॉजी से संपन्न है।
संवृत ग्राफ़ प्रमेय कार्यात्मक विश्लेषण में एक महत्वपूर्ण परिणाम है जो गारंटी देता है कि कुछ प्रतिबंध के तहत एक संवृत रैखिक ऑपरेटर निरंतर है।
मूल परिणाम को कई बार सामान्यीकृत किया गया है। संवृत ग्राफ प्रमेयों का एक प्रसिद्ध संस्करण निम्नलिखित है।
प्रमेय[5][6] — दो F- स्पेसेस (जैसे बंच स्पेसेस s) के बीच एक रेखीय नक्शा निरंतर होता है अगर और केवल अगर इसका ग्राफ बंद हो।
यह भी देखें
- लगभग विवृत रेखीय मानचित्र
- बैरल स्थान
- संवृत ग्राफ़
- संवृत रैखिक ऑपरेटर
- असंतत रेखीय मानचित्र
- काकुतानी निश्चित-बिंदु प्रमेय
- ओपन मैपिंग प्रमेय (कार्यात्मक विश्लेषण)
- उर्सेस्कु प्रमेय
- जालयुक्त स्थान
- ज़ारिस्की का मुख्य प्रमेय
संदर्भ
- ↑ Rudin 1991, p. 51-52.
- ↑ Rudin 1991, p. 50.
- ↑ Narici & Beckenstein 2011, pp. 459–483.
- ↑ 4.0 4.1 Munkres 2000, pp. 163–172.
- ↑ Schaefer & Wolff 1999, p. 78.
- ↑ Trèves (2006), p. 173
ग्रन्थसूची
- Bourbaki, Nicolas (1987) [1981]. Topological Vector Spaces: Chapters 1–5. Éléments de mathématique. Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag. ISBN 3-540-13627-4. OCLC 17499190.
- Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
- Jarchow, Hans (1981). Locally convex spaces. Stuttgart: B.G. Teubner. ISBN 978-3-519-02224-4. OCLC 8210342.
- Köthe, Gottfried (1983) [1969]. Topological Vector Spaces I. Grundlehren der mathematischen Wissenschaften. Vol. 159. Translated by Garling, D.J.H. New York: Springer Science & Business Media. ISBN 978-3-642-64988-2. MR 0248498. OCLC 840293704.
- Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
- Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
- Zălinescu, Constantin (30 July 2002). Convex Analysis in General Vector Spaces. River Edge, N.J. London: World Scientific Publishing. ISBN 978-981-4488-15-0. MR 1921556. OCLC 285163112 – via Internet Archive.
- "Proof of closed graph theorem". PlanetMath.