लॉग-सामान्य वितरण: Difference between revisions
No edit summary |
No edit summary |
||
| (21 intermediate revisions by 4 users not shown) | |||
| Line 21: | Line 21: | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
=== पीढ़ी और | === पीढ़ी और मापदंड === | ||
जब <math>Z</math> एक मानक सामान्य चर हों, और <math>\mu</math> और <math>\sigma>0</math> दो वास्तविक संख्याएँ हों। फिर, यादृच्छिक चर का वितरण | जब <math>Z</math> एक मानक सामान्य चर हों, और <math>\mu</math> और <math>\sigma>0</math> दो वास्तविक संख्याएँ हों। फिर, यादृच्छिक चर का वितरण | ||
:<math> X=e^{\mu+\sigma Z} </math> | :<math> X=e^{\mu+\sigma Z} </math> | ||
मापदंडों के साथ लॉग-सामान्य वितरण कहा जाता है <math>\mu</math> और <math>\sigma</math>। ये चर के प्राकृतिक लघुगणक का अपेक्षित मान (या माध्य) और [[मानक विचलन]] हैं, न कि अपेक्षा और मानक विचलन <math>X</math> ही है। | |||
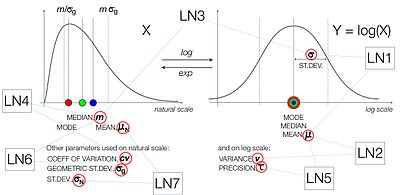
[[File:Lognormal Distribution.svg|thumb|upright=1.5|सामान्य और लॉग-सामान्य वितरण के बीच संबंध। यदि <math>Y=\mu+\sigma Z</math> तब सामान्य रूप से वितरित किया जाता है, तो <math>X\sim e^{Y}</math> लॉग-सामान्य रूप से वितरित है।]]लघुगणक या घातांक फलन के आधार पर ध्यान दिए बिना यह संबंध सत्य है: यदि <math>\log_a(X)</math> सामान्य रूप से वितरित किया जाता है, तो ऐसा है <math>\log_b(X)</math> किन्हीं दो धनात्मक संख्याओं के लिए <math>a,b\neq 1</math>। इसी तरह यदि <math>e^Y</math> लॉग-सामान्य रूप से वितरित है, तो ऐसा ही है <math>a^Y</math>, जहां <math>0 < a \neq 1</math>।[[File:Lognormal Distribution.svg|thumb|upright=1.5]]अभीष्ट माध्य के साथ वितरण की उत्पत्ति करने के लिए <math>\mu_X</math> और विचरण <math>\sigma_X^2</math>, एक उपयोग करता है | [[File:Lognormal Distribution.svg|thumb|upright=1.5|सामान्य और लॉग-सामान्य वितरण के बीच संबंध। यदि <math>Y=\mu+\sigma Z</math> तब सामान्य रूप से वितरित किया जाता है, तो <math>X\sim e^{Y}</math> लॉग-सामान्य रूप से वितरित है।]]लघुगणक या घातांक फलन के आधार पर ध्यान दिए बिना यह संबंध सत्य है: यदि <math>\log_a(X)</math> सामान्य रूप से वितरित किया जाता है, तो ऐसा है <math>\log_b(X)</math> किन्हीं दो धनात्मक संख्याओं के लिए <math>a,b\neq 1</math>। इसी तरह यदि <math>e^Y</math> लॉग-सामान्य रूप से वितरित है, तो ऐसा ही है <math>a^Y</math>, जहां <math>0 < a \neq 1</math>।[[File:Lognormal Distribution.svg|thumb|upright=1.5]]अभीष्ट माध्य के साथ वितरण की उत्पत्ति करने के लिए <math>\mu_X</math> और विचरण <math>\sigma_X^2</math>, एक उपयोग करता है | ||
<math>\mu = \ln\left(\frac{\mu_X^2}{\sqrt{\mu_X^2+\sigma_X^2}}\right) </math> और <math>\sigma^2 = \ln\left(1+\frac{\sigma_X^2}{\mu_X^2}\right). </math> | <math>\mu = \ln\left(\frac{\mu_X^2}{\sqrt{\mu_X^2+\sigma_X^2}}\right) </math> और <math>\sigma^2 = \ln\left(1+\frac{\sigma_X^2}{\mu_X^2}\right). </math> | ||
वैकल्पिक रूप से, गुणात्मक या ज्यामितीय | वैकल्पिक रूप से, गुणात्मक या ज्यामितीय मापदंडों <math>\mu^*=e^\mu</math> और <math>\sigma^*=e^\sigma</math> का उपयोग किया जा सकता है। उनकी अधिक प्रत्यक्ष व्याख्या है: <math>\mu^*</math> वितरण की माध्यिका है, और <math>\sigma^*</math> "तितर बितर" अंतराल निर्धारित करने के लिए उपयोगी है। | ||
=== संभाव्यता घनत्व फलन === | === संभाव्यता घनत्व फलन === | ||
एक धनात्मक यादृच्छिक चर X लॉग-सामान्य रूप से वितरित होता (अर्थात, <math> X \sim \operatorname{Lognormal}(\mu_x,\sigma_x^2)</math>), यदि X का प्राकृतिक लघुगणक सामान्य रूप से माध्य के साथ वितरित किया जाता है <math> \mu</math> और विचरण <math> \sigma^2</math>: | एक धनात्मक यादृच्छिक चर X लॉग-सामान्य रूप से वितरित होता है (अर्थात, <math> X \sim \operatorname{Lognormal}(\mu_x,\sigma_x^2)</math>), यदि X का प्राकृतिक लघुगणक सामान्य रूप से माध्य के साथ वितरित किया जाता है <math> \mu</math> और विचरण <math> \sigma^2</math>: | ||
:<math> \ln(X) \sim \mathcal N(\mu,\sigma^2)</math> | :<math> \ln(X) \sim \mathcal N(\mu,\sigma^2)</math> | ||
<math>\Phi</math> और <math>\varphi</math> क्रमशः N(0,1) वितरण का संचयी संभाव्यता वितरण फलन और संभाव्यता घनत्व फलन हो, तो हमारे पास वह है<ref name=":1" /><ref name="JKB" /> | |||
: <math> | : <math> | ||
| Line 71: | Line 71: | ||
:<math>\operatorname{Var}[\boldsymbol Y]_{ij}=e^{\mu_i+\mu_j + \frac{1}{2}(\Sigma_{ii}+\Sigma_{jj}) }( e^{\Sigma_{ij}} - 1) . </math> | :<math>\operatorname{Var}[\boldsymbol Y]_{ij}=e^{\mu_i+\mu_j + \frac{1}{2}(\Sigma_{ii}+\Sigma_{jj}) }( e^{\Sigma_{ij}} - 1) . </math> | ||
चूंकि बहुभिन्नरूपी लॉग-सामान्य वितरण का व्यापक रूप से उपयोग नहीं किया जाता है, इसलिए इस प्रविष्टि का शेष भाग केवल एक अविभाज्य वितरण | चूंकि बहुभिन्नरूपी लॉग-सामान्य वितरण का व्यापक रूप से उपयोग नहीं किया जाता है, इसलिए इस प्रविष्टि का शेष भाग केवल एक अविभाज्य वितरण से संबंधित है। | ||
=== विशेषता कार्य और क्षण उत्पन्न करने वाला कार्य === | === विशेषता कार्य और क्षण उत्पन्न करने वाला कार्य === | ||
| Line 78: | Line 78: | ||
:<math>\operatorname{E}[X^n]= e^{n\mu+n^2\sigma^2/2}</math> | :<math>\operatorname{E}[X^n]= e^{n\mu+n^2\sigma^2/2}</math> | ||
इसे रख कर प्राप्त किया जा सकता है <math>z=\tfrac{\ln(x) - (\mu+n\sigma^2)}{\sigma}</math> समाकल के भीतर। चूंकि, लॉग-सामान्य वितरण इसके क्षणों से निर्धारित नहीं होता है।<ref name="Heyde">{{Citation|last=Heyde|first=CC.|title=On a property of the lognormal distribution|work=Journal of the Royal Statistical Society, Series B|volume=25|issue=2|pages=392–393|year=1963|doi=10.1007/978-1-4419-5823-5_6|isbn=978-1-4419-5822-8|doi-access=free}}</ref> इसका तात्पर्य यह है कि शून्य के निकटतम में इसका परिभाषित क्षण उत्पन्न करने वाला कार्य नहीं हो सकता है।<ref>{{Cite book|last=Billingsley|first=Patrick|url=https://www.worldcat.org/oclc/780289503|title=Probability and Measure|date=2012|publisher=Wiley|isbn=978-1-118-12237-2|edition=Anniversary|location=Hoboken, N.J.|pages=415|oclc=780289503}}</ref> दरअसल, अपेक्षित मूल्य <math>\operatorname{E}[e^{t X}]</math> तर्क के किसी सकारात्मक | इसे रख कर प्राप्त किया जा सकता है <math>z=\tfrac{\ln(x) - (\mu+n\sigma^2)}{\sigma}</math> समाकल के भीतर। चूंकि, लॉग-सामान्य वितरण इसके क्षणों से निर्धारित नहीं होता है।<ref name="Heyde">{{Citation|last=Heyde|first=CC.|title=On a property of the lognormal distribution|work=Journal of the Royal Statistical Society, Series B|volume=25|issue=2|pages=392–393|year=1963|doi=10.1007/978-1-4419-5823-5_6|isbn=978-1-4419-5822-8|doi-access=free}}</ref> इसका तात्पर्य यह है कि शून्य के निकटतम में इसका परिभाषित क्षण उत्पन्न करने वाला कार्य नहीं हो सकता है।<ref>{{Cite book|last=Billingsley|first=Patrick|url=https://www.worldcat.org/oclc/780289503|title=Probability and Measure|date=2012|publisher=Wiley|isbn=978-1-118-12237-2|edition=Anniversary|location=Hoboken, N.J.|pages=415|oclc=780289503}}</ref> दरअसल, अपेक्षित मूल्य <math>\operatorname{E}[e^{t X}]</math> तर्क के किसी सकारात्मक मान के लिए परिभाषित नहीं है <math>t</math>, परिभाषित है समाकल विचलन के पश्चात से। | ||
[[विशेषता समारोह (संभावना सिद्धांत)]] <math>\operatorname{E}[e^{i t X}]</math>को t के वास्तविक मानों के लिए परिभाषित किया गया है, लेकिन t के किसी भी सम्मिश्र मान के लिए परिभाषित नहीं किया गया है जिसमें एक नकारात्मक काल्पनिक भाग है, और इसलिए विशेषता कार्य मूल पर [[विश्लेषणात्मक कार्य]] नहीं है। परिणामस्वरूप, लॉग-सामान्य वितरण की विशेषता फलन को अनंत अभिसरण श्रृंखला के रूप में प्रदर्शित नहीं किया जा सकता है।<ref name="Holgate">{{Cite journal |last=Holgate |first=P. |year=1989 |title=The lognormal characteristic function, vol. 18, pp. 4539–4548, 1989 |journal=Communications in Statistics - Theory and Methods |volume=18 |issue=12 |pages=4539–4548 |doi=10.1080/03610928908830173}}</ref> विशेष रूप से, इसकी टेलर [[औपचारिक श्रृंखला]] भिन्न होती है: | [[विशेषता समारोह (संभावना सिद्धांत)|विशेषता फलन (संभावना सिद्धांत)]] <math>\operatorname{E}[e^{i t X}]</math> को t के वास्तविक मानों के लिए परिभाषित किया गया है, लेकिन t के किसी भी सम्मिश्र मान के लिए परिभाषित नहीं किया गया है जिसमें एक नकारात्मक काल्पनिक भाग है, और इसलिए विशेषता कार्य मूल पर [[विश्लेषणात्मक कार्य]] नहीं है। परिणामस्वरूप, लॉग-सामान्य वितरण की विशेषता फलन को अनंत अभिसरण श्रृंखला के रूप में प्रदर्शित नहीं किया जा सकता है।<ref name="Holgate">{{Cite journal |last=Holgate |first=P. |year=1989 |title=The lognormal characteristic function, vol. 18, pp. 4539–4548, 1989 |journal=Communications in Statistics - Theory and Methods |volume=18 |issue=12 |pages=4539–4548 |doi=10.1080/03610928908830173}}</ref> विशेष रूप से, इसकी टेलर [[औपचारिक श्रृंखला]] भिन्न होती है: | ||
: <math>\sum_{n=0}^\infty \frac{(it)^n}{n!}e^{n\mu+n^2\sigma^2/2}</math> | : <math>\sum_{n=0}^\infty \frac{(it)^n}{n!}e^{n\mu+n^2\sigma^2/2}</math> | ||
| Line 97: | Line 97: | ||
=== विभिन्न डोमेन में संभावना === | === विभिन्न डोमेन में संभावना === | ||
किसी भी | किसी भी स्वैच्छिक डोमेन में लॉग-सामान्य वितरण की संभाव्यता सामग्री को पहले चर को सामान्य में बदलकर, फिर रे-ट्रेस विधि का उपयोग करके संख्यात्मक रूप से एकीकृत करके वांछित सटीकता की गणना की जा सकती है।<ref name="Das">{{cite arXiv |last=Das|first=Abhranil|eprint=2012.14331|title=A method to integrate and classify normal distributions|date=2020|class=stat.ML}}</ref> ([https://www.mathworks.com/matlabcentral/fileexchange/84973-integrate-and-classify-normal-distributions मैटलैब कोड]) | ||
==== लॉग-सामान्य चर के कार्यों की संभावनाएं ==== | ==== लॉग-सामान्य चर के कार्यों की संभावनाएं ==== | ||
| Line 106: | Line 106: | ||
लॉग-सामान्य वितरण का ज्यामितीय माध्य है <math>\operatorname{GM}[X] = e^\mu = \mu^*</math>. यह माध्यिका के बराबर होता है। [[ज्यामितीय मानक विचलन]] है <math>\operatorname{GSD}[X] = e^{\sigma} = \sigma^*</math>.<ref name="ReferenceA">{{cite journal |last1=Kirkwood |first1=Thomas BL |title=Geometric means and measures of dispersion |journal=Biometrics |date=Dec 1979 |volume=35 |issue=4 |pages=908–9|jstor=2530139 }}</ref><ref>{{cite journal |last1=Limpert |first1=E |last2=Stahel |first2=W |last3=Abbt |first3=M |title=Lognormal distributions across the sciences: keys and clues |journal=BioScience |year=2001 |volume=51 |issue=5 |pages=341–352 |doi=10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2|doi-access=free }}</ref> | लॉग-सामान्य वितरण का ज्यामितीय माध्य है <math>\operatorname{GM}[X] = e^\mu = \mu^*</math>. यह माध्यिका के बराबर होता है। [[ज्यामितीय मानक विचलन]] है <math>\operatorname{GSD}[X] = e^{\sigma} = \sigma^*</math>.<ref name="ReferenceA">{{cite journal |last1=Kirkwood |first1=Thomas BL |title=Geometric means and measures of dispersion |journal=Biometrics |date=Dec 1979 |volume=35 |issue=4 |pages=908–9|jstor=2530139 }}</ref><ref>{{cite journal |last1=Limpert |first1=E |last2=Stahel |first2=W |last3=Abbt |first3=M |title=Lognormal distributions across the sciences: keys and clues |journal=BioScience |year=2001 |volume=51 |issue=5 |pages=341–352 |doi=10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2|doi-access=free }}</ref> | ||
अंकगणितीय आँकड़ों के अनुरूप, एक ज्यामितीय विचरण को परिभाषित कर सकते है, <math>\operatorname{GVar}[X] = e^{\sigma^2}</math>द्वारा, और सापेक्ष मानक विचलन<ref name="ReferenceA" /> को<math>\operatorname{GCV}[X] = e^{\sigma} - 1</math>, द्वारा प्रस्थापित किया गया है। लॉग-सामान्य आंकड़े में गुणात्मक भिन्नता का वर्णन करने के लिए, इस शब्द का अभिप्रेत सापेक्ष मानक विचलन के अनुरूप होना था, लेकिन जीसीवी की इस परिभाषा का आकलन के रूप में कोई सैद्धांतिक आधार | अंकगणितीय आँकड़ों के अनुरूप, एक ज्यामितीय विचरण को परिभाषित कर सकते है, <math>\operatorname{GVar}[X] = e^{\sigma^2}</math>द्वारा, और सापेक्ष मानक विचलन<ref name="ReferenceA" /> को<math>\operatorname{GCV}[X] = e^{\sigma} - 1</math>, द्वारा प्रस्थापित किया गया है। लॉग-सामान्य आंकड़े में गुणात्मक भिन्नता का वर्णन करने के लिए, इस शब्द का अभिप्रेत सापेक्ष मानक विचलन के अनुरूप होना था, लेकिन जीसीवी की इस परिभाषा का आकलन के रूप में कोई सैद्धांतिक आधार <math>\operatorname{CV}</math> स्वयं नहीं है (सापेक्ष मानक विचलन भी देखें)। | ||
ध्यान दें कि ज्यामितीय माध्य अंकगणितीय माध्य से छोटा होता है। यह एएम-जीएम असमानता के कारण होता है और लघुगणक के अवतल फलन होने का परिणाम है। वास्तव में, | ध्यान दें कि ज्यामितीय माध्य अंकगणितीय माध्य से छोटा होता है। यह एएम-जीएम असमानता के कारण होता है और लघुगणक के अवतल फलन होने का परिणाम है। वास्तव में, | ||
| Line 117: | Line 117: | ||
किसी भी वास्तविक या सम्मिश्र संख्या {{math|''n''}} के लिए, लॉग-सामान्य रूप से वितरित चर {{math|''X''}} का n-वें क्षण द्वारा दिया गया है<ref name=JKB/>: <math>\operatorname{E}[X^n] = e^{n\mu + \frac12n^2\sigma^2}.</math> | किसी भी वास्तविक या सम्मिश्र संख्या {{math|''n''}} के लिए, लॉग-सामान्य रूप से वितरित चर {{math|''X''}} का n-वें क्षण द्वारा दिया गया है<ref name=JKB/>: <math>\operatorname{E}[X^n] = e^{n\mu + \frac12n^2\sigma^2}.</math> | ||
विशेष रूप से, अंकगणितीय माध्य, अपेक्षित वर्ग, अंकगणितीय विचरण, और अंकगणितीय मानक विचलन एक लॉग-सामान्य रूप से वितरित चर {{math|''X''}} | विशेष रूप से, अंकगणितीय माध्य, अपेक्षित वर्ग, अंकगणितीय विचरण, और अंकगणितीय मानक विचलन एक लॉग-सामान्य रूप से वितरित चर {{math|''X''}} क्रमशः द्वारा दिया जाता हैं:<ref name=":1" /> | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 132: | Line 132: | ||
इस अनुमान को कभी-कभी इसके ज्यामितीय विचरण के उपयोग के कारण ज्यामितीय सीवी (जीसीवी) के रूप में संदर्भित किया जाता है।<ref>Sawant,S.; Mohan, N. (2011) [http://pharmasug.org/proceedings/2011/PO/PharmaSUG-2011-PO08.pdf "FAQ: Issues with Efficacy Analysis of Clinical Trial Data Using SAS"] {{webarchive|url=https://web.archive.org/web/20110824094357/http://pharmasug.org/proceedings/2011/PO/PharmaSUG-2011-PO08.pdf |date=24 August 2011 }}, ''PharmaSUG2011'', Paper PO08</ref><ref>{{cite journal | last1 = Schiff | first1 = MH | display-authors = etal | year = 2014 | title = Head-to-head, randomised, crossover study of oral versus subcutaneous methotrexate in patients with rheumatoid arthritis: drug-exposure limitations of oral methotrexate at doses >=15 mg may be overcome with subcutaneous administration| journal = Ann Rheum Dis | volume = 73| issue = 8| pages = 1–3 | doi = 10.1136/annrheumdis-2014-205228 | pmid = 24728329 | pmc = 4112421}}</ref> अंकगणितीय मानक विचलन के विपरीत, अंकगणितीय सापेक्ष मानक विचलन अंकगणितीय माध्य से स्वतंत्र है। | इस अनुमान को कभी-कभी इसके ज्यामितीय विचरण के उपयोग के कारण ज्यामितीय सीवी (जीसीवी) के रूप में संदर्भित किया जाता है।<ref>Sawant,S.; Mohan, N. (2011) [http://pharmasug.org/proceedings/2011/PO/PharmaSUG-2011-PO08.pdf "FAQ: Issues with Efficacy Analysis of Clinical Trial Data Using SAS"] {{webarchive|url=https://web.archive.org/web/20110824094357/http://pharmasug.org/proceedings/2011/PO/PharmaSUG-2011-PO08.pdf |date=24 August 2011 }}, ''PharmaSUG2011'', Paper PO08</ref><ref>{{cite journal | last1 = Schiff | first1 = MH | display-authors = etal | year = 2014 | title = Head-to-head, randomised, crossover study of oral versus subcutaneous methotrexate in patients with rheumatoid arthritis: drug-exposure limitations of oral methotrexate at doses >=15 mg may be overcome with subcutaneous administration| journal = Ann Rheum Dis | volume = 73| issue = 8| pages = 1–3 | doi = 10.1136/annrheumdis-2014-205228 | pmid = 24728329 | pmc = 4112421}}</ref> अंकगणितीय मानक विचलन के विपरीत, अंकगणितीय सापेक्ष मानक विचलन अंकगणितीय माध्य से स्वतंत्र है। | ||
अंकगणित माध्य और अंकगणितीय विचलन ज्ञात होने पर | अंकगणित माध्य और अंकगणितीय विचलन ज्ञात होने पर मापदंड {{math|''μ''}} और {{math|''σ''}} प्राप्त किए जा सकते हैं: | ||
: <math>\begin{align} | : <math>\begin{align} | ||
| Line 208: | Line 208: | ||
=== स्वतंत्र, लॉग-सामान्य यादृच्छिक चर का गुणन और विभाजन === | === स्वतंत्र, लॉग-सामान्य यादृच्छिक चर का गुणन और विभाजन === | ||
यदि दो स्वतंत्र, लॉग-सामान्य चर <math>X_1</math> और <math>X_2</math> गुणा [विभाजित] हैं, उत्पाद [अनुपात] | यदि दो स्वतंत्र, लॉग-सामान्य चर <math>X_1</math> और <math>X_2</math> गुणा [विभाजित] हैं, उत्पाद [अनुपात] मापदंडों के साथ फिर से लॉग-सामान्य है <math>\mu=\mu_1+\mu_2</math> [<math>\mu=\mu_1-\mu_2</math>] और <math>\sigma</math>, जहां <math>\sigma^2=\sigma_1^2+\sigma_2^2</math>. यह आसानी से <math>n</math> जैसे चर उत्पाद के लिए सामान्यीकृत है। | ||
सामान्यतः अधिक, यदि <math>X_j \sim \operatorname{Lognormal} (\mu_j, \sigma_j^2)</math> हैं <math>n</math> स्वतंत्र, लॉग-सामान्य रूप से वितरित चर, फिर <math>Y = \textstyle\prod_{j=1}^n X_j \sim \operatorname{Lognormal} \Big(\textstyle \sum_{j=1}^n\mu_j,\ \sum_{j=1}^n \sigma_j^2 \Big).</math>है। | |||
=== गुणक केंद्रीय सीमा प्रमेय === | === गुणक केंद्रीय सीमा प्रमेय === | ||
{{See also|जिब्रात का नियम}} | {{See also|जिब्रात का नियम}} | ||
का ज्यामितीय या गुणक माध्य <math>n</math> स्वतंत्र, समान रूप से वितरित, सकारात्मक यादृच्छिक चर <math>X_i</math> दिखाता है, के लिए <math>n \to\infty</math> | का ज्यामितीय या गुणक माध्य <math>n</math> स्वतंत्र, समान रूप से वितरित, सकारात्मक यादृच्छिक चर <math>X_i</math> दिखाता है, के लिए <math>n \to\infty</math> मापदंडों के साथ लगभग एक लॉग-सामान्य वितरण <math>\mu = E[\ln(X_i)]</math> और <math>\sigma^2 = \mbox{var}[\ln(X_i)]/n</math>, मानते हुए <math>\sigma^2</math> परिमित है। | ||
वास्तव में, यादृच्छिक चरों को समान रूप से वितरित करने की आवश्यकता नहीं है। के वितरण के लिए पर्याप्त है <math>\ln(X_i)</math> सभी के पास परिमित प्रसरण है और केंद्रीय सीमा प्रमेय के कई रूपों में से किसी एक की अन्य शर्तों को पूरा करते हैं। | वास्तव में, यादृच्छिक चरों को समान रूप से वितरित करने की आवश्यकता नहीं है। के वितरण के लिए पर्याप्त है <math>\ln(X_i)</math> सभी के पास परिमित प्रसरण है और केंद्रीय सीमा प्रमेय के कई रूपों में से किसी एक की अन्य शर्तों को पूरा करते हैं। | ||
| Line 231: | Line 231: | ||
| year = 2000 | volume = 81 | issue = 4 | pages = 1139–1142 | | year = 2000 | volume = 81 | issue = 4 | pages = 1139–1142 | ||
}}</ref> | }}</ref> | ||
हार्मोनिक <math>H</math>, ज्यामितीय <math>G</math> और अंकगणित <math>A</math> इस वितरण के द्वारा संबंधित हैं;<ref name=Rossman1990>{{cite journal|last=Rossman |first=Lewis A |date=July 1990 |title=Design stream flows based on harmonic means |journal=Journal of Hydraulic Engineering |volume=116 |issue=7 |pages=946–950 |doi=10.1061/(ASCE)0733-9429(1990)116:7(946)}}</ref> ऐसा संबंध द्वारा दिया गया है | |||
हार्मोनिक <math>H</math>, ज्यामितीय <math>G</math> और अंकगणित <math>A</math> इस वितरण के द्वारा संबंधित हैं;<ref name="Rossman1990">{{cite journal|last=Rossman |first=Lewis A |date=July 1990 |title=Design stream flows based on harmonic means |journal=Journal of Hydraulic Engineering |volume=116 |issue=7 |pages=946–950 |doi=10.1061/(ASCE)0733-9429(1990)116:7(946)}}</ref> ऐसा संबंध द्वारा दिया गया है | |||
: <math>H = \frac{G^2} A.</math> | : <math>H = \frac{G^2} A.</math> | ||
लॉग-सामान्य वितरण [[अनंत विभाज्यता (संभावना)]] हैं,<ref name=OlofThorin1978LNInfDivi/>लेकिन वे [[स्थिर वितरण]] नहीं हैं, जिन्हें आसानी से निकाला जा सकता है।<ref name=Gao/> | लॉग-सामान्य वितरण [[अनंत विभाज्यता (संभावना)]] हैं,<ref name=OlofThorin1978LNInfDivi/>लेकिन वे [[स्थिर वितरण]] नहीं हैं, जिन्हें आसानी से निकाला जा सकता है।<ref name=Gao/> | ||
== संबंधित वितरण == | == संबंधित वितरण == | ||
* यदि <math>X \sim \mathcal{N}(\mu, \sigma^2)</math> एक सामान्य वितरण है, | * यदि <math>X \sim \mathcal{N}(\mu, \sigma^2)</math> एक सामान्य वितरण है, फिर <math>\exp(X) \sim \operatorname{Lognormal}(\mu, \sigma^2).</math> | ||
* यदि <math>X \sim \operatorname{Lognormal}(\mu, \sigma^2)</math> लॉग-सामान्य रूप से वितरित किया जाता है, तब <math>\ln(X) \sim \mathcal{N}(\mu, \sigma^2)</math> एक सामान्य यादृच्छिक चर है। | * यदि <math>X \sim \operatorname{Lognormal}(\mu, \sigma^2)</math> लॉग-सामान्य रूप से वितरित किया जाता है, तब <math>\ln(X) \sim \mathcal{N}(\mu, \sigma^2)</math> एक सामान्य यादृच्छिक चर है। | ||
* | * <math>X_j \sim \operatorname{Lognormal}(\mu_j, \sigma_j^2)</math> स्वतंत्र लॉग-सामान्य रूप से वितरित चर हो सकते हैं जिनमें संभवतः भिन्नता हो <math>\sigma</math> और <math>\mu</math> मापदंड, और <math display="inline">Y = \sum_{j=1}^n X_j</math>. का वितरण <math>Y</math> की कोई बंद-रूप अभिव्यक्ति नहीं है, लेकिन एक अन्य लॉग-सामान्य वितरण द्वारा यथोचित अनुमान लगाया जा सकता है की <math>Z</math> दाहिने अंतिम भाग पर है।<ref name="Asmussen2">{{cite journal| first1=S. |last1=Asmussen |first2=L. |last2=Rojas-Nandayapa |title=Asymptotics of Sums of Lognormal Random Variables with Gaussian Copula |journal=Statistics and Probability Letters |volume=78 |issue=16 |pages=2709–2714 |year=2008 |doi=10.1016/j.spl.2008.03.035 |url=https://hal.archives-ouvertes.fr/hal-00595951/file/PEER_stage2_10.1016%252Fj.spl.2008.03.035.pdf }}</ref> संभाव्यता घनत्व फलन की विशेषता 0 के निकटतम में<ref name=Gao/> होती है और यह किसी लॉग-सामान्य वितरण के समान नहीं है। एल.एफ. फेंटन के कारण सामान्यतः उपयोग किया जाने वाला सन्निकटन (लेकिन पहले आर.आई. विल्किंसन द्वारा कहा गया था और मार्लो द्वारा गणितीय औचित्य<ref name="Marlow">{{cite journal |first=NA. |last=Marlow |title=A normal limit theorem for power sums of independent normal random variables |journal=Bell System Technical Journal |volume=46 |issue=9 |pages=2081–2089 |date=Nov 1967 |doi=10.1002/j.1538-7305.1967.tb04244.x}}</ref>) एक अन्य लॉग-सामान्य वितरण के माध्य और विचरण से मेल करके प्राप्त किया जाता है:<math display="block">\begin{align} | ||
\sigma^2_Z &= \ln\!\left[ \frac{\sum e^{2\mu_j+\sigma_j^2}(e^{\sigma_j^2}-1)}{(\sum e^{\mu_j+\sigma_j^2/2})^2} + 1\right], \\ | \sigma^2_Z &= \ln\!\left[ \frac{\sum e^{2\mu_j+\sigma_j^2}(e^{\sigma_j^2}-1)}{(\sum e^{\mu_j+\sigma_j^2/2})^2} + 1\right], \\ | ||
\mu_Z &= \ln\!\left[ \sum e^{\mu_j+\sigma_j^2/2} \right] - \frac{\sigma^2_Z}{2}. | \mu_Z &= \ln\!\left[ \sum e^{\mu_j+\sigma_j^2/2} \right] - \frac{\sigma^2_Z}{2}. | ||
\end{align}</math> स्थिति में यह सब <math>X_j</math> एक ही विचरण | \end{align}</math> स्थिति में यह सब <math>X_j</math> एक ही विचरण मापदंडों है <math>\sigma_j=\sigma</math>, ये सूत्र सरल करते हैं <math display="block">\begin{align} | ||
\sigma^2_Z &= \ln\!\left[ (e^{\sigma^2}-1)\frac{\sum e^{2\mu_j}}{(\sum e^{\mu_j})^2} + 1\right], \\ | \sigma^2_Z &= \ln\!\left[ (e^{\sigma^2}-1)\frac{\sum e^{2\mu_j}}{(\sum e^{\mu_j})^2} + 1\right], \\ | ||
\mu_Z &= \ln\!\left[ \sum e^{\mu_j} \right] + \frac{\sigma^2}{2} - \frac{\sigma^2_Z}{2}. | \mu_Z &= \ln\!\left[ \sum e^{\mu_j} \right] + \frac{\sigma^2}{2} - \frac{\sigma^2_Z}{2}. | ||
| Line 282: | Line 283: | ||
\mu_Z &= \ln\left( S_+ \right) - \sigma_{Z}^2/2 | \mu_Z &= \ln\left( S_+ \right) - \sigma_{Z}^2/2 | ||
\end{align}</math> | \end{align}</math> | ||
* यदि <math>X \sim \operatorname{Lognormal}(\mu, \sigma^2)</math> तब <math>X+c</math> कहा जाता है कि समर्थन के साथ तीन-फलन लॉग-सामान्य वितरण है <math>x\in (c, +\infty)</math>.<ref name="Sangal1970">{{cite journal|first1=B. |last1=Sangal |first2=A. |last2=Biswas |title=The 3-Parameter Lognormal Distribution Applications in Hydrology |journal=Water Resources Research |volume=6 |issue=2 |pages=505–515 |year=1970 |doi=10.1029/WR006i002p00505}}</ref> <math>\operatorname{E}[X+c] = \operatorname{E}[X] + c</math>, <math>\operatorname{Var}[X+c] = \operatorname{Var}[X]</math> | * यदि <math>X \sim \operatorname{Lognormal}(\mu, \sigma^2)</math> तब <math>X+c</math> कहा जाता है कि समर्थन के साथ तीन-फलन लॉग-सामान्य वितरण है <math>x\in (c, +\infty)</math>.<ref name="Sangal1970">{{cite journal|first1=B. |last1=Sangal |first2=A. |last2=Biswas |title=The 3-Parameter Lognormal Distribution Applications in Hydrology |journal=Water Resources Research |volume=6 |issue=2 |pages=505–515 |year=1970 |doi=10.1029/WR006i002p00505}}</ref> <math>\operatorname{E}[X+c] = \operatorname{E}[X] + c</math>, <math>\operatorname{Var}[X+c] = \operatorname{Var}[X]</math> | ||
* कहा जाता है कि समर्थन के साथ तीन-फलन प्रारंभिक-सामान्य वितरण है।<ref name="Johnson1949">{{cite journal |author-link=Norman Lloyd Johnson |last=Johnson |first=N. L. |date=1949 |title=Systems of Frequency Curves Generated by Methods of Translation| journal=[[Biometrika]] |volume=36 |issue=1/2 |pages=149–176 |jstor=2332539 |doi=10.2307/2332539| pmid=18132090 }}</ref> | * कहा जाता है कि समर्थन के साथ तीन-फलन प्रारंभिक-सामान्य वितरण है।<ref name="Johnson1949">{{cite journal |author-link=Norman Lloyd Johnson |last=Johnson |first=N. L. |date=1949 |title=Systems of Frequency Curves Generated by Methods of Translation| journal=[[Biometrika]] |volume=36 |issue=1/2 |pages=149–176 |jstor=2332539 |doi=10.2307/2332539| pmid=18132090 }}</ref> | ||
* यदि <math>X\mid Y \sim \operatorname{Rayleigh}(Y)</math> साथ <math> Y \sim \operatorname{Lognormal}(\mu, \sigma^2)</math>, तब <math> X \sim \operatorname{Suzuki}(\mu, \sigma)</math> ([[सुजुकी वितरण]])। | * यदि <math>X\mid Y \sim \operatorname{Rayleigh}(Y)</math> साथ <math> Y \sim \operatorname{Lognormal}(\mu, \sigma^2)</math>, तब <math> X \sim \operatorname{Suzuki}(\mu, \sigma)</math> ([[सुजुकी वितरण]])। | ||
| Line 291: | Line 292: | ||
=== मापदंडों का अनुमान === | === मापदंडों का अनुमान === | ||
लॉग-सामान्य वितरण | लॉग-सामान्य वितरण मापदंडों μ और σ के अधिकतम संभावना अनुमानक का निर्धारण करने के लिए, हम सामान्य वितरण के समान प्रक्रिया का उपयोग कर सकते हैं। ध्यान दें कि | ||
<math display="block">L(\mu, \sigma) = \prod_{i=1}^n \frac 1 {x_i} \varphi_{\mu,\sigma} (\ln x_i),</math> | <math display="block">L(\mu, \sigma) = \prod_{i=1}^n \frac 1 {x_i} \varphi_{\mu,\sigma} (\ln x_i),</math> | ||
जहां <math>\varphi</math> सामान्य वितरण का घनत्व फलन है <math>\mathcal N(\mu,\sigma^2)</math>. इसलिए, लॉग-संभावित फलन है | जहां <math>\varphi</math> सामान्य वितरण का घनत्व फलन है <math>\mathcal N(\mu,\sigma^2)</math>. इसलिए, लॉग-संभावित फलन है | ||
| Line 300: | Line 301: | ||
परिमित ''n'' के लिए, अनुमानक के लिए <math>\mu</math> निष्पक्ष है, लेकिन एक के लिए <math>\sigma</math> पक्षपाती है। सामान्य वितरण के लिए, एक निष्पक्ष अनुमानक के लिए समीकरण में हर n को n−1 से प्रतिस्थापित करके <math>\sigma</math> प्राप्त किया जा सकता है <math>\widehat\sigma^2</math> में। | परिमित ''n'' के लिए, अनुमानक के लिए <math>\mu</math> निष्पक्ष है, लेकिन एक के लिए <math>\sigma</math> पक्षपाती है। सामान्य वितरण के लिए, एक निष्पक्ष अनुमानक के लिए समीकरण में हर n को n−1 से प्रतिस्थापित करके <math>\sigma</math> प्राप्त किया जा सकता है <math>\widehat\sigma^2</math> में। | ||
जब मूलभूत स्तंभ <math>x_1, x_2, \ldots, x_n</math> उपलब्ध नहीं हैं, लेकिन प्रतिरूप का मतलब है <math>\bar x</math> और मानक विचलन एस है, तो संबंधित | जब मूलभूत स्तंभ <math>x_1, x_2, \ldots, x_n</math> उपलब्ध नहीं हैं, लेकिन प्रतिरूप का मतलब है <math>\bar x</math> और मानक विचलन एस है, तो संबंधित मापदंडों को निम्नलिखित सूत्रों द्वारा निर्धारित किया जाता है, जो अपेक्षा के लिए समीकरणों को हल करने से प्राप्त होते हैं <math>\operatorname{E}[X]</math> और विचरण <math>\operatorname{Var}[X]</math> के लिए <math>\mu</math> और <math>\sigma</math>: | ||
<math display="block"> \mu = \ln\left(\bar x\ \Big/ \ \sqrt{1+\frac{\widehat\sigma^2}{\bar x^2}}\right), | <math display="block"> \mu = \ln\left(\bar x\ \Big/ \ \sqrt{1+\frac{\widehat\sigma^2}{\bar x^2}}\right), | ||
\qquad \sigma^2 = \ln\left(1 + \frac{\widehat\sigma^2}{\bar x^2}\right).</math> | \qquad \sigma^2 = \ln\left(1 + \frac{\widehat\sigma^2}{\bar x^2}\right).</math> | ||
| Line 309: | Line 310: | ||
तितर-बितर अंतराल द्वारा एक बुनियादी उदाहरण दिया जाता है: सामान्य वितरण के लिए, अंतराल <math>[\mu-\sigma,\mu+\sigma]</math> में संभाव्यता (या एक बड़े नमूने) का लगभग दो तिहाई (68%) होता है, और <math>[\mu-2\sigma,\mu+2\sigma]</math> में 95% होता हैं। इसलिए, लॉग-सामान्य वितरण के लिए, | तितर-बितर अंतराल द्वारा एक बुनियादी उदाहरण दिया जाता है: सामान्य वितरण के लिए, अंतराल <math>[\mu-\sigma,\mu+\sigma]</math> में संभाव्यता (या एक बड़े नमूने) का लगभग दो तिहाई (68%) होता है, और <math>[\mu-2\sigma,\mu+2\sigma]</math> में 95% होता हैं। इसलिए, लॉग-सामान्य वितरण के लिए, | ||
<math display="block">[\mu^*/\sigma^*,\mu^*\cdot\sigma^*]=[\mu^* {}^\times\!\!/ \sigma^*]</math> 2/3 सम्मलित है, और | <math display="block">[\mu^*/\sigma^*,\mu^*\cdot\sigma^*]=[\mu^* {}^\times\!\!/ \sigma^*]</math> 2/3 सम्मलित है, और | ||
<math display="block">[\mu^*/(\sigma^*)^2,\mu^*\cdot(\sigma^*)^2] = [\mu^* {}^\times\!\!/ (\sigma^*)^2]</math> संभावना का 95% सम्मलित है। अनुमानित | <math display="block">[\mu^*/(\sigma^*)^2,\mu^*\cdot(\sigma^*)^2] = [\mu^* {}^\times\!\!/ (\sigma^*)^2]</math> संभावना का 95% सम्मलित है। अनुमानित मापदंडों का उपयोग करते हुए, इन अंतरालों में आंकड़ों का लगभग समान प्रतिशत होना चाहिए। | ||
=== मुक्त | === मुक्त मापदंड σ को हल करने के लिए एन्ट्रापी का चरम सिद्धांत=== | ||
अनुप्रयोगों में, <math>\sigma</math> निर्धारित करने के लिए एक | अनुप्रयोगों में, <math>\sigma</math> निर्धारित करने के लिए एक मापदंड है। उत्पादन और विसरण द्वारा संतुलित बढ़ती प्रक्रियाओं के लिए, एंट्रॉपी के चरम सिद्धांत का उपयोग दर्शाता है कि<ref name="bai">{{cite journal| last1=Wu|first1=Ziniu| last2=Li|first2=Juan| last3=Bai|first3=Chenyuan| title=Scaling Relations of Lognormal Type Growth Process with an Extremal Principle of Entropy| journal=Entropy| volume=19| issue=56| year=2017| pages=1–14| doi=10.3390/e19020056| bibcode=2017Entrp..19...56W| doi-access=free}}</ref> | ||
<math display="block">\sigma = \frac 1 \sqrt{6} </math>इसके पश्चात इस मान का उपयोग मोड़ बिंदु और लॉग-सामान्य वितरण के अधिकतम बिंदु के बीच कुछ स्केलिंग संबंध देने के लिए किया जा सकता है। यह संबंध प्राकृतिक लघुगणक के आधार से निर्धारित होता है, <math>e = 2.718\ldots</math>, और न्यूनतम सतह ऊर्जा सिद्धांत के लिए कुछ ज्यामितीय समानता प्रदर्शित करता है। | <math display="block">\sigma = \frac 1 \sqrt{6} </math>इसके पश्चात इस मान का उपयोग मोड़ बिंदु और लॉग-सामान्य वितरण के अधिकतम बिंदु के बीच कुछ स्केलिंग संबंध देने के लिए किया जा सकता है। यह संबंध प्राकृतिक लघुगणक के आधार से निर्धारित होता है, <math>e = 2.718\ldots</math>, और न्यूनतम सतह ऊर्जा सिद्धांत के लिए कुछ ज्यामितीय समानता प्रदर्शित करता है। | ||
| Line 344: | Line 345: | ||
| isbn = 978-0-486-61114-3 | | isbn = 978-0-486-61114-3 | ||
}}</ref> | }}</ref> | ||
* अत्यधिक संचारी महामारी के लिए, जैसे कि 2003 में सार्स, में यदि सार्वजनिक हस्तक्षेप नियंत्रण नीतियां सम्मलित हैं, तो अस्पताल में भर्ती स्थितियों की संख्या लॉग-सामान्य वितरण को बिना किसी मुक्त | * अत्यधिक संचारी महामारी के लिए, जैसे कि 2003 में सार्स, में यदि सार्वजनिक हस्तक्षेप नियंत्रण नीतियां सम्मलित हैं, तो अस्पताल में भर्ती स्थितियों की संख्या लॉग-सामान्य वितरण को बिना किसी मुक्त मापदंडों के संतुष्ट करने के लिए दिखाई जाती है और यदि एक एंट्रॉपी मान ली जाती है तो मानक विचलन [[एन्ट्रापी उत्पादन]] की अधिकतम दर के सिद्धांत द्वारा निर्धारित किया जाता है।<ref>{{cite journal |last1=S. K. Chan |first1=Jennifer |last2=Yu |first2=Philip L. H. |title=Modelling SARS data using threshold geometric process |journal=Statistics in Medicine |date=2006 |volume=25 |issue=11 |pages=1826–1839 |doi=10.1002/sim.2376 |pmid=16345017 |s2cid=46599163 }}</ref> | ||
* वृद्धि की दिशा में जैविक प्रतिरूप के अक्रिय उपांगों (बाल, पंजे, नाखून, दांत) की लंबाई। | * वृद्धि की दिशा में जैविक प्रतिरूप के अक्रिय उपांगों (बाल, पंजे, नाखून, दांत) की लंबाई। | ||
* किसी भी जीनोमिक क्षेत्र के लिए सामान्यीकृत आरएनए-सेक रीडकाउंट को लॉग-सामान्य वितरण द्वारा अच्छी तरह से अनुमानित किया जा सकता है। | * किसी भी जीनोमिक क्षेत्र के लिए सामान्यीकृत आरएनए-सेक रीडकाउंट को लॉग-सामान्य वितरण द्वारा अच्छी तरह से अनुमानित किया जा सकता है। | ||
| Line 409: | Line 410: | ||
== अग्रिम पठन == | == अग्रिम पठन == | ||
* {{Citation | * {{Citation | ||
| editor-last = | | editor-last = क्रो | ||
| editor-first = | | editor-first = एडविन एल. | ||
| editor-last2 = | | editor-last2 = शिमिजु | ||
| editor-first2 = | | editor-first2 = कुनियो | ||
| title = | | title = लॉगनॉर्मल वितरण, सिद्धांत और अनुप्रयोग | ||
| place = | | place = न्यूयॉर्क | ||
| publisher = | | publisher = मार्सेल डेकर, इंक | ||
| series = | | series = सांख्यिकी: पाठ्यपुस्तकें और मोनोग्राफ | ||
| volume = 88 | | volume = 88 | ||
| year = 1988 | | year = 1988 | ||
| Line 423: | Line 424: | ||
| mr = 0939191 | | mr = 0939191 | ||
| zbl = 0644.62014}} | | zbl = 0644.62014}} | ||
* | * एचिसन, जे. और ब्राउन, जे.ए.सी. (1957) द लॉगनॉर्मल डिस्ट्रीब्यूशन, कैम्ब्रिज यूनिवर्सिटी प्रेस। | ||
* {{cite journal |last1= | * {{cite journal |last1=लिम्पर्ट |first1=E |last2=स्थल |first2=W |last3=एबट |first3=M |title=विज्ञान में लॉगनॉर्मल वितरण: कुंजियाँ और सुराग |journal=जिव शस्त्र |year=2001 |volume=51 |issue=5 |pages=341–352 |doi=10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2|doi-access=free }} | ||
* {{Cite journal | last1 = | * {{Cite journal | last1 = होलगेट | first1 = P. | title = लॉगनॉर्मल विशेषता फ़ंक्शन | doi = 10.1080/03610928908830173 | journal = सांख्यिकी में संचार - सिद्धांत और तरीके | volume = 18 | issue = 12 | pages = 4539–4548 | year = 1989 }} | ||
* {{cite journal | last1 = | * {{cite journal | last1 = ब्रुक्स | first1 = रॉबर्ट | author-link3 = जिम्बो वेल्स | last2 = कोर्सन | first2 = जॉन | last3 = डोनल | first3 = वेल्स | title = सूचकांक विकल्पों का मूल्य निर्धारण तब होता है जब सभी अंतर्निहित परिसंपत्तियाँ एक सामान्य प्रसार का पालन करती हैं | ssrn = 5735 | journal = वायदा और विकल्प अनुसंधान में प्रगति | volume = 7 | year = 1994 }} | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
{{Commons category}} | {{Commons category}} | ||
*[https://stat.ethz.ch/~stahel/talks/lognormal.pdf सामान्य वितरण लॉग-सामान्य वितरण है।] | *[https://stat.ethz.ch/~stahel/talks/lognormal.pdf सामान्य वितरण लॉग-सामान्य वितरण है।] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Log-Normal Distribution]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 errors]] | |||
[[Category:Collapse templates|Log-Normal Distribution]] | |||
[[Category:Commons category link is the pagename|Log-Normal Distribution]] | |||
[[Category:Created On 08/02/2023|Log-Normal Distribution]] | |||
[[Category:Lua-based templates]] | |||
[[Category: | [[Category:Machine Translated Page|Log-Normal Distribution]] | ||
[[Category: | [[Category:Navigational boxes| ]] | ||
[[Category:Navigational boxes without horizontal lists|Log-Normal Distribution]] | |||
[[Category:Pages using infobox probability distribution with unknown parameters|सीडीएफलॉग-सामान्य वितरण]] | |||
[[Category:Pages with math errors|Log-Normal Distribution]] | |||
[[Category:Pages with math render errors|Log-Normal Distribution]] | |||
[[Category:Pages with maths render errors]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Webarchive template wayback links]] | |||
Latest revision as of 17:46, 19 September 2023
|
Probability density function  Identical parameter but differing parameters | |||
|
Cumulative distribution function  | |||
| Notation | |||
|---|---|---|---|
| Parameters |
, | ||
| Support | |||
| Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "ऍ" found.in 1:46"): {\displaystyle \frac 1 {x\sigma\sqrt{2\pi}}\ ऍक्स्प \ लेफ्ट ( - \ frac {\ लेफ्ट (\ ln x - \ mu \ राइट) ^ 2} {2 \ सिग्मा ^ 2} \ राइट) } | |||
प्रायिकता सिद्धांत में, एक लॉग-सामान्य (या लॉगनोर्मल) वितरण एक यादृच्छिक चर का निरंतर संभावना वितरण होता है जिसका लघुगणक सामान्य रूप से वितरित किया जाता है। इस प्रकार, यदि यादृच्छिक चर X लॉग-सामान्य रूप से वितरित किया जाता है, तो Y = ln(X) का सामान्य वितरण होता है।[1][2] समतुल्य रूप से, यदि Y का सामान्य वितरण है, तो Y, X = exp(Y) के घातीय फलन का लॉग-सामान्य वितरण होगा। एक यादृच्छिक चर जो लॉग-सामान्य रूप से वितरित होता है, केवल सकारात्मक वास्तविक मान लेता है। यह सटीक और अभियांत्रिकी विज्ञान, साथ ही चिकित्सा, अर्थशास्त्र और अन्य विषयों (जैसे, ऊर्जा, संकेंद्रण, लंबाई, वित्तीय साधनों की कीमतों और अन्य मीटरी पद्धति) में मापन के लिए एक सुविधाजनक और उपयोगी प्रतिरूप है।
फ्रांसिस गैल्टन के पश्चात वितरण को कभी-कभी गैल्टन वितरण या गैल्टन के वितरण के रूप में जाना जाता है।[3]लॉग-सामान्य वितरण को अन्य नामों से भी संबंधित किया गया है, जैसे मैकएलिस्टर, जिब्राट का नियम और कॉब-डगलस।[3]
एक लॉग-सामान्य प्रक्रिया कई स्वतंत्र यादृच्छिक चर के गुणात्मक उत्पाद का सांख्यिकीय स्वतंत्रता बोध है, जिनमें से प्रत्येक सकारात्मक है। यह लॉग डोमेन में केंद्रीय सीमा प्रमेय (कभी-कभी जिब्रत का नियम कहा जाता है) पर विचार करने के लिए उचित है। लॉग-सामान्य वितरण एक यादृच्छिक चर X- के लिए अधिकतम एन्ट्रापी प्रायिकता वितरण है - जिसके लिए ln(X) का माध्य और विचरण निर्दिष्ट किया गया है।[4]
परिभाषाएँ
पीढ़ी और मापदंड
जब एक मानक सामान्य चर हों, और और दो वास्तविक संख्याएँ हों। फिर, यादृच्छिक चर का वितरण
मापदंडों के साथ लॉग-सामान्य वितरण कहा जाता है और । ये चर के प्राकृतिक लघुगणक का अपेक्षित मान (या माध्य) और मानक विचलन हैं, न कि अपेक्षा और मानक विचलन ही है।
लघुगणक या घातांक फलन के आधार पर ध्यान दिए बिना यह संबंध सत्य है: यदि सामान्य रूप से वितरित किया जाता है, तो ऐसा है किन्हीं दो धनात्मक संख्याओं के लिए । इसी तरह यदि लॉग-सामान्य रूप से वितरित है, तो ऐसा ही है , जहां ।
अभीष्ट माध्य के साथ वितरण की उत्पत्ति करने के लिए और विचरण , एक उपयोग करता है
और
वैकल्पिक रूप से, गुणात्मक या ज्यामितीय मापदंडों और का उपयोग किया जा सकता है। उनकी अधिक प्रत्यक्ष व्याख्या है: वितरण की माध्यिका है, और "तितर बितर" अंतराल निर्धारित करने के लिए उपयोगी है।
संभाव्यता घनत्व फलन
एक धनात्मक यादृच्छिक चर X लॉग-सामान्य रूप से वितरित होता है (अर्थात, ), यदि X का प्राकृतिक लघुगणक सामान्य रूप से माध्य के साथ वितरित किया जाता है और विचरण :
और क्रमशः N(0,1) वितरण का संचयी संभाव्यता वितरण फलन और संभाव्यता घनत्व फलन हो, तो हमारे पास वह है[1][3]
संचयी वितरण फलन
संचयी वितरण फलन है
जहां
मानक सामान्य वितरण (अर्थात्, N(0,1)) का संचयी वितरण फलन है।
इसे इस प्रकार भी व्यक्त किया जा सकता है:[1]
जहां इआरएफसी पूरक त्रुटि फलन है।
बहुभिन्नरूपी लॉग-सामान्य
यदि एक बहुभिन्नरूपी सामान्य वितरण है, तो एक बहुभिन्नरूपी लॉग-सामान्य वितरण होगा।[5][6] घातांक को यादृच्छिक सदिश पर तत्व अनुसार लागू किया जाता है . का मतलब है
और इसका सहप्रसरण मैट्रिक्स है
चूंकि बहुभिन्नरूपी लॉग-सामान्य वितरण का व्यापक रूप से उपयोग नहीं किया जाता है, इसलिए इस प्रविष्टि का शेष भाग केवल एक अविभाज्य वितरण से संबंधित है।
विशेषता कार्य और क्षण उत्पन्न करने वाला कार्य
लॉग-सामान्य वितरण के सभी क्षण उपस्थित हैं और
इसे रख कर प्राप्त किया जा सकता है समाकल के भीतर। चूंकि, लॉग-सामान्य वितरण इसके क्षणों से निर्धारित नहीं होता है।[7] इसका तात्पर्य यह है कि शून्य के निकटतम में इसका परिभाषित क्षण उत्पन्न करने वाला कार्य नहीं हो सकता है।[8] दरअसल, अपेक्षित मूल्य तर्क के किसी सकारात्मक मान के लिए परिभाषित नहीं है , परिभाषित है समाकल विचलन के पश्चात से।
विशेषता फलन (संभावना सिद्धांत) को t के वास्तविक मानों के लिए परिभाषित किया गया है, लेकिन t के किसी भी सम्मिश्र मान के लिए परिभाषित नहीं किया गया है जिसमें एक नकारात्मक काल्पनिक भाग है, और इसलिए विशेषता कार्य मूल पर विश्लेषणात्मक कार्य नहीं है। परिणामस्वरूप, लॉग-सामान्य वितरण की विशेषता फलन को अनंत अभिसरण श्रृंखला के रूप में प्रदर्शित नहीं किया जा सकता है।[9] विशेष रूप से, इसकी टेलर औपचारिक श्रृंखला भिन्न होती है:
चूंकि, कई वैकल्पिक अपसारी श्रृंखला निरूपण प्राप्त किए हुए हैं।[9][10][11][12]
अभिलाक्षणिक फलन के लिए एक बंद रूप सूत्र के साथ अभिसरण के क्षेत्र में ज्ञात नहीं है। एक अपेक्षाकृत सरल अनुमानित सूत्र बंद रूप में उपलब्ध है, और इसके द्वारा दिया गया है[13]
जहां लैम्बर्ट डब्ल्यू फलन है। यह सन्निकटन एक स्पर्शोन्मुख विधि के माध्यम से प्राप्त किया गया है, लेकिन यह अभिसरण के पूरे कार्यक्षेत्र में तीव्र रहता है .
गुण

विभिन्न डोमेन में संभावना
किसी भी स्वैच्छिक डोमेन में लॉग-सामान्य वितरण की संभाव्यता सामग्री को पहले चर को सामान्य में बदलकर, फिर रे-ट्रेस विधि का उपयोग करके संख्यात्मक रूप से एकीकृत करके वांछित सटीकता की गणना की जा सकती है।[14] (मैटलैब कोड)
लॉग-सामान्य चर के कार्यों की संभावनाएं
चूंकि लॉग-सामान्य की संभाव्यता की गणना किसी भी डोमेन में की जा सकती है, इसका मतलब यह है कि लॉग-सामान्य चर के किसी भी फलन के सीडीएफ (और परिणामस्वरूप पीडीएफ और व्युत्क्रम सीडीएफ) की भी गणना की जा सकती है।[14](मैटलैब कोड)
ज्यामितीय या गुणात्मक क्षण
लॉग-सामान्य वितरण का ज्यामितीय माध्य है . यह माध्यिका के बराबर होता है। ज्यामितीय मानक विचलन है .[15][16]
अंकगणितीय आँकड़ों के अनुरूप, एक ज्यामितीय विचरण को परिभाषित कर सकते है, द्वारा, और सापेक्ष मानक विचलन[15] को, द्वारा प्रस्थापित किया गया है। लॉग-सामान्य आंकड़े में गुणात्मक भिन्नता का वर्णन करने के लिए, इस शब्द का अभिप्रेत सापेक्ष मानक विचलन के अनुरूप होना था, लेकिन जीसीवी की इस परिभाषा का आकलन के रूप में कोई सैद्धांतिक आधार स्वयं नहीं है (सापेक्ष मानक विचलन भी देखें)।
ध्यान दें कि ज्यामितीय माध्य अंकगणितीय माध्य से छोटा होता है। यह एएम-जीएम असमानता के कारण होता है और लघुगणक के अवतल फलन होने का परिणाम है। वास्तव में,
गणितीय वित्त में, शब्द को कभी-कभी उत्तलता सुधार के रूप में व्याख्या किया जाता है। स्टोचैस्टिक कैलकुलस के दृष्टिकोण से, यह वही सुधार शब्द है जो ज्यामितीय ब्राउनियन गति के लिए गणित में, इतो का लेम्मा या इतो का सूत्र में है।
अंकगणितीय क्षण
किसी भी वास्तविक या सम्मिश्र संख्या n के लिए, लॉग-सामान्य रूप से वितरित चर X का n-वें क्षण द्वारा दिया गया है[3]:
विशेष रूप से, अंकगणितीय माध्य, अपेक्षित वर्ग, अंकगणितीय विचरण, और अंकगणितीय मानक विचलन एक लॉग-सामान्य रूप से वितरित चर X क्रमशः द्वारा दिया जाता हैं:[1]
अंकगणितीय सापेक्ष मानक विचलन का अनुपात है। लॉग-सामान्य वितरण के लिए यह समान है[2]:
इस अनुमान को कभी-कभी इसके ज्यामितीय विचरण के उपयोग के कारण ज्यामितीय सीवी (जीसीवी) के रूप में संदर्भित किया जाता है।[18][19] अंकगणितीय मानक विचलन के विपरीत, अंकगणितीय सापेक्ष मानक विचलन अंकगणितीय माध्य से स्वतंत्र है।
अंकगणित माध्य और अंकगणितीय विचलन ज्ञात होने पर मापदंड μ और σ प्राप्त किए जा सकते हैं:
संभाव्यता वितरण विशिष्ट रूप से क्षणों E[Xn] = enμ + 1/2n2σ2 द्वारा निर्धारित नहीं होता है n ≥ 1. के लिए। अर्थात्, समान क्षणों के साथ अन्य वितरण उपस्थित होते।[3]वास्तव में, लॉग-सामान्य वितरण के समान क्षणों के साथ वितरण की एक पूरी श्रेणी होती है।
मोड, माध्यिका, क्वांटाइल्स
मोड (सांख्यिकी) संभाव्यता घनत्व फलन का सार्वत्रिक अधिकतम बिंदु है। विशेष रूप से, समीकरण को हल करके , हमें वह मिलता है:
लघुगणक परिवर्तन चर के पश्चात से का एक सामान्य वितरण है, और मात्रात्मक को एकदिष्ट परिवर्तनों के तहत संरक्षित किया जाता है, मात्रात्मक हैं
जहां मानक सामान्य वितरण का परिमाण है।
विशेष रूप से, एक लॉग-सामान्य वितरण का माध्य इसके गुणक माध्य के बराबर होता है,[20]
आंशिक अपेक्षा
एक यादृच्छिक चर की आंशिक अपेक्षा एक प्रारंभ के संबंध में के रूप में परिभाषित किया गया है
वैकल्पिक रूप से, सशर्त अपेक्षा की परिभाषा का उपयोग करके, इसे इस रूप में लिखा जा सकता है . लॉग-सामान्य सांयोगिक चर के लिए, आंशिक अपेक्षा इसके द्वारा दी जाती है:
जहां सामान्य वितरण या गॉसियन वितरण है। सूत्र की व्युत्पत्ति वार्ता पृष्ठ में दी गई है। आंशिक अपेक्षा सूत्र में बीमा और अर्थशास्त्र अनुप्रयोग हैं, इसका उपयोग ब्लैक-स्कोल्स सूत्र के लिए आंशिक अंतर समीकरण को हल करने में किया जाता है।
सशर्त अपेक्षा
लॉग-सामान्य यादृच्छिक चर की सशर्त अपेक्षा - प्रारंभ के संबंध में —इसकी आंशिक अपेक्षा को उस सीमा में होने की संचयी संभावना से विभाजित करता है:
वैकल्पिक मानकीकरण
या द्वारा लक्षण वर्णन के अतिरिक्त, लॉग-सामान्य वितरण को मानकीकरण करने के कई उपाय हैं। प्रोबऑन्टो, संभाव्यता वितरण के ज्ञान का आधार और ऑन्कोलॉजी[21][22] ऐसे सात रूपों को सूचीबद्ध करता है:
- लॉग-स्तर पर माध्य, μ और मानक विचलन, σ, दोनों के साथ लॉग-सामान्य 1(μ,σ) [23]
- लॉग-सामान्य 2(μ,υ) माध्य, μ और विचरण के साथ, υ, दोनों लॉग-स्तर पर
- लॉग-सामान्य 3(m,σ) मध्यिका के साथ, m, प्राकृतिक पैमाने पर और मानक विचलन, σ, लॉग-पैमाने पर[23]
- लॉग-सामान्य 4(m,सी वी) माध्यिका, m, और भिन्नता के गुणांक, सी वी, दोनों के साथ प्राकृतिक पैमाने पर
- लॉग-सामान्य 5(μ,τ) माध्य, μ और सटीक, τ, दोनों के साथ लॉग-पैमाने पर[24]
- लॉग-सामान्य 6 (m,σg) माध्यिका, मी और ज्यामितीय मानक विचलन, σg, दोनों के साथ प्राकृतिक पैमाने पर[25]
- लॉग-सामान्य(μN, पीN) माध्य के साथ, μN, और मानक विचलन, σN, दोनों प्राकृतिक पैमाने पर[26]
पुन: मानकीकरण के उदाहरण
उस स्थिति पर विचार करें जब कोई दो अलग-अलग सर्वोत्तम डिज़ाइन उपकरण का उपयोग करके एक प्रतिरूप चलाना चाहेगा, उदाहरण के लिए पीएफआईएम[27] और पॉपपेड।[28] पूर्व क्रमशः एलएन2, पश्चात वाले एलएन7 के मानकीकरण का समर्थन करता है। इसलिए, पुन: मानकीकरण की आवश्यकता है, अन्यथा दो उपकरण अलग-अलग परिणाम देंगे।
संक्र्रांति के लिए निम्नलिखित सूत्र धारण करते हैं और .
संक्र्रांति के लिए निम्नलिखित सूत्र धारण करते हैं और .
शेष सभी पुनः-मानकीकरण सूत्र परियोजना की वेबसाइट पर विनिर्देश प्रलेख में पाए जा सकते हैं।[29]
एकाधिक, पारस्परिक, शक्ति
- एक एकाधिक से गुणा: यदि तब के लिए
- पारस्परिक: यदि तब
- शक्ति: यदि तब के लिए
स्वतंत्र, लॉग-सामान्य यादृच्छिक चर का गुणन और विभाजन
यदि दो स्वतंत्र, लॉग-सामान्य चर और गुणा [विभाजित] हैं, उत्पाद [अनुपात] मापदंडों के साथ फिर से लॉग-सामान्य है [] और , जहां . यह आसानी से जैसे चर उत्पाद के लिए सामान्यीकृत है।
सामान्यतः अधिक, यदि हैं स्वतंत्र, लॉग-सामान्य रूप से वितरित चर, फिर है।
गुणक केंद्रीय सीमा प्रमेय
का ज्यामितीय या गुणक माध्य स्वतंत्र, समान रूप से वितरित, सकारात्मक यादृच्छिक चर दिखाता है, के लिए मापदंडों के साथ लगभग एक लॉग-सामान्य वितरण और , मानते हुए परिमित है।
वास्तव में, यादृच्छिक चरों को समान रूप से वितरित करने की आवश्यकता नहीं है। के वितरण के लिए पर्याप्त है सभी के पास परिमित प्रसरण है और केंद्रीय सीमा प्रमेय के कई रूपों में से किसी एक की अन्य शर्तों को पूरा करते हैं।
इसे सामान्यतः जिब्रात के नियम के रूप में जाना जाता है।
अन्य
लॉग-सामान्य वितरण से उत्पन्न होने वाले आंकड़े के एक सेट में एक सममित लॉरेंज वक्र होता है (लॉरेंज विषमता गुणांक भी देखें)।[30]
हार्मोनिक , ज्यामितीय और अंकगणित इस वितरण के द्वारा संबंधित हैं;[31] ऐसा संबंध द्वारा दिया गया है
लॉग-सामान्य वितरण अनंत विभाज्यता (संभावना) हैं,[32]लेकिन वे स्थिर वितरण नहीं हैं, जिन्हें आसानी से निकाला जा सकता है।[33]
संबंधित वितरण
- यदि एक सामान्य वितरण है, फिर
- यदि लॉग-सामान्य रूप से वितरित किया जाता है, तब एक सामान्य यादृच्छिक चर है।
- स्वतंत्र लॉग-सामान्य रूप से वितरित चर हो सकते हैं जिनमें संभवतः भिन्नता हो और मापदंड, और . का वितरण की कोई बंद-रूप अभिव्यक्ति नहीं है, लेकिन एक अन्य लॉग-सामान्य वितरण द्वारा यथोचित अनुमान लगाया जा सकता है की दाहिने अंतिम भाग पर है।[34] संभाव्यता घनत्व फलन की विशेषता 0 के निकटतम में[33] होती है और यह किसी लॉग-सामान्य वितरण के समान नहीं है। एल.एफ. फेंटन के कारण सामान्यतः उपयोग किया जाने वाला सन्निकटन (लेकिन पहले आर.आई. विल्किंसन द्वारा कहा गया था और मार्लो द्वारा गणितीय औचित्य[35]) एक अन्य लॉग-सामान्य वितरण के माध्य और विचरण से मेल करके प्राप्त किया जाता है:स्थिति में यह सब एक ही विचरण मापदंडों है , ये सूत्र सरल करते हैं
अधिक सटीक समीपता के लिए, संचयी वितरण फलन, पीडीएफ और सही अंतिम भाग का अनुमान लगाने के लिए मोंटे कार्लो विधि का उपयोग कर सकते हैं।[36][37] सहसंबद्ध लॉग-सामान्य रूप से वितरित यादृच्छिक चर का योग भी लॉग-सामान्य वितरण द्वारा अनुमानित किया जा सकता हैं।
- यदि तब कहा जाता है कि समर्थन के साथ तीन-फलन लॉग-सामान्य वितरण है .[38] ,
- कहा जाता है कि समर्थन के साथ तीन-फलन प्रारंभिक-सामान्य वितरण है।[39]
- यदि साथ , तब (सुजुकी वितरण)।
- लॉग-सामान्य के लिए एक विकल्प जिसका समाकलित तत्व अधिक प्राथमिक फलन के संदर्भ में व्यक्त किया जा सकता है[40] सीडीएफ के लिए एक समीपता प्राप्त करने के लिए उसे रसद वितरण के आधार पर प्राप्त किया जा सकता हैयह एक लॉग-लॉजिस्टिक वितरण है।
सांख्यिकीय निष्कर्ष
मापदंडों का अनुमान
लॉग-सामान्य वितरण मापदंडों μ और σ के अधिकतम संभावना अनुमानक का निर्धारण करने के लिए, हम सामान्य वितरण के समान प्रक्रिया का उपयोग कर सकते हैं। ध्यान दें कि
जब मूलभूत स्तंभ उपलब्ध नहीं हैं, लेकिन प्रतिरूप का मतलब है और मानक विचलन एस है, तो संबंधित मापदंडों को निम्नलिखित सूत्रों द्वारा निर्धारित किया जाता है, जो अपेक्षा के लिए समीकरणों को हल करने से प्राप्त होते हैं और विचरण के लिए और :
सांख्यिकी
लॉग-सामान्य रूप से वितरित आंकड़े का विश्लेषण करने का सबसे कुशल उपाए लघुगणकीय रूप से रूपांतरित आंकड़े के लिए सामान्य वितरण के आधार पर प्रसिद्ध विधियों को लागू करना है और यदि उपयुक्त हो तो परिणामों को वापस-परिवरतित करना है।
तितर बितर अंतराल
तितर-बितर अंतराल द्वारा एक बुनियादी उदाहरण दिया जाता है: सामान्य वितरण के लिए, अंतराल में संभाव्यता (या एक बड़े नमूने) का लगभग दो तिहाई (68%) होता है, और में 95% होता हैं। इसलिए, लॉग-सामान्य वितरण के लिए,
मुक्त मापदंड σ को हल करने के लिए एन्ट्रापी का चरम सिद्धांत
अनुप्रयोगों में, निर्धारित करने के लिए एक मापदंड है। उत्पादन और विसरण द्वारा संतुलित बढ़ती प्रक्रियाओं के लिए, एंट्रॉपी के चरम सिद्धांत का उपयोग दर्शाता है कि[41]
ये स्केलिंग संबंध कई विकास प्रक्रियाओं (महामारी फैलना, बूंदों के छींटे, जनसंख्या वृद्धि, बाथटब भंवर की घूमने की दर, भाषा वर्णों का वितरण, विक्षोभ का वेग प्रोफ़ाइल, आदि) की भविष्यवाणी करने के लिए उपयोगी हैं।उदाहरण के लिए, लॉग--सामान्य फलन के साथ छोटी बूंदों के प्रभाव और एक महामारी रोग के प्रसार के समय माध्यमिक रूप से उत्पादित बूंदों के आकार के साथ अच्छी तरह से फिट बैठता है। [42]
मूल्य का उपयोग ड्रेक समीकरण के लिए एक संभाव्य समाधान प्रदान करने के लिए किया जाता है।[43]
घटना और अनुप्रयोग
प्राकृतिक परिघटनाओं के वर्णन में लॉग-सामान्य वितरण महत्वपूर्ण है। कई प्राकृतिक विकास प्रक्रियाएं कई छोटे प्रतिशत परिवर्तनों के संचय द्वारा संचालित होती हैं जो लॉग मापने पर योगात्मक हो जाती हैं। उपयुक्त नियमितता की शर्तों के तहत, परिणामी संचित परिवर्तनों का वितरण एक लॉग-सामान्य द्वारा तेजी से अच्छी तरह से अनुमानित होगा, जैसा कि "गुणात्मक केंद्रीय सीमा प्रमेय" पर ऊपर दिए गए अनुभाग में बताया गया है। रॉबर्ट जिब्रत (1904-1980) के पश्चात इसे जिब्राट के सिद्धांत के रूप में भी जाना जाता है, जिन्होंने इसे कंपनियों के लिए तैयार किया था।[44] यदि इन छोटे परिवर्तनों के संचय की दर समय के साथ भिन्न नहीं होती है, तो वृद्धि आकार से स्वतंत्र हो जाती है। यहां तक कि यदि यह धारणा सही नहीं है, तो समय के साथ बढ़ने वाली किसी भी उम्र में आकार का वितरण लॉग-सामान्य हो जाता है। परिणामस्वरूप, स्वस्थ व्यक्तियों में शारीरिक माप के लिए संदर्भ श्रेणी या संदर्भ अंतराल माध्य के बारे में एक सममित वितरण मानकर एक लॉग-सामान्य वितरण मानकर अधिक सटीक रूप से अनुमान लगाया जाता है।
एक दूसरा औचित्य इस अवलोकन पर आधारित है कि मौलिक प्राकृतिक नियम सकारात्मक चरों के गुणन और विभाजन को लागू करते हैं। उदाहरण परिणामी बल के साथ द्रव्यमान और दूरी को जोड़ने वाला सरल गुरुत्वाकर्षण नियम हैं, या एक समाधान में रसायनों की साम्य सांद्रता के लिए सूत्र है जो उत्पादों और उत्पादों की सांद्रता को जोड़ता है। सम्मलित चरों के लॉग-सामान्य वितरण को मानने से इन स्थितियों में सुसंगत प्रारूप बनते हैं।
निम्नलिखित उपखंडों में विशिष्ट उदाहरण दिए गए हैं।
मानव व्यवहार
- अंतरजाल चर्चा मंचों में पोस्ट की गई टिप्पणियों की लंबाई लॉग-सामान्य वितरण का अनुसरण करती है।[45]
- ऑनलाइन लेखों (चुटकुले, समाचार आदि) पर उपयोगकर्ताओं का समय एक लॉग-सामान्य वितरण का अनुसरण करता है।[46]
- शतरंज के खेल की लंबाई लॉग-सामान्य वितरण का अनुसरण करती है।[47]
- एक मानक उत्तेजना से मेल खाने वाली ध्वनिक तुलना उत्तेजनाओं की प्रारंभ की अवधि एक लॉग-सामान्य वितरण का पालन करती है।[17]
- रूबिक घन हल करता है, दोनों सामान्य या व्यक्तिगत रूप से, लॉग-सामान्य वितरण का पालन करते प्रतीत होते हैं।
जीव विज्ञान और चिकित्सा
- जीवित ऊतक के आकार का माप (लंबाई, त्वचा क्षेत्र, वजन)।[48]
- अत्यधिक संचारी महामारी के लिए, जैसे कि 2003 में सार्स, में यदि सार्वजनिक हस्तक्षेप नियंत्रण नीतियां सम्मलित हैं, तो अस्पताल में भर्ती स्थितियों की संख्या लॉग-सामान्य वितरण को बिना किसी मुक्त मापदंडों के संतुष्ट करने के लिए दिखाई जाती है और यदि एक एंट्रॉपी मान ली जाती है तो मानक विचलन एन्ट्रापी उत्पादन की अधिकतम दर के सिद्धांत द्वारा निर्धारित किया जाता है।[49]
- वृद्धि की दिशा में जैविक प्रतिरूप के अक्रिय उपांगों (बाल, पंजे, नाखून, दांत) की लंबाई।
- किसी भी जीनोमिक क्षेत्र के लिए सामान्यीकृत आरएनए-सेक रीडकाउंट को लॉग-सामान्य वितरण द्वारा अच्छी तरह से अनुमानित किया जा सकता है।
- प्रशांत बायोसाइंसेज अनुक्रमण पढ़ने की लंबाई लॉग-सामान्य वितरण का अनुसरण करती है।[50]
- कुछ शारीरिक माप, जैसे कि वयस्क मनुष्यों का रक्तचाप (पुरुष/महिला उप-जनसंख्या पर अलग होने के पश्चात)।[51]
- कई फार्माकोकाइनेटिक्स चर, जैसे कि सी अधिकतम, उन्मूलन जैविक आधा जीवन और उन्मूलन दर स्थिर।[52]
- तंत्रिका विज्ञान में, न्यूरॉन्स की आबादी में फायरिंग दरों का वितरण अधिकांशतः लगभग लॉग-सामान्य होता है। यह पहले कॉर्टेक्स और स्ट्रिएटम [53] में और पश्चात में हिप्पोकैम्पस और एंटोरहिनल कॉर्टेक्स,[54] और मस्तिष्क में कहीं देखा गया है।[55][56]साथ ही,आंतरिक लाभ वितरण और सिनैप्टिक वजन वितरण लॉग-सामान्य[57]भी प्रतीत होते हैं।
- ऑपरेटिंग-रूम प्रबंधन में, सर्जरी की अवधि का वितरण।
- जीवित कोशिकाओं के साइटोस्केलेटन में फ्रैक्चर के ऐवलैन्च के आकार में, लॉग-सामान्य वितरण दिखा रहा है, स्वस्थ लोगों की तुलना में कैंसर कोशिकाओं में काफी अधिक आकार के साथ। [58]
रसायन विज्ञान
रसायन विज्ञान में, लॉग-सामान्य वितरण का उपयोग पार्टिकल साइज वितरण और मोलर द्रव्यमान वितरण को प्रतिरूप करने के लिए किया जाता है।
जल विज्ञान
- जल विज्ञान में, लॉग-सामान्य वितरण का उपयोग ऐसे चर के चरम मूल्यों का विश्लेषण करने के लिए किया जाता है जैसे दैनिक वर्षा और नदी निर्वहन मात्रा के मासिक और वार्षिक अधिकतम मूल्यों के लिए।[59]
- दाईं ओर का प्रतिबिंब, कम फ्रीक के साथ बनाई गई, वार्षिक अधिकतम एक-दिवसीय वर्षा के लिए लॉग-सामान्य वितरण को फिट करने का एक उदाहरण दिखाता है, जो द्विपद वितरण के आधार पर 90% आत्मविश्वास बेल्ट भी दिखाता है।[60]
- संचयी बारंबारता विश्लेषण के भाग के रूप में वर्षा के आंकड़ों को प्लॉटिंग पोजीशन द्वारा दर्शाया जाता है।
सामाजिक विज्ञान और जनसांख्यिकी
- अर्थशास्त्र में, इस बात के प्रमाण हैं कि 97% -99% जनसंख्या की आय सामान्य रूप से वितरित की जाती है।[61] (उच्च आय वाले व्यक्तियों का वितरण पारेटो वितरण का अनुसरण करता है)।[62]
- यदि आय वितरण मानक विचलन के साथ लॉग-सामान्य वितरण का अनुसरण करता है , तो गिनी गुणांक, सामान्यतः आय असमानता का मूल्यांकन करने के लिए उपयोग किया जाता है, इसकी गणना की जा सकती है जहां त्रुटि फलन है, चूंकि , जहां एक मानक सामान्य वितरण का संचयी वितरण फलन है।
- वित्त में, विशेष रूप से ब्लैक-स्कोल्स प्रारूप, विनिमय दरों, मूल्य सूचकांकों और शेयर बाजार सूचकांकों के लघुगणक में परिवर्तन को सामान्य माना जाता है।[63] (ये चर चक्रवृद्धि ब्याज की तरह व्यवहार करते हैं, साधारण ब्याज की तरह नहीं, और इसलिए गुणक हैं)। चूंकि, बेनोइट मंडेलब्रॉट जैसे कुछ गणितज्ञों ने तर्क दिया है[64] कि लॉग-लेवी वितरण, जिसमें भारी पूंछ होती है, एक अधिक उपयुक्त प्रारूप होता है, विशेष रूप से शेयर बाजार में गिरावट के विश्लेषण के लिए। वास्तव में, स्टॉक मूल्य वितरण सामान्यतः एक मोटी पूंछ प्रदर्शित करते हैं।[65] स्टॉक मार्केट क्रैश के समय परिवर्तनों की मोटी पूंछ वितरण केंद्रीय सीमा प्रमेय की धारणाओं को अमान्य कर देता है।
- साइनोमेट्रिक्स में, दैनिक लेखों और पेटेंट के उद्धरणों की संख्या असतत लॉग-सामान्य वितरण का अनुसरण करती है।[66][67]
- ऐतिहासिक शहरी समुदाय आकार (जनसंख्या) जिब्रात के नियम को संतुष्ट करता है।[68] शहर के आकार की विकास प्रक्रिया आकार के संबंध में आनुपातिक और अपरिवर्तनीय होती है। केंद्रीय सीमा प्रमेय से इसलिए, शहर के आकार को लॉग सामान्य रूप से वितरित किया जाता है।
- लॉग-सामान्य वितरण द्वारा यौन भागीदारों की संख्या का सबसे अच्छा वर्णन किया गया प्रतीत होता है।[69]
प्रौद्योगिकी
- विश्वसनीयता (सांख्यिकी) विश्लेषण में, लॉग-सामान्य वितरण का उपयोग अधिकांशतः एक अनुरक्षण योग्य प्रणाली की मरम्मत के लिए प्रारूप समय के लिए किया जाता है।[70]
- बेतार संचार में, लघुगणक मानों में व्यक्त स्थानीय-माध्य शक्ति, जैसे डीबी या नेपर, का सामान्य (अर्थात, गॉसियन) वितरण होता है।[71] साथ ही, बड़ी इमारतों और पहाड़ियों के कारण रेडियो संकेतों की यादृच्छिक रुकावट, जिसे लुप्त होती कहा जाता है, को अधिकांशतः लॉग-सामान्य वितरण के रूप में प्रतिरूपित किया जाता है।
- बॉल मिलिंग जैसे यादृच्छिक प्रभावों के साथ टुकड़े टुकड़े करने द्वारा उत्पादित कण आकार वितरण।
- सार्वजनिक रूप से उपलब्ध ऑडियो और वीडियो आंकड़े फ़ाइलों (एमआईएमइ प्रकार) का फ़ाइल आकार वितरण परिमाण के पाँच आदेशों पर एक लॉग-सामान्य वितरण का अनुसरण करता है।[72]
- कंप्यूटर नेटवर्क और इंटरनेट यातायात विश्लेषण में, लॉग-सामान्य को प्रति यूनिट समय ट्रैफ़िक की मात्रा का प्रतिनिधित्व करने के लिए एक अच्छे सांख्यिकीय प्रारूप के रूप में दिखाया गया है। यह वास्तविक इंटरनेट अंशों के एक बड़े समूह पर एक मजबूत सांख्यिकीय दृष्टिकोण लागू करके दिखाया गया है। इस संदर्भ में, लॉग-सामान्य वितरण ने दो मुख्य उपयोग स्थितियों में अच्छा प्रदर्शन दिखाया है: (1) समय यातायात के अनुपात की भविष्यवाणी एक निश्चित स्तर से अधिक हो जाएगी (सेवा स्तर समझौते या लिंक क्षमता अनुमान के लिए) अर्थात बैंडविड्थ प्रावधान के आधार पर लिंक आयाम और (2) 95वें प्रतिशतता मूल्य निर्धारण की भविष्यवाणी करना।[73]
यह भी देखें
टिप्पणियाँ
- ↑ 1.0 1.1 1.2 1.3 Weisstein, Eric W. "Log Normal Distribution". mathworld.wolfram.com (in English). Retrieved 2020-09-13.
- ↑ 2.0 2.1 "1.3.6.6.9. Lognormal Distribution". www.itl.nist.gov. Retrieved 2020-09-13.
- ↑ 3.0 3.1 3.2 3.3 3.4 Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1994), "14: Lognormal Distributions", Continuous univariate distributions. Vol. 1, Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-58495-7, MR 1299979
- ↑ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model" (PDF). Journal of Econometrics. 150 (2): 219–230. CiteSeerX 10.1.1.511.9750. doi:10.1016/j.jeconom.2008.12.014. Archived from the original (PDF) on 2016-03-07. Retrieved 2011-06-02. Table 1, p. 221.
- ↑ Tarmast, Ghasem (2001). Multivariate Log–Normal Distribution (PDF). ISI Proceedings: 53rd Session. Seoul.
- ↑ Halliwell, Leigh (2015). The Lognormal Random Multivariate (PDF). Casualty Actuarial Society E-Forum, Spring 2015. Arlington, VA.
- ↑ Heyde, CC. (1963), "On a property of the lognormal distribution", Journal of the Royal Statistical Society, Series B, vol. 25, no. 2, pp. 392–393, doi:10.1007/978-1-4419-5823-5_6, ISBN 978-1-4419-5822-8
- ↑ Billingsley, Patrick (2012). Probability and Measure (Anniversary ed.). Hoboken, N.J.: Wiley. p. 415. ISBN 978-1-118-12237-2. OCLC 780289503.
- ↑ 9.0 9.1 Holgate, P. (1989). "The lognormal characteristic function, vol. 18, pp. 4539–4548, 1989". Communications in Statistics - Theory and Methods. 18 (12): 4539–4548. doi:10.1080/03610928908830173.
- ↑ Barakat, R. (1976). "Sums of independent lognormally distributed random variables". Journal of the Optical Society of America. 66 (3): 211–216. Bibcode:1976JOSA...66..211B. doi:10.1364/JOSA.66.000211.
- ↑ Barouch, E.; Kaufman, GM.; Glasser, ML. (1986). "On sums of lognormal random variables" (PDF). Studies in Applied Mathematics. 75 (1): 37–55. doi:10.1002/sapm198675137. hdl:1721.1/48703.
- ↑ Leipnik, Roy B. (January 1991). "On Lognormal Random Variables: I – The Characteristic Function" (PDF). Journal of the Australian Mathematical Society, Series B. 32 (3): 327–347. doi:10.1017/S0334270000006901.
- ↑ S. Asmussen, J.L. Jensen, L. Rojas-Nandayapa (2016). "On the Laplace transform of the Lognormal distribution", Methodology and Computing in Applied Probability 18 (2), 441-458. Thiele report 6 (13).
- ↑ 14.0 14.1 14.2 Das, Abhranil (2020). "A method to integrate and classify normal distributions". arXiv:2012.14331 [stat.ML].
- ↑ 15.0 15.1 Kirkwood, Thomas BL (Dec 1979). "Geometric means and measures of dispersion". Biometrics. 35 (4): 908–9. JSTOR 2530139.
- ↑ Limpert, E; Stahel, W; Abbt, M (2001). "Lognormal distributions across the sciences: keys and clues". BioScience. 51 (5): 341–352. doi:10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2.
- ↑ 17.0 17.1 Heil P, Friedrich B (2017). "Onset-Duration Matching of Acoustic Stimuli Revisited: Conventional Arithmetic vs. Proposed Geometric Measures of Accuracy and Precision". Frontiers in Psychology. 7: 2013. doi:10.3389/fpsyg.2016.02013. PMC 5216879. PMID 28111557.
- ↑ Sawant,S.; Mohan, N. (2011) "FAQ: Issues with Efficacy Analysis of Clinical Trial Data Using SAS" Archived 24 August 2011 at the Wayback Machine, PharmaSUG2011, Paper PO08
- ↑ Schiff, MH; et al. (2014). "Head-to-head, randomised, crossover study of oral versus subcutaneous methotrexate in patients with rheumatoid arthritis: drug-exposure limitations of oral methotrexate at doses >=15 mg may be overcome with subcutaneous administration". Ann Rheum Dis. 73 (8): 1–3. doi:10.1136/annrheumdis-2014-205228. PMC 4112421. PMID 24728329.
- ↑ Daly, Leslie E.; Bourke, Geoffrey Joseph (2000). Interpretation and uses of medical statistics. p. 89. doi:10.1002/9780470696750. ISBN 978-0-632-04763-5. PMC 1059583.
{{cite book}}:|journal=ignored (help) - ↑ "ProbOnto". Retrieved 1 July 2017.
- ↑ Swat, MJ; Grenon, P; Wimalaratne, S (2016). "ProbOnto: ontology and knowledge base of probability distributions". Bioinformatics. 32 (17): 2719–21. doi:10.1093/bioinformatics/btw170. PMC 5013898. PMID 27153608.
- ↑ 23.0 23.1 Forbes et al. Probability Distributions (2011), John Wiley & Sons, Inc.
- ↑ Lunn, D. (2012). The BUGS book: a practical introduction to Bayesian analysis. Texts in statistical science. CRC Press.
- ↑ Limpert, E.; Stahel, W. A.; Abbt, M. (2001). "Log-normal distributions across the sciences: Keys and clues". BioScience. 51 (5): 341–352. doi:10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2.
- ↑ Nyberg, J.; et al. (2012). "PopED - An extended, parallelized, population optimal design tool". Comput Methods Programs Biomed. 108 (2): 789–805. doi:10.1016/j.cmpb.2012.05.005. PMID 22640817.
- ↑ Retout, S; Duffull, S; Mentré, F (2001). "Development and implementation of the population Fisher information matrix for the evaluation of population pharmacokinetic designs". Comp Meth Pro Biomed. 65 (2): 141–151. doi:10.1016/S0169-2607(00)00117-6. PMID 11275334.
- ↑ The PopED Development Team (2016). PopED Manual, Release version 2.13. Technical report, Uppsala University.
- ↑ ProbOnto website, URL: http://probonto.org
- ↑ Damgaard, Christian; Weiner, Jacob (2000). "Describing inequality in plant size or fecundity". Ecology. 81 (4): 1139–1142. doi:10.1890/0012-9658(2000)081[1139:DIIPSO]2.0.CO;2.
- ↑ Rossman, Lewis A (July 1990). "Design stream flows based on harmonic means". Journal of Hydraulic Engineering. 116 (7): 946–950. doi:10.1061/(ASCE)0733-9429(1990)116:7(946).
- ↑ Thorin, Olof (1977). "On the infinite divisibility of the lognormal distribution". Scandinavian Actuarial Journal. 1977 (3): 121–148. doi:10.1080/03461238.1977.10405635. ISSN 0346-1238.
- ↑ 33.0 33.1 Gao, Xin (2009). "Asymptotic Behavior of Tail Density for Sum of Correlated Lognormal Variables". International Journal of Mathematics and Mathematical Sciences. 2009: 1–28. doi:10.1155/2009/630857.
- ↑ Asmussen, S.; Rojas-Nandayapa, L. (2008). "Asymptotics of Sums of Lognormal Random Variables with Gaussian Copula" (PDF). Statistics and Probability Letters. 78 (16): 2709–2714. doi:10.1016/j.spl.2008.03.035.
- ↑ Marlow, NA. (Nov 1967). "A normal limit theorem for power sums of independent normal random variables". Bell System Technical Journal. 46 (9): 2081–2089. doi:10.1002/j.1538-7305.1967.tb04244.x.
- ↑ Botev, Z. I.; L'Ecuyer, P. (2017). "Accurate computation of the right tail of the sum of dependent log-normal variates". 2017 Winter Simulation Conference (WSC), 3rd–6th Dec 2017. Las Vegas, NV, USA: IEEE. pp. 1880–1890. arXiv:1705.03196. doi:10.1109/WSC.2017.8247924. ISBN 978-1-5386-3428-8.
- ↑ Asmussen, A.; Goffard, P.-O.; Laub, P. J. (2016). "Orthonormal polynomial expansions and lognormal sum densities". arXiv:1601.01763v1 [math.PR].
- ↑ Sangal, B.; Biswas, A. (1970). "The 3-Parameter Lognormal Distribution Applications in Hydrology". Water Resources Research. 6 (2): 505–515. doi:10.1029/WR006i002p00505.
- ↑ Johnson, N. L. (1949). "Systems of Frequency Curves Generated by Methods of Translation". Biometrika. 36 (1/2): 149–176. doi:10.2307/2332539. JSTOR 2332539. PMID 18132090.
- ↑ Swamee, P. K. (2002). "Near Lognormal Distribution". Journal of Hydrologic Engineering. 7 (6): 441–444. doi:10.1061/(ASCE)1084-0699(2002)7:6(441).
- ↑ Wu, Ziniu; Li, Juan; Bai, Chenyuan (2017). "Scaling Relations of Lognormal Type Growth Process with an Extremal Principle of Entropy". Entropy. 19 (56): 1–14. Bibcode:2017Entrp..19...56W. doi:10.3390/e19020056.
- ↑ Wu, Zi-Niu (2003). "Prediction of the size distribution of secondary ejected droplets by crown splashing of droplets impinging on a solid wall". Probabilistic Engineering Mechanics. 18 (3): 241–249. doi:10.1016/S0266-8920(03)00028-6.
- ↑ Bloetscher, Frederick (2019). "Using predictive Bayesian Monte Carlo- Markov Chain methods to provide a probabilistic solution for the Drake equation". Acta Astronautica. 155: 118–130. Bibcode:2019AcAau.155..118B. doi:10.1016/j.actaastro.2018.11.033. S2CID 117598888.
- ↑ Sutton, John (Mar 1997). "Gibrat's Legacy". Journal of Economic Literature. 32 (1): 40–59. JSTOR 2729692.
- ↑ Pawel, Sobkowicz; et al. (2013). "Lognormal distributions of user post lengths in Internet discussions - a consequence of the Weber-Fechner law?". EPJ Data Science.
- ↑ Yin, Peifeng; Luo, Ping; Lee, Wang-Chien; Wang, Min (2013). Silence is also evidence: interpreting dwell time for recommendation from psychological perspective. ACM International Conference on KDD.
- ↑ "What is the average length of a game of chess?". chess.stackexchange.com. Retrieved 14 April 2018.
- ↑ Huxley, Julian S. (1932). Problems of relative growth. London. ISBN 978-0-486-61114-3. OCLC 476909537.
- ↑ S. K. Chan, Jennifer; Yu, Philip L. H. (2006). "Modelling SARS data using threshold geometric process". Statistics in Medicine. 25 (11): 1826–1839. doi:10.1002/sim.2376. PMID 16345017. S2CID 46599163.
- ↑ Ono, Yukiteru; Asai, Kiyoshi; Hamada, Michiaki (2013-01-01). "PBSIM: PacBio reads simulator—toward accurate genome assembly". Bioinformatics (in English). 29 (1): 119–121. doi:10.1093/bioinformatics/bts649. ISSN 1367-4803. PMID 23129296.
- ↑ Makuch, Robert W.; D.H. Freeman; M.F. Johnson (1979). "Justification for the lognormal distribution as a model for blood pressure". Journal of Chronic Diseases. 32 (3): 245–250. doi:10.1016/0021-9681(79)90070-5. PMID 429469.
- ↑ Lacey, L. F.; Keene, O. N.; Pritchard, J. F.; Bye, A. (1997-01-01). "Common noncompartmental pharmacokinetic variables: are they normally or log-normally distributed?". Journal of Biopharmaceutical Statistics (in English). 7 (1): 171–178. doi:10.1080/10543409708835177. ISSN 1054-3406. PMID 9056596.
- ↑ Scheler, Gabriele; Schumann, Johann (2006-10-08). Diversity and stability in neuronal output rates. 36th Society for Neuroscience Meeting, Atlanta.
- ↑ Mizuseki, Kenji; Buzsáki, György (2013-09-12). "Preconfigured, skewed distribution of firing rates in the hippocampus and entorhinal cortex". Cell Reports. 4 (5): 1010–1021. doi:10.1016/j.celrep.2013.07.039. ISSN 2211-1247. PMC 3804159. PMID 23994479.
- ↑ Buzsáki, György; Mizuseki, Kenji (2017-01-06). "The log-dynamic brain: how skewed distributions affect network operations". Nature Reviews. Neuroscience. 15 (4): 264–278. doi:10.1038/nrn3687. ISSN 1471-003X. PMC 4051294. PMID 24569488.
- ↑ Wohrer, Adrien; Humphries, Mark D.; Machens, Christian K. (2013-04-01). "Population-wide distributions of neural activity during perceptual decision-making". Progress in Neurobiology. 103: 156–193. doi:10.1016/j.pneurobio.2012.09.004. ISSN 1873-5118. PMC 5985929. PMID 23123501.
- ↑ Scheler, Gabriele (2017-07-28). "Logarithmic distributions prove that intrinsic learning is Hebbian". F1000Research. 6: 1222. doi:10.12688/f1000research.12130.2. PMC 5639933. PMID 29071065.
- ↑ Polizzi, S., Laperrousaz, B., Perez-Reche, F. J., Nicolini, F. E., Satta, V. M., Arneodo, A., & Argoul, F. (2018). A minimal rupture cascade model for living cell plasticity. New Journal of Physics, 20(5), 053057. doi: https://doi.org/10.1088/1367-2630/aac3c7
- ↑ Oosterbaan, R.J. (1994). "6: Frequency and Regression Analysis" (PDF). In Ritzema, H.P. (ed.). Drainage Principles and Applications, Publication 16. Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement (ILRI). pp. 175–224. ISBN 978-90-70754-33-4.
- ↑ CumFreq, free software for distribution fitting
- ↑ Clementi, Fabio; Gallegati, Mauro (2005) "Pareto's law of income distribution: Evidence for Germany, the United Kingdom, and the United States", EconWPA
- ↑ Wataru, Souma (2002-02-22). "Physics of Personal Income". In Takayasu, Hideki (ed.). Empirical Science of Financial Fluctuations: The Advent of Econophysics. Springer. arXiv:cond-mat/0202388. doi:10.1007/978-4-431-66993-7.
- ↑ Black, F.; Scholes, M. (1973). "The Pricing of Options and Corporate Liabilities". Journal of Political Economy. 81 (3): 637. doi:10.1086/260062. S2CID 154552078.
- ↑ Mandelbrot, Benoit (2004). The (mis-)Behaviour of Markets. Basic Books. ISBN 9780465043552.
- ↑ Bunchen, P., Advanced Option Pricing, University of Sydney coursebook, 2007
- ↑ Thelwall, Mike; Wilson, Paul (2014). "Regression for citation data: An evaluation of different methods". Journal of Informetrics. 8 (4): 963–971. arXiv:1510.08877. doi:10.1016/j.joi.2014.09.011. S2CID 8338485.
- ↑ Sheridan, Paul; Onodera, Taku (2020). "A Preferential Attachment Paradox: How Preferential Attachment Combines with Growth to Produce Networks with Log-normal In-degree Distributions". Scientific Reports. 8 (1): 2811. arXiv:1703.06645. doi:10.1038/s41598-018-21133-2. PMC 5809396. PMID 29434232.
- ↑ Eeckhout, Jan (2004). "Gibrat's Law for (All) Cities". American Economic Review. 94 (5): 1429–1451. doi:10.1257/0002828043052303. JSTOR 3592829 – via JSTOR.
- ↑ Kault, David (1996). "The Shape of the Distribution of the Number of Sexual Partners". Statistics in Medicine. 15 (2): 221–230. doi:10.1002/(SICI)1097-0258(19960130)15:2<221::AID-SIM148>3.0.CO;2-Q. PMID 8614756.
- ↑ O'Connor, Patrick; Kleyner, Andre (2011). Practical Reliability Engineering. John Wiley & Sons. p. 35. ISBN 978-0-470-97982-2.
- ↑ "Shadowing". www.WirelessCommunication.NL. Archived from the original on January 13, 2012.
- ↑ Gros, C; Kaczor, G.; Markovic, D (2012). "Neuropsychological constraints to human data production on a global scale". The European Physical Journal B. 85 (28): 28. arXiv:1111.6849. Bibcode:2012EPJB...85...28G. doi:10.1140/epjb/e2011-20581-3. S2CID 17404692.
- ↑ Alamsar, Mohammed; Parisis, George; Clegg, Richard; Zakhleniuk, Nickolay (2019). "On the Distribution of Traffic Volumes in the Internet and its Implications". arXiv:1902.03853 [cs.NI].
अग्रिम पठन
- क्रो, एडविन एल.; शिमिजु, कुनियो, eds. (1988), लॉगनॉर्मल वितरण, सिद्धांत और अनुप्रयोग, सांख्यिकी: पाठ्यपुस्तकें और मोनोग्राफ, vol. 88, न्यूयॉर्क: मार्सेल डेकर, इंक, pp. xvi+387, ISBN 978-0-8247-7803-3, MR 0939191, Zbl 0644.62014
- एचिसन, जे. और ब्राउन, जे.ए.सी. (1957) द लॉगनॉर्मल डिस्ट्रीब्यूशन, कैम्ब्रिज यूनिवर्सिटी प्रेस।
- लिम्पर्ट, E; स्थल, W; एबट, M (2001). "विज्ञान में लॉगनॉर्मल वितरण: कुंजियाँ और सुराग". जिव शस्त्र. 51 (5): 341–352. doi:10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2.
- होलगेट, P. (1989). "लॉगनॉर्मल विशेषता फ़ंक्शन". सांख्यिकी में संचार - सिद्धांत और तरीके. 18 (12): 4539–4548. doi:10.1080/03610928908830173.
- ब्रुक्स, रॉबर्ट; कोर्सन, जॉन; डोनल, वेल्स (1994). "सूचकांक विकल्पों का मूल्य निर्धारण तब होता है जब सभी अंतर्निहित परिसंपत्तियाँ एक सामान्य प्रसार का पालन करती हैं". वायदा और विकल्प अनुसंधान में प्रगति. 7. SSRN 5735.