श्रांति सीमा: Difference between revisions

Latest revision as of 07:33, 27 September 2023

प्रयुक्त तनाव के प्रतिनिधि वक्र बनाम चक्रों की संख्या स्टील (श्रांति सीमा दिखा रहा है) और एल्यूमीनियम (ऐसी कोई सीमा नहीं दिखा रहा है)।

श्रांति सीमा (फटीग लिमिट) या सहनशक्ति सीमा वह तनाव (यांत्रिकी) स्तर है जिसके नीचे फटीग पदार्थ की विफलता के बिना किसी पदार्थ पर अनंत संख्या में लोडिंग चक्र प्रयुक्त किए जा सकते हैं।^[1] कुछ धातुओं जैसे लौह मिश्र धातु और टाइटेनियम मिश्र धातु की पृथक सीमा होती है,^[2] जबकि अन्य जैसे अल्युमीनियम और तांबा छोटे तनाव आयामों से भी विफल नहीं होते हैं और अंततः विफल हो जाएंगे। जहां पदार्थो की कोई भिन्न सीमा नहीं होती है वहां फटीग शक्ति या सहनशक्ति शक्ति शब्द का उपयोग किया जाता है और इसे पूर्ण रूप से विपरीत झुकाव वाले तनाव का अधिकतम मान जो पदार्थ फटीग विफलता के बिना चक्रों की निर्दिष्ट संख्या तक सामना कर सकती है जिसे इस रूप में परिभाषित किया गया है।^[3]^[4]

परिभाषाएँ

इस प्रकार एएसटीएम फटीग शक्ति $S_{N_{f}}$ को परिभाषित करता है, "तनाव का वह मान जिस पर $N_{f}$ चक्र के पश्चात विफलता होती है", और श्रांति सीमा $S_{f}$ को "तनाव का सीमित मान" के रूप में परिभाषित करता है। जो विफलता तब होती है जब $N_{f}$ बहुत बड़ा हो जाता है"। इस प्रकार एएसटीएम सहनशक्ति सीमा को परिभाषित नहीं करता है, वह तनाव मान जिसके नीचे पदार्थ अनेक भार चक्रों का सामना करती है ^[1] किन्तु इसका तात्पर्य यह है कि यह श्रांति सीमा के समान है। ^[5]

कुछ लेखक उस तनाव के लिए सहनशक्ति सीमा $S_{e}$ का उपयोग करते हैं, जिसके नीचे विफलता कभी नहीं होती है, यहां तक कि अनिश्चित काल तक बड़ी संख्या में लोडिंग चक्रों के लिए भी, जैसा कि स्टील के स्थिति में होता है; और इस प्रकार तनाव के लिए श्रांति सीमा या फटीग शक्ति $S_{f}$ जिस पर एल्युमीनियम के स्थिति में 500 मिलियन जैसे लोडिंग चक्रों की एक निर्दिष्ट संख्या के पश्चात विफलता होती है। ^[1]^[6]^[7] अन्य लेखक अभिव्यक्तियों के मध्य अंतर नहीं करते, तथापि वह दो प्रकार की पदार्थो के मध्य अंतर करते है।^[8]^[9]^[10]

विशिष्ट मान

इस प्रकार स्टील्स के लिए सीमा ( $S_{e}$ ) के विशिष्ट मान अंतिम तन्य शक्ति का आधा, अधिकतम 290 MPa (42 ksi) हैं। इस प्रकार लोहा, एल्युमीनियम और तांबे की मिश्रधातुओं के लिए $S_{e}$ सामान्यतः अंतिम तन्यता बल का 0.4 गुना है। लोहे के लिए अधिकतम विशिष्ट मान 170 MPa (24 ksi) एल्युमीनियम 130 MPa (19 ksi), और तांबे के लिए 97 MPa (14 ksi) हैं। ^[2] ध्यान दें कि यह मान सुचारू "अन- नोट्च्द" परीक्षण प्रतिरूपों के लिए हैं। नोट्च्द प्रतिरूपों (और इस प्रकार विभिन्न व्यावहारिक डिजाइन स्थितियों के लिए) के लिए सहनशक्ति सीमा अधिक कम है।

इस प्रकार बहुलक पदार्थो के लिए, श्रांति सीमा को बहुलक श्रृंखलाओं में सहसंयोजक बंधनों की आंतरिक बल को प्रतिबिंबित करने के लिए दिखाया गया है जिन्हें विच्छेद का विस्तार करने के लिए टूटना होगा। जब तक अन्य थर्मो रासायनिक प्रक्रियाएं पॉलिमर श्रृंखला (अर्थात एजिंग या ओजोन आक्रमण ) को नहीं तोड़ती हैं, तब तक पॉलिमर बिना विच्छेद वृद्धि के अनिश्चित काल तक कार्य कर सकता है जब भार आंतरिक बल से नीचे रखा जाता है।^[11]^[12]

श्रांति सीमा की अवधारणा, और इस प्रकार आईएसओ 281:2007 रोलिंग बियरिंग जीवनकाल पूर्वानुमान जैसे श्रांति सीमा पर आधारित मानक, कम से कम अमेरिका में विवादास्पद बने हुए हैं।^[13]^[14]

श्रांति सीमा के कारकों को संशोधित करना

मशीन घटक, एसई की श्रांति सीमा, संशोधित कारकों नामक तत्वों की श्रृंखला से प्रभावित होती है। इनमें से कुछ कारक नीचे सूचीबद्ध हैं।

सतह कारक

$k_{S}$ , पदार्थ की तन्य शक्ति, $S_{ut}$ और मशीन घटक की सतह फिनिश दोनों से संबंधित है।

$k_{S}=aS_{ut}^{b}$

जहां समीकरण में उपस्थित कारक A और घातांक B सतह समाप्त से संबंधित हैं।

प्रवणता कारक

सतह की फिनिश को ध्यान में रखने के अतिरिक्त आकार प्रवणता कारक $k_{G}$ पर विचार करना भी महत्वपूर्ण है। जब झुकाव और घूर्णन वाली लोडिंग की स्थिति आती है, तो प्रवणता कारक को भी ध्यान में रखा जाता है।

भार कारक

भार संशोधित कारक के रूप में पहचाना जा सकता है।

$k_{L}=0.85$ अक्षीय के लिए

$k Subscript upper L Baseline equals 1$

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

@@ Line 1: / Line 1: @@
 {{Short description|Maximum stress that won't cause fatigue failure}}
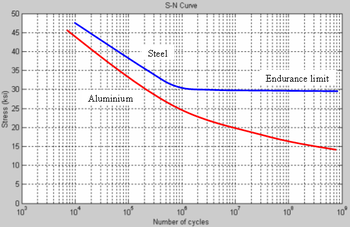
-[[Image:S-N curves.PNG|thumb|350px|लागू तनाव के प्रतिनिधि वक्र बनाम चक्रों की संख्या {{colorbox|blue}}{{nbsp}}स्टील (धीरज सीमा दिखा रहा है) और {{colorbox|red}}{{nbsp}}एल्यूमीनियम (ऐसी कोई सीमा नहीं दिखा रहा है)।]]थकान सीमा या सहनशक्ति सीमा वह [[तनाव (यांत्रिकी)]] स्तर है जिसके नीचे [[थकान (सामग्री)]] की विफलता के बिना किसी सामग्री पर अनंत संख्या में लोडिंग चक्र लागू किए जा सकते हैं।<ref name="BandJ">{{cite book
+[[Image:S-N curves.PNG|thumb|350px|प्रयुक्त तनाव के प्रतिनिधि वक्र बनाम चक्रों की संख्या {{colorbox|blue}}स्टील (श्रांति सीमा दिखा रहा है) और {{colorbox|red}}एल्यूमीनियम (ऐसी कोई सीमा नहीं दिखा रहा है)।]]'''श्रांति सीमा (फटीग लिमिट)''' या '''सहनशक्ति सीमा''' वह [[तनाव (यांत्रिकी)]] स्तर है जिसके नीचे [[थकान (सामग्री)|फटीग]] पदार्थ की विफलता के बिना किसी पदार्थ पर अनंत संख्या में लोडिंग चक्र प्रयुक्त किए जा सकते हैं।<ref name="BandJ">{{cite book
 | title = Mechanics of Materials
 | url = https://archive.org/details/mechanicsofmater00ferd_1
@@ Line 12: / Line 12: @@
 | isbn = 978-0-07-837340-4
 | page = [https://archive.org/details/mechanicsofmater00ferd_1/page/51 51]
-| author-link = Ferdinand Beer}}</ref> कुछ धातुओं जैसे [[लौह]] मिश्र धातु और [[टाइटेनियम]] मिश्र धातु की एक अलग सीमा होती है,<ref name = "MFandE">{{cite web
+| author-link = Ferdinand Beer}}</ref> कुछ धातुओं जैसे [[लौह]] मिश्र धातु और [[टाइटेनियम]] मिश्र धातु की पृथक सीमा होती है,<ref name = "MFandE">{{cite web
 | url = http://www.roymech.co.uk/Useful_Tables/Fatigue/Fatigue.html
 | title = Metal Fatigue and Endurance
@@ Line 19: / Line 19: @@
 | archive-date = 2012-04-15
 | url-status = dead
-}}</ref> जबकि अन्य जैसे [[अल्युमीनियम]] और तांबा छोटे तनाव आयामों से भी विफल नहीं होते हैं और अंततः विफल हो जाएंगे। जहां सामग्रियों की कोई अलग सीमा नहीं होती है वहां थकान शक्ति या सहनशक्ति शक्ति शब्द का उपयोग किया जाता है और इसे ''पूरी तरह से उलट झुकने वाले तनाव का अधिकतम मूल्य जो एक सामग्री थकान विफलता के बिना चक्रों की एक निर्दिष्ट संख्या तक झेल सकती है'' के रूप में परिभाषित किया गया है।<ref>{{cite book |title=इंजीनियरिंग सामग्री की प्रकृति और गुण|first=D. |last=Jastrzebski |publisher=John Wiley & Sons, Inc |edition=Wiley International |year=1959}}</ref><ref name="suresh04">{{cite book |last1=Suresh |first1=S. |author-link=Subra Suresh |year=2004 |title=सामग्री की थकान|publisher=Cambridge University Press |isbn=978-0-521-57046-6}}</ref>
+}}</ref> जबकि अन्य जैसे [[अल्युमीनियम]] और तांबा छोटे तनाव आयामों से भी विफल नहीं होते हैं और अंततः विफल हो जाएंगे। जहां पदार्थो की कोई भिन्न सीमा नहीं होती है वहां फटीग शक्ति या सहनशक्ति शक्ति शब्द का उपयोग किया जाता है और इसे ''पूर्ण रूप से विपरीत झुकाव वाले तनाव का अधिकतम मान जो पदार्थ फटीग विफलता के बिना चक्रों की निर्दिष्ट संख्या तक सामना कर सकती है'' जिसे इस रूप में परिभाषित किया गया है।<ref>{{cite book |title=इंजीनियरिंग सामग्री की प्रकृति और गुण|first=D. |last=Jastrzebski |publisher=John Wiley & Sons, Inc |edition=Wiley International |year=1959}}</ref><ref name="suresh04">{{cite book |last1=Suresh |first1=S. |author-link=Subra Suresh |year=2004 |title=सामग्री की थकान|publisher=Cambridge University Press |isbn=978-0-521-57046-6}}</ref>
 ==परिभाषाएँ==
-[[एएसटीएम इंटरनेशनल]] थकान शक्ति को परिभाषित करता है, <math>S_{N_f}</math>, तनाव के मूल्य के रूप में जिसके बाद विफलता होती है <math>N_f</math> चक्र, और थकान सीमा, <math>S_f</math>, तनाव के सीमित मूल्य के रूप में जिस पर विफलता होती है <math>N_f</math> बहुत बड़ा हो जाता है. एएसटीएम सहनशक्ति सीमा को परिभाषित नहीं करता है, वह तनाव मान जिसके नीचे सामग्री कई भार चक्रों का सामना करेगी,<ref name="BandJ"/>लेकिन तात्पर्य यह है कि यह थकान सीमा के समान है।<ref name="Stephens">{{cite book
+इस प्रकार [[एएसटीएम इंटरनेशनल|एएसटीएम]] फटीग शक्ति <math>S_{N_f}</math> को परिभाषित करता है, "तनाव का वह मान जिस पर <math>N_f</math> चक्र के पश्चात विफलता होती है", और श्रांति सीमा <math>S_f</math> को "तनाव का सीमित मान" के रूप में परिभाषित करता है। जो विफलता तब होती है जब <math>N_f</math> बहुत बड़ा हो जाता है"। इस प्रकार एएसटीएम सहनशक्ति सीमा को परिभाषित नहीं करता है, वह तनाव मान जिसके नीचे पदार्थ अनेक भार चक्रों का सामना करती है <ref name="BandJ"/> किन्तु इसका तात्पर्य यह है कि यह श्रांति सीमा के समान है। <ref name="Stephens">{{cite book
 | title = Metal Fatigue in Engineering
 | url = https://archive.org/details/metalfatigueengi00step
@@ Line 34: / Line 32: @@
 | isbn = 978-0-471-51059-8
 | page = [https://archive.org/details/metalfatigueengi00step/page/n46 69]}}</ref>
-कुछ लेखक सहनशक्ति सीमा का उपयोग करते हैं, <math>S_e</math>, उस तनाव के लिए जिसके नीचे विफलता कभी नहीं होती, यहां तक कि अनिश्चित काल तक बड़ी संख्या में लोडिंग चक्रों के लिए भी, जैसा कि [[ इस्पात ]] के मामले में होता है; और थकान की सीमा या थकान की ताकत, <math>S_f</math>, उस तनाव के लिए जिस पर लोडिंग चक्रों की एक निर्दिष्ट संख्या के बाद विफलता होती है, जैसे कि 500 मिलियन, जैसा कि एल्यूमीनियम के मामले में होता है।<ref name="BandJ"/><ref name = "Bydynas">{{cite book
+कुछ लेखक उस तनाव के लिए सहनशक्ति सीमा <math>S_e</math> का उपयोग करते हैं, जिसके नीचे विफलता कभी नहीं होती है, यहां तक कि अनिश्चित काल तक बड़ी संख्या में लोडिंग चक्रों के लिए भी, जैसा कि स्टील के स्थिति में होता है; और इस प्रकार तनाव के लिए श्रांति सीमा या फटीग शक्ति <math>S_f</math> जिस पर एल्युमीनियम के स्थिति में 500 मिलियन जैसे लोडिंग चक्रों की एक निर्दिष्ट संख्या के पश्चात विफलता होती है। <ref name="BandJ" /><ref name="Bydynas">{{cite book
 | title = Advanced Strength and Applied Stress Analysis
 | url = https://archive.org/details/advancedstrength00budy
@@ Line 44: / Line 43: @@
 | publisher = McGraw-Hill, Inc.
 | isbn = 978-0-07-008985-3
-| pages = [https://archive.org/details/advancedstrength00budy/page/n549 532]–533}}</ref><ref name="Askeland">{{cite book|last=Askeland|first=Donald R.|title=सामग्री का विज्ञान और इंजीनियरिंग|author2=Pradeep P. Phule|publisher=Brooks/Cole|year=2003|isbn=978-0-534-95373-7|edition=4th|page=248}}</ref> अन्य लेखक दो प्रकार की सामग्रियों में अंतर करते हुए भी भावों में अंतर नहीं करते।<ref name="Hibbeler">{{cite book
+| pages = [https://archive.org/details/advancedstrength00budy/page/n549 532]–533}}</ref><ref name="Askeland">{{cite book|last=Askeland|first=Donald R.|title=सामग्री का विज्ञान और इंजीनियरिंग|author2=Pradeep P. Phule|publisher=Brooks/Cole|year=2003|isbn=978-0-534-95373-7|edition=4th|page=248}}</ref> अन्य लेखक अभिव्यक्तियों के मध्य अंतर नहीं करते, तथापि वह दो प्रकार की पदार्थो के मध्य अंतर करते है।<ref name="Hibbeler">{{cite book
 | title = Mechanics of Materials
 | edition = 5th
@@ Line 68: / Line 67: @@
 | isbn = 978-0-07-232519-5
 | page = 65}}</ref>
 ==विशिष्ट मान==
-सीमा के विशिष्ट मान (<math>S_e</math>) स्टील्स के लिए अधिकतम तन्य शक्ति का आधा हिस्सा है {{convert|290|MPa|ksi|abbr=on}}. लोहा, एल्युमीनियम और तांबा मिश्रधातु के लिए, <math>S_e</math> आमतौर पर परम तन्यता ताकत का 0.4 गुना है। आयरन के लिए अधिकतम विशिष्ट मान हैं {{convert|24|ksi|MPa|abbr=on|disp=flip}}, एल्यूमीनियम {{convert|19|ksi|MPa|abbr=on|disp=flip}}, और तांबे {{convert|14|ksi|MPa|abbr=on|disp=flip}}.<ref name = "MFandE"/>ध्यान दें कि ये मान सुचारू बिना नोकदार परीक्षण नमूनों के लिए हैं। नोकदार नमूनों (और इस प्रकार कई व्यावहारिक डिजाइन स्थितियों के लिए) के लिए सहनशक्ति सीमा काफी कम है।
+इस प्रकार स्टील्स के लिए सीमा (<math>S_e</math>) के विशिष्ट मान अंतिम तन्य शक्ति का आधा, अधिकतम {{convert|290|MPa|ksi|abbr=on}} हैं। इस प्रकार लोहा, एल्युमीनियम और तांबे की मिश्रधातुओं के लिए <math>S_e</math> सामान्यतः अंतिम तन्यता बल का 0.4 गुना है। लोहे के लिए अधिकतम विशिष्ट मान {{convert|24|ksi|MPa|abbr=on|disp=flip}} एल्युमीनियम {{convert|19|ksi|MPa|abbr=on|disp=flip}}, और तांबे के लिए {{convert|14|ksi|MPa|abbr=on|disp=flip}} हैं। <ref name = "MFandE"/> ध्यान दें कि यह मान सुचारू "अन- नोट्च्द" परीक्षण प्रतिरूपों के लिए हैं। नोट्च्द प्रतिरूपों (और इस प्रकार विभिन्न व्यावहारिक डिजाइन स्थितियों के लिए) के लिए सहनशक्ति सीमा अधिक कम है।
-बहुलक सामग्रियों के लिए, थकान सीमा को बहुलक श्रृंखलाओं में सहसंयोजक बंधनों की आंतरिक ताकत को प्रतिबिंबित करने के लिए दिखाया गया है जिन्हें दरार का विस्तार करने के लिए टूटना होगा। जब तक अन्य थर्मो रासायनिक प्रक्रियाएं पॉलिमर श्रृंखला (यानी उम्र बढ़ने या [[ ओजोन का टूटना ]]) को नहीं तोड़ती हैं, तब तक पॉलिमर बिना दरार वृद्धि के अनिश्चित काल तक काम कर सकता है जब भार आंतरिक ताकत से नीचे रखा जाता है।<ref name ="LakeLundley">{{cite journal
+इस प्रकार बहुलक पदार्थो के लिए, श्रांति सीमा को बहुलक श्रृंखलाओं में सहसंयोजक बंधनों की आंतरिक बल को प्रतिबिंबित करने के लिए दिखाया गया है जिन्हें विच्छेद का विस्तार करने के लिए टूटना होगा। जब तक अन्य थर्मो रासायनिक प्रक्रियाएं पॉलिमर श्रृंखला (अर्थात एजिंग या [[ ओजोन का टूटना |ओजोन आक्रमण]] ) को नहीं तोड़ती हैं, तब तक पॉलिमर बिना विच्छेद वृद्धि के अनिश्चित काल तक कार्य कर सकता है जब भार आंतरिक बल से नीचे रखा जाता है।<ref name ="LakeLundley">{{cite journal
 | journal = Journal of Applied Polymer Science
 | volume = 9
@@ Line 98: / Line 95: @@
 | s2cid = 138395281
 }}</ref>
-थकान सीमा की अवधारणा, और इस प्रकार आईएसओ 281:2007 [[घूमने वाली बियरिंग]] लाइफटाइम भविष्यवाणी जैसे थकान सीमा पर आधारित मानक, कम से कम अमेरिका में विवादास्पद बने हुए हैं।<ref name="STLE, Zaretsky">{{Cite journal
+श्रांति सीमा की अवधारणा, और इस प्रकार आईएसओ 281:2007 रोलिंग बियरिंग जीवनकाल पूर्वानुमान जैसे श्रांति सीमा पर आधारित मानक, कम से कम अमेरिका में विवादास्पद बने हुए हैं।<ref name="STLE, Zaretsky">{{Cite journal
   |title       = In search of a fatigue limit: A critique of ISO standard 281:2007
   |author      = Erwin V. Zaretsky
@@ Line 118: / Line 116: @@
   |archive-date = 2013-10-24
 }}</ref>
+== श्रांति सीमा के कारकों को संशोधित करना ==
+मशीन घटक, एसई की श्रांति सीमा, संशोधित कारकों नामक तत्वों की श्रृंखला से प्रभावित होती है। इनमें से कुछ कारक नीचे सूचीबद्ध हैं।
-== थकान सीमा के कारकों को संशोधित करना ==
-एक मशीन घटक, एसई की थकान सीमा, संशोधित कारकों नामक तत्वों की एक श्रृंखला से प्रभावित होती है। इनमें से कुछ कारक नीचे सूचीबद्ध हैं।
 === सतह कारक ===
-सतह संशोधित कारक, <math>k_S</math>, दोनों तन्य शक्ति से संबंधित है, <math>S_{ut}</math>, मशीन घटक की सामग्री और सतह की समाप्ति।
+<math>k_S</math>, पदार्थ की तन्य शक्ति, <math>S_{ut}</math> और मशीन घटक की सतह फिनिश दोनों से संबंधित है।
 <math>k_{S}=aS_{ut}^b</math>
-जहां समीकरण में मौजूद कारक ए और घातांक बी सतह खत्म से संबंधित हैं।
-=== ग्रेडियेंट कारक ===
+जहां समीकरण में उपस्थित कारक A और घातांक B सतह समाप्त से संबंधित हैं।
-सतह की फिनिश को ध्यान में रखने के अलावा, आकार ढाल कारक पर विचार करना भी महत्वपूर्ण है <math>k_{G}</math>. जब झुकने और मरोड़ने वाली लोडिंग की बात आती है, तो ढाल कारक को भी ध्यान में रखा जाता है।
-=== लोड फैक्टर ===
+=== प्रवणता कारक ===
-लोड संशोधित कारक के रूप में पहचाना जा सकता है।
+सतह की फिनिश को ध्यान में रखने के अतिरिक्त आकार प्रवणता कारक <math>k_{G}</math> पर विचार करना भी महत्वपूर्ण है। जब झुकाव और घूर्णन वाली लोडिंग की स्थिति आती है, तो प्रवणता कारक को भी ध्यान में रखा जाता है।
+=== भार कारक ===
+भार संशोधित कारक के रूप में पहचाना जा सकता है।
 <math>k_{L}=0.85
@@ Line 140: / Line 137: @@
 <math>k_{L}=1
-</math> झुकने के लिए
+</math> झुकाव के लिए
 <math>k_{L}=0.59
@@ Line 152: / Line 149: @@
 <math>S_o
-</math> ऑपरेटिंग तापमान पर तन्य शक्ति है
+</math> परिचालन तापमान पर तन्य शक्ति है
 <math>S_{r}
@@ Line 176: / Line 173: @@
 ==इतिहास==
-सहनशक्ति सीमा की अवधारणा 1870 में अगस्त वोहलर द्वारा पेश की गई थी।<ref name=schutz>W. Schutz (1996). A history of fatigue. ''Engineering Fracture Mechanics'' 54: 263-300. [https://dx.doi.org/10.1016/0013-7944(95)00178-6 DOI]</ref> हालाँकि, हाल के शोध से पता चलता है कि धातु सामग्री के लिए सहनशक्ति सीमाएँ मौजूद नहीं हैं, यदि पर्याप्त तनाव चक्र किए जाते हैं, तो सबसे छोटा तनाव भी अंततः थकान विफलता उत्पन्न करेगा।<ref name = "Askeland"/><ref name ="Bathias">{{cite journal
+सहनशक्ति सीमा की अवधारणा 1870 में अगस्त वोहलर द्वारा प्रस्तुत की गई थी।<ref name=schutz>W. Schutz (1996). A history of fatigue. ''Engineering Fracture Mechanics'' 54: 263-300. [https://dx.doi.org/10.1016/0013-7944(95)00178-6 DOI]</ref> चूंकि, वर्तमान शोध से पता चलता है कि धातु पदार्थ के लिए सहनशक्ति सीमाएँ उपस्थित नहीं हैं, यदि पर्याप्त तनाव चक्र किए जाते हैं, इस प्रकार सबसे छोटा तनाव भी अंततः फटीग विफलता उत्पन्न करता है।<ref name = "Askeland"/><ref name ="Bathias">{{cite journal
 | journal = Fatigue & Fracture of Engineering Materials & Structures
 | volume = 22
@@ Line 187: / Line 184: @@
 | doi = 10.1046/j.1460-2695.1999.00183.x
 }}</ref>
 ==यह भी देखें==
-* थकान (सामग्री)
+* फटीग (पदार्थ)
-* {{ill|Smith fatigue strength diagram|de|Dauerfestigkeitsschaubild nach Smith}}, ब्रिटिश मैकेनिकल इंजीनियर द्वारा एक आरेख {{ill|James Henry Smith|de}}
+* ब्रिटिश मैकेनिकल इंजीनियर द्वारा आरेख {{ill|जेम्स हेनरी स्मिथ|डीई}}
 ==संदर्भ==
@@ Line 201: / Line 196: @@
 [[Category: Machine Translated Page]]
 [[Category:Created On 14/08/2023]]
+[[Category:Vigyan Ready]]

Anonymous

Search

श्रांति सीमा: Difference between revisions

Namespaces

More

Page actions