बंडल मानचित्र: Difference between revisions
| Line 9: | Line 9: | ||
==फाइबर बंडलों की सामान्य आकृतियाँ== | ==फाइबर बंडलों की सामान्य आकृतियाँ== | ||
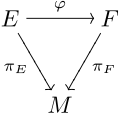
चलो π<sub>''E''</sub>:E→ M और π<sub>''F''</sub>:F→ N क्रमशः रिक्त स्थान M और N पर फाइबर बंडल बनें। फिर एक सतत मानचित्र <math>\varphi : E \to F</math> ''ई'' से ''एफ'' तक एक बंडल मानचित्र कहा जाता है यदि कोई सतत मानचित्र ''एफ'':''एम''→ ''एन'' ऐसा हो कि आरेख | चलो π<sub>''E''</sub>:E→ M और π<sub>''F''</sub>:F→ N क्रमशः रिक्त स्थान M और N पर फाइबर बंडल बनें। फिर एक सतत मानचित्र <math>\varphi : E \to F</math> ''ई'' से ''एफ'' तक एक बंडल मानचित्र कहा जाता है यदि कोई सतत मानचित्र ''एफ'':''एम''→ ''एन'' ऐसा हो कि आरेख | ||
[[Image:BundleMorphism-04.svg|150px|center]]आवागमन, अर्थात्, <math> \pi_F\circ\varphi = f\circ\pi_E </math>. दूसरे शब्दों में, <math>\varphi</math> फाइबर-संरक्षण है, और ''एफ'' ''ई'' के फाइबर के स्थान पर प्रेरित मानचित्र है: चूंकि π<sub>''E''</sub> विशेषण है, f विशिष्ट रूप से निर्धारित होता है <math>\varphi</math>. किसी दिए गए f के लिए, ऐसा बंडल मानचित्र <math>\varphi</math> कहा जाता है कि यह एक बंडल मैप ''कवरिंग एफ'' | [[Image:BundleMorphism-04.svg|150px|center]]आवागमन, अर्थात्, <math> \pi_F\circ\varphi = f\circ\pi_E </math>. दूसरे शब्दों में, <math>\varphi</math> फाइबर-संरक्षण है, और ''एफ'' ''ई'' के फाइबर के स्थान पर प्रेरित मानचित्र है: चूंकि π<sub>''E''</sub> विशेषण है, f विशिष्ट रूप से निर्धारित होता है <math>\varphi</math>. किसी दिए गए f के लिए, ऐसा बंडल मानचित्र <math>\varphi</math> कहा जाता है कि यह एक बंडल मैप ''कवरिंग एफ'' है | ||
==दो धारणाओं के बीच संबंध== | ==दो धारणाओं के बीच संबंध== | ||
Revision as of 00:59, 8 August 2023
गणित में, बंडल मानचित्र या बंडल संरूप एक ऐसा मानचित्र है जो तन्तु बंडलों के श्रेणी में एक आकारिता होता है।
बंडल मानचित्र के दो भिन्न और गहरे संबंधित अर्थ होते हैं, जो इस बात पर निर्भर करते हैं कि क्या विचार में आने वाले तंतु बंडलों के पास एक समान बेस स्पेस होता है। इसी तरह, जिन भी श्रेणी के तंतु बंडल विचार किए जा रहे होते हैं, उन परिवर्तनों के साथ कई विविधताएं हो सकती हैं। पहले तीन खंडों में, हम शीर्षकीय रूप से संस्थानिक स्पेस के श्रेणी में सामान्य तंतु बंडलों को विचार करेंगे। तब चौथे खंड में, कुछ अन्य उदाहरण दिए जाएंगे।
सामान्य बेस के ऊपर बंडल मानचित्र
यदि और एक स्थान M पर तंतु बंडल हैं, तो E से F तक एक बंडल मानचित्र एक ऐसा नियमित चित्र है जिसका निम्नलिखित रूप होता है अर्थात आरेख
परिवर्तित होता है । बंडल मानचित्र, M में किसी भी बिंदु x के लिए, तन्तु को आरेखित करता है तन्तु से x के ऊपर E का F के ऊपर x के साथ संबंधित रूप से आरेखित करता है।
फाइबर बंडलों की सामान्य आकृतियाँ
चलो πE:E→ M और πF:F→ N क्रमशः रिक्त स्थान M और N पर फाइबर बंडल बनें। फिर एक सतत मानचित्र ई से एफ तक एक बंडल मानचित्र कहा जाता है यदि कोई सतत मानचित्र एफ:एम→ एन ऐसा हो कि आरेख
आवागमन, अर्थात्, . दूसरे शब्दों में, फाइबर-संरक्षण है, और एफ ई के फाइबर के स्थान पर प्रेरित मानचित्र है: चूंकि πE विशेषण है, f विशिष्ट रूप से निर्धारित होता है . किसी दिए गए f के लिए, ऐसा बंडल मानचित्र कहा जाता है कि यह एक बंडल मैप कवरिंग एफ है
दो धारणाओं के बीच संबंध
परिभाषाओं से यह तुरंत पता चलता है कि एम पर एक बंडल मैप (पहले अर्थ में) एम के पहचान मानचित्र को कवर करने वाले बंडल मैप के समान है।
इसके विपरीत, पुलबैक बंडल की धारणा का उपयोग करके सामान्य बंडल मानचित्रों को एक निश्चित आधार स्थान पर बंडल मानचित्रों में कम किया जा सकता है। यदि πF:F→ N, N के ऊपर एक फाइबर बंडल है और f:M→ N एक सतत मानचित्र है, तो F द्वारा F का 'पुलबैक' एक फाइबर बंडल f है*M के ऊपर F जिसका x के ऊपर का फाइबर (f) द्वारा दिया गया है*एफ)x = एफf(x). इसके बाद यह निष्कर्ष निकलता है कि E से F तक f को कवर करने वाला बंडल मैप E से f तक बंडल मैप के समान है*एम के ऊपर एफ।
विकल्प और सामान्यीकरण
बंडल मानचित्र की सामान्य अवधारणा में दो प्रकार की भिन्नताएँ हैं।
सबसे पहले, कोई विभिन्न श्रेणी के स्थानों में फाइबर बंडलों पर विचार कर सकता है। यह, उदाहरण के लिए, एक चिकने मैनिफोल्ड पर चिकने फाइबर बंडलों के बीच एक चिकने बंडल मानचित्र की धारणा की ओर ले जाता है।
दूसरा, कोई अपने फाइबर में अतिरिक्त संरचना वाले फाइबर बंडलों पर विचार कर सकता है, और इस संरचना को संरक्षित करने वाले बंडल मानचित्रों पर ध्यान केंद्रित कर सकता है। यह, उदाहरण के लिए, वेक्टर बंडलों के बीच एक (वेक्टर) बंडल होमोमोर्फिज्म की धारणा की ओर ले जाता है, जिसमें फाइबर वेक्टर रिक्त स्थान होते हैं, और एक बंडल मैप φ को प्रत्येक फाइबर पर एक रैखिक मानचित्र होना आवश्यक है। इस मामले में, ऐसे बंडल मैप φ (एफ को कवर करते हुए) को वेक्टर बंडल होम(ई,एफ के एक अनुभाग (फाइबर बंडल) के रूप में भी देखा जा सकता है*F) या M, जिसका x से अधिक का फाइबर वेक्टर स्पेस होम हैx,एफf(x)) (एल(ई) को भी दर्शाया गया हैx,एफf(x))) से रेखीय मानचित्रों की इxएफ कोf(x).
श्रेणी:फाइबर बंडल
श्रेणी:निरंतर कार्यों का सिद्धांत