ऑप एम्प इंटीग्रेटर: Difference between revisions
No edit summary |
m (12 revisions imported from alpha:ऑप_एम्प_इंटीग्रेटर) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Circuit component performing mathematical integration}}'''[[ ऑपरेशनल एंप्लीफायर |संक्रियात्मक प्रवर्द्धन]] [[ जोड़नेवाला |समाकलक]]'''एक समाकलन परिपथ है। यह संक्रियात्मक प्रवर्धक (ऑप-एम्प) पर आधारित है। यह समय के सापेक्ष, गणितीय [[एकीकरण (गणित)|समाकलन]] करता है; अर्थात्, इसका निर्गत [[वोल्टेज|विभव]], समय के सापेक्ष | {{Short description|Circuit component performing mathematical integration}}'''[[ ऑपरेशनल एंप्लीफायर |संक्रियात्मक प्रवर्द्धन]] [[ जोड़नेवाला |समाकलक]]''' एक समाकलन परिपथ है। यह संक्रियात्मक प्रवर्धक (ऑप-एम्प) पर आधारित है। यह समय के सापेक्ष, गणितीय [[एकीकरण (गणित)|समाकलन]] करता है; अर्थात्, इसका निर्गत [[वोल्टेज|विभव]], समय के सापेक्ष समाकलित निविष्ट विभव के समानुपाती होता है। | ||
==अनुप्रयोग== | ==अनुप्रयोग== | ||
समाकलन परिपथ का उपयोग अधिकतर [[एनालॉग कंप्यूटर]], [[एनॉलॉग से डिजिटल परिवर्तित करने वाला उपकरण|एनॉलॉग से डिजिटल परिवर्तक]] और तरंग-संरूपण परिपथ में किया जाता है।किसी सामान्य तरंग-संरूपण का उपयोग [[ आवेश प्रवर्धक |आवेश प्रवर्धक]] के रूप में किया जाता है और इन्हें सामान्यतः एक संक्रिया प्रवर्धक का उपयोग करके निर्मित किया जाता है, यद्यपि वे उच्च लाभ असतत ट्रांजिस्टर समाकृति का उपयोग कर सकते हैं। | समाकलन परिपथ का उपयोग अधिकतर [[एनालॉग कंप्यूटर]], [[एनॉलॉग से डिजिटल परिवर्तित करने वाला उपकरण|एनॉलॉग से डिजिटल परिवर्तक]] और तरंग-संरूपण परिपथ में किया जाता है।किसी सामान्य तरंग-संरूपण का उपयोग [[ आवेश प्रवर्धक |आवेश प्रवर्धक]] के रूप में किया जाता है और इन्हें सामान्यतः एक संक्रिया प्रवर्धक का उपयोग करके निर्मित किया जाता है, यद्यपि वे उच्च लाभ असतत ट्रांजिस्टर समाकृति का उपयोग कर सकते हैं। | ||
== | == प्रारूप == | ||
निविष्ट धारा की भरपाई संधारित्र में प्रवाहित होने वाली नकारात्मक प्रतिपुष्टि धारा से होती है, जो प्रवर्धक के निर्गत विभव में वृद्धि से उत्पन्न होती है। इसलिए निर्गत विभव निविष्ट धारा के मान पर निर्भर होता है जो प्रतिपुष्टि संधारित्र में प्रवाहित होने वाली धारा का व्युत्क्रम होता है। संधारित्र का मान जितना अधिक होगा, एक विशेष प्रतिपुष्टी धारा प्रवाह उत्पन्न करने के लिए उतना ही कम निर्गत विभव उत्पन्न करना होगा। | |||
[[मिलर प्रभाव]] के कारण परिपथ की | [[मिलर प्रभाव]] के कारण परिपथ की निविष्ट प्रतिबाधा लगभग शून्य है। इसलिए सभी अवांछित धारिता वस्तुतः भूसंपर्कित हैं और निर्गत संकेत पर उनका कोई प्रभाव नहीं पड़ता है।<ref>[http://www.mmf.de/instrumentation.htm Transducers with Charge Output]</ref> | ||
===आदर्श परिपथ=== | ===आदर्श परिपथ=== | ||
यह परिपथ एक | यह परिपथ एक ऐसी धारा प्रवाहित करके संचालित किया जाता है जो [[संधारित्र]] <math>C_\text{F}</math>को आवेशित या अनावेशित करता है। यह निविष्ट धारा के प्रभाव को निष्क्रिय करके निविष्ट पर [[ आभासी मैदान |आभासी भूसंपर्क]] स्थिति को बनाए रखने का प्रयास करता है: | ||
[[File:Integrator_circuit.png|500x500px]]उपरोक्त आरेख के संदर्भ में, यदि ऑप-एम्प को | [[File:Integrator_circuit.png|500x500px]]उपरोक्त आरेख के संदर्भ में, यदि ऑप-एम्प को आदर्श ऑप एम्प्स माना जाता है, तो प्रतिलोम (-) निविष्ट पर विभव को आभाषी रूप में गैर-प्रतिलोम (+) निविष्ट पर भू संपर्क विभव के बराबर रखा जाता है। निविष्ट विभव द्वारा आभासी भू संपर्क को बनाए रखने के लिए श्रृंखला संधारित्र के माध्यम से एक प्रतिकारी धारा प्रवाह उत्पन्न करने वाले [[अवरोध]] से <math>V_\text{in}/{R_1}</math> धारा प्रवाहित होती है। यह समय के साथ संधारित्र को आवेशित या अनावेशित करता है। क्योंकि अवरोधक और संधारित्र एक आभासी भू संपर्क से जुड़े होते हैं, निविष्ट धारा संधारित्र आवेश के साथ भिन्न नहीं होती है, इसलिए एक [[रैखिकता|रैखिक]] समाकलन प्राप्त होता है जो {{Slink|आरसी परिपथ|समाकलक}} के विपरीत सभी आवृत्तियों पर कार्य करता है। | ||
प्रतिलोम निविष्ट पर किरचॉफ के धारा नियम को लागू करके परिपथ का विश्लेषण किया जा सकता है: | |||
:<math>i_{\text{1}} = I_{\text{B}} + i_{\text{F}}</math> | :<math>i_{\text{1}} = I_{\text{B}} + i_{\text{F}}</math> | ||
किसी आदर्श ऑप-एम्प के लिए, <math>I_{\text{B}} = 0</math> ऐम्पीयर हो , तो: | |||
:<math>i_{\text{1}} = i_{\text{F}}</math> | :<math>i_{\text{1}} = i_{\text{F}}</math> | ||
इसके | इसके अतिरिक्त, संधारित्र का विभव-धारा संबंध निम्नलिखित समीकरण द्वारा नियंत्रित होता है: | ||
:<math>i_{\text{F}} = C_\text{F} \frac{d(V_\text{2} - V_\text{o})}{dt}</math> | :<math>i_{\text{F}} = C_\text{F} \frac{d(V_\text{2} - V_\text{o})}{dt}</math> | ||
उपयुक्त चरों को प्रतिस्थापित | उपयुक्त चरों को प्रतिस्थापित करने पर : | ||
:<math>\frac{V_{\text{in}} - V_{\text{2}}}{R_{\text{1}}} = C_{\text{F}}\frac{d(V_{\text{2}} - V_{\text{o}})}{dt}</math> | :<math>\frac{V_{\text{in}} - V_{\text{2}}}{R_{\text{1}}} = C_{\text{F}}\frac{d(V_{\text{2}} - V_{\text{o}})}{dt}</math> | ||
एक आदर्श ऑप-एम्प के लिए, <math>V_2 = 0</math> वोल्ट, तो: | एक आदर्श ऑप-एम्प के लिए, <math>V_2 = 0</math> वोल्ट हो, तो: | ||
:<math>\frac{V_{\text{in}}}{R_{\text{1}}} = -C_{\text{F}}\frac{dV_{\text{o}}}{dt}</math> | :<math>\frac{V_{\text{in}}}{R_{\text{1}}} = -C_{\text{F}}\frac{dV_{\text{o}}}{dt}</math> | ||
समय के संबंध में दोनों पक्षों को | समय के संबंध में दोनों पक्षों को समाकलित करने पर: | ||
:<math> \int_0^t\frac{V_{\text{in}}}{R_{\text{1}}} \ dt\ = - \int_0^t C_{\text{F}} \frac{dV_{\text{o}}}{dt} \, dt</math> | :<math> \int_0^t\frac{V_{\text{in}}}{R_{\text{1}}} \ dt\ = - \int_0^t C_{\text{F}} \frac{dV_{\text{o}}}{dt} \, dt</math> | ||
यदि प्रारंभिक मान <math> V_\text{o}</math> 0 वोल्ट माना जाता है, | यदि प्रारंभिक मान <math> V_\text{o}</math> 0 वोल्ट माना जाता है, तो निर्गत विभव केवल निविष्ट विभव के समाकलन के समानुपाती होगा:<ref name="microchip-opa-dc">{{cite web | ||
|title = AN1177 Op Amp Precision Design: DC Errors | |title = AN1177 Op Amp Precision Design: DC Errors | ||
|publisher = Microchip | |publisher = Microchip | ||
| Line 46: | Line 46: | ||
=== | ===व्यावहारिक परिपथ=== | ||
यह व्यावहारिक समाकलन आदर्श समाकलन परिपथ की कई | यह व्यावहारिक समाकलन आदर्श समाकलन परिपथ की कई कमियों को दूर करने का प्रयास करता है: | ||
[[File:Practical_integrator.png|500x500px]]वास्तविक ऑप-एम्प्स में एक सीमित [[ओपन-लूप लाभ]], एक [[ निवेश समायोजन विद्युत संचालन शक्ति | [[File:Practical_integrator.png|500x500px]]वास्तविक ऑप-एम्प्स में एक सीमित [[ओपन-लूप लाभ|ओपन-लूप गेन]], एक [[ निवेश समायोजन विद्युत संचालन शक्ति |निविष्ट समायोजन विद्युत संचालन शक्ति <math>(V_\text{OS})</math>]] और निविष्ट बायस धारा <math>(I_\text{B})</math>, जो उपयुक्त रूप से समान नहीं होतें है। इन्हे प्रातलोम निविष्ट धारा <math>I_\text{B-}</math>और गैर प्रतिलोम निविष्ट धारा <math>I_\text{B+}</math> के रूप में दर्शाया जाता है। यह आदर्श प्रारूप के लिए विभिन्न समस्याएँ उत्पन्न कर सकता है; सबसे महत्वपूर्ण तथ्य, यदि <math>V_{\text{in}} = 0</math> हों तो निर्गत ऑफसेट विभव और निविष्ट बायस धारा <math>I_\text{B-}</math> दोनों संधारित्र के माध्यम से प्रवाहित हो सकता है, जिससे निर्गत विभव, समय के साथ ऑप-एम्प पूर्ण होने तक प्रवाहित होता रहता है। इसी प्रकार, यदि <math>V_{\text{in}}</math> संकेत, शून्य वोल्ट पर केन्द्रित हो (अर्थात प्रत्यक्ष धारा घटक के बिना), तो एक आदर्श परिपथ में किसी बहाव की संभावना नहीं होगी, परंतु वास्तविक परिपथ में ऐसा हो सकता है। | ||
निविष्ट बायस धारा के प्रभाव को निष्क्रिय करने के लिए, गैर-प्रतिलोम सीमा के सापेक्ष एक अवरोधक <math>R_{\text{om}}=R_1 || R_\text{F} || R_\text{L} ,</math> को सम्मिलित करना आवश्यक है जो <math>R_1</math> को सरल बनाता है परंतु इसके लिए <math>R_1</math>, भार प्रतिरोध <math>R_L</math>और प्रतिपुष्टी प्रतिरोध <math>R_F</math> से अत्यधिक छोटा होना चाहिए। उपयुक्त रूप से समान निविष्ट बायस धाराएं दोनों अंतकों पर समान प्रतिलोम तथा गैर-प्रतिलोम विभव कमी <math>R_1 I_\text{B}</math> का कारण बनती हैं। यह उस निविष्ट पर बायस धारा के प्रभाव को प्रभावी ढंग से निष्क्रिय कर देती है। | |||
इसके | इसके अतिरिक्त, डीसी स्थिर अवस्था में, संधारित्र एक खुले परिपथ के रूप में कार्य करता है। इसलिए आदर्श परिपथ का डीसी लाभ या व्यवहार में, एक गैर-आदर्श ऑप-एम्प का ओपन-लूप लाभ, अनंत है। इसका सामना करने के लिए, एक बड़ा अवरोधक <math>R_\text{F}</math>, प्रतिपुष्टी संधारित्र के समानांतर लगाया जाता है। यह परिपथ के डीसी लाभ को एक परिमित मान तक सीमित करता है। | ||
इन प्रतिरोधों को जोड़ने से | इन प्रतिरोधों को जोड़ने से निर्गत बहाव एक सीमित, अधिमानतः छोटे, डीसी त्रुटि विभव में परिवर्तित हो जाता है: | ||
:<math>V_\text{error} = \left( \frac{R_\text{F}}{R_1} + 1 \right) \left( V_\text{OS} + I_\text{B-} \left( R_\text{F} \parallel R_1 \right) \right) .</math> | :<math>V_\text{error} = \left( \frac{R_\text{F}}{R_1} + 1 \right) \left( V_\text{OS} + I_\text{B-} \left( R_\text{F} \parallel R_1 \right) \right) .</math> | ||
| Line 61: | Line 61: | ||
==आवृत्ति प्रतिक्रिया== | ==आवृत्ति प्रतिक्रिया== | ||
[[File:Frequency_response_of_ideal_and_practical_integrator.png|500x500px]]व्यावहारिक और आदर्श समाकलन की आवृत्ति प्रतिक्रियाएं उपरोक्त [[बोडे प्लॉट|बोड आरेख]] में प्रदर्शित की गई हैं। दोनों परिपथ के लिए, विनिमय आवृत्ति <math>f_\text{b}</math>, जिस पर लाभ 0 dB है, निम्नलिखित सामिकरण द्वारा प्रदर्शित किया गया है: | |||
:<math>f_{\text{b}}=\frac{1}{{2\pi}{R_{\text{1}}}{ C_{\text{F}}}}</math> | :<math>f_{\text{b}}=\frac{1}{{2\pi}{R_{\text{1}}}{ C_{\text{F}}}}</math> | ||
| Line 68: | Line 67: | ||
:<math>f_{\text{a}}=\frac{1}{{2\pi}{R_{\text{F}}}{ C_{\text{F}}}}</math> | :<math>f_{\text{a}}=\frac{1}{{2\pi}{R_{\text{F}}}{ C_{\text{F}}}}</math> | ||
व्यावहारिक समाकलन परिपथ एक सक्रिय प्रथम-क्रम [[लो पास फिल्टर]] के बराबर है। कटऑफ आवृत्ति तक लाभ अपेक्षाकृत स्थिर रहता है और इसके बाद प्रति दशक 20 डीबी कम हो जाता है। एकीकरण | व्यावहारिक समाकलन परिपथ एक सक्रिय प्रथम-क्रम [[लो पास फिल्टर]] के बराबर है। कटऑफ आवृत्ति तक लाभ अपेक्षाकृत स्थिर रहता है और इसके बाद प्रति दशक 20 डीबी कम हो जाता है। एकीकरण संक्रिया क्षेत्र में <math>\left[ f_\text{a}, f_\text{b} \right]</math> आवृत्तियों के लिए समान होता है इस स्थिति को <math>R_\text{F}C_\text{F}</math> और <math>R_1 C_\text{F}</math> समय स्थिरांक के उचित चयन द्वारा प्राप्त किया जा सकता है। | ||
==संदर्भ== | ==संदर्भ== | ||
| Line 90: | Line 89: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 10/08/2023]] | [[Category:Created On 10/08/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 07:21, 28 September 2023
संक्रियात्मक प्रवर्द्धन समाकलक एक समाकलन परिपथ है। यह संक्रियात्मक प्रवर्धक (ऑप-एम्प) पर आधारित है। यह समय के सापेक्ष, गणितीय समाकलन करता है; अर्थात्, इसका निर्गत विभव, समय के सापेक्ष समाकलित निविष्ट विभव के समानुपाती होता है।
अनुप्रयोग
समाकलन परिपथ का उपयोग अधिकतर एनालॉग कंप्यूटर, एनॉलॉग से डिजिटल परिवर्तक और तरंग-संरूपण परिपथ में किया जाता है।किसी सामान्य तरंग-संरूपण का उपयोग आवेश प्रवर्धक के रूप में किया जाता है और इन्हें सामान्यतः एक संक्रिया प्रवर्धक का उपयोग करके निर्मित किया जाता है, यद्यपि वे उच्च लाभ असतत ट्रांजिस्टर समाकृति का उपयोग कर सकते हैं।
प्रारूप
निविष्ट धारा की भरपाई संधारित्र में प्रवाहित होने वाली नकारात्मक प्रतिपुष्टि धारा से होती है, जो प्रवर्धक के निर्गत विभव में वृद्धि से उत्पन्न होती है। इसलिए निर्गत विभव निविष्ट धारा के मान पर निर्भर होता है जो प्रतिपुष्टि संधारित्र में प्रवाहित होने वाली धारा का व्युत्क्रम होता है। संधारित्र का मान जितना अधिक होगा, एक विशेष प्रतिपुष्टी धारा प्रवाह उत्पन्न करने के लिए उतना ही कम निर्गत विभव उत्पन्न करना होगा।
मिलर प्रभाव के कारण परिपथ की निविष्ट प्रतिबाधा लगभग शून्य है। इसलिए सभी अवांछित धारिता वस्तुतः भूसंपर्कित हैं और निर्गत संकेत पर उनका कोई प्रभाव नहीं पड़ता है।[1]
आदर्श परिपथ
यह परिपथ एक ऐसी धारा प्रवाहित करके संचालित किया जाता है जो संधारित्र को आवेशित या अनावेशित करता है। यह निविष्ट धारा के प्रभाव को निष्क्रिय करके निविष्ट पर आभासी भूसंपर्क स्थिति को बनाए रखने का प्रयास करता है:
 उपरोक्त आरेख के संदर्भ में, यदि ऑप-एम्प को आदर्श ऑप एम्प्स माना जाता है, तो प्रतिलोम (-) निविष्ट पर विभव को आभाषी रूप में गैर-प्रतिलोम (+) निविष्ट पर भू संपर्क विभव के बराबर रखा जाता है। निविष्ट विभव द्वारा आभासी भू संपर्क को बनाए रखने के लिए श्रृंखला संधारित्र के माध्यम से एक प्रतिकारी धारा प्रवाह उत्पन्न करने वाले अवरोध से धारा प्रवाहित होती है। यह समय के साथ संधारित्र को आवेशित या अनावेशित करता है। क्योंकि अवरोधक और संधारित्र एक आभासी भू संपर्क से जुड़े होते हैं, निविष्ट धारा संधारित्र आवेश के साथ भिन्न नहीं होती है, इसलिए एक रैखिक समाकलन प्राप्त होता है जो आरसी परिपथ § समाकलक के विपरीत सभी आवृत्तियों पर कार्य करता है।
उपरोक्त आरेख के संदर्भ में, यदि ऑप-एम्प को आदर्श ऑप एम्प्स माना जाता है, तो प्रतिलोम (-) निविष्ट पर विभव को आभाषी रूप में गैर-प्रतिलोम (+) निविष्ट पर भू संपर्क विभव के बराबर रखा जाता है। निविष्ट विभव द्वारा आभासी भू संपर्क को बनाए रखने के लिए श्रृंखला संधारित्र के माध्यम से एक प्रतिकारी धारा प्रवाह उत्पन्न करने वाले अवरोध से धारा प्रवाहित होती है। यह समय के साथ संधारित्र को आवेशित या अनावेशित करता है। क्योंकि अवरोधक और संधारित्र एक आभासी भू संपर्क से जुड़े होते हैं, निविष्ट धारा संधारित्र आवेश के साथ भिन्न नहीं होती है, इसलिए एक रैखिक समाकलन प्राप्त होता है जो आरसी परिपथ § समाकलक के विपरीत सभी आवृत्तियों पर कार्य करता है।
प्रतिलोम निविष्ट पर किरचॉफ के धारा नियम को लागू करके परिपथ का विश्लेषण किया जा सकता है:
किसी आदर्श ऑप-एम्प के लिए, ऐम्पीयर हो , तो:
इसके अतिरिक्त, संधारित्र का विभव-धारा संबंध निम्नलिखित समीकरण द्वारा नियंत्रित होता है:
उपयुक्त चरों को प्रतिस्थापित करने पर :
एक आदर्श ऑप-एम्प के लिए, वोल्ट हो, तो:
समय के संबंध में दोनों पक्षों को समाकलित करने पर:
यदि प्रारंभिक मान 0 वोल्ट माना जाता है, तो निर्गत विभव केवल निविष्ट विभव के समाकलन के समानुपाती होगा:[2]
व्यावहारिक परिपथ
यह व्यावहारिक समाकलन आदर्श समाकलन परिपथ की कई कमियों को दूर करने का प्रयास करता है:
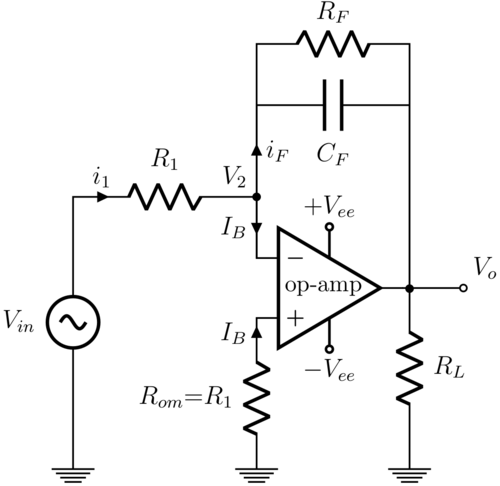 वास्तविक ऑप-एम्प्स में एक सीमित ओपन-लूप गेन, एक निविष्ट समायोजन विद्युत संचालन शक्ति और निविष्ट बायस धारा , जो उपयुक्त रूप से समान नहीं होतें है। इन्हे प्रातलोम निविष्ट धारा और गैर प्रतिलोम निविष्ट धारा के रूप में दर्शाया जाता है। यह आदर्श प्रारूप के लिए विभिन्न समस्याएँ उत्पन्न कर सकता है; सबसे महत्वपूर्ण तथ्य, यदि हों तो निर्गत ऑफसेट विभव और निविष्ट बायस धारा दोनों संधारित्र के माध्यम से प्रवाहित हो सकता है, जिससे निर्गत विभव, समय के साथ ऑप-एम्प पूर्ण होने तक प्रवाहित होता रहता है। इसी प्रकार, यदि संकेत, शून्य वोल्ट पर केन्द्रित हो (अर्थात प्रत्यक्ष धारा घटक के बिना), तो एक आदर्श परिपथ में किसी बहाव की संभावना नहीं होगी, परंतु वास्तविक परिपथ में ऐसा हो सकता है।
वास्तविक ऑप-एम्प्स में एक सीमित ओपन-लूप गेन, एक निविष्ट समायोजन विद्युत संचालन शक्ति और निविष्ट बायस धारा , जो उपयुक्त रूप से समान नहीं होतें है। इन्हे प्रातलोम निविष्ट धारा और गैर प्रतिलोम निविष्ट धारा के रूप में दर्शाया जाता है। यह आदर्श प्रारूप के लिए विभिन्न समस्याएँ उत्पन्न कर सकता है; सबसे महत्वपूर्ण तथ्य, यदि हों तो निर्गत ऑफसेट विभव और निविष्ट बायस धारा दोनों संधारित्र के माध्यम से प्रवाहित हो सकता है, जिससे निर्गत विभव, समय के साथ ऑप-एम्प पूर्ण होने तक प्रवाहित होता रहता है। इसी प्रकार, यदि संकेत, शून्य वोल्ट पर केन्द्रित हो (अर्थात प्रत्यक्ष धारा घटक के बिना), तो एक आदर्श परिपथ में किसी बहाव की संभावना नहीं होगी, परंतु वास्तविक परिपथ में ऐसा हो सकता है।
निविष्ट बायस धारा के प्रभाव को निष्क्रिय करने के लिए, गैर-प्रतिलोम सीमा के सापेक्ष एक अवरोधक को सम्मिलित करना आवश्यक है जो को सरल बनाता है परंतु इसके लिए , भार प्रतिरोध और प्रतिपुष्टी प्रतिरोध से अत्यधिक छोटा होना चाहिए। उपयुक्त रूप से समान निविष्ट बायस धाराएं दोनों अंतकों पर समान प्रतिलोम तथा गैर-प्रतिलोम विभव कमी का कारण बनती हैं। यह उस निविष्ट पर बायस धारा के प्रभाव को प्रभावी ढंग से निष्क्रिय कर देती है।
इसके अतिरिक्त, डीसी स्थिर अवस्था में, संधारित्र एक खुले परिपथ के रूप में कार्य करता है। इसलिए आदर्श परिपथ का डीसी लाभ या व्यवहार में, एक गैर-आदर्श ऑप-एम्प का ओपन-लूप लाभ, अनंत है। इसका सामना करने के लिए, एक बड़ा अवरोधक , प्रतिपुष्टी संधारित्र के समानांतर लगाया जाता है। यह परिपथ के डीसी लाभ को एक परिमित मान तक सीमित करता है।
इन प्रतिरोधों को जोड़ने से निर्गत बहाव एक सीमित, अधिमानतः छोटे, डीसी त्रुटि विभव में परिवर्तित हो जाता है:
आवृत्ति प्रतिक्रिया
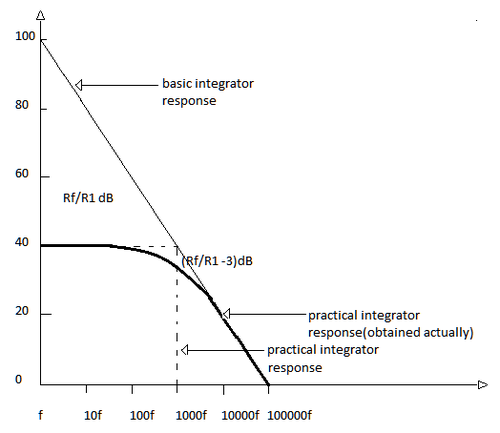 व्यावहारिक और आदर्श समाकलन की आवृत्ति प्रतिक्रियाएं उपरोक्त बोड आरेख में प्रदर्शित की गई हैं। दोनों परिपथ के लिए, विनिमय आवृत्ति , जिस पर लाभ 0 dB है, निम्नलिखित सामिकरण द्वारा प्रदर्शित किया गया है:
व्यावहारिक और आदर्श समाकलन की आवृत्ति प्रतिक्रियाएं उपरोक्त बोड आरेख में प्रदर्शित की गई हैं। दोनों परिपथ के लिए, विनिमय आवृत्ति , जिस पर लाभ 0 dB है, निम्नलिखित सामिकरण द्वारा प्रदर्शित किया गया है:
3 डीबी कटऑफ़ आवृत्ति व्यावहारिक परिपथ का विवरण इस प्रकार दिया गया है:
व्यावहारिक समाकलन परिपथ एक सक्रिय प्रथम-क्रम लो पास फिल्टर के बराबर है। कटऑफ आवृत्ति तक लाभ अपेक्षाकृत स्थिर रहता है और इसके बाद प्रति दशक 20 डीबी कम हो जाता है। एकीकरण संक्रिया क्षेत्र में आवृत्तियों के लिए समान होता है इस स्थिति को और समय स्थिरांक के उचित चयन द्वारा प्राप्त किया जा सकता है।
संदर्भ
- ↑ Transducers with Charge Output
- ↑ "AN1177 Op Amp Precision Design: DC Errors" (PDF). Microchip. 2 January 2008. Archived (PDF) from the original on 2019-07-09. Retrieved 26 December 2012.