सर्वदिशी संधि

"U-joint" redirects here. For the plumbing fixture, see U-bend.

एक सर्वदिशी संधि

सर्वदिशी संधि (जिसे सार्विक युग्मन या यू-संधि भी कहा जाता है) दृढ़ शाफ्ट को जोड़ने वालासंधि (यांत्रिकी) या युग्मन है जिनकी अक्ष एक-दूसरे की ओर झुकी होती है। इसका उपयोग आमतौर पर उन शाफ्टों में किया जाता है जो घूर्णन गति संचारित करते हैं। इसमें एक-दूसरे के आस पास, एक-दूसरे से 90° पर उन्मुख, अनुप्रस्थ ईषा (क्रॉस शाफ्ट) द्वारा जुड़े हुए, द्वारसन्धि की युग्म होती है। सर्वदिशी संधि एक सतत वेग संधि नहीं है।

यू-संधि को कभी-कभी विभिन्न समान नामों से भी बुलाया जाता है, जो इस प्रकार हैं:

• कार्डन संधि, जेरोम कार्डानो के बाद, 16वीं शताब्दी का बहुज्ञ जिसने गिम्बल्स सहित विभिन्न योग्य तंत्रों के ज्ञान में योगदान दिया है।
• हुक संधि या हुक का संधि, रॉबर्ट हुक के नाम पर, 17वीं शताब्दी का बहुविज्ञ जिसने विभिन्न योग्य तंत्रों के ज्ञान में योगदान दिया है।
• स्पाइसर संधि, क्लेरेंस डब्ल्यू स्पाइसर और स्पाइसर निर्माण कंपनी के बाद, जिसने यू संधि का निर्माण किया है।
• हार्डी स्पाइसर संधि, हार्डी स्पाइसर ब्रांड के बाद, स्पाइसर ब्रांड का उत्तराधिकारी है।

इतिहास

यह वीडियो यूनिवर्सल शाफ्ट के विभिन्न भागों और संचालन को दिखाता है।

मोटर कारों के लिए स्पाइसर सर्वदिशी संधि, 1916।

सर्वदिशी संधि की मुख्य अवधारणा गिम्बल्स के डिज़ाइन पर आधारित है, जो प्राचीन काल से उपयोग में रहे हैं। सर्वदिशी संधि की प्रत्याशा प्राचीन यूनानियों द्वारा बैलिस्टा पर इसका उपयोग था। यूरोप में सर्वदिशी संधि को अक्सर इतालवी गणितज्ञ गेरोलामो कार्डानो के बाद कार्डानो संधि (और चालन शैफ्ट जो संधि का उपयोग करता है, कार्डन शाफ्ट) कहा जाता है, जो कि गिंबल्स पर प्रारंभिक लेखक थे, हालांकि उनके लेखन में केवल जिम्बल आलंबन का उल्लेख था, सर्वदिशी संधि का नहीं था।

इस तंत्र का वर्णन बाद में गैस्पर शॉट द्वारा टेक्निका क्यूरियोसा सिव मिराबिलिया आर्टिस (1664) में किया गया था, जिन्होंने गलती से दावा किया था कि यह सतत वेग संधि संधि था। कुछ ही समय बाद, 1667 और 1675 के बीच, रॉबर्ट हुक ने संधि का विश्लेषण किया और पाया कि इसकी घूर्णन गति असमान थी, लेकिन इस गुण का उपयोग धूपघड़ी के अग्रभाग पर छाया की गति को पता करने के लिए किया जा सकता था।वास्तव में, समय के समीकरण का वह घटक जो क्रांतिवृत्त के सापेक्ष भूमध्यरेखीय तल के झुकाव को दर्शाता है, पूरी तरह से सर्वदिशी संधि के गणितीय विवरण के अनुरूप है। इस उपकरण के लिए सर्वदिशी संधि शब्द का पहला लेखाबद्ध किया गया उपयोग 1676 में हुक द्वारा अपनी पुस्तक हेलियोस्कोप्स में किया गया था। उन्होंने 1678 में एक विवरण प्रकाशित किया, जिसके परिणामस्वरूप अंग्रेजी भाषी दुनिया में हुक्स संधि शब्द का प्रयोग प्रारंभ हुआ। 1683 में, हुक ने सर्वदिशी संधि की गैर-समान घूर्णन गति का समाधान प्रस्तावित किया: मध्यवर्ती शाफ्ट के दोनों छोर पर चरण से 90° बाहर हुक के संधि की युग्म, ऐसी व्यवस्था जिसे अब एक प्रकार के सतत वेग संधि के रूप में जाना जाता है। स्वीडन के क्रिस्टोफर पोल्हेम ने बाद में सर्वदिशी संधि का पुन: आविष्कार किया, जिससे स्वीडिश में पोलहेमस्कनट ("पोलहेम बंधन") नाम सामने आया था।

1841 में, अंग्रेजी वैज्ञानिक रॉबर्ट विलिस (इंजीनियर) ने सर्वदिशी संधि की गति का विश्लेषण किया। 1845 तक, फ्रांसीसी इंजीनियर और गणितज्ञ जीन-विक्टर पोंसलेट ने गोलाकार त्रिकोणमिति का उपयोग करके सर्वदिशी संधि की गति का विश्लेषण किया था।

सर्वदिशी संधि शब्द का प्रयोग 18वीं शताब्दी में किया गया थाऔर 19वीं सदी में उपयोग में था। धातु कोटिंग मशीन के लिए एडमंड मोरवुड के 1844 के पेटेंट में इंजन और वेल्लक मिल शाफ्ट के बीच छोटी संरेखण त्रुटियों को समायोजित करने के लिए, उस नाम से सर्वदिशी संधि की आवश्यकता थी। उदाहरण के लिए, एफ़्रिअम शाय के 1881 के गतिशील पेटेंट में गतिशील के चालन शैफ्ट में युग्म सर्वदिशी संधि का उपयोग किया गया था। चार्ल्स एमिडॉन ने 1884 में पेटेंट कराए गए अपने बिट-ब्रेस (उपकरण) में बहुत छोटे सर्वदिशी संधि का उपयोग किया। ब्यूचैम्प टावर के गोलाकार, घूर्णन, उच्च गति वाले भाप इंजन ने लगभग 1885 में सार्विक संधि c के अनुकूलन का उपयोग किया।

कार्डन संधि शब्द अंग्रेजी भाषा में देर से आया प्रतीत होता है। 19वीं शताब्दी के कई प्रारंभिक उपयोग फ्रांसीसी भाषा के अनुवादों में दिखाई देते हैं या फ्रांसीसी उपयोग से काफी प्रभावित हैं। उदाहरणों में शामिल हैं 1867 की प्रतिपादक सर्वदिशी पर 1868 की रिपोर्ट और डाइनेमोमीटर पर 1881 में फ्रेंच से अनुवादित लेख शामिल हैं।

20वीं सदी में, क्लेरेंस डब्ल्यू स्पाइसर और स्पाइसर विनिर्माण कंपनी, साथ ही हार्डी स्पाइसर उत्तराधिकारी ब्रांड ने स्वचालित उद्योग, कृषि मशीनरी, भारी उपकरण और औद्योगिक मशीनरी उद्योगों की रूपरेखा में सार्विक संधि को और अधिक लोकप्रिय बनाने में मदद की थी।

गति का समीकरण

सर्वदिशी संधि के लिए चर का आरेख। धुरी 1 लाल तल के लंबवत है और धुरी 2 हर समय नीले तल के लंबवत है। ये तल एक दूसरे के सापेक्ष β कोण पर हैं। प्रत्येक धुरी का कोणीय विस्थापन (घूर्णी स्थिति) निम्न द्वारा दिया जाता है $\gamma _{1}$ और $\gamma _{2}$ क्रमशः, जो इकाई सदिशों के कोण हैं ${\hat {x}}_{1}$ और ${\hat {x}}_{2}$ x और y अक्ष के साथ उनकी प्रारंभिक स्थिति के संबंध में। ${\hat {x}}_{1}$ एच> और ${\hat {x}}_{2}$ वेक्टर दो धुरियों को जोड़ने वाले जिम्बल द्वारा तय किए जाते हैं और इसलिए हर समय एक-दूसरे के लंबवत बने रहने के लिए बाध्य होते हैं।

A sample universal joint colour-coded to the diagrams about the equation of motion. The red and blue planes are visible.

Angular (rotational) output shaft speed $\omega _{2}\,$ versus rotation angle $\gamma _{1}\,$ for different bend angles $\beta \,$ of the joint

Output shaft rotation angle, $\gamma _{2}\,$ versus input shaft rotation angle $\gamma _{1}\,$ for different bend angles $\beta \,$ of the joint

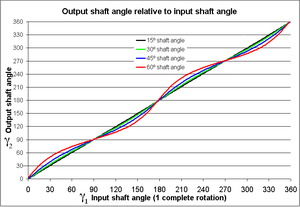
कार्डन संधि एक बड़ी समस्या से ग्रस्त है: यहां तक ​​कि जब निविष्ट चालन शैफ्ट एक्सल एक स्थिर गति से घूमता है, तो निर्गम चालन शैफ्ट एक्सल एक चर गति से घूमता है, जिससे कंपन और घिसाव होता है। चालित शाफ्ट की गति में भिन्नता संधि के विन्यास पर निर्भर करती है, जो तीन चर द्वारा निर्दिष्ट है:

1. $\gamma _{1}$ धुरी 1 के लिए घूर्णन का कोण
2. $\gamma _{2}$ धुरा 2 के लिए घूर्णन का कोण
3. $\beta$ संधि का मोड़ कोण, या एक दूसरे के संबंध में धुरी का कोण, जिसमें शून्य समानांतर या सीधा होता है।

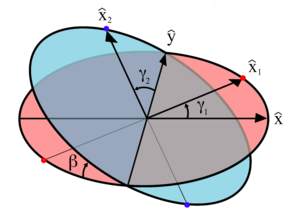
इन चरों को दाईं ओर के चित्र में दर्शाया गया है। इकाई सदिशों के साथ निश्चित निर्देशांक अक्षों का एक सेट भी दिखाया गया है ${\hat {\mathbf {x} }}$ और ${\hat {\mathbf {y} }}$ और प्रत्येक धुरी के घूमने का तल। घूर्णन के ये तल घूर्णन अक्षों के लंबवत होते हैं और धुरी के घूमने पर गति नहीं करते हैं। दोनों धुरियाँ एक जिम्बल से जुड़ी हुई हैं जो दिखाया नहीं गया है। हालाँकि, एक्सल 1 आरेख में घूर्णन के लाल तल पर लाल बिंदुओं पर जिम्बल से जुड़ता है, और एक्सल 2 नीले तल पर नीले बिंदुओं पर जुड़ता है। घूर्णन धुरी के संबंध में तय की गई समन्वय प्रणालियों को उनके एक्स-अक्ष इकाई वैक्टर के रूप में परिभाषित किया गया है (${\hat {\mathbf {x} }}_{1}$ और ${\hat {\mathbf {x} }}_{2}$) मूल से किसी एक कनेक्शन बिंदु की ओर इशारा करते हुए। जैसा कि चित्र में दिखाया गया है, ${\hat {\mathbf {x} }}_{1}$ कोण पर है $\gamma _{1}$ x अक्ष के साथ इसकी आरंभिक स्थिति के संबंध में और ${\hat {\mathbf {x} }}_{2}$ कोण पर है $\gamma _{2}$ y अक्ष के साथ इसकी आरंभिक स्थिति के संबंध में।

${\hat {\mathbf {x} }}_{1}$ आरेख में लाल तल तक ही सीमित है और संबंधित है $\gamma _{1}$ द्वारा:

$${\hat {\mathbf {x} }}_{1}=\left[\cos \gamma _{1}\,,\,\sin \gamma _{1}\,,\,0\right]$$

${\hat {\mathbf {x} }}_{2}$ आरेख में नीले तल तक ही सीमित है और x अक्ष पर इकाई वेक्टर का परिणाम है ${\hat {x}}=[1,0,0]$ यूलर कोणों से घुमाया जा रहा है $[\pi \!/2\,,\,\beta \,,\,\gamma _{2}$]:

$${\hat {\mathbf {x} }}_{2}=\left[-\cos \beta \sin \gamma _{2}\,,\,\cos \gamma _{2}\,,\,\sin \beta \sin \gamma _{2}\right]$$

पर एक बाधा ${\hat {\mathbf {x} }}_{1}$ और ${\hat {\mathbf {x} }}_{2}$ वैक्टर का अर्थ यह है कि चूँकि वे जिम्बल में स्थिर हैं, इसलिए उन्हें एक-दूसरे के ओर्थोगोनालिटी पर रहना चाहिए। ऐसा तब होता है जब उनका डॉट उत्पाद शून्य के बराबर होता है:

$${\hat {\mathbf {x} }}_{1}\cdot {\hat {\mathbf {x} }}_{2}=0$$

इस प्रकार दो कोणीय स्थितियों से संबंधित गति का समीकरण इस प्रकार दिया गया है:

$$\tan \gamma _{1}=\cos \beta \tan \gamma _{2}\,$$

के लिए एक औपचारिक समाधान के साथ $\gamma _{2}$:

$$\gamma _{2}=\tan ^{-1}\left[\tan \gamma _{1}\sec \beta \right]\,$$

के लिए समाधान $\gamma _{2}$ यह अद्वितीय नहीं है क्योंकि आर्कटेंजेंट फ़ंक्शन बहुमूल्यांकित है, हालांकि इसके लिए समाधान की आवश्यकता है $\gamma _{2}$ रुचि के कोणों पर निरंतर रहें। उदाहरण के लिए, atan2(y, x) फ़ंक्शन का उपयोग करने वाला निम्नलिखित स्पष्ट समाधान मान्य होगा $-\pi <\gamma _{1}<\pi$:

$$\gamma _{2}=\operatorname {atan2} \left(\sin \gamma _{1},\cos \beta \,\cos \gamma _{1}\right)$$

कोण $\gamma _{1}$ और $\gamma _{2}$ एक घूमने वाले संधि में समय के कार्य होंगे। समय के संबंध में गति के समीकरण को अलग करना और एक चर को खत्म करने के लिए गति के समीकरण का उपयोग करने से कोणीय वेगों के बीच संबंध प्राप्त होता है $\omega _{1}=d\gamma _{1}/dt$ और $\omega _{2}=d\gamma _{2}/dt$:

$$\omega _{2}=\omega _{1}\left({\frac {\cos \beta }{1-\sin ^{2}\beta \,\cos ^{2}\gamma _{1}}}\right)$$

जैसा कि भूखंडों में दिखाया गया है, कोणीय वेग रैखिक रूप से संबंधित नहीं हैं, बल्कि घूर्णन शाफ्ट की आधी अवधि के साथ आवधिक हैं। कोणीय त्वरणों के बीच संबंध प्राप्त करने के लिए कोणीय वेग समीकरण को फिर से विभेदित किया जा सकता है $a_{1}$ और $a_{2}$:

$$a_{2}={\frac {a_{1}\cos \beta }{1-\sin ^{2}\beta \,\cos ^{2}\gamma _{1}}}-{\frac {\omega _{1}^{2}\cos \beta \,\sin ^{2}\beta \,\sin 2\gamma _{1}}{\left(1-\sin ^{2}\beta \,\cos ^{2}\gamma _{1}\right)^{2}}}$$

युग्म कार्डन शाफ्ट

ड्राइवशाफ्ट में सर्वदिशी संधि

युग्म कार्डन संधि चालन शैफ्ट के रूप में जाना जाने वाला कॉन्फ़िगरेशन आंशिक रूप से झटकेदार रोटेशन की समस्या को दूर करता है। यह कॉन्फ़िगरेशन एक मध्यवर्ती शाफ्ट द्वारा जुड़े हुए दो यू-संधि का उपयोग करता है, जिसमें बदलते कोणीय वेग को रद्द करने के लिए पहले यू-संधि के संबंध में दूसरे यू-संधि को चरणबद्ध किया जाता है। इस कॉन्फ़िगरेशन में, संचालित शाफ्ट का कोणीय वेग ड्राइविंग शाफ्ट से मेल खाएगा, बशर्ते कि ड्राइविंग शाफ्ट और संचालित शाफ्ट दोनों मध्यवर्ती शाफ्ट के संबंध में समान कोण पर हों (लेकिन जरूरी नहीं कि एक ही विमान में हों) और वह दो सर्वदिशी संधि चरण से 90 डिग्री बाहर हैं। यह असेंबली आमतौर पर रियर व्हील ड्राइव वाहनों में नियोजित होती है, जहां इसे चालन शैफ्ट या प्रोपेलर (प्रोप) शाफ्ट के रूप में जाना जाता है।

यहां तक ​​कि जब ड्राइविंग और संचालित शाफ्ट मध्यवर्ती शाफ्ट के संबंध में समान कोण पर होते हैं, यदि ये कोण शून्य से अधिक हैं, तो घूमते समय तीन शाफ्ट पर दोलन क्षण लागू होते हैं। ये उन्हें शाफ्ट के सामान्य तल के लंबवत दिशा में मोड़ते हैं। यह सपोर्ट बियरिंग्स पर बल लागू करता है और रियर व्हील ड्राइव वाहनों में लॉन्च कंपकंपी पैदा कर सकता है। मध्यवर्ती शाफ्ट के कोणीय वेग में एक साइन लहर घटक भी होगा, जो कंपन और तनाव में योगदान देता है।

गणितीय रूप से, इसे इस प्रकार दर्शाया जा सकता है: यदि $\gamma _{1}\,$ और $\gamma _{2}\,$ क्रमशः ड्राइव और मध्यवर्ती शाफ्ट को जोड़ने वाले सर्वदिशी संधि के निविष्ट और निर्गम के कोण हैं, और $\gamma _{3}\,$ और $\gamma _{4}\,$ मध्यवर्ती और निर्गम शाफ्ट को जोड़ने वाले सर्वदिशी संधि के निविष्ट और निर्गम के लिए क्रमशः कोण हैं, और प्रत्येक युग्म कोण पर है $\beta \,$ एक दूसरे के संबंध में, तो:

$$\tan \gamma _{2}=\cos \beta \,\tan \gamma _{1}\qquad \tan \gamma _{4}=\cos \beta \,\tan \gamma _{3}$$

यदि दूसरे सर्वदिशी संधि को पहले के संबंध में 90 डिग्री घुमाया जाए, तो $\gamma _{3}=\gamma _{2}+\pi /2$. इस तथ्य का उपयोग करते हुए कि $\tan(\gamma +\pi /2)=1/\tan \gamma$ पैदावार:

$$\tan \gamma _{4}={\frac {\cos \beta }{\tan \gamma _{2}}}={\frac {1}{\tan \gamma _{1}}}=\tan \left(\gamma _{1}+{\frac {\pi }{2}}\right)\,$$

और यह देखा गया है कि निर्गम ड्राइव निविष्ट शाफ्ट के चरण से केवल 90 डिग्री बाहर है, जिससे एक सतत वेग ड्राइव उत्पन्न होती है।

नोट: सर्वदिशी संधि के निविष्ट और निर्गम शाफ्ट के कोणों को मापने के लिए संदर्भ परस्पर लंबवत अक्ष हैं। तो, पूर्ण अर्थ में मध्यवर्ती शाफ्ट के कांटे एक दूसरे के समानांतर होते हैं। (चूंकि, एक कांटा निविष्ट के रूप में कार्य कर रहा है और दूसरा कांटा शाफ्ट के लिए निर्गम के रूप में कार्य कर रहा है और कांटों के बीच 90 डिग्री से ऊपर चरण अंतर का उल्लेख किया गया है।)

युग्म कार्डन संधि

Main article: सतत वेग संधि § युग्म कार्डन

युग्म कार्डन संधि में दो सर्वदिशी संधि होते हैं जो मध्य युग्मक के साथ एक के पीछे एक लगे होते हैं; मध्य युग्मक मध्यवर्ती शाफ्ट की जगह लेता है। बशर्ते कि निविष्ट शाफ्ट और मध्य युग्मक के बीच का कोण मध्य युग्मक और निर्गम शाफ्ट के बीच के कोण के बराबर हो, दूसरा कार्डन संधि पहले कार्डन संधि द्वारा प्रारंभ की गई वेग त्रुटियों को रद्द कर देगा और संरेखित युग्म कार्डन संधि एक के रूप में कार्य करेगा। CV संधि।

थॉम्पसन युग्मन

Main article: सतत वेग संधि § थॉम्पसन युग्मन

थॉम्पसन युग्मन कार्डन संधि का परिष्कृत संस्करण है। यह जटिलता में अत्यधिक वृद्धि के शास्ति के साथ थोड़ी बढ़ी हुई दक्षता प्रदान करता है।

यह भी देखें

• कैनफील्ड जोड़
• निरंतर-वेग जोड़
• लोचदार युग्मन
• गियर कपलिंग
• हॉचकिस ड्राइव
• चिथड़े का जोड़
• कपलिंग#ट्विन स्प्रिंग कपलिंग

संदर्भ

• Theory of Machines 3 from National University of Ireland

बाहरी संबंध

• [1] by Sándor Kabai, Wolfram Demonstrations Project.
• DIY: Replacing Universal Joints at About.com.
• Thompson Couplings Limited explanation of the Thompson coupling.
• Universal Joint Failure - Custom Solutions Address Common Problems
• Universal Joint Phasing - The Concept and Importance of Drive Shaft Phasing and Alignment Archived 2020-06-15 at the Wayback Machine
• The Thompson Coupling - invented by Glenn Thompson by ABC Television (The New Inventors, broadcast Feb 2007).
• U.S. Patent 7,144,326 (constant-velocity coupling).
• About universal joints at McMaster Carr.
• Cardan Shaft at McMaster Carr.