सहसंबंधित वर्ण ताप

शिखर उत्सर्जन तवर्ण दैर्ध्य और दीप्तिमान निकास के प्रति ब्लैक बॉडी ताप के लॉग-लॉग ग्राफ़ रेड एरो दिखाते हैं कि 5780 K ब्लैक बॉडीज में 501 nm और 63.3 मेगावाट/मीटर² उज्ज्वल निकास है।

सहसंबंधित वर्ण ताप (CCT, T_cp) को प्लैंकियन रेडिएटर के ताप के रूप में परिभाषित किया गया है जिसका अनुमानित वर्ण समान चमक और निर्दिष्ट देखने की स्थितियों के अंतर्गत दिए गए उत्तेजना के समान होता है।

प्रेरणा

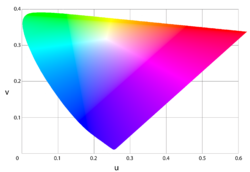
ब्लैक-बॉडी रेडिएटर वह संदर्भ है जिसके द्वारा प्रकाश स्रोतों की वाइटनेस का आकलन किया जाता है। ब्लैक बॉडी का वर्णन उस ताप से किया जा सकता है और यह विशेष वर्ण का प्रकाश उत्पन्न करता है, जैसा कि ऊपर दर्शाया गया है। वर्णों के इस सेट को वर्ण ताप कहा जाता है। सादृश्य से, लगभग प्लैंकियन प्रकाश स्रोतों जैसे कि कुछ फ्लोरोसेंट लैंप या उच्च-तीव्रता वाले डिस्चार्ज लैंप को उनके सहसंबंधित वर्ण ताप (सीसीटी) से आंकलन किया जा सकता है, प्लैंकियन रेडिएटर का ताप जिसका वर्ण उनके सबसे निकट होता है। प्रकाश स्रोत स्पेक्ट्रा के लिए जो प्लैंकियन नहीं हैं, उन ब्लैक बॉडी का संयुग्मन उत्तम रूप से परिभाषित नहीं है; सहसंबंधित वर्ण ताप की अवधारणा को ऐसे स्रोतों को यथासंभव वर्ण ताप के आयामी पैमाने पर मैप करने के लिए विस्तारित किया गया था, जहां यथासंभव उद्देश्य वर्ण स्थान के संदर्भ में परिभाषित किया गया है।

पृष्ठभूमि

जड का (r,g) आरेख। संकेंद्रित वक्र निरंतर शुद्धता के लोकी को दर्शाते हैं।

जड का मैक्सवेल त्रिकोण भूरे वर्ण में प्लैंकियन लोकस। त्रिरेखीय निर्देशांक से कार्तीय निर्देशांक में अनुवाद करने से अगला आरेख प्राप्त होता है।

जुड का एकसमान वर्णिकता स्थान (UCS), प्लैंकियन लोकस और 1000 K से 10000 K तक इज़ोटेर्म के साथ, लोकस के लंबवत है। जुड ने इस स्थान में इज़ोटेर्म की गणना उन्हें वापस (x,y) वर्णिकता स्थान में अनुवाद करने से पहले की, जैसा कि लेख के शीर्ष पर चित्र में दर्शाया गया है।

सीआईई 1960 यूसीएस में प्लैंकियन लोकस का पास से चित्र, जिसमें समताप रेखाएँ मिरेड्स में हैं। पारस्परिक ताप पैमाने का उपयोग करते समय समताप रेखाओं की सम दूरी पर ध्यान दें और नीचे दिए गए समान आंकड़े से तुलना करें। स्थान पर समतापी रेखाओं के मध्य समान दूरी का तात्पर्य यह है कि ताप पैमाने की तुलना में मायर्ड स्केल अवधारणात्मक वर्ण अंतर का उत्तम माप है।

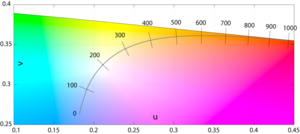
अन्य प्रकाश स्रोतों का मूल्यांकन करने के लिए प्लैंकियन रेडिएटर्स को पैरामीटर के रूप में उपयोग करने की धारणा नई नहीं है।1923 में, वर्ण की गुणवत्ता के संदर्भ में प्रकाश की ग्रेडिंग वर्ण की गुणवत्ता के सूचकांक के रूप में स्रोत के ताप, के बारे में लिखते हुए, प्रीस्ट ने अनिवार्य रूप से सीसीटी का वर्णन किया जैसा कि हम आज इसे समझते हैं, यहां तक ​​​​कि इसका उपयोग करने के लिए भी शब्द "स्पष्ट वर्ण ताप", और तीन स्थितियों को सूक्ष्मता से पहचाना गया:

• "जिनके लिए ऊर्जा का वर्णक्रमीय वितरण प्लैंकियन सूत्र द्वारा दिए गए वितरण के समान है।"
• "जिनके लिए ऊर्जा का वर्णक्रमीय वितरण प्लैंकियन सूत्र द्वारा दिए गए समान नहीं है, किंतु फिर भी इस प्रकार का है कि उत्पन्न वर्ण की गुणवत्ता वही है जो प्लैंकियन रेडिएटर से ऊर्जा द्वारा उत्पन्न वर्ण ताप होगा।"
• 'जिनके लिए ऊर्जा का वर्णक्रमीय वितरण ऐसा है कि वर्ण का युग्मन वर्णक्रमीय वितरण के प्लैंकियन रूप की उत्तेजना से ही किया जा सकता है।"

1931 में कई महत्वपूर्ण विकास हुए। कालानुक्रमिक क्रम में:

1. रेमंड डेविस ने "सहसंबंधित वर्ण ताप" (उनका कार्यकाल) पर पेपर प्रकाशित किया। आर-जी आरेख पर प्लैंकियन लोकस का उल्लेख करते हुए, उन्होंने त्रिरेखीय निर्देशांक का उपयोग करते हुए सीसीटी को "प्राथमिक घटक ताप" (आरजीबी सीसीटी) के औसत के रूप में परिभाषित किया।
2. सीआईई ने एक्सवाईजेड कलर स्पेस की घोषणा की।
3. डीन बी. जुड ने वर्णीन उत्तेजनाओं के संबंध में "कम से कम बोधगम्य अंतर" की प्रकृति पर पेपर प्रकाशित किया। अनुभवजन्य विधियों से उन्होंने निर्धारित किया कि संवेदना में अंतर, जिसे उन्होंने "वर्णों के मध्य भेदभावपूर्ण चरण एम्प्फाइंडुंग" (संवेदना के लिए जर्मन) के लिए ΔE कहा था, वर्णिकता आरेख पर वर्णों की दूरी के समानुपाती था। एक ओर दर्शाए गए (r,g) वर्णिकता आरेख का उल्लेख करते हुए, उन्होंने इसकी परिकल्पना की।

KΔE = |c₁ − c₂| = max(|r₁ − r₂|, |g₁ − g₂|)

इन विकासों ने नए वर्णिकता स्थानों के विकास का मार्ग प्रशस्त किया जो सहसंबंधित वर्ण ताप और वर्णिकता अंतर का अनुमान लगाने के लिए अधिक उपयुक्त हैं। वर्ण अंतर और ताप की अवधारणाओं को जोड़ते हुए, प्रीस्ट ने अवलोकन किया कि आंख "पारस्परिक" ताप में निरंतर अंतर के प्रति संवेदनशील है:

एक सूक्ष्म-पारस्परिक-डिग्री (μrd) का अंतर अवलोकन की सबसे अनुकूल परिस्थितियों के अंतर्गत संदिग्ध रूप से बोधगम्य अंतर का अधिक सीमा तक प्रतिनिधि है।

प्रीस्ट ने "क्रमिक क्रम में कई प्रकाशकों की वर्णिकताओं को व्यवस्थित करने के लिए ताप के पैमाने के रूप में उपयोग करने का प्रस्ताव रखा"। अगले कुछ वर्षों में, जुड ने तीन और महत्वपूर्ण पत्र प्रकाशित किए:

पहले ने प्रीस्ट,डेविसऔर जड,के निष्कर्षों को वर्ण ताप में परिवर्तन के प्रति संवेदनशीलता पर पेपर के साथ सत्यापित किया।

दूसरे ने नए वर्णिकता स्थान का प्रस्ताव रखा, जो सिद्धांत द्वारा निर्देशित है जो वर्ण स्थानों की हौली ग्रेल बन गया है: अवधारणात्मक एकरूपता (वर्णीनता की दूरी अवधारणात्मक अंतर के अनुरूप होनी चाहिए) प्रक्षेपी परिवर्तन के माध्यम से, जुड को अधिक "यूनिफ़ॉर्म क्रोमैटिकिटी स्पेस" (यूसीएस) प्राप्त हुआ जिसमें सीसीटी प्राप्त किया जा सकता था। जुड ने जेम्स क्लर्क मैक्सवेल के वर्ण त्रिकोण पर उत्तेजना की वर्णिकता के निकटतम प्लैंकियन लोकस पर बिंदु को ज्ञात करके निकटतम वर्ण ताप निर्धारित किया। जिसे एक ओर दर्शाया गया है। X,Y,Z ट्रिस्टिमुलस मानों को R,G,B निर्देशांक में परिवर्तित करने के लिए उन्होंने जिस परिवर्तन आव्यूह का उपयोग किया वह था:

${\begin{bmatrix}R\\G\\B\end{bmatrix}}={\begin{bmatrix}3.1956&2.4478&-0.1434\\-2.5455&7.0492&0.9963\\0.0000&0.0000&1.0000\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}.$

इससे, कोई इन वर्णिकताओं को ज्ञात कर सकता है:

$u={\frac {0.4661x+0.1593y}{y-0.15735x+0.2424}},\quad v={\frac {0.6581y}{y-0.15735x+0.2424}}.$

तीसरे ने सीआईई 1931 x,y क्रोमैटिकिटी आरेख पर इज़ोटेर्मल क्रोमैटिकिटीज़ के स्थान को दर्शाया। चूंकि इज़ोटेर्मल बिंदुओं ने उनके यूसीएस आरेख पर सामान्य (ज्यामिति) रूप से गठन किया था, xy तल में वापस परिवर्तन से ज्ञात हुआ कि वे अभी भी रेखाएं हैं, किंतु अब लोकस के लंबवत नहीं हैं।

मैकएडम का "यूनिफ़ॉर्म क्रोमैटिकिटी स्केल" आरेख; जड के यूसीएस का सरलीकरण।

गणना

समान वर्णिकता स्थान पर प्लैंकियन लोकस के निकटतम बिंदु को निर्धारित करने का जुड का विचार वर्तमान है। 1937 में, मैकएडम ने कुछ सरलीकृत ज्यामितीय विचारों के आधार पर "संशोधित समान वर्णिकता पैमाने आरेख" का विचार दिया:

$u={\frac {4x}{-2x+12y+3}},\quad v={\frac {6y}{-2x+12y+3}}.$

यह (u,v) क्रोमैटिकिटी स्पेस सीआईई 1960 कलर स्पेस बन गया, जिसका उपयोग अभी भी सीसीटी की गणना के लिए किया जाता है (मैकएडम ने इसे इस उद्देश्य को ध्यान में रखकर तैयार नहीं किया था)। अन्य वर्णिकता रिक्त स्थान, जैसे कि u'v', का उपयोग करने से अमानक परिणाम प्राप्त होते हैं जो फिर भी अवधारणात्मक रूप से सार्थक हो सकते हैं।

सीआईई 1960 यूसीएस का क्लोज़अप। इज़ोटेर्म प्लैंकियन लोकस के लंबवत हैं, और लोकस से अधिकतम दूरी को प्रदर्शित करने के लिए खींचे जाते हैं जिसे सीआईई सहसंबंधित वर्ण ताप को सार्थक मानता है: $\Delta uv=\pm 0.05$

लोकस से दूरी (अर्थात, ब्लैक बॉडी से प्रस्थान की डिग्री) पारंपरिक रूप से इकाइयों $\Delta uv$ में प्रदर्शित किया जाता है, लोकस के ऊपर के बिंदुओं के लिए धनात्मक दूरी की यह अवधारणा विकसित होकर डेल्टा E बन गई है, जिसका उपयोग आज भी प्रारंभ है।

रॉबर्टसन की विधि

शक्तिशाली व्यक्तिगत कंप्यूटरों के आगमन से पूर्व, लुक-अप टेबल्स और चार्ट इन्टरपोलेशन के माध्यम से सहसंबंधित वर्ण ताप का अनुमान लगाना सरल था।इस प्रकार की सबसे प्रसिद्ध विधि रॉबर्टसन की है, जिन्होंने इज़ोटेर्म के मायर्ड वैल्यूज के रैखिक इन्टरपोलेशन का उपयोग करके CCT T_c की गणना करने के लिए मायर्ड स्केल (ऊपर देखें) की अपेक्षाकृत समान दूरी का लाभ उठाया:

वर्णिकता निर्देशांक के अनुरूप CCT T_c की गणना $\scriptstyle (u_{T},v_{T})$।

:${\frac {1}{T_{c}}}={\frac {1}{T_{i}}}+{\frac {\theta _{1}}{\theta _{1}+\theta _{2}}}\left({\frac {1}{T_{i+1}}}-{\frac {1}{T_{i}}}\right),$

जहाँ $T_{i}$ और $T_{i+1}$ लुक-अप इज़ोटेर्म का वर्ण ताप है और i का इस प्रकार $T_{i}<T_{c}<T_{i+1}$ चयन किया गया है (इसके अतिरिक्त, परीक्षण वर्णिकता केवल दो आसन्न रेखाओं के मध्य होती है जिसके लिए $d_{i}/d_{i+1}<0$ है।)

यदि इज़ोटेर्म पर्याप्त रूप से टाइट हैं, तो कोई मान सकता है $\theta _{1}/\theta _{2}\approx \sin \theta _{1}/\sin \theta _{2}$, के लिए अग्रणी

${\frac {1}{T_{c}}}={\frac {1}{T_{i}}}+{\frac {d_{i}}{d_{i}-d_{i+1}}}\left({\frac {1}{T_{i+1}}}-{\frac {1}{T_{i}}}\right).$

परीक्षण बिंदु की i-वें इज़ोटेर्म से दूरी निम्न द्वारा दी गई है:

$d_{i}={\frac {(v_{T}-v_{i})-m_{i}(u_{T}-u_{i})}{\sqrt {1+m_{i}^{2}}}},$

जहाँ $(u_{i},v_{i})$ प्लैंकियन लोकस पर i-वें इज़ोटेर्म का वर्णिकता समन्वय है और m_i इज़ोटेर्म का स्लोप है चूँकि यह बिन्दुपथ के लंबवत है, यह इसका $m_{i}=-1/l_{i}$ अनुसरण करता है जहाँ l_i बिंदु का स्लोप $(u_{i},v_{i})$ है।

सावधानियाँ

यद्यपि सीसीटी की गणना किसी भी वर्णिकता समन्वय के लिए की जा सकती है, किंतु परिणाम केवल तभी सार्थक होता है जब प्रकाश स्रोत कुछ सीमा तक प्लैंकियन रेडिएटर का अनुमान लगाता है। सीआईई अनुशंसा करता है कि यदि परीक्षण स्रोत की वर्णिकता इससे अधिक भिन्न हो तो सहसंबंधित वर्ण ताप की अवधारणा का उपयोग नहीं किया जाना चाहिए। प्लैंकियन रेडिएटर से $\scriptstyle \Delta _{uv}=5\times 10^{-2}$के निश्चित मान से $\scriptstyle \Delta uv$, वर्णिकता समन्वय स्थान पर दो बिंदुओं के समान दूरी पर हो सकता है, जिससे सीसीटी में अस्पष्टता उत्पन्न हो सकती है।

अनुमान

यदि वर्ण ताप की संकीर्ण सीमा पर विचार किया जाता है- जो दिन के प्रकाश को घेरता है, तो यह सबसे व्यावहारिक स्तिथि है- कोई वर्णिकता निर्देशांक के संदर्भ में सीसीटी की गणना करने के लिए प्लैंकियन लोकस का अनुमान लगा सकता है। केली के अवलोकन के पश्चात कि इज़ोटेर्म बैंगनी क्षेत्र में (x = 0.325, y = 0.154) के पास प्रतिच्छेद करते हैं, मैककेमी ने इस घन अनुमानता का प्रस्ताव रखा:

$CCT(x,y)=-449n^{3}+3525n^{2}-6823.3n+5520.33,$

जहां n = (x − x_e)/(y - y_e) व्युत्क्रम स्लोप रेखा है, और (x_e = 0.3320, y_e = 0.1858) "उपरिकेंद्र" है; केली द्वारा उल्लिखित इंटरसेक्शन बिंदु के अधिक निकट 2856 K (इल्यूमिनेंट A) से 6504 K (सीआईई मानक इलुमिनेंट डी65) तक के वर्ण ताप के लिए अधिकतम निरपेक्ष त्रुटि 2 K से कम है।

वर्तमान प्रस्ताव, घातीय शब्दों का उपयोग करते हुए, उच्च वर्ण ताप के लिए दूसरा उपरिकेंद्र जोड़कर प्रारम्भ सीमा को अधिक सीमा तक बढ़ाता है:

$CCT(x,y)=A_{0}+A_{1}\exp(-n/t_{1})+A_{2}\exp(-n/t_{2})+A_{3}\exp(-n/t_{3})$

जहां n पहले जैसा है और अन्य स्थिरांक नीचे परिभाषित हैं:

	3–50 kK	50–800 kK
xe	0.3366	0.3356
ye	0.1735	0.1691
A0	−949.86315	36284.48953
A1	6253.80338	0.00228
t1	0.92159	0.07861
A2	28.70599	5.4535×10−36
t2	0.20039	0.01543
A3	0.00004
t3	0.07125

लेखक का विचार है कि उच्च ताप पैरामीटर की आवश्यकता है या नहीं यह निर्धारित करने के लिए निम्न-ताप समीकरण का उपयोग किया जाता है।

वर्ण ताप से संबंधित वर्णिकता निर्देशांक तक व्युत्क्रम गणना प्लैंकियन लोकस § एप्प्रोक्सिमशन पर वर्णन किया गया है।