इकाई घन: Difference between revisions
From Vigyanwiki
No edit summary |
m (4 revisions imported from alpha:इकाई_घन) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 29: | Line 29: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 07/07/2023]] | [[Category:Created On 07/07/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 07:24, 13 October 2023
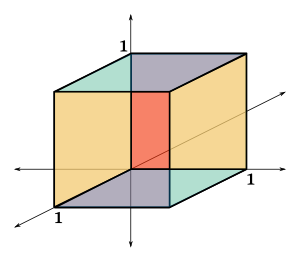
एक इकाई घन (यूनिट क्यूब), अधिक औपचारिक रूप से 1 भुजा वाला घन, एक ऐसा घन है जिसकी भुजाएँ 1 इकाई लंबी होती हैं।[1][2] एक त्रि-आयामी इकाई घन का आयतन 1 घन इकाई है, और इसका कुल सतह क्षेत्र 6 वर्ग इकाई है।[3]
इकाई अतिविम (यूनिट हाइपरक्यूब)
इकाई घन या 'इकाई अतिविम' शब्द का उपयोग अतिविम या n-डायमेंशनल स्पेस में ''क्यूब्स'' के लिए भी किया जाता है, या 3 और किनारे की लंबाई 1 के अलावा n के अन्य मान के लिए किया जाता है।[1][2]
कभी-कभी 'इकाई घन' शब्द विशेष रूप से समुच्चय को संदर्भित करता है [0, 1]nअंतराल में संख्याओं के सभी n-टुपल्स का [0, 1]।[1]
n आयामों के एक इकाई अतिविम के सबसे लंबे विकर्ण की लंबाई है , n का वर्गमूल और n-आयामी स्पेस में सदिश की (यूक्लिडियन) लंबाई (1,1,1,....1,1)।[2]
यह भी देखें
- घन को दोगुना करना
- के-सेल (गणित)
- रॉबिन्स स्थिरांक, एक इकाई घन में दो यादृच्छिक बिंदुओं के बीच की औसत दूरी
- टाइकोनोफ़ क्यूब, यूनिट क्यूब का एक अनंत-आयामी एनालॉग
- इकाई वर्ग
- इकाई क्षेत्र
संदर्भ
- ↑ 1.0 1.1 1.2 Ball, Keith (2010), "High-dimensional geometry and its probabilistic analogues", in Gowers, Timothy (ed.), The Princeton Companion to Mathematics, Princeton University Press, pp. 670–680, ISBN 9781400830398. See in particular p. 671.
- ↑ 2.0 2.1 2.2 Gardner, Martin (2001), "Chapter 13: Hypercubes", The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems : Number Theory, Algebra, Geometry, Probability, Topology, Game Theory, Infinity, and Other Topics of Recreational Mathematics, W. W. Norton & Company, pp. 162–174, ISBN 9780393020236.
- ↑ Geometry: Reteaching Masters, Holt Rinehart & Winston, 2001, p. 74, ISBN 9780030543289.