त्रिकोणमितीय फलन: Difference between revisions

Latest revision as of 15:49, 17 October 2023

त्रिकोणमिति का आधार: यदि दो समकोण त्रिभुजों में समान न्यूनकोण होते हैं, तो वे समान होते हैं, इसलिए उनकी भुजाओं की लंबाई समानुपाती होती है।

गणित में, त्रिकोणमितीय फलन (जिन्हें वृत्तीय फलन, कोण फलन या गोनीमितीय फलन भी कहा जाता है^[1]^[2]) वास्तविक फलन होते हैं जो एक समकोण त्रिभुज के कोण को दो भुजाओं की लंबाई के अनुपात से संबंधित करते हैं। वे सभी विज्ञानों में व्यापक रूप से उपयोग किए जाते हैं जो कि ज्यामिति से संबंधित हैं, जैसे कि नौसंचालन, ठोस यांत्रिकी, खगोलीय यांत्रिकी, भूगणित और कई अन्य। वे सबसे सरल आवर्ती फलनों में से हैं, और जैसे कि फुरिये विश्लेषण के माध्यम से आवर्ती घटनाओं का अध्ययन करने के लिए भी व्यापक रूप से उपयोग किए जाते हैं।

आधुनिक गणित में सबसे व्यापक रूप से उपयोग किए जाने वाले त्रिकोणमितीय फलन ज्या, कोज्या और स्पर्शरेखा हैं। इनके व्युत्क्रम क्रमश: व्युत्क्रमज्या, व्युत्क्रम कोटिज्या और कोटिस्पर्श रेखा हैं, जिनका प्रयोग कम होता है। इन छह त्रिकोणमितीय फलनों में से प्रत्येक में एक समान प्रतिलोम फलन होता है, और अतिपरवलयिक फलनों के मध्य एक अनुरूप होता है।

समकोण त्रिभुजों से संबंधित त्रिकोणमितीय फलनों की सबसे पुरानी परिभाषाएँ उन्हें केवल न्यून कोणों के लिए परिभाषित करती हैं। ज्या और कोज्या फलन को उन फलन तक विस्तारित करने के लिए जिनका प्रक्षेत्र संपूर्ण वास्तविक रेखा है, मानक इकाई वृत्त (अर्थात, त्रिज्या 1 इकाई वाला एक वृत्त) का उपयोग करते हुए ज्यामितीय परिभाषाएं प्रायः उपयोग की जाती हैं; तो अन्य फलनों का प्रक्षेत्र वास्तविक रेखा है जिसमें कुछ वियुक्त बिंदु अलग कर दिए गए हैं। आधुनिक परिभाषाएँ त्रिकोणमितीय फलनों को अनंत श्रृंखला या अंतर समीकरणों के समाधान के रूप में व्यक्त करती हैं। यह ज्या और कोज्या फलनों के प्रक्षेत्र को पूरे सम्मिश्र समतल में विस्तारित करने की अनुमति देती है, और अन्य त्रिकोणमितीय फलनों के प्रक्षेत्र को कुछ वियुक्त बिंदुओं को अलग करके सम्मिश्र समतल पर ले जाती है।

संकेतन

परंपरागत रूप से, प्रत्येक त्रिकोणमितीय फलन के नाम का एक संक्षिप्त नाम सूत्रों में इसके प्रतीक के रूप में उपयोग किया जाता है। आज, इन संक्षेपों के सबसे सामान्य संस्करण ज्या के लिए ''सिन'' है, कोज्या के लिए ''कॉस'', या ''टीजी'' स्पर्शरेखा के लिए, व्युत्क्रम कोटिज्या के लिए ''सेकंड'', व्युत्क्रमज्या के लिए ''सीएससी'' या ''कोसेक'', और कोटिस्पर्श रेखा के लिए ''कॉट'' या ''सीटीजी'' है। ऐतिहासिक रूप से, इन संक्षिप्ताक्षरों का उपयोग पहली बार गद्य वाक्यों में उपयोग किया गया था ताकि विशेष रेखा खंडों या उनकी लंबाई को एक स्वेच्छ वृत्त के एक चाप कर्ण से संबंधित किया जा सके, और बाद में लंबाई के अनुपात को इंगित करने के लिए, जैसा कि 17वीं-18वीं शताब्दी में फलन की अवधारणा विकसित हुई, उन्हें वास्तविक-संख्या-मूल्यवान कोण मापक के फलनों के रूप में माना जाने लगा, और फलनात्मक संकेतन के साथ लिखा गया, उदाहरण के लिए $sin(x)$ है। अव्यवस्था को कम करने के लिए कोष्ठक अभी भी प्रायः कम किए जाते हैं, लेकिन कभी-कभी आवश्यक होते हैं; उदाहरण के लिए अभिव्यक्ति $\sin x+y$ को विशिष्ट रूप से $\sin(x)+y,$ के अर्थ में व्याख्या की जाएगी, इसलिए $\sin(x+y)$ को व्यक्त करने के लिए कोष्ठकों की आवश्यकता होती है।

फलन के प्रतीक के बाद एक अधिलेख के रूप में प्रकट होने वाला एक सकारात्मक पूर्णांक घातांक को दर्शाता है, फलन संयोजन को नहीं दर्शाता है। उदाहरण के लिए $\sin ^{2}x$ और $\sin ^{2}(x)$ $\sin(x)\cdot \sin(x)$ को लक्षित करते हैं, $\sin(\sin x)$ को लक्षित नहीं करते हैं। यह (ऐतिहासिक रूप से बाद में) सामान्य फलनात्मक संकेतन से भिन्न है जिसमें $f^{2}(x)=(f\circ f)(x)=f(f(x))$ है।

हालाँकि, घातांक ${-1}$ का प्रयोग सामान्यतः प्रतिलोम फलन को निरूपित करने के लिए किया जाता है, पारस्परिक करने के लिए नहीं किया जाता है। उदाहरण $\sin ^{-1}x$ और $\sin ^{-1}(x)$ प्रतिलोम त्रिकोणमितीय फलन को वैकल्पिक रूप से लिखे गए $\arcsin x\colon$ को लक्षित करते हैं: समीकरण $\theta =\sin ^{-1}x$ का तात्पर्य $\sin \theta =x$ है, $\theta \cdot \sin x=1$ नहीं हैं। इस प्रकरण में, अधिलेख को एक रचित या पुनरावृत्त फलन को निरूपित करने के रूप में माना जा सकता है, लेकिन ${-1}$ के अलावा अन्य नकारात्मक अधिलेख सामान्य प्रयोग में नहीं हैं।

समकोण त्रिभुज की परिभाषाएँ

इस समकोण त्रिभुज में, कोण BAC की माप को A के रूप में निरूपित करते हुए:

sin A = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}a/c

;

cos A = b / c

;

tan A = a / b

.

छह त्रिकोणमितीय फलनों का प्लॉट, इकाई वृत्त और कोण

θ = 0.7 radians

के लिए एक रेखा है। 1, Sec(θ), Csc(θ) चिह्नित वाले बिंदु मूल से उस बिंदु तक रेखा खंड की लंबाई का प्रतिनिधित्व करते हैं। Sin(θ), Tan(θ), और 1

x

-अक्ष से प्रारम्भ होने वाली रेखा की ऊँचाई हैं, जबकि Cos(θ), 1, और Cot(θ) मूल बिंदु से प्रारम्भ होने वाली

x

-अक्ष की लंबाई हैं।

यदि न्यूनकोण $θ$ दिया गया है, तो कोई भी समकोण त्रिभुज जिसका कोण $θ$ है, एक दूसरे से समरूप होते हैं। इसका अर्थ है कि किन्हीं दो भुजाओं की लंबाई का अनुपात केवल $θ$ पर निर्भर करता हैं। इस प्रकार ये छह अनुपात $θ$ के छह फलनों को परिभाषित करते हैं, जो कि त्रिकोणमितीय फलन हैं। निम्नलिखित परिभाषाओं में, कर्ण समकोण के विपरीत भुजा की लंबाई है, विपरीत दिए गए कोण $θ$ के विपरीत भुजा का प्रतिनिधित्व करते है, और आसन्न कोण $θ$ और समकोण के मध्य की भुजा का प्रतिनिधित्व करते है।^[3]^[4]

sine $\sin \theta ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}$	cosecant $\csc \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}$
cosine $\cos \theta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}$	secant $\sec \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}$
tangent $\tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}$	cotangent $\cot \theta ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}$

एक समकोण त्रिभुज में, दो न्यून कोणों का योग समकोण होता है, अर्थात, $90°$ या $π / 2 रेडियन$ होता है। इसलिए $\sin(\theta )$ और $\cos(90^{\circ }-\theta )$ समान अनुपात का प्रतिनिधित्व करते हैं, और इस प्रकार समान हैं। यह समरूपता और अन्य त्रिकोणमितीय फलनों के मध्य समान संबंधों को निम्न तालिका में संक्षेपित किया गया है।

शीर्ष: त्रिकोणमितीय फलन

sin θ

चयनित कोणों के लिए

θ

,

π - θ

,

π + θ

, और

2 π - θ

चार चतुर्भुजों में है।
नीचे: ज्या फलन बनाम कोण का लेखाचित्र। शीर्ष सूची के कोणों की पहचान की जाती है।

त्रिकोणमितीय फलानो के मध्य संबंधों का सारांश^[5]
फलन	विवरण	सम्बन्ध
फलन	विवरण	रेडियंस का उपयोग करना	डिग्रियों का उपयोग करना
sine	$opposite / hypotenuse$	$\sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\csc \theta }}$	$\sin x=\cos \left(90^{\circ }-x\right)={\frac {1}{\csc x}}$
cosine	$adjacent / hypotenuse$	$\cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\sec \theta }}\,$	$\cos x=\sin \left(90^{\circ }-x\right)={\frac {1}{\sec x}}\,$
tangent	$opposite / adjacent$	$\tan \theta ={\frac {\sin \theta }{\cos \theta }}=\cot \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cot \theta }}$	$\tan x={\frac {\sin x}{\cos x}}=\cot \left(90^{\circ }-x\right)={\frac {1}{\cot x}}$
cotangent	$adjacent / opposite$	$\cot \theta ={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\tan \theta }}$	$\cot x={\frac {\cos x}{\sin x}}=\tan \left(90^{\circ }-x\right)={\frac {1}{\tan x}}$
secant	$hypotenuse / adjacent$	$\sec \theta =\csc \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cos \theta }}$	$\sec x=\csc \left(90^{\circ }-x\right)={\frac {1}{\cos x}}$
cosecant	$hypotenuse / opposite$	$\csc \theta =\sec \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\sin \theta }}$	$\csc x=\sec \left(90^{\circ }-x\right)={\frac {1}{\sin x}}$

रेडियंस बनाम डिग्री

ज्यामितीय अनुप्रयोगों में, त्रिकोणमितीय फलन का तर्क सामान्यतः एक कोण का माप होता है। इस प्रयोजन के लिए, कोई भी कोणीय इकाई उपयुक्त है। एक सामान्य इकाई डिग्री है, जिसमें एक समकोण 90°और एक पूर्ण घूर्णन 360° होता है (विशेष रूप से प्राथमिक गणित में)।

हालांकि, गणना और गणितीय विश्लेषण में, त्रिकोणमितीय फलनों को सामान्यतः कोणों के बदले वास्तविक संख्या या सम्मिश्र संख्याओं के फलनों के रूप में अधिक अमूर्त माना जाता है। वास्तव में, फलन sin और cos को सभी सम्मिश्र संख्याओं के लिए चरघातांकी फलन के संदर्भ में घात श्रृंखला के माध्यम से परिभाषित किया जा सकता है,^[6] ^[7] या किसी भी ज्यामितीय धारणा के संदर्भ के बिना, विशेष प्रारंभिक मान दिए गए अंतर समीकरणों के समाधान के रूप में (नीचे देखें) किसी भी ज्यामितीय धारणाओं के संदर्भ के बिना है। अन्य चार त्रिकोणमितीय फलनों (tan, cot, sec, csc) को sin और cos के भागफल और व्युत्क्रम के रूप में परिभाषित किया जा सकता है, अतिरिक्त इसके कि जहाँ भाजक में शून्य होता है। वास्तविक तर्कों के लिए यह सिद्ध किया जा सकता है कि ये परिभाषाएँ प्रारंभिक ज्यामितीय परिभाषाओं के अनुरूप हैं यदि तर्क को रेडियन में दिए गए कोण के रूप में माना जाता है।^[6] इसके अलावा, इन परिभाषाओं के परिणामस्वरूप त्रिकोणमितीय फलनों के लिए व्युत्पन्न और अनिशिचित समाकल के लिए सरल अभिव्यक्तियां होती हैं।^[8] इस प्रकार, प्रारंभिक ज्यामिति से अतिरिक्त समायोजन में, रेडियंस को कोण मापों का वर्णन करने के लिए गणितीय रूप से प्राकृतिक इकाई माना जाता है।

जब रेडियन (रेड) लगाए जाते हैं, तो कोण को इसके द्वारा अंतरित इकाई वृत्त के चाप कर्ण (ज्यामिति) की लंबाई के रूप में दिया जाता है: इकाई वृत्त पर लंबाई 1 के चाप कर्ण को अंतरित करने वाला कोण 1 रेड (≈ 57.3°) और एक पूर्ण घूर्णन (360°) 2 $π$ (≈ 6.28) रेड का कोण है। वास्तविक संख्या x के लिए, चिह्न sin x, cos x, आदि x रेड के कोण पर मूल्यांकन किए गए त्रिकोणमितीय फलनों के मान को संदर्भित करते हैं। यदि डिग्री की इकाइयों का अभीष्ट है, तो डिग्री चिह्न स्पष्ट रूप से दिखाया जाना चाहिए (उदाहरण के लिए, sin x°, cos x°, आदि)। इस मानक संकेतन का उपयोग करते हुए, त्रिकोणमितीय फलनों के लिए तर्क x संबंध x = (180x/ $π$ )° को संतुष्ट करता है, इसलिए, उदाहरण के लिए, sin π = sin 180° जब हम x = $π$ लेते है। इस प्रकार, डिग्री प्रतीक को गणितीय स्थिरांक के रूप में माना जा सकता है जैसे कि 1° = $π$ /180 ≈ 0.0175 है।

इकाई-वृत्त परिभाषाएँ

इस उदाहरण में, एक स्वेच्छ कोण

θ

के छह त्रिकोणमितीय फलानो को इकाई वृत्त से संबंधित बिंदुओं के कार्टेशियन निर्देशांक के रूप में प्रतिनिधित्व किया जाता है।

A

,

B

और

D

के निर्देशांक क्रमशः

sin θ

,

tan θ

और

csc θ

हैं, जबकि

A

,

C

और

E

के भुज क्रमशः

cos θ

,

cot θ

और

sec θ

हैं।

प्रत्येक चतुर्थांश में त्रिकोणमितीय फलनों के संकेत। स्मरक ''सभी विज्ञान शिक्षक क्षीण (हैं) उन फलनों को सूचीबद्ध करता है जो चतुर्भुज I से IV तक सकारात्मक हैं।^[9] यह स्मरक सभी छात्र गणना लेते हैं का एक रूपांतर है।

छह त्रिकोणमितीय फलनों को इकाई-वृत्त से संबंधित यूक्लिडियन समतल बिंदुओं के समन्वय मूल्यों के रूप में परिभाषित किया जा सकता है, जो इस समन्वय प्रणाली के मूल $O$ पर केंद्रित त्रिज्या का वृत्त है। जबकि समकोण त्रिभुज परिभाषाएँ $0$ और ${\textstyle {\frac {\pi }{2}}}$ रेडियंस $(90°)$ के मध्य के कोणों के लिए त्रिकोणमितीय फलनों की परिभाषा की अनुमति देती हैं, इकाई वृत्त परिभाषाएं त्रिकोणमितीय फलनों के प्रक्षेत्र को सभी सकारात्मक और नकारात्मक वास्तविक संख्याओं तक विस्तारित करने की अनुमति देती हैं।

${\mathcal {L}}$ को $x$ -अक्ष के सकारात्मक आधे कोण $θ$ द्वारा घूर्णन करके प्राप्त रे होने दें ( $\theta >0,$ के लिए वामावर्त घूर्णन, और $\theta <0$ के लिए दक्षिणावर्त घूर्णन)। यह रे इकाई वृत्त को बिंदु $\mathrm {A} =(x_{\mathrm {A} },y_{\mathrm {A} })$ पर प्रतिच्छेद हैं। रे ${\mathcal {L}},$ यदि आवश्यक हो तो एक रेखा विस्तारित, समीकरण $x=1$ की रेखा को बिंदु $\mathrm {B} =(1,y_{\mathrm {B} })$ पर और समीकरण $y=1$ की रेखा को बिंदु $\mathrm {C} =(x_{\mathrm {C} },1)$ प्रतिच्छेद करती है। बिंदु $A$ पर इकाई वृत्त की स्पर्श रेखा, ${\mathcal {L}}$ के लंबवत है, और $y$ - और $x$ -अक्षों को बिंदु $\mathrm {D} =(0,y_{\mathrm {D} })$ और $\mathrm {E} =(x_{\mathrm {E} },0)$ प्रतिच्छेद करती है। इन बिंदुओं के निर्देशांक $θ$ के किसी भी स्वेच्छ वास्तविक मूल्य के लिए सभी त्रिकोणमितीय फलनों के मान निम्नलिखित प्रकार से देते हैं।

त्रिकोणमितीय फलन $cos$ और $sin$ को क्रमशः बिंदु $A$ के x- और y-निर्देशांक मान के रूप में परिभाषित किया गया हैं। अर्थात्,

\cos \theta =x_{\mathrm {A} }\quad

और

\quad \sin \theta =y_{\mathrm {A} }.

^[10]

$0\leq \theta \leq \pi /2$ , श्रेणी में, यह परिभाषा समकोण त्रिभुज की परिभाषा के अनुरूप है, इकाई त्रिज्या $OA$ को कर्ण के रूप में रखने के लिए समकोण त्रिभुज हैं। समीकरण $x^{2}+y^{2}=1$ इकाई वृत्त पर सभी बिंदुओं $\mathrm {P} =(x,y)$ के लिए है, कोज्या और ज्या की यह परिभाषा पाइथागोरस की पहचान को भी संतुष्ट करती है।

\cos ^{2}\theta +\sin ^{2}\theta =1.

अन्य त्रिकोणमितीय फलनों को इकाई वृत्त के रूप में पाया जा सकता है

\tan \theta =y_{\mathrm {B} }\quad

और

\quad \cot \theta =x_{\mathrm {C} },

\csc \theta \ =y_{\mathrm {D} }\quad

और

\quad \sec \theta =x_{\mathrm {E} }.

पायथागॉरियन पहचान और ज्यामितीय प्रमाण विधियों को उपयोजित करके, इन परिभाषाओं को ज्या और कोज्या के संदर्भ में स्पर्शरेखा, कोटिस्पर्श, व्युत्क्रम कोटिज्या और व्युत्क्रमज्या की परिभाषाओं के अनुरूप के लिए आसानी से दिखाया जा सकता है, अर्थात

\tan \theta ={\frac {\sin \theta }{\cos \theta }},\quad \cot \theta ={\frac {\cos \theta }{\sin \theta }},\quad \sec \theta ={\frac {1}{\cos \theta }},\quad \csc \theta ={\frac {1}{\sin \theta }}.

त्रिकोणमितीय फलन: ज्या, कोज्या, स्पर्शरेखा, व्युत्क्रमज्या (बिंदुकित), छेदक रेखा (बिंदुकित), कोस्पर्शरेखा (बिंदुकित) – एनीमेशन

क्योंकि $\pm 2\pi$ के कोण के घूर्णन से आकृति की स्थिति या आकार में कोई परिवर्तन नहीं होता है, बिंदु $A$ , $B$ , $C$ , $D$ , और $E$ दो कोणों के लिए समान होते हैं जिनका अंतर $2\pi$ का पूर्णांक गुणज होता है। इस प्रकार त्रिकोणमितीय फलन आवर्ती फलन हैं जिनकी अवधि $2\pi$ है। अर्थात

\sin \theta =\sin \left(\theta +2k\pi \right)\quad

और

\quad \cos \theta =\cos \left(\theta +2k\pi \right)

किसी भी कोण $θ$ और किसी भी पूर्णांक $k$ के लिए समानताएँ उपयोजित होती हैं। चार अन्य त्रिकोणमितीय फलनों के लिए भी यही यथार्थ है। चार चतुर्भुजों में ज्या, कोज्या, व्युत्क्रमज्या और व्युत्क्रम कोटिज्या के फलनों के संकेत और एकदिष्टता को देखकर, कोई यह दिखा सकता है कि $2\pi$ सबसे छोटा मान है जिसके लिए वे आवर्ती हैं (अर्थात, $2\pi$ इन फलनों की मौलिक अवधि है)। हालाँकि, एक कोण $\pi$ द्वारा घूर्णन जाने के बाद, बिन्दु $B$ और $C$ पहले से ही अपनी मूल स्थिति में वापस आ जाते हैं, जिससे कि स्पर्शरेखा फलन और कोटिस्पर्श रेखा फलन में $\pi$ की मौलिक अवधि होती हैं। अर्थात्,

\tan \theta =\tan(\theta +k\pi )\quad

और

\quad \cot \theta =\cot(\theta +k\pi )

किसी भी कोण $θ$ और किसी भी पूर्णांक $k$ के लिए समानताएँ उपयोजित होती हैं।

बीजगणितीय मान

इकाई वृत्त, कुछ बिंदुओं के साथ उनके कोज्या और ज्या (इस क्रम में), और रेडियन और डिग्री में संबंधित कोण।

सबसे महत्वपूर्ण कोणों के लिए बीजगणितीय व्यंजक इस प्रकार हैं:

\sin 0=\sin 0^{\circ }\quad ={\frac {\sqrt {0}}{2}}=0

(शून्य कोण)

\sin {\frac {\pi }{6}}=\sin 30^{\circ }={\frac {\sqrt {1}}{2}}={\frac {1}{2}}

\sin {\frac {\pi }{4}}=\sin 45^{\circ }={\frac {\sqrt {2}}{2}}={\frac {1}{\sqrt {2}}}

\sin {\frac {\pi }{3}}=\sin 60^{\circ }={\frac {\sqrt {3}}{2}}

\sin {\frac {\pi }{2}}=\sin 90^{\circ }={\frac {\sqrt {4}}{2}}=1

(समकोण)

अंशों को लगातार गैर-ऋणात्मक पूर्णांकों के वर्गमूल के रूप में लिखना, 2 के भाजक के साथ, मानों को याद रखने का एक आसान प्रकार प्रदान करता है।^[11]

ऐसे सरल व्यंजक सामान्यतः अन्य कोणों के लिए उपस्तिथ नहीं होते हैं जो एक समकोण के परिमेय गुणज होते हैं।

ऐसे कोण के लिए, जो डिग्री में मापा जाता है, तीन का गुणक है, ज्या और कोज्या के यथार्थ त्रिकोणमितीय मान वर्गमूल के रूप में व्यक्त किए जा सकते हैं। इस प्रकार ज्या और कोज्या के ये मान मापक और दिक्सूचक द्वारा निर्मित किए जा सकते हैं।
पूर्णांक संख्या के डिग्री के कोण के लिए, ज्या और कोज्या को वर्गमूल और गैर-वास्तविक सम्मिश्र संख्या के घनमूल के रूप में व्यक्त किया जा सकता है। गाल्वा सिद्धांत एक प्रमाण की अनुमति देता है कि, यदि कोण 3° का गुणक नहीं है, तो गैर-वास्तविक घनमूल अपरिहार्य हैं।
एक कोण के लिए, जो डिग्री में व्यक्त किया जाता है, एक परिमेय संख्या है, ज्या और कोज्या बीजगणितीय संख्याएँ हैं, जिन्हें nवें मूल के रूप में व्यक्त किया जा सकता है। यह इस तथ्य से परिणामित होता है कि साइक्लोटोमिक बहुपदों के गाल्वा समूह वृत्तीय हैं।
एक कोण के लिए, जो डिग्री में व्यक्त किया जाता है, एक परिमेय संख्या नहीं है, तब या तो कोण या ज्या और कोज्या दोनों ही पारलौकिक संख्याएँ हैं। यह 1966 में सिद्ध हुई बेकर प्रमेय का परिणाम है।

सरल बीजगणितीय मान

निम्न तालिका 0 से 90 डिग्री तक 15 डिग्री के गुणकों की ज्या, कोज्या और स्पर्शरेखा सूचीबद्ध करती है।

Angle, θ, in		$\sin(\theta )$	$\cos(\theta )$	$\tan(\theta )$
radians	degrees	$\sin(\theta )$	$\cos(\theta )$	$\tan(\theta )$
$0$	$0^{\circ }$	$0$	$1$	$0$
${\frac {\pi }{12}}$	$15^{\circ }$	${\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$	${\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}$	$2-{\sqrt {3}}$
${\frac {\pi }{6}}$	$30^{\circ }$	${\frac {1}{2}}$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {3}}{3}}$
${\frac {\pi }{4}}$	$45^{\circ }$	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {2}}{2}}$	$1$
${\frac {\pi }{3}}$	$60^{\circ }$	${\frac {\sqrt {3}}{2}}$	${\frac {1}{2}}$	${\sqrt {3}}$
${\frac {5\pi }{12}}$	$75^{\circ }$	${\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}$	${\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$	$2+{\sqrt {3}}$
${\frac {\pi }{2}}$	$90^{\circ }$	$1$	$0$	Undefined

गणना

ज्या, कोज्या और स्पर्शरेखा के रेखांकन

मूल पर केंद्रित एक पूर्ण चक्र के लिए ज्या फलन (नीला) डिग्री 7 (गुलाबी) के टेलर के प्रमेय द्वारा ध्यानपूर्वक अनुमानित है।

टेलर बहुपदों के माध्यम से कोज्या के सन्निकटन के लिए अनुप्राणन।

\cos(x)

पहले टेलर बहुपदों के साथ

p_{n}(x)=\sum _{k=0}^{n}(-1)^{k}{\frac {x^{2k}}{(2k)!}}

गणित में आधुनिक प्रवृत्ति विपरीत के बदले गणना से ज्यामिति का गठन करना है।^{[citation needed]} इसलिए, बहुत प्रारंभिक स्तर के अतिरिक्त, त्रिकोणमितीय फलनों को गणना की विधियों का उपयोग करके परिभाषित किया जाता है।

त्रिकोणमितीय फलन हर उस बिंदु पर अवगणनाीय फलन और विश्लेषणात्मक होते हैं जहां उन्हें परिभाषित किया जाता है; अर्थात्, ज्या और कोज्या के लिए सर्वत्र, और स्पर्शरेखा के लिए, प्रत्येक पूर्णांक $k$ के लिए $π /2 + k π$ के अतिरिक्त सर्वत्र है।

त्रिकोणमितीय फलन आवर्ती फलन हैं, और उनकी आधारी आवर्तक ज्या और कोज्या के लिए $2 π$ है, और स्पर्शरेखा के लिए $π$ है, जो प्रत्येक विवृत अंतराल में $(π /2 + k π, π /2 + (k + 1) π)$ बढ़ रही है। इन अंतरालों के प्रत्येक अंत बिंदु पर, स्पर्शरेखा फलन में एक ऊर्ध्वाधर स्पर्शोन्मुख होता है।

गणना में, त्रिकोणमितीय फलनों की दो समतुल्य परिभाषाएँ हैं, या तो घात श्रृंखला या अवकल समीकरणों का उपयोग करते हुए। ये परिभाषाएँ समतुल्य हैं, क्योंकि उनमें से एक से प्रारम्भ होकर, दूसरे को गुण के रूप में पुनः प्राप्त करना आसान है। हालाँकि अवकल समीकरणों के माध्यम से परिभाषा किसी तरह अधिक स्वाभाविक है, उदाहरण के लिए, घात श्रृंखला के गुणांकों का चयन अत्यंत स्वेच्छ लग सकता है, और पाइथागोरस की पहचान अवकल समीकरणों से निकालना बहुत आसान है।

अंतर समीकरणों द्वारा परिभाषा

ज्या और कोज्या को प्रारंभिक मूल्य समस्या के अद्वितीय समाधान के रूप में परिभाषित किया जा सकता है:

{\frac {d}{dx}}\sin x=\cos x,\ {\frac {d}{dx}}\cos x=-\sin x,\ \sin(0)=0,\ \cos(0)=1.

फिर से भेद करना, ${\textstyle {\frac {d^{2}}{dx^{2}}}\sin x={\frac {d}{dx}}\cos x=-\sin x}$ और ${\textstyle {\frac {d^{2}}{dx^{2}}}\cos x=-{\frac {d}{dx}}\sin x=-\cos x}$ , इसलिए ज्या और कोज्या दोनों साधारण अवकल समीकरण के समाधान हैं

y''+y=0.

स्पर्शरेखा $\tan x=\sin x/\cos x$ पर भागफल नियम उपयोजित करके, हम प्राप्त करते हैं

{\frac {d}{dx}}\tan x={\frac {\cos ^{2}x+\sin ^{2}x}{\cos ^{2}x}}=1+\tan ^{2}x=\sec ^{2}x.

घात श्रेणी विस्तार

अनिश्चित गुणांकों वाली घात श्रृंखला में अवकल समीकरणों को उपयोजित करने पर, ज्या और कोज्या फलनों की टेलर श्रृंखला के गुणांकों के लिए पुनरावृत्ति संबंध प्राप्त किया जा सकता है। इन पुनरावर्तन संबंधों का समाधान करना आसान है, और श्रृंखला विस्तार प्रदान करते हैं^[12]: ${\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[6mu]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\\[8pt]\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\[6mu]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}.\end{aligned}}$

इन श्रृंखलाओं के अभिसरण की त्रिज्या अनंत है। इसलिए, ज्या और कोज्या को संपूर्ण फलनों (जिन्हें ज्या और कोज्या भी कहा जाता है) तक विस्तृत किया जा सकता है, जो कि (परिभाषा के अनुसार) सम्मिश्र-मूल्यवान फलन हैं जो पूरे सम्मिश्र समतल पर परिभाषित और पूर्णसममितिक हैं।

संपूर्ण फलनों के अंशों के रूप में परिभाषित होने के कारण, अन्य त्रिकोणमितीय फलनों को मेरोमॉर्फिक फलन तक विस्तृत किया जा सकता है, जो कि ऐसे फलन हैं जो पूरे सम्मिश्र समतल में पूर्णसममितिक होते हैं, कुछ वियुक्त बिंदुओं के अलावा जिन्हें शून्य और ध्रुव कहा जाता है। यहाँ, ध्रुव स्पर्शरेखा और व्युत्क्रम कोटिज्या के लिए ${\textstyle (2k+1){\frac {\pi }{2}}}$ के रूप की संख्याएँ हैं, या कोटिस्पर्श रेखा और व्युत्क्रमज्या के लिए $k\pi$ हैं, जहाँ $k$ एक स्वेच्छ पूर्णांक है।

अन्य त्रिकोणमितीय फलनों की टेलर श्रृंखला के गुणांकों के लिए पुनरावृत्ति संबंधों की गणना भी की जा सकती है। इन श्रृंखलाओं में अभिसरण की परिमित त्रिज्या होती है। उनके गुणांकों की एक संयोजक व्याख्या है: वे परिमित समुच्चय के वैकल्पिक क्रमपरिवर्तनों की गणना करते हैं।^[13]

अधिक यथार्थ, परिभाषित करना

U n

,

n

वां ऊपर/नीचे संख्या,

B n

,

n

वां बरनौली संख्या, और

E n

,

n

वां यूलर संख्या,

एक में निम्नलिखित श्रृंखला विस्तार हैं:^[14]

{\begin{aligned}\tan x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n+1}}{(2n+1)!}}x^{2n+1}\\[8mu]&{}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}\left(2^{2n}-1\right)B_{2n}}{(2n)!}}x^{2n-1}\\[5mu]&{}=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}.\end{aligned}}

{\begin{aligned}\csc x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2\left(2^{2n-1}-1\right)B_{2n}}{(2n)!}}x^{2n-1}\\[5mu]&=x^{-1}+{\frac {1}{6}}x+{\frac {7}{360}}x^{3}+{\frac {31}{15120}}x^{5}+\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}

{\begin{aligned}\sec x&=\sum _{n=0}^{\infty }{\frac {U_{2n}}{(2n)!}}x^{2n}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}\\[5mu]&=1+{\frac {1}{2}}x^{2}+{\frac {5}{24}}x^{4}+{\frac {61}{720}}x^{6}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}.\end{aligned}}

{\begin{aligned}\cot x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}}{(2n)!}}x^{2n-1}\\[5mu]&=x^{-1}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}

निरंतर भिन्न विस्तार

निम्नलिखित विस्तार पूरे सम्मिश्र समतल में मान्य हैं:

\sin x={\cfrac {x}{1+{\cfrac {x^{2}}{2\cdot 3-x^{2}+{\cfrac {2\cdot 3x^{2}}{4\cdot 5-x^{2}+{\cfrac {4\cdot 5x^{2}}{6\cdot 7-x^{2}+\ddots }}}}}}}}

\cos x={\cfrac {1}{1+{\cfrac {x^{2}}{1\cdot 2-x^{2}+{\cfrac {1\cdot 2x^{2}}{3\cdot 4-x^{2}+{\cfrac {3\cdot 4x^{2}}{5\cdot 6-x^{2}+\ddots }}}}}}}}

\tan x={\cfrac {x}{1-{\cfrac {x^{2}}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-\ddots }}}}}}}}={\cfrac {1}{{\cfrac {1}{x}}-{\cfrac {1}{{\cfrac {3}{x}}-{\cfrac {1}{{\cfrac {5}{x}}-{\cfrac {1}{{\cfrac {7}{x}}-\ddots }}}}}}}}

अन्तिम वाले का उपयोग ऐतिहासिक रूप से पहले प्रमाण में किया गया था कि π अपरिमेय है।^[15]

आंशिक भिन्न विस्तार

आंशिक भिन्न विस्तार के रूप में एक श्रृंखला प्रतिनिधित्व होता है जहां सिर्फ अनुवादित पारस्परिक फलन को अभिव्यक्त किया जाता है, जैसे कि कोटिस्पर्श रेखा फलन के ध्रुव समान होते हैं:^[16]: $\pi \cot \pi x=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{x+n}}.$

यह सर्वसमिका को हर्ग्लोट्ज़ युक्ति से सिद्ध किया जा सकता है।^[17] $(- n)$ वें को nवें पद के साथ मिलाने से पूरी तरह से अभिसारी श्रृंखला बनती है:

\pi \cot \pi x={\frac {1}{x}}+2x\sum _{n=1}^{\infty }{\frac {1}{x^{2}-n^{2}}}.

इसी प्रकार, व्युत्क्रम कोटिज्या, व्युत्क्रमज्या और स्पर्शरेखा फलनों के लिए एक आंशिक भिन्न विस्तार कर सकते हैं:

\pi \csc \pi x=\sum _{n=-\infty }^{\infty }{\frac {(-1)^{n}}{x+n}}={\frac {1}{x}}+2x\sum _{n=1}^{\infty }{\frac {(-1)^{n}}{x^{2}-n^{2}}},

\pi ^{2}\csc ^{2}\pi x=\sum _{n=-\infty }^{\infty }{\frac {1}{(x+n)^{2}}},

\pi \sec \pi x=\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n+1)}{(n+{\tfrac {1}{2}})^{2}-x^{2}}},

\pi \tan \pi x=2x\sum _{n=0}^{\infty }{\frac {1}{(n+{\tfrac {1}{2}})^{2}-x^{2}}}.

अनंत उत्पाद विस्तार

सम्मिश्र विश्लेषण में ज्या के लिए निम्नलिखित अनंत उत्पाद का बहुत महत्व है:

\sin z=z\prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{n^{2}\pi ^{2}}}\right),\quad z\in \mathbb {C} .

इस विस्तार के प्रमाण के लिए, ज्या देखें। इससे यह अनुमान लगाया जा सकता है

\cos z=\prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{(n-1/2)^{2}\pi ^{2}}}\right),\quad z\in \mathbb {C} .

चरघातांकी फलन से संबंध (यूलर का सूत्र)

\cos(\theta )

और

\sin(\theta )

क्रमशः

e^{i\theta }

के वास्तविक और काल्पनिक भाग हैं।

यूलर का सूत्र ज्या और कोज्या को घातीय फलन से संबंधित करता है:

e^{ix}=\cos x+i\sin x.

यह सूत्र सामान्यतः

x

के वास्तविक मूल्यों के लिए माना जाता है, लेकिन यह सभी सम्मिश्र मूल्यों के लिए सही रहता है।

प्रमाण: अनुमान $f_{1}(x)=\cos x+i\sin x,$ और $f_{2}(x)=e^{ix}$ है। किसी के पास $df_{j}(x)/dx=if_{j}(x)$ के लिए $j = 1, 2$ है। भागफल नियम का तात्पर्य इस $d/dx\,(f_{1}(x)/f_{2}(x))=0$ प्रकार है। इसलिए, $f_{1}(x)/f_{2}(x)$ एक स्थिर फलन है, जो 1 के समान है, $f_{1}(0)=f_{2}(0)=1$ के रूप में है। यह सूत्र सिद्ध करता है।

किसी के पास

{\begin{aligned}e^{ix}&=\cos x+i\sin x\\[5pt]e^{-ix}&=\cos x-i\sin x.\end{aligned}}

ज्या और कोज्या में इस रैखिक प्रणाली का समाधान करते हुए, उन्हें घातीय फलन के संदर्भ में व्यक्त किया जा सकता है:

{\begin{aligned}\sin x&={\frac {e^{ix}-e^{-ix}}{2i}}\\[5pt]\cos x&={\frac {e^{ix}+e^{-ix}}{2}}.\end{aligned}}

कब $x$ वास्तविक हो, तो इसे इस रूप में फिर से लिखा जा सकता है

\cos x=\operatorname {Re} \left(e^{ix}\right),\qquad \sin x=\operatorname {Im} \left(e^{ix}\right).

उपरोक्त सूत्रों का उपयोग करके त्रिकोणमितीय फलनों को सम्मिश्र चरघातांकी फलन के संदर्भ में व्यक्त करके और फिर परिणाम को सरल बनाने के लिए अस्मिता $e^{a+b}=e^{a}e^{b}$ का उपयोग करके अधिकांश त्रिकोणमितीय सर्वसमिका सिद्ध की जा सकती हैं।

फलनिक समीकरण का उपयोग करके परिभाषाएं

विभिन्न फलनात्मक समीकरणों का उपयोग करके त्रिकोणमितीय फलनों को भी परिभाषित किया जा सकता है।

उदाहरण के लिए,^[18]ज्या और कोज्या निरंतर फलनों की अद्वितीय जोड़ी बनाते हैं जो अंतर सूत्र को संतुष्ट करते हैं

\cos(x-y)=\cos x\cos y+\sin x\sin y\,

और अतिरिक्त स्थिति

0<x\cos x<\sin x<x\quad {\text{ for }}\quad 0<x<1.

सम्मिश्र समतल में

एक सम्मिश्र संख्या $z=x+iy$ की ज्या और कोज्या को वास्तविक ज्या, कोज्या और अतिशयोक्तिपूर्ण फलनों के संदर्भ में निम्नानुसार व्यक्त किया जा सकता है:

{\begin{aligned}\sin z&=\sin x\cosh y+i\cos x\sinh y\\[5pt]\cos z&=\cos x\cosh y-i\sin x\sinh y\end{aligned}}

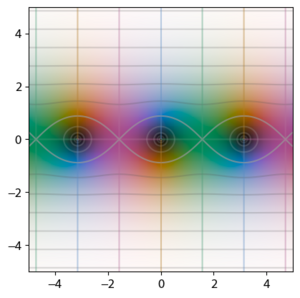
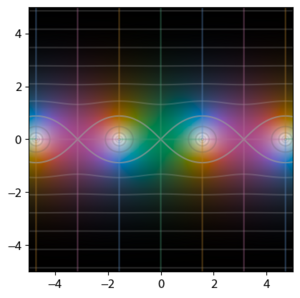
प्रक्षेत्र रंजक का लाभ उठाते हुए, त्रिकोणमितीय फलनों को सम्मिश्र-मूल्यवान फलनों के रूप में आलेख करना संभव है। आलेख से सम्मिश्र फलनों के लिए अद्वितीय विभिन्न विशेषताओं को देखा जा सकता है; उदाहरण के लिए, ज्या और कोज्या फलनों को अपरिबद्ध देखा जा सकता है क्योंकि $z$ का काल्पनिक भाग बड़ा हो जाता है (क्योंकि रंग सफेद अनंतता का प्रतिनिधित्व करता है), और तथ्य यह है कि फलनों में सरल शून्य और ध्रुव होते हैं, इस तथ्य से स्पष्ट है कि रंग प्रत्येक शून्य या ध्रुव के आसपास एक बार चक्कर लगाता है। इन आलेखों की तुलना संबंधित अतिपरवलयिक फलन के साथ करने से दोनों के मध्य संबंधों पर प्रकाश पड़ता है।

**सम्मिश्र समतल में त्रिकोणमितीय फलन**
$\sin z\,$ $\cos z\,$	$\tan z\,$ $\cot z\,$	$\sec z\,$ $\csc z\,$

मूल सर्वसमिका

कई सर्वसमिकाएं त्रिकोणमितीय फलनों से संबंधित हैं। इस खंड में सबसे आधारिक सम्मिलित हैं; अधिक सर्वसमिकाओं के लिए, त्रिकोणमितीय सर्वसमिकाओं की सूची देखें। इन सर्वसमिकाओं को इकाई-वृत्त परिभाषाओं या समकोण-त्रिकोण परिभाषाओं से ज्यामितीय रूप से सिद्ध किया जा सकता है (हालांकि, बाद की परिभाषाओं के लिए, उन कोणों का ध्यान रखना चाहिए जो अंतराल $[0, π /2]$ में नहीं हैं, त्रिकोणमितीय सर्वसमिकाओं के प्रमाण देखें)। गणना के केवल उपकरणों का उपयोग करने वाले गैर-ज्यामितीय प्रमाणों के लिए, सीधे अवकलन समीकरणों का उपयोग किया जा सकता है, जो यूलर की पहचान के उपरोक्त प्रमाण के समान है। सभी त्रिकोणमितीय फलनों को सम्मिश्र घातांकों के रूप में व्यक्त करने और घातीय फलन के गुणों का उपयोग करने के लिए यूलर की पहचान का भी उपयोग किया जा सकता है।

समता

कोज्या और व्युत्क्रम कोटिज्या सम फलन हैं; अन्य त्रिकोणमितीय फलन विषम फलन हैं। वह है:

{\begin{aligned}\sin(-x)&=-\sin x\\\cos(-x)&=\cos x\\\tan(-x)&=-\tan x\\\cot(-x)&=-\cot x\\\csc(-x)&=-\csc x\\\sec(-x)&=\sec x.\end{aligned}}

अवधि

सभी त्रिकोणमितीय फलन अवधि $2 π$ के आवर्ती फलन है। स्पर्शरेखा और कोटिस्पर्श के अतिरिक्त यह सबसे छोटी अवधि है, जिसमें $π$ सबसे छोटी अवधि है। इसका अर्थ है कि, प्रत्येक पूर्णांक $k$ के लिए, किसी के पास

{\begin{aligned}\sin(x+2k\pi )&=\sin x\\\cos(x+2k\pi )&=\cos x\\\tan(x+k\pi )&=\tan x\\\cot(x+k\pi )&=\cot x\\\csc(x+2k\pi )&=\csc x\\\sec(x+2k\pi )&=\sec x.\end{aligned}}

पायथागॉरियन सर्वसमिका

पायथागॉरियन सर्वसमिका, त्रिकोणमितीय फलनों के संदर्भ में पायथागॉरियन प्रमेय की अभिव्यक्ति है। यह है

\sin ^{2}x+\cos ^{2}x=1

.

$\cos ^{2}x$ या $\sin ^{2}x$ से विभाजित करने पर प्राप्त होता है

\tan ^{2}x+1=\sec ^{2}x

और

1+\cot ^{2}x=\csc ^{2}x

.

योग और अंतर सूत्र

योग और अंतर सूत्र ज्या, कोज्या, और योग के स्पर्शरेखा या दो कोणों के अंतर को ज्या और कोज्या और स्वयं कोणों की स्पर्शरेखा के संदर्भ में विस्तारित करने की अनुमति देते हैं। टॉलेमी तिथि के तर्कों का उपयोग करके इन्हें ज्यामितीय रूप से प्राप्त किया जा सकता है। यूलर के सूत्र का उपयोग करके बीजगणितीय रूप से भी उनका उत्पादन किया जा सकता है।

योग: ${\begin{aligned}\sin \left(x+y\right)&=\sin x\cos y+\cos x\sin y,\\[5mu]\cos \left(x+y\right)&=\cos x\cos y-\sin x\sin y,\\[5mu]\tan(x+y)&={\frac {\tan x+\tan y}{1-\tan x\tan y}}.\end{aligned}}$
अंतर: ${\begin{aligned}\sin \left(x-y\right)&=\sin x\cos y-\cos x\sin y,\\[5mu]\cos \left(x-y\right)&=\cos x\cos y+\sin x\sin y,\\[5mu]\tan(x-y)&={\frac {\tan x-\tan y}{1+\tan x\tan y}}.\end{aligned}}$

जब दो कोण समान होते हैं, योग सूत्र सरल समीकरणों में परिवर्तित हो जाते हैं जिन्हें द्वि-कोण सूत्र कहा जाता है।

{\begin{aligned}\sin 2x&=2\sin x\cos x={\frac {2\tan x}{1+\tan ^{2}x}},\\[5mu]\cos 2x&=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}},\\[5mu]\tan 2x&={\frac {2\tan x}{1-\tan ^{2}x}}.\end{aligned}}

इन सर्वसमिका का उपयोग उत्पाद-से-योग सर्वसमिका प्राप्त करने के लिए किया जा सकता है।

$t=\tan {\tfrac {1}{2}}\theta$ समायोजन करके, $\theta$ के सभी त्रिकोणमितीय फलन को $t$ के तपरिमेय भिन्न के रूप में व्यक्त किया जा सकता है :

{\begin{aligned}\sin \theta &={\frac {2t}{1+t^{2}}},\\[5mu]\cos \theta &={\frac {1-t^{2}}{1+t^{2}}},\\[5mu]\tan \theta &={\frac {2t}{1-t^{2}}}.\end{aligned}}

के साथ साथ

d\theta ={\frac {2}{1+t^{2}}}\,dt,

यह स्पर्शरेखा आधा-कोण प्रतिस्थापन है, जो तर्कसंगत अंशों के त्रिकोणमितीय फलनों के पूर्ण और एंटीडेरिवेटिव की गणना को कम करता है।

व्युत्पन्न और एंटीडेरिवेटिव्स

त्रिकोणमितीय फलनों के व्युत्पन्न का परिणाम भागफल नियम उपयोजित करने से ज्या और कोज्या के परिणाम से होता है। निम्नलिखित सारणी में एंटीडेरिवेटिव्स के लिए दिए गए मानों को उनमें विभेद करके सत्यापित किया जा सकता है। संख्या $C$ एकीकरण का एक स्थिरांक है।

$f(x)$	$f'(x)$	${\textstyle \int f(x)\,dx}$
$\sin x$	$\cos x$	$-\cos x+C$
$\cos x$	$-\sin x$	$\sin x+C$
$\tan x$	$\sec ^{2}x=1+\tan ^{2}x$	$-\ln \left\|\cos x\right\|+C$
$\csc x$	$-\csc x\cot x$	$-\ln \left\|\csc x+\cot x\right\|+C$
$\sec x$	$\sec x\tan x$	$\ln \left\|\sec x+\tan x\right\|+C$
$\cot x$	$-\csc ^{2}x=-1-\cot ^{2}x$	$\ln \left\|\sin x\right\|+C$

वैकल्पिक रूप से, 'सह-फलन' के व्युत्पन्न को त्रिकोणमितीय सर्वसमिका और श्रृंखला नियम का उपयोग करके प्राप्त किया जा सकता है:

{\begin{aligned}{\frac {d\cos x}{dx}}&={\frac {d}{dx}}\sin(\pi /2-x)=-\cos(\pi /2-x)=-\sin x\,,\\{\frac {d\csc x}{dx}}&={\frac {d}{dx}}\sec(\pi /2-x)=-\sec(\pi /2-x)\tan(\pi /2-x)=-\csc x\cot x\,,\\{\frac {d\cot x}{dx}}&={\frac {d}{dx}}\tan(\pi /2-x)=-\sec ^{2}(\pi /2-x)=-\csc ^{2}x\,.\end{aligned}}

प्रतिलोम फलन

त्रिकोणमितीय फलन आवर्ती होते हैं, और इसलिए अंतःक्षेपक नहीं होते हैं, इसलिए कठोरता से बोलते हुए, उनके पास प्रतिलोम फलन नहीं होते है। हालांकि, प्रत्येक अंतराल जिस पर एक त्रिकोणमितीय फलन एकदिष्‍ट होता है, एक प्रतिलोम फलन को परिभाषित कर सकता है, और यह प्रतिलोम त्रिकोणमितीय फलन को बहु-मूल्यवान फलन के रूप में परिभाषित करता है। एक सच्चे प्रतिलोम फलन को परिभाषित करने के लिए, किसी को प्रक्षेत्र को एक अंतराल तक सीमित करना चाहिए जहां फलन एकदिष्‍ट है, और इस प्रकार फलन द्वारा इस अंतराल से इसके प्रतिबिंब के लिए विशेषण है। इस अंतराल के लिए सामान्य विकल्प, जिसे प्रमुख मूल्यों का समुच्चय कहा जाता है, निम्नलिखित तालिका में दिया गया है। हमेशा की तरह, व्युत्क्रम त्रिकोणमितीय फलनों को फलन के नाम या इसके संक्षिप्त नाम से पहले पूर्वलग्‍न ''चाप कर्ण'' के साथ दर्शाया जाता है।

फलन	परिभाषा	प्रक्षेत्र	प्रमुख मूल्यों का समुच्चय
$y=\arcsin x$	$\sin y=x$	$-1\leq x\leq 1$	${\textstyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}}$
$y=\arccos x$	$\cos y=x$	$-1\leq x\leq 1$	${\textstyle 0\leq y\leq \pi }$
$y=\arctan x$	$\tan y=x$	$-\infty <x<\infty$	${\textstyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}}$
$y=\operatorname {arccot} x$	$\cot y=x$	$-\infty <x<\infty$	${\textstyle 0<y<\pi }$
$y=\operatorname {arcsec} x$	$\sec y=x$	$x<-1{\text{ or }}x>1$	${\textstyle 0\leq y\leq \pi ,\;y\neq {\frac {\pi }{2}}}$
$y=\operatorname {arccsc} x$	$\csc y=x$	$x<-1{\text{ or }}x>1$	${\textstyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},\;y\neq 0}$

अंकन $sin -1$ , $cos -1$ आदि प्राय: $arcsin$ और $arccos$ आदि के लिए उपयोग किए जाते हैं। जब इस संकेतन का उपयोग किया जाता है, तो प्रतिलोम फलनों को गुणात्मक व्युत्क्रमों के साथ अस्पष्ट किया जा सकता है। ''आर्क'' पूर्वलग्‍न के साथ अंकन इस तरह के अस्पष्ट से परिहार जाता है, हालांकि आर्कव्युत्क्रम कोटिज्या के लिए ''आर्कसेक'' को ''आर्कसेकंड'' के साथ भ्रमित किया जा सकता है।

ज्या और कोज्या की तरह, व्युत्क्रम त्रिकोणमितीय फलनों को भी अनंत श्रृंखला के संदर्भ में व्यक्त किया जा सकता है। उन्हें सम्मिश्र लघुगणक के रूप में भी व्यक्त किया जा सकता है।

अनुप्रयोग

त्रिभुज के कोण और भुजाएँ

इस अनुभाग में $A$ , $B$ , $C$ त्रिकोण के तीन (आंतरिक) कोणों को लक्षित करते हैं, और $a$ , $b$ , $c$ संबंधित विपरीत किनारों की लंबाई को दर्शाते है। वे विभिन्न सूत्र से संबंधित हैं, जिन्हें उनके द्वारा सम्मिलित त्रिकोणमितीय फलनों द्वारा नामित किया गया है।

ज्या का नियम

ज्या के नियम में कहा गया है कि $a$ , $b$ , और $c$ के साथ एक स्वेच्छ त्रिकोण के लिए और उन भुजाओं के विपरीत कोण $A$ , $B$ और $C$ के लिए:

{\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}={\frac {2\Delta }{abc}},

जहाँ

Δ

त्रिभुज का क्षेत्रफल है, या, समतुल्य,

{\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R,

जहाँ

R

त्रिभुज की परित्रिज्या है।

इसे त्रिभुज को दो समकोणों में विभाजित करके और ज्या की उपरोक्त परिभाषा का उपयोग करके सिद्ध किया जा सकता है। ज्या का नियम एक त्रिभुज में अज्ञात भुजाओं की लंबाई की गणना करने के लिए उपयोगी होता है यदि दो कोण और एक भुजा ज्ञात हो। यह त्रिकोणासन में होने वाली एक सामान्य स्थिति है, दो कोणों और एक सुलभ संलग्न दूरी को मापकर अज्ञात दूरियों को निर्धारित करने की एक तकनीक है।

कोज्या का नियम

कोज्या का नियम (कोज्या सूत्र या कोज्या नियम के रूप में भी जाना जाता है) पाइथागोरस प्रमेय का एक विस्तार है:

c^{2}=a^{2}+b^{2}-2ab\cos C,

या समतुल्य,

\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}.

इस सूत्र में

C

पर कोण भुजा

c

के विपरीत है। इस प्रमेय को त्रिभुज को दो समकोण में विभाजित करके और पाइथागोरस प्रमेय का उपयोग करके सिद्ध किया जा सकता है।

कोज्या के नियम का उपयोग त्रिभुज की एक भुजा निर्धारित करने के लिए किया जा सकता है यदि दो भुजाएँ और उनके मध्य का कोण ज्ञात हो। यदि सभी भुजाओ की लंबाई ज्ञात हो तो इसका उपयोग कोण (और इसके परिणामस्वरूप स्वयं कोण) के कोज्या को खोजने के लिए भी किया जा सकता है।

स्पर्शरेखा का नियम

स्पर्शरेखा का नियम कहता है कि:

{\frac {\tan {\frac {A-B}{2}}}{\tan {\frac {A+B}{2}}}}={\frac {a-b}{a+b}}

.

स्पर्शरेखा का नियम

यदि s त्रिभुज का अर्द्धपरिधि है, (a + b + c)/2, और r त्रिभुज के अंत:वृत्त की त्रिज्या है, तो rs त्रिभुज का क्षेत्रफल है। इसलिए हीरोन के सूत्र का तात्पर्य है कि:

r={\sqrt {{\frac {1}{s}}(s-a)(s-b)(s-c)}}

.

कोटिस्पर्श रेखा का नियम कहता है कि:^[19]

$\cot {\frac {A}{2}}={\frac {s-a}{r}}$

यह इस प्रकार है कि

{\frac {\cot {\dfrac {A}{2}}}{s-a}}={\frac {\cot {\dfrac {B}{2}}}{s-b}}={\frac {\cot {\dfrac {C}{2}}}{s-c}}={\frac {1}{r}}.

आवर्ती फलन

एक लिसाजस वक्र, त्रिकोणमिति-आधारित फलन के साथ बनाई गई एक आकृति।

हार्मोनिक्स की बढ़ती संख्या के साथ एक वर्ग तरंग के योगात्मक संश्लेषण का एक अनुप्राणन

ज्यासॉइडल आधार फलन (नीचे) जोड़े जाने पर एक आरादंती तरंग (शीर्ष) बना सकते हैं। सभी आधार फलनों में आरादंती के नोड्स पर नोड्स होते हैं, और मूलभूत (

k = 1

) अतिरिक्त नोड होते हैं। जब k बड़ा होता है तो आरादंत के बारे में देखा जाने वाला दोलन गिब्स घटना कहलाता है।

भौतिकी में त्रिकोणमितीय फलन भी महत्वपूर्ण हैं। उदाहरण के लिए, ज्या और कोज्या फलन का उपयोग सरल हरात्मक गति का वर्णन करने के लिए किया जाता है, जो कई प्राकृतिक घटनाओं को प्रतिरूप करता है, जैसे किसी स्प्रिंग से जुड़े द्रव्यमान की गति और, छोटे कोणों के लिए, किसी डोरी से लटके द्रव्यमान की दोलन गति, ज्या और कोज्या फलन एकसमान वृत्तीय गति के एक आयामी प्रक्षेपण हैं।

त्रिकोणमितीय फलन सामान्य आवर्ती फलनों के अध्ययन में भी उपयोगी सिद्ध होते हैं। आवर्ती फलनों के विशिष्ट तरंग प्रतिरूप आवर्ती घटनाओं जैसे ध्वनि या प्रकाश तरंगों के मॉडलिंग के लिए उपयोगी होते हैं।^[20]

वस्तुत सामान्य परिस्थितियों में, एक आवर्ती फलन $f (x)$ को फूरियर श्रृंखला में ज्या तरंगों या कोज्या तरंगों के योग के रूप में व्यक्त किया जा सकता है।^[21] $φ k$ द्वारा ज्या या कोज्या आधार फलनों को लक्षित करते हुए, आवर्ती फलनों का विस्तार $f (t)$ रूप लेता है:

f(t)=\sum _{k=1}^{\infty }c_{k}\varphi _{k}(t).

उदाहरण के लिए, वर्ग तरंग को फुरिये श्रृंखला के रूप में लिखा जा सकता है

f_{\text{square}}(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\sin {\big (}(2k-1)t{\big )} \over 2k-1}.

शीर्ष दाईं ओर एक वर्ग तरंग के एनीमेशन में यह देखा जा सकता है कि केवल कुछ शब्द पहले से ही अत्यंत अच्छा सन्निकटन उत्पन्न करते हैं। एक आरादंती तरंग के विस्तार में कई पदों के अधिस्थापन को नीचे दिखाया गया है।

इतिहास

जबकि त्रिकोणमिति के प्रारंभिक अध्ययन से पुरातनता का पता लगाया जा सकता है, त्रिकोणमितीय फलनों के रूप में वे आज उपयोग में हैं, मध्यकाल में विकसित किए गए थे। कॉर्ड फलन की खोज नाइसिया के हिप्पार्कस (180–125 बीसीई) और रोमन मिस्र के टॉलेमी (90-165 सीई) द्वारा की गई थी। ज्या और वर्साइन (1 - कोज्या) के फलनों को गुप्ता काल के भारतीय खगोल विज्ञान (आर्यभटीय, सूर्य सिद्धांत) में संस्कृत से अरबी और फिर अरबी से लैटिन में अनुवाद के माध्यम से उपयोग किए गए जया और कोटि-ज्या फलानो में खोजा जा सकता है।^[22](आर्यभट्ट की ज्या तालिका देखें।)

वर्तमान उपयोग में सभी छह त्रिकोणमितीय फलनों को 9वीं शताब्दी तक इस्लामी गणित में जाना जाता था, जैसा कि त्रिकोणों का समाधान करने में प्रयुक्त होने वाली त्रिभुज का नियम था।^[23] ज्या (जो भारतीय गणित से स्वीकृत किया गया था) के अपवाद के साथ, अन्य पांच आधुनिक त्रिकोणमितीय फलनों की खोज फ़ारसी और अरब गणितज्ञों द्वारा की गई, जिनमें कोज्या, स्पर्शरेखा, कोटिस्पर्श, व्युत्क्रम कोटिज्या और व्युत्क्रमज्या सम्मिलित हैं।^[23]अल-ख़्वारिज़्मी (सी.-780-850) ने ज्या, कोज्या और स्पर्शरेखाओं की सूची बनाईं। लगभग 830, हबश अल-हकूब अल-मरवाज़ी ने कोटिस्पर्श रेखा की खोज की, और स्पर्शरेखा और कॉटैंगेंट की सूची प्रस्तुत की थी।^[24]^[25] मुहम्मद इब्न जाबिर अल-हररानी अल-बट्टानी (853–929) ने व्युत्क्रम कोटिज्या और व्युत्क्रमज्या के पारस्परिक फलनों की खोज की, और 1° से 90° तक प्रत्येक डिग्री के लिए व्युत्क्रमज्या की पहली तालिका प्रस्तुत की थी।^[25]बाद में ओमर खय्याम, भास्कर II, नासिर अल-दीन अल-तुसी, जमशेद अल-काशी (14वीं सदी), उलूग बेग (14वीं सदी), रेजीओमोंटानस (1464), और जॉर्ज जोआचिम रेटिकस के छात्र सहित गणितज्ञों द्वारा त्रिकोणमितीय फलनों का अध्ययन किया गया।

संगमग्राम के माधव (सी। 1400) ने श्रृंखला के संदर्भ में त्रिकोणमितीय फलनों के गणितीय विश्लेषण में पूर्व प्रगति की थी।^[26](माधव श्रृंखला और माधव की ज्या तालिका देखें।)

1467 में जियोवन्नी बियांचिनी द्वारा तारकीय निर्देशांक की गणना का समर्थन करने के लिए बनाई गई त्रिकोणमिति तालिकाओं में स्पर्शरेखा फलन यूरोप में लाया गया था।^[27]

स्पर्शरेखा और व्युत्क्रम कोटिज्या शब्द पहली बार डेनिश गणितज्ञ थॉमस फिनके ने अपनी पुस्तक जियोमेट्रिया रोटुंडी (1583) में प्रस्तावित किए थे।^[28]

17वीं शताब्दी के फ्रांसीसी गणितज्ञ अल्बर्ट गिरार्ड ने अपनी पुस्तक त्रिकोणमिति में सिन, कॉस और टैन संक्षिप्त रूपों का पहला प्रकाशित उपयोग किया।^[29]

1682 में प्रकाशित एक पत्र में गॉटफ्रीड लीबनिज ने यह सिद्ध किया कि $sin x$ $x$ का बीजगणितीय फलन नहीं है।^[30] यद्यपि एक समकोण त्रिभुज की भुजाओं के अनुपात के रूप में प्रस्तावित किया गया, और इस प्रकार तर्कसंगत फलनों के रूप में प्रकट होता है, लीबनिट्ज परिणाम ने स्थापित किया कि वे वास्तव में उनके तर्क के अबीजीय फलन हैं। वृत्तीय फलनों को बीजगणितीय व्यंजकों में समावेश करने का फलन यूलर द्वारा अनंत के विश्लेषण के अपने परिचय (1748) में पूरा किया गया था। उनकी विधि यह दिखाने के लिए थी कि ज्या और कोज्या फलन घातांक श्रृंखला के क्रमशः सम और विषम शब्दों से बनने वाली प्रत्यावर्ती श्रृंखला हैं। उन्होंने ''यूलर के सूत्र'', साथ ही निकट-आधुनिक संक्षिप्ताक्षर (sin., cos., tang., cot., sec., और cosec.) प्रस्तुत किए।^[22]

कुछ फलन ऐतिहासिक रूप से सामान्य थे, लेकिन अब सम्भावित ही कभी इसका उपयोग किया जाता है, जैसे कि तार, वरसाइन (जो सबसे पूर्वतर तालिकाओं में दिखाई देता है)^[22]), कवरज्या, हावेरसिन,^[31] एक्ससेकेंट और एक्सोसेकेंट है। त्रिकोणमितीय सर्वसमिकाओं की सूची इन फलनों के मध्य अधिक संबंध सिध्द करती है।

$crd(θ) = 2 sin(θ / 2)$
$versin(θ) = 1 - cos(θ) = 2 sin 2 (θ / 2)$
$coversin(θ) = 1 - sin(θ) = versin(π / 2 - θ)$
$haversin(θ) = 1 / 2 versin(θ) = sin 2 (θ / 2)$
$exsec(θ) = sec(θ) - 1$
$excsc(θ) = exsec(π / 2 - θ) = csc(θ) - 1$

व्युत्पत्ति विज्ञान

ज्या शब्द ^[32] लैटिन साइनस से निकला है: जिसका अर्थ है "बेंड; बे", और अधिक विशेष रूप से ''एक टोगा के ऊपरी भाग की निलम्बी हुई तह'', ''एक परिधान की बोसोम'', जिसे अरबी शब्द जैब के रूप में व्याख्या किए गए अनुवाद के रूप में चयन किया गया था, मध्यकालीन लैटिन में अल-बट्टानी और मुहम्मद इब्न मूसा अल-ख़्वारिज़्मी द्वारा किए गए कार्यों के बारहवीं शताब्दी के अनुवाद में "पॉकेट" या "फोल्ड" का अर्थ है।^[33] यह विकल्प अरबी लिखित रूप j-y-b (جيب) के गलत अर्थ पर आधारित था, जो स्वयं संस्कृत जिवा से एक लिप्यंतरण के रूप में उत्पन्न हुआ था, जो इसके पर्यायवाची jyā (ज्या के लिए मानक संस्कृत शब्द) के साथ "धनुर्ज्या " में अनुवाद करता है, जिसे प्राचीन ग्रीक χορδή "तंतु" से अपनाया गया है।^[34]

स्पर्शरेखा शब्द लैटिन टैंगेंस से आया है जिसका अर्थ है ''संस्पर्श'', क्योंकि रेखा इकाई त्रिज्या के वृत्त को स्पर्श करती है, जबकि व्युत्क्रम कोटिज्या लैटिन सेकान से उत्पन्न होता है- "काटना"- क्योंकि रेखा वृत्त को काटती है।^[35]

उपसर्ग सह- (कोज्या में, कोटिस्पर्श रेखा, व्युत्क्रम ज्या) एडमंड गुंटर के कैनन त्रिकोणीय (1620) में पाया जाता है, जो कोसिनस को साइनस पूरक (पूरक कोण की ज्या) के संक्षिप्त नाम के रूप में परिभाषित करता है और इसी तरह कोटांगेंस को परिभाषित करने के लिए आगे बढ़ता है।^[36]^[37]

यह भी देखें

सभी छात्र गणना लेते हैं - एक कार्तीय तल के एक विशेष चतुर्भुज में त्रिकोणमितीय फलानो के संकेतों को याद करने के लिए एक स्मरक
भास्कर प्रथम का ज्या सन्निकटन सूत्र
त्रिकोणमितीय फलानो का विभेदन
सामान्यीकृत त्रिकोणमिति
त्रिकोणमितीय तालिकाएँ बनाना
अतिशयोक्तिपूर्ण फलान
त्रिकोणमितीय फलानो के समाकलन की सूची
आवधिक फलानो की सूची
त्रिकोणमितीय सर्वसमिका की सूची
ध्रुवीय ज्या - शीर्ष कोणों के लिए एक सामान्यीकरण
त्रिकोणमितीय सर्वसमिकाओं के प्रमाण
वर्साइन - कई कम उपयोग किए जाने वाले त्रिकोणमितीय फलानो के लिए

↑ Klein, Christian Felix (1924) [1902]. Elementarmathematik vom höheren Standpunkt aus: Arithmetik, Algebra, Analysis (in Deutsch). Vol. 1 (3rd ed.). Berlin: J. Springer.
↑ Klein, Christian Felix (2004) [1932]. Elementary Mathematics from an Advanced Standpoint: Arithmetic, Algebra, Analysis. Translated by Hedrick, E. R.; Noble, C. A. (Translation of 3rd German ed.). Dover Publications, Inc. / The Macmillan Company. ISBN 978-0-48643480-3. Archived from the original on 15 February 2018. Retrieved 13 August 2017.
↑ Protter & Morrey (1970, pp. APP-2, APP-3)
↑ "साइन, कोसाइन, स्पर्शरेखा". www.mathsisfun.com. Retrieved 29 August 2020.
↑ Protter & Morrey (1970, p. APP-7)
↑ ^6.0 ^6.1 Rudin, Walter, 1921–2010. गणितीय विश्लेषण के सिद्धांत (Third ed.). New York. ISBN 0-07-054235-X. OCLC 1502474.{{cite book}}: CS1 maint: multiple names: authors list (link)
↑ Diamond, Harvey (2014). "विभेदक समीकरणों का उपयोग करके घातीय और त्रिकोणमितीय कार्यों को परिभाषित करना". Mathematics Magazine (in English). 87 (1): 37–42. doi:10.4169/math.mag.87.1.37. ISSN 0025-570X. S2CID 126217060.
↑ Spivak, Michael (1967). "15". गणना. Addison-Wesley. pp. 256–257. LCCN 67-20770.
↑ Heng, Cheng and Talbert, "Additional Mathematics" Archived 20 March 2015 at the Wayback Machine, page 228
↑ Bityutskov, V.I. (7 February 2011). "त्रिकोणमितीय कार्य". Encyclopedia of Mathematics (in English). Archived from the original on 29 December 2017. Retrieved 29 December 2017.
↑ Larson, Ron (2013). Trigonometry (9th ed.). Cengage Learning. p. 153. ISBN 978-1-285-60718-4. Archived from the original on 15 February 2018. Extract of page 153 Archived 15 February 2018 at the Wayback Machine
↑ See Ahlfors, pp. 43–44.
↑ Stanley, Enumerative Combinatorics, Vol I., p. 149
↑ Abramowitz; Weisstein.
↑ Lambert, Johann Heinrich (2004) [1768], "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", in Berggren, Lennart; Borwein, Jonathan M.; Borwein, Peter B. (eds.), Pi, a source book (3rd ed.), New York: Springer-Verlag, pp. 129–140, ISBN 0-387-20571-3
↑ Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (Second ed.). Springer-Verlag. p. 149. ISBN 978-3-642-00855-9. Archived from the original on 8 March 2014.
↑ Remmert, Reinhold (1991). Theory of complex functions. Springer. p. 327. ISBN 978-0-387-97195-7. Archived from the original on 20 March 2015. Extract of page 327 Archived 20 March 2015 at the Wayback Machine
↑ Kannappan, Palaniappan (2009). Functional Equations and Inequalities with Applications. Springer. ISBN 978-0387894911.
↑ The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, pp. 529–530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.
↑ Farlow, Stanley J. (1993). Partial differential equations for scientists and engineers (Reprint of Wiley 1982 ed.). Courier Dover Publications. p. 82. ISBN 978-0-486-67620-3. Archived from the original on 20 March 2015.
↑ See for example, Folland, Gerald B. (2009). "Convergence and completeness". Fourier Analysis and its Applications (Reprint of Wadsworth & Brooks/Cole 1992 ed.). American Mathematical Society. pp. 77ff. ISBN 978-0-8218-4790-9. Archived from the original on 19 March 2015.
↑ ^22.0 ^22.1 ^22.2 Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc. ISBN 0-471-54397-7, p. 210.
↑ ^23.0 ^23.1 Gingerich, Owen (1986). "Islamic Astronomy". Scientific American. Vol. 254. p. 74. Archived from the original on 19 October 2013. Retrieved 13 July 2010.
↑ Jacques Sesiano, "Islamic mathematics", p. 157, in Selin, Helaine; D'Ambrosio, Ubiratan, eds. (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer Science+Business Media. ISBN 978-1-4020-0260-1.
↑ ^25.0 ^25.1 "त्रिकोणमिति". Encyclopedia Britannica.
↑ O'Connor, J. J.; Robertson, E. F. "Madhava of Sangamagrama". School of Mathematics and Statistics University of St Andrews, Scotland. Archived from the original on 14 May 2006. Retrieved 8 September 2007.
↑ Van Brummelen, Glen (2018). "एक त्रुटि का अंत: बियांचिनी, रेजीओमोंटानस, और तारकीय निर्देशांक का सारणीकरण". Archive for History of Exact Sciences. 72 (5): 547–563. doi:10.1007/s00407-018-0214-2. JSTOR 45211959. S2CID 240294796.
↑ "Fincke biography". Archived from the original on 7 January 2017. Retrieved 15 March 2017.
↑ O'Connor, John J.; Robertson, Edmund F., "त्रिकोणमितीय फलन", MacTutor History of Mathematics archive, University of St Andrews
↑ Bourbaki, Nicolás (1994). Elements of the History of Mathematics. Springer. ISBN 9783540647676.
↑ Nielsen (1966, pp. xxiii–xxiv)
↑ The anglicized form is first recorded in 1593 in Thomas Fale's Horologiographia, the Art of Dialling.
↑
Various sources credit the first use of sinus to either
- Plato Tiburtinus's 1116 translation of the Astronomy of Al-Battani
- Gerard of Cremona's translation of the Algebra of al-Khwārizmī
- Robert of Chester's 1145 translation of the tables of al-Khwārizmī
See Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004
See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
See Katx, Victor (July 2008). A history of mathematics (in English) (3rd ed.). Boston: Pearson. p. 210 (sidebar). ISBN 978-0321387004.
↑ See Plofker, Mathematics in India, Princeton University Press, 2009, p. 257
See "Clark University". Archived from the original on 15 June 2008.
See Maor (1998), chapter 3, regarding the etymology.
↑ Oxford English Dictionary
↑ Gunter, Edmund (1620). Canon triangulorum.
↑ Roegel, Denis, ed. (6 December 2010). "A reconstruction of Gunter's Canon triangulorum (1620)" (Research report). HAL. inria-00543938. Archived from the original on 28 July 2017. Retrieved 28 July 2017.

संदर्भ

Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
Lars Ahlfors, Complex Analysis: an introduction to the theory of analytic functions of one complex variable, second edition, McGraw-Hill Book Company, New York, 1966.
Boyer, Carl B., A History of Mathematics, John Wiley & Sons, Inc., 2nd edition. (1991). ISBN 0-471-54397-7.
Cajori, Florian (1929). "§2.2.1. Trigonometric Notations". A History of Mathematical Notations. Vol. 2. Open Court. pp. 142–179 (¶511–537).
Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991).
Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, 2nd ed. Penguin Books, London. (2000). ISBN 0-691-00659-8.
Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
Maor, Eli, Trigonometric Delights, Princeton Univ. Press. (1998). Reprint edition (2002): ISBN 0-691-09541-8.
Needham, Tristan, "Preface"" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9.
Nielsen, Kaj L. (1966), Logarithmic and Trigonometric Tables to Five Places (2nd ed.), New York: Barnes & Noble, LCCN 61-9103
O'Connor, J. J., and E. F. Robertson, "Trigonometric functions", MacTutor History of Mathematics archive. (1996).
O'Connor, J. J., and E. F. Robertson, "Madhava of Sangamagramma", MacTutor History of Mathematics archive. (2000).
Pearce, Ian G., "Madhava of Sangamagramma" Archived 2006-05-05 at the Wayback Machine, MacTutor History of Mathematics archive. (2002).
Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
Weisstein, Eric W., "Tangent" from MathWorld, accessed 21 January 2006.

बाहरी कड़ियाँ

"Trigonometric functions", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Visionlearning Module on Wave Mathematics
GonioLab Visualization of the unit circle, trigonometric and hyperbolic functions
q-Sine Article about the q-analog of sin at MathWorld
q-Cosine Article about the q-analog of cos at MathWorld

श्रेणी:कोण श्रेणी: त्रिकोणमिति श्रेणी: प्रारंभिक विशेष फलन श्रेणी:विश्लेषणात्मक फलन श्रेणी: अनुपात श्रेणी:आयामहीन संख्या

[Klein_1924-1] Klein, Christian Felix (1924) [1902]. Elementarmathematik vom höheren Standpunkt aus: Arithmetik, Algebra, Analysis (in Deutsch). Vol. 1 (3rd ed.). Berlin: J. Springer.

[Klein_2004-2] Klein, Christian Felix (2004) [1932]. Elementary Mathematics from an Advanced Standpoint: Arithmetic, Algebra, Analysis. Translated by Hedrick, E. R.; Noble, C. A. (Translation of 3rd German ed.). Dover Publications, Inc. / The Macmillan Company. ISBN 978-0-48643480-3. Archived from the original on 15 February 2018. Retrieved 13 August 2017.

[3] Protter & Morrey (1970, pp. APP-2, APP-3)

[4] "साइन, कोसाइन, स्पर्शरेखा". www.mathsisfun.com. Retrieved 29 August 2020.

[5] Protter & Morrey (1970, p. APP-7)

[:0-6] 6.0 ^6.1 Rudin, Walter, 1921–2010. गणितीय विश्लेषण के सिद्धांत (Third ed.). New York. ISBN 0-07-054235-X. OCLC 1502474.{{cite book}}: CS1 maint: multiple names: authors list (link)

[7] Diamond, Harvey (2014). "विभेदक समीकरणों का उपयोग करके घातीय और त्रिकोणमितीय कार्यों को परिभाषित करना". Mathematics Magazine (in English). 87 (1): 37–42. doi:10.4169/math.mag.87.1.37. ISSN 0025-570X. S2CID 126217060.

[:1-8] Spivak, Michael (1967). "15". गणना. Addison-Wesley. pp. 256–257. LCCN 67-20770.

[Heng-9] Heng, Cheng and Talbert, "Additional Mathematics" Archived 20 March 2015 at the Wayback Machine, page 228

[10] Bityutskov, V.I. (7 February 2011). "त्रिकोणमितीय कार्य". Encyclopedia of Mathematics (in English). Archived from the original on 29 December 2017. Retrieved 29 December 2017.

[Larson_2013-11] Larson, Ron (2013). Trigonometry (9th ed.). Cengage Learning. p. 153. ISBN 978-1-285-60718-4. Archived from the original on 15 February 2018. Extract of page 153 Archived 15 February 2018 at the Wayback Machine

[12] See Ahlfors, pp. 43–44.

[13] Stanley, Enumerative Combinatorics, Vol I., p. 149

[14] Abramowitz; Weisstein.

[15] Lambert, Johann Heinrich (2004) [1768], "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", in Berggren, Lennart; Borwein, Jonathan M.; Borwein, Peter B. (eds.), Pi, a source book (3rd ed.), New York: Springer-Verlag, pp. 129–140, ISBN 0-387-20571-3

[Aigner_2000-16] Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (Second ed.). Springer-Verlag. p. 149. ISBN 978-3-642-00855-9. Archived from the original on 8 March 2014.

[Remmert_1991-17] Remmert, Reinhold (1991). Theory of complex functions. Springer. p. 327. ISBN 978-0-387-97195-7. Archived from the original on 20 March 2015. Extract of page 327 Archived 20 March 2015 at the Wayback Machine

[Kannappan_2009-18] Kannappan, Palaniappan (2009). Functional Equations and Inequalities with Applications. Springer. ISBN 978-0387894911.

[Allen_1976-19] The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, pp. 529–530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.

[Farlow_1993-20] Farlow, Stanley J. (1993). Partial differential equations for scientists and engineers (Reprint of Wiley 1982 ed.). Courier Dover Publications. p. 82. ISBN 978-0-486-67620-3. Archived from the original on 20 March 2015.

[Folland_1992-21] See for example, Folland, Gerald B. (2009). "Convergence and completeness". Fourier Analysis and its Applications (Reprint of Wadsworth & Brooks/Cole 1992 ed.). American Mathematical Society. pp. 77ff. ISBN 978-0-8218-4790-9. Archived from the original on 19 March 2015.

[Boyer_1991-22] 22.0 ^22.1 ^22.2 Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc. ISBN 0-471-54397-7, p. 210.

[Gingerich_1986-23] 23.0 ^23.1 Gingerich, Owen (1986). "Islamic Astronomy". Scientific American. Vol. 254. p. 74. Archived from the original on 19 October 2013. Retrieved 13 July 2010.

[Sesiano-24] Jacques Sesiano, "Islamic mathematics", p. 157, in Selin, Helaine; D'Ambrosio, Ubiratan, eds. (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer Science+Business Media. ISBN 978-1-4020-0260-1.

[Britannica-25] 25.0 ^25.1 "त्रिकोणमिति". Encyclopedia Britannica.

[mact-biog-26] O'Connor, J. J.; Robertson, E. F. "Madhava of Sangamagrama". School of Mathematics and Statistics University of St Andrews, Scotland. Archived from the original on 14 May 2006. Retrieved 8 September 2007.

[27] Van Brummelen, Glen (2018). "एक त्रुटि का अंत: बियांचिनी, रेजीओमोंटानस, और तारकीय निर्देशांक का सारणीकरण". Archive for History of Exact Sciences. 72 (5): 547–563. doi:10.1007/s00407-018-0214-2. JSTOR 45211959. S2CID 240294796.

[Fincke-28] "Fincke biography". Archived from the original on 7 January 2017. Retrieved 15 March 2017.

[MacTutor-29] O'Connor, John J.; Robertson, Edmund F., "त्रिकोणमितीय फलन", MacTutor History of Mathematics archive, University of St Andrews

[Bourbaki_1994-30] Bourbaki, Nicolás (1994). Elements of the History of Mathematics. Springer. ISBN 9783540647676.

[31] Nielsen (1966, pp. xxiii–xxiv)

[32] The anglicized form is first recorded in 1593 in Thomas Fale's Horologiographia, the Art of Dialling.

[33] Various sources credit the first use of sinus to either
Plato Tiburtinus's 1116 translation of the Astronomy of Al-Battani

Gerard of Cremona's translation of the Algebra of al-Khwārizmī

Robert of Chester's 1145 translation of the tables of al-Khwārizmī
See Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004
See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
See Katx, Victor (July 2008). A history of mathematics (in English) (3rd ed.). Boston: Pearson. p. 210 (sidebar). ISBN 978-0321387004.

[34] Plato Tiburtinus's 1116 translation of the Astronomy of Al-Battani

[35] Gerard of Cremona's translation of the Algebra of al-Khwārizmī

[36] Robert of Chester's 1145 translation of the tables of al-Khwārizmī

[Plofker_2009-34] See Plofker, Mathematics in India, Princeton University Press, 2009, p. 257
See "Clark University". Archived from the original on 15 June 2008.
See Maor (1998), chapter 3, regarding the etymology.

[35] Oxford English Dictionary

[Gunter_1620-36] Gunter, Edmund (1620). Canon triangulorum.

[Roegel_2010-37] Roegel, Denis, ed. (6 December 2010). "A reconstruction of Gunter's Canon triangulorum (1620)" (Research report). HAL. inria-00543938. Archived from the original on 28 July 2017. Retrieved 28 July 2017.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

v t e Trigonometric and hyperbolic functions
Groups	Trigonometric Sine and cosine Inverse trigonometric Hyperbolic Inverse hyperbolic
Other	Versine Exsecant Jyā, koti-jyā and utkrama-jyā atan2

@@ Line 2: / Line 2: @@
 {{Trigonometry}}
-[[File:Academ Base of trigonometry.svg|thumb|300px|upright=2|त्रिकोणमिति का आधार: यदि दो समकोण त्रिभुजों में समान न्यूनकोण होते हैं, तो वे [[समानता (ज्यामिति)]] होते हैं, इसलिए उनकी भुजाओं की लंबाई [[आनुपातिकता (गणित)]] होती है।]]गणित में, त्रिकोणमितीय फलन (जिन्हें वृत्तीय फलन, कोण फलन या गोनीमितीय फलन भी कहा जाता है<ref name="Klein_1924"/><ref name="Klein_2004"/>) वास्तविक फलन होते हैं जो एक समकोण त्रिभुज के कोण को दो भुजाओं की लंबाई के अनुपात से संबंधित करते हैं। वे सभी विज्ञानों में व्यापक रूप से उपयोग किए जाते हैं जो कि [[ज्यामिति]] से संबंधित हैं, जैसे कि [[पथ प्रदर्शन|नौसंचालन]], [[ठोस यांत्रिकी]], [[आकाशीय यांत्रिकी|खगोलीय यांत्रिकी]], भूगणित और कई अन्य। वे सबसे सरल आवर्ती फलनों में से हैं, और जैसे कि [[फूरियर विश्लेषण|फुरिये विश्लेषण]] के माध्यम से आवर्ती घटनाओं का अध्ययन करने के लिए भी व्यापक रूप से उपयोग किया जाता है।
+[[File:Academ Base of trigonometry.svg|thumb|300px|upright=2|त्रिकोणमिति का आधार: यदि दो समकोण त्रिभुजों में समान न्यूनकोण होते हैं, तो वे [[समानता (ज्यामिति)|समान]] होते हैं, इसलिए उनकी भुजाओं की लंबाई [[आनुपातिकता (गणित)|समानुपाती]] होती है।]]गणित में, त्रिकोणमितीय फलन (जिन्हें वृत्तीय फलन, कोण फलन या गोनीमितीय फलन भी कहा जाता है<ref name="Klein_1924"/><ref name="Klein_2004"/>) वास्तविक फलन होते हैं जो एक समकोण त्रिभुज के कोण को दो भुजाओं की लंबाई के अनुपात से संबंधित करते हैं। वे सभी विज्ञानों में व्यापक रूप से उपयोग किए जाते हैं जो कि [[ज्यामिति]] से संबंधित हैं, जैसे कि [[पथ प्रदर्शन|नौसंचालन]], [[ठोस यांत्रिकी]], [[आकाशीय यांत्रिकी|खगोलीय यांत्रिकी]], भूगणित और कई अन्य। वे सबसे सरल आवर्ती फलनों में से हैं, और जैसे कि [[फूरियर विश्लेषण|फुरिये विश्लेषण]] के माध्यम से आवर्ती घटनाओं का अध्ययन करने के लिए भी व्यापक रूप से उपयोग किए जाते हैं।
-आधुनिक गणित में सबसे व्यापक रूप से उपयोग किए जाने वाले त्रिकोणमितीय फलन ज्या, [[कोज्या]] और स्पर्शरेखा हैं। इनके व्युत्क्रम क्रमश: व्युत्क्रमज्या, छेदक रेखा और कोटिस्पर्श रेखा हैं, जिनका प्रयोग कम होता है। इन छह त्रिकोणमितीय फलनों में से प्रत्येक में एक समान [[उलटा त्रिकोणमितीय कार्य|प्रतिलोम फलन]] होता है, और [[अतिशयोक्तिपूर्ण कार्य|अतिपरवलयिक फलनों]] के मध्य एक अनुरूप होता है।
+आधुनिक गणित में सबसे व्यापक रूप से उपयोग किए जाने वाले त्रिकोणमितीय फलन ज्या, [[कोज्या]] और स्पर्शरेखा हैं। इनके व्युत्क्रम क्रमश: व्युत्क्रमज्या, व्युत्क्रम कोटिज्या और कोटिस्पर्श रेखा हैं, जिनका प्रयोग कम होता है। इन छह त्रिकोणमितीय फलनों में से प्रत्येक में एक समान [[उलटा त्रिकोणमितीय कार्य|प्रतिलोम फलन]] होता है, और [[अतिशयोक्तिपूर्ण कार्य|अतिपरवलयिक फलनों]] के मध्य एक अनुरूप होता है।
-समकोण त्रिभुजों से संबंधित त्रिकोणमितीय फलनों की सबसे पुरानी परिभाषाएँ उन्हें केवल न्यून कोणों के लिए परिभाषित करती हैं। ज्या और कोज्या फलन को उन फलन तक विस्तारित करने के लिए जिनका प्रक्षेत्र संपूर्ण [[वास्तविक रेखा]] है, मानक [[यूनिट सर्कल|इकाई वृत्त]] (अर्थात, त्रिज्या 1 इकाई वाला एक वृत्त) का उपयोग करते हुए ज्यामितीय परिभाषाएं प्रायः उपयोग की जाती हैं; तो अन्य फलनों का प्रक्षेत्र वास्तविक रेखा है जिसमें कुछ वियुक्त बिंदु अलग कर दिए गए हैं। आधुनिक परिभाषाएँ त्रिकोणमितीय फलनों को अनंत [[श्रृंखला (गणित)|श्रृंखला]] या [[अंतर समीकरण|अंतर समीकरणों]] के समाधान के रूप में व्यक्त करती हैं। यह ज्या और कोज्या फलनों के प्रक्षेत्र को पूरे [[जटिल विमान|सम्मिश्र समतल]] में विस्तारित करने की अनुमति देता है, और अन्य त्रिकोणमितीय फलनों के प्रक्षेत्र को कुछ वियुक्त बिंदुओं को अलग करके सम्मिश्र समतल पर ले जाता है।
+समकोण त्रिभुजों से संबंधित त्रिकोणमितीय फलनों की सबसे पुरानी परिभाषाएँ उन्हें केवल न्यून कोणों के लिए परिभाषित करती हैं। ज्या और कोज्या फलन को उन फलन तक विस्तारित करने के लिए जिनका प्रक्षेत्र संपूर्ण [[वास्तविक रेखा]] है, मानक [[यूनिट सर्कल|इकाई वृत्त]] (अर्थात, त्रिज्या 1 इकाई वाला एक वृत्त) का उपयोग करते हुए ज्यामितीय परिभाषाएं प्रायः उपयोग की जाती हैं; तो अन्य फलनों का प्रक्षेत्र वास्तविक रेखा है जिसमें कुछ वियुक्त बिंदु अलग कर दिए गए हैं। आधुनिक परिभाषाएँ त्रिकोणमितीय फलनों को अनंत [[श्रृंखला (गणित)|श्रृंखला]] या [[अंतर समीकरण|अंतर समीकरणों]] के समाधान के रूप में व्यक्त करती हैं। यह ज्या और कोज्या फलनों के प्रक्षेत्र को पूरे [[जटिल विमान|सम्मिश्र समतल]] में विस्तारित करने की अनुमति देती है, और अन्य त्रिकोणमितीय फलनों के प्रक्षेत्र को कुछ वियुक्त बिंदुओं को अलग करके सम्मिश्र समतल पर ले जाती है।
 == संकेतन ==
-परंपरागत रूप से, प्रत्येक त्रिकोणमितीय फलन के नाम का एक संक्षिप्त नाम सूत्रों में इसके प्रतीक के रूप में उपयोग किया जाता है। आज, इन संक्षेपों के सबसे सामान्य संस्करण ज्या के लिए <nowiki>''सिन'' है, कोज्या के लिए ''कॉस'', या ''टीजी'' स्पर्शरेखा के लिए, छेदक रेखा के लिए ''सेकंड'', व्युत्क्रमज्या के लिए ''सीएससी'' या ''कोसेक'', और कोटिस्पर्श रेखा के लिए ''कॉट'' या ''सीटीजी''</nowiki>। ऐतिहासिक रूप से, इन संक्षिप्ताक्षरों का उपयोग पहली बार गद्य वाक्यों में उपयोग किया गया था ताकि विशेष [[रेखा खंड|रेखा खंडों]] या उनकी लंबाई को एक स्वेच्छ वृत्त के एक चाप से संबंधित किया जा सके, और बाद में लंबाई के अनुपात को इंगित करने के लिए, लेकिन जैसा कि 17वीं-18वीं शताब्दी में फलन की अवधारणा विकसित हुई, उन्हें वास्तविक-संख्या-मूल्यवान कोण मापक के फलनों के रूप में माना जाने लगा, और [[कार्यात्मक अंकन|फलनात्मक संकेतन]] के साथ लिखा गया,  उदाहरण के लिए {{math|sin(''x'')}} है। अव्यवस्था को कम करने के लिए कोष्ठक अभी भी प्रायः कम किए जाते हैं, लेकिन कभी-कभी आवश्यक होते हैं; उदाहरण के लिए अभिव्यक्ति <math>\sin x+y</math>  को विशिष्ट रूप से <math>\sin (x)+y,</math> के अर्थ में व्याख्या की जाएगी, इसलिए <math>\sin (x+y)</math> को व्यक्त करने के लिए कोष्ठकों की आवश्यकता होती है।
+परंपरागत रूप से, प्रत्येक त्रिकोणमितीय फलन के नाम का एक संक्षिप्त नाम सूत्रों में इसके प्रतीक के रूप में उपयोग किया जाता है। आज, इन संक्षेपों के सबसे सामान्य संस्करण ज्या के लिए <nowiki>''सिन'' है, कोज्या के लिए ''कॉस'', या ''टीजी'' स्पर्शरेखा के लिए, व्युत्क्रम कोटिज्या के लिए ''सेकंड'', व्युत्क्रमज्या के लिए ''सीएससी'' या ''कोसेक'', और कोटिस्पर्श रेखा के लिए ''कॉट'' या ''सीटीजी''</nowiki> है। ऐतिहासिक रूप से, इन संक्षिप्ताक्षरों का उपयोग पहली बार गद्य वाक्यों में उपयोग किया गया था ताकि विशेष [[रेखा खंड|रेखा खंडों]] या उनकी लंबाई को एक स्वेच्छ वृत्त के एक चाप कर्ण से संबंधित किया जा सके, और बाद में लंबाई के अनुपात को इंगित करने के लिए, जैसा कि 17वीं-18वीं शताब्दी में फलन की अवधारणा विकसित हुई, उन्हें वास्तविक-संख्या-मूल्यवान कोण मापक के फलनों के रूप में माना जाने लगा, और [[कार्यात्मक अंकन|फलनात्मक संकेतन]] के साथ लिखा गया,  उदाहरण के लिए {{math|sin(''x'')}} है। अव्यवस्था को कम करने के लिए कोष्ठक अभी भी प्रायः कम किए जाते हैं, लेकिन कभी-कभी आवश्यक होते हैं; उदाहरण के लिए अभिव्यक्ति <math>\sin x+y</math>  को विशिष्ट रूप से <math>\sin (x)+y,</math> के अर्थ में व्याख्या की जाएगी, इसलिए <math>\sin (x+y)</math> को व्यक्त करने के लिए कोष्ठकों की आवश्यकता होती है।
-फलन के प्रतीक के बाद एक अधिलेख के रूप में प्रकट होने वाला एक [[सकारात्मक पूर्णांक]] [[घातांक]] को दर्शाता है, फलन संयोजन को नहीं दर्शाता है। उदाहरण के लिए <math>\sin^2 x</math> और <math>\sin^2 (x)</math> <math>\sin(x) \cdot \sin(x)</math> को दर्शाते हैं, <math>\sin(\sin x)</math> को नहीं दर्शाते हैं। यह (ऐतिहासिक रूप से बाद में) सामान्य फलनात्मक संकेतन से भिन्न है जिसमें <math>f^2(x) = (f \circ f)(x) = f(f(x))</math> है।
+फलन के प्रतीक के बाद एक अधिलेख के रूप में प्रकट होने वाला एक [[सकारात्मक पूर्णांक]] [[घातांक]] को दर्शाता है, फलन संयोजन को नहीं दर्शाता है। उदाहरण के लिए <math>\sin^2 x</math> और <math>\sin^2 (x)</math> <math>\sin(x) \cdot \sin(x)</math> को लक्षित करते हैं, <math>\sin(\sin x)</math> को लक्षित नहीं करते हैं। यह (ऐतिहासिक रूप से बाद में) सामान्य फलनात्मक संकेतन से भिन्न है जिसमें <math>f^2(x) = (f \circ f)(x) = f(f(x))</math> है।
-हालाँकि, घातांक <math>{-1}</math> का प्रयोग सामान्यतः प्रतिलोम फलन को निरूपित करने के लिए किया जाता है, पारस्परिक करने के लिए नहीं किया जाता है। उदाहरण  <math>\sin^{-1}x</math> और <math>\sin^{-1}(x)</math> प्रतिलोम त्रिकोणमितीय फलन को वैकल्पिक रूप से लिखे गए <math>\arcsin x\colon</math> को दर्शाते हैं: समीकरण <math>\theta = \sin^{-1}x</math> का तात्पर्य <math>\sin \theta = x</math> है, <math>\theta \cdot \sin x = 1</math> नहीं हैं। इस प्रकरण में, अधिलेख को एक रचित या पुनरावृत्त फलन को निरूपित करने के रूप में माना जा सकता है, लेकिन <math>{-1}</math> के अलावा अन्य नकारात्मक अधिलेख सामान्य प्रयोग में नहीं हैं।
+हालाँकि, घातांक <math>{-1}</math> का प्रयोग सामान्यतः प्रतिलोम फलन को निरूपित करने के लिए किया जाता है, पारस्परिक करने के लिए नहीं किया जाता है। उदाहरण  <math>\sin^{-1}x</math> और <math>\sin^{-1}(x)</math> प्रतिलोम त्रिकोणमितीय फलन को वैकल्पिक रूप से लिखे गए <math>\arcsin x\colon</math> को लक्षित करते हैं: समीकरण <math>\theta = \sin^{-1}x</math> का तात्पर्य <math>\sin \theta = x</math> है, <math>\theta \cdot \sin x = 1</math> नहीं हैं। इस प्रकरण में, अधिलेख को एक रचित या पुनरावृत्त फलन को निरूपित करने के रूप में माना जा सकता है, लेकिन <math>{-1}</math> के अलावा अन्य नकारात्मक अधिलेख सामान्य प्रयोग में नहीं हैं।
 == समकोण त्रिभुज की परिभाषाएँ ==
-[[File:TrigonometryTriangle.svg|thumb|इस समकोण त्रिभुज में, कोण BAC की माप को A के रूप में निरूपित करते हुए: {{math|1=sin ''A'' = {{sfrac|''a''|''c''}}}}; {{math|1=cos ''A'' = {{sfrac|''b''|''c''}}}}; {{math|1=tan ''A'' = {{sfrac|''a''|''b''}}}}.]]
+[[File:TrigonometryTriangle.svg|thumb|इस समकोण त्रिभुज में, कोण BAC की माप को A के रूप में निरूपित करते हुए:{{math|1=sin ''A'' = {{sfrac|''a''|''c''}}}}; {{math|1=cos ''A'' = {{sfrac|''b''|''c''}}}}; {{math|1=tan ''A'' = {{sfrac|''a''|''b''}}}}.]]
-[[File:TrigFunctionDiagram.svg|thumb|छह त्रिकोणमितीय फलनों का प्लॉट, इकाई वृत्त और कोण के लिए एक रेखा {{math|1=''θ'' = 0.7 radians}}. लेबल किए गए बिंदु {{color|#D00|1}}, {{color|#02D|Sec(''θ'')}}, {{color|#0D1|Csc(''θ'')}} मूल बिंदु से उस बिंदु तक रेखा खंड की लंबाई का प्रतिनिधित्व करते हैं। {{color|#D00|Sin(''θ'')}}, {{color|#02D|Tan(''θ'')}}, और {{color|#0D1|1}} से प्रारम्भ होने वाली रेखा की ऊँचाई हैं {{mvar|x}}-अक्ष, जबकि {{color|#D00|Cos(''θ'')}}, {{color|#02D|1}}, और {{color|#0D1|Cot(''θ'')}} लंबाई के साथ हैं {{mvar|x}}-अक्ष मूल से प्रारम्भ होता है।]]यदि न्यूनकोण {{mvar|θ}} दिया गया है, तो कोई भी समकोण त्रिभुज जिसका कोण {{mvar|θ}} है, एक दूसरे से समरूप होते हैं। इसका अर्थ है कि किन्हीं दो भुजाओं की लंबाई का अनुपात केवल {{mvar|θ}} पर निर्भर करता हैं। इस प्रकार ये छह अनुपात {{mvar|θ}} के छह फलनों को परिभाषित करते हैं, जो कि त्रिकोणमितीय फलन हैं। निम्नलिखित परिभाषाओं में, [[कर्ण]] समकोण के विपरीत भुजा की लंबाई है, विपरीत दिए गए कोण {{mvar|θ}} के विपरीत भुजा का प्रतिनिधित्व करता है, और आसन्न कोण {{mvar|θ}} और समकोण के मध्य की भुजा का प्रतिनिधित्व करता है।<ref>{{harvtxt|Protter|Morrey|1970|pp=APP-2, APP-3}}</ref><ref>{{Cite web|title=साइन, कोसाइन, स्पर्शरेखा|url=https://www.mathsisfun.com/sine-cosine-tangent.html|access-date=29 August 2020|website=www.mathsisfun.com}}</ref>
+[[File:TrigFunctionDiagram.svg|thumb|छह त्रिकोणमितीय फलनों का प्लॉट, इकाई वृत्त और कोण {{math|1=''θ'' = 0.7 radians}} के लिए एक रेखा है।  {{color|#D00|1}}, {{color|#02D|Sec(''θ'')}}, {{color|#0D1|Csc(''θ'')}} चिह्नित वाले बिंदु मूल से उस बिंदु तक रेखा खंड की लंबाई का प्रतिनिधित्व करते हैं। {{color|#D00|Sin(''θ'')}}, {{color|#02D|Tan(''θ'')}}, और {{color|#0D1|1}} {{mvar|x}}-अक्ष से प्रारम्भ होने वाली रेखा की ऊँचाई हैं, जबकि {{color|#D00|Cos(''θ'')}}, {{color|#02D|1}}, और {{color|#0D1|Cot(''θ'')}} मूल बिंदु से प्रारम्भ होने वाली {{mvar|x}}-अक्ष की लंबाई हैं। ]]यदि न्यूनकोण {{mvar|θ}} दिया गया है, तो कोई भी समकोण त्रिभुज जिसका कोण {{mvar|θ}} है, एक दूसरे से समरूप होते हैं। इसका अर्थ है कि किन्हीं दो भुजाओं की लंबाई का अनुपात केवल {{mvar|θ}} पर निर्भर करता हैं। इस प्रकार ये छह अनुपात {{mvar|θ}} के छह फलनों को परिभाषित करते हैं, जो कि त्रिकोणमितीय फलन हैं। निम्नलिखित परिभाषाओं में, [[कर्ण]] समकोण के विपरीत भुजा की लंबाई है, विपरीत दिए गए कोण {{mvar|θ}} के विपरीत भुजा का प्रतिनिधित्व करते है, और आसन्न कोण {{mvar|θ}} और समकोण के मध्य की भुजा का प्रतिनिधित्व करते है।<ref>{{harvtxt|Protter|Morrey|1970|pp=APP-2, APP-3}}</ref><ref>{{Cite web|title=साइन, कोसाइन, स्पर्शरेखा|url=https://www.mathsisfun.com/sine-cosine-tangent.html|access-date=29 August 2020|website=www.mathsisfun.com}}</ref>
 {|
 | style="padding-left: 2em; padding-right: 2em; |
@@ Line 34: / Line 34: @@
 ;cotangent: <math>\cot \theta = \frac \mathrm{adjacent}\mathrm{opposite}</math>
 |}
-एक समकोण त्रिभुज में, दो न्यून कोणों का योग समकोण होता है, अर्थात, {{math|90°}} या {{math|{{sfrac|π|2}} [[रेडियन]]}} होता है। इसलिए <math>\sin(\theta)</math> और <math>\cos(90^\circ - \theta)</math> समान अनुपात का प्रतिनिधित्व करते हैं, और इस प्रकार समान हैं। यह पहचान और अन्य त्रिकोणमितीय फलनों के मध्य समान संबंधों को निम्न तालिका में संक्षेपित किया गया है।
+एक समकोण त्रिभुज में, दो न्यून कोणों का योग समकोण होता है, अर्थात, {{math|90°}} या {{math|{{sfrac|π|2}} [[रेडियन]]}} होता है। इसलिए <math>\sin(\theta)</math> और <math>\cos(90^\circ - \theta)</math> समान अनुपात का प्रतिनिधित्व करते हैं, और इस प्रकार समान हैं। यह समरूपता और अन्य त्रिकोणमितीय फलनों के मध्य समान संबंधों को निम्न तालिका में संक्षेपित किया गया है।
-[[File:Periodic sine.PNG|thumb|शीर्ष: त्रिकोणमितीय फलन {{math|sin ''θ''}} चयनित कोणों के लिए {{math|''θ''}}, {{math|{{pi}} − ''θ''}}, {{math|{{pi}} + ''θ''}}, और {{math|2{{pi}} − ''θ''}} चार चतुर्भुजों में।<br>नीचे: ज्या फलन बनाम कोण का ग्राफ। शीर्ष पैनल के कोणों की पहचान की जाती है।]]
+[[File:Periodic sine.PNG|thumb|शीर्ष: त्रिकोणमितीय फलन {{math|sin ''θ''}} चयनित कोणों के लिए {{math|''θ''}}, {{math|{{pi}} − ''θ''}}, {{math|{{pi}} + ''θ''}}, और {{math|2{{pi}} − ''θ''}} चार चतुर्भुजों में है।<br>नीचे: ज्या फलन बनाम कोण का लेखाचित्र। शीर्ष सूची के कोणों की पहचान की जाती है।]]
 {| class="wikitable sortable"
@@ Line 80: / Line 80: @@
 == रेडियंस बनाम डिग्री ==
-ज्यामितीय अनुप्रयोगों में, त्रि[[कोण]]मितीय फलन का तर्क सामान्यतः एक कोण का माप होता है। इस प्रयोजन के लिए, कोई भी [[कोणीय इकाई]] उपयुक्त है। एक सामान्य इकाई [[डिग्री (कोण)|डिग्री]] है, जिसमें एक समकोण 90°और एक पूर्ण घूर्णन 360° होता है (विशेष रूप से प्राथमिक गणित में)।
+ज्यामितीय अनुप्रयोगों में, त्रिकोणमितीय फलन का तर्क सामान्यतः एक कोण का माप होता है। इस प्रयोजन के लिए, कोई भी [[कोणीय इकाई]] उपयुक्त है। एक सामान्य इकाई [[डिग्री (कोण)|डिग्री]] है, जिसमें एक समकोण 90°और एक पूर्ण घूर्णन 360° होता है (विशेष रूप से प्राथमिक गणित में)।
-हालांकि, गणना और [[गणितीय विश्लेषण]] में, त्रिकोणमितीय फलनों को सामान्यतः कोणों के बदले [[वास्तविक संख्या]] या [[जटिल संख्या|सम्मिश्र संख्याओं]] के फलनों के रूप में अधिक अमूर्त माना जाता है। वास्तव में, फलन sin और cos को सभी सम्मिश्र संख्याओं के लिए चरघातांकी फलन के संदर्भ में घात श्रृंखला के माध्यम से परिभाषित किया जा सकता है,<ref name=":0">{{Cite book|last=Rudin, Walter, 1921–2010|url=https://www.worldcat.org/oclc/1502474|title=गणितीय विश्लेषण के सिद्धांत|isbn=0-07-054235-X|edition=Third |location=New York|oclc=1502474}}</ref> <ref>{{Cite journal|last=Diamond|first=Harvey|date=2014|title=विभेदक समीकरणों का उपयोग करके घातीय और त्रिकोणमितीय कार्यों को परिभाषित करना|url=https://www.tandfonline.com/doi/full/10.4169/math.mag.87.1.37|journal=Mathematics Magazine|language=en|volume=87|issue=1|pages=37–42|doi=10.4169/math.mag.87.1.37|s2cid=126217060|issn=0025-570X}}</ref> या किसी भी ज्यामितीय धारणा के संदर्भ के बिना, विशेष प्रारंभिक मान दिए गए अंतर समीकरणों के समाधान के रूप में (नीचे देखें) किसी भी ज्यामितीय धारणाओं के संदर्भ के बिना है। अन्य चार त्रिकोणमितीय फलनों (tan, cot, sec, csc) को sin और cos के भागफल और व्युत्क्रम के रूप में परिभाषित किया जा सकता है,अतिरिक्त इसके कि जहाँ भाजक में शून्य होता है। वास्तविक तर्कों के लिए यह सिद्ध किया जा सकता है कि ये परिभाषाएँ प्रारंभिक ज्यामितीय परिभाषाओं के अनुरूप हैं यदि तर्क को रेडियन में दिए गए कोण के रूप में माना जाता है।<ref name=":0" /> इसके अलावा, इन परिभाषाओं के परिणामस्वरूप त्रिकोणमितीय फलनों के लिए [[यौगिक|व्युत्पन्न]] और [[antiderivative|अनिशिचित समाकल]] के लिए सरल अभिव्यक्तियां होती हैं।<ref name=":1">{{Cite book|last=Spivak|first=Michael|title=गणना|publisher=Addison-Wesley|year=1967|chapter=15|pages=256–257|lccn=67-20770}}</ref> इस प्रकार, प्रारंभिक ज्यामिति से अतिरिक्त समायोजन में, रेडियंस को कोण मापों का वर्णन करने के लिए गणितीय रूप से प्राकृतिक इकाई माना जाता है।
+हालांकि, गणना और [[गणितीय विश्लेषण]] में, त्रिकोणमितीय फलनों को सामान्यतः कोणों के बदले [[वास्तविक संख्या]] या [[जटिल संख्या|सम्मिश्र संख्याओं]] के फलनों के रूप में अधिक अमूर्त माना जाता है। वास्तव में, फलन sin और cos को सभी सम्मिश्र संख्याओं के लिए चरघातांकी फलन के संदर्भ में घात श्रृंखला के माध्यम से परिभाषित किया जा सकता है,<ref name=":0">{{Cite book|last=Rudin, Walter, 1921–2010|url=https://www.worldcat.org/oclc/1502474|title=गणितीय विश्लेषण के सिद्धांत|isbn=0-07-054235-X|edition=Third |location=New York|oclc=1502474}}</ref> <ref>{{Cite journal|last=Diamond|first=Harvey|date=2014|title=विभेदक समीकरणों का उपयोग करके घातीय और त्रिकोणमितीय कार्यों को परिभाषित करना|url=https://www.tandfonline.com/doi/full/10.4169/math.mag.87.1.37|journal=Mathematics Magazine|language=en|volume=87|issue=1|pages=37–42|doi=10.4169/math.mag.87.1.37|s2cid=126217060|issn=0025-570X}}</ref> या किसी भी ज्यामितीय धारणा के संदर्भ के बिना, विशेष प्रारंभिक मान दिए गए अंतर समीकरणों के समाधान के रूप में (नीचे देखें) किसी भी ज्यामितीय धारणाओं के संदर्भ के बिना है। अन्य चार त्रिकोणमितीय फलनों (tan, cot, sec, csc) को sin और cos के भागफल और व्युत्क्रम के रूप में परिभाषित किया जा सकता है, अतिरिक्त इसके कि जहाँ भाजक में शून्य होता है। वास्तविक तर्कों के लिए यह सिद्ध किया जा सकता है कि ये परिभाषाएँ प्रारंभिक ज्यामितीय परिभाषाओं के अनुरूप हैं यदि तर्क को रेडियन में दिए गए कोण के रूप में माना जाता है।<ref name=":0" /> इसके अलावा, इन परिभाषाओं के परिणामस्वरूप त्रिकोणमितीय फलनों के लिए [[यौगिक|व्युत्पन्न]] और [[antiderivative|अनिशिचित समाकल]] के लिए सरल अभिव्यक्तियां होती हैं।<ref name=":1">{{Cite book|last=Spivak|first=Michael|title=गणना|publisher=Addison-Wesley|year=1967|chapter=15|pages=256–257|lccn=67-20770}}</ref> इस प्रकार, प्रारंभिक ज्यामिति से अतिरिक्त समायोजन में, रेडियंस को कोण मापों का वर्णन करने के लिए गणितीय रूप से प्राकृतिक इकाई माना जाता है।
-जब [[कांति|रेडियन]] (रेड) लगाए जाते हैं, तो कोण को इसके द्वारा अंतरित इकाई वृत्त के [[चाप (ज्यामिति)]] की लंबाई के रूप में दिया जाता है: इकाई वृत्त पर लंबाई 1 के चाप को अंतरित करने वाला कोण 1 रेड (≈ 57.3°) और एक पूर्ण [[मोड़ (कोण)|घूर्णन]] (360°) 2{{pi}} (≈ 6.28) रेड का कोण है। वास्तविक संख्या x के लिए, चिह्न sin x, cos x, आदि x रेड के कोण पर मूल्यांकन किए गए त्रिकोणमितीय फलनों के मान को संदर्भित करते हैं। यदि डिग्री की इकाइयों का अभीष्ट है, तो डिग्री चिह्न स्पष्ट रूप से दिखाया जाना चाहिए (उदाहरण के लिए, sin x°, cos x°, आदि)। इस मानक संकेतन का उपयोग करते हुए, त्रिकोणमितीय फलनों के लिए तर्क x संबंध x = (180x/{{pi}}) °को संतुष्ट करता है, इसलिए, उदाहरण के लिए, sin π = sin 180° जब हम x = {{pi}} लेते है। इस प्रकार, डिग्री प्रतीक को गणितीय स्थिरांक के रूप में माना जा सकता है जैसे कि 1° = {{pi}}/180 ≈ 0.0175 है।
+जब [[कांति|रेडियन]] (रेड) लगाए जाते हैं, तो कोण को इसके द्वारा अंतरित इकाई वृत्त के [[चाप (ज्यामिति)|चाप कर्ण (ज्यामिति)]] की लंबाई के रूप में दिया जाता है: इकाई वृत्त पर लंबाई 1 के चाप कर्ण को अंतरित करने वाला कोण 1 रेड (≈ 57.3°) और एक पूर्ण [[मोड़ (कोण)|घूर्णन]] (360°) 2{{pi}} (≈ 6.28) रेड का कोण है। वास्तविक संख्या x के लिए, चिह्न sin x, cos x, आदि x रेड के कोण पर मूल्यांकन किए गए त्रिकोणमितीय फलनों के मान को संदर्भित करते हैं। यदि डिग्री की इकाइयों का अभीष्ट है, तो डिग्री चिह्न स्पष्ट रूप से दिखाया जाना चाहिए (उदाहरण के लिए, sin x°, cos x°, आदि)। इस मानक संकेतन का उपयोग करते हुए, त्रिकोणमितीय फलनों के लिए तर्क x संबंध x = (180x/{{pi}})° को संतुष्ट करता है, इसलिए, उदाहरण के लिए, sin π = sin 180° जब हम x = {{pi}} लेते है। इस प्रकार, डिग्री प्रतीक को गणितीय स्थिरांक के रूप में माना जा सकता है जैसे कि 1° = {{pi}}/180 ≈ 0.0175 है।
 == इकाई-वृत्त परिभाषाएँ ==
-[[File:Unit Circle Definitions of Six Trigonometric Functions.png|thumb|300x300px|इस उदाहरण में, एक स्वेच्छ कोण के छह त्रिकोणमितीय फलन {{math|''θ''}} इकाई वृत्त से संबंधित बिंदुओं के कार्टेशियन निर्देशांक के रूप में प्रतिनिधित्व किया जाता है। के निर्देशांक {{math|A}}, {{math|B}} और {{math|D}} हैं {{math|sin ''θ''}}, {{math|tan ''θ''}} और {{math|csc ''θ''}}, क्रमशः, जबकि के फरसा {{math|A}}, {{math|C}} और {{math|E}} हैं {{math|cos ''θ''}}, {{math|cot ''θ''}} और {{math|sec ''θ''}}, क्रमश।]]
+[[File:Unit Circle Definitions of Six Trigonometric Functions.png|thumb|300x300px|इस उदाहरण में, एक स्वेच्छ कोण {{math|''θ''}} के छह त्रिकोणमितीय फलानो को इकाई वृत्त से संबंधित बिंदुओं के कार्टेशियन निर्देशांक के रूप में प्रतिनिधित्व किया जाता है। {{math|A}}, {{math|B}} और {{math|D}} के निर्देशांक क्रमशः {{math|sin ''θ''}}, {{math|tan ''θ''}} और {{math|csc ''θ''}} हैं, जबकि {{math|A}}, {{math|C}} और {{math|E}} के भुज क्रमशः {{math|cos ''θ''}}, {{math|cot ''θ''}} और {{math|sec ''θ''}} हैं।]]
-[[File:trigonometric function quadrant sign.svg|thumb|प्रत्येक चतुर्थांश में त्रिकोणमितीय फलनों के संकेत। स्मरक सभी विज्ञान शिक्षक (हैं) पागल उन फलनों को सूचीबद्ध करते हैं जो चतुर्थांश I से IV तक सकारात्मक हैं।<ref name="Heng"/>यह स्मरक [[सभी छात्र कैलकुलस लेते हैं|सभी छात्र गणना लेते हैं]] का एक रूपांतर है।]]छह त्रिकोणमितीय फलनों को इकाई-वृत्त से संबंधित [[यूक्लिडियन विमान|यूक्लिडियन समतल]] बिंदुओं के समन्वय मूल्यों के रूप में परिभाषित किया जा सकता है, जो इस समन्वय प्रणाली के मूल {{math|O}} पर केंद्रित त्रिज्या का वृत्त है। जबकि समकोण त्रिभुज परिभाषाएँ | समकोण त्रिभुज परिभाषाएँ  {{math|0}} और <math display="inline">\frac{\pi}{2}</math> रेडियंस {{math|(90°)}} के मध्य के कोणों के लिए त्रिकोणमितीय फलनों की परिभाषा की अनुमति देती हैं, इकाई वृत्त परिभाषाएं त्रिकोणमितीय फलनों के प्रक्षेत्र को सभी सकारात्मक और नकारात्मक वास्तविक संख्याओं तक विस्तारित करने की अनुमति देती हैं।
+[[File:trigonometric function quadrant sign.svg|thumb|प्रत्येक चतुर्थांश में त्रिकोणमितीय फलनों के संकेत। स्मरक <nowiki>''</nowiki>सभी विज्ञान शिक्षक क्षीण (हैं) उन फलनों को सूचीबद्ध करता है जो चतुर्भुज I से IV तक सकारात्मक हैं।<ref name="Heng"/> यह स्मरक [[सभी छात्र कैलकुलस लेते हैं|सभी छात्र गणना लेते हैं]] का एक रूपांतर है।]]छह त्रिकोणमितीय फलनों को इकाई-वृत्त से संबंधित [[यूक्लिडियन विमान|यूक्लिडियन समतल]] बिंदुओं के समन्वय मूल्यों के रूप में परिभाषित किया जा सकता है, जो इस समन्वय प्रणाली के मूल {{math|O}} पर केंद्रित त्रिज्या का वृत्त है। जबकि समकोण त्रिभुज परिभाषाएँ {{math|0}} और <math display="inline">\frac{\pi}{2}</math> रेडियंस {{math|(90°)}} के मध्य के कोणों के लिए त्रिकोणमितीय फलनों की परिभाषा की अनुमति देती हैं, इकाई वृत्त परिभाषाएं त्रिकोणमितीय फलनों के प्रक्षेत्र को सभी सकारात्मक और नकारात्मक वास्तविक संख्याओं तक विस्तारित करने की अनुमति देती हैं।
-<math>\mathcal L</math> को  {{math|''x''}}-अक्ष के सकारात्मक आधे कोण {{mvar|θ}} द्वारा घूर्णन करके प्राप्त रे होने दें (<math>\theta > 0,</math> के लिए [[वामावर्त]] घूर्णन, और <math>\theta < 0</math> के लिए दक्षिणावर्त घूर्णन)। यह रे इकाई वृत्त को बिंदु <math>\mathrm{A} = (x_\mathrm{A},y_\mathrm{A})</math> पर प्रतिच्छेद हैं।  रे <math>\mathcal L,</math> यदि आवश्यक हो तो एक [[रेखा (ज्यामिति)|रेखा]] विस्तारित, समीकरण <math>x=1</math> की रेखा को बिंदु <math>\mathrm{B} = (1,y_\mathrm{B})</math>पर और समीकरण <math>y=1</math> की रेखा को बिंदु <math>\mathrm{C} = (x_\mathrm{C},1)</math> प्रतिच्छेद करती है। बिंदु {{math|A}} पर इकाई वृत्त की स्पर्श रेखा, <math>\mathcal L</math> के लंबवत है, और {{math|''y''}}- और {{math|''x''}}-अक्षों को बिंदु <math>\mathrm{D} = (0,y_\mathrm{D})</math> और <math>\mathrm{E} = (x_\mathrm{E},0)</math> प्रतिच्छेद करती है। इन बिंदुओं के निर्देशांक {{mvar|θ}} के किसी भी स्वेच्छ वास्तविक मूल्य के लिए सभी त्रिकोणमितीय फलनों के मान निम्नलिखित प्रकार से देते हैं।
+<math>\mathcal L</math> को  {{math|''x''}}-अक्ष के सकारात्मक आधे कोण {{mvar|θ}} द्वारा घूर्णन करके प्राप्त रे होने दें (<math>\theta > 0,</math> के लिए [[वामावर्त]] घूर्णन, और <math>\theta < 0</math> के लिए दक्षिणावर्त घूर्णन)। यह रे इकाई वृत्त को बिंदु <math>\mathrm{A} = (x_\mathrm{A},y_\mathrm{A})</math> पर प्रतिच्छेद हैं। रे <math>\mathcal L,</math> यदि आवश्यक हो तो एक [[रेखा (ज्यामिति)|रेखा]] विस्तारित, समीकरण <math>x=1</math> की रेखा को बिंदु <math>\mathrm{B} = (1,y_\mathrm{B})</math> पर और समीकरण <math>y=1</math> की रेखा को बिंदु <math>\mathrm{C} = (x_\mathrm{C},1)</math> प्रतिच्छेद करती है। बिंदु {{math|A}} पर इकाई वृत्त की स्पर्श रेखा, <math>\mathcal L</math> के लंबवत है, और {{math|''y''}}- और {{math|''x''}}-अक्षों को बिंदु <math>\mathrm{D} = (0,y_\mathrm{D})</math> और <math>\mathrm{E} = (x_\mathrm{E},0)</math> प्रतिच्छेद करती है। इन बिंदुओं के निर्देशांक {{mvar|θ}} के किसी भी स्वेच्छ वास्तविक मूल्य के लिए सभी त्रिकोणमितीय फलनों के मान निम्नलिखित प्रकार से देते हैं।
 त्रिकोणमितीय फलन {{math|cos}} और {{math|sin}} को क्रमशः बिंदु {{math|A}} के x- और y-निर्देशांक मान के रूप में परिभाषित किया गया हैं। अर्थात्,
 :<math>\cos \theta = x_\mathrm{A} \quad</math> और <math>\quad \sin \theta = y_\mathrm{A}.</math><ref>{{Cite web|url=https://www.encyclopediaofmath.org/index.php/Trigonometric_functions|title=त्रिकोणमितीय कार्य|last=Bityutskov|first=V.I.|date=7 February 2011|website=Encyclopedia of Mathematics|language=en|archive-url=https://web.archive.org/web/20171229231821/https://www.encyclopediaofmath.org/index.php/Trigonometric_functions|archive-date=29 December 2017|url-status=live|access-date=29 December 2017}}</ref>
-<math>0 \le \theta \le \pi/2</math>, श्रेणी में, यह परिभाषा समकोण त्रिभुज की परिभाषा के अनुरूप है, इकाई त्रिज्या {{math|OA}} को कर्ण के रूप में रखने के लिए समकोण त्रिभुज लेकर हैं। समीकरण <math>x^2+y^2=1</math> इकाई वृत्त पर सभी बिंदुओं <math>\mathrm{P} = (x,y)</math> के लिए है, कोज्या और ज्या की यह परिभाषा पाइथागोरस की पहचान को भी संतुष्ट करती है।
+<math>0 \le \theta \le \pi/2</math>, श्रेणी में, यह परिभाषा समकोण त्रिभुज की परिभाषा के अनुरूप है, इकाई त्रिज्या {{math|OA}} को कर्ण के रूप में रखने के लिए समकोण त्रिभुज हैं। समीकरण <math>x^2+y^2=1</math> इकाई वृत्त पर सभी बिंदुओं <math>\mathrm{P} = (x,y)</math> के लिए है, कोज्या और ज्या की यह परिभाषा पाइथागोरस की पहचान को भी संतुष्ट करती है।
 :<math>\cos^2\theta+\sin^2\theta=1.</math>
 अन्य त्रिकोणमितीय फलनों को इकाई वृत्त के रूप में पाया जा सकता है
 :<math>\tan \theta = y_\mathrm{B} \quad</math> और <math> \quad\cot \theta = x_\mathrm{C},</math>
 :<math>\csc \theta\ = y_\mathrm{D} \quad</math> और <math> \quad\sec \theta = x_\mathrm{E}.</math>
-पायथागॉरियन पहचान और ज्यामितीय प्रमाण विधियों को उपयोजित करके, इन परिभाषाओं को ज्या और कोज्या के संदर्भ में स्पर्शरेखा, कोटिस्पर्श, छेदक रेखा और व्युत्क्रमज्या की परिभाषाओं के अनुरूप के लिए आसानी से दिखाया जा सकता है, अर्थात
+पायथागॉरियन पहचान और ज्यामितीय प्रमाण विधियों को उपयोजित करके, इन परिभाषाओं को ज्या और कोज्या के संदर्भ में स्पर्शरेखा, कोटिस्पर्श, व्युत्क्रम कोटिज्या और व्युत्क्रमज्या की परिभाषाओं के अनुरूप के लिए आसानी से दिखाया जा सकता है, अर्थात
 : <math>\tan \theta =\frac{\sin \theta}{\cos\theta},\quad \cot\theta=\frac{\cos\theta}{\sin\theta},\quad \sec\theta=\frac{1}{\cos\theta},\quad \csc\theta=\frac{1}{\sin\theta}.</math>
-[[File:Trigonometric functions.svg|right|thumb|300px|लिंक ={{filepath:trigonometric_functions_derivation_animation.svg}}<nowiki/>त्रिकोणमितीय फलन:
+[[File:Trigonometric functions.svg|right|thumb|300px|त्रिकोणम<nowiki/>ितीय फलन:
-{{color|#00A|Sine}},
+{{color|#00A|ज्या}},
-{{color|#0A0|Cosine}},
+{{color|#0A0|कोज्या}},
-{{color|#A00|Tangent}},
+{{color|#A00|स्पर्शरेखा}},
-{{color|#00A|Cosecant (dotted)}},
+{{color|#00A|व्युत्क्रमज्या (बिंदुकित)}},
-{{color|#0A0|Secant (dotted)}},
+{{color|#0A0|छेदक रेखा (बिंदुकित)}},
-{{color|#A00|Cotangent (dotted)}}
+{{color|#A00|कोस्पर्शरेखा (बिंदुकित)}}
 – [{{filepath:trigonometric_functions_derivation_animation.svg}} एनीमेशन]]]क्योंकि <math>\pm2\pi</math> के कोण के घूर्णन से आकृति की स्थिति या आकार में कोई परिवर्तन नहीं होता है, बिंदु {{math|A}}, {{math|B}}, {{math|C}}, {{math|D}}, और {{math|E}} दो कोणों के लिए समान होते हैं जिनका अंतर <math>2\pi</math> का पूर्णांक गुणज होता है। इस प्रकार त्रिकोणमितीय फलन आवर्ती फलन हैं जिनकी अवधि <math>2\pi</math> है। अर्थात
 : <math> \sin\theta = \sin\left(\theta + 2 k \pi \right)\quad</math> और <math>\quad \cos\theta = \cos\left(\theta + 2 k \pi \right)</math>
-किसी भी कोण {{mvar|θ}} और किसी भी पूर्णांक {{mvar|k}} के लिए समानताएँ उपयोजित होती हैं। चार अन्य त्रिकोणमितीय फलनों के लिए भी यही यथार्थ है। चार चतुर्भुजों में ज्या, कोज्या, व्युत्क्रमज्या और छेदक रेखा के फलनों के संकेत और एकदिष्टता को देखकर, कोई यह दिखा सकता है कि <math>2\pi</math> सबसे छोटा मान है जिसके लिए वे आवर्ती हैं (अर्थात, <math>2\pi</math> इन फलनों की मौलिक अवधि है)। हालाँकि, एक कोण <math>\pi</math> द्वारा घूर्णन जाने के बाद, बिन्दु {{mvar|B}} और {{mvar|C}} पहले से ही अपनी मूल स्थिति में वापस आ जाते हैं, जिससे कि स्पर्शरेखा फलन और कोटिस्पर्श रेखा फलन में <math>\pi</math> की मौलिक अवधि होती हैं। अर्थात्,
+किसी भी कोण {{mvar|θ}} और किसी भी पूर्णांक {{mvar|k}} के लिए समानताएँ उपयोजित होती हैं। चार अन्य त्रिकोणमितीय फलनों के लिए भी यही यथार्थ है। चार चतुर्भुजों में ज्या, कोज्या, व्युत्क्रमज्या और व्युत्क्रम कोटिज्या के फलनों के संकेत और एकदिष्टता को देखकर, कोई यह दिखा सकता है कि <math>2\pi</math> सबसे छोटा मान है जिसके लिए वे आवर्ती हैं (अर्थात, <math>2\pi</math> इन फलनों की मौलिक अवधि है)। हालाँकि, एक कोण <math>\pi</math> द्वारा घूर्णन जाने के बाद, बिन्दु {{mvar|B}} और {{mvar|C}} पहले से ही अपनी मूल स्थिति में वापस आ जाते हैं, जिससे कि स्पर्शरेखा फलन और कोटिस्पर्श रेखा फलन में <math>\pi</math> की मौलिक अवधि होती हैं। अर्थात्,
 : <math> \tan\theta = \tan(\theta + k\pi) \quad</math> और <math>\quad \cot\theta = \cot(\theta + k\pi)</math>
 किसी भी कोण {{mvar|θ}} और किसी भी पूर्णांक {{mvar|k}} के लिए समानताएँ उपयोजित होती हैं।
@@ Line 124: / Line 124: @@
 :<math>\sin \frac\pi2 = \sin 90^\circ = \frac{\sqrt4}2 = 1</math> ([[समकोण]])
-अंशों को लगातार गैर-ऋणात्मक पूर्णांकों के [[वर्गमूल]] के रूप में लिखना, 2 के भाजक के साथ, मानों को याद रखने का एक आसान तरीका प्रदान करता है।<ref name="Larson_2013"/>
+अंशों को लगातार गैर-ऋणात्मक पूर्णांकों के [[वर्गमूल]] के रूप में लिखना, 2 के भाजक के साथ, मानों को याद रखने का एक आसान प्रकार प्रदान करता है।<ref name="Larson_2013"/>
 ऐसे सरल व्यंजक सामान्यतः अन्य कोणों के लिए उपस्तिथ नहीं होते हैं जो एक समकोण के परिमेय गुणज होते हैं।
-*ऐसे कोण के लिए, जो डिग्री में मापा जाता है, तीन का गुणक है, ज्या और कोज्या के [[सटीक त्रिकोणमितीय मान|यथार्थ त्रिकोणमितीय मान]] वर्गमूल के रूप में व्यक्त किए जा सकते हैं। इस प्रकार ज्या और कोज्या के ये मान मापक और परकारइस द्वारा निर्मित किए जा सकते हैं।
+*ऐसे कोण के लिए, जो डिग्री में मापा जाता है, तीन का गुणक है, ज्या और कोज्या के [[सटीक त्रिकोणमितीय मान|यथार्थ त्रिकोणमितीय मान]] वर्गमूल के रूप में व्यक्त किए जा सकते हैं। इस प्रकार ज्या और कोज्या के ये मान मापक और दिक्सूचक द्वारा निर्मित किए जा सकते हैं।
 *पूर्णांक संख्या के डिग्री के कोण के लिए, ज्या और कोज्या को वर्गमूल और गैर-वास्तविक सम्मिश्र संख्या के [[घनमूल]] के रूप में व्यक्त किया जा सकता है। [[गाल्वा सिद्धांत]] एक प्रमाण की अनुमति देता है कि, यदि कोण 3° का गुणक नहीं है, तो गैर-वास्तविक घनमूल अपरिहार्य हैं।
-*एक कोण के लिए, जो डिग्री में व्यक्त किया जाता है, एक परिमेय संख्या है, ज्या और कोज्या [[बीजगणितीय संख्या|बीजगणितीय संख्याएँ]] हैं, जिन्हें nवें मूल के रूप में व्यक्त किया जा सकता है। यह इस तथ्य से परिणामित होता है कि [[साइक्लोटोमिक बहुपद|साइक्लोटोमिक बहुपदों]] के [[गाल्वा समूह]] [[चक्रीय समूह|चक्रीय]] हैं।
+*एक कोण के लिए, जो डिग्री में व्यक्त किया जाता है, एक परिमेय संख्या है, ज्या और कोज्या [[बीजगणितीय संख्या|बीजगणितीय संख्याएँ]] हैं, जिन्हें nवें मूल के रूप में व्यक्त किया जा सकता है। यह इस तथ्य से परिणामित होता है कि [[साइक्लोटोमिक बहुपद|साइक्लोटोमिक बहुपदों]] के [[गाल्वा समूह]] [[चक्रीय समूह|वृत्तीय]] हैं।
 *एक कोण के लिए, जो डिग्री में व्यक्त किया जाता है, एक परिमेय संख्या नहीं है, तब या तो कोण या ज्या और कोज्या दोनों ही [[पारलौकिक संख्या|पारलौकिक संख्याएँ]] हैं। यह 1966 में सिद्ध हुई बेकर प्रमेय का परिणाम है।
@@ Line 190: / Line 190: @@
 == गणना ==
-[[file:Trigonometrija-graf.png|thumb|right|ज्या, कोज्या और स्पर्शरेखा के [[एक समारोह का ग्राफ|एक समारोह का आलेख]]]]
+[[file:Trigonometrija-graf.png|thumb|right|ज्या, कोज्या और स्पर्शरेखा के [[एक समारोह का ग्राफ|रेखांकन]]]]
-[[File:Taylorsine.svg|thumb|right|मूल पर केंद्रित एक पूर्ण चक्र के लिए ज्या समारोह (नीला) डिग्री 7 (गुलाबी) के टेलर के प्रमेय द्वारा बारीकी से अनुमानित है।]]
+[[File:Taylorsine.svg|thumb|right|मूल पर केंद्रित एक पूर्ण चक्र के लिए ज्या फलन (नीला) डिग्री 7 (गुलाबी) के टेलर के प्रमेय द्वारा ध्यानपूर्वक अनुमानित है।]]
-[[File:Taylor cos.gif|thumb|टेलर बहुपदों के माध्यम से कोज्या के सन्निकटन के लिए एनिमेशन।]]
+[[File:Taylor cos.gif|thumb|टेलर बहुपदों के माध्यम से कोज्या के सन्निकटन के लिए अनुप्राणन।]]
 [[File:Taylorreihenentwicklung des Kosinus.svg|thumb|<math>\cos(x)</math> पहले टेलर बहुपदों के साथ <math>p_n(x)=\sum_{k=0}^n (-1)^k \frac{x^{2k}}{(2k)!}</math>]]गणित में आधुनिक प्रवृत्ति विपरीत के बदले गणना से ज्यामिति का गठन करना है।{{citation needed|date=November 2020}} इसलिए, बहुत प्रारंभिक स्तर के अतिरिक्त, त्रिकोणमितीय फलनों को गणना की विधियों का उपयोग करके परिभाषित किया जाता है।
 त्रिकोणमितीय फलन हर उस बिंदु पर अवगणनाीय फलन और विश्लेषणात्मक होते हैं जहां उन्हें परिभाषित किया जाता है; अर्थात्, ज्या और कोज्या के लिए सर्वत्र, और स्पर्शरेखा के लिए, प्रत्येक पूर्णांक {{mvar|k}} के लिए {{math|{{pi}}/2 + ''k''{{pi}}}}  के अतिरिक्त सर्वत्र है।
-त्रिकोणमितीय फलन आवर्ती फलन हैं, और उनकी आधारी आवर्तक ज्या और कोज्या के लिए {{math|2{{pi}}}} है, और स्पर्शरेखा के लिए {{pi}} है, जो प्रत्येक विवृत अंतराल में बढ़ रही है {{math|({{pi}}/2 + ''k''{{pi}}, {{pi}}/2 + (''k'' + 1){{pi}})}}। इन अंतरालों के प्रत्येक अंत बिंदु पर, स्पर्शरेखा फलन में एक ऊर्ध्वाधर स्पर्शोन्मुख होता है।
+त्रिकोणमितीय फलन आवर्ती फलन हैं, और उनकी आधारी आवर्तक ज्या और कोज्या के लिए {{math|2{{pi}}}} है, और स्पर्शरेखा के लिए {{pi}} है, जो प्रत्येक विवृत अंतराल में {{math|({{pi}}/2 + ''k''{{pi}}, {{pi}}/2 + (''k'' + 1){{pi}})}} बढ़ रही है। इन अंतरालों के प्रत्येक अंत बिंदु पर, स्पर्शरेखा फलन में एक ऊर्ध्वाधर स्पर्शोन्मुख होता है।
 गणना में, त्रिकोणमितीय फलनों की दो समतुल्य परिभाषाएँ हैं, या तो घात श्रृंखला या अवकल समीकरणों का उपयोग करते हुए। ये परिभाषाएँ समतुल्य हैं, क्योंकि उनमें से एक से प्रारम्भ होकर, दूसरे को गुण के रूप में पुनः प्राप्त करना आसान है। हालाँकि अवकल समीकरणों के माध्यम से परिभाषा किसी तरह अधिक स्वाभाविक है, उदाहरण के लिए, घात श्रृंखला के गुणांकों का चयन अत्यंत स्वेच्छ लग सकता है, और पाइथागोरस की पहचान अवकल समीकरणों से निकालना बहुत आसान है।
@@ Line 210: / Line 210: @@
 :<math>\frac{d}{dx}\tan x = \frac{\cos^2 x + \sin^2 x}{\cos^2 x} = 1+\tan^2 x = \sec^2 x.</math>
 === घात श्रेणी विस्तार ===
-अनिश्चित गुणांकों वाली घात श्रृंखला में अवकल समीकरणों को उपयोजित करने पर, ज्या और कोज्या फलनों की [[टेलर श्रृंखला]] के गुणांकों के लिए [[पुनरावृत्ति संबंध]] प्राप्त किया जा सकता है। इन पुनरावर्तन संबंधों का समाधान करना आसान है, और श्रृंखला विस्तार प्रदान करते हैं<ref>See Ahlfors, pp. 43–44.</ref> :<math>
+अनिश्चित गुणांकों वाली घात श्रृंखला में अवकल समीकरणों को उपयोजित करने पर, ज्या और कोज्या फलनों की [[टेलर श्रृंखला]] के गुणांकों के लिए [[पुनरावृत्ति संबंध]] प्राप्त किया जा सकता है। इन पुनरावर्तन संबंधों का समाधान करना आसान है, और श्रृंखला विस्तार प्रदान करते हैं<ref>See Ahlfors, pp. 43–44.</ref>:<math>
 \begin{align}
 \sin x & = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\[6mu]
@@ Line 221: / Line 221: @@
 इन श्रृंखलाओं के [[अभिसरण की त्रिज्या]] अनंत है। इसलिए, ज्या और कोज्या को संपूर्ण फलनों (जिन्हें ज्या और कोज्या भी कहा जाता है) तक विस्तृत किया जा सकता है, जो कि (परिभाषा के अनुसार) [[जटिल-मूल्यवान कार्य|सम्मिश्र-मूल्यवान फलन]] हैं जो पूरे सम्मिश्र समतल पर परिभाषित और [[होलोमार्फिक|पूर्णसममितिक]] हैं।
-संपूर्ण फलनों के अंशों के रूप में परिभाषित होने के कारण, अन्य त्रिकोणमितीय फलनों को [[मेरोमॉर्फिक फ़ंक्शन|मेरोमॉर्फिक फलन]] तक विस्तृत किया जा सकता है, जो कि ऐसे फलन हैं जो पूरे सम्मिश्र समतल में पूर्णसममितिक होते हैं, कुछ वियुक्त बिंदुओं के अलावा जिन्हें [[शून्य और ध्रुव]] कहा जाता है। यहाँ, ध्रुव स्पर्शरेखा और छेदक रेखा के लिए <math display="inline">(2k+1)\frac \pi 2</math> के रूप की संख्याएँ हैं, या कोटिस्पर्श रेखा और व्युत्क्रमज्या के लिए <math>k\pi</math> हैं, जहाँ {{mvar|k}} एक स्वेच्छ पूर्णांक है।
+संपूर्ण फलनों के अंशों के रूप में परिभाषित होने के कारण, अन्य त्रिकोणमितीय फलनों को [[मेरोमॉर्फिक फ़ंक्शन|मेरोमॉर्फिक फलन]] तक विस्तृत किया जा सकता है, जो कि ऐसे फलन हैं जो पूरे सम्मिश्र समतल में पूर्णसममितिक होते हैं, कुछ वियुक्त बिंदुओं के अलावा जिन्हें [[शून्य और ध्रुव]] कहा जाता है। यहाँ, ध्रुव स्पर्शरेखा और व्युत्क्रम कोटिज्या के लिए <math display="inline">(2k+1)\frac \pi 2</math> के रूप की संख्याएँ हैं, या कोटिस्पर्श रेखा और व्युत्क्रमज्या के लिए <math>k\pi</math> हैं, जहाँ {{mvar|k}} एक स्वेच्छ पूर्णांक है।
 अन्य त्रिकोणमितीय फलनों की टेलर श्रृंखला के गुणांकों के लिए पुनरावृत्ति संबंधों की गणना भी की जा सकती है। इन श्रृंखलाओं में अभिसरण की परिमित त्रिज्या होती है। उनके गुणांकों की एक संयोजक व्याख्या है: वे परिमित समुच्चय के [[वैकल्पिक क्रमपरिवर्तन|वैकल्पिक क्रमपरिवर्तनों]] की गणना करते हैं।<ref>Stanley, Enumerative Combinatorics, Vol I., p. 149</ref>
@@ Line 277: / Line 277: @@
 \pi \cot \pi x = \frac{1}{x} + 2x\sum_{n=1}^\infty \frac{1}{x^2-n^2}.
 </math>
-इसी प्रकार, छेदक रेखा, व्युत्क्रमज्या और स्पर्शरेखा फलनों के लिए एक आंशिक भिन्न विस्तार कर सकते हैं:
+इसी प्रकार, व्युत्क्रम कोटिज्या, व्युत्क्रमज्या और स्पर्शरेखा फलनों के लिए एक आंशिक भिन्न विस्तार कर सकते हैं:
 :<math>
 \pi\csc\pi x = \sum_{n=-\infty}^\infty \frac{(-1)^n}{x+n}=\frac{1}{x} + 2x\sum_{n=1}^\infty \frac{(-1)^n}{x^2-n^2},
@@ Line 291: / Line 291: @@
 सम्मिश्र विश्लेषण में ज्या के लिए निम्नलिखित अनंत उत्पाद का बहुत महत्व है:
 :<math>\sin z = z \prod_{n=1}^\infty \left(1-\frac{z^2}{n^2 \pi^2}\right), \quad z\in\mathbb C.</math>
-इस विस्तार के प्रमाण के लिए, ज्या देखें। इससे यह अनुमान लगाना जा सकता है
+इस विस्तार के प्रमाण के लिए, ज्या देखें। इससे यह अनुमान लगाया जा सकता है
 :<math>\cos z = \prod_{n=1}^\infty \left(1-\frac{z^2}{(n-1/2)^2 \pi^2}\right), \quad z\in\mathbb C.</math>
 === चरघातांकी फलन से संबंध (यूलर का सूत्र) ===
-[[File:Sinus und Kosinus am Einheitskreis 3.svg|thumb|<math>\cos(\theta)</math> और <math>\sin(\theta)</math> का वास्तविक और काल्पनिक हिस्सा हैं <math>e^{i\theta}</math> क्रमश।]]यूलर का सूत्र ज्या और कोज्या को घातीय फलन से संबंधित करता है:
+[[File:Sinus und Kosinus am Einheitskreis 3.svg|thumb|<math>\cos(\theta)</math> और <math>\sin(\theta)</math> क्रमशः <math>e^{i\theta}</math> के वास्तविक और काल्पनिक भाग हैं।]]यूलर का सूत्र ज्या और कोज्या को घातीय फलन से संबंधित करता है:
 :<math> e^{ix}  = \cos x + i\sin x.</math>
 :यह सूत्र सामान्यतः {{mvar|x}} के वास्तविक मूल्यों के लिए माना जाता है, लेकिन यह सभी सम्मिश्र मूल्यों के लिए सही रहता है।
@@ Line 359: / Line 359: @@
 === समता ===
-कोज्या और छेदक रेखा सम फलन हैं; अन्य त्रिकोणमितीय फलन विषम फलन हैं। वह है:
+कोज्या और व्युत्क्रम कोटिज्या सम फलन हैं; अन्य त्रिकोणमितीय फलन विषम फलन हैं। वह है:
 :<math>\begin{align}
 \sin(-x) &=-\sin x\\
@@ Line 439: / Line 439: @@
 |<math>\cot x</math>||<math>-\csc^2 x = - 1 - \cot^2 x</math>||<math>\ln \left| \sin x \right| + C</math>
 |}
 वैकल्पिक रूप से, 'सह-फलन' के व्युत्पन्न को त्रिकोणमितीय सर्वसमिका और श्रृंखला नियम का उपयोग करके प्राप्त किया जा सकता है:
@@ Line 453: / Line 452: @@
 {{Main|प्रतिलोम त्रिकोणमितीय फलन}}
-त्रिकोणमितीय फलन आवर्ती होते हैं, और इसलिए अंतःक्षेपक नहीं होते हैं, इसलिए कठोरता से बोलते हुए, उनके पास प्रतिलोम फलन नहीं होता है। हालांकि, प्रत्येक अंतराल जिस पर एक त्रिकोणमितीय फलन [[मोनोटोनिक|एकदिष्‍ट]] होता है, एक प्रतिलोम फलन को परिभाषित कर सकता है, और यह प्रतिलोम त्रिकोणमितीय फलन को बहु-मूल्यवान फलन के रूप में परिभाषित करता है। एक सच्चे प्रतिलोम फलन को परिभाषित करने के लिए, किसी को प्रक्षेत्र को एक अंतराल तक सीमित करना चाहिए जहां फलन एकदिष्‍ट है, और इस प्रकार फलन द्वारा इस अंतराल से इसके प्रतिबिंब के लिए विशेषण है। इस अंतराल के लिए सामान्य विकल्प, जिसे [[प्रमुख मूल्य|प्रमुख मूल्यों]] का समुच्चय कहा जाता है, निम्नलिखित तालिका में दिया गया है। हमेशा की तरह, व्युत्क्रम त्रिकोणमितीय फलनों को फलन के नाम या इसके संक्षिप्त नाम से पहले पूर्वलग्‍न <nowiki>''चाप''</nowiki> के साथ दर्शाया जाता है।
+त्रिकोणमितीय फलन आवर्ती होते हैं, और इसलिए अंतःक्षेपक नहीं होते हैं, इसलिए कठोरता से बोलते हुए, उनके पास प्रतिलोम फलन नहीं होते है। हालांकि, प्रत्येक अंतराल जिस पर एक त्रिकोणमितीय फलन [[मोनोटोनिक|एकदिष्‍ट]] होता है, एक प्रतिलोम फलन को परिभाषित कर सकता है, और यह प्रतिलोम त्रिकोणमितीय फलन को बहु-मूल्यवान फलन के रूप में परिभाषित करता है। एक सच्चे प्रतिलोम फलन को परिभाषित करने के लिए, किसी को प्रक्षेत्र को एक अंतराल तक सीमित करना चाहिए जहां फलन एकदिष्‍ट है, और इस प्रकार फलन द्वारा इस अंतराल से इसके प्रतिबिंब के लिए विशेषण है। इस अंतराल के लिए सामान्य विकल्प, जिसे [[प्रमुख मूल्य|प्रमुख मूल्यों]] का समुच्चय कहा जाता है, निम्नलिखित तालिका में दिया गया है। हमेशा की तरह, व्युत्क्रम त्रिकोणमितीय फलनों को फलन के नाम या इसके संक्षिप्त नाम से पहले पूर्वलग्‍न <nowiki>''चाप कर्ण''</nowiki> के साथ दर्शाया जाता है।
 {| class="wikitable" style="text-align: center;"
 !फलन
@@ Line 472: / Line 471: @@
 | <math>y = \arccsc x</math> || <math>\csc y = x</math> || <math>x<-1 \text{ or } x>1</math> || <math display="inline">-\frac{\pi}{2} \le y \le \frac{\pi}{2},\; y \ne 0</math>
 |}
-अंकन {{math|sin<sup>−1</sup>}}, {{math|cos<sup>−1</sup>}}आदि प्राय: {{math|arcsin}} और {{math|arccos}} आदि के लिए उपयोग किए जाते हैं। जब इस संकेतन का उपयोग किया जाता है, तो प्रतिलोम फलनों को गुणात्मक व्युत्क्रमों के साथ अस्पष्ट किया जा सकता है। <nowiki>''आर्क'' पूर्वलग्‍न के साथ अंकन इस तरह के अस्पष्ट से परिहार जाता है, हालांकि आर्कसेकेंट के लिए ''</nowiki>[[arcsecond|आर्कसेक]]<nowiki>'' को ''आर्कसेकंड''</nowiki> के साथ भ्रमित किया जा सकता है।
+अंकन {{math|sin<sup>−1</sup>}}, {{math|cos<sup>−1</sup>}}आदि प्राय: {{math|arcsin}} और {{math|arccos}} आदि के लिए उपयोग किए जाते हैं। जब इस संकेतन का उपयोग किया जाता है, तो प्रतिलोम फलनों को गुणात्मक व्युत्क्रमों के साथ अस्पष्ट किया जा सकता है। <nowiki>''आर्क'' पूर्वलग्‍न के साथ अंकन इस तरह के अस्पष्ट से परिहार जाता है, हालांकि आर्कव्युत्क्रम कोटिज्या के लिए ''</nowiki>[[arcsecond|आर्कसेक]]<nowiki>'' को ''आर्कसेकंड''</nowiki> के साथ भ्रमित किया जा सकता है।
 ज्या और कोज्या की तरह, व्युत्क्रम त्रिकोणमितीय फलनों को भी अनंत श्रृंखला के संदर्भ में व्यक्त किया जा सकता है। उन्हें [[जटिल लघुगणक|सम्मिश्र लघुगणक]] के रूप में भी व्यक्त किया जा सकता है।
@@ Line 480: / Line 479: @@
 === त्रिभुज के कोण और भुजाएँ ===
-इस अनुभाग में {{mvar|A}}, {{mvar|B}}, {{mvar|C}} त्रिकोण के तीन (आंतरिक) कोणों को दर्शाते हैं, और {{mvar|a}}, {{mvar|b}}, {{mvar|c}} संबंधित विपरीत किनारों की लंबाई को दर्शाता है। वे विभिन्न सूत्र से संबंधित हैं, जिन्हें उनके द्वारा सम्मिलित त्रिकोणमितीय फलनों द्वारा नामित किया गया है।
+इस अनुभाग में {{mvar|A}}, {{mvar|B}}, {{mvar|C}} त्रिकोण के तीन (आंतरिक) कोणों को लक्षित करते हैं, और {{mvar|a}}, {{mvar|b}}, {{mvar|c}} संबंधित विपरीत किनारों की लंबाई को दर्शाते है। वे विभिन्न सूत्र से संबंधित हैं, जिन्हें उनके द्वारा सम्मिलित त्रिकोणमितीय फलनों द्वारा नामित किया गया है।
 ==== ज्या का नियम ====
@@ Line 497: / Line 496: @@
 कोज्या का नियम (कोज्या सूत्र या कोज्या नियम के रूप में भी जाना जाता है) पाइथागोरस प्रमेय का एक विस्तार है:
 <math display="block">c^2=a^2+b^2-2ab\cos C,</math>
-या समतुल्य,
+या समतुल्य,<math display="block">\cos C=\frac{a^2+b^2-c^2}{2ab}.</math>
-<math display="block">\cos C=\frac{a^2+b^2-c^2}{2ab}.</math>
 इस सूत्र में {{mvar|C}} पर कोण भुजा {{mvar|c}} के विपरीत है। इस प्रमेय को त्रिभुज को दो समकोण में विभाजित करके और पाइथागोरस प्रमेय का उपयोग करके सिद्ध किया जा सकता है।
@@ Line 522: / Line 520: @@
 === आवर्ती फलन ===
 [[File:Lissajous curve 5by4.svg|thumb|right|एक [[लिसाजस वक्र]], त्रिकोणमिति-आधारित फलन के साथ बनाई गई एक आकृति।]]
-[[File:Synthesis square.gif|thumb|340px|right|हार्मोनिक्स की बढ़ती संख्या के साथ एक [[स्क्वेर वेव|स्क्वेर तरंग]] के योगात्मक संश्लेषण का एक एनीमेशन]]
+[[File:Synthesis square.gif|thumb|340px|right|हार्मोनिक्स की बढ़ती संख्या के साथ एक [[स्क्वेर वेव|वर्ग तरंग]] के योगात्मक संश्लेषण का एक अनुप्राणन]]
-[[File:Sawtooth Fourier Animation.gif|thumb|280px|ज्यासॉइडल आधार फलन (नीचे) जोड़े जाने पर एक आरादंती  तरंग (शीर्ष) बना सकते हैं। सभी आधार फलनों में आरादंती  के नोड्स पर नोड्स होते हैं, और सभी मौलिक ({{math|1=''k'' = 1}}) अतिरिक्त नोड हैं। आरी के बारे में देखा गया दोलन जब {{mvar|k}} बड़ा है [[गिब्स घटना]] कहा जाता है]]भौतिकी में त्रिकोणमितीय फलन भी महत्वपूर्ण हैं। उदाहरण के लिए, ज्या और कोज्या फलन का उपयोग सरल हरात्मक गति का वर्णन करने के लिए किया जाता है, जो कई प्राकृतिक घटनाओं को प्रतिरूप करता है, जैसे किसी स्प्रिंग से जुड़े द्रव्यमान की गति और, छोटे कोणों के लिए, किसी डोरी से लटके द्रव्यमान की दोलन गति। ज्या और कोज्या फलन एकसमान वृत्तीय गति के एक आयामी प्रक्षेपण हैं।
+[[File:Sawtooth Fourier Animation.gif|thumb|280px|ज्यासॉइडल आधार फलन (नीचे) जोड़े जाने पर एक आरादंती तरंग (शीर्ष) बना सकते हैं। सभी आधार फलनों में आरादंती के नोड्स पर नोड्स होते हैं, और मूलभूत ({{math|1=''k'' = 1}}) अतिरिक्त नोड होते हैं। जब k बड़ा होता है तो आरादंत के बारे में देखा जाने वाला दोलन [[गिब्स घटना]] कहलाता है।]]भौतिकी में त्रिकोणमितीय फलन भी महत्वपूर्ण हैं। उदाहरण के लिए, ज्या और कोज्या फलन का उपयोग सरल हरात्मक गति का वर्णन करने के लिए किया जाता है, जो कई प्राकृतिक घटनाओं को प्रतिरूप करता है, जैसे किसी स्प्रिंग से जुड़े द्रव्यमान की गति और, छोटे कोणों के लिए, किसी डोरी से लटके द्रव्यमान की दोलन गति, ज्या और कोज्या फलन एकसमान वृत्तीय गति के एक आयामी प्रक्षेपण हैं।
 त्रिकोणमितीय फलन सामान्य आवर्ती फलनों के अध्ययन में भी उपयोगी सिद्ध होते हैं। आवर्ती फलनों के विशिष्ट तरंग प्रतिरूप आवर्ती घटनाओं जैसे ध्वनि या प्रकाश तरंगों के मॉडलिंग के लिए उपयोगी होते हैं।<ref name="Farlow_1993"/>
@@ Line 536: / Line 534: @@
 {{Main|त्रिकोणमिति का इतिहास}}
-जबकि त्रिकोणमिति के प्रारंभिक अध्ययन से पुरातनता का पता लगाया जा सकता है, त्रिकोणमितीय फलनों के रूप में वे आज उपयोग में हैं, मध्यकाल में विकसित किए गए थे। कॉर्ड फलन की खोज नाइसिया के [[हिप्पार्कस]] (180–125 बीसीई) और रोमन मिस्र के टॉलेमी (90-165 सीई) द्वारा की गई थी। ज्या और वर्साइन (1 - कोज्या) के फलनों को गुप्ता काल के  [[भारतीय खगोल विज्ञान]] ([[आर्यभटीय]], [[सूर्य सिद्धांत]]) में संस्कृत से अरबी और फिर अरबी से लैटिन में अनुवाद के माध्यम से उपयोग किए गए जया और कोटि-ज्या फलानो में खोजा जा सकता है।<ref name="Boyer_1991"/>(आर्यभट्ट की ज्या तालिका देखें।)
+जबकि त्रिकोणमिति के प्रारंभिक अध्ययन से पुरातनता का पता लगाया जा सकता है, त्रिकोणमितीय फलनों के रूप में वे आज उपयोग में हैं, मध्यकाल में विकसित किए गए थे। कॉर्ड फलन की खोज नाइसिया के [[हिप्पार्कस]] (180–125 बीसीई) और रोमन मिस्र के टॉलेमी (90-165 सीई) द्वारा की गई थी। ज्या और वर्साइन (1 - कोज्या) के फलनों को गुप्ता काल के [[भारतीय खगोल विज्ञान]] ([[आर्यभटीय]], [[सूर्य सिद्धांत]]) में संस्कृत से अरबी और फिर अरबी से लैटिन में अनुवाद के माध्यम से उपयोग किए गए जया और कोटि-ज्या फलानो में खोजा जा सकता है।<ref name="Boyer_1991"/>(आर्यभट्ट की ज्या तालिका देखें।)
+वर्तमान उपयोग में सभी छह त्रिकोणमितीय फलनों को 9वीं शताब्दी तक [[इस्लामी गणित]] में जाना जाता था, जैसा कि त्रिकोणों का समाधान करने में प्रयुक्त होने वाली त्रिभुज का नियम था।<ref name="Gingerich_1986"/> ज्या (जो भारतीय गणित से स्वीकृत किया गया था) के अपवाद के साथ, अन्य पांच आधुनिक त्रिकोणमितीय फलनों की खोज फ़ारसी और अरब गणितज्ञों द्वारा की गई, जिनमें कोज्या, स्पर्शरेखा, कोटिस्पर्श, व्युत्क्रम कोटिज्या और व्युत्क्रमज्या सम्मिलित हैं।<ref name="Gingerich_1986"/>अल-ख़्वारिज़्मी (सी.-780-850) ने ज्या, कोज्या और स्पर्शरेखाओं की सूची बनाईं। लगभग 830, [[हबश अल-हकूब अल-मरवाज़ी]] ने कोटिस्पर्श रेखा की खोज की, और स्पर्शरेखा और कॉटैंगेंट की सूची प्रस्तुत की थी।<ref name="Sesiano">Jacques Sesiano, "Islamic mathematics", p. 157, in {{Cite book |title=Mathematics Across Cultures: The History of Non-western Mathematics |editor1-first=Helaine |editor1-last=Selin |editor1-link=Helaine Selin |editor2-first=Ubiratan |editor2-last=D'Ambrosio |editor2-link=Ubiratan D'Ambrosio |year=2000 |publisher=[[Springer Science+Business Media]] |isbn=978-1-4020-0260-1}}</ref><ref name="Britannica">{{cite web |title=त्रिकोणमिति|url=http://www.britannica.com/EBchecked/topic/605281/त्रिकोणमिति|publisher=Encyclopedia Britannica}}</ref> मुहम्मद इब्न जाबिर अल-हररानी अल-बट्टानी (853–929) ने व्युत्क्रम कोटिज्या और व्युत्क्रमज्या के पारस्परिक फलनों की खोज की, और 1° से 90° तक प्रत्येक डिग्री के लिए व्युत्क्रमज्या की पहली तालिका प्रस्तुत की थी।<ref name="Britannica"/>बाद में ओमर खय्याम, भास्कर II, [[नासिर अल-दीन अल-तुसी]], जमशेद अल-काशी (14वीं सदी), [[उलूग बेग]] (14वीं सदी), [[रेजीओमोंटानस]] (1464), और [[जॉर्ज जोआचिम रेटिकस]] के छात्र सहित गणितज्ञों द्वारा त्रिकोणमितीय फलनों का अध्ययन किया गया।
+संगमग्राम के माधव (सी। 1400) ने श्रृंखला के संदर्भ में त्रिकोणमितीय फलनों के गणितीय विश्लेषण में पूर्व प्रगति की थी।<ref name="mact-biog"/>([[माधव श्रृंखला]] और माधव की ज्या तालिका देखें।)
-वर्तमान उपयोग में सभी छह त्रिकोणमितीय फलनों को 9वीं शताब्दी तक [[इस्लामी गणित]] में जाना जाता था, जैसा कि त्रिकोणों को हल करने में इस्तेमाल होने वाली ज्याओं का नियम था।<ref name="Gingerich_1986"/>ज्या (जो भारतीय गणित से अपनाया गया था) के अपवाद के साथ, अन्य पांच आधुनिक त्रिकोणमितीय फलनों की खोज फ़ारसी और अरब गणितज्ञों द्वारा की गई, जिनमें कोज्या, स्पर्शरेखा, कोटिस्पर्श, छेदक रेखा और व्युत्क्रमज्या सम्मिलित हैं।<ref name="Gingerich_1986"/>अल-ख़्वारिज़्मी (सी.-780-850) ने ज्या, कोज्या और स्पर्शरेखाओं की सारणियाँ बनाईं। लगभग 830, [[हबश अल-हकूब अल-मरवाज़ी]] ने कोटिस्पर्श रेखा की खोज की, और टेंगेंट और कॉटैंगेंट की टेबल तैयार की।<ref name="Sesiano">Jacques Sesiano, "Islamic mathematics", p. 157, in {{Cite book |title=Mathematics Across Cultures: The History of Non-western Mathematics |editor1-first=Helaine |editor1-last=Selin |editor1-link=Helaine Selin |editor2-first=Ubiratan |editor2-last=D'Ambrosio |editor2-link=Ubiratan D'Ambrosio |year=2000 |publisher=[[Springer Science+Business Media]] |isbn=978-1-4020-0260-1}}</ref><ref name="Britannica">{{cite web |title=त्रिकोणमिति|url=http://www.britannica.com/EBchecked/topic/605281/त्रिकोणमिति|publisher=Encyclopedia Britannica}}</ref> मुहम्मद इब्न जाबिर अल-हररानी अल-बट्टानी (853–929) ने छेदक रेखा और व्युत्क्रमज्या के पारस्परिक फलनों की खोज की, और 1° से 90° तक प्रत्येक डिग्री के लिए व्युत्क्रमज्या की पहली तालिका तैयार की।<ref name="Britannica"/>बाद में ओमर खय्याम, भास्कर II, [[नासिर अल-दीन अल-तुसी]], जमशेद अल-काशी (14वीं सदी), [[उलूग बेग]] (14वीं सदी), [[रेजीओमोंटानस]] (1464), और [[जॉर्ज जोआचिम रेटिकस]] के छात्र सहित गणितज्ञों द्वारा त्रिकोणमितीय फलनों का अध्ययन किया गया। [[वेलेंटाइन ओथो]]
+में [[Giovanni Bianchini|जियोवन्नी बियांचिनी]] द्वारा तारकीय निर्देशांक की गणना का समर्थन करने के लिए बनाई गई त्रिकोणमिति तालिकाओं में स्पर्शरेखा फलन यूरोप में लाया गया था।<ref>{{cite journal | url=https://www.jstor.org/stable/45211959 | jstor=45211959 | title=एक त्रुटि का अंत: बियांचिनी, रेजीओमोंटानस, और तारकीय निर्देशांक का सारणीकरण| last1=Van Brummelen | first1=Glen | journal=Archive for History of Exact Sciences | year=2018 | volume=72 | issue=5 | pages=547–563 | doi=10.1007/s00407-018-0214-2 | s2cid=240294796 }}</ref>
-संगमग्राम के माधव (सी। 1400) ने श्रृंखला (गणित) के संदर्भ में त्रिकोणमितीय फलनों के गणितीय विश्लेषण में शुरुआती प्रगति की।<ref name="mact-biog"/>([[माधव श्रृंखला]] और माधव की ज्या तालिका देखें।)
+स्पर्शरेखा और व्युत्क्रम कोटिज्या शब्द पहली बार डेनिश गणितज्ञ [[थॉमस फिनके]] ने अपनी पुस्तक जियोमेट्रिया रोटुंडी (1583) में प्रस्तावित किए थे।<ref name="Fincke" />
-में [[Giovanni Bianchini]] द्वारा तारकीय निर्देशांक की गणना का समर्थन करने के लिए बनाई गई त्रिकोणमिति तालिकाओं में स्पर्शरेखा समारोह यूरोप में लाया गया था।<ref>{{cite journal | url=https://www.jstor.org/stable/45211959 | jstor=45211959 | title=एक त्रुटि का अंत: बियांचिनी, रेजीओमोंटानस, और तारकीय निर्देशांक का सारणीकरण| last1=Van Brummelen | first1=Glen | journal=Archive for History of Exact Sciences | year=2018 | volume=72 | issue=5 | pages=547–563 | doi=10.1007/s00407-018-0214-2 | s2cid=240294796 }}</ref> टेंगेंट और सेकेंट शब्द पहली बार डेनिश गणितज्ञ [[थॉमस फिनके]] ने अपनी पुस्तक जियोमेट्रिया रोटुंडी (1583) में पेश किए थे।<ref name="Fincke"/>
+वीं शताब्दी के फ्रांसीसी गणितज्ञ [[अल्बर्ट गिरार्ड]] ने अपनी पुस्तक त्रिकोणमिति में सिन, कॉस और टैन संक्षिप्त रूपों का पहला प्रकाशित उपयोग किया।<ref name="MacTutor">{{MacTutor|id=Girard_Albert}}</ref>
-वीं सदी के फ्रांसीसी गणितज्ञ [[अल्बर्ट गिरार्ड]] ने अपनी पुस्तक त्रिकोणमिति में पाप, कॉस और टैन संक्षिप्त रूपों का पहला प्रकाशित उपयोग किया।<ref name=MacTutor>{{MacTutor|id=Girard_Albert}}</ref>
+में प्रकाशित एक पत्र में [[गॉटफ्रीड लीबनिज]] ने यह सिद्ध किया कि {{math|sin ''x''}} {{mvar|x}} का बीजगणितीय फलन नहीं है।<ref name="Bourbaki_1994" /> यद्यपि एक समकोण त्रिभुज की भुजाओं के अनुपात के रूप में प्रस्तावित किया गया, और इस प्रकार [[तर्कसंगत कार्य|तर्कसंगत फलनों]] के रूप में प्रकट होता है, लीबनिट्ज परिणाम ने स्थापित किया कि वे वास्तव में उनके तर्क के अबीजीय फलन हैं। वृत्तीय फलनों को बीजगणितीय व्यंजकों में समावेश करने का फलन यूलर द्वारा अनंत के विश्लेषण के अपने परिचय (1748) में पूरा किया गया था। उनकी विधि यह दिखाने के लिए थी कि ज्या और कोज्या फलन घातांक श्रृंखला के क्रमशः सम और विषम शब्दों से बनने वाली प्रत्यावर्ती श्रृंखला हैं। उन्होंने <nowiki>''</nowiki>यूलर के सूत्र<nowiki>''</nowiki>, साथ ही निकट-आधुनिक संक्षिप्ताक्षर (sin., cos., tang., cot., sec., और cosec.) प्रस्तुत किए।<ref name="Boyer_1991" />
-में प्रकाशित एक पत्र में [[गॉटफ्रीड लीबनिज]] ने यह साबित किया {{math|sin ''x''}} का बीजगणितीय फलन नहीं है {{mvar|x}}.<ref name="Bourbaki_1994"/>यद्यपि एक समकोण त्रिभुज की भुजाओं के अनुपात के रूप में पेश किया गया, और इस प्रकार [[तर्कसंगत कार्य|तर्कसंगत फलन]]ों के रूप में प्रकट होता है, लीबनिट्ज परिणाम ने स्थापित किया कि वे वास्तव में उनके तर्क के पारलौकिक फलन हैं। चक्रीय फलनों को बीजगणितीय व्यंजकों में आत्मसात करने का फलन यूलर द्वारा अनंत के विश्लेषण के अपने परिचय (1748) में पूरा किया गया था। उनकी विधि यह दिखाने के लिए थी कि ज्या और कोज्या फलन घातीय फलन के क्रमशः सम और विषम पदों से बनने वाली प्रत्यावर्ती श्रृंखला हैं। उन्होंने यूलर के सूत्र के साथ-साथ निकट-आधुनिक संक्षिप्त रूपों (sin., cos., tang., cot., sec., और cosec.) को प्रस्तुत किया।<ref name="Boyer_1991"/>
-कुछ फलन ऐतिहासिक रूप से सामान्य थे, लेकिन अब शायद ही कभी इसका उपयोग किया जाता है, जैसे कि राग (ज्यामिति), छंद (जो सबसे शुरुआती तालिकाओं में दिखाई देता है)<ref name="Boyer_1991"/>), [[कवरसाइन|कवरज्या]], [[haversine]],<ref>{{harvtxt|Nielsen|1966|pp=xxiii–xxiv}}</ref> [[exsecant]] और [[excosecant]]। त्रिकोणमितीय सर्वसमिकाओं की सूची इन फलनों के मध्य अधिक संबंध दर्शाती है।
+कुछ फलन ऐतिहासिक रूप से सामान्य थे, लेकिन अब सम्भावित ही कभी इसका उपयोग किया जाता है, जैसे कि तार, वरसाइन (जो सबसे पूर्वतर तालिकाओं में दिखाई देता है)<ref name="Boyer_1991" />), [[कवरसाइन|कवरज्या]], [[haversine|हावेरसिन]],<ref>{{harvtxt|Nielsen|1966|pp=xxiii–xxiv}}</ref> [[exsecant|एक्ससेकेंट]] और [[excosecant|एक्सोसेकेंट]] है। त्रिकोणमितीय सर्वसमिकाओं की सूची इन फलनों के मध्य अधिक संबंध सिध्द करती है।
 * {{math|1=crd(''θ'') = 2 sin({{sfrac|''θ''|2}})}}
@@ Line 555: / Line 556: @@
 * {{math|1=exsec(''θ'') = sec(''θ'') − 1}}
 * {{math|1=excsc(''θ'') = exsec({{sfrac|{{pi}}|2}} − ''θ'') = csc(''θ'') − 1}}
-== व्युत्पत्ति ==
+== व्युत्पत्ति विज्ञान ==
-{{main|History of trigonometry#Etymology}}
+{{main|त्रिकोणमिति का इतिहास#व्युत्पत्ति विज्ञान}}
-शब्द {{Lang|la-x-medieval|sine}} व्युत्पन्न<ref>The anglicized form is first recorded in 1593 in [[Thomas Fale]]'s ''Horologiographia, the Art of Dialling''.</ref> [[लैटिन]] शब्द से: ज्यास, जिसका अर्थ है झुकना; बे, और अधिक विशेष रूप से एक [[टोगा]] के ऊपरी हिस्से की लटकती हुई तह, एक परिधान की छाती, जिसे अरबी शब्द जैब के रूप में व्याख्या के रूप में चुना गया था, जिसका अर्थ है कि काम के बारहवीं शताब्दी के अनुवादों में पॉकेट या फोल्ड [[मध्यकालीन लैटिन]] में अल-बट्टानी और मुहम्मद इब्न मूसा अल-ख़्वारिज़्मी द्वारा।<ref>Various sources credit the first use of {{Lang|la-x-medieval|sinus}} to either
+ज्या शब्द <ref>The anglicized form is first recorded in 1593 in [[Thomas Fale]]'s ''Horologiographia, the Art of Dialling''.</ref> [[लैटिन]] साइनस से निकला है: जिसका अर्थ है "बेंड; बे", और अधिक विशेष रूप से <nowiki>''</nowiki>एक [[टोगा]] के ऊपरी भाग की निलम्बी हुई तह<nowiki>'', ''एक परिधान की बोसोम''</nowiki>, जिसे अरबी शब्द जैब के रूप में व्याख्या किए गए अनुवाद के रूप में चयन किया गया था, [[मध्यकालीन लैटिन]] में अल-बट्टानी और मुहम्मद इब्न मूसा अल-ख़्वारिज़्मी द्वारा किए गए कार्यों के बारहवीं शताब्दी के अनुवाद में "पॉकेट" या "फोल्ड" का अर्थ है।<ref>Various sources credit the first use of {{Lang|la-x-medieval|sinus}} to either
 * [[Plato Tiburtinus]]'s 1116 translation of the ''Astronomy'' of [[Al-Battani]]
 * [[Gerard of Cremona]]'s translation of the ''Algebra'' of [[Muḥammad ibn Mūsā al-Khwārizmī|al-Khwārizmī]]
 * [[Robert of Chester]]'s 1145 translation of the tables of al-Khwārizmī
-See Merlet, [https://link.springer.com/chapter/10.1007/1-4020-2204-2_16#page-1 ''A Note on the History of the Trigonometric Functions''] in Ceccarelli (ed.), ''International Symposium on History of Machines and Mechanisms'', Springer, 2004<br>See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.<br>See {{cite book |last=Katx |first=Victor |date=July 2008 |title=A history of mathematics |edition=3rd |location=Boston |publisher=[[Pearson (publisher)|Pearson]] |page=210 (sidebar) |isbn= 978-0321387004 |language=en }}</ref>
+See Merlet, [https://link.springer.com/chapter/10.1007/1-4020-2204-2_16#page-1 ''A Note on the History of the Trigonometric Functions''] in Ceccarelli (ed.), ''International Symposium on History of Machines and Mechanisms'', Springer, 2004<br>See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.<br>See {{cite book |last=Katx |first=Victor |date=July 2008 |title=A history of mathematics |edition=3rd |location=Boston |publisher=[[Pearson (publisher)|Pearson]] |page=210 (sidebar) |isbn= 978-0321387004 |language=en }}</ref> यह विकल्प अरबी लिखित रूप ''j-y-b'' (جيب) के गलत अर्थ पर आधारित था, जो स्वयं संस्कृत जिवा से एक [[लिप्यंतरण]] के रूप में उत्पन्न हुआ था, जो इसके पर्यायवाची {{IAST|jyā}} (ज्या के लिए मानक संस्कृत शब्द) के साथ "धनुर्ज्या " में अनुवाद करता है, जिसे प्राचीन ग्रीक {{lang|grc|[[Chord (geometry)|χορδή]]}} "तंतु" से अपनाया गया है।<ref name="Plofker_2009"/>
-यह चुनाव अरबी लिखित रूप j-y-b () की गलत व्याख्या पर आधारित था।{{lang|ar|[[:wikt:جيب|جيب]]}}), जिसकी उत्पत्ति स्वयं संस्कृत से [[लिप्यंतरण]] के रूप में हुई थी{{IAST|jīvā}}, जो इसके पर्यायवाची के साथ{{IAST|jyā}}(ज्या के लिए मानक संस्कृत शब्द) का अनुवाद बॉलिंग में होता है, जिसे प्राचीन ग्रीक भाषा से अपनाया जाता है {{lang|grc|[[Chord (geometry)|χορδή]]}} डोरी ।<ref name="Plofker_2009"/>
-टेंगेंट शब्द लैटिन टैंगेंस से आया है जिसका अर्थ है स्पर्श करना, चूंकि रेखा इकाई त्रिज्या के वृत्त को छूती है, जबकि सेकेंट लैटिन सेकान से उत्पन्न होता है- कटिंग-चूंकि रेखा वृत्त को काटती है।<ref>Oxford English Dictionary</ref>
+स्पर्शरेखा शब्द लैटिन टैंगेंस से आया है जिसका अर्थ है <nowiki>''</nowiki>संस्पर्श<nowiki>''</nowiki>, क्योंकि रेखा इकाई त्रिज्या के वृत्त को स्पर्श करती है, जबकि व्युत्क्रम कोटिज्या लैटिन सेकान से उत्पन्न होता है- "काटना"- क्योंकि रेखा वृत्त को काटती है।<ref>Oxford English Dictionary</ref>
-पूर्वलग्‍न सह (फलन प्रीफ़िक्स)|सह- (cosine में, cotangent, cosecant) [[एडमंड गुंटर]] के कैनन त्रिकोणीय (1620) में पाया जाता है, जो कोसिनस को ज्यास पूरक ([[पूरक कोण]] की ज्या) के संक्षिप्त नाम के रूप में परिभाषित करता है और आगे बढ़ता है cotangens को इसी तरह परिभाषित करें।<ref name="Gunter_1620"/><ref name="Roegel_2010"/>
+उपसर्ग सह- (कोज्या में, कोटिस्पर्श रेखा, व्युत्क्रम ज्या) [[एडमंड गुंटर]] के कैनन त्रिकोणीय (1620) में पाया जाता है, जो कोसिनस को साइनस पूरक ([[पूरक कोण]] की ज्या) के संक्षिप्त नाम के रूप में परिभाषित करता है और इसी तरह कोटांगेंस को परिभाषित करने के लिए आगे बढ़ता है।<ref name="Gunter_1620" /><ref name="Roegel_2010" />
 == यह भी देखें ==
 {{colbegin|colwidth=25em}}
-* सभी छात्र कैलकुलस लेते हैं - एक कार्तीय तल के एक विशेष चतुर्भुज में त्रिकोणमितीय कार्यों के संकेतों को याद करने के लिए एक स्मरक
+* सभी छात्र गणना लेते हैं - एक कार्तीय तल के एक विशेष चतुर्भुज में त्रिकोणमितीय फलानो के संकेतों को याद करने के लिए एक स्मरक
 * भास्कर प्रथम का ज्या सन्निकटन सूत्र
-* [[त्रिकोणमितीय कार्यों का विभेदन]]
+* [[त्रिकोणमितीय फलानो का विभेदन]]
 * [[सामान्यीकृत त्रिकोणमिति]]
 * [[त्रिकोणमितीय तालिकाएँ बनाना]]
-* अतिशयोक्तिपूर्ण समारोह
+* अतिशयोक्तिपूर्ण फलान
-* [[त्रिकोणमितीय कार्यों के इंटीग्रल की सूची]]
+* [[त्रिकोणमितीय फलानो के समाकलन  की सूची]]
-* [[आवधिक कार्यों की सूची]]
+* [[आवधिक फलानो की सूची]]
-* त्रिकोणमितीय पहचान की सूची
+* त्रिकोणमितीय सर्वसमिका की सूची
 * ध्रुवीय ज्या - शीर्ष कोणों के लिए एक सामान्यीकरण
 * त्रिकोणमितीय सर्वसमिकाओं के प्रमाण
-* वर्साइन - कई कम उपयोग किए जाने वाले त्रिकोणमितीय कार्यों के लिए
+* वर्साइन - कई कम उपयोग किए जाने वाले त्रिकोणमितीय फलानो के लिए
 {{colend}}
@@ Line 647: / Line 649: @@
 [[श्रेणी:आयामहीन संख्या]]
+[[Category:All articles with unsourced statements|Trigonometric Functions]]
-[[Category: Machine Translated Page]]
+[[Category:Articles containing Ancient Greek (to 1453)-language text|Trigonometric Functions]]
-[[Category:Created On 17/12/2022]]
+[[Category:Articles containing Medieval Latin-language text]]
+[[Category:Articles with hatnote templates targeting a nonexistent page|Trigonometric Functions]]
+[[Category:Articles with unsourced statements from November 2020|Trigonometric Functions]]
+[[Category:CS1 Deutsch-language sources (de)]]
+[[Category:CS1 English-language sources (en)]]
+[[Category:CS1 maint]]
+[[Category:Citation Style 1 templates|M]]
+[[Category:Collapse templates|Trigonometric Functions]]
+[[Category:Created On 17/12/2022|Trigonometric Functions]]
+[[Category:Lua-based templates|Trigonometric Functions]]
+[[Category:Machine Translated Page|Trigonometric Functions]]
+[[Category:Mathematics sidebar templates|Trigonometric Functions]]
+[[Category:Multi-column templates|Trigonometric Functions]]
+[[Category:Navigational boxes| ]]
+[[Category:Navigational boxes without horizontal lists|Trigonometric Functions]]
+[[Category:Pages using div col with small parameter|Trigonometric Functions]]
+[[Category:Pages with broken file links|Trigonometric Functions]]
+[[Category:Pages with maths render errors|Trigonometric Functions]]
+[[Category:Pages with script errors|Trigonometric Functions]]
+[[Category:Sidebars with styles needing conversion|Trigonometric Functions]]
+[[Category:Template documentation pages|Documentation/doc]]
+[[Category:Templates Vigyan Ready|Trigonometric Functions]]
+[[Category:Templates based on the Citation/CS1 Lua module]]
+[[Category:Templates generating COinS|Cite magazine]]
+[[Category:Templates generating microformats|Trigonometric Functions]]
+[[Category:Templates that add a tracking category|Trigonometric Functions]]
+[[Category:Templates that are not mobile friendly|Trigonometric Functions]]
+[[Category:Templates that generate short descriptions|Trigonometric Functions]]
+[[Category:Templates using TemplateData|Trigonometric Functions]]
+[[Category:Templates using under-protected Lua modules|Trigonometric Functions]]
+[[Category:Webarchive template wayback links|Trigonometric Functions]]
+[[Category:Wikipedia fully protected templates|Div col]]
+[[Category:Wikipedia metatemplates|Trigonometric Functions]]

Anonymous

Search

त्रिकोणमितीय फलन: Difference between revisions

Latest revision as of 15:49, 17 October 2023

संकेतन

समकोण त्रिभुज की परिभाषाएँ

रेडियंस बनाम डिग्री

इकाई-वृत्त परिभाषाएँ

बीजगणितीय मान

सरल बीजगणितीय मान

गणना

अंतर समीकरणों द्वारा परिभाषा

घात श्रेणी विस्तार

निरंतर भिन्न विस्तार

आंशिक भिन्न विस्तार

अनंत उत्पाद विस्तार

चरघातांकी फलन से संबंध (यूलर का सूत्र)

फलनिक समीकरण का उपयोग करके परिभाषाएं

सम्मिश्र समतल में

मूल सर्वसमिका

समता

अवधि

पायथागॉरियन सर्वसमिका

योग और अंतर सूत्र

व्युत्पन्न और एंटीडेरिवेटिव्स

प्रतिलोम फलन

अनुप्रयोग

त्रिभुज के कोण और भुजाएँ

ज्या का नियम

कोज्या का नियम

स्पर्शरेखा का नियम

स्पर्शरेखा का नियम

आवर्ती फलन

इतिहास

व्युत्पत्ति विज्ञान

यह भी देखें

टिप्पणियाँ

संदर्भ

बाहरी कड़ियाँ

Navigation

Wiki tools

Page tools

Other projects

Hidden categories