ग्राहम स्कैन: Difference between revisions
No edit summary |
No edit summary |
||
| Line 42: | Line 42: | ||
== टिप्पणियाँ == | == टिप्पणियाँ == | ||
यदि मूल विचार तब ही कार्य करता है जब इनपुट को कोण के अतिरिक्त एक्स-समन्वय पर क्रमबद्ध किया जाता है, और पतवार की गणना क्रमशः पतवार के ऊपरी और निचले भागो का निर्माण करते हुए दो चरणों में की जाती है। यह संशोधन ए. एम. एंड्रयू द्वारा तैयार किया गया था। | यदि मूल विचार तब ही कार्य करता है जब इनपुट को कोण के अतिरिक्त एक्स-समन्वय पर क्रमबद्ध किया जाता है, और पतवार की गणना क्रमशः पतवार के ऊपरी और निचले भागो का निर्माण करते हुए दो चरणों में की जाती है। यह संशोधन ए. एम. एंड्रयू द्वारा तैयार किया गया था।<ref name=":0">{{cite journal|title=Another efficient algorithm for convex hulls in two dimensions|first=A. M.|last=Andrew|journal=Information Processing Letters|year=1979|volume=9|issue=5|pages=216–219|doi=10.1016/0020-0190(79)90072-3}}</ref> इसमें ग्राहम के स्कैन के समान ही मूल गुण हैं।<ref name=":1">{{Cite book | ||
| last1 = De Berg | | last1 = De Berg | ||
| first1 = Mark | | first1 = Mark | ||
Revision as of 18:04, 18 July 2023
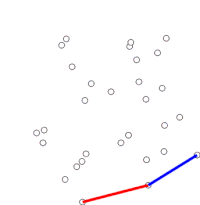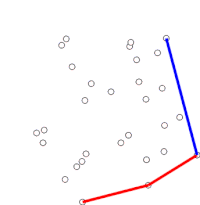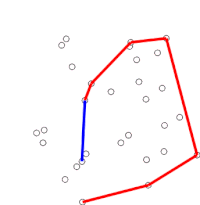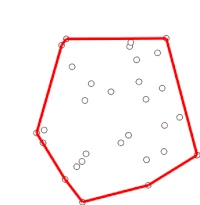
ग्राहम स्कैन समय जटिलता बिग ओ अंकन (n log n) के साथ विमान में बिंदुओं के सीमित समूह के उत्तल पतवार को खोजने की विधि है। इसका नाम रोनाल्ड ग्राहम के नाम पर रखा गया है, जिन्होंने 1972 में मूल एल्गोरिदम प्रकाशित किया था।[1] एल्गोरिथ्म अपनी सीमा के साथ क्रमबद्ध उत्तल पतवार के सभी शीर्षों को ढूंढता है। यह सीमा में अवतलताओं का कुशलतापूर्वक पता लगाने और उन्हें हटाने के लिए स्टैक (अमूर्त डेटा प्रकार) का उपयोग करता है।
एल्गोरिथम
इस एल्गोरिदम में पहला कदम सबसे कम y-निर्देशांक वाला बिंदु ढूंढना है। यदि समूह में एक से अधिक बिंदुओं पर सबसे कम y-निर्देशांक उपस्थित है, तो अभ्यर्थी में से सबसे कम x-निर्देशांक वाले बिंदु को चुना जाना चाहिए। इस बिंदु P पर कॉल करें। यह चरण बिग O नोटेशन (n) लेता है, जहां n प्रश्न में अंकों की संख्या है।
इसके बाद, बिंदुओं के समूह को उनके और बिंदु P द्वारा x-अक्ष के साथ बनाए जाने वाले कोण के बढ़ते क्रम में क्रमबद्ध किया जाना चाहिए। कोई भी सामान्य प्रयोजन सॉर्टिंग एल्गोरिथ्म इसके लिए उपयुक्त है, उदाहरण के लिए हेप्सोर्ट (जो O (n log n है))।
कोण के क्रम में क्रमबद्ध करने के लिए कोण की गणना करने की आवश्यकता नहीं होती है। कोण के किसी भी कार्य का उपयोग करना संभव है जो अंतराल (गणित) में मोनोटोनिक है। डॉट उत्पाद का उपयोग करके कोसाइन की गणना सरलता से की जाती है, या रेखा के ढलान का उपयोग किया जा सकता है। यदि संख्यात्मक परिशुद्धता दांव पर है, तो सॉर्टिंग एल्गोरिदम द्वारा उपयोग किया जाने वाला तुलना कार्य सापेक्ष कोण निर्धारित करने के लिए क्रॉस उत्पाद के संकेत का उपयोग कर सकता है।
यदि कई बिंदु एक ही कोण के हैं, तो या तो दूरी बढ़ाकर संबंधों को तोड़ दें (आसान गणना के लिए यूक्लिडियन दूरी के अतिरिक्त टैक्सीकैब ज्यामिति या चेबीशेव दूरी की दूरी का उपयोग किया जा सकता है, क्योंकि बिंदु एक ही किरण पर स्थित हैं), या सबसे दूर के बिंदु को छोड़कर सभी को हटा दिया जाता है।
एल्गोरिथ्म क्रमबद्ध सरणी में प्रत्येक बिंदु पर क्रम से विचार करके आगे बढ़ता है। प्रत्येक बिंदु के लिए, पहले यह निर्धारित किया जाता है कि इस बिंदु से ठीक पहले वाले दो बिंदुओं से यात्रा करना बाएँ मुड़ना है या दाएँ मुड़ना है। यदि दाएं मुड़ते हैं, तो दूसरा-से-अंतिम बिंदु उत्तल पतवार का भाग नहीं है, और इसके 'अंदर' स्थित है। यही निर्धारण फिर नवीनतम बिंदु के समूह और दो बिंदुओं के लिए किया जाता है जो पतवार के अंदर पाए जाने वाले बिंदु से तुरंत पहले होते हैं, और तब तक दोहराया जाता है जब तक कि बाएं मोड़ का समूह सामने नहीं आता है, जिस बिंदु पर एल्गोरिदम आगे बढ़ता है क्रमबद्ध सरणी में बिंदुओं के समूह में अगला बिंदु तक कोई भी बिंदु जो पतवार के अंदर पाया गया था; इन बिंदुओं पर दोबारा विचार करने की जरूरत नहीं है. (यदि किसी भी स्तर पर तीन बिंदु संरेख हैं, तो कोई इसे त्यागने या रिपोर्ट करने का विकल्प चुन सकता है, क्योंकि कुछ अनुप्रयोगों में उत्तल पतवार की सीमा पर सभी बिंदुओं को ढूंढना आवश्यक है।)
इस के अतिरिक्त, यह निर्धारित करने के लिए कि क्या तीन बिंदु बाएं मोड़ या दाएं मोड़ का गठन करते हैं, दो रेखा खंडों के बीच वास्तविक कोण की गणना करने की आवश्यकता नहीं है, और वास्तव में केवल सरल अंकगणित के साथ प्राप्त किया जा सकता है। तीन अंक , और के लिए, दो वेक्टर (ज्यामितीय) और के क्रॉस उत्पाद के z-निर्देशांक की गणना करते है, जो अभिव्यक्ति द्वारा दिया गया है। यदि परिणाम 0 है, तो बिंदु संरेख हैं; यदि यह सकारात्मक है, तो तीन बिंदु बाएं मोड़ या वामावर्त अभिविन्यास का गठन करते हैं, अन्यथा दाएं मोड़ या दक्षिणावर्त अभिविन्यास (वामावर्त क्रमांकित बिंदुओं के लिए) का गठन करते हैं।
यह प्रक्रिया अंततः उसी बिंदु पर वापस आ जाएगी जहां से यह प्रारंभ हुई थी, जिस बिंदु पर एल्गोरिदम पूरा हो गया है और स्टैक में अब उत्तल पतवार पर वामावर्त क्रम में बिंदु सम्मिलित हैं।
समय जटिलता
बिंदुओं को क्रमबद्ध करने में समय जटिलता O(n log n) होती है। चूँकि ऐसा लग सकता है कि लूप की समय जटिलता O(n2) है, क्योंकि प्रत्येक बिंदु के लिए यह जांचने के लिए वापस जाता है कि क्या पिछले बिंदुओं में से कोई दाहिनी ओर मुड़ता है, यह वास्तव में O(n) है, क्योंकि प्रत्येक बिंदु को कुछ अर्थों में अधिकतम दो बार माना जाता है। प्रत्येक बिंदु एक बार बाएं मोड़ में एक बिंदु के रूप में प्रकट हो सकता है (क्योंकि एल्गोरिदम इसके बाद अगले बिंदु पर आगे बढ़ता है), और दाएँ मोड़ में एक बिंदु के रूप में (क्योंकि बिंदु हटा दिया जाता है)। इसलिए समग्र समय जटिलता O(n log n) है, क्योंकि क्रमबद्ध करने का समय वास्तव में उत्तल पतवार की गणना करने के समय पर हावी होता है।
स्यूडोकोड
नीचे दिया गया स्यूडोकोड कार्य का उपयोग करता है: 0 यदि तीन बिंदु वामावर्त घुमाते हैं, यदि है तो दक्षिणावर्त घुमाएँ, और यदि ccw = 0 है तो संरेख करते है। (वास्तविक अनुप्रयोगों में, यदि निर्देशांक इच्छानुसार से वास्तविक संख्याएँ हैं, तो कार्य की आवश्यकता होती है फ़्लोटिंग-पॉइंट संख्याओं की स्पष्ट तुलना, और लगभग संरेख बिंदुओं के लिए संख्यात्मक विलक्षणताओं से सावधान रहना रहा जाता है।)
फिर परिणाम को stack में संग्रहीत होने दें।
let points be the list of points
let stack = empty_stack()
find the lowest y-coordinate and leftmost point, called P0
sort points by polar angle with P0, if several points have the same polar angle then only keep the farthest
for point in points:
# pop the last point from the stack if we turn clockwise to reach this point
while count stack > 1 and ccw(next_to_top(stack), top(stack), point) <= 0:
pop stack
push point to stack
endअब स्टैक में उत्तल पतवार है, जहां बिंदु वामावर्त उन्मुख हैं और P0 पहला बिंदु है।
यहाँ, next_to_top() स्टैक को बदले बिना, आइटम को स्टैक के शीर्ष के नीचे प्रविष्टि में वापस करने का कार्य है, और इसी तरह, top() सर्वोच्च तत्व को वापस करने के लिए है।
यह स्यूडोकोड एल्गोरिदम के परिचय से अनुकूलित है।
टिप्पणियाँ
यदि मूल विचार तब ही कार्य करता है जब इनपुट को कोण के अतिरिक्त एक्स-समन्वय पर क्रमबद्ध किया जाता है, और पतवार की गणना क्रमशः पतवार के ऊपरी और निचले भागो का निर्माण करते हुए दो चरणों में की जाती है। यह संशोधन ए. एम. एंड्रयू द्वारा तैयार किया गया था।[2] इसमें ग्राहम के स्कैन के समान ही मूल गुण हैं।[3]
Graham's original description involved sorting around an interior point of the convex hull, rather than one of its vertices.[1] For the same choice of a pivot point for the sorting algorithm, connecting all of the other points in their sorted order around this point rather than performing the remaining steps of the Graham scan produces a star-shaped polygon, a polygonalization of the input.[4]
The stack technique used in Graham's scan is very similar to that for the all nearest smaller values problem, and parallel algorithms for all nearest smaller values may also be used (like Graham's scan) to compute convex hulls of sorted sequences of points efficiently.[5]
संख्यात्मक सुदृढ़ता
संख्यात्मक सुदृढ़ता उन एल्गोरिदम में निपटने के लिए उद्देश्य है जो परिमित-स्पष्ट फ़्लोटिंग-पॉइंट कंप्यूटर अंकगणित का उपयोग करते हैं। 2004 के पेपर में सरल वृद्धिशील रणनीति का विश्लेषण किया गया था, जिसका उपयोग, विशेष रूप से, ग्राहम स्कैन के कार्यान्वयन के लिए किया जा सकता है।[6] पेपर का घोषित लक्ष्य विशेष रूप से एल्गोरिदम का विश्लेषण करना नहीं था, किंतु कम्प्यूटेशनल ज्यामिति में फ़्लोटिंग-पॉइंट गणनाओं के कारण क्या और कैसे विफल हो सकता है, इसका पाठ्यपुस्तक उदाहरण प्रदान करना था।[6] बाद में डी. जियांग और एन.एफ. स्टीवर्ट[7] इस पर विस्तार से बताया और पिछड़े त्रुटि विश्लेषण का उपयोग करके दो प्राथमिक निष्कर्ष निकाले है। पहला यह है कि उत्तल पतवार अच्छी तरह से वातानुकूलित समस्या है, और इसलिए कोई ऐसे एल्गोरिदम की अपेक्षा कर सकता है जो उचित त्रुटि मार्जिन के अंदर उत्तर उत्पन्न करता है। दूसरा, वे प्रदर्शित करते हैं कि ग्राहम स्कैन का संशोधन जिसे वे ग्राहम-फॉर्च्यून कहते हैं (संख्यात्मक स्थिरता के लिए स्टीवन फॉर्च्यून के विचारों को सम्मिलित करते हुए[8]) जिस भी सीमा तक ऐसा करना संभव हो सकता है, तब परिमित परिशुद्धता और अयथार्थ डेटा की समस्याओं को दूर करता है।
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 Graham, R.L. (1972). "एक परिमित तलीय सेट के उत्तल पतवार को निर्धारित करने के लिए एक कुशल एल्गोरिदम" (PDF). Information Processing Letters. 1 (4): 132–133. doi:10.1016/0020-0190(72)90045-2.
- ↑ Andrew, A. M. (1979). "Another efficient algorithm for convex hulls in two dimensions". Information Processing Letters. 9 (5): 216–219. doi:10.1016/0020-0190(79)90072-3.
- ↑ De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars, Mark (2008). Computational Geometry Algorithms and Applications. Berlin: Springer. pp. 2–14. doi:10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5.
- ↑ Arkin, Esther M.; Fekete, Sándor P.; Hurtado, Ferran; Mitchell, Joseph S. B.; Noy, Marc; Sacristán, Vera; Sethia, Saurabh (2003). "On the reflexivity of point sets". In Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha (eds.). Discrete and Computational Geometry: The Goodman-Pollack Festschrift. Algorithms and Combinatorics. Vol. 25. Berlin: Springer. pp. 139–156. doi:10.1007/978-3-642-55566-4_6. MR 2038472.
- ↑ Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993). "Optimal double logarithmic parallel algorithms based on finding all nearest smaller values". Journal of Algorithms. 14 (3): 344–370. CiteSeerX 10.1.1.55.5669. doi:10.1006/jagm.1993.1018..
- ↑ 6.0 6.1 Kettner, Lutz; Mehlhorn, Kurt; Pion, Sylvain; Schirra, Stefan; Yap, Chee (2008). "ज्यामितीय संगणनाओं में मजबूती की समस्याओं के कक्षा उदाहरण" (PDF). Computational Geometry. 40 (1): 61–78. doi:10.1016/j.comgeo.2007.06.003. (An earlier version was reported in 2004 at ESA'2004)
- ↑ D. Jiang and N. F. Stewart, Backward error analysis in computational geometry Archived 2017-08-09 at the Wayback Machine, Computational Science and Its Applications - ICCSA 2006 Volume 3980 of the series Lecture Notes in Computer Science, pp 50-59
- ↑ Fortune, S. Stable maintenance of point set triangulations in two dimensions. Proceedings of the 30th annual IEEE Symposium on Foundations of Computer Science Vol. 30, 494-499, 1989.
अग्रिम पठन
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "33.3: Finding the convex hull". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 949–955. ISBN 0-262-03293-7.