यूबी-ट्री: Difference between revisions
m (added Category:Vigyan Ready using HotCat) |
m (10 revisions imported from alpha:यूबी-ट्री) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 34: | Line 34: | ||
==संदर्भ == | ==संदर्भ == | ||
<references/> | <references/> | ||
[[Category: डेटाबेस सूचकांक तकनीक]] | [[Category: डेटाबेस सूचकांक तकनीक]] | ||
Latest revision as of 07:11, 19 October 2023
| UB-tree | ||||
|---|---|---|---|---|
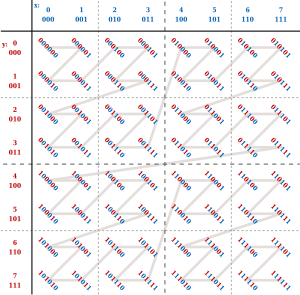 Two dimensional Z-order | ||||
| Type | tree | |||
| Invented by | Rudolf Bayer and Volker Markl | |||
| Time complexity in big O notation | ||||
| ||||
रूडोल्फ बायर और वोल्कर मार्कल द्वारा प्रस्तावित यूबी-ट्री बहुआयामी डेटा को संग्रहीत करने और कुशलतापूर्वक पुनर्प्राप्त करने के लिए एक संतुलित ट्री है। यह मूल रूप से एक B+ पेड़ है (जानकारी केवल पत्तियों में) जिसमें रिकॉर्ड Z-ऑर्डर (वक्र) के अनुसार संग्रहीत होते हैं, जिन्हें मॉर्टन ऑर्डर भी कहा जाता है। Z-ऑर्डर की गणना केवल कुंजियों को बिटवाइज़ इंटरलेसिंग करके की जाती है।
सम्मिलन, विलोपन और बिंदु क्वेरी सामान्य B+ ट्री की तरह ही की जाती है। चूँकि बहुआयामी बिंदु डेटा में श्रेणी खोज करने के लिए डेटा बेस में सामने आए एक बिंदु से, अगले Z-मान की गणना करने के लिए एक एल्गोरिदम प्रदान किया जाना चाहिए जो बहुआयामी खोज सीमा में है।
इस मुख्य समस्या को हल करने के लिए मूल एल्गोरिदम आयामीता के साथ घातीय था और इसलिए वह संभव नहीं था[1] ( गेटनेक्स्टज़-एड्रेस ). ज़ेड-एड्रेस बिट लंबाई के साथ यूबी-ट्री रेंज क्वेरी लीनियर के इस महत्वपूर्ण भाग का समाधान बाद में वर्णित किया गया है।[2] इस विधि का वर्णन पहले ही एक पुराने पेपर में किया जा चुका है[3] जहां खोज वृक्षों के साथ Z-ऑर्डर का उपयोग पहली बार प्रस्तावित किया गया है।
संदर्भ
- ↑ Markl, V. (1999). "MISTRAL: Processing Relational Queries using a Multidimensional Access Technique". CiteSeerX 10.1.1.32.6487.
- ↑ Ramsak, Frank; Markl, Volker; Fenk, Robert; Zirkel, Martin; Elhardt, Klaus; Bayer, Rudolf (September 10–14, 2000). यूबी-ट्री को डेटाबेस सिस्टम कर्नेल में एकीकृत करना (PDF). 26th International Conference on Very Large Data Bases. pp. 263–272.
- ↑ Tropf, H.; Herzog, H. "गतिशील रूप से संतुलित पेड़ों में बहुआयामी रेंज खोज" (PDF). Angewandte Informatik (Applied Informatics) (2/1981): 71–77. ISSN 0013-5704.