चार्ज-पंप फेज-लॉक लूप: Difference between revisions
No edit summary |
|||
| (15 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
चार्ज-पंप [[चरण बंद लूप| | [[File:CP-PLL.pdf|thumb|चार्ज-पंप पीएलएल]] | ||
'''चार्ज-पंप [[चरण बंद लूप|फेज -लॉक लूप]]''' (सीपी-पीएलएल) फेज-आवृत्ति डिटेक्टर और वर्गाकार तरंग संकेतों के साथ फेज-लॉक लूप का एक संशोधन है।<ref>{{cite patent |country= USA|number=US3714463A |status= |title=Digital frequency and/or phase detector charge pump |pubdate=1973-01-30 |gdate= |fdate= |pridate=1971-01-04 |inventor=Jon M. Laune |invent1= |invent2= |assign1= |assign2= |class= |url=https://patents.google.com/patent/US3714463A}}</ref> सीपी-पीएलएल आने वाले संकेतों के फेज को त्वरित रूप से लॉक करने की अनुमति देता है, जिससे कम स्थिर अवस्था फेज त्रुटि प्राप्त होती है।<ref name="Gardner-1980">{{cite journal |author = F. Gardner |author-link=Floyd M. Gardner | |||
|title = चार्ज-पंप चरण-लॉक लूप| journal = IEEE Transactions on Communications | volume = 28 |issue=11 | pages = 1849–1858| year = 1980|doi=10.1109/TCOM.1980.1094619 | |title = चार्ज-पंप चरण-लॉक लूप| journal = IEEE Transactions on Communications | volume = 28 |issue=11 | pages = 1849–1858| year = 1980|doi=10.1109/TCOM.1980.1094619 | ||
|bibcode=1980ITCom..28.1849G | |bibcode=1980ITCom..28.1849G | ||
}}</ref> | }}</ref> | ||
== | == फेज-आवृत्ति डिटेक्टर (पीएफडी) == | ||
[[File:Phase-frequency-detector.pdf|thumb|फेज-आवृत्ति डिटेक्टर गतिशीलता]] | |||
फेज-आवृत्ति डिटेक्टर (पीएफडी) को संदर्भ (रेफ) और नियंत्रित (वीसीओ) संकेतों के पिछला किनारों द्वारा रोका गया है। पीएफडी का आउटपुट संकेत <math>i(t)</math> में केवल तीन अवस्थाएँ हो सकती हैं: 0, <math>+I_p</math>, और <math>-I_p</math>. संदर्भ संकेत का पिछला किनारा पीएफडी को उच्च अवस्था में स्विच करने के लिए मजबूर करता है, जब तक कि वह पहले से ही इस अवस्था में न हो <math>+I_p</math>.वीसीओ संकेत का पिछला किनारा पीएफडी को निचले अवस्था में जाने के लिए मजबूर करता है, जब तक कि वह पहले से ही इस अवस्था में न हो <math>-I_p</math>.यदि दोनों पिछला किनारे एक ही समय में होते हैं, तो पीएफडी शून्य पर स्विच हो जाता है। | |||
== सीपी-पीएलएल के गणितीय मॉडल == | == सीपी-पीएलएल के गणितीय मॉडल == | ||
दूसरे क्रम के सीपी-पीएलएल के पहला रैखिक गणितीय मॉडल 1980 में एफ. गार्डनर द्वारा सुझाव दिया गया था। <ref name="Gardner-1980" /> 1994 में एम. वैन पैमेल द्वारा वीसीओ अधिभार के बिना एक अरैखिक मॉडल का सुझाव दिया गया था <ref name="Paemel-1984">{{cite journal |author = M. van Paemel | |||
|title = Analysis of a charge-pump pll: A new model | |title = Analysis of a charge-pump pll: A new model | ||
| journal = IEEE Transactions on Communications | volume = 42 |issue=7 | pages = 2490–2498| year = 1994|doi = 10.1109/26.297861 | | journal = IEEE Transactions on Communications | volume = 42 |issue=7 | pages = 2490–2498| year = 1994|doi = 10.1109/26.297861 | ||
}}</ref> और फिर एन. कुज़नेत्सोव एट अल द्वारा परिष्कृत किया | }}</ref> और फिर एन. कुज़नेत्सोव एट अल द्वारा परिष्कृत किया गया था। 2019 में।<ref name="Kuznetsov-2019-JDECP">{{cite journal |author = N. Kuznetsov, M. Yuldashev, R. Yuldashev, M. Blagov, E. Kudryashova, O. Kuznetsova, and T. Mokaev | ||
|title = Comments on van Paemel's mathematical model of charge-pump phase-locked loop | |title = Comments on van Paemel's mathematical model of charge-pump phase-locked loop | ||
| journal = Differential Equations and Control Processes | volume = 1 | pages = 109–120 | url=https://diffjournal.spbu.ru/pdf/19107-jdecp-kuznetsov.pdf| year = 2019}}</ref> वीसीओ अधिभार को ध्यान में रखते हुए सीपी-पीएलएल का बंद | | journal = Differential Equations and Control Processes | volume = 1 | pages = 109–120 | url=https://diffjournal.spbu.ru/pdf/19107-jdecp-kuznetsov.pdf| year = 2019}}</ref> वीसीओ अधिभार को ध्यान में रखते हुए सीपी-पीएलएल का बंद रूप गणितीय मॉडल प्राप्त किया गया है।<ref name="KuznetsovYYBKKM-2020">{{cite journal |author = N. Kuznetsov, M. Yuldashev, R. Yuldashev, M. Blagov, E. Kudryashova, O. Kuznetsova, T. Mokaev |title = Charge pump phase-locked loop with phase-frequency detector: closed form mathematical model| issue=1468 | year = 2020 |volume = 1901|arxiv = 1901.01468}}</ref> | ||
सीपी-पीएलएल के ये गणितीय मॉडल होल्ड-इन रेंज (इनपुट संकेत अवधि की अधिकतम सीमा जैसे कि वहाँ एक बंद अवस्था उपस्थित है जिस पर वीसीओ अतिभारित नहीं है) और पुल-इन रेंज (ए) के विश्लेषणात्मक अनुमान प्राप्त करने की अनुमति देते हैं। होल्ड-इन रेंज के भीतर इनपुट संकेत अवधि की अधिकतम सीमा, जैसे कि किसी भी प्रारंभिक स्थिति के लिए सीपी-पीएलएल लॉक स्थिति प्राप्त कर लेता है)।<ref name="KuznetsovMYY-2020" /> | |||
=== दूसरे क्रम सीपी-पीएलएल और गार्डनर के अनुमान का निरंतर समय रैखिक मॉडल === | |||
=== दूसरे क्रम | गार्डनर का विश्लेषण निम्नलिखित समीपता पर आधारित है<ref name=Gardner-1980/> समय अंतराल जिस पर संदर्भ संकेत की प्रत्येक अवधि पर पीएफडी की गैर-शून्य स्थिति होती है | ||
गार्डनर का विश्लेषण निम्नलिखित | |||
:<math>t_p = |\theta_e|/\omega_{\rm ref},\ \theta_e = \theta_{\rm ref} - \theta_{\rm vco}.</math> | :<math>t_p = |\theta_e|/\omega_{\rm ref},\ \theta_e = \theta_{\rm ref} - \theta_{\rm vco}.</math> | ||
चार्ज-पंप | फिर चार्ज-पंप पीएफडी का औसत आउटपुट है | ||
:<math>i_d = I_p \theta_e/2\pi</math> | :<math>i_d = I_p \theta_e/2\pi</math> | ||
संगत स्थानांतरण कार्य के साथ | |||
:<math>I_d(s) = I_p\theta_e(s)/2\pi</math> | :<math>I_d(s) = I_p\theta_e(s)/2\pi</math> | ||
फ़िल्टर ट्रांसफर फ़ंक्शन का उपयोग करना <math>F(s) = R + \frac{1}{Cs}</math> और वीसीओ स्थानांतरण समारोह <math>\theta_{\rm vco}(s) = K_{\rm vco}I_d(s)F(s)/s</math> एक को दूसरे क्रम के | फ़िल्टर ट्रांसफर फ़ंक्शन का उपयोग करना <math>F(s) = R + \frac{1}{Cs}</math> और वीसीओ स्थानांतरण समारोह <math>\theta_{\rm vco}(s) = K_{\rm vco}I_d(s)F(s)/s</math> एक को दूसरे क्रम के सीपी-पीएलएल का गार्डनर का रैखिक अनुमानित औसत मॉडल मिलता है | ||
:<math> | :<math> | ||
\frac{\theta_e(s)}{\theta_{\rm ref}(s)} = \frac{2\pi s}{2\pi s + K_{\rm vco}I_p\left(R + \frac{1}{Cs}\right)}. | \frac{\theta_e(s)}{\theta_{\rm ref}(s)} = \frac{2\pi s}{2\pi s + K_{\rm vco}I_p\left(R + \frac{1}{Cs}\right)}. | ||
</math> | </math> | ||
1980 में, | 1980 में, एम. गार्डनर ने उपरोक्त तर्क के आधार पर अनुमान लगाया कि ''व्यावहारिक चार्ज-पंप पीएलएल की क्षणिक प्रतिक्रिया समकक्ष शास्त्रीय पीएलएल की प्रतिक्रिया के लगभग समान होने की उम्मीद की जा सकती है''।<ref name=Gardner-1980/>1856 (सीपी-पीएलएल पर गार्डनर का अनुमान <ref name=2021-TCAS-KuznetsovMYY>{{cite journal | ||
| last1=Kuznetsov | first1=N.V.| last2=Matveev | first2=A.S.| last3=Yuldashev | first3=M.V.| last4=Yuldashev | first4=R.V. | | last1=Kuznetsov | first1=N.V.| last2=Matveev | first2=A.S.| last3=Yuldashev | first3=M.V.| last4=Yuldashev | first4=R.V. | ||
| title=Nonlinear Analysis of Charge-Pump Phase-Locked Loop: The Hold-In and Pull-In Ranges | journal= IEEE Transactions on Circuits and Systems I: Regular Papers | | title=Nonlinear Analysis of Charge-Pump Phase-Locked Loop: The Hold-In and Pull-In Ranges | journal= IEEE Transactions on Circuits and Systems I: Regular Papers | ||
| volume= 68| pages=4049–4061| doi=10.1109/TCSI.2021.3101529 | | volume= 68| pages=4049–4061| doi=10.1109/TCSI.2021.3101529 | ||
| year=2021 | | year=2021 | ||
| issue=10| doi-access=free}}</ref>) | | issue=10| doi-access=free}}</ref>) गार्डनर के परिणामों के बाद, टाइप 2 एपीएलएल की पुल-इन रेंज पर ईगन अनुमान के अनुरूप, अम्र एम. फहीम ने अपने पुस्तक में अनुमान लगाया<ref name="2005-Fahim">{{cite book | first= Amr M. | last=Fahim | year = 2005| title = Clock Generators for SOC Processors: Circuits and Architecture | publisher = Kluwer Academic Publishers| location = Boston-Dordrecht-London }}</ref> {{rp|6}} कि एक अनंत पुल-इन (कैप्चर) रेंज रखने के लिए, सीपी-पीएलएल में लूप फ़िल्टर के लिए सक्रिय फ़िल्टर का उपयोग किया जाना चाहिए ( टाइप II सीपी-पीएलएल के पुल-इन रेंज पर फहीम-ईगन का अनुमान)। | ||
गार्डनर के परिणामों के बाद, | |||
===दूसरे क्रम के | === दूसरे क्रम के सीपी-पीएलएल का निरंतर समय अरैखिक मॉडल === | ||
व्यापकता के नुकसान के बिना यह माना जाता है कि वीसीओ और रेफ संकेतों के | व्यापकता के नुकसान के बिना यह माना जाता है कि वीसीओ और रेफ संकेतों के पिछला किनारे होते हैं जब संबंधित फेज पूर्णांक संख्या तक पहुँचता है। मान लीजिए कि रेफ संकेत के पहले पिछला किनारे का समय उदाहरण को इस रूप में परिभाषित किया गया है <math>t = 0</math>.पीएफडी अवस्था <math>i(0)</math> पीएफडी प्रारंभिक अवस्था द्वारा निर्धारित किया जाता है <math>i(0-)</math>,वीसीओ के प्रारंभिक फेज में बदलाव <math>\theta_{vco}(0)</math> और रेफरी <math>\theta_{ref}(0)</math> संकेत। | ||
जब संबंधित | |||
पीएफडी अवस्था <math>i(0)</math> पीएफडी प्रारंभिक अवस्था द्वारा निर्धारित किया जाता है <math>i(0-)</math>, | |||
इनपुट करंट के बीच संबंध <math>i(t)</math> और आउटपुट वोल्टेज <math>v_F(t)</math> | इनपुट करंट के बीच संबंध <math>i(t)</math> और आउटपुट वोल्टेज <math>v_F(t)</math> के लिए प्रतिरोधी और संधारित्र के आधार पर आनुपातिक रूप से एकीकृत (परिपूर्ण पीआई) फ़िल्टर के लिए इस प्रकार है | ||
प्रतिरोधी और संधारित्र के आधार पर आनुपातिक रूप से एकीकृत (परिपूर्ण पीआई) फ़िल्टर | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 56: | Line 46: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहाँ <math>R>0</math> प्रतिरोध है, <math>C>0</math> धारिता है, और <math>v_c(t)</math> संधारित्र आवेश है। नियंत्रण संकेत <math>v_F(t)</math> वीसीओ आवृत्ति समायोजित करता है | |||
और <math>v_c(t)</math> | |||
नियंत्रण संकेत <math>v_F(t)</math> | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 66: | Line 54: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहाँ <math>\omega_{vco}^{\text{free}}</math> वीसीओ फ्री-रनिंग (शांत) आवृत्ति है (अर्थात <math>v_F(t)\equiv 0</math>) के लिए, <math>K_{vco}</math> वीसीओ लाभ (संवेदनशीलता) है, और <math>\theta_{vco}(t)</math> वीसीओ फेज है। अंत में, सीपी-पीएलएल का निरंतर समय अरेखीय गणितीय मॉडल इस प्रकार है | |||
( | |||
अंत में, सीपी-पीएलएल का निरंतर समय | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 81: | Line 66: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
निम्नलिखित | निम्नलिखित असंतत टुकड़ा-वार निरंतर रैखिकता के साथ | ||
:<math> | :<math> | ||
i(t) = i\big(i(t-), \theta_{ref}(t), \theta_{vco}(t)\big) | i(t) = i\big(i(t-), \theta_{ref}(t), \theta_{vco}(t)\big) | ||
</math> | </math> | ||
और प्रारंभिक शर्तें <math>\big(v_c(0), \theta_{vco}(0)\big)</math>. | और प्रारंभिक शर्तें <math>\big(v_c(0), \theta_{vco}(0)\big)</math>. यह मॉडल अरैखिक, गैर-स्वायत्त, असंतुलित, स्विचिंग प्रणाली है। | ||
यह मॉडल | |||
===दूसरे क्रम के | === दूसरे क्रम के सीपी-पीएलएल का असतत समय अरेखीय मॉडल === | ||
[[File:PDF time intervals.jpg|thumb|500px|पीएफडी | [[File:PDF time intervals.jpg|thumb|500px|पीएफडी गतिशीलता का समय अंतराल]]संदर्भ संकेत आवृत्ति को स्थिर मानी जाती है: | ||
<math> | <math> | ||
\theta_{ref}(t) = \omega_{ref}t = \frac{t}{T_{ref}}, | \theta_{ref}(t) = \omega_{ref}t = \frac{t}{T_{ref}}, | ||
</math> | </math> जहाँ <math>T_{ref}</math>, <math>\omega_{ref}</math> और <math>\theta_{ref}(t)</math> संदर्भ संकेत की एक अवधि, आवृत्ति और एक फेज है। होने देना <math>t_0 = 0</math>. द्वारा निरूपित करें <math>t_0^{\rm middle}</math> समय का पहला क्षण ऐसा है कि पीएफडी आउटपुट शून्य हो जाता है (यदि <math>i(0)=0</math>, तब <math>t_0^{\rm middle}=0</math>) और तक <math>t_1</math> वीसीओ या Ref का पहला पिछला किनारा। आगे तदनुरूप बढ़ते क्रम <math>\{t_k\}</math> और <math>\{t_k^{\rm middle}\}</math> के लिए <math>k=0,1,2...</math> परिभाषित किया गया हैं। होने देना <math>t_k < t_k^{\rm middle}</math>. तब <math>t \in [t_k,t_k^{\rm middle})</math> <math>\text{sign}(i(t))</math> के लिए एक गैर-शून्य स्थिरांक है (<math>\pm1</math>). द्वारा निरूपित करें <math>\tau_k</math> पीएफडी पल्स चौड़ाई (समय अंतराल की लंबाई, जहां पीएफडी आउटपुट गैर-शून्य स्थिरांक है), पीएफडी आउटपुट के संकेत से गुणा किया जाता है अर्थात। <math> \tau_k = (t_k^{\rm middle} - t_k)\text{sign}(i(t)) </math> के लिए <math> t \in [t_k,t_k^{\rm middle}) </math> और <math> \tau_k = 0 </math> के लिए <math> t_k=t_k^{\rm middle} </math> यदि वीसीओ ट्रेलिंग एज Ref ट्रेलिंग एज से पहले हिट करता है,तब <math>\tau_k < 0</math> और विपरीत अवस्था में हमारे पास है <math>\tau_k > 0</math>, अर्थात। <math>\tau_k</math> दिखाता है कि कैसे एक संकेत दूसरे से पिछड़ जाता है। पीएफडी का शून्य उत्पादन <math>i(t) \equiv 0</math> अंतराल पर <math>(t_k^{\rm middle},t_{k+1})</math>:<math> v_F(t) \equiv v_k </math> के लिए <math> t \in [t_k^{\rm middle},t_{k+1}) </math>. चर का परिवर्तन<ref>{{cite journal |author = P. Curran, C. Bi, and O. Feely |title = चार्ज-पंप चरण-लॉक लूप की गतिशीलता| journal = International Journal of Circuit Theory and Applications | volume = 41 |issue=11 | pages = 1109–1135| year = 2013|doi = 10.1002/cta.1814| s2cid=3792988 }}</ref> <math>(\tau_k,v_k)</math> को<math> | ||
एक अवधि, आवृत्ति और | |||
होने देना <math>t_0 = 0</math>. | |||
द्वारा निरूपित करें <math>t_0^{\rm middle}</math> समय का पहला | |||
( | |||
और तक <math>t_1</math> | |||
आगे | |||
होने देना <math>t_k < t_k^{\rm middle}</math>. | |||
द्वारा निरूपित करें <math>\tau_k</math> पीएफडी पल्स चौड़ाई (समय अंतराल की लंबाई, | |||
जहां पीएफडी आउटपुट गैर-शून्य | |||
अर्थात। <math> \tau_k = (t_k^{\rm middle} - t_k)\text{sign}(i(t)) </math> के लिए <math> t \in [t_k,t_k^{\rm middle}) </math> और | |||
<math> \tau_k = 0 </math> के लिए <math> t_k=t_k^{\rm middle} </math> | |||
यदि | |||
तब <math>\tau_k < 0</math> और विपरीत अवस्था में हमारे पास है <math>\tau_k > 0</math>, अर्थात। <math>\tau_k</math> दिखाता है कि कैसे एक | |||
<math> v_F(t) \equiv v_k </math> के लिए <math> t \in [t_k^{\rm middle},t_{k+1}) </math>. | |||
चर का परिवर्तन<ref>{{cite journal |author = P. Curran, C. Bi, and O. Feely |title = चार्ज-पंप चरण-लॉक लूप की गतिशीलता| journal = International Journal of Circuit Theory and Applications | volume = 41 |issue=11 | pages = 1109–1135| year = 2013|doi = 10.1002/cta.1814| s2cid=3792988 }}</ref> <math>(\tau_k,v_k)</math> को | |||
<math> | |||
p_k = \frac{\tau_k}{T_{\rm ref}}, | p_k = \frac{\tau_k}{T_{\rm ref}}, | ||
u_k=T_{\rm ref} | u_k=T_{\rm ref} | ||
| Line 116: | Line 82: | ||
\omega_{\rm vco}^{\text{free}} + K_{\rm vco}v_k | \omega_{\rm vco}^{\text{free}} + K_{\rm vco}v_k | ||
) - 1, | ) - 1, | ||
</math> | </math> पैरामीटर की संख्या को दो तक कम करने की अनुमति देता है:<math> | ||
पैरामीटर की संख्या को दो तक कम करने की अनुमति देता है: | |||
<math> | |||
\alpha = K_{\rm vco}I_pT_{\rm ref}R, | \alpha = K_{\rm vco}I_pT_{\rm ref}R, | ||
\beta = \frac{K_{\rm vco}I_pT_{\rm ref}^2}{2C}. | \beta = \frac{K_{\rm vco}I_pT_{\rm ref}^2}{2C}. | ||
</math> | </math> यहाँ <math>p_k</math> सामान्यीकृत फेज बदलाव है और <math>u_k+1</math> वीसीओ आवृत्ति का अनुपात है <math>\omega_{\rm vco}^{\text{free}} + K_{\rm vco}v_k</math> संदर्भ आवृत्ति के लिए <math>\frac{1}{T_{\rm ref}}</math>.अंत में, वीसीओ अधिभार के बिना दूसरे क्रम सीपी-पीएलएल का असतत-समय मॉडल<ref name=Kuznetsov-2019-JDECP/><ref name=KuznetsovMYY-2020>{{cite journal |author = N.V. Kuznetsov, A.S. Matveev, M.V. Yuldashev, R.V. Yuldashev | ||
यहाँ <math>p_k</math> | |||
अंत में, | |||
|title = Nonlinear analysis of charge-pump phase-locked loop: the hold-in and pull-in ranges | |title = Nonlinear analysis of charge-pump phase-locked loop: the hold-in and pull-in ranges | ||
| journal = IFAC World Congress |year = 2020 |arxiv = 2005.00864 | | journal = IFAC World Congress |year = 2020 |arxiv = 2005.00864 | ||
| Line 146: | Line 108: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहाँ | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 155: | Line 117: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
इस असतत-समय | इस असतत-समय मॉडल की एकमात्र स्थिर अवस्था है <math>(u_k=0,p_k=0)</math> और होल्ड-इन और पुल-इन रेंज का अनुमान लगाने की अनुमति देता है।<ref name=KuznetsovMYY-2020/> | ||
यदि | यदि वीसीओ अतिभारित है, अर्थात <math> \dot\theta_{\rm vco}(t)</math> शून्य है, या समान है: | ||
या | |||
<math> (p_k>0, u_k<2\beta p_k-1)</math> या | <math> (p_k>0, u_k<2\beta p_k-1)</math> या | ||
<math>(p_k<0, u_k<\alpha-1)</math>, | <math>(p_k<0, u_k<\alpha-1)</math>, फिर सीपी-पीएलएल गतिशीलता के अतिरिक्त मामलों को ध्यान में रखा जाना है।<ref name=KuznetsovYYBKKM-2020/> किसी भी पैरामीटर के लिए वीसीओ अधिभार वीसीओ और संदर्भ संकेतों के बीच पर्याप्त रूप से बड़े आवृत्ति अंतर के लिए हो सकता है।व्यवहार में वीसीओ अधिभार से बचना चाहिए। | ||
फिर | |||
ध्यान में रखा जाना है।<ref name=KuznetsovYYBKKM-2020/>किसी भी पैरामीटर के लिए वीसीओ अधिभार वीसीओ और संदर्भ संकेतों के बीच पर्याप्त रूप से बड़े आवृत्ति अंतर के लिए हो सकता | |||
=== उच्च-क्रम सीपी-पीएलएल के अरैखिक मॉडल === | |||
उच्च-क्रम सीपी-पीएलएल के गैर-रैखिक गणितीय मॉडल की व्युत्पत्ति पारलौकिक फेज समीकरणों की ओर ले जाती है जिन्हें विश्लेषणात्मक रूप से हल नहीं किया जा सकता है और शास्त्रीय निश्चित-बिंदु विधि या न्यूटन-रैपसन दृष्टिकोण जैसे संख्यात्मक दृष्टिकोण की आवश्यकता होती है।<ref>{{cite journal |author = C. Hedayat, A. Hachem, Y. Leduc, and G. Benbassat |title = Modeling and characterization of the 3rd order charge-pump PLL: a fully event-driven approach| journal = Analog Integrated Circuits and Signal Processing | issue= 1| year = 1999 |volume = 19| pages = 25–45|doi = 10.1023/A:1008326315191|s2cid = 58204942}}</ref> | |||
== संदर्भ == | == संदर्भ == | ||
{{Reflist}} | {{Reflist}} | ||
[[Category: | [[Category:CS1 errors]] | ||
[[Category:CS1 maint]] | |||
[[Category:Created On 19/06/2023]] | [[Category:Created On 19/06/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:विद्युत सर्किट]] | |||
Latest revision as of 15:56, 26 October 2023
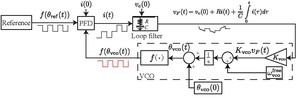
चार्ज-पंप फेज -लॉक लूप (सीपी-पीएलएल) फेज-आवृत्ति डिटेक्टर और वर्गाकार तरंग संकेतों के साथ फेज-लॉक लूप का एक संशोधन है।[1] सीपी-पीएलएल आने वाले संकेतों के फेज को त्वरित रूप से लॉक करने की अनुमति देता है, जिससे कम स्थिर अवस्था फेज त्रुटि प्राप्त होती है।[2]
फेज-आवृत्ति डिटेक्टर (पीएफडी)
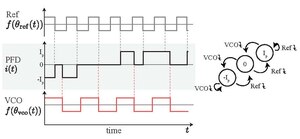
फेज-आवृत्ति डिटेक्टर (पीएफडी) को संदर्भ (रेफ) और नियंत्रित (वीसीओ) संकेतों के पिछला किनारों द्वारा रोका गया है। पीएफडी का आउटपुट संकेत में केवल तीन अवस्थाएँ हो सकती हैं: 0, , और . संदर्भ संकेत का पिछला किनारा पीएफडी को उच्च अवस्था में स्विच करने के लिए मजबूर करता है, जब तक कि वह पहले से ही इस अवस्था में न हो .वीसीओ संकेत का पिछला किनारा पीएफडी को निचले अवस्था में जाने के लिए मजबूर करता है, जब तक कि वह पहले से ही इस अवस्था में न हो .यदि दोनों पिछला किनारे एक ही समय में होते हैं, तो पीएफडी शून्य पर स्विच हो जाता है।
सीपी-पीएलएल के गणितीय मॉडल
दूसरे क्रम के सीपी-पीएलएल के पहला रैखिक गणितीय मॉडल 1980 में एफ. गार्डनर द्वारा सुझाव दिया गया था। [2] 1994 में एम. वैन पैमेल द्वारा वीसीओ अधिभार के बिना एक अरैखिक मॉडल का सुझाव दिया गया था [3] और फिर एन. कुज़नेत्सोव एट अल द्वारा परिष्कृत किया गया था। 2019 में।[4] वीसीओ अधिभार को ध्यान में रखते हुए सीपी-पीएलएल का बंद रूप गणितीय मॉडल प्राप्त किया गया है।[5]
सीपी-पीएलएल के ये गणितीय मॉडल होल्ड-इन रेंज (इनपुट संकेत अवधि की अधिकतम सीमा जैसे कि वहाँ एक बंद अवस्था उपस्थित है जिस पर वीसीओ अतिभारित नहीं है) और पुल-इन रेंज (ए) के विश्लेषणात्मक अनुमान प्राप्त करने की अनुमति देते हैं। होल्ड-इन रेंज के भीतर इनपुट संकेत अवधि की अधिकतम सीमा, जैसे कि किसी भी प्रारंभिक स्थिति के लिए सीपी-पीएलएल लॉक स्थिति प्राप्त कर लेता है)।[6]
दूसरे क्रम सीपी-पीएलएल और गार्डनर के अनुमान का निरंतर समय रैखिक मॉडल
गार्डनर का विश्लेषण निम्नलिखित समीपता पर आधारित है[2] समय अंतराल जिस पर संदर्भ संकेत की प्रत्येक अवधि पर पीएफडी की गैर-शून्य स्थिति होती है
फिर चार्ज-पंप पीएफडी का औसत आउटपुट है
संगत स्थानांतरण कार्य के साथ
फ़िल्टर ट्रांसफर फ़ंक्शन का उपयोग करना और वीसीओ स्थानांतरण समारोह एक को दूसरे क्रम के सीपी-पीएलएल का गार्डनर का रैखिक अनुमानित औसत मॉडल मिलता है
1980 में, एम. गार्डनर ने उपरोक्त तर्क के आधार पर अनुमान लगाया कि व्यावहारिक चार्ज-पंप पीएलएल की क्षणिक प्रतिक्रिया समकक्ष शास्त्रीय पीएलएल की प्रतिक्रिया के लगभग समान होने की उम्मीद की जा सकती है।[2]1856 (सीपी-पीएलएल पर गार्डनर का अनुमान [7]) गार्डनर के परिणामों के बाद, टाइप 2 एपीएलएल की पुल-इन रेंज पर ईगन अनुमान के अनुरूप, अम्र एम. फहीम ने अपने पुस्तक में अनुमान लगाया[8] : 6 कि एक अनंत पुल-इन (कैप्चर) रेंज रखने के लिए, सीपी-पीएलएल में लूप फ़िल्टर के लिए सक्रिय फ़िल्टर का उपयोग किया जाना चाहिए ( टाइप II सीपी-पीएलएल के पुल-इन रेंज पर फहीम-ईगन का अनुमान)।
दूसरे क्रम के सीपी-पीएलएल का निरंतर समय अरैखिक मॉडल
व्यापकता के नुकसान के बिना यह माना जाता है कि वीसीओ और रेफ संकेतों के पिछला किनारे होते हैं जब संबंधित फेज पूर्णांक संख्या तक पहुँचता है। मान लीजिए कि रेफ संकेत के पहले पिछला किनारे का समय उदाहरण को इस रूप में परिभाषित किया गया है .पीएफडी अवस्था पीएफडी प्रारंभिक अवस्था द्वारा निर्धारित किया जाता है ,वीसीओ के प्रारंभिक फेज में बदलाव और रेफरी संकेत।
इनपुट करंट के बीच संबंध और आउटपुट वोल्टेज के लिए प्रतिरोधी और संधारित्र के आधार पर आनुपातिक रूप से एकीकृत (परिपूर्ण पीआई) फ़िल्टर के लिए इस प्रकार है
जहाँ प्रतिरोध है, धारिता है, और संधारित्र आवेश है। नियंत्रण संकेत वीसीओ आवृत्ति समायोजित करता है
जहाँ वीसीओ फ्री-रनिंग (शांत) आवृत्ति है (अर्थात ) के लिए, वीसीओ लाभ (संवेदनशीलता) है, और वीसीओ फेज है। अंत में, सीपी-पीएलएल का निरंतर समय अरेखीय गणितीय मॉडल इस प्रकार है
निम्नलिखित असंतत टुकड़ा-वार निरंतर रैखिकता के साथ
और प्रारंभिक शर्तें . यह मॉडल अरैखिक, गैर-स्वायत्त, असंतुलित, स्विचिंग प्रणाली है।
दूसरे क्रम के सीपी-पीएलएल का असतत समय अरेखीय मॉडल
संदर्भ संकेत आवृत्ति को स्थिर मानी जाती है:
जहाँ , और संदर्भ संकेत की एक अवधि, आवृत्ति और एक फेज है। होने देना . द्वारा निरूपित करें समय का पहला क्षण ऐसा है कि पीएफडी आउटपुट शून्य हो जाता है (यदि , तब ) और तक वीसीओ या Ref का पहला पिछला किनारा। आगे तदनुरूप बढ़ते क्रम और के लिए परिभाषित किया गया हैं। होने देना . तब के लिए एक गैर-शून्य स्थिरांक है (). द्वारा निरूपित करें पीएफडी पल्स चौड़ाई (समय अंतराल की लंबाई, जहां पीएफडी आउटपुट गैर-शून्य स्थिरांक है), पीएफडी आउटपुट के संकेत से गुणा किया जाता है अर्थात। के लिए और के लिए यदि वीसीओ ट्रेलिंग एज Ref ट्रेलिंग एज से पहले हिट करता है,तब और विपरीत अवस्था में हमारे पास है , अर्थात। दिखाता है कि कैसे एक संकेत दूसरे से पिछड़ जाता है। पीएफडी का शून्य उत्पादन अंतराल पर : के लिए . चर का परिवर्तन[9] को पैरामीटर की संख्या को दो तक कम करने की अनुमति देता है: यहाँ सामान्यीकृत फेज बदलाव है और वीसीओ आवृत्ति का अनुपात है संदर्भ आवृत्ति के लिए .अंत में, वीसीओ अधिभार के बिना दूसरे क्रम सीपी-पीएलएल का असतत-समय मॉडल[4][6]
जहाँ
इस असतत-समय मॉडल की एकमात्र स्थिर अवस्था है और होल्ड-इन और पुल-इन रेंज का अनुमान लगाने की अनुमति देता है।[6]
यदि वीसीओ अतिभारित है, अर्थात शून्य है, या समान है:
या
, फिर सीपी-पीएलएल गतिशीलता के अतिरिक्त मामलों को ध्यान में रखा जाना है।[5] किसी भी पैरामीटर के लिए वीसीओ अधिभार वीसीओ और संदर्भ संकेतों के बीच पर्याप्त रूप से बड़े आवृत्ति अंतर के लिए हो सकता है।व्यवहार में वीसीओ अधिभार से बचना चाहिए।
उच्च-क्रम सीपी-पीएलएल के अरैखिक मॉडल
उच्च-क्रम सीपी-पीएलएल के गैर-रैखिक गणितीय मॉडल की व्युत्पत्ति पारलौकिक फेज समीकरणों की ओर ले जाती है जिन्हें विश्लेषणात्मक रूप से हल नहीं किया जा सकता है और शास्त्रीय निश्चित-बिंदु विधि या न्यूटन-रैपसन दृष्टिकोण जैसे संख्यात्मक दृष्टिकोण की आवश्यकता होती है।[10]
संदर्भ
- ↑ USA US3714463A, Jon M. Laune, "Digital frequency and/or phase detector charge pump", published 1973-01-30
- ↑ 2.0 2.1 2.2 2.3 F. Gardner (1980). "चार्ज-पंप चरण-लॉक लूप". IEEE Transactions on Communications. 28 (11): 1849–1858. Bibcode:1980ITCom..28.1849G. doi:10.1109/TCOM.1980.1094619.
- ↑ M. van Paemel (1994). "Analysis of a charge-pump pll: A new model". IEEE Transactions on Communications. 42 (7): 2490–2498. doi:10.1109/26.297861.
- ↑ 4.0 4.1 N. Kuznetsov, M. Yuldashev, R. Yuldashev, M. Blagov, E. Kudryashova, O. Kuznetsova, and T. Mokaev (2019). "Comments on van Paemel's mathematical model of charge-pump phase-locked loop" (PDF). Differential Equations and Control Processes. 1: 109–120.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ 5.0 5.1 N. Kuznetsov, M. Yuldashev, R. Yuldashev, M. Blagov, E. Kudryashova, O. Kuznetsova, T. Mokaev (2020). "Charge pump phase-locked loop with phase-frequency detector: closed form mathematical model". 1901 (1468). arXiv:1901.01468.
{{cite journal}}: Cite journal requires|journal=(help)CS1 maint: multiple names: authors list (link) - ↑ 6.0 6.1 6.2 N.V. Kuznetsov, A.S. Matveev, M.V. Yuldashev, R.V. Yuldashev (2020). "Nonlinear analysis of charge-pump phase-locked loop: the hold-in and pull-in ranges". IFAC World Congress. arXiv:2005.00864.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Kuznetsov, N.V.; Matveev, A.S.; Yuldashev, M.V.; Yuldashev, R.V. (2021). "Nonlinear Analysis of Charge-Pump Phase-Locked Loop: The Hold-In and Pull-In Ranges". IEEE Transactions on Circuits and Systems I: Regular Papers. 68 (10): 4049–4061. doi:10.1109/TCSI.2021.3101529.
- ↑ Fahim, Amr M. (2005). Clock Generators for SOC Processors: Circuits and Architecture. Boston-Dordrecht-London: Kluwer Academic Publishers.
- ↑ P. Curran, C. Bi, and O. Feely (2013). "चार्ज-पंप चरण-लॉक लूप की गतिशीलता". International Journal of Circuit Theory and Applications. 41 (11): 1109–1135. doi:10.1002/cta.1814. S2CID 3792988.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ C. Hedayat, A. Hachem, Y. Leduc, and G. Benbassat (1999). "Modeling and characterization of the 3rd order charge-pump PLL: a fully event-driven approach". Analog Integrated Circuits and Signal Processing. 19 (1): 25–45. doi:10.1023/A:1008326315191. S2CID 58204942.
{{cite journal}}: CS1 maint: multiple names: authors list (link)