अनुकूली फिल्टर: Difference between revisions
No edit summary |
(→स्रोत) |
||
| (5 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
'''अनुकूलनशील फ़िल्टर''' रेखीय [[फ़िल्टर (सिग्नल प्रोसेसिंग)|फ़िल्टर (संकेत प्रोसेसिंग)]] वाली प्रणाली होती है जिसमें चर मापदंडों द्वारा नियंत्रित स्थानांतरण फ़ंक्शन होता है और अनुकूलन एल्गोरिथम के अनुसार उन मापदंडों को समायोजित करने का साधन होता है। अनुकूलन एल्गोरिदम की जटिलता के कारण, लगभग सभी अनुकूलनशील फ़िल्टर [[डिजिटल फिल्टर]] के रूप में होते हैं। कुछ अनुप्रयोगों के लिए अनुकूलनशील फिल्टर की आवश्यकता होती है क्योंकि वांछित प्रसंस्करण संचालन के कुछ पैरामीटर (उदाहरण के लिए, प्रतिध्वनि स्थान में परावर्तक सतहों के स्थान) पहले से ज्ञात नहीं होते हैं या बदल रहे हैं। बंद लूप अनुकूलनशील फ़िल्टर अपने स्थानांतरण फ़ंक्शन को परिष्कृत करने के लिए त्रुटि संकेत के रूप में प्रतिक्रिया का उपयोग करता है। | |||
सामान्यतः बंद लूप अनुकूलनशील प्रक्रिया में | सामान्यतः बंद लूप अनुकूलनशील प्रक्रिया में [[लॉस फंकशन|लॉस फ़ंक्शन]] का उपयोग सम्मलित होता है, जो फ़िल्टर के इष्टतम प्रदर्शन के लिए मान्यता होता है, और इसे एल्गोरिदम को खिलाने के लिए, जो यह निर्धारित करता है कि अगले पुनरावृत्ति पर लागत को कम करने के लिए फ़िल्टर [[स्थानांतरण प्रकार्य]] को कैसे संशोधित किया जाता है। सबसे सामान्य लागत फलन त्रुटि संकेत का माध्य वर्ग है। | ||
चूंकि [[डिजिटल सिग्नल प्रोसेसर|डिजिटल संकेत प्रोसेसर]] की शक्ति में वृद्धि हुई है, अनुकूलनशील फिल्टर अधिक सामान्य हो गए हैं और अब नियमित रूप से मोबाइल फोन और अन्य संचार उपकरणों, कैमकोर्डर और डिजिटल कैमरे, और चिकित्सा निगरानी उपकरण जैसे उपकरणों में उपयोग किए जाते हैं। | चूंकि [[डिजिटल सिग्नल प्रोसेसर|डिजिटल संकेत प्रोसेसर]] की शक्ति में वृद्धि हुई है, अनुकूलनशील फिल्टर अधिक सामान्य हो गए हैं और अब नियमित रूप से मोबाइल फोन और अन्य संचार उपकरणों, कैमकोर्डर और डिजिटल कैमरे, और चिकित्सा निगरानी उपकरण जैसे उपकरणों में उपयोग किए जाते हैं। | ||
== उदाहरण आवेदन == | == उदाहरण आवेदन == | ||
दिल की धड़कन ( | दिल की धड़कन ( [[ईसीजी]]) की रिकॉर्डिंग, [[बिजली की आपूर्ति]] से शोर से दूषित हो सकती है। शक्ति और उसके [[हार्मोनिक्स]] की सटीक आवृत्ति पल-पल भिन्न हो सकती है। | ||
शोर को दूर करने का | शोर को दूर करने का विधि मुख्य आवृत्ति और उसके आसपास के क्षेत्र में पायदान फिल्टर के साथ संकेत को फ़िल्टर करना है, किन्तु यह ईसीजी की गुणवत्ता को अत्यधिक कम कर सकता है क्योंकि दिल की धड़कन में भी अस्वीकृत सीमा में आवृत्ति घटक होते है । | ||
सूचना के इस संभावित हानि को रोकने के लिए, | सूचना के इस संभावित हानि को रोकने के लिए, अनुकूलनशील फ़िल्टर का उपयोग किया जा सकता है। अनुकूलनशील फ़िल्टर रोगी और मुख्य दोनों से इनपुट लेगा और इस प्रकार शोर की वास्तविक आवृत्ति को ट्रैक करने में सक्षम होगा क्योंकि यह रिकॉर्डिंग से शोर घटाता है और घटाता है। ऐसी अनुकूलनशील तकनीक सामान्यतः छोटी अस्वीकृति सीमा के साथ फिल्टर की अनुमति देती है, जिसका अर्थ है, इस स्थितियों में, चिकित्सा उद्देश्यों के लिए आउटपुट संकेत की गुणवत्ता अधिक सटीक है।<ref>{{Cite journal|title = Applications of adaptive filtering to ECG analysis: noise cancellation and arrhythmia detection|journal = IEEE Transactions on Biomedical Engineering|date = 1991-08-01|issn = 0018-9294|pages = 785–794|volume = 38|issue = 8|doi = 10.1109/10.83591|pmid = 1937512|first1 = N.V.|last1 = Thakor|first2 = Yi-Sheng|last2 = Zhu| s2cid=11271450 }}</ref><ref name="Widrow">{{cite book|last1=Widrow |first1=Bernard |last2= Stearns|first2= Samuel D. |year= 1985 |title=अनुकूली सिग्नल प्रोसेसिंग|url=https://archive.org/details/adaptivesignalpr00widr |url-access=limited |edition= 1st | page = [https://archive.org/details/adaptivesignalpr00widr/page/n173 329]| publisher= Prentice-Hall|isbn= 978-0130040299 }}</ref> | ||
== ब्लॉक आरेख == | == ब्लॉक आरेख == | ||
बंद लूप अनुकूलनशील फ़िल्टर के पीछे की विचारधारा है कि परिवर्तनशील फ़िल्टर को तब तक समायोजित किया जाता है जब तक कि त्रुटि (फ़िल्टर आउटपुट और वांछित संकेत के बीच का अंतर)को कम से कम नहीं किया जाता है। न्यूनतम माध्य वर्ग (एलएमएस ) फ़िल्टर और पुनरावर्ती न्यूनतम वर्ग (आरएलएस) फ़िल्टर अनुकूलनशील फ़िल्टर के रूप में होते हैं। | |||
:[[File:Adaptive Filter General.png|thumb|400px|alt=A block diagram of an adaptive filter with a separate block for the adaptation processअनुकूली फिल्टर। k = नमूना संख्या, x = संदर्भ इनपुट, X = x के हाल के मानों का सेट, d = वांछित इनपुट, W = फ़िल्टर गुणांक का सेट, ε = त्रुटि आउटपुट, f = फ़िल्टर आवेग प्रतिक्रिया, * = दृढ़ संकल्प, Σ = योग, ऊपरी बॉक्स = रैखिक फ़िल्टर, निचला बॉक्स = अनुकूलन एल्गोरिदम|एडैप्टिव फ़िल्टर। k = सैंपल नंबर, x = संदर्भ इनपुट, X = हाल के x मानों का सेट, d = वांछित इनपुट, W = फ़िल्टर संख्याओं का सेट, ε = त्रुटि आउटपुट, f = फ़िल्टर प्रेरणा प्रतिक्रिया, * = संवेगण, Σ = योग, ऊपरी बक्सा = रैखिक फ़िल्टर, निचली बक्सा = अनुकूलन एल्गोरिदम।]] | :[[File:Adaptive Filter General.png|thumb|400px|alt=A block diagram of an adaptive filter with a separate block for the adaptation processअनुकूली फिल्टर। k = नमूना संख्या, x = संदर्भ इनपुट, X = x के हाल के मानों का सेट, d = वांछित इनपुट, W = फ़िल्टर गुणांक का सेट, ε = त्रुटि आउटपुट, f = फ़िल्टर आवेग प्रतिक्रिया, * = दृढ़ संकल्प, Σ = योग, ऊपरी बॉक्स = रैखिक फ़िल्टर, निचला बॉक्स = अनुकूलन एल्गोरिदम|एडैप्टिव फ़िल्टर। k = सैंपल नंबर, x = संदर्भ इनपुट, X = हाल के x मानों का सेट, d = वांछित इनपुट, W = फ़िल्टर संख्याओं का सेट, ε = त्रुटि आउटपुट, f = फ़िल्टर प्रेरणा प्रतिक्रिया, * = संवेगण, Σ = योग, ऊपरी बक्सा = रैखिक फ़िल्टर, निचली बक्सा = अनुकूलन एल्गोरिदम।]] | ||
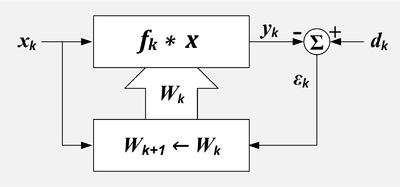
[[File:Adaptive Filter Compact.png|thumb|400px|alt=A compact block diagram of an adaptive filter without a separate block for the adaptation processअनुकूली फ़िल्टर, कॉम्पैक्ट प्रतिनिधित्व। के = नमूना संख्या, एक्स = संदर्भ इनपुट, डी = वांछित इनपुट, ε = त्रुटि आउटपुट, एफ = फ़िल्टर आवेग प्रतिक्रिया, Σ = सारांश, बॉक्स = रैखिक फ़िल्टर और अनुकूलन एल्गोरिदम।|एडैप्टिव फ़िल्टर, संक्षिप्त प्रतिस्थापन। k = सैंपल नंबर, x = संदर्भ इनपुट, d = वांछित इनपुट, ε = त्रुटि आउटपुट, f = फ़िल्टर प्रेरणा प्रतिक्रिया, Σ = योग, बक्सा = रैखिक फ़िल्टर और अनुकूलन | [[File:Adaptive Filter Compact.png|thumb|400px|alt=A compact block diagram of an adaptive filter without a separate block for the adaptation processअनुकूली फ़िल्टर, कॉम्पैक्ट प्रतिनिधित्व। के = नमूना संख्या, एक्स = संदर्भ इनपुट, डी = वांछित इनपुट, ε = त्रुटि आउटपुट, एफ = फ़िल्टर आवेग प्रतिक्रिया, Σ = सारांश, बॉक्स = रैखिक फ़िल्टर और अनुकूलन एल्गोरिदम।|एडैप्टिव फ़िल्टर, संक्षिप्त प्रतिस्थापन। k = सैंपल नंबर, x = संदर्भ इनपुट, d = वांछित इनपुट, ε = त्रुटि आउटपुट, f = फ़िल्टर प्रेरणा प्रतिक्रिया, Σ = योग, बक्सा = रैखिक फ़िल्टर और अनुकूलन एल्गोरिदम होता है ।]]अनुकूलनशील फ़िल्टर के लिए दो इनपुट संकेत हैं: <math> d_k </math> और <math> x_k </math> जिन्हें कभी-कभी क्रमशः प्राथमिक इनपुट और संदर्भ इनपुट कहा जाता है।<ref>Widrow p 304</ref> अनुकूलन एल्गोरिदम अवशिष्ट संकेत को कम करके वांछित इनपुट की प्रतिकृति में संदर्भ इनपुट को फ़िल्टर करने का प्रयास करता है, <math> \epsilon_k </math>. जब अनुकूलन सफल होता है, तो फ़िल्टर का आउटपुट <math> y_k </math> प्रभावी रूप से वांछित संकेत का अनुमान है। | ||
:<math> d_k </math> जिसमें वांछित संकेत प्लस अवांछित हस्तक्षेप सम्मलित है और | :<math> d_k </math> जिसमें वांछित संकेत प्लस अवांछित हस्तक्षेप सम्मलित है ,और | ||
:<math> x_k </math> जिसमें ऐसे संकेत सम्मलित हैं जो कुछ अवांछित हस्तक्षेप से संबंधित हैं <math> d_k </math>. | :<math> x_k </math> जिसमें ऐसे संकेत सम्मलित हैं जो कुछ अवांछित हस्तक्षेप से संबंधित हैं <math> d_k </math>. | ||
:k असतत नमूना संख्या का प्रतिनिधित्व करता है। | :k असतत नमूना संख्या का प्रतिनिधित्व करता है। | ||
| Line 29: | Line 29: | ||
::ये परिवर्तन नमूना समय k के बाद और नमूना समय k+1 पर उपयोग किए जाने से पहले लागू किए जाएंगे। | ::ये परिवर्तन नमूना समय k के बाद और नमूना समय k+1 पर उपयोग किए जाने से पहले लागू किए जाएंगे। | ||
आउटपुट सामान्यतः <math> \epsilon_k </math> होता है | आउटपुट सामान्यतः <math> \epsilon_k </math> होता है किन्तु यह हो सकता है <math> y_k </math> या यह फ़िल्टर गुणांक भी हो सकता है।<ref>Widrow p 212</ref>(विधवा) | ||
इनपुट संकेतों को निम्नानुसार परिभाषित किया गया है: | इनपुट संकेतों को निम्नानुसार परिभाषित किया गया है: | ||
| Line 37: | Line 37: | ||
:यहां: | :यहां: | ||
::g = वांछित संकेत, | ::g = वांछित संकेत, | ||
::g{{'}} = | ::g{{'}} = संकेत जो वांछित संकेत जी से संबंधित होता है, | ||
::u = g में जोड़े जाने वाले अनुचित संकेत, लेकिन g या g{{'}} के संबंध में नहीं होता है, | ::u = g में जोड़े जाने वाले अनुचित संकेत, लेकिन g या g{{'}} के संबंध में नहीं होता है, | ||
::u{{'}} = अनुचित संकेत u से संबंधित होता है, लेकिन g या g{{'}} के संबंध में नहीं होता है, | ::u{{'}} = अनुचित संकेत u से संबंधित होता है, लेकिन g या g{{'}} के संबंध में नहीं होता है, | ||
| Line 55: | Line 55: | ||
:<math> y_k= \sum_{l=0}^L w_{lk} \ x_{(k-l)} = \hat{g}_k + \hat{u}_k + \hat{v}_k </math> | :<math> y_k= \sum_{l=0}^L w_{lk} \ x_{(k-l)} = \hat{g}_k + \hat{u}_k + \hat{v}_k </math> | ||
::जहाँ <math> w_{lk} </math> यह आपकी जानकारी के लिए है <math>l</math>'जन्म के समय | ::जहाँ <math> w_{lk} </math> यह आपकी जानकारी के लिए है <math>l</math>'जन्म के समय वजन होता है । | ||
=== आदर्श स्थिति === | === आदर्श स्थिति === | ||
आदर्श स्थिति में <math> v \equiv 0, v' \equiv 0, g' \equiv 0 </math> होता है। सभी अवांछित संकेत अंदर <math> d_k </math> द्वारा प्रतिनिधित्व किया जाता है <math> u_k </math> <math> \ x_k </math> में अवांछित संकेत के साथ सहसंबद्ध | आदर्श स्थिति में <math> v \equiv 0, v' \equiv 0, g' \equiv 0 </math> होता है। सभी अवांछित संकेत अंदर <math> d_k </math> द्वारा प्रतिनिधित्व किया जाता है <math> u_k </math> <math> \ x_k </math> में अवांछित संकेत के साथ सहसंबद्ध संकेत के पूरी तरह से होते हैं <math> u_k </math>. | ||
आदर्श स्थितियों में वेरिएबल फ़िल्टर का आउटपुट | आदर्श स्थितियों में वेरिएबल फ़िल्टर का आउटपुट होता है | ||
:<math> y_k = \hat{u}_k</math> . | :<math> y_k = \hat{u}_k</math> . | ||
त्रुटि संकेत या हानि फंक्शन के बीच का अंतर है <math> d_k </math> और <math> y_k </math> | त्रुटि संकेत या हानि फंक्शन के बीच का अंतर होता है <math> d_k </math> और <math> y_k </math> | ||
:<math> \epsilon_k = d_k-y_k = g_k+ u_k - \hat{u}_k </math>. वांछित संकेत ''g''<sub>k</sub> बिना बदले गुजरता है। | :<math> \epsilon_k = d_k-y_k = g_k+ u_k - \hat{u}_k </math>. वांछित संकेत ''g''<sub>k</sub> बिना बदले गुजरता है। | ||
| Line 75: | Line 75: | ||
:<math> \epsilon_k = d_k-y_k = g_k - \hat{g}_k+ u_k - \hat{u}_k </math>. वांछित संकेत संशोधित किया जाएगा (सामान्यतः घटाया गया)। | :<math> \epsilon_k = d_k-y_k = g_k - \hat{g}_k+ u_k - \hat{u}_k </math>. वांछित संकेत संशोधित किया जाएगा (सामान्यतः घटाया गया)। | ||
आउटपुट संकेत टू इंटरफेरेंस अनुपात का | आउटपुट संकेत टू इंटरफेरेंस अनुपात का सरल सूत्र है जिसे पावर इनवर्जन कहा जाता है। | ||
: <math> \rho_{\mathsf{out}}(z) = \frac{1}{ \rho_{\mathsf{ref}}(z)} </math>. | : <math> \rho_{\mathsf{out}}(z) = \frac{1}{ \rho_{\mathsf{ref}}(z)} </math>. | ||
::यहां, | ::यहां, | ||
| Line 82: | Line 82: | ||
:::<math> z \ </math> = z-डोमेन में आवृत्ति। | :::<math> z \ </math> = z-डोमेन में आवृत्ति। | ||
यह सूत्र यह मतलब है कि | यह सूत्र यह मतलब है कि विशेष आवृत्ति पर आउटपुट संकेत से प्रतिरोध अनुपात संदर्भ संकेत से प्रतिरोध अनुपात का उलट होता है।<ref>Widrow p 313</ref> | ||
उदाहरण: | उदाहरण: फास्ट फूड रेस्तरां में ड्राइव-अप विंडो होती है। विंडो पर जाने से पहले, ग्राहक माइक्रोफ़ोन में बोलकर अपना ऑर्डर देते हैं। माइक्रोफोन इंजन और पर्यावरण से शोर भी उठाता है। यह माइक्रोफोन प्राथमिक संकेत प्रदान करता है। ग्राहक की आवाज से संकेत की शक्ति और इंजन से शोर की शक्ति समान होती है। रेस्टोरेंट के कर्मचारियों के लिए ग्राहक को समझना मुश्किल होता है। प्राथमिक माइक्रोफ़ोन में व्यवधान की मात्रा को कम करने के लिए, दूसरा माइक्रोफ़ोन उस स्थान पर स्थित होता है जहाँ इसका निश्चय इंजन से ध्वनियाँ लेने का होता है। यह ग्राहक की आवाज भी उठाता है। यह माइक्रोफोन संदर्भ संकेत का स्रोत है। ऐसे में इंजन का शोर ग्राहक की आवाज से 50 गुना अधिक शक्तिशाली होता है। बार कैंसिलर के अभिसरण हो जाने के बाद, प्राथमिक संकेत और हस्तक्षेप अनुपात 1:1 से 50:1 तक सुधर जाएगा। | ||
=== अनुकूलनशील रैखिक संयोजन === | === अनुकूलनशील रैखिक संयोजन === | ||
:[[File:Adaptive Linear Combiner General.png|thumb|400px|alt=A block diagram of an adaptive linear combiner with a separate block for the adaptation processअनुकूली रेखीय कॉम्बिनर जो कॉम्बिनर और अनुकूलन प्रक्रिया दिखा रहा है। के = नमूना संख्या, एन = इनपुट चर सूचकांक, एक्स = संदर्भ इनपुट, डी = वांछित इनपुट, डब्ल्यू = फिल्टर गुणांक का सेट, ε = त्रुटि आउटपुट, Σ = योग, ऊपरी बॉक्स = रैखिक संयोजन, निचला बॉक्स = अनुकूलन एल्गोरिदम।| | :[[File:Adaptive Linear Combiner General.png|thumb|400px|alt=A block diagram of an adaptive linear combiner with a separate block for the adaptation processअनुकूली रेखीय कॉम्बिनर जो कॉम्बिनर और अनुकूलन प्रक्रिया दिखा रहा है। के = नमूना संख्या, एन = इनपुट चर सूचकांक, एक्स = संदर्भ इनपुट, डी = वांछित इनपुट, डब्ल्यू = फिल्टर गुणांक का सेट, ε = त्रुटि आउटपुट, Σ = योग, ऊपरी बॉक्स = रैखिक संयोजन, निचला बॉक्स = अनुकूलन एल्गोरिदम।|एडाप्टिव रैखिक कम्बाइनर जो कम्बाइनर और एडेप्शन प्रक्रिया दिखाता है। k = सैंपल नंबर, n = इनपुट चर नंबर, x = संदर्भ इनपुट, d = वांछित इनपुट, W = फ़िल्टर संख्याएँ का सेट, ε = त्रुटि आउटपुट, Σ = योग, ऊपरी बॉक्स = रैखिक कम्बाइनर, निचले बॉक्स = एडेप्शन एल्गोरिदम।]] [[File:Adaptive Linear Combiner Compact.png|thumb|400px|alt=A compact block diagram of an adaptive linear combiner without a separate block for the adaptation processअनुकूली रैखिक संयोजक, कॉम्पैक्ट प्रतिनिधित्व। के = नमूना संख्या, एन = इनपुट चर सूचकांक, एक्स = संदर्भ इनपुट, डी = वांछित इनपुट, ε = त्रुटि आउटपुट, Σ = योग।|एडाप्टिव रैखिक कम्बाइनर, संक्षेपित प्रतिष्ठान। k = सैंपल नंबर, n = इनपुट चर सूची, x = संदर्भ इनपुट, d = वांछित इनपुट, ε = त्रुटि आउटपुट, Σ = योग।]]एडेप्टिव लीनियर कॉम्बिनर (एएलसी) एडेप्टिव टैप्ड डिले लाइन FIR फिल्टर जैसा दिखता है सिवाय इसके कि X वैल्यू के बीच कोई अनुमानित संबंध नहीं है। यदि X मान टैप की गई विलंब रेखा के आउटपुट से थे, तो टैप की गई विलंब रेखा और ALC के संयोजन में अनुकूलनशील फ़िल्टर सम्मलित होगा। चूँकि , X मान पिक्सेल की सरणी के मान हो सकते हैं। या वे एकाधिक टैप की गई विलंब लाइनों के आउटपुट हो सकते हैं। एएलसी को हाइड्रोफ़ोन या एंटेना के सरणी के लिए पूर्व अनुकूलनशील बीम के रूप में उपयोग मिलता है। | ||
:<math> y_k= \sum_{l=0}^L w_{lk} \ x_{lk} = \mathbf{W}_k^T \mathbf{x}_k </math> ::जहाँ<math> w_{lk} </math> यह आपकी जानकारी के लिए है <math>l</math>'जन्म के समय वजन। | :<math> y_k= \sum_{l=0}^L w_{lk} \ x_{lk} = \mathbf{W}_k^T \mathbf{x}_k </math> ::जहाँ<math> w_{lk} </math> यह आपकी जानकारी के लिए है <math>l</math>'जन्म के समय वजन। | ||
=== | === एलएमएस एल्गोरिथ्म === | ||
{{Main|कम से कम औसत वर्ग फ़िल्टर}} | {{Main|कम से कम औसत वर्ग फ़िल्टर}} | ||
यदि चर फ़िल्टर में टैप की गई विलंब रेखा FIR संरचना होती है, तो | यदि चर फ़िल्टर में टैप की गई विलंब रेखा FIR संरचना होती है, तो एलएमएस अपडेट एल्गोरिथ्म विशेष रूप से सरल होता है। सामान्यतः, प्रत्येक नमूने के बाद, FIR फ़िल्टर के गुणांक निम्नानुसार समायोजित किए जाते हैं:<ref>Widrow p 100</ref>(विद्रो ) | ||
: के लिए <math> l = 0 \dots L </math> | : के लिए <math> l = 0 \dots L </math> | ||
:<math> w_{l,k+1} = w_{lk} + 2 \mu \ \epsilon_k \ x_{k-l} </math> :::μ को अभिसरण कारक कहा जाता है। | :<math> w_{l,k+1} = w_{lk} + 2 \mu \ \epsilon_k \ x_{k-l} </math> :::μ को अभिसरण कारक कहा जाता है। | ||
एलएमएस एल्गोरिथम के लिए यह आवश्यक नहीं है कि X मानों का कोई विशेष संबंध हो; इसलिए इसका उपयोग लीनियर कॉम्बिनर के साथ-साथ FIR फिल्टर को अनुकूलित करने के लिए किया जा सकता है। इस स्थितियों में अद्यतन सूत्र इस प्रकार लिखा गया है: | |||
:<math> w_{l,k+1} = w_{lk} + 2 \mu \ \epsilon_k \ x_{lk} </math> | :<math> w_{l,k+1} = w_{lk} + 2 \mu \ \epsilon_k \ x_{lk} </math> | ||
एलएमएस एल्गोरिथम का प्रभाव प्रत्येक समय, k, प्रत्येक भार में छोटा परिवर्तन करने के लिए होता है। परिवर्तन की दिशा ऐसी है कि यदि इसे समय k पर लागू किया गया होता तो यह त्रुटि को कम कर देता। प्रत्येक भार में परिवर्तन का परिमाण μ, संबद्ध X मान और समय k पर त्रुटि पर निर्भर करता है। भार उत्पादन में सबसे बड़ा योगदान देता है, <math> y_k </math>, सबसे ज्यादा बदले जाते हैं। यदि त्रुटि शून्य है, तो भार में कोई परिवर्तन नहीं होना चाहिए। यदि X का संबंधित मान शून्य है, तो वजन बदलने से कोई अंतर नहीं पड़ता, इसलिए इसे नहीं बदला जाता है। | |||
==== अभिसरण ==== | ==== अभिसरण ==== | ||
| Line 109: | Line 109: | ||
μ नियंत्रित करता है कि एल्गोरिथ्म कितनी तेजी से और कितनी अच्छी तरह से इष्टतम फिल्टर गुणांक में परिवर्तित होता है। यदि μ बहुत बड़ा है, तो एल्गोरिथम एकाग्र नहीं होगा। यदि μ बहुत छोटा है तो एल्गोरिदम धीरे-धीरे अभिसरण करता है और बदलती स्थितियों को ट्रैक करने में सक्षम नहीं हो सकता है। यदि μ बड़ा है किन्तु अभिसरण को रोकने के लिए बहुत बड़ा नहीं है, एल्गोरिथ्म तेजी से स्थिर स्थिति तक पहुंचता है किन्तु इष्टतम वजन वेक्टर को लगातार ओवरशूट करता है। कभी-कभी, μ को पहले तेजी से अभिसरण के लिए बड़ा बनाया जाता है और फिर ओवरशूट को कम करने के लिए घटाया जाता है। | μ नियंत्रित करता है कि एल्गोरिथ्म कितनी तेजी से और कितनी अच्छी तरह से इष्टतम फिल्टर गुणांक में परिवर्तित होता है। यदि μ बहुत बड़ा है, तो एल्गोरिथम एकाग्र नहीं होगा। यदि μ बहुत छोटा है तो एल्गोरिदम धीरे-धीरे अभिसरण करता है और बदलती स्थितियों को ट्रैक करने में सक्षम नहीं हो सकता है। यदि μ बड़ा है किन्तु अभिसरण को रोकने के लिए बहुत बड़ा नहीं है, एल्गोरिथ्म तेजी से स्थिर स्थिति तक पहुंचता है किन्तु इष्टतम वजन वेक्टर को लगातार ओवरशूट करता है। कभी-कभी, μ को पहले तेजी से अभिसरण के लिए बड़ा बनाया जाता है और फिर ओवरशूट को कम करने के लिए घटाया जाता है। | ||
विड्रो और स्टर्न्स ने 1985 में कहा कि उन्हें इस बात का कोई ज्ञान नहीं है कि | विड्रो और स्टर्न्स ने 1985 में कहा कि उन्हें इस बात का कोई ज्ञान नहीं है कि एलएमएस एल्गोरिथम सभी स्थितियों में अभिसरण करता है।<ref name="Widrow p 103">Widrow p 103</ref> | ||
चूँकि स्थिरता और स्वतंत्रता के बारे में कुछ धारणाओं के अनुसार यह दिखाया जा सकता है कि एल्गोरिथम अभिसरण करेगा यदि | चूँकि स्थिरता और स्वतंत्रता के बारे में कुछ धारणाओं के अनुसार यह दिखाया जा सकता है कि एल्गोरिथम अभिसरण करेगा यदि | ||
| Line 119: | Line 119: | ||
:::<math>\sigma_l</math> का मूल माध्य वर्ग मान है <math>l </math> वें इनपुट | :::<math>\sigma_l</math> का मूल माध्य वर्ग मान है <math>l </math> वें इनपुट | ||
टैप किए गए विलंब लाइन फ़िल्टर के स्थितियों में, प्रत्येक इनपुट का समान | टैप किए गए विलंब लाइन फ़िल्टर के स्थितियों में, प्रत्येक इनपुट का समान एलएमएस मान होता है क्योंकि वे केवल वही मान विलंबित होते हैं। इस स्थितियों में कुल शक्ति ये होती है | ||
:<math> \sigma^2 = (L+1) \sigma_0^2 </math> | :<math> \sigma^2 = (L+1) \sigma_0^2 </math> | ||
::जहाँ | ::जहाँ | ||
:::<math>\sigma_0</math> का | :::<math>\sigma_0</math> का एलएमएस मान है <math>x_k</math>, इनपुट स्ट्रीम होता है।<ref name="Widrow p 103" /> | ||
यह सामान्यीकृत | यह सामान्यीकृत एलएमएस एल्गोरिदम की ओर जाता है: | ||
:<math> w_{l,k+1} = w_{lk} + \left ( \frac { 2 \mu_{\sigma} } {\sigma^2} \right ) \epsilon_k \ x_{k-l} </math> किस स्थितियों में अभिसरण मानदंड बन जाता है: <math> 0 < \mu_{\sigma} < 1 </math>. | :<math> w_{l,k+1} = w_{lk} + \left ( \frac { 2 \mu_{\sigma} } {\sigma^2} \right ) \epsilon_k \ x_{k-l} </math> किस स्थितियों में अभिसरण मानदंड बन जाता है: <math> 0 < \mu_{\sigma} < 1 </math>. | ||
=== अरेखीय अनुकूलनशील फिल्टर === | === अरेखीय अनुकूलनशील फिल्टर === | ||
गैर-रैखिक फिल्टर का लक्ष्य रैखिक मॉडल की सीमा को दूर करना है। कुछ सामान्य रूप से उपयोग किए जाने वाले दृष्टिकोण हैं: वोलटेर्रा | गैर-रैखिक फिल्टर का लक्ष्य रैखिक मॉडल की सीमा को दूर करना होता है। कुछ सामान्य रूप से उपयोग किए जाने वाले दृष्टिकोण हैं: वोलटेर्रा एलएमएस , [[कर्नेल अनुकूली फ़िल्टर|कर्नेल अनुकूलनशील फ़िल्टर]], तख़्ता अनुकूलनशील फ़िल्टर <ref>{{cite book|author1=Danilo Comminiello |author2= José C. Príncipe |title= गैर-रैखिक प्रणाली मॉडलिंग के लिए अनुकूली सीखने के तरीके|date= 2018 |publisher=Elsevier Inc. |isbn= 978-0-12-812976-0}}</ref> और उरीसोहन अनुकूलनशील फ़िल्टर होते है ।<ref>M.Poluektov and A.Polar. [http://ezcodesample.com/UAF/UAF.html Urysohn Adaptive Filter]. 2019.</ref><ref>{{Cite web|url=http://ezcodesample.com/NAF/index.html|title=गैर रेखीय अनुकूली फ़िल्टरिंग|website=ezcodesample.com}}</ref> कई लेखक <ref name=Liu2010>{{cite book|author1=Weifeng Liu |author2=José C. Principe |author3=Simon Haykin |title=Kernel Adaptive Filtering: A Comprehensive Introduction|date=March 2010|publisher=Wiley|isbn=978-0-470-44753-6|pages=12–20|url=http://media.wiley.com/product_data/excerpt/32/04704475/0470447532.pdf}}</ref> इस सूची में तंत्रिका नेटवर्क भी सम्मलित करें। वोलटेर्रा एलएमएस और कर्नेल एलएमएस के पीछे सामान्य विचार यह है कि डेटा नमूनों को अलग-अलग अरैखिक बीजगणितीय व्यंजकों द्वारा प्रतिस्थापित किया जाता है । वोलटेर्रा एलएमएस के लिए यह अभिव्यक्ति [[Volterra series|वोलटेर्रा सीरीज]] है। तख़्ता अनुकूलनशील फ़िल्टर में मॉडल रैखिक गतिशील ब्लॉक और स्थैतिक गैर-रैखिकता का झरना है, जिसे स्प्लिन द्वारा अनुमानित किया जाता है। उरिसोह्न अनुकूलनशील फ़िल्टर में मॉडल में रैखिक शब्द | ||
:<math> y_i= \sum_{j=0}^m w_{j} \ x_{ij} </math> टुकड़ों के रैखिक कार्यों द्वारा प्रतिस्थापित किया जाता है | :<math> y_i= \sum_{j=0}^m w_{j} \ x_{ij} </math> टुकड़ों के रैखिक कार्यों द्वारा प्रतिस्थापित किया जाता है | ||
| Line 153: | Line 153: | ||
* कर्नेल अनुकूलनशील फ़िल्टर | * कर्नेल अनुकूलनशील फ़िल्टर | ||
* रेखीय भविष्यवाणी | * रेखीय भविष्यवाणी | ||
* [[एमएमएसई | * [[एमएमएसई अनुमानक]] | ||
* [[ विनीज़ फ़िल्टर ]] | * [[ विनीज़ फ़िल्टर ]] | ||
* [[वीनर-हॉफ समीकरण]] | * [[वीनर-हॉफ समीकरण]] | ||
| Line 168: | Line 168: | ||
*{{cite book |last1=Widrow |first1=Bernard |last2=Stearns |first2=Samuel D. |title=अनुकूली सिग्नल प्रोसेसिंग|year=1985 |publisher=Prentice Hall |location=Englewood Cliffs, NJ |isbn=978-0-13-004029-9}} | *{{cite book |last1=Widrow |first1=Bernard |last2=Stearns |first2=Samuel D. |title=अनुकूली सिग्नल प्रोसेसिंग|year=1985 |publisher=Prentice Hall |location=Englewood Cliffs, NJ |isbn=978-0-13-004029-9}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Adaptive Filter]] | |||
[[Category:Created On 31/05/2023|Adaptive Filter]] | |||
[[Category:Machine Translated Page|Adaptive Filter]] | |||
[[Category:Pages with script errors|Adaptive Filter]] | |||
[[Category:Templates Vigyan Ready|Adaptive Filter]] | |||
[[Category: Machine Translated Page]] | |||
[[Category: | |||
Latest revision as of 16:27, 26 October 2023
अनुकूलनशील फ़िल्टर रेखीय फ़िल्टर (संकेत प्रोसेसिंग) वाली प्रणाली होती है जिसमें चर मापदंडों द्वारा नियंत्रित स्थानांतरण फ़ंक्शन होता है और अनुकूलन एल्गोरिथम के अनुसार उन मापदंडों को समायोजित करने का साधन होता है। अनुकूलन एल्गोरिदम की जटिलता के कारण, लगभग सभी अनुकूलनशील फ़िल्टर डिजिटल फिल्टर के रूप में होते हैं। कुछ अनुप्रयोगों के लिए अनुकूलनशील फिल्टर की आवश्यकता होती है क्योंकि वांछित प्रसंस्करण संचालन के कुछ पैरामीटर (उदाहरण के लिए, प्रतिध्वनि स्थान में परावर्तक सतहों के स्थान) पहले से ज्ञात नहीं होते हैं या बदल रहे हैं। बंद लूप अनुकूलनशील फ़िल्टर अपने स्थानांतरण फ़ंक्शन को परिष्कृत करने के लिए त्रुटि संकेत के रूप में प्रतिक्रिया का उपयोग करता है।
सामान्यतः बंद लूप अनुकूलनशील प्रक्रिया में लॉस फ़ंक्शन का उपयोग सम्मलित होता है, जो फ़िल्टर के इष्टतम प्रदर्शन के लिए मान्यता होता है, और इसे एल्गोरिदम को खिलाने के लिए, जो यह निर्धारित करता है कि अगले पुनरावृत्ति पर लागत को कम करने के लिए फ़िल्टर स्थानांतरण प्रकार्य को कैसे संशोधित किया जाता है। सबसे सामान्य लागत फलन त्रुटि संकेत का माध्य वर्ग है।
चूंकि डिजिटल संकेत प्रोसेसर की शक्ति में वृद्धि हुई है, अनुकूलनशील फिल्टर अधिक सामान्य हो गए हैं और अब नियमित रूप से मोबाइल फोन और अन्य संचार उपकरणों, कैमकोर्डर और डिजिटल कैमरे, और चिकित्सा निगरानी उपकरण जैसे उपकरणों में उपयोग किए जाते हैं।
उदाहरण आवेदन
दिल की धड़कन ( ईसीजी) की रिकॉर्डिंग, बिजली की आपूर्ति से शोर से दूषित हो सकती है। शक्ति और उसके हार्मोनिक्स की सटीक आवृत्ति पल-पल भिन्न हो सकती है।
शोर को दूर करने का विधि मुख्य आवृत्ति और उसके आसपास के क्षेत्र में पायदान फिल्टर के साथ संकेत को फ़िल्टर करना है, किन्तु यह ईसीजी की गुणवत्ता को अत्यधिक कम कर सकता है क्योंकि दिल की धड़कन में भी अस्वीकृत सीमा में आवृत्ति घटक होते है ।
सूचना के इस संभावित हानि को रोकने के लिए, अनुकूलनशील फ़िल्टर का उपयोग किया जा सकता है। अनुकूलनशील फ़िल्टर रोगी और मुख्य दोनों से इनपुट लेगा और इस प्रकार शोर की वास्तविक आवृत्ति को ट्रैक करने में सक्षम होगा क्योंकि यह रिकॉर्डिंग से शोर घटाता है और घटाता है। ऐसी अनुकूलनशील तकनीक सामान्यतः छोटी अस्वीकृति सीमा के साथ फिल्टर की अनुमति देती है, जिसका अर्थ है, इस स्थितियों में, चिकित्सा उद्देश्यों के लिए आउटपुट संकेत की गुणवत्ता अधिक सटीक है।[1][2]
ब्लॉक आरेख
बंद लूप अनुकूलनशील फ़िल्टर के पीछे की विचारधारा है कि परिवर्तनशील फ़िल्टर को तब तक समायोजित किया जाता है जब तक कि त्रुटि (फ़िल्टर आउटपुट और वांछित संकेत के बीच का अंतर)को कम से कम नहीं किया जाता है। न्यूनतम माध्य वर्ग (एलएमएस ) फ़िल्टर और पुनरावर्ती न्यूनतम वर्ग (आरएलएस) फ़िल्टर अनुकूलनशील फ़िल्टर के रूप में होते हैं।
अनुकूलनशील फ़िल्टर के लिए दो इनपुट संकेत हैं: और जिन्हें कभी-कभी क्रमशः प्राथमिक इनपुट और संदर्भ इनपुट कहा जाता है।[3] अनुकूलन एल्गोरिदम अवशिष्ट संकेत को कम करके वांछित इनपुट की प्रतिकृति में संदर्भ इनपुट को फ़िल्टर करने का प्रयास करता है, . जब अनुकूलन सफल होता है, तो फ़िल्टर का आउटपुट प्रभावी रूप से वांछित संकेत का अनुमान है।
- जिसमें वांछित संकेत प्लस अवांछित हस्तक्षेप सम्मलित है ,और
- जिसमें ऐसे संकेत सम्मलित हैं जो कुछ अवांछित हस्तक्षेप से संबंधित हैं .
- k असतत नमूना संख्या का प्रतिनिधित्व करता है।
फ़िल्टर को L+1 गुणांक या भार के सेट द्वारा नियंत्रित किया जाता है।
- वज़न के सेट या वेक्टर का प्रतिनिधित्व करता है, जो नमूना समय k पर फ़िल्टर को नियंत्रित करता है।
- यहां, यह आपकी जानकारी के लिए है 'जन्म के समय वजन।
- नमूना समय k पर गणना किए गए समायोजन के परिणामस्वरूप होने वाले वज़न में परिवर्तन का प्रतिनिधित्व करता है।
- ये परिवर्तन नमूना समय k के बाद और नमूना समय k+1 पर उपयोग किए जाने से पहले लागू किए जाएंगे।
आउटपुट सामान्यतः होता है किन्तु यह हो सकता है या यह फ़िल्टर गुणांक भी हो सकता है।[4](विधवा)
इनपुट संकेतों को निम्नानुसार परिभाषित किया गया है:
- यहां:
- g = वांछित संकेत,
- g' = संकेत जो वांछित संकेत जी से संबंधित होता है,
- u = g में जोड़े जाने वाले अनुचित संकेत, लेकिन g या g' के संबंध में नहीं होता है,
- u' = अनुचित संकेत u से संबंधित होता है, लेकिन g या g' के संबंध में नहीं होता है,
- v =g, g', u, u' या v के संबंध में नहीं होने वाला अनुचित संकेत (सामान्यतः यादृच्छिक शोर),
- v' = g, g', u, u' या v के संबंध में नहीं होने वाला अनुचित संकेत (सामान्यतः यादृच्छिक शोर)।
आउटपुट संकेत निम्नानुसार परिभाषित किए गए हैं:
- .
- जहाँ:
- = फ़िल्टर का आउटपुट यदि इनपुट केवल g था',
- = फ़िल्टर का आउटपुट यदि इनपुट केवल u था',
- = फ़िल्टर का आउटपुट यदि इनपुट केवल v था'.
टैप की गई देरी लाइन FIR फ़िल्टर
यदि चर फ़िल्टर में टैप की गई विलंब रेखा परिमित आवेग प्रतिक्रिया (FIR) संरचना है, तो आवेग प्रतिक्रिया फ़िल्टर गुणांक के समान होती है। फ़िल्टर का आउटपुट द्वारा दिया जाता है
-
- जहाँ यह आपकी जानकारी के लिए है 'जन्म के समय वजन होता है ।
आदर्श स्थिति
आदर्श स्थिति में होता है। सभी अवांछित संकेत अंदर द्वारा प्रतिनिधित्व किया जाता है में अवांछित संकेत के साथ सहसंबद्ध संकेत के पूरी तरह से होते हैं .
आदर्श स्थितियों में वेरिएबल फ़िल्टर का आउटपुट होता है
- .
त्रुटि संकेत या हानि फंक्शन के बीच का अंतर होता है और
- . वांछित संकेत gk बिना बदले गुजरता है।
त्रुटि संकेत माध्य वर्ग अर्थ में न्यूनतम किया जाता है जब कम किया जाता है। दूसरे शब्दों में, का सर्वोत्तम माध्य वर्ग अनुमान है . आदर्श स्थिति में, और , और घटाव के बाद जो कुछ बचा है वह है जो अपरिवर्तित वांछित संकेत है जिसमें सभी अवांछित संकेत हटा दिए गए हैं।
संदर्भ इनपुट में संकेत घटक
कुछ स्थितियों में, संदर्भ इनपुट वांछित संकेत के घटक सम्मलित हैं। इसका अर्थ है g' ≠ 0 होता है।
स्थितियों में अवांछित हस्तक्षेप का पूर्ण रद्दीकरण संभव नहीं है, किन्तु हस्तक्षेप अनुपात के संकेत में सुधार संभव है। आउटपुट होगा
- . वांछित संकेत संशोधित किया जाएगा (सामान्यतः घटाया गया)।
आउटपुट संकेत टू इंटरफेरेंस अनुपात का सरल सूत्र है जिसे पावर इनवर्जन कहा जाता है।
- .
- यहां,
- = हस्तक्षेप अनुपात के लिए आउटपुट सिग्नल।
- = हस्तक्षेप अनुपात के संदर्भ संकेत।
- = z-डोमेन में आवृत्ति।
- यहां,
यह सूत्र यह मतलब है कि विशेष आवृत्ति पर आउटपुट संकेत से प्रतिरोध अनुपात संदर्भ संकेत से प्रतिरोध अनुपात का उलट होता है।[5]
उदाहरण: फास्ट फूड रेस्तरां में ड्राइव-अप विंडो होती है। विंडो पर जाने से पहले, ग्राहक माइक्रोफ़ोन में बोलकर अपना ऑर्डर देते हैं। माइक्रोफोन इंजन और पर्यावरण से शोर भी उठाता है। यह माइक्रोफोन प्राथमिक संकेत प्रदान करता है। ग्राहक की आवाज से संकेत की शक्ति और इंजन से शोर की शक्ति समान होती है। रेस्टोरेंट के कर्मचारियों के लिए ग्राहक को समझना मुश्किल होता है। प्राथमिक माइक्रोफ़ोन में व्यवधान की मात्रा को कम करने के लिए, दूसरा माइक्रोफ़ोन उस स्थान पर स्थित होता है जहाँ इसका निश्चय इंजन से ध्वनियाँ लेने का होता है। यह ग्राहक की आवाज भी उठाता है। यह माइक्रोफोन संदर्भ संकेत का स्रोत है। ऐसे में इंजन का शोर ग्राहक की आवाज से 50 गुना अधिक शक्तिशाली होता है। बार कैंसिलर के अभिसरण हो जाने के बाद, प्राथमिक संकेत और हस्तक्षेप अनुपात 1:1 से 50:1 तक सुधर जाएगा।
अनुकूलनशील रैखिक संयोजन
- एडेप्टिव लीनियर कॉम्बिनर (एएलसी) एडेप्टिव टैप्ड डिले लाइन FIR फिल्टर जैसा दिखता है सिवाय इसके कि X वैल्यू के बीच कोई अनुमानित संबंध नहीं है। यदि X मान टैप की गई विलंब रेखा के आउटपुट से थे, तो टैप की गई विलंब रेखा और ALC के संयोजन में अनुकूलनशील फ़िल्टर सम्मलित होगा। चूँकि , X मान पिक्सेल की सरणी के मान हो सकते हैं। या वे एकाधिक टैप की गई विलंब लाइनों के आउटपुट हो सकते हैं। एएलसी को हाइड्रोफ़ोन या एंटेना के सरणी के लिए पूर्व अनुकूलनशील बीम के रूप में उपयोग मिलता है।
- ::जहाँ यह आपकी जानकारी के लिए है 'जन्म के समय वजन।
एलएमएस एल्गोरिथ्म
यदि चर फ़िल्टर में टैप की गई विलंब रेखा FIR संरचना होती है, तो एलएमएस अपडेट एल्गोरिथ्म विशेष रूप से सरल होता है। सामान्यतः, प्रत्येक नमूने के बाद, FIR फ़िल्टर के गुणांक निम्नानुसार समायोजित किए जाते हैं:[6](विद्रो )
- के लिए
- :::μ को अभिसरण कारक कहा जाता है।
एलएमएस एल्गोरिथम के लिए यह आवश्यक नहीं है कि X मानों का कोई विशेष संबंध हो; इसलिए इसका उपयोग लीनियर कॉम्बिनर के साथ-साथ FIR फिल्टर को अनुकूलित करने के लिए किया जा सकता है। इस स्थितियों में अद्यतन सूत्र इस प्रकार लिखा गया है:
एलएमएस एल्गोरिथम का प्रभाव प्रत्येक समय, k, प्रत्येक भार में छोटा परिवर्तन करने के लिए होता है। परिवर्तन की दिशा ऐसी है कि यदि इसे समय k पर लागू किया गया होता तो यह त्रुटि को कम कर देता। प्रत्येक भार में परिवर्तन का परिमाण μ, संबद्ध X मान और समय k पर त्रुटि पर निर्भर करता है। भार उत्पादन में सबसे बड़ा योगदान देता है, , सबसे ज्यादा बदले जाते हैं। यदि त्रुटि शून्य है, तो भार में कोई परिवर्तन नहीं होना चाहिए। यदि X का संबंधित मान शून्य है, तो वजन बदलने से कोई अंतर नहीं पड़ता, इसलिए इसे नहीं बदला जाता है।
अभिसरण
μ नियंत्रित करता है कि एल्गोरिथ्म कितनी तेजी से और कितनी अच्छी तरह से इष्टतम फिल्टर गुणांक में परिवर्तित होता है। यदि μ बहुत बड़ा है, तो एल्गोरिथम एकाग्र नहीं होगा। यदि μ बहुत छोटा है तो एल्गोरिदम धीरे-धीरे अभिसरण करता है और बदलती स्थितियों को ट्रैक करने में सक्षम नहीं हो सकता है। यदि μ बड़ा है किन्तु अभिसरण को रोकने के लिए बहुत बड़ा नहीं है, एल्गोरिथ्म तेजी से स्थिर स्थिति तक पहुंचता है किन्तु इष्टतम वजन वेक्टर को लगातार ओवरशूट करता है। कभी-कभी, μ को पहले तेजी से अभिसरण के लिए बड़ा बनाया जाता है और फिर ओवरशूट को कम करने के लिए घटाया जाता है।
विड्रो और स्टर्न्स ने 1985 में कहा कि उन्हें इस बात का कोई ज्ञान नहीं है कि एलएमएस एल्गोरिथम सभी स्थितियों में अभिसरण करता है।[7]
चूँकि स्थिरता और स्वतंत्रता के बारे में कुछ धारणाओं के अनुसार यह दिखाया जा सकता है कि एल्गोरिथम अभिसरण करेगा यदि
-
- जहाँ
- = सभी इनपुट शक्ति का योग
- जहाँ
- का मूल माध्य वर्ग मान है वें इनपुट
टैप किए गए विलंब लाइन फ़िल्टर के स्थितियों में, प्रत्येक इनपुट का समान एलएमएस मान होता है क्योंकि वे केवल वही मान विलंबित होते हैं। इस स्थितियों में कुल शक्ति ये होती है
-
- जहाँ
- का एलएमएस मान है , इनपुट स्ट्रीम होता है।[7]
- जहाँ
यह सामान्यीकृत एलएमएस एल्गोरिदम की ओर जाता है:
- किस स्थितियों में अभिसरण मानदंड बन जाता है: .
अरेखीय अनुकूलनशील फिल्टर
गैर-रैखिक फिल्टर का लक्ष्य रैखिक मॉडल की सीमा को दूर करना होता है। कुछ सामान्य रूप से उपयोग किए जाने वाले दृष्टिकोण हैं: वोलटेर्रा एलएमएस , कर्नेल अनुकूलनशील फ़िल्टर, तख़्ता अनुकूलनशील फ़िल्टर [8] और उरीसोहन अनुकूलनशील फ़िल्टर होते है ।[9][10] कई लेखक [11] इस सूची में तंत्रिका नेटवर्क भी सम्मलित करें। वोलटेर्रा एलएमएस और कर्नेल एलएमएस के पीछे सामान्य विचार यह है कि डेटा नमूनों को अलग-अलग अरैखिक बीजगणितीय व्यंजकों द्वारा प्रतिस्थापित किया जाता है । वोलटेर्रा एलएमएस के लिए यह अभिव्यक्ति वोलटेर्रा सीरीज है। तख़्ता अनुकूलनशील फ़िल्टर में मॉडल रैखिक गतिशील ब्लॉक और स्थैतिक गैर-रैखिकता का झरना है, जिसे स्प्लिन द्वारा अनुमानित किया जाता है। उरिसोह्न अनुकूलनशील फ़िल्टर में मॉडल में रैखिक शब्द
- टुकड़ों के रैखिक कार्यों द्वारा प्रतिस्थापित किया जाता है
- जिनकी पहचान डेटा नमूनों से की जाती है।
अनुकूलनशील फिल्टर के अनुप्रयोग
- अनुकूलनशील शोर रद्द करना
- सक्रिय शोर नियंत्रण
- रैखिक भविष्यवाणी
- अनुकूलनशील प्रतिक्रिया रद्द करना
- गूंज रद्दीकरण
फ़िल्टर कार्यान्वयन
- कम से कम औसत वर्ग फ़िल्टर
- पुनरावर्ती कम से कम वर्ग फ़िल्टर
- बहुविलंब ब्लॉक आवृत्ति डोमेन अनुकूलनशील फ़िल्टर
यह भी देखें
- 2D अनुकूलनशील फिल्टर
- फ़िल्टर (संकेत प्रोसेसिंग)
- कलमन फिल्टर
- कर्नेल अनुकूलनशील फ़िल्टर
- रेखीय भविष्यवाणी
- एमएमएसई अनुमानक
- विनीज़ फ़िल्टर
- वीनर-हॉफ समीकरण
संदर्भ
- ↑ Thakor, N.V.; Zhu, Yi-Sheng (1991-08-01). "Applications of adaptive filtering to ECG analysis: noise cancellation and arrhythmia detection". IEEE Transactions on Biomedical Engineering. 38 (8): 785–794. doi:10.1109/10.83591. ISSN 0018-9294. PMID 1937512. S2CID 11271450.
- ↑ Widrow, Bernard; Stearns, Samuel D. (1985). अनुकूली सिग्नल प्रोसेसिंग (1st ed.). Prentice-Hall. p. 329. ISBN 978-0130040299.
- ↑ Widrow p 304
- ↑ Widrow p 212
- ↑ Widrow p 313
- ↑ Widrow p 100
- ↑ 7.0 7.1 Widrow p 103
- ↑ Danilo Comminiello; José C. Príncipe (2018). गैर-रैखिक प्रणाली मॉडलिंग के लिए अनुकूली सीखने के तरीके. Elsevier Inc. ISBN 978-0-12-812976-0.
- ↑ M.Poluektov and A.Polar. Urysohn Adaptive Filter. 2019.
- ↑ "गैर रेखीय अनुकूली फ़िल्टरिंग". ezcodesample.com.
- ↑ Weifeng Liu; José C. Principe; Simon Haykin (March 2010). Kernel Adaptive Filtering: A Comprehensive Introduction (PDF). Wiley. pp. 12–20. ISBN 978-0-470-44753-6.
स्रोत
- Hayes, Monson H. (1996). सांख्यिकीय डिजिटल सिग्नल प्रोसेसिंग और मॉडलिंग. Wiley. ISBN 978-0-471-59431-4.
- Haykin, Simon (2002). अनुकूली फ़िल्टर सिद्धांत. Prentice Hall. ISBN 978-0-13-048434-5.
- Widrow, Bernard; Stearns, Samuel D. (1985). अनुकूली सिग्नल प्रोसेसिंग. Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0-13-004029-9.