प्रक्षेप (रैखिक बीजगणित): Difference between revisions
m (Abhishek moved page एक बिन्दु से एक रेखा की दूरी to बिन्दु से रेखा की दूरी without leaving a redirect) |
No edit summary |
||
| (8 intermediate revisions by 5 users not shown) | |||
| Line 2: | Line 2: | ||
[[यूक्लिडियन ज्यामिति]] में, एक बिंदु से एक रेखा तक की दूरी किसी दिए गए [[बिंदु (ज्यामिति)]] से एक अनंत [[रेखा (गणित)]] पर किसी भी बिंदु तक की सबसे छोटी [[यूक्लिडियन दूरी]] होती है। यह बिंदु की रेखा से [[लंबवत दूरी]] है, [[रेखा खंड]] की लंबाई जो बिंदु को रेखा पर निकटतम बिंदु से जोड़ती है। इसकी गणना करने का सूत्र कई तरीकों से निकाला और व्यक्त किया जा सकता है। | [[यूक्लिडियन ज्यामिति]] में, एक बिंदु से एक रेखा तक की दूरी किसी दिए गए [[बिंदु (ज्यामिति)]] से एक अनंत [[रेखा (गणित)]] पर किसी भी बिंदु तक की सबसे छोटी [[यूक्लिडियन दूरी]] होती है। यह बिंदु की रेखा से [[लंबवत दूरी]] है, [[रेखा खंड]] की लंबाई जो बिंदु को रेखा पर निकटतम बिंदु से जोड़ती है। इसकी गणना करने का सूत्र कई तरीकों से निकाला और व्यक्त किया जा सकता है। | ||
एक बिंदु से एक रेखा तक की दूरी को जानना विभिन्न स्थितियों में उपयोगी हो सकता है—उदाहरण के लिए, एक सड़क तक पहुँचने के लिए सबसे छोटी दूरी का पता लगाना, एक ग्राफ पर | एक बिंदु से एक रेखा तक की दूरी को जानना विभिन्न स्थितियों में उपयोगी हो सकता है—उदाहरण के लिए, एक सड़क तक पहुँचने के लिए सबसे छोटी दूरी का पता लगाना, एक ग्राफ पर प्रकीर्णन की मात्रा निर्धारित करना, आदि। [[डेमिंग प्रतिगमन]] में, एक प्रकार का रेखीय [[Index.php?title=वक्र समंजन|वक्र समंजन]], यदि आश्रित और स्वतंत्र चर के समान भिन्नता होती है जिसके परिणामस्वरूप [[Index.php?title=लांबिक प्रतिगमन|लांबिक प्रतिगमन]] होता है जिसमें योग्य की अपूर्णता की डिग्री प्रत्येक दत्तानुसारी बिन्दु के लिए प्रतिगमन रेखा से बिंदु की लंबवत दूरी के रूप में मापी जाती है। | ||
== एक समीकरण द्वारा परिभाषित रेखा == | == एक समीकरण द्वारा परिभाषित रेखा == | ||
समीकरण द्वारा दिए गए | समीकरण द्वारा दिए गए समतल रेखा कि स्थितियों में {{math|1=''ax'' + ''by'' + ''c'' = 0}}, जहाँ {{mvar|a}}, {{mvar|b}} और {{mvar|c}} [[वास्तविक संख्या]] स्थिरांक हैं {{mvar|a}} और {{mvar|b}} दोनों शून्य नहीं हैं, रेखा से एक बिंदु तक की दूरी {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} है<ref>{{harvnb|Larson|Hostetler|2007|loc=p. 452}}</ref><ref>{{harvnb|Spain|2007}}</ref>{{rp|p.14}} | ||
:<math>\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. </math> | :<math>\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. </math> | ||
इस रेखा पर वह बिंदु जो सबसे निकट है {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} निर्देशांक हैं:<ref name="Larson 2007 loc=p. 522">{{harvnb|Larson|Hostetler|2007|loc=p. 522}}</ref> | इस रेखा पर वह बिंदु जो सबसे निकट है {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} निर्देशांक हैं:<ref name="Larson 2007 loc=p. 522">{{harvnb|Larson|Hostetler|2007|loc=p. 522}}</ref> | ||
:<math>x = \frac{b(bx_0 - ay_0)-ac}{a^2 + b^2} \text{ and } y = \frac{a(-bx_0 + ay_0) - bc}{a^2+b^2}.</math> | :<math>x = \frac{b(bx_0 - ay_0)-ac}{a^2 + b^2} \text{ and } y = \frac{a(-bx_0 + ay_0) - bc}{a^2+b^2}.</math> | ||
क्षैतिज और लंबवत रेखाएं | '''क्षैतिज और लंबवत रेखाएं''' | ||
एक रेखा के सामान्य समीकरण में, {{math|1=''ax'' + ''by'' + ''c'' = 0}}, {{mvar|a}} और {{mvar|b}} जब तक दोनों शून्य नहीं हो सकते {{mvar|c}} भी शून्य है, | एक रेखा के सामान्य समीकरण में, {{math|1=''ax'' + ''by'' + ''c'' = 0}}, {{mvar|a}} और {{mvar|b}} जब तक दोनों शून्य नहीं हो सकते {{mvar|c}} भी शून्य है, इस स्थिति में समीकरण एक रेखा को परिभाषित नहीं करता है। यदि {{math|1=''a'' = 0}} और {{math|''b'' ≠ 0}}, रेखा क्षैतिज है और समीकरण है {{math|1=''y'' = −{{sfrac|''c''|''b''}}}}. से दूरी {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} इस रेखा को लंबाई के एक ऊर्ध्वाधर रेखा खंड के साथ मापा जाता है {{math|1={{!}}''y''<sub>0</sub> − (−{{sfrac|''c''|''b''}}){{!}} = {{sfrac|{{!}}''by''<sub>0</sub> + ''c''{{!}}|{{!}}''b''{{!}}}}}} सूत्र के अनुसार। इसी प्रकार, ऊर्ध्वाधर रेखाओं के लिए (b = 0) समान बिंदु और रेखा के बीच की दूरी है {{math|1={{sfrac|{{!}}''ax''<sub>0</sub> + ''c''{{!}}|{{!}}''a''{{!}}}} }}, जैसा कि एक क्षैतिज रेखा खंड के साथ मापा जाता है। | ||
== दो बिंदुओं द्वारा परिभाषित रेखा == | == दो बिंदुओं द्वारा परिभाषित रेखा == | ||
यदि रेखा दो बिन्दुओं से होकर गुजरती है {{math|1=''P''<sub>1</sub> = (''x''<sub>1</sub>, ''y''<sub>1</sub>)}} और {{math|1=''P''<sub>2</sub> = (''x<sub>2</sub>'', ''y<sub>2</sub>'')}} फिर | यदि रेखा दो बिन्दुओं से होकर गुजरती है {{math|1=''P''<sub>1</sub> = (''x''<sub>1</sub>, ''y''<sub>1</sub>)}} और {{math|1=''P''<sub>2</sub> = (''x<sub>2</sub>'', ''y<sub>2</sub>'')}} फिर लाइन से दूरी {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} है:<ref name=GEO /> | ||
इस व्यंजक | |||
<nowiki>:</nowiki><math>\operatorname{distance}(P_1, P_2, (x_0, y_0)) = \frac{|(x_2-x_1)(y_1-y_0)-(x_1-x_0)(y_2-y_1)|}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}. </math> | |||
इस व्यंजक के भाजक के बीच की दूरी है {{math|''P''<sub>1</sub>}} और {{math|''P''<sub>2</sub>}}. अंश तीन बिंदुओं पर इसके शीर्षों के साथ त्रिभुज के क्षेत्रफल का दुगुना है, {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}}, {{math|''P''<sub>1</sub>}} और {{math|''P''<sub>2</sub>}}. देखना: {{slink|त्रिभुज का क्षेत्रफल|निर्देशांकों का उपयोग}}. अभिव्यक्ति के बराबर है {{math|1=''h'' = {{sfrac|2''A''|''b''}}}}, जिसे त्रिभुज के क्षेत्रफल के लिए मानक सूत्र को पुनर्व्यवस्थित करके प्राप्त किया जा सकता है: {{math|1=''A'' = {{sfrac|1|2}} ''bh''}}, जहाँ {{mvar|b}} भुजा की लंबाई है, और {{mvar|h}} विपरीत शीर्ष से लंबवत ऊंचाई है। | |||
== बिंदु और कोण द्वारा परिभाषित रेखा == | == बिंदु और कोण द्वारा परिभाषित रेखा == | ||
| Line 31: | Line 32: | ||
=== एक बीजगणितीय प्रमाण === | === एक बीजगणितीय प्रमाण === | ||
यह प्रमाण केवल तभी मान्य होता है जब रेखा न तो लंबवत हो और न ही क्षैतिज, | यह प्रमाण केवल तभी मान्य होता है जब रेखा न तो लंबवत हो और न ही क्षैतिज, अर्थात हम मानते हैं कि न तो {{mvar|a}} और न {{mvar|b}} रेखा के समीकरण में शून्य है। | ||
समीकरण वाली रेखा {{math|1=''ax'' + ''by'' + ''c'' = 0}} में | समीकरण वाली रेखा {{math|1=''ax'' + ''by'' + ''c'' = 0}} में ढाल है {{math|−''a''/''b''}}, इसलिए इसके लम्बवत किसी भी रेखा पर ढाल होगा {{math|''b''/''a''}} (नकारात्मक पारस्परिक)।माना (m, n) रेखा ax + by + c = 0 का प्रतिच्छेदन बिंदु है और रेखा इसके लंबवत है जो बिंदु (x0, y0) से गुजरती है। इन दो बिंदुओं के माध्यम से रेखा मूल रेखा के लंबवत है, इसलिए | ||
:<math>\frac{y_0 - n}{x_0 - m}=\frac{b}{a}.</math> | :<math>\frac{y_0 - n}{x_0 - m}=\frac{b}{a}.</math> | ||
इस प्रकार, | इस प्रकार, | ||
<math>a(y_0 -n) - b(x_0 - m) = 0,</math> | <math>a(y_0 -n) - b(x_0 - m) = 0,</math> | ||
और इस समीकरण का वर्ग करके हम प्राप्त करते हैं: | और इस समीकरण का वर्ग करके हम प्राप्त करते हैं: | ||
:<math>a^2(y_0 - n)^2 + b^2(x_0 - m)^2 = 2ab(y_0 - n)(x_0 - m).</math> | :<math>a^2(y_0 - n)^2 + b^2(x_0 - m)^2 = 2ab(y_0 - n)(x_0 - m).</math> | ||
अब विचार | अब विचार कीजिए, | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 46: | Line 48: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
उपरोक्त वर्ग समीकरण का उपयोग करना। लेकिन हमारे पास | उपरोक्त वर्ग समीकरण का उपयोग करना। लेकिन हमारे पास है, | ||
:<math> (a(x_0 - m) + b(y_0 - n))^2 = (ax_0 + by_0 - am - bn)^2 = (ax_0 + by_0 + c)^2</math> | :<math> (a(x_0 - m) + b(y_0 - n))^2 = (ax_0 + by_0 - am - bn)^2 = (ax_0 + by_0 + c)^2</math> | ||
चूँकि (m, n) ax + by + c = 0 पर है। इस प्रकार, | |||
इस प्रकार, | |||
:<math>\left(a^2 + b^2\right) \left((x_0 - m)^2 + (y_0 - n)^2\right) = (ax_0 + by_0 + c)^2 </math> | :<math>\left(a^2 + b^2\right) \left((x_0 - m)^2 + (y_0 - n)^2\right) = (ax_0 + by_0 + c)^2 </math> | ||
और हम इन दो बिंदुओं द्वारा निर्धारित रेखा खंड की लंबाई प्राप्त करते हैं, | और हम इन दो बिंदुओं द्वारा निर्धारित रेखा खंड की लंबाई प्राप्त करते हैं, | ||
| Line 57: | Line 58: | ||
=== एक ज्यामितीय प्रमाण === | === एक ज्यामितीय प्रमाण === | ||
[[File:point-to-line2.svg|thumb|ज्यामितीय प्रमाण के लिए आरेख]]यह प्रमाण तभी मान्य होता है जब रेखा क्षैतिज या लंबवत न हो।<ref>{{harvnb|Ballantine|Jerbert|1952}} do not mention this restriction in their article</ref> | [[File:point-to-line2.svg|thumb|ज्यामितीय प्रमाण के लिए आरेख]]यह प्रमाण तभी मान्य होता है जब रेखा क्षैतिज या लंबवत न हो।<ref>{{harvnb|Ballantine|Jerbert|1952}} do not mention this restriction in their article</ref> | ||
निर्देशांक (x<sub>0</sub>, y<sub>0</sub>) वाले बिंदु P से समीकरण Ax + By + C = 0 वाली रेखा पर लंब डालें। लंब R के आधार को लेबल करें। P से होकर एक ऊर्ध्वाधर रेखा खींचें और दी गई रेखा S के साथ इसके प्रतिच्छेदन को चिह्नित करें। रेखा के किसी भी बिंदु T पर, एक समकोण त्रिभुज बनाएँ। TVU जिसकी भुजाएँ दी गई रेखा पर कर्ण TU के साथ क्षैतिज और ऊर्ध्वाधर रेखाखंड हैं और लंबाई की क्षैतिज भुजा |B| (आरेख देखें)। ∆TVU की उर्ध्वाधर भुजा की लंबाई |A| होगी चूँकि रेखा का ढाल -A/B है। | |||
∆PRS और ∆TVU समरूप त्रिभुज हैं, क्योंकि ये दोनों समकोण त्रिभुज हैं और ∠PSR ≅ ∠TUV क्योंकि ये समांतर रेखाओं PS और UV (दोनों लंबवत रेखाएँ हैं) के तिर्यक रेखा के संगत कोण हैं।<ref>If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.</ref> इन त्रिभुजों की संगत भुजाएँ समान अनुपात में हैं, इसलिए: | ∆PRS और ∆TVU समरूप त्रिभुज हैं, क्योंकि ये दोनों समकोण त्रिभुज हैं और ∠PSR ≅ ∠TUV हैं क्योंकि ये समांतर रेखाओं PS और UV (दोनों लंबवत रेखाएँ हैं) के तिर्यक रेखा के संगत कोण हैं।<ref>If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.</ref> इन त्रिभुजों की संगत भुजाएँ समान अनुपात में हैं, इसलिए: | ||
:<math>\frac{|\overline{PR}|}{|\overline{PS}|} = \frac{|\overline{TV}|}{|\overline{TU}|}.</math> | :<math>\frac{|\overline{PR}|}{|\overline{PS}|} = \frac{|\overline{TV}|}{|\overline{TU}|}.</math> | ||
यदि बिंदु S के निर्देशांक | यदि बिंदु S के निर्देशांक (x<sub>0</sub>, m)हैं तब |''PS''| = |''y''<sub>0</sub> - ''m''| P से लाइन की दूरी है: | ||
:<math> |\overline{PR} | = \frac{|y_0 - m||B|}{\sqrt{A^2 + B^2}}.</math> | :<math> |\overline{PR} | = \frac{|y_0 - m||B|}{\sqrt{A^2 + B^2}}.</math> | ||
चूँकि S रेखा पर है, हम m का मान ज्ञात कर सकते हैं, | चूँकि S रेखा पर है, हम m का मान ज्ञात कर सकते हैं, | ||
:<math>m = \frac{-Ax_0 - C}{B},</math> | :<math>m = \frac{-Ax_0 - C}{B},</math> | ||
और अंत में प्राप्त | और अंत में प्राप्त होगा:<ref>{{harvnb|Ballantine|Jerbert|1952}}</ref> | ||
:<math> |\overline{PR}| = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}.</math> | :<math> |\overline{PR}| = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}.</math> | ||
इस प्रमाण का एक रूपांतर V को P पर रखना है और त्रिभुज ∆UVT के क्षेत्रफल की गणना दो तरीकों से प्राप्त करना है। <math>D|\overline{TU}| = |\overline{VU}||\overline{VT}|</math> | इस प्रमाण का एक रूपांतर V को P पर रखना है और त्रिभुज ∆UVT के क्षेत्रफल की गणना दो तरीकों से प्राप्त करना है। <math>D|\overline{TU}| = |\overline{VU}||\overline{VT}|</math> | ||
जहाँ D P से ∆UVT के कर्ण के लिए खींची गई ∆UVT की ऊँचाई है। तब दूरी सूत्र का उपयोग व्यक्त करने के लिए किया जा सकता है <math>|\overline{TU}|</math>, <math>|\overline{VU}|</math>, और <math>|\overline{VT}|</math>संकेतित सूत्र प्राप्त करने के लिए P के निर्देशांक और रेखा के समीकरण के गुणांक के संदर्भ में।{{citation needed|date=April 2015}} | जहाँ D P से ∆UVT के कर्ण के लिए खींची गई ∆UVT की ऊँचाई है। तब दूरी सूत्र का उपयोग व्यक्त करने के लिए किया जा सकता है <math>|\overline{TU}|</math>, <math>|\overline{VU}|</math>, और <math>|\overline{VT}|</math>संकेतित सूत्र प्राप्त करने के लिए P के निर्देशांक और रेखा के समीकरण के गुणांक के संदर्भ में।{{citation needed|date=April 2015}} | ||
=== एक | === एक सदिश प्रोजेक्शन प्रूफ === | ||
[[File:vectorpoint-to-line.svg|250px|left| | [[File:vectorpoint-to-line.svg|250px|left|सदिश प्रोजेक्शन प्रूफ के लिए आरेख]]मान लीजिए P निर्देशांक वाला बिंदु (x<sub>0</sub>, y<sub>0</sub>)है और मान लीजिए कि दी गई रेखा का समीकरण ax + by + c = 0 है। साथ ही, मान लीजिए Q = (x<sub>1</sub>, और<sub>1</sub>) इस रेखा पर कोई बिंदु हो और n सदिश (''a'', ''b'') बिंदु ''Q'' से प्रारंभ हो। सदिश n रेखा के लंबवत है, और बिंदु ''P'' से रेखा तक की दूरी ''d'' के लांबिक प्रतिगमन की लंबाई के बराबर है <math>\overrightarrow{QP}</math> n पर है। इस प्रक्षेपण की लंबाई इसके द्वारा दी गई है: | ||
:<math>d = \frac{|\overrightarrow{QP} \cdot \mathbf{n}|}{\| \mathbf{n}\|}.</math> | :<math>d = \frac{|\overrightarrow{QP} \cdot \mathbf{n}|}{\| \mathbf{n}\|}.</math> | ||
तब, | |||
:<math> \overrightarrow{QP} = (x_0 - x_1, y_0 - y_1),</math> इसलिए <math> \overrightarrow{QP} \cdot \mathbf{n} = a(x_0 - x_1) + b(y_0 - y_1)</math> और <math> \| \mathbf{n} \| = \sqrt{a^2 + b^2},</math> | :<math> \overrightarrow{QP} = (x_0 - x_1, y_0 - y_1),</math> इसलिए <math> \overrightarrow{QP} \cdot \mathbf{n} = a(x_0 - x_1) + b(y_0 - y_1)</math> और <math> \| \mathbf{n} \| = \sqrt{a^2 + b^2},</math> | ||
इस प्रकार | इस प्रकार | ||
| Line 79: | Line 80: | ||
चूँकि Q रेखा पर एक बिंदु है, <math>c = -ax_1 - by_1</math>, इसलिए,<ref>{{harvnb|Anton|1994|loc=pp. 138-9}}</ref> | चूँकि Q रेखा पर एक बिंदु है, <math>c = -ax_1 - by_1</math>, इसलिए,<ref>{{harvnb|Anton|1994|loc=pp. 138-9}}</ref> | ||
:<math> d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}}.</math> | :<math> d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}}.</math> | ||
चूंकि दूरी को गुणांक के रूप में दिया जाता है, संकेत सामान्य सदिश (A, B) की दिशा द्वारा निर्धारित अर्थ में, यह निर्धारित करने के लिए उपयोगी हो सकता है कि बिंदु किस तरफ है। | |||
== अन्य सूत्र == | == अन्य सूत्र == | ||
| Line 85: | Line 86: | ||
बिंदु P निर्देशांक के साथ दिया गया है (<math>x_0, y_0</math>). | बिंदु P निर्देशांक के साथ दिया गया है (<math>x_0, y_0</math>). | ||
एक रेखा का समीकरण | |||
एक रेखा का समीकरण दिया जाता है <math>y=mx+k</math>. बिंदु P से गुजरने वाली उस रेखा के अभिलम्ब का समीकरण दिया गया है <math>y=\frac{x_0-x}{m}+y_0</math>. | |||
जिस बिंदु पर ये दो रेखाएँ प्रतिच्छेद करती हैं, वह मूल रेखा पर बिंदु P का निकटतम बिंदु है। इसलिए: | जिस बिंदु पर ये दो रेखाएँ प्रतिच्छेद करती हैं, वह मूल रेखा पर बिंदु P का निकटतम बिंदु है। इसलिए: | ||
| Line 91: | Line 93: | ||
हम इस समीकरण को x के लिए हल कर सकते हैं, | हम इस समीकरण को x के लिए हल कर सकते हैं, | ||
:<math>x=\frac{x_0+my_0-mk}{m^2+1}.</math> | :<math>x=\frac{x_0+my_0-mk}{m^2+1}.</math> | ||
अंतरायोजी के बिंदु का y निर्देशांक मूल रेखा के समीकरण में x के इस मान को प्रतिस्थापित करके पाया जा सकता है, | |||
:<math>y=m\frac{(x_0+my_0-mk)}{m^2+1}+k.</math> | :<math>y=m\frac{(x_0+my_0-mk)}{m^2+1}+k.</math> | ||
2 बिंदुओं के बीच की दूरी ज्ञात करने के लिए समीकरण का उपयोग | 2 बिंदुओं के बीच की दूरी ज्ञात करने के लिए समीकरण का उपयोग करके, <math>d=\sqrt{(X_2-X_1)^2+(Y_2-Y_1)^2}</math>, हम यह निष्कर्ष निकाल सकते हैं कि एक रेखा और एक बिंदु के बीच की न्यूनतम दूरी ज्ञात करने का सूत्र निम्नलिखित है: | ||
:<math>d=\sqrt{ \left( {\frac{x_0 + m y_0-mk}{m^2+1}-x_0 } \right) ^2 + \left( {m\frac{x_0+m y_0-mk}{m^2+1}+k-y_0 }\right) ^2 } = \frac{|k + m x_0 - y_0|}\sqrt{1 + m^2} .</math> | :<math>d=\sqrt{ \left( {\frac{x_0 + m y_0-mk}{m^2+1}-x_0 } \right) ^2 + \left( {m\frac{x_0+m y_0-mk}{m^2+1}+k-y_0 }\right) ^2 } = \frac{|k + m x_0 - y_0|}\sqrt{1 + m^2} .</math> | ||
| Line 99: | Line 101: | ||
== | == सदिश फॉर्मूलेशन == | ||
[[File:Distance from a point to a line.svg|thumb|300px| | [[File:Distance from a point to a line.svg|thumb|300px|सदिश फॉर्मूलेशन का चित्रण।]]यूक्लिडियन सदिश रूप में एक रेखा का समीकरण दिया जा सकता है: | ||
: <math> \mathbf{x} = \mathbf{a} + t\mathbf{n}</math> | : <math> \mathbf{x} = \mathbf{a} + t\mathbf{n}</math> | ||
यहाँ {{math|'''a'''}} रेखा पर एक बिंदु है, और {{math|'''n'''}} रेखा की दिशा में एक इकाई सदिश है। फिर जैसे | यहाँ {{math|'''a'''}} रेखा पर एक बिंदु है, और {{math|'''n'''}} रेखा की दिशा में एक इकाई सदिश है। फिर जैसे अदिश ''t'' भिन्न होता है, {{math|'''x'''}} रेखा का स्थान (बिंदुपथ) देता है। | ||
एक | इस पंक्ति के लिए एक स्वच्छंद द्वारा बिंदु p की दूरी दी गई है | ||
: <math>\operatorname{distance}(\mathbf{x} = \mathbf{a} + t\mathbf{n}, \mathbf{p}) = \| (\mathbf{p}-\mathbf{a}) - ((\mathbf{p}-\mathbf{a}) \cdot \mathbf{n})\mathbf{n} \|. </math> | : <math>\operatorname{distance}(\mathbf{x} = \mathbf{a} + t\mathbf{n}, \mathbf{p}) = \| (\mathbf{p}-\mathbf{a}) - ((\mathbf{p}-\mathbf{a}) \cdot \mathbf{n})\mathbf{n} \|. </math> | ||
यह सूत्र इस प्रकार निकाला जा सकता है: <math>\mathbf{p}-\mathbf{a}</math> से एक | यह सूत्र इस प्रकार निकाला जा सकता है: <math>\mathbf{p}-\mathbf{a}</math> से एक सदिश है {{math|'''a'''}} से {{math|'''p'''}} तक. तब <math>(\mathbf{p} - \mathbf{a}) \cdot \mathbf{n}</math> लाइन पर अनुमानित लंबाई है और इसलिए | ||
:<math>\mathbf{a} + ((\mathbf{p} - \mathbf{a}) \cdot \mathbf{n})\mathbf{n}</math> | :<math>\mathbf{a} + ((\mathbf{p} - \mathbf{a}) \cdot \mathbf{n})\mathbf{n}</math> | ||
एक | एक सदिश है, जो कि [[प्रक्षेपण (रैखिक बीजगणित)]] है <math>\mathbf{p}-\mathbf{a}</math> लाइन पर और निकटतम रेखा पर बिंदु <math>\mathbf{p}</math> का प्रतिनिधित्व करता है। इस प्रकार | ||
:<math>(\mathbf{p}-\mathbf{a}) - ((\mathbf{p}-\mathbf{a}) \cdot \mathbf{n})\mathbf{n}</math> | :<math>(\mathbf{p}-\mathbf{a}) - ((\mathbf{p}-\mathbf{a}) \cdot \mathbf{n})\mathbf{n}</math> | ||
का | का घटक है <math>\mathbf{p}-\mathbf{a}</math> रेखा के लंबवत। बिंदु से रेखा तक की दूरी तब उस सदिश का आदर्श (मानक) है।<ref name=GEO>{{cite web|last=Sunday|first=Dan|title=रेखाएँ और एक बिंदु से एक रेखा की दूरी|url=https://geomalgorithms.com/a02-_lines.html|publisher=softSurfer|url-status=dead|archive-url=https://web.archive.org/web/20210507021429/https://geomalgorithms.com/a02-_lines.html|archive-date=2021-05-07}}</ref> यह अधिक सामान्य सूत्र दो आयामों तक सीमित नहीं है। | ||
== एक और सदिश सूत्रीकरण == | == एक और सदिश सूत्रीकरण == | ||
यदि सदिश स्थान [[ | यदि सदिश स्थान [[Index.php?title=लांबिक|लांबिक]] है और यदि रेखा बिंदु {{math|'''a'''}} से होकर जाती है और एक यूक्लिडियन सदिश {{math|'''n'''}} है , बिंदु {{math|'''p'''}} और रेखा के बीच की दूरी है <ref>{{Cite web|last=Weisstein|first=Eric W.|title=Point-Line Distance--3-Dimensional | ||
|url=https://mathworld.wolfram.com/Point-LineDistance3-Dimensional.html|access-date=2021-06-06|website=mathworld.wolfram.com|language=en}}</ref> | |url=https://mathworld.wolfram.com/Point-LineDistance3-Dimensional.html|access-date=2021-06-06|website=mathworld.wolfram.com|language=en}}</ref> | ||
: <math>\operatorname{distance}(\mathbf{x} = \mathbf{a} + t\mathbf{n}, \mathbf{p}) = \frac{\left\|(\mathbf{p}-\mathbf{a}) \times \mathbf{n}\right\|}{\|\mathbf{n}\|}.</math> | : <math>\operatorname{distance}(\mathbf{x} = \mathbf{a} + t\mathbf{n}, \mathbf{p}) = \frac{\left\|(\mathbf{p}-\mathbf{a}) \times \mathbf{n}\right\|}{\|\mathbf{n}\|}.</math> | ||
ध्यान दें कि | ध्यान दें कि सदिश गुणनफल केवल आयाम 3 और 7 में सम्मलित हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 142: | Line 144: | ||
==अग्रिम पठन== | ==अग्रिम पठन== | ||
*{{citation|title=Encyclopedia of Distances|first1=Michel Marie|last1=Deza|author1-link=Michel Deza|first2=Elena|last2=Deza|author2-link=Elena Deza|edition=2nd|publisher=Springer|year=2013|isbn=9783642309588|page=86|url=https://books.google.com/books?id=QxX2CX5OVMsC&pg=PA86}} | *{{citation|title=Encyclopedia of Distances|first1=Michel Marie|last1=Deza|author1-link=Michel Deza|first2=Elena|last2=Deza|author2-link=Elena Deza|edition=2nd|publisher=Springer|year=2013|isbn=9783642309588|page=86|url=https://books.google.com/books?id=QxX2CX5OVMsC&pg=PA86}} | ||
[[Category: | [[Category:All articles with unsourced statements]] | ||
[[Category:Articles with unsourced statements from April 2015]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:Created On 28/02/2023]] | [[Category:Created On 28/02/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:दूरी]] | |||
[[Category:यूक्लिडियन ज्यामिति]] | |||
[[Category:वैक्टर (गणित और भौतिकी)]] | |||
Latest revision as of 11:43, 27 October 2023
यूक्लिडियन ज्यामिति में, एक बिंदु से एक रेखा तक की दूरी किसी दिए गए बिंदु (ज्यामिति) से एक अनंत रेखा (गणित) पर किसी भी बिंदु तक की सबसे छोटी यूक्लिडियन दूरी होती है। यह बिंदु की रेखा से लंबवत दूरी है, रेखा खंड की लंबाई जो बिंदु को रेखा पर निकटतम बिंदु से जोड़ती है। इसकी गणना करने का सूत्र कई तरीकों से निकाला और व्यक्त किया जा सकता है।
एक बिंदु से एक रेखा तक की दूरी को जानना विभिन्न स्थितियों में उपयोगी हो सकता है—उदाहरण के लिए, एक सड़क तक पहुँचने के लिए सबसे छोटी दूरी का पता लगाना, एक ग्राफ पर प्रकीर्णन की मात्रा निर्धारित करना, आदि। डेमिंग प्रतिगमन में, एक प्रकार का रेखीय वक्र समंजन, यदि आश्रित और स्वतंत्र चर के समान भिन्नता होती है जिसके परिणामस्वरूप लांबिक प्रतिगमन होता है जिसमें योग्य की अपूर्णता की डिग्री प्रत्येक दत्तानुसारी बिन्दु के लिए प्रतिगमन रेखा से बिंदु की लंबवत दूरी के रूप में मापी जाती है।
एक समीकरण द्वारा परिभाषित रेखा
समीकरण द्वारा दिए गए समतल रेखा कि स्थितियों में ax + by + c = 0, जहाँ a, b और c वास्तविक संख्या स्थिरांक हैं a और b दोनों शून्य नहीं हैं, रेखा से एक बिंदु तक की दूरी (x0, y0) है[1][2]: p.14
इस रेखा पर वह बिंदु जो सबसे निकट है (x0, y0) निर्देशांक हैं:[3]
क्षैतिज और लंबवत रेखाएं
एक रेखा के सामान्य समीकरण में, ax + by + c = 0, a और b जब तक दोनों शून्य नहीं हो सकते c भी शून्य है, इस स्थिति में समीकरण एक रेखा को परिभाषित नहीं करता है। यदि a = 0 और b ≠ 0, रेखा क्षैतिज है और समीकरण है y = −c/b. से दूरी (x0, y0) इस रेखा को लंबाई के एक ऊर्ध्वाधर रेखा खंड के साथ मापा जाता है |y0 − (−c/b)| = |by0 + c|/|b| सूत्र के अनुसार। इसी प्रकार, ऊर्ध्वाधर रेखाओं के लिए (b = 0) समान बिंदु और रेखा के बीच की दूरी है |ax0 + c|/|a|, जैसा कि एक क्षैतिज रेखा खंड के साथ मापा जाता है।
दो बिंदुओं द्वारा परिभाषित रेखा
यदि रेखा दो बिन्दुओं से होकर गुजरती है P1 = (x1, y1) और P2 = (x2, y2) फिर लाइन से दूरी (x0, y0) है:[4]
:
इस व्यंजक के भाजक के बीच की दूरी है P1 और P2. अंश तीन बिंदुओं पर इसके शीर्षों के साथ त्रिभुज के क्षेत्रफल का दुगुना है, (x0, y0), P1 और P2. देखना: त्रिभुज का क्षेत्रफल § निर्देशांकों का उपयोग. अभिव्यक्ति के बराबर है h = 2A/b, जिसे त्रिभुज के क्षेत्रफल के लिए मानक सूत्र को पुनर्व्यवस्थित करके प्राप्त किया जा सकता है: A = 1/2 bh, जहाँ b भुजा की लंबाई है, और h विपरीत शीर्ष से लंबवत ऊंचाई है।
बिंदु और कोण द्वारा परिभाषित रेखा
यदि रेखा बिंदु से होकर गुजरती है P = (Px, Py) कोण के साथ θ, फिर किसी बिंदु की दूरी (x0, y0) लाइन के लिए है
प्रमाण
एक बीजगणितीय प्रमाण
यह प्रमाण केवल तभी मान्य होता है जब रेखा न तो लंबवत हो और न ही क्षैतिज, अर्थात हम मानते हैं कि न तो a और न b रेखा के समीकरण में शून्य है।
समीकरण वाली रेखा ax + by + c = 0 में ढाल है −a/b, इसलिए इसके लम्बवत किसी भी रेखा पर ढाल होगा b/a (नकारात्मक पारस्परिक)।माना (m, n) रेखा ax + by + c = 0 का प्रतिच्छेदन बिंदु है और रेखा इसके लंबवत है जो बिंदु (x0, y0) से गुजरती है। इन दो बिंदुओं के माध्यम से रेखा मूल रेखा के लंबवत है, इसलिए
इस प्रकार,
और इस समीकरण का वर्ग करके हम प्राप्त करते हैं:
अब विचार कीजिए,
उपरोक्त वर्ग समीकरण का उपयोग करना। लेकिन हमारे पास है,
चूँकि (m, n) ax + by + c = 0 पर है। इस प्रकार,
और हम इन दो बिंदुओं द्वारा निर्धारित रेखा खंड की लंबाई प्राप्त करते हैं,
एक ज्यामितीय प्रमाण
यह प्रमाण तभी मान्य होता है जब रेखा क्षैतिज या लंबवत न हो।[6]
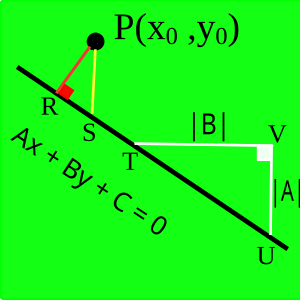
निर्देशांक (x0, y0) वाले बिंदु P से समीकरण Ax + By + C = 0 वाली रेखा पर लंब डालें। लंब R के आधार को लेबल करें। P से होकर एक ऊर्ध्वाधर रेखा खींचें और दी गई रेखा S के साथ इसके प्रतिच्छेदन को चिह्नित करें। रेखा के किसी भी बिंदु T पर, एक समकोण त्रिभुज बनाएँ। TVU जिसकी भुजाएँ दी गई रेखा पर कर्ण TU के साथ क्षैतिज और ऊर्ध्वाधर रेखाखंड हैं और लंबाई की क्षैतिज भुजा |B| (आरेख देखें)। ∆TVU की उर्ध्वाधर भुजा की लंबाई |A| होगी चूँकि रेखा का ढाल -A/B है।
∆PRS और ∆TVU समरूप त्रिभुज हैं, क्योंकि ये दोनों समकोण त्रिभुज हैं और ∠PSR ≅ ∠TUV हैं क्योंकि ये समांतर रेखाओं PS और UV (दोनों लंबवत रेखाएँ हैं) के तिर्यक रेखा के संगत कोण हैं।[7] इन त्रिभुजों की संगत भुजाएँ समान अनुपात में हैं, इसलिए:
यदि बिंदु S के निर्देशांक (x0, m)हैं तब |PS| = |y0 - m| P से लाइन की दूरी है:
चूँकि S रेखा पर है, हम m का मान ज्ञात कर सकते हैं,
और अंत में प्राप्त होगा:[8]
इस प्रमाण का एक रूपांतर V को P पर रखना है और त्रिभुज ∆UVT के क्षेत्रफल की गणना दो तरीकों से प्राप्त करना है। जहाँ D P से ∆UVT के कर्ण के लिए खींची गई ∆UVT की ऊँचाई है। तब दूरी सूत्र का उपयोग व्यक्त करने के लिए किया जा सकता है , , और संकेतित सूत्र प्राप्त करने के लिए P के निर्देशांक और रेखा के समीकरण के गुणांक के संदर्भ में।[citation needed]
एक सदिश प्रोजेक्शन प्रूफ
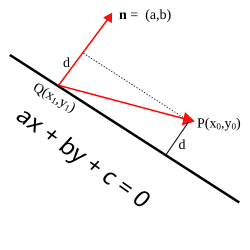
मान लीजिए P निर्देशांक वाला बिंदु (x0, y0)है और मान लीजिए कि दी गई रेखा का समीकरण ax + by + c = 0 है। साथ ही, मान लीजिए Q = (x1, और1) इस रेखा पर कोई बिंदु हो और n सदिश (a, b) बिंदु Q से प्रारंभ हो। सदिश n रेखा के लंबवत है, और बिंदु P से रेखा तक की दूरी d के लांबिक प्रतिगमन की लंबाई के बराबर है n पर है। इस प्रक्षेपण की लंबाई इसके द्वारा दी गई है:
तब,
- इसलिए और
इस प्रकार
चूँकि Q रेखा पर एक बिंदु है, , इसलिए,[9]
चूंकि दूरी को गुणांक के रूप में दिया जाता है, संकेत सामान्य सदिश (A, B) की दिशा द्वारा निर्धारित अर्थ में, यह निर्धारित करने के लिए उपयोगी हो सकता है कि बिंदु किस तरफ है।
अन्य सूत्र
एक बिंदु से एक रेखा की सबसे छोटी दूरी का पता लगाने के लिए एक और अभिव्यक्ति उत्पन्न करना संभव है। इस व्युत्पत्ति के लिए यह भी आवश्यक है कि रेखा लंबवत या क्षैतिज न हो।
बिंदु P निर्देशांक के साथ दिया गया है ().
एक रेखा का समीकरण दिया जाता है . बिंदु P से गुजरने वाली उस रेखा के अभिलम्ब का समीकरण दिया गया है .
जिस बिंदु पर ये दो रेखाएँ प्रतिच्छेद करती हैं, वह मूल रेखा पर बिंदु P का निकटतम बिंदु है। इसलिए:
हम इस समीकरण को x के लिए हल कर सकते हैं,
अंतरायोजी के बिंदु का y निर्देशांक मूल रेखा के समीकरण में x के इस मान को प्रतिस्थापित करके पाया जा सकता है,
2 बिंदुओं के बीच की दूरी ज्ञात करने के लिए समीकरण का उपयोग करके, , हम यह निष्कर्ष निकाल सकते हैं कि एक रेखा और एक बिंदु के बीच की न्यूनतम दूरी ज्ञात करने का सूत्र निम्नलिखित है:
समीकरण ax + by + c = 0 वाली रेखा के लिए m = -a/b और k = - c/b को याद करते हुए, थोड़ा बीजगणितीय सरलीकरण इसे मानक अभिव्यक्ति में कम कर देता है।[3]
सदिश फॉर्मूलेशन
यूक्लिडियन सदिश रूप में एक रेखा का समीकरण दिया जा सकता है:
यहाँ a रेखा पर एक बिंदु है, और n रेखा की दिशा में एक इकाई सदिश है। फिर जैसे अदिश t भिन्न होता है, x रेखा का स्थान (बिंदुपथ) देता है।
इस पंक्ति के लिए एक स्वच्छंद द्वारा बिंदु p की दूरी दी गई है
यह सूत्र इस प्रकार निकाला जा सकता है: से एक सदिश है a से p तक. तब लाइन पर अनुमानित लंबाई है और इसलिए
एक सदिश है, जो कि प्रक्षेपण (रैखिक बीजगणित) है लाइन पर और निकटतम रेखा पर बिंदु का प्रतिनिधित्व करता है। इस प्रकार
का घटक है रेखा के लंबवत। बिंदु से रेखा तक की दूरी तब उस सदिश का आदर्श (मानक) है।[4] यह अधिक सामान्य सूत्र दो आयामों तक सीमित नहीं है।
एक और सदिश सूत्रीकरण
यदि सदिश स्थान लांबिक है और यदि रेखा बिंदु a से होकर जाती है और एक यूक्लिडियन सदिश n है , बिंदु p और रेखा के बीच की दूरी है [10]
ध्यान दें कि सदिश गुणनफल केवल आयाम 3 और 7 में सम्मलित हैं।
यह भी देखें
- हेस्से सामान्य रूप
- लाइन-लाइन चौराहा
- दो रेखाओं के बीच की दूरी
- एक बिंदु से एक विमान की दूरी
- तिरछी रेखाएँ#दूरी
टिप्पणियाँ
- ↑ Larson & Hostetler 2007, p. 452
- ↑ Spain 2007
- ↑ 3.0 3.1 Larson & Hostetler 2007, p. 522
- ↑ 4.0 4.1 Sunday, Dan. "रेखाएँ और एक बिंदु से एक रेखा की दूरी". softSurfer. Archived from the original on 2021-05-07.
- ↑ Between Certainty and Uncertainty: Statistics and Probability in Five Units With Notes on Historical Origins and Illustrative Numerical Examples
- ↑ Ballantine & Jerbert 1952 do not mention this restriction in their article
- ↑ If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.
- ↑ Ballantine & Jerbert 1952
- ↑ Anton 1994, pp. 138-9
- ↑ Weisstein, Eric W. "Point-Line Distance--3-Dimensional". mathworld.wolfram.com (in English). Retrieved 2021-06-06.
संदर्भ
- Anton, Howard (1994), Elementary Linear Algebra (7th ed.), John Wiley & Sons, ISBN 0-471-58742-7
- Ballantine, J.P.; Jerbert, A.R. (1952), "Distance from a line or plane to a point", American Mathematical Monthly, 59 (4): 242–243, doi:10.2307/2306514, JSTOR 2306514
- Larson, Ron; Hostetler, Robert (2007), Precalculus: A Concise Course, Houghton Mifflin Co., ISBN 978-0-618-62719-6
- Spain, Barry (2007) [1957], Analytical Conics, Dover Publications, ISBN 978-0-486-45773-4
- Weisstein, Eric W. "Point-Line Distance--3-Dimensional". MathWorld.
अग्रिम पठन
- Deza, Michel Marie; Deza, Elena (2013), Encyclopedia of Distances (2nd ed.), Springer, p. 86, ISBN 9783642309588