सम्मिलन सॉर्ट: Difference between revisions

सम्मिलन सॉर्ट
	Animation of insertion sort
Class	Sorting algorithm
Data structure	Array
Worst-case performance	comparisons and swaps
Best-case performance	comparisons, swaps
Average performance	comparisons and swaps
Worst-case space complexity	total, auxiliary

Latest revision as of 16:57, 28 October 2023

सम्मिलन सॉर्टिंग एक सरल सॉर्टिंग एल्गोरिथ्म है जो अंतिम क्रमबद्ध सरणी (या सूची) एक समय में एक वस्तु समानता प्रकार बनाता है। यह अधिक उन्नत एल्गोरिदम जैसे कि जल्दी से सुलझाएं, ढेर बनाएं और सॉर्ट या मर्ज़ सॉर्ट की समानता में बड़ी सूचियों पर बहुत कम कुशल है। चूँकि, सम्मिलन क्रम कई लाभ प्रदान करता है:

सरल कार्यान्वयन: जॉन बेंटले (कंप्यूटर वैज्ञानिक) एक तीन-पंक्ति सी (प्रोग्रामिंग भाषा) / C++ (प्रोग्रामिंग भाषा) दिखाता है। C++ संस्करण जो प्रोग्राम अनुकूलन के समय पांच पंक्तियों का होता है।^[1]* (अधिक ) छोटे डेटा सेट के लिए कुशल, अन्य द्विघात की प्रकार (अर्थात , बिग ओ नोटेशन (एन)² सॉर्टिंग एल्गोरिदम
चयन सॉर्ट या बुलबुले की प्रकार जैसे अधिकांश अन्य सरल द्विघात एल्गोरिदम की समानता में अभ्यास में अधिक कुशल
अनुकूली सॉर्ट, अर्थात , डेटा सेट के लिए कुशल जो पहले से ही पर्याप्त रूप से सॉर्ट किए गए हैं: समय की जटिलता बड़ी O नोटेशन (kn) है जब इनपुट में प्रत्येक तत्व इससे अधिक नहीं है $k$ अपनी क्रमबद्ध स्थिति से दूर रखता है
स्थिर प्रकार; अर्थात समान कुंजी वाले तत्वों के सापेक्ष क्रम को नहीं बदलता है
इन-प्लेस एल्गोरिदम | इन-प्लेस; अर्थात , एकमात्र अतिरिक्त मेमोरी स्पेस की निरंतर राशि ओ (1) की आवश्यकता होती है
ऑनलाइन एल्गोरिदम; अर्थात , एक सूची को प्राप्त करते ही उसे क्रमबद्ध कर सकते हैं

जब लोग ठेके का पुल हैंड में कार्ड्स को मैन्युअल रूप स्थिर सॉर्टिंग करते हैं, तो अधिकांश एक ऐसी विधि का उपयोग करते हैं जो इंसर्शन सॉर्ट के समान होती है।^[2]

एल्गोरिथम

सम्मिलन प्रकार का एक चित्रमय उदाहरण है। आंशिक रूप से सॉर्ट की गई सूची (काली) प्रारंभ में सूची के एकमात्र पहले तत्व को ही सम्मलित करती है। प्रत्येक अवर्तन के साथ, एक तत्व (लाल) "अभी तक क्रम के लिए जांच नहीं की गई" इनपुट डेटा से हटाया जाता है और संरेखित सूची में अपनी जगह पर डाला जाता है।

इंसर्शन सॉर्ट यात्रा , एक ऐसा विधि है जो एक इनपुट सूची को लेकर काम करता है। यह हर बार एक इनपुट तत्व का उपभोग करता है, और एक संरेखित आउटपुट सूची बढ़ाता है। प्रत्येक अवर्तन में, इन्सर्शन सॉर्ट इनपुट डेटा से एक तत्व को हटाता है, संरेखित सूची में उसकी जगह खोजता है, और उस जगह में इसे डालता है। इस प्रक्रिया को इनपुट तत्व शेष नहीं रहने तक दोहराया जाता है।

सॉर्टिंग सामान्यतः स्थान में ही की जाती है, चूँकि एक्सएरे के साथ ऊपर की ओर चला जाता है और इसके पीछे संरेखित सूची को बढ़ाता है। प्रत्येक एक्सएरे स्थिति पर, यह संरेखित सूची में सबसे बड़े मान (जो पिछले एक्सएरे स्थिति में स्थित होता है) के खिलाफ वहाँ के मूल्य की जाँच करता है। यदि अधिक बड़ा हो, तो यह तत्व उसी स्थान पर छोड़ देता है और अगले मूल्य के लिए आगे बढ़ता है। यदि छोटा हो, तो यह संरेखित सूची में सही स्थान खोजता है, सभी अधिक बड़े मूल्यों को एक जगह ऊपर खिसकता है और उस सही स्थान में डालता है।

k अवर्तनों के बाद परिणामस्वरूप का एक्सएरे ऐसी गुणवत्ता होती है जहाँ पहले k + 1 प्रविष्टियाँ सॉर्ट होती हैं ("+1" क्योंकि पहली प्रविष्टि को छोड़ दिया जाता है)। प्रत्येक अवर्तन में इनपुट के पहले शेष तत्व को हटाया जाता है और सही स्थान पर परिणाम में डाला जाता है, इस प्रकार परिणाम को बढ़ाते हुए।

बन जाता है

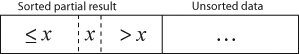x से अधिक प्रत्येक तत्व के साथ हर एक तत्व को x से बड़ा मान जब x से समानता की जाती है तो उसे उसके दाएं तरफ कॉपी किया जाता है।

इंसर्शन सॉर्ट का सबसे सामान्य रूप जो एरे पर काम करता है, उसे निम्न विधियां से वर्णित किया जा सकता है:

यदि सम्मिलित एक संचयी में एक मूल्य को डालने के लिए डिज़ाइन किया गया एक फ़ंक्शन हो, जिसे एक सॉर्टेड सीक्वेंस के प्रारंभ में एक एरे में डालने के लिए बनाया गया हो। यह सीक्वेंस के अंत में प्रारंभ होकर, नए तत्व के लिए एक उपयुक्त स्थान मिलने तक प्रत्येक तत्व को दाएं तरफ़ एक स्थान बढ़ाता है। फ़ंक्शन का साइड इफ़ेक्ट यह होता है कि यह सॉर्टेड सीक्वेंस के तुरंत बाद में संचय में संग्रहीत मूल्य को अधिलेखित कर देता है।
इन्सर्शन सॉर्ट करने के लिए, एरे के बाएं से सबसे बाएं तत्व पर प्रारंभ करें और प्रत्येक तत्व को सही स्थान पर डालने के लिए इंसर्ट को अभिह्राय करें। तत्व को डालने के लिए व्यवस्थित अनुक्रम सबसे पहले एरे के प्रारंभ में संग्रहीत होता है, जिसमें पहले से ही जांचे गए अनुक्रमों का सेट होता है। प्रत्येक इंसर्ट एकल मान को अधिलेखित करता है: डाले जा रहे मान को।

पूर्ण एल्गोरिथ्म का स्यूडोकोड इस प्रकार है, जहां सरणियाँ शून्य-आधारित संख्या हैं | शून्य-आधारित:^[1]

i ← 1
while i < length(A)    
  j ← i
    while j > 0 and A[j-1] > A[j]
        swap A[j] and A[j-1]
        j ← j - 1
    end while
    i ← i + 1
end while

बाहरी लूप पहले वाले को छोड़कर सभी तत्वों पर चलता है, क्योंकि एकल-तत्व उपसर्ग A[0:1] सरल रूप से क्रमबद्ध किया जाता है, इसलिए इनवेरिएंट (कंप्यूटर विज्ञान) कि पहले i प्रविष्टियों को क्रमबद्ध किया गया है यह प्रारंभ से सत्य है। आंतरिक पाश तत्व को स्थानांतरित करता है A[i] अपनी सही जगह पर जिससे लूप के बाद, पहले i+1 तत्वों को क्रमबद्ध किया जाता है। ध्यान दें कि andपरीक्षण में -ऑपरेटर को शॉर्ट सर्किट मूल्यांकन का उपयोग करना चाहिए, अन्यथा परीक्षण के परिणामस्वरूप सीमा जांच हो सकती है, जब j=0 और यह मूल्यांकन करने की कोशिश करता है A[j-1] > A[j] (अर्थात एक्सेस करना A[-1] विफल)।

विस्तार करने के बाद swap ऑपरेशन इन-प्लेस के रूप में x ← A[j]; A[j] ← A[j-1]; A[j-1] ← x (कहाँ x एक अस्थायी चर है), थोड़ा तेज संस्करण तैयार किया जा सकता है जो चलता है A[i] एक बार में अपनी स्थिति के लिए और आंतरिक लूप बॉडी में एकमात्र एक असाइनमेंट करता है:^[1]

while i < length(A)
    x ← A[i]
    j ← i - 1
    while j >= 0 and A[j] > x
        A[j+1] ← A[j]
        j ← j - 1
    end while
    A[j+1] ← x
    i ← i + 1
end while

नया इनर लूप एलिमेंट्स को स्पॉट क्लियर करने के लिए दाईं ओर शिफ्ट करता है x = A[i].

एल्गोरिथ्म को पुनरावर्ती विधियां से भी लागू किया जा सकता है। रिकर्सन एकमात्र बाहरी लूप को प्रतिस्थापित करता है, खुद को कॉल करता है और स्टैक पर n के क्रमिक रूप से छोटे मानों को n के समान 0 तक संग्रहीत करता है, जहां फ़ंक्शन तब प्रत्येक पुनरावर्ती कॉल के बाद कोड को निष्पादित करने के लिए कॉल श्रृंखला को वापस करता है, जो n के समान 1 से प्रारंभ होता है। n 1 से बढ़ रहा है क्योंकि फ़ंक्शन का प्रत्येक उदाहरण पूर्व उदाहरण पर लौटता है। प्रारंभिक कॉल सम्मिलन सॉर्टआर (ए, लंबाई (ए) -1) होगी।

function insertionSortR(array A, int n)
    if n > 0
        insertionSortR(A, n-1)
        x ← A[n]
        j ← n-1
        while j >= 0 and A[j] > x
            A[j+1] ← A[j]
            j ← j-1
        end while
        A[j+1] ← x
    end if
end function

यह कोड $O(1)$ को $O(N)$ में बदल देता है, किन्तु इससे कोड का आकार और निष्पादन समय परिवर्तित नहीं होता है। कोड में एक सरणीA होती है, जिसमें प्रत्येक चर के साथn से $N$ तक के मूल्य होते हैं।"

सर्वोत्तम, सबसे खराब और औसत स्थितियों े

इस स्थितियों में, सबसे अच्छा केस इनपुट एक सरणी होती है जो पहले से ही क्रमबद्ध होती है। इस स्थितियों में सम्मिलन क्रम में एक रैखिक चलने का समय होता है (अर्थात , ओ (एन))। प्रत्येक पुनरावृत्ति के समय, इनपुट के पहले शेष तत्व की समानता एकमात्र सरणी के क्रमबद्ध उपखंड के सबसे दाहिने तत्व से की जाती है।

सबसे सरल सबसे खराब स्थिति इनपुट रिवर्स ऑर्डर में क्रमबद्ध एक सरणी है। सभी सबसे खराब स्थिति वाले इनपुट के सेट में सभी सरणियाँ होती हैं जहाँ प्रत्येक तत्व इससे पहले सबसे छोटा या दूसरा सबसे छोटा तत्व होता है। इन स्थितियों ों में आंतरिक लूप का प्रत्येक पुनरावृत्ति अगला तत्व डालने से पहले सरणी के पूरे क्रमबद्ध उपखंड को स्कैन और स्थानांतरित करेगा। यह सम्मिलन क्रम को द्विघात चलने का समय देता है (अर्थात , O(n²))।

औसत स्थितियों ा भी द्विघात है,^[3] जो बड़े सरणियों को छाँटने के लिए सम्मिलन प्रकार को अव्यावहारिक बनाता है। यद्यपि , सम्मिलन सॉर्टिंग बहुत छोटी सरणियों को छाँटने के लिए सबसे तेज़ एल्गोरिदम में से एक है, यहाँ तक कि क्विकसॉर्ट से भी तेज़; वास्तव में, अच्छे क्विकसॉर्ट कार्यान्वयन उप-समस्याओं के रूप में उत्पन्न होने पर भी एक निश्चित सीमा से छोटे सरणियों के लिए सम्मिलन प्रकार का उपयोग करते हैं; त्रुटिहीन दहलीज प्रयोगात्मक रूप से निर्धारित की जानी चाहिए और मशीन पर निर्भर करती है, किन्तु सामान्यतः दस के आसपास होती है।

उदाहरण: निम्न तालिका क्रम {3, 7, 4, 9, 5, 2, 6, 1} को क्रमबद्ध करने के चरणों को दर्शाती है। प्रत्येक चरण में, विचाराधीन कुंजी को रेखांकित किया गया है। पिछले चरण में जिस कुंजी को स्थानांतरित किया गया था (या जगह में छोड़ दिया गया था क्योंकि यह अभी तक सबसे बड़ा माना जाता था) को तारांकन चिह्न के साथ चिह्नित किया गया है।

3  7  4  9  5  2  6  1
3* 7  4  9  5  2  6  1
3  7* 4  9  5  2  6  1
3  4* 7  9  5  2  6  1
3  4  7  9* 5  2  6  1
3  4  5* 7  9  2  6  1
2* 3  4  5  7  9  6  1
2  3  4  5  6* 7  9  1
1* 2  3  4  5  6  7  9

अन्य सॉर्टिंग एल्गोरिदम से संबंध

सम्मिलन सॉर्टिंग चयन सॉर्टिंग के समान है। जैसा कि चयन क्रम में, k सरणी से गुजरने के बाद, पहले k तत्व क्रमबद्ध क्रम में होते हैं। यद्यपि , दो एल्गोरिदम के बीच मूलभूत अंतर यह है कि सम्मिलन क्रम वर्तमान कुंजी से पीछे की ओर स्कैन करता है, चूँकि चयन क्रम आगे की ओर स्कैन करता है। इसके परिणामस्वरूप चयन सॉर्ट पहले k तत्वों को बिना इनपुट के k सबसे छोटा तत्व बना देता है, चूँकि सम्मिलन क्रम में वे इनपुट के पहले k तत्व होते हैं।

चयन सॉर्टिंग की समानता में सम्मिलन सॉर्टिंग का प्राथमिक लाभ यह है कि चयन सॉर्टिंग को हमेशा शेष सभी तत्वों को सूची के अवर्गीकृत भाग में सबसे छोटे तत्व को खोजने के लिए स्कैन करना चाहिए, चूँकि सम्मिलन क्रम में एकमात्र एक समानता की आवश्यकता होती है जब (k+1)-st तत्व k-वें तत्व से बड़ा है; जब यह अधिकांशतः सत्य होता है (जैसे कि यदि इनपुट सरणी पहले से ही क्रमबद्ध या आंशिक रूप से क्रमबद्ध है), तो सम्मिलन प्रकार चयन प्रकार की समानता में स्पष्ट रूप से अधिक कुशल है। औसतन (यह मानते हुए कि (k + 1)-st एलिमेंट रैंक का रैंक रैंडम है), इंसर्शन सॉर्ट को पिछले k एलिमेंट्स के आधे हिस्से की समानता करने और स्थानांतरित करने की आवश्यकता होगी, जिसका अर्थ है कि इंसर्शन सॉर्ट, चयन सॉर्ट की समानता में अधिकतर आधी समानता करेगा औसत।

सम्मिलन प्रकार के लिए सबसे खराब स्थिति में (जब इनपुट सरणी रिवर्स-सॉर्ट की जाती है), सम्मिलन सॉर्ट चयन सॉर्ट के रूप में कई समानता करता है। चूंकि, चयन सॉर्टिंग की समानता में सम्मिलन सॉर्टिंग का एक हानि यह है कि इस तथ्य के कारण अधिक लिखने की आवश्यकता होती है, क्योंकि प्रत्येक पुनरावृत्ति पर, (k+1)-st तत्व को सरणी के क्रमबद्ध भाग में सम्मिलित करने के लिए सभी तत्वों को स्थानांतरित करने के लिए कई तत्वों की अदला-बदली की आवश्यकता होती है। निम्नलिखित तत्वों में से, चूँकि चयन प्रकार के प्रत्येक पुनरावृत्ति के लिए एकमात्र एक स्वैप की आवश्यकता होती है। सामान्यतः, सम्मिलन प्रकार सरणी O (n²) बार, चूँकि चयन सॉर्ट एकमात्र O(लिखेगा) $n$ ) बार। इस कारण चयन सॉर्टिंग उन स्थितियों ों में बेहतर हो सकती है जहाँ मेमोरी में लिखना पढ़ने की समानता में अधिक अधिक महंगा है, जैसे कि EEPROM या फ्लैश मेमोरी के साथ।

चूँकि कुछ फूट डालो और जीतो एल्गोरिथ्म जैसे क्विकसॉर्ट और मर्ज़ सॉर्ट बड़ी सरणियों के लिए इंसर्शन सॉर्ट से बेहतर प्रदर्शन करते हैं, गैर-पुनरावर्ती सॉर्टिंग एल्गोरिदम जैसे इंसर्शन सॉर्ट या सिलेक्शन सॉर्ट सामान्यतः बहुत छोटे सरणियों के लिए तेज़ होते हैं (त्रुटिहीन आकार पर्यावरण और कार्यान्वयन के अनुसार भिन्न होता है, किन्तु सामान्यतः पर 7 और 50 तत्वों के बीच होता है)। इसलिए, उन एल्गोरिदम के कार्यान्वयन में एक उपयोगी अनुकूलन एक संकर दृष्टिकोण है, सरल एल्गोरिदम का उपयोग करते हुए जब सरणी को छोटे आकार में विभाजित किया गया हो।^[1]

वेरिएंट

डोनाल्ड शेल|डी.एल. शेल ने एल्गोरिद्म में पर्याप्त सुधार किए; संशोधित संस्करण को शैलसॉर्ट कहा जाता है। सॉर्टिंग एल्गोरिथ्म प्रत्येक पास पर घटने वाली दूरी से अलग किए गए तत्वों की समानता करता है। शेल सॉर्ट ने व्यावहारिक कार्य में विशिष्ट रूप से चलने के समय में सुधार किया है, जिसमें दो सरल प्रकारों के लिए O(n^3/2) और O(n^4/3) चलने का समय।^[4]^[5]

यदि समानता की लागत अदला-बदली की लागत से अधिक हो जाती है, जैसा कि उदाहरण के लिए संदर्भ के माध्यम से संग्रहीत स्ट्रिंग कुंजियों के साथ या मानवीय अंतःक्रिया के साथ होता है (जैसे कि साथ-साथ प्रदर्शित जोड़ी में से एक को चुनना), तो बाइनरी सम्मिलन प्रकार का उपयोग करने से उपज हो सकती है बेहतर प्रदर्शन।^[6] बाइनरी इंसर्शन सॉर्ट नए तत्वों को सम्मिलित करने के लिए सही स्थान निर्धारित करने के लिए एक द्विआधारी खोज एल्गोरिथ्म को नियोजित करता है, और इसलिए ⌈log करता है₂n⌉ सबसे खराब स्थिति में समानता । जब सरणी में प्रत्येक तत्व को खोजा जाता है और डाला जाता है तो यह ओ (एन लॉग एन) होता है।^[6]समग्र रूप से एल्गोरिथ्म में अभी भी O(n²) औसतन प्रत्येक प्रविष्टि के लिए आवश्यक स्वैप की श्रृंखला के कारण।^[6]

कई तत्वों को स्थानांतरित करने से पहले उनकी स्थिति की गणना करके स्वैप की संख्या कम की जा सकती है। उदाहरण के लिए, यदि दो तत्वों की लक्ष्य स्थिति की गणना उन्हें उचित स्थिति में ले जाने से पहले की जाती है, तो यादृच्छिक डेटा के लिए स्वैप की संख्या को अधिकतर 25% कम किया जा सकता है। चरम स्थिति में, यह संस्करण मर्ज सॉर्ट के समान काम करता है।

बाइनरी मर्ज सॉर्ट नाम का एक वेरिएंट 32 तत्वों के समूह को सॉर्ट करने के लिए बाइनरी इंसर्शन सॉर्ट का उपयोग करता है, इसके बाद मर्ज सॉर्ट का उपयोग करके अंतिम सॉर्ट किया जाता है। यह बड़े डेटा सेट पर मर्ज सॉर्ट की गति के साथ छोटे डेटा सेट पर सम्मिलन सॉर्ट की गति को जोड़ती है।^[7]

प्रत्येक सम्मिलन के लिए स्वैप की एक श्रृंखला बनाने से बचने के लिए, इनपुट को एक लिंक की गई सूची में संग्रहीत किया जा सकता है, जो सूची में स्थिति ज्ञात होने पर तत्वों को निरंतर समय में सूची में या बाहर विभाजित करने की अनुमति देता है। चूंकि, एक लिंक की गई सूची को खोजने के लिए वांछित स्थिति के लिंक का क्रमिक रूप से अनुसरण करने की आवश्यकता होती है: एक लिंक की गई सूची में यादृच्छिक अभिगम नहीं होता है, इसलिए यह बाइनरी खोज जैसी तेज विधि का उपयोग नहीं कर सकता है। इसलिए, खोज के लिए आवश्यक रनिंग टाइम O (n) है, और सॉर्ट करने का समय O (n) है²). यदि अधिक परिष्कृत डेटा संरचना (जैसे, हीप (डेटा संरचना) या बाइनरी ट्री) का उपयोग किया जाता है, तो खोज और सम्मिलन के लिए आवश्यक समय को अधिक कम किया जा सकता है; यह ढेर बनाएं और सॉर्ट और बाइनरी ट्री सॉर्ट का सार है।

2006 में बेंडर, मार्टिन फ़राच-कोल्टन, और मोस्टियोरो ने इंसर्शन सॉर्ट का एक नया संस्करण प्रकाशित किया जिसे पुस्तकालय सॉर्टिंग या गैप्ड इंसर्शन सॉर्ट कहा जाता है जो कम संख्या में अप्रयुक्त रिक्त स्थान (अर्थात , अंतराल) को पूरे सरणी में फैला देता है। लाभ यह है कि सम्मिलन को एकमात्र तब तक तत्वों को स्थानांतरित करने की आवश्यकता होती है जब तक कि कोई अंतर न हो जाए। लेखक दिखाते हैं कि यह सॉर्टिंग एल्गोरिथ्म O(n log n) समय में उच्च संभावना के साथ चलता है।^[8]

यदि स्किप सूची का उपयोग किया जाता है, तो सम्मिलन समय को O(log n) पर लाया जाता है, और स्वैप की आवश्यकता नहीं होती है क्योंकि स्किप सूची को लिंक की गई सूची संरचना पर लागू किया जाता है। सम्मिलन के लिए अंतिम चलने का समय ओ (एन लॉग एन) होगा।

=== सी === में सूची सम्मिलन सॉर्ट कोड

यदि आइटम लिंक की गई सूची में संग्रहीत हैं, तो सूची को O(1) अतिरिक्त स्थान के साथ क्रमबद्ध किया जा सकता है। एल्गोरिदम प्रारंभिक रूप से खाली (और इसलिए सरल रूप से क्रमबद्ध) सूची से प्रारंभ होता है। इनपुट आइटम एक बार में सूची से हटा दिए जाते हैं, और फिर क्रमबद्ध सूची में उचित स्थान पर डाले जाते हैं। जब इनपुट सूची खाली होती है, तो क्रमबद्ध सूची में वांछित परिणाम होता है।

struct LIST * SortList1(struct LIST * pList) 
{
    // zero or one element in list
    if (pList == NULL || pList->pNext == NULL)
        return pList;
    // head is the first element of resulting sorted list
    struct LIST * head = NULL;
    while (pList != NULL) {
        struct LIST * current = pList;
        pList = pList->pNext;
        if (head == NULL || current->iValue < head->iValue) {
            // insert into the head of the sorted list
            // or as the first element into an empty sorted list
            current->pNext = head;
            head = current;
        } else {
            // insert current element into proper position in non-empty sorted list
            struct LIST * p = head;
            while (p != NULL) {
                if (p->pNext == NULL || // last element of the sorted list
                    current->iValue < p->pNext->iValue) // middle of the list
                {
                    // insert into middle of the sorted list or as the last element
                    current->pNext = p->pNext;
                    p->pNext = current;
                    break; // done
                }
                p = p->pNext;
            }
        }
    }
    return head;
}

नीचे दिया गया एल्गोरिदम अनुगामी सूचक का उपयोग करता है^[9] क्रमबद्ध सूची में सम्मिलन के लिए। एक सरल पुनरावर्ती विधि हर बार सूची का पुनर्निर्माण करती है (स्प्लिसिंग के अतिरिक्त) और O(n) स्टैक स्पेस का उपयोग कर सकती है।

struct LIST
{
  struct LIST * pNext;
  int           iValue;
};

struct LIST * SortList(struct LIST * pList)
{
  // zero or one element in list
  if (!pList || !pList->pNext)
      return pList;

  /* build up the sorted array from the empty list */
  struct LIST * pSorted = NULL;

  /* take items off the input list one by one until empty */
  while (pList != NULL) {
      /* remember the head */
      struct LIST *   pHead  = pList;
      /* trailing pointer for efficient splice */
      struct LIST ** ppTrail = &pSorted;

      /* pop head off list */
      pList = pList->pNext;

      /* splice head into sorted list at proper place */
      while (!(*ppTrail == NULL || pHead->iValue < (*ppTrail)->iValue)) { /* does head belong here? */
          /* no - continue down the list */
          ppTrail = &(*ppTrail)->pNext;
      }

      pHead->pNext = *ppTrail;
      *ppTrail = pHead;
  }

  return pSorted;
}

संदर्भ

↑ ^1.0 ^1.1 ^1.2 ^1.3 Bentley, Jon (2000). "Column 11: Sorting". प्रोग्रामिंग मोती (2nd ed.). ACM Press / Addison-Wesley. pp. 115–116. ISBN 978-0-201-65788-3. OCLC 1047840657.
↑ Sedgewick, Robert (1983). एल्गोरिदम. Addison-Wesley. p. 95. ISBN 978-0-201-06672-2.
↑ Schwarz, Keith. "Why is insertion sort Θ(n^2) in the average case? (answer by "templatetypedef")". Stack Overflow.
↑ Frank, R. M.; Lazarus, R. B. (1960). "A High-Speed Sorting Procedure". Communications of the ACM. 3 (1): 20–22. doi:10.1145/366947.366957. S2CID 34066017.
↑ Sedgewick, Robert (1986). "A New Upper Bound for Shellsort". Journal of Algorithms. 7 (2): 159–173. doi:10.1016/0196-6774(86)90001-5.
↑ ^6.0 ^6.1 ^6.2 Samanta, Debasis (2008). क्लासिक डेटा संरचनाएं. PHI Learning. p. 549. ISBN 9788120337312.
↑ "Binary Merge Sort"
↑ Bender, Michael A.; Farach-Colton, Martín; Mosteiro, Miguel A. (2006), "Insertion sort is O(n log n)", Theory of Computing Systems, 39 (3): 391–397, arXiv:cs/0407003, doi:10.1007/s00224-005-1237-z, MR 2218409, S2CID 14701669
↑ Hill, Curt (ed.), "Trailing Pointer Technique", Euler, Valley City State University, archived from the original on 26 April 2012, retrieved 22 September 2012.

अग्रिम पठन

Knuth, Donald (1998), "5.2.1: Sorting by Insertion", The Art of Computer Programming, vol. 3. Sorting and Searching (second ed.), Addison-Wesley, pp. 80–105, ISBN 0-201-89685-0.

बाहरी संबंध

Animated Sorting Algorithms: Insertion Sort at the Wayback Machine (archived 8 March 2015) – graphical demonstration
Adamovsky, John Paul, Binary Insertion Sort – Scoreboard – Complete Investigation and C Implementation, Pathcom.
Insertion Sort – a comparison with other O(n²) sorting algorithms, UK: Core war.
Insertion sort (C) (wiki), LiteratePrograms – implementations of insertion sort in C and several other programming languages

[pearls-1] 1.0 ^1.1 ^1.2 ^1.3 Bentley, Jon (2000). "Column 11: Sorting". प्रोग्रामिंग मोती (2nd ed.). ACM Press / Addison-Wesley. pp. 115–116. ISBN 978-0-201-65788-3. OCLC 1047840657.

[2] Sedgewick, Robert (1983). एल्गोरिदम. Addison-Wesley. p. 95. ISBN 978-0-201-06672-2.

[3] Schwarz, Keith. "Why is insertion sort Θ(n^2) in the average case? (answer by "templatetypedef")". Stack Overflow.

[4] Frank, R. M.; Lazarus, R. B. (1960). "A High-Speed Sorting Procedure". Communications of the ACM. 3 (1): 20–22. doi:10.1145/366947.366957. S2CID 34066017.

[Sedgewick2-5] Sedgewick, Robert (1986). "A New Upper Bound for Shellsort". Journal of Algorithms. 7 (2): 159–173. doi:10.1016/0196-6774(86)90001-5.

[:0-6] 6.0 ^6.1 ^6.2 Samanta, Debasis (2008). क्लासिक डेटा संरचनाएं. PHI Learning. p. 549. ISBN 9788120337312.

[7] "Binary Merge Sort"

[8] Bender, Michael A.; Farach-Colton, Martín; Mosteiro, Miguel A. (2006), "Insertion sort is O(n log n)", Theory of Computing Systems, 39 (3): 391–397, arXiv:cs/0407003, doi:10.1007/s00224-005-1237-z, MR 2218409, S2CID 14701669

[9] Hill, Curt (ed.), "Trailing Pointer Technique", Euler, Valley City State University, archived from the original on 26 April 2012, retrieved 22 September 2012.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

@@ Line 259: / Line 259: @@
 * {{Citation | url = https://literateprograms.org/insertion_sort__c_.html | title = Insertion sort (C) | publisher = LiteratePrograms | type = wiki}} – implementations of insertion sort in C and several other programming languages
-{{sorting}}
+[[Category:CS1|Insertion Sort]]
+[[Category:Collapse templates|Insertion Sort]]
-{{DEFAULTSORT:Insertion Sort}}[[Category: छँटाई एल्गोरिदम]] [[Category: तुलना प्रकार]] [[Category: स्थिर प्रकार]] [[Category: स्यूडोकोड के उदाहरण वाले लेख]] [[Category: ऑनलाइन छँटाई]]
+[[Category:Commons category link is locally defined|Insertion Sort]]
+[[Category:Created On 21/03/2023|Insertion Sort]]
-[[no:Sorteringsalgoritme#Innstikksortering]]
+[[Category:Machine Translated Page|Insertion Sort]]
+[[Category:Navigational boxes| ]]
+[[Category:Navigational boxes without horizontal lists|Insertion Sort]]
+[[Category:Pages with broken file links|Insertion Sort]]
-[[Category: Machine Translated Page]]
+[[Category:Pages with script errors|Insertion Sort]]
-[[Category:Created On 21/03/2023]]
+[[Category:Vigyan Ready]]

Anonymous

Search

सम्मिलन सॉर्ट: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 16:57, 28 October 2023

Contents

एल्गोरिथम

सर्वोत्तम, सबसे खराब और औसत स्थितियों े

अन्य सॉर्टिंग एल्गोरिदम से संबंध

वेरिएंट

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

सम्मिलन सॉर्ट: Difference between revisions

Latest revision as of 16:57, 28 October 2023

एल्गोरिथम

सर्वोत्तम, सबसे खराब और औसत स्थितियों े

अन्य सॉर्टिंग एल्गोरिदम से संबंध

वेरिएंट

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Hidden categories