ब्रैग का नियम: Difference between revisions
(Created page with "{{short description|Physical law regarding scattering angles of radiation through a medium}} भौतिकी और रसायन विज्ञान में, ब्...") |
|||
| (21 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Physical law regarding scattering angles of radiation through a medium}} | {{short description|Physical law regarding scattering angles of radiation through a medium}} | ||
भौतिकी और रसायन विज्ञान में, ब्रैग का नियम, [[जॉर्ज वुल्फ]]-ब्रैग की स्थिति या लाउ-ब्रैग हस्तक्षेप, लाउ विवर्तन का | भौतिकी और रसायन विज्ञान में, ब्रैग का नियम, [[जॉर्ज वुल्फ|वुल्फ]]-ब्रैग की स्थिति या लाउ-ब्रैग हस्तक्षेप, लाउ विवर्तन का विशेष स्तिथियों , क्रिस्टल जाली से तरंगों के सुसंगत प्रकीर्णन के लिए कोण देता है। यह जाली विमानों द्वारा बिखरे तरंग मोर्चों के सुपरपोजिशन को सम्मिलित करता है, जिससे तरंग दैर्ध्य और [[बिखरने]] वाले कोण के मध्य अत्यधिक संबंध होता है, क्रिस्टल जाली के संबंध में वेववेक्टर ट्रांसफर होता है। इस प्रकार के नियम को प्रारंभ में क्रिस्टल पर एक्स-रे के लिए प्रस्तुत किया गया था। चूँकि, यह सभी प्रकार के क्वांटम बीम पर प्रारम्भ होता है, जिसमें परमाणु दूरी पर न्यूट्रॉन और इलेक्ट्रॉन तरंगों के साथ-साथ कृत्रिम आवधिक सूक्ष्म जाली पर दृश्य प्रकाश भी सम्मिलित है। | ||
== इतिहास == | == इतिहास == | ||
[[File:Diffusion rayleigh et diffraction.svg|thumb|450px| | [[File:Diffusion rayleigh et diffraction.svg|thumb|450px|्स-रे [[क्रिस्टल]] में परमाणुओं के साथ परस्पर क्रिया करते हैं।]]ब्रैग विवर्तन (जिसे एक्स-रे विवर्तन के ब्रैग सूत्रीकरण के रूप में भी जाना जाता है) प्रथम बार [[लॉरेंस ब्रैग]] और उनके पिता, [[विलियम हेनरी ब्रैग]] द्वारा 1913<ref>{{cite journal|first1=W. H.|last1=Bragg|first2=W. L.|last2=Bragg|journal=Proc. R. Soc. Lond. A|year=1913|volume=88|pages=428–38|author-link=William Henry Bragg|author-link2=Lawrence Bragg|title=क्रिस्टल द्वारा एक्स-रे का प्रतिबिंब|doi=10.1098/rspa.1913.0040|issue=605|bibcode = 1913RSPSA..88..428B|doi-access=free}}</ref> में उनकी अविष्कार के उपकार में प्रस्तावित किया गया था कि क्रिस्टलीय ठोस परावर्तित एक्स-रे के आश्चर्यजनक पैटर्न का उत्पादन करते हैं। (इसके विपरीत, कहते हैं, तरल)। उन्होंने पाया कि ये क्रिस्टल, कुछ विशिष्ट तरंग दैर्ध्य और घटना कोणों पर, परावर्तित विकिरण की तीव्र चोटियों का उत्पादन करते हैं। व्युत्पन्न ब्रैग का नियम लाउ विवर्तन की विशेष व्याख्या है, जहां ब्रैग्स ने क्रिस्टल जाली विमानों से तरंगों के प्रतिबिंब द्वारा ज्यामितीय विधि से रचनात्मक लाउ-ब्रैग हस्तक्षेप की व्याख्या की, जैसे कि पथ-अंतर घटना तरंगदैर्ध्य का गुणक बन जाता है। | ||
[[Image:Braggs Law.svg|thumb|450px|के अनुसार {{math|2''θ''}} विचलन, चरण बदलाव रचनात्मक (बाएं आंकड़ा) या विनाशकारी (दायां आंकड़ा) हस्तक्षेप का कारण बनता है।]]लॉरेंस ब्रैग ने क्रिस्टल को | [[Image:Braggs Law.svg|thumb|450px|के अनुसार {{math|2''θ''}} विचलन, चरण बदलाव रचनात्मक (बाएं आंकड़ा) या विनाशकारी (दायां आंकड़ा) हस्तक्षेप का कारण बनता है।]]लॉरेंस ब्रैग ने क्रिस्टल को स्थिर पैरामीटर {{mvar|d}} द्वारा अलग किए गए असतत समानांतर विमानों के सेट के रूप में मॉडलिंग करके इस परिणाम की व्याख्या की। यह प्रस्तावित किया गया था कि घटना एक्स-रे विकिरण ब्रैग चोटी का उत्पादन करेगा यदि विभिन्न विमानों से उनका प्रतिबिंब रचनात्मक रूप से हस्तक्षेप करता है। हस्तक्षेप रचनात्मक होता है जब चरण परिवर्तन {{math|2''π''}} का गुणक होता है; इस स्थिति को ब्रैग के नियम द्वारा व्यक्त किया जा सकता है (नीचे ब्रैग स्थिति अनुभाग देखें) और पहली बार लॉरेंस ब्रैग द्वारा 11 नवंबर 1912 को [[कैम्ब्रिज फिलोसोफिकल सोसायटी]] को प्रस्तुत किया गया था।<ref>See, for example, [http://www.encalc.com/?expr=n%20lambda%20%2F%20(2*sin(theta))%20in%20nanometers&var1=n&val1=1&var2=lambda&val2=620%20nm&var3=theta&val3=45%20degrees&var4=&val4= this example calculation] {{webarchive|url=https://web.archive.org/web/20110710191659/http://www.encalc.com/?expr=n%20lambda%20%2F%20%282%2Asin%28theta%29%29%20in%20nanometers&var1=n&val1=1&var2=lambda&val2=620%20nm&var3=theta&val3=45%20degrees&var4=&val4= |date=July 10, 2011 }} of interatomic spacing with Bragg's law.</ref><ref>There are some sources, like the ''Academic American Encyclopedia'', that attribute the discovery of the law to both W.L Bragg and his father W.H. Bragg, but the [http://nobelprize.org/nobel_prizes/physics/laureates/1915/present.html official Nobel Prize site] and the biographies written about him ("Light Is a Messenger: The Life and Science of William Lawrence Bragg", Graeme K. Hunter, 2004 and "Great Solid State Physicists of the 20th Century", Julio Antonio Gonzalo, Carmen Aragó López) make a clear statement that Lawrence Bragg alone derived the law.</ref> चूँकि सरल, ब्रैग के नियम ने परमाणु मापक पर वास्तविक कणों के अस्तित्व की पुष्टि की, साथ ही एक्स-रे और [[न्यूट्रॉन विवर्तन]] के रूप में क्रिस्टल का अध्ययन करने के लिए शक्तिशाली आधुनिक उपकरण प्रदान किया। लॉरेंस ब्रैग और उनके पिता, विलियम हेनरी ब्रैग को 1915 में [[सोडियम क्लोराइड]], [[जिंक सल्फाइड]] और हीरे से शुरू होने वाली क्रिस्टल संरचनाओं के निर्धारण में उनके कार्य के लिए भौतिकी में [[नोबेल पुरस्कार]] से सम्मानित किया गया था। वे संयुक्त रूप से जीतने वाली एकमात्र पिता-पुत्र टीम हैं। | ||
ब्रैग विवर्तन की अवधारणा न्यूट्रॉन विवर्तन और [[इलेक्ट्रॉन विवर्तन]] प्रक्रियाओं पर समान रूप से लागू होती है।<ref>John M. Cowley (1975) ''Diffraction physics'' (North-Holland, Amsterdam) {{ISBN|0-444-10791-6}}.</ref> [[न्यूट्रॉन]] और एक्स-रे दोनों तरंग दैर्ध्य अंतर-परमाणु दूरी (~ 150 pm) के साथ तुलनीय हैं और इस प्रकार इस लंबाई के पैमाने के लिए | ब्रैग विवर्तन की अवधारणा न्यूट्रॉन विवर्तन और [[इलेक्ट्रॉन विवर्तन]] प्रक्रियाओं पर समान रूप से लागू होती है।<ref>John M. Cowley (1975) ''Diffraction physics'' (North-Holland, Amsterdam) {{ISBN|0-444-10791-6}}.</ref> [[न्यूट्रॉन]]और एक्स-रे दोनों तरंग दैर्ध्य अंतर-परमाणु दूरी (~ 150 pm) के साथ तुलनीय हैं और इस प्रकार इस लंबाई के पैमाने के लिए उत्कृष्ट जांच है। | ||
== डींग मारने की स्थिति == | == डींग मारने की स्थिति == | ||
[[File:Bragg diffraction 2.svg|thumb|400px|ब्रैग विवर्तन<ref name="bragg">{{citation |last1=Bragg |first1=Henry W. |last2=Bragg |first2=Lawrence W. |date=January 1915|title=X RAYS AND CRYSTAL STRUCTURE |url=https://archive.org/details/xrayscrystalstru00braguoft/page/n5/mode/2up?ref=ol&view=theater |editor=G. Bell and sons L.T.D. London |pages=228 |access-date=2021-05-12}}</ref>{{rp|16}} | [[File:Bragg diffraction 2.svg|thumb|400px|ब्रैग विवर्तन<ref name="bragg">{{citation |last1=Bragg |first1=Henry W. |last2=Bragg |first2=Lawrence W. |date=January 1915|title=X RAYS AND CRYSTAL STRUCTURE |url=https://archive.org/details/xrayscrystalstru00braguoft/page/n5/mode/2up?ref=ol&view=theater |editor=G. Bell and sons L.T.D. London |pages=228 |access-date=2021-05-12}}</ref>{{rp|16}} | ||
समान तरंग दैर्ध्य और चरण वाले दो बीम क्रिस्टलीय ठोस के पास आते हैं और इसके भीतर दो अलग-अलग परमाणुओं से बिखर जाते हैं। निचला बीम 2dsinθ की अतिरिक्त लंबाई का पता लगाता है। रचनात्मक हस्तक्षेप तब होता है जब यह लंबाई विकिरण के तरंग दैर्ध्य के पूर्णांक गुणक के बराबर होती है।]]ब्रैग विवर्तन तब होता है जब [[तरंग दैर्ध्य]] {{mvar|λ}} का विकिरण परमाणु अंतराल के बराबर होता है, क्रिस्टलीय प्रणाली के परमाणुओं द्वारा स्पेक्युलर परावर्तन फैशन (दर्पण जैसा प्रतिबिंब) में बिखरा हुआ है,और रचनात्मक हस्तक्षेप से निर्वाह करता है। | |||
क्रिस्टलीय ठोस के लिए, तरंगें दूरी | क्रिस्टलीय ठोस के लिए, तरंगें परमाणुओं की क्रमिक परतों के मध्य की दूरी {{mvar|d}} द्वारा अलग किए गए जाली विमानों से बिखरी होती हैं। <ref name="moseley1913a"/>{{rp|223}} जब बिखरी हुई तरंगें रचनात्मक रूप से [[हस्तक्षेप (लहर प्रसार)]] करती हैं तो वे चरण में रहती हैं। वे तभी परावर्तित होते हैं जब वे सतह पर निश्चित कोण, दृष्टि कोण (ऑप्टिक्स) {{mvar|θ}} पर प्रहार करते हैं (दाईं ओर की आकृति देखें, और ध्यान दें कि यह स्नेल के नियम की परंपरा से भिन्न है जहां {{mvar|θ}} सामान्य सतह से मापा जाता है), तरंग दैर्ध्य {{mvar|λ}}, और क्रिस्टल का "ग्रेटिंग स्थिरांक" {{mvar|d}} संबंध से जुड़ा है।<ref name="Mose1913" />{{rp|1026}} | ||
<math display="block">n\lambda = 2 d\sin\theta</math> | <math display="block">n\lambda = 2 d\sin\theta</math> | ||
<math> n </math> [[विवर्तन क्रम]] है (<math> n = 1 </math> पहला आदेश है, <math> n = 2 </math> दूसरा क्रम है,<ref name="moseley1913a">{{cite journal |last1=Moseley |first1=Henry H. G. J. |last2=Darwin |first2=Charles G. |date=July 1913 |title=एक्स-रे के प्रतिबिंब पर|url=https://archive.org/details/londonedinburg6261913lond/page/210/mode/2up |journal=The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science|volume=26 |issue=151 |pages=210–232 |doi=10.1080/14786441308634968 |access-date=2021-04-27}}</ref>{{rp|221}} <math> n = 3 </math> तीसरा क्रम है<ref name="Mose1913">{{Cite journal |title=तत्वों की उच्च-आवृत्ति स्पेक्ट्रा|journal=The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science |last=Moseley |first=Henry G. J. |year=1913 |publisher=London : Taylor & Francis |others=Smithsonian Libraries |location=London-Edinburgh |series=6 |volume=26 |pages=1024–1034 |doi=10.1080/14786441308635052 |url=https://archive.org/details/londonedinburg6261913lond/page/1024/mode/2up}}</ref>{{rp|1028}} | <math> n </math> [[विवर्तन क्रम]] है (<math> n = 1 </math> पहला आदेश है, <math> n = 2 </math> दूसरा क्रम है,<ref name="moseley1913a">{{cite journal |last1=Moseley |first1=Henry H. G. J. |last2=Darwin |first2=Charles G. |date=July 1913 |title=एक्स-रे के प्रतिबिंब पर|url=https://archive.org/details/londonedinburg6261913lond/page/210/mode/2up |journal=The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science|volume=26 |issue=151 |pages=210–232 |doi=10.1080/14786441308634968 |access-date=2021-04-27}}</ref>{{rp|221}} <math> n = 3 </math> तीसरा क्रम है)<ref name="Mose1913">{{Cite journal |title=तत्वों की उच्च-आवृत्ति स्पेक्ट्रा|journal=The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science |last=Moseley |first=Henry G. J. |year=1913 |publisher=London : Taylor & Francis |others=Smithsonian Libraries |location=London-Edinburgh |series=6 |volume=26 |pages=1024–1034 |doi=10.1080/14786441308635052 |url=https://archive.org/details/londonedinburg6261913lond/page/1024/mode/2up}}</ref>{{rp|1028}}। रचनात्मक या विनाशकारी हस्तक्षेप का प्रभाव क्रिस्टलीय जाली के क्रमिक [[क्रिस्टलोग्राफिक विमान|क्रिस्टलोग्राफिक विमानों]] (एच, के, एल) में प्रतिबिंब के संचयी प्रभाव के कारण तेज हो जाता है (जैसा कि [[ मिलर सूचकांक ]] द्वारा वर्णित है)। यह ब्रैग के नियम की ओर जाता है, जो रचनात्मक हस्तक्षेप के सबसे मजबूत होने के लिए θ पर स्थिति का वर्णन करता है।<ref>{{Cite book| title=परिचयात्मक ठोस अवस्था भौतिकी|author=H. P. Myers|publisher=Taylor & Francis|year=2002|isbn=0-7484-0660-3}}</ref> | ||
ध्यान दें कि गतिमान कणों, जिनमें [[इलेक्ट्रॉन]], [[प्रोटॉन]] और न्यूट्रॉन सम्मिलित हैं, की संबंधित तरंग दैर्ध्य होती है जिसे [[डी ब्रोगली तरंग दैर्ध्य]] कहा जाता है। प्रकीर्णन कोण के फलन के रूप में प्रकीर्णित तरंगों की तीव्रता को मापकर विवर्तन पैटर्न प्राप्त किया जाता है। ब्रैग चोटियों के रूप में जानी जाने वाली बहुत मजबूत तीव्रता विवर्तन पैटर्न में उन बिंदुओं पर प्राप्त की जाती है जहां प्रकीर्णन कोण ब्रैग स्थिति को संतुष्ट करते हैं। जैसा कि परिचय में उल्लेख किया गया है, यह स्थिति अधिक सामान्य लाउ समीकरणों का विशेष स्थिति है, और लाउ समीकरणों को अतिरिक्त धारणाओं के तहत ब्रैग की स्थिति को कम करने के लिए दिखाया जा सकता है। | |||
क्रिस्टल जाली द्वारा ब्रैग विवर्तन की घटना [[पतली फिल्म हस्तक्षेप]] के साथ समान विशेषताओं को साझा करती है, जिसकी सीमा में समान स्थिति होती है जहां निकट के माध्यम (जैसे हवा) और हस्तक्षेप करने वाले माध्यम (जैसे तेल) के अपवर्तक सूचकांक बराबर होते हैं। | |||
== प्रकीर्णन प्रक्रियाओं को रेखांकित करना == | == प्रकीर्णन प्रक्रियाओं को रेखांकित करना == | ||
जब | जब एक्स-रे किसी परमाणु पर आपतित होते हैं, तो वे इलेक्ट्रॉनिक बादल को गतिमान बनाते हैं, जैसा कि कोई [[विद्युत चुम्बकीय तरंग]] करती है। इन आवेशों की गति ही [[आवृत्ति]] के साथ तरंगों को पुनः से विकीर्ण करती है, विभिन्न प्रकार के प्रभावों के कारण अल्प धुंधला हो जाता है; इस घटना को [[रेले स्कैटरिंग]] (इलास्टिक स्कैटरिंग) के रूप में जाना जाता है। बिखरी हुई तरंगें स्वयं बिखर सकती हैं किंतु यह द्वितीयक विस्तार नगण्य माना जाता है। | ||
इसी | इसी प्रकार की प्रक्रिया [[परमाणु नाभिक|नाभिक]] से न्यूट्रॉन तरंगों को विस्तार या अयुग्मित इलेक्ट्रॉन के साथ [[जुटना (भौतिकी)|सुसंगत]] [[स्पिन (भौतिकी)|स्पिन]] इंटरैक्शन द्वारा होती है। ये पुन: उत्सर्जित तरंग क्षेत्र एक दूसरे के साथ या तो रचनात्मक या विनाशकारी रूप से हस्तक्षेप करते हैं (अतिव्यापी तरंगें या तो स्थिर चोटियों का उत्पादन करने के लिए साथ जुड़ती हैं या दूसरे से कुछ सीमा तक घटाई जाती हैं), डिटेक्टर या फिल्म पर [[विवर्तन]] [[ नमूना |नमूना]] का उत्पादन करती हैं। परिणामी तरंग हस्तक्षेप पैटर्न विवर्तन विश्लेषण का आधार है। इस विश्लेषण को ब्रैग विवर्तन कहा जाता है। | ||
== अनुमानी व्युत्पत्ति == | == अनुमानी व्युत्पत्ति == | ||
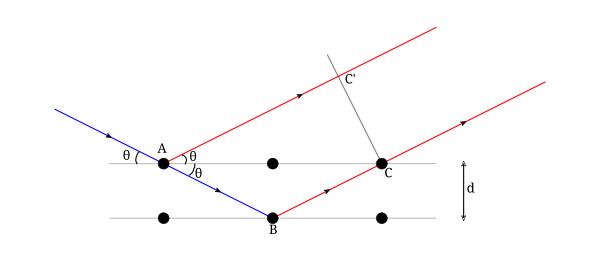
मान लीजिए कि | मान लीजिए कि[[ एकरंगा | मोनोक्रोमैटिक]] तरंग (किसी भी प्रकार की) जाली बिंदुओं के संरेखित विमानों पर तलों पर आपतित होती है <math>d</math>, कोण पर <math>\theta</math> है। बिंदु A और C तल पर हैं, और B नीचे तल पर है। बिंदु ABCC' चतुर्भुज बनाते हैं। | ||
[[File:Bragg's law.svg|center|600px]] | [[File:Bragg's law.svg|center|600px]]AC' के अनुदिश परावर्तित होने वाली किरण AB के साथ संचरित होने वाली किरण, पुनः BC के अनुदिश परावर्तित होने वाली किरण के मध्य पथांतर होगा। यह पथ भेद है | ||
<math display="block">(AB + BC) - \left(AC'\right) \,.</math> | <math display="block">(AB + BC) - \left(AC'\right) \,.</math> | ||
दो अलग-अलग तरंगें एक ही चरण (तरंगों) के साथ | दो अलग-अलग तरंगें एक ही चरण (तरंगों) के साथ बिंदु (इन जाली विमानों से असीम रूप से विस्थापित) पर पहुंचेंगी, और इसलिए रचनात्मक हस्तक्षेप से गुजरती हैं, यदि यह पथ अंतर तरंग दैर्ध्य के किसी भी पूर्णांक मान के बराबर है,अर्थात। | ||
<math display="block"> n\lambda =(AB + BC) - \left(AC'\right) </math> | <math display="block"> n\lambda =(AB + BC) - \left(AC'\right) </math> | ||
<math>n</math> और <math>\lambda</math> पूर्णांक और घटना तरंग की तरंग दैर्ध्य क्रमशः हैं। | |||
इसलिए, | इसलिए, | ||
| Line 37: | Line 37: | ||
जिससे यह अनुसरण करता है | जिससे यह अनुसरण करता है | ||
<math display="block">AC' = AC\cdot\cos\theta = \frac{2d}{\tan\theta}\cos\theta = \left(\frac{2d}{\sin\theta}\cos\theta\right)\cos\theta = \frac{2d}{\sin\theta}\cos^2\theta \,.</math> | <math display="block">AC' = AC\cdot\cos\theta = \frac{2d}{\tan\theta}\cos\theta = \left(\frac{2d}{\sin\theta}\cos\theta\right)\cos\theta = \frac{2d}{\sin\theta}\cos^2\theta \,.</math> | ||
सब कुछ | सब कुछ साथ रखकर, | ||
<math display="block">n\lambda = \frac{2d}{\sin\theta} - \frac{2d}{\sin\theta}\cos^2\theta = \frac{2d}{\sin\theta}\left(1 - \cos^2\theta\right) = \frac{2d}{\sin\theta}\sin^2\theta</math> | <math display="block">n\lambda = \frac{2d}{\sin\theta} - \frac{2d}{\sin\theta}\cos^2\theta = \frac{2d}{\sin\theta}\left(1 - \cos^2\theta\right) = \frac{2d}{\sin\theta}\sin^2\theta</math> | ||
जो सरल करता है <math>n\lambda = 2d\sin\theta \,,</math> जो ब्रैग का नियम ऊपर दिखाया गया है। | जो सरल करता है <math>n\lambda = 2d\sin\theta \,,</math> जो ब्रैग का नियम ऊपर दिखाया गया है। | ||
यदि चित्रों में दिखाए गए अनुसार परमाणुओं के | यदि चित्रों में दिखाए गए अनुसार परमाणुओं के दो विमान विवर्तन कर रहे थे, तो रचनात्मक से विनाशकारी हस्तक्षेप का संक्रमण कोण के समारोह के रूप में धीरे-धीरे होगा, ब्रैग कोणों पर कोमल [[मैक्सिमा और मिनिमा]] के साथ।चूंकि कई परमाणु विमान अधिकांश वास्तविक सामग्रियों में हस्तक्षेप में भाग ले रहे हैं, अधिकतर विनाशकारी हस्तक्षेप परिणाम से घिरे बहुत तेज शिखर है।<ref>{{cite web|url=http://electrons.wikidot.com/x-ray-diffraction-and-bragg-s-law|title=एक्स-रे विवर्तन, ब्रैग का नियम और लाऊ समीकरण|publisher=electrons.wikidot.com}}</ref> | ||
अधिक सामान्य लाउ समीकरणों से | |||
अधिक सामान्य लाउ समीकरणों से कठोर व्युत्पत्ति उपलब्ध है (पृष्ठ देखें: लाउ समीकरण)। | |||
== कोलाइड्स द्वारा दृश्यमान प्रकाश का प्रकीर्णन == | == कोलाइड्स द्वारा दृश्यमान प्रकाश का प्रकीर्णन == | ||
[[कोलाइडल क्रिस्टल]] कणों का उच्च क्रम (क्रिस्टल जाली) वाली सरणी है जो लंबी सीमा (कुछ [[मिलीमीटर]] से लंबाई में [[सेंटीमीटर]] तक) में बनता है; कोलाइडल क्रिस्टल का स्वरूप और गुण लगभग उनके परमाणु या आणविक समकक्षों के अनुरूप होते हैं। <ref name='Pieranski_1983'>{{Cite journal|title=कोलाइडल क्रिस्टल|journal=Contemporary Physics|year=1983|first=P|last=Pieranski|volume=24|pages=25–73 |doi=10.1080/00107518308227471 |bibcode = 1983ConPh..24...25P }</ref> यह कई वर्षों से ज्ञात है कि, प्रतिकारक [[कूलम्बिक]] अंतःक्रियाओं के कारण, [[जलीय]] वातावरण में [[विद्युत आवेशित]] [[बड़े अणुओं|मैक्रोमोलेक्युलस]] लंबी दूरी के क्रिस्टल-जैसे सहसंबंध प्रदर्शित कर सकते हैं, जिसमें इंटरपार्टिकल पृथक्करण दूरी अधिकतर व्यक्तिगत कण व्यास से अधिक होती है। गोलाकार कणों की आवधिक सरणी अंतरालीय [[रिक्ति दोष]] (कणों के मध्य का स्थान) को जन्म देती है, जो दृश्य प्रकाश तरंग के लिए प्राकृतिक विवर्तन झंझरी के रूप में कार्य करती है, जब अंतरालीय रिक्ति घटना प्रकाश तरंग के समान परिमाण के समान क्रम की होती है।<ref name='Hiltner_1969'>{{Cite journal|title=आदेशित निलंबन द्वारा प्रकाश का विवर्तन|journal=Journal of Physical Chemistry|year=1969|first=PA|last=Hiltner|author2=IM Krieger| volume=73|issue=7|pages=2386–2389 |doi=10.1021/j100727a049}}</ref><ref name='Aksay_1984'>{{Cite journal| title=कोलाइडल समेकन के माध्यम से माइक्रोस्ट्रक्चरल कंट्रोल|journal=Proceedings of the American Ceramic Society| year=1984| first=IA|last=Aksay| volume=9|pages=94 }}</ref><ref name="LuckKlier1963">{{cite journal|last1=Luck|first1=Werner|last2=Klier|first2=Manfred| last3=Wesslau|first3=Hermann|title=Über Bragg-Reflexe mit sichtbarem Licht an monodispersen Kunststofflatices. II| journal=Berichte der Bunsengesellschaft für physikalische Chemie|volume=67|issue=1|year=1963|pages=84–85| issn=0005-9021| doi=10.1002/bbpc.19630670114}}</ref> प्रकृति में इन स्तिथियों में, क्रिस्टलीय ठोस में एक्स-रे के प्रकीर्णन के समान मामले में ब्रैग के नियम के अनुसार दृश्यमान प्रकाश तरंगों के विवर्तन और रचनात्मक हस्तक्षेप के लिए ब्रिलियंट इंद्रधनुषी (रंगों का खेल) को उत्तरदायी ठहराया जाता है। प्रभाव दृश्य तरंग दैर्ध्य पर होते हैं क्योंकि पृथक्करण पैरामीटर {{mvar|d}} सच्चे क्रिस्टल की समानता में बहुत बड़ा है। बहुमूल्य [[ ओपीएएल |ओपीएएल]] कोलाइडल क्रिस्टल का उदाहरण है जो हड़ताली ऑप्टिकल प्रभाव उत्पन्न करता है। | |||
== वॉल्यूम ब्रैग झंझरी == | == वॉल्यूम ब्रैग झंझरी == | ||
{{main| | {{main|वॉल्यूम होलोग्राम}} | ||
वॉल्यूम ब्रैग ग्रेटिंग्स (वीबीजी) या [[वॉल्यूम होलोग्राम]] (वीएचजी) में | वॉल्यूम ब्रैग ग्रेटिंग्स (वीबीजी) या [[वॉल्यूम होलोग्राम|वॉल्यूम होलोग्राफिक]] (वीएचजी) में होता है जहां [[अपवर्तक सूचकांक]] में आवधिक परिवर्तन होता है। अपवर्तक सूचकांक के मॉड्यूलेशन के उन्मुखीकरण के आधार पर, वीबीजी का उपयोग या तो [[तरंग दैर्ध्य]] की छोटी बैंडविड्थ को संचारित या प्रतिबिंबित करने के लिए किया जा सकता है।<ref>{{cite journal| last1=Barden|first1=S.C.|last2=Williams|first2=J.B.|last3=Arns|first3=J.A.|last4=Colburn|first4=W.S.| title=Tunable Gratings: Imaging the Universe in 3-D with Volume-Phase Holographic Gratings (Review)|journal=ASP Conf. Ser.| date=2000|volume=195|page=552|bibcode=2000ASPC..195..552B}}</ref> ब्रैग का नियम (वॉल्यूम होलोग्राम के लिए अनुकूलित) निर्धारित करता है कि किस तरंग दैर्ध्य को विवर्तित किया जाएगा:<ref>{{cite book|last1=C. Kress|first1=Bernard|title=Applied Digital Optics : From Micro-optics to Nanophotonics| date=2009|isbn=978-0-470-02263-4}}</ref> | ||
<math display="block">2\Lambda\sin(\theta + \varphi)=m\lambda_B \,,</math> | <math display="block">2\Lambda\sin(\theta + \varphi)=m\lambda_B \,,</math> | ||
जहाँ {{mvar|m}} ब्रैग क्रम ( धनात्मक पूर्णांक) है, {{math|''λ''<sub>B</sub>}} विचलित तरंग दैर्ध्य, Λ झंझरी की फ्रिंज रिक्ति, {{mvar|θ}} घटना बीम और प्रवेश सतह के सामान्य ('''N''') के मध्य का कोण और {{mvar|φ}} सामान्य के मध्य का कोण और झंझरी वेक्टर ({{math|'''K<sub>G</sub>'''}})। विकिरण जो ब्रैग के नियम से मेल नहीं खाता है, वह बिना विचलित हुए वीबीजी से होकर गुजरेगा। घटना कोण ({{mvar|θ}}) को बदलकर कुछ सौ नैनोमीटर पर आउटपुट वेवलेंथ को ट्यून किया जा सकता है। वीबीजी का उपयोग व्यापक रूप से ट्यून करने योग्य लेजर स्रोत का उत्पादन करने या वैश्विक [[हाइपरस्पेक्ट्रल इमेजिंग]] (फोटॉन आदि देखें) करने के लिए किया जा रहा है। | |||
== चयन नियम और व्यावहारिक क्रिस्टलोग्राफी == | == चयन नियम और व्यावहारिक क्रिस्टलोग्राफी == | ||
| Line 58: | Line 59: | ||
<math display="block">d = \frac{a}{\sqrt{h^2 + k^2 + \ell^2}} \,,</math> | <math display="block">d = \frac{a}{\sqrt{h^2 + k^2 + \ell^2}} \,,</math> | ||
<math>a</math> [[ घन क्रिस्टल ]]की जाली रिक्ति है, और {{mvar|h}}, {{mvar|k}}, और {{mvar|ℓ}} ब्रैग प्लेन के मिलर सूचकांक हैं। ब्रैग के नियम के साथ इस संबंध का संयोजन देता है: | |||
<math display="block">\left(\frac{\lambda}{2a}\right)^2 = \left(\frac{\lambda}{2d}\right)^2 \frac{1}{h^2 + k^2 + \ell^2}</math> | <math display="block">\left(\frac{\lambda}{2a}\right)^2 = \left(\frac{\lambda}{2d}\right)^2 \frac{1}{h^2 + k^2 + \ell^2}</math> | ||
मिलर सूचकांकों के लिए अलग-अलग क्यूबिक [[ब्राविस जाली]] के लिए चयन नियम प्राप्त कर सकते हैं; यहां, | मिलर सूचकांकों के लिए अलग-अलग क्यूबिक [[ब्राविस जाली]] के लिए चयन नियम प्राप्त कर सकते हैं; यहां, चयन नियम इस प्रकार दिए जाएंगे। | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ मिलर सूचकांकों के लिए चयन नियम | ||
! | ! ब्रावाइस जाली | ||
! | ! उदाहरण यौगिक | ||
! | ! अनुमत प्रतिबिंब | ||
! | ! निषिद्ध प्रतिबिंब | ||
|- | |- | ||
| | | साधारण घन | ||
| Po | | Po | ||
| Any ''h'', ''k'', ''ℓ'' | | Any ''h'', ''k'', ''ℓ'' | ||
| | | कोई नहीं | ||
|- | |- | ||
| | | शरीर केंद्रित घन | ||
| Fe, W, Ta, Cr | | Fe, W, Ta, Cr | ||
| ''h'' + ''k'' + ''ℓ'' = | | ''h'' + ''k'' + ''ℓ'' =सम | ||
| ''h'' + ''k'' + ''ℓ'' = | | ''h'' + ''k'' + ''ℓ'' = विषम | ||
|- | |- | ||
| | | चेहरा केंद्रित घन (एफसीसी) | ||
| Cu, Al, Ni, NaCl, LiH, PbS | | Cu, Al, Ni, NaCl, LiH, PbS | ||
| ''h'', ''k'', ''ℓ'' | | ''h'', ''k'', ''ℓ'' सभी विषम या सभी सम | ||
| ''h'', ''k'', ''ℓ'' | | ''h'', ''k'', ''ℓ'' मिश्रित विषम और सम | ||
|- | |- | ||
| | | डायमंड एफसीसी | ||
| Si, Ge | | Si, Ge | ||
| | | सभी विषम, या सम सभी के ''h'' + ''k'' + ''ℓ'' = 4''n'' | ||
| ''h'', ''k'', ''ℓ'' | | ''h'', ''k'', ''ℓ'' मिश्रित विषम और सम, या सभी सम के साथ ''h'' + ''k'' + ''ℓ'' ≠ 4''n'' | ||
|- | |- | ||
| [[Triangular lattice]] | | [[Triangular lattice|त्रिकोणीय जाली]] | ||
| Ti, Zr, Cd, Be | | Ti, Zr, Cd, Be | ||
| ''ℓ'' | | ''ℓ'' सम, ''h'' + 2''k'' ≠ 3''n'' | ||
| ''h'' + 2''k'' = 3''n'' | | ''h'' + 2''k'' = 3''n'' विषम के लिए ''ℓ'' | ||
|} | |} | ||
इन चयन नियमों का उपयोग दी गई क्रिस्टल संरचना वाले किसी भी क्रिस्टल के लिए किया जा सकता है। KCl में फलक-केन्द्रित घनीय [[ब्रावाइस जाली]] होता है। | इन चयन नियमों का उपयोग दी गई क्रिस्टल संरचना वाले किसी भी क्रिस्टल के लिए किया जा सकता है। KCl में फलक-केन्द्रित घनीय [[ब्रावाइस जाली]] होता है। चूँकि, K<sup>+</sup> और Cl<sup>−</sup> आयन में इलेक्ट्रॉनों की समान संख्या होती है और आकार में करीब होते हैं, जिससे कि विवर्तन पैटर्न अनिवार्य रूप से आधे लैटिस पैरामीटर के साथ साधारण क्यूबिक संरचना के लिए होता है। अन्य संरचनाओं के लिए चयन नियमों को अन्यत्र या [[संरचना कारक]] के रूप में संदर्भित किया जा सकता है। अन्य क्रिस्टल प्रणालियों के लिए जाली रिक्ति पाई जा सकती है। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 100: | Line 101: | ||
* [[क्रिस्टल लैटिस]] | * [[क्रिस्टल लैटिस]] | ||
* विवर्तन | * विवर्तन | ||
* [[वितरित ब्रैग परावर्तक]] | * [[वितरित ब्रैग परावर्तक]] | ||
*[[फाइबर ब्रैग झंझरी]] | |||
* [[विवर्तन का गतिशील सिद्धांत]] | * [[विवर्तन का गतिशील सिद्धांत]] | ||
* इलेक्ट्रॉन विवर्तन | * इलेक्ट्रॉन विवर्तन | ||
| Line 110: | Line 111: | ||
* राडार एन्जिल्स | * राडार एन्जिल्स | ||
* संरचना कारक | * संरचना कारक | ||
* [[एक्स - रे क्रिस्टलोग्राफी]] | * [[एक्स - रे क्रिस्टलोग्राफी|्स - रे क्रिस्टलोग्राफी]] | ||
== संदर्भ == | == संदर्भ == | ||
| Line 126: | Line 127: | ||
* [http://www.xtal.iqfr.csic.es/Cristalografia/index-en.html Learning crystallography] | * [http://www.xtal.iqfr.csic.es/Cristalografia/index-en.html Learning crystallography] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Bragg's Law]] | |||
[[Category:Collapse templates|Bragg's Law]] | |||
[[Category:Created On 27/03/2023|Bragg's Law]] | |||
[[Category:Lua-based templates|Bragg's Law]] | |||
[[Category:Machine Translated Page|Bragg's Law]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category: | [[Category:Navigational boxes without horizontal lists|Bragg's Law]] | ||
[[Category: | [[Category:Pages with script errors|Bragg's Law]] | ||
[[Category:Short description with empty Wikidata description|Bragg's Law]] | |||
[[Category:Sidebars with styles needing conversion|Bragg's Law]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Bragg's Law]] | |||
[[Category:Templates generating microformats|Bragg's Law]] | |||
[[Category:Templates that add a tracking category|Bragg's Law]] | |||
[[Category:Templates that are not mobile friendly|Bragg's Law]] | |||
[[Category:Templates that generate short descriptions|Bragg's Law]] | |||
[[Category:Templates using TemplateData|Bragg's Law]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:Wikipedia metatemplates|Bragg's Law]] | |||
[[Category:एक्स-रे|Bragg's Law]] | |||
[[Category:क्रिस्टलोग्राफी|Bragg's Law]] | |||
[[Category:न्यूट्रॉन|Bragg's Law]] | |||
[[Category:विवर्तन|Bragg's Law]] | |||
Latest revision as of 13:18, 30 October 2023
भौतिकी और रसायन विज्ञान में, ब्रैग का नियम, वुल्फ-ब्रैग की स्थिति या लाउ-ब्रैग हस्तक्षेप, लाउ विवर्तन का विशेष स्तिथियों , क्रिस्टल जाली से तरंगों के सुसंगत प्रकीर्णन के लिए कोण देता है। यह जाली विमानों द्वारा बिखरे तरंग मोर्चों के सुपरपोजिशन को सम्मिलित करता है, जिससे तरंग दैर्ध्य और बिखरने वाले कोण के मध्य अत्यधिक संबंध होता है, क्रिस्टल जाली के संबंध में वेववेक्टर ट्रांसफर होता है। इस प्रकार के नियम को प्रारंभ में क्रिस्टल पर एक्स-रे के लिए प्रस्तुत किया गया था। चूँकि, यह सभी प्रकार के क्वांटम बीम पर प्रारम्भ होता है, जिसमें परमाणु दूरी पर न्यूट्रॉन और इलेक्ट्रॉन तरंगों के साथ-साथ कृत्रिम आवधिक सूक्ष्म जाली पर दृश्य प्रकाश भी सम्मिलित है।
इतिहास

ब्रैग विवर्तन (जिसे एक्स-रे विवर्तन के ब्रैग सूत्रीकरण के रूप में भी जाना जाता है) प्रथम बार लॉरेंस ब्रैग और उनके पिता, विलियम हेनरी ब्रैग द्वारा 1913[1] में उनकी अविष्कार के उपकार में प्रस्तावित किया गया था कि क्रिस्टलीय ठोस परावर्तित एक्स-रे के आश्चर्यजनक पैटर्न का उत्पादन करते हैं। (इसके विपरीत, कहते हैं, तरल)। उन्होंने पाया कि ये क्रिस्टल, कुछ विशिष्ट तरंग दैर्ध्य और घटना कोणों पर, परावर्तित विकिरण की तीव्र चोटियों का उत्पादन करते हैं। व्युत्पन्न ब्रैग का नियम लाउ विवर्तन की विशेष व्याख्या है, जहां ब्रैग्स ने क्रिस्टल जाली विमानों से तरंगों के प्रतिबिंब द्वारा ज्यामितीय विधि से रचनात्मक लाउ-ब्रैग हस्तक्षेप की व्याख्या की, जैसे कि पथ-अंतर घटना तरंगदैर्ध्य का गुणक बन जाता है।
लॉरेंस ब्रैग ने क्रिस्टल को स्थिर पैरामीटर d द्वारा अलग किए गए असतत समानांतर विमानों के सेट के रूप में मॉडलिंग करके इस परिणाम की व्याख्या की। यह प्रस्तावित किया गया था कि घटना एक्स-रे विकिरण ब्रैग चोटी का उत्पादन करेगा यदि विभिन्न विमानों से उनका प्रतिबिंब रचनात्मक रूप से हस्तक्षेप करता है। हस्तक्षेप रचनात्मक होता है जब चरण परिवर्तन 2π का गुणक होता है; इस स्थिति को ब्रैग के नियम द्वारा व्यक्त किया जा सकता है (नीचे ब्रैग स्थिति अनुभाग देखें) और पहली बार लॉरेंस ब्रैग द्वारा 11 नवंबर 1912 को कैम्ब्रिज फिलोसोफिकल सोसायटी को प्रस्तुत किया गया था।[2][3] चूँकि सरल, ब्रैग के नियम ने परमाणु मापक पर वास्तविक कणों के अस्तित्व की पुष्टि की, साथ ही एक्स-रे और न्यूट्रॉन विवर्तन के रूप में क्रिस्टल का अध्ययन करने के लिए शक्तिशाली आधुनिक उपकरण प्रदान किया। लॉरेंस ब्रैग और उनके पिता, विलियम हेनरी ब्रैग को 1915 में सोडियम क्लोराइड, जिंक सल्फाइड और हीरे से शुरू होने वाली क्रिस्टल संरचनाओं के निर्धारण में उनके कार्य के लिए भौतिकी में नोबेल पुरस्कार से सम्मानित किया गया था। वे संयुक्त रूप से जीतने वाली एकमात्र पिता-पुत्र टीम हैं।
ब्रैग विवर्तन की अवधारणा न्यूट्रॉन विवर्तन और इलेक्ट्रॉन विवर्तन प्रक्रियाओं पर समान रूप से लागू होती है।[4] न्यूट्रॉनऔर एक्स-रे दोनों तरंग दैर्ध्य अंतर-परमाणु दूरी (~ 150 pm) के साथ तुलनीय हैं और इस प्रकार इस लंबाई के पैमाने के लिए उत्कृष्ट जांच है।
डींग मारने की स्थिति

ब्रैग विवर्तन तब होता है जब तरंग दैर्ध्य λ का विकिरण परमाणु अंतराल के बराबर होता है, क्रिस्टलीय प्रणाली के परमाणुओं द्वारा स्पेक्युलर परावर्तन फैशन (दर्पण जैसा प्रतिबिंब) में बिखरा हुआ है,और रचनात्मक हस्तक्षेप से निर्वाह करता है।
क्रिस्टलीय ठोस के लिए, तरंगें परमाणुओं की क्रमिक परतों के मध्य की दूरी d द्वारा अलग किए गए जाली विमानों से बिखरी होती हैं। [6]: 223 जब बिखरी हुई तरंगें रचनात्मक रूप से हस्तक्षेप (लहर प्रसार) करती हैं तो वे चरण में रहती हैं। वे तभी परावर्तित होते हैं जब वे सतह पर निश्चित कोण, दृष्टि कोण (ऑप्टिक्स) θ पर प्रहार करते हैं (दाईं ओर की आकृति देखें, और ध्यान दें कि यह स्नेल के नियम की परंपरा से भिन्न है जहां θ सामान्य सतह से मापा जाता है), तरंग दैर्ध्य λ, और क्रिस्टल का "ग्रेटिंग स्थिरांक" d संबंध से जुड़ा है।[7]: 1026
ध्यान दें कि गतिमान कणों, जिनमें इलेक्ट्रॉन, प्रोटॉन और न्यूट्रॉन सम्मिलित हैं, की संबंधित तरंग दैर्ध्य होती है जिसे डी ब्रोगली तरंग दैर्ध्य कहा जाता है। प्रकीर्णन कोण के फलन के रूप में प्रकीर्णित तरंगों की तीव्रता को मापकर विवर्तन पैटर्न प्राप्त किया जाता है। ब्रैग चोटियों के रूप में जानी जाने वाली बहुत मजबूत तीव्रता विवर्तन पैटर्न में उन बिंदुओं पर प्राप्त की जाती है जहां प्रकीर्णन कोण ब्रैग स्थिति को संतुष्ट करते हैं। जैसा कि परिचय में उल्लेख किया गया है, यह स्थिति अधिक सामान्य लाउ समीकरणों का विशेष स्थिति है, और लाउ समीकरणों को अतिरिक्त धारणाओं के तहत ब्रैग की स्थिति को कम करने के लिए दिखाया जा सकता है।
क्रिस्टल जाली द्वारा ब्रैग विवर्तन की घटना पतली फिल्म हस्तक्षेप के साथ समान विशेषताओं को साझा करती है, जिसकी सीमा में समान स्थिति होती है जहां निकट के माध्यम (जैसे हवा) और हस्तक्षेप करने वाले माध्यम (जैसे तेल) के अपवर्तक सूचकांक बराबर होते हैं।
प्रकीर्णन प्रक्रियाओं को रेखांकित करना
जब एक्स-रे किसी परमाणु पर आपतित होते हैं, तो वे इलेक्ट्रॉनिक बादल को गतिमान बनाते हैं, जैसा कि कोई विद्युत चुम्बकीय तरंग करती है। इन आवेशों की गति ही आवृत्ति के साथ तरंगों को पुनः से विकीर्ण करती है, विभिन्न प्रकार के प्रभावों के कारण अल्प धुंधला हो जाता है; इस घटना को रेले स्कैटरिंग (इलास्टिक स्कैटरिंग) के रूप में जाना जाता है। बिखरी हुई तरंगें स्वयं बिखर सकती हैं किंतु यह द्वितीयक विस्तार नगण्य माना जाता है।
इसी प्रकार की प्रक्रिया नाभिक से न्यूट्रॉन तरंगों को विस्तार या अयुग्मित इलेक्ट्रॉन के साथ सुसंगत स्पिन इंटरैक्शन द्वारा होती है। ये पुन: उत्सर्जित तरंग क्षेत्र एक दूसरे के साथ या तो रचनात्मक या विनाशकारी रूप से हस्तक्षेप करते हैं (अतिव्यापी तरंगें या तो स्थिर चोटियों का उत्पादन करने के लिए साथ जुड़ती हैं या दूसरे से कुछ सीमा तक घटाई जाती हैं), डिटेक्टर या फिल्म पर विवर्तन नमूना का उत्पादन करती हैं। परिणामी तरंग हस्तक्षेप पैटर्न विवर्तन विश्लेषण का आधार है। इस विश्लेषण को ब्रैग विवर्तन कहा जाता है।
अनुमानी व्युत्पत्ति
मान लीजिए कि मोनोक्रोमैटिक तरंग (किसी भी प्रकार की) जाली बिंदुओं के संरेखित विमानों पर तलों पर आपतित होती है , कोण पर है। बिंदु A और C तल पर हैं, और B नीचे तल पर है। बिंदु ABCC' चतुर्भुज बनाते हैं।
AC' के अनुदिश परावर्तित होने वाली किरण AB के साथ संचरित होने वाली किरण, पुनः BC के अनुदिश परावर्तित होने वाली किरण के मध्य पथांतर होगा। यह पथ भेद है
इसलिए,
यदि चित्रों में दिखाए गए अनुसार परमाणुओं के दो विमान विवर्तन कर रहे थे, तो रचनात्मक से विनाशकारी हस्तक्षेप का संक्रमण कोण के समारोह के रूप में धीरे-धीरे होगा, ब्रैग कोणों पर कोमल मैक्सिमा और मिनिमा के साथ।चूंकि कई परमाणु विमान अधिकांश वास्तविक सामग्रियों में हस्तक्षेप में भाग ले रहे हैं, अधिकतर विनाशकारी हस्तक्षेप परिणाम से घिरे बहुत तेज शिखर है।[9]
अधिक सामान्य लाउ समीकरणों से कठोर व्युत्पत्ति उपलब्ध है (पृष्ठ देखें: लाउ समीकरण)।
कोलाइड्स द्वारा दृश्यमान प्रकाश का प्रकीर्णन
कोलाइडल क्रिस्टल कणों का उच्च क्रम (क्रिस्टल जाली) वाली सरणी है जो लंबी सीमा (कुछ मिलीमीटर से लंबाई में सेंटीमीटर तक) में बनता है; कोलाइडल क्रिस्टल का स्वरूप और गुण लगभग उनके परमाणु या आणविक समकक्षों के अनुरूप होते हैं। [10] यह कई वर्षों से ज्ञात है कि, प्रतिकारक कूलम्बिक अंतःक्रियाओं के कारण, जलीय वातावरण में विद्युत आवेशित मैक्रोमोलेक्युलस लंबी दूरी के क्रिस्टल-जैसे सहसंबंध प्रदर्शित कर सकते हैं, जिसमें इंटरपार्टिकल पृथक्करण दूरी अधिकतर व्यक्तिगत कण व्यास से अधिक होती है। गोलाकार कणों की आवधिक सरणी अंतरालीय रिक्ति दोष (कणों के मध्य का स्थान) को जन्म देती है, जो दृश्य प्रकाश तरंग के लिए प्राकृतिक विवर्तन झंझरी के रूप में कार्य करती है, जब अंतरालीय रिक्ति घटना प्रकाश तरंग के समान परिमाण के समान क्रम की होती है।[11][12][13] प्रकृति में इन स्तिथियों में, क्रिस्टलीय ठोस में एक्स-रे के प्रकीर्णन के समान मामले में ब्रैग के नियम के अनुसार दृश्यमान प्रकाश तरंगों के विवर्तन और रचनात्मक हस्तक्षेप के लिए ब्रिलियंट इंद्रधनुषी (रंगों का खेल) को उत्तरदायी ठहराया जाता है। प्रभाव दृश्य तरंग दैर्ध्य पर होते हैं क्योंकि पृथक्करण पैरामीटर d सच्चे क्रिस्टल की समानता में बहुत बड़ा है। बहुमूल्य ओपीएएल कोलाइडल क्रिस्टल का उदाहरण है जो हड़ताली ऑप्टिकल प्रभाव उत्पन्न करता है।
वॉल्यूम ब्रैग झंझरी
वॉल्यूम ब्रैग ग्रेटिंग्स (वीबीजी) या वॉल्यूम होलोग्राफिक (वीएचजी) में होता है जहां अपवर्तक सूचकांक में आवधिक परिवर्तन होता है। अपवर्तक सूचकांक के मॉड्यूलेशन के उन्मुखीकरण के आधार पर, वीबीजी का उपयोग या तो तरंग दैर्ध्य की छोटी बैंडविड्थ को संचारित या प्रतिबिंबित करने के लिए किया जा सकता है।[14] ब्रैग का नियम (वॉल्यूम होलोग्राम के लिए अनुकूलित) निर्धारित करता है कि किस तरंग दैर्ध्य को विवर्तित किया जाएगा:[15]
चयन नियम और व्यावहारिक क्रिस्टलोग्राफी
जैसा कि ऊपर कहा गया है, ब्रैग के नियम का उपयोग निम्नलिखित संबंधों के माध्यम से किसी विशेष घन प्रणाली की जाली रिक्ति प्राप्त करने के लिए किया जा सकता है:
| ब्रावाइस जाली | उदाहरण यौगिक | अनुमत प्रतिबिंब | निषिद्ध प्रतिबिंब |
|---|---|---|---|
| साधारण घन | Po | Any h, k, ℓ | कोई नहीं |
| शरीर केंद्रित घन | Fe, W, Ta, Cr | h + k + ℓ =सम | h + k + ℓ = विषम |
| चेहरा केंद्रित घन (एफसीसी) | Cu, Al, Ni, NaCl, LiH, PbS | h, k, ℓ सभी विषम या सभी सम | h, k, ℓ मिश्रित विषम और सम |
| डायमंड एफसीसी | Si, Ge | सभी विषम, या सम सभी के h + k + ℓ = 4n | h, k, ℓ मिश्रित विषम और सम, या सभी सम के साथ h + k + ℓ ≠ 4n |
| त्रिकोणीय जाली | Ti, Zr, Cd, Be | ℓ सम, h + 2k ≠ 3n | h + 2k = 3n विषम के लिए ℓ |
इन चयन नियमों का उपयोग दी गई क्रिस्टल संरचना वाले किसी भी क्रिस्टल के लिए किया जा सकता है। KCl में फलक-केन्द्रित घनीय ब्रावाइस जाली होता है। चूँकि, K+ और Cl− आयन में इलेक्ट्रॉनों की समान संख्या होती है और आकार में करीब होते हैं, जिससे कि विवर्तन पैटर्न अनिवार्य रूप से आधे लैटिस पैरामीटर के साथ साधारण क्यूबिक संरचना के लिए होता है। अन्य संरचनाओं के लिए चयन नियमों को अन्यत्र या संरचना कारक के रूप में संदर्भित किया जा सकता है। अन्य क्रिस्टल प्रणालियों के लिए जाली रिक्ति पाई जा सकती है।
यह भी देखें
- ब्रैग विमान
- क्रिस्टल लैटिस
- विवर्तन
- वितरित ब्रैग परावर्तक
- फाइबर ब्रैग झंझरी
- विवर्तन का गतिशील सिद्धांत
- इलेक्ट्रॉन विवर्तन
- जॉर्ज वुल्फ
- हेंडरसन सीमा
- हँसने की स्थिति
- पाउडर विवर्तन
- राडार एन्जिल्स
- संरचना कारक
- ्स - रे क्रिस्टलोग्राफी
संदर्भ
- ↑ Bragg, W. H.; Bragg, W. L. (1913). "क्रिस्टल द्वारा एक्स-रे का प्रतिबिंब". Proc. R. Soc. Lond. A. 88 (605): 428–38. Bibcode:1913RSPSA..88..428B. doi:10.1098/rspa.1913.0040.
- ↑ See, for example, this example calculation Archived July 10, 2011, at the Wayback Machine of interatomic spacing with Bragg's law.
- ↑ There are some sources, like the Academic American Encyclopedia, that attribute the discovery of the law to both W.L Bragg and his father W.H. Bragg, but the official Nobel Prize site and the biographies written about him ("Light Is a Messenger: The Life and Science of William Lawrence Bragg", Graeme K. Hunter, 2004 and "Great Solid State Physicists of the 20th Century", Julio Antonio Gonzalo, Carmen Aragó López) make a clear statement that Lawrence Bragg alone derived the law.
- ↑ John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN 0-444-10791-6.
- ↑ Bragg, Henry W.; Bragg, Lawrence W. (January 1915), G. Bell and sons L.T.D. London (ed.), X RAYS AND CRYSTAL STRUCTURE, p. 228, retrieved 2021-05-12
- ↑ 6.0 6.1 Moseley, Henry H. G. J.; Darwin, Charles G. (July 1913). "एक्स-रे के प्रतिबिंब पर". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (151): 210–232. doi:10.1080/14786441308634968. Retrieved 2021-04-27.
- ↑ 7.0 7.1 Moseley, Henry G. J. (1913). Smithsonian Libraries. "तत्वों की उच्च-आवृत्ति स्पेक्ट्रा". The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science. 6. London-Edinburgh: London : Taylor & Francis. 26: 1024–1034. doi:10.1080/14786441308635052.
- ↑ H. P. Myers (2002). परिचयात्मक ठोस अवस्था भौतिकी. Taylor & Francis. ISBN 0-7484-0660-3.
- ↑ "एक्स-रे विवर्तन, ब्रैग का नियम और लाऊ समीकरण". electrons.wikidot.com.
- ↑ {{Cite journal|title=कोलाइडल क्रिस्टल|journal=Contemporary Physics|year=1983|first=P|last=Pieranski|volume=24|pages=25–73 |doi=10.1080/00107518308227471 |bibcode = 1983ConPh..24...25P }
- ↑ Hiltner, PA; IM Krieger (1969). "आदेशित निलंबन द्वारा प्रकाश का विवर्तन". Journal of Physical Chemistry. 73 (7): 2386–2389. doi:10.1021/j100727a049.
- ↑ Aksay, IA (1984). "कोलाइडल समेकन के माध्यम से माइक्रोस्ट्रक्चरल कंट्रोल". Proceedings of the American Ceramic Society. 9: 94.
- ↑ Luck, Werner; Klier, Manfred; Wesslau, Hermann (1963). "Über Bragg-Reflexe mit sichtbarem Licht an monodispersen Kunststofflatices. II". Berichte der Bunsengesellschaft für physikalische Chemie. 67 (1): 84–85. doi:10.1002/bbpc.19630670114. ISSN 0005-9021.
- ↑ Barden, S.C.; Williams, J.B.; Arns, J.A.; Colburn, W.S. (2000). "Tunable Gratings: Imaging the Universe in 3-D with Volume-Phase Holographic Gratings (Review)". ASP Conf. Ser. 195: 552. Bibcode:2000ASPC..195..552B.
- ↑ C. Kress, Bernard (2009). Applied Digital Optics : From Micro-optics to Nanophotonics. ISBN 978-0-470-02263-4.
अग्रिम पठन
- Neil W. Ashcroft and N. David Mermin, Solid State Physics (Harcourt: Orlando, 1976).
- Bragg W (1913). "The Diffraction of Short Electromagnetic Waves by a Crystal". Proceedings of the Cambridge Philosophical Society. 17: 43–57.