रडार चार्ट: Difference between revisions

From Vigyanwiki
m (14 revisions imported from alpha:रडार_चार्ट)
No edit summary
 
(One intermediate revision by one other user not shown)
Line 1: Line 1:
{{Short description|Type of chart}}
 
{{Redirect|
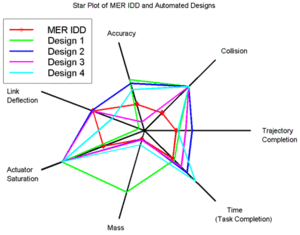
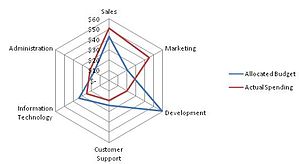
[[Image:MER Star Plot.gif|thumb|300px|right|नासा के स्टार प्लॉट का उदाहरण, कुछ सबसे वांछनीय डिज़ाइन परिणामों को केंद्र में दर्शाया गया है।]] [[File:Spider Chart2.jpg|right|thumb|300px|यह स्पाइडर चार्ट किसी दिए गए संगठन के लिए आवंटित बजट के प्रति वास्तविक व्यय का प्रतिनिधित्व करता है।]]'''रडार [[चार्ट]]''' ही बिंदु से प्रारम्भ होने वाले अक्षों पर दर्शाए गए तीन या अधिक मात्रात्मक चर के दो-आयामी चार्ट के रूप में बहुभिन्नरूपी सांख्यिकी डेटा प्रदर्शित करने के ग्राफिकल प्रविधियो की सूची है। अक्षों की सापेक्ष स्थिति एवं कोण सामान्यतः सूचनात्मक नहीं है, किन्तु विभिन्न [[आंकड़े]], जैसे कि एल्गोरिदम जो डेटा को अधिकतम कुल क्षेत्र के रूप में प्लॉट करते हैं, को चर (अक्षों) को सापेक्ष स्थितियों में क्रमबद्ध करने के लिए प्रारम्भ किया जा सकता है जो भिन्न-भिन्न सहसंबंध, व्यापार-विवृत प्रकट करते हैं, एवं कई अन्य तुलनात्मक प्रविधि प्रकट करते हैं।<ref>{{cite journal |last1=Porter |first1=Michael M |last2=Niksiar |first2=Pooya |title=Multidimensional mechanics: Performance mapping of natural biological systems using permutated radar charts |journal=PLOS ONE |date=2018 |volume=13 |issue=9 |page=e0204309 |doi=10.1371/journal.pone.0204309|pmid=30265707 |pmc=6161877 |bibcode=2018PLoSO..1304309P |doi-access=free }}</ref>
स्पाइडर चार्ट|
यूलर आरेख का विस्तार|स्पाइडर आरेख}}
[[Image:MER Star Plot.gif|thumb|300px|right|नासा के स्टार प्लॉट का उदाहरण, कुछ सबसे वांछनीय डिज़ाइन परिणामों को केंद्र में दर्शाया गया है।]] [[File:Spider Chart2.jpg|right|thumb|300px|यह स्पाइडर चार्ट किसी दिए गए संगठन के लिए आवंटित बजट के प्रति वास्तविक व्यय का प्रतिनिधित्व करता है।]]रडार [[चार्ट]] ही बिंदु से प्रारम्भ होने वाले अक्षों पर दर्शाए गए तीन या अधिक मात्रात्मक चर के दो-आयामी चार्ट के रूप में बहुभिन्नरूपी सांख्यिकी डेटा प्रदर्शित करने के ग्राफिकल प्रविधियो की सूची है। अक्षों की सापेक्ष स्थिति एवं कोण सामान्यतः सूचनात्मक नहीं है, किन्तु विभिन्न [[आंकड़े]], जैसे कि एल्गोरिदम जो डेटा को अधिकतम कुल क्षेत्र के रूप में प्लॉट करते हैं, को चर (अक्षों) को सापेक्ष स्थितियों में क्रमबद्ध करने के लिए प्रारम्भ किया जा सकता है जो भिन्न-भिन्न सहसंबंध, व्यापार-विवृत प्रकट करते हैं, एवं कई अन्य तुलनात्मक प्रविधि प्रकट करते हैं।<ref>{{cite journal |last1=Porter |first1=Michael M |last2=Niksiar |first2=Pooya |title=Multidimensional mechanics: Performance mapping of natural biological systems using permutated radar charts |journal=PLOS ONE |date=2018 |volume=13 |issue=9 |page=e0204309 |doi=10.1371/journal.pone.0204309|pmid=30265707 |pmc=6161877 |bibcode=2018PLoSO..1304309P |doi-access=free }}</ref>
रडार चार्ट को वेब चार्ट, स्पाइडर चार्ट, स्पाइडर ग्राफ, स्पाइडर वेब चार्ट, स्टार चार्ट, के रूप में भी जाना जाता है।<ref>Nancy R. Tague (2005) ''The quality toolbox''. page 437.</ref> स्टार प्लॉट, कोबवेब चार्ट, अनियमित बहुभुज, ध्रुवीय चार्ट, या किविएट आरेख,<ref>{{cite journal|last1=Kolence|first1=Kenneth W.|title=सॉफ्टवेयर अनुभववादी|journal=ACM SIGMETRICS Performance Evaluation Review|date=1973|volume=2|issue=2|pages=31–36|doi=10.1145/1113644.1113647 |s2cid=18600391|quote=Dr. [[Philip J. Kiviat]] suggested at a recent NBS/ACM workshop on performance measurement that a circular graph, using radii as the variable axes might be a useful form. […] I recommend they be called "Kiviat Plots" or "Kiviat Graphs" to recognize his insight as to their importance.|doi-access=free}}</ref><ref name=radarandpolar>{{cite web|url=http://www.content-workshops.com/toolbox/2015/2/find-content-gaps-using-radar-charts |title=रडार चार्ट का उपयोग करके सामग्री अंतराल खोजें|publisher=Content Strategy Workshops |date=March 3, 2015 |access-date=December 17, 2015}}</ref> यह [[समानांतर निर्देशांक]] प्लॉट के समतुल्य है, जिसमें अक्ष रेडियल रूप से व्यवस्थित हैं।
रडार चार्ट को वेब चार्ट, स्पाइडर चार्ट, स्पाइडर ग्राफ, स्पाइडर वेब चार्ट, स्टार चार्ट, के रूप में भी जाना जाता है।<ref>Nancy R. Tague (2005) ''The quality toolbox''. page 437.</ref> स्टार प्लॉट, कोबवेब चार्ट, अनियमित बहुभुज, ध्रुवीय चार्ट, या किविएट आरेख,<ref>{{cite journal|last1=Kolence|first1=Kenneth W.|title=सॉफ्टवेयर अनुभववादी|journal=ACM SIGMETRICS Performance Evaluation Review|date=1973|volume=2|issue=2|pages=31–36|doi=10.1145/1113644.1113647 |s2cid=18600391|quote=Dr. [[Philip J. Kiviat]] suggested at a recent NBS/ACM workshop on performance measurement that a circular graph, using radii as the variable axes might be a useful form. […] I recommend they be called "Kiviat Plots" or "Kiviat Graphs" to recognize his insight as to their importance.|doi-access=free}}</ref><ref name=radarandpolar>{{cite web|url=http://www.content-workshops.com/toolbox/2015/2/find-content-gaps-using-radar-charts |title=रडार चार्ट का उपयोग करके सामग्री अंतराल खोजें|publisher=Content Strategy Workshops |date=March 3, 2015 |access-date=December 17, 2015}}</ref> यह [[समानांतर निर्देशांक]] प्लॉट के समतुल्य है, जिसमें अक्ष रेडियल रूप से व्यवस्थित हैं।


== सिंहावलोकन ==
== अवलोकन ==
रडार चार्ट चार्ट एवं/या [[प्लॉट (ग्राफिक्स)]] है जिसमें सम-कोणीय तीलियों का क्रम होता है, जिसे रेडी कहा जाता है, जिसमें प्रत्येक तीली चर का प्रतिनिधित्व करती है। किसी स्पोक की डेटा लंबाई सभी डेटा बिंदुओं पर चर के अधिकतम परिमाण के सापेक्ष डेटा बिंदु के लिए चर के परिमाण के समानुपाती होती है। प्रत्येक स्पोक के लिए डेटा मानों को जोड़ने वाली रेखा खींची जाती है। इससे कथानक को तारे जैसा स्वरूप मिलता है एवं इस कथानक के लिए लोकप्रिय नामों में से की उत्पत्ति होती है। स्टार प्लॉट का उपयोग निम्नलिखित प्रश्नों के उत्तर देने के लिए किया जा सकता है:<ref name="NIST03"/>* कौन से अवलोकन सबसे अधिक समान हैं, अर्थात, क्या अवलोकनों के समूह हैं? (रडार चार्ट का उपयोग एकल डेटा बिंदु के सापेक्ष मूल्यों की परिक्षण करने के लिए किया जाता है (उदाहरण के लिए, बिंदु 3 चर 2 एवं 4 के लिए बड़ा है, चर 1, 3, 5, एवं 6 के लिए अल्प है) एवं समान बिंदुओं या असमान बिंदुओं की जानकारी ज्ञात करने के लिए।)<ref name="NIST03"/>*क्या आउटलेयर हैं?
रडार चार्ट चार्ट एवं/या [[प्लॉट (ग्राफिक्स)]] है जिसमें सम-कोणीय तीलियों का क्रम होता है, जिसे रेडी कहा जाता है, जिसमें प्रत्येक तीली चर का प्रतिनिधित्व करती है। किसी स्पोक की डेटा लंबाई सभी डेटा बिंदुओं पर चर के अधिकतम परिमाण के सापेक्ष डेटा बिंदु के लिए चर के परिमाण के समानुपाती होती है। प्रत्येक स्पोक के लिए डेटा मानों को जोड़ने वाली रेखा खींची जाती है। इससे कथानक को तारे जैसा स्वरूप मिलता है एवं इस कथानक के लिए लोकप्रिय नामों में से की उत्पत्ति होती है। स्टार प्लॉट का उपयोग निम्नलिखित प्रश्नों के उत्तर देने के लिए किया जा सकता है:<ref name="NIST03"/>* कौन से अवलोकन सबसे अधिक समान हैं, अर्थात, क्या अवलोकनों के समूह हैं? (रडार चार्ट का उपयोग एकल डेटा बिंदु के सापेक्ष मूल्यों की परिक्षण करने के लिए किया जाता है (उदाहरण के लिए, बिंदु 3 चर 2 एवं 4 के लिए बड़ा है, चर 1, 3, 5, एवं 6 के लिए अल्प है) एवं समान बिंदुओं या असमान बिंदुओं की जानकारी ज्ञात करने के लिए।)<ref name="NIST03"/>*क्या आउटलेयर हैं?


Line 14: Line 11:
[[File:MLB2021ShoheivsLeague.png|alt=Shohei Ohtaniके बल्लेबाजी आँकड़े बनाम एमएलबी औसत बल्लेबाजी आँकड़े|अंगूठे |300px |2021 एमएलबी सीज़न से बल्लेबाजी के आँकड़े दिखाने वाला एक रडार चार्ट। शूही ओहतानी, हरा, उस सीज़न के लिए डीएच, लाल और एमएलबी, नीले, औसत से बेहतर प्रदर्शन करता है, लेकिन अधिक बार स्ट्राइक भी करता है। https://www.baseball-reference.com/ से डेटा।]]
[[File:MLB2021ShoheivsLeague.png|alt=Shohei Ohtaniके बल्लेबाजी आँकड़े बनाम एमएलबी औसत बल्लेबाजी आँकड़े|अंगूठे |300px |2021 एमएलबी सीज़न से बल्लेबाजी के आँकड़े दिखाने वाला एक रडार चार्ट। शूही ओहतानी, हरा, उस सीज़न के लिए डीएच, लाल और एमएलबी, नीले, औसत से बेहतर प्रदर्शन करता है, लेकिन अधिक बार स्ट्राइक भी करता है। https://www.baseball-reference.com/ से डेटा।]]


रडार चार्ट का उपयोग खेल में खिलाड़ियों की शक्ति एवं शक्तिहीन को चार्ट करने के लिए किया जा सकता है।<ref>[http://howtowatchsports.com/spider-graphs-charting-basketball-statistics/ Spider Graphs: Charting Basketball Statistics]</ref> खिलाड़ी से संबंधित विभिन्न आँकड़ों की गणना करके जिसे चार्ट के केंद्रीय अक्ष के साथ ट्रैक किया जा सकता है। उदाहरणों में बास्केट खिलाड़ी द्वारा लगाए गए शॉट, रिबाउंड, सहायता आदि, या बेसबॉल खिलाड़ी की बल्लेबाजी या पिचिंग आँकड़े सम्मिलित हैं। यह किसी खिलाड़ी की शक्ति एवं कमजोरियों का केंद्रीकृत दृश्य बनाता है, एवं यदि अन्य खिलाड़ियों या लीग औसत के आंकड़ों के साथ ओवरलैप किया जाता है, तो यह प्रदर्शित हो सकता है कि खिलाड़ी कहां उत्कृष्टता प्राप्त करता है एवं वे कहां सुधार कर सकते हैं।<ref>{{cite web |title=डेटा विज़ुअलाइज़ेशन को समझना|author=Seeing Data |publisher=Seeing Data|url=http://seeingdata.org/taketime/inside-the-chart-radar-chart/ |language=en-US}}</ref> खिलाड़ी की ताकत एवं कमजोरी के बारे में ये अंतर्दृष्टि खिलाड़ी के विकास के लिए महत्वपूर्ण प्रमाणित हो सकती है क्योंकि यह कोच एवं प्रशिक्षकों को खिलाड़ी की कमजोरियों को सुधारने में सहायता करने के लिए उनकी प्रशिक्षण रेजिमेंट को समायोजित करने की अनुमति देती है। रडार चार्ट के परिणाम स्थितिजन्य खेल में भी उपयोगी हो सकते हैं। यदि किसी बल्लेबाज को बाएं हाथ की पिचिंग के विरुद्ध निकृष्ट हिट करते हुए दिखाया गया है, तो उसकी टीम बाएं हाथ के पिचर्स के विरुद्ध अपनी प्लेट की उपस्थिति को सीमित करना जानती है, जबकि विरोधी टीम ऐसी स्थिति को विवश करने का प्रयत्न कर सकती है जहां बल्लेबाज को पिचर के विरुद्ध हिट करने के लिए विवश किया जाता है।[[File:3VehiclePerformanceMetrics.png|alt=The performance metrics of 3 different types of vehicle|thumb |300px |सेडान, स्पोर्ट्स कार एवं पिकअप ट्रक के प्रदर्शन मेट्रिक्स में अंतर दिखाने वाला रडार चार्ट।]]रडार चार्ट का अन्य अनुप्रयोग कंप्यूटर प्रोग्राम सहित विभिन्न वस्तुओं के प्रदर्शन मेट्रिक्स को प्रदर्शित करने के लिए [[गुणवत्ता प्रबंधन]] का नियंत्रण है,<ref>Ron Basu (2004). ''Implementing Quality: A Practical Guide to Tools and Techniques''. p.131.</ref> कंप्यूटर, फ़ोन, वाहन, एवं आदि होते है। कंप्यूटर प्रोग्रामर प्रायः दूसरों की तुलना में अपने प्रोग्राम के प्रदर्शन का परीक्षण करने के लिए एनालिटिक्स का उपयोग करते हैं। इसका उदाहरण जहां रडार चार्ट उपयोगी हो सकते हैं, वह विभिन्न सॉर्टिंग एल्गोरिदम का प्रदर्शन विश्लेषण है। प्रोग्रामर चयन, बबल एवं क्विक जैसे कई भिन्न-भिन्न सॉर्टिंग एल्गोरिदम एकत्र कर सकता है, तत्पश्चात उनकी गति, मेमोरी उपयोग एवं पावर उपयोग को मापकर इन एल्गोरिदम के प्रदर्शन का विश्लेषण कर सकता है, तत्पश्चात इन्हें रडार चार्ट पर ग्राफ़ करके देख सकता है कि प्रत्येक सॉर्ट कैसा प्रदर्शन करता है। डेटा के विभिन्न आकारों के अंतर्गत अन्य प्रदर्शन अनुप्रयोग दूसरे के प्रतिस्पर्धा समान कारों के प्रदर्शन को माप रहा है। उपभोक्ता कारों की शीर्ष गति, मील प्रति गैलन, अश्वशक्ति एवं टॉर्क जैसे चर देख सकता है। तत्पश्चात डेटा की कल्पना करने के लिए रडार चार्ट का उपयोग करने के पश्चात, वे परिणामों के आधार पर यह निर्धारित कर सकते हैं कि कौन सी कार उनके लिए सबसे उत्तम है।
रडार चार्ट का उपयोग खेल में खिलाड़ियों की शक्ति एवं शक्तिहीन को चार्ट करने के लिए किया जा सकता है।<ref>[http://howtowatchsports.com/spider-graphs-charting-basketball-statistics/ Spider Graphs: Charting Basketball Statistics]</ref> खिलाड़ी से संबंधित विभिन्न आँकड़ों की गणना करके जिसे चार्ट के केंद्रीय अक्ष के साथ ट्रैक किया जा सकता है। उदाहरणों में बास्केट खिलाड़ी द्वारा लगाए गए शॉट, रिबाउंड, सहायता आदि, या बेसबॉल खिलाड़ी की बल्लेबाजी या पिचिंग आँकड़े सम्मिलित हैं। यह किसी खिलाड़ी की शक्ति एवं कमजोरियों का केंद्रीकृत दृश्य बनाता है, एवं यदि अन्य खिलाड़ियों या लीग औसत के आंकड़ों के साथ ओवरलैप किया जाता है, तो यह प्रदर्शित हो सकता है कि खिलाड़ी कहां उत्कृष्टता प्राप्त करता है एवं वे कहां सुधार कर सकते हैं।<ref>{{cite web |title=डेटा विज़ुअलाइज़ेशन को समझना|author=Seeing Data |publisher=Seeing Data|url=http://seeingdata.org/taketime/inside-the-chart-radar-chart/ |language=en-US}}</ref> खिलाड़ी की ताकत एवं कमजोरी के बारे में ये अंतर्दृष्टि खिलाड़ी के विकास के लिए महत्वपूर्ण प्रमाणित हो सकती है क्योंकि यह कोच एवं प्रशिक्षकों को खिलाड़ी की कमजोरियों को सुधारने में सहायता करने के लिए उनकी प्रशिक्षण रेजिमेंट को समायोजित करने की अनुमति देती है। रडार चार्ट के परिणाम स्थितिजन्य खेल में भी उपयोगी हो सकते हैं। यदि किसी बल्लेबाज को बाएं हाथ की पिचिंग के विरुद्ध निकृष्ट हिट करते हुए दिखाया गया है, तो उसकी टीम बाएं हाथ के पिचर्स के विरुद्ध अपनी प्लेट की उपस्थिति को सीमित करना जानती है, जबकि विरोधी टीम ऐसी स्थिति को विवश करने का प्रयत्न कर सकती है जहां बल्लेबाज को पिचर के विरुद्ध हिट करने के लिए विवश किया जाता है।[[File:3VehiclePerformanceMetrics.png|alt=The performance metrics of 3 different types of vehicle|thumb |300px |सेडान, स्पोर्ट्स कार एवं पिकअप ट्रक के प्रदर्शन मेट्रिक्स में अंतर दिखाने वाला रडार चार्ट।]]रडार चार्ट का अन्य अनुप्रयोग कंप्यूटर प्रोग्राम सहित विभिन्न वस्तुओं के प्रदर्शन मेट्रिक्स को प्रदर्शित करने के लिए [[गुणवत्ता प्रबंधन]] का नियंत्रण है,<ref>Ron Basu (2004). ''Implementing Quality: A Practical Guide to Tools and Techniques''. p.131.</ref> कंप्यूटर, फ़ोन, वाहन, एवं आदि होते है। कंप्यूटर प्रोग्रामर प्रायः दूसरों की अपेक्षा में अपने प्रोग्राम के प्रदर्शन का परीक्षण करने के लिए एनालिटिक्स का उपयोग करते हैं। इसका उदाहरण जहां रडार चार्ट उपयोगी हो सकते हैं, वह विभिन्न सॉर्टिंग एल्गोरिदम का प्रदर्शन विश्लेषण है। प्रोग्रामर चयन, बबल एवं क्विक जैसे कई भिन्न-भिन्न सॉर्टिंग एल्गोरिदम एकत्र कर सकता है, तत्पश्चात उनकी गति, मेमोरी उपयोग एवं पावर उपयोग को मापकर इन एल्गोरिदम के प्रदर्शन का विश्लेषण कर सकता है, तत्पश्चात इन्हें रडार चार्ट पर ग्राफ़ करके देख सकता है कि प्रत्येक सॉर्ट कैसा प्रदर्शन करता है। डेटा के विभिन्न आकारों के अंतर्गत अन्य प्रदर्शन अनुप्रयोग दूसरे के प्रतिस्पर्धा समान कारों के प्रदर्शन को माप रहा है। उपभोक्ता कारों की शीर्ष गति, मील प्रति गैलन, अश्वशक्ति एवं टॉर्क जैसे चर देख सकता है। तत्पश्चात डेटा की कल्पना करने के लिए रडार चार्ट का उपयोग करने के पश्चात, वे परिणामों के आधार पर यह निर्धारित कर सकते हैं कि कौन सी कार उनके लिए सबसे उत्तम है।
[[Image:Wiki Radar Chart Example.png|thumb|300px|रडार चार्ट जो दो समुदायों की समानता दर्शाता है, जिसमें कनेक्टेड जीनोमिक विंडो सम्मिलित हैं; [[ जीनोम वास्तुकला मानचित्रण | जीनोम वास्तुकला मानचित्रण]] देखें।]]रडार चार्ट का उपयोग जीवन विज्ञान में औषिधियो एवं अन्य औषिधियो की शक्ति एवं कमजोरी को प्रदर्शित करने के लिए किया जा सकता है।<ref>{{cite web |title=रडार चार्ट का प्रभावी उपयोग|author=Model Systems Knowledge Translation Center |publisher=Model Systems Knowledge Translation Center |url=https://msktc.org/lib/docs/KT_Toolkit/Charts_and_Graphs/Charts_and_Graphics_Radar_508c.pdf |language=en-US}}</ref> दो अवसाद रोधी औषिधियो के उदाहरण का उपयोग करके, शोधकर्ता से दस के स्तर पर प्रभावकारिता, दुष्प्रभाव, वित्त आदि जैसे चर को रैंक कर सकता है। तत्पश्चात वे चर के प्रसार को देखने के लिए रडार चार्ट का उपयोग करके परिणामों को ग्राफ़ कर सकते हैं एवं जानकारी ज्ञात कर सकते हैं कि वे कैसे भिन्न हैं, जैसे कि एंटी-डिप्रेसेंट सस्ता एवं तीव्र कार्य करता है, किन्तु समय के साथ आराम नहीं देता है। इसके मध्य, अन्य अवसाद रोधी औषिधि ठोस आराम प्रदान करती है एवं समय के साथ उत्तम बनी रहती है किन्तु अधिक मूल्यवान होती है। जीवन विज्ञान का अन्य अनुप्रयोग रोगी विश्लेषण में है। रडार चार्ट का उपयोग किसी व्यक्ति के स्वास्थ्य को प्रभावित करने वाले जीवन के चरों को रेखांकन करने के लिए किया जा सकता है, एवं तत्पश्चात उनकी सहायता के लिए उनका विश्लेषण किया जा सकता है। अधिक विशिष्ट उदाहरण एथलीटों के विषय में है, जिनकी विभिन्न स्वास्थ्य आदतों जैसे नींद, आहार एवं तनाव का परिक्षण किया जाता है, जिससे यह सुनिश्चित किया जा सके कि वे चरम शारीरिक स्थिति में रहें।<ref>{{cite web |title=डी-सामान्यीकृत स्पाइडर और रडार ग्राफ़|author=John Maguire |publisher=Kitman Labs |url=https://www.kitmanlabs.com/ |language=en-US}}</ref> यदि किसी भी क्षेत्र में गिरावट दिखाई देती है, तो डॉक्टर एवं प्रशिक्षक एथलीट की सहायता के लिए आगे आ सकते हैं एवं उनके स्वास्थ्य में सुधार कर सकते हैं।
[[Image:Wiki Radar Chart Example.png|thumb|300px|रडार चार्ट जो दो समुदायों की समानता दर्शाता है, जिसमें कनेक्टेड जीनोमिक विंडो सम्मिलित हैं; [[ जीनोम वास्तुकला मानचित्रण | जीनोम वास्तुकला मानचित्रण]] देखें।]]रडार चार्ट का उपयोग जीवन विज्ञान में औषिधियो एवं अन्य औषिधियो की शक्ति एवं कमजोरी को प्रदर्शित करने के लिए किया जा सकता है।<ref>{{cite web |title=रडार चार्ट का प्रभावी उपयोग|author=Model Systems Knowledge Translation Center |publisher=Model Systems Knowledge Translation Center |url=https://msktc.org/lib/docs/KT_Toolkit/Charts_and_Graphs/Charts_and_Graphics_Radar_508c.pdf |language=en-US}}</ref> दो अवसाद रोधी औषिधियो के उदाहरण का उपयोग करके, शोधकर्ता से दस के स्तर पर प्रभावकारिता, दुष्प्रभाव, वित्त आदि जैसे चर को रैंक कर सकता है। तत्पश्चात वे चर के प्रसार को देखने के लिए रडार चार्ट का उपयोग करके परिणामों को ग्राफ़ कर सकते हैं एवं जानकारी ज्ञात कर सकते हैं कि वे कैसे भिन्न हैं, जैसे कि एंटी-डिप्रेसेंट सस्ता एवं तीव्र कार्य करता है, किन्तु समय के साथ आराम नहीं देता है। इसके मध्य, अन्य अवसाद रोधी औषिधि ठोस आराम प्रदान करती है एवं समय के साथ उत्तम बनी रहती है किन्तु अधिक मूल्यवान होती है। जीवन विज्ञान का अन्य अनुप्रयोग रोगी विश्लेषण में है। रडार चार्ट का उपयोग किसी व्यक्ति के स्वास्थ्य को प्रभावित करने वाले जीवन के चरों को रेखांकन करने के लिए किया जा सकता है, एवं तत्पश्चात उनकी सहायता के लिए उनका विश्लेषण किया जा सकता है। अधिक विशिष्ट उदाहरण एथलीटों के विषय में है, जिनकी विभिन्न स्वास्थ्य आदतों जैसे नींद, आहार एवं तनाव का परिक्षण किया जाता है, जिससे यह सुनिश्चित किया जा सके कि वे चरम शारीरिक स्थिति में रहें।<ref>{{cite web |title=डी-सामान्यीकृत स्पाइडर और रडार ग्राफ़|author=John Maguire |publisher=Kitman Labs |url=https://www.kitmanlabs.com/ |language=en-US}}</ref> यदि किसी भी क्षेत्र में गिरावट दिखाई देती है, तो डॉक्टर एवं प्रशिक्षक एथलीट की सहायता के लिए आगे आ सकते हैं एवं उनके स्वास्थ्य में सुधार कर सकते हैं।


== सीमाएँ ==
== सीमाएँ ==
रडार चार्ट मुख्य रूप से आउटलेर्स एवं [[समानता]] दिखाने के लिए उपयुक्त होते हैं, या जब चार्ट दूसरे की तुलना में प्रत्येक चर में अधिक होता है, एवं मुख्य रूप से सामान्य स्केल के लिए उपयोग किया जाता है, जहां प्रत्येक चर कुछ विषयो में उत्तम से मिलता है, एवं सभी चर ही स्तर पर होते हैं।
रडार चार्ट मुख्य रूप से आउटलेर्स एवं [[समानता]] दिखाने के लिए उपयुक्त होते हैं, या जब चार्ट दूसरे की अपेक्षा में प्रत्येक चर में अधिक होता है, एवं मुख्य रूप से सामान्य स्केल के लिए उपयोग किया जाता है, जहां प्रत्येक चर कुछ विषयो में उत्तम से मिलता है, एवं सभी चर ही स्तर पर होते हैं।


इसके विपरीत, रडार चार्ट की आलोचना की गई है क्योंकि यह व्यापार-विवृत निर्णय लेने के लिए उपयुक्त नहीं है, जब चार्ट कुछ चर पर दूसरे से अधिक होता है, किन्तु दूसरों पर अर्घ्य होता है।<ref>[http://chandoo.org/wp/2008/09/18/better-radar-charts-excel/ You are NOT spider man, so why do you use radar charts?], by Chandoo, September 18th, 2008</ref>इसके अतिरिक्त, विभिन्न तीलियों की लंबाई की तुलना करना कठिन है, क्योंकि रेडियल दूरियों का आकलन करना कठिन है, चूंकि संकेंद्रित वृत्त ग्रिड लाइनों के रूप में सहायता करते हैं। इसके अतिरिक्त, कोई सरल रेखा ग्राफ़ का उपयोग कर सकता है, विशेष रूप से समय श्रृंखला के लिए उपयोग कर सकता है।<ref name="ratc" />
इसके विपरीत, रडार चार्ट की आलोचना की गई है क्योंकि यह व्यापार-विवृत निर्णय लेने के लिए उपयुक्त नहीं है, जब चार्ट कुछ चर पर दूसरे से अधिक होता है, किन्तु दूसरों पर अर्घ्य होता है।<ref>[http://chandoo.org/wp/2008/09/18/better-radar-charts-excel/ You are NOT spider man, so why do you use radar charts?], by Chandoo, September 18th, 2008</ref>इसके अतिरिक्त, विभिन्न तीलियों की लंबाई की अपेक्षा करना कठिन है, क्योंकि रेडियल दूरियों का आकलन करना कठिन है, चूंकि संकेंद्रित वृत्त ग्रिड लाइनों के रूप में सहायता करते हैं। इसके अतिरिक्त, कोई सरल रेखा ग्राफ़ का उपयोग कर सकता है, विशेष रूप से समय श्रृंखला के लिए उपयोग कर सकता है।<ref name="ratc" />


रडार चार्ट कुछ सीमा तक डेटा को विकृत कर सकते हैं, विशेष रूप से जब क्षेत्र भरे हुए हों, क्योंकि इसमें सम्मिलित क्षेत्र रैखिक माप के वर्ग के समानुपाती हो जाता है। उदाहरण के लिए, 1 से 100 तक के 5 चर वाले चार्ट में, जब सभी माप 90 होते हैं, तो 5 बिंदुओं से घिरे बहुभुज में निहित क्षेत्र 82 के सभी मान वाले चार्ट की तुलना में 10% से अधिक विस्तृत होता है।
रडार चार्ट कुछ सीमा तक डेटा को विकृत कर सकते हैं, विशेष रूप से जब क्षेत्र भरे हुए हों, क्योंकि इसमें सम्मिलित क्षेत्र रैखिक माप के वर्ग के समानुपाती हो जाता है। उदाहरण के लिए, 1 से 100 तक के 5 चर वाले चार्ट में, जब सभी माप 90 होते हैं, तो 5 बिंदुओं से घिरे बहुभुज में निहित क्षेत्र 82 के सभी मान वाले चार्ट की अपेक्षा में 10% से अधिक विस्तृत होता है।


रडार चार्ट पर विभिन्न प्रारूपों के मध्य दृष्टिगत रूप से तुलना करना भी कठिन हो सकता है जब उनके मान निकट होते हैं क्योंकि उनकी रेखाएं या क्षेत्र एक-दूसरे में प्रवाहित होते हैं, जैसा कि चित्र 5 में दिखाया गया है।
रडार चार्ट पर विभिन्न प्रारूपों के मध्य दृष्टिगत रूप से अपेक्षा करना भी कठिन हो सकता है जब उनके मान निकट होते हैं क्योंकि उनकी रेखाएं या क्षेत्र एक-दूसरे में प्रवाहित होते हैं, जैसा कि चित्र 5 में दिखाया गया है।


=== कृत्रिम संरचना ===
=== कृत्रिम संरचना ===
Line 38: Line 35:
'''*''' आपको सामान्य स्तर पर स्थिति के अतिरिक्त स्टैक्ड क्षेत्रों को पढ़ने में कोई आपत्ति नहीं है (क्लीवलैंड के पदानुक्रम देखें)।
'''*''' आपको सामान्य स्तर पर स्थिति के अतिरिक्त स्टैक्ड क्षेत्रों को पढ़ने में कोई आपत्ति नहीं है (क्लीवलैंड के पदानुक्रम देखें)।
* डेटा समूह वास्तव में चक्रीय है, रैखिक नहीं, एवं
* डेटा समूह वास्तव में चक्रीय है, रैखिक नहीं, एवं
* एक- दूसरी से अधिक अल्प तुलना करने के लिए दो श्रृंखलाएँ हैं।
* एक- दूसरी से अधिक अल्प अपेक्षा करने के लिए दो श्रृंखलाएँ हैं।


=== [[डेटा सेट]] का आकार ===
=== [[डेटा सेट]] का आकार ===
Line 45: Line 42:
इसके अतिरिक्त, जब कई आयामों या प्रारूपों के साथ रडार चार्ट का उपयोग किया जाता है, तो प्रारूपों की संख्या बढ़ने पर रडार चार्ट अव्यवस्थित हो सकता है एवं इसकी व्याख्या करना कठिन हो सकता है।
इसके अतिरिक्त, जब कई आयामों या प्रारूपों के साथ रडार चार्ट का उपयोग किया जाता है, तो प्रारूपों की संख्या बढ़ने पर रडार चार्ट अव्यवस्थित हो सकता है एवं इसकी व्याख्या करना कठिन हो सकता है।


उदाहरण के लिए, एमएलबी 2021 एमवीपी शोहेई ओहतानी की तुलना लीग के औसत नामित हिटरों एवं कुछ हॉल ऑफ फेम खिलाड़ियों के आंकड़ों से तुलना करने वाली बल्लेबाजी सांख्यिकी सारणी को लें। ये आँकड़े किसी खिलाड़ी के बल्ले पर हिट, होम रन, स्ट्राइक आउट आदि का प्रतिशत दर्शाते हैं। सारणी में प्रयुक्त प्रत्येक आँकड़ा क्या दर्शाता है, इसके विषय में अधिक जानकारी के लिए, आप एमएलबी के इस संदर्भ का संदर्भ ले सकते हैं।<ref>{{Cite web |title=मानक आँकड़े|url=https://www.mlb.com/glossary/standard-stats |access-date=2022-04-26 |website=www.mlb.com}}</ref> प्रदर्शन मेट्रिक्स की कल्पना करने एवं स्पष्ट रूप से इस निष्कर्ष पर पहुंचने के प्रयत्न में कि हम नामित हिटर्स एवं नियमित बल्लेबाजों के लिए 2021 एमवीपी बल्लेबाजी आंकड़ों की लीग औसत से तुलना करते हुए रडार चार्ट बनाने के लिए नीचे दी गई इस सारणी का उपयोग करेंगे एवं इस निष्कर्ष पर पहुंचेंगे कि शोहेई ने औसत खिलाड़ी का प्रदर्शन किया है। इसके पश्चात हम हॉल ऑफ फेम खिलाड़ियों जैकी रॉबिन्सन, जिम थॉम एवं फ्रैंक थॉमस का उपयोग करके रडार चार्ट में अतिरिक्त प्रतिरूप सम्मिलित करेंगे, जिससे शोहेई की तुलना सभी समय के कुछ महानतम बल्लेबाजों से की जा सके। यह राडार चार्ट न केवल हमें यह अंतर्ज्ञान दे सकता है कि शोहेई शीर्ष ऐतिहासिक खिलाड़ियों की तुलना कैसे करता है, अन्यथा राडार चार्ट में अत्यधिक प्रतिरूप होने की सीमाओं को दिखाने में भी उद्देश्य पूर्ण करेगा।
उदाहरण के लिए, एमएलबी 2021 एमवीपी शोहेई ओहतानी की अपेक्षा लीग के औसत नामित हिटरों एवं कुछ हॉल ऑफ फेम खिलाड़ियों के आंकड़ों से अपेक्षा करने वाली बल्लेबाजी सांख्यिकी सारणी को लें। ये आँकड़े किसी खिलाड़ी के बल्ले पर हिट, होम रन, स्ट्राइक आउट आदि का प्रतिशत दर्शाते हैं। सारणी में प्रयुक्त प्रत्येक आँकड़ा क्या दर्शाता है, इसके विषय में अधिक जानकारी के लिए, आप एमएलबी के इस संदर्भ का संदर्भ ले सकते हैं।<ref>{{Cite web |title=मानक आँकड़े|url=https://www.mlb.com/glossary/standard-stats |access-date=2022-04-26 |website=www.mlb.com}}</ref> प्रदर्शन मेट्रिक्स की कल्पना करने एवं स्पष्ट रूप से इस निष्कर्ष पर पहुंचने के प्रयत्न में कि हम नामित हिटर्स एवं नियमित बल्लेबाजों के लिए 2021 एमवीपी बल्लेबाजी आंकड़ों की लीग औसत से अपेक्षा करते हुए रडार चार्ट बनाने के लिए नीचे दी गई इस सारणी का उपयोग करेंगे एवं इस निष्कर्ष पर पहुंचेंगे कि शोहेई ने औसत खिलाड़ी का प्रदर्शन किया है। इसके पश्चात हम हॉल ऑफ फेम खिलाड़ियों जैकी रॉबिन्सन, जिम थॉम एवं फ्रैंक थॉमस का उपयोग करके रडार चार्ट में अतिरिक्त प्रतिरूप सम्मिलित करेंगे, जिससे शोहेई की अपेक्षा सभी समय के कुछ महानतम बल्लेबाजों से की जा सके। यह राडार चार्ट न केवल हमें यह अंतर्ज्ञान दे सकता है कि शोहेई शीर्ष ऐतिहासिक खिलाड़ियों की अपेक्षा कैसे करता है, अन्यथा राडार चार्ट में अत्यधिक प्रतिरूप होने की सीमाओं को दिखाने में भी उद्देश्य पूर्ण करेगा।


{| class="wikitable"
{| class="wikitable"
Line 69: Line 66:
| 0.301 || 0.419 || 0.555 || 0.974 || 0.063 || 0.17 || 0.203
| 0.301 || 0.419 || 0.555 || 0.974 || 0.063 || 0.17 || 0.203
|}
|}
हम चित्र 10 में देख सकते हैं कि जब तीलियों एवं प्रारूपों की संख्या अपेक्षाकृत अर्घ्य होती है तो रडार चार्ट की सरलता से व्याख्या कैसे की जा सकती है। जब हम चित्र 11 में अधिक प्रारूपों की तुलना करते हैं, यहां तक ​​​​कि रडार चार्ट पर कोई क्षेत्र भरे बिना भी, यह स्पष्ट हो जाता है कि व्याख्या करना या व्यापार-विवृत निर्णय लेना कितना कठिन हो सकता है।
हम चित्र 10 में देख सकते हैं कि जब तीलियों एवं प्रारूपों की संख्या अपेक्षाकृत अर्घ्य होती है तो रडार चार्ट की सरलता से व्याख्या कैसे की जा सकती है। जब हम चित्र 11 में अधिक प्रारूपों की अपेक्षा करते हैं, यहां तक ​​​​कि रडार चार्ट पर कोई क्षेत्र भरे बिना भी, यह स्पष्ट हो जाता है कि व्याख्या करना या व्यापार-विवृत निर्णय लेना कितना कठिन हो सकता है।


== उदाहरण ==
== उदाहरण ==
Line 85: Line 82:
#  लंबाई
#  लंबाई


हम इन भूखंडों को व्यक्तिगत रूप से देख सकते हैं या समान सुविधाओं वाली कारों के समूहों की पहचान करने के लिए उनका उपयोग कर सकते हैं। उदाहरण के लिए, हम [[कैडिलैक]] सेविले (छवि पर आखिरी वाली) के स्टार प्लॉट को देख सकते हैं एवं देख सकते हैं कि यह सबसे मूल्यवान कारों में से है, औसत से नीचे (किन्तु सबसे निकृष्ट में से नहीं) गैस माइलेज देती है, औसत है त्रुटिनिवारण रिकॉर्ड, एवं इसमें औसत से ऊपर का स्थान एवं आकार है। तत्पश्चात हम कैडिलैक मॉडल (अंतिम तीन प्लॉट) की तुलना एएमसी मॉडल (प्रथम तीन प्लॉट) से कर सकते हैं। यह तुलना भिन्न-भिन्न सारणी दिखाती है। एएमसी मॉडल अल्पमूल्य होते हैं, उनका गैस माइलेज औसत से अर्घ्य होता है, एवं ऊंचाई, वजन एवं स्थान दोनों में अल्प होते हैं। कैडिलैक मॉडल मूल्यवान होते हैं, गैस माइलेज अर्घ्य है, एवं आकार एवं स्थान दोनों में बड़े हैं।<ref name="NIST03"/>
हम इन भूखंडों को व्यक्तिगत रूप से देख सकते हैं या समान सुविधाओं वाली कारों के समूहों की पहचान करने के लिए उनका उपयोग कर सकते हैं। उदाहरण के लिए, हम [[कैडिलैक]] सेविले (छवि पर आखिरी वाली) के स्टार प्लॉट को देख सकते हैं एवं देख सकते हैं कि यह सबसे मूल्यवान कारों में से है, औसत से नीचे (किन्तु सबसे निकृष्ट में से नहीं) गैस माइलेज देती है, औसत है त्रुटिनिवारण रिकॉर्ड, एवं इसमें औसत से ऊपर का स्थान एवं आकार है। तत्पश्चात हम कैडिलैक मॉडल (अंतिम तीन प्लॉट) की अपेक्षा एएमसी मॉडल (प्रथम तीन प्लॉट) से कर सकते हैं। यह अपेक्षा भिन्न-भिन्न सारणी दिखाती है। एएमसी मॉडल अल्पमूल्य होते हैं, उनका गैस माइलेज औसत से अर्घ्य होता है, एवं ऊंचाई, वजन एवं स्थान दोनों में अल्प होते हैं। कैडिलैक मॉडल मूल्यवान होते हैं, गैस माइलेज अर्घ्य है, एवं आकार एवं स्थान दोनों में बड़े हैं।<ref name="NIST03"/>


== विकल्प ==
== विकल्प ==
कोई समय श्रृंखला एवं अन्य डेटा के लिए लाइन ग्राफ़ का उपयोग कर सकता है,<ref name="ratc" />समानांतर निर्देशांक के रूप में कई चरों में 2-आयामी सारणीबद्ध डेटा की ग्राफिकल गुणात्मक तुलना के लिए, सामान्य विकल्प [[हार्वे बॉल्स]] हैं, जिनका [[उपभोक्ता रिपोर्ट]] द्वारा बड़े स्तर पर उपयोग किया जाता है।<ref>{{cite web |url=http://supportanalytics.com/blog/2007/12/qualitative-comparison/ |title=गुणात्मक तुलना|author=<!--Staff writer(s); no by-line.--> |date=11 December 2007 |website=Support Analytics Blog |publisher=<!--Substantially similar to website.--> |archive-url=https://web.archive.org/web/20120408192509/http://supportanalytics.com/blog/2007/12/qualitative-comparison/ |archive-date=2012-04-08}}</ref> हार्वे गेंदों (एवं रडार चार्ट) में तुलना को क्रम में जोड़ने के लिए एल्गोरिदमिक रूप से चर को क्रमबद्ध करके महत्वपूर्ण सहायता मिल सकती है।<ref name="reorder" />
कोई समय श्रृंखला एवं अन्य डेटा के लिए लाइन ग्राफ़ का उपयोग कर सकता है,<ref name="ratc" />समानांतर निर्देशांक के रूप में कई चरों में 2-आयामी सारणीबद्ध डेटा की ग्राफिकल गुणात्मक अपेक्षा के लिए, सामान्य विकल्प [[हार्वे बॉल्स]] हैं, जिनका [[उपभोक्ता रिपोर्ट]] द्वारा बड़े स्तर पर उपयोग किया जाता है।<ref>{{cite web |url=http://supportanalytics.com/blog/2007/12/qualitative-comparison/ |title=गुणात्मक तुलना|author=<!--Staff writer(s); no by-line.--> |date=11 December 2007 |website=Support Analytics Blog |publisher=<!--Substantially similar to website.--> |archive-url=https://web.archive.org/web/20120408192509/http://supportanalytics.com/blog/2007/12/qualitative-comparison/ |archive-date=2012-04-08}}</ref> हार्वे गेंदों (एवं रडार चार्ट) में अपेक्षा को क्रम में जोड़ने के लिए एल्गोरिदमिक रूप से चर को क्रमबद्ध करके महत्वपूर्ण सहायता मिल सकती है।<ref name="reorder" />


बहुभिन्नरूपी डेटा के अंदर संरचनाओं को देखने का उत्कृष्ट प्रविधि प्रमुख घटक विश्लेषण (पीसीए) द्वारा प्रस्तुत किया जाता है।
बहुभिन्नरूपी डेटा के अंदर संरचनाओं को देखने का उत्कृष्ट प्रविधि प्रमुख घटक विश्लेषण (पीसीए) द्वारा प्रस्तुत किया जाता है।


अन्य विकल्प अल्प, इनलाइन बार चार्ट का उपयोग करना है, जिसकी तुलना [[स्पार्कलाइन]] से की जा सकती है।<ref name="reorder">{{cite web|url=http://i-ocean.blogspot.com/2008/09/reorderable-tables-ii-bertin-versus.html |title=Information Ocean: Reorderable tables II: Bertin versus the Spiders |publisher=I-ocean.blogspot.com |date=2008-09-24 |access-date=2013-09-11}}</ref>चूंकि रडार एवं ध्रुवीय चार्ट को प्रायः ही चार्ट प्रकार के रूप में वर्णित किया जाता है,<ref name="radarandpolar" />कुछ स्रोत उनके मध्य अंतर करते हैं एवं यहां तक ​​कि रडार चार्ट को ध्रुवीय चार्ट का रूपांतर मानते हैं जो ध्रुवीय समन्वय के संदर्भ में डेटा प्रदर्शित नहीं करता है।<ref>{{cite web|url=https://msdn.microsoft.com/en-us/library/dd239337.aspx |title=ध्रुवीय चार्ट (रिपोर्ट बिल्डर और एसएसआरएस)|publisher=Microsoft Developer Network |access-date=December 17, 2015}}</ref>
अन्य विकल्प अल्प, इनलाइन बार चार्ट का उपयोग करना है, जिसकी अपेक्षा [[स्पार्कलाइन]] से की जा सकती है।<ref name="reorder">{{cite web|url=http://i-ocean.blogspot.com/2008/09/reorderable-tables-ii-bertin-versus.html |title=Information Ocean: Reorderable tables II: Bertin versus the Spiders |publisher=I-ocean.blogspot.com |date=2008-09-24 |access-date=2013-09-11}}</ref>चूंकि रडार एवं ध्रुवीय चार्ट को प्रायः ही चार्ट प्रकार के रूप में वर्णित किया जाता है,<ref name="radarandpolar" />कुछ स्रोत उनके मध्य अंतर करते हैं एवं यहां तक ​​कि रडार चार्ट को ध्रुवीय चार्ट का रूपांतर मानते हैं जो ध्रुवीय समन्वय के संदर्भ में डेटा प्रदर्शित नहीं करता है।<ref>{{cite web|url=https://msdn.microsoft.com/en-us/library/dd239337.aspx |title=ध्रुवीय चार्ट (रिपोर्ट बिल्डर और एसएसआरएस)|publisher=Microsoft Developer Network |access-date=December 17, 2015}}</ref>


== यह भी देखें ==
== यह भी देखें ==
Line 99: Line 96:
* [[ध्रुवीय क्षेत्र आरेख]]
* [[ध्रुवीय क्षेत्र आरेख]]
* समानांतर निर्देशांक
* समानांतर निर्देशांक
*[[रेडियल वृक्ष]]
*[[रेडियल ट्री]]


== संदर्भ ==
== संदर्भ ==
Line 110: Line 107:
* [http://www.itl.nist.gov/div898/handbook/eda/section3/starplot.htm Star Plot] – ''[[NIST]]/SEMATECH e-Handbook of Statistical Methods''
* [http://www.itl.nist.gov/div898/handbook/eda/section3/starplot.htm Star Plot] – ''[[NIST]]/SEMATECH e-Handbook of Statistical Methods''


{{Statistics|descriptive}}
[[Category:Articles with hatnote templates targeting a nonexistent page]]
[[Category: चार्ट]] [[Category: सांख्यिकीय चार्ट और आरेख]]  
[[Category:CS1 Deutsch-language sources (de)]]
 
[[Category:CS1 English-language sources (en)]]
 
[[Category:Collapse templates]]
 
[[Category:Commons category link is locally defined]]
[[Category: Machine Translated Page]]
[[Category:Created On 10/07/2023]]
[[Category:Created On 10/07/2023]]
[[Category:Vigyan Ready]]
[[Category:Lua-based templates]]
[[Category:Machine Translated Page]]
[[Category:Missing redirects]]
[[Category:Navigational boxes| ]]
[[Category:Navigational boxes without horizontal lists]]
[[Category:Pages with broken file links]]
[[Category:Pages with empty portal template]]
[[Category:Pages with script errors]]
[[Category:Portal-inline template with redlinked portals]]
[[Category:Short description with empty Wikidata description]]
[[Category:Sidebars with styles needing conversion]]
[[Category:Template documentation pages|Documentation/doc]]
[[Category:Templates Vigyan Ready]]
[[Category:Templates generating microformats]]
[[Category:Templates that add a tracking category]]
[[Category:Templates that are not mobile friendly]]
[[Category:Templates that generate short descriptions]]
[[Category:Templates using TemplateData]]
[[Category:Webarchive template wayback links]]
[[Category:Wikipedia articles incorporating text from the National Institute of Standards and Technology]]
[[Category:Wikipedia metatemplates]]
[[Category:चार्ट]]
[[Category:सांख्यिकीय चार्ट और आरेख]]

Latest revision as of 12:22, 1 November 2023

नासा के स्टार प्लॉट का उदाहरण, कुछ सबसे वांछनीय डिज़ाइन परिणामों को केंद्र में दर्शाया गया है।
यह स्पाइडर चार्ट किसी दिए गए संगठन के लिए आवंटित बजट के प्रति वास्तविक व्यय का प्रतिनिधित्व करता है।

रडार चार्ट ही बिंदु से प्रारम्भ होने वाले अक्षों पर दर्शाए गए तीन या अधिक मात्रात्मक चर के दो-आयामी चार्ट के रूप में बहुभिन्नरूपी सांख्यिकी डेटा प्रदर्शित करने के ग्राफिकल प्रविधियो की सूची है। अक्षों की सापेक्ष स्थिति एवं कोण सामान्यतः सूचनात्मक नहीं है, किन्तु विभिन्न आंकड़े, जैसे कि एल्गोरिदम जो डेटा को अधिकतम कुल क्षेत्र के रूप में प्लॉट करते हैं, को चर (अक्षों) को सापेक्ष स्थितियों में क्रमबद्ध करने के लिए प्रारम्भ किया जा सकता है जो भिन्न-भिन्न सहसंबंध, व्यापार-विवृत प्रकट करते हैं, एवं कई अन्य तुलनात्मक प्रविधि प्रकट करते हैं।[1]

रडार चार्ट को वेब चार्ट, स्पाइडर चार्ट, स्पाइडर ग्राफ, स्पाइडर वेब चार्ट, स्टार चार्ट, के रूप में भी जाना जाता है।[2] स्टार प्लॉट, कोबवेब चार्ट, अनियमित बहुभुज, ध्रुवीय चार्ट, या किविएट आरेख,[3][4] यह समानांतर निर्देशांक प्लॉट के समतुल्य है, जिसमें अक्ष रेडियल रूप से व्यवस्थित हैं।

अवलोकन

रडार चार्ट चार्ट एवं/या प्लॉट (ग्राफिक्स) है जिसमें सम-कोणीय तीलियों का क्रम होता है, जिसे रेडी कहा जाता है, जिसमें प्रत्येक तीली चर का प्रतिनिधित्व करती है। किसी स्पोक की डेटा लंबाई सभी डेटा बिंदुओं पर चर के अधिकतम परिमाण के सापेक्ष डेटा बिंदु के लिए चर के परिमाण के समानुपाती होती है। प्रत्येक स्पोक के लिए डेटा मानों को जोड़ने वाली रेखा खींची जाती है। इससे कथानक को तारे जैसा स्वरूप मिलता है एवं इस कथानक के लिए लोकप्रिय नामों में से की उत्पत्ति होती है। स्टार प्लॉट का उपयोग निम्नलिखित प्रश्नों के उत्तर देने के लिए किया जा सकता है:[5]* कौन से अवलोकन सबसे अधिक समान हैं, अर्थात, क्या अवलोकनों के समूह हैं? (रडार चार्ट का उपयोग एकल डेटा बिंदु के सापेक्ष मूल्यों की परिक्षण करने के लिए किया जाता है (उदाहरण के लिए, बिंदु 3 चर 2 एवं 4 के लिए बड़ा है, चर 1, 3, 5, एवं 6 के लिए अल्प है) एवं समान बिंदुओं या असमान बिंदुओं की जानकारी ज्ञात करने के लिए।)[5]*क्या आउटलेयर हैं?

रडार चार्ट मनमाने रूप से चर की संख्या के साथ बहुभिन्नरूपी सांख्यिकी अवलोकन प्रदर्शित करने की उपयोगी विधि है।[6] प्रत्येक तारा एकल अवलोकन का प्रतिनिधित्व करता है। सामान्यतः रडार चार्ट मल्टी-प्लॉट प्रारूप में प्रस्तुत किए जाते हैं, जिसमें प्रत्येक पृष्ठ पर कई सितारे होते हैं एवं प्रत्येक सितारा अवलोकन का प्रतिनिधित्व करता है।[5] स्टार प्लॉट का उपयोग प्रथम बार 1877 में जॉर्ज वॉन मेयर द्वारा किया गया था।[7][8] रडार चार्ट ग्लिफ़ प्लॉट से इसमें भिन्न होते हैं कि प्लॉट किए गए स्टार आकृति के निर्माण के लिए सभी चर का उपयोग किया जाता है। अग्रभूमि चर एवं पृष्ठभूमि चर में कोई पृथक्करण नहीं है। इसके अतिरिक्त, तारे के आकार की आकृतियाँ सामान्यतः पृष्ठ पर आयताकार सारणी में व्यवस्थित होती हैं। यदि अवलोकनों को कुछ गैर-इच्छानुसार क्रम में व्यवस्थित किया जाता है (यदि चर को कुछ सार्थक क्रम में तारे की किरणों को समर्पित किया गया है) तो डेटा में पैटर्न देखना कुछ सीमा तक सरल है।[9]

अनुप्रयोग

Shohei Ohtaniके बल्लेबाजी आँकड़े बनाम एमएलबी औसत बल्लेबाजी आँकड़े

रडार चार्ट का उपयोग खेल में खिलाड़ियों की शक्ति एवं शक्तिहीन को चार्ट करने के लिए किया जा सकता है।[10] खिलाड़ी से संबंधित विभिन्न आँकड़ों की गणना करके जिसे चार्ट के केंद्रीय अक्ष के साथ ट्रैक किया जा सकता है। उदाहरणों में बास्केट खिलाड़ी द्वारा लगाए गए शॉट, रिबाउंड, सहायता आदि, या बेसबॉल खिलाड़ी की बल्लेबाजी या पिचिंग आँकड़े सम्मिलित हैं। यह किसी खिलाड़ी की शक्ति एवं कमजोरियों का केंद्रीकृत दृश्य बनाता है, एवं यदि अन्य खिलाड़ियों या लीग औसत के आंकड़ों के साथ ओवरलैप किया जाता है, तो यह प्रदर्शित हो सकता है कि खिलाड़ी कहां उत्कृष्टता प्राप्त करता है एवं वे कहां सुधार कर सकते हैं।[11] खिलाड़ी की ताकत एवं कमजोरी के बारे में ये अंतर्दृष्टि खिलाड़ी के विकास के लिए महत्वपूर्ण प्रमाणित हो सकती है क्योंकि यह कोच एवं प्रशिक्षकों को खिलाड़ी की कमजोरियों को सुधारने में सहायता करने के लिए उनकी प्रशिक्षण रेजिमेंट को समायोजित करने की अनुमति देती है। रडार चार्ट के परिणाम स्थितिजन्य खेल में भी उपयोगी हो सकते हैं। यदि किसी बल्लेबाज को बाएं हाथ की पिचिंग के विरुद्ध निकृष्ट हिट करते हुए दिखाया गया है, तो उसकी टीम बाएं हाथ के पिचर्स के विरुद्ध अपनी प्लेट की उपस्थिति को सीमित करना जानती है, जबकि विरोधी टीम ऐसी स्थिति को विवश करने का प्रयत्न कर सकती है जहां बल्लेबाज को पिचर के विरुद्ध हिट करने के लिए विवश किया जाता है।

The performance metrics of 3 different types of vehicle
सेडान, स्पोर्ट्स कार एवं पिकअप ट्रक के प्रदर्शन मेट्रिक्स में अंतर दिखाने वाला रडार चार्ट।

रडार चार्ट का अन्य अनुप्रयोग कंप्यूटर प्रोग्राम सहित विभिन्न वस्तुओं के प्रदर्शन मेट्रिक्स को प्रदर्शित करने के लिए गुणवत्ता प्रबंधन का नियंत्रण है,[12] कंप्यूटर, फ़ोन, वाहन, एवं आदि होते है। कंप्यूटर प्रोग्रामर प्रायः दूसरों की अपेक्षा में अपने प्रोग्राम के प्रदर्शन का परीक्षण करने के लिए एनालिटिक्स का उपयोग करते हैं। इसका उदाहरण जहां रडार चार्ट उपयोगी हो सकते हैं, वह विभिन्न सॉर्टिंग एल्गोरिदम का प्रदर्शन विश्लेषण है। प्रोग्रामर चयन, बबल एवं क्विक जैसे कई भिन्न-भिन्न सॉर्टिंग एल्गोरिदम एकत्र कर सकता है, तत्पश्चात उनकी गति, मेमोरी उपयोग एवं पावर उपयोग को मापकर इन एल्गोरिदम के प्रदर्शन का विश्लेषण कर सकता है, तत्पश्चात इन्हें रडार चार्ट पर ग्राफ़ करके देख सकता है कि प्रत्येक सॉर्ट कैसा प्रदर्शन करता है। डेटा के विभिन्न आकारों के अंतर्गत अन्य प्रदर्शन अनुप्रयोग दूसरे के प्रतिस्पर्धा समान कारों के प्रदर्शन को माप रहा है। उपभोक्ता कारों की शीर्ष गति, मील प्रति गैलन, अश्वशक्ति एवं टॉर्क जैसे चर देख सकता है। तत्पश्चात डेटा की कल्पना करने के लिए रडार चार्ट का उपयोग करने के पश्चात, वे परिणामों के आधार पर यह निर्धारित कर सकते हैं कि कौन सी कार उनके लिए सबसे उत्तम है।

रडार चार्ट जो दो समुदायों की समानता दर्शाता है, जिसमें कनेक्टेड जीनोमिक विंडो सम्मिलित हैं; जीनोम वास्तुकला मानचित्रण देखें।

रडार चार्ट का उपयोग जीवन विज्ञान में औषिधियो एवं अन्य औषिधियो की शक्ति एवं कमजोरी को प्रदर्शित करने के लिए किया जा सकता है।[13] दो अवसाद रोधी औषिधियो के उदाहरण का उपयोग करके, शोधकर्ता से दस के स्तर पर प्रभावकारिता, दुष्प्रभाव, वित्त आदि जैसे चर को रैंक कर सकता है। तत्पश्चात वे चर के प्रसार को देखने के लिए रडार चार्ट का उपयोग करके परिणामों को ग्राफ़ कर सकते हैं एवं जानकारी ज्ञात कर सकते हैं कि वे कैसे भिन्न हैं, जैसे कि एंटी-डिप्रेसेंट सस्ता एवं तीव्र कार्य करता है, किन्तु समय के साथ आराम नहीं देता है। इसके मध्य, अन्य अवसाद रोधी औषिधि ठोस आराम प्रदान करती है एवं समय के साथ उत्तम बनी रहती है किन्तु अधिक मूल्यवान होती है। जीवन विज्ञान का अन्य अनुप्रयोग रोगी विश्लेषण में है। रडार चार्ट का उपयोग किसी व्यक्ति के स्वास्थ्य को प्रभावित करने वाले जीवन के चरों को रेखांकन करने के लिए किया जा सकता है, एवं तत्पश्चात उनकी सहायता के लिए उनका विश्लेषण किया जा सकता है। अधिक विशिष्ट उदाहरण एथलीटों के विषय में है, जिनकी विभिन्न स्वास्थ्य आदतों जैसे नींद, आहार एवं तनाव का परिक्षण किया जाता है, जिससे यह सुनिश्चित किया जा सके कि वे चरम शारीरिक स्थिति में रहें।[14] यदि किसी भी क्षेत्र में गिरावट दिखाई देती है, तो डॉक्टर एवं प्रशिक्षक एथलीट की सहायता के लिए आगे आ सकते हैं एवं उनके स्वास्थ्य में सुधार कर सकते हैं।

सीमाएँ

रडार चार्ट मुख्य रूप से आउटलेर्स एवं समानता दिखाने के लिए उपयुक्त होते हैं, या जब चार्ट दूसरे की अपेक्षा में प्रत्येक चर में अधिक होता है, एवं मुख्य रूप से सामान्य स्केल के लिए उपयोग किया जाता है, जहां प्रत्येक चर कुछ विषयो में उत्तम से मिलता है, एवं सभी चर ही स्तर पर होते हैं।

इसके विपरीत, रडार चार्ट की आलोचना की गई है क्योंकि यह व्यापार-विवृत निर्णय लेने के लिए उपयुक्त नहीं है, जब चार्ट कुछ चर पर दूसरे से अधिक होता है, किन्तु दूसरों पर अर्घ्य होता है।[15]इसके अतिरिक्त, विभिन्न तीलियों की लंबाई की अपेक्षा करना कठिन है, क्योंकि रेडियल दूरियों का आकलन करना कठिन है, चूंकि संकेंद्रित वृत्त ग्रिड लाइनों के रूप में सहायता करते हैं। इसके अतिरिक्त, कोई सरल रेखा ग्राफ़ का उपयोग कर सकता है, विशेष रूप से समय श्रृंखला के लिए उपयोग कर सकता है।[16]

रडार चार्ट कुछ सीमा तक डेटा को विकृत कर सकते हैं, विशेष रूप से जब क्षेत्र भरे हुए हों, क्योंकि इसमें सम्मिलित क्षेत्र रैखिक माप के वर्ग के समानुपाती हो जाता है। उदाहरण के लिए, 1 से 100 तक के 5 चर वाले चार्ट में, जब सभी माप 90 होते हैं, तो 5 बिंदुओं से घिरे बहुभुज में निहित क्षेत्र 82 के सभी मान वाले चार्ट की अपेक्षा में 10% से अधिक विस्तृत होता है।

रडार चार्ट पर विभिन्न प्रारूपों के मध्य दृष्टिगत रूप से अपेक्षा करना भी कठिन हो सकता है जब उनके मान निकट होते हैं क्योंकि उनकी रेखाएं या क्षेत्र एक-दूसरे में प्रवाहित होते हैं, जैसा कि चित्र 5 में दिखाया गया है।

कृत्रिम संरचना

रडार चार्ट डेटा पर कई संरचनाएं लगाते हैं, जो प्रायः कृत्रिम होती हैं:

  • निकटतम की संबद्धता - रडार चार्ट का उपयोग प्रायः तब किया जाता है जब निकटतम चर असंबंधित होते हैं, जिससे कृत्रिम सम्बन्ध बनते हैं।
  • चक्रीय संरचना - प्रथम एवं अंतिम चर दूसरे के निकट में रखे गए हैं।
  • लंबाई - चर प्रायः सबसे स्वाभाविक रूप से क्रमिक होते हैं: उत्तम, चूंकि अंतर की डिग्री कृत्रिम हो सकती है।
  • क्षेत्रफल - क्षेत्रफल को मानों के वर्ग के रूप में मापा जाता है, जो बड़ी संख्याओं के प्रभाव को बढ़ाकर बताता है। उदाहरण के लिए, 2, 2, 1, 1 के क्षेत्रफल का 4 गुना लेता है। क्षेत्रफल ग्राफ़ के साथ यह सामान्य समस्या है, एवं क्षेत्रफल का निर्धारण करना कठिन है, क्लीवलैंड का पदानुक्रम देखें।[17]

उदाहरण के लिए, वैकल्पिक डेटा 9, 1, 9, 1, 9, 1 स्पाइकिंग रडार चार्ट उत्पन्न करता है (जो अंदर एवं बाहर जाता है), जबकि 9, 9, 9, 1, 1, 1 के रूप में डेटा को पुन: व्यवस्थित करने के अतिरिक्त दो भिन्न-भिन्न परिणाम मिलते हैं (सेक्टर)।

कुछ विषयो में प्राकृतिक संरचना होती है, एवं रडार चार्ट उपयुक्त हो सकते हैं। उदाहरण के लिए, डेटा के आरेखों के लिए जो 24-घंटे के चक्र में भिन्न होते हैं, प्रति घंटा डेटा स्वाभाविक रूप से स्वयं निकटतम से संबंधित होता है, एवं इसमें चक्रीय संरचना होती है, इसलिए इसे स्वाभाविक रूप से रडार चार्ट के रूप में प्रदर्शित किया जा सकता है।[16][18][19] रडार चार्ट (या अन्यथा निकट से संबंधित ध्रुवीय क्षेत्र ग्राफ) के उपयोग पर दिशानिर्देशों का समूह है:[19]

* आपको सामान्य स्तर पर स्थिति के अतिरिक्त स्टैक्ड क्षेत्रों को पढ़ने में कोई आपत्ति नहीं है (क्लीवलैंड के पदानुक्रम देखें)।

  • डेटा समूह वास्तव में चक्रीय है, रैखिक नहीं, एवं
  • एक- दूसरी से अधिक अल्प अपेक्षा करने के लिए दो श्रृंखलाएँ हैं।

डेटा सेट का आकार

रडार चार्ट अल्प से मध्यम आकार के बहुभिन्नरूपी डेटा समूह के लिए सहायक होते हैं। उनकी प्राथमिक कमजोरी यह है कि उनकी प्रभावशीलता कुछ सौ अंकों से भी कम डेटा सेट तक सीमित है। उसके पश्चात, वे प्रबल हो जाते हैं।[5]

इसके अतिरिक्त, जब कई आयामों या प्रारूपों के साथ रडार चार्ट का उपयोग किया जाता है, तो प्रारूपों की संख्या बढ़ने पर रडार चार्ट अव्यवस्थित हो सकता है एवं इसकी व्याख्या करना कठिन हो सकता है।

उदाहरण के लिए, एमएलबी 2021 एमवीपी शोहेई ओहतानी की अपेक्षा लीग के औसत नामित हिटरों एवं कुछ हॉल ऑफ फेम खिलाड़ियों के आंकड़ों से अपेक्षा करने वाली बल्लेबाजी सांख्यिकी सारणी को लें। ये आँकड़े किसी खिलाड़ी के बल्ले पर हिट, होम रन, स्ट्राइक आउट आदि का प्रतिशत दर्शाते हैं। सारणी में प्रयुक्त प्रत्येक आँकड़ा क्या दर्शाता है, इसके विषय में अधिक जानकारी के लिए, आप एमएलबी के इस संदर्भ का संदर्भ ले सकते हैं।[20] प्रदर्शन मेट्रिक्स की कल्पना करने एवं स्पष्ट रूप से इस निष्कर्ष पर पहुंचने के प्रयत्न में कि हम नामित हिटर्स एवं नियमित बल्लेबाजों के लिए 2021 एमवीपी बल्लेबाजी आंकड़ों की लीग औसत से अपेक्षा करते हुए रडार चार्ट बनाने के लिए नीचे दी गई इस सारणी का उपयोग करेंगे एवं इस निष्कर्ष पर पहुंचेंगे कि शोहेई ने औसत खिलाड़ी का प्रदर्शन किया है। इसके पश्चात हम हॉल ऑफ फेम खिलाड़ियों जैकी रॉबिन्सन, जिम थॉम एवं फ्रैंक थॉमस का उपयोग करके रडार चार्ट में अतिरिक्त प्रतिरूप सम्मिलित करेंगे, जिससे शोहेई की अपेक्षा सभी समय के कुछ महानतम बल्लेबाजों से की जा सके। यह राडार चार्ट न केवल हमें यह अंतर्ज्ञान दे सकता है कि शोहेई शीर्ष ऐतिहासिक खिलाड़ियों की अपेक्षा कैसे करता है, अन्यथा राडार चार्ट में अत्यधिक प्रतिरूप होने की सीमाओं को दिखाने में भी उद्देश्य पूर्ण करेगा।

लक्ष्य BA OBP SLG OPS HR% SO% BB%
एमएलबी 0.244 0.317 0.411 0.728 0.037 0.232 0.087
डीएच 0.239 0.316 0.434 0.75 0.047 0.256 0.093
शोहेई ओहटानी 0.257 0.372 0.592 0.965 0.086 0.296 0.15
जैकी रॉबिन्सन 0.313 0.41 0.477 0.887 0.0282 0.0582 0.151
जिम थोम 0.276 0.402 0.554 0.956 0.072 0.302 0.207
फ्रैंक थॉमस 0.301 0.419 0.555 0.974 0.063 0.17 0.203

हम चित्र 10 में देख सकते हैं कि जब तीलियों एवं प्रारूपों की संख्या अपेक्षाकृत अर्घ्य होती है तो रडार चार्ट की सरलता से व्याख्या कैसे की जा सकती है। जब हम चित्र 11 में अधिक प्रारूपों की अपेक्षा करते हैं, यहां तक ​​​​कि रडार चार्ट पर कोई क्षेत्र भरे बिना भी, यह स्पष्ट हो जाता है कि व्याख्या करना या व्यापार-विवृत निर्णय लेना कितना कठिन हो सकता है।

उदाहरण

354 x 4 छवि
File:Star plot Detail.gif
कैडिलैक सेविले के स्टार प्लॉट का विवरण

दाईं ओर का चार्ट[5] इसमें 15 कारों के स्टार प्लॉट सम्मिलित हैं। प्रतिरूप स्टार प्लॉट के लिए परिवर्तनीय सूची है:

  1. मूल्य
  2. माइलेज (एमपीजी)
  3. 1978 त्रुटिनिवारण रिकॉर्ड (1 = सबसे निकृष्ट, 5 = सर्वोत्तम)
  4. 1977 त्रुटिनिवारण रिकॉर्ड (1 = सबसे निकृष्ट, 5 = सर्वोत्तम)
  5. हेडरूम
  6. पूर्व की सीट का कमरा
  7. ट्रंक स्पेस
  8. वज़न
  9. लंबाई

हम इन भूखंडों को व्यक्तिगत रूप से देख सकते हैं या समान सुविधाओं वाली कारों के समूहों की पहचान करने के लिए उनका उपयोग कर सकते हैं। उदाहरण के लिए, हम कैडिलैक सेविले (छवि पर आखिरी वाली) के स्टार प्लॉट को देख सकते हैं एवं देख सकते हैं कि यह सबसे मूल्यवान कारों में से है, औसत से नीचे (किन्तु सबसे निकृष्ट में से नहीं) गैस माइलेज देती है, औसत है त्रुटिनिवारण रिकॉर्ड, एवं इसमें औसत से ऊपर का स्थान एवं आकार है। तत्पश्चात हम कैडिलैक मॉडल (अंतिम तीन प्लॉट) की अपेक्षा एएमसी मॉडल (प्रथम तीन प्लॉट) से कर सकते हैं। यह अपेक्षा भिन्न-भिन्न सारणी दिखाती है। एएमसी मॉडल अल्पमूल्य होते हैं, उनका गैस माइलेज औसत से अर्घ्य होता है, एवं ऊंचाई, वजन एवं स्थान दोनों में अल्प होते हैं। कैडिलैक मॉडल मूल्यवान होते हैं, गैस माइलेज अर्घ्य है, एवं आकार एवं स्थान दोनों में बड़े हैं।[5]

विकल्प

कोई समय श्रृंखला एवं अन्य डेटा के लिए लाइन ग्राफ़ का उपयोग कर सकता है,[16]समानांतर निर्देशांक के रूप में कई चरों में 2-आयामी सारणीबद्ध डेटा की ग्राफिकल गुणात्मक अपेक्षा के लिए, सामान्य विकल्प हार्वे बॉल्स हैं, जिनका उपभोक्ता रिपोर्ट द्वारा बड़े स्तर पर उपयोग किया जाता है।[21] हार्वे गेंदों (एवं रडार चार्ट) में अपेक्षा को क्रम में जोड़ने के लिए एल्गोरिदमिक रूप से चर को क्रमबद्ध करके महत्वपूर्ण सहायता मिल सकती है।[22]

बहुभिन्नरूपी डेटा के अंदर संरचनाओं को देखने का उत्कृष्ट प्रविधि प्रमुख घटक विश्लेषण (पीसीए) द्वारा प्रस्तुत किया जाता है।

अन्य विकल्प अल्प, इनलाइन बार चार्ट का उपयोग करना है, जिसकी अपेक्षा स्पार्कलाइन से की जा सकती है।[22]चूंकि रडार एवं ध्रुवीय चार्ट को प्रायः ही चार्ट प्रकार के रूप में वर्णित किया जाता है,[4]कुछ स्रोत उनके मध्य अंतर करते हैं एवं यहां तक ​​कि रडार चार्ट को ध्रुवीय चार्ट का रूपांतर मानते हैं जो ध्रुवीय समन्वय के संदर्भ में डेटा प्रदर्शित नहीं करता है।[23]

यह भी देखें

संदर्भ

Public Domain This article incorporates public domain material from the National Institute of Standards and Technology.

  1. ↑ Porter, Michael M; Niksiar, Pooya (2018). "Multidimensional mechanics: Performance mapping of natural biological systems using permutated radar charts". PLOS ONE. 13 (9): e0204309. Bibcode:2018PLoSO..1304309P. doi:10.1371/journal.pone.0204309. PMC 6161877. PMID 30265707.
  2. ↑ Nancy R. Tague (2005) The quality toolbox. page 437.
  3. ↑ Kolence, Kenneth W. (1973). "सॉफ्टवेयर अनुभववादी". ACM SIGMETRICS Performance Evaluation Review. 2 (2): 31–36. doi:10.1145/1113644.1113647. S2CID 18600391. Dr. Philip J. Kiviat suggested at a recent NBS/ACM workshop on performance measurement that a circular graph, using radii as the variable axes might be a useful form. […] I recommend they be called "Kiviat Plots" or "Kiviat Graphs" to recognize his insight as to their importance.
  4. ↑ 4.0 4.1 "रडार चार्ट का उपयोग करके सामग्री अंतराल खोजें". Content Strategy Workshops. March 3, 2015. Retrieved December 17, 2015.
  5. ↑ 5.0 5.1 5.2 5.3 5.4 5.5 NIST/SEMATECH (2003). Star Plot in: e-Handbook of Statistical Methods. 6/01/2003 (Date created)
  6. ↑ Chambers, John, William Cleveland, Beat Kleiner, and Paul Tukey, (1983). Graphical Methods for Data Analysis. Wadsworth. pp. 158–162
  7. ↑ Mayr, Georg von (1877), Die Gesetzmäßigkeit im Gesellschaftsleben (in Deutsch), Munich: Oldenbourg, OL 23294909M, p.78. Linien-Diagramme im Kreise: Line charts in circles.
  8. ↑ Michael Friendly (2008). "Milestones in the history of thematic cartography, statistical graphics, and data visualization" Archived 2018-09-26 at the Wayback Machine.
  9. ↑ Michael Friendly (1991). "Statistical Graphics for Multivariate Data". Paper presented at the SAS SUGI 16 Conference, Apr, 1991.
  10. ↑ Spider Graphs: Charting Basketball Statistics
  11. ↑ Seeing Data. "डेटा विज़ुअलाइज़ेशन को समझना" (in English). Seeing Data.
  12. ↑ Ron Basu (2004). Implementing Quality: A Practical Guide to Tools and Techniques. p.131.
  13. ↑ Model Systems Knowledge Translation Center. "रडार चार्ट का प्रभावी उपयोग" (PDF) (in English). Model Systems Knowledge Translation Center.
  14. ↑ John Maguire. "डी-सामान्यीकृत स्पाइडर और रडार ग्राफ़" (in English). Kitman Labs.
  15. ↑ You are NOT spider man, so why do you use radar charts?, by Chandoo, September 18th, 2008
  16. ↑ 16.0 16.1 16.2 Peltier, Jon (2008-08-14). "रॉक अराउंड द क्लॉक - पेल्टियर टेक ब्लॉग". Peltiertech.com. Retrieved 2013-09-11.
  17. ↑ Cleveland, William; McGill, Robert (1984). "Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods". Journal of the American Statistical Association. 79 (387): 531–554. JSTOR 2288400. Summary of Cleveland's hierarchy
  18. ↑ "चौबीस घंटे चार्टिंग एक्सेल चार्ट ब्लॉग". Excelcharts.com. 2008-08-15. Retrieved 2013-09-11.
  19. ↑ 19.0 19.1 Clock This
  20. ↑ "मानक आँकड़े". www.mlb.com. Retrieved 2022-04-26.
  21. ↑ "गुणात्मक तुलना". Support Analytics Blog. 11 December 2007. Archived from the original on 2012-04-08.
  22. ↑ 22.0 22.1 "Information Ocean: Reorderable tables II: Bertin versus the Spiders". I-ocean.blogspot.com. 2008-09-24. Retrieved 2013-09-11.
  23. ↑ "ध्रुवीय चार्ट (रिपोर्ट बिल्डर और एसएसआरएस)". Microsoft Developer Network. Retrieved December 17, 2015.


बाहरी संबंध

Wikimedia Commons has media related to Radar charts.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=रडार_चार्ट&oldid=272049’