व्युत्क्रम अतिपरवलयिक फलन

इकाई अतिपरवलय के माध्यम से एक किरण $\scriptstyle x^{2}\ -\ y^{2}\ =\ 1$ बिंदु में $\scriptstyle (\cosh \,a,\,\sinh \,a)$, कहाँ $\scriptstyle a$ किरण, अतिपरवलय और के बीच का क्षेत्र दोगुना है $\scriptstyle x$-एक्सिस

प्रतिलोम अतिपरवलयिक फलन करता है

अतिपरवलयिक फलन के दिए गए मान के लिए, संबंधित व्युत्क्रम अतिपरवलयिक फलन संबंधित अतिपरवलयिक कोण प्रदान करता है। अतिपरवलयिक कोण का आकार अतिशयोक्ति के संगत अतिपरवलयिक क्षेत्र के क्षेत्रफल के बराबर होता है xy = 1, या इकाई हाइपरबोला के संबंधित क्षेत्र के क्षेत्र का दोगुना x² − y² = 1, ठीक वैसे ही जैसे एक कोण इकाई वृत्त के वृत्तीय त्रिज्यखंड के क्षेत्रफल का दुगुना होता है। कुछ लेखकों ने अतिपरवलयिक कोणों को अनुभूत करने के लिए व्युत्क्रम अतिपरवलयिक फलनों को क्षेत्र फलन कहा है।

अतिपरवलयिक ज्यामिति में कोणों और दूरियों की गणना में अतिपरवलयिक फलन होते हैं। यह कई रेखीय अंतर समीकरणों के समाधान में भी होता है (जैसे कि एक ज़ंजीर का को परिभाषित करने वाला समीकरण), क्यूबिक समीकरण और कार्टेशियन निर्देशांक में लाप्लास का समीकरण। लाप्लास के समीकरण भौतिकी के कई क्षेत्रों में महत्वपूर्ण हैं, जिनमें विद्युत चुम्बकीय सिद्धांत, गर्मी हस्तांतरण, द्रव गतिकी और विशेष सापेक्षता सम्मिलित हैं।

नोटेशन

ISO 80000-2 मानक संक्षिप्ताक्षरों में एआर- के बाद संबंधित अतिपरवलयिक फलन (जैसे, आर्कसिंह, आर्ककोश) का संक्षिप्त नाम सम्मिलित है।

पूर्वयोजन एआरसी- इसके बाद संबंधित अतिपरवलयिक फलन (उदाहरण के लिए, आर्कसिंह, आर्ककोश) भी सामान्यतः व्युत्क्रम त्रिकोणमितीय फलनों के लिए नामकरण के अनुरूप देखा जाता है। ये मिथ्या नाम हैं, क्योंकि उपसर्ग आर्क आर्कस का संक्षिप्त नाम है, जबकि उपसर्ग आर क्षेत्र के लिए है; अतिपरवलयिक फलन सीधे चाप से संबंधित नहीं हैं।

अन्य लेखक संकेतन अर्गसिंह, अर्गकोश, अर्गतन्ह, इत्यादि का उपयोग करना पसंद करते हैं, जहाँ उपसर्ग एआरजी लैटिन तर्क का संक्षिप्त नाम है। कंप्यूटर विज्ञान में, इसे अधिकांशतः असिंह के रूप में संक्षिप्त किया जाता है।

संकेत sinh⁻¹(x), cosh⁻¹(x), आदि का भी प्रयोग किया जाता है, इस तथ्य के अतिरिक्त कि सुपरस्क्रिप्ट -1 की एक शक्ति के रूप में गलत व्याख्या से बचने के लिए सावधानी बरतनी चाहिए, जैसा कि विपरीत फलन को दर्शाने के लिए एक आशुलिपि के विपरीत है (उदाहरण के लिए, cosh⁻¹(x) बनाम cosh(x)⁻¹).

लघुगणक के संदर्भ में परिभाषाएँ

चूँकि अतिपरवलयिक फलन e^xतर्कसंगत फलन हैं जिनके अंश और हर अधिक से अधिक दो डिग्री के हैं, इन फलनों को द्विघात सूत्र का उपयोग करके e^x के संदर्भ में हल किया जा सकता है ; फिर, प्राकृतिक लघुगणक लेने से व्युत्क्रम अतिपरवलयिक फलनों के लिए निम्नलिखित भाव मिलते हैं।

जटिल संख्या तर्कों के लिए, प्रतिलोम अतिपरवलयिक फलन, वर्गमूल और लघुगणक बहु-मूल्यवान फलन हैं, और अगले उपखंडों की समानता को बहु-मूल्यवान फलनों की समानता के रूप में देखा जा सकता है।

सभी व्युत्क्रम अतिपरवलयिक फलनों के लिए (प्रतिलोम अतिपरवलयिक कोटिस्पर्श और व्युत्क्रम अतिपरवलयिक व्युत्क्रमज्या को बचाएं), वास्तविक फलन का डोमेन जुड़ा हुआ स्थान है।

व्युत्क्रम अतिपरवलयिक साइन

व्युत्क्रम अतिपरवलयिक साइन (उर्फ क्षेत्र अतिपरवलयिक साइन) (लैटिन: क्षेत्र साइनस अतिपरवलयिक):

$\operatorname {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)$

डोमेन वास्तविक संख्या है।

व्युत्क्रम अतिपरवलयिक कोसाइन

व्युत्क्रम अतिपरवलयिक कोज्या(उर्फ क्षेत्र अतिपरवलयिक कोसाइन) (लैटिन: क्षेत्र कोसिनस अतिपरवलयिक):

$\operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)$

डोमेन बंद अंतराल है [1, +∞ ).

प्रतिलोम अतिपरवलयिक स्पर्शज्या

व्युत्क्रम अतिपरवलयिक स्पर्शरेखा (उर्फ क्षेत्र अतिपरवलयिक स्पर्शरेखा) (लैटिन: क्षेत्र स्पर्शरेखा अतिपरवलयिक):

$\operatorname {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)$

डोमेन खुला अंतराल है (−1, 1).

व्युत्क्रम अतिपरवलयिक कोटिस्पर्श

व्युत्क्रम अतिपरवलयिक कोटिस्पर्श(उर्फ, क्षेत्र अतिपरवलयिक कोटिस्पर्श) (लैटिन: क्षेत्र कोटिस्पर्श अतिपरवलयिक):

$\operatorname {arcoth} x={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)$

डोमेन खुले अंतराल का संघ है (−∞, −1) और (1, +∞).

प्रतिलोम अतिपरवलयिक कोटिज्या

व्युत्क्रम अतिपरवलयिक कोटिज्या (उर्फ, क्षेत्र अतिपरवलयिक कोटिज्या) (लैटिन: क्षेत्र कोटिज्या अतिपरवलयिक):

$\operatorname {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)$

डोमेन अर्ध-खुला अंतराल है (0, 1].

व्युत्क्रम अतिपरवलयिक व्युत्क्रमज्या

व्युत्क्रम अतिपरवलयिक व्युत्क्रमज्या (उर्फ, क्षेत्र अतिपरवलयिक व्युत्क्रमज्या) (लैटिन: क्षेत्र व्युत्क्रमज्या अतिपरवलयिक):

$\operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)$

डोमेन 0 को छोड़कर सभी वास्तविक संख्याएँ हैं।

जोड़ सूत्र

$\operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)$

$\operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)$

$\operatorname {artanh} u\pm \operatorname {artanh} v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)$

$\operatorname {arcoth} u\pm \operatorname {arcoth} v=\operatorname {arcoth} \left({\frac {1\pm uv}{u\pm v}}\right)$

${\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}$

अन्य पहचान

${\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ for }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ for }}x\geq 1\\2\operatorname {arsinh} x&=\operatorname {arcosh} (2x^{2}+1)&\quad {\hbox{ for }}x\geq 0\\4\operatorname {arsinh} x&=\operatorname {arcosh} (8x^{4}+8x^{2}+1)&\quad {\hbox{ for }}x\geq 0\end{aligned}}$

$\ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)$

अतिपरवलयिक और प्रतिलोम अतिपरवलयिक फलनों की संरचना

${\begin{aligned}&\sinh(\operatorname {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{for}}\quad |x|>1\\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\cosh(\operatorname {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatorname {artanh} x)={\frac {1}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{\sqrt {1+x^{2}}}}\\&\tanh(\operatorname {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad {\text{for}}\quad |x|>1\end{aligned}}$

व्युत्क्रम अतिपरवलयिक और त्रिकोणमितीय फलनों की संरचना

$\operatorname {arsinh} \left(\tan \alpha \right)=\operatorname {artanh} \left(\sin \alpha \right)=\ln \left({\frac {1+\sin \alpha }{\cos \alpha }}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\cos \alpha }}\right)$

$\ln \left(\left|\tan \alpha \right|\right)=-\operatorname {artanh} \left(\cos 2\alpha \right)$

रूपांतरण

$\ln x=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\pm \operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)$

$\operatorname {artanh} x=\operatorname {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\sqrt {1-x^{2}}}}\right)$

$\operatorname {arsinh} x=\operatorname {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\sqrt {1+x^{2}}}\right)$

$\operatorname {arcosh} x=\left|\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)\right|=\left|\operatorname {artanh} \left({\frac {\sqrt {x^{2}-1}}{x}}\right)\right|$

साधित

${\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{\text{ for all real }}x\\{\frac {d}{dx}}\operatorname {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}},{\text{ for all real }}x>1\\{\frac {d}{dx}}\operatorname {artanh} x&{}={\frac {1}{1-x^{2}}},{\text{ for all real }}|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&{}={\frac {1}{1-x^{2}}},{\text{ for all real }}|x|>1\\{\frac {d}{dx}}\operatorname {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ for all real }}x\in (0,1)\\{\frac {d}{dx}}\operatorname {arcsch} x&{}={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ for all real }}x{\text{, except }}0\\\end{aligned}}$

एक उदाहरण अवकलन के लिए: मान लीजिए θ = arsinh x, इसलिए (जहां sinh² θ = (sinh θ)²):

${\frac {d\,\operatorname {arsinh} x}{dx}}={\frac {d\theta }{d\sinh \theta }}={\frac {1}{\cosh \theta }}={\frac {1}{\sqrt {1+\sinh ^{2}\theta }}}={\frac {1}{\sqrt {1+x^{2}}}}.$

श्रृंखला विस्तार

उपरोक्त फलनों के लिए विस्तार श्रृंखला प्राप्त की जा सकती है:

${\begin{aligned}\operatorname {arsinh} x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}$

${\begin{aligned}\operatorname {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{aligned}}$

${\begin{aligned}\operatorname {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}$

${\begin{aligned}\operatorname {arcsch} x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}$

${\begin{aligned}\operatorname {arsech} x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\end{aligned}}$

${\begin{aligned}\operatorname {arcoth} x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}$

arsinh के लिए एक स्पर्शोन्मुख विस्तार द्वारा दिया गया है

$\operatorname {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}$

जटिल सतह में प्रमुख मूल्य

एक जटिल चर के फलनों के रूप में, व्युत्क्रम अतिपरवलयिक फलन बहुविकल्पीय फलन होते हैं जो विश्लेषणात्मक फलन होते हैं, बिंदुओं की सीमित संख्या को छोड़कर। इस तरह के एक फलन के लिए, एक प्रमुख मूल्य को परिभाषित करना सामान्य है, जो एक एकल मूल्यवान विश्लेषणात्मक फलन है जो जटिल विमान से युक्त एक डोमेन पर बहु-मूल्यवान फलन की एक विशिष्ट शाखा के साथ मेल खाता है जिसमें चाप (ज्यामिति) की एक परिमित संख्या होती है। (सामान्यतः आधी लाइन या रेखा खंड ) हटा दिए गए हैं। इन आर्क्स को शाखा कट कहा जाता है। शाखा को निर्दिष्ट करने के लिए, अर्थात्, प्रत्येक बिंदु पर बहुविकल्पी फलनो का कौन सा मान माना जाता है, इसे परिभाषित करने के लिए, सामान्यतः इसे एक विशेष बिंदु पर परिभाषित किया जाता है, और विश्लेषणात्मक निरंतरता द्वारा प्रमुख मूल्य की परिभाषा के डोमेन में हर स्थान मूल्य घटाया जाता है। जब संभव हो, मुख्य मूल्य को सीधे परिभाषित करना उत्तम होता है—विश्लेषणात्मक निरंतरता का जिक्र किए बिना।

उदाहरण के लिए, वर्गमूल के लिए, मुख्य मान को उस वर्गमूल के रूप में परिभाषित किया जाता है जिसका एक धनात्मक वास्तविक भाग होता है। यह एक एकल मूल्यवान विश्लेषणात्मक फलन को परिभाषित करता है, जिसे चर के गैर-सकारात्मक वास्तविक मानों को छोड़कर (जहां दो वर्गमूलों का शून्य वास्तविक भाग होता है) को छोड़कर, हर स्थान परिभाषित किया जाता है। वर्गमूल फलन के इस मुख्य मान को निम्नलिखित में${\sqrt {x}}$ निरूपित किया जाता है। इसी तरह, लघुगणक का मुख्य मूल्य, जिसे $\operatorname {Log}$ निरूपित किया जाता है, को उस मान के रूप में परिभाषित किया गया है जिसके लिए काल्पनिक भाग का सबसे छोटा निरपेक्ष मान है। यह चर के गैर-सकारात्मक वास्तविक मूल्यों को छोड़कर हर स्थान परिभाषित किया गया है, जिसके लिए लघुगणक के दो अलग-अलग मान न्यूनतम तक पहुँचते हैं।

सभी व्युत्क्रम अतिपरवलयिक फलनों के लिए, मुख्य मूल्य को वर्गमूल के प्रमुख मूल्यों और लघुगणक फलनो के संदर्भ में परिभाषित किया जा सकता है। चूँकि, कुछ स्थितियों में, के सूत्र लघुगणक के संदर्भ में और परिभाषाओं के सूत्र एक सही मूल मान नहीं देते हैं, क्योंकि परिभाषा का एक डोमेन बहुत छोटा है और एक स्थिति में गैर-जुड़ा हुआ है।

व्युत्क्रम अतिपरवलय ज्या का मुख्य मूल्य

व्युत्क्रम अतिपरवलय ज्या का मुख्य मूल्य द्वारा दिया जाता है

$\operatorname {arsinh} z=\operatorname {Log} (z+{\sqrt {z^{2}+1}}\,)\,.$

वर्गमूल का तर्क एक गैर-सकारात्मक वास्तविक संख्या है, यदि और केवल यदि z काल्पनिक अक्ष के अंतराल [i, +i∞) और (−i∞, −i] में से एक से संबंधित है। यदि लघुगणक का तर्क वास्तविक है, तो यह धनात्मक है। इस प्रकार यह सूत्र शाखाओं में कटौती के साथ अरसिंह के लिए एक प्रमुख मूल्य को परिभाषित करता है [i, +i∞) और (−i∞, −i]. यह इष्टतम है, क्योंकि शाखा कटौती को एकवचन बिंदुओं को जोड़ना चाहिए i और −i अनंत की ओर इंगित करता है।

व्युत्क्रम अतिपरवलयिक कोज्या का मूल मूल्य

व्युत्क्रम अतिपरवलयिक कोज्या के लिए सूत्र दिया गया है और व्युत्क्रम अतिपरवलयिक कोज्या सुविधाजनक नहीं है, क्योंकि लघुगणक और वर्गमूल के प्रमुख मानों के समान, चाप का मुख्य मान काल्पनिक के लिए परिभाषित नहीं किया जाएगा z. इस प्रकार वर्गमूल को कारक बनाना होगा, जिसके कारण

$\operatorname {arcosh} z=\operatorname {Log} (z+{\sqrt {z+1}}{\sqrt {z-1}}\,)\,.$

वर्गमूलों के प्रमुख मान दोनों परिभाषित हैं, यदि को छोड़कर z वास्तविक अंतराल से संबंधित है (−∞, 1]. यदि लघुगणक का तर्क वास्तविक है, तब z वास्तविक है और उसका चिह्न समान है। इस प्रकार, उपरोक्त सूत्र वास्तविक अंतराल के बाहर आर्कोश के एक प्रमुख मूल्य को परिभाषित करता है (−∞, 1], जो इस प्रकार अद्वितीय शाखा कट है।

प्रतिलोम अतिपरवलयिक स्पर्शरेखा और कोटिस्पर्श के प्रमुख मूल्य

और परिभाषाओं में दिए गए सूत्र लघुगणक के रूप में सुझाते हैं

${\begin{aligned}\operatorname {artanh} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {1+z}{1-z}}\right)\\\operatorname {arcoth} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {z+1}{z-1}}\right)\end{aligned}}$

व्युत्क्रम अतिपरवलयिक स्पर्शरेखा और कोटिस्पर्श के प्रमुख मूल्यों की परिभाषा के लिए। इन सूत्रों में, लघुगणक का तर्क वास्तविक है यदि और केवल यदि z यह सचमुच का है। अर्तन्ह के लिए, यह तर्क वास्तविक अंतराल में है (−∞, 0], यदि z या तो से संबंधित है (−∞, −1] या करने के लिए [1, ∞). आर्कोथ के लिए, लघुगणक का तर्क अंदर है (−∞, 0], यदि और केवल यदि z वास्तविक अंतराल से [−1, 1] संबंधित है|

इसलिए, ये सूत्र सुविधाजनक प्रमुख मूल्यों को परिभाषित करते हैं, जिसके लिए व्युत्क्रम अतिपरवलयिक स्पर्शरेखा के लिए शाखा कट (−∞, −1] और [1, ∞) हैं,व्युत्क्रम अतिपरवलयिक स्पर्शरेखा के लिए, और [−1, 1] हैं।

शाखा कटौती के पास उत्तम संख्यात्मक मूल्यांकन को देखते हुए, कुछ लेखक प्रमुख मूल्यों की निम्नलिखित परिभाषाओं का उपयोग करें, चूंकि दूसरा z = 0 पर एक हटाने योग्य विलक्षणता का परिचय देता है | $\operatorname {artanh}$ की दो परिभाषाएँ अलग-अलग हैं $z>1$ के साथ $z$ के वास्तविक मान है| $\operatorname {arcoth}$ वाले $z\in [0,1)$ के साथ $z$ के वास्तविक मानों के लिए भिन्न होते हैं।

${\begin{aligned}\operatorname {artanh} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+z}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-z}\right)\\\operatorname {arcoth} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+{\frac {1}{z}}}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-{\frac {1}{z}}}\right)\end{aligned}}$

प्रतिलोम अतिपरवलयिक व्युत्क्रमज्या का मुख्य मूल्य

व्युत्क्रम अतिपरवलयिक व्युत्क्रमज्या के लिए, मुख्य मान को इस प्रकार परिभाषित किया जाता है

$\operatorname {arcsch} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}+1}}\,\right)$.

इसे तब परिभाषित किया जाता है जब लघुगणक और वर्गमूल के तर्क गैर-धनात्मक वास्तविक संख्याएँ नहीं होते हैं। वर्गमूल का मुख्य मान इस प्रकार काल्पनिक रेखा के अंतराल [−i, i] के बाहर परिभाषित किया गया है यदि लघुगणक का तर्क वास्तविक है, तब z एक गैर-शून्य वास्तविक संख्या है, और इसका तात्पर्य है कि लघुगणक का तर्क धनात्मक है।

इस प्रकार, प्रमुख मूल्य काल्पनिक रेखा के अंतराल [−i, i] से युक्त शाखा कट के बाहर उपरोक्त सूत्र द्वारा परिभाषित किया गया है।

z = 0के लिए, एक विलक्षण बिंदु है जो शाखा कट में सम्मिलित है।

प्रतिलोम अतिपरवलयिक कोटिज्या का मुख्य मूल्य

यहाँ, जैसा कि व्युत्क्रम अतिपरवलयिक कोज्याके स्थितियों में है, हमें वर्गमूल का गुणनखंडन करना होगा। यह मुख्य मूल्य देता है

$\operatorname {arsech} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z}}+1}}\,{\sqrt {{\frac {1}{z}}-1}}\right).$

यदि वर्गमूल का तर्क वास्तविक है, तब z वास्तविक है, और यह अनुसरण करता है कि वर्गमूल के दोनों प्रमुख मान परिभाषित हैं, यदि को छोड़कर z वास्तविक है और एक अंतराल से संबंधित है (−∞, 0] और [1, +∞). यदि लघुगणक का तर्क वास्तविक और ऋणात्मक है, तब z भी वास्तविक और ऋणात्मक है। कि आर्सेक का मुख्य मूल्य उपरोक्त सूत्र द्वारा अच्छी तरह से परिभाषित है दो शाखाओं के बाहर वास्तविक अंतराल(−∞, 0] और [1, +∞) को काटता है।

z = 0 के लिए, एक विलक्षण बिंदु है जो एक शाखा कटौती में सम्मिलित है।

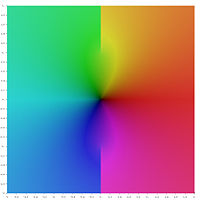
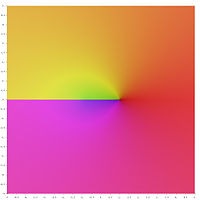
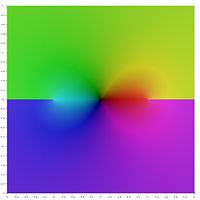
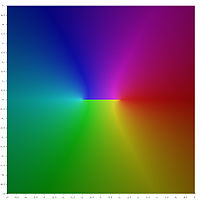
चित्रात्मक प्रतिनिधित्व

व्युत्क्रम अतिपरवलयिक फलनों के प्रमुख मूल्यों के निम्नलिखित चित्रमय प्रतिनिधित्व में, शाखा कटौती रंग की असततता के रूप में दिखाई देती है। तथ्य यह है कि पूरी शाखा कटौती विच्छेदन के रूप में दिखाई देती है, यह दर्शाता है कि इन प्रमुख मूल्यों को बड़े डोमेन पर परिभाषित विश्लेषणात्मक फलनों में विस्तारित नहीं किया जा सकता है। दूसरे शब्दों में, ऊपर परिभाषित शाखाओं में कटौती न्यूनतम है।

$\operatorname {arsinh} (z)$

$\operatorname {arcosh} (z)$

$\operatorname {artanh} (z)$

$\operatorname {arcoth} (z)$

$\operatorname {arsech} (z)$

$\operatorname {arcsch} (z)$

Inverse hyperbolic functions in the complex z-plane: the colour at each point in the plane represents the complex value of the respective function at that point

यह भी देखें

• जटिल लघुगणक
• अतिपरवलयिक कोटिज्या वितरण
• आईएसओ 80000-2
• प्रतिलोम अतिपरवलयिक फलनों के अभिन्न की सूची

ग्रन्थसूची

• Herbert Busemann and Paul J. Kelly (1953) Projective Geometry and Projective Metrics, page 207, Academic Press.

बाहरी संबंध

• "Inverse hyperbolic functions", Encyclopedia of Mathematics, EMS Press, 2001 [1994]