विशिष्ट आपेक्षिकता में द्रव्यमान: Difference between revisions
mNo edit summary |
No edit summary |
||
| (14 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
विशिष्ट आपेक्षिकता में [[ द्रव्यमान ]] शब्द के दो अर्थ हैं: [[ अपरिवर्तनीय द्रव्यमान | निश्चर द्रव्यमान]] (जिसे ''[[विराम द्रव्यमान]]'' भी कहा जाता है) एक [[ अपरिवर्तनीय मात्रा | निश्चर मात्रा]] है जो सभी [[निर्देश फ्रेमों]] में सभी [[परिदर्शक]] ([[ विशेष सापेक्षता | विशिष्ट आपेक्षिकता]] ) के लिए समान है, जबकि '''<nowiki/>'आपेक्षिकीय द्रव्यमान'''' परिदर्शक के वेग पर निर्भर है। [[द्रव्यमान-ऊर्जा तुल्यता]] की अवधारणा के अनुसार, निश्चर द्रव्यमान [[विराम ऊर्जा]] के बराबर है, जबकि आपेक्षिकीय द्रव्यमान [[सापेक्षतावादी ऊर्जा|आपेक्षिकीय ऊर्जा]] (जिसे कुल ऊर्जा भी कहा जाता है) के बराबर है। | विशिष्ट आपेक्षिकता में [[ द्रव्यमान ]] शब्द के दो अर्थ हैं: [[ अपरिवर्तनीय द्रव्यमान | निश्चर द्रव्यमान]] (जिसे ''[[विराम द्रव्यमान]]'' भी कहा जाता है) एक [[ अपरिवर्तनीय मात्रा | निश्चर मात्रा]] है जो सभी [[निर्देश फ्रेमों]] में सभी [[परिदर्शक]] ([[ विशेष सापेक्षता | विशिष्ट आपेक्षिकता]] ) के लिए समान है, जबकि '''<nowiki/>'आपेक्षिकीय द्रव्यमान'''' परिदर्शक के वेग पर निर्भर है। [[द्रव्यमान-ऊर्जा तुल्यता]] की अवधारणा के अनुसार, निश्चर द्रव्यमान [[विराम ऊर्जा]] के बराबर है, जबकि आपेक्षिकीय द्रव्यमान [[सापेक्षतावादी ऊर्जा|आपेक्षिकीय ऊर्जा]] (जिसे कुल ऊर्जा भी कहा जाता है) के बराबर है। | ||
| Line 66: | Line 65: | ||
== आपेक्षिक बनाम विराम द्रव्यमान == | == आपेक्षिक बनाम विराम द्रव्यमान == | ||
आपेक्षिक द्रव्यमान और विराम द्रव्यमान दोनों भौतिकी में पारंपरिक अवधारणाएं हैं, लेकिन आपेक्षिकीय द्रव्यमान कुल ऊर्जा से मेल खाता है। आपेक्षिकीय द्रव्यमान पद्धति का द्रव्यमान है क्योंकि इसे एक मानदंड पर मापा जाएगा, लेकिन कुछ स्थितियों में (जैसे कि ऊपर का डिब्बा)। उदाहरण के लिए, यदि [[ साइक्लोट्रॉन ]] में एक अतिसूक्ष्म परमाणु सापेक्ष वेग के साथ घेरे में घूम रहा है, तो साइक्लोट्रॉन + अतिसूक्ष्म परमाणु पद्धति का द्रव्यमान अतिसूक्ष्म परमाणु के सापेक्षिक द्रव्यमान से बढ़ जाता है, न कि अतिसूक्ष्म परमाणु के विराम द्रव्यमान से। लेकिन यह किसी भी बंद पद्धति के बारे में भी सच है, जैसे अतिसूक्ष्म परमाणु-और-डिब्बा, अगर अतिसूक्ष्म परमाणु डिब्बे के अंदर उच्च गति से उछलता है। यह केवल पद्धति में कुल संवेग की कमी है (पद्धति संवेग शून्य है) जो अतिसूक्ष्म परमाणु की गतिज ऊर्जा को तौलने की अनुमति देता है। यदि अतिसूक्ष्म परमाणु को रोका जाता है और तौला जाता है, या | आपेक्षिक द्रव्यमान और विराम द्रव्यमान दोनों भौतिकी में पारंपरिक अवधारणाएं हैं, लेकिन आपेक्षिकीय द्रव्यमान कुल ऊर्जा से मेल खाता है। आपेक्षिकीय द्रव्यमान पद्धति का द्रव्यमान है क्योंकि इसे एक मानदंड पर मापा जाएगा, लेकिन कुछ स्थितियों में (जैसे कि ऊपर का डिब्बा)। उदाहरण के लिए, यदि [[ साइक्लोट्रॉन ]] में एक अतिसूक्ष्म परमाणु सापेक्ष वेग के साथ घेरे में घूम रहा है, तो साइक्लोट्रॉन + अतिसूक्ष्म परमाणु पद्धति का द्रव्यमान अतिसूक्ष्म परमाणु के सापेक्षिक द्रव्यमान से बढ़ जाता है, न कि अतिसूक्ष्म परमाणु के विराम द्रव्यमान से। लेकिन यह किसी भी बंद पद्धति के बारे में भी सच है, जैसे अतिसूक्ष्म परमाणु-और-डिब्बा, अगर अतिसूक्ष्म परमाणु डिब्बे के अंदर उच्च गति से उछलता है। यह केवल पद्धति में कुल संवेग की कमी है (पद्धति संवेग शून्य है) जो अतिसूक्ष्म परमाणु की गतिज ऊर्जा को तौलने की अनुमति देता है। यदि अतिसूक्ष्म परमाणु को रोका जाता है और तौला जाता है, या मानदंड को किसी तरह उसके बाद भेजा जाता है, तो यह मानदंड के संबंध में आगे नहीं बढ़ेगा, और फिर से आपेक्षिकीय और विराम द्रव्यमान एकल अतिसूक्ष्म परमाणु के लिए समान होंगे (और छोटे होंगे)। सामान्य तौर पर, सापेक्षतावादी और विराम द्रव्यमान केवल उन पद्धतियों में समान होते हैं जिनमें कोई नेट संवेग नहीं होता है और द्रव्यमान का पद्धति केंद्र स्थिर होता है; अन्यथा वे भिन्न हो सकते हैं। | ||
निश्चर द्रव्यमान एक निर्देश फ्रेम में कुल ऊर्जा के मूल्य के समानुपाती होता है, वह फ्रेम जहां संपूर्ण वस्तु | निश्चर द्रव्यमान एक निर्देश फ्रेम में कुल ऊर्जा के मूल्य के समानुपाती होता है, वह फ्रेम जहां संपूर्ण वस्तु स्थिर होती है (जैसा कि द्रव्यमान के केंद्र के संदर्भ में नीचे परिभाषित किया गया है)। यही कारण है कि निश्चर द्रव्यमान एकल कणों के लिए विराम द्रव्यमान के समान होता है। हालांकि, निश्चर द्रव्यमान भी मापा द्रव्यमान का प्रतिनिधित्व करता है जब द्रव्यमान का केंद्र कई कणों की पद्धतियों के लिए स्थिर होता है। यह फ्रेम जहां ऐसा होता है उसे संवेग फ्रेम का केंद्र भी कहा जाता है, और इसे [[ जड़त्वीय फ्रेम ]] के रूप में परिभाषित किया जाता है जिसमें वस्तु के द्रव्यमान का केंद्र स्थिर होता है (यह कहने का दूसरा तरीका यह है कि यह वह फ्रेम है जिसमें संवेग पद्धति के पुर्जों का योग शून्य हो जाता है)। यौगिक वस्तुओं के लिए (कई छोटी वस्तुओं से बना है, जिनमें से कुछ गतिमान हो सकती हैं) और अपरिबद्ध वस्तुओं के सेट (जिनमें से कुछ गतिमान भी हो सकते हैं), केवल पद्धति के द्रव्यमान के केंद्र को वस्तु के लिए आराम की आवश्यकता होती है आपेक्षिक द्रव्यमान अपने विराम द्रव्यमान के बराबर होना चाहिए। | ||
एक तथाकथित [[ द्रव्यमान रहित कण ]] (जैसे एक फोटॉन, या एक सैद्धांतिक गुरुत्वाकर्षण) निर्देश के प्रत्येक फ्रेम में प्रकाश की गति से चलता है। इस स्थिति में कोई परिवर्तन नहीं होता है जो कण को आराम में लाएगा। ऐसे कणों की कुल ऊर्जा फ्रेम में छोटी और छोटी होती जाती है जो एक ही दिशा में तेजी से और तेजी से आगे बढ़ते हैं। जैसे, उनके पास कोई विराम द्रव्यमान नहीं है, क्योंकि उन्हें कभी भी उस फ्रेम में नहीं मापा जा सकता है जहां वे | एक तथाकथित [[ द्रव्यमान रहित कण ]] (जैसे एक फोटॉन, या एक सैद्धांतिक गुरुत्वाकर्षण) निर्देश के प्रत्येक फ्रेम में प्रकाश की गति से चलता है। इस स्थिति में कोई परिवर्तन नहीं होता है जो कण को आराम में लाएगा। ऐसे कणों की कुल ऊर्जा फ्रेम में छोटी और छोटी होती जाती है जो एक ही दिशा में तेजी से और तेजी से आगे बढ़ते हैं। जैसे, उनके पास कोई विराम द्रव्यमान नहीं है, क्योंकि उन्हें कभी भी उस फ्रेम में नहीं मापा जा सकता है जहां वे स्थिर हैं। विराम द्रव्यमान न होने का यह गुण इन कणों को "द्रव्यमान रहित" कहलाने का कारण बनता है। हालांकि, द्रव्यमान रहित कणों में भी एक आपेक्षिकीय द्रव्यमान होता है, जो संदर्भ के विभिन्न फ्रेमों में उनकी देखी गई ऊर्जा के साथ भिन्न होता है। | ||
== निश्चर द्रव्यमान == | == निश्चर द्रव्यमान == | ||
निश्चर द्रव्यमान | निश्चर द्रव्यमान चतुर्विम-संवेग ([[ शास्त्रीय त्रि-आयामी गति ]] के चार-आयामी सामान्यीकरण) का [[ चार-वेग | चतुरंग वेग]] का अनुपात है:<ref>{{Citation | ||
|title=Introduction to relativity | |title=Introduction to relativity | ||
|first1=William D. | |first1=William D. | ||
| Line 85: | Line 84: | ||
</ref> | </ref> | ||
<math display="block">p^\mu = m v^\mu</math> | <math display="block">p^\mu = m v^\mu</math> | ||
और विराम द्रव्यमान स्थिर होने पर [[ चार-त्वरण ]] से | और विराम द्रव्यमान स्थिर होने पर [[ चार-त्वरण | चतुरंग-त्वरण]] से चतुरंग बल का अनुपात भी है। न्यूटन के द्वितीय नियम का चतुर्विमीय रूप है: | ||
<math display="block">F^\mu = m A^\mu.</math> | <math display="block">F^\mu = m A^\mu.</math> | ||
==आपेक्षिकीय ऊर्जा–संवेग समीकरण== | ==आपेक्षिकीय ऊर्जा–संवेग समीकरण== | ||
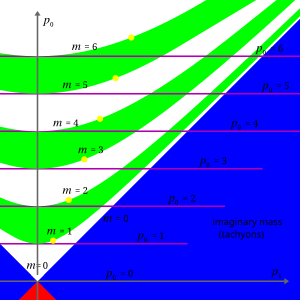
[[File:Invariant and additive masses.svg|thumb|right]]{{mvar|E}} और {{mvar|p}} के लिए आपेक्षिकीय भाव आपेक्षिकीय ऊर्जा-संवेग संबंध का पालन करते हैं:<ref name=taylor /> | |||
[[File:Invariant and additive masses.svg|thumb|right | |||
<math display="block">E^2 - (pc)^2 = \left(mc^2\right)^2</math> | <math display="block">E^2 - (pc)^2 = \left(mc^2\right)^2</math> | ||
जहां <var>m</var> | जहां <var>m</var> विराम द्रव्यमान है, या पद्धति के लिए निश्चर द्रव्यमान है, और {{mvar|E}} कुल ऊर्जा है। | ||
समीकरण फोटॉनों के लिए भी मान्य है, जिनके | समीकरण फोटॉनों के लिए भी मान्य है, जिनके {{math|1=<var>m</var> = 0}} है: | ||
<math display="block">E^2 - (pc)^2 = 0</math> | <math display="block">E^2 - (pc)^2 = 0</math> | ||
और इसीलिए | और इसीलिए | ||
<math display="block">E = pc</math> | <math display="block">E = pc</math> | ||
एक फोटॉन का संवेग उसकी ऊर्जा का एक कार्य है, लेकिन यह वेग के समानुपाती नहीं है, जो हमेशा | एक फोटॉन का संवेग उसकी ऊर्जा का एक कार्य है, लेकिन यह वेग के समानुपाती नहीं है, जो हमेशा {{math|''c''}} होता है | ||
किसी वस्तु | किसी स्थिर वस्तु के लिए, संवेग {{mvar|<var>p</var>}} शून्य है, इसलिए | ||
<math display="block">E = mc^2.</math> ध्यान दें कि सूत्र केवल शून्य गति वाले कणों या पद्धतियों के लिए सही है। | <math display="block">E = mc^2.</math> ध्यान दें कि सूत्र केवल शून्य गति वाले कणों या पद्धतियों के लिए सही है। | ||
विराम द्रव्यमान वस्तु के विराम फ्रेम में कुल ऊर्जा के समानुपाती होता है। | विराम द्रव्यमान वस्तु के विराम फ्रेम में कुल ऊर्जा के समानुपाती होता है। | ||
जब वस्तु गतिमान होती है, तो कुल ऊर्जा | जब वस्तु गतिमान होती है, तो कुल ऊर्जा निम्न द्वारा दी जाती है | ||
<math display="block">E = \sqrt{\left(mc^2\right)^2 + (pc)^2}</math> | <math display="block">E = \sqrt{\left(mc^2\right)^2 + (pc)^2}</math> | ||
वेग के फलन के रूप में संवेग और ऊर्जा का रूप ज्ञात करने के लिए यह ध्यान दिया जा सकता है कि | वेग के फलन के रूप में संवेग और ऊर्जा का रूप ज्ञात करने के लिए यह ध्यान दिया जा सकता है कि चतुरंग वेग , जो <math>\left(c, \vec{v}\right)</math>, के समानुपाती है। कण की गति से जुड़ा एकमात्र चतुर्विम सदिश है, ताकि अगर कोई संरक्षित चतुर्विम-संवेग हो <math>\left(E, \vec{p}c\right)</math>, तो यह इस सदिश के समानुपाती होना चाहिए। यह ऊर्जा के अनुपात को गति के रूप में व्यक्त करने की अनुमति देता है | ||
<math display="block">pc = E \frac{v}{c} ,</math> | <math display="block">pc = E \frac{v}{c} ,</math> | ||
परिणामस्वरूप {{mvar|<var>E</var>}} और {{mvar|<var>v</var>}} के बीच संबंध: | |||
<math display="block">E^2 = \left(mc^2\right)^2 + E^2 \frac{v^2}{c^2},</math> | <math display="block">E^2 = \left(mc^2\right)^2 + E^2 \frac{v^2}{c^2},</math> | ||
इस में यह परिणाम | इस में यह परिणाम | ||
| Line 123: | Line 121: | ||
\end{align}</math> | \end{align}</math> | ||
जहां कारक <math display="inline">\gamma = {1}/{\sqrt{1-\frac{v^2}{c^2}}}.</math> | जहां कारक <math display="inline">\gamma = {1}/{\sqrt{1-\frac{v^2}{c^2}}}.</math> | ||
[[ इकाइयों की प्रणाली | इकाइयों | |||
[[ इकाइयों की प्रणाली |इकाइयों]] में काम करते समय जहां {{math|1=''c'' = 1}}, जिसे [[ प्राकृतिक इकाई प्रणाली | प्राकृतिक इकाई पद्धति]] के रूप में जाना जाता है, सभी आपेक्षिकीय समीकरणों को सरल किया जाता है और मात्रा [[ ऊर्जा | ऊर्जा]] , संवेग और द्रव्यमान का एक ही प्राकृतिक आयाम होता है:<ref name="QFT">{{cite book |title=क्वांटम फील्ड थ्योरी|edition=2nd |first1=Franz |last1=Mandl |first2=Graham |last2=Shaw |publisher=John Wiley & Sons |year=2013 |isbn=978-1-118-71665-6 |page=70 |url=https://books.google.com/books?id=jTBzQfctvHAC}} [https://books.google.com/books?id=jTBzQfctvHAC&pg=PT70 Extract of page 70]</ref> | |||
<math display="block">m^2 = E^2 - p^2.</math> | <math display="block">m^2 = E^2 - p^2.</math> | ||
समीकरण को प्रायः इस तरह लिखा जाता है क्योंकि अंतर <math>E^2 - p^2</math> ऊर्जा संवेग चतुर्विम सदिश की आपेक्षिक लंबाई है, एक लंबाई जो पद्धति में विराम द्रव्यमान या निश्चर द्रव्यमान से जुड़ी होती है। जहां {{math|''m'' > 0}} और {{math|1=''p'' = 0}}, यह समीकरण फिर से द्रव्यमान-ऊर्जा तुल्यता {{math|1=''E'' = ''m''}} को व्यक्त करता है। | |||
== समग्र पद्धतियों का द्रव्यमान == | == समग्र पद्धतियों का द्रव्यमान == | ||
एक समग्र पद्धति का विराम द्रव्यमान भागों के विराम द्रव्यमानों का योग नहीं है, जब तक कि सभी भाग स्थिर न हों। एक समग्र पद्धति के कुल द्रव्यमान में पद्धति में गतिज ऊर्जा और क्षेत्र ऊर्जा समिलित होती है। | |||
एक समग्र पद्धति का विराम द्रव्यमान भागों के विराम द्रव्यमानों का योग नहीं है, जब तक कि सभी भाग | |||
कुल ऊर्जा {{mvar|E}} | एक समग्र पद्धति की कुल ऊर्जा {{mvar|E}} को इसके घटकों की ऊर्जाओं के योग को एक साथ जोड़कर निर्धारित किया जा सकता है। पद्धति का कुल संवेग <math>\vec{p}</math> एक सदिश मात्रा, की गणना उसके सभी घटकों के संवेगों को एक साथ जोड़कर भी की जा सकती है। कुल ऊर्जा {{mvar|E}} और कुल संवेग सदिश {{mvar|\vec{p<nowiki>}</nowiki>}} की लंबाई (परिणाम) कुलका <math>p</math>, को देखते हुए, निश्चर द्रव्यमान इस प्रकार दिया जाता है: | ||
<math display="block"> m = \frac{\sqrt{E^2 - (pc)^2}}{c^2}</math> | <math display="block"> m = \frac{\sqrt{E^2 - (pc)^2}}{c^2}</math> | ||
प्राकृतिक इकाइयों की पद्धति में जहां {{math|1=''c'' = 1}}, कणों की पद्धतियों के लिए (चाहे | प्राकृतिक इकाइयों की पद्धति में जहां {{math|1=''c'' = 1}}, कणों की पद्धतियों के लिए (चाहे बाध्य या अपरिबद्ध) कुल पद्धति निश्चर द्रव्यमान निम्नलिखित द्वारा समान रूप से दिया गया है: | ||
<math display="block"> m^2 = \left(\sum E\right)^2 - \left\|\sum \vec{p} \ \right\|^2</math> | <math display="block"> m^2 = \left(\sum E\right)^2 - \left\|\sum \vec{p} \ \right\|^2</math> | ||
कहाँ, फिर से, कण संवेग <math>\vec{p}</math> पहले सदिशों के रूप में अभिव्यक्त किया जाता है, और फिर उनके परिणामी कुल परिमाण ([[ यूक्लिडियन मानदंड ]]) के वर्ग का उपयोग किया जाता है। इसका परिणाम एक अदिश संख्या में होता है, जिसे कुल ऊर्जा के वर्ग के अदिश मान से घटाया जाता है। | कहाँ, फिर से, कण संवेग <math>\vec{p}</math> पहले सदिशों के रूप में अभिव्यक्त किया जाता है, और फिर उनके परिणामी कुल परिमाण ([[ यूक्लिडियन मानदंड ]]) के वर्ग का उपयोग किया जाता है। इसका परिणाम एक अदिश संख्या में होता है, जिसे कुल ऊर्जा के वर्ग के अदिश मान से घटाया जाता है। | ||
ऐसी पद्धति के लिए, संवेग फ्रेम के विशेष केंद्र में जहां संवेग का योग शून्य होता है, फिर से पद्धति द्रव्यमान (जिसे निश्चर द्रव्यमान कहा जाता है) कुल पद्धति ऊर्जा से मेल खाता है या इकाइयों में जहां {{math|1=''c'' = 1}}, | ऐसी पद्धति के लिए, संवेग फ्रेम के विशेष केंद्र में जहां संवेग का योग शून्य होता है, फिर से पद्धति द्रव्यमान (जिसे निश्चर द्रव्यमान कहा जाता है) कुल पद्धति ऊर्जा से मेल खाता है या इकाइयों में जहां {{math|1=''c'' = 1}}, इसके समान है। एक पद्धति के लिए यह निश्चर द्रव्यमान किसी भी जड़त्वीय फ्रेम में समान मात्रा में रहता है, हालांकि पद्धति की कुल ऊर्जा और कुल संवेग चुने गए विशेष जड़त्वीय फ्रेम के कार्य हैं, और जड़त्वीय फ्रेम के बीच इस तरह से भिन्न होंगे जैसे कि निश्चर द्रव्यमान सभी परिदर्शकों के लिए समान। निश्चर द्रव्यमान इस प्रकार उसी क्षमता में कणों की पद्धतियों के लिए कार्य करता है जैसे "विराम द्रव्यमान" एकल कणों के लिए करता है। | ||
ध्यान दें कि एक पृथक पद्धति का निश्चर द्रव्यमान (अर्थात, द्रव्यमान और ऊर्जा दोनों के लिए बंद) भी परिदर्शक या जड़त्वीय फ्रेम से स्वतंत्र है, और पृथक पद्धतियों और एकल परिदर्शकों के लिए एक स्थिर, संरक्षित मात्रा | ध्यान दें कि एक पृथक पद्धति का निश्चर द्रव्यमान (अर्थात, द्रव्यमान और ऊर्जा दोनों के लिए बंद) भी परिदर्शक या जड़त्वीय फ्रेम से स्वतंत्र है, और रासायनिक और परमाणु प्रतिक्रियाओं के दौरान भी पृथक पद्धतियों और एकल परिदर्शकों के लिए एक स्थिर, संरक्षित मात्रा है। [[ कण भौतिकी ]] में निश्चर द्रव्यमान की अवधारणा का व्यापक रूप से उपयोग किया जाता है, क्योंकि एक कण के क्षय उत्पादों का निश्चर द्रव्यमान उसके विराम द्रव्यमान के बराबर होता है। इसका उपयोग [[Z बोसॉन]] या [[ शीर्ष क्वार्क ]] जैसे कणों के द्रव्यमान का मापन करने के लिए किया जाता है। | ||
== विशिष्ट आपेक्षिकता में द्रव्यमान का संरक्षण बनाम निश्चरता == | == विशिष्ट आपेक्षिकता में द्रव्यमान का संरक्षण बनाम निश्चरता == | ||
कुल ऊर्जा एक योगात्मक संरक्षित मात्रा है (एकल परिदर्शकों के लिए) पद्धतियों और कणों के बीच प्रतिक्रियाओं में, लेकिन विराम द्रव्यमान (कण विराम द्रव्यमानों के योग होने के अर्थ में) एक घटना के माध्यम से संरक्षित नहीं किया जा सकता है जिसमें कणों के विराम द्रव्यमान हैं अन्य प्रकार की ऊर्जा में परिवर्तित, जैसे गतिज ऊर्जा। अलग-अलग कण विराम द्रव्यमानों का योग खोजने के लिए कई परिदर्शकों की आवश्यकता होगी, प्रत्येक कण जड़त्वीय फ्रेम के लिए एक, और ये परिदर्शक व्यक्तिगत कण गतिज ऊर्जा की उपेक्षा करते हैं। संरक्षण सिद्धांतो के लिए एक एकल परिदर्शक और एक जड़त्वीय फ्रेम की आवश्यकता होती है। | |||
कुल ऊर्जा एक योगात्मक संरक्षित मात्रा है (एकल परिदर्शकों के लिए) | |||
सामान्य तौर पर, पृथक पद्धतियों और एकल परिदर्शकों के लिए, आपेक्षिकीय द्रव्यमान संरक्षित होता है (प्रत्येक परिदर्शक इसे समय के साथ स्थिर देखता है), लेकिन अपरिवर्तनीय नहीं है (अर्थात, अलग-अलग परिदर्शक अलग-अलग मान देखते हैं)। निश्चर द्रव्यमान, हालांकि, संरक्षित और अपरिवर्तनीय दोनों है (सभी एकल परिदर्शकों को समान मान दिखाई देता है, जो समय के साथ नहीं बदलता है)। | सामान्य तौर पर, पृथक पद्धतियों और एकल परिदर्शकों के लिए, आपेक्षिकीय द्रव्यमान संरक्षित होता है (प्रत्येक परिदर्शक इसे समय के साथ स्थिर देखता है), लेकिन यह अपरिवर्तनीय नहीं है (अर्थात, अलग-अलग परिदर्शक अलग-अलग मान देखते हैं)। निश्चर द्रव्यमान, हालांकि, संरक्षित और अपरिवर्तनीय दोनों ही है (सभी एकल परिदर्शकों को समान मान दिखाई देता है, जो समय के साथ नहीं बदलता है)। | ||
आपेक्षिकीय द्रव्यमान ऊर्जा से मेल खाता है, इसलिए ऊर्जा के संरक्षण का स्वचालित रूप से मतलब है कि किसी दिए गए परिदर्शक और जड़त्वीय फ्रेम के लिए आपेक्षिकीय द्रव्यमान संरक्षित है। हालाँकि, यह मात्रा, कण की कुल ऊर्जा की तरह, अपरिवर्तनीय नहीं है। इसका मतलब यह है कि, भले ही यह प्रतिक्रिया के | आपेक्षिकीय द्रव्यमान ऊर्जा से मेल खाता है, इसलिए ऊर्जा के संरक्षण का स्वचालित रूप से मतलब है कि किसी दिए गए परिदर्शक और जड़त्वीय फ्रेम के लिए आपेक्षिकीय द्रव्यमान संरक्षित है। हालाँकि, यह मात्रा, कण की कुल ऊर्जा की तरह, अपरिवर्तनीय नहीं है। इसका मतलब यह है कि, भले ही यह प्रतिक्रिया के बीच किसी भी परिदर्शक के लिए संरक्षित है, परिदर्शक के फ्रेम के साथ और अलग-अलग परिदर्शकों के लिए अलग-अलग फ्रेम में इसका पूर्ण मूल्य बदल जाएगा। | ||
इसके विपरीत, पद्धति और कणों के विराम द्रव्यमान और निश्चर द्रव्यमान | इसके विपरीत, पद्धति और कणों के विराम द्रव्यमान और निश्चर द्रव्यमान {{em|both}} संरक्षित {{em|and}} अपरिवर्तनीय भी हैं। उदाहरण के लिए: गैस के एक बंद पात्र (ऊर्जा के लिए भी बंद) में पद्धति विराम द्रव्यमान इस अर्थ में होता है कि इसे विराम मानदंड पर तौला जा सकता है, भले ही इसमें गतिमान घटक क्यू न हों। यह द्रव्यमान निश्चर द्रव्यमान है, जो पात्र की कुल सापेक्ष ऊर्जा (गैस की गतिज ऊर्जा सहित) के बराबर होता है, जब इसे संवेग फ्रेम के केंद्र में मापा जाता है। जैसा कि एकल कणों की स्थिति में होता है, गैस के ऐसे पात्र का परिकलित विराम द्रव्यमान गति में होने पर नहीं बदलता है, हालांकि इसका "आपेक्षिकीय द्रव्यमान" बदलता है। | ||
पात्र को एक बल के अधीन भी किया जा सकता है जो इसे एक समग्र वेग देता है, या फिर (समतुल्य रूप से) इसे जड़त्वीय फ्रेम से देखा जा सकता है जिसमें इसका समग्र वेग होता है (अर्थात, तकनीकी रूप से, एक फ्रेम जिसमें द्रव्यमान का केंद्र होता है) वेग है)। इस स्थिति में, इसका कुल आपेक्षिकीय द्रव्यमान और ऊर्जा बढ़ जाती है। हालांकि, ऐसी स्थिति में, हालांकि पात्र की कुल सापेक्ष ऊर्जा और कुल गति में वृद्धि होती है, इन ऊर्जा और गति में वृद्धि निश्चर द्रव्यमान परिभाषा में घट जाती है, जिससे चलते पात्र के निश्चर द्रव्यमान की गणना उसी मान के रूप में की जाएगी मानो इसे स्थिर मानदंड पर मापा गया हो। | |||
=== बंद (मतलब पूरी तरह से | === बंद (मतलब पूरी तरह से अश्लिष्ट) पद्धति === | ||
विशिष्ट आपेक्षिकता (ऊर्जा, द्रव्यमान और संवेग के लिए) में सभी संरक्षण | विशिष्ट आपेक्षिकता (ऊर्जा, द्रव्यमान और संवेग के लिए) में सभी संरक्षण नियम के लिए पृथक पद्धतियों की आवश्यकता होती है, जिसका अर्थ है कि ऐसी पद्धतियाँ जो पूरी तरह से पृथक हैं, जिनमें समय के साथ-साथ द्रव्यमान-ऊर्जा की अनुमति नहीं है। यदि एक पद्धति को अलग किया जाता है, तो पद्धति में कुल ऊर्जा और कुल गति दोनों किसी भी जड़त्वीय फ्रेम में किसी भी परिदर्शक के लिए समय के साथ संरक्षित होते हैं, हालांकि अलग-अलग जड़त्वीय फ्रेम में अलग-अलग परिदर्शकों के अनुसार उनके पूर्ण मूल्य अलग-अलग होंगे। पद्धति का निश्चर द्रव्यमान भी संरक्षित है, लेकिन यह विभिन्न परिदर्शकों के साथ नहीं बदलता है। यह एकल कणों के साथ परिचित स्थिति भी है: सभी परिदर्शक एक ही कण विराम द्रव्यमान (निश्चर द्रव्यमान की एक विशेष स्थिति) की गणना करते हैं, इससे कोई असमानता नहीं होती है कि वे कैसे चलते हैं (वे किस जड़त्वीय फ्रेम को चुनते हैं), लेकिन वही कण अलग-अलग परिदर्शक अलग-अलग कुल ऊर्जा और संवेग देखते हैं । | ||
निश्चर द्रव्यमान के संरक्षण के लिए भी पद्धति को संलग्न करने की आवश्यकता होती है ताकि कोई गर्मी और विकिरण (और इस प्रकार निश्चर द्रव्यमान) बच न सके। जैसा कि ऊपर दिए गए उदाहरण में, भौतिक रूप से बंद या बाध्य पद्धति को अपने द्रव्यमान को स्थिर रखने के लिए बाहरी ताकतों से पूरी तरह अलग होने की आवश्यकता नहीं है, क्योंकि बाध्य पद्धतियों के लिए ये केवल पद्धति या परिदर्शक के जड़त्वीय फ्रेम को बदलने के लिए कार्य करते हैं। हालांकि इस तरह की कार्रवाइयाँ बाध्य पद्धति की कुल ऊर्जा या गति को बदल सकती हैं, ये दो परिवर्तन रद्द हो जाते हैं, जिससे पद्धति के निश्चर द्रव्यमान में कोई परिवर्तन नहीं होता है। यह एकल कणों के समान ही परिणाम है: उनका परिकलित विराम द्रव्यमान भी स्थिर रहता है, चाहे वे कितनी भी तेजी से चलते हों, या कोई प्रेक्षक उन्हें कितनी तेजी से चलता हुआ देखता हो। | निश्चर द्रव्यमान के संरक्षण के लिए भी पद्धति को संलग्न करने की आवश्यकता होती है ताकि कोई गर्मी और विकिरण (और इस प्रकार निश्चर द्रव्यमान) बच न सके। जैसा कि ऊपर दिए गए उदाहरण में, भौतिक रूप से बंद या बाध्य पद्धति को अपने द्रव्यमान को स्थिर रखने के लिए बाहरी ताकतों से पूरी तरह अलग होने की आवश्यकता नहीं है, क्योंकि बाध्य पद्धतियों के लिए ये केवल पद्धति या परिदर्शक के जड़त्वीय फ्रेम को बदलने के लिए कार्य करते हैं। हालांकि इस तरह की कार्रवाइयाँ बाध्य पद्धति की कुल ऊर्जा या गति को बदल सकती हैं, ये दो परिवर्तन रद्द हो जाते हैं, जिससे पद्धति के निश्चर द्रव्यमान में कोई परिवर्तन नहीं होता है। यह एकल कणों के समान ही परिणाम है: उनका परिकलित विराम द्रव्यमान भी स्थिर रहता है, चाहे वे कितनी भी तेजी से चलते हों, या कोई प्रेक्षक उन्हें कितनी तेजी से चलता हुआ देखता हो। | ||
दूसरी ओर, उन पद्धतियों के लिए जो | दूसरी ओर, उन पद्धतियों के लिए जो अपरिबद्ध हैं, पद्धति के "बंद" होने को एक आदर्श सतह द्वारा लागू किया जा सकता है, क्योंकि समय के साथ परीक्षण-मात्रा में या बाहर कोई द्रव्यमान-ऊर्जा की अनुमति नहीं दी जा सकती है। यदि किसी बल को इस तरह के एक अपरिबद्ध पद्धति के केवल एक अंश पर कार्य करने की अनुमति दी जाती है, तो यह ऊर्जा को पद्धति में या बाहर जाने की अनुमति देने के बराबर है, और द्रव्यमान-ऊर्जा (कुल अलगाव) के बंद होने की स्थिति का उल्लंघन किया जाता है। इस स्थिति में, पद्धति के निश्चर द्रव्यमान का संरक्षण भी अब नहीं रहेगा। {{math|1=''E'' = ''mc''{{i sup|2}}}} के अनुसार जहाँ {{mvar|E}} ऊर्जा को हटा दिया जाता है, और {{mvar|m}} विराम द्रव्यमान में परिवर्तन है, ऊर्जा के संचलन से जुड़े द्रव्यमान के परिवर्तनों को दर्शाता है, न कि द्रव्यमान का ऊर्जा में "रूपांतरण"। | ||
=== पद्धति | === पद्धति निश्चर द्रव्यमान बनाम पद्धति के कुछ अंशों के अलग-अलग विराम द्रव्यमान === | ||
फिर से, विशिष्ट आपेक्षिकता में, पद्धति के विराम द्रव्यमान को भागों के विराम द्रव्यमानों के योग के बराबर होने की आवश्यकता नहीं है (एक ऐसी स्थिति जो रसायन विज्ञान में सकल द्रव्यमान-संरक्षण के अनुरूप होगी)। उदाहरण के लिए, एक विशाल कण फोटॉनों में क्षय हो सकता है, जिसमें व्यक्तिगत रूप से कोई द्रव्यमान नहीं होता है, लेकिन जो (एक पद्धति के रूप में) उस कण के निश्चर द्रव्यमान को संरक्षित करता है जिसने उन्हें उत्पन्न किया। साथ ही गैर-अंतःक्रियात्मक कणों (जैसे, फोटॉन, या एक आदर्श गैस) के एक | फिर से, विशिष्ट आपेक्षिकता में, पद्धति के विराम द्रव्यमान को भागों के विराम द्रव्यमानों के योग के बराबर होने की आवश्यकता नहीं है (एक ऐसी स्थिति जो रसायन विज्ञान में सकल द्रव्यमान-संरक्षण के अनुरूप होगी)। उदाहरण के लिए, एक विशाल कण फोटॉनों में क्षय हो सकता है, जिसमें व्यक्तिगत रूप से कोई द्रव्यमान नहीं होता है, लेकिन जो (एक पद्धति के रूप में) उस कण के निश्चर द्रव्यमान को संरक्षित करता है जिसने उन्हें उत्पन्न किया। साथ ही गैर-अंतःक्रियात्मक कणों (जैसे, फोटॉन, या एक आदर्श गैस) के एक डिब्बा में कणों के विराम द्रव्यमानों के योग की तुलना में एक बड़ा निश्चर द्रव्यमान होगा जो इसे बनाते हैं। ऐसा इसलिए है क्योंकि एक पद्धति में सभी कणों और क्षेत्रों की कुल ऊर्जा का योग होना चाहिए, और यह मात्रा, जैसा कि संवेग फ्रेम के केंद्र में देखा गया है, और {{math|''c''{{i sup|2}}}} द्वारा विभाजित, पद्धति का निश्चर द्रव्यमान है। | ||
विशिष्ट आपेक्षिकता में, द्रव्यमान को ऊर्जा में परिवर्तित नहीं किया जाता है, क्योंकि सभी प्रकार की ऊर्जा अभी भी अपने संबद्ध द्रव्यमान को बनाए रखती है। विशिष्ट आपेक्षिकता में न तो ऊर्जा और न ही निश्चर द्रव्यमान को नष्ट किया जा सकता है, और प्रत्येक बंद पद्धतियों में समय के साथ अलग-अलग संरक्षित होता है। इस प्रकार, एक पद्धति का निश्चर द्रव्यमान केवल इसलिए बदल सकता है क्योंकि निश्चर द्रव्यमान को प्रकाश या गर्मी के रूप में बचने की अनुमति है। इस प्रकार, जब प्रतिक्रियाएँ (चाहे रासायनिक या परमाणु) गर्मी और प्रकाश के रूप में ऊर्जा छोड़ती हैं, अगर गर्मी और प्रकाश को बाहर निकलने की अनुमति नहीं है (पद्धति बंद और पृथक है), तो ऊर्जा पद्धति के विराम द्रव्यमान में योगदान देना जारी रखेगी , और पद्धति द्रव्यमान नहीं बदलेगा। यदि ऊर्जा को पर्यावरण में छोड़ा जाता है तो ही द्रव्यमान नष्ट होगा; ऐसा इसलिए है क्योंकि संबंधित द्रव्यमान को पद्धति से बाहर जाने दिया गया है, जहां यह आसपास के द्रव्यमान में योगदान देता है।<ref name=taylor> | विशिष्ट आपेक्षिकता में, द्रव्यमान को ऊर्जा में परिवर्तित नहीं किया जाता है, क्योंकि सभी प्रकार की ऊर्जा अभी भी अपने संबद्ध द्रव्यमान को बनाए रखती है। विशिष्ट आपेक्षिकता में न तो ऊर्जा और न ही निश्चर द्रव्यमान को नष्ट किया जा सकता है, और प्रत्येक बंद पद्धतियों में यह समय के साथ अलग-अलग संरक्षित होता है। इस प्रकार, एक पद्धति का निश्चर द्रव्यमान केवल इसलिए बदल सकता है क्योंकि निश्चर द्रव्यमान को प्रकाश या गर्मी के रूप में बचने की अनुमति है। इस प्रकार, जब प्रतिक्रियाएँ (चाहे रासायनिक या परमाणु) गर्मी और प्रकाश के रूप में ऊर्जा छोड़ती हैं, अगर गर्मी और प्रकाश को बाहर निकलने की अनुमति नहीं है (पद्धति बंद और पृथक है), तो ऊर्जा पद्धति के विराम द्रव्यमान में योगदान देना जारी रखेगी, और पद्धति द्रव्यमान नहीं बदलेगा। यदि ऊर्जा को पर्यावरण में छोड़ा जाता है तो ही द्रव्यमान नष्ट होगा; ऐसा इसलिए है क्योंकि संबंधित द्रव्यमान को पद्धति से बाहर जाने दिया गया है, जहां यह आसपास के द्रव्यमान में योगदान देता है।<ref name=taylor> | ||
{{Citation | {{Citation | ||
|author1=E. F. Taylor |author2=J. A. Wheeler |date=1992 | |author1=E. F. Taylor |author2=J. A. Wheeler |date=1992 | ||
| Line 181: | Line 178: | ||
=== अनुप्रस्थ और अनुदैर्ध्य द्रव्यमान === | === अनुप्रस्थ और अनुदैर्ध्य द्रव्यमान === | ||
{{Further| | {{Further|विद्युत चुम्बकीय द्रव्यमान}} | ||
ऐसी अवधारणाएं जो आज आपेक्षिकीय द्रव्यमान कहलाती हैं | ऐसी अवधारणाएं जो आज "आपेक्षिकीय द्रव्यमान" कहलाती हैं, विशिष्ट आपेक्षिकता के आगमन से पहले ही विकसित हो चुकी थीं। उदाहरण के लिए, 1881 में J. J. थॉमसन द्वारा यह माना गया था कि एक आवेशित पिंड को एक अपरिवर्तित पिंड की तुलना में गति में स्थापित करना कठिन होता है, जिसे [[ ओलिवर हीविसाइड ]] (1889) और [[ जॉर्ज फ्रेडरिक चार्ल्स सियरल ]] (1897) द्वारा अधिक विस्तार से काम किया गया था। तो स्थिर वैद्युत ऊर्जा कुछ इस प्रकार के विद्युत चुम्बकीय द्रव्यमान के रूप में व्यवहार करती है <math display="inline">m_\text{em} = \frac{4}{3} E_\text{em}/c^2</math>, जो निकायों के सामान्य यांत्रिक द्रव्यमान को बढ़ा सकता है।<ref>{{Citation |author=J. J. Thomson |date=1881 |title=On the Electric and Magnetic Effects produced by the Motion of Electrified Bodies |journal=[[Philosophical Magazine]] |series=5 |volume=11 |issue=68 |pages=229–249 |doi=10.1080/14786448108627008 | title-link=s:On the Electric and Magnetic Effects produced by the Motion of Electrified Bodies }}</ref><ref>{{Citation |author=G. F. C. Searle |date=1897 |title=On the Steady Motion of an Electrified Ellipsoid |journal=[[Philosophical Magazine]] |series=5 |volume=44 |issue=269 |pages=329–341 |doi=10.1080/14786449708621072 |title-link=s:On the Steady Motion of an Electrified Ellipsoid }}</ref> | ||
गैर-शून्य विराम द्रव्यमान | फिर, थॉमसन और सियरल द्वारा यह बताया गया कि यह विद्युत चुम्बकीय द्रव्यमान भी वेग के साथ बढ़ता है। [[ लोरेंत्ज़ ईथर सिद्धांत | लोरेंत्ज़ ईथर सिद्धांत]] के ढांचे में [[ हेंड्रिक लोरेंत्ज़ | हेंड्रिक लोरेंत्ज़]] (1899, 1904) द्वारा इसे और विस्तृत किया गया था। उन्होंने द्रव्यमान को त्वरण और बल के अनुपात के रूप में परिभाषित किया, न कि संवेग के वेग के अनुपात के रूप में, इसलिए उन्हें द्रव्यमान <math>m_\text{L} = \gamma^3 m</math> गति की दिशा और द्रव्यमान के समानांतर <math>m_\text{T} = \gamma m</math> गति की दिशा के लंबवत (जहाँ <math display="inline">\gamma = 1/\sqrt{1 - v^2/c^2}</math> [[ लोरेंत्ज़ कारक | लोरेंत्ज़ कारक]] है, {{math|''v''}} ईथर और वस्तु के बीच सापेक्ष वेग है, और {{math|''c''}} प्रकाश की गति है)। केवल जब बल वेग के लम्बवत् होता है, लोरेंत्ज़ का द्रव्यमान उस द्रव्यमान के बराबर होता है जिसे अब आपेक्षिक द्रव्यमान कहा जाता है। [[ मैक्स अब्राहम | मैक्स अब्राहम]] (1902) को <math>m_\text{L}</math> अनुदैर्ध्य द्रव्यमान और <math>m_\text{T}</math> [[ अनुप्रस्थ द्रव्यमान | अनुप्रस्थ द्रव्यमान]] (हालांकि इब्राहीम ने लोरेंत्ज़ के आपेक्षिकता द्रव्यमान की तुलना में अधिक जटिल अभिव्यक्तियों का उपयोग किया)। इसलिए, लोरेंत्ज़ के सिद्धांत के अनुसार कोई भी पिंड प्रकाश की गति तक नहीं पहुँच सकता क्योंकि इस वेग पर द्रव्यमान असीम रूप से बड़ा हो जाता है।<ref>{{Citation |author=H. A. Lorentz |date=1899 |title=Simplified Theory of Electrical and Optical Phenomena in Moving Systems |journal=[[Proceedings of the Royal Netherlands Academy of Arts and Sciences]] |volume=1 |pages=427–442 |title-link=s:Simplified Theory of Electrical and Optical Phenomena in Moving Systems }}</ref><ref>{{Citation |author=H. A. Lorentz |date=1904 |title=Electromagnetic phenomena in a system moving with any velocity smaller than that of light |journal=[[Proceedings of the Royal Netherlands Academy of Arts and Sciences]] |volume=6 |pages=809–831 |title-link=s:Electromagnetic phenomena }}</ref><ref>{{Citation |author=M. Abraham |date=1903 |title=Prinzipien der Dynamik des Elektrons |journal=[[Annalen der Physik]] |volume=315 |issue=1 |pages=105–179 |doi=10.1002/andp.19023150105 |bibcode = 1902AnP...315..105A |url=https://de.wikisource.org/wiki/Prinzipien_der_Dynamik_des_Elektrons_(1903)}}</ref> | ||
[[ अल्बर्ट आइंस्टीन |अल्बर्ट आइंस्टीन]] ने भी शुरू में अपने 1905 के वैद्युतगतिकी पेपर में अनुदैर्ध्य और अनुप्रस्थ द्रव्यमान की अवधारणाओं का उपयोग किया था (लोरेंत्ज़ के समान, लेकिन एक अलग <math>m_\text{T}</math> दुर्भाग्यपूर्ण बल परिभाषा के साथ, जिसे बाद में 1906 में अन्य पेपर में सुधारा गया) <ref>{{Citation |author=A. Einstein |date=1905 |title=Zur Elektrodynamik bewegter Körper |journal=[[Annalen der Physik]] |volume=322 |issue=10 | pages=891–921 |url=http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1905_17_891-921.pdf |doi=10.1002/andp.19053221004 |bibcode = 1905AnP...322..891E |language=de|doi-access=free }} ([http://www.fourmilab.ch/etexts/einstein/specrel/ English translation])</ref><ref>{{Citation |author=A. Einstein |date=1906 |title=Über eine Methode zur Bestimmung des Verhältnisses der transversalen und longitudinalen Masse des Elektrons |url=http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1906_21_583-586.pdf |journal=[[Annalen der Physik]] |volume =21 | pages =583–586 |doi=10.1002/andp.19063261310 |bibcode = 1906AnP...326..583E |issue=13 |language=de}}</ref> हालांकि, बाद में उन्होंने वेग पर निर्भर द्रव्यमान अवधारणाओं को छोड़ दिया। | |||
गैर-शून्य विराम द्रव्यमान <math>m</math> के साथ एक कण के लिए बल और त्वरण से संबंधित सटीक आपेक्षिकता अभिव्यक्ति (जो लोरेंत्ज़ के समतुल्य है) वेग v के साथ <math>x</math> दिशा में आगे बढ़ रहा है और संबंधित लोरेंत्ज़ कारक <math>\gamma</math> है | |||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
f_\text{x} &= m \gamma^3 a_\text{x} &= m_\text{L} a_\text{x}, \\ | f_\text{x} &= m \gamma^3 a_\text{x} &= m_\text{L} a_\text{x}, \\ | ||
| Line 197: | Line 197: | ||
विशिष्ट आपेक्षिकता में, शून्येतर विराम द्रव्यमान वाली वस्तु प्रकाश की गति से यात्रा नहीं कर सकती है। जैसे-जैसे वस्तु प्रकाश की गति के करीब आती है, वस्तु की ऊर्जा और गति बिना किसी सीमा के बढ़ती जाती है। | विशिष्ट आपेक्षिकता में, शून्येतर विराम द्रव्यमान वाली वस्तु प्रकाश की गति से यात्रा नहीं कर सकती है। जैसे-जैसे वस्तु प्रकाश की गति के करीब आती है, वस्तु की ऊर्जा और गति बिना किसी सीमा के बढ़ती जाती है। | ||
1905 के बाद के पहले वर्षों में, लोरेंत्ज़ और आइंस्टीन के बाद, अनुदैर्ध्य और अनुप्रस्थ द्रव्यमान शब्द अभी भी उपयोग में थे। हालाँकि, उन अभिव्यक्तियों को आपेक्षिकीय द्रव्यमान की अवधारणा द्वारा प्रतिस्थापित किया गया था, एक अभिव्यक्ति जिसे पहली बार 1909 में गिल्बर्ट | 1905 के बाद के पहले वर्षों में, लोरेंत्ज़ और आइंस्टीन के बाद, अनुदैर्ध्य और अनुप्रस्थ द्रव्यमान शब्द अभी भी उपयोग में थे। हालाँकि, उन अभिव्यक्तियों को आपेक्षिकीय द्रव्यमान की अवधारणा द्वारा प्रतिस्थापित किया गया था, एक अभिव्यक्ति जिसे पहली बार 1909 में गिल्बर्ट N. लुईस और रिचर्ड C. टोलमैन द्वारा परिभाषित किया गया था।<ref>{{Citation|author1=Lewis, Gilbert N. |author2=Tolman, Richard C. |name-list-style=amp |date=1909|title=The Principle of Relativity, and Non-Newtonian Mechanics |journal=Proceedings of the American Academy of Arts and Sciences|volume=44 |pages=709–726|doi=10.2307/20022495 |issue=25 |title-link=s:The Principle of Relativity, and Non-Newtonian Mechanics |jstor=20022495 }}</ref> उन्होंने किसी पिंड की कुल ऊर्जा और द्रव्यमान को इस रूप में परिभाषित किया | ||
<math display="block">m_\text{rel} = \frac{E}{c^2},</math> | <math display="block">m_\text{rel} = \frac{E}{c^2},</math> | ||
और एक | और एक पिंड स्थिर है | ||
<math display="block">m_0 = \frac{E_0}{c^2},</math> | <math display="block">m_0 = \frac{E_0}{c^2},</math> | ||
अनुपात के साथ | अनुपात के साथ | ||
<math display="block">\frac{m_\text{rel}}{m_0} = \gamma.</math> | <math display="block">\frac{m_\text{rel}}{m_0} = \gamma.</math> | ||
1912 में टॉल्मन ने इस अवधारणा पर और विस्तार किया, और कहा: अभिव्यक्ति | 1912 में टॉल्मन ने इस अवधारणा पर और विस्तार किया, और कहा: अभिव्यक्ति m<sub>0</sub>(1 - v{{i sup|2}}/c{{i sup|2}})<sup>−1/2</sup> गतिमान पिंड के द्रव्यमान के लिए सबसे उपयुक्त है।<ref name="RT">{{citation |author=R. Tolman |date=1911 |title=Note on the Derivation from the Principle of Relativity of the Fifth Fundamental Equation of the Maxwell–Lorentz Theory |journal=Philosophical Magazine |volume=21|issue=123 | pages=296–301 |doi=10.1080/14786440308637034|title-link=s:Derivation of Fifth Fundamental Equation }}</ref><ref>{{citation |author=R. Tolman |date=1911 |title=Non-Newtonian Mechanics :— The Direction of Force and Acceleration.|journal=Philosophical Magazine |volume=22|issue=129 |pages=458–463 |doi=10.1080/14786440908637142 |title-link=s:The Direction of Force and Acceleration }}</ref><ref>{{citation |author=R. Tolman |date=1912 |title=Non-Newtonian Mechanics. The Mass of a Moving Body.|journal=Philosophical Magazine |volume=23|issue=135 | pages=375–380 |doi=10.1080/14786440308637231 |title-link=s:The Mass of a Moving Body }}</ref> | ||
1934 में, टॉल्मन ने तर्क दिया कि आपेक्षिकीय द्रव्यमान सूत्र <math>m_\text{rel} = E / c^2 </math> प्रकाश की गति से चलने वाले कणों सहित सभी कणों के लिए सूत्र | |||
1934 में, टॉल्मन ने तर्क दिया कि आपेक्षिकीय द्रव्यमान सूत्र <math>m_\text{rel} = E / c^2 </math> प्रकाश की गति से चलने वाले कणों सहित सभी कणों के लिए सूत्र लागू होता है, जबकि सूत्र <math>m_\text{rel} = \gamma m_0 </math> केवल एक धीमी-से-प्रकाश कण पर लागू होता है (एक गैर-शून्य विराम द्रव्यमान वाला कण)। टॉल्मन ने इस संबंध पर टिप्पणी की कि, "इसके अलावा, हमारे पास निश्चित रूप से गतिमान अतिसूक्ष्म परमाणुों की स्थिति में अभिव्यक्ति का प्रायोगिक सत्यापन है ... इसलिए हमें गतिमान कण के द्रव्यमान के लिए अभिव्यक्ति को सामान्य रूप से सही मानने में कोई असमंजस नहीं होगी।<ref name="RT34"> | |||
{{Citation | {{Citation | ||
|author=R.C. Tolman | |author=R.C. Tolman | ||
| Line 214: | Line 215: | ||
|lccn=34032023 | |lccn=34032023 | ||
}} Reissued (1987), New York: [[Dover]], {{ISBN|0-486-65383-8}}.</ref> | }} Reissued (1987), New York: [[Dover]], {{ISBN|0-486-65383-8}}.</ref> | ||
जब सापेक्ष वेग शून्य होता है, <math>\gamma</math> बस 1 के बराबर है, और आपेक्षिक द्रव्यमान को विराम द्रव्यमान तक कम कर दिया जाता है जैसा कि नीचे दिए गए अगले दो समीकरणों में देखा जा सकता है। जैसे-जैसे वेग प्रकाश की गति c की ओर बढ़ता है, दाहिनी ओर का | |||
जब सापेक्ष वेग शून्य होता है, <math>\gamma</math> बस 1 के बराबर है, और आपेक्षिक द्रव्यमान को विराम द्रव्यमान तक कम कर दिया जाता है जैसा कि नीचे दिए गए अगले दो समीकरणों में देखा जा सकता है। जैसे-जैसे वेग प्रकाश की गति c की ओर बढ़ता है, दाहिनी ओर का हर शून्य की ओर बढ़ता है, और परिणामस्वरूप <math>\gamma</math> अनंत तक पहुँचता है। जबकि न्यूटन के द्वितीय नियम के रूप में वैध रहता है | |||
<math display="block">\mathbf{f} = \frac{d(m_\text{rel}\mathbf{v})}{dt}, </math> | <math display="block">\mathbf{f} = \frac{d(m_\text{rel}\mathbf{v})}{dt}, </math> | ||
व्युत्पन्न रूप <math>\mathbf{f} = m_\text{rel} \mathbf{a}</math> मान्य नहीं है क्योंकि <math>m_\text{rel}</math> में <math>{d(m_\text{rel}\mathbf{v})}</math> समान्यतः स्थिर नहीं होता है<ref>{{cite web |url=http://math.ucr.edu/home/baez/physics/Relativity/SR/mass.html | title=सापेक्षतावादी द्रव्यमान क्या है?|author1=Philip Gibbs| author2=Jim Carr|access-date=2011-09-27}}</ref> (अनुप्रस्थ और अनुदैर्ध्य द्रव्यमान पर ऊपर अनुभाग देखें)। | व्युत्पन्न रूप <math>\mathbf{f} = m_\text{rel} \mathbf{a}</math> मान्य नहीं है क्योंकि <math>m_\text{rel}</math> में <math>{d(m_\text{rel}\mathbf{v})}</math> समान्यतः स्थिर नहीं होता है<ref>{{cite web |url=http://math.ucr.edu/home/baez/physics/Relativity/SR/mass.html | title=सापेक्षतावादी द्रव्यमान क्या है?|author1=Philip Gibbs| author2=Jim Carr|access-date=2011-09-27}}</ref> (अनुप्रस्थ और अनुदैर्ध्य द्रव्यमान पर ऊपर अनुभाग देखें)। | ||
भले ही आइंस्टीन ने | भले ही आइंस्टीन ने शुरु में अपने पहले पेपर में "अनुदैर्ध्य" और "अनुप्रस्थ" द्रव्यमान को दो पेपरों में प्रयोग किया था <math>E = mc^2</math> (1905) में अपने पहले पेपर में उन्होंने {{mvar|m}} को अभिक्रियित किया जिसे अब विराम द्रव्यमान कहा जाएगा।<ref name="inertia" />आइंस्टीन ने आपेक्षिकीय द्रव्यमान के लिए कभी कोई समीकरण नहीं बनाया, और बाद के वर्षों में उन्होंने इस विचार के प्रति अपनी नापसंदगी व्यक्त की:<ref>{{cite journal |author=Eugene Hecht |date=19 August 2009 |title=आइंस्टीन ने कभी सापेक्षतावादी द्रव्यमान का अनुमोदन नहीं किया|journal=The Physics Teacher |volume=47 |issue=6 |pages=336–341 |doi=10.1119/1.3204111 |bibcode=2009PhTea..47..336H |citeseerx=10.1.1.205.5072 }}</ref> | ||
{{Quotation| | |||
{{Quotation|गतिमान पिंड के द्रव्यमान <math display="inline">M = m/\sqrt{1 - v^2/c^2}</math> की अवधारणा को पेश करना अच्छा नहीं है, जिसके लिए कोई स्पष्ट परिभाषा नहीं दी जा सकती दिया जाए। 'विश्राम द्रव्यमान' 'm'' के अतिरिक्त कोई अन्य द्रव्यमान अवधारणा प्रस्तुत करना ठीक नहीं है। 'm'' प्रस्तुत करने के अतिरिक्त गतिमान शरीर की गति और ऊर्जा के लिए अभिव्यक्ति का उल्लेख करना अच्छा है।|[[लिंकन बार्नेट]] को अल्बर्ट आइंस्टीन का पत्र, 19 जून 1948}} | |||
=== लोकप्रिय विज्ञान और पाठ्यपुस्तकें === | === लोकप्रिय विज्ञान और पाठ्यपुस्तकें === | ||
लोकप्रिय विज्ञान लेखन और हाई स्कूल और स्नातक पाठ्यपुस्तकों में आपेक्षिकीय द्रव्यमान की अवधारणा का व्यापक रूप से उपयोग किया जाता है। ओकुन और | लोकप्रिय विज्ञान लेखन और हाई स्कूल और स्नातक पाठ्यपुस्तकों में आपेक्षिकीय द्रव्यमान की अवधारणा का व्यापक रूप से उपयोग किया जाता है। ओकुन और A. B. एरोन्स जैसे लेखकों ने इसके विपरीत तर्क दिया है कि यह पुरातन और भ्रमित करने वाला है, और आधुनिक आपेक्षिकीय सिद्धांत के अनुरूप नहीं है।<ref name=okun /><ref name=Arons> | ||
{{citation |author=A.B. Arons |date=1990 |title=A Guide to Introductory Physics Teaching |page=263}} | {{citation |author=A.B. Arons |date=1990 |title=A Guide to Introductory Physics Teaching |page=263}} | ||
Also in {{citation |date=2001 |title=Teaching Introductory Physics |page=308}}</ref> | Also in {{citation |date=2001 |title=Teaching Introductory Physics |page=308}}</ref> | ||
एरोन्स ने लिखा:<ref name=Arons/><blockquote>कई वर्षों तक आपेक्षिकीय द्रव्यमान की व्युत्पत्ति के माध्यम से गतिशीलता की चर्चा में प्रवेश करना पारंपरिक था, जो कि द्रव्यमान-वेग संबंध है, और यह | एरोन्स ने लिखा:<ref name=Arons/><blockquote>कई वर्षों तक आपेक्षिकीय द्रव्यमान की व्युत्पत्ति के माध्यम से गतिशीलता की चर्चा में प्रवेश करना पारंपरिक था, जो कि द्रव्यमान-वेग संबंध है, और यह कदाचित् अभी भी पाठ्यपुस्तकों में प्रमुख विधा है। हाल ही में, हालांकि, यह तेजी से मान्यता प्राप्त हुई है कि आपेक्षिकीय द्रव्यमान एक परेशानी और संदिग्ध अवधारणा है। [देखें, उदाहरण के लिए, ओकुन (1989)।<ref name=okun />]... सापेक्षतावादी गतिशीलता के लिए ध्वनि और कठोर दृष्टिकोण गति के लिए उस अभिव्यक्ति के प्रत्यक्ष विकास के माध्यम से है जो सभी फ्रेमों में गति के संरक्षण को सुनिश्चित करता है: <math display="block">p = {m_0 v \over {\sqrt{1 - \frac{v^2}{c^2}}}} </math> आपेक्षिकीय द्रव्यमान के विपरीत।</blockquote> | ||
C. एल्डर सापेक्षता में द्रव्यमान पर समान रूप से बहिष्कृत करने वाला रूप अपनाते है। उक्त विषय वस्तु पर लिखते हुए, वे कहते हैं कि "विशिष्ट आपेक्षिकता के सिद्धांत में इसका परिचय एक ऐतिहासिक दुर्घटना के रूप में हुआ था", {{math|1=''E'' = ''mc''<sup>2</sup>}} जो व्यापक ज्ञान की ओर ध्यान दे रहा था और कैसे समीकरण की जनता की व्याख्या ने बड़े मानदंड पर इसे सूचित किया है कि उच्च शिक्षा में इसे कैसे पढ़ाया जाए।<ref>{{Cite journal| last=Adler | first=Carl|date=September 30, 1986| title=क्या द्रव्यमान वास्तव में वेग पर निर्भर करता है, पिताजी?|url=https://sites.fas.harvard.edu/~phys191r/References/b5/Adler1987.pdf |journal=American Journal of Physics | volume=55| issue=8|pages=739–743|via=HUIT Sites Hosting|doi=10.1119/1.15314| bibcode=1987AmJPh..55..739A}}</ref> इसके विपरीत वह मानते है कि स्थिरता और आपेक्षिकीय द्रव्यमान के बीच का अंतर स्पष्ट रूप से सिखाया जाना चाहिए, ताकि छात्रों को पता चल सके कि जड़त्व की अधिकांश चर्चाओं में द्रव्यमान को अपरिवर्तनीय क्यों माना जाना चाहिए। | |||
कई समकालीन लेखक जैसे टेलर और व्हीलर आपेक्षिकीय द्रव्यमान की अवधारणा का पूरी तरह से उपयोग करने से बचते हैं: | कई समकालीन लेखक जैसे टेलर और व्हीलर आपेक्षिकीय द्रव्यमान की अवधारणा का पूरी तरह से उपयोग करने से बचते हैं: | ||
{{quote| | {{quote|"सापेक्षतावादी द्रव्यमान" की अवधारणा गलतफहमी के अधीन है। इसलिए हम इसका उपयोग नहीं करते हैं। सबसे पहले, यह नाम द्रव्यमान - चतुरंग वेग के परिमाण से संबंधित - को एक बहुत अलग अवधारणा पर लागू करता है, एक का समय घटक चतुरंग वेग । दूसरा, यह किसी वस्तु की ऊर्जा में वृद्धि को वेग या संवेग के साथ वस्तु की आंतरिक संरचना में कुछ बदलाव के साथ जुड़ा हुआ प्रतीत करता है। वास्तव में, वेग के साथ ऊर्जा की वृद्धि वस्तु में नहीं बल्कि ज्यामितीय में उत्पन्न होती है अंतरिक्ष समय के ही गुण।}} | ||
जबकि अंतरिक्ष-समय में मिन्कोवस्की अंतरिक्ष की असीमित ज्यामिति है, वेग-अंतरिक्ष | |||
जबकि अंतरिक्ष-समय में मिन्कोवस्की अंतरिक्ष की असीमित ज्यामिति है, वेग-अंतरिक्ष {{math|''c''}} इससे घिरा होता है और बेल्ट्रामी-क्लेन प्रतिरूप की ज्यामिति होती है जहां सापेक्षवादी द्रव्यमान [[ यूक्लिडियन ज्यामिति ]] के बेरिकेंट्रिक निर्देशांक में न्यूटोनियन द्रव्यमान के अनुरूप भूमिका निभाता है।<ref>{{Cite book |last=Ungar |first=Abraham A. |url=https://www.worldcat.org/oclc/663096629 |title=अतिशयोक्तिपूर्ण त्रिभुज केंद्र: विशेष सापेक्षतावादी दृष्टिकोण|date=2010 |publisher=Springer |isbn=978-90-481-8636-5 |location=Dordrecht |oclc=663096629}}</ref> अतिशयोक्तिपूर्ण ज्यामिति के वेग का संबंध 3-वेग-निर्भर आपेक्षिकीय द्रव्यमान को चतुरंग वेग मिन्कोव्स्की औपचारिकता से संबंधित होने में सक्षम बनाता है।<ref>[https://projecteuclid.org/journals/communications-in-mathematical-analysis/volume-10/issue-1/When-Relativistic-Mass-Meets-Hyperbolic-Geometry/cma/1305810734.full When Relativistic Mass Meets Hyperbolic Geometry], Abraham A. Ungar, Commun. Math. Anal. Volume 10, Number 1 (2011), 30–56.</ref> | |||
| Line 259: | Line 264: | ||
[[श्रेणी:द्रव्यमान]] | [[श्रेणी:द्रव्यमान]] | ||
[[Category:CS1 Deutsch-language sources (de)]] | |||
[[Category: | [[Category:CS1 English-language sources (en)]] | ||
[[Category:Created On 29/12/2022]] | [[Category:Collapse templates|Mass In Special Relativity]] | ||
[[Category:Created On 29/12/2022|Mass In Special Relativity]] | |||
[[Category:Lua-based templates|Mass In Special Relativity]] | |||
[[Category:Machine Translated Page|Mass In Special Relativity]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Mass In Special Relativity]] | |||
[[Category:Pages with empty portal template|Mass In Special Relativity]] | |||
[[Category:Pages with script errors|Mass In Special Relativity]] | |||
[[Category:Portal templates with redlinked portals|Mass In Special Relativity]] | |||
[[Category:Sidebars with styles needing conversion|Mass In Special Relativity]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Mass In Special Relativity]] | |||
[[Category:Templates generating microformats|Mass In Special Relativity]] | |||
[[Category:Templates that add a tracking category|Mass In Special Relativity]] | |||
[[Category:Templates that are not mobile friendly|Mass In Special Relativity]] | |||
[[Category:Templates that generate short descriptions|Mass In Special Relativity]] | |||
[[Category:Templates using TemplateData|Mass In Special Relativity]] | |||
[[Category:Wikipedia metatemplates|Mass In Special Relativity]] | |||
Latest revision as of 16:53, 3 November 2023
विशिष्ट आपेक्षिकता में द्रव्यमान शब्द के दो अर्थ हैं: निश्चर द्रव्यमान (जिसे विराम द्रव्यमान भी कहा जाता है) एक निश्चर मात्रा है जो सभी निर्देश फ्रेमों में सभी परिदर्शक ( विशिष्ट आपेक्षिकता ) के लिए समान है, जबकि 'आपेक्षिकीय द्रव्यमान' परिदर्शक के वेग पर निर्भर है। द्रव्यमान-ऊर्जा तुल्यता की अवधारणा के अनुसार, निश्चर द्रव्यमान विराम ऊर्जा के बराबर है, जबकि आपेक्षिकीय द्रव्यमान आपेक्षिकीय ऊर्जा (जिसे कुल ऊर्जा भी कहा जाता है) के बराबर है।
आपेक्षिकीय द्रव्यमान शब्द का उपयोग कण और परमाणु भौतिकी में नहीं किया जाता है और शरीर की सापेक्ष ऊर्जा के संदर्भ में, विशिष्ट आपेक्षिकता पर लेखकों द्वारा प्रायः इससे बचा जाता है।[1] इसके विपरीत, निश्चर द्रव्यमान को समान्यतः विराम ऊर्जा से अधिक पसंद किया जाता है। मापने योग्य जड़त्व और निर्देश में दिए गए फ्रेम में किसी पिंड द्वारा अंतरिक्ष समय का आवलन उसके आपेक्षिकीय द्रव्यमान से निर्धारित होता है, न कि केवल इसके निश्चर द्रव्यमान से। उदाहरण के लिए, फोटॉनों में शून्य विराम द्रव्यमान होता है, लेकिन उनमें उपस्थित किसी भी पद्धति की जड़त्व (और गुरुत्वाकर्षण क्षेत्र में वजन) में योगदान होता है।
सामान्य आपेक्षिकीय में द्रव्यमान में अवधारणा सामान्यीकृत है।
विराम द्रव्यमान
विशिष्ट आपेक्षिकता में शब्द द्रव्यमान समान्यतः वस्तु के विराम द्रव्यमान को संदर्भित करता है, जो न्यूटनी द्रव्यमान है जिसे वस्तु के साथ चलने वाले परिदर्शक द्वारा मापा गया। निश्चर द्रव्यमान एकल कणों के विराम द्रव्यमान का दूसरा नाम है। अधिक सामान्य निश्चर द्रव्यमान (अधिक जटिल सूत्र के साथ गणना) " पद्धति" के "विराम द्रव्यमान" से शिथिल रूप से मेल खाती है। इस प्रकार, निश्चर द्रव्यमान द्रव्यमान की एक प्राकृतिक इकाई है जिसका उपयोग उन पद्धतियों के लिए किया जाता है जिन्हें उनके संवेग केंद्र (COM फ्रेम) के केंद्र से देखा जा रहा है, जैसे कि जब किसी बंद पद्धति (उदाहरण के लिए गर्म गैस की एक बोतल) का वजन किया जाता है, जिसके लिए आवश्यक है कि माप को संवेग फ्रेम के केंद्र में लिया जाए जहां पद्धति में कोई नेट संवेग नहीं है। ऐसी परिस्थितियों में निश्चर द्रव्यमान आपेक्षिकीय द्रव्यमान (नीचे चर्चा की गई) के बराबर है, जो कि पद्धति की कुल ऊर्जा है जिसे C2 (प्रकाश की गति का वर्ग) से विभाजित किया जाता है।
हालांकि, निश्चर द्रव्यमान की अवधारणा को कणों की बाध्य पद्धतियों की आवश्यकता नहीं होती है। जैसे, यह उच्च गति सापेक्ष गति में अपरिबद्ध कणों की पद्धतियों पर भी लागू किया जा सकता है। इस वजह से, यह प्रायः कण भौतिकी में उन पद्धतियों के लिए नियोजित होता है जिनमें व्यापक रूप से अलग-अलग उच्च-ऊर्जा कण होते हैं। यदि ऐसी प्रणालियाँ एक कण से प्राप्त की गई थीं, तो ऐसी पद्धतियों के निश्चर द्रव्यमान की गणना, जो कभी न बदलने वाली मात्रा है, मूल कण का विराम द्रव्यमान प्रदान करेगी (क्योंकि यह समय के साथ संरक्षित है)।
गणना में प्रायः यह सुविधाजनक होता है कि किसी पद्धति का निश्चर द्रव्यमान COM फ्रेम में पद्धति की कुल ऊर्जा (c2 द्वारा विभाजित) होता है (जहां, परिभाषा के अनुसार, पद्धति का संवेग शून्य है)। हालाँकि, चूंकि किसी भी पद्धति का निश्चर द्रव्यमान भी सभी जड़त्वीय फ़्रेमों में समान मात्रा में होता है, यह प्रायः COM फ़्रेम में कुल ऊर्जा से गणना की जाने वाली मात्रा होती है, फिर अन्य फ़्रेमों में पद्धति ऊर्जा और संवेग की गणना करने के लिए उपयोग किया जाता है जहां संवेग शून्य नहीं होते हैं, और पद्धति की कुल ऊर्जा निश्चित रूप से COM फ्रेम की तुलना में एक अलग मात्रा होगी। जैसा कि ऊर्जा और संवेग की स्थिति में होता है, एक पद्धति के निश्चर द्रव्यमान को नष्ट या परिवर्तित नहीं किया जा सकता, और इस प्रकार इसे संरक्षित किया जाता है, जब तक कि पद्धति सभी प्रभावों के लिए बंद हो जाती है। (तकनीकी शब्द पृथक पद्धति है जिसका अर्थ है कि पद्धति के चारों ओर एक आदर्श सीमा रेखा खींची गई है, और इसके पार कोई द्रव्यमान/ऊर्जा की अनुमति नहीं है।)
आपेक्षिकीय द्रव्यमान
आपेक्षिकीय द्रव्यमान एक शरीर या पद्धति में ऊर्जा की कुल मात्रा है ( c2 द्वारा विभाजित)। इस प्रकार सूत्र में द्रव्यमान
सापेक्षिक द्रव्यमान भी वेग और संवेग के बीच आनुपातिकता कारक है,
न्यूटनी यांत्रिकी से किसी वस्तु के गुण के रूप में द्रव्यमान की धारणा का आपेक्षिकता में अवधारणा के लिए एक सटीक संबंध नहीं होता है।[9] परमाणु और कण भौतिकी में आपेक्षिकता द्रव्यमान का संदर्भ नहीं दिया गया है, और 2005 में परिचयात्मक पाठ्यपुस्तकों के एक सर्वेक्षण से पता चला है कि 24 में से केवल 5 ग्रंथों ने अवधारणा का उपयोग किया है, हालांकि यह अभी भी लोकप्रियकरण में प्रचलित है
यदि एक स्थिर डिब्बे में कई कण होते हैं, तो इसका वजन उसके विराम फ्रेम में अधिक होता है, कण तेजी से आगे बढ़ते रहते हैं। डिब्बे में कोई भी ऊर्जा (कणों की गतिज ऊर्जा सहित) द्रव्यमान में जुड़ जाती है, जिससे कणों की सापेक्ष गति डिब्बे के द्रव्यमान में योगदान करती है। लेकिन अगर डिब्बा खुद चल रहा है (इसका द्रव्यमान का केंद्र चल रहा है), तो यह सवाल बना रहता है कि क्या समग्र गति की गतिज ऊर्जा को पद्धति के द्रव्यमान में समिलित किया जाना चाहिए। निश्चर द्रव्यमान की गणना समग्र रूप से पद्धति की गतिज ऊर्जा को छोड़कर की जाती है (डिब्बे के एकल वेग का उपयोग करके गणना की जाती है, जिसे डिब्बे के द्रव्यमान के केंद्र के वेग का कहना है), जबकि आपेक्षिकीय द्रव्यमान की गणना निश्चर द्रव्यमान और पद्धति की गतिज ऊर्जा सहित की जाती है जिसकी गणना द्रव्यमान के केंद्र के वेग से होती है।
आपेक्षिक बनाम विराम द्रव्यमान
आपेक्षिक द्रव्यमान और विराम द्रव्यमान दोनों भौतिकी में पारंपरिक अवधारणाएं हैं, लेकिन आपेक्षिकीय द्रव्यमान कुल ऊर्जा से मेल खाता है। आपेक्षिकीय द्रव्यमान पद्धति का द्रव्यमान है क्योंकि इसे एक मानदंड पर मापा जाएगा, लेकिन कुछ स्थितियों में (जैसे कि ऊपर का डिब्बा)। उदाहरण के लिए, यदि साइक्लोट्रॉन में एक अतिसूक्ष्म परमाणु सापेक्ष वेग के साथ घेरे में घूम रहा है, तो साइक्लोट्रॉन + अतिसूक्ष्म परमाणु पद्धति का द्रव्यमान अतिसूक्ष्म परमाणु के सापेक्षिक द्रव्यमान से बढ़ जाता है, न कि अतिसूक्ष्म परमाणु के विराम द्रव्यमान से। लेकिन यह किसी भी बंद पद्धति के बारे में भी सच है, जैसे अतिसूक्ष्म परमाणु-और-डिब्बा, अगर अतिसूक्ष्म परमाणु डिब्बे के अंदर उच्च गति से उछलता है। यह केवल पद्धति में कुल संवेग की कमी है (पद्धति संवेग शून्य है) जो अतिसूक्ष्म परमाणु की गतिज ऊर्जा को तौलने की अनुमति देता है। यदि अतिसूक्ष्म परमाणु को रोका जाता है और तौला जाता है, या मानदंड को किसी तरह उसके बाद भेजा जाता है, तो यह मानदंड के संबंध में आगे नहीं बढ़ेगा, और फिर से आपेक्षिकीय और विराम द्रव्यमान एकल अतिसूक्ष्म परमाणु के लिए समान होंगे (और छोटे होंगे)। सामान्य तौर पर, सापेक्षतावादी और विराम द्रव्यमान केवल उन पद्धतियों में समान होते हैं जिनमें कोई नेट संवेग नहीं होता है और द्रव्यमान का पद्धति केंद्र स्थिर होता है; अन्यथा वे भिन्न हो सकते हैं।
निश्चर द्रव्यमान एक निर्देश फ्रेम में कुल ऊर्जा के मूल्य के समानुपाती होता है, वह फ्रेम जहां संपूर्ण वस्तु स्थिर होती है (जैसा कि द्रव्यमान के केंद्र के संदर्भ में नीचे परिभाषित किया गया है)। यही कारण है कि निश्चर द्रव्यमान एकल कणों के लिए विराम द्रव्यमान के समान होता है। हालांकि, निश्चर द्रव्यमान भी मापा द्रव्यमान का प्रतिनिधित्व करता है जब द्रव्यमान का केंद्र कई कणों की पद्धतियों के लिए स्थिर होता है। यह फ्रेम जहां ऐसा होता है उसे संवेग फ्रेम का केंद्र भी कहा जाता है, और इसे जड़त्वीय फ्रेम के रूप में परिभाषित किया जाता है जिसमें वस्तु के द्रव्यमान का केंद्र स्थिर होता है (यह कहने का दूसरा तरीका यह है कि यह वह फ्रेम है जिसमें संवेग पद्धति के पुर्जों का योग शून्य हो जाता है)। यौगिक वस्तुओं के लिए (कई छोटी वस्तुओं से बना है, जिनमें से कुछ गतिमान हो सकती हैं) और अपरिबद्ध वस्तुओं के सेट (जिनमें से कुछ गतिमान भी हो सकते हैं), केवल पद्धति के द्रव्यमान के केंद्र को वस्तु के लिए आराम की आवश्यकता होती है आपेक्षिक द्रव्यमान अपने विराम द्रव्यमान के बराबर होना चाहिए।
एक तथाकथित द्रव्यमान रहित कण (जैसे एक फोटॉन, या एक सैद्धांतिक गुरुत्वाकर्षण) निर्देश के प्रत्येक फ्रेम में प्रकाश की गति से चलता है। इस स्थिति में कोई परिवर्तन नहीं होता है जो कण को आराम में लाएगा। ऐसे कणों की कुल ऊर्जा फ्रेम में छोटी और छोटी होती जाती है जो एक ही दिशा में तेजी से और तेजी से आगे बढ़ते हैं। जैसे, उनके पास कोई विराम द्रव्यमान नहीं है, क्योंकि उन्हें कभी भी उस फ्रेम में नहीं मापा जा सकता है जहां वे स्थिर हैं। विराम द्रव्यमान न होने का यह गुण इन कणों को "द्रव्यमान रहित" कहलाने का कारण बनता है। हालांकि, द्रव्यमान रहित कणों में भी एक आपेक्षिकीय द्रव्यमान होता है, जो संदर्भ के विभिन्न फ्रेमों में उनकी देखी गई ऊर्जा के साथ भिन्न होता है।
निश्चर द्रव्यमान
निश्चर द्रव्यमान चतुर्विम-संवेग (शास्त्रीय त्रि-आयामी गति के चार-आयामी सामान्यीकरण) का चतुरंग वेग का अनुपात है:[10]
आपेक्षिकीय ऊर्जा–संवेग समीकरण
E और p के लिए आपेक्षिकीय भाव आपेक्षिकीय ऊर्जा-संवेग संबंध का पालन करते हैं:[11]
समीकरण फोटॉनों के लिए भी मान्य है, जिनके m = 0 है:
किसी स्थिर वस्तु के लिए, संवेग p शून्य है, इसलिए
विराम द्रव्यमान वस्तु के विराम फ्रेम में कुल ऊर्जा के समानुपाती होता है।
जब वस्तु गतिमान होती है, तो कुल ऊर्जा निम्न द्वारा दी जाती है
और
इकाइयों में काम करते समय जहां c = 1, जिसे प्राकृतिक इकाई पद्धति के रूप में जाना जाता है, सभी आपेक्षिकीय समीकरणों को सरल किया जाता है और मात्रा ऊर्जा , संवेग और द्रव्यमान का एक ही प्राकृतिक आयाम होता है:[12]
समग्र पद्धतियों का द्रव्यमान
एक समग्र पद्धति का विराम द्रव्यमान भागों के विराम द्रव्यमानों का योग नहीं है, जब तक कि सभी भाग स्थिर न हों। एक समग्र पद्धति के कुल द्रव्यमान में पद्धति में गतिज ऊर्जा और क्षेत्र ऊर्जा समिलित होती है।
एक समग्र पद्धति की कुल ऊर्जा E को इसके घटकों की ऊर्जाओं के योग को एक साथ जोड़कर निर्धारित किया जा सकता है। पद्धति का कुल संवेग एक सदिश मात्रा, की गणना उसके सभी घटकों के संवेगों को एक साथ जोड़कर भी की जा सकती है। कुल ऊर्जा E और कुल संवेग सदिश \vec{p} की लंबाई (परिणाम) कुलका , को देखते हुए, निश्चर द्रव्यमान इस प्रकार दिया जाता है:
ऐसी पद्धति के लिए, संवेग फ्रेम के विशेष केंद्र में जहां संवेग का योग शून्य होता है, फिर से पद्धति द्रव्यमान (जिसे निश्चर द्रव्यमान कहा जाता है) कुल पद्धति ऊर्जा से मेल खाता है या इकाइयों में जहां c = 1, इसके समान है। एक पद्धति के लिए यह निश्चर द्रव्यमान किसी भी जड़त्वीय फ्रेम में समान मात्रा में रहता है, हालांकि पद्धति की कुल ऊर्जा और कुल संवेग चुने गए विशेष जड़त्वीय फ्रेम के कार्य हैं, और जड़त्वीय फ्रेम के बीच इस तरह से भिन्न होंगे जैसे कि निश्चर द्रव्यमान सभी परिदर्शकों के लिए समान। निश्चर द्रव्यमान इस प्रकार उसी क्षमता में कणों की पद्धतियों के लिए कार्य करता है जैसे "विराम द्रव्यमान" एकल कणों के लिए करता है।
ध्यान दें कि एक पृथक पद्धति का निश्चर द्रव्यमान (अर्थात, द्रव्यमान और ऊर्जा दोनों के लिए बंद) भी परिदर्शक या जड़त्वीय फ्रेम से स्वतंत्र है, और रासायनिक और परमाणु प्रतिक्रियाओं के दौरान भी पृथक पद्धतियों और एकल परिदर्शकों के लिए एक स्थिर, संरक्षित मात्रा है। कण भौतिकी में निश्चर द्रव्यमान की अवधारणा का व्यापक रूप से उपयोग किया जाता है, क्योंकि एक कण के क्षय उत्पादों का निश्चर द्रव्यमान उसके विराम द्रव्यमान के बराबर होता है। इसका उपयोग Z बोसॉन या शीर्ष क्वार्क जैसे कणों के द्रव्यमान का मापन करने के लिए किया जाता है।
विशिष्ट आपेक्षिकता में द्रव्यमान का संरक्षण बनाम निश्चरता
कुल ऊर्जा एक योगात्मक संरक्षित मात्रा है (एकल परिदर्शकों के लिए) पद्धतियों और कणों के बीच प्रतिक्रियाओं में, लेकिन विराम द्रव्यमान (कण विराम द्रव्यमानों के योग होने के अर्थ में) एक घटना के माध्यम से संरक्षित नहीं किया जा सकता है जिसमें कणों के विराम द्रव्यमान हैं अन्य प्रकार की ऊर्जा में परिवर्तित, जैसे गतिज ऊर्जा। अलग-अलग कण विराम द्रव्यमानों का योग खोजने के लिए कई परिदर्शकों की आवश्यकता होगी, प्रत्येक कण जड़त्वीय फ्रेम के लिए एक, और ये परिदर्शक व्यक्तिगत कण गतिज ऊर्जा की उपेक्षा करते हैं। संरक्षण सिद्धांतो के लिए एक एकल परिदर्शक और एक जड़त्वीय फ्रेम की आवश्यकता होती है।
सामान्य तौर पर, पृथक पद्धतियों और एकल परिदर्शकों के लिए, आपेक्षिकीय द्रव्यमान संरक्षित होता है (प्रत्येक परिदर्शक इसे समय के साथ स्थिर देखता है), लेकिन यह अपरिवर्तनीय नहीं है (अर्थात, अलग-अलग परिदर्शक अलग-अलग मान देखते हैं)। निश्चर द्रव्यमान, हालांकि, संरक्षित और अपरिवर्तनीय दोनों ही है (सभी एकल परिदर्शकों को समान मान दिखाई देता है, जो समय के साथ नहीं बदलता है)।
आपेक्षिकीय द्रव्यमान ऊर्जा से मेल खाता है, इसलिए ऊर्जा के संरक्षण का स्वचालित रूप से मतलब है कि किसी दिए गए परिदर्शक और जड़त्वीय फ्रेम के लिए आपेक्षिकीय द्रव्यमान संरक्षित है। हालाँकि, यह मात्रा, कण की कुल ऊर्जा की तरह, अपरिवर्तनीय नहीं है। इसका मतलब यह है कि, भले ही यह प्रतिक्रिया के बीच किसी भी परिदर्शक के लिए संरक्षित है, परिदर्शक के फ्रेम के साथ और अलग-अलग परिदर्शकों के लिए अलग-अलग फ्रेम में इसका पूर्ण मूल्य बदल जाएगा।
इसके विपरीत, पद्धति और कणों के विराम द्रव्यमान और निश्चर द्रव्यमान both संरक्षित and अपरिवर्तनीय भी हैं। उदाहरण के लिए: गैस के एक बंद पात्र (ऊर्जा के लिए भी बंद) में पद्धति विराम द्रव्यमान इस अर्थ में होता है कि इसे विराम मानदंड पर तौला जा सकता है, भले ही इसमें गतिमान घटक क्यू न हों। यह द्रव्यमान निश्चर द्रव्यमान है, जो पात्र की कुल सापेक्ष ऊर्जा (गैस की गतिज ऊर्जा सहित) के बराबर होता है, जब इसे संवेग फ्रेम के केंद्र में मापा जाता है। जैसा कि एकल कणों की स्थिति में होता है, गैस के ऐसे पात्र का परिकलित विराम द्रव्यमान गति में होने पर नहीं बदलता है, हालांकि इसका "आपेक्षिकीय द्रव्यमान" बदलता है।
पात्र को एक बल के अधीन भी किया जा सकता है जो इसे एक समग्र वेग देता है, या फिर (समतुल्य रूप से) इसे जड़त्वीय फ्रेम से देखा जा सकता है जिसमें इसका समग्र वेग होता है (अर्थात, तकनीकी रूप से, एक फ्रेम जिसमें द्रव्यमान का केंद्र होता है) वेग है)। इस स्थिति में, इसका कुल आपेक्षिकीय द्रव्यमान और ऊर्जा बढ़ जाती है। हालांकि, ऐसी स्थिति में, हालांकि पात्र की कुल सापेक्ष ऊर्जा और कुल गति में वृद्धि होती है, इन ऊर्जा और गति में वृद्धि निश्चर द्रव्यमान परिभाषा में घट जाती है, जिससे चलते पात्र के निश्चर द्रव्यमान की गणना उसी मान के रूप में की जाएगी मानो इसे स्थिर मानदंड पर मापा गया हो।
बंद (मतलब पूरी तरह से अश्लिष्ट) पद्धति
विशिष्ट आपेक्षिकता (ऊर्जा, द्रव्यमान और संवेग के लिए) में सभी संरक्षण नियम के लिए पृथक पद्धतियों की आवश्यकता होती है, जिसका अर्थ है कि ऐसी पद्धतियाँ जो पूरी तरह से पृथक हैं, जिनमें समय के साथ-साथ द्रव्यमान-ऊर्जा की अनुमति नहीं है। यदि एक पद्धति को अलग किया जाता है, तो पद्धति में कुल ऊर्जा और कुल गति दोनों किसी भी जड़त्वीय फ्रेम में किसी भी परिदर्शक के लिए समय के साथ संरक्षित होते हैं, हालांकि अलग-अलग जड़त्वीय फ्रेम में अलग-अलग परिदर्शकों के अनुसार उनके पूर्ण मूल्य अलग-अलग होंगे। पद्धति का निश्चर द्रव्यमान भी संरक्षित है, लेकिन यह विभिन्न परिदर्शकों के साथ नहीं बदलता है। यह एकल कणों के साथ परिचित स्थिति भी है: सभी परिदर्शक एक ही कण विराम द्रव्यमान (निश्चर द्रव्यमान की एक विशेष स्थिति) की गणना करते हैं, इससे कोई असमानता नहीं होती है कि वे कैसे चलते हैं (वे किस जड़त्वीय फ्रेम को चुनते हैं), लेकिन वही कण अलग-अलग परिदर्शक अलग-अलग कुल ऊर्जा और संवेग देखते हैं ।
निश्चर द्रव्यमान के संरक्षण के लिए भी पद्धति को संलग्न करने की आवश्यकता होती है ताकि कोई गर्मी और विकिरण (और इस प्रकार निश्चर द्रव्यमान) बच न सके। जैसा कि ऊपर दिए गए उदाहरण में, भौतिक रूप से बंद या बाध्य पद्धति को अपने द्रव्यमान को स्थिर रखने के लिए बाहरी ताकतों से पूरी तरह अलग होने की आवश्यकता नहीं है, क्योंकि बाध्य पद्धतियों के लिए ये केवल पद्धति या परिदर्शक के जड़त्वीय फ्रेम को बदलने के लिए कार्य करते हैं। हालांकि इस तरह की कार्रवाइयाँ बाध्य पद्धति की कुल ऊर्जा या गति को बदल सकती हैं, ये दो परिवर्तन रद्द हो जाते हैं, जिससे पद्धति के निश्चर द्रव्यमान में कोई परिवर्तन नहीं होता है। यह एकल कणों के समान ही परिणाम है: उनका परिकलित विराम द्रव्यमान भी स्थिर रहता है, चाहे वे कितनी भी तेजी से चलते हों, या कोई प्रेक्षक उन्हें कितनी तेजी से चलता हुआ देखता हो।
दूसरी ओर, उन पद्धतियों के लिए जो अपरिबद्ध हैं, पद्धति के "बंद" होने को एक आदर्श सतह द्वारा लागू किया जा सकता है, क्योंकि समय के साथ परीक्षण-मात्रा में या बाहर कोई द्रव्यमान-ऊर्जा की अनुमति नहीं दी जा सकती है। यदि किसी बल को इस तरह के एक अपरिबद्ध पद्धति के केवल एक अंश पर कार्य करने की अनुमति दी जाती है, तो यह ऊर्जा को पद्धति में या बाहर जाने की अनुमति देने के बराबर है, और द्रव्यमान-ऊर्जा (कुल अलगाव) के बंद होने की स्थिति का उल्लंघन किया जाता है। इस स्थिति में, पद्धति के निश्चर द्रव्यमान का संरक्षण भी अब नहीं रहेगा। E = mc2 के अनुसार जहाँ E ऊर्जा को हटा दिया जाता है, और m विराम द्रव्यमान में परिवर्तन है, ऊर्जा के संचलन से जुड़े द्रव्यमान के परिवर्तनों को दर्शाता है, न कि द्रव्यमान का ऊर्जा में "रूपांतरण"।
पद्धति निश्चर द्रव्यमान बनाम पद्धति के कुछ अंशों के अलग-अलग विराम द्रव्यमान
फिर से, विशिष्ट आपेक्षिकता में, पद्धति के विराम द्रव्यमान को भागों के विराम द्रव्यमानों के योग के बराबर होने की आवश्यकता नहीं है (एक ऐसी स्थिति जो रसायन विज्ञान में सकल द्रव्यमान-संरक्षण के अनुरूप होगी)। उदाहरण के लिए, एक विशाल कण फोटॉनों में क्षय हो सकता है, जिसमें व्यक्तिगत रूप से कोई द्रव्यमान नहीं होता है, लेकिन जो (एक पद्धति के रूप में) उस कण के निश्चर द्रव्यमान को संरक्षित करता है जिसने उन्हें उत्पन्न किया। साथ ही गैर-अंतःक्रियात्मक कणों (जैसे, फोटॉन, या एक आदर्श गैस) के एक डिब्बा में कणों के विराम द्रव्यमानों के योग की तुलना में एक बड़ा निश्चर द्रव्यमान होगा जो इसे बनाते हैं। ऐसा इसलिए है क्योंकि एक पद्धति में सभी कणों और क्षेत्रों की कुल ऊर्जा का योग होना चाहिए, और यह मात्रा, जैसा कि संवेग फ्रेम के केंद्र में देखा गया है, और c2 द्वारा विभाजित, पद्धति का निश्चर द्रव्यमान है।
विशिष्ट आपेक्षिकता में, द्रव्यमान को ऊर्जा में परिवर्तित नहीं किया जाता है, क्योंकि सभी प्रकार की ऊर्जा अभी भी अपने संबद्ध द्रव्यमान को बनाए रखती है। विशिष्ट आपेक्षिकता में न तो ऊर्जा और न ही निश्चर द्रव्यमान को नष्ट किया जा सकता है, और प्रत्येक बंद पद्धतियों में यह समय के साथ अलग-अलग संरक्षित होता है। इस प्रकार, एक पद्धति का निश्चर द्रव्यमान केवल इसलिए बदल सकता है क्योंकि निश्चर द्रव्यमान को प्रकाश या गर्मी के रूप में बचने की अनुमति है। इस प्रकार, जब प्रतिक्रियाएँ (चाहे रासायनिक या परमाणु) गर्मी और प्रकाश के रूप में ऊर्जा छोड़ती हैं, अगर गर्मी और प्रकाश को बाहर निकलने की अनुमति नहीं है (पद्धति बंद और पृथक है), तो ऊर्जा पद्धति के विराम द्रव्यमान में योगदान देना जारी रखेगी, और पद्धति द्रव्यमान नहीं बदलेगा। यदि ऊर्जा को पर्यावरण में छोड़ा जाता है तो ही द्रव्यमान नष्ट होगा; ऐसा इसलिए है क्योंकि संबंधित द्रव्यमान को पद्धति से बाहर जाने दिया गया है, जहां यह आसपास के द्रव्यमान में योगदान देता है।[11]
सापेक्षतावादी जन अवधारणा का इतिहास
अनुप्रस्थ और अनुदैर्ध्य द्रव्यमान
ऐसी अवधारणाएं जो आज "आपेक्षिकीय द्रव्यमान" कहलाती हैं, विशिष्ट आपेक्षिकता के आगमन से पहले ही विकसित हो चुकी थीं। उदाहरण के लिए, 1881 में J. J. थॉमसन द्वारा यह माना गया था कि एक आवेशित पिंड को एक अपरिवर्तित पिंड की तुलना में गति में स्थापित करना कठिन होता है, जिसे ओलिवर हीविसाइड (1889) और जॉर्ज फ्रेडरिक चार्ल्स सियरल (1897) द्वारा अधिक विस्तार से काम किया गया था। तो स्थिर वैद्युत ऊर्जा कुछ इस प्रकार के विद्युत चुम्बकीय द्रव्यमान के रूप में व्यवहार करती है , जो निकायों के सामान्य यांत्रिक द्रव्यमान को बढ़ा सकता है।[13][14]
फिर, थॉमसन और सियरल द्वारा यह बताया गया कि यह विद्युत चुम्बकीय द्रव्यमान भी वेग के साथ बढ़ता है। लोरेंत्ज़ ईथर सिद्धांत के ढांचे में हेंड्रिक लोरेंत्ज़ (1899, 1904) द्वारा इसे और विस्तृत किया गया था। उन्होंने द्रव्यमान को त्वरण और बल के अनुपात के रूप में परिभाषित किया, न कि संवेग के वेग के अनुपात के रूप में, इसलिए उन्हें द्रव्यमान गति की दिशा और द्रव्यमान के समानांतर गति की दिशा के लंबवत (जहाँ लोरेंत्ज़ कारक है, v ईथर और वस्तु के बीच सापेक्ष वेग है, और c प्रकाश की गति है)। केवल जब बल वेग के लम्बवत् होता है, लोरेंत्ज़ का द्रव्यमान उस द्रव्यमान के बराबर होता है जिसे अब आपेक्षिक द्रव्यमान कहा जाता है। मैक्स अब्राहम (1902) को अनुदैर्ध्य द्रव्यमान और अनुप्रस्थ द्रव्यमान (हालांकि इब्राहीम ने लोरेंत्ज़ के आपेक्षिकता द्रव्यमान की तुलना में अधिक जटिल अभिव्यक्तियों का उपयोग किया)। इसलिए, लोरेंत्ज़ के सिद्धांत के अनुसार कोई भी पिंड प्रकाश की गति तक नहीं पहुँच सकता क्योंकि इस वेग पर द्रव्यमान असीम रूप से बड़ा हो जाता है।[15][16][17]
अल्बर्ट आइंस्टीन ने भी शुरू में अपने 1905 के वैद्युतगतिकी पेपर में अनुदैर्ध्य और अनुप्रस्थ द्रव्यमान की अवधारणाओं का उपयोग किया था (लोरेंत्ज़ के समान, लेकिन एक अलग दुर्भाग्यपूर्ण बल परिभाषा के साथ, जिसे बाद में 1906 में अन्य पेपर में सुधारा गया) [18][19] हालांकि, बाद में उन्होंने वेग पर निर्भर द्रव्यमान अवधारणाओं को छोड़ दिया।
गैर-शून्य विराम द्रव्यमान के साथ एक कण के लिए बल और त्वरण से संबंधित सटीक आपेक्षिकता अभिव्यक्ति (जो लोरेंत्ज़ के समतुल्य है) वेग v के साथ दिशा में आगे बढ़ रहा है और संबंधित लोरेंत्ज़ कारक है
आपेक्षिकीय द्रव्यमान
विशिष्ट आपेक्षिकता में, शून्येतर विराम द्रव्यमान वाली वस्तु प्रकाश की गति से यात्रा नहीं कर सकती है। जैसे-जैसे वस्तु प्रकाश की गति के करीब आती है, वस्तु की ऊर्जा और गति बिना किसी सीमा के बढ़ती जाती है।
1905 के बाद के पहले वर्षों में, लोरेंत्ज़ और आइंस्टीन के बाद, अनुदैर्ध्य और अनुप्रस्थ द्रव्यमान शब्द अभी भी उपयोग में थे। हालाँकि, उन अभिव्यक्तियों को आपेक्षिकीय द्रव्यमान की अवधारणा द्वारा प्रतिस्थापित किया गया था, एक अभिव्यक्ति जिसे पहली बार 1909 में गिल्बर्ट N. लुईस और रिचर्ड C. टोलमैन द्वारा परिभाषित किया गया था।[20] उन्होंने किसी पिंड की कुल ऊर्जा और द्रव्यमान को इस रूप में परिभाषित किया
1934 में, टॉल्मन ने तर्क दिया कि आपेक्षिकीय द्रव्यमान सूत्र प्रकाश की गति से चलने वाले कणों सहित सभी कणों के लिए सूत्र लागू होता है, जबकि सूत्र केवल एक धीमी-से-प्रकाश कण पर लागू होता है (एक गैर-शून्य विराम द्रव्यमान वाला कण)। टॉल्मन ने इस संबंध पर टिप्पणी की कि, "इसके अलावा, हमारे पास निश्चित रूप से गतिमान अतिसूक्ष्म परमाणुों की स्थिति में अभिव्यक्ति का प्रायोगिक सत्यापन है ... इसलिए हमें गतिमान कण के द्रव्यमान के लिए अभिव्यक्ति को सामान्य रूप से सही मानने में कोई असमंजस नहीं होगी।[24]
जब सापेक्ष वेग शून्य होता है, बस 1 के बराबर है, और आपेक्षिक द्रव्यमान को विराम द्रव्यमान तक कम कर दिया जाता है जैसा कि नीचे दिए गए अगले दो समीकरणों में देखा जा सकता है। जैसे-जैसे वेग प्रकाश की गति c की ओर बढ़ता है, दाहिनी ओर का हर शून्य की ओर बढ़ता है, और परिणामस्वरूप अनंत तक पहुँचता है। जबकि न्यूटन के द्वितीय नियम के रूप में वैध रहता है
भले ही आइंस्टीन ने शुरु में अपने पहले पेपर में "अनुदैर्ध्य" और "अनुप्रस्थ" द्रव्यमान को दो पेपरों में प्रयोग किया था (1905) में अपने पहले पेपर में उन्होंने m को अभिक्रियित किया जिसे अब विराम द्रव्यमान कहा जाएगा।[2]आइंस्टीन ने आपेक्षिकीय द्रव्यमान के लिए कभी कोई समीकरण नहीं बनाया, और बाद के वर्षों में उन्होंने इस विचार के प्रति अपनी नापसंदगी व्यक्त की:[26]
गतिमान पिंड के द्रव्यमान की अवधारणा को पेश करना अच्छा नहीं है, जिसके लिए कोई स्पष्ट परिभाषा नहीं दी जा सकती दिया जाए। 'विश्राम द्रव्यमान' 'm के अतिरिक्त कोई अन्य द्रव्यमान अवधारणा प्रस्तुत करना ठीक नहीं है। 'm प्रस्तुत करने के अतिरिक्त गतिमान शरीर की गति और ऊर्जा के लिए अभिव्यक्ति का उल्लेख करना अच्छा है।
— लिंकन बार्नेट को अल्बर्ट आइंस्टीन का पत्र, 19 जून 1948
लोकप्रिय विज्ञान और पाठ्यपुस्तकें
लोकप्रिय विज्ञान लेखन और हाई स्कूल और स्नातक पाठ्यपुस्तकों में आपेक्षिकीय द्रव्यमान की अवधारणा का व्यापक रूप से उपयोग किया जाता है। ओकुन और A. B. एरोन्स जैसे लेखकों ने इसके विपरीत तर्क दिया है कि यह पुरातन और भ्रमित करने वाला है, और आधुनिक आपेक्षिकीय सिद्धांत के अनुरूप नहीं है।[5][27]
एरोन्स ने लिखा:[27]
कई वर्षों तक आपेक्षिकीय द्रव्यमान की व्युत्पत्ति के माध्यम से गतिशीलता की चर्चा में प्रवेश करना पारंपरिक था, जो कि द्रव्यमान-वेग संबंध है, और यह कदाचित् अभी भी पाठ्यपुस्तकों में प्रमुख विधा है। हाल ही में, हालांकि, यह तेजी से मान्यता प्राप्त हुई है कि आपेक्षिकीय द्रव्यमान एक परेशानी और संदिग्ध अवधारणा है। [देखें, उदाहरण के लिए, ओकुन (1989)।[5]]... सापेक्षतावादी गतिशीलता के लिए ध्वनि और कठोर दृष्टिकोण गति के लिए उस अभिव्यक्ति के प्रत्यक्ष विकास के माध्यम से है जो सभी फ्रेमों में गति के संरक्षण को सुनिश्चित करता है:
आपेक्षिकीय द्रव्यमान के विपरीत।
C. एल्डर सापेक्षता में द्रव्यमान पर समान रूप से बहिष्कृत करने वाला रूप अपनाते है। उक्त विषय वस्तु पर लिखते हुए, वे कहते हैं कि "विशिष्ट आपेक्षिकता के सिद्धांत में इसका परिचय एक ऐतिहासिक दुर्घटना के रूप में हुआ था", E = mc2 जो व्यापक ज्ञान की ओर ध्यान दे रहा था और कैसे समीकरण की जनता की व्याख्या ने बड़े मानदंड पर इसे सूचित किया है कि उच्च शिक्षा में इसे कैसे पढ़ाया जाए।[28] इसके विपरीत वह मानते है कि स्थिरता और आपेक्षिकीय द्रव्यमान के बीच का अंतर स्पष्ट रूप से सिखाया जाना चाहिए, ताकि छात्रों को पता चल सके कि जड़त्व की अधिकांश चर्चाओं में द्रव्यमान को अपरिवर्तनीय क्यों माना जाना चाहिए।
कई समकालीन लेखक जैसे टेलर और व्हीलर आपेक्षिकीय द्रव्यमान की अवधारणा का पूरी तरह से उपयोग करने से बचते हैं:
"सापेक्षतावादी द्रव्यमान" की अवधारणा गलतफहमी के अधीन है। इसलिए हम इसका उपयोग नहीं करते हैं। सबसे पहले, यह नाम द्रव्यमान - चतुरंग वेग के परिमाण से संबंधित - को एक बहुत अलग अवधारणा पर लागू करता है, एक का समय घटक चतुरंग वेग । दूसरा, यह किसी वस्तु की ऊर्जा में वृद्धि को वेग या संवेग के साथ वस्तु की आंतरिक संरचना में कुछ बदलाव के साथ जुड़ा हुआ प्रतीत करता है। वास्तव में, वेग के साथ ऊर्जा की वृद्धि वस्तु में नहीं बल्कि ज्यामितीय में उत्पन्न होती है अंतरिक्ष समय के ही गुण।
जबकि अंतरिक्ष-समय में मिन्कोवस्की अंतरिक्ष की असीमित ज्यामिति है, वेग-अंतरिक्ष c इससे घिरा होता है और बेल्ट्रामी-क्लेन प्रतिरूप की ज्यामिति होती है जहां सापेक्षवादी द्रव्यमान यूक्लिडियन ज्यामिति के बेरिकेंट्रिक निर्देशांक में न्यूटोनियन द्रव्यमान के अनुरूप भूमिका निभाता है।[29] अतिशयोक्तिपूर्ण ज्यामिति के वेग का संबंध 3-वेग-निर्भर आपेक्षिकीय द्रव्यमान को चतुरंग वेग मिन्कोव्स्की औपचारिकता से संबंधित होने में सक्षम बनाता है।[30]
यह भी देखें
- आपेक्षिकीय ऊर्जा और संवेग का परीक्षण
संदर्भ
- ↑ Roche, J (2005). "द्रव्यमान क्या है?" (PDF). European Journal of Physics. 26 (2): 225. Bibcode:2005EJPh...26..225R. doi:10.1088/0143-0807/26/2/002.
- ↑ 2.0 2.1 A. Einstein (1905), "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?" (PDF), Annalen der Physik (in Deutsch), 18 (13): 639–643, Bibcode:1905AnP...323..639E, doi:10.1002/andp.19053231314 (English translation)
- ↑ 3.0 3.1 3.2 T. R. Sandin (1991), "In defense of relativistic mass", American Journal of Physics, 59 (11): 1032–1036, Bibcode:1991AmJPh..59.1032S, doi:10.1119/1.16642
- ↑ Ketterle, W. and Jamison, A. O. (2020). "An atomic physics perspective on the kilogram’s new definition", "Physics Today" 73, 32-38
- ↑ 5.0 5.1 5.2 L. B. Okun (1989), "The Concept of Mass" (PDF), Physics Today, 42 (6): 31–36, Bibcode:1989PhT....42f..31O, doi:10.1063/1.881171, archived from the original (PDF) on 2011-06-07
- ↑ L. B. Okun (2009), "Mass versus relativistic and rest masses", American Journal of Physics, 77 (5): 430–431, Bibcode:2009AmJPh..77..430O, doi:10.1119/1.3056168
- ↑ Pitzer, Kenneth S. (1979). "रासायनिक गुणों पर सापेक्ष प्रभाव" (PDF). Accounts of Chemical Research. 12 (8): 271–276. doi:10.1021/ar50140a001.
- ↑ Norrby, Lars J. (1991). "पारा तरल क्यों होता है? या, सापेक्षतावादी प्रभाव रसायन विज्ञान की पाठ्यपुस्तकों में क्यों नहीं आते?". Journal of Chemical Education (in English). 68 (2): 110–113. doi:10.1021/ed068p110. ISSN 0021-9584.
- ↑ E. Eriksen; K. Vøyenli (1976), "The classical and relativistic concepts of mass", Foundations of Physics, 6 (1): 115–124, Bibcode:1976FoPh....6..115E, doi:10.1007/BF00708670, S2CID 120139174</रेफरी> परमाणु और कण भौतिकी में आपेक्षिक द्रव्यमान का संदर्भ नहीं दिया जाता है,और 2005 में परिचयात्मक पाठ्यपुस्तकों के एक सर्वेक्षण से पता चला कि 24 में से केवल 5 पाठों ने अवधारणा का उपयोग किया,<ref>Oas, "On the Abuse and Use of Relativistic Mass," 2005, http://arxiv.org/abs/physics/0504110
- ↑ McGlinn, William D. (2004), Introduction to relativity, JHU Press, p. 43, ISBN 978-0-8018-7047-7 Extract of page 43
- ↑ 11.0 11.1 E. F. Taylor; J. A. Wheeler (1992), Spacetime Physics (second ed.), New York: W.H. Freeman and Company, pp. 248–249, ISBN 978-0-7167-2327-1
- ↑ Mandl, Franz; Shaw, Graham (2013). क्वांटम फील्ड थ्योरी (2nd ed.). John Wiley & Sons. p. 70. ISBN 978-1-118-71665-6. Extract of page 70
- ↑ J. J. Thomson (1881), , Philosophical Magazine, 5, 11 (68): 229–249, doi:10.1080/14786448108627008
- ↑ G. F. C. Searle (1897), , Philosophical Magazine, 5, 44 (269): 329–341, doi:10.1080/14786449708621072
- ↑ H. A. Lorentz (1899), , Proceedings of the Royal Netherlands Academy of Arts and Sciences, 1: 427–442
- ↑ H. A. Lorentz (1904), , Proceedings of the Royal Netherlands Academy of Arts and Sciences, 6: 809–831
- ↑ M. Abraham (1903), "Prinzipien der Dynamik des Elektrons", Annalen der Physik, 315 (1): 105–179, Bibcode:1902AnP...315..105A, doi:10.1002/andp.19023150105
- ↑ A. Einstein (1905), "Zur Elektrodynamik bewegter Körper" (PDF), Annalen der Physik (in Deutsch), 322 (10): 891–921, Bibcode:1905AnP...322..891E, doi:10.1002/andp.19053221004 (English translation)
- ↑ A. Einstein (1906), "Über eine Methode zur Bestimmung des Verhältnisses der transversalen und longitudinalen Masse des Elektrons" (PDF), Annalen der Physik (in Deutsch), 21 (13): 583–586, Bibcode:1906AnP...326..583E, doi:10.1002/andp.19063261310
- ↑ Lewis, Gilbert N. & Tolman, Richard C. (1909), , Proceedings of the American Academy of Arts and Sciences, 44 (25): 709–726, doi:10.2307/20022495, JSTOR 20022495
- ↑ R. Tolman (1911), , Philosophical Magazine, 21 (123): 296–301, doi:10.1080/14786440308637034
- ↑ R. Tolman (1911), , Philosophical Magazine, 22 (129): 458–463, doi:10.1080/14786440908637142
- ↑ R. Tolman (1912), , Philosophical Magazine, 23 (135): 375–380, doi:10.1080/14786440308637231
- ↑ R.C. Tolman (1934), Relativity, Thermodynamics, and Cosmology, Oxford: Clarendon Press, ISBN 978-0-486-65383-9, LCCN 34032023 Reissued (1987), New York: Dover, ISBN 0-486-65383-8.
- ↑ Philip Gibbs; Jim Carr. "सापेक्षतावादी द्रव्यमान क्या है?". Retrieved 2011-09-27.
- ↑ Eugene Hecht (19 August 2009). "आइंस्टीन ने कभी सापेक्षतावादी द्रव्यमान का अनुमोदन नहीं किया". The Physics Teacher. 47 (6): 336–341. Bibcode:2009PhTea..47..336H. CiteSeerX 10.1.1.205.5072. doi:10.1119/1.3204111.
- ↑ 27.0 27.1 A.B. Arons (1990), A Guide to Introductory Physics Teaching, p. 263 Also in Teaching Introductory Physics, 2001, p. 308
- ↑ Adler, Carl (September 30, 1986). "क्या द्रव्यमान वास्तव में वेग पर निर्भर करता है, पिताजी?" (PDF). American Journal of Physics. 55 (8): 739–743. Bibcode:1987AmJPh..55..739A. doi:10.1119/1.15314 – via HUIT Sites Hosting.
- ↑ Ungar, Abraham A. (2010). अतिशयोक्तिपूर्ण त्रिभुज केंद्र: विशेष सापेक्षतावादी दृष्टिकोण. Dordrecht: Springer. ISBN 978-90-481-8636-5. OCLC 663096629.
- ↑ When Relativistic Mass Meets Hyperbolic Geometry, Abraham A. Ungar, Commun. Math. Anal. Volume 10, Number 1 (2011), 30–56.
बाहरी कड़ियाँ
- Silagadze, Z. K. (2008), "Relativity without tears", Acta Physica Polonica B, 39 (4): 811–885, arXiv:0708.0929, Bibcode:2008AcPPB..39..811S
- Oas, Gary (2005), "On the Abuse and Use of Relativistic Mass", arXiv:physics/0504110
- Usenet Physics FAQ
- "Does mass change with velocity?" by Philip Gibbs et al., 2002, retrieved August 10, 2006
- "What is the mass of a photon?" by Matt Austern et al., 1998, retrieved June 27, 2007
- Max Jammer (1997), Concepts of Mass in Classical and Modern Physics, Courier Dover Publications, pp. 177–178, ISBN 978-0-486-29998-3
- Mass as a Variable Quantity