निरंतर समान वितरण: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 5 users not shown) | |||
| Line 35: | Line 35: | ||
}} | }} | ||
संभाव्यता सिद्धांत और सांख्यिकी में, निरंतर समान वितरण या आयताकार वितरण [[सममित वितरण]] [[संभाव्यता वितरण]] का एक वर्ग है। ऐसा वितरण एक प्रयोग का वर्णन करता है जहां एक यादृच्छिक परिणाम होता है जो कुछ सीमाओं के मध्य होता है।<ref name=":0">{{Cite book|title=A modern introduction to probability and statistics : understanding why and how|url=https://archive.org/details/modernintroducti00fmde|url-access=limited|last=Dekking|first=Michel|publisher=Springer|year=2005|isbn=978-1-85233-896-1|location=London, UK|pages=[https://archive.org/details/modernintroducti00fmde/page/n71 60]–61}}</ref> सीमाएं मापदंडों | संभाव्यता सिद्धांत और सांख्यिकी में, निरंतर समान वितरण या आयताकार वितरण [[सममित वितरण|सममित]] [[संभाव्यता वितरण]] का एक वर्ग है। ऐसा वितरण एक प्रयोग का वर्णन करता है जहां एक यादृच्छिक परिणाम होता है जो कुछ सीमाओं के मध्य होता है।<ref name=":0">{{Cite book|title=A modern introduction to probability and statistics : understanding why and how|url=https://archive.org/details/modernintroducti00fmde|url-access=limited|last=Dekking|first=Michel|publisher=Springer|year=2005|isbn=978-1-85233-896-1|location=London, UK|pages=[https://archive.org/details/modernintroducti00fmde/page/n71 60]–61}}</ref> सीमाएं मापदंडों, <math>a</math> और <math>b</math> द्वारा परिभाषित की जाती हैं जो न्यूनतम और अधिकतम मान हैं। अंतराल या तो [[बंद अंतराल|संवृत]] (अर्थात, <math>[a,b]</math>) या [[खुला अंतराल|विवृत]] (अर्थात् <math>(a,b)</math>) हो सकता है।<ref name=":3">{{Cite book|title=इंजीनियरों और वैज्ञानिकों के लिए संभाव्यता और सांख्यिकी|last=Walpole |display-authors=etal |first=Ronald|publisher=Prentice Hall|year=2012|isbn=978-0-321-62911-1|location=Boston, USA|pages=171–172}}</ref> इसलिए, वितरण <math>U(a,b)</math>, प्रायः संक्षिप्त किया जाता है जहाँ <math>U</math> का अर्थ समान वितरण है।<ref name=":0" />सीमाओं के मध्य का अंतर, अंतराल की लंबाई को परिभाषित करता है; वितरण के [[समर्थन (गणित)]] पर समान लंबाई के सभी [[अंतराल (गणित)]] समान रूप से संभावित हैं। यह एक यादृच्छिक चर <math>X</math> के लिए [[अधिकतम एन्ट्रापी संभाव्यता वितरण]] है। इसके अतिरिक्त कोई प्रतिबंध नहीं है कि यह वितरण के समर्थन में सम्मिलित है।<ref>{{cite journal |last1=Park |first1=Sung Y. |last2=Bera |first2=Anil K. |year=2009 |title=अधिकतम एन्ट्रापी ऑटोरेग्रेसिव कंडीशनल हेटेरोस्केडैस्टिसिटी मॉडल|journal=[[Journal of Econometrics]] |volume=150 |issue=2 |pages=219–230 |doi=10.1016/j.jeconom.2008.12.014 |citeseerx=10.1.1.511.9750 }}</ref> | ||
| Line 45: | Line 45: | ||
f(x) = \begin{cases} | f(x) = \begin{cases} | ||
\frac{1}{b-a} & \text{for } a \le x \le b, \\[8pt] | \frac{1}{b-a} & \text{for } a \le x \le b, \\[8pt] | ||
0 & \text{for } x < a \ \text{ or } \ x > b | 0 & \text{for } x < a \ \text{ or } \ x > b | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
<math>f(x)</math> के मान, दो सीमाओं <math>a</math> और <math>b</math> पर, सामान्यतः महत्वहीन होते हैं, क्योंकि वे किसी भी अंतराल <math>[c,d]</math> और न ही <math display="inline">\int_a^b xf(x)dx,</math> किसी उच्चतर आघूर्ण पर, <math display="inline">\int_c^d f(x)dx</math> के मान में परिवर्तन नहीं करते हैं। कभी-कभी उन्हें शून्य और कभी-कभी <math>\tfrac{1}{b-a} </math> चुना जाता है। अधिकतम संभावना की विधि द्वारा अनुमान के संदर्भ में उत्तरार्द्ध उपयुक्त है। [[फूरियर विश्लेषण]] के संदर्भ में, कोई <math>f(a)</math> या <math>f(b)</math> का मान <math>\tfrac{1}{2(b-a)} </math> ले सकता है, क्योंकि तब इस समान फलन के कई [[अभिन्न परिवर्तन|अभिन्न परिवर्तनों]] का व्युत्क्रम परिवर्तन फलन को वापस लाएगा, न कि एक फलन जो, अर्थात शून्य [[माप सिद्धांत|माप]] वाले बिंदुओं के एक समुच्चय को छोड़कर [[लगभग हर जगह]] समान है। साथ ही, यह [[साइन फ़ंक्शन|संकेत फलन]] के अनुरूप है, जिसमें ऐसी कोई अस्पष्टता नहीं है। | |||
कोई भी संभाव्यता घनत्व फलन | कोई भी संभाव्यता घनत्व फलन <math>1</math> एकीकृत होता है इसलिए निरंतर समान वितरण की संभाव्यता घनत्व फलनों को सुचित्रित रूप से एक आयत के रूप में चित्रित किया गया है, जहाँ {{tmath|b-a}} आधार लंबाई और {{tmath|\tfrac{1}{b-a} }} ऊंचाई है। जैसे-जैसे आधार की लंबाई बढ़ती है, ऊंचाई (वितरण सीमाओं के भीतर किसी विशेष मान पर घनत्व) कम हो जाती है।<ref name=":1">{{Cite web|url=https://www.mathworks.com/help/stats/uniform-distribution-continuous.html|title=समान वितरण (निरंतर)|date=2019|website=MathWorks|access-date=November 22, 2019}}</ref> | ||
माध्य | |||
माध्य <math>\mu</math> और विचरण <math>\sigma ^2 </math> की दृष्टि से, निरंतर समान वितरण की संभाव्यता घनत्व फलन है: | |||
:<math> | :<math> | ||
f(x) = \begin{cases} | f(x) = \begin{cases} | ||
| Line 71: | Line 72: | ||
इसका व्युत्क्रम है: | इसका व्युत्क्रम है: | ||
:<math>F^{-1} (p) = a + p (b - a) \quad \text{ for } 0 < p < 1.</math> | :<math>F^{-1} (p) = a + p (b - a) \quad \text{ for } 0 < p < 1.</math> | ||
माध्य | माध्य <math>\mu</math> और विचरण <math>\sigma ^2 </math> की दृष्टि से सतत समान वितरण का संचयी वितरण फलन है: | ||
:<math>F(x) = \begin{cases} | :<math>F(x) = \begin{cases} | ||
0 & \text{for } x - \mu < - \sigma \sqrt{3} , \\ | 0 & \text{for } x - \mu < - \sigma \sqrt{3} , \\ | ||
| Line 81: | Line 82: | ||
==== <u>उदाहरण 1.</u> सतत समान वितरण फलन का उपयोग | ==== <u>उदाहरण 1.</u> सतत समान वितरण फलन का उपयोग ==== | ||
एक यादृच्छिक चर <math>X \sim U(0,23)</math> के लिए, | एक यादृच्छिक चर <math>X \sim U(0,23)</math> के लिए, <math>P(2 < X < 18)</math> प्राप्त करें: | ||
:<math>P(2 < X < 18) = (18-2) \cdot \frac{1}{23-0} = \frac{16}{23} .</math> | :<math>P(2 < X < 18) = (18-2) \cdot \frac{1}{23-0} = \frac{16}{23} .</math> | ||
निरंतर समान वितरण फलन | निरंतर समान वितरण फलन<math>[f(x) \text{ vs } x]</math> के चित्रमय प्रतिनिधित्व में, निर्दिष्ट सीमा के भीतर वक्र के नीचे का क्षेत्र, संभाव्यता प्रदर्शित करते हुए, एक आयत है। उपरोक्त विशिष्ट उदाहरण के लिए, आधार {{tmath|16}} होगा और ऊंचाई {{tmath|\tfrac{1}{23} }}<ref name=":2">{{Cite book|title=परिचयात्मक सांख्यिकी|url=https://archive.org/details/IntroductoryStatistics_201904|last=Illowsky |display-authors=etal |first=Barbara|publisher=OpenStax College|year=2013|isbn=978-1-938168-20-8|location=Rice University, Houston, Texas, USA|pages=[https://archive.org/details/IntroductoryStatistics_201904/page/n303 296]–304}}</ref>होगी। | ||
==== <u>उदाहरण 2.</u> निरंतर समान वितरण फलन (सशर्त) का उपयोग | ==== <u>उदाहरण 2.</u> निरंतर समान वितरण फलन (सशर्त) का उपयोग ==== | ||
एक यादृच्छिक चर <math>X \sim U(0,23)</math> के लिए , | एक यादृच्छिक चर <math>X \sim U(0,23)</math> के लिए, <math>P(X > 12 \ | \ X > 8)</math> प्राप्त करें: | ||
:<math>P(X > 12 \ | \ X > 8) = (23-12) \cdot \frac{1}{23-8} = \frac{11}{15}</math> | :<math>P(X > 12 \ | \ X > 8) = (23-12) \cdot \frac{1}{23-8} = \frac{11}{15}</math> | ||
उपरोक्त उदाहरण निरंतर समान वितरण के लिए एक [[सशर्त संभाव्यता]] | उपरोक्त उदाहरण निरंतर समान वितरण के लिए एक [[सशर्त संभाव्यता]] स्थिति है: मान लें कि {{tmath|X > 8}} सत्य है, {{tmath|X > 12}} की क्या प्रायिकता है ? सशर्त संभाव्यता प्रतिदर्श स्थान को परिवर्तित कर देती है, इसलिए एक नई अंतराल लंबाई {{tmath|b-a'}} की गणना करनी होगी, जहाँ <math>b = 23</math> और <math>a' = 8</math> है।<ref name=":2" />आलेखीय प्रतिनिधित्व अभी भी उदाहरण 1 का अनुसरण करेगा, जहां निर्दिष्ट सीमा के भीतर वक्र के नीचे का क्षेत्र संभाव्यता प्रदर्शित करता है; आयत का आधार {{tmath|11}} होगा और ऊंचाई {{tmath|\tfrac{1}{15} }} होगी।<ref name=":2" /> | ||
| Line 98: | Line 99: | ||
सतत एकसमान वितरण का आघूर्ण-जनक फलन है:<ref>{{harvnb|Casella|Berger|2001|page=626}}</ref> | सतत एकसमान वितरण का आघूर्ण-जनक फलन है:<ref>{{harvnb|Casella|Berger|2001|page=626}}</ref> | ||
:<math>M_X = \mathrm{E} ( \mathrm{e} ^{tX}) = \int_a^b \mathrm{e} ^{tx} \frac{dx}{b-a} = \frac{ \mathrm{e} ^{tb} - \mathrm{e} ^{ta} }{t(b-a)} = \frac{B^t - A^t}{t(b-a)} </math><ref>https://www.stat.washington.edu/~nehemyl/files/UW_MATH-STAT395_moment-functions.pdf {{Bare URL PDF|date=March 2022}}</ref> | :<math>M_X = \mathrm{E} ( \mathrm{e} ^{tX}) = \int_a^b \mathrm{e} ^{tx} \frac{dx}{b-a} = \frac{ \mathrm{e} ^{tb} - \mathrm{e} ^{ta} }{t(b-a)} = \frac{B^t - A^t}{t(b-a)} </math><ref>https://www.stat.washington.edu/~nehemyl/files/UW_MATH-STAT395_moment-functions.pdf {{Bare URL PDF|date=March 2022}}</ref> | ||
जिससे हम [[कच्चे क्षण| | जिससे हम [[कच्चे क्षण|अपरिष्कृत]] आघूर्णों <math>m_k </math> की गणना कर सकते हैं: | ||
:<math>m_1 = \frac{a+b}{2} </math> | :<math>m_1 = \frac{a+b}{2} </math> | ||
:<math>m_2 = \frac{a^2+ab+b^2}{3} </math> | :<math>m_2 = \frac{a^2+ab+b^2}{3} </math> | ||
:<math>m_k = \frac{ \sum_{i=0}^k a^i b^{k-i} }{k+1} </math> | :<math>m_k = \frac{ \sum_{i=0}^k a^i b^{k-i} }{k+1} </math> | ||
निरंतर समान वितरण के बाद एक यादृच्छिक चर के लिए, [[अपेक्षित मूल्य|अपेक्षित मान]] | निरंतर समान वितरण के बाद एक यादृच्छिक चर के लिए, [[अपेक्षित मूल्य|अपेक्षित मान]] <math>m_1 = \tfrac{a+b}{2} </math> और भिन्नता <math>m_2 - m_1 ^2 = \tfrac{(b-a)^2}{12} </math> है। | ||
विशेष स्थिति | |||
विशेष स्थिति <math>a = -b</math> के लिए, निरंतर समान वितरण की संभाव्यता घनत्व फलन है: | |||
:<math> | :<math> | ||
f(x) = \begin{cases} | f(x) = \begin{cases} | ||
| Line 115: | Line 117: | ||
==== संचयी-जनक फलन ==== | ==== संचयी-जनक फलन ==== | ||
{{tmath|n \ge 2}} के लिए, अंतराल{{tmath|[- \tfrac{1}{2} , \tfrac{1}{2}]}} पर निरंतर समान वितरण का 𝑛-वाँ संचयी <math>\tfrac{B_n}{n} </math> है। जहाँ <math>B_n</math>, <math>n</math>-वीं [[ बर्नौली संख्या |बर्नौली संख्या]] है।<ref>https://galton.uchicago.edu/~wichura/Stat304/Handouts/L18.cumulants.pdf {{Bare URL PDF|date=March 2022}}</ref> | |||
=== मानक समान वितरण === | === मानक समान वितरण === | ||
मापदंडों | मापदंडों <math>a = 0</math> और <math>b = 1</math> के साथ निरंतर समान वितरण, अर्थात, <math>U(0,1)</math> को मानक समान वितरण कहा जाता है। | ||
मानक समान वितरण | मानक समान वितरण का एक रोचक गुणधर्म यह है कि यदि <math>u_1</math> एक मानक समान वितरण है, फिर <math>1 - u_1 </math> वैसा ही होता है। इस गुणधर्म का उपयोग अन्य चीजों के अतिरिक्त, [[विपरीत भिन्नताएँ]] उत्पन्न करने के लिए किया जा सकता है। दूसरे शब्दों में, इस गुणधर्म को व्युत्क्रम विधि के रूप में जाना जाता है जहां निरंतर मानक समान वितरण का उपयोग किसी अन्य निरंतर वितरण के लिए [[सांख्यिकीय यादृच्छिकता|यादृच्छिक संख्या]] उत्पन्न करने के लिए किया जा सकता है।<ref name=":1" />यदि <math>u_1</math>मानक समान वितरण के साथ एक समान यादृच्छिक संख्या है, अर्थात, <math>U(0,1),</math> निर्दिष्ट संचयी वितरण फलनों <math>F</math> के साथ किसी भी निरंतर वितरण से, तब <math>x = F^{-1} (u_1)</math> एक यादृच्छिक संख्या <math>x</math> उत्पन्न करता है।<ref name=":1" /> | ||
=== अन्य फलनों से संबंध === | === अन्य फलनों से संबंध === | ||
जब तक | जब तक परिवर्तन बिंदुओं पर समान परिपाटियों का पालन किया जाता है, तब तक निरंतर समान वितरण की संभाव्यता घनत्व फलनों को हेविसाइड चरण फलनों के संदर्भ में भी व्यक्त किया जा सकता है: | ||
:<math>f(x) = \frac{ \operatorname{H} (x-a) - \operatorname{H} (x-b) }{b-a} | :<math>f(x) = \frac{ \operatorname{H} (x-a) - \operatorname{H} (x-b) }{b-a} </math> | ||
या आयत | या आयत फलनों के संदर्भ में: | ||
:<math>f(x) = \frac{1}{b-a} \ \operatorname{rect} \left( \frac{x - \frac{a+b}{2}}{b-a} \right) | :<math>f(x) = \frac{1}{b-a} \ \operatorname{rect} \left( \frac{x - \frac{a+b}{2}}{b-a} \right) </math> | ||
संकेत | संकेत फलनों के परिवर्तन बिंदुओं पर कोई अस्पष्टता नहीं है। परिवर्तन बिंदुओं पर अर्ध-अधिकतम परिपाटियों का उपयोग करते हुए, निरंतर समान वितरण को संकेत फलनों के संदर्भ में इस प्रकार व्यक्त किया जा सकता है: | ||
:<math>f(x) = \frac{ \sgn{(x-a)} - \sgn{(x-b)} }{2(b-a)} | :<math>f(x) = \frac{ \sgn{(x-a)} - \sgn{(x-b)} }{2(b-a)} </math> | ||
== | == गुणधर्म == | ||
=== आघूर्ण === | === आघूर्ण === | ||
सतत एकसमान वितरण का माध्य (पहला | सतत एकसमान वितरण का माध्य (पहला अपरिष्कृत [[क्षण (गणित)|आघूर्ण]]) है: | ||
:<math>E(X) = \int_a^b x \frac{dx}{b-a} = \frac{b^2 - a^2}{2(b-a)} | :<math>E(X) = \int_a^b x \frac{dx}{b-a} = \frac{b^2 - a^2}{2(b-a)} </math> | ||
इस वितरण का दूसरा | इस वितरण का दूसरा अपरिष्कृत आघूर्ण है: | ||
:<math>E(X^2) = \int_a^b x^2 \frac{dx}{b-a} = \frac{b^3 - a^3}{3(b-a)} | :<math>E(X^2) = \int_a^b x^2 \frac{dx}{b-a} = \frac{b^3 - a^3}{3(b-a)} </math> | ||
सामान्य तौर पर, <math>n</math>- | सामान्य तौर पर, इस वितरण का <math>n</math>-वाँ अपरिष्कृत आघूर्ण है: | ||
:<math>E(X^n) = \int_a^b x^n \frac{dx}{b-a} = \frac{b^{n+1} - a^{n+1}}{(n+1)(b-a)} | :<math>E(X^n) = \int_a^b x^n \frac{dx}{b-a} = \frac{b^{n+1} - a^{n+1}}{(n+1)(b-a)} </math> | ||
इस वितरण का विचरण (दूसरा [[केंद्रीय क्षण|केंद्रीय आघूर्ण]]) है: | इस वितरण का विचरण (दूसरा [[केंद्रीय क्षण|केंद्रीय आघूर्ण]]) है: | ||
:<math>V(X) = E \left( \big( X-E(X) \big) ^2 \right) = \int_a^b \left( x - \frac{a+b}{2} \right) ^2 \frac{dx}{b-a} = \frac{(b-a)^2}{12} | :<math>V(X) = E \left( \big( X-E(X) \big) ^2 \right) = \int_a^b \left( x - \frac{a+b}{2} \right) ^2 \frac{dx}{b-a} = \frac{(b-a)^2}{12} </math> | ||
=== | === क्रम सांख्यिकी === | ||
मान लीजिए कि <math>X_1 , ..., X_n</math> एक आई.आई.डी. | मान लीजिए कि <math>X_1 , ..., X_n</math> एक आई.आई.डी. <math>U(0,1)</math> और <math>X_{(k)}</math>है। इस प्रतिदर्श से <math>k</math>-वें क्रम की सांख्यिकी है। | ||
<math>X_{(k)}</math> मापदंडों | <math>X_{(k)}</math>में मापदंडों <math>k</math> और {{tmath|n-k+1}} के साथ [[बीटा वितरण]] है। | ||
अपेक्षित मान है: | अपेक्षित मान है: | ||
:<math>\operatorname{E} (X_{(k)}) = {k \over n+1} | :<math>\operatorname{E} (X_{(k)}) = {k \over n+1} </math> | ||
Q-Q | Q-Q भूखंड बनाते समय यह तथ्य उपयोगी होता है। | ||
भिन्नता है: | भिन्नता है: | ||
:<math>\operatorname{V} (X_{(k)}) = {k(n-k+1) \over (n+1)^2 (n+2)} | :<math>\operatorname{V} (X_{(k)}) = {k(n-k+1) \over (n+1)^2 (n+2)} </math> | ||
{{See also| | {{See also|क्रम सांख्यिकी#क्रम सांख्यिकीयों की संभाव्यता वितरण}} | ||
=== एकरूपता === | === एकरूपता === | ||
संभावना है कि एक निरंतर समान रूप से वितरित यादृच्छिक चर निश्चित लंबाई के किसी भी अंतराल के भीतर आता है, अंतराल के स्थान से स्वतंत्र है (परन्तु यह अंतराल के आकार | संभावना है कि एक निरंतर समान रूप से वितरित यादृच्छिक चर निश्चित लंबाई के किसी भी अंतराल के भीतर आता है, अंतराल के स्थान से स्वतंत्र है (परन्तु यह अंतराल के आकार <math>( \ell )</math> पर निर्भर है), जब तक अंतराल वितरण के समर्थन में निहित है। | ||
वास्तव में, यदि <math>X \sim U(a,b)</math> और | वास्तव में, यदि <math>X \sim U(a,b)</math> और <math>[x,x+ \ell ]</math> का एक उप-अंतराल <math>[a,b]</math> है। स्थिर <math>\ell > 0</math> के साथ, तब: | ||
:<math> | :<math> | ||
P \big( X \in [x,x+ \ell ] \big) | P \big( X \in [x,x+ \ell ] \big) | ||
= \int_{x}^{x+ \ell} \frac{dy}{b-a} | = \int_{x}^{x+ \ell} \frac{dy}{b-a} | ||
= \frac{ \ell }{b-a} | = \frac{ \ell }{b-a} | ||
</math> | </math> | ||
जो स्वतंत्र | जो स्वतंत्र <math>x</math> है। यह तथ्य वितरण के नाम को प्रेरित करता है। | ||
=== बोरेल | === बोरेल समुच्चय का सामान्यीकरण === | ||
इस वितरण को अंतरालों की तुलना में अधिक जटिल | इस वितरण को अंतरालों की तुलना में अधिक जटिल समुच्चयों के लिए सामान्यीकृत किया जा सकता है। मान लीजिए कि <math>S</math> धनात्मक, परिमित [[लेब्सेग माप]] <math>\lambda (S)</math> का एक [[बोरेल सेट|बोरेल समुच्चय]], अर्थात, <math>0 < \lambda (S) < + \infty </math> है। समान वितरण <math>S</math> पर, संभाव्यता घनत्व फलन <math>S</math> को शून्य के बाहर परिभाषित करके निर्दिष्ट किया जा सकता है और <math>S</math> पर, <math>\tfrac{1}{\lambda (S)}</math> सदैव बराबर है। | ||
== संबंधित वितरण == | == संबंधित वितरण == | ||
* यदि X का मानक समान वितरण है, तो [[व्युत्क्रम परिवर्तन नमूनाकरण|व्युत्क्रम परिवर्तन | * यदि X का मानक समान वितरण है, तो [[व्युत्क्रम परिवर्तन नमूनाकरण|व्युत्क्रम परिवर्तन प्रतिदर्श]] विधि द्वारा, Y = - λ<sup>−1</sup> में (X) का (दर) मापदण्ड λ के साथ एक घातीय वितरण है। | ||
* यदि X का मानक समान वितरण है, तो Y = X<sup>n</sup> में | * यदि X का मानक समान वितरण है, तो Y = X<sup>n</sup> में मापदण्ड (1/n,1) के साथ बीटा वितरण है। जैसे की, | ||
* मानक समान वितरण बीटा वितरण | * मापदण्ड (1,1) के साथ, मानक समान वितरण बीटा वितरण की एक विशेष स्थिति है। | ||
*इरविन-हॉल वितरण n | *इरविन-हॉल वितरण n आई.आई.डी, ''U''(0,1) वितरण का योग है। | ||
* दो स्वतंत्र, समान रूप से वितरित, समान वितरण का योग एक सममित [[त्रिकोणीय वितरण]] उत्पन्न करता है। | * दो स्वतंत्र, समान रूप से वितरित, समान वितरण का योग एक सममित [[त्रिकोणीय वितरण]] उत्पन्न करता है। | ||
* दो आई.आई.डी. के मध्य की दूरी समान यादृच्छिक चर का भी त्रिकोणीय वितरण होता है, हालांकि सममित नहीं। | * दो आई.आई.डी. के मध्य की दूरी समान यादृच्छिक चर का भी त्रिकोणीय वितरण होता है, हालांकि सममित नहीं। | ||
| Line 190: | Line 192: | ||
===== न्यूनतम-विचरण निष्पक्ष अनुमानक ===== | ===== न्यूनतम-विचरण निष्पक्ष अनुमानक ===== | ||
{{Main| | {{Main|जर्मन टैंक समस्या}} | ||
:<math>\hat{b} _\text{UMVU} = \frac{k+1}{k} m = m + \frac{m}{k} | अज्ञात <math>b</math> के साथ, <math>[0,b]</math> पर एक समान वितरण दिया गया है। अधिकतम के लिए न्यूनतम-विचरण निष्पक्ष अनुमानक (UMVUE) है: | ||
जहाँ <math>m</math> [[नमूना अधिकतम|प्रतिदर्श अधिकतम]] | :<math>\hat{b} _\text{UMVU} = \frac{k+1}{k} m = m + \frac{m}{k} </math> | ||
जहाँ <math>m</math> [[नमूना अधिकतम|प्रतिदर्श अधिकतम]] और <math>k</math> प्रतिदर्श आकार है, प्रतिस्थापन के बिना प्रतिदर्श (हालांकि यह अंतर लगभग निश्चित रूप से निरंतर वितरण के लिए कोई असमानता नहीं है)। यह असतत वितरण के अनुमान के समान कारणों से होता है और इसे अधिकतम अंतर अनुमान के एक बहुत ही सरल स्थिति के रूप में देखा जा सकता है। [[द्वितीय विश्व युद्ध]] के पर्यन्त जर्मन टैंक उत्पादन के अनुमानों के लिए अधिकतम अनुमान अनुप्रयुक्त करने के कारण, इस समस्या को सामान्यतः [[जर्मन टैंक समस्या]] के रूप में जाना जाता है। | |||
===== अधिकतम संभावना अनुमानक ===== | ===== अधिकतम संभावना अनुमानक ===== | ||
अधिकतम संभावना अनुमानक है: | अधिकतम संभावना अनुमानक है: | ||
:<math>\hat{b} _{ML} = m | :<math>\hat{b} _{ML} = m </math> | ||
जहाँ <math>m</math> प्रतिदर्श अधिकतम है, | जहाँ <math>m</math> प्रतिदर्श अधिकतम है, जिसे <math>m = X_{(n)} </math>के रूप में भी दर्शाया गया है। प्रतिदर्श की अधिकतम क्रम सांख्यिकी है। | ||
===== आघूर्ण अनुमानक की विधि ===== | ===== आघूर्ण अनुमानक की विधि ===== | ||
[[क्षणों की विधि (सांख्यिकी)|आघूर्णों की विधि (सांख्यिकी)]] अनुमानक है: | [[क्षणों की विधि (सांख्यिकी)|आघूर्णों की विधि (सांख्यिकी)]] अनुमानक है: | ||
:<math>\hat{b} _{MM} = 2 \bar{X} | :<math>\hat{b} _{MM} = 2 \bar{X} </math> | ||
जहाँ <math>\bar{X}</math> प्रतिदर्श माध्य | जहाँ <math>\bar{X}</math> प्रतिदर्श माध्य है। | ||
==== मध्यबिंदु का अनुमान ==== | ==== मध्यबिंदु का अनुमान ==== | ||
वितरण | वितरण <math>\tfrac{a+b}{2} </math> का मध्यबिंदु, समान वितरण की माध्य और मध्यिका दोनों है। यद्यपि प्रतिदर्श माध्य और प्रतिदर्श माध्यिका दोनों ही मध्यबिंदु के निष्पक्ष अनुमानक हैं, इनमें से कोई भी प्रतिदर्श मध्य-सीमा जितना कुशल नहीं है, अर्थात, प्रतिदर्श अधिकतम और प्रतिदर्श न्यूनतम का अंकगणितीय माध्य, जो मध्यबिंदु का यूएमवीयू अनुमानक है (और अधिकतम संभावना अनुमान भी)। | ||
=== | === विश्वास्यता अंतराल === | ||
==== अधिकतम के लिए ==== | ==== अधिकतम के लिए ==== | ||
मान लीजिए कि <math>X_1 , X_2 , X_3 , ..., X_n</math> से एक प्रतिदर्श | मान लीजिए कि <math>X_1 , X_2 , X_3 , ..., X_n</math> से एक प्रतिदर्श <math>U_{[0,L]} </math>है, जहाँ <math>L</math> जनसंख्या में अधिकतम मान है। तब, <math>X_{(n)} = \max ( X_1 , X_2 , X_3 , ..., X_n )</math> लेब्सग्यू-बोरेल-घनत्व <math>f = \frac{ d \Pr _{X_{(n)}} }{ d \lambda } </math><ref name=Nechval2002>Nechval KN, Nechval NA, Vasermanis EK, Makeev VY (2002) [https://www.researchgate.net/profile/Konstantin_Nechval/publication/267986471_CONSTRUCTING_SHORTEST-LENGTH_CONFIDENCE_INTERVALS/links/55c37b3008aeb97567400f29.pdf Constructing shortest-length confidence intervals]. Transport and Telecommunication 3 (1) 95-103</ref> है। | ||
:<math>f(t) = n \frac{1}{L} \left( \frac{t}{L} \right) ^{n-1} \! = n \frac{ t^{n-1} }{ L^n } 1 \! \! 1 _{[0,L]} (t),</math> जहाँ <math>1 \! \! 1 _{[0,L]}</math> का [[सूचक कार्य|सूचक फलन]] | :<math>f(t) = n \frac{1}{L} \left( \frac{t}{L} \right) ^{n-1} \! = n \frac{ t^{n-1} }{ L^n } 1 \! \! 1 _{[0,L]} (t),</math> जहाँ <math>1 \! \! 1 _{[0,L]}</math> का [[सूचक कार्य|सूचक फलन]] <math>[0,L] </math> है। | ||
पहले दिया गया | पहले दिया गया विश्वास्यता अंतराल गणितीय रूप से गलत है: | ||
:<math>\Pr \big( [ \hat{\theta}, \hat{\theta} + \varepsilon ] \ni \theta \big) \ge 1 - \alpha</math> | :<math>\Pr \big( [ \hat{\theta}, \hat{\theta} + \varepsilon ] \ni \theta \big) \ge 1 - \alpha</math> | ||
<math>\theta</math> की जानकारी के बिना, <math>\varepsilon</math> के लिए हल नहीं किया जा सकता है, हालाँकि, कोई भी हल कर सकता है। | |||
:<math>\Pr \big( [ \hat{\theta}, \hat{\theta} (1 + \varepsilon) ] \ni \theta \big) \ge 1 - \alpha</math> के लिए <math>\varepsilon \ge (1 - \alpha) ^{-1/n} - 1</math> किसी भी अज्ञात परन्तु | :<math>\Pr \big( [ \hat{\theta}, \hat{\theta} (1 + \varepsilon) ] \ni \theta \big) \ge 1 - \alpha</math> के लिए <math>\varepsilon \ge (1 - \alpha) ^{-1/n} - 1</math>, किसी भी अज्ञात परन्तु <math>\theta </math> के लिए मान्य है। | ||
फिर कोई सबसे छोटा | फिर कोई सबसे छोटा <math>\varepsilon</math> चुनता है। उपरोक्त स्थिति को पूर्ण करना संभव है। ध्यान दें कि अंतराल की लंबाई यादृच्छिक चर <math>\hat{\theta} </math> पर निर्भर करती है। | ||
== घटना और अनुप्रयोग == | == घटना और अनुप्रयोग == | ||
फलन रूप की सरलता के कारण समान वितरण फलन की संभावनाओं की गणना करना | फलन रूप की सरलता के कारण समान वितरण फलन की संभावनाओं की गणना करना सरल है।<ref name=":3" />इसलिए, ऐसे कई अनुप्रयोग हैं जिनके लिए इस वितरण का उपयोग किया जा सकता है जैसा कि नीचे दर्शाया गया है: परिकल्पना परीक्षण स्थितियां, यादृच्छिक प्रतिदर्श स्थितियां, वित्त, आदि। इसके अतिरिक्त, सामान्यतः, भौतिक उत्पत्ति के प्रयोग एक समान वितरण का पालन करते हैं (उदाहरण के लिए रेडियोधर्मी [[रेडियोधर्मी क्षय|कणों]] का उत्सर्जन)।<ref name=":0" />हालाँकि, यह ध्यान रखना महत्वपूर्ण है कि किसी भी अनुप्रयोग में, यह अपरिवर्तनीय धारणा है कि निश्चित लंबाई के अंतराल में गिरने की संभावना स्थिर है।<ref name=":3" /> | ||
=== समान वितरण के लिए अर्थशास्त्र उदाहरण === | === समान वितरण के लिए अर्थशास्त्र उदाहरण === | ||
अर्थशास्त्र के क्षेत्र में, सामान्यतः मांग और | अर्थशास्त्र के क्षेत्र में, सामान्यतः मांग और पुनःपूर्ति अपेक्षित सामान्य वितरण का पालन नहीं कर सकती है। परिणामस्वरूप, अन्य वितरण प्रतिरुपों का उपयोग संभावनाओं और प्रवृतियों की उन्नत भविष्यवाणी करने के लिए किया जाता है जैसे कि [[बर्नौली प्रक्रिया]] है।<ref name=":4">{{Cite journal|last=Wanke|first=Peter|date=2008|title=नए उत्पाद सूची प्रबंधन के लिए पहले व्यावहारिक दृष्टिकोण के रूप में समान वितरण|url=https://www.researchgate.net/publication/223280031|journal=International Journal of Production Economics|volume=114|issue=2|pages=811–819|via=Research Gate|doi=10.1016/j.ijpe.2008.04.004}}</ref> परन्तु वान्के (2008) के अनुसार, जीवन-चक्र मानांकन के प्रारम्भ में विस्तृत सूची प्रबंधन के लिए अग्रिम काल की जांच की विशेष स्थिति में, जब एक पूर्णतया से नए उत्पाद का विश्लेषण किया जा रहा है, तो समान वितरण अधिक उपयोगी सिद्ध होता है।<ref name=":4" />इस स्थिति में, अन्य वितरण व्यवहार्य नहीं हो सकता है क्योंकि नए उत्पाद पर कोई उपस्थित आंकड़े नहीं है या मांग इतिहास अनुपलब्ध है इसलिए वास्तव में कोई उचित या ज्ञात वितरण नहीं है।<ref name=":4" />इस स्थिति में समान वितरण आदर्श होगा क्योंकि नए उत्पाद के लिए अग्रिम काल (मांग से संबंधित) का यादृच्छिक चर अज्ञात है, परन्तु परिणाम दो मानों की एक प्रशंसनीय सीमा के मध्य होने की संभावना है।<ref name=":4" />अग्रिम काल इस प्रकार यादृच्छिक चर का प्रतिनिधित्व करेगा। समान वितरण प्रतिरुप से, अग्रिम काल से संबंधित अन्य कारकों की गणना करने में सक्षम थे जैसे कि [[चक्र सेवा स्तर]] और [[प्रति चक्र कमी]] है। यह भी ध्यान दिया गया कि गणना की सरलता के कारण समान वितरण का भी उपयोग किया गया था।<ref name=":4" /> | ||
=== एक यादृच्छिक वितरण से | === एक यादृच्छिक वितरण से प्रतिचयन === | ||
{{Main| | {{Main|व्युत्क्रम परिवर्तन प्रतिदर्श}} | ||
एकसमान वितरण यादृच्छिक वितरण से प्रतिदर्श लेने के लिए उपयोगी है। एक सामान्य विधि व्युत्क्रम परिवर्तन | |||
एकसमान वितरण यादृच्छिक वितरण से प्रतिदर्श लेने के लिए उपयोगी है। एक सामान्य विधि व्युत्क्रम परिवर्तन प्रतिचयन विधि है, जो लक्ष्य यादृच्छिक चर के संचयी वितरण फलन (CDF) का उपयोग करती है। यह विधि सैद्धान्तिक कार्यों में बहुत उपयोगी है। चूंकि इस पद्धति का उपयोग करने वाले अनुकरण के लिए लक्ष्य चर के सीडीएफ को उलटने की आवश्यकता होती है, ऐसी स्थितियों के लिए वैकल्पिक तरीके तैयार किए गए हैं जहां सीडीएफ संवृत रूप में ज्ञात नहीं है। ऐसी ही एक विधि [[अस्वीकृति नमूनाकरण|अस्वीकृति प्रतिचयन]] है। | |||
[[सामान्य वितरण]] एक महत्वपूर्ण उदाहरण है जहां व्युत्क्रम परिवर्तन विधि कुशल नहीं है। हालाँकि, एक सटीक विधि है, बॉक्स-मुलर परिवर्तन, जो दो स्वतंत्र समान यादृच्छिक चर को दो स्वतंत्र सामान्य वितरण यादृच्छिक चर में परिवर्तित करने के लिए व्युत्क्रम परिवर्तन का उपयोग करता है। | [[सामान्य वितरण]] एक महत्वपूर्ण उदाहरण है जहां व्युत्क्रम परिवर्तन विधि कुशल नहीं है। हालाँकि, एक सटीक विधि है, बॉक्स-मुलर परिवर्तन, जो दो स्वतंत्र समान यादृच्छिक चर को दो स्वतंत्र सामान्य वितरण यादृच्छिक चर में परिवर्तित करने के लिए व्युत्क्रम परिवर्तन का उपयोग करता है। | ||
=== परिमाणीकरण त्रुटि === | === परिमाणीकरण त्रुटि === | ||
{{Main| | {{Main|परिमाणीकरण त्रुटि}} | ||
अनुरूप-से-अंकीय रूपांतरण में, एक परिमाणीकरण त्रुटि उत्पन्न होती है। यह त्रुटि या तो पूर्णांकन या खंडन के कारण है। जब मूल संकेत एक [[कम से कम महत्वपूर्ण बिट|कम-से-कम महत्वपूर्ण बिट]] (LSB) से बहुत बड़ा होता है, तो परिमाणीकरण त्रुटि संकेत के साथ महत्वपूर्ण रूप से सहसंबद्ध नहीं होता है और लगभग समान वितरण होता है। इसलिए [[आरएमएस त्रुटि]] इस वितरण के भिन्नता से उत्पन्न होती है। | |||
== यादृच्छिक भिन्न युग == | |||
ऐसे कई अनुप्रयोग हैं जिनमें अनुकरण प्रयोग चलाना उपयोगी है। कई [[प्रोग्रामिंग भाषा|क्रमदेशन भाषाएं]] छद्म-यादृच्छिक संख्याएं उत्पन्न करने के लिए कार्यान्वयन के साथ आती हैं जिन्हें मानक समान वितरण के अनुसार प्रभावी ढंग से वितरित किया जाता है। | |||
यदि <math>u</math> मानक समान वितरण से प्रतिदर्श लिया गया मान है, फिर मान <math>a+(b-a)u</math> द्वारा मानकीकृत समान वितरण | दूसरी ओर, समान रूप से वितरित संख्याओं को प्रायः [[गैर-समान यादृच्छिक विविधता पीढ़ी|गैर-समान यादृच्छिक विविधता युग]] के आधार के रूप में उपयोग किया जाता है। | ||
यदि <math>u</math> मानक समान वितरण से प्रतिदर्श लिया गया मान है, फिर मान <math>a+(b-a)u</math> द्वारा मानकीकृत समान वितरण <math>a</math> और <math>b</math> का अनुसरण करता है, जैसा ऊपर वर्णित है। | |||
== इतिहास == | == इतिहास == | ||
जबकि समान वितरण की अवधारणा में ऐतिहासिक उत्पत्ति अनिर्णीत है, यह अनुमान लगाया गया है कि | जबकि समान वितरण की अवधारणा में ऐतिहासिक उत्पत्ति अनिर्णीत है, यह अनुमान लगाया गया है कि एकसमान शब्द पासा खेल में [[समसंभाव्यता]] की अवधारणा से उत्पन्न हुआ है (ध्यान दें कि पासा खेल में असतत समान वितरण होगा और निरंतर समान प्रतिदर्श स्थान नहीं होगा)। समसंभाव्यता का उल्लेख [[ जेरोम कार्डानो |जेरोम कार्डानो]] के लिबर डी लूडो एले में किया गया था, जो 16वीं शताब्दी में लिखी गयी एक नियमावली थी और पासे के संबंध में उन्नत संभाव्यता कलन पर विस्तृत था।<ref>{{Cite journal|last=Bellhouse|first=David|date=May 2005|title=कार्डानो के लिबर डी लूडो को डिकोड करना|journal=Historia Mathematica|volume=32|pages=180–202|doi=10.1016/j.hm.2004.04.001|doi-access=free}}</ref> | ||
| Line 255: | Line 260: | ||
* बॉक्स-मुलर परिवर्तन | * बॉक्स-मुलर परिवर्तन | ||
* [[संभाव्यता कथानक (बहुविकल्पी)]] | * [[संभाव्यता कथानक (बहुविकल्पी)]] | ||
* | * Q-Q भूखंड | ||
* [[आयताकार कार्य|आयताकार फलन]] | * [[आयताकार कार्य|आयताकार फलन]] | ||
* इरविन-हॉल वितरण - पतित स्थिति में जहां n=1, इरविन-हॉल वितरण 0 और 1 के मध्य एक समान वितरण उत्पन्न करता है। | * इरविन-हॉल वितरण - पतित स्थिति में जहां n=1, इरविन-हॉल वितरण 0 और 1 के मध्य एक समान वितरण उत्पन्न करता है। | ||
| Line 285: | Line 290: | ||
{{Authority control}} | {{Authority control}} | ||
{{DEFAULTSORT:Uniform Distribution (Continuous)}} | {{DEFAULTSORT:Uniform Distribution (Continuous)}} | ||
[[su:Sebaran seragam#Kasus kontinyu]] | [[su:Sebaran seragam#Kasus kontinyu]] | ||
[[Category:All articles with bare URLs for citations]] | |||
[[Category:Articles with PDF format bare URLs for citations]] | |||
[[Category: | [[Category:Articles with bare URLs for citations from March 2022]] | ||
[[Category:Created On 06/07/2023]] | [[Category:Articles with hatnote templates targeting a nonexistent page|Uniform Distribution (Continuous)]] | ||
[[Category:Collapse templates|Uniform Distribution (Continuous)]] | |||
[[Category:Created On 06/07/2023|Uniform Distribution (Continuous)]] | |||
[[Category:Lua-based templates|Uniform Distribution (Continuous)]] | |||
[[Category:Machine Translated Page|Uniform Distribution (Continuous)]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists|Uniform Distribution (Continuous)]] | |||
[[Category:Pages that use a deprecated format of the math tags|Uniform Distribution (Continuous)]] | |||
[[Category:Pages with maths render errors|Uniform Distribution (Continuous)]] | |||
[[Category:Pages with script errors|Uniform Distribution (Continuous)]] | |||
[[Category:Sidebars with styles needing conversion|Uniform Distribution (Continuous)]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready|Uniform Distribution (Continuous)]] | |||
[[Category:Templates generating microformats|Uniform Distribution (Continuous)]] | |||
[[Category:Templates that add a tracking category|Uniform Distribution (Continuous)]] | |||
[[Category:Templates that are not mobile friendly|Uniform Distribution (Continuous)]] | |||
[[Category:Templates that generate short descriptions|Uniform Distribution (Continuous)]] | |||
[[Category:Templates using TemplateData|Uniform Distribution (Continuous)]] | |||
[[Category:Wikipedia metatemplates|Uniform Distribution (Continuous)]] | |||
[[Category:निरंतर वितरण|Uniform Distribution (Continuous)]] | |||
[[Category:स्थान-पैमाने पर पारिवारिक संभाव्यता वितरण|Uniform Distribution (Continuous)]] | |||
Latest revision as of 12:27, 6 November 2023
|
Probability density function 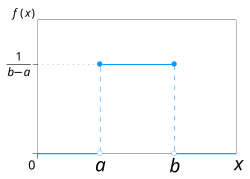 Using maximum convention | |||
|
Cumulative distribution function  | |||
| Notation | |||
|---|---|---|---|
| Parameters | |||
| Support | |||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| MAD | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
| MGF | |||
| CF | |||
संभाव्यता सिद्धांत और सांख्यिकी में, निरंतर समान वितरण या आयताकार वितरण सममित संभाव्यता वितरण का एक वर्ग है। ऐसा वितरण एक प्रयोग का वर्णन करता है जहां एक यादृच्छिक परिणाम होता है जो कुछ सीमाओं के मध्य होता है।[1] सीमाएं मापदंडों, और द्वारा परिभाषित की जाती हैं जो न्यूनतम और अधिकतम मान हैं। अंतराल या तो संवृत (अर्थात, ) या विवृत (अर्थात् ) हो सकता है।[2] इसलिए, वितरण , प्रायः संक्षिप्त किया जाता है जहाँ का अर्थ समान वितरण है।[1]सीमाओं के मध्य का अंतर, अंतराल की लंबाई को परिभाषित करता है; वितरण के समर्थन (गणित) पर समान लंबाई के सभी अंतराल (गणित) समान रूप से संभावित हैं। यह एक यादृच्छिक चर के लिए अधिकतम एन्ट्रापी संभाव्यता वितरण है। इसके अतिरिक्त कोई प्रतिबंध नहीं है कि यह वितरण के समर्थन में सम्मिलित है।[3]
परिभाषाएँ
संभाव्यता घनत्व फलन
सतत समान वितरण का संभाव्यता घनत्व फलन है:
के मान, दो सीमाओं और पर, सामान्यतः महत्वहीन होते हैं, क्योंकि वे किसी भी अंतराल और न ही किसी उच्चतर आघूर्ण पर, के मान में परिवर्तन नहीं करते हैं। कभी-कभी उन्हें शून्य और कभी-कभी चुना जाता है। अधिकतम संभावना की विधि द्वारा अनुमान के संदर्भ में उत्तरार्द्ध उपयुक्त है। फूरियर विश्लेषण के संदर्भ में, कोई या का मान ले सकता है, क्योंकि तब इस समान फलन के कई अभिन्न परिवर्तनों का व्युत्क्रम परिवर्तन फलन को वापस लाएगा, न कि एक फलन जो, अर्थात शून्य माप वाले बिंदुओं के एक समुच्चय को छोड़कर लगभग हर जगह समान है। साथ ही, यह संकेत फलन के अनुरूप है, जिसमें ऐसी कोई अस्पष्टता नहीं है।
कोई भी संभाव्यता घनत्व फलन एकीकृत होता है इसलिए निरंतर समान वितरण की संभाव्यता घनत्व फलनों को सुचित्रित रूप से एक आयत के रूप में चित्रित किया गया है, जहाँ आधार लंबाई और ऊंचाई है। जैसे-जैसे आधार की लंबाई बढ़ती है, ऊंचाई (वितरण सीमाओं के भीतर किसी विशेष मान पर घनत्व) कम हो जाती है।[4]
माध्य और विचरण की दृष्टि से, निरंतर समान वितरण की संभाव्यता घनत्व फलन है:
संचयी वितरण फलन
सतत समान वितरण का संचयी वितरण फलन है:
इसका व्युत्क्रम है:
माध्य और विचरण की दृष्टि से सतत समान वितरण का संचयी वितरण फलन है:
इसका व्युत्क्रम है:
उदाहरण 1. सतत समान वितरण फलन का उपयोग
एक यादृच्छिक चर के लिए, प्राप्त करें:
निरंतर समान वितरण फलन के चित्रमय प्रतिनिधित्व में, निर्दिष्ट सीमा के भीतर वक्र के नीचे का क्षेत्र, संभाव्यता प्रदर्शित करते हुए, एक आयत है। उपरोक्त विशिष्ट उदाहरण के लिए, आधार होगा और ऊंचाई [5]होगी।
उदाहरण 2. निरंतर समान वितरण फलन (सशर्त) का उपयोग
एक यादृच्छिक चर के लिए, प्राप्त करें:
उपरोक्त उदाहरण निरंतर समान वितरण के लिए एक सशर्त संभाव्यता स्थिति है: मान लें कि सत्य है, की क्या प्रायिकता है ? सशर्त संभाव्यता प्रतिदर्श स्थान को परिवर्तित कर देती है, इसलिए एक नई अंतराल लंबाई की गणना करनी होगी, जहाँ और है।[5]आलेखीय प्रतिनिधित्व अभी भी उदाहरण 1 का अनुसरण करेगा, जहां निर्दिष्ट सीमा के भीतर वक्र के नीचे का क्षेत्र संभाव्यता प्रदर्शित करता है; आयत का आधार होगा और ऊंचाई होगी।[5]
जनक फलन
आघूर्ण जनक फलन
सतत एकसमान वितरण का आघूर्ण-जनक फलन है:[6]
जिससे हम अपरिष्कृत आघूर्णों की गणना कर सकते हैं:
निरंतर समान वितरण के बाद एक यादृच्छिक चर के लिए, अपेक्षित मान और भिन्नता है।
विशेष स्थिति के लिए, निरंतर समान वितरण की संभाव्यता घनत्व फलन है:
आघूर्ण-जनक फलन सरल रूप में कम हो जाता है:
संचयी-जनक फलन
के लिए, अंतराल पर निरंतर समान वितरण का 𝑛-वाँ संचयी है। जहाँ , -वीं बर्नौली संख्या है।[8]
मानक समान वितरण
मापदंडों और के साथ निरंतर समान वितरण, अर्थात, को मानक समान वितरण कहा जाता है।
मानक समान वितरण का एक रोचक गुणधर्म यह है कि यदि एक मानक समान वितरण है, फिर वैसा ही होता है। इस गुणधर्म का उपयोग अन्य चीजों के अतिरिक्त, विपरीत भिन्नताएँ उत्पन्न करने के लिए किया जा सकता है। दूसरे शब्दों में, इस गुणधर्म को व्युत्क्रम विधि के रूप में जाना जाता है जहां निरंतर मानक समान वितरण का उपयोग किसी अन्य निरंतर वितरण के लिए यादृच्छिक संख्या उत्पन्न करने के लिए किया जा सकता है।[4]यदि मानक समान वितरण के साथ एक समान यादृच्छिक संख्या है, अर्थात, निर्दिष्ट संचयी वितरण फलनों के साथ किसी भी निरंतर वितरण से, तब एक यादृच्छिक संख्या उत्पन्न करता है।[4]
अन्य फलनों से संबंध
जब तक परिवर्तन बिंदुओं पर समान परिपाटियों का पालन किया जाता है, तब तक निरंतर समान वितरण की संभाव्यता घनत्व फलनों को हेविसाइड चरण फलनों के संदर्भ में भी व्यक्त किया जा सकता है:
या आयत फलनों के संदर्भ में:
संकेत फलनों के परिवर्तन बिंदुओं पर कोई अस्पष्टता नहीं है। परिवर्तन बिंदुओं पर अर्ध-अधिकतम परिपाटियों का उपयोग करते हुए, निरंतर समान वितरण को संकेत फलनों के संदर्भ में इस प्रकार व्यक्त किया जा सकता है:
गुणधर्म
आघूर्ण
सतत एकसमान वितरण का माध्य (पहला अपरिष्कृत आघूर्ण) है:
इस वितरण का दूसरा अपरिष्कृत आघूर्ण है:
सामान्य तौर पर, इस वितरण का -वाँ अपरिष्कृत आघूर्ण है:
इस वितरण का विचरण (दूसरा केंद्रीय आघूर्ण) है:
क्रम सांख्यिकी
मान लीजिए कि एक आई.आई.डी. और है। इस प्रतिदर्श से -वें क्रम की सांख्यिकी है।
में मापदंडों और के साथ बीटा वितरण है।
अपेक्षित मान है:
Q-Q भूखंड बनाते समय यह तथ्य उपयोगी होता है।
भिन्नता है:
एकरूपता
संभावना है कि एक निरंतर समान रूप से वितरित यादृच्छिक चर निश्चित लंबाई के किसी भी अंतराल के भीतर आता है, अंतराल के स्थान से स्वतंत्र है (परन्तु यह अंतराल के आकार पर निर्भर है), जब तक अंतराल वितरण के समर्थन में निहित है।
वास्तव में, यदि और का एक उप-अंतराल है। स्थिर के साथ, तब:
जो स्वतंत्र है। यह तथ्य वितरण के नाम को प्रेरित करता है।
बोरेल समुच्चय का सामान्यीकरण
इस वितरण को अंतरालों की तुलना में अधिक जटिल समुच्चयों के लिए सामान्यीकृत किया जा सकता है। मान लीजिए कि धनात्मक, परिमित लेब्सेग माप का एक बोरेल समुच्चय, अर्थात, है। समान वितरण पर, संभाव्यता घनत्व फलन को शून्य के बाहर परिभाषित करके निर्दिष्ट किया जा सकता है और पर, सदैव बराबर है।
संबंधित वितरण
- यदि X का मानक समान वितरण है, तो व्युत्क्रम परिवर्तन प्रतिदर्श विधि द्वारा, Y = - λ−1 में (X) का (दर) मापदण्ड λ के साथ एक घातीय वितरण है।
- यदि X का मानक समान वितरण है, तो Y = Xn में मापदण्ड (1/n,1) के साथ बीटा वितरण है। जैसे की,
- मापदण्ड (1,1) के साथ, मानक समान वितरण बीटा वितरण की एक विशेष स्थिति है।
- इरविन-हॉल वितरण n आई.आई.डी, U(0,1) वितरण का योग है।
- दो स्वतंत्र, समान रूप से वितरित, समान वितरण का योग एक सममित त्रिकोणीय वितरण उत्पन्न करता है।
- दो आई.आई.डी. के मध्य की दूरी समान यादृच्छिक चर का भी त्रिकोणीय वितरण होता है, हालांकि सममित नहीं।
सांख्यिकीय अनुमान
मापदंडों का अनुमान
अधिकतम का अनुमान
न्यूनतम-विचरण निष्पक्ष अनुमानक
अज्ञात के साथ, पर एक समान वितरण दिया गया है। अधिकतम के लिए न्यूनतम-विचरण निष्पक्ष अनुमानक (UMVUE) है:
जहाँ प्रतिदर्श अधिकतम और प्रतिदर्श आकार है, प्रतिस्थापन के बिना प्रतिदर्श (हालांकि यह अंतर लगभग निश्चित रूप से निरंतर वितरण के लिए कोई असमानता नहीं है)। यह असतत वितरण के अनुमान के समान कारणों से होता है और इसे अधिकतम अंतर अनुमान के एक बहुत ही सरल स्थिति के रूप में देखा जा सकता है। द्वितीय विश्व युद्ध के पर्यन्त जर्मन टैंक उत्पादन के अनुमानों के लिए अधिकतम अनुमान अनुप्रयुक्त करने के कारण, इस समस्या को सामान्यतः जर्मन टैंक समस्या के रूप में जाना जाता है।
अधिकतम संभावना अनुमानक
अधिकतम संभावना अनुमानक है:
जहाँ प्रतिदर्श अधिकतम है, जिसे के रूप में भी दर्शाया गया है। प्रतिदर्श की अधिकतम क्रम सांख्यिकी है।
आघूर्ण अनुमानक की विधि
आघूर्णों की विधि (सांख्यिकी) अनुमानक है:
जहाँ प्रतिदर्श माध्य है।
मध्यबिंदु का अनुमान
वितरण का मध्यबिंदु, समान वितरण की माध्य और मध्यिका दोनों है। यद्यपि प्रतिदर्श माध्य और प्रतिदर्श माध्यिका दोनों ही मध्यबिंदु के निष्पक्ष अनुमानक हैं, इनमें से कोई भी प्रतिदर्श मध्य-सीमा जितना कुशल नहीं है, अर्थात, प्रतिदर्श अधिकतम और प्रतिदर्श न्यूनतम का अंकगणितीय माध्य, जो मध्यबिंदु का यूएमवीयू अनुमानक है (और अधिकतम संभावना अनुमान भी)।
विश्वास्यता अंतराल
अधिकतम के लिए
मान लीजिए कि से एक प्रतिदर्श है, जहाँ जनसंख्या में अधिकतम मान है। तब, लेब्सग्यू-बोरेल-घनत्व [9] है।
- जहाँ का सूचक फलन है।
पहले दिया गया विश्वास्यता अंतराल गणितीय रूप से गलत है:
की जानकारी के बिना, के लिए हल नहीं किया जा सकता है, हालाँकि, कोई भी हल कर सकता है।
- के लिए , किसी भी अज्ञात परन्तु के लिए मान्य है।
फिर कोई सबसे छोटा चुनता है। उपरोक्त स्थिति को पूर्ण करना संभव है। ध्यान दें कि अंतराल की लंबाई यादृच्छिक चर पर निर्भर करती है।
घटना और अनुप्रयोग
फलन रूप की सरलता के कारण समान वितरण फलन की संभावनाओं की गणना करना सरल है।[2]इसलिए, ऐसे कई अनुप्रयोग हैं जिनके लिए इस वितरण का उपयोग किया जा सकता है जैसा कि नीचे दर्शाया गया है: परिकल्पना परीक्षण स्थितियां, यादृच्छिक प्रतिदर्श स्थितियां, वित्त, आदि। इसके अतिरिक्त, सामान्यतः, भौतिक उत्पत्ति के प्रयोग एक समान वितरण का पालन करते हैं (उदाहरण के लिए रेडियोधर्मी कणों का उत्सर्जन)।[1]हालाँकि, यह ध्यान रखना महत्वपूर्ण है कि किसी भी अनुप्रयोग में, यह अपरिवर्तनीय धारणा है कि निश्चित लंबाई के अंतराल में गिरने की संभावना स्थिर है।[2]
समान वितरण के लिए अर्थशास्त्र उदाहरण
अर्थशास्त्र के क्षेत्र में, सामान्यतः मांग और पुनःपूर्ति अपेक्षित सामान्य वितरण का पालन नहीं कर सकती है। परिणामस्वरूप, अन्य वितरण प्रतिरुपों का उपयोग संभावनाओं और प्रवृतियों की उन्नत भविष्यवाणी करने के लिए किया जाता है जैसे कि बर्नौली प्रक्रिया है।[10] परन्तु वान्के (2008) के अनुसार, जीवन-चक्र मानांकन के प्रारम्भ में विस्तृत सूची प्रबंधन के लिए अग्रिम काल की जांच की विशेष स्थिति में, जब एक पूर्णतया से नए उत्पाद का विश्लेषण किया जा रहा है, तो समान वितरण अधिक उपयोगी सिद्ध होता है।[10]इस स्थिति में, अन्य वितरण व्यवहार्य नहीं हो सकता है क्योंकि नए उत्पाद पर कोई उपस्थित आंकड़े नहीं है या मांग इतिहास अनुपलब्ध है इसलिए वास्तव में कोई उचित या ज्ञात वितरण नहीं है।[10]इस स्थिति में समान वितरण आदर्श होगा क्योंकि नए उत्पाद के लिए अग्रिम काल (मांग से संबंधित) का यादृच्छिक चर अज्ञात है, परन्तु परिणाम दो मानों की एक प्रशंसनीय सीमा के मध्य होने की संभावना है।[10]अग्रिम काल इस प्रकार यादृच्छिक चर का प्रतिनिधित्व करेगा। समान वितरण प्रतिरुप से, अग्रिम काल से संबंधित अन्य कारकों की गणना करने में सक्षम थे जैसे कि चक्र सेवा स्तर और प्रति चक्र कमी है। यह भी ध्यान दिया गया कि गणना की सरलता के कारण समान वितरण का भी उपयोग किया गया था।[10]
एक यादृच्छिक वितरण से प्रतिचयन
एकसमान वितरण यादृच्छिक वितरण से प्रतिदर्श लेने के लिए उपयोगी है। एक सामान्य विधि व्युत्क्रम परिवर्तन प्रतिचयन विधि है, जो लक्ष्य यादृच्छिक चर के संचयी वितरण फलन (CDF) का उपयोग करती है। यह विधि सैद्धान्तिक कार्यों में बहुत उपयोगी है। चूंकि इस पद्धति का उपयोग करने वाले अनुकरण के लिए लक्ष्य चर के सीडीएफ को उलटने की आवश्यकता होती है, ऐसी स्थितियों के लिए वैकल्पिक तरीके तैयार किए गए हैं जहां सीडीएफ संवृत रूप में ज्ञात नहीं है। ऐसी ही एक विधि अस्वीकृति प्रतिचयन है।
सामान्य वितरण एक महत्वपूर्ण उदाहरण है जहां व्युत्क्रम परिवर्तन विधि कुशल नहीं है। हालाँकि, एक सटीक विधि है, बॉक्स-मुलर परिवर्तन, जो दो स्वतंत्र समान यादृच्छिक चर को दो स्वतंत्र सामान्य वितरण यादृच्छिक चर में परिवर्तित करने के लिए व्युत्क्रम परिवर्तन का उपयोग करता है।
परिमाणीकरण त्रुटि
अनुरूप-से-अंकीय रूपांतरण में, एक परिमाणीकरण त्रुटि उत्पन्न होती है। यह त्रुटि या तो पूर्णांकन या खंडन के कारण है। जब मूल संकेत एक कम-से-कम महत्वपूर्ण बिट (LSB) से बहुत बड़ा होता है, तो परिमाणीकरण त्रुटि संकेत के साथ महत्वपूर्ण रूप से सहसंबद्ध नहीं होता है और लगभग समान वितरण होता है। इसलिए आरएमएस त्रुटि इस वितरण के भिन्नता से उत्पन्न होती है।
यादृच्छिक भिन्न युग
ऐसे कई अनुप्रयोग हैं जिनमें अनुकरण प्रयोग चलाना उपयोगी है। कई क्रमदेशन भाषाएं छद्म-यादृच्छिक संख्याएं उत्पन्न करने के लिए कार्यान्वयन के साथ आती हैं जिन्हें मानक समान वितरण के अनुसार प्रभावी ढंग से वितरित किया जाता है।
दूसरी ओर, समान रूप से वितरित संख्याओं को प्रायः गैर-समान यादृच्छिक विविधता युग के आधार के रूप में उपयोग किया जाता है।
यदि मानक समान वितरण से प्रतिदर्श लिया गया मान है, फिर मान द्वारा मानकीकृत समान वितरण और का अनुसरण करता है, जैसा ऊपर वर्णित है।
इतिहास
जबकि समान वितरण की अवधारणा में ऐतिहासिक उत्पत्ति अनिर्णीत है, यह अनुमान लगाया गया है कि एकसमान शब्द पासा खेल में समसंभाव्यता की अवधारणा से उत्पन्न हुआ है (ध्यान दें कि पासा खेल में असतत समान वितरण होगा और निरंतर समान प्रतिदर्श स्थान नहीं होगा)। समसंभाव्यता का उल्लेख जेरोम कार्डानो के लिबर डी लूडो एले में किया गया था, जो 16वीं शताब्दी में लिखी गयी एक नियमावली थी और पासे के संबंध में उन्नत संभाव्यता कलन पर विस्तृत था।[11]
यह भी देखें
- पृथक समान वितरण
- बीटा वितरण
- बॉक्स-मुलर परिवर्तन
- संभाव्यता कथानक (बहुविकल्पी)
- Q-Q भूखंड
- आयताकार फलन
- इरविन-हॉल वितरण - पतित स्थिति में जहां n=1, इरविन-हॉल वितरण 0 और 1 के मध्य एक समान वितरण उत्पन्न करता है।
- बेट्स वितरण - इरविन-हॉल वितरण के समान, परन्तु n के लिए पुनर्स्केल किया गया। इरविन-हॉल वितरण की तरह, पतित स्थिति में जहां n=1, बेट्स वितरण 0 और 1 के मध्य एक समान वितरण उत्पन्न करता है।
संदर्भ
- ↑ 1.0 1.1 1.2 Dekking, Michel (2005). A modern introduction to probability and statistics : understanding why and how. London, UK: Springer. pp. 60–61. ISBN 978-1-85233-896-1.
- ↑ 2.0 2.1 2.2 Walpole, Ronald; et al. (2012). इंजीनियरों और वैज्ञानिकों के लिए संभाव्यता और सांख्यिकी. Boston, USA: Prentice Hall. pp. 171–172. ISBN 978-0-321-62911-1.
- ↑ Park, Sung Y.; Bera, Anil K. (2009). "अधिकतम एन्ट्रापी ऑटोरेग्रेसिव कंडीशनल हेटेरोस्केडैस्टिसिटी मॉडल". Journal of Econometrics. 150 (2): 219–230. CiteSeerX 10.1.1.511.9750. doi:10.1016/j.jeconom.2008.12.014.
- ↑ 4.0 4.1 4.2 "समान वितरण (निरंतर)". MathWorks. 2019. Retrieved November 22, 2019.
- ↑ 5.0 5.1 5.2 Illowsky, Barbara; et al. (2013). परिचयात्मक सांख्यिकी. Rice University, Houston, Texas, USA: OpenStax College. pp. 296–304. ISBN 978-1-938168-20-8.
- ↑ Casella & Berger 2001, p. 626
- ↑ https://www.stat.washington.edu/~nehemyl/files/UW_MATH-STAT395_moment-functions.pdf[bare URL PDF]
- ↑ https://galton.uchicago.edu/~wichura/Stat304/Handouts/L18.cumulants.pdf[bare URL PDF]
- ↑ Nechval KN, Nechval NA, Vasermanis EK, Makeev VY (2002) Constructing shortest-length confidence intervals. Transport and Telecommunication 3 (1) 95-103
- ↑ 10.0 10.1 10.2 10.3 10.4 Wanke, Peter (2008). "नए उत्पाद सूची प्रबंधन के लिए पहले व्यावहारिक दृष्टिकोण के रूप में समान वितरण". International Journal of Production Economics. 114 (2): 811–819. doi:10.1016/j.ijpe.2008.04.004 – via Research Gate.
- ↑ Bellhouse, David (May 2005). "कार्डानो के लिबर डी लूडो को डिकोड करना". Historia Mathematica. 32: 180–202. doi:10.1016/j.hm.2004.04.001.
अग्रिम पठन
- Casella, George; Roger L. Berger (2001), Statistical Inference (2nd ed.), ISBN 978-0-534-24312-8, LCCN 2001025794