रम्ब रेखा: Difference between revisions

Latest revision as of 16:45, 6 November 2023

एकदिश नौपथ, या रम्ब रेखाओं की छवि, जो उत्तरी ध्रुव की ओर बढ़ती है।

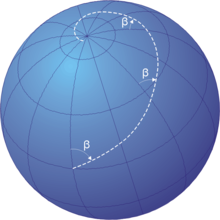
मार्गनिर्देशन में, एक रम्ब रेखा, रम्ब (/rʌm/), या एकदिश नौपथ एक चाप है जो एक ही कोण पर देशांतर के सभी भूमध्य रेखाओं को पार करता है, जोकि वास्तविक उत्तर दिशा के सापेक्ष मापा गया स्थिर दिक्कोण वाला पथ है।

परिचय

भूमंडल की सतहों पर रम्ब रेखा पाठ्यक्रम का पालन करने के प्रभाव पर पहली बार 1537 में पुर्तगाली गणितज्ञ पेड्रो नून्स ने 1590 के दशक में थॉमस हैरियट द्वारा आगे के गणितीय विकास के साथ समुद्रीय रेखाचित्र की रक्षा में अपने ग्रंथ में चर्चा की थी।

रम्ब रेखाओं की तुलना एक बड़े वृत्त से की जा सकती है, जो वृत्त की सतह पर दो बिंदुओं के मध्य की सबसे छोटी दूरी का पथ है। एक बड़े वृत्त पर, गंतव्य बिंदु का दिक्कोण स्थिर नहीं रहता है। यदि किसी को बृहत् वृत के साथ एक मोटर गाड़ी चलानी होती है तो वह चालन चक्र को स्थिर रखता है, परन्तु रम्ब रेखाओं का पालन करने के लिए पहिये को घुमाना पड़ता है, जैसे-जैसे स्तंभ पास आते हैं, इसे और अधिक तीव्रता से घुमाते हैं। दूसरे शब्दों में, एक बड़ा वृत्त शून्य अल्पांतरी वक्रता के साथ स्थानीय रूप से "सीधा" होता है, जबकि रम्ब रेखाओं में गैर-शून्य अल्पांतरी वक्रता होती है।

देशांतर के याम्योत्तर और अक्षांश के समानांतर रम्ब रेखाओं की विशेष स्थितियां प्रदान करते हैं, जहां उनके प्रतिच्छेदन के कोण क्रमशः 0° और 90° होते हैं। उत्तर-दक्षिण पथ पर रम्ब रेखा पाठ्यक्रम बृहत् वृत्तों के अनुरूप है, जैसे कि यह भूमध्य रेखाओं के साथ पूर्व-पश्चिम पथ पर होता है।

मर्केटर प्रक्षेपण मानचित्र पर, कोई भी रम्ब रेखा एक सीधी रेखा है; इस प्रकार के मानचित्रों पर पृथ्वी पर किन्हीं दो बिंदुओं के मध्य बिना मानचित्र के किनारे से हटे रम्ब रेखा खींची जा सकती है। परन्तु सैद्धांतिक रूप से एकदिश नौपथ मानचित्र के दाहिने किनारे से आगे बढ़ सकता है, जहां यह फिर उसी प्रवणता के साथ बाएं किनारे पर जारी रहता है (यह मानते हुए कि प्रतिचित्र बिल्कुल 360 डिग्री देशांतर को आच्छादित करता है)।

रम्ब रेखाएं जो भूमध्य रेखाओं को तिर्यक् कोणों पर काटती हैं, वे एकदिश नौपथ वक्र हैं जो ध्रुवों की ओर कुंडलित होती हैं।^[1] मर्केटर प्रक्षेपण पर उत्तरी ध्रुव और दक्षिणी ध्रुव अनंत पर होते हैं और इसलिए इन्हें कभी दर्शाया नहीं जाता है। हालांकि असीमित उच्च मानचित्रों पर पूर्ण एकदिश नौपथ में दो किनारों के मध्य अनंततः कई रेखा खंड सम्मिलित होंगे। त्रिविम प्रक्षेपण मानचित्र पर, एकदिश नौपथ समकोणीय कुंडली है जिसका केंद्र उत्तर या दक्षिण ध्रुव है।

सभी एकदिश नौपथ एक ध्रुव से दूसरे ध्रुव की ओर कुंडलित होते हैं। ध्रुवों के पास, वे लागेरिथ्मीय कुंडली होने के निकट हैं (जो कि वे त्रिविम प्रक्षेपण पर हैं, नीचे देखें) इसलिए वे प्रत्येक ध्रुव के चारों ओर अनंत बार चक्कर लगाते हैं परन्तु एक सीमित दूरी में ध्रुव तक पहुंचते हैं। एकदिश नौपथ की ध्रुव-से-ध्रुव लंबाई (एक आदर्श क्षेत्र मानते हुए) वास्तविक उत्तर दिशा से दूर दिक्कोण के कोज्या द्वारा विभाजित भूमध्य रेखाओं की लंबाई है। एकदिश नौपथो को ध्रुवों पर परिभाषित नहीं किया गया है।

व्युत्पत्ति और ऐतिहासिक विवरण

एकदिश नौपथ शब्द प्राचीन यूनानी भाषा λοξός loxos से आया है: तिर्यक् + δρόμος drómos: संचालन (δραμεῖν drameîn से: चलाने के लिए) है। रम्ब शब्द स्पेनी भाषा या पुर्तगाली भाषा रम्बो/रंमो (पाठ्यक्रम या दिशा) और यूनानी ῥόμβος rhómbos^[2] से आया हो सकता है।

सार्वभौमिक सूचना के भूमंडलीय विश्वज्ञानकोष के 1878 संस्करण में एकदिश नौपथ रेखाओं का वर्णन इस प्रकार है:^[3]

एकदिश नौपथ रेखा एक वक्र है जो किसी दिए गए सतह की वक्रता की रेखाओं की प्रणाली के प्रत्येक भागो को एक ही कोण पर काटती है। दिक्सूचक के एक ही बिंदु की ओर जाने वाला पोत एक ऐसी रेखा का वर्णन करता है जो सभी याम्योत्तरों को एक ही कोण पर काटती है। मर्केटर के प्रक्षेपण (q.v.) में एकदिश नौपथ रेखाएँ स्पष्ट रूप से सीधी होती हैं।^[3]
एक असम्मति उत्पन्न हो सकती है क्योंकि शब्द "रम्ब" का प्रयोग में आने पर इसका कोई सटीक अर्थ नहीं था। यह पवन आरेख रेखाओं के लिए समान रूप से अच्छी तरह से अनुप्रयुक्त होता है क्योंकि यह एकदिश नौपथो के लिए किया जाता है क्योंकि यह शब्द केवल स्थानीय रूप से अनुप्रयुक्त होता है और इसका अर्थ है कि एक नौकाचालक ने स्थिर दिक्कोण के साथ नौकायन करने के लिए जो कुछ भी किया है, जोकि सभी अशुद्धियों के साथ होता है। इसलिए, रम्ब पत्तन दर्शिकाओं पर सीधी रेखाओं पर अनुप्रयुक्त होता था, जब पत्तन दर्शिका उपयोग में होते थे, साथ ही सदैव मर्केटर रेखाचित्र पर सीधी रेखाओं पर भी अनुप्रयुक्त होते थे। छोटी दूरी के लिए पत्तन दर्शिका "रम्ब" अर्थपूर्ण रूप से मर्केटर रम्ब से भिन्न नहीं होते हैं, लेकिन इन दिनों "रम्ब" गणितीय रूप से सटीक "एकदिश नौपथ" का पर्याय बन गया है क्योंकि इसे पूर्वव्यापी रूप से समानार्थी बना दिया गया है।
जैसा कि लियो बग्रो कहते हैं:^[4] शब्द "रम्ब रेखा" इस अवधि के समुद्रीय-रेखाचित्रों पर अनुचित तरीके से अनुप्रयुक्त किया गया है क्योंकि एकदिश नौपथ केवल एक सटीक पाठ्यक्रम देता है, जब रेखाचित्र एक उपयुक्त प्रक्षेपण पर खींचा जाता है। मानचित्रमितीय जांच से पता चला है कि प्रारम्भिक रेखाचित्रों में किसी प्रक्षेपण का उपयोग नहीं किया गया था, इसलिए हम "पत्तन दर्शिका" नाम रखते हैं।

गणितीय विवरण

त्रिज्या 1 के वृत्तों के लिए, दिगंशीय कोण $λ$ , ध्रुवीय कोण $−.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}π/2 ≤ φ ≤ π/2$ (अक्षांश के अनुरूप यहां परिभाषित) और कार्तीय इकाई सदिश $i$ , $j$ , और $k$ का उपयोग त्रिज्या सदिश $r$ को लिखने के लिए किया जा सकता है।

$\mathbf {r} (\lambda ,\varphi )=(\cos {\lambda }\cdot \cos {\varphi })\mathbf {i} +(\sin {\lambda }\cdot \cos {\varphi })\mathbf {j} +(\sin {\varphi })\mathbf {k} \,$

वृत्तों के दिगंशीय और ध्रुवीय दिशाओं में लंबकोणीय इकाई सदिश लिखे जा सकते हैं;

${\begin{aligned}{\boldsymbol {\hat {\lambda }}}(\lambda ,\varphi )&=\sec {\varphi }{\frac {\partial \mathbf {r} }{\partial \lambda }}=(-\sin {\lambda })\mathbf {i} +(\cos {\lambda })\mathbf {j} \,\\[8pt]{\boldsymbol {\hat {\varphi }}}(\lambda ,\varphi )&={\frac {\partial \mathbf {r} }{\partial \varphi }}=(-\cos {\lambda }\cdot \sin {\varphi })\mathbf {i} +(-\sin {\lambda }\cdot \sin {\varphi })\mathbf {j} +(\cos {\varphi })\mathbf {k} \,\end{aligned}}$

जिनके पास अदिश गुणनफल है

${\boldsymbol {\hat {\lambda }}}\cdot {\boldsymbol {\hat {\varphi }}}={\boldsymbol {\hat {\lambda }}}\cdot \mathbf {r} ={\boldsymbol {\hat {\varphi }}}\cdot \mathbf {r} =0\,$

नियतांक $φ$ के लिए $λ̂$ अक्षांश के समानांतर का पता लगाता है, जबकि नियतांक $λ$ के लिए $φ̂$ देशांतर के भूमध्य रेखाओं का पता लगाता है और साथ में वे वृत्तों के लिए समतल स्पर्शरेखा उत्पन्न करते हैं।
इकाई सदिश

$\mathbf {\boldsymbol {\hat {\beta }}} (\lambda ,\varphi )=(\sin {\beta }){\boldsymbol {\hat {\lambda }}}+(\cos {\beta }){\boldsymbol {\hat {\varphi }}}$

किसी भी $λ$ और $φ$ के लिए इकाई सदिश $φ̂$ के साथ एक स्थिर कोण $β$ है, क्योंकि उनका अदिश गुणनफल है।

${\boldsymbol {\hat {\beta }}}\cdot {\boldsymbol {\hat {\varphi }}}=\cos {\beta }\,$

एकदिश नौपथो को वृत्तों पर एक वक्र के रूप में परिभाषित किया जाता है जिसमें देशांतर के सभी याम्योत्तरों के साथ एक स्थिर कोण $β$ होता है और इसलिए इकाई सदिश $β̂$ के समानांतर होना चाहिए। फलस्वरूप, एकदिश नौपथो के साथ अंतर लंबाई $ds$ एक अंतर विस्थापन का उत्पादन करेगा।

$\begin{aligned} d r & = \hat{β} d s \\ \frac{\partial r}{\partial λ} d λ + \frac{\partial r}{\partial φ} d φ & = ((\sin β) \hat{λ} + (\cos β) \hat{φ}) d s \\ (\cos φ) d λ \hat{λ} + d φ \hat{φ} & = (\sin β) d s \hat{λ} + (\cos β) d s \hat{φ} \\ d s & = \frac{\cos φ}{\sin β} d λ = \frac{d φ}{\cos β} \\ \frac{d λ}{d φ} & = \tan β \cdot \sec φ \\ λ (φ | β, λ_{0}, φ_{0}) & = \tan β \cdot ({gd}^{- 1} φ - {gd}^{- 1} φ_{0}) + λ_{0} \\ φ (λ | β, λ_{0}, φ_{0}) & = gd ((λ - λ_{0}) \cot β + {gd}^{} \end{aligned}$
जहाँ $\operatorname {gd}$ और $\operatorname {gd} ^{-1}$ गुडेरमैनियन फलन और इसके व्युत्क्रम, $\operatorname {gd} \psi =\arctan(\sinh \psi ),$ $\operatorname {gd} ^{-1}\varphi =\operatorname {arsinh} (\tan \varphi )$ हैं और $\operatorname {arsinh}$ व्युत्क्रम अतिपरवलीय द्विज्या है।
$λ$ और $φ$ के मध्य इस संबंध के साथ, त्रिज्या सदिश एक चर का प्राचलिक फलन बन जाता है, जो वृत्तों पर एकदिश नौपथो का पता लगाता है:

$\mathbf {r} (\lambda \,|\,\beta ,\lambda _{0},\varphi _{0})={\big (}\cos {\lambda }\cdot \operatorname {sech} \psi {\big )}\mathbf {i} +{\big (}\sin {\lambda }\cdot \operatorname {sech} \psi {\big )}\mathbf {j} +{\big (}\tanh \psi {\big )}\mathbf {k} \,$

जहाँ

$\psi \equiv (\lambda -\lambda _{0})\cot \beta +\operatorname {gd} ^{-1}\varphi _{0}=\operatorname {gd} ^{-1}\varphi$

सममितीय अक्षांश है।^[5]
रम्ब रेखाओं में, जैसे-जैसे अक्षांश ध्रुवों $φ \to \pm π / 2$ , $sin φ \to \pm1$ की ओर जाता है, सममितीय अक्षांश $arsinh(tan φ) \to \pm \infty$ और देशांतर $λ$ बिना किसी सीमा के बढ़ता है, ध्रुवों की ओर एक कुंडली में इतनी तीव्रता से वृत्त का चक्कर लगाता है, जबकि एक परिमित कुल चाप लंबाई Δs द्वारा दी जाती है।

$\Delta s=R\,{\big |}(\pm \pi /2-\varphi _{0})\cdot \sec \beta {\big |}$

मर्केटर प्रक्षेपण से सम्बन्ध

लिस्बन, पुर्तगाल और हवाना, क्यूबा के मध्य एक बृहत् वृत चाप (लाल) की तुलना में रम्ब रेखा (नीली) है। शीर्ष पर: लंबकोणीय प्रक्षेपण और नीचे: मर्केटर प्रक्षेपण है।
मान लीजिए $λ$ वृत्त पर एक बिंदु का देशांतर है और $φ$ इसका अक्षांश है। फिर, यदि हम मर्केटर प्रक्षेपण के मानचित्र निर्देशांकों को परिभाषित करते हैं;
${\begin{aligned}x&=\lambda -\lambda _{0}\,\\y&=\operatorname {gd} ^{-1}\varphi =\operatorname {arsinh} (\tan \varphi )\,\end{aligned}}$

वास्तविक उत्तर दिशा से स्थिर दिक्कोण $β$ एकदिश नौपथ एक सीधी रेखा होगी, क्योंकि (पिछले अनुभाग में अभिव्यक्ति का उपयोग करके)

$y=mx$

प्रवणता के साथ

$m=\cot \beta \,$

दो दिए गए बिंदुओं के मध्य एकदिश नौपथो का पता लगाना एक मर्केटर प्रतिचित्र पर सुचित्रित रूप से किया जा सकता है, या दो अज्ञात $m = cot β$ और $λ 0$ में दो समीकरणों की एक गैर-रैखिक प्रणाली को हल करके किया जा सकता है। अपरिमित रूप से अनेक हल हैं; सबसे छोटा वह है जो वास्तविक देशांतर अन्तरो को आच्छादित करता है, अर्थात अतिरिक्त चक्कर नहीं लगाता है और "अनुचित तरीके से नहीं" जाता है।
एकदिश नौपथो के साथ मापी गई दो बिंदुओं $Δ s$ के मध्य की दूरी, उत्तर-दक्षिण दूरी (अक्षांश के वृत्तों को छोड़कर जिसके लिए दूरी अनंत हो जाती है) के दिक्कोण (दिगंश) के छेदक का पूर्ण मान है:

$\Delta s=R\,{\big |}(\varphi -\varphi _{0})\cdot \sec \beta {\big |}$

जहाँ $R$ पृथ्वी की औसत त्रिज्याओं में से एक है।

अनुप्रयोग

मार्गनिर्देशन में इसका उपयोग सीधे शैली से जुड़ा हुआ है, या कुछ मार्गनिर्देशक मानचित्रों का प्रक्षेपण है। मर्केटर प्रक्षेपण प्रतिचित्रों पर एक रम्ब रेखा एक सीधी रेखा के रूप में दिखाई देती है।^[1]
यह नाम क्रमशः पुराने फ्रांसीसी या स्पेनी से लिया गया है: "रम्ब" या "रम्बो" रेखाचित्र पर एक रेखा जो एक ही कोण पर सभी मध्याह्न रेखाओं को काटती है।^[1]समतल सतहों पर यह दो बिंदुओं के मध्य की सबसे छोटी दूरी होगी। पृथ्वी की सतहों पर कम अक्षांशों पर या कम दूरी पर इसका उपयोग किसी वाहन, विमान या पोतो के पाठ्यक्रमों का आलेखन रचने के लिए किया जा सकता है।^[1]लंबी दूरी और/या उच्च अक्षांशों पर बृहत् वृत पथ समान दो बिंदुओं के मध्य की रेखाओं से काफी छोटा है। हालांकि, एक बृहत् वृत पथ का आवागमन करते समय दिक्कोणो को निरन्तर परिवर्तित करने की असुविधा कुछ उदाहरणों में रम्ब रेखा मार्गनिर्देशनो को आकर्षक बनाती है।^[1]
बिंदु को भूमध्य रेखाओं के साथ 90 डिग्री देशांतरों पर एक पूर्व-पश्चिम पंथ के साथ चित्रित किया जा सकता है, जिसके लिए 10,000 किलोमीटर (5,400 समुद्रीय मील) पर बृहत् वृत्तों और रम्ब रेखाओं की दूरी समान हैं, 20 डिग्री उत्तर में बृहत् वृत्तों की दूरी 9,254 किमी (4,997 एनएमआई) है, जबकि रम्ब रेखाओं की दूरी 9,397 किमी (5,074 एनएमआई) है, लगभग 1.5% आगे है। परन्तु 60 डिग्री उत्तर में बृहत् वृत्तों की दूरी 4,602 किमी (2,485 समुद्रीय मील) है, जबकि रम्ब रेखा 5,000 किमी (2,700 समुद्रीय मील) है, जो 8.5% का अंतर है। एक अधिक चरम परिस्थिति न्यूयॉर्क शहर और हांगकांग के मध्य का विमान मार्ग है, जिसके लिए रम्ब रेखा पथ 18,000 किमी (9,700 एनएमआई) है। उत्तरी ध्रुवों पर बृहत् वृत्त पंथ 13,000 किमी (7,000 एनएमआई) है, या सामान्य परिभ्रमण गति पर 5+1⁄2 घंटे कम उड़ान समय है।
मर्केटर प्रक्षेपण के कुछ पुराने मानचित्रों में अक्षांश और देशांतर की रेखाओं से बने संजाल होते हैं, परन्तु रम्ब रेखाएं भी दिखाई देती हैं, जो सीधे उत्तर की ओर, उत्तर से समकोण पर, या उत्तर से कुछ कोण पर होती हैं जोकि एक समकोण कुछ सरल तर्कसंगत अंश है। ये रम्ब रेखाएँ खींची जाएँगी ताकि वे मानचित्रों के कुछ बिंदुओं पर अभिसरित हों। प्रत्येक दिशाओं में जाने वाली रेखाएँ इनमें से प्रत्येक बिंदु पर अभिसरित होंगी। दिक्सूचकआरेख देखें। इस प्रकार के प्रतिचित्र आवश्यक रूप से मर्केटर प्रक्षेपण में रहे होंगे इसलिए सभी पुराने मानचित्र रम्ब रेखा चिह्नों को दर्शाने में सक्षम नहीं रहे होंगे।
दिक्सूचक आरेख पर त्रिज्यीय रेखाओं को रम्ब भी कहा जाता है। 16वीं-19वीं शताब्दी में एक विशेष दिक्सूचक शीर्षक को इंगित करने के लिए अनुसरण "रम्ब पर नौचालन" का उपयोग किया गया था।^[1]
समुद्रीय कालमापी के आविष्कार से पूर्व के प्रारम्भिक नौनिर्देशकों ने लंबे समुद्रीय मार्गों पर रम्ब रेखाओं पाठ्यक्रमों का उपयोग किया था, क्योंकि पोत का अक्षांश सूर्य या तारों को देखकर सटीक रूप से स्थापित किया जा सकता था परन्तु देशांतर निर्धारित करने का कोई सटीक तरीका नहीं था। गंतव्य के अक्षांश तक पहुंचने तक पोत उत्तर या दक्षिण की ओर जाएगा और पोत तब पूर्व या पश्चिम में रम्ब रेखाओं (वास्तव में एक समानांतर, जो कि एकदिश नौपथ की एक विशेष स्थिति है) के साथ एक स्थिर अक्षांश बनाए रखेगा और भूमि के साक्ष्य देखे जाने तक तय की गई दूरी के नियमित अनुमानों को अंकित करना है।^[6]

सामान्यीकरण

रीमैन क्षेत्र पर

Main article: मोबियस परिवर्तन

पृथ्वी की सतहों को गणितीय रूप से रीमैन क्षेत्र के रूप में समझा जा सकता है, अर्थात, वृत्तों के एक जटिल तल के प्रक्षेपण के रूप में समझा जा सकता है। इस स्थिति में, एकदिश नौपथो को मोबियस परिवर्तनों के कुछ वर्गों के रूप में समझा जा सकता है।

गोलाभ

उपरोक्त सूत्रीकरण को सरलता से गोलाभ तक बढ़ाया जा सकता है।^[7]^[8]^[9]^[10]^[11] रम्ब रेखाओं का पथ केवल दीर्घवृत्ताभ सममितीय अक्षांश का उपयोग करके पाया जाता है। इस पृष्ठ पर उपरोक्त सूत्रों में, वृत्तों पर अक्षांश के लिए दीर्घवृत्ताभ पर अनुरूप अक्षांश को प्रतिस्थापित किया जाता है। इसी तरह, दिगंश के छेदक द्वारा दीर्घवृत्ताकार याम्योत्तर चाप की लंबाई को गुणा करके दूरियां प्राप्त की जाती हैं।

यह भी देखें

बृहत् वृत

दीर्घवृत्ताभ पर अल्पांतरी

बृहत् दीर्घवृत्त

इसोआज़ीमुथल

एकदिश नौपथ संजाल

सीफ़र्ट की कुंडली

लघु वृत्त

संदर्भ

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 Oxford University Press Rhumb Line. The Oxford Companion to Ships and the Sea, Oxford University Press, 2006. Retrieved from Encyclopedia.com 18 July 2009.

↑ Rhumb at TheFreeDictionary

↑ ^3.0 ^3.1 Ross, J.M. (editor) (1878). The Globe Encyclopaedia of Universal Information, Vol. IV, Edinburgh-Scotland, Thomas C. Jack, Grange Publishing Works, retrieved from Google Books 2009-03-18;

↑ Leo Bagrow (2010). कार्टोग्राफी का इतिहास. Transaction Publishers. p. 65. ISBN 978-1-4128-2518-4.

↑ James Alexander, Loxodromes: A Rhumb Way to Go, "Mathematics Magazine", Vol. 77. No. 5, Dec. 2004. [1]

↑ A Brief History of British Seapower, David Howarth, pub. Constable & Robinson, London, 2003, chapter 8.

↑ Smart, W. M. (1946). "On a Problem in Navigation". Monthly Notices of the Royal Astronomical Society. 106 (2): 124–127. Bibcode:1946MNRAS.106..124S. doi:10.1093/mnras/106.2.124.

↑ Williams, J. E. D. (1950). "Loxodromic Distances on the Terrestrial Spheroid". Journal of Navigation. 3 (2): 133–140. doi:10.1017/S0373463300045549. S2CID 128651304.

↑ Carlton-Wippern, K. C. (1992). "On Loxodromic Navigation". Journal of Navigation. 45 (2): 292–297. doi:10.1017/S0373463300010791. S2CID 140735736.

↑ Bennett, G. G. (1996). "Practical Rhumb Line Calculations on the Spheroid". Journal of Navigation. 49 (1): 112–119. Bibcode:1996JNav...49..112B. doi:10.1017/S0373463300013151. S2CID 128764133.

↑ Botnev, V.A; Ustinov, S.M. (2014). Методы решения прямой и обратной геодезических задач с высокой точностью [Methods for direct and inverse geodesic problems solving with high precision] (PDF). St. Petersburg State Polytechnical University Journal (in Russian). 3 (198): 49–58.{{cite journal}}: CS1 maint: unrecognized language (link)

अग्रिम पठन

Monmonier, Mark (2004). Rhumb lines and map wars. A social history of the Mercator projection. Chicago: University of Chicago Press. ISBN 9780226534329.

बाहरी संबंध

Constant Headings and Rhumb Lines at MathPages.

RhumbSolve(1), a utility for ellipsoidal rhumb line calculations (a component of GeographicLib); supplementary documentation.

An online version of RhumbSolve.

Navigational Algorithms Archived 16 October 2018 at the Wayback Machine Paper: The Sailings.

Chart Work - Navigational Algorithms Chart Work free software: Rhumb line, Great Circle, Composite sailing, Meridional parts. Lines of position Piloting - currents and coastal fix.

Mathworld Loxodrome.

[EOS-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 Oxford University Press Rhumb Line. The Oxford Companion to Ships and the Sea, Oxford University Press, 2006. Retrieved from Encyclopedia.com 18 July 2009.

[2] Rhumb at TheFreeDictionary

[Globe-3] 3.0 ^3.1 Ross, J.M. (editor) (1878). The Globe Encyclopaedia of Universal Information, Vol. IV, Edinburgh-Scotland, Thomas C. Jack, Grange Publishing Works, retrieved from Google Books 2009-03-18;

[Bagrow2010-4] Leo Bagrow (2010). कार्टोग्राफी का इतिहास. Transaction Publishers. p. 65. ISBN 978-1-4128-2518-4.

[5] James Alexander, Loxodromes: A Rhumb Way to Go, "Mathematics Magazine", Vol. 77. No. 5, Dec. 2004. [1]

[6] A Brief History of British Seapower, David Howarth, pub. Constable & Robinson, London, 2003, chapter 8.

[7] Smart, W. M. (1946). "On a Problem in Navigation". Monthly Notices of the Royal Astronomical Society. 106 (2): 124–127. Bibcode:1946MNRAS.106..124S. doi:10.1093/mnras/106.2.124.

[8] Williams, J. E. D. (1950). "Loxodromic Distances on the Terrestrial Spheroid". Journal of Navigation. 3 (2): 133–140. doi:10.1017/S0373463300045549. S2CID 128651304.

[9] Carlton-Wippern, K. C. (1992). "On Loxodromic Navigation". Journal of Navigation. 45 (2): 292–297. doi:10.1017/S0373463300010791. S2CID 140735736.

[10] Bennett, G. G. (1996). "Practical Rhumb Line Calculations on the Spheroid". Journal of Navigation. 49 (1): 112–119. Bibcode:1996JNav...49..112B. doi:10.1017/S0373463300013151. S2CID 128764133.

[11] Botnev, V.A; Ustinov, S.M. (2014). Методы решения прямой и обратной геодезических задач с высокой точностью [Methods for direct and inverse geodesic problems solving with high precision] (PDF). St. Petersburg State Polytechnical University Journal (in Russian). 3 (198): 49–58.{{cite journal}}: CS1 maint: unrecognized language (link)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

@@ Line 1: / Line 1: @@
-{{short description|Arc crossing all meridians of longitude at the same angle}}
-{{Use dmy dates|date=October 2019}}
+[[File:Loxodrome.png|thumb|right|220px|एकदिश नौपथ, या रम्ब रेखाओं की छवि, जो [[उत्तरी ध्रुव]] की ओर बढ़ती है।]][[ मार्गदर्शन |मार्गनिर्देशन]] में, एक '''रम्ब रेखा''', रम्ब ({{IPAc-en|r|ʌ|m}}), या एकदिश नौपथ एक [[चाप (ज्यामिति)|चाप]] है जो एक ही [[कोण]] पर देशांतर के सभी [[मेरिडियन (भूगोल)|भूमध्य रेखाओं]] को पार करता है, जोकि वास्तविक उत्तर दिशा के सापेक्ष मापा गया स्थिर दिक्कोण वाला पथ है।
-[[File:Loxodrome.png|thumb|right|220px|एकदिश नौपथ, या रंब रेखाओं की छवि, जो [[उत्तरी ध्रुव]] की ओर बढ़ती है।]][[ मार्गदर्शन |मार्गनिर्देशन]] में, एक रंब रेखा, रंब ({{IPAc-en|r|ʌ|m}}), या एकदिश नौपथ एक [[चाप (ज्यामिति)|चाप]] है जो एक ही [[कोण]] पर देशांतर के सभी [[मेरिडियन (भूगोल)|भूमध्य रेखाओं]] को पार करता है, जोकि वास्तविक उत्तर दिशा के सापेक्ष मापा गया स्थिर [[असर (नेविगेशन)|दिक्कोण]] वाला पथ है।
 == परिचय ==
-एक भूमंडल की सतह पर रंब रेखा पाठ्यक्रम का पालन करने के प्रभाव पर पहली बार 1537 में [[पुर्तगाली लोग|पुर्तगाली]] [[गणितज्ञ]] [[पेड्रो नून्स]] ने 1590 के दशक में [[थॉमस हैरियट]] द्वारा आगे के गणितीय विकास के साथ समुद्रीय रेखाचित्र की रक्षा में अपने ग्रंथ में चर्चा की थी।
+भूमंडल की सतहों पर रम्ब रेखा पाठ्यक्रम का पालन करने के प्रभाव पर पहली बार 1537 में पुर्तगाली [[गणितज्ञ]] [[पेड्रो नून्स]] ने 1590 के दशक में थॉमस हैरियट द्वारा आगे के गणितीय विकास के साथ समुद्रीय रेखाचित्र की रक्षा में अपने ग्रंथ में चर्चा की थी।
-एक रंब रेखा की तुलना एक बड़े वृत्त से की जा सकती है, जो एक वृत्त की सतह पर दो बिंदुओं के मध्य की सबसे छोटी दूरी का पथ है। एक बड़े वृत्त पर, गंतव्य बिंदु का दिक्कोण स्थिर नहीं रहता है। यदि किसी को बृहत् वृत के साथ एक मोटर गाड़ी चलानी होती है तो वह चालन चक्र को स्थिर रखता है, परन्तु रंब रेखाओं का पालन करने के लिए पहिये को घुमाना पड़ता है, जैसे-जैसे स्तंभ पास आते हैं, इसे और अधिक तीव्रता से घुमाते हैं। दूसरे शब्दों में, एक बड़ा वृत्त शून्य [[जियोडेसिक वक्रता|अल्पांतरी वक्रता]] के साथ स्थानीय रूप से "सीधा" होता है, जबकि एक रंब रेखा में गैर-शून्य अल्पांतरी वक्रता होती है।
+रम्ब रेखाओं की तुलना एक बड़े वृत्त से की जा सकती है, जो वृत्त की सतह पर दो बिंदुओं के मध्य की सबसे छोटी दूरी का पथ है। एक बड़े वृत्त पर, गंतव्य बिंदु का दिक्कोण स्थिर नहीं रहता है। यदि किसी को बृहत् वृत के साथ एक मोटर गाड़ी चलानी होती है तो वह चालन चक्र को स्थिर रखता है, परन्तु रम्ब रेखाओं का पालन करने के लिए पहिये को घुमाना पड़ता है, जैसे-जैसे स्तंभ पास आते हैं, इसे और अधिक तीव्रता से घुमाते हैं। दूसरे शब्दों में, एक बड़ा वृत्त शून्य [[जियोडेसिक वक्रता|अल्पांतरी वक्रता]] के साथ स्थानीय रूप से "सीधा" होता है, जबकि रम्ब रेखाओं में गैर-शून्य अल्पांतरी वक्रता होती है।
-देशांतर के याम्योत्तर और अक्षांश के समानांतर रंब रेखाओं की विशेष स्थितियां प्रदान करते हैं, जहां उनके प्रतिच्छेदन के कोण क्रमशः 0° और 90° होते हैं। एक उत्तर-दक्षिण पथ पर रंब रेखा पाठ्यक्रम एक बृहत् वृत के अनुरूप है, जैसे कि यह [[भूमध्य रेखा|भूमध्य रेखाओं]] के साथ पूर्व-पश्चिम पथ पर होता है।
+देशांतर के याम्योत्तर और अक्षांश के समानांतर रम्ब रेखाओं की विशेष स्थितियां प्रदान करते हैं, जहां उनके प्रतिच्छेदन के कोण क्रमशः 0° और 90° होते हैं। उत्तर-दक्षिण पथ पर रम्ब रेखा पाठ्यक्रम बृहत् वृत्तों के अनुरूप है, जैसे कि यह [[भूमध्य रेखा|भूमध्य रेखाओं]] के साथ पूर्व-पश्चिम पथ पर होता है।
-[[मर्केटर प्रोजेक्शन|मर्केटर]] [[त्रिविम प्रक्षेपण|प्रक्षेपण]] मानचित्र पर, कोई भी रंब रेखा एक सीधी रेखा है; इस प्रकार के मानचित्रों पर पृथ्वी पर किन्हीं दो बिंदुओं के मध्य बिना मानचित्र के किनारे से हटे रंब रेखा खींची जा सकती है। परन्तु सैद्धांतिक रूप से एकदिश नौपथ मानचित्र के दाहिने किनारे से आगे बढ़ सकता है, जहां यह फिर उसी प्रवणता के साथ बाएं किनारे पर जारी रहता है (यह मानते हुए कि प्रतिचित्र बिल्कुल 360 डिग्री देशांतर को आच्छादित करता है)।
+[[मर्केटर प्रोजेक्शन|मर्केटर]] प्रक्षेपण मानचित्र पर, कोई भी रम्ब रेखा एक सीधी रेखा है; इस प्रकार के मानचित्रों पर पृथ्वी पर किन्हीं दो बिंदुओं के मध्य बिना मानचित्र के किनारे से हटे रम्ब रेखा खींची जा सकती है। परन्तु सैद्धांतिक रूप से एकदिश नौपथ मानचित्र के दाहिने किनारे से आगे बढ़ सकता है, जहां यह फिर उसी प्रवणता के साथ बाएं किनारे पर जारी रहता है (यह मानते हुए कि प्रतिचित्र बिल्कुल 360 डिग्री देशांतर को आच्छादित करता है)।
-रंब रेखाएं जो [[भूमध्य रेखा|भूमध्य रेखाओं]] को तिर्यक् कोणों पर काटती हैं, वे एकदिश नौपथ वक्र हैं जो ध्रुवों की ओर कुंडलित होती हैं।<ref name="EOS" />मर्केटर प्रक्षेपण पर [[उत्तरी ध्रुव]] और [[दक्षिणी ध्रुव]] अनंत पर होते हैं और इसलिए इन्हें कभी दर्शाया नहीं जाता है। हालांकि असीमित उच्च मानचित्रों पर पूर्ण एकदिश नौपथ में दो किनारों के मध्य अनंततः कई रेखा खंड सम्मिलित होंगे। त्रिविम प्रक्षेपण मानचित्र पर, एकदिश नौपथ एक [[समकोणीय सर्पिल|समकोणीय कुंडली]] है जिसका केंद्र उत्तर या दक्षिण ध्रुव है।
+रम्ब रेखाएं जो [[भूमध्य रेखा|भूमध्य रेखाओं]] को तिर्यक् कोणों पर काटती हैं, वे एकदिश नौपथ वक्र हैं जो ध्रुवों की ओर कुंडलित होती हैं।<ref name="EOS" /> मर्केटर प्रक्षेपण पर [[उत्तरी ध्रुव]] और [[दक्षिणी ध्रुव]] अनंत पर होते हैं और इसलिए इन्हें कभी दर्शाया नहीं जाता है। हालांकि असीमित उच्च मानचित्रों पर पूर्ण एकदिश नौपथ में दो किनारों के मध्य अनंततः कई रेखा खंड सम्मिलित होंगे। त्रिविम प्रक्षेपण मानचित्र पर, एकदिश नौपथ समकोणीय कुंडली है जिसका केंद्र उत्तर या दक्षिण ध्रुव है।
-सभी एकदिश नौपथ एक ध्रुव से दूसरे ध्रुव की ओर कुंडलित होते हैं। ध्रुवों के पास, वे लागेरिथ्मीय कुंडली होने के निकट हैं (जो कि वे एक [[त्रिविम प्रक्षेपण]] पर हैं, नीचे देखें), इसलिए वे प्रत्येक ध्रुव के चारों ओर अनंत बार चक्कर लगाते हैं परन्तु एक सीमित दूरी में ध्रुव तक पहुंचते हैं। एकदिश नौपथ की ध्रुव-से-ध्रुव लंबाई (एक आदर्श क्षेत्र मानते हुए) वास्तविक उत्तर दिशा से दूर दिक्कोण के [[ कोज्या |कोज्या]] द्वारा विभाजित [[भूमध्य रेखा|भूमध्य रेखाओं]] की लंबाई है। एकदिश नौपथो को ध्रुवों पर परिभाषित नहीं किया गया है।
+सभी एकदिश नौपथ एक ध्रुव से दूसरे ध्रुव की ओर कुंडलित होते हैं। ध्रुवों के पास, वे लागेरिथ्मीय कुंडली होने के निकट हैं (जो कि वे त्रिविम प्रक्षेपण पर हैं, नीचे देखें) इसलिए वे प्रत्येक ध्रुव के चारों ओर अनंत बार चक्कर लगाते हैं परन्तु एक सीमित दूरी में ध्रुव तक पहुंचते हैं। एकदिश नौपथ की ध्रुव-से-ध्रुव लंबाई (एक आदर्श क्षेत्र मानते हुए) वास्तविक उत्तर दिशा से दूर दिक्कोण के कोज्या द्वारा विभाजित [[भूमध्य रेखा|भूमध्य रेखाओं]] की लंबाई है। एकदिश नौपथो को ध्रुवों पर परिभाषित नहीं किया गया है।
 == व्युत्पत्ति और ऐतिहासिक विवरण ==
-एकदिश नौपथ शब्द प्राचीन यूनानी भाषा λοξός loxos से आया है: तिर्यक् + δρόμος ''drómos'': संचालन (δραμεῖν drameîn से: चलाने के लिए) है। रंब शब्द [[स्पेनिश भाषा|स्पेनी भाषा]] या [[पुर्तगाली भाषा]] रंबो/रंमो ("पाठ्यक्रम" या "दिशा") और यूनानी ῥόμβος rhómbos,<ref>''[http://www.thefreedictionary.com/rhumb Rhumb]'' at TheFreeDictionary</ref> से आया हो सकता है।
+एकदिश नौपथ शब्द प्राचीन यूनानी भाषा λοξός loxos से आया है: तिर्यक् + δρόμος ''drómos'': संचालन (δραμεῖν drameîn से: चलाने के लिए) है। रम्ब शब्द स्पेनी भाषा या [[पुर्तगाली भाषा]] रम्बो/रंमो (पाठ्यक्रम या दिशा) और यूनानी ῥόμβος rhómbos<ref>''[http://www.thefreedictionary.com/rhumb Rhumb]'' at TheFreeDictionary</ref> से आया हो सकता है।
 सार्वभौमिक सूचना के भूमंडलीय विश्वज्ञानकोष के 1878 संस्करण में एकदिश नौपथ रेखाओं का वर्णन इस प्रकार है:<ref name="Globe"/>
@@ Line 23: / Line 22: @@
 <blockquote>एकदिश नौपथ रेखा एक वक्र है जो किसी दिए गए सतह की वक्रता की रेखाओं की प्रणाली के प्रत्येक भागो को एक ही कोण पर काटती है। दिक्सूचक के एक ही बिंदु की ओर जाने वाला पोत एक ऐसी रेखा का वर्णन करता है जो सभी याम्योत्तरों को एक ही कोण पर काटती है। मर्केटर के प्रक्षेपण (q.v.) में एकदिश नौपथ रेखाएँ स्पष्ट रूप से सीधी होती हैं।<ref name="Globe">Ross, J.M. (editor) (1878). ''[https://archive.org/details/globeencyclopae01rossgoog The Globe Encyclopaedia of Universal Information]'', Vol. IV, Edinburgh-Scotland, Thomas C. Jack, Grange Publishing Works, retrieved from [[Google Books]] 2009-03-18;</ref>
-एक असम्मति उत्पन्न हो सकती है क्योंकि शब्द "रंब" का प्रयोग में आने पर इसका कोई सटीक अर्थ नहीं था। यह [[इन्द्रोंसे लाइन|पवन आरेख]] रेखाओं के लिए समान रूप से अच्छी तरह से अनुप्रयुक्त होता है क्योंकि यह एकदिश नौपथो के लिए किया जाता है क्योंकि यह शब्द केवल स्थानीय रूप से अनुप्रयुक्त होता है और इसका अर्थ है कि एक नौकाचालक ने स्थिर दिक्कोण के साथ नौकायन करने के लिए जो कुछ भी किया है, जोकि सभी अशुद्धियों के साथ होता है। इसलिए, रंब [[पोर्टोलन|पत्तन दर्शिकाओं]] पर सीधी रेखाओं पर अनुप्रयुक्त होता था, जब पत्तन दर्शिका उपयोग में होते थे, साथ ही सदैव मर्केटर रेखाचित्र पर सीधी रेखाओं पर भी अनुप्रयुक्त होते थे। छोटी दूरी के लिए पत्तन दर्शिका "रंब" अर्थपूर्ण रूप से मर्केटर रंब से भिन्न नहीं होते हैं, लेकिन इन दिनों "रंब" गणितीय रूप से सटीक "एकदिश नौपथ" का पर्याय बन गया है क्योंकि इसे पूर्वव्यापी रूप से समानार्थी बना दिया गया है।
+एक असम्मति उत्पन्न हो सकती है क्योंकि शब्द "रम्ब" का प्रयोग में आने पर इसका कोई सटीक अर्थ नहीं था। यह पवन आरेख रेखाओं के लिए समान रूप से अच्छी तरह से अनुप्रयुक्त होता है क्योंकि यह एकदिश नौपथो के लिए किया जाता है क्योंकि यह शब्द केवल स्थानीय रूप से अनुप्रयुक्त होता है और इसका अर्थ है कि एक नौकाचालक ने स्थिर दिक्कोण के साथ नौकायन करने के लिए जो कुछ भी किया है, जोकि सभी अशुद्धियों के साथ होता है। इसलिए, रम्ब [[पोर्टोलन|पत्तन दर्शिकाओं]] पर सीधी रेखाओं पर अनुप्रयुक्त होता था, जब पत्तन दर्शिका उपयोग में होते थे, साथ ही सदैव मर्केटर रेखाचित्र पर सीधी रेखाओं पर भी अनुप्रयुक्त होते थे। छोटी दूरी के लिए पत्तन दर्शिका "रम्ब" अर्थपूर्ण रूप से मर्केटर रम्ब से भिन्न नहीं होते हैं, लेकिन इन दिनों "रम्ब" गणितीय रूप से सटीक "एकदिश नौपथ" का पर्याय बन गया है क्योंकि इसे पूर्वव्यापी रूप से समानार्थी बना दिया गया है।
-जैसा कि लियो बग्रो कहते हैं:<ref name="Bagrow2010">{{cite book|author=Leo Bagrow|title=कार्टोग्राफी का इतिहास|url=https://books.google.com/books?id=OBeB4tDmJv8C&pg=PA65|year=2010|publisher=Transaction Publishers|isbn=978-1-4128-2518-4|page=65}}</ref> शब्द ('रंब रेखा') इस अवधि के समुद्रीय-रेखाचित्रों पर अनुचित तरीके से अनुप्रयुक्त किया गया है, क्योंकि एक एकदिश नौपथ केवल एक सटीक पाठ्यक्रम देता है, जब रेखाचित्र एक उपयुक्त प्रक्षेपण पर खींचा जाता है। मानचित्रमितीय जांच से पता चला है कि प्रारम्भिक रेखाचित्रों में किसी प्रक्षेपण का उपयोग नहीं किया गया था, इसलिए हम 'पत्तन दर्शिका' नाम रखते हैं।
+जैसा कि लियो बग्रो कहते हैं:<ref name="Bagrow2010">{{cite book|author=Leo Bagrow|title=कार्टोग्राफी का इतिहास|url=https://books.google.com/books?id=OBeB4tDmJv8C&pg=PA65|year=2010|publisher=Transaction Publishers|isbn=978-1-4128-2518-4|page=65}}</ref> शब्द "रम्ब रेखा" इस अवधि के समुद्रीय-रेखाचित्रों पर अनुचित तरीके से अनुप्रयुक्त किया गया है क्योंकि एकदिश नौपथ केवल एक सटीक पाठ्यक्रम देता है, जब रेखाचित्र एक उपयुक्त प्रक्षेपण पर खींचा जाता है। मानचित्रमितीय जांच से पता चला है कि प्रारम्भिक रेखाचित्रों में किसी प्रक्षेपण का उपयोग नहीं किया गया था, इसलिए हम "पत्तन दर्शिका" नाम रखते हैं।
 == गणितीय विवरण ==
@@ Line 41: / Line 40: @@
 :<math>\boldsymbol{\hat\lambda} \cdot \boldsymbol{\hat\varphi} = \boldsymbol{\hat\lambda} \cdot \mathbf{r} = \boldsymbol{\hat\varphi} \cdot \mathbf{r} = 0 \, </math>
-नियतांक {{mvar|φ}} के लिए {{math|'''λ̂'''}} अक्षांश के समानांतर का पता लगाता है, जबकि नियतांक {{mvar|λ}} के लिए {{math|'''φ̂'''}}  देशांतर के भूमध्य रेखाओं का पता लगाता है और साथ में वे वृत्तों के लिए एक समतल स्पर्शरेखा उत्पन्न करते हैं।
+नियतांक {{mvar|φ}} के लिए {{math|'''λ̂'''}}  अक्षांश के समानांतर का पता लगाता है, जबकि नियतांक {{mvar|λ}} के लिए {{math|'''φ̂'''}}  देशांतर के भूमध्य रेखाओं का पता लगाता है और साथ में वे वृत्तों के लिए समतल स्पर्शरेखा उत्पन्न करते हैं।
 इकाई सदिश
@@ Line 47: / Line 46: @@
 किसी भी {{mvar|λ}} और {{mvar|φ}} के लिए इकाई सदिश {{math|'''φ̂'''}}  के साथ एक स्थिर कोण {{mvar|β}} है, क्योंकि उनका अदिश गुणनफल है।
-:<math>\boldsymbol{\hat\beta} \cdot \boldsymbol{\hat\varphi} = \cos{\beta} \, .</math>
+:<math>\boldsymbol{\hat\beta} \cdot \boldsymbol{\hat\varphi} = \cos{\beta} \, </math>
-एकदिश नौपथो को वृत्तों पर एक वक्र के रूप में परिभाषित किया जाता है जिसमें देशांतर के सभी याम्योत्तरों के साथ एक स्थिर कोण {{mvar|β}} होता है और इसलिए इकाई सदिश {{math|'''β̂'''}} के समानांतर होना चाहिए। फलस्वरूप, एकदिश नौपथो के साथ एक अंतर लंबाई {{mvar|ds}}  एक अंतर विस्थापन का उत्पादन करेगा।
+एकदिश नौपथो को वृत्तों पर एक वक्र के रूप में परिभाषित किया जाता है जिसमें देशांतर के सभी याम्योत्तरों के साथ एक स्थिर कोण {{mvar|β}} होता है और इसलिए इकाई सदिश {{math|'''β̂'''}}  के समानांतर होना चाहिए। फलस्वरूप, एकदिश नौपथो के साथ अंतर लंबाई {{mvar|ds}} एक अंतर विस्थापन का उत्पादन करेगा।
 :<math>\begin{align}
@@ Line 59: / Line 58: @@
 \varphi(\lambda\,|\,\beta,\lambda_0,\varphi_0) &= \operatorname{gd} \big((\lambda - \lambda_0) \cot\beta + \operatorname{gd}^{-1}\varphi_0\big)
 \end{align}</math>
-जहाँ <math>\operatorname{gd}</math> और <math>\operatorname{gd}^{-1}</math> [[गुडरमैनियन समारोह|गुडेरमैनियन फलन]] और इसके व्युत्क्रम, <math>\operatorname{gd}\psi = \arctan(\sinh\psi),</math> <math>\operatorname{gd}^{-1}\varphi = \operatorname{arsinh}(\tan\varphi)</math> हैं और <math>\operatorname{arsinh}</math> [[उलटा अतिशयोक्तिपूर्ण कार्य|व्युत्क्रम अतिपरवलीय द्विज्या]] है।
+जहाँ <math>\operatorname{gd}</math> और <math>\operatorname{gd}^{-1}</math> गुडेरमैनियन फलन और इसके व्युत्क्रम, <math>\operatorname{gd}\psi = \arctan(\sinh\psi),</math> <math>\operatorname{gd}^{-1}\varphi = \operatorname{arsinh}(\tan\varphi)</math> हैं और <math>\operatorname{arsinh}</math> [[उलटा अतिशयोक्तिपूर्ण कार्य|व्युत्क्रम अतिपरवलीय द्विज्या]] है।
 {{mvar|λ}} और {{mvar|φ}} के मध्य इस संबंध के साथ, त्रिज्या सदिश एक चर का प्राचलिक फलन बन जाता है, जो वृत्तों पर एकदिश नौपथो का पता लगाता है:
@@ Line 70: / Line 69: @@
 सममितीय अक्षांश है।<ref>James Alexander, Loxodromes: A Rhumb Way to Go, "Mathematics Magazine", Vol. 77. No. 5, Dec. 2004. [http://hans.fugal.net/src/lindbergh/mathmag349-356.pdf]</ref>
-रंब रेखाओं में, जैसे-जैसे अक्षांश ध्रुवों, {{math|''φ'' → ±{{sfrac|π|2}}}}, {{math|sin ''φ'' → ±1}} की ओर जाता है, सममितीय अक्षांश {{math|arsinh(tan ''φ'') → ± ∞}} और देशांतर {{mvar|λ}} बिना किसी सीमा के बढ़ता है, ध्रुवों की ओर एक कुंडली में इतनी तीव्रता से वृत्त का चक्कर लगाता है, जबकि एक परिमित कुल चाप लंबाई Δs द्वारा दी जाती है।
+रम्ब रेखाओं में, जैसे-जैसे अक्षांश ध्रुवों {{math|''φ'' → ±{{sfrac|π|2}}}}, {{math|sin ''φ'' → ±1}} की ओर जाता है, सममितीय अक्षांश {{math|arsinh(tan ''φ'') → ± ∞}} और देशांतर {{mvar|λ}} बिना किसी सीमा के बढ़ता है, ध्रुवों की ओर एक कुंडली में इतनी तीव्रता से वृत्त का चक्कर लगाता है, जबकि एक परिमित कुल चाप लंबाई Δs द्वारा दी जाती है।
 :<math>\Delta s = R \, \big|(\pm\pi/2 - \varphi_0) \cdot \sec \beta\big|</math>
 == मर्केटर प्रक्षेपण से सम्बन्ध ==
-[[File:Rhumb line vs great-circle arc.png|thumb|upright=1.3|लिस्बन, पुर्तगाल और हवाना, क्यूबा के मध्य एक बृहत् वृत चाप (लाल) की तुलना में एकदिश नौपथ (नीला) है। शीर्ष पर: लंबकोणीय प्रक्षेपण और नीचे: मर्केटर प्रक्षेपण है।]]मान लीजिए {{mvar|λ}} वृत्त पर एक बिंदु का देशांतर है और {{mvar|φ}} इसका अक्षांश है। फिर, यदि हम मर्केटर प्रक्षेपण के मानचित्र निर्देशांकों को परिभाषित करते हैं
+[[File:Rhumb line vs great-circle arc.png|thumb|upright=1.3|लिस्बन, पुर्तगाल और हवाना, क्यूबा के मध्य एक बृहत् वृत चाप (लाल) की तुलना में रम्ब रेखा (नीली) है। शीर्ष पर: लंबकोणीय प्रक्षेपण और नीचे: मर्केटर प्रक्षेपण है।]]मान लीजिए {{mvar|λ}} वृत्त पर एक बिंदु का देशांतर है और {{mvar|φ}} इसका अक्षांश है। फिर, यदि हम मर्केटर प्रक्षेपण के मानचित्र निर्देशांकों को परिभाषित करते हैं;
 :<math>\begin{align}
 x &= \lambda - \lambda_0 \,  \\
@@ Line 92: / Line 91: @@
 == अनुप्रयोग ==
-मार्गनिर्देशन में इसका उपयोग सीधे शैली से जुड़ा हुआ है, या कुछ मार्गनिर्देशक मानचित्रों का प्रक्षेपण है। [[नक्शा प्रक्षेपण|मर्केटर प्रक्षेपण]] प्रतिचित्रों पर एक रंब रेखा एक सीधी रेखा के रूप में दिखाई देती है।<ref name="EOS">Oxford University Press [http://www.encyclopedia.com/doc/1O225-rhumbline.html Rhumb Line]. The Oxford Companion to Ships and the Sea, Oxford University Press, 2006. Retrieved from Encyclopedia.com 18 July 2009.</ref>
+मार्गनिर्देशन में इसका उपयोग सीधे शैली से जुड़ा हुआ है, या कुछ मार्गनिर्देशक मानचित्रों का प्रक्षेपण है। मर्केटर प्रक्षेपण प्रतिचित्रों पर एक रम्ब रेखा एक सीधी रेखा के रूप में दिखाई देती है।<ref name="EOS">Oxford University Press [http://www.encyclopedia.com/doc/1O225-rhumbline.html Rhumb Line]. The Oxford Companion to Ships and the Sea, Oxford University Press, 2006. Retrieved from Encyclopedia.com 18 July 2009.</ref>
-यह नाम क्रमशः पुराने फ्रांसीसी या स्पेनी से लिया गया है: "रंब" या "रंबो" रेखाचित्र पर एक रेखा जो एक ही कोण पर सभी मध्याह्न रेखाओं को काटती है।<ref name="EOS" />समतल सतहों पर यह दो बिंदुओं के मध्य की सबसे छोटी दूरी होगी। पृथ्वी की सतहों पर कम अक्षांशों पर या कम दूरी पर इसका उपयोग किसी वाहन, विमान या पोतो के पाठ्यक्रमों का आलेखन रचने के लिए किया जा सकता है।<ref name="EOS" />लंबी दूरी और/या उच्च अक्षांशों पर बृहत् वृत पथ समान दो बिंदुओं के मध्य की रेखाओं से काफी छोटा है। हालांकि, एक बृहत् वृत पथ का आवागमन करते समय दिक्कोणो को निरन्तर परिवर्तित करने की असुविधा कुछ उदाहरणों में रंब रेखा मार्गनिर्देशनो को आकर्षक बनाती है।<ref name="EOS" />
+यह नाम क्रमशः पुराने फ्रांसीसी या स्पेनी से लिया गया है: "रम्ब" या "रम्बो" रेखाचित्र पर एक रेखा जो एक ही कोण पर सभी मध्याह्न रेखाओं को काटती है।<ref name="EOS" />समतल सतहों पर यह दो बिंदुओं के मध्य की सबसे छोटी दूरी होगी। पृथ्वी की सतहों पर कम अक्षांशों पर या कम दूरी पर इसका उपयोग किसी वाहन, विमान या पोतो के पाठ्यक्रमों का आलेखन रचने के लिए किया जा सकता है।<ref name="EOS" />लंबी दूरी और/या उच्च अक्षांशों पर बृहत् वृत पथ समान दो बिंदुओं के मध्य की रेखाओं से काफी छोटा है। हालांकि, एक बृहत् वृत पथ का आवागमन करते समय दिक्कोणो को निरन्तर परिवर्तित करने की असुविधा कुछ उदाहरणों में रम्ब रेखा मार्गनिर्देशनो को आकर्षक बनाती है।<ref name="EOS" />
-बिंदु को भूमध्य रेखाओं के साथ [[90 डिग्री]] देशांतरों पर एक पूर्व-पश्चिम पंथ के साथ चित्रित किया जा सकता है, जिसके लिए 10,000 किलोमीटर (5,400 समुद्रीय मील) पर बृहत् वृत्तों और रंब रेखाओं की दूरी समान हैं, 20 डिग्री उत्तर में बृहत् वृत्तों की दूरी 9,254 किमी (4,997 एनएमआई) है, जबकि रंब रेखाओं की दूरी 9,397 किमी (5,074 एनएमआई) है, लगभग 1.5% आगे है। परन्तु 60 डिग्री उत्तर में बृहत् वृत्तों की दूरी 4,602 किमी (2,485 समुद्रीय मील) है, जबकि रंब रेखा 5,000 किमी (2,700 समुद्रीय मील) है, जो 8.5% का अंतर है। एक अधिक चरम परिस्थिति [[न्यूयॉर्क शहर]] और [[हांगकांग]] के मध्य का विमान मार्ग है, जिसके लिए रंब रेखा पथ 18,000 किमी (9,700 एनएमआई) है। उत्तरी ध्रुवों पर बृहत् वृत्त पंथ 13,000 किमी (7,000 एनएमआई) है, या सामान्य [[क्रूज (उड़ान)|परिभ्रमण गति]] पर {{frac|5|1|2}} घंटे कम उड़ान समय है।
+बिंदु को भूमध्य रेखाओं के साथ 90 डिग्री देशांतरों पर एक पूर्व-पश्चिम पंथ के साथ चित्रित किया जा सकता है, जिसके लिए 10,000 किलोमीटर (5,400 समुद्रीय मील) पर बृहत् वृत्तों और रम्ब रेखाओं की दूरी समान हैं, 20 डिग्री उत्तर में बृहत् वृत्तों की दूरी 9,254 किमी (4,997 एनएमआई) है, जबकि रम्ब रेखाओं की दूरी 9,397 किमी (5,074 एनएमआई) है, लगभग 1.5% आगे है। परन्तु 60 डिग्री उत्तर में बृहत् वृत्तों की दूरी 4,602 किमी (2,485 समुद्रीय मील) है, जबकि रम्ब रेखा 5,000 किमी (2,700 समुद्रीय मील) है, जो 8.5% का अंतर है। एक अधिक चरम परिस्थिति [[न्यूयॉर्क शहर]] और हांगकांग के मध्य का विमान मार्ग है, जिसके लिए रम्ब रेखा पथ 18,000 किमी (9,700 एनएमआई) है। उत्तरी ध्रुवों पर बृहत् वृत्त पंथ 13,000 किमी (7,000 एनएमआई) है, या सामान्य परिभ्रमण गति पर {{frac|5|1|2}} घंटे कम उड़ान समय है।
-मर्केटर प्रक्षेपण के कुछ पुराने मानचित्रों में [[अक्षांश]] और देशांतर की रेखाओं से बने संजाल होते हैं, परन्तु रंब रेखाएं भी दिखाई देती हैं, जो सीधे उत्तर की ओर, उत्तर से समकोण पर, या उत्तर से कुछ कोण पर होती हैं, जोकि एक समकोण कुछ सरल तर्कसंगत अंश है। ये रंब रेखाएँ खींची जाएँगी ताकि वे मानचित्रों के कुछ बिंदुओं पर अभिसरित हों: प्रत्येक दिशाओं में जाने वाली रेखाएँ इनमें से प्रत्येक बिंदु पर अभिसरित होंगी। [[कम्पास गुलाब|दिक्सूचकआरेख]] देखें। इस प्रकार के प्रतिचित्र आवश्यक रूप से मर्केटर प्रक्षेपण में रहे होंगे इसलिए सभी पुराने मानचित्र रंब रेखा चिह्नों को दर्शाने में सक्षम नहीं रहे होंगे।
+मर्केटर प्रक्षेपण के कुछ पुराने मानचित्रों में [[अक्षांश]] और देशांतर की रेखाओं से बने संजाल होते हैं, परन्तु रम्ब रेखाएं भी दिखाई देती हैं, जो सीधे उत्तर की ओर, उत्तर से समकोण पर, या उत्तर से कुछ कोण पर होती हैं जोकि एक समकोण कुछ सरल तर्कसंगत अंश है। ये रम्ब रेखाएँ खींची जाएँगी ताकि वे मानचित्रों के कुछ बिंदुओं पर अभिसरित हों। प्रत्येक दिशाओं में जाने वाली रेखाएँ इनमें से प्रत्येक बिंदु पर अभिसरित होंगी। [[कम्पास गुलाब|दिक्सूचकआरेख]] देखें। इस प्रकार के प्रतिचित्र आवश्यक रूप से मर्केटर प्रक्षेपण में रहे होंगे इसलिए सभी पुराने मानचित्र रम्ब रेखा चिह्नों को दर्शाने में सक्षम नहीं रहे होंगे।
-दिक्सूचक आरेख पर त्रिज्यीय रेखाओं को रंब भी कहा जाता है। 16वीं-19वीं शताब्दी में एक विशेष दिक्सूचक शीर्षक को इंगित करने के लिए अनुसरण "रंब पर नौचालन" का उपयोग किया गया था।<ref name="EOS" />
+दिक्सूचक आरेख पर त्रिज्यीय रेखाओं को रम्ब भी कहा जाता है। 16वीं-19वीं शताब्दी में एक विशेष दिक्सूचक शीर्षक को इंगित करने के लिए अनुसरण "रम्ब पर नौचालन" का उपयोग किया गया था।<ref name="EOS" />
-[[समुद्री क्रोनोमीटर|समुद्रीय कालमापी]] के आविष्कार से पूर्व के प्रारम्भिक नौनिर्देशकों ने लंबे समुद्रीय मार्गों पर रंब रेखाओं पाठ्यक्रमों का उपयोग किया था, क्योंकि पोत का अक्षांश सूर्य या तारों को देखकर सटीक रूप से स्थापित किया जा सकता था परन्तु देशांतर निर्धारित करने का कोई सटीक तरीका नहीं था। गंतव्य के अक्षांश तक पहुंचने तक पोत उत्तर या दक्षिण की ओर जाएगा और पोत तब पूर्व या पश्चिम में रंब रेखाओं (वास्तव में एक समानांतर, जो कि एकदिश नौपथ की एक विशेष स्थिति है) के साथ एक स्थिर अक्षांश बनाए रखेगा और भूमि के साक्ष्य देखे जाने तक तय की गई दूरी के नियमित अनुमानों को अंकित करना है।<ref>A Brief History of British Seapower, David Howarth, pub. Constable & Robinson, London, 2003, chapter 8.</ref>
+समुद्रीय कालमापी के आविष्कार से पूर्व के प्रारम्भिक नौनिर्देशकों ने लंबे समुद्रीय मार्गों पर रम्ब रेखाओं पाठ्यक्रमों का उपयोग किया था, क्योंकि पोत का अक्षांश सूर्य या तारों को देखकर सटीक रूप से स्थापित किया जा सकता था परन्तु देशांतर निर्धारित करने का कोई सटीक तरीका नहीं था। गंतव्य के अक्षांश तक पहुंचने तक पोत उत्तर या दक्षिण की ओर जाएगा और पोत तब पूर्व या पश्चिम में रम्ब रेखाओं (वास्तव में एक समानांतर, जो कि एकदिश नौपथ की एक विशेष स्थिति है) के साथ एक स्थिर अक्षांश बनाए रखेगा और भूमि के साक्ष्य देखे जाने तक तय की गई दूरी के नियमित अनुमानों को अंकित करना है।<ref>A Brief History of British Seapower, David Howarth, pub. Constable & Robinson, London, 2003, chapter 8.</ref>
@@ Line 135: / Line 134: @@
 |url = http://ntv.spbstu.ru/fulltext/T3.198.2014_05.PDF
 }}
-</ref> रंब रेखाओं का पथ केवल दीर्घवृत्ताभ [[सममितीय अक्षांश]] का उपयोग करके पाया जाता है। इस पृष्ठ पर उपरोक्त सूत्रों में, वृत्तों पर अक्षांश के लिए दीर्घवृत्ताभ पर अनुरूप अक्षांश को प्रतिस्थापित किया जाता है। इसी तरह, दिगंश के छेदक द्वारा दीर्घवृत्ताकार याम्योत्तर चाप की लंबाई को गुणा करके दूरियां प्राप्त की जाती हैं।
+</ref> रम्ब रेखाओं का पथ केवल दीर्घवृत्ताभ [[सममितीय अक्षांश]] का उपयोग करके पाया जाता है। इस पृष्ठ पर उपरोक्त सूत्रों में, वृत्तों पर अक्षांश के लिए दीर्घवृत्ताभ पर अनुरूप अक्षांश को प्रतिस्थापित किया जाता है। इसी तरह, दिगंश के छेदक द्वारा दीर्घवृत्ताकार याम्योत्तर चाप की लंबाई को गुणा करके दूरियां प्राप्त की जाती हैं।
 == यह भी देखें ==
 * बृहत् वृत
-* एक दीर्घवृत्ताभ पर अल्पांतरी
+* दीर्घवृत्ताभ पर अल्पांतरी
 * [[महान दीर्घवृत्त|बृहत् दीर्घवृत्त]]
-* [[इसोआज़ीमुथल]]
+* इसोआज़ीमुथल
-* [[रंबलाइन नेटवर्क|एकदिश नौपथ संजाल]]
+* एकदिश नौपथ संजाल
-* सीफ़र्ट का कुंडली
+* सीफ़र्ट की कुंडली
-* [[छोटा घेरा|लघु वृत्त]]
+* लघु वृत्त
 ==संदर्भ==
 {{reflist|30em}}
-'''''Note:''' this article incorporates text from the 1878 edition of '''The Globe Encyclopaedia of Universal Information''', a work in the public domain''
 ==अग्रिम पठन==
@@ Line 155: / Line 152: @@
 *{{cite book|last1=Monmonier|first1=Mark|title=Rhumb lines and map wars. A social history of the Mercator projection|url=https://archive.org/details/rhumblinesmapwar00monm|url-access=registration|date=2004|publisher=University of Chicago Press|location=Chicago|isbn=9780226534329}}
 {{Refend}}
 ==बाहरी संबंध==
-{{wiktionary|loxodrome|rhumb}}
 * [http://www.mathpages.com/home/kmath502/kmath502.htm Constant Headings and Rhumb Lines] at MathPages.
 * [https://geographiclib.sourceforge.io/C++/doc/RhumbSolve.1.html RhumbSolve(1)], a utility for ellipsoidal rhumb line calculations (a component of [https://geographiclib.sourceforge.io GeographicLib]); [https://geographiclib.sourceforge.io/C++/doc/rhumb.html supplementary documentation].
@@ Line 166: / Line 160: @@
 * [http://mathworld.wolfram.com/Loxodrome.html Mathworld] Loxodrome.
-{{DEFAULTSORT:Rhumb Line}}[[Category: नक्शानवीसी]] [[Category: सर्पिल]] [[Category: गोलाकार वक्र]] [[Category: मार्गदर्शन]] [[Category: भूमंडल नापने का शास्र]]
+{{DEFAULTSORT:Rhumb Line}}
-[[Category: Machine Translated Page]]
+[[Category:Articles with hatnote templates targeting a nonexistent page|Rhumb Line]]
-[[Category:Created On 17/04/2023]]
+[[Category:CS1 maint]]
+[[Category:CS1 uses русский-language script (ru)]]
+[[Category:Created On 17/04/2023|Rhumb Line]]
+[[Category:Lua-based templates|Rhumb Line]]
+[[Category:Machine Translated Page|Rhumb Line]]
+[[Category:Pages with maths render errors|Rhumb Line]]
+[[Category:Pages with script errors|Rhumb Line]]
+[[Category:Templates Vigyan Ready|Rhumb Line]]
+[[Category:Templates that add a tracking category|Rhumb Line]]
+[[Category:Templates that generate short descriptions|Rhumb Line]]
+[[Category:Templates using TemplateData|Rhumb Line]]
+[[Category:Use dmy dates from October 2019|Rhumb Line]]
+[[Category:Webarchive template wayback links|Rhumb Line]]
+[[Category:गोलाकार वक्र|Rhumb Line]]
+[[Category:नक्शानवीसी|Rhumb Line]]
+[[Category:भूमंडल नापने का शास्र|Rhumb Line]]
+[[Category:मार्गदर्शन|Rhumb Line]]
+[[Category:सर्पिल|Rhumb Line]]

Anonymous

Search

रम्ब रेखा: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 16:45, 6 November 2023

Contents

परिचय

व्युत्पत्ति और ऐतिहासिक विवरण

गणितीय विवरण

मर्केटर प्रक्षेपण से सम्बन्ध

अनुप्रयोग

सामान्यीकरण

रीमैन क्षेत्र पर

गोलाभ

यह भी देखें

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

रम्ब रेखा: Difference between revisions

Latest revision as of 16:45, 6 November 2023

परिचय

व्युत्पत्ति और ऐतिहासिक विवरण

गणितीय विवरण

मर्केटर प्रक्षेपण से सम्बन्ध

अनुप्रयोग

सामान्यीकरण

रीमैन क्षेत्र पर

गोलाभ

यह भी देखें

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories