परिणाम की पुष्टि: Difference between revisions
(Created page with "{{Short description|Type of fallacious argument (logical fallacy)}} {{Use dmy dates|date=June 2013}} {{redirect3|False conversion|the Islamic doctrine|Taqiya}} प्रस...") |
No edit summary |
||
| (4 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[प्रस्तावात्मक कलन]] में, '''परिणामी की पुष्टि''' करना, जिसे कभी-कभी विपरीत त्रुटि, विपरीत की भ्रांति, या आवश्यकता और पर्याप्तता का भ्रम कहा जाता है, एक वास्तविक [[सांकेतिक सशर्त|सांकेतिक सपरिस्थिति]] कथन लेने की एक [[औपचारिक भ्रांति]] है (उदाहरण के लिए, यदि दीपक टूट गया था, तो कमरा अंधेरा होगा), और अमान्य रूप से इसके विपरीत का अनुमान लगाना (कमरा अंधेरा है, संभवतः दीपक टूट गया होगा), भले ही वह कथन सत्य न हो। यह तब उत्पन्न होता है जब परिणामी (कमरा अंधेरा होगा) के अन्य संभावित पूर्ववृत्त (तर्क) हैं (उदाहरण के लिए, दीपक काम करने की स्थिति में है, लेकिन बंद है या कमरे में कोई दीपक नहीं है)। | |||
परिणाम को नकारने वाले विपरीत कथन को [[विधि को हटाना]] कहा जाता है और | प्रतिदिन की सोच और संचार में बातचीत संबंधी त्रुटियां सामान्य हैं और अन्य कारणों के अतिरिक्त, संचार संबंधी समस्याएं, तर्क के बारे में गलत धारणाएं और अन्य कारणों पर विचार करने में विफलता के परिणामस्वरूप हो सकती हैं। | ||
परिणाम को नकारने वाले विपरीत कथन को [[विधि को हटाना|निषेधक हेतु फलानुमान]] कहा जाता है और यह तर्क का एक वैध रूप है। <ref name="Hurley2012">{{Cite book |last=Hurley |first=Patrick J. |url=https://books.google.com/books?id=foDDbwAACAAJ |page=362 |title=तर्क का संक्षिप्त परिचय|date=2012 |isbn=9781111346232 |publisher=Cengage Learning |location=Boston, Massachusetts |oclc=711774631|edition=11th }}</ref> | |||
==औपचारिक विवरण== | ==औपचारिक विवरण== | ||
[[File:In Quest of Univeral Logic HypoSyll.png|right|thumbnail|400px|काल्पनिक न्यायवाक्य के चार संभावित रूप हैं, जिनमें से दो वैध हैं, जबकि दो अमान्य हैं। एक बहुत ही सरल उदाहरण पर विचार करने से आपको यह समझने में मदद मिल सकती है कि ये फॉर्म वैध या अमान्य क्यों हैं। यदि p दर्शाता है कि कैंडिरू एक मछली है और q दर्शाता है कि कैंडिरू तैर सकता है, तो उपरोक्त तालिका में इन कथनों को p और q से प्रतिस्थापित करके स्वयं को समझाने का प्रयास करें।<ref name="Kashef2023">{{citation |last1=Kashef |first1=Arman |year=2023 |title= In Quest of Univeral Logic: A brief overview of formal logic's evolution |doi=10.13140/RG.2.2.24043.82724/1 |url=https://www.researchgate.net/publication/366867569}}</ref>]]परिणाम की पुष्टि करना सत्य कथन | [[File:In Quest of Univeral Logic HypoSyll.png|right|thumbnail|400px|काल्पनिक न्यायवाक्य के चार संभावित रूप हैं, जिनमें से दो वैध हैं, जबकि दो अमान्य हैं। एक बहुत ही सरल उदाहरण पर विचार करने से आपको यह समझने में मदद मिल सकती है कि ये फॉर्म वैध या अमान्य क्यों हैं। यदि p दर्शाता है कि कैंडिरू एक मछली है और q दर्शाता है कि कैंडिरू तैर सकता है, तो उपरोक्त तालिका में इन कथनों को p और q से प्रतिस्थापित करके स्वयं को समझाने का प्रयास करें।<ref name="Kashef2023">{{citation |last1=Kashef |first1=Arman |year=2023 |title= In Quest of Univeral Logic: A brief overview of formal logic's evolution |doi=10.13140/RG.2.2.24043.82724/1 |url=https://www.researchgate.net/publication/366867569}}</ref>]]परिणाम की पुष्टि करना सत्य कथन <math>P \to Q</math> लेने और इसके वार्तालाप को अमान्य रूप <math>Q \to P</math> से समाप्त करने की क्रिया है। परिणामी की पुष्टि करने वाला नाम परिणामी, Q, के उपयोग से निकला <math>P \to Q</math> है, पूर्ववर्ती पी का निष्कर्ष निकालने के लिए इस भ्रांति को औपचारिक रूप से संक्षेप में <math>(P \to Q, Q)\to P</math> या, वैकल्पिक रूप से, <math>\frac{P \to Q, Q}{\therefore P}</math> प्रस्तुत किया जा सकता है। <ref>Hurley, Patrick J. (2010), ''A Concise Introduction to Logic'' (11th edition). Wadsworth Cengage Learning, pp. 362–63.</ref> | ||
ऐसी तार्किक त्रुटि का मूल कारण कभी-कभी यह | ऐसी तार्किक त्रुटि का मूल कारण कभी-कभी यह अनुभव करने में विफलता है कि सिर्फ इसलिए कि P, Q के लिए एक संभावित स्थिति है, P, Q के लिए एकमात्र परिस्थिति नहीं हो सकती है, यानी Q किसी अन्य स्थिति से भी उत्पन्न हो सकता है। <ref>{{cite web|url=http://www.fallacyfiles.org/afthecon.html|title=परिणाम की पुष्टि|website=Fallacy Files|publisher=Fallacy Files|access-date=9 May 2013}}</ref><ref>{{cite book|title=दोषपूर्ण तर्क पर हमला|last=Damer|first=T. Edward|publisher=Wadsworth|year=2001|edition=4th|page=150|chapter=Confusion of a Necessary with a Sufficient Condition |isbn=0-534-60516-8}}</ref> | ||
परिणाम की पुष्टि करने का परिणाम सत्य वार्तालाप वाले कई कथनों के अनुभव को अतिसामान्यीकरण करना भी हो सकता है। यदि P और Q समतुल्य कथन हैं, अर्थात <math>P \leftrightarrow Q</math>, | |||
परिणाम की पुष्टि करने का परिणाम सत्य वार्तालाप वाले कई कथनों के अनुभव को अतिसामान्यीकरण करना भी हो सकता है। यदि P और Q समतुल्य कथन हैं, अर्थात <math>P \leftrightarrow Q</math>, परिस्थिति Q के अंतर्गत P का अनुमान लगाना संभव है। "यह 13 अगस्त है, इसलिए यह मेरा जन्मदिन है" <math>P \leftrightarrow Q</math> और "यह मेरा जन्मदिन है, इसलिए यह 13 अगस्त है" <math>Q \to P</math> समतुल्य हैं और कथन के दोनों सही परिणाम "13 अगस्त मेरा जन्मदिन है" (<math>P \to Q</math>) का संक्षिप्त रूप है। | |||
मिश्रित [[काल्पनिक न्यायवाक्य]] के संभावित रूपों में से दो मान्य हैं और दो अमान्य हैं। पूर्ववर्ती ([[ मूड सेट करना |विधानात्मक हेतुफलानुमान]]) की पुष्टि करना और परिणामी (मोडस पोनेन्स) को नकारना वैध है। परिणामी की पुष्टि करना और [[पूर्ववृत्त को नकारना]] अमान्य है (तालिका देखें)। <ref>Kelley, David (1998), ''The Art of Reasoning'' (3rd edition). Norton, pp. 290–94.</ref> | |||
| Line 24: | Line 24: | ||
:यदि कोई [[सैन डिएगो]] में रहता है, तो वह [[कैलिफोर्निया]] में रहता है। | :यदि कोई [[सैन डिएगो]] में रहता है, तो वह [[कैलिफोर्निया]] में रहता है। | ||
: | :जोइ कैलिफ़ोर्निया में रहता है। | ||
:इसलिए, | :इसलिए, जोइ सैन डिएगो में रहता है। | ||
कैलिफ़ोर्निया में सैन डिएगो के अतिरिक्त रहने के लिए कई जगहें हैं; हालाँकि, कोई निश्चितता के साथ पुष्टि कर सकता है कि यदि कोई कैलिफ़ोर्निया (नॉन-क्यू) में नहीं रहता है, तो यह व्यक्ति सैन डिएगो (नॉन-पी) में नहीं रहता है। यह पहले कथन का प्रतिधनात्मक है, और यह तभी सत्य होना चाहिए जब मूल कथन सत्य हो। | |||
| Line 38: | Line 40: | ||
:इसलिए, मेरी बिल्ली एक कुत्ता है। | :इसलिए, मेरी बिल्ली एक कुत्ता है। | ||
यहां, यह तुरंत सहज ज्ञान युक्त है कि किसी भी अन्य पूर्ववृत्त (यदि कोई जानवर हिरण है..., यदि कोई जानवर हाथी है..., यदि कोई जानवर मूस है..., | यहां, यह तुरंत सहज ज्ञान युक्त है कि किसी भी अन्य पूर्ववृत्त (यदि कोई जानवर हिरण है..., यदि कोई जानवर हाथी है..., यदि कोई जानवर मूस है..., आदि) परिणाम को उत्पन्न कर सकता है (तब इसके चार पैर हैं), और यह मान लेना बेतुका है कि चार पैर होने का अर्थ यह होना चाहिए कि जानवर एक कुत्ता है और कुछ नहीं। यह एक शिक्षण उदाहरण के रूप में उपयोगी है क्योंकि अधिकांश लोग तुरंत पहचान सकते हैं कि जो निष्कर्ष निकाला गया है वह गलत होना चाहिए (सहज रूप से, एक बिल्ली कुत्ता नहीं हो सकती), और जिस तरीके से यह निष्कर्ष निकाला गया वह गलत होना चाहिए। | ||
उदाहरण 3 | उदाहरण 3 | ||
| Line 45: | Line 47: | ||
:अगर ब्रायन को [[एफिल टॉवर]] के ऊपर से फेंक दिया गया होता, तो वह मर गया होता। | :अगर ब्रायन को [[एफिल टॉवर]] के ऊपर से फेंक दिया गया होता, तो वह मर गया होता। | ||
:ब्रायन मर चुका | :ब्रायन मर चुका है। | ||
:इसलिए, ब्रायन को एफिल टॉवर के ऊपर से फेंक दिया गया। | :इसलिए, ब्रायन को एफिल टॉवर के ऊपर से फेंक दिया गया। | ||
एफिल टॉवर के ऊपर से फेंक दिया जाना | एफिल टॉवर के ऊपर से फेंक दिया जाना मृत्यु का एकमात्र कारण नहीं है, क्योंकि मृत्यु के कई अलग-अलग कारण उपस्थित हैं। | ||
उदाहरण 4 | उदाहरण 4 | ||
| Line 55: | Line 57: | ||
: हालाँकि, आप पढ़ सकते हैं, है ना? कर्नल व्यंग्य करता रहा। लेखक ने अपने नाम पर हस्ताक्षर किये। | : हालाँकि, आप पढ़ सकते हैं, है ना? कर्नल व्यंग्य करता रहा। लेखक ने अपने नाम पर हस्ताक्षर किये। | ||
: वहां मेरा नाम यही | : वहां मेरा नाम यही है। | ||
: फिर आपने इसे लिखा। क्यू.ई.डी. | : फिर आपने इसे लिखा। क्यू.ई.डी. | ||
इस | इस स्तिथि में P है 'पादरी अपने नाम पर हस्ताक्षर करता है', और Q 'पादरी का नाम लिखा है'। पादरी का नाम लिखा जा सकता है, लेकिन जरूरी नहीं कि उसने इसे लिखा हो, जैसा कि कर्नल ने गलत निष्कर्ष निकाला है। <ref name=":0" /> | ||
उदाहरण 5 | उदाहरण 5 | ||
वैज्ञानिक पद्धति सिखाते समय, निम्नलिखित उदाहरण का उपयोग यह बताने के लिए किया जाता है कि क्यों, परिणाम की पुष्टि करने की भ्रांति के माध्यम से, कोई भी वैज्ञानिक सिद्धांत कभी भी सत्य | वैज्ञानिक पद्धति सिखाते समय, निम्नलिखित उदाहरण का उपयोग यह बताने के लिए किया जाता है कि क्यों, परिणाम की पुष्टि करने की भ्रांति के माध्यम से, कोई भी वैज्ञानिक सिद्धांत कभी भी सत्य सिद्ध नहीं होता है, बल्कि मिथ्या सिद्ध होने में विफल रहता है। | ||
: यदि यह सिद्धांत सही है, तो हम एक्स का अवलोकन करेंगे। | : यदि यह सिद्धांत सही है, तो हम एक्स का अवलोकन करेंगे। | ||
| Line 68: | Line 70: | ||
: अत: यह सिद्धांत सही है। | : अत: यह सिद्धांत सही है। | ||
यह निष्कर्ष निकालना या मान लेना कि कोई सिद्धांत किसी भविष्यवाणी के कारण सत्य है, जिसे देखा जा रहा है, अमान्य है। यह वैज्ञानिक पद्धति को लागू करने की चुनौतियों में से एक है, हालांकि इसे अकादमिक संदर्भों में | यह निष्कर्ष निकालना या मान लेना कि कोई सिद्धांत किसी भविष्यवाणी के कारण सत्य है, जिसे देखा जा रहा है, अमान्य है। यह वैज्ञानिक पद्धति को लागू करने की चुनौतियों में से एक है, हालांकि इसे अकादमिक संदर्भों में संभवतः ही कभी लाया जाता है क्योंकि इसका अध्ययन के परिणामों पर कोई प्रभाव पड़ने की संभावना नहीं है। सिद्धांत की वैधता, अवलोकन की भविष्यवाणी करने वाले सिद्धांत की अपेक्षा की वैधता, और/या स्वयं अवलोकन की वैधता पर सवाल उठाना अधिक सामान्य है। | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 85: | Line 87: | ||
{{reflist}} | {{reflist}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Collapse templates]] | |||
[[Category: | |||
[[Category:Created On 30/06/2023]] | [[Category:Created On 30/06/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Missing redirects]] | |||
[[Category:Multi-column templates]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
[[Category:Use dmy dates from June 2013]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:औपचारिक भ्रांतियाँ]] | |||
[[Category:तर्कपूर्ण लेखों पर विशेषज्ञ ध्यान देने की आवश्यकता है]] | |||
Latest revision as of 17:00, 7 November 2023
प्रस्तावात्मक कलन में, परिणामी की पुष्टि करना, जिसे कभी-कभी विपरीत त्रुटि, विपरीत की भ्रांति, या आवश्यकता और पर्याप्तता का भ्रम कहा जाता है, एक वास्तविक सांकेतिक सपरिस्थिति कथन लेने की एक औपचारिक भ्रांति है (उदाहरण के लिए, यदि दीपक टूट गया था, तो कमरा अंधेरा होगा), और अमान्य रूप से इसके विपरीत का अनुमान लगाना (कमरा अंधेरा है, संभवतः दीपक टूट गया होगा), भले ही वह कथन सत्य न हो। यह तब उत्पन्न होता है जब परिणामी (कमरा अंधेरा होगा) के अन्य संभावित पूर्ववृत्त (तर्क) हैं (उदाहरण के लिए, दीपक काम करने की स्थिति में है, लेकिन बंद है या कमरे में कोई दीपक नहीं है)।
प्रतिदिन की सोच और संचार में बातचीत संबंधी त्रुटियां सामान्य हैं और अन्य कारणों के अतिरिक्त, संचार संबंधी समस्याएं, तर्क के बारे में गलत धारणाएं और अन्य कारणों पर विचार करने में विफलता के परिणामस्वरूप हो सकती हैं।
परिणाम को नकारने वाले विपरीत कथन को निषेधक हेतु फलानुमान कहा जाता है और यह तर्क का एक वैध रूप है। [1]
औपचारिक विवरण
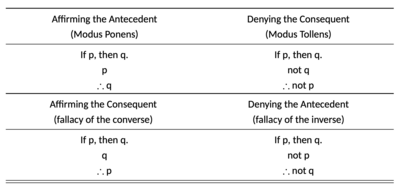
परिणाम की पुष्टि करना सत्य कथन लेने और इसके वार्तालाप को अमान्य रूप से समाप्त करने की क्रिया है। परिणामी की पुष्टि करने वाला नाम परिणामी, Q, के उपयोग से निकला है, पूर्ववर्ती पी का निष्कर्ष निकालने के लिए इस भ्रांति को औपचारिक रूप से संक्षेप में या, वैकल्पिक रूप से, प्रस्तुत किया जा सकता है। [3]
ऐसी तार्किक त्रुटि का मूल कारण कभी-कभी यह अनुभव करने में विफलता है कि सिर्फ इसलिए कि P, Q के लिए एक संभावित स्थिति है, P, Q के लिए एकमात्र परिस्थिति नहीं हो सकती है, यानी Q किसी अन्य स्थिति से भी उत्पन्न हो सकता है। [4][5]
परिणाम की पुष्टि करने का परिणाम सत्य वार्तालाप वाले कई कथनों के अनुभव को अतिसामान्यीकरण करना भी हो सकता है। यदि P और Q समतुल्य कथन हैं, अर्थात , परिस्थिति Q के अंतर्गत P का अनुमान लगाना संभव है। "यह 13 अगस्त है, इसलिए यह मेरा जन्मदिन है" और "यह मेरा जन्मदिन है, इसलिए यह 13 अगस्त है" समतुल्य हैं और कथन के दोनों सही परिणाम "13 अगस्त मेरा जन्मदिन है" () का संक्षिप्त रूप है।
मिश्रित काल्पनिक न्यायवाक्य के संभावित रूपों में से दो मान्य हैं और दो अमान्य हैं। पूर्ववर्ती (विधानात्मक हेतुफलानुमान) की पुष्टि करना और परिणामी (मोडस पोनेन्स) को नकारना वैध है। परिणामी की पुष्टि करना और पूर्ववृत्त को नकारना अमान्य है (तालिका देखें)। [6]
अतिरिक्त उदाहरण
उदाहरण 1
इस तर्क प्रपत्र की अमान्यता को प्रदर्शित करने का एक तरीका सही परिसर के साथ एक प्रति उदाहरण है लेकिन एक स्पष्ट रूप से गलत निष्कर्ष है। उदाहरण के लिए:
- यदि कोई सैन डिएगो में रहता है, तो वह कैलिफोर्निया में रहता है।
- जोइ कैलिफ़ोर्निया में रहता है।
- इसलिए, जोइ सैन डिएगो में रहता है।
कैलिफ़ोर्निया में सैन डिएगो के अतिरिक्त रहने के लिए कई जगहें हैं; हालाँकि, कोई निश्चितता के साथ पुष्टि कर सकता है कि यदि कोई कैलिफ़ोर्निया (नॉन-क्यू) में नहीं रहता है, तो यह व्यक्ति सैन डिएगो (नॉन-पी) में नहीं रहता है। यह पहले कथन का प्रतिधनात्मक है, और यह तभी सत्य होना चाहिए जब मूल कथन सत्य हो।
उदाहरण 2
यहाँ एक और उपयोगी, स्पष्ट रूप से भ्रामक उदाहरण है।
- अगर कोई जानवर कुत्ता है तो उसके चार पैर होते हैं।
- मेरी बिल्ली के चार पैर हैं।
- इसलिए, मेरी बिल्ली एक कुत्ता है।
यहां, यह तुरंत सहज ज्ञान युक्त है कि किसी भी अन्य पूर्ववृत्त (यदि कोई जानवर हिरण है..., यदि कोई जानवर हाथी है..., यदि कोई जानवर मूस है..., आदि) परिणाम को उत्पन्न कर सकता है (तब इसके चार पैर हैं), और यह मान लेना बेतुका है कि चार पैर होने का अर्थ यह होना चाहिए कि जानवर एक कुत्ता है और कुछ नहीं। यह एक शिक्षण उदाहरण के रूप में उपयोगी है क्योंकि अधिकांश लोग तुरंत पहचान सकते हैं कि जो निष्कर्ष निकाला गया है वह गलत होना चाहिए (सहज रूप से, एक बिल्ली कुत्ता नहीं हो सकती), और जिस तरीके से यह निष्कर्ष निकाला गया वह गलत होना चाहिए।
उदाहरण 3
एक ही रूप के तर्क कभी-कभी सतही रूप से ठोस प्रतीत हो सकते हैं, जैसा कि निम्नलिखित उदाहरण में है:
- अगर ब्रायन को एफिल टॉवर के ऊपर से फेंक दिया गया होता, तो वह मर गया होता।
- ब्रायन मर चुका है।
- इसलिए, ब्रायन को एफिल टॉवर के ऊपर से फेंक दिया गया।
एफिल टॉवर के ऊपर से फेंक दिया जाना मृत्यु का एकमात्र कारण नहीं है, क्योंकि मृत्यु के कई अलग-अलग कारण उपस्थित हैं।
उदाहरण 4
कैच-22 में,[7] कथित तौर पर वाशिंगटन इरविंग/इरविंग वाशिंगटन होने के कारण पादरी से पूछताछ की जाती है, जो सैनिकों के पत्रों के बड़े हिस्से को घर भेजने से रोक रहा है। कर्नल को ऐसा एक पत्र मिला है, लेकिन उस पर पादरी के नाम के हस्ताक्षर हैं।
- हालाँकि, आप पढ़ सकते हैं, है ना? कर्नल व्यंग्य करता रहा। लेखक ने अपने नाम पर हस्ताक्षर किये।
- वहां मेरा नाम यही है।
- फिर आपने इसे लिखा। क्यू.ई.डी.
इस स्तिथि में P है 'पादरी अपने नाम पर हस्ताक्षर करता है', और Q 'पादरी का नाम लिखा है'। पादरी का नाम लिखा जा सकता है, लेकिन जरूरी नहीं कि उसने इसे लिखा हो, जैसा कि कर्नल ने गलत निष्कर्ष निकाला है। [7]
उदाहरण 5
वैज्ञानिक पद्धति सिखाते समय, निम्नलिखित उदाहरण का उपयोग यह बताने के लिए किया जाता है कि क्यों, परिणाम की पुष्टि करने की भ्रांति के माध्यम से, कोई भी वैज्ञानिक सिद्धांत कभी भी सत्य सिद्ध नहीं होता है, बल्कि मिथ्या सिद्ध होने में विफल रहता है।
- यदि यह सिद्धांत सही है, तो हम एक्स का अवलोकन करेंगे।
- हम एक्स का निरीक्षण करते हैं।
- अत: यह सिद्धांत सही है।
यह निष्कर्ष निकालना या मान लेना कि कोई सिद्धांत किसी भविष्यवाणी के कारण सत्य है, जिसे देखा जा रहा है, अमान्य है। यह वैज्ञानिक पद्धति को लागू करने की चुनौतियों में से एक है, हालांकि इसे अकादमिक संदर्भों में संभवतः ही कभी लाया जाता है क्योंकि इसका अध्ययन के परिणामों पर कोई प्रभाव पड़ने की संभावना नहीं है। सिद्धांत की वैधता, अवलोकन की भविष्यवाणी करने वाले सिद्धांत की अपेक्षा की वैधता, और/या स्वयं अवलोकन की वैधता पर सवाल उठाना अधिक सामान्य है।
यह भी देखें
- अपहरणात्मक तर्क
- परिणाम की अपील
- व्युत्क्रम का भ्रम
- पूर्ववृत्त को नकारना
- एकल कारण की भ्रांति
- अवितरित मध्य की भ्रान्ति
- एक वैध, सरल तर्क और निष्कर्ष के नियम के रूप
- आवश्यकता एवं पर्याप्तता
संदर्भ
- ↑ Hurley, Patrick J. (2012). तर्क का संक्षिप्त परिचय (11th ed.). Boston, Massachusetts: Cengage Learning. p. 362. ISBN 9781111346232. OCLC 711774631.
- ↑ Kashef, Arman (2023), In Quest of Univeral Logic: A brief overview of formal logic's evolution, doi:10.13140/RG.2.2.24043.82724/1
- ↑ Hurley, Patrick J. (2010), A Concise Introduction to Logic (11th edition). Wadsworth Cengage Learning, pp. 362–63.
- ↑ "परिणाम की पुष्टि". Fallacy Files. Fallacy Files. Retrieved 9 May 2013.
- ↑ Damer, T. Edward (2001). "Confusion of a Necessary with a Sufficient Condition". दोषपूर्ण तर्क पर हमला (4th ed.). Wadsworth. p. 150. ISBN 0-534-60516-8.
- ↑ Kelley, David (1998), The Art of Reasoning (3rd edition). Norton, pp. 290–94.
- ↑ 7.0 7.1 Heller, Joseph (1994). Catch-22. Vintage. pp. 438, 8. ISBN 0-09-947731-9.