आर्किमिडीज़ का ट्रैमेल: Difference between revisions

Latest revision as of 12:27, 8 November 2023

आर्किमिडीज़ का बंधन अनुप्राणित प्रतिरूप।

आर्किमिडीज़ का ट्रैमेल (दीर्घवृत्तलेखी) एक तंत्र (इंजीनियरिंग) है जो दीर्घवृत्त का आकार उत्पन्न करता है। ^[1] इसमें दो तुरी होते हैं जो लंबवत प्रणाल या छड़ तक सीमित (बंधन) रखे जाते हैं और एक छड़ी होती है जो छड़ी के साथ निश्चित स्थानों पर केंद्रबिंदु द्वारा तुरी से जुड़ी होती है।

जैसे ही तुरी अपने प्रणाल के साथ आगे-पीछे चलती हैं, छड़ी पर सभी बिंदु अण्डाकार पथ में चलते हैं। छड़ की गति को अण्डाकार गति कहा जाता है। दीर्घवृत्त के अर्ध-अक्ष a और b की लंबाई छड़ पर बिंदु से प्रत्येक दो धुरी तक की दूरी के बराबर होती है।

धुरी द्वारा वर्णित सीधी रेखाएँ दीर्घवृत्त की विशेष स्तिथियाँ हैं, जहाँ एक अक्ष की लंबाई धुरी के बीच की दूरी से दोगुनी है और दूसरे की लंबाई शून्य है। दो धुरी द्वारा परिभाषित व्यास वाले वृत्त पर सभी बिंदु ऐसी सीधी रेखाओं में परस्पर मिलते हैं। यह वृत्त तुसी जोड़े के छोटे वृत्त से मेल खाता है।

धुरी के बीच का बिंदु उस बिंदु के चारों ओर एक वृत्त में परिक्रमा करता है जहां प्रणाल पार करते हैं। यह वृत्त भी दीर्घवृत्त की एक विशेष स्तिथि है। यहां अक्षों की लंबाई समान है। वृत्त का व्यास धुरी के बीच की दूरी के बराबर है। कक्षा के चारों ओर यात्रा की दिशा ट्रामेल के घूमने की भावना के विपरीत है। इस प्रकार, यदि प्रणाल के प्रतिच्छेद बिंदु पर केंद्रित वक्रोक्ति का उपयोग ट्रामेल को चलाने के लिए मध्य बिंदु पर संलग्न करने के लिए किया जाता है, तो क्रैंकपिन और बंधन का घूर्णन बराबर और विपरीत होता है, जिसके परिणामस्वरूप व्यावहारिक अनुप्रयोगों में अतिरिक्त घर्षण होता है और त्वरित घिसाव होता है। यह केंद्रबिंदु की केवल 1/4 यात्रा के वक्रोक्ति के कम प्रक्षेप के कारण उच्च बलों द्वारा मिश्रित होता है।

अनुचित ग्राइंडर खिलौना (सीए. 1960)

आर्किमिडीज़ के बंधन के लकड़ी के संस्करणों को दीर्घवृत्त खींचने या काटने के लिए उपकरणों के रूप में तैयार किया गया है, जिन्हें दीर्घवृत्तचित्र के रूप में जाना जाता है। संस्करण खिलौने या विलक्षणता वस्तुओं के रूप में भी बनाए जाते हैं (केंटकी डू-नथिंग्स, नथिंग ग्राइंडर, डू नथिंग मशीन, स्मोक ग्राइंडर, या बुलशिट ग्राइंडर के नाम से बेचे जाते हैं)। इन खिलौनों में आलेखन उपकरण को वक्रोक्ति (तंत्र) हस्तक द्वारा प्रतिस्थापित किया जाता है, और विसर्पण तुरी की स्थिति सामान्यतः तय की जाती है.

गणित

Concept

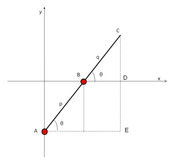
दीर्घवृत्तचित्र के रूप में आर्किमिडीज़ का ट्रैमेल
आरेख
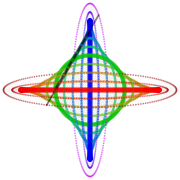
आर्किमिडीज़ के ट्रामेल के साथ और उससे आगे कुछ बिंदुओं का बिंदुपथ, हरा वृत्त इसके मध्यबिंदु का बिंदुपथ है - SVG फ़ाइल में, ट्रैमेल को स्थानांतरित करने के लिए संकेतक को आरेख पर ले जाएं
तीन सर्पक के साथ आर्किमिडीज़ का ट्रैमेल

होने देना $C$ छड़ का बाहरी सिरा हो, और $A$ , $B$ सर्पक की धुरी बनें। होने देना $AB$ और $BC$ से दूरियां हो $A$ को $B$ और $B$ को $C$ , क्रमश। आइए मान लें कि स्लाइडर $A$ और $B$ के साथ आगे बढ़ें $y$ और $x$ कार्टेशियन क्रमशः अक्षों का समन्वय करता है। जब छड़ एक कोण बनाती है $θ$ x-अक्ष के साथ, बिंदु के निर्देशांक $C$ द्वारा दिए गए हैं

x=(AB+BC)\cos \theta \,

y=BC\sin \theta \,

ये विहित स्थिति में दीर्घवृत्त के लिए मानक पैरामीट्रिक समीकरण के रूप में हैं। आगे का समीकरण

{\frac {x^{2}}{(AB+BC)^{2}}}+{\frac {y^{2}}{(BC)^{2}}}=1

सन्निहित भी है।

आर्किमिडीज़ का ट्रैमेल दो सर्पक और दो केंद्रबिंदु के साथ चार-बार लिंकेज का एक उदाहरण है, और अधिक सामान्य तिरछे ट्रैमेल की विशेष स्तिथि है। धुरी को बाधित करने वाली अक्षों को लंबवत नहीं होना चाहिए और बिंदु ए, बी और सी एक त्रिकोण बना सकते हैं। C का परिणामी स्थान अभी भी एक दीर्घवृत्त है। ^[2]

दीर्घवृत्तचित्र

लकड़ी का दीर्घवृत्तचित्र (सीए. 1900) अब स्मिथसोनियन इंस्टीट्यूशन एलिप्सोग्राफ में है

जिनेवा शहर के विज्ञान के इतिहास के संग्रहालय में प्रदर्शन पर एलिप्सोग्राफ

एक दीर्घवृत्तचित्र आर्किमिडीज का एक बंधन है जिसका उद्देश्य दीर्घवृत्त को खींचना, काटना या दीर्घवृत्त करना है, उदाहरण के लिए लकड़ी या अन्य शीट सामग्री। दीर्घवृत्ताकार में छड़ से जुड़ा उपयुक्त उपकरण (पेंसिल, चाकू, लकड़ी का अनुर्मागक, आदि) होता है। सामान्यतः दूरियाँ a और b समायोज्य होती हैं, ताकि दीर्घवृत्त का आकार और आकार भिन्न हो सके।

ऐसे दीर्घवृत्तचित्रों का इतिहास निश्चित नहीं है, लेकिन माना जाता है कि वे प्रोक्लस और संभवतः आर्किमिडीज़ के समय के भी हैं। ^[2]

यह भी देखें

↑ Schwartzman, Steven (1996). गणित के शब्द. The Mathematical Association of America. ISBN 0-88385-511-9. (restricted online copy, p. 223, at Google Books)
↑ ^2.0 ^2.1 Wetzel, John E. (February 2010). "एक प्राचीन अण्डाकार स्थान". American Mathematical Monthly. 117 (2): 161–167. doi:10.4169/000298910x476068. JSTOR 10. S2CID 117701083.

संदर्भ

J. W. Downs: Practical Conic Sections: The Geometric Properties of Ellipses, Parabolas and Hyperbolas. Courier Dover 2003, ISBN 978-0-486-42876-5, pp. 4–5 (restricted online copy, p. 4, at Google Books)
I. I. Artobolevskii Mechanisms for the Generation of Plane Curves. Pergamon Press 1964, ISBN 978-1483120003.

बाहरी संबंध

Video of various trammel designs in action
Cutting ellipses in wood
Photo of a Kentucky Do-Nothing
Instructions on how to build a Kentucky Do-Nothing
Video of a Do-Nothing made from Lego bricks
"Wonky Trammel of Archimedes" An exploration of a generalized trammel.
US-Patent 4306598 for ellipse cutting guide allowing small ellipses
Secrets of the Nothing Grinder YouTube video by Mathologer

[1] Schwartzman, Steven (1996). गणित के शब्द. The Mathematical Association of America. ISBN 0-88385-511-9. (restricted online copy, p. 223, at Google Books)

[AMM-2] 2.0 ^2.1 Wetzel, John E. (February 2010). "एक प्राचीन अण्डाकार स्थान". American Mathematical Monthly. 117 (2): 161–167. doi:10.4169/000298910x476068. JSTOR 10. S2CID 117701083.

[1]

[2]

@@ Line 1: / Line 1: @@
-{{Short description|Ellipse-drawing mechanism}}
+[[File:Trammel of Archimedes Small White.gif|thumb|आर्किमिडीज़ का बंधन अनुप्राणित प्रतिरूप।]]'''आर्किमिडीज़ का ट्रैमेल''' ('''दीर्घवृत्तलेखी''') एक [[तंत्र (इंजीनियरिंग)]] है जो '''दीर्घवृत्त''' का आकार उत्पन्न करता है। <ref>{{cite book |title=गणित के शब्द|url=https://archive.org/details/wordsofmathemati0000schw |url-access=registration |last=Schwartzman |first=Steven |year=1996 |publisher=The [[Mathematical Association of America]] |isbn=0-88385-511-9}} ({{Google books|SRw4PevE4zUC|restricted online copy|page=223}})</ref> इसमें दो तुरी होते हैं जो लंबवत प्रणाल या छड़ तक सीमित (बंधन) रखे जाते हैं और एक छड़ी होती है जो छड़ी के साथ निश्चित स्थानों पर केंद्रबिंदु द्वारा तुरी से जुड़ी होती है।
-[[File:Trammel of Archimedes Small White.gif|thumb|आर्किमिडीज़ का बंधन अनुप्राणित प्रतिरूप।]]'''आर्किमिडीज़ का बंधन''' एक [[तंत्र (इंजीनियरिंग)]] है जो दीर्घवृत्त का आकार उत्पन्न करता है। <ref>{{cite book |title=गणित के शब्द|url=https://archive.org/details/wordsofmathemati0000schw |url-access=registration |last=Schwartzman |first=Steven |year=1996 |publisher=The [[Mathematical Association of America]] |isbn=0-88385-511-9}} ({{Google books|SRw4PevE4zUC|restricted online copy|page=223}})</ref> इसमें दो तुरी होते हैं जो लंबवत प्रणाल या छड़ तक सीमित (बंधन) रखे जाते हैं और एक छड़ी होती है जो छड़ी के साथ निश्चित स्थानों पर केंद्रबिंदु द्वारा तुरी से जुड़ी होती है।
 जैसे ही तुरी अपने प्रणाल के साथ आगे-पीछे चलती हैं, छड़ी पर सभी बिंदु अण्डाकार पथ में चलते हैं। छड़ की गति को अण्डाकार गति कहा जाता है। दीर्घवृत्त के अर्ध-अक्ष a और b की लंबाई छड़ पर बिंदु से प्रत्येक दो धुरी तक की दूरी के बराबर होती है।
@@ Line 36: / Line 35: @@
 ऐसे दीर्घवृत्तचित्रों का इतिहास निश्चित नहीं है, लेकिन माना जाता है कि वे प्रोक्लस और संभवतः आर्किमिडीज़ के समय के भी हैं। <ref name=AMM/>
 ==यह भी देखें==
 * [[किरण कम्पास]]
@@ Line 50: / Line 47: @@
 ==टिप्पणियाँ==
 {{reflist}}
 ==संदर्भ==
 * J. W. Downs: ''Practical Conic Sections: The Geometric Properties of Ellipses, Parabolas and Hyperbolas''. Courier Dover 2003, {{ISBN|978-0-486-42876-5}}, pp.&nbsp;4–5 ({{Google books|pHxTQTiYkGYC|restricted online copy|page=4}})
 * I. I. Artobolevskii ''Mechanisms for the Generation of Plane Curves''. Pergamon Press 1964, {{ISBN|978-1483120003}}.
 ==बाहरी संबंध==
-{{commonscat|Trammel of Archimedes}}
 *[https://www.youtube.com/watch?v=pid70tRkDJo Video of various trammel designs in action]
 *[http://www.woodweb.com/knowledge_base/A_Jig_for_Drawing_or_Cutting_Ellipses.html Cutting ellipses in wood]
@@ Line 67: / Line 59: @@
 *[http://www.freepatentsonline.com/4306598.html US-Patent 4306598 for ellipse cutting guide allowing small ellipses]
 *[https://www.youtube.com/watch?v=7Fn-26Jmi5E ''Secrets of the Nothing Grinder''] YouTube video by [[Mathologer]]
-[[Category: पारंपरिक खिलौने]] [[Category: तंत्र (इंजीनियरिंग)]] [[Category: लिंकेज (यांत्रिक)]] [[Category: शंक्वाकार खंड]] [[Category: नोवेल्टी आइटम]] [[Category: शैक्षिक खिलौने]] [[Category: आर्किमिडीज]]
-[[Category: Machine Translated Page]]
+[[Category:Commons category link is locally defined]]
 [[Category:Created On 13/07/2023]]
-[[Category:Vigyan Ready]]
+[[Category:Lua-based templates]]
+[[Category:Machine Translated Page]]
+[[Category:Pages with script errors]]
+[[Category:Templates Vigyan Ready]]
+[[Category:Templates that add a tracking category]]
+[[Category:Templates that generate short descriptions]]
+[[Category:Templates using TemplateData]]
+[[Category:आर्किमिडीज]]
+[[Category:तंत्र (इंजीनियरिंग)]]
+[[Category:नोवेल्टी आइटम]]
+[[Category:पारंपरिक खिलौने]]
+[[Category:लिंकेज (यांत्रिक)]]
+[[Category:शंक्वाकार खंड]]
+[[Category:शैक्षिक खिलौने]]

Anonymous

Search

आर्किमिडीज़ का ट्रैमेल: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 12:27, 8 November 2023

Contents

गणित

दीर्घवृत्तचित्र

यह भी देखें

टिप्पणियाँ

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

आर्किमिडीज़ का ट्रैमेल: Difference between revisions

Latest revision as of 12:27, 8 November 2023

गणित

दीर्घवृत्तचित्र

यह भी देखें

टिप्पणियाँ

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories