पोलैनी का संभावित सिद्धांत: Difference between revisions
No edit summary |
No edit summary |
||
| Line 18: | Line 18: | ||
पोलानी और आइंस्टीन अगले 20 वर्षों तक एक-दूसरे को लिखते रहे। | पोलानी और आइंस्टीन अगले 20 वर्षों तक एक-दूसरे को लिखते रहे। | ||
==== | ====क्रिटिसिज़म ==== | ||
पोलानी के एडसोर्प्शन मॉडल को प्रकाशन को कई वर्षों के बाद दशकों तक बहुत | पोलानी के एडसोर्प्शन मॉडल को प्रकाशन को कई वर्षों के बाद दशकों तक बहुत क्रिटिसिज़म का सामना करना पड़ा था। इस प्रकार एडसोर्प्शन के निर्धारण के लिए उनका सरलीकृत मॉडल डेबी के निश्चित द्विध्रुव और बोह्र के परमाणु मॉडल की खोज के समय बनाया गया था और साथ ही डब्ल्यू.एच. ब्रैग, डब्ल्यू.एल. ब्रैग, और [[विलेम हेंड्रिक कीसोम]] सहित रसायन विज्ञान की दुनिया में प्रमुख हस्तियों द्वारा अंतर-आणविक बलों और इलेक्ट्रोस्टैटिक बलों के विकासशील सिद्धांत के समय बनाया गया था। उनके मॉडल के विरोधियों ने दावा किया कि पोलैनी के सिद्धांत ने इन उभरते सिद्धांतों को ध्यान में नहीं रखा है और क्रिटिसिज़म यह थी कि मॉडल ने गैस और सतह के विद्युतीय संबंधों को ध्यान में नहीं रखा और अन्य अणुओं की उपस्थिति से गैस के आकर्षण को रोक देती है। 1916 से 1918 तक [[लैंगमुइर समीकरण|इरविंग]] के प्रायोगिक दावों के बाद पोलानी के मॉडल को जांच की सीमा में रखा गया था, जिसके शोध के माध्यम से अंततः 1932 में [[नोबेल पुरस्कार]] जीता गया था। चूंकि, पोलानी इनमें से कई चर्चाओं में भाग लेने में सक्षम नहीं थे क्योंकि उन्होंने [[प्रथम विश्व युद्ध में हंगरी]] के समय 1914-1916 में [[ऑस्ट्रिया-हंगरी]] सर्बियाई मोर्चे पर ऑस्ट्रो-हंगेरियन सेना के लिए एक चिकित्सा अधिकारी के रूप में कार्य किया था। पोलानी ने इस अनुभव के बारे में इस प्रकार लिखा हैं | ||
अगस्त 1914 से अक्टूबर 1918 तक ऑस्ट्रो-हंगेरियन सेना में एक चिकित्सा अधिकारी के रूप में सेवा करके और 1919 के अंत तक चली बाद की क्रांतियों और जवाबी क्रांतियों से मैं स्वयं कुछ समय के लिए इन विकासों के बारे में किसी भी जानकारी से सुरक्षित था। अन्यत्र कम-अच्छी जानकारी वाले मंडल के सदस्य कुछ समय तक मेरे सिद्धांत की सरलता और इसके व्यापक प्रयोगात्मक सत्यापन से प्रभावित होते रहे हैं।<ref name="polanyi" /> | अगस्त 1914 से अक्टूबर 1918 तक ऑस्ट्रो-हंगेरियन सेना में एक चिकित्सा अधिकारी के रूप में सेवा करके और 1919 के अंत तक चली बाद की क्रांतियों और जवाबी क्रांतियों से मैं स्वयं कुछ समय के लिए इन विकासों के बारे में किसी भी जानकारी से सुरक्षित था। अन्यत्र कम-अच्छी जानकारी वाले मंडल के सदस्य कुछ समय तक मेरे सिद्धांत की सरलता और इसके व्यापक प्रयोगात्मक सत्यापन से प्रभावित होते रहे हैं।<ref name="polanyi" /> | ||
==== | ====डिफेन्स ==== | ||
पोलानी ने वर्णन किया कि उनके एडसोर्प्शन के मॉडल की स्वीकृति का "महत्वपूर्ण मोड़" तब आया जब [[फ़्रिट्ज़ हैबर]] ने उन्हें बर्लिन | पोलानी ने वर्णन किया कि उनके एडसोर्प्शन के मॉडल की स्वीकृति का "महत्वपूर्ण मोड़" तब आया जब [[फ़्रिट्ज़ हैबर]] ने उन्हें बर्लिन जर्मनी में [[भौतिक रसायन विज्ञान के लिए कैसर विल्हेम संस्थान]] में अपने सिद्धांत का पूर्ण बचाव करने के लिए कहा था और इस बैठक में अल्बर्ट आइंस्टीन सहित वैज्ञानिक जगत के कई प्रमुख खिलाड़ी उपस्थित थे। इस प्रकार अपने मॉडल के बारे में पोलैनी की पूरी व्याख्या सुनने के बाद हैबर और आइंस्टीन ने दावा किया कि पोलैनी ने "इस स्थिति की वैज्ञानिक रूप से स्थापित संरचना के प्रति पूर्ण उपेक्षा प्रदर्शित की थी" और वर्षों बाद पोलैनी ने निष्कर्ष निकालते हुए अपनी आप बीती का वर्णन इस प्रकार किया था, | ||
<blockquote> | <blockquote>व्यावसायिक रूप से, मैं इस अवसर पर केवल अपने दाँतों की खाल के सहारे बच गया था।</blockquote> | ||
इस बैठक के बाद पोलानी ने वर्षों के अपने मॉडल की वैधता को साबित करने के लिए सहायक साक्ष्य के रूप में जारी रखा था।<ref name="polanyi"/> | |||
==== | ====रेफ्यूटशन ==== | ||
अपने मॉडल की इन अस्वीकृतियों और | अपने मॉडल की इन अस्वीकृतियों और क्रिटिसिज़म से पोलानी की 'मुक्ति' 1930 में हुई थी, जैसा कि उन्होंने इसका वर्णन किया है जब [[फ़्रिट्ज़ लंदन]] ने इलेक्ट्रॉनिक प्रणालियों के ध्रुवीकरण पर क्वांटम यांत्रिकी के सिद्धांतों पर स्थापित एकजुट बलों का एक नया सिद्धांत प्रस्तावित किया था और इस प्रकार पोलानी ने लंदन को पत्र लिखकर पूछा कि, | ||
क्या ये बल हस्तक्षेप करने वाले अणुओं द्वारा स्क्रीनिंग के अधीन हैं, क्या इन बलों के ठोस कार्य में स्थानिक रूप से निश्चित एडसोर्प्शन की क्षमता होती है | क्या ये बल हस्तक्षेप करने वाले अणुओं द्वारा स्क्रीनिंग के अधीन हैं, क्या इन बलों के ठोस कार्य में स्थानिक रूप से निश्चित एडसोर्प्शन की क्षमता होती है | ||
| Line 63: | Line 63: | ||
:<math>\varepsilon_{s}= - RT \ln \frac{c_{\rm s}}{c}</math> | :<math>\varepsilon_{s}= - RT \ln \frac{c_{\rm s}}{c}</math> | ||
जहाँ <math>c_{\rm s}</math> एडसोर्बेन्ट की सैचुरेटेड सांद्रता है c | जहाँ <math>c_{\rm s}</math> एडसोर्बेन्ट की सैचुरेटेड सांद्रता है c एडसोर्बेन्ट की संतुलन सांद्रता है। | ||
===पोलैनी एडसोर्प्शन सिद्धांत पर आधारित सिद्धांत=== | ===पोलैनी एडसोर्प्शन सिद्धांत पर आधारित सिद्धांत=== | ||
अपनी पहली रिपोर्ट के बाद से संभावित सिद्धांत में कई वर्षों के समय कई परिशोधन और परिवर्तन हुए हैं। पोलैनी के सिद्धांत का उपयोग करके विकसित किए गए प्रमुख सिद्धांतों में से एक डुबिनिन सिद्धांत, डुबिनिन-रादुशकिवेच और डुबिनिन-अस्ताखोव समीकरण थे। | अपनी पहली रिपोर्ट के बाद से संभावित सिद्धांत में कई वर्षों के समय कई परिशोधन और परिवर्तन हुए हैं। पोलैनी के सिद्धांत का उपयोग करके विकसित किए गए प्रमुख सिद्धांतों में से एक डुबिनिन सिद्धांत, डुबिनिन-रादुशकिवेच और डुबिनिन-अस्ताखोव समीकरण के रूप में थे। | ||
एडसोर्प्शन क्षमता का उपयोग करते हुए | एडसोर्प्शन क्षमता का उपयोग करते हुए एडसोर्प्शन स्थान की डिग्री <math>\theta</math> के रूप में गणना की जा सकती है | ||
:<math>\theta = a/a_0 = \mathrm{e}^{{({A / E})}^b }</math> | :<math>\theta = a/a_0 = \mathrm{e}^{{({A / E})}^b }</math> | ||
जहाँ <math>a</math> तापमान T और संतुलन दबाव p पर एडसोर्प्शन का मान है | जहाँ <math>a</math> तापमान T और संतुलन दबाव p पर एडसोर्प्शन का मान है और इस प्रकार <math>a_0</math> एडसोर्प्शन का अधिकतम मूल्य है और <math>E</math> एडसोर्प्शन की विशिष्ट ऊर्जा केजे/मोल में है, <math>A</math> एडसोर्प्शन में [[गिब्स मुक्त ऊर्जा]] <math>\Delta G = - RT \log (p_0/p) </math> में होने वाली हानि के बराबर है और <math>b</math> फिटिंग गुणांक है.<ref>{{Cite journal | last = Dubinin | first = M. M. | author2 = Astakhov, V. A.|title = माइक्रोपोरस अधिशोषक द्वारा गैसों और वाष्पों के अधिशोषण में माइक्रोप्रोर्स की मात्रा भरने की अवधारणाओं का विकास| journal = Bulletin of the Academy of Sciences of the USSR, Division of Chemical Science | volume = 20 | issue = 1 | pages = 3–7 | doi=10.1007/bf00849307| year = 1971 }}</ref> डबिनिन-राडुष्किवेच समीकरण जहाँ <math>b</math> 2 के बराबर है और अनुकूलित डुबिनिन-अस्ताखोव समीकरण है इस प्रकार <math>b</math> प्रयोगात्मक डेटा के लिए उपयुक्त है और इसे सरल बनाया जा सकता है | ||
:<math>\log a = \log a_0 + 0.434 \left(\frac{A}{E}\right)^b</math> | :<math>\log a = \log a_0 + 0.434 \left(\frac{A}{E}\right)^b</math> | ||
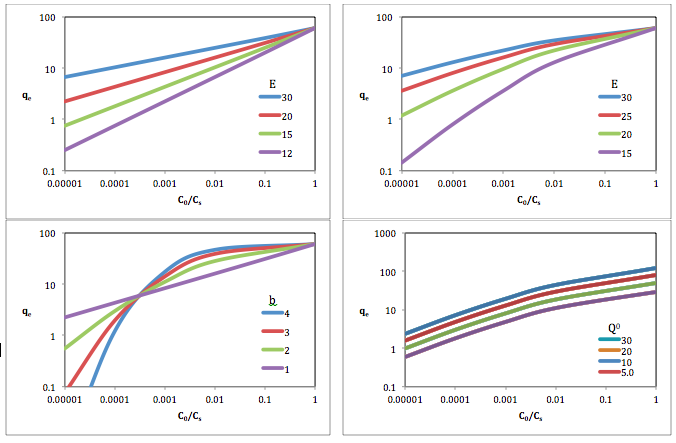
[[File:Dubinin-Astakhov Curves.png|thumb|800px|''Q''<sup>0</sup>, में वृद्धि के कारण डुबिनिन-अस्ताखोव वक्र में परिवर्तन ''E'', और b सॉर्बेंट बनाम सापेक्ष विलेय सांद्रता पर विलेय इज़ोटे र्म लॉग-लॉग स्केल प्लॉट इस प्रकार है। <br />Top-left: ''Q''<sup>0</sup> = 60; ''b'' = 1Top-right: ''Q''<sup>0</sup> = 60; ''b'' = 1.5Bottom-left: ''Q''<sup>0</sup> = 60; ''E'' = 20Bottom-right: ''E'' = 20; ''b'' = 1.5]]अन्य अध्ययनों में | [[File:Dubinin-Astakhov Curves.png|thumb|800px|''Q''<sup>0</sup>, में वृद्धि के कारण डुबिनिन-अस्ताखोव वक्र में परिवर्तन ''E'', और b सॉर्बेंट बनाम सापेक्ष विलेय सांद्रता पर विलेय इज़ोटे र्म लॉग-लॉग स्केल प्लॉट इस प्रकार है। <br />Top-left: ''Q''<sup>0</sup> = 60; ''b'' = 1Top-right: ''Q''<sup>0</sup> = 60; ''b'' = 1.5Bottom-left: ''Q''<sup>0</sup> = 60; ''E'' = 20Bottom-right: ''E'' = 20; ''b'' = 1.5]]अन्य अध्ययनों में डबिनिन अस्ताखोव का उपयोग इसी रूप में किया गया है | ||
<math>\log q_{\rm e} = \log Q^0 + (\varepsilon_{\rm sw}/E)^b</math>, | <math>\log q_{\rm e} = \log Q^0 + (\varepsilon_{\rm sw}/E)^b</math>, | ||
जहाँ <math>q_{\rm e}</math> | जहाँ <math>q_{\rm e}</math>, में एडसोर्बेन्ट की संतुलन अधिशोषित सांद्रता है, <math>Q^0</math>, mg/g में एडसोर्एडसोर्बेन्ट अधिशोषित सांद्रता है जहां mg/g, <math>\varepsilon_{\rm sw}</math> प्रभावी एएडसोर्बेन्ट क्षमता के बराबर है <math>\varepsilon_{\rm sw} = -RT \ln (c_{\rm e}/c_{\rm s})</math>, <math>c_{\rm e}</math> समाधान चरण में एडसोर्बेन्ट की संतुलन सांद्रता mg/L के रूप में होती है और <math>c_{\rm s}</math> पानी में एडसोर्बेन्ट घुलनशीलता mg/L के रूप में होती है।<ref name=Xing /> | ||
एडसोर्प्शन की विशिष्ट ऊर्जा को एक ही सतह पर एक मानक वाष्प के लिए एडसोर्प्शन की विशिष्ट ऊर्जा से संबंधित | एडसोर्प्शन की विशिष्ट ऊर्जा को एक ही सतह पर एक मानक वाष्प के लिए एडसोर्प्शन की विशिष्ट ऊर्जा से संबंधित होती है और इस प्रकार <math>E_0</math>, एक एफिनिटी गुणांक के उपयोग के माध्यम से, <math>\beta</math> के रूप में होते है | ||
:<math>E= \beta E_0</math> | :<math>E= \beta E_0</math> | ||
एफिनिटी गुणांक नमूना और मानक वाष्प के गुणों का अनुपात इस प्रकार है | |||
:<math>\beta = \frac{\alpha}{\alpha_0}</math> | :<math>\beta = \frac{\alpha}{\alpha_0}</math> | ||
जहाँ <math>\alpha</math> और <math>\alpha_0</math> क्रमशः नमूने और मानक वाष्प की ध्रुवीकरण क्षमताएं हैं। | जहाँ <math>\alpha</math> और <math>\alpha_0</math> क्रमशः नमूने और मानक वाष्प की ध्रुवीकरण क्षमताएं हैं। ऑप्टीमल फिटिंग गुणांक निर्धारित करने के लिए कई अध्ययन किए गए हैं, <math>b</math>, और एफिनिटी गुणांक <math>\beta</math> ठोस पदार्थों पर गैसों और वाष्पों के एडसोर्प्शन का सर्वोत्तम वर्णन करने के लिए हैं। इस प्रकार परिणामस्वरूप प्रयोगात्मक परिणामों के साथ फिट होने पर प्राप्त होने वाली सटीकता के कारण डबिनिन-अस्ताखोव समीकरण एडसोर्प्शन अध्ययन के रूप में उपयोग होता है। | ||
====वाष्प और गैसों के लिए डबिनिन-अस्ताखोव पैरामीटर==== | ====वाष्प और गैसों के लिए डबिनिन-अस्ताखोव पैरामीटर==== | ||
| Line 126: | Line 118: | ||
===कार्बन नैनोकणों काएडसोर्बेन्ट र्अएडसोर्बेन्ट === | ===कार्बन नैनोकणों काएडसोर्बेन्ट र्अएडसोर्बेन्ट === | ||
ऐतिहासिक रूअधिशोषक ंत का उपयोग गैर-समान एडसोर्बेन्ट औरएडसोर्बेन्ट विएडसोर्बेन्ट ॉडअधिशोषक ए कअधिशोषक एडसोर्बेन्ट और एडसोर्बेन्ट के कुछ जोड़े के लिए, पॉलीनी सिद्धांत के गणितीय पैरामीटर एडसोर्बेन्ट और एडसोर्बेन्ट दोनों के भौतिक रासायनिक गुणों से संबंधित हो सकते हैं। सिद्धांत का उपयोग कार्बन नैनोट्यूब और कार्बन नैनोकणों के एडसोर्प्शन के मॉडल के लिए किया गया है। यांग और ज़िंग द्वारा किए गए अध्ययन में,<ref name=Xing>{{Cite journal | last = Yang | first = K. | author2 = Xing, B. | title = Adsorption of organic compounds by carbon nanomaterials in aqueous phase: Polanyi theory and its application | journal = Chemical Reviews | volume = 110 | issue = 10 | pages = 5989–6008 | doi=10.1021/cr100059s | pmid=20518459| year = 2010 }}</ref> सिद्धांत को [[लैंगमुइर सोखना मॉडल|इरविंग एडसोर्प्शन मॉडल]], फ्रायंडलिच समीकरण और विभाजन की तुलना में एडसोर्प्शन इसोथर्म के लिए बेहतर रूप से फिट दिखाया गया है। प्रयोग में कार्बन नैनोकणों और कार्बन नैनोट्यूब पर कार्बनिक अणुओं के एडसोर्प्शन का अध्ययन किया गया। पॉलीनी सिद्धांत के अनुसार कार्बन नैनोकणों की सतह दोष वक्रता उनके एडसोर्प्शन को प्रभावित कर सकती है। कणों पर सपाट सतह अधिक सतह परमाणुओं को एडसोर्प्शन वाले कार्बनिक अणुओं के पास जाने की अनुमति देगी जिससे क्षमता में वृद्धि होगी, जिससे मजबूत अंतःक्रिया होगी। यह सिद्धांत कार्बन नैनोकणों पर कार्बनिक यौगिकों के एडसोर्प्शन के तंत्र को समझने और एडसोर्प्शन की क्षमता और | ऐतिहासिक रूअधिशोषक ंत का उपयोग गैर-समान एडसोर्बेन्ट औरएडसोर्बेन्ट विएडसोर्बेन्ट ॉडअधिशोषक ए कअधिशोषक एडसोर्बेन्ट और एडसोर्बेन्ट के कुछ जोड़े के लिए, पॉलीनी सिद्धांत के गणितीय पैरामीटर एडसोर्बेन्ट और एडसोर्बेन्ट दोनों के भौतिक रासायनिक गुणों से संबंधित हो सकते हैं। सिद्धांत का उपयोग कार्बन नैनोट्यूब और कार्बन नैनोकणों के एडसोर्प्शन के मॉडल के लिए किया गया है। यांग और ज़िंग द्वारा किए गए अध्ययन में,<ref name=Xing>{{Cite journal | last = Yang | first = K. | author2 = Xing, B. | title = Adsorption of organic compounds by carbon nanomaterials in aqueous phase: Polanyi theory and its application | journal = Chemical Reviews | volume = 110 | issue = 10 | pages = 5989–6008 | doi=10.1021/cr100059s | pmid=20518459| year = 2010 }}</ref> सिद्धांत को [[लैंगमुइर सोखना मॉडल|इरविंग एडसोर्प्शन मॉडल]], फ्रायंडलिच समीकरण और विभाजन की तुलना में एडसोर्प्शन इसोथर्म के लिए बेहतर रूप से फिट दिखाया गया है। प्रयोग में कार्बन नैनोकणों और कार्बन नैनोट्यूब पर कार्बनिक अणुओं के एडसोर्प्शन का अध्ययन किया गया। पॉलीनी सिद्धांत के अनुसार कार्बन नैनोकणों की सतह दोष वक्रता उनके एडसोर्प्शन को प्रभावित कर सकती है। कणों पर सपाट सतह अधिक सतह परमाणुओं को एडसोर्प्शन वाले कार्बनिक अणुओं के पास जाने की अनुमति देगी जिससे क्षमता में वृद्धि होगी, जिससे मजबूत अंतःक्रिया होगी। यह सिद्धांत कार्बन नैनोकणों पर कार्बनिक यौगिकों के एडसोर्प्शन के तंत्र को समझने और एडसोर्प्शन की क्षमता और एफिनिटी का अनुमान लगाने में फायदेमंद रहा है। इस सिद्धांत का उपयोग करके, शोधकर्ता विशिष्ट आवश्यकताओं के लिए कार्बन नैनोकणों को डिजाइन करने में सक्षम होने की उम्मीद कर रहे हैं जैसे कि उन्हें पर्यावरण अध्ययन में शर्बत के रूप में उपयोग करना। | ||
[[File:Surface adsorption onto carbon nanoparticles.png|कार्बन नैनोकणों पर सतह सोखना]] | [[File:Surface adsorption onto carbon nanoparticles.png|कार्बन नैनोकणों पर सतह सोखना]] | ||
Revision as of 09:27, 27 July 2023
पोलानी का संभावित सिद्धांत, जिसे पोलानी एडसोर्प्शन संभावित सिद्धांत भी कहा जाता है और इस प्रकार माइकल पोलानी द्वारा प्रस्तावित एडसोर्प्शन का एक मॉडल है, जहां सतह के पास गैस की रासायनिक क्षमता और बड़ी दूरी सतह से गैस की रासायनिक क्षमता के बीच रासायनिक संतुलन के माध्यम से एडसोर्प्शन को मापा जा सकता है। इस मॉडल में, उन्होंने माना कि सतह पर गैस के वान डर वाल्स बलों के कारण मुख्य रूप से आकर्षण सतह से गैस कण की स्थिति से निर्धारित होता है और गैस कान्डेन्सेशन एक आदर्श गैस के रूप में व्यवहार करती है जहां गैस अपने संतुलन वाष्प दबाव से अधिक हो जाती है। जबकि हेनरी का एडसोर्प्शन सिद्धांत कम दबाव में अधिक प्रयुक्त होता है और बीईटी सिद्धांत एडसोर्प्शन इसोथर्म समीकरण 0.05 to 0.35 P/Po पर अधिक उपयोगी होता है और इस प्रकार पोलानी संभावित सिद्धांत का उच्च P/Po (~0.1–0.8) पर बहुत अधिक अनुप्रयोग होता है।
अवलोकन
माइकल पोलानी
माइकल पोलानी, FRS 11 मार्च 1891 से 22 फरवरी 1976 के एक हंगेरियन पालीमैथ के रूप में थे, जिन्होंने भौतिक रसायन विज्ञान अर्थशास्त्र और दर्शनशास्त्र में सैद्धांतिक योगदान दिया था। पोलानी एक प्रसिद्ध सैद्धांतिक रसायनज्ञ के रूप में थे, जिन्होंने अध्ययन के तीन मुख्य क्षेत्रों के माध्यम से ठोस पदार्थों के साक्ष एक्स-रे संरचना विश्लेषण और रासायनिक प्रतिक्रियाओं की दर पर गैसों का एडसोर्प्शन के माध्यम से रसायन विज्ञान के क्षेत्र में योगदान दिया था। चूंकि, पोलानी रसायन विज्ञान क्षेत्र में सैद्धांतिक और प्रायोगिक दोनों अध्ययनों में सक्रिय रूप में थे। पोलानी ने 1913 में चिकित्सा में डिग्री के साथ-साथ पीएच.डी. भी प्राप्त की थी और इस प्रकार वर्ष 1917 में बुडापेस्ट विश्वविद्यालय से भौतिक रसायन विज्ञान में और बाद में अपने जीवन में उन्होंने बर्लिन में कैसर विल्हेम संस्थान के साथ-साथ इंग्लैंड के मैनचेस्टर में मैनचेस्टर विश्वविद्यालय में रसायन विज्ञान के प्रोफेसर के रूप में पढ़ाया था।
इतिहास
प्रस्तावित सिद्धांत
1914 में, पोलैनी ने एडसोर्प्शन पर प्रस्तावित अपना पहला पेपर लिखा जहां उन्होंने एक ठोस सतह पर गैस के एडसोर्प्शन के लिए एक मॉडल प्रस्तावित किया था।[1] और बाद में, उन्होंने 1916 में एक पूर्ण विकसित पेपर प्रकाशित किया था जिसमें उनके छात्रों और अन्य लेखकों द्वारा प्रयोगात्मक सत्यापन सम्मलित था। बुडापेस्ट विश्वविद्यालय में अपने शोध के समय उनके गुरु प्रोफेसर जॉर्ज ब्रेडिग ने अपने शोध निष्कर्ष अल्बर्ट आइंस्टीन को भेजे थे और इस प्रकार आइंस्टीन ने ब्रेडिग को जवाब देते हुए लिखा था कि,
आपके एम. पोलानी के कागजात मुझे बहुत प्रसन्न करते हैं। मैंने उनमें आवश्यक चीज़ों की जाँच की है और उन्हें मौलिक रूप से सही पाया है।
पोलानी ने बाद में इस फेनोमेनन का वर्णन यह कहकर किया:
बैंग ! मैं एक वैज्ञानिक था. पोलानी और आइंस्टीन अगले 20 वर्षों तक एक-दूसरे को लिखते रहे।
क्रिटिसिज़म
पोलानी के एडसोर्प्शन मॉडल को प्रकाशन को कई वर्षों के बाद दशकों तक बहुत क्रिटिसिज़म का सामना करना पड़ा था। इस प्रकार एडसोर्प्शन के निर्धारण के लिए उनका सरलीकृत मॉडल डेबी के निश्चित द्विध्रुव और बोह्र के परमाणु मॉडल की खोज के समय बनाया गया था और साथ ही डब्ल्यू.एच. ब्रैग, डब्ल्यू.एल. ब्रैग, और विलेम हेंड्रिक कीसोम सहित रसायन विज्ञान की दुनिया में प्रमुख हस्तियों द्वारा अंतर-आणविक बलों और इलेक्ट्रोस्टैटिक बलों के विकासशील सिद्धांत के समय बनाया गया था। उनके मॉडल के विरोधियों ने दावा किया कि पोलैनी के सिद्धांत ने इन उभरते सिद्धांतों को ध्यान में नहीं रखा है और क्रिटिसिज़म यह थी कि मॉडल ने गैस और सतह के विद्युतीय संबंधों को ध्यान में नहीं रखा और अन्य अणुओं की उपस्थिति से गैस के आकर्षण को रोक देती है। 1916 से 1918 तक इरविंग के प्रायोगिक दावों के बाद पोलानी के मॉडल को जांच की सीमा में रखा गया था, जिसके शोध के माध्यम से अंततः 1932 में नोबेल पुरस्कार जीता गया था। चूंकि, पोलानी इनमें से कई चर्चाओं में भाग लेने में सक्षम नहीं थे क्योंकि उन्होंने प्रथम विश्व युद्ध में हंगरी के समय 1914-1916 में ऑस्ट्रिया-हंगरी सर्बियाई मोर्चे पर ऑस्ट्रो-हंगेरियन सेना के लिए एक चिकित्सा अधिकारी के रूप में कार्य किया था। पोलानी ने इस अनुभव के बारे में इस प्रकार लिखा हैं
अगस्त 1914 से अक्टूबर 1918 तक ऑस्ट्रो-हंगेरियन सेना में एक चिकित्सा अधिकारी के रूप में सेवा करके और 1919 के अंत तक चली बाद की क्रांतियों और जवाबी क्रांतियों से मैं स्वयं कुछ समय के लिए इन विकासों के बारे में किसी भी जानकारी से सुरक्षित था। अन्यत्र कम-अच्छी जानकारी वाले मंडल के सदस्य कुछ समय तक मेरे सिद्धांत की सरलता और इसके व्यापक प्रयोगात्मक सत्यापन से प्रभावित होते रहे हैं।[1]
डिफेन्स
पोलानी ने वर्णन किया कि उनके एडसोर्प्शन के मॉडल की स्वीकृति का "महत्वपूर्ण मोड़" तब आया जब फ़्रिट्ज़ हैबर ने उन्हें बर्लिन जर्मनी में भौतिक रसायन विज्ञान के लिए कैसर विल्हेम संस्थान में अपने सिद्धांत का पूर्ण बचाव करने के लिए कहा था और इस बैठक में अल्बर्ट आइंस्टीन सहित वैज्ञानिक जगत के कई प्रमुख खिलाड़ी उपस्थित थे। इस प्रकार अपने मॉडल के बारे में पोलैनी की पूरी व्याख्या सुनने के बाद हैबर और आइंस्टीन ने दावा किया कि पोलैनी ने "इस स्थिति की वैज्ञानिक रूप से स्थापित संरचना के प्रति पूर्ण उपेक्षा प्रदर्शित की थी" और वर्षों बाद पोलैनी ने निष्कर्ष निकालते हुए अपनी आप बीती का वर्णन इस प्रकार किया था,
व्यावसायिक रूप से, मैं इस अवसर पर केवल अपने दाँतों की खाल के सहारे बच गया था।
इस बैठक के बाद पोलानी ने वर्षों के अपने मॉडल की वैधता को साबित करने के लिए सहायक साक्ष्य के रूप में जारी रखा था।[1]
रेफ्यूटशन
अपने मॉडल की इन अस्वीकृतियों और क्रिटिसिज़म से पोलानी की 'मुक्ति' 1930 में हुई थी, जैसा कि उन्होंने इसका वर्णन किया है जब फ़्रिट्ज़ लंदन ने इलेक्ट्रॉनिक प्रणालियों के ध्रुवीकरण पर क्वांटम यांत्रिकी के सिद्धांतों पर स्थापित एकजुट बलों का एक नया सिद्धांत प्रस्तावित किया था और इस प्रकार पोलानी ने लंदन को पत्र लिखकर पूछा कि,
क्या ये बल हस्तक्षेप करने वाले अणुओं द्वारा स्क्रीनिंग के अधीन हैं, क्या इन बलों के ठोस कार्य में स्थानिक रूप से निश्चित एडसोर्प्शन की क्षमता होती है
कम्प्यूटेशनल विश्लेषण के बाद, पोलानी और लंदन के बीच एक संयुक्त प्रकाशन किया गया था, जिसमें दावा किया गया कि एडसोर्प्शन वाली ताकतें उस मॉडल के समान व्यवहार करती हैं जो पोलानी ने प्रस्तावित किया था।[1]
आगे का शोध
पोलैनी के सिद्धांत का ऐतिहासिक महत्व है, जिनके काम का उपयोग अन्य मॉडलों के लिए एक आधार के रूप में किया जाता है , जैसे कि वॉल्यूम भरने वाले माइक्रोप्रोर्स (टीवीएफएम) का सिद्धांत और डुबिनिन-राडशकेविच सिद्धांत के रूप में होता है। पोलैनी के संभावित सिद्धांत को सम्मलित करते हुए अन्य शोध किए गए हैं, जैसे कि ज़्सिग्मोंडी द्वारा खोजी गई कैपलेरी कान्डेन्सेशन फेनोमेनन इत्यादि । पोयलानी के सिद्धांत के विपरीत इसमें एक सपाट सतह सम्मलित है, ज़िग्मोंडी के शोध में सिलिका सामग्री जैसी छिद्रपूर्ण संरचना के रूप में सम्मलित होती है और इस प्रकार उनके शोध ने साबित किया कि वाष्प का कान्डेन्सेशन मानक सैचुरेटेड वाष्प दबाव के नीचे संकीर्ण छिद्रों में हो सकता है।[2]
सिद्धांत
पोलैनी संभावित एडसोर्प्शन सिद्धांत
पोलैनी संभावित एडसोर्प्शन सिद्धांत इस धारणा पर आधारित होता है कि सतह के पास के अणु गुरुत्वाकर्षण या विद्युत क्षेत्र के समान क्षमता के अनुसार चलते हैं।[3] यह मॉडल स्थिर तापमान पर सतह पर गैसों के स्थिति में प्रयुक्त होता है। जब दबाव संतुलन वाष्प दबाव से अधिक होता है तो गैस के अणु उस सतह के निकट चले जाते हैं। इस प्रकार सतह से दूरी के सापेक्ष क्षमता में परिवर्तन की गणना रासायनिक क्षमता के अंतर के सूत्र का उपयोग करके की जाती है,
जहाँ रासायनिक क्षमता है, मोलर एन्ट्रापी है, मोलर की मात्रा है, और मोलर आंतरिक ऊर्जा है.
इक्विलिब्रियम पर, किसी सतह से r दूरी पर गैस की रासायनिक क्षमता, , सतह से असीम रूप से बड़ी दूरी पर गैस की रासायनिक क्षमता के बराबर होती है, . परिणामस्वरूप, सतह से अनंत दूरी से r दूरी तक एकीकरण होता है
जहाँ दूरी r और पर आंशिक दबाव है इस प्रकार सतह से अनंत दूरी पर आंशिक दबाव है।
चूँकि तापमान स्थिर रहता है और इस प्रकार रासायनिक क्षमता सूत्र में अंतर को दबाव और पर एकीकृत किया जा सकता है
सेटिंग करके , समीकरण को सरल बनाया जा सकता है
आदर्श गैस नियम का उपयोग करते हुए, , निम्नलिखित सूत्र प्राप्त होता है
चूंकि गैस किसी सतह पर तब संघनित होकर तरल में बदल जाती है जब गैस का दबाव संतुलन वाष्प दबाव से अधिक हो जाता है, , हम मान सकते हैं कि मोटाई की सतह पर एक तरल फिल्म बनती है, . पर ऊर्जा के रूप में होता है
यह मानते हुए कि गैसों का आंशिक दबाव सांद्रता एडसोर्प्शन की क्षमता से संबंधित होता है, के रूप में गणना की जा सकती है
जहाँ एडसोर्बेन्ट की सैचुरेटेड सांद्रता है c एडसोर्बेन्ट की संतुलन सांद्रता है।
पोलैनी एडसोर्प्शन सिद्धांत पर आधारित सिद्धांत
अपनी पहली रिपोर्ट के बाद से संभावित सिद्धांत में कई वर्षों के समय कई परिशोधन और परिवर्तन हुए हैं। पोलैनी के सिद्धांत का उपयोग करके विकसित किए गए प्रमुख सिद्धांतों में से एक डुबिनिन सिद्धांत, डुबिनिन-रादुशकिवेच और डुबिनिन-अस्ताखोव समीकरण के रूप में थे।
एडसोर्प्शन क्षमता का उपयोग करते हुए एडसोर्प्शन स्थान की डिग्री के रूप में गणना की जा सकती है
जहाँ तापमान T और संतुलन दबाव p पर एडसोर्प्शन का मान है और इस प्रकार एडसोर्प्शन का अधिकतम मूल्य है और एडसोर्प्शन की विशिष्ट ऊर्जा केजे/मोल में है, एडसोर्प्शन में गिब्स मुक्त ऊर्जा में होने वाली हानि के बराबर है और फिटिंग गुणांक है.[4] डबिनिन-राडुष्किवेच समीकरण जहाँ 2 के बराबर है और अनुकूलित डुबिनिन-अस्ताखोव समीकरण है इस प्रकार प्रयोगात्मक डेटा के लिए उपयुक्त है और इसे सरल बनाया जा सकता है
अन्य अध्ययनों में डबिनिन अस्ताखोव का उपयोग इसी रूप में किया गया है
,
जहाँ , में एडसोर्बेन्ट की संतुलन अधिशोषित सांद्रता है, , mg/g में एडसोर्एडसोर्बेन्ट अधिशोषित सांद्रता है जहां mg/g, प्रभावी एएडसोर्बेन्ट क्षमता के बराबर है , समाधान चरण में एडसोर्बेन्ट की संतुलन सांद्रता mg/L के रूप में होती है और पानी में एडसोर्बेन्ट घुलनशीलता mg/L के रूप में होती है।[5]
एडसोर्प्शन की विशिष्ट ऊर्जा को एक ही सतह पर एक मानक वाष्प के लिए एडसोर्प्शन की विशिष्ट ऊर्जा से संबंधित होती है और इस प्रकार , एक एफिनिटी गुणांक के उपयोग के माध्यम से, के रूप में होते है
एफिनिटी गुणांक नमूना और मानक वाष्प के गुणों का अनुपात इस प्रकार है
जहाँ और क्रमशः नमूने और मानक वाष्प की ध्रुवीकरण क्षमताएं हैं। ऑप्टीमल फिटिंग गुणांक निर्धारित करने के लिए कई अध्ययन किए गए हैं, , और एफिनिटी गुणांक ठोस पदार्थों पर गैसों और वाष्पों के एडसोर्प्शन का सर्वोत्तम वर्णन करने के लिए हैं। इस प्रकार परिणामस्वरूप प्रयोगात्मक परिणामों के साथ फिट होने पर प्राप्त होने वाली सटीकता के कारण डबिनिन-अस्ताखोव समीकरण एडसोर्प्शन अध्ययन के रूप में उपयोग होता है।
वाष्प और गैसों के लिए डबिनिन-अस्ताखोव पैरामीटर
| मिश्रण | सक्रिय कार्बन | , केजे/मोल | स्रोत | ||
|---|---|---|---|---|---|
| बेंजीन | कार्बन आणविक सीव | 1.78 | 11.52 | 1.00 | [6] |
| एसीटोन | कार्बन आणविक सीव | 2.00 | 9.774 | 0.85 | [6] |
| बेंजीन | CAL AC | 2 | 18.23 | 1.00 | [7] |
| एसीटोन | CAL AC | 2 | 13.21 | 0.72 | [7] |
| एसीटोन | कार्बन आणविक सीव | 2.8 | 20.29 | 0.72 | [8] |
| बेंजीन | कार्बन आणविक सीव | 3.1 | 28.87 | 1.00 | [8] |
| नाइट्रोजन | कार्बन आणविक सीव | 2.6 | 11.72 | 0.41 | [8] |
| ऑक्सीजन | कार्बन आणविक सीव | 2.3 | 9.21 | 0.32 | [8] |
| हाइड्रोजन | कार्बन आणविक सीव | 2.5 | 5.44 | 0.19 | [8] |
आवेदन
कई आधुनिक अध्ययनों में, सक्रिय कार्बन या कार्बन ब्लैक के अध्ययन में पोलैनी सिद्धांत का व्यापक रूप से उपयोग किया जाता है। सिद्धांत का उपयोग विभिन्न प्रकार के परिदृश्यों जैसे सक्रिय कार्बन पर गैस एडसोर्प्शन और नॉनऑनिक पॉलीसाइक्लिक एरोमैटिक हाइड्रोकार्बन की एडसोर्प्शन की प्रक्रिया को मॉडल करने के लिए सफलतापूर्वक किया गया है।[9] बाद में, प्रयोगों से यह भी पता चला कि यह फिनोल और रंगों का रासायनिक आधार जैसे आयनिक यौगिक पॉलीसाइक्लिक एरोमैटिक हाइड्रोकार्बन का मॉडल बना सकता है। हाल ही में, पॉलीनी एडसोर्प्शन इसोथर्म का उपयोग कार्बन नैनोकणों एडसोर्बेन्ट ्पअधिशोषक के लिए किया गया है।
कार्बन नैनोकणों काएडसोर्बेन्ट र्अएडसोर्बेन्ट
ऐतिहासिक रूअधिशोषक ंत का उपयोग गैर-समान एडसोर्बेन्ट औरएडसोर्बेन्ट विएडसोर्बेन्ट ॉडअधिशोषक ए कअधिशोषक एडसोर्बेन्ट और एडसोर्बेन्ट के कुछ जोड़े के लिए, पॉलीनी सिद्धांत के गणितीय पैरामीटर एडसोर्बेन्ट और एडसोर्बेन्ट दोनों के भौतिक रासायनिक गुणों से संबंधित हो सकते हैं। सिद्धांत का उपयोग कार्बन नैनोट्यूब और कार्बन नैनोकणों के एडसोर्प्शन के मॉडल के लिए किया गया है। यांग और ज़िंग द्वारा किए गए अध्ययन में,[5] सिद्धांत को इरविंग एडसोर्प्शन मॉडल, फ्रायंडलिच समीकरण और विभाजन की तुलना में एडसोर्प्शन इसोथर्म के लिए बेहतर रूप से फिट दिखाया गया है। प्रयोग में कार्बन नैनोकणों और कार्बन नैनोट्यूब पर कार्बनिक अणुओं के एडसोर्प्शन का अध्ययन किया गया। पॉलीनी सिद्धांत के अनुसार कार्बन नैनोकणों की सतह दोष वक्रता उनके एडसोर्प्शन को प्रभावित कर सकती है। कणों पर सपाट सतह अधिक सतह परमाणुओं को एडसोर्प्शन वाले कार्बनिक अणुओं के पास जाने की अनुमति देगी जिससे क्षमता में वृद्धि होगी, जिससे मजबूत अंतःक्रिया होगी। यह सिद्धांत कार्बन नैनोकणों पर कार्बनिक यौगिकों के एडसोर्प्शन के तंत्र को समझने और एडसोर्प्शन की क्षमता और एफिनिटी का अनुमान लगाने में फायदेमंद रहा है। इस सिद्धांत का उपयोग करके, शोधकर्ता विशिष्ट आवश्यकताओं के लिए कार्बन नैनोकणों को डिजाइन करने में सक्षम होने की उम्मीद कर रहे हैं जैसे कि उन्हें पर्यावरण अध्ययन में शर्बत के रूप में उपयोग करना।
विभिन्न प्रणालियों से एडसोर्प्शन
मैन्स, एम., और होफ़र, एल. जे. ई. द्वारा किए गए पहले अध्ययनों में से एक में,[10] पॉलीनी सिद्धांत का उपयोग कार्बनिक विलायक की एक विस्तृत श्रृंखला का उपयोग करके सक्रिय कार्बन के विभिन्न सांद्रता पर तरल-चरण एडसोर्प्शन इसोथर्म को चिह्नित करने के लिए किया गया था। पोलियानी सिद्धांत को इन विभिन्न प्रणालियों के लिए उपयुक्त दिखाया गया है। इस प्रकार परिणामों के कारण अध्ययन ने न्यूनतम डेटा का उपयोग करके समान प्रणालियों के लिए इसोथर्म की भविष्यवाणी करने की संभावना प्रस्तुत की है। चूंकि, सीमा यह है कि बड़ी संख्या में सॉल्वैंट्स के लिए एडसोर्प्शन इसोथर्म केवल एक सीमित सीमा तक ही फिट हो सकते हैं। इस प्रकार वक्र उच्च क्षमता सीमा पर डेटा को फिट करने में सक्षम नहीं था और अध्ययन में यह भी निष्कर्ष निकाला कि परिणामों में कुछ विसंगतियाँ थीं। सक्रिय कार्बन पर कार्बन टेट्राक्लोराइड, साइक्लोहैक्सेन और कार्बन डाइसल्फ़ाइड से एडसोर्प्शन वक्र में अच्छी तरह से फिट नहीं हो पा रहा था और इसे समझाया जाना बाकी है और इस प्रकार प्रयोग करने वाले शोधकर्ताओं का अनुमान है कि कार्बन टेट्राक्लोराइड और साइक्लोहेक्सेन के स्टेरिक प्रभावों ने इसमें भूमिका होती है। यह अध्ययन विभिन्न प्रणालियों के साथ किया गया है जैसे कि पानी के घोल से कार्बनिक तरल पदार्थ और पानी के घोल से कार्बनिक ठोस इत्यादि के रूप में होते है।
कंपीटिटिव एडसोर्प्शन
चूंकि विभिन्न प्रणालियों की जांच की गई है, इसलिए मिश्रित समाधान के व्यक्तिगत एडसोर्प्शन की जांच के लिए एक अध्ययन किया गया था। इस फेनोमेनन को इरविंग एडसोर्प्शन मॉडल कंपीटिटिव एडसोर्प्शन भी कहा जाता है क्योंकि विलेय समान एडसोर्प्शन साइटों के लिए प्रतिस्पर्धा करते हैं। रोसेन और मेन्स द्वारा किए गए प्रयोग में,[11] ग्लूकोज, यूरिया, बेंज़ोइक एसिड , थैलाइड और पी-नाइट्रोफेनोल का कंपीटिटिव एडसोर्प्शन है । पोलैनी एडसोर्प्शन मॉडल का उपयोग करके वे सक्रिय कार्बन की सतह पर प्रत्येक यौगिक के सापेक्ष एडसोर्प्शन की गणना करने में सक्षम थे।
यह भी देखें
- एडसोर्प्शन
- कार्बन नैनोट्यूब
- सक्रिय कार्बन
- फ़्रायंडलिच एडसोर्प्शन
- बेट एडसोर्प्शन सिद्धांत
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 Polanyi, M (1963). "सोखना का संभावित सिद्धांत". Science. 141 (3585): 1010–013. Bibcode:1963Sci...141.1010P. doi:10.1126/science.141.3585.1010. PMID 17739484.
- ↑ http://web.iitd.ac.in/~arunku/files/CEL311_Y13/Adsorption%20Theory%20to%20practice_Dabrowski.pdf[bare URL PDF]
- ↑ Butt, Hans-Jürgen; Graf, Karlheinz; Kappl, Michael (2003). "इंटरफेस की भौतिकी और रसायन विज्ञान": 193–195.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Dubinin, M. M.; Astakhov, V. A. (1971). "माइक्रोपोरस अधिशोषक द्वारा गैसों और वाष्पों के अधिशोषण में माइक्रोप्रोर्स की मात्रा भरने की अवधारणाओं का विकास". Bulletin of the Academy of Sciences of the USSR, Division of Chemical Science. 20 (1): 3–7. doi:10.1007/bf00849307.
- ↑ 5.0 5.1 Yang, K.; Xing, B. (2010). "Adsorption of organic compounds by carbon nanomaterials in aqueous phase: Polanyi theory and its application". Chemical Reviews. 110 (10): 5989–6008. doi:10.1021/cr100059s. PMID 20518459.
- ↑ 6.0 6.1 Doong, S. J.; Yang, R. T. (1988). "A simple potential theory model for predicting mixed-gas adsorption". Industrial & Engineering Chemistry Research. 27 (4): 630–635. doi:10.1021/ie00076a017.
- ↑ 7.0 7.1 Tamon, H.; Okazaki, M. (1996). "Influence of acidic surface oxides of activated carbon on gas adsorption characteristics". Carbon. 34 (6): 741–746. doi:10.1016/0008-6223(96)00029-2.
- ↑ 8.0 8.1 8.2 8.3 8.4 Kawazoe, K.; Kawai, T.; Eguchi, Y.; Itoga, K. (1974). "Correlation of adsorption equilibrium data of various gases and vapors on molecular-sieving carbon". Journal of Chemical Engineering of Japan. 7 (3): 158–162. doi:10.1252/jcej.7.158.
- ↑ Yang, K.; Wu, W.; Jing, Q & Zhu, L. (2008). "बहु-दीवार वाले कार्बन नैनोट्यूब द्वारा एनिलिन, फिनोल और उनके विकल्प का जलीय सोखना". Environmental Science and Technology. 42 (21): 7931–6. Bibcode:2008EnST...42.7931Y. doi:10.1021/es801463v. PMID 19031883.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Manes, M.; Hofer, B.J.E. (1969). "सक्रिय कार्बन पर समाधान से सोखने के लिए पोलैनी सोखना संभावित सिद्धांत का अनुप्रयोग". The Journal of Physical Chemistry. 73 (3): 584–590. doi:10.1021/j100723a018.
- ↑ Manes, M.R.; Manes, M. (1976). "सक्रिय कार्बन पर समाधान से सोखने के लिए पोलैनी सोखना संभावित सिद्धांत का अनुप्रयोग। सातवीं. जल विलयन से ठोस पदार्थों का प्रतिस्पर्धी अधिशोषण". The Journal of Physical Chemistry. 80 (9): 953–959. doi:10.1021/j100550a007.