एफआईआर अंतरण प्रकार्य: Difference between revisions
No edit summary |
m (15 revisions imported from alpha:एफआईआर_अंतरण_प्रकार्य) |
||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
फ़िल्टर (सिग्नल प्रोसेसिंग) | फ़िल्टर (सिग्नल प्रोसेसिंग) या '''ट्रांसफर फ़ंक्शन''' फ़िल्टर बनाने के लिए ट्रांसफ़र फ़ंक्शन और कन्वोल्यूशन प्रमेय का उपयोग करता है। इस लेख में, परिमित आवेग प्रतिक्रिया का उपयोग करते हुए ऐसे फ़िल्टर के उदाहरण पर चर्चा की गई है और वास्तविक वर्ड डेटा में फ़िल्टर के अनुप्रयोग को दिखाया गया है। | ||
== एफआईआर ([[परिमित आवेग प्रतिक्रिया]]) रैखिक फिल्टर == | == एफआईआर ([[परिमित आवेग प्रतिक्रिया]]) रैखिक फिल्टर == | ||
डिजिटल प्रोसेसिंग में, परिमित आवेग प्रतिक्रिया समय-निरंतर फ़िल्टर है जो समय के साथ अपरिवर्तनीय है। इसका | डिजिटल प्रोसेसिंग में, परिमित आवेग प्रतिक्रिया समय-निरंतर फ़िल्टर है जो समय के साथ अपरिवर्तनीय है। इसका अर्थ यह है कि फ़िल्टर समय के विशिष्ट बिंदु पर निर्भर नहीं करता है, किंतु समय अवधि पर निर्भर करता है। इस फ़िल्टर के विनिर्देशन में लीनियर फ़िल्टर या एफआईआर ट्रांसफर फ़ंक्शंस का उपयोग किया जाता है जिसमें आवृत्ति प्रतिक्रिया होती है जो केवल इनपुट की वांछित आवृत्तियों को पारित करती है। इस प्रकार का फ़िल्टर गैर-पुनरावर्ती है, जिसका अर्थ है कि आउटपुट को आउटपुट के किसी भी पुनरावर्ती मान के बिना इनपुट के संयोजन से पूरी तरह से प्राप्त किया जा सकता है। इसका अर्थ यह है कि कोई फीडबैक लूप नहीं है जो नए आउटपुट को पिछले आउटपुट के मूल्यों को फीड करता है। यह उन अनुप्रयोगों में [[अनंत आवेग प्रतिक्रिया|IIR फ़िल्टर (अनंत आवेग प्रतिक्रिया)]] जैसे पुनरावर्ती फ़िल्टर पर लाभ है, जिन्हें रैखिक चरण प्रतिक्रिया की आवश्यकता होती है क्योंकि यह चरण विरूपण के बिना इनपुट को पास कर देता है।<ref>IIR Filters and FIR Filters. (2012, June). Retrieved May 04, 2017, from http://zone.ni.com/reference/en-XX/help/370858K-01/genmaths/genmaths/calc_filterfir_iir/</ref> | ||
== गणितीय मॉडल == | == गणितीय मॉडल == | ||
आउटपुट फ़ंक्शन | मान लीजिए कि आउटपुट फ़ंक्शन <math>y(t)</math> है और इनपुट <math>x(t)</math> हैं। स्थानांतरण फ़ंक्शन <math>h(t)</math> के साथ इनपुट का कनवल्शन फ़िल्टर्ड आउटपुट प्रदान करता है। इस प्रकार के फ़िल्टर का गणितीय मॉडल है: | ||
: <math>y(t) = \int_{0}^{T} x(t-\tau)\, h(\tau)\, d\tau</math> | : <math>y(t) = \int_{0}^{T} x(t-\tau)\, h(\tau)\, d\tau</math> | ||
h(<math>\tau</math>) इनपुट के लिए आवेग प्रतिक्रिया का स्थानांतरण फ़ंक्शन है। कन्वोल्यूशन या विज़ुअल स्पष्टीकरण फ़िल्टर को केवल तभी सक्रिय करने की अनुमति देता है जब इनपुट ने उसी समय मान पर सिग्नल रिकॉर्ड करता है। यदि k फ़ंक्शन h के समर्थन क्षेत्र में आता है तो यह फ़िल्टर इनपुट मान (x(t)) लौटाता है। यही कारण है कि इस फ़िल्टर को परिमित प्रतिक्रिया कहा जाता है। यदि k समर्थन क्षेत्र के बाहर है, तो आवेग प्रतिक्रिया शून्य है जो आउटपुट को शून्य बनाती है। इसका केंद्रीय विचार h(<math>\tau</math>) फ़ंक्शन को दो फ़ंक्शनों के भागफल के रूप में विचार किया जा सकता है।<ref>Nagai, N. (1990). Linear circuits, systems, and signal processing: Advanced theory and applications. New York: M. Dekker.</ref> | |||
हुआंग के अनुसार (1981)<ref>Huang, T. S. (1981). Topics in applied physics: Two-Dimensional Digital Signal Processing I (3rd ed., Vol. 42, Topics in Applied Physics). Berlin: Springer.</ref> इस गणितीय मॉडल का उपयोग करते हुए, विभिन्न परिमित आवेग प्रतिक्रिया | |||
हुआंग के अनुसार (1981)<ref>Huang, T. S. (1981). Topics in applied physics: Two-Dimensional Digital Signal Processing I (3rd ed., Vol. 42, Topics in Applied Physics). Berlin: Springer.</ref> इस गणितीय मॉडल का उपयोग करते हुए, विभिन्न परिमित आवेग प्रतिक्रिया या फ़िल्टर डिज़ाइन के साथ गैर-पुनरावर्ती रैखिक फ़िल्टर को डिज़ाइन करने की चार विधियाँ हैं: | |||
# विंडो डिज़ाइन विधि | |||
# आवृत्ति नमूनाकरण विधि | # आवृत्ति नमूनाकरण विधि | ||
# पारंपरिक रैखिक प्रोग्रामिंग | # पारंपरिक रैखिक प्रोग्रामिंग | ||
# पुनरावृत्तीय रैखिक प्रोग्रामिंग | # पुनरावृत्तीय रैखिक प्रोग्रामिंग | ||
== | == एकल-पक्षीय रैखिक फ़िल्टर == | ||
=== इनपुट फ़ंक्शन === | === इनपुट फ़ंक्शन === | ||
| Line 22: | Line 22: | ||
[[File:Sin with random function.jpg|यादृच्छिक फ़ंक्शन के साथ साइन]] | [[File:Sin with random function.jpg|यादृच्छिक फ़ंक्शन के साथ साइन]] | ||
=== | === एकल-पक्षीय फिल्टर === | ||
धनात्मक मूल्यों के समर्थन क्षेत्र के लिए आवेग प्रतिक्रिया के रूप में घातीय फ़ंक्शन का उपयोग करें। | |||
:<math>h(t) = \begin{cases} 0, & \forall &-\infty &\le & t &\le 0 \\ e^{-t}, \quad & \forall &0 &\le & t &\le +\infty \end{cases}</math> | :<math>h(t) = \begin{cases} 0, & \forall &-\infty &\le & t &\le 0 \\ e^{-t}, \quad & \forall &0 &\le & t &\le +\infty \end{cases}</math> | ||
| Line 31: | Line 31: | ||
[[File:Single sided filter.jpg|एकल-पक्षीय फ़िल्टरिंग परिणाम]] | [[File:Single sided filter.jpg|एकल-पक्षीय फ़िल्टरिंग परिणाम]] | ||
== दो | == दो पक्षीय फिल्टर == | ||
इनपुट सिग्नल को सिंगल-साइडेड फ़ंक्शन के समान होने दें। | इनपुट सिग्नल को सिंगल-साइडेड फ़ंक्शन के समान होने दें। पहले की तरह धनात्मक मूल्यों के समर्थन क्षेत्र के लिए आवेग प्रतिक्रिया के रूप में घातीय फ़ंक्शन का उपयोग करें। इस दोतरफा फ़िल्टर में, अन्य घातीय फ़ंक्शन भी प्रयुक्त करें। घातांक की शक्तियों के संकेतों में विपरीत घातीय कार्यों की गणना करते समय गैर-अनंत परिणामों को बनाए रखना है। | ||
पहले की तरह | |||
<math> h(t) = \begin{cases} e^{t}, & \forall & -\infty &\le & t &\le 0 \\ e^{-t}, &\forall & 0 &\le &t &\le +\infty \end{cases} </math> | <math> h(t) = \begin{cases} e^{t}, & \forall & -\infty &\le & t &\le 0 \\ e^{-t}, &\forall & 0 &\le &t &\le +\infty \end{cases} </math> | ||
इस फ़िल्टर को इसके आवृत्ति डोमेन में जांचें, हम देखते हैं कि परिमाण प्रतिक्रिया एकल पक्षीय फ़िल्टर के समान प्रवृत्ति है। | |||
इस फ़िल्टर को इसके आवृत्ति डोमेन में जांचें, हम देखते हैं कि परिमाण प्रतिक्रिया एकल पक्षीय फ़िल्टर के समान प्रवृत्ति है। चूँकि, जिन आवृत्तियों को पारित किया जा सकता है वे एकल-पक्षीय फ़िल्टर की तुलना में छोटी हैं। इसके परिणामस्वरूप श्रेष्ठ आउटपुट प्राप्त हुआ है। इस परिणाम का महत्वपूर्ण यह है कि दो पक्षीय फिल्टर प्रकार के रैखिक फिल्टर श्रेष्ठ फिल्टर होते हैं। | |||
[[File:Double sided filter frequency response.jpg|दो तरफा फ़िल्टर आवृत्ति प्रतिक्रिया]] | [[File:Double sided filter frequency response.jpg|दो तरफा फ़िल्टर आवृत्ति प्रतिक्रिया]] | ||
| Line 42: | Line 42: | ||
== एफआईआर ट्रांसफर फ़ंक्शन रैखिक फ़िल्टर अनुप्रयोग == | == एफआईआर ट्रांसफर फ़ंक्शन रैखिक फ़िल्टर अनुप्रयोग == | ||
रैखिक फ़िल्टर तब | रैखिक फ़िल्टर तब श्रेष्ठ प्रदर्शन करता है जब यह दो पक्षीय फ़िल्टर होता है। इसके लिए डेटा को पहले से जानना आवश्यक है जिससे इन फ़िल्टरों के लिए उन स्थितियों में उचित प्रकार से काम करना चुनौती बन जाता है जहां सिग्नल को समय से पहले नहीं जाना जा सकता है जैसे कि रेडियो सिग्नल प्रोसेसिंग। चूँकि, इसका अर्थ यह है कि रैखिक फ़िल्टर प्री-लोडेड डेटा को फ़िल्टर करने में अत्यधिक उपयोगी हैं। इसके अतिरिक्त, इसकी गैर-पुनरावर्ती प्रकृति के कारण जो इनपुट के चरण कोणों को संरक्षित करता है, इस प्रकार रैखिक फिल्टर सामान्यतः छवि प्रसंस्करण, इमेज प्रोसेसिंग, विडियो प्रोसेसिंग या पैटर्न का पता लगाने में उपयोग किया जाता है। कुछ उदाहरण वर्णक्रमीय विश्लेषण के लिए छवि वृद्धि, पुनर्स्थापन और पूर्व-श्वेतीकरण हैं।<ref>Huang, T. S. (1981). Topics in applied physics: Two-Dimensional Digital Signal Processing I (3rd ed., Vol. 42, Topics in Applied Physics). Berlin: Springer.</ref> इसके अतिरिक्त, रैखिक गैर-पुनरावर्ती फ़िल्टर सदैव स्थिर होते हैं और सामान्यतः पूरी तरह से वास्तविक आउटपुट उत्पन्न करते हैं जो उन्हें अधिक अनुकूल बनाता है। वे कम्प्यूटेशनल रूप से भी सरल हैं जो सामान्यतः इस एफआईआर रैखिक फ़िल्टर का उपयोग करने के लिए बड़ा लाभ उत्पन्न करता है। | ||
== संदर्भ == | == संदर्भ == | ||
| Line 52: | Line 52: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 16/08/2023]] | [[Category:Created On 16/08/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 09:50, 1 December 2023
फ़िल्टर (सिग्नल प्रोसेसिंग) या ट्रांसफर फ़ंक्शन फ़िल्टर बनाने के लिए ट्रांसफ़र फ़ंक्शन और कन्वोल्यूशन प्रमेय का उपयोग करता है। इस लेख में, परिमित आवेग प्रतिक्रिया का उपयोग करते हुए ऐसे फ़िल्टर के उदाहरण पर चर्चा की गई है और वास्तविक वर्ड डेटा में फ़िल्टर के अनुप्रयोग को दिखाया गया है।
एफआईआर (परिमित आवेग प्रतिक्रिया) रैखिक फिल्टर
डिजिटल प्रोसेसिंग में, परिमित आवेग प्रतिक्रिया समय-निरंतर फ़िल्टर है जो समय के साथ अपरिवर्तनीय है। इसका अर्थ यह है कि फ़िल्टर समय के विशिष्ट बिंदु पर निर्भर नहीं करता है, किंतु समय अवधि पर निर्भर करता है। इस फ़िल्टर के विनिर्देशन में लीनियर फ़िल्टर या एफआईआर ट्रांसफर फ़ंक्शंस का उपयोग किया जाता है जिसमें आवृत्ति प्रतिक्रिया होती है जो केवल इनपुट की वांछित आवृत्तियों को पारित करती है। इस प्रकार का फ़िल्टर गैर-पुनरावर्ती है, जिसका अर्थ है कि आउटपुट को आउटपुट के किसी भी पुनरावर्ती मान के बिना इनपुट के संयोजन से पूरी तरह से प्राप्त किया जा सकता है। इसका अर्थ यह है कि कोई फीडबैक लूप नहीं है जो नए आउटपुट को पिछले आउटपुट के मूल्यों को फीड करता है। यह उन अनुप्रयोगों में IIR फ़िल्टर (अनंत आवेग प्रतिक्रिया) जैसे पुनरावर्ती फ़िल्टर पर लाभ है, जिन्हें रैखिक चरण प्रतिक्रिया की आवश्यकता होती है क्योंकि यह चरण विरूपण के बिना इनपुट को पास कर देता है।[1]
गणितीय मॉडल
मान लीजिए कि आउटपुट फ़ंक्शन है और इनपुट हैं। स्थानांतरण फ़ंक्शन के साथ इनपुट का कनवल्शन फ़िल्टर्ड आउटपुट प्रदान करता है। इस प्रकार के फ़िल्टर का गणितीय मॉडल है:
h() इनपुट के लिए आवेग प्रतिक्रिया का स्थानांतरण फ़ंक्शन है। कन्वोल्यूशन या विज़ुअल स्पष्टीकरण फ़िल्टर को केवल तभी सक्रिय करने की अनुमति देता है जब इनपुट ने उसी समय मान पर सिग्नल रिकॉर्ड करता है। यदि k फ़ंक्शन h के समर्थन क्षेत्र में आता है तो यह फ़िल्टर इनपुट मान (x(t)) लौटाता है। यही कारण है कि इस फ़िल्टर को परिमित प्रतिक्रिया कहा जाता है। यदि k समर्थन क्षेत्र के बाहर है, तो आवेग प्रतिक्रिया शून्य है जो आउटपुट को शून्य बनाती है। इसका केंद्रीय विचार h() फ़ंक्शन को दो फ़ंक्शनों के भागफल के रूप में विचार किया जा सकता है।[2]
हुआंग के अनुसार (1981)[3] इस गणितीय मॉडल का उपयोग करते हुए, विभिन्न परिमित आवेग प्रतिक्रिया या फ़िल्टर डिज़ाइन के साथ गैर-पुनरावर्ती रैखिक फ़िल्टर को डिज़ाइन करने की चार विधियाँ हैं:
- विंडो डिज़ाइन विधि
- आवृत्ति नमूनाकरण विधि
- पारंपरिक रैखिक प्रोग्रामिंग
- पुनरावृत्तीय रैखिक प्रोग्रामिंग
एकल-पक्षीय रैखिक फ़िल्टर
इनपुट फ़ंक्शन
इनपुट सिग्नल को परिभाषित करें:
साइनसॉइडल फ़ंक्शन में 1 से 200 तक यादृच्छिक संख्या जोड़ता है जो डेटा को विकृत करने का कार्य करता है।
एकल-पक्षीय फिल्टर
धनात्मक मूल्यों के समर्थन क्षेत्र के लिए आवेग प्रतिक्रिया के रूप में घातीय फ़ंक्शन का उपयोग करें।
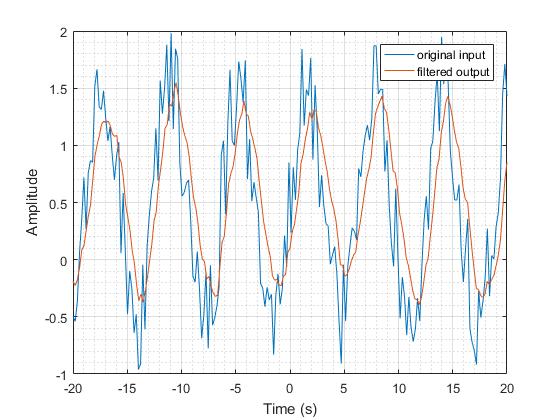
इस फ़िल्टर की आवृत्ति प्रतिक्रिया निम्न आवृत्ति की तरह लो पास फिल्टर के समान होती है।
दो पक्षीय फिल्टर
इनपुट सिग्नल को सिंगल-साइडेड फ़ंक्शन के समान होने दें। पहले की तरह धनात्मक मूल्यों के समर्थन क्षेत्र के लिए आवेग प्रतिक्रिया के रूप में घातीय फ़ंक्शन का उपयोग करें। इस दोतरफा फ़िल्टर में, अन्य घातीय फ़ंक्शन भी प्रयुक्त करें। घातांक की शक्तियों के संकेतों में विपरीत घातीय कार्यों की गणना करते समय गैर-अनंत परिणामों को बनाए रखना है।
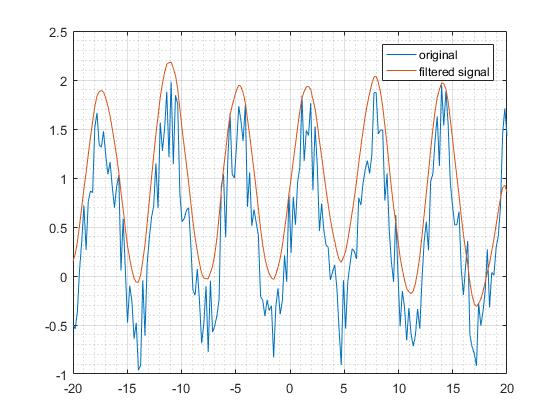
इस फ़िल्टर को इसके आवृत्ति डोमेन में जांचें, हम देखते हैं कि परिमाण प्रतिक्रिया एकल पक्षीय फ़िल्टर के समान प्रवृत्ति है। चूँकि, जिन आवृत्तियों को पारित किया जा सकता है वे एकल-पक्षीय फ़िल्टर की तुलना में छोटी हैं। इसके परिणामस्वरूप श्रेष्ठ आउटपुट प्राप्त हुआ है। इस परिणाम का महत्वपूर्ण यह है कि दो पक्षीय फिल्टर प्रकार के रैखिक फिल्टर श्रेष्ठ फिल्टर होते हैं।
एफआईआर ट्रांसफर फ़ंक्शन रैखिक फ़िल्टर अनुप्रयोग
रैखिक फ़िल्टर तब श्रेष्ठ प्रदर्शन करता है जब यह दो पक्षीय फ़िल्टर होता है। इसके लिए डेटा को पहले से जानना आवश्यक है जिससे इन फ़िल्टरों के लिए उन स्थितियों में उचित प्रकार से काम करना चुनौती बन जाता है जहां सिग्नल को समय से पहले नहीं जाना जा सकता है जैसे कि रेडियो सिग्नल प्रोसेसिंग। चूँकि, इसका अर्थ यह है कि रैखिक फ़िल्टर प्री-लोडेड डेटा को फ़िल्टर करने में अत्यधिक उपयोगी हैं। इसके अतिरिक्त, इसकी गैर-पुनरावर्ती प्रकृति के कारण जो इनपुट के चरण कोणों को संरक्षित करता है, इस प्रकार रैखिक फिल्टर सामान्यतः छवि प्रसंस्करण, इमेज प्रोसेसिंग, विडियो प्रोसेसिंग या पैटर्न का पता लगाने में उपयोग किया जाता है। कुछ उदाहरण वर्णक्रमीय विश्लेषण के लिए छवि वृद्धि, पुनर्स्थापन और पूर्व-श्वेतीकरण हैं।[4] इसके अतिरिक्त, रैखिक गैर-पुनरावर्ती फ़िल्टर सदैव स्थिर होते हैं और सामान्यतः पूरी तरह से वास्तविक आउटपुट उत्पन्न करते हैं जो उन्हें अधिक अनुकूल बनाता है। वे कम्प्यूटेशनल रूप से भी सरल हैं जो सामान्यतः इस एफआईआर रैखिक फ़िल्टर का उपयोग करने के लिए बड़ा लाभ उत्पन्न करता है।
संदर्भ
- ↑ IIR Filters and FIR Filters. (2012, June). Retrieved May 04, 2017, from http://zone.ni.com/reference/en-XX/help/370858K-01/genmaths/genmaths/calc_filterfir_iir/
- ↑ Nagai, N. (1990). Linear circuits, systems, and signal processing: Advanced theory and applications. New York: M. Dekker.
- ↑ Huang, T. S. (1981). Topics in applied physics: Two-Dimensional Digital Signal Processing I (3rd ed., Vol. 42, Topics in Applied Physics). Berlin: Springer.
- ↑ Huang, T. S. (1981). Topics in applied physics: Two-Dimensional Digital Signal Processing I (3rd ed., Vol. 42, Topics in Applied Physics). Berlin: Springer.