विशेष सापेक्षता के परीक्षण: Difference between revisions

From Vigyanwiki
 
(7 intermediate revisions by 2 users not shown)
Line 1: Line 1:
{{Short description|Experiments probing the accuracy of special relativity's predictions}}[[विशेष सापेक्षता]] एक [[भौतिक सिद्धांत]] है जो सभी भौतिक घटनाओं के वर्णन में एक मौलिक भूमिका निभाता है, जब तक कि गुरुत्वाकर्षण महत्वपूर्ण न हो। कई प्रयोगों ने इसके विकास और औचित्य में महत्वपूर्ण भूमिका निभाई (और अब भी निभाते हैं)। सिद्धांत की ताकत अत्यंत विविध प्रकार के प्रयोगों के परिणाम की उच्च परिशुद्धता के साथ सही भविष्यवाणी करने की इसकी अद्वितीय क्षमता में निहित है। उनमें से कई प्रयोगों की पुनरावृत्ति अभी भी लगातार बढ़ी हुई सटीकता के साथ की जा रही है, जिसमें आधुनिक प्रयोग [[प्लैंक स्केल]] और [[ न्युट्रीनो ]] क्षेत्र जैसे प्रभावों पर ध्यान केंद्रित कर रहे हैं। उनके परिणाम विशेष सापेक्षता की भविष्यवाणियों के अनुरूप हैं। [[जेकब लाउब]] द्वारा विभिन्न परीक्षणों का संग्रह दिया गया,<ref name="laub" />झांग,<ref name="zhang" />मैटिंगली,<ref name="mattingly" />[[क्लिफोर्ड विल]],<ref name="will" />और रॉबर्ट्स/श्लीफ़।<ref name="faq" />
{{Short description|Experiments probing the accuracy of special relativity's predictions}}[[विशेष सापेक्षता|'''विशेष सापेक्षता''']] एक [[भौतिक सिद्धांत]] है, जब तक कि गुरुत्वाकर्षण महत्वपूर्ण न हो जो सभी भौतिक घटनाओं के वर्णन में मौलिक भूमिका निभाता है। अनेक प्रयोगों ने इसके विकास और औचित्य में महत्वपूर्ण भूमिका निभाई (और अब भी निभाते हैं)। इस प्रकार से सिद्धांत की शक्ति अत्यंत विविध प्रकार के प्रयोगों के परिणाम की उच्च परिशुद्धता के साथ सही पूर्वानुमान करने की इसकी अद्वितीय क्षमता में निहित है। किन्तु उनमें से अनेक प्रयोगों की पुनरावृत्ति अभी भी निरंतर बढ़ी हुई स्पष्टतः के साथ की जा रही है, जिसमें आधुनिक प्रयोग [[प्लैंक स्केल]] और [[ न्युट्रीनो |न्युट्रीनो]] क्षेत्र जैसे प्रभावों पर ध्यान केंद्रित कर रहे हैं। उनके परिणाम विशेष सापेक्षता की पूर्वानुमानो के अनुरूप हैं। [[जेकब लाउब]],<ref name="laub" /> झांग,<ref name="zhang" /> मैटिंगली,<ref name="mattingly" /> [[क्लिफोर्ड विल]],<ref name="will" /> और रॉबर्ट्स/श्लीफ़ द्वारा विभिन्न परीक्षणों का संग्रह दिया गया था।<ref name="faq" />


विशेष सापेक्षता मिन्कोव्स्की अंतरिक्ष तक ही सीमित है, अर्थात, गुरुत्वाकर्षण के महत्वपूर्ण प्रभाव के बिना सभी घटनाओं तक। उत्तरार्द्ध [[सामान्य सापेक्षता]] के क्षेत्र में है और सामान्य सापेक्षता के संबंधित परीक्षणों पर विचार किया जाना चाहिए।
अर्थात, गुरुत्वाकर्षण के महत्वपूर्ण प्रभाव के बिना सभी घटनाओं तक विशेष सापेक्षता मिन्कोव्स्की अंतरिक्ष तक ही सीमित है। इस प्रकार से उत्तरार्द्ध [[सामान्य सापेक्षता]] के क्षेत्र में है और सामान्य सापेक्षता के संबंधित परीक्षणों पर विचार किया जाना चाहिए।


== सापेक्षता का मार्ग प्रशस्त करने वाले प्रयोग ==
== सापेक्षता का मार्ग प्रशस्त करने वाले प्रयोग ==


19वीं शताब्दी में प्रकाश का प्रमुख सिद्धांत [[चमकदार ईथर]] का था, एक स्थिर माध्यम जिसमें प्रकाश उसी तरह फैलता है जैसे ध्वनि हवा के माध्यम से फैलती है। सादृश्य से, यह इस प्रकार है कि [[प्रकाश की गति]] ईथर में सभी दिशाओं में स्थिर है और स्रोत के वेग से स्वतंत्र है। इस प्रकार ईथर के सापेक्ष गति करने वाले एक पर्यवेक्षक को किसी प्रकार की ईथर हवा को मापना चाहिए, वैसे ही जैसे वायु के सापेक्ष गति करने वाला एक पर्यवेक्षक [[स्पष्ट हवा]] को मापता है।
19वीं शताब्दी में प्रकाश का प्रमुख सिद्धांत [[चमकदार ईथर|ल्यूमिनिफेरस ईथर]] का था, स्थिर माध्यम जिसमें प्रकाश उसी तरह फैलता है जैसे ध्वनि वायु के माध्यम से फैलती है। सादृश्य से, यह इस प्रकार है कि [[प्रकाश की गति]] ईथर में सभी दिशाओं में स्थिर है और स्रोत के वेग से स्वतंत्र है। इस प्रकार ईथर के सापेक्ष गति करने वाले पर्यवेक्षक को किसी प्रकार की ईथर वायु को मापना चाहिए, वैसे ही जैसे वायु के सापेक्ष गति करने वाला पर्यवेक्षक [[स्पष्ट हवा|स्पष्ट वायु]] को मापता है।


===प्रथम-क्रम प्रयोग===
===प्रथम-क्रम प्रयोग===
{{Main|Luminiferous aether#First order experiments}}
{{Main| ल्यूमिनिफेरस ईथर#प्रथम क्रम प्रयोग}}
[[File:Fizeau-Mascart2.png|thumb|right|[[फ़िज़ो प्रयोग]], 1851]]फ्रांकोइस अरागो (1810) के काम की शुरुआत में, ऑप्टिकल प्रयोगों की एक श्रृंखला आयोजित की गई थी, जिसे पहले क्रम के परिमाण के लिए सकारात्मक परिणाम देना चाहिए था। <math>v/c</math> (अर्थात, का <math>(v/c)^1</math>) और इस प्रकार ईथर की सापेक्ष गति को प्रदर्शित करना चाहिए था। फिर भी परिणाम नकारात्मक थे. [[ऑगस्टिन फ़्रेज़नेल]] (1818) द्वारा एक सहायक परिकल्पना, तथाकथित ड्रैगिंग गुणांक, की शुरूआत के साथ एक स्पष्टीकरण प्रदान किया गया था, अर्थात, पदार्थ ईथर को कुछ हद तक खींच रहा है। इस गुणांक को फ़िज़ो प्रयोग (1851) द्वारा सीधे प्रदर्शित किया गया था। बाद में यह दिखाया गया कि सभी प्रथम-क्रम ऑप्टिकल प्रयोगों को इस गुणांक के कारण नकारात्मक परिणाम देना होगा। इसके अलावा, कुछ इलेक्ट्रोस्टैटिक प्रथम-क्रम प्रयोग आयोजित किए गए, जिनके फिर से नकारात्मक परिणाम आए। सामान्य तौर पर, [[हेंड्रिक लोरेंत्ज़]] (1892, 1895) ने गतिमान पर्यवेक्षकों के लिए कई नए सहायक चर पेश किए, यह प्रदर्शित करते हुए कि सभी प्रथम-क्रम ऑप्टिकल और इलेक्ट्रोस्टैटिक प्रयोगों ने शून्य परिणाम क्यों दिए हैं। उदाहरण के लिए, लोरेंत्ज़ ने एक स्थान चर प्रस्तावित किया जिसके द्वारा इलेक्ट्रोस्टैटिक क्षेत्र गति की रेखा में सिकुड़ते हैं और एक अन्य चर (स्थानीय समय) जिसके द्वारा गतिमान पर्यवेक्षकों के लिए समय निर्देशांक उनके वर्तमान स्थान पर निर्भर करते हैं।<ref name=laub />
[[File:Fizeau-Mascart2.png|thumb|right|[[फ़िज़ो प्रयोग]], 1851]]फ्रांकोइस अरागो (1810) के काम की प्रारंभ करते हुए, ऑप्टिकल प्रयोगों की श्रृंखला आयोजित की गई थी, जिसे <math>v/c</math> (अर्थात, का <math>(v/c)^1</math>) पहले क्रम के परिमाण के लिए धनात्मक परिणाम देना चाहिए था। और इस प्रकार ईथर की सापेक्ष गति को प्रदर्शित करना चाहिए था। फिर भी परिणाम ऋणात्मक थे. [[ऑगस्टिन फ़्रेज़नेल]] (1818) द्वारा सहायक परिकल्पना, तथाकथित कर्षणिंग गुणांक, के प्रारंभ के साथ स्पष्टीकरण प्रदान किया गया था, अर्थात, पदार्थ ईथर को कुछ सीमा तक खींच रहा है। इस गुणांक को फ़िज़ो प्रयोग (1851) द्वारा सीधे प्रदर्शित किया गया था। तत्पश्चात यह दिखाया गया कि सभी प्रथम-क्रम ऑप्टिकल प्रयोगों को इस गुणांक के कारण ऋणात्मक परिणाम देना होगा। इसके अतिरिक्त, कुछ इलेक्ट्रोस्टैटिक प्रथम-क्रम प्रयोग आयोजित किए गए, जिनके फिर से ऋणात्मक परिणाम आए। सामान्य रूप से, [[हेंड्रिक लोरेंत्ज़]] (1892, 1895) ने गतिमान पर्यवेक्षकों के लिए अनेक नए सहायक वेरिएबल प्रस्तुत किए, यह प्रदर्शित करते हुए कि सभी प्रथम-क्रम ऑप्टिकल और इलेक्ट्रोस्टैटिक प्रयोगों ने शून्य परिणाम क्यों दिए हैं। उदाहरण के लिए, लोरेंत्ज़ ने स्थान वेरिएबल प्रस्तावित किया जिसके द्वारा इलेक्ट्रोस्टैटिक क्षेत्र गति की रेखा में संकुचन हैं और अन्य वेरिएबल (स्थानीय समय) जिसके द्वारा गतिमान पर्यवेक्षकों के लिए समय निर्देशांक उनके वर्तमान स्थान पर निर्भर करते हैं।<ref name=laub />
===द्वतीय क्रम के प्रयोग===
{{Main| ल्यूमिनिफेरस ईथर#द्वितीय क्रम प्रयोग}}
[[File:Michelson-Morley experiment conducted with white light.png|thumb|माइकलसन-मॉर्ले इंटरफेरोमीटर]]चूंकि, स्थिर ईथर सिद्धांत धनात्मक परिणाम देगा जब प्रयोग <math>v/c</math>(अर्थात, का <math>(v/c)^2</math>) द्वतीय क्रम के परिमाण को मापने के लिए पर्याप्त स्पष्ट होंगे। इस प्रकार से अल्बर्ट ए. माइकलसन ने 1881 में माइकलसन-मॉर्ले प्रयोग या मिशेलसन प्रयोग (1881) किया, इसके बाद 1887 में अधिक परिष्कृत माइकलसन-मॉर्ले प्रयोग किया गया। किन्तु अलग-अलग दिशाओं में कुछ समय के लिए यात्रा करने वाली प्रकाश की दो किरणों को हस्तक्षेप के लिए लाया गया, जिससे ईथर पवन के सापेक्ष भिन्न-भिन्न झुकावों से व्यतिकरण फ्रिंजों का विस्थापन होना चाहिए। किन्तु परिणाम पुनः ऋणात्मक रहा. इस दुविधा से बाहर निकलने का रास्ता [[जॉर्ज फ्रांसिस फिट्जगेराल्ड]] (1889) और लोरेंत्ज़ (1892) का प्रस्ताव था कि पदार्थ ईथर ([[लंबाई संकुचन]]) के संबंध में गति की रेखा में अनुबंधित होता है। अर्थात्, इलेक्ट्रोस्टैटिक क्षेत्रों के संकुचन की पुरानी परिकल्पना को अंतर-आणविक बलों तक विस्तारित किया गया था। चूँकि इसका कोई सैद्धांतिक कारण नहीं था, इसलिए संकुचन परिकल्पना को तदर्थ माना गया था।


ऑप्टिकल माइकलसन-मॉर्ले प्रयोग के अतिरिक्त, इसके इलेक्ट्रोडायनामिक समकक्ष, ट्राउटन-नोबल प्रयोग भी आयोजित किया गया था। इसके द्वारा यह प्रदर्शित किया जाना चाहिए कि गतिशील कंडेनसर को [[ टॉर्कः |टॉर्कः]] के अधीन किया जाना चाहिए। इसके अतिरिक्त, [[रेले और ब्रेस के प्रयोग|रेले और ब्रेस के प्रयोगो]] का उद्देश्य प्रयोगशाला फ्रेम में लंबाई संकुचन के कुछ परिणामों को मापना था, उदाहरण के लिए यह धारणा कि इससे द्विअपवर्तन हो सकता है। चूंकि उन सभी प्रयोगों के ऋणात्मक परिणाम आये। (1908 में किए गए ट्राउटन-रैंकिन प्रयोग ने भी [[विद्युत चुम्बकीय कुंडल]] पर लंबाई संकुचन के प्रभाव को मापते समय ऋणात्मक परिणाम दिया था।)<ref name=laub />


===दूसरे क्रम के प्रयोग===
इस प्रकार से 1904 से पहले किए गए सभी प्रयोगों को समझाने के लिए, लोरेंत्ज़ को संपूर्ण [[लोरेंत्ज़ परिवर्तन]] की प्रारंभ करके अपने सिद्धांत को फिर से विस्तारित करने के लिए विवश होना पड़ा। हेनरी पोंकारे ने 1905 में घोषणा की कि पूर्ण गति ([[सापेक्षता का सिद्धांत]]) प्रदर्शित करने की असंभवता स्पष्ट रूप से प्रकृति का नियम है।
{{Main|Luminiferous aether#Second order experiments}}
[[File:Michelson-Morley experiment conducted with white light.png|thumb|माइकलसन-मॉर्ले इंटरफेरोमीटर]]हालाँकि, स्थिर ईथर सिद्धांत सकारात्मक परिणाम देगा जब प्रयोग दूसरे क्रम के परिमाण को मापने के लिए पर्याप्त सटीक होंगे<math>v/c</math>(अर्थात, का <math>(v/c)^2</math>). अल्बर्ट ए. माइकलसन ने 1881 में माइकलसन-मॉर्ले प्रयोग#मिशेलसन प्रयोग (1881) किया, इसके बाद 1887 में अधिक परिष्कृत माइकलसन-मॉर्ले प्रयोग किया गया। अलग-अलग दिशाओं में कुछ समय के लिए यात्रा करने वाली प्रकाश की दो किरणों को हस्तक्षेप के लिए लाया गया, ताकि ईथर पवन के सापेक्ष भिन्न-भिन्न झुकावों से व्यतिकरण फ्रिंजों का विस्थापन होना चाहिए। लेकिन नतीजा फिर नकारात्मक रहा. इस दुविधा से बाहर निकलने का रास्ता [[जॉर्ज फ्रांसिस फिट्जगेराल्ड]] (1889) और लोरेंत्ज़ (1892) का प्रस्ताव था कि पदार्थ ईथर ([[लंबाई संकुचन]]) के संबंध में गति की रेखा में अनुबंधित होता है। अर्थात्, इलेक्ट्रोस्टैटिक क्षेत्रों के संकुचन की पुरानी परिकल्पना को अंतर-आणविक बलों तक विस्तारित किया गया था। हालाँकि, चूँकि इसका कोई सैद्धांतिक कारण नहीं था, इसलिए संकुचन परिकल्पना को तदर्थ माना गया।


ऑप्टिकल माइकलसन-मॉर्ले प्रयोग के अलावा, इसके इलेक्ट्रोडायनामिक समकक्ष, ट्राउटन-नोबल प्रयोग भी आयोजित किया गया था। इसके द्वारा यह प्रदर्शित किया जाना चाहिए कि एक गतिशील कंडेनसर को एक [[ टॉर्कः ]] के अधीन किया जाना चाहिए। इसके अलावा, [[रेले और ब्रेस के प्रयोग]]ों का उद्देश्य प्रयोगशाला फ्रेम में लंबाई संकुचन के कुछ परिणामों को मापना था, उदाहरण के लिए यह धारणा कि इससे द्विअपवर्तन हो सकता है। हालाँकि उन सभी प्रयोगों के नकारात्मक परिणाम आये। (1908 में किए गए ट्राउटन-रैंकिन प्रयोग ने भी [[विद्युत चुम्बकीय कुंडल]] पर लंबाई संकुचन के प्रभाव को मापते समय एक नकारात्मक परिणाम दिया था।)<ref name=laub />
===पूर्ण ईथर कर्षण का खंडन===
{{Main|ईथर ड्रैग परिकल्पना}}
[[File:Lodge's ether machine DE.svg|thumb|200px|लॉज की ईथर मशीन. स्टील डिस्क का व्यास गज था। श्वेत प्रकाश को किरण विभाजक द्वारा विभाजित किया गया था और फ्रिंज बनाने के लिए पुन: एकजुट होने से पहले उपकरण के चारों ओर तीन बार दौड़ा।]]यह विचार कि ईथर को पूरी तरह से पृथ्वी के अन्दर या उसके समीप खींचा जा सकता है, जिससे ऋणात्मक ईथर धारा प्रयोगों को समझाया जा सकता है, विभिन्न प्रयोगों द्वारा खंडन किया गया था।
*[[ओलिवर लॉज]] (1893) ने पाया कि संवेदनशील [[सामान्य-पथ इंटरफेरोमीटर]] के ऊपर और नीचे तेजी से घूर्णन वाली स्टील डिस्क मापने योग्य फ्रिंज परिवर्तन उत्पन्न करने में विफल रही।
*[[गुस्ताफ हैमर]] (1935) हैमर प्रयोग में सामान्य-पथ इंटरफेरोमीटर का उपयोग किया गया, जिसकी भुजा लीड से प्लग की गई मोटी दीवार वाली पाइप से घिरी हुई थी, जबकि दूसरी भुजा स्वतंत्र थी।
*[[सैग्नैक प्रभाव]] से पता चला कि पृथ्वी के कर्षण के कारण होने वाली ईथर वायु का प्रदर्शन नहीं किया जा सकता है।
*प्रकाश के विपथन का अस्तित्व ईथर कर्षण परिकल्पना के साथ असंगत था।
*यह धारणा कि ईथर कर्षण द्रव्यमान के समानुपाती होता है और इस प्रकार केवल संपूर्ण पृथ्वी के संबंध में होता है, माइकलसन-गेल-पियर्सन प्रयोग द्वारा खंडन किया गया था, जिसने पृथ्वी की गति के माध्यम से सैग्नैक प्रभाव का प्रदर्शन किया था।


1904 से पहले किए गए सभी प्रयोगों को समझाने के लिए, लोरेंत्ज़ को संपूर्ण [[लोरेंत्ज़ परिवर्तन]] की शुरुआत करके अपने सिद्धांत को फिर से विस्तारित करने के लिए मजबूर होना पड़ा। हेनरी पोंकारे ने 1905 में घोषणा की कि पूर्ण गति ([[सापेक्षता का सिद्धांत]]) प्रदर्शित करने की असंभवता स्पष्ट रूप से प्रकृति का नियम है।
लॉज ने उस विरोधाभासी स्थिति को व्यक्त किया जिसमें भौतिकविदों ने स्वयं को इस प्रकार पाया: ... किसी भी व्यावहारिक गति पर ... पदार्थ की ईथर पर कोई सराहनीय श्यान पकड़ नहीं होती है। यदि परमाणु पर्याप्त गति से दोलन कर रहे हैं या घूम रहे हैं, तो उन्हें कंपन में फेंकने में सक्षम होना चाहिए; अन्यथा वे प्रकाश या किसी भी प्रकार का विकिरण उत्सर्जित नहीं करेंगे; किन्तु किसी भी स्थिति में वे इसे अपने साथ कर्षण करते हुए, या इसके माध्यम से किसी भी समान गति में प्रतिरोध का सामना करते हुए दिखाई नहीं देते हैं।<ref name=Lodge1909>{{cite book|last=Lodge|first=Oliver, Sir|title=अंतरिक्ष का ईथर|year=1909|publisher=Harper and Brothers|location=New York|url=https://archive.org/details/etherofspace00lodguoft}}</ref>
 
===पूर्ण ईथर ड्रैग का खंडन===
{{Main|Aether drag hypothesis}}
[[File:Lodge's ether machine DE.svg|thumb|200px|लॉज की ईथर मशीन. स्टील डिस्क का व्यास एक गज था। श्वेत प्रकाश को किरण विभाजक द्वारा विभाजित किया गया था और फ्रिंज बनाने के लिए पुन: एकजुट होने से पहले उपकरण के चारों ओर तीन बार दौड़ा।]]यह विचार कि ईथर को पूरी तरह से पृथ्वी के भीतर या उसके आसपास खींचा जा सकता है, जिससे नकारात्मक ईथर बहाव प्रयोगों को समझाया जा सकता है, विभिन्न प्रयोगों द्वारा खंडन किया गया था।
*[[ओलिवर लॉज]] (1893) ने पाया कि एक संवेदनशील [[सामान्य-पथ इंटरफेरोमीटर]] के ऊपर और नीचे तेजी से घूमने वाली स्टील डिस्क एक मापने योग्य फ्रिंज शिफ्ट उत्पन्न करने में विफल रही।
*[[गुस्ताफ हैमर]] (1935) हैमर प्रयोग में एक सामान्य-पथ इंटरफेरोमीटर का उपयोग किया गया, जिसकी एक भुजा सीसे से प्लग की गई मोटी दीवार वाली पाइप से घिरी हुई थी, जबकि दूसरी भुजा स्वतंत्र थी।
*[[सैग्नैक प्रभाव]] से पता चला कि पृथ्वी के खिंचाव के कारण होने वाली ईथर हवा का प्रदर्शन नहीं किया जा सकता है।
*प्रकाश के विपथन का अस्तित्व ईथर ड्रैग परिकल्पना के साथ असंगत था।
*यह धारणा कि ईथर ड्रैग द्रव्यमान के समानुपाती होता है और इस प्रकार केवल संपूर्ण पृथ्वी के संबंध में होता है, माइकलसन-गेल-पियर्सन प्रयोग द्वारा खंडन किया गया था, जिसने पृथ्वी की गति के माध्यम से सैग्नैक प्रभाव का प्रदर्शन किया था।
 
लॉज ने उस विरोधाभासी स्थिति को व्यक्त किया जिसमें भौतिकविदों ने खुद को इस प्रकार पाया: ... किसी भी व्यावहारिक गति पर ... पदार्थ की ईथर पर कोई सराहनीय चिपचिपी पकड़ नहीं होती। यदि परमाणु पर्याप्त गति से दोलन कर रहे हैं या घूम रहे हैं, तो उन्हें कंपन में फेंकने में सक्षम होना चाहिए; अन्यथा वे प्रकाश या किसी भी प्रकार का विकिरण उत्सर्जित नहीं करेंगे; लेकिन किसी भी स्थिति में वे इसे अपने साथ खींचते हुए, या इसके माध्यम से किसी भी समान गति में प्रतिरोध का सामना करते हुए दिखाई नहीं देते हैं।<ref name=Lodge1909>{{cite book|last=Lodge|first=Oliver, Sir|title=अंतरिक्ष का ईथर|year=1909|publisher=Harper and Brothers|location=New York|url=https://archive.org/details/etherofspace00lodguoft}}</ref>




Line 35: Line 33:


=== अवलोकन ===
=== अवलोकन ===
अंततः, [[अल्बर्ट आइंस्टीन]] (1905) ने निष्कर्ष निकाला कि उस समय ज्ञात स्थापित सिद्धांत और तथ्य केवल एक तार्किक सुसंगत प्रणाली बनाते हैं जब अंतरिक्ष और समय की अवधारणाओं को मौलिक संशोधन के अधीन किया जाता है। उदाहरण के लिए:
अंततः, [[अल्बर्ट आइंस्टीन]] (1905) ने निष्कर्ष निकाला कि उस समय ज्ञात स्थापित सिद्धांत और तथ्य केवल तार्किक सुसंगत प्रणाली बनाते हैं जब अंतरिक्ष और समय की अवधारणाओं को मौलिक संशोधन के अधीन किया जाता है। उदाहरण के लिए:


*मैक्सवेल-लोरेंत्ज़ का इलेक्ट्रोडायनामिक्स (स्रोत की गति से प्रकाश की गति की स्वतंत्रता),
*मैक्सवेल-लोरेंत्ज़ का इलेक्ट्रोडायनामिक्स (स्रोत की गति से प्रकाश की गति की स्वतंत्रता),
*नकारात्मक ईथर बहाव प्रयोग (कोई पसंदीदा संदर्भ फ्रेम नहीं),
*ऋणात्मक ईथर धारा प्रयोग (कोई वरीय संदर्भ फ्रेम नहीं),
*चल चुंबक और चालक समस्या (केवल सापेक्ष गति ही प्रासंगिक है),
*चल चुंबक और चालक समस्या (केवल सापेक्ष गति ही प्रासंगिक है),
*फ़िज़ो प्रयोग और प्रकाश का विपथन (दोनों संशोधित वेग वृद्धि और पूर्ण ईथर ड्रैग नहीं होने का संकेत देते हैं)।
*फ़िज़ो प्रयोग और प्रकाश का विपथन (दोनों संशोधित वेग वृद्धि और पूर्ण ईथर कर्षण नहीं होने का संकेत देते हैं)।


परिणाम विशेष सापेक्षता सिद्धांत है, जो संदर्भ के सभी जड़त्वीय फ्रेम में प्रकाश की गति की स्थिरता और सापेक्षता के सिद्धांत पर आधारित है। यहां, लोरेंत्ज़ परिवर्तन अब केवल सहायक परिकल्पनाओं का संग्रह नहीं है, बल्कि मौलिक [[लोरेंत्ज़ समरूपता]] को दर्शाता है और [[क्वांटम इलेक्ट्रोडायनामिक्स]] जैसे सफल सिद्धांतों का आधार बनता है। विशेष सापेक्षता बड़ी संख्या में परीक्षण योग्य भविष्यवाणियाँ प्रदान करती है, जैसे:<ref name=laem />
परिणाम विशेष सापेक्षता सिद्धांत है, जो संदर्भ के सभी जड़त्वीय फ्रेम में प्रकाश की गति की स्थिरता और सापेक्षता के सिद्धांत पर आधारित है। यहां, लोरेंत्ज़ परिवर्तन अब केवल सहायक परिकल्पनाओं का संग्रह नहीं है, किन्तु मौलिक [[लोरेंत्ज़ समरूपता]] को दर्शाता है और [[क्वांटम इलेक्ट्रोडायनामिक्स]] जैसे सफल सिद्धांतों का आधार बनता है। विशेष सापेक्षता बड़ी संख्या में परीक्षण योग्य पूर्वसूचना प्रदान करती है, जैसे:<ref name=laem />


{| class=wikitable
{| class=wikitable
!Principle of relativity||Constancy of the speed of light||[[Time dilation]]
!सापेक्षता का सिद्धांत||प्रकाश की गति की स्थिरता||[[Time dilation|समय का विस्तार]]
|-
|-
|Any uniformly moving observer in an inertial frame cannot determine his "absolute" state of motion by a co-moving experimental arrangement.
|जड़त्वीय फ्रेम में कोई भी समान रूप से गतिमान पर्यवेक्षक सह-गतिशील प्रयोगात्मक व्यवस्था द्वारा अपनी "पूर्ण" गति की स्थिति निर्धारित नहीं कर सकता है।
|In all inertial frames the measured speed of light is equal in all directions ([[isotropy]]), independent of the speed of the source, and cannot be reached by [[mass]]ive bodies.
|सभी जड़त्वीय फ़्रेमों में प्रकाश की मापी गई गति सभी दिशाओं (आइसोट्रॉपी) में समान होती है, जो स्रोत की गति से स्वतंत्र होती है, और बड़े पिंडों द्वारा उस तक नहीं पहुंचा जा सकता है।
|The rate of a clock C (= any periodic process) traveling between two synchronized clocks A and B at rest in an inertial frame is retarded with respect to the two clocks.
|एक जड़त्वीय फ्रेम में विश्राम कर रही दो सिंक्रनाइज़ क्लॉक A और B के मध्य यात्रा करने वाली क्लॉक C(= कोई आवधिक प्रक्रिया) की दर दो क्लॉक के संबंध में मंद है।
|-
|-
|colspan=3|Also other relativistic effects such as [[length contraction]], [[Doppler effect]], [[Relativistic aberration|aberration]] and the experimental predictions of relativistic theories such as the [[Standard Model]] can be measured.
|colspan=3|इसके अतिरिक्त अन्य सापेक्षतावादी प्रभाव जैसे लंबाई संकुचन, डॉपलर प्रभाव, विपथन और मानक मॉडल जैसे सापेक्षतावादी सिद्धांतों की प्रयोगात्मक पूर्वसूचना को भी मापा जा सकता है।
|}
|}


=== मौलिक प्रयोग ===
=== मौलिक प्रयोग ===
Line 60: Line 57:
*मिशेलसन-मॉर्ले प्रयोग, जिसके द्वारा मापने वाले उपकरण की दिशा पर प्रकाश की गति की निर्भरता का परीक्षण किया जा सकता है। यह गतिमान पिंडों की अनुदैर्ध्य और अनुप्रस्थ लंबाई के बीच संबंध स्थापित करता है।
*मिशेलसन-मॉर्ले प्रयोग, जिसके द्वारा मापने वाले उपकरण की दिशा पर प्रकाश की गति की निर्भरता का परीक्षण किया जा सकता है। यह गतिमान पिंडों की अनुदैर्ध्य और अनुप्रस्थ लंबाई के बीच संबंध स्थापित करता है।
*कैनेडी-थॉर्नडाइक प्रयोग, जिसके द्वारा मापने वाले उपकरण के वेग पर प्रकाश की गति की निर्भरता का परीक्षण किया जा सकता है। यह अनुदैर्ध्य लंबाई और गतिशील पिंडों के समय की अवधि के बीच संबंध स्थापित करता है।
*कैनेडी-थॉर्नडाइक प्रयोग, जिसके द्वारा मापने वाले उपकरण के वेग पर प्रकाश की गति की निर्भरता का परीक्षण किया जा सकता है। यह अनुदैर्ध्य लंबाई और गतिशील पिंडों के समय की अवधि के बीच संबंध स्थापित करता है।
*इव्स-स्टिलवेल प्रयोग, जिसके द्वारा [[समय फैलाव]] का सीधे परीक्षण किया जा सकता है।
*इव्स-स्टिलवेल प्रयोग, जिसके द्वारा [[समय फैलाव|समय विस्तार]] का सीधे परीक्षण किया जा सकता है।
 
इन तीन प्रयोगों से और [[आइंस्टीन तुल्यकालन]] का उपयोग करके, संपूर्ण लोरेंत्ज़ परिवर्तन निम्नानुसार है जिसमें <math display="inline">\gamma = 1/\sqrt{1-v^{2}/c^{2}}</math> [[लोरेंत्ज़ कारक]] होना:<ref name=rob />


इन तीन प्रयोगों से और [[आइंस्टीन तुल्यकालन]] का उपयोग करके, संपूर्ण लोरेंत्ज़ परिवर्तन निम्नानुसार है <math display="inline">\gamma = 1/\sqrt{1-v^{2}/c^{2}}</math> [[लोरेंत्ज़ कारक]] होना:<ref name=rob />
<math display="block">x'=\gamma(x-vt),\ y'=y,\ z'=z,\ t'=\gamma\left(t-\frac{vx}{c^{2}}\right)</math>
<math display="block">x'=\gamma(x-vt),\ y'=y,\ z'=z,\ t'=\gamma\left(t-\frac{vx}{c^{2}}\right)</math>
लोरेंत्ज़ परिवर्तन की व्युत्पत्ति के अलावा, इन प्रयोगों का संयोजन भी महत्वपूर्ण है क्योंकि व्यक्तिगत रूप से देखे जाने पर उनकी व्याख्या अलग-अलग तरीकों से की जा सकती है। उदाहरण के लिए, माइकलसन-मॉर्ले जैसे आइसोट्रॉपी प्रयोगों को सापेक्षता सिद्धांत के एक सरल परिणाम के रूप में देखा जा सकता है, जिसके अनुसार कोई भी जड़ता से गतिशील पर्यवेक्षक खुद को आराम की स्थिति में मान सकता है। इसलिए, अपने आप में, एमएम प्रयोग [[उत्सर्जन सिद्धांत (सापेक्षता)]] या एथर ड्रैग परिकल्पना#पूर्ण ईथर ड्रैगिंग जैसे गैलिलियन-अपरिवर्तनीय सिद्धांतों के अनुकूल है, जिसमें कुछ प्रकार के सापेक्षता सिद्धांत भी शामिल हैं। हालाँकि, जब गैलिलियन-अपरिवर्तनीय सिद्धांतों को बाहर करने वाले अन्य प्रयोगों पर विचार किया जाता है (अर्थात इवेस-स्टिलवेल प्रयोग, उत्सर्जन सिद्धांत (सापेक्षता) और ईथर ड्रैग परिकल्पना#पूर्ण ईथर ड्रैगिंग), लोरेंत्ज़-अपरिवर्तनीय सिद्धांत और इस प्रकार विशेष सापेक्षता ही एकमात्र सिद्धांत हैं जो व्यवहार्य बने रहें.
 
लोरेंत्ज़ परिवर्तन की व्युत्पत्ति के अतिरिक्त, इन प्रयोगों का संयोजन भी महत्वपूर्ण है क्योंकि व्यक्तिगत रूप से देखे जाने पर उनकी व्याख्या अलग-अलग विधियों से की जा सकती है। उदाहरण के लिए, माइकलसन-मॉर्ले जैसे आइसोट्रॉपी प्रयोगों को सापेक्षता सिद्धांत के सरल परिणाम के रूप में देखा जा सकता है, जिसके अनुसार कोई भी जड़ता से गतिशील पर्यवेक्षक स्वयं को विश्राम की स्थिति में मान सकता है। इसलिए, अपने आप में, MM प्रयोग [[उत्सर्जन सिद्धांत (सापेक्षता)]] या एथर कर्षण परिकल्पना या पूर्ण ईथर कर्षणिंग जैसे गैलिलियन-अपरिवर्तनीय सिद्धांतों के अनुकूल है, जिसमें कुछ प्रकार के सापेक्षता सिद्धांत भी सम्मिलित हैं। चूंकि, जब गैलिलियन-अपरिवर्तनीय सिद्धांतों को बाहर करने वाले अन्य प्रयोगों पर विचार किया जाता है (अर्थात इवेस-स्टिलवेल प्रयोग, उत्सर्जन सिद्धांत (सापेक्षता) और ईथर कर्षण परिकल्पना या पूर्ण ईथर कर्षणिंग), लोरेंत्ज़-अपरिवर्तनीय सिद्धांत और इस प्रकार विशेष सापेक्षता ही एकमात्र सिद्धांत हैं जो गतिविधि्य बने रहें.


===प्रकाश की गति की स्थिरता===
===प्रकाश की गति की स्थिरता===


==== इंटरफेरोमीटर, रेज़ोनेटर ====
==== इंटरफेरोमीटर, रेज़ोनेटर ====
[[File:MMX with optical resonators.svg|thumb|250px |माइकलसन-मॉर्ले ने क्रायोजेनिक ऑप्टिकल रेज़ोनेटर के साथ प्रयोग किया, जैसा कि मुलर एट अल द्वारा उपयोग किया गया था। (2003), माइकलसन-मॉर्ले प्रयोग#हाल के ऑप्टिकल रेज़ोनेटर प्रयोग देखें]]
[[File:MMX with optical resonators.svg|thumb|250px |माइकलसन-मॉर्ले ने क्रायोजेनिक ऑप्टिकल रेज़ोनेटर के साथ प्रयोग किया, जैसा कि मुलर एट अल द्वारा उपयोग किया गया था। (2003), माइकलसन-मॉर्ले प्रयोग वर्त्तमान के ऑप्टिकल रेज़ोनेटर प्रयोग देखें]]
{{See also|Michelson–Morley experiment#Recent optical resonator experiments|l1=Recent Michelson-Morley experiments|Kennedy–Thorndike experiment#Recent experiments|l2=Recent Kennedy–Thorndike experiments}}
{{See also|माइकलसन-मॉर्ले प्रयोग#वर्तमान के ऑप्टिकल रेज़ोनेटर प्रयोग|l1=वर्तमान के माइकलसन-मॉर्ले प्रयोग|कैनेडी-थॉर्नडाइक प्रयोग#वर्तमान के प्रयोग|l2=वर्तमान कैनेडी-थार्नडाइक प्रयोग}}


प्रकाश की गति की [[आइसोट्रॉपी]] का परीक्षण करने के लिए माइकलसन-मॉर्ले और कैनेडी-थॉर्नडाइक प्रयोगों के आधुनिक संस्करण आयोजित किए गए हैं। माइकलसन-मॉर्ले के विपरीत, कैनेडी-थॉर्नडाइक प्रयोग अलग-अलग बांह की लंबाई का उपयोग करते हैं, और मूल्यांकन कई महीनों तक चलता है। इस तरह, सूर्य के चारों ओर पृथ्वी की परिक्रमा के दौरान विभिन्न वेगों का प्रभाव देखा जा सकता है। [[लेज़र]], मेज़र और [[ ऑप्टिकल गुंजयमान यंत्र ]] का उपयोग किया जाता है, जिससे प्रकाश की गति की किसी भी अनिसोट्रॉपी की संभावना 10 तक कम हो जाती है<sup>−17</sup>स्तर. स्थलीय परीक्षणों के अलावा, कैनेडी-थॉर्नडाइक-प्रयोग के एक रूपांतर के रूप में [[चंद्र लेजर रेंजिंग प्रयोग]] भी आयोजित किए गए हैं।<ref name=will />
प्रकाश की गति की [[आइसोट्रॉपी]] का परीक्षण करने के लिए माइकलसन-मॉर्ले और कैनेडी-थॉर्नडाइक प्रयोगों के आधुनिक संस्करण आयोजित किए गए हैं। माइकलसन-मॉर्ले के विपरीत, कैनेडी-थॉर्नडाइक प्रयोग अलग-अलग बांह की लंबाई का उपयोग करते हैं, और मूल्यांकन अनेक महीनों तक चलता है। इस प्रकार, सूर्य के चारों ओर पृथ्वी की परिक्रमा के समय विभिन्न वेगों का प्रभाव देखा जा सकता है। चूंकि [[लेज़र]], मेज़र और [[ ऑप्टिकल गुंजयमान यंत्र |ऑप्टिकल गुंजयमान यंत्र]] का उपयोग किया जाता है, जिससे प्रकाश की गति की किसी भी अनिसोट्रॉपी की संभावना 10<sup>−17</sup> तक कम हो जाती है स्तर. स्थलीय परीक्षणों के अतिरिक्त, कैनेडी-थॉर्नडाइक-प्रयोग के रूपांतर के रूप में [[चंद्र लेजर रेंजिंग प्रयोग]] भी आयोजित किए गए हैं।<ref name=will />


एक अन्य प्रकार के आइसोट्रॉपी प्रयोग हैं Ives-Stilwell प्रयोग#Mössbauer रोटर प्रयोग|1960 के दशक में Mössbauer रोटर प्रयोग, जिसके द्वारा Mossbauer प्रभाव का उपयोग करके एक घूर्णन डिस्क पर डॉपलर प्रभाव की अनिसोट्रॉपी देखी जा सकती है (उन प्रयोगों का उपयोग भी किया जा सकता है) समय फैलाव मापने के लिए, नीचे देखें)।
एक अन्य प्रकार के आइसोट्रॉपी प्रयोग 1960 के दशक में मोसबाउर रोटर प्रयोग हैं, जिसके द्वारा घूर्णन वाली डिस्क पर डॉपलर प्रभाव की अनिसोट्रॉपी को मोसबाउर प्रभाव का उपयोग करके देखा जा सकता है (उन प्रयोगों का उपयोग समय के विस्तार को मापने के लिए भी किया जा सकता है, नीचे देखें)।


====स्रोत वेग या ऊर्जा पर कोई निर्भरता नहीं====
====स्रोत वेग या ऊर्जा पर कोई निर्भरता नहीं====
[[File:SitterKonstanz.png|thumb|[[डी सिटर डबल स्टार प्रयोग]], बाद में विलुप्त होने के प्रमेय पर विचार के तहत ब्रेचर द्वारा दोहराया गया।]]उत्सर्जन सिद्धांत (सापेक्षता), जिसके अनुसार प्रकाश की गति स्रोत के वेग पर निर्भर करती है, ईथर बहाव प्रयोगों के नकारात्मक परिणाम को स्पष्ट रूप से समझा सकता है। 1960 के दशक के मध्य तक प्रकाश की गति की स्थिरता को निश्चित रूप से प्रयोग द्वारा नहीं दिखाया गया था, क्योंकि 1965 में, जे.जी. फॉक्स ने दिखाया कि इवाल्ड और ओसीन के विलुप्त होने प्रमेय के प्रभावों ने पिछले सभी प्रयोगों के परिणामों को प्रस्तुत किया समय अनिर्णायक है, और इसलिए विशेष सापेक्षता और उत्सर्जन सिद्धांत दोनों के साथ संगत है।<ref name=fox>{{Citation|author=Fox, J. G.|title=Evidence Against Emission Theories|journal=American Journal of Physics|volume=33|issue=1|year=1965|pages=1–17|doi=10.1119/1.1971219|postscript=.|bibcode = 1965AmJPh..33....1F }}</ref><ref>{{Citation|author=Martínez, Alberto A.|journal=Physics in Perspective|title=Ritz, Einstein, and the Emission Hypothesis|pages= 4–28|volume=6|issue=1|doi=10.1007/s00016-003-0195-6|bibcode = 2004PhP.....6....4M|year=2004 |s2cid=123043585}}</ref> हाल के प्रयोगों ने निश्चित रूप से उत्सर्जन मॉडल को खारिज कर दिया है: सबसे पहले फिलिप्पस और फॉक्स (1964) के प्रयोग थे,<ref name=FilippasFox>{{cite journal|last=Filippas|first=T.A.|author2=Fox, J.G.|title=गतिशील स्रोत से गामा किरणों का वेग|journal=Physical Review|year=1964|volume=135|issue=4B|pages=B1071-1075|bibcode = 1964PhRv..135.1071F |doi = 10.1103/PhysRev.135.B1071 }}</ref> गामा किरणों के गतिमान स्रोतों और अल्वेगर एट अल का उपयोग करना। (1964),<ref>{{Citation|author1=Alväger, T. |author2=Farley, F. J. M. |author3=Kjellman, J. |author4=Wallin, L. |title=Test of the second postulate of special relativity in the GeV region|journal=Physics Letters|volume=12|issue=3|year=1964|pages=260–262|doi=10.1016/0031-9163(64)91095-9|postscript=.|bibcode=1964PhL....12..260A}}</ref> जिससे पता चला कि फोटॉनों ने उच्च गति वाले क्षयकारी मेसॉन की गति हासिल नहीं की, जो उनका स्रोत था। इसके अलावा, डी सिटर डबल स्टार प्रयोग (1913) को विलुप्त होने के प्रमेय पर विचार करते हुए ब्रेचर (1977) द्वारा दोहराया गया था, साथ ही स्रोत निर्भरता को भी खारिज कर दिया गया था।<ref>{{Cite journal|author=Brecher, K.|title=क्या प्रकाश की गति स्रोत के वेग से स्वतंत्र है?|journal=Physical Review Letters|volume=39|year=1977|pages=1051–1054|doi=10.1103/PhysRevLett.39.1051|bibcode=1977PhRvL..39.1051B|issue=17}}</ref>
[[File:SitterKonstanz.png|thumb|[[डी सिटर डबल स्टार प्रयोग]], बाद में विलुप्त होने के प्रमेय पर विचार के अधीन ब्रेचर द्वारा दोहराया गया।]]इस प्रकार से उत्सर्जन सिद्धांत (सापेक्षता), जिसके अनुसार प्रकाश की गति स्रोत के वेग पर निर्भर करती है, ईथर धारा प्रयोगों के ऋणात्मक परिणाम को स्पष्ट रूप से समझा सकता है। किन्तु 1960 के दशक के मध्य तक प्रकाश की गति की स्थिरता को निश्चित रूप से प्रयोग द्वारा नहीं दिखाया गया था, क्योंकि 1965 में, जे.जी. फॉक्स ने दिखाया कि इवाल्ड और ओसीन के विलुप्त होने प्रमेय के प्रभावों ने पिछले सभी प्रयोगों के परिणामों को प्रस्तुत किया समय अनिर्णायक है, और इसलिए विशेष सापेक्षता और उत्सर्जन सिद्धांत दोनों के साथ संगत है।<ref name=fox>{{Citation|author=Fox, J. G.|title=Evidence Against Emission Theories|journal=American Journal of Physics|volume=33|issue=1|year=1965|pages=1–17|doi=10.1119/1.1971219|postscript=.|bibcode = 1965AmJPh..33....1F }}</ref><ref>{{Citation|author=Martínez, Alberto A.|journal=Physics in Perspective|title=Ritz, Einstein, and the Emission Hypothesis|pages= 4–28|volume=6|issue=1|doi=10.1007/s00016-003-0195-6|bibcode = 2004PhP.....6....4M|year=2004 |s2cid=123043585}}</ref> वर्तमान के प्रयोगों ने निश्चित रूप से उत्सर्जन मॉडल को बहिष्कृत कर दिया है: सबसे पहले फिलिप्पस और फॉक्स (1964) के प्रयोग थे,<ref name=FilippasFox>{{cite journal|last=Filippas|first=T.A.|author2=Fox, J.G.|title=गतिशील स्रोत से गामा किरणों का वेग|journal=Physical Review|year=1964|volume=135|issue=4B|pages=B1071-1075|bibcode = 1964PhRv..135.1071F |doi = 10.1103/PhysRev.135.B1071 }}</ref> गामा किरणों के गतिमान स्रोतों और अल्वेगर एट अल (1964), का उपयोग करना था। <ref>{{Citation|author1=Alväger, T. |author2=Farley, F. J. M. |author3=Kjellman, J. |author4=Wallin, L. |title=Test of the second postulate of special relativity in the GeV region|journal=Physics Letters|volume=12|issue=3|year=1964|pages=260–262|doi=10.1016/0031-9163(64)91095-9|postscript=.|bibcode=1964PhL....12..260A}}</ref> जिससे पता चला कि फोटॉनों ने उच्च गति वाले क्षयकारी मेसॉन की गति प्राप्त नहीं की, जो उनका स्रोत था। इसके अतिरिक्त, डी सिटर डबल स्टार प्रयोग (1913) को विलुप्त होने के प्रमेय पर विचार करते हुए ब्रेचर (1977) द्वारा दोहराया गया था, इसी के साथ ही स्रोत निर्भरता को भी बहिष्कृत कर दिया गया था।<ref>{{Cite journal|author=Brecher, K.|title=क्या प्रकाश की गति स्रोत के वेग से स्वतंत्र है?|journal=Physical Review Letters|volume=39|year=1977|pages=1051–1054|doi=10.1103/PhysRevLett.39.1051|bibcode=1977PhRvL..39.1051B|issue=17}}</ref>
गामा-किरण विस्फोटों के अवलोकन से यह भी पता चला कि प्रकाश की गति प्रकाश किरणों की आवृत्ति और ऊर्जा से स्वतंत्र है।<ref>{{cite journal |author=Fermi LAT Collaboration|title=क्वांटम गुरुत्व प्रभाव से उत्पन्न होने वाली प्रकाश की गति की भिन्नता पर एक सीमा|journal=Nature|volume=462|issue=7271 |year=2009|pages=331–334|doi=10.1038/nature08574|arxiv=0908.1832|pmid=19865083|bibcode = 2009Natur.462..331A |s2cid=205218977}}</ref>
इस प्रकार से गामा-किरण विस्फोटों के अवलोकन से यह भी पता चला कि प्रकाश की गति प्रकाश किरणों की आवृत्ति और ऊर्जा से स्वतंत्र है।<ref>{{cite journal |author=Fermi LAT Collaboration|title=क्वांटम गुरुत्व प्रभाव से उत्पन्न होने वाली प्रकाश की गति की भिन्नता पर एक सीमा|journal=Nature|volume=462|issue=7271 |year=2009|pages=331–334|doi=10.1038/nature08574|arxiv=0908.1832|pmid=19865083|bibcode = 2009Natur.462..331A |s2cid=205218977}}</ref>




====प्रकाश की एकतरफ़ा गति====
====प्रकाश की एकपक्षीय गति====
{{Main|One-way speed of light}}
{{Main|प्रकाश की एकपक्षीय गति}}


एक-तरफ़ा मापों की एक श्रृंखला शुरू की गई, वे सभी प्रकाश की गति की आइसोट्रॉपी की पुष्टि करते हैं।<ref name=faq />हालाँकि, केवल प्रकाश की दो-तरफ़ा गति (ए से बी से वापस ए तक) को स्पष्ट रूप से मापा जा सकता है, क्योंकि एक-तरफ़ा गति एक साथ की परिभाषा पर निर्भर करती है और इसलिए सिंक्रनाइज़ेशन की विधि पर निर्भर करती है। आइंस्टीन सिंक्रोनाइज़ेशन कन्वेंशन एक-तरफ़ा गति को दो-तरफ़ा गति के बराबर बनाता है। हालाँकि, ऐसे कई मॉडल हैं जिनमें प्रकाश की आइसोट्रोपिक दो-तरफ़ा गति होती है, जिसमें अलग-अलग सिंक्रनाइज़ेशन योजनाओं को चुनकर एक-तरफ़ा गति को अनिसोट्रोपिक किया जाता है। वे प्रयोगात्मक रूप से विशेष सापेक्षता के समतुल्य हैं क्योंकि इन सभी मॉडलों में चलती घड़ियों के समय विस्तार जैसे प्रभाव शामिल हैं, जो किसी भी मापने योग्य अनिसोट्रॉपी की भरपाई करते हैं। हालाँकि, आइसोट्रोपिक दो-तरफा गति वाले सभी मॉडलों में से केवल विशेष सापेक्षता ही भौतिकविदों के भारी बहुमत के लिए स्वीकार्य है क्योंकि अन्य सभी सिंक्रनाइज़ेशन बहुत अधिक जटिल हैं, और वे अन्य मॉडल (जैसे [[लोरेंत्ज़ ईथर सिद्धांत]]) चरम और अविश्वसनीय मान्यताओं पर आधारित हैं कुछ गतिशील प्रभावों के संबंध में, जिनका उद्देश्य पसंदीदा फ्रेम को अवलोकन से छिपाना है।
एकपक्षीय मापों की श्रृंखला प्रारंभ की गई, वे सभी प्रकाश की गति की आइसोट्रॉपी की पुष्टि करते हैं।<ref name=faq /> चूंकि, केवल प्रकाश की दो-तरफ़ा गति (a से b से वापस a तक) को स्पष्ट रूप से मापा जा सकता है, क्योंकि एकपक्षीय गति साथ की परिभाषा पर निर्भर करती है और इसलिए सिंक्रनाइज़ेशन की विधि पर निर्भर करती है। इस प्रकार से आइंस्टीन सिंक्रोनाइज़ेशन कन्वेंशन एकपक्षीय गति को दो-पक्षीय गति के समान बनाता है। चूंकि, ऐसे अनेक मॉडल हैं जिनमें प्रकाश की आइसोट्रोपिक दो-तरफ़ा गति होती है, जिसमें अलग-अलग सिंक्रनाइज़ेशन योजनाओं को चुनकर एकपक्षीय गति को अनिसोट्रोपिक किया जाता है। वे प्रयोगात्मक रूप से विशेष सापेक्षता के समतुल्य हैं क्योंकि इन सभी मॉडलों में चलती क्लॉक के समय विस्तार जैसे प्रभाव सम्मिलित हैं, जो किसी भी मापने योग्य अनिसोट्रॉपी की भरपाई करते हैं। चूंकि, आइसोट्रोपिक दो-तरफा गति वाले सभी मॉडलों में से केवल विशेष सापेक्षता ही भौतिकविदों के भारी बहुमत के लिए स्वीकार्य है क्योंकि अन्य सभी सिंक्रनाइज़ेशन बहुत अधिक सम्मिश्र हैं, और वे अन्य मॉडल (जैसे [[लोरेंत्ज़ ईथर सिद्धांत]]) चरम और अविश्वसनीय मान्यताओं पर आधारित हैं कुछ गतिशील प्रभावों के संबंध में, जिनका उद्देश्य वरीय फ्रेम को अवलोकन से छिपाना है।


=== द्रव्यमान, ऊर्जा और स्थान की आइसोट्रॉपी ===
=== द्रव्यमान, ऊर्जा और स्थान की आइसोट्रॉपी ===
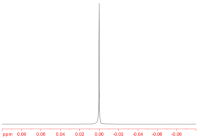
[[File:Lithium-7-NMR spectrum of LiCl (1M) in D2O.gif|thumb|200px|<sup>7</sup>D में LiCl (1M) का Li-NMR स्पेक्ट्रम<sub>2</sub>O. लिथियम के इस आइसोटोप की तेज, बिना विभाजित एनएमआर रेखा द्रव्यमान और स्थान की आइसोट्रॉपी का प्रमाण है।]]
[[File:Lithium-7-NMR spectrum of LiCl (1M) in D2O.gif|thumb|200px|D<sub>2</sub>O में LiCl (1M) का <sup>7</sup>Li-NMR स्पेक्ट्रम. लिथियम के इस आइसोटोप की तेज, बिना विभाजित एनएमआर रेखा द्रव्यमान और स्थान की आइसोट्रॉपी का प्रमाण है।]]
{{See also|Hughes–Drever experiment}}
{{See also|ह्यूजेस-ड्रेवर प्रयोग}}


घड़ी-तुलना प्रयोग (आवधिक प्रक्रियाओं और आवृत्तियों को घड़ियों के रूप में माना जा सकता है) जैसे ह्यूजेस-ड्रेवर प्रयोग [[लोरेंट्ज़ इनवेरिएंस]] के कड़े परीक्षण प्रदान करते हैं। वे माइकलसन-मॉर्ले की तरह फोटॉन क्षेत्र तक ही सीमित नहीं हैं, बल्कि [[परमाणु नाभिक]] की जमीनी स्थिति को मापकर सीधे द्रव्यमान, ऊर्जा या स्थान की किसी भी अनिसोट्रॉपी का निर्धारण करते हैं। ऐसी अनिसोट्रॉपियों की ऊपरी सीमा 10 है<sup>−33</sup> [[GeV]] प्रदान किया गया है। इस प्रकार ये प्रयोग लोरेंत्ज़ इनवेरिएंस के अब तक किए गए सबसे सटीक सत्यापनों में से एक हैं।<ref name=mattingly /><ref name=will />
क्लॉक-तुलना प्रयोग (आवधिक प्रक्रियाओं और आवृत्तियों को क्लॉक के रूप में माना जा सकता है) जैसे ह्यूजेस-ड्रेवर प्रयोग [[लोरेंट्ज़ इनवेरिएंस]] के कड़े परीक्षण प्रदान करते हैं। वे माइकलसन-मॉर्ले की तरह फोटॉन क्षेत्र तक ही सीमित नहीं हैं, किन्तु [[परमाणु नाभिक]] की भूमि स्थिति को मापकर सीधे द्रव्यमान, ऊर्जा या स्थान की किसी भी अनिसोट्रॉपी का निर्धारण करते हैं। चूंकि 10<sup>−33</sup> [[GeV]] की ऐसी अनिसोट्रॉपी की ऊपरी सीमा प्रदान की गई है। इस प्रकार ये प्रयोग लोरेंत्ज़ इनवेरिएंस के अब तक किए गए सबसे स्पष्ट सत्यापनों में से हैं।<ref name=mattingly /><ref name=will />




===समय फैलाव और लंबाई संकुचन===
===समय विस्तार और लंबाई संकुचन===
[[File:Ives-Stilwell experiment.svg|thumb|250px|इवेस-स्टिलवेल प्रयोग (1938)।)]]
[[File:Ives-Stilwell experiment.svg|thumb|250px|इवेस-स्टिलवेल प्रयोग (1938)।)]]
   {{Main|Ives–Stilwell experiment|Experimental testing of time dilation|Length contraction#Experimental verifications|l3 = Confirmations of length contraction}}
   {{Main|इव्स-स्टिलवेल प्रयोग|समय प्रसार का प्रायोगिक परीक्षण|लंबाई संकुचन#प्रायोगिक सत्यापन|l3 = लंबाई संकुचन की पुष्टि}}


[[अनुप्रस्थ डॉपलर प्रभाव]] और परिणामस्वरूप समय फैलाव को पहली बार इवेस-स्टिलवेल प्रयोग (1938) में सीधे देखा गया था। Ives-Stilwell प्रयोग#आधुनिक प्रयोग|[[संतृप्त स्पेक्ट्रोस्कोपी]] का उपयोग करके भारी आयन भंडारण रिंगों में आधुनिक Ives-Stilwell प्रयोगों में, सापेक्षतावादी भविष्यवाणी से समय फैलाव का अधिकतम मापा विचलन ≤10 तक सीमित कर दिया गया है<sup>−8</sup>. समय फैलाव की अन्य पुष्टियों में इवेस-स्टिलवेल प्रयोग#मोसबाउर रोटर प्रयोग|मोसबाउर रोटर प्रयोग शामिल हैं जिसमें [[गामा किरण]]ों को एक घूर्णन डिस्क के मध्य से डिस्क के किनारे पर एक रिसीवर तक भेजा गया था, ताकि अनुप्रस्थ डॉपलर प्रभाव का मूल्यांकन किया जा सके मोसबाउर प्रभाव के माध्यम से। वायुमंडल और कण त्वरक में म्यूऑन के जीवनकाल को मापकर, गतिमान कणों के समय विस्तार को भी सत्यापित किया गया। दूसरी ओर, हाफेल-कीटिंग प्रयोग ने [[जुड़वां विरोधाभास]] के समाधान की पुष्टि की, यानी कि ए से बी से वापस ए पर जाने वाली घड़ी प्रारंभिक घड़ी के संबंध में मंद है। हालाँकि, इस प्रयोग में सामान्य सापेक्षता के प्रभाव भी एक आवश्यक भूमिका निभाते हैं।
[[अनुप्रस्थ डॉपलर प्रभाव]] और परिणामस्वरूप समय विस्तार को पहली बार इवेस-स्टिलवेल प्रयोग (1938) में सीधे देखा गया था। [[संतृप्त स्पेक्ट्रोस्कोपी]] का उपयोग करके भारी आयन भंडारण वलय में आधुनिक इवेस-स्टिलवेल प्रयोगों में, सापेक्षतावादी पूर्वानुमान से समय फैलाव का अधिकतम मापा विचलन ≤10<sup>−8</sup> तक सीमित कर दिया गया है। समय विस्तार की अन्य पुष्टियों में इवेस-स्टिलवेल मोसबाउर रोटर प्रयोग प्रयोग सम्मिलित हैं जिसमें [[गामा किरण|गामा किरणों]] को घूर्णन डिस्क के मध्य से डिस्क के किनारे पर रिसीवर तक भेजा गया था, जिससे अनुप्रस्थ डॉपलर प्रभाव का मूल्यांकन मोसबाउर प्रभाव के माध्यम से किया जा सके। वायुमंडल और कण त्वरक में म्यूऑन के जीवनकाल को मापकर, गतिमान कणों के समय विस्तार को भी सत्यापित किया गया। किन्तु दूसरी ओर, हाफेल-कीटिंग प्रयोग ने [[जुड़वां विरोधाभास|ट्विन पैराडॉक्स]] के समाधान की पुष्टि की, यानी कि a से b से वापस a पर जाने वाली क्लॉक प्रारंभिक क्लॉक के संबंध में मंद है। चूंकि, इस प्रयोग में सामान्य सापेक्षता के प्रभाव भी आवश्यक भूमिका निभाते हैं।


व्यवहार में लंबाई संकुचन की प्रत्यक्ष पुष्टि प्राप्त करना कठिन है क्योंकि प्रेक्षित कणों के आयाम लुप्त हो रहे हैं। हालाँकि, अप्रत्यक्ष पुष्टियाँ हैं; उदाहरण के लिए, भारी [[आयन]]ों के टकराने के व्यवहार को केवल तभी समझाया जा सकता है जब लोरेंत्ज़ संकुचन के कारण उनके बढ़े हुए घनत्व पर विचार किया जाए। संकुचन से गति की दिशा के लंबवत कूलम्ब के नियम की तीव्रता में भी वृद्धि होती है, जिसका प्रभाव पहले ही देखा जा चुका है। परिणामस्वरूप, कण त्वरक में प्रयोग करते समय समय फैलाव और लंबाई संकुचन दोनों पर विचार किया जाना चाहिए।
इस प्रकार से गतिविधि में लंबाई संकुचन की प्रत्यक्ष पुष्टि प्राप्त करना कठिन है क्योंकि प्रेक्षित कणों के आयाम लुप्त हो रहे हैं। चूंकि, अप्रत्यक्ष पुष्टियाँ हैं; उदाहरण के लिए, भारी [[आयन|आयनो]] के टकराने के गतिविधि को केवल तभी समझाया जा सकता है जब लोरेंत्ज़ संकुचन के कारण उनके बढ़े हुए घनत्व पर विचार किया जाए। संकुचन से गति की दिशा के लंबवत कूलम्ब के नियम की तीव्रता में भी वृद्धि होती है, जिसका प्रभाव पहले ही देखा जा चुका है। परिणामस्वरूप, कण त्वरक में प्रयोग करते समय समय विस्तार और लंबाई संकुचन दोनों पर विचार किया जाना चाहिए।


===सापेक्षिक संवेग और ऊर्जा===
===सापेक्षिक संवेग और ऊर्जा===
[[File:Bucherer expt-en.svg|thumb|right|β के विशिष्ट आवेश e/m को मापने के लिए ब्यूचरर का प्रायोगिक सेटअप<sup>−</sup>इलेक्ट्रॉन अपनी गति v/c के फलन के रूप में। (चुंबकीय क्षेत्र एच के संबंध में एक कोण α पर, इसके केंद्र में बीटा-स्रोत के साथ एक गोलाकार संधारित्र की धुरी के माध्यम से क्रॉस-सेक्शन)]]
[[File:Bucherer expt-en.svg|thumb|right|β के विशिष्ट आवेश e/m को मापने के लिए ब्यूचरर का प्रायोगिक सेटअप<sup>−</sup>इलेक्ट्रॉन अपनी गति v/c के फलन के रूप में। (चुंबकीय क्षेत्र एच के संबंध में कोण α पर, इसके केंद्र में बीटा-स्रोत के साथ वृत्ताकार संधारित्र की धुरी के माध्यम से क्रॉस-सेक्शन)]]
{{Main|Tests of relativistic energy and momentum|Kaufmann–Bucherer–Neumann experiments}}
{{Main|सापेक्षिक ऊर्जा और संवेग का परीक्षण|कॉफ़मैन-बुचेरर-न्यूमैन प्रयोग}}


1901 से प्रारंभ होकर, [[इलेक्ट्रॉन]]ों के द्रव्यमान की वेग निर्भरता को प्रदर्शित करने के उद्देश्य से मापों की एक श्रृंखला आयोजित की गई थी। परिणामों ने वास्तव में ऐसी निर्भरता दिखाई लेकिन प्रतिस्पर्धी सिद्धांतों के बीच अंतर करने के लिए आवश्यक सटीकता पर लंबे समय तक विवाद रहा। अंततः, विशेष सापेक्षता को छोड़कर सभी प्रतिस्पर्धी मॉडलों को निश्चित रूप से खारिज करना संभव हो गया।
इस प्रकार से 1901 से प्रारंभ होकर, [[इलेक्ट्रॉन|इलेक्ट्रॉनो]] के द्रव्यमान की वेग निर्भरता को प्रदर्शित करने के उद्देश्य से मापों की श्रृंखला आयोजित की गई थी। परिणामों ने वास्तव में ऐसी निर्भरता दिखाई किन्तु प्रतिस्पर्धी सिद्धांतों के बीच अंतर करने के लिए आवश्यक स्पष्टतः पर लंबे समय तक विवाद रहा है। अंततः, विशेष सापेक्षता को छोड़कर सभी प्रतिस्पर्धी मॉडलों को निश्चित रूप से बहिष्कृत करना संभव हो गया था।


आज, [[सापेक्षतावादी भारी आयन कोलाइडर]] जैसे [[कण त्वरक]] में विशेष सापेक्षता की भविष्यवाणियों की नियमित रूप से पुष्टि की जाती है। उदाहरण के लिए, सापेक्षतावादी [[गति]] और ऊर्जा की वृद्धि को न केवल सटीक रूप से मापा जाता है, बल्कि [[साइक्लोट्रॉन]] और [[ सिंक्रोटॉन ]] आदि के व्यवहार को समझने के लिए भी आवश्यक है, जिसके द्वारा कणों को प्रकाश की गति के करीब त्वरित किया जाता है।
वर्तमान, [[सापेक्षतावादी भारी आयन कोलाइडर]] जैसे [[कण त्वरक]] में विशेष सापेक्षता की पूर्वानुमानो की नियमित रूप से पुष्टि की जाती है। उदाहरण के लिए, सापेक्षतावादी [[गति]] और ऊर्जा की वृद्धि को न केवल स्पष्ट रूप से मापा जाता है, किन्तु [[साइक्लोट्रॉन]] और [[ सिंक्रोटॉन |सिंक्रोटॉन]] आदि के गतिविधि को समझने के लिए भी आवश्यक है, जिसके द्वारा कणों को प्रकाश की गति के समीप त्वरित किया जाता है।


===सैग्नैक और फ़िज़ो===
===सैग्नैक और फ़िज़ो===
[[File:Sagnac-Interferometer.png|thumb|मूल सैग्नैक इंटरफेरोमीटर]]
[[File:Sagnac-Interferometer.png|thumb|मूल सैग्नैक इंटरफेरोमीटर]]
{{Main|Sagnac interferometer|Fizeau experiment}}
{{Main|सैग्नैक इंटरफेरोमीटर|फ़िज़ो प्रयोग}}
विशेष सापेक्षता यह भी भविष्यवाणी करती है कि एक घूमते हुए बंद पथ (उदाहरण के लिए एक लूप) के चारों ओर विपरीत दिशाओं में यात्रा करने वाली दो प्रकाश किरणों को गतिमान उत्सर्जक/रिसीवर पर वापस आने के लिए अलग-अलग उड़ान समय की आवश्यकता होती है (यह प्रकाश की गति की स्वतंत्रता का परिणाम है) स्रोत का वेग, ऊपर देखें)। यह प्रभाव वास्तव में देखा गया और इसे सैग्नैक प्रभाव कहा जाता है। वर्तमान में, इस आशय पर विचार कई प्रायोगिक सेटअपों और [[ग्लोबल पोजिशनिंग सिस्टम]] के सही कामकाज के लिए आवश्यक है।
विशेष सापेक्षता यह भी पूर्वानुमान करती है कि घूमते हुए बंद पथ (उदाहरण के लिए लूप) के चारों ओर विपरीत दिशाओं में यात्रा करने वाली दो प्रकाश किरणों को गतिमान उत्सर्जक/रिसीवर पर वापस आने के लिए अलग-अलग उड़ान समय की आवश्यकता होती है (यह प्रकाश की गति की स्वतंत्रता का परिणाम है) स्रोत का वेग, ऊपर देखें)। यह प्रभाव वास्तव में देखा गया और इसे सैग्नैक प्रभाव कहा जाता है। वर्तमान में, इस आशय पर विचार अनेक प्रायोगिक सेटअपों और [[ग्लोबल पोजिशनिंग सिस्टम]] के सही कार्यप्रणाली के लिए आवश्यक है।


यदि ऐसे प्रयोग गतिशील मीडिया (उदाहरण के लिए पानी, या ग्लास [[ प्रकाशित तंतु ]]) में आयोजित किए जाते हैं, तो फ़्रेज़नेल के ड्रैगिंग गुणांक पर विचार करना भी आवश्यक है जैसा कि फ़िज़ो प्रयोग द्वारा प्रदर्शित किया गया है। हालाँकि इस प्रभाव को शुरू में लगभग स्थिर ईथर या आंशिक ईथर ड्रैग का प्रमाण देने के रूप में समझा गया था, इसे वेग-जोड़ सूत्र#सापेक्षता के विशेष सिद्धांत का उपयोग करके विशेष सापेक्षता के साथ आसानी से समझाया जा सकता है।
यदि ऐसे प्रयोग गतिशील मीडिया (उदाहरण के लिए जल, या ग्लास [[ प्रकाशित तंतु |प्रकाशित तंतु]] ) में आयोजित किए जाते हैं, तो फ़्रेज़नेल के कर्षणिंग गुणांक पर विचार करना भी आवश्यक है जैसा कि फ़िज़ो प्रयोग द्वारा प्रदर्शित किया गया है। चूंकि इस प्रभाव को प्रारंभ में लगभग स्थिर ईथर या आंशिक ईथर कर्षण का प्रमाण देने के रूप में समझा गया था, इसे वेग-जोड़ सूत्र या सापेक्षता के विशेष सिद्धांत का उपयोग करके विशेष सापेक्षता के साथ सरलता से समझाया जा सकता है।


===परीक्षण सिद्धांत===
===परीक्षण सिद्धांत===
{{Main|Test theories of special relativity}}
{{Main|विशेष सापेक्षता के सिद्धांतों का परीक्षण करें}}
मानक समीकरणों में कुछ पैरामीटर जोड़कर लोरेंत्ज़ उल्लंघन प्रयोगों में संभावित सकारात्मक परिणाम का आकलन करने के लिए कई परीक्षण सिद्धांत विकसित किए गए हैं। इनमें रॉबर्टसन-मंसौरी-सेक्सएल फ्रेमवर्क (आरएमएस) और [[ मानक-मॉडल विस्तार ]] (एसएमई) शामिल हैं। आरएमएस में लंबाई संकुचन और समय फैलाव के संबंध में तीन परीक्षण योग्य पैरामीटर हैं। उससे, प्रकाश की गति की किसी भी अनिसोट्रॉपी का आकलन किया जा सकता है। दूसरी ओर, एसएमई में न केवल विशेष सापेक्षता के लिए, बल्कि [[मानक मॉडल]] और सामान्य सापेक्षता के लिए भी कई लोरेंत्ज़ उल्लंघन पैरामीटर शामिल हैं; इस प्रकार इसमें परीक्षण योग्य मापदंडों की बहुत बड़ी संख्या है।
मानक समीकरणों में कुछ पैरामीटर जोड़कर लोरेंत्ज़ उल्लंघन प्रयोगों में संभावित धनात्मक परिणाम का आकलन करने के लिए अनेक परीक्षण सिद्धांत विकसित किए गए हैं। इनमें रॉबर्टसन-मंसौरी-सेक्सएल फ्रेमवर्क (आरएमएस) और [[ मानक-मॉडल विस्तार |मानक-मॉडल विस्तार]] (एसएमई) सम्मिलित हैं। इस प्रकार से आरएमएस में लंबाई संकुचन और समय विस्तार के संबंध में तीन परीक्षण योग्य पैरामीटर हैं। उससे, प्रकाश की गति की किसी भी अनिसोट्रॉपी का आकलन किया जा सकता है। दूसरी ओर, एसएमई में न केवल विशेष सापेक्षता के लिए, किन्तु [[मानक मॉडल]] और सामान्य सापेक्षता के लिए भी अनेक लोरेंत्ज़ उल्लंघन पैरामीटर सम्मिलित हैं; इस प्रकार इसमें परीक्षण योग्य मापदंडों की बहुत बड़ी संख्या है।


===अन्य आधुनिक परीक्षण===
===अन्य आधुनिक परीक्षण===
{{Main|Modern searches for Lorentz violation}}
{{Main|लोरेंत्ज़ उल्लंघन के लिए आधुनिक खोजें}}
हाल के वर्षों में [[क्वांटम गुरुत्व]] के विभिन्न मॉडलों से संबंधित विकास के कारण, लोरेंत्ज़ इनवेरिएंस के विचलन (संभवतः उन मॉडलों से अनुसरण करते हुए) फिर से प्रयोगवादियों का लक्ष्य हैं। क्योंकि स्थानीय लोरेंत्ज़ इनवेरिएंस (एलएलआई) भी स्वतंत्र रूप से गिरने वाले फ्रेम में रहता है, कमजोर सम[[तुल्यता सिद्धांत]] से संबंधित प्रयोग भी परीक्षणों के इस वर्ग से संबंधित हैं। परिणामों का विश्लेषण आरएमएस जैसे परीक्षण सिद्धांतों (जैसा कि ऊपर बताया गया है) या, अधिक महत्वपूर्ण बात, एसएमई द्वारा किया जाता है।<ref name=mattingly />
वर्तमान के वर्षों में [[क्वांटम गुरुत्व]] के विभिन्न मॉडलों से संबंधित विकास के कारण, लोरेंत्ज़ इनवेरिएंस के विचलन (संभवतः उन मॉडलों से अनुसरण करते हुए) फिर से प्रयोगवादियों का लक्ष्य हैं। क्योंकि स्थानीय लोरेंत्ज़ इनवेरिएंस (एलएलआई) भी स्वतंत्र रूप से गिरने वाले फ्रेम में रहता है, अशक्त सम[[तुल्यता सिद्धांत]] से संबंधित प्रयोग भी परीक्षणों के इस वर्ग से संबंधित हैं। परिणामों का विश्लेषण आरएमएस जैसे परीक्षण सिद्धांतों (जैसा कि ऊपर बताया गया है) या, अधिक महत्वपूर्ण बात, एसएमई द्वारा किया जाता है।<ref name=mattingly />


*माइकलसन-मॉर्ले और कैनेडी-थॉर्नडाइक प्रयोगों की उल्लिखित विविधताओं के अलावा, [[प्रोटोन]] और [[न्यूट्रॉन]] क्षेत्र में आइसोट्रॉपी परीक्षणों के लिए ह्यूजेस-ड्रेवर प्रयोग जारी हैं। इलेक्ट्रॉन क्षेत्र में संभावित विचलन का पता लगाने के लिए, [[स्पिन ध्रुवीकरण]] | स्पिन-ध्रुवीकृत [[मरोड़ संतुलन]] का उपयोग किया जाता है।
*माइकलसन-मॉर्ले और कैनेडी-थॉर्नडाइक प्रयोगों की उल्लिखित विविधताओं के अतिरिक्त, [[प्रोटोन]] और [[न्यूट्रॉन]] क्षेत्र में आइसोट्रॉपी परीक्षणों के लिए ह्यूजेस-ड्रेवर प्रयोग जारी हैं। इलेक्ट्रॉन क्षेत्र में संभावित विचलन का पता लगाने के लिए, [[स्पिन ध्रुवीकरण]] [[मरोड़ संतुलन|आघूर्ण संतुलन]] का उपयोग किया जाता है।
*[[लिथियम]] के डॉपलर प्रभाव के अवलोकन से [[मैक्स प्लैंक इंस्टीट्यूट फॉर न्यूक्लियर फिजिक्स]] में टीएसआर जैसे भारी आयन भंडारण रिंगों में समय फैलाव की पुष्टि की जाती है, और वे प्रयोग इलेक्ट्रॉन, प्रोटॉन और फोटॉन क्षेत्र में मान्य हैं।
*[[लिथियम]] के डॉपलर प्रभाव के अवलोकन से [[मैक्स प्लैंक इंस्टीट्यूट फॉर न्यूक्लियर फिजिक्स]] में टीएसआर जैसे भारी आयन संचय वलय में समय विस्तार की पुष्टि की जाती है, और वे प्रयोग इलेक्ट्रॉन, प्रोटॉन और फोटॉन क्षेत्र में मान्य हैं।
*अन्य प्रयोग इलेक्ट्रोस्टैटिक और चुंबकीय क्षेत्रों में [[साइक्लोट्रॉन गति]] और [[लार्मोर प्रीसेशन]] के विचलन का निरीक्षण करने के लिए [[ पेनिंग जाल ]] का उपयोग करते हैं।
*अन्य प्रयोग इलेक्ट्रोस्टैटिक और चुंबकीय क्षेत्रों में [[साइक्लोट्रॉन गति]] और [[लार्मोर प्रीसेशन]] के विचलन का निरीक्षण करने के लिए [[ पेनिंग जाल |पेनिंग जाल]] का उपयोग करते हैं।
*[[सीपीटी समरूपता]] से संभावित विचलन (जिसका उल्लंघन लोरेंत्ज़ इनवेरिएंस के उल्लंघन का भी प्रतिनिधित्व करता है) तटस्थ [[मेसन]], पेनिंग ट्रैप और म्यूऑन के प्रयोगों में निर्धारित किया जा सकता है, लोरेंत्ज़ उल्लंघन के एंटीमैटर टेस्ट देखें।
*[[सीपीटी समरूपता]] से संभावित विचलन (जिसका उल्लंघन लोरेंत्ज़ इनवेरिएंस के उल्लंघन का भी प्रतिनिधित्व करता है) तटस्थ [[मेसन]], पेनिंग ट्रैप और म्यूऑन के प्रयोगों में निर्धारित किया जा सकता है, लोरेंत्ज़ उल्लंघन के एंटीमैटर टेस्ट देखें।
*खगोलीय परीक्षण फोटॉन के उड़ान समय के संबंध में आयोजित किए जाते हैं, जहां लोरेंत्ज़ उल्लंघन करने वाले कारक असामान्य फैलाव और द्विअपवर्तन का कारण बन सकते हैं, जिससे [[ऊर्जा]], [[आवृत्ति]] या ध्रुवीकरण (तरंगों) पर फोटॉन की निर्भरता हो सकती है।
*खगोलीय परीक्षण फोटॉन के उड़ान समय के संबंध में आयोजित किए जाते हैं, जहां लोरेंत्ज़ उल्लंघन करने वाले कारक असामान्य विस्तार और द्विअपवर्तन का कारण बन सकते हैं, जिससे [[ऊर्जा]], [[आवृत्ति]] या ध्रुवीकरण (तरंगों) पर फोटॉन की निर्भरता हो सकती है।
*दूरस्थ खगोलीय पिंडों की [[दहलीज ऊर्जा]] के संबंध में, बल्कि स्थलीय स्रोतों के संबंध में, लोरेंत्ज़ उल्लंघन से उस ऊर्जा से होने वाली प्रक्रियाओं के लिए मानक मूल्यों में परिवर्तन हो सकता है, जैसे वैक्यूम [[चेरेनकोव विकिरण]], या [[सिंक्रोट्रॉन विकिरण]] में संशोधन।
*दूरस्थ खगोलीय पिंडों की [[दहलीज ऊर्जा|प्रारम्भ ऊर्जा]] के संबंध में, किन्तु स्थलीय स्रोतों के संबंध में, लोरेंत्ज़ उल्लंघन से उस ऊर्जा से उत्पन्न होने वाली प्रक्रियाओं जैसे वैक्यूम [[चेरेनकोव विकिरण]], या [[सिंक्रोट्रॉन विकिरण]] के संशोधनों के लिए मानक मूल्यों में परिवर्तन हो सकता है।
*[[न्यूट्रिनो दोलन]] ([[लोरेंत्ज़-उल्लंघन न्यूट्रिनो दोलन]] देखें) और न्यूट्रिनो की गति (न्यूट्रिनो गति की माप देखें) की संभावित लोरेंत्ज़ उल्लंघन के लिए जांच की जा रही है।
*[[न्यूट्रिनो दोलन]] ([[लोरेंत्ज़-उल्लंघन न्यूट्रिनो दोलन]] देखें) और न्यूट्रिनो की गति (न्यूट्रिनो गति की माप देखें) की संभावित लोरेंत्ज़ उल्लंघन के लिए जांच की जा रही है।
*खगोलीय अवलोकन के लिए अन्य उम्मीदवार ग्रीसेन-ज़त्सेपिन-कुज़मिन सीमा और [[हवादार डिस्क]] हैं। उत्तरार्द्ध की जांच लोरेंत्ज़ इनवेरिएंस के संभावित विचलन को खोजने के लिए की गई है जो फोटॉनों को चरण से बाहर कर सकता है।
*खगोलीय अवलोकन के लिए अन्य उम्मीदवार ग्रीसेन-ज़त्सेपिन-कुज़मिन सीमा और [[हवादार डिस्क|एयरी डिस्क]] हैं। उत्तरार्द्ध की जांच लोरेंत्ज़ इनवेरिएंस के संभावित विचलन को खोजने के लिए की गई है जो फोटॉनों को चरण से बाहर कर सकता है।
*[[हिग्स बॉसन]] क्षेत्र में अवलोकन चल रहे हैं।
*[[हिग्स बॉसन]] क्षेत्र में अवलोकन चल रहे हैं।


Line 161: Line 160:
[[Category: Machine Translated Page]]
[[Category: Machine Translated Page]]
[[Category:Created On 17/11/2023]]
[[Category:Created On 17/11/2023]]
[[Category:Vigyan Ready]]

Latest revision as of 10:11, 1 December 2023

विशेष सापेक्षता एक भौतिक सिद्धांत है, जब तक कि गुरुत्वाकर्षण महत्वपूर्ण न हो जो सभी भौतिक घटनाओं के वर्णन में मौलिक भूमिका निभाता है। अनेक प्रयोगों ने इसके विकास और औचित्य में महत्वपूर्ण भूमिका निभाई (और अब भी निभाते हैं)। इस प्रकार से सिद्धांत की शक्ति अत्यंत विविध प्रकार के प्रयोगों के परिणाम की उच्च परिशुद्धता के साथ सही पूर्वानुमान करने की इसकी अद्वितीय क्षमता में निहित है। किन्तु उनमें से अनेक प्रयोगों की पुनरावृत्ति अभी भी निरंतर बढ़ी हुई स्पष्टतः के साथ की जा रही है, जिसमें आधुनिक प्रयोग प्लैंक स्केल और न्युट्रीनो क्षेत्र जैसे प्रभावों पर ध्यान केंद्रित कर रहे हैं। उनके परिणाम विशेष सापेक्षता की पूर्वानुमानो के अनुरूप हैं। जेकब लाउब,[1] झांग,[2] मैटिंगली,[3] क्लिफोर्ड विल,[4] और रॉबर्ट्स/श्लीफ़ द्वारा विभिन्न परीक्षणों का संग्रह दिया गया था।[5]

अर्थात, गुरुत्वाकर्षण के महत्वपूर्ण प्रभाव के बिना सभी घटनाओं तक विशेष सापेक्षता मिन्कोव्स्की अंतरिक्ष तक ही सीमित है। इस प्रकार से उत्तरार्द्ध सामान्य सापेक्षता के क्षेत्र में है और सामान्य सापेक्षता के संबंधित परीक्षणों पर विचार किया जाना चाहिए।

सापेक्षता का मार्ग प्रशस्त करने वाले प्रयोग

19वीं शताब्दी में प्रकाश का प्रमुख सिद्धांत ल्यूमिनिफेरस ईथर का था, स्थिर माध्यम जिसमें प्रकाश उसी तरह फैलता है जैसे ध्वनि वायु के माध्यम से फैलती है। सादृश्य से, यह इस प्रकार है कि प्रकाश की गति ईथर में सभी दिशाओं में स्थिर है और स्रोत के वेग से स्वतंत्र है। इस प्रकार ईथर के सापेक्ष गति करने वाले पर्यवेक्षक को किसी प्रकार की ईथर वायु को मापना चाहिए, वैसे ही जैसे वायु के सापेक्ष गति करने वाला पर्यवेक्षक स्पष्ट वायु को मापता है।

प्रथम-क्रम प्रयोग

Main article: ल्यूमिनिफेरस ईथर § प्रथम क्रम प्रयोग
फ़िज़ो प्रयोग, 1851

फ्रांकोइस अरागो (1810) के काम की प्रारंभ करते हुए, ऑप्टिकल प्रयोगों की श्रृंखला आयोजित की गई थी, जिसे (अर्थात, का ) पहले क्रम के परिमाण के लिए धनात्मक परिणाम देना चाहिए था। और इस प्रकार ईथर की सापेक्ष गति को प्रदर्शित करना चाहिए था। फिर भी परिणाम ऋणात्मक थे. ऑगस्टिन फ़्रेज़नेल (1818) द्वारा सहायक परिकल्पना, तथाकथित कर्षणिंग गुणांक, के प्रारंभ के साथ स्पष्टीकरण प्रदान किया गया था, अर्थात, पदार्थ ईथर को कुछ सीमा तक खींच रहा है। इस गुणांक को फ़िज़ो प्रयोग (1851) द्वारा सीधे प्रदर्शित किया गया था। तत्पश्चात यह दिखाया गया कि सभी प्रथम-क्रम ऑप्टिकल प्रयोगों को इस गुणांक के कारण ऋणात्मक परिणाम देना होगा। इसके अतिरिक्त, कुछ इलेक्ट्रोस्टैटिक प्रथम-क्रम प्रयोग आयोजित किए गए, जिनके फिर से ऋणात्मक परिणाम आए। सामान्य रूप से, हेंड्रिक लोरेंत्ज़ (1892, 1895) ने गतिमान पर्यवेक्षकों के लिए अनेक नए सहायक वेरिएबल प्रस्तुत किए, यह प्रदर्शित करते हुए कि सभी प्रथम-क्रम ऑप्टिकल और इलेक्ट्रोस्टैटिक प्रयोगों ने शून्य परिणाम क्यों दिए हैं। उदाहरण के लिए, लोरेंत्ज़ ने स्थान वेरिएबल प्रस्तावित किया जिसके द्वारा इलेक्ट्रोस्टैटिक क्षेत्र गति की रेखा में संकुचन हैं और अन्य वेरिएबल (स्थानीय समय) जिसके द्वारा गतिमान पर्यवेक्षकों के लिए समय निर्देशांक उनके वर्तमान स्थान पर निर्भर करते हैं।[1]

द्वतीय क्रम के प्रयोग

Main article: ल्यूमिनिफेरस ईथर § द्वितीय क्रम प्रयोग
माइकलसन-मॉर्ले इंटरफेरोमीटर

चूंकि, स्थिर ईथर सिद्धांत धनात्मक परिणाम देगा जब प्रयोग (अर्थात, का ) द्वतीय क्रम के परिमाण को मापने के लिए पर्याप्त स्पष्ट होंगे। इस प्रकार से अल्बर्ट ए. माइकलसन ने 1881 में माइकलसन-मॉर्ले प्रयोग या मिशेलसन प्रयोग (1881) किया, इसके बाद 1887 में अधिक परिष्कृत माइकलसन-मॉर्ले प्रयोग किया गया। किन्तु अलग-अलग दिशाओं में कुछ समय के लिए यात्रा करने वाली प्रकाश की दो किरणों को हस्तक्षेप के लिए लाया गया, जिससे ईथर पवन के सापेक्ष भिन्न-भिन्न झुकावों से व्यतिकरण फ्रिंजों का विस्थापन होना चाहिए। किन्तु परिणाम पुनः ऋणात्मक रहा. इस दुविधा से बाहर निकलने का रास्ता जॉर्ज फ्रांसिस फिट्जगेराल्ड (1889) और लोरेंत्ज़ (1892) का प्रस्ताव था कि पदार्थ ईथर (लंबाई संकुचन) के संबंध में गति की रेखा में अनुबंधित होता है। अर्थात्, इलेक्ट्रोस्टैटिक क्षेत्रों के संकुचन की पुरानी परिकल्पना को अंतर-आणविक बलों तक विस्तारित किया गया था। चूँकि इसका कोई सैद्धांतिक कारण नहीं था, इसलिए संकुचन परिकल्पना को तदर्थ माना गया था।

ऑप्टिकल माइकलसन-मॉर्ले प्रयोग के अतिरिक्त, इसके इलेक्ट्रोडायनामिक समकक्ष, ट्राउटन-नोबल प्रयोग भी आयोजित किया गया था। इसके द्वारा यह प्रदर्शित किया जाना चाहिए कि गतिशील कंडेनसर को टॉर्कः के अधीन किया जाना चाहिए। इसके अतिरिक्त, रेले और ब्रेस के प्रयोगो का उद्देश्य प्रयोगशाला फ्रेम में लंबाई संकुचन के कुछ परिणामों को मापना था, उदाहरण के लिए यह धारणा कि इससे द्विअपवर्तन हो सकता है। चूंकि उन सभी प्रयोगों के ऋणात्मक परिणाम आये। (1908 में किए गए ट्राउटन-रैंकिन प्रयोग ने भी विद्युत चुम्बकीय कुंडल पर लंबाई संकुचन के प्रभाव को मापते समय ऋणात्मक परिणाम दिया था।)[1]

इस प्रकार से 1904 से पहले किए गए सभी प्रयोगों को समझाने के लिए, लोरेंत्ज़ को संपूर्ण लोरेंत्ज़ परिवर्तन की प्रारंभ करके अपने सिद्धांत को फिर से विस्तारित करने के लिए विवश होना पड़ा। हेनरी पोंकारे ने 1905 में घोषणा की कि पूर्ण गति (सापेक्षता का सिद्धांत) प्रदर्शित करने की असंभवता स्पष्ट रूप से प्रकृति का नियम है।

पूर्ण ईथर कर्षण का खंडन

Main article: ईथर ड्रैग परिकल्पना
लॉज की ईथर मशीन. स्टील डिस्क का व्यास गज था। श्वेत प्रकाश को किरण विभाजक द्वारा विभाजित किया गया था और फ्रिंज बनाने के लिए पुन: एकजुट होने से पहले उपकरण के चारों ओर तीन बार दौड़ा।

यह विचार कि ईथर को पूरी तरह से पृथ्वी के अन्दर या उसके समीप खींचा जा सकता है, जिससे ऋणात्मक ईथर धारा प्रयोगों को समझाया जा सकता है, विभिन्न प्रयोगों द्वारा खंडन किया गया था।

  • ओलिवर लॉज (1893) ने पाया कि संवेदनशील सामान्य-पथ इंटरफेरोमीटर के ऊपर और नीचे तेजी से घूर्णन वाली स्टील डिस्क मापने योग्य फ्रिंज परिवर्तन उत्पन्न करने में विफल रही।
  • गुस्ताफ हैमर (1935) हैमर प्रयोग में सामान्य-पथ इंटरफेरोमीटर का उपयोग किया गया, जिसकी भुजा लीड से प्लग की गई मोटी दीवार वाली पाइप से घिरी हुई थी, जबकि दूसरी भुजा स्वतंत्र थी।
  • सैग्नैक प्रभाव से पता चला कि पृथ्वी के कर्षण के कारण होने वाली ईथर वायु का प्रदर्शन नहीं किया जा सकता है।
  • प्रकाश के विपथन का अस्तित्व ईथर कर्षण परिकल्पना के साथ असंगत था।
  • यह धारणा कि ईथर कर्षण द्रव्यमान के समानुपाती होता है और इस प्रकार केवल संपूर्ण पृथ्वी के संबंध में होता है, माइकलसन-गेल-पियर्सन प्रयोग द्वारा खंडन किया गया था, जिसने पृथ्वी की गति के माध्यम से सैग्नैक प्रभाव का प्रदर्शन किया था।

लॉज ने उस विरोधाभासी स्थिति को व्यक्त किया जिसमें भौतिकविदों ने स्वयं को इस प्रकार पाया: ... किसी भी व्यावहारिक गति पर ... पदार्थ की ईथर पर कोई सराहनीय श्यान पकड़ नहीं होती है। यदि परमाणु पर्याप्त गति से दोलन कर रहे हैं या घूम रहे हैं, तो उन्हें कंपन में फेंकने में सक्षम होना चाहिए; अन्यथा वे प्रकाश या किसी भी प्रकार का विकिरण उत्सर्जित नहीं करेंगे; किन्तु किसी भी स्थिति में वे इसे अपने साथ कर्षण करते हुए, या इसके माध्यम से किसी भी समान गति में प्रतिरोध का सामना करते हुए दिखाई नहीं देते हैं।[6]


विशेष सापेक्षता

अवलोकन

अंततः, अल्बर्ट आइंस्टीन (1905) ने निष्कर्ष निकाला कि उस समय ज्ञात स्थापित सिद्धांत और तथ्य केवल तार्किक सुसंगत प्रणाली बनाते हैं जब अंतरिक्ष और समय की अवधारणाओं को मौलिक संशोधन के अधीन किया जाता है। उदाहरण के लिए:

  • मैक्सवेल-लोरेंत्ज़ का इलेक्ट्रोडायनामिक्स (स्रोत की गति से प्रकाश की गति की स्वतंत्रता),
  • ऋणात्मक ईथर धारा प्रयोग (कोई वरीय संदर्भ फ्रेम नहीं),
  • चल चुंबक और चालक समस्या (केवल सापेक्ष गति ही प्रासंगिक है),
  • फ़िज़ो प्रयोग और प्रकाश का विपथन (दोनों संशोधित वेग वृद्धि और पूर्ण ईथर कर्षण नहीं होने का संकेत देते हैं)।

परिणाम विशेष सापेक्षता सिद्धांत है, जो संदर्भ के सभी जड़त्वीय फ्रेम में प्रकाश की गति की स्थिरता और सापेक्षता के सिद्धांत पर आधारित है। यहां, लोरेंत्ज़ परिवर्तन अब केवल सहायक परिकल्पनाओं का संग्रह नहीं है, किन्तु मौलिक लोरेंत्ज़ समरूपता को दर्शाता है और क्वांटम इलेक्ट्रोडायनामिक्स जैसे सफल सिद्धांतों का आधार बनता है। विशेष सापेक्षता बड़ी संख्या में परीक्षण योग्य पूर्वसूचना प्रदान करती है, जैसे:[7]

सापेक्षता का सिद्धांत प्रकाश की गति की स्थिरता समय का विस्तार
जड़त्वीय फ्रेम में कोई भी समान रूप से गतिमान पर्यवेक्षक सह-गतिशील प्रयोगात्मक व्यवस्था द्वारा अपनी "पूर्ण" गति की स्थिति निर्धारित नहीं कर सकता है। सभी जड़त्वीय फ़्रेमों में प्रकाश की मापी गई गति सभी दिशाओं (आइसोट्रॉपी) में समान होती है, जो स्रोत की गति से स्वतंत्र होती है, और बड़े पिंडों द्वारा उस तक नहीं पहुंचा जा सकता है। एक जड़त्वीय फ्रेम में विश्राम कर रही दो सिंक्रनाइज़ क्लॉक A और B के मध्य यात्रा करने वाली क्लॉक C(= कोई आवधिक प्रक्रिया) की दर दो क्लॉक के संबंध में मंद है।
इसके अतिरिक्त अन्य सापेक्षतावादी प्रभाव जैसे लंबाई संकुचन, डॉपलर प्रभाव, विपथन और मानक मॉडल जैसे सापेक्षतावादी सिद्धांतों की प्रयोगात्मक पूर्वसूचना को भी मापा जा सकता है।

मौलिक प्रयोग

कैनेडी-थॉर्नडाइक प्रयोग

विशेष सापेक्षता के प्रभाव को घटनात्मक रूप से निम्नलिखित तीन मौलिक प्रयोगों से प्राप्त किया जा सकता है:[8]

  • मिशेलसन-मॉर्ले प्रयोग, जिसके द्वारा मापने वाले उपकरण की दिशा पर प्रकाश की गति की निर्भरता का परीक्षण किया जा सकता है। यह गतिमान पिंडों की अनुदैर्ध्य और अनुप्रस्थ लंबाई के बीच संबंध स्थापित करता है।
  • कैनेडी-थॉर्नडाइक प्रयोग, जिसके द्वारा मापने वाले उपकरण के वेग पर प्रकाश की गति की निर्भरता का परीक्षण किया जा सकता है। यह अनुदैर्ध्य लंबाई और गतिशील पिंडों के समय की अवधि के बीच संबंध स्थापित करता है।
  • इव्स-स्टिलवेल प्रयोग, जिसके द्वारा समय विस्तार का सीधे परीक्षण किया जा सकता है।

इन तीन प्रयोगों से और आइंस्टीन तुल्यकालन का उपयोग करके, संपूर्ण लोरेंत्ज़ परिवर्तन निम्नानुसार है जिसमें लोरेंत्ज़ कारक होना:[8]

लोरेंत्ज़ परिवर्तन की व्युत्पत्ति के अतिरिक्त, इन प्रयोगों का संयोजन भी महत्वपूर्ण है क्योंकि व्यक्तिगत रूप से देखे जाने पर उनकी व्याख्या अलग-अलग विधियों से की जा सकती है। उदाहरण के लिए, माइकलसन-मॉर्ले जैसे आइसोट्रॉपी प्रयोगों को सापेक्षता सिद्धांत के सरल परिणाम के रूप में देखा जा सकता है, जिसके अनुसार कोई भी जड़ता से गतिशील पर्यवेक्षक स्वयं को विश्राम की स्थिति में मान सकता है। इसलिए, अपने आप में, MM प्रयोग उत्सर्जन सिद्धांत (सापेक्षता) या एथर कर्षण परिकल्पना या पूर्ण ईथर कर्षणिंग जैसे गैलिलियन-अपरिवर्तनीय सिद्धांतों के अनुकूल है, जिसमें कुछ प्रकार के सापेक्षता सिद्धांत भी सम्मिलित हैं। चूंकि, जब गैलिलियन-अपरिवर्तनीय सिद्धांतों को बाहर करने वाले अन्य प्रयोगों पर विचार किया जाता है (अर्थात इवेस-स्टिलवेल प्रयोग, उत्सर्जन सिद्धांत (सापेक्षता) और ईथर कर्षण परिकल्पना या पूर्ण ईथर कर्षणिंग), लोरेंत्ज़-अपरिवर्तनीय सिद्धांत और इस प्रकार विशेष सापेक्षता ही एकमात्र सिद्धांत हैं जो गतिविधि्य बने रहें.

प्रकाश की गति की स्थिरता

इंटरफेरोमीटर, रेज़ोनेटर

माइकलसन-मॉर्ले ने क्रायोजेनिक ऑप्टिकल रेज़ोनेटर के साथ प्रयोग किया, जैसा कि मुलर एट अल द्वारा उपयोग किया गया था। (2003), माइकलसन-मॉर्ले प्रयोग वर्त्तमान के ऑप्टिकल रेज़ोनेटर प्रयोग देखें
See also: वर्तमान के माइकलसन-मॉर्ले प्रयोग and वर्तमान कैनेडी-थार्नडाइक प्रयोग

प्रकाश की गति की आइसोट्रॉपी का परीक्षण करने के लिए माइकलसन-मॉर्ले और कैनेडी-थॉर्नडाइक प्रयोगों के आधुनिक संस्करण आयोजित किए गए हैं। माइकलसन-मॉर्ले के विपरीत, कैनेडी-थॉर्नडाइक प्रयोग अलग-अलग बांह की लंबाई का उपयोग करते हैं, और मूल्यांकन अनेक महीनों तक चलता है। इस प्रकार, सूर्य के चारों ओर पृथ्वी की परिक्रमा के समय विभिन्न वेगों का प्रभाव देखा जा सकता है। चूंकि लेज़र, मेज़र और ऑप्टिकल गुंजयमान यंत्र का उपयोग किया जाता है, जिससे प्रकाश की गति की किसी भी अनिसोट्रॉपी की संभावना 10−17 तक कम हो जाती है स्तर. स्थलीय परीक्षणों के अतिरिक्त, कैनेडी-थॉर्नडाइक-प्रयोग के रूपांतर के रूप में चंद्र लेजर रेंजिंग प्रयोग भी आयोजित किए गए हैं।[4]

एक अन्य प्रकार के आइसोट्रॉपी प्रयोग 1960 के दशक में मोसबाउर रोटर प्रयोग हैं, जिसके द्वारा घूर्णन वाली डिस्क पर डॉपलर प्रभाव की अनिसोट्रॉपी को मोसबाउर प्रभाव का उपयोग करके देखा जा सकता है (उन प्रयोगों का उपयोग समय के विस्तार को मापने के लिए भी किया जा सकता है, नीचे देखें)।

स्रोत वेग या ऊर्जा पर कोई निर्भरता नहीं

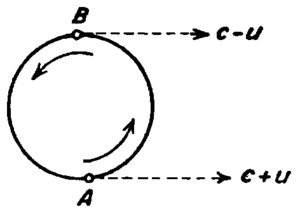
डी सिटर डबल स्टार प्रयोग, बाद में विलुप्त होने के प्रमेय पर विचार के अधीन ब्रेचर द्वारा दोहराया गया।

इस प्रकार से उत्सर्जन सिद्धांत (सापेक्षता), जिसके अनुसार प्रकाश की गति स्रोत के वेग पर निर्भर करती है, ईथर धारा प्रयोगों के ऋणात्मक परिणाम को स्पष्ट रूप से समझा सकता है। किन्तु 1960 के दशक के मध्य तक प्रकाश की गति की स्थिरता को निश्चित रूप से प्रयोग द्वारा नहीं दिखाया गया था, क्योंकि 1965 में, जे.जी. फॉक्स ने दिखाया कि इवाल्ड और ओसीन के विलुप्त होने प्रमेय के प्रभावों ने पिछले सभी प्रयोगों के परिणामों को प्रस्तुत किया समय अनिर्णायक है, और इसलिए विशेष सापेक्षता और उत्सर्जन सिद्धांत दोनों के साथ संगत है।[9][10] वर्तमान के प्रयोगों ने निश्चित रूप से उत्सर्जन मॉडल को बहिष्कृत कर दिया है: सबसे पहले फिलिप्पस और फॉक्स (1964) के प्रयोग थे,[11] गामा किरणों के गतिमान स्रोतों और अल्वेगर एट अल (1964), का उपयोग करना था। [12] जिससे पता चला कि फोटॉनों ने उच्च गति वाले क्षयकारी मेसॉन की गति प्राप्त नहीं की, जो उनका स्रोत था। इसके अतिरिक्त, डी सिटर डबल स्टार प्रयोग (1913) को विलुप्त होने के प्रमेय पर विचार करते हुए ब्रेचर (1977) द्वारा दोहराया गया था, इसी के साथ ही स्रोत निर्भरता को भी बहिष्कृत कर दिया गया था।[13]

इस प्रकार से गामा-किरण विस्फोटों के अवलोकन से यह भी पता चला कि प्रकाश की गति प्रकाश किरणों की आवृत्ति और ऊर्जा से स्वतंत्र है।[14]


प्रकाश की एकपक्षीय गति

Main article: प्रकाश की एकपक्षीय गति

एकपक्षीय मापों की श्रृंखला प्रारंभ की गई, वे सभी प्रकाश की गति की आइसोट्रॉपी की पुष्टि करते हैं।[5] चूंकि, केवल प्रकाश की दो-तरफ़ा गति (a से b से वापस a तक) को स्पष्ट रूप से मापा जा सकता है, क्योंकि एकपक्षीय गति साथ की परिभाषा पर निर्भर करती है और इसलिए सिंक्रनाइज़ेशन की विधि पर निर्भर करती है। इस प्रकार से आइंस्टीन सिंक्रोनाइज़ेशन कन्वेंशन एकपक्षीय गति को दो-पक्षीय गति के समान बनाता है। चूंकि, ऐसे अनेक मॉडल हैं जिनमें प्रकाश की आइसोट्रोपिक दो-तरफ़ा गति होती है, जिसमें अलग-अलग सिंक्रनाइज़ेशन योजनाओं को चुनकर एकपक्षीय गति को अनिसोट्रोपिक किया जाता है। वे प्रयोगात्मक रूप से विशेष सापेक्षता के समतुल्य हैं क्योंकि इन सभी मॉडलों में चलती क्लॉक के समय विस्तार जैसे प्रभाव सम्मिलित हैं, जो किसी भी मापने योग्य अनिसोट्रॉपी की भरपाई करते हैं। चूंकि, आइसोट्रोपिक दो-तरफा गति वाले सभी मॉडलों में से केवल विशेष सापेक्षता ही भौतिकविदों के भारी बहुमत के लिए स्वीकार्य है क्योंकि अन्य सभी सिंक्रनाइज़ेशन बहुत अधिक सम्मिश्र हैं, और वे अन्य मॉडल (जैसे लोरेंत्ज़ ईथर सिद्धांत) चरम और अविश्वसनीय मान्यताओं पर आधारित हैं कुछ गतिशील प्रभावों के संबंध में, जिनका उद्देश्य वरीय फ्रेम को अवलोकन से छिपाना है।

द्रव्यमान, ऊर्जा और स्थान की आइसोट्रॉपी

D2O में LiCl (1M) का 7Li-NMR स्पेक्ट्रम. लिथियम के इस आइसोटोप की तेज, बिना विभाजित एनएमआर रेखा द्रव्यमान और स्थान की आइसोट्रॉपी का प्रमाण है।
See also: ह्यूजेस-ड्रेवर प्रयोग

क्लॉक-तुलना प्रयोग (आवधिक प्रक्रियाओं और आवृत्तियों को क्लॉक के रूप में माना जा सकता है) जैसे ह्यूजेस-ड्रेवर प्रयोग लोरेंट्ज़ इनवेरिएंस के कड़े परीक्षण प्रदान करते हैं। वे माइकलसन-मॉर्ले की तरह फोटॉन क्षेत्र तक ही सीमित नहीं हैं, किन्तु परमाणु नाभिक की भूमि स्थिति को मापकर सीधे द्रव्यमान, ऊर्जा या स्थान की किसी भी अनिसोट्रॉपी का निर्धारण करते हैं। चूंकि 10−33 GeV की ऐसी अनिसोट्रॉपी की ऊपरी सीमा प्रदान की गई है। इस प्रकार ये प्रयोग लोरेंत्ज़ इनवेरिएंस के अब तक किए गए सबसे स्पष्ट सत्यापनों में से हैं।[3][4]


समय विस्तार और लंबाई संकुचन

इवेस-स्टिलवेल प्रयोग (1938)।)
Main articles: इव्स-स्टिलवेल प्रयोग, समय प्रसार का प्रायोगिक परीक्षण, and लंबाई संकुचन की पुष्टि

अनुप्रस्थ डॉपलर प्रभाव और परिणामस्वरूप समय विस्तार को पहली बार इवेस-स्टिलवेल प्रयोग (1938) में सीधे देखा गया था। संतृप्त स्पेक्ट्रोस्कोपी का उपयोग करके भारी आयन भंडारण वलय में आधुनिक इवेस-स्टिलवेल प्रयोगों में, सापेक्षतावादी पूर्वानुमान से समय फैलाव का अधिकतम मापा विचलन ≤10−8 तक सीमित कर दिया गया है। समय विस्तार की अन्य पुष्टियों में इवेस-स्टिलवेल मोसबाउर रोटर प्रयोग प्रयोग सम्मिलित हैं जिसमें गामा किरणों को घूर्णन डिस्क के मध्य से डिस्क के किनारे पर रिसीवर तक भेजा गया था, जिससे अनुप्रस्थ डॉपलर प्रभाव का मूल्यांकन मोसबाउर प्रभाव के माध्यम से किया जा सके। वायुमंडल और कण त्वरक में म्यूऑन के जीवनकाल को मापकर, गतिमान कणों के समय विस्तार को भी सत्यापित किया गया। किन्तु दूसरी ओर, हाफेल-कीटिंग प्रयोग ने ट्विन पैराडॉक्स के समाधान की पुष्टि की, यानी कि a से b से वापस a पर जाने वाली क्लॉक प्रारंभिक क्लॉक के संबंध में मंद है। चूंकि, इस प्रयोग में सामान्य सापेक्षता के प्रभाव भी आवश्यक भूमिका निभाते हैं।

इस प्रकार से गतिविधि में लंबाई संकुचन की प्रत्यक्ष पुष्टि प्राप्त करना कठिन है क्योंकि प्रेक्षित कणों के आयाम लुप्त हो रहे हैं। चूंकि, अप्रत्यक्ष पुष्टियाँ हैं; उदाहरण के लिए, भारी आयनो के टकराने के गतिविधि को केवल तभी समझाया जा सकता है जब लोरेंत्ज़ संकुचन के कारण उनके बढ़े हुए घनत्व पर विचार किया जाए। संकुचन से गति की दिशा के लंबवत कूलम्ब के नियम की तीव्रता में भी वृद्धि होती है, जिसका प्रभाव पहले ही देखा जा चुका है। परिणामस्वरूप, कण त्वरक में प्रयोग करते समय समय विस्तार और लंबाई संकुचन दोनों पर विचार किया जाना चाहिए।

सापेक्षिक संवेग और ऊर्जा

β के विशिष्ट आवेश e/m को मापने के लिए ब्यूचरर का प्रायोगिक सेटअप−इलेक्ट्रॉन अपनी गति v/c के फलन के रूप में। (चुंबकीय क्षेत्र एच के संबंध में कोण α पर, इसके केंद्र में बीटा-स्रोत के साथ वृत्ताकार संधारित्र की धुरी के माध्यम से क्रॉस-सेक्शन)
Main articles: सापेक्षिक ऊर्जा और संवेग का परीक्षण and कॉफ़मैन-बुचेरर-न्यूमैन प्रयोग

इस प्रकार से 1901 से प्रारंभ होकर, इलेक्ट्रॉनो के द्रव्यमान की वेग निर्भरता को प्रदर्शित करने के उद्देश्य से मापों की श्रृंखला आयोजित की गई थी। परिणामों ने वास्तव में ऐसी निर्भरता दिखाई किन्तु प्रतिस्पर्धी सिद्धांतों के बीच अंतर करने के लिए आवश्यक स्पष्टतः पर लंबे समय तक विवाद रहा है। अंततः, विशेष सापेक्षता को छोड़कर सभी प्रतिस्पर्धी मॉडलों को निश्चित रूप से बहिष्कृत करना संभव हो गया था।

वर्तमान, सापेक्षतावादी भारी आयन कोलाइडर जैसे कण त्वरक में विशेष सापेक्षता की पूर्वानुमानो की नियमित रूप से पुष्टि की जाती है। उदाहरण के लिए, सापेक्षतावादी गति और ऊर्जा की वृद्धि को न केवल स्पष्ट रूप से मापा जाता है, किन्तु साइक्लोट्रॉन और सिंक्रोटॉन आदि के गतिविधि को समझने के लिए भी आवश्यक है, जिसके द्वारा कणों को प्रकाश की गति के समीप त्वरित किया जाता है।

सैग्नैक और फ़िज़ो

मूल सैग्नैक इंटरफेरोमीटर
Main articles: सैग्नैक इंटरफेरोमीटर and फ़िज़ो प्रयोग

विशेष सापेक्षता यह भी पूर्वानुमान करती है कि घूमते हुए बंद पथ (उदाहरण के लिए लूप) के चारों ओर विपरीत दिशाओं में यात्रा करने वाली दो प्रकाश किरणों को गतिमान उत्सर्जक/रिसीवर पर वापस आने के लिए अलग-अलग उड़ान समय की आवश्यकता होती है (यह प्रकाश की गति की स्वतंत्रता का परिणाम है) स्रोत का वेग, ऊपर देखें)। यह प्रभाव वास्तव में देखा गया और इसे सैग्नैक प्रभाव कहा जाता है। वर्तमान में, इस आशय पर विचार अनेक प्रायोगिक सेटअपों और ग्लोबल पोजिशनिंग सिस्टम के सही कार्यप्रणाली के लिए आवश्यक है।

यदि ऐसे प्रयोग गतिशील मीडिया (उदाहरण के लिए जल, या ग्लास प्रकाशित तंतु ) में आयोजित किए जाते हैं, तो फ़्रेज़नेल के कर्षणिंग गुणांक पर विचार करना भी आवश्यक है जैसा कि फ़िज़ो प्रयोग द्वारा प्रदर्शित किया गया है। चूंकि इस प्रभाव को प्रारंभ में लगभग स्थिर ईथर या आंशिक ईथर कर्षण का प्रमाण देने के रूप में समझा गया था, इसे वेग-जोड़ सूत्र या सापेक्षता के विशेष सिद्धांत का उपयोग करके विशेष सापेक्षता के साथ सरलता से समझाया जा सकता है।

परीक्षण सिद्धांत

Main article: विशेष सापेक्षता के सिद्धांतों का परीक्षण करें

मानक समीकरणों में कुछ पैरामीटर जोड़कर लोरेंत्ज़ उल्लंघन प्रयोगों में संभावित धनात्मक परिणाम का आकलन करने के लिए अनेक परीक्षण सिद्धांत विकसित किए गए हैं। इनमें रॉबर्टसन-मंसौरी-सेक्सएल फ्रेमवर्क (आरएमएस) और मानक-मॉडल विस्तार (एसएमई) सम्मिलित हैं। इस प्रकार से आरएमएस में लंबाई संकुचन और समय विस्तार के संबंध में तीन परीक्षण योग्य पैरामीटर हैं। उससे, प्रकाश की गति की किसी भी अनिसोट्रॉपी का आकलन किया जा सकता है। दूसरी ओर, एसएमई में न केवल विशेष सापेक्षता के लिए, किन्तु मानक मॉडल और सामान्य सापेक्षता के लिए भी अनेक लोरेंत्ज़ उल्लंघन पैरामीटर सम्मिलित हैं; इस प्रकार इसमें परीक्षण योग्य मापदंडों की बहुत बड़ी संख्या है।

अन्य आधुनिक परीक्षण

Main article: लोरेंत्ज़ उल्लंघन के लिए आधुनिक खोजें

वर्तमान के वर्षों में क्वांटम गुरुत्व के विभिन्न मॉडलों से संबंधित विकास के कारण, लोरेंत्ज़ इनवेरिएंस के विचलन (संभवतः उन मॉडलों से अनुसरण करते हुए) फिर से प्रयोगवादियों का लक्ष्य हैं। क्योंकि स्थानीय लोरेंत्ज़ इनवेरिएंस (एलएलआई) भी स्वतंत्र रूप से गिरने वाले फ्रेम में रहता है, अशक्त समतुल्यता सिद्धांत से संबंधित प्रयोग भी परीक्षणों के इस वर्ग से संबंधित हैं। परिणामों का विश्लेषण आरएमएस जैसे परीक्षण सिद्धांतों (जैसा कि ऊपर बताया गया है) या, अधिक महत्वपूर्ण बात, एसएमई द्वारा किया जाता है।[3]

  • माइकलसन-मॉर्ले और कैनेडी-थॉर्नडाइक प्रयोगों की उल्लिखित विविधताओं के अतिरिक्त, प्रोटोन और न्यूट्रॉन क्षेत्र में आइसोट्रॉपी परीक्षणों के लिए ह्यूजेस-ड्रेवर प्रयोग जारी हैं। इलेक्ट्रॉन क्षेत्र में संभावित विचलन का पता लगाने के लिए, स्पिन ध्रुवीकरण आघूर्ण संतुलन का उपयोग किया जाता है।
  • लिथियम के डॉपलर प्रभाव के अवलोकन से मैक्स प्लैंक इंस्टीट्यूट फॉर न्यूक्लियर फिजिक्स में टीएसआर जैसे भारी आयन संचय वलय में समय विस्तार की पुष्टि की जाती है, और वे प्रयोग इलेक्ट्रॉन, प्रोटॉन और फोटॉन क्षेत्र में मान्य हैं।
  • अन्य प्रयोग इलेक्ट्रोस्टैटिक और चुंबकीय क्षेत्रों में साइक्लोट्रॉन गति और लार्मोर प्रीसेशन के विचलन का निरीक्षण करने के लिए पेनिंग जाल का उपयोग करते हैं।
  • सीपीटी समरूपता से संभावित विचलन (जिसका उल्लंघन लोरेंत्ज़ इनवेरिएंस के उल्लंघन का भी प्रतिनिधित्व करता है) तटस्थ मेसन, पेनिंग ट्रैप और म्यूऑन के प्रयोगों में निर्धारित किया जा सकता है, लोरेंत्ज़ उल्लंघन के एंटीमैटर टेस्ट देखें।
  • खगोलीय परीक्षण फोटॉन के उड़ान समय के संबंध में आयोजित किए जाते हैं, जहां लोरेंत्ज़ उल्लंघन करने वाले कारक असामान्य विस्तार और द्विअपवर्तन का कारण बन सकते हैं, जिससे ऊर्जा, आवृत्ति या ध्रुवीकरण (तरंगों) पर फोटॉन की निर्भरता हो सकती है।
  • दूरस्थ खगोलीय पिंडों की प्रारम्भ ऊर्जा के संबंध में, किन्तु स्थलीय स्रोतों के संबंध में, लोरेंत्ज़ उल्लंघन से उस ऊर्जा से उत्पन्न होने वाली प्रक्रियाओं जैसे वैक्यूम चेरेनकोव विकिरण, या सिंक्रोट्रॉन विकिरण के संशोधनों के लिए मानक मूल्यों में परिवर्तन हो सकता है।
  • न्यूट्रिनो दोलन (लोरेंत्ज़-उल्लंघन न्यूट्रिनो दोलन देखें) और न्यूट्रिनो की गति (न्यूट्रिनो गति की माप देखें) की संभावित लोरेंत्ज़ उल्लंघन के लिए जांच की जा रही है।
  • खगोलीय अवलोकन के लिए अन्य उम्मीदवार ग्रीसेन-ज़त्सेपिन-कुज़मिन सीमा और एयरी डिस्क हैं। उत्तरार्द्ध की जांच लोरेंत्ज़ इनवेरिएंस के संभावित विचलन को खोजने के लिए की गई है जो फोटॉनों को चरण से बाहर कर सकता है।
  • हिग्स बॉसन क्षेत्र में अवलोकन चल रहे हैं।

यह भी देखें

संदर्भ

  1. ↑ 1.0 1.1 1.2 Laub, Jakob (1910). "Über die experimentellen Grundlagen des Relativitätsprinzips". Jahrbuch der Radioaktivität und Elektronik. 7: 405–463.
  2. ↑ Zhang, Yuan Zhong (1997). Special Relativity and Its Experimental Foundations. World Scientific. ISBN 978-981-02-2749-4.
  3. ↑ 3.0 3.1 3.2 Mattingly, David (2005). "Modern Tests of Lorentz Invariance". Living Rev. Relativ. 8 (5): 5. arXiv:gr-qc/0502097. Bibcode:2005LRR.....8....5M. doi:10.12942/lrr-2005-5. PMC 5253993. PMID 28163649.
  4. ↑ 4.0 4.1 4.2 Will, C.M (2005). "Special Relativity: A Centenary Perspective". In T. Damour; O. Darrigol; B. Duplantier; V. Rivasseau (eds.). Poincare Seminar 2005. Basel: Birkhauser. pp. 33–58. arXiv:gr-qc/0504085. Bibcode:2006eins.book...33W. doi:10.1007/3-7643-7436-5_2. ISBN 978-3-7643-7435-8. S2CID 17329576.
  5. ↑ 5.0 5.1 Roberts, T; Schleif, S (2007). Dlugosz, JM (ed.). "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. University of California, Riverside. Retrieved 2010-10-31.
  6. ↑ Lodge, Oliver, Sir (1909). अंतरिक्ष का ईथर. New York: Harper and Brothers.{{cite book}}: CS1 maint: multiple names: authors list (link)
  7. ↑ Lämmerzahl, C. (2005). "Special Relativity and Lorentz Invariance". Annalen der Physik. 517 (1): 71–102. Bibcode:2005AnP...517...71L. doi:10.1002/andp.200410127. S2CID 119383407.
  8. ↑ 8.0 8.1 Robertson, H. P. (1949). "Postulate versus Observation in the Special Theory of Relativity". Reviews of Modern Physics. 21 (3): 378–382. Bibcode:1949RvMP...21..378R. doi:10.1103/RevModPhys.21.378.
  9. ↑ Fox, J. G. (1965), "Evidence Against Emission Theories", American Journal of Physics, 33 (1): 1–17, Bibcode:1965AmJPh..33....1F, doi:10.1119/1.1971219.
  10. ↑ Martínez, Alberto A. (2004), "Ritz, Einstein, and the Emission Hypothesis", Physics in Perspective, 6 (1): 4–28, Bibcode:2004PhP.....6....4M, doi:10.1007/s00016-003-0195-6, S2CID 123043585
  11. ↑ Filippas, T.A.; Fox, J.G. (1964). "गतिशील स्रोत से गामा किरणों का वेग". Physical Review. 135 (4B): B1071-1075. Bibcode:1964PhRv..135.1071F. doi:10.1103/PhysRev.135.B1071.
  12. ↑ Alväger, T.; Farley, F. J. M.; Kjellman, J.; Wallin, L. (1964), "Test of the second postulate of special relativity in the GeV region", Physics Letters, 12 (3): 260–262, Bibcode:1964PhL....12..260A, doi:10.1016/0031-9163(64)91095-9.
  13. ↑ Brecher, K. (1977). "क्या प्रकाश की गति स्रोत के वेग से स्वतंत्र है?". Physical Review Letters. 39 (17): 1051–1054. Bibcode:1977PhRvL..39.1051B. doi:10.1103/PhysRevLett.39.1051.
  14. ↑ Fermi LAT Collaboration (2009). "क्वांटम गुरुत्व प्रभाव से उत्पन्न होने वाली प्रकाश की गति की भिन्नता पर एक सीमा". Nature. 462 (7271): 331–334. arXiv:0908.1832. Bibcode:2009Natur.462..331A. doi:10.1038/nature08574. PMID 19865083. S2CID 205218977.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=विशेष_सापेक्षता_के_परीक्षण&oldid=275460’