चिरल पॉट्स मॉडल

चिरल पॉट्स मॉडल सांख्यिकीय यांत्रिकी में एक समतल जालक (समूह) पर एक स्पिन मॉडल है जिसका अध्ययन हेलेन औ-यांग पर्क और जैक्स पर्क सहित अन्य लोगों ने किया है। इसे पॉट्स मॉडल के सामान्यीकरण के रूप में देखा जा सकता है, और पॉट्स मॉडल की तरह, मॉडल को कॉन्फ़िगरेशन द्वारा परिभाषित किया गया है जो आरेख (अलग गणित) के प्रत्येक शीर्ष पर स्पिन (भौतिकी) के असाइनमेंट हैं, जहां प्रत्येक स्पिन $N$ मानों में से एक ले सकता है। प्रत्येक किनारे को नियत स्पिन $n$ और $n'$ के साथ शीर्षों को जोड़ने वाले प्रत्येक किनारे के लिए, एक, बोल्ट्ज़मान कारक $W(n,n')$ सौंपा गया है। इस मॉडल के लिए चिरल का अर्थ$W(n,n')\neq W(n',n)$ होता है। जब भार यांग-बैक्सटर समीकरण को संतुष्ट करते हैं, तो यह पूर्णांक है, इस अर्थ में कि कुछ मात्राओं का त्रुटिहीन मूल्यांकन किया जा सकता है।

इंटीग्रेबल चिरल पॉट्स मॉडल के लिए, भार को उच्च जीनस (गणित) बीजगणितीय वक्र, चिरल पॉट्स वक्र द्वारा परिभाषित किया गया है। अन्य सॉल्व करने योग्य मॉडलों के विपरीत, जिनके भार को एक से कम या उसके समान जीनस के वक्रों द्वारा पैरामीट्रिज्ड किया जाता है, जिससे उन्हें त्रिकोणमितीय फलनों, जीनस शून्य स्थितियों के लिए तर्कसंगत फलनों, या जीनस 1 स्थिति के लिए थीटा फलन द्वारा व्यक्त किया जा सके, इस मॉडल में उच्च जीनस थीटा फलन सम्मिलित है कार्य, जिनके लिए सिद्धांत कम विकसित है।

संबंधित चिरल क्लॉक मॉडल, जिसे 1980 के दशक में डेविड ह्युस और स्टेलन ओस्टलुंड द्वारा स्वतंत्र रूप से प्रस्तुत किया गया था, चिरल पॉट्स मॉडल के विपरीत, बिल्कुल सॉल्व करने योग्य नहीं है।

मॉडल

यह मॉडल पहले से ज्ञात सभी मॉडलों की श्रेणी से बाहर है और कई अनसुलझे प्रश्न उठाता है जो बीजगणितीय ज्यामिति की कुछ सबसे सम्मिश्र समस्याओं से संबंधित हैं जो 150 वर्षों से हमारे साथ हैं। चिरल पॉट्स मॉडल का उपयोग अनुरूप-असमान चरण संक्रमण को समझने के लिए किया जाता है। N = 3 और 4 के लिए, अभिन्न स्थिति 1986 में स्टोनी ब्रुक में खोजा गया और अगले वर्ष प्रकाशित हुआ था।

सेल्फ-डुअल स्थिति

यदि वेट फलन का फूरियर रूपांतरण समान फलन लौटाता है तो मॉडल को सेल्फ-डुअल कहा जाता है। एक विशेष (जीनस 1) स्थिति 1982 में फतेयेव और अलेक्जेंडर ज़मोलोडचिकोव द्वारा सॉल्व किया गया था। अलकराज और सैंटोस के काम पर लगे कुछ प्रतिबंधों को हटाकर, इंटीग्रेबल चिरल पॉट्स मॉडल का एक अधिक सामान्य सेल्फ-डुअल स्थिति खोजा गया था। भार उत्पाद के रूप में दिया गया है और भार में पैरामीटर्स को फ़र्मेट वक्र पर दिखाया गया है, जिसमें जीनस 1 से अधिक है।

सामान्य स्थिति

सभी k (तापमान परिवर्तन) के लिए सामान्य समाधान मिल गया। भार भी उत्पाद के रूप में दिया गया था और यह कम्प्यूटेशनल रूप से (फोरट्रान पर) परीक्षण किया गया था कि वे स्टार-त्रिकोण संबंध को संतुष्ट करते हैं। इसका प्रमाण बाद में प्रकाशित हुआ।

परिणाम

ऑर्डर पैरामीटर

श्रृंखला से ऑर्डर पैरामीटर को सरल रूप,

$$\langle \sigma ^{n}\rangle =(1-k'^{2})^{\beta },\quad \beta =n(N-n)/2N^{2}$$

के रूप में अनुमान लगाया गया था।

इस अनुमान को सिद्ध करने में कई साल लग गए, क्योंकि उच्च जीनस वक्र के कारण सामान्य कॉर्नर ट्रांसफर मैट्रिक्स विधि का उपयोग नहीं किया जा सका। इस अनुमान को 2005 में कार्यात्मक समीकरणों और मिचियो जिम्बो एट अल की टूटी हुई रैपिडिटी लाइन विधि का उपयोग करके सिद्ध किया था। यांग-बैक्सटर इंटीग्रेबल मॉडल के क्षेत्र में सामान्यतः पर उपयोग की जाने वाली प्रकार की दो हल्की विश्लेषणात्मक स्थितियाँ है। वर्तमान में, पत्रों की श्रृंखला में ऑर्डर पैरामीटर प्राप्त करने का बीजगणितीय (आइसिंग मॉडल) प्रणाली दिया गया है, जो बीजगणितीय संरचना में अधिक जानकारी देता है।

छह शीर्ष मॉडल से संबंध

1990 में बज़ानोव और स्ट्रोगनोव ने दिखाया कि L-ऑपरेटर (लैक्स जोड़ी) उपस्थित हैं जो यांग-बैक्सटर समीकरण

$L_{i_{1}\alpha }^{j_{1}\beta }(x)L_{i_{2}\beta }^{j_{2}\gamma }(y)R_{j_{1}j_{2}}^{k_{1}k_{2}}(y/x)=R_{i_{1}i_{2}}^{j_{1}j_{2}}(y/x)L_{j_{2}\alpha }^{k_{2}\beta }(y)L_{j_{1}\beta }^{k_{1}\gamma }(x),\quad 0<i,j,k\leq 1,\quad 0\leq \alpha ,\beta ,\gamma \leq N-1.$

को संतुष्ट करते हैं। जहां 2 × 2 R-ऑपरेटर (आर-मैट्रिक्स) छह शीर्ष मॉडल R-मैट्रिक्स (शीर्ष मॉडल देखें) है।

चार चिरल पॉट्स भार S के उत्पाद को दो L-ऑपरेटरों को आपस में जोड़ते हुए दिखाया गया था

$L_{i_{1}\alpha _{1}}^{i_{2}\alpha _{2}}{\hat {L}}_{i_{2}\beta _{1}}^{i_{3}\beta _{2}}S_{\alpha _{2}\beta _{2}}^{\alpha _{3}\beta _{3}}=S_{\alpha _{1}\beta _{1}}^{\alpha _{2}\beta _{2}}{\hat {L}}_{i_{1}\beta _{2}}^{i_{2}\beta _{3}}L_{i_{2}\alpha _{2}}^{i_{3}\alpha _{3}},\quad 0<i_{i}\leq 1,\quad 0\leq \alpha _{i},\beta _{i}\leq N-1.$

इसने सफलता को प्रेरित किया, अर्थात् चिरल पॉट्स मॉडल के स्थानांतरण मैट्रिक्स के लिए कार्यात्मक संबंधों की खोज की गई।

मुक्त ऊर्जा और अंतरापृष्ठीय तनाव

इन कार्यात्मक संबंधों का उपयोग करते हुए, बैक्सटर चिरल पॉट्स मॉडल के स्थानांतरण मैट्रिक्स के आइगेनवैल्यू ​​​​की गणना करने में सक्षम था, और विशिष्ट ऊष्मा α=1-2/N के लिए महत्वपूर्ण घातांक प्राप्त किया, जिसे संदर्भ 12 में भी अनुमानित किया गया था। अंतरापृष्ठीय तनाव की गणना भी उनके द्वारा घातांक μ=1/2+1/N के साथ की गई थी।

क्नॉट सिद्धांत से संबंध

इंटीग्रेबल चिरल पॉट्स भार उत्पाद के रूप में दिए गए हैं जैसा

$W_{pq}(n)\!=\!{\Big (}{\mu _{p} \over \mu _{q}}{\Big )}^{\!\!n}\prod _{j=1}^{n}{y_{q}-x_{p}\omega ^{j} \over y_{p}-x_{q}\omega ^{j}},\quad {\overline {W}}_{pq}(n)\!=\!{\big (}{\mu _{p}\mu _{q}}{\big )}^{\!n}\!\prod _{j=1}^{n}{\omega x_{p}\!-\!x_{q}\omega ^{j} \over y_{q}\!-\!y_{p}\omega ^{j}},$

जहाँ $\omega ^{N}=1$ एकता की अभाज्य मूल है और हम प्रत्येक रैपिडिटी वैरिएबल P के साथ तीन वैरिएबल $(x_{p},y_{p},\mu _{p})$ को जोड़ते हैं जो

$x_{p}^{N}+y_{p}^{N}=k(1+x_{p}^{N}y_{p}^{N}),\quad k'^{2}+k^{2}=1,\quad k'\mu _{p}^{N}=1-ky_{p}^{N},\quad k'\mu _{p}^{-N}=1-kx_{p}^{N}.$

को संतुष्ट करते हैं। यह देखना आसान है

$W_{pp}(a-b)=1,\quad {\overline {W}}_{pp}(a-b)=\delta _{a,b}$

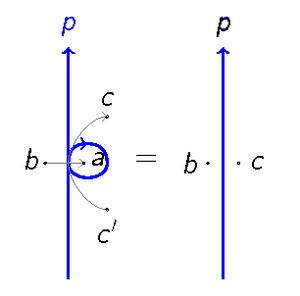
जो रिडेमिस्टर चाल I के समान है। यह भी ज्ञात था कि भार व्युत्क्रम संबंध को संतुष्ट करते हैं,

$W_{pq}(a-b)W_{qp}(a-b)=1,\quad \sum _{d=0}^{N-1}{\overline {W}}_{pq}(a-d){\overline {W}}_{qp}(d-a')=r_{pq}\delta _{a,a'}.$

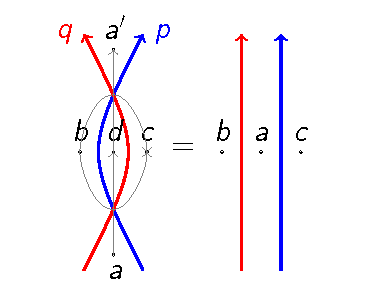
यह रिडेमिस्टर चाल II के समान है। स्टार-त्रिकोण संबंध

$\sum _{d=1}^{N}\,{\overline {W}}_{pr}(a-d)\,W_{pq}(d-c)\,{\overline {W}}_{rq}(d-b)=R_{pqr}\,{\overline {W}}_{pq}(a-b)\,{W}_{pr}(b-c)\,W_{rq}(a-c)$

रिडेमिस्टर चाल III के समान है। इन्हें नीचे दिए गए आंकड़ों में दिखाया गया है।

Property of the Weights: Reidemeister Move I

Inversion Relation of the Weights: Reidemeister Move II

Star-triangle relation: Reidemeister Move III

इंटीग्रेबल चिरल पॉट्स मॉडल का भार

यह भी देखें

• जेडएन मॉडल