स्वतःस्फूर्त सममिति भंजन: Difference between revisions
No edit summary |
m (6 revisions imported from alpha:स्वतःस्फूर्त_सममिति_भंजन) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 176: | Line 176: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 29/11/2023]] | [[Category:Created On 29/11/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 09:03, 13 December 2023
स्वतःस्फूर्त सममिति भंजन सममित भंजन की एक सहज प्रक्रिया है, जिसके द्वारा सममित (भौतिकी) अवस्था में एक भौतिक प्रणाली स्वतः ही असममित अवस्था में समाप्त हो जाती है।[1][2][3] विशेष रूप से, यह उन प्रणालियों का वर्णन कर सकता है जहां गति के समीकरण या लैग्रेंजियन (क्षेत्र सिद्धांत) सममित का पालन करते हैं, लेकिन सबसे कम ऊर्जा वाले वैक्यूम समाधान उसी सममित (भौतिकी) को प्रदर्शित नहीं करते हैं। जब प्रणाली उन वैक्यूम समाधानों में से एक में जाता है, तो उस वैक्यूम के चारों ओर अस्तव्यस्तता के लिए सममित टूट जाती है, भले ही संपूर्ण लैग्रेंजियन उस सममित को निरंतर रखता है।
सिंहावलोकन
परिभाषा के अनुसार, सहज सममित तोड़ने के लिए भौतिक नियमों (उदाहरण के लिए क्वांटम यांत्रिकी) के अस्तित्व की आवश्यकता होती है जो सममित (भौतिकी) परिवर्तन (जैसे अनुवाद या आवर्तन) के अनुसार अपरिवर्तनीय (भौतिकी) हैं, जिससे कि परिणामों की कोई भी जोड़ी केवल उस परिवर्तन से भिन्न हो समान संभाव्यता वितरण. उदाहरण के लिए, यदि किन्हीं दो अलग-अलग स्थितियों पर किसी अवलोकनीय वस्तु के माप में समान संभाव्यता वितरण होता है, तो अवलोकनीय में अनुवादात्मक सममित होती है।
जब यह संबंध टूट जाता है तो सहज सममित टूट जाती है, जबकि अंतर्निहित भौतिक नियम सममित रहते हैं।
इसके विपरीत, स्पष्ट सममित तोड़ने में, यदि दो परिणामों पर विचार किया जाता है, तो परिणामों की एक जोड़ी की संभाव्यता वितरण भिन्न हो सकता है। उदाहरण के लिए, एक विद्युत क्षेत्र में, एक आवेशित कण पर बल अलग-अलग दिशाओं में भिन्न होते हैं, इसलिए घूर्णी सममित विद्युत क्षेत्र द्वारा स्पष्ट रूप से टूट जाती है जिसमें यह सममित नहीं होती है।
पदार्थ के चरण, जैसे कि क्रिस्टल, चुंबक और पारंपरिक सुपरकंडक्टर्स (अतिचालक), साथ ही सरल चरण परिवर्तन को सहज सममित को तोड़कर वर्णित किया जा सकता है। उल्लेखनीय अपवादों में भिन्नात्मक क्वांटम हॉल प्रभाव जैसे पदार्थ के टोपोलॉजिकल चरण सम्मलित हैं।
सामान्यत:, जब सहज सममित टूटती है, तो प्रणाली के अवलोकन योग्य गुण कई तरीकों से बदल जाते हैं। उदाहरण के लिए, जब कोई तरल ठोस बन जाता है तो घनत्व, संपीड्यता, तापीय विस्तार का गुणांक और विशिष्ट ऊष्मा में बदलाव की उम्मीद की जाएगी।
उदाहरण
संब्रेरो क्षमता
एक सममित ऊपर की ओर गुंबद पर विचार करें जिसके नीचे एक गर्त घूम रहा है। यदि एक गेंद को गुंबद के शीर्ष पर रखा जाता है, तो प्रणाली केंद्र अक्ष के चारों ओर घूमने के संबंध में सममित होती है। लेकिन गेंद गुम्बद से नीचे गर्त में, जो सबसे कम ऊर्जा वाला बिंदु है, लुढ़क कर इस सममित को अनायास तोड़ सकती है। इसके बाद, गेंद परिधि पर किसी निश्चित बिंदु पर रुक गई है। गुंबद और गेंद अपनी व्यक्तिगत सममित बनाए रखते हैं, लेकिन प्रणाली ऐसा नहीं करती है।[4]
सबसे सरल आदर्शीकृत सापेक्षतावादी मॉडल में, अनायास भंजन हुई सममित को एक उदाहरणात्मक अदिश क्षेत्र सिद्धांत के माध्यम से संक्षेपित किया गया है। अदिश क्षेत्र का प्रासंगिक लैग्रेंजियन (क्षेत्र सिद्धांत) है। , जो अनिवार्य रूप से यह तय करता है कि एक प्रणाली कैसे व्यवहार करती है, इसे गतिक और संभावित शब्दों में विभाजित किया जा सकता है,
-
(1)
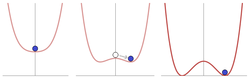
यह इस संभावित अवधि में है कि सममित का भंजन आरंभ हो गया है। जेफरी गोल्डस्टोन के कारण क्षमता का एक उदाहरण[5] बाईं ओर ग्राफ़ में दर्शाया गया है।
-
.
(2)
इस क्षमता में संभावित न्यूनतम (वैक्यूम अवस्थाएँ) की अनंत संख्या दी गई है
-
.
(3)
0 और 2π के बीच किसी भी वास्तविक θ के लिए प्रणाली में एक अस्थिर वैक्यूम स्थिति भी होती है Φ = 0. इस अवस्था में एकात्मक समूह U(1) सममित है। चूंकि, एक बार जब प्रणाली एक विशिष्ट स्थिर वैक्यूम स्थिति (θ की पसंद के बराबर) में गिर जाता है, तो यह सममित खो जाती है, या स्वचालित रूप से टूट जाती है।
वास्तव में, θ के किसी भी अन्य विकल्प में बिल्कुल समान ऊर्जा होगी, और परिभाषित समीकरण सममित का सम्मान करते हैं लेकिन सिद्धांत की जमीनी स्थिति (वैक्यूम) सममित को तोड़ देती है, जिसका अर्थ है कि द्रव्यमान रहित गोल्डस्टोन बोसोन नंबू-गोल्डस्टोन बोसोन का अस्तित्व मोड इस क्षमता के न्यूनतम पर वृत्त के चारों ओर चल रहा है, और यह दर्शाता है कि लैग्रेंजियन में मूल सममित की कुछ स्मृति है।[6][7]
अन्य उदाहरण
- लौहचुंबकीय सामग्रियों के लिए, स्थानिक घुमाव के अनुसार अंतर्निहित नियम अपरिवर्तनीय हैं। यहां, कोटि प्राचल चुंबकत्व है, जो चुंबकीय द्विध्रुव घनत्व को मापता है। क्यूरी तापमान के ऊपर, कोटि प्राचल शून्य है, जो स्थानिक रूप से अपरिवर्तनीय है, और कोई सममित नहीं टूट रही है। क्यूरी तापमान के नीचे, चूंकि, चुंबकत्व एक निरंतर गैर-लुप्त होने वाला तत्व प्राप्त करता है, जो एक निश्चित दिशा में इंगित करता है (आदर्श स्थिति में जहां हमारे पास पूर्ण संतुलन है; अन्यथा, अनुवादात्मक सममित भी टूट जाती है)। अवशिष्ट घूर्णी सममितएं जो इस सदिश अपरिवर्तनीय के अभिविन्यास को छोड़ती हैं, अन्य घुमावों के विपरीत, जो नहीं टूटती हैं और इस प्रकार अनायास टूट जाती हैं, अखंड रहती हैं।
- ठोस का वर्णन करने वाले नियम पूर्ण यूक्लिडियन समूह के अंतर्गत अपरिवर्तनीय हैं, लेकिन ठोस स्वयं ही इस समूह को एक त्रिविम ग्रुप में तोड़ देता है। विस्थापन और अभिविन्यास कोटि प्राचल हैं।
- सामान्य सापेक्षता में लोरेंत्ज़ सममित होती है, लेकिन फ्रीडमैन-लेमेत्रे-रॉबर्टसन-वॉकर मीट्रिक में, आकाशगंगाओं के वेगों के औसत से परिभाषित औसत 4-वेग क्षेत्र (आकाशगंगाएँ ब्रह्माण्ड संबंधी तराजू पर गैस कणों की तरह कार्य करती हैं) एक कोटि प्राचल के रूप में कार्य करती हैं। कॉस्मिक माइक्रोवेव पृष्ठभूमि के बारे में भी ऐसी ही टिप्पणियाँ की जा सकती हैं।
- इलेक्ट्रोवीक(विद्युत् दुर्बल) मॉडल के लिए, जैसा कि पहले बताया गया है, हिग्स फ़ील्ड का एक घटक इलेक्ट्रोवीक गेज सममित को इलेक्ट्रोमैग्नेटिक गेज सममित को तोड़ने वाला कोटि प्राचल प्रदान करता है। लौहचुंबकीय उदाहरण की तरह, इलेक्ट्रोकम तापमान पर एक चरण घटक होता है। हमारे बारे में वही टिप्पणी जो भंजन हुई सममितओं पर ध्यान नहीं देती है, यह बताती है कि इलेक्ट्रोवीक एकीकरण की खोज करने में हमें इतना समय क्यों लगा था।
- अतिचालकता में, एक संघनित-पदार्थ सामूहिक क्षेत्र ψ होता है, जो विद्युत चुम्बकीय गेज सममित को तोड़ने वाले कोटि प्राचल के रूप में कार्य करता है।
- एक पतली बेलनाकार प्लास्टिक की छड़ लें और दोनों सिरों को एक साथ दबाएं बकलिंग से पहले, प्रणाली आवर्तन के अनुसार सममित होता है, और इसलिए स्पष्ट रूप से बेलनाकार रूप से सममित होता है। लेकिन बकलिंग के बाद, यह अलग और असममित दिखता है। फिर भी, बेलनाकार समरूपता की विशेषताएं अभी भी सम्मलित हैं: घर्षण को नजरअंदाज करते हुए, छड़ी को चारों ओर स्वतंत्र रूप से घुमाने के लिए कोई बल नहीं लगेगा, समय में जमीन की स्थिति विस्थापित हो जाएगी, और दिशा में रेडियल दोलनों के विपरीत, गायब आवृत्ति के दोलन की मात्रा होगी। बकल. यह प्रचक्रण मोड प्रभावी रूप से अपेक्षित नंबू-गोल्डस्टोन बोसोन है
- अनंत क्षैतिज तल पर तरल पदार्थ की एक समान परत पर विचार करें। इस प्रणाली में यूक्लिडियन तल की सभी सममितएँ हैं। लेकिन अब निचली सतह को समान रूप से गर्म करें जिससे कि यह ऊपरी सतह की तुलना में अधिक गर्म हो जाए। जब तापमान प्रवणता काफी बड़ी हो जाती है, तो संवहन कोशिकाएं बन जाएंगी, जिससे यूक्लिडियन सममित टूट जाएगी।
- एक गोलाकार घेरे पर एक मनके पर विचार करें जो ऊर्ध्वाधर व्यास के चारों ओर घूमता है। जैसे-जैसे आराम से घूर्णी वेग धीरे-धीरे बढ़ता है, मनका आरंभ में घेरा के नीचे अपने प्रारंभिक संतुलन बिंदु (सहज रूप से स्थिर, सबसे कम गुरुत्वाकर्षण क्षमता) पर रहेगा, एक निश्चित महत्वपूर्ण घूर्णी वेग पर, यह बिंदु अस्थिर हो जाएगी और मनका केंद्र से समान दूरी पर दो अन्य नव निर्मित संतुलनों में से एक पर कूद जाएगा। प्रारंभ में, प्रणाली व्यास के संबंध में सममित है, फिर भी महत्वपूर्ण वेग से गुजरने के बाद, मनका दो नए संतुलन बिंदुओं में से एक में समाप्त होता है, इस प्रकार सममित टूट जाती है।
* दो-गुब्बारे का प्रयोग स्वतःस्फूर्त सममित भंजन का एक उदाहरण है जब दोनों गुब्बारे आरंभ में स्थानीय अधिकतम दबाव तक फुलाए जाते हैं। जब कुछ हवा एक गुब्बारे से दूसरे गुब्बारे में प्रवाहित होती है, तो दोनों गुब्बारों में दबाव कम हो जाएगा, जिससे प्रणाली असममित अवस्था में अधिक स्थिर हो जाएगी।
कण भौतिकी में
कण भौतिकी में, बल वाहक कणों को सामान्यतः गेज सममित के साथ क्षेत्र समीकरणों द्वारा निर्दिष्ट किया जाता है; उनके समीकरण पूर्वानुमान करते हैं कि क्षेत्र में किसी भी बिंदु पर कुछ माप समान होंगे। उदाहरण के लिए, फ़ील्ड समीकरण यह अनुमान लगा सकते हैं कि दो क्वार्क का द्रव्यमान स्थिर है। प्रत्येक क्वार्क का द्रव्यमान ज्ञात करने के लिए समीकरणों को हल करने से दो समाधान मिल सकते हैं। एक विलयन में, क्वार्क ए, क्वार्क बी से भारी है। दूसरे विलयन में, क्वार्क बी, क्वार्क ए से समान मात्रा में भारी है। समीकरणों की सममित व्यक्तिगत समाधानों द्वारा प्रतिबिंबित नहीं होती है, बल्कि यह समाधानों की सीमा से परिलक्षित होती है।
एक वास्तविक माप केवल एक समाधान को दर्शाता है, जो अंतर्निहित सिद्धांत की सममित में खराबी का प्रतिनिधित्व करता है। "विच्छिन्न" हुआ शब्द की तुलना में "प्रच्छन्न" हुआ एक बेहतर शब्द है, क्योंकि इन समीकरणों में सममित हमेशा सम्मलित रहती है। इस घटना को सहज चुंबकीयकरण सममित भंजन (एसएसबी) कहा जाता है क्योंकि कुछ भी (जिसे हम जानते हैं) समीकरणों में सममित को नहीं तोड़ता है।[8]: 194–195 सहज सममित भंजन की प्रकृति से, प्रारंभिक ब्रह्मांड के विभिन्न हिस्से अलग-अलग दिशाओं में सममित तोड़ देंगे, जिससे सांस्थितिक दोष हो जाएंगे, जैसे कि दो-आयामी डोमेन दीवारें, एक-आयामी ब्रह्मांडीय स्ट्रिंग, शून्य-आयामी मोनोपोल (गणित), और/या बनावट (ब्रह्मांड विज्ञान), प्रासंगिक होमोटॉपी समूह और सिद्धांत की गतिकीयता पर निर्भर करता है। उदाहरण के लिए, हिग्स सममित तोड़ने से उपोत्पाद के रूप में आदिम ब्रह्मांडीय तार बन सकते हैं। काल्पनिक ग्रैंड यूनिफाइड थ्योरी सममित को तोड़ने से सामान्य रूप से मोनोपोल (गणित) उत्पन्न होता है, जो जीयूटी के लिए कठिनाइयाँ पैदा करता है जब तक कि मोनोपोल (किसी भी जीयूटी डोमेन दीवारों के साथ) को ब्रह्मांडीय स्फीति के माध्यम से हमारे अवलोकन योग्य ब्रह्मांड से निष्कासित नहीं किया जाता है।[9]
चिरल सममित
चिरल सममित भंजन सहज सममित भंजन का एक उदाहरण है जो कण भौतिकी में मजबूत अंतःक्रियाओं की चिरल सममित को प्रभावित करता है। यह क्वांटम क्रोमोडायनामिक्स का एक गुण है, क्वांटम क्षेत्र सिद्धांत इन अंतः क्रिया का वर्णन करता है, और न्यूक्लियॉन के द्रव्यमान (99% से अधिक) और इस प्रकार सभी सामान्य पदार्थों के लिए ज़िम्मेदार है, क्योंकि यह बहुत हल्के बाध्य क्वार्क को 100 में परिवर्तित करता है बेरियनों के कई गुना भारी घटक है। इस सहज सममित तोड़ने की प्रक्रिया में अनुमानित नंबू-गोल्डस्टोन बोसॉन पियोन हैं, जिनका द्रव्यमान न्युक्लियोन के द्रव्यमान की तुलना में हल्के परिमाण का एक क्रम है। यह इलेक्ट्रोवीक सममित तोड़ने के अंतर्निहित हिग्स तंत्र के प्रोटोटाइप और महत्वपूर्ण घटक के रूप में कार्य करता है।
हिग्स तंत्र
मजबूत, कमजोर और विद्युत चुम्बकीय बल सभी को गेज सममित से उत्पन्न होने के रूप में समझा जा सकता है, जो सममित के विवरण में अतिरेक है। हिग्स तंत्र, गेज सममित का सहज सममित भंजन, कण भौतिकी के मानक मॉडल में धातुओं की अतिचालकता और कण द्रव्यमान की उत्पत्ति को समझने में एक महत्वपूर्ण घटक है।
स्वतःस्फूर्त सममित भंजन शब्द यहां एक मिथ्या नाम है क्योंकि एलिट्ज़ुर के प्रमेय में कहा गया है कि स्थानीय गेज सममितएं कभी भी स्वतःस्फूर्त रूप से नहीं तोड़ी जा सकती हैं। बल्कि, गेज फिक्सिंग के बाद, वैश्विक सममित (या अतिरेक) को औपचारिक रूप से सहज सममित तोड़ने के समान तरीके से तोड़ा जा सकता है।
यथार्त सममित और गेज सममित के बीच अंतर का एक महत्वपूर्ण परिणाम यह है कि गेज सममित के सहज भंजन से उत्पन्न द्रव्यमान रहित नंबू-गोल्डस्टोन गेज सदिश क्षेत्र के विवरण में अवशोषित हो जाते हैं, जो प्लाज्मा मोड की तरह बड़े पैमाने पर सदिश क्षेत्र मोड प्रदान करते हैं। एक सुपरकंडक्टर (अतिसंवाहक), या कण भौतिकी में देखा गया हिग्स मोड है।
कण भौतिकी के मानक मॉडल में, सहज सममित का भंजन SU(2) × U(1) इलेक्ट्रो-कमजोर बल से जुड़ी गेज सममित कई कणों के लिए द्रव्यमान उत्पन्न करती है, और विद्युत चुम्बकीय और कमजोर बलों को अलग करती है। डब्ल्यू और जेड बोसॉन प्राथमिक कण हैं जो कमजोर अंतः क्रिया में मध्यस्थता करते हैं, जबकि फोटॉन विद्युत चुम्बकीय अंतः क्रिया में मध्यस्थता करते हैं। 100 GeV से कहीं अधिक ऊर्जा पर, ये सभी कण एक समान तरीके से व्यवहार करते हैं। एकीकृत क्षेत्र सिद्धांत#आधुनिक प्रगति वेनबर्ग-सलाम सिद्धांत पूर्वानुमान करता है कि, कम ऊर्जा पर, यह सममित टूट जाती है जिससे कि फोटॉन और बड़े पैमाने पर डब्ल्यू और जेड बोसोन उभरें।[10] इसके अतिरिक्त, फर्मियन लगातार द्रव्यमान विकसित करते हैं।
सहज सममित को तोड़े बिना, प्राथमिक कण अंतःक्रिया के मानक मॉडल को कई कणों के अस्तित्व की आवश्यकता होती है। चूंकि, कुछ कणों (डब्ल्यू और जेड बोसॉन) के द्रव्यमान रहित होने की पूर्वानुमान की जाएगी, जब वास्तव में, उनमें द्रव्यमान देखा जाएगा। इस पर काबू पाने के लिए, इन कणों को द्रव्यमान देने के लिए हिग्स तंत्र द्वारा सहज सममित भंजन को बढ़ाया जाता है। यह 2012 में खोजे गए एक नए कण, हिग्स बॉसन की उपस्थिति का भी सुझाव देता है।
धातुओं की अतिचालकता हिग्स घटना का एक संघनित-पदार्थ एनालॉग है, जिसमें इलेक्ट्रॉनों के कूपर जोड़े का संघनन प्रकाश और विद्युत चुंबकत्व से जुड़े यू (1) गेज सममित को स्वचालित रूप से तोड़ देता है।
गतिकीय सममित तोड़ना
गतिकीय सममित भंजन (डीएसबी) सहज सममित भंजन का एक विशेष रूप है जिसमें प्रणाली की जमीनी स्थिति ने इसके सैद्धांतिक विवरण (अर्थात, लैग्रेंजियन (क्षेत्र सिद्धांत)) की तुलना में सममित गुणों को कम कर दिया है।
वैश्विक सममित का गतिकीय भंजन एक सहज सममित भंजन है, जो (शास्त्रीय) ट्री स्तर पर नहीं होता है (अर्थात, नंगे कार्रवाई के स्तर पर), लेकिन क्वांटम सुधार के कारण (अर्थात, प्रभावी कार्रवाई के स्तर पर) .
गेज सममित का गतिकीय भंजन अधिक सूक्ष्म होता है। पारंपरिक सहज गेज सममित तोड़ने में, सिद्धांत में एक अस्थिर हिग्स कण सम्मलित होता है, जो निर्वात को सममित-टूटे हुए चरण (अर्थात, विद्युत कमजोर अंतःक्रिया) में ले जाता है। गतिकीय गेज सममित तोड़ने में, चूंकि, सिद्धांत में कोई अस्थिर हिग्स कण संचालित नहीं होता है। , लेकिन प्रणाली की बाध्य अवस्थाएँ ही अस्थिर क्षेत्र प्रदान करती हैं जो चरण घटक को प्रस्तुत करती हैं। उदाहरण के लिए, बार्डीन, हिल और लिंडनर ने एक पेपर प्रकाशित किया जो मानक मॉडल में पारंपरिक हिग्स तंत्र को एक डीएसबी द्वारा प्रतिस्थापित करने का प्रयास करता है जो शीर्ष-एंटीटॉप क्वार्क की एक बाध्य स्थिति द्वारा संचालित होता है। (ऐसे मॉडल, जिनमें एक मिश्रित कण हिग्स बोसोन की भूमिका निभाता है, उन्हें अधिकांशत: समग्र हिग्स मॉडल कहा जाता है।)[11] गेज सममित का गतिकीय भंजन अधिकांशत: फर्मिओनिक संघनन के निर्माण के कारण होता है - उदाहरण के लिए, क्वार्क संघनन , जो क्वांटम क्रोमोडायनामिक्स में चिरल सममित भंजन से जुड़ा होता है। पारंपरिक अतिचालकता संघनित पदार्थ पक्ष से प्रतिमानात्मक उदाहरण है, जहां फोनन-मध्यस्थ आकर्षण इलेक्ट्रॉनों को जोड़े में बांधते हैं और फिर संघनित होते हैं, जिससे विद्युत चुम्बकीय गेज सममित टूट जाती है।
संघनित पदार्थ भौतिकी में
पदार्थ के अधिकांश चरणों को स्वतःस्फूर्त सममित भंजन के लेंस के माध्यम से समझा जा सकता है। उदाहरण के लिए, क्रिस्टल परमाणुओं की आवधिक सारणी हैं जो सभी अनुवादों के अनुसार अपरिवर्तनीय नहीं हैं (केवल एक जाली सदिश द्वारा अनुवादों के एक छोटे उपसमूह के अनुसार)। चुम्बकों में उत्तरी और दक्षिणी ध्रुव होते हैं जो घूर्णी सममित को तोड़ते हुए एक विशिष्ट दिशा में उन्मुख होते हैं। इन उदाहरणों के अतिरिक्त, पदार्थ के अन्य सममित-तोड़ने वाले चरणों की एक पूरी श्रृंखला है - जिसमें तरल स्फ़टिक के नेमैटिक चरण, चार्ज- और स्पिन-घनत्व तरंगें, सुपरफ्लुइड्स और कई अन्य सम्मलित हैं।
पदार्थ के ऐसे कई ज्ञात उदाहरण हैं जिनका वर्णन स्वतःस्फूर्त सममित भंजन से नहीं किया जा सकता है, जिनमें सम्मलित हैं: पदार्थ के स्थलाकृतिक रूप से क्रमित चरण, जैसे फ्रैक्शनल क्वांटम हॉल प्रभाव, और क्वांटम स्पिन तरल पदार्थ। ये अवस्थाएँ किसी भी सममित को नहीं तोड़ती हैं, बल्कि पदार्थ की अलग-अलग अवस्थाएँ हैं। स्वतःस्फूर्त सममित भंजन की स्थिति के विपरीत, ऐसी अवस्थाओं का वर्णन करने के लिए कोई सामान्य रूपरेखा नहीं है।[12]
सतत सममित
फेरोमैग्नेट विहित प्रणाली है जो क्यूरी तापमान के नीचे और पर स्पिन की निरंतर सममित को स्वचालित रूप से तोड़ देती है h = 0, जहां h बाहरी चुंबकीय क्षेत्र है। क्यूरी तापमान के नीचे, प्रणाली की ऊर्जा चुंबकीयकरण m('x') के व्युत्क्रमण के अनुसार अपरिवर्तनीय है जैसे कि m(x) = −m(−x). सममित अनायास ही टूट जाती है h → 0जब व्युत्क्रम परिवर्तन के अनुसार हैमिल्टनियन अपरिवर्तनीय हो जाता है, लेकिन अपेक्षा तत्व अपरिवर्तनीय नहीं होता है।
पदार्थ के अनायास-सममित-टूटे हुए चरणों को एक कोटि प्राचल द्वारा चित्रित किया जाता है जो उस मात्रा का वर्णन करता है जो विचाराधीन सममित को तोड़ता है। उदाहरण के लिए, एक चुंबक में, कोटि प्राचल स्थानीय चुंबकत्व है।
निरंतर सममित का सहज भंजन अनिवार्य रूप से गैपलेस के साथ होता है (जिसका अर्थ है कि इन मोडों को उत्तेजित करने के लिए कोई ऊर्जा खर्च नहीं होती है) नंबू-गोल्डस्टोन मोड कोटि प्राचल के धीमे, लंबे-तरंगदैर्ध्य उतार-चढ़ाव से जुड़े होते हैं। उदाहरण के लिए, एक क्रिस्टल में कंपन मोड, जिसे फोनन के रूप में जाना जाता है, क्रिस्टल के परमाणुओं के धीमे घनत्व में उतार-चढ़ाव से जुड़ा होता है। चुम्बकों के लिए संबद्ध गोल्डस्टोन मोड स्पिन की दोलन तरंगें हैं जिन्हें स्पिन-तरंगों के रूप में जाना जाता है। सममित-तोड़ने वाली अवस्था के लिए, जिनका कोटि प्राचल एक संरक्षित मात्रा नहीं है, नंबू-गोल्डस्टोन मोड सामान्यत: द्रव्यमान रहित होते हैं और स्थिर वेग से फैलते हैं।
मर्मिन और वैगनर के कारण एक महत्वपूर्ण प्रमेय बताता है कि, सीमित तापमान पर, नंबू-गोल्डस्टोन मोड के थर्मल सक्रिय उतार-चढ़ाव लंबी दूरी के क्रम को नष्ट कर देते हैं, और एक- और दो-आयामी प्रणालियों में सहज सममित को तोड़ने से रोकते हैं। इसी प्रकार, कोटि प्राचल के क्वांटम उतार-चढ़ाव शून्य तापमान पर भी एक-आयामी प्रणालियों में अधिकांश प्रकार की निरंतर सममित को तोड़ने से रोकते हैं। (एक महत्वपूर्ण अपवाद लौहचुंबक है, जिसका कोटि प्राचल, चुंबकत्व, बिल्कुल संरक्षित मात्रा है और इसमें कोई क्वांटम उतार-चढ़ाव नहीं होता है।)
अन्य लंबी दूरी की अन्योन्यकारी प्रणालियाँ, जैसे कि कूलम्ब क्षमता या युकावा क्षमता के माध्यम से बातचीत करने वाली बेलनाकार घुमावदार सतहों को अनुवादात्मक और घूर्णी सममित को तोड़ने के लिए दिखाया गया है।[13] यह दिखाया गया था, एक सममित हैमिल्टनियन की उपस्थिति में, और अनंत मात्रा की सीमा में, प्रणाली स्वचालित रूप से एक चिरल कॉन्फ़िगरेशन को अपनाता है - अर्थात, दर्पण विमान सममित को तोड़ देता है।
सामान्यीकरण और तकनीकी उपयोग
सहज सममित भंजन के लिए, एक ऐसी प्रणाली होनी चाहिए जिसमें कई समान रूप से संभावित परिणाम हों। इसलिए संपूर्ण प्रणाली इन परिणामों के संबंध में सममित (भौतिकी) है। चूंकि, यदि प्रणाली का नमूना लिया गया है (अर्थात यदि प्रणाली वास्तव में उपयोग किया जाता है या किसी भी तरह से अंतःक्रिया किया जाता है), तो एक विशिष्ट परिणाम अवश्य आना चाहिए। चूंकि संपूर्ण प्रणाली सममित है, इसका सामना कभी भी इस सममित से नहीं होता है, बल्कि केवल एक विशिष्ट असममित स्थिति में होता है। इसलिए, उस सिद्धांत में सममित को अनायास विच्छिन्न हुआ कहा जाता है। फिर भी, यह तथ्य कि प्रत्येक परिणाम समान रूप से संभावित है, अंतर्निहित सममित का प्रतिबिंब है, जिसे अधिकांशत: छिपी हुई सममित कहा जाता है, और इसके महत्वपूर्ण औपचारिक परिणाम होते हैं। (नंबू-गोल्डस्टोन बोसोन पर लेख देखें।)
जब एक सिद्धांत सममित समूह के संबंध में सममित होता है, लेकिन इसके लिए आवश्यक है कि समूह का एक तत्व अलग हो, तो सहज सममित टूट जाती है। सिद्धांत को यह निर्देशित नहीं करना चाहिए कि कौन सा सदस्य विशिष्ट है, केवल वही है। इस बिंदु से, सिद्धांत को ऐसे माना जा सकता है जैसे कि यह तत्व वास्तव में अलग है, इस प्रावधान के साथ कि इस तरह से पाए गए किसी भी परिणाम को समूह के प्रत्येक तत्व के औसत को अलग मानकर, पुन: सममित किया जाना चाहिए।
भौतिकी सिद्धांतों में महत्वपूर्ण अवधारणा कोटि प्राचल है। यदि कोई फ़ील्ड (अधिकांशत: एक पृष्ठभूमि फ़ील्ड) है जो एक अपेक्षा तत्व प्राप्त करता है (जरूरी नहीं कि एक वैक्यूम अपेक्षा तत्व) जो प्रश्न में सममित के अनुसार अपरिवर्तनीय नहीं है, तो हम कहते हैं कि प्रणाली आदेशित चरण में है, और सममित स्वचालित रूप से है विच्छिन्न हुआ है। ऐसा इसलिए है क्योंकि अन्य सबप्रणाली कोटि प्राचल के साथ अंतःक्रिया करते हैं, जो मापे जाने वाले संदर्भ के एक फ्रेम को निर्दिष्ट करता है। उस स्थिति में, निर्वात अवस्था प्रारंभिक सममित का पालन नहीं करती है (जो इसे रैखिक रूप से महसूस किए गए 'विग्नर मोड' में अपरिवर्तनीय बनाए रखेगी, जिसमें यह एक एकल होगा), और, इसके अतिरिक्त (छिपी हुई) सममित के अनुसार परिवर्तन होता है, जिसे अब लागू किया गया है (नॉनलाइनर) 'नंबू-गोल्डस्टोन मोड' में। सामान्यत:, हिग्स तंत्र की अनुपस्थिति में, द्रव्यमान रहित गोल्डस्टोन बोसॉन उत्पन्न होते हैं।
सममित समूह असतत हो सकता है, जैसे कि क्रिस्टल का अंतरिक्ष समूह, या निरंतर (उदाहरण के लिए, एक झूठ समूह), जैसे कि अंतरिक्ष की घूर्णी सममित, चूंकि, यदि प्रणाली में केवल एक ही स्थानिक आयाम है, तो पूर्ण क्वांटम यांत्रिकी की निर्वात स्थिति में केवल असतत सममित को तोड़ा जा सकता है, चूंकि एक शास्त्रीय समाधान निरंतर सममित को तोड़ सकता है।
नोबेल पुरस्कार
7 अक्टूबर 2008 को, रॉयल स्वीडिश एकेडमी ऑफ साइंसेज ने उप-परमाणु भौतिकी सममित तोड़ने में उनके काम के लिए तीन वैज्ञानिकों को भौतिकी में 2008 के नोबेल पुरस्कार से सम्मानित किया। शिकागो विश्वविद्यालय के योइचिरो नंबु ने मजबूत अंतःक्रियाओं, विशेष रूप से चिरल सममित तोड़ने के संदर्भ में सहज भंजन सममित के तंत्र की खोज के लिए आधा पुरस्कार जीता। क्योटो विश्वविद्यालय के भौतिक विज्ञानी मकोतो कोबायाशी (भौतिक विज्ञानी) और तिथि के अनुसार मास ने कमजोर अंतःक्रियाओं में सीपी सममित को तोड़ने वाली स्पष्ट सममित की उत्पत्ति की खोज के लिए पुरस्कार का दूसरा भाग साझा किया।[14] यह उत्पत्ति अंततः हिग्स तंत्र पर निर्भर है, लेकिन, अब तक हिग्स कपलिंग की बस इतनी ही विशेषता के रूप में समझा जाता है, न कि अनायास भंजन हुई सममित घटना।
यह भी देखें
- ऑटोकैटलिटिक प्रतिक्रियाएं और आदेश निर्माण
- प्रलय सिद्धांत
- चिरल समरूपता का टूटना
- सीपी-उल्लंघन
- फर्मी बॉल
- गुरुत्वाकर्षण सिद्धांत को मापें
- गोल्डस्टोन बोसोन
- भव्य एकीकृत सिद्धांत
- हिग्स तंत्र
- हिग्स बॉसन
- हिग्स फील्ड (शास्त्रीय)
- अपरिवर्तनीयता
- चिरल समरूपता को तोड़ने का चुंबकीय उत्प्रेरण
- मर्मिन-वैग्नर प्रमेय
- नॉर्टन का गुंबद
- दूसरे क्रम का चरण संक्रमण
- रसायन विज्ञान में सहज पूर्ण असममित संश्लेषण
- समरूपता का टूटना
- टैच्योन संघनन
- 1964 पीआरएल समरूपता कागज तोड़ना
टिप्पणियाँ
- ^ Note that (as in fundamental Higgs driven spontaneous gauge symmetry breaking) the term "symmetry breaking" is a misnomer when applied to gauge symmetries.
संदर्भ
- ↑ Miransky, Vladimir A. (1993). क्वांटम क्षेत्र सिद्धांतों में गतिशील समरूपता को तोड़ना. World Scientific. p. 15. ISBN 9810215584.
- ↑ Arodz, Henryk; Dziarmaga, Jacek; Zurek, Wojciech Hubert, eds. (30 November 2003). समरूपता तोड़ने के पैटर्न. Springer. p. 141. ISBN 9781402017452.
- ↑ Cornell, James, ed. (21 November 1991). Bubbles, Voids and Bumps in Time: The New Cosmology. Cambridge University Press. p. 125. ISBN 9780521426732.
- ↑ Edelman, Gerald M. (1992). Bright Air, Brilliant Fire: On the Matter of the Mind. New York: BasicBooks. p. 203.
- ↑ Goldstone, J. (1961). ""सुपरकंडक्टर" समाधान के साथ क्षेत्र सिद्धांत". Il Nuovo Cimento. 19 (1): 154–164. Bibcode:1961NCim...19..154G. doi:10.1007/BF02812722. S2CID 120409034.
- ↑ Muñoz-Vega, R.; García-Quiroz, A.; López-Chávez, Ernesto; Salinas-Hernández, Encarnación (2012). "गैर-सापेक्षतावादी क्वांटम यांत्रिकी में सहज समरूपता टूटना". American Journal of Physics. 80 (10): 891–897. arXiv:1205.4773. Bibcode:2012AmJPh..80..891M. doi:10.1119/1.4739927. S2CID 119131875.
- ↑ Kibble, T W B. (2015). "इलेक्ट्रोवीक समरूपता टूटने का इतिहास". Journal of Physics: Conference Series. 626 (1): 012001. arXiv:1502.06276. Bibcode:2015JPhCS.626a2001K. doi:10.1088/1742-6596/626/1/012001. S2CID 119290021.
- ↑ Steven Weinberg (20 April 2011). Dreams of a Final Theory: The Scientist's Search for the Ultimate Laws of Nature. Knopf Doubleday Publishing Group. ISBN 978-0-307-78786-6.
- ↑ Jeannerot, Rachel; Rocher, Jonathan; Sakellariadou, Mairi (24 November 2003). "सुपरसिमेट्रिक ग्रैंड यूनिफाइड सिद्धांतों में ब्रह्मांडीय स्ट्रिंग गठन कितना सामान्य है". Physical Review D. 68 (10): 103514. arXiv:hep-ph/0308134. Bibcode:2003PhRvD..68j3514J. doi:10.1103/PhysRevD.68.103514.
- ↑ A Brief History of Time, Stephen Hawking, Bantam; 10th anniversary edition (1998). pp. 73–74.[ISBN missing]
- ↑ William A. Bardeen; Christopher T. Hill; Manfred Lindner (1990). "Minimal dynamical symmetry breaking of the standard model". Physical Review D. 41 (5): 1647–1660. Bibcode:1990PhRvD..41.1647B. doi:10.1103/PhysRevD.41.1647. PMID 10012522.
- ↑ Chen, Xie; Gu, Zheng-Cheng; Wen, Xiao-Gang (2010). "स्थानीय एकात्मक परिवर्तन, लंबी दूरी की क्वांटम उलझाव, तरंग फ़ंक्शन पुनर्सामान्यीकरण, और टोपोलॉजिकल ऑर्डर". Phys. Rev. B. 82 (15): 155138. arXiv:1004.3835. Bibcode:2010PhRvB..82o5138C. doi:10.1103/physrevb.82.155138. S2CID 14593420.
- ↑ Kohlstedt, K.L.; Vernizzi, G.; Solis, F.J.; Olvera de la Cruz, M. (2007). "Spontaneous Chirality via Long-range Electrostatic Forces". Physical Review Letters. 99 (3): 030602. arXiv:0704.3435. Bibcode:2007PhRvL..99c0602K. doi:10.1103/PhysRevLett.99.030602. PMID 17678276. S2CID 37983980.
- ↑ The Nobel Foundation. "The Nobel Prize in Physics 2008". nobelprize.org. Retrieved January 15, 2008.
बाहरी संबंध
- For a pedagogic introduction to electroweak symmetry breaking with step by step derivations, not found in texts, of many key relations, see http://www.quantumfieldtheory.info/Electroweak_Sym_breaking.pdf
- Spontaneous symmetry breaking
- Physical Review Letters – 50th Anniversary Milestone Papers
- In CERN Courier, Steven Weinberg reflects on spontaneous symmetry breaking
- Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia
- History of Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia
- The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles
- International Journal of Modern Physics A: The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles
- Guralnik, G S; Hagen, C R and Kibble, T W B (1967). Broken Symmetries and the Goldstone Theorem. Advances in Physics, vol. 2 Interscience Publishers, New York. pp. 567–708 ISBN 0-470-17057-3
- Spontaneous Symmetry Breaking in Gauge Theories: a Historical Survey
- The Royal Society Publishing: Spontaneous symmetry breaking in gauge theories
- University of Cambridge, David Tong: Lectures on Quantum Field Theory for masters level students.

