चतुर्भुज (ज्यामिति): Difference between revisions
No edit summary |
m (5 revisions imported from alpha:चतुर्भुज_(ज्यामिति)) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Mathematical term for squaring a plane figure}} | {{short description|Mathematical term for squaring a plane figure}} | ||
{{Other uses| | {{Other uses|चतुर्भुज (बहुविकल्पी)}} | ||
गणित में, विशेष रूप से [[ज्यामिति]] में, '''चतुर्भुज''' (जिसे स्क्वेरिंग भी कहा जाता है) किसी दिए गए [[समतल आकृति]] के समान [[क्षेत्र]] के साथ [[वर्ग]] बनाने या उस क्षेत्र के संख्यात्मक मान की [[गणना]] करने की ऐतिहासिक प्रक्रिया है। शास्त्रीय उदाहरण [[वृत्त का चतुर्भुज]] (या वृत्त का वर्ग करना) है। चतुर्भुज समस्याएं कलन के विकास में समस्याओं के मुख्य स्रोतों के रूप में कार्य करती हैं। वे [[गणितीय विश्लेषण]] में महत्वपूर्ण विषयों का परिचय देते हैं। | गणित में, विशेष रूप से [[ज्यामिति]] में, '''चतुर्भुज''' (जिसे स्क्वेरिंग भी कहा जाता है) किसी दिए गए [[समतल आकृति]] के समान [[क्षेत्र]] के साथ [[वर्ग]] बनाने या उस क्षेत्र के संख्यात्मक मान की [[गणना]] करने की ऐतिहासिक प्रक्रिया है। शास्त्रीय उदाहरण [[वृत्त का चतुर्भुज]] (या वृत्त का वर्ग करना) है। चतुर्भुज समस्याएं कलन के विकास में समस्याओं के मुख्य स्रोतों के रूप में कार्य करती हैं। वे [[गणितीय विश्लेषण]] में महत्वपूर्ण विषयों का परिचय देते हैं। | ||
| Line 8: | Line 8: | ||
=== प्राचीनता === | === प्राचीनता === | ||
[[File:Lune.svg|thumb|हिप्पोक्रेट्स की लून प्रथम घूर्णन आकृति थी जिसके त्रुटिहीन क्षेत्रफल की गणना गणितीय रूप से की गई थी।]]ग्रीक गणित ने किसी आकृति के क्षेत्रफल के निर्धारण को ज्यामितीय रूप से समान क्षेत्रफल (वर्गीकरण) वाले [[वर्ग (ज्यामिति)]] के निर्माण की प्रक्रिया के रूप में समझा, इस प्रकार इस प्रक्रिया को चतुर्भुज नाम दिया गया। ग्रीक जियोमीटर सदैव सफल नहीं थे ([[वृत्त का वर्ग करना]] देखें), किंतु उन्होंने कुछ आकृतियों का चतुर्भुज बनाया, जिनकी भुजाएँ केवल रेखा खंड नहीं थीं, जैसे कि हिप्पोक्रेट्स का लून और परबोला का चतुर्भुज है। निश्चित यूनानी परंपरा के अनुसार, इन निर्माणों को केवल [[कम्पास और स्ट्रेटएज निर्माण|कम्पास और स्ट्रेटएज]] का उपयोग करके किया जाना था, चूँकि सभी [[यूनानी गणित|ग्रीक गणितज्ञ]] इस सिद्धांत का पालन नहीं करते थे। | [[File:Lune.svg|thumb|हिप्पोक्रेट्स की लून प्रथम घूर्णन आकृति थी जिसके त्रुटिहीन क्षेत्रफल की गणना गणितीय रूप से की गई थी।]]ग्रीक गणित ने किसी आकृति के क्षेत्रफल के निर्धारण को ज्यामितीय रूप से समान क्षेत्रफल (वर्गीकरण) वाले [[वर्ग (ज्यामिति)]] के निर्माण की प्रक्रिया के रूप में समझा, इस प्रकार इस प्रक्रिया को चतुर्भुज नाम दिया गया। ग्रीक जियोमीटर सदैव सफल नहीं थे ([[वृत्त का वर्ग करना]] देखें), किंतु उन्होंने कुछ आकृतियों का चतुर्भुज बनाया, जिनकी भुजाएँ केवल रेखा खंड नहीं थीं, जैसे कि हिप्पोक्रेट्स का लून और परबोला का चतुर्भुज है। निश्चित यूनानी परंपरा के अनुसार, इन निर्माणों को केवल [[कम्पास और स्ट्रेटएज निर्माण|कम्पास और स्ट्रेटएज]] का उपयोग करके किया जाना था, चूँकि सभी [[यूनानी गणित|ग्रीक गणितज्ञ]] इस सिद्धांत का पालन नहीं करते थे। | ||
[[File:Geometric mean.svg|thumb|left|220px|ज्यामितीय माध्य ज्ञात करने की प्राचीन विधि]]a और b भुजाओं वाले [[आयत]] के चतुर्भुज <math>x =\sqrt {ab}</math> के लिए भुजा वाले वर्ग का निर्माण करना आवश्यक है (a और b का ज्यामितीय माध्य)। इस प्रयोजन के लिए निम्नलिखित का उपयोग करना संभव है: यदि कोई लंबाई a और b के रेखा खंडों को जोड़ने से बने व्यास के साथ वृत्त खींचता है, तो व्यास से लंबवत खींचे गए रेखा खंड की ऊंचाई (आरेख में बीएच) है। उस बिंदु से उनके संबंध का बिंदु जहां यह वृत्त को पार करता है, a और b के ज्यामितीय माध्य के समान होता है। समान ज्यामितीय निर्माण समांतर चतुर्भुज और त्रिभुज के चतुर्भुज की समस्याओं का समाधान करता है। | [[File:Geometric mean.svg|thumb|left|220px|ज्यामितीय माध्य ज्ञात करने की प्राचीन विधि]]a और b भुजाओं वाले [[आयत]] के चतुर्भुज <math>x =\sqrt {ab}</math> के लिए भुजा वाले वर्ग का निर्माण करना आवश्यक है (a और b का ज्यामितीय माध्य)। इस प्रयोजन के लिए निम्नलिखित का उपयोग करना संभव है: यदि कोई लंबाई a और b के रेखा खंडों को जोड़ने से बने व्यास के साथ वृत्त खींचता है, तो व्यास से लंबवत खींचे गए रेखा खंड की ऊंचाई (आरेख में बीएच) है। उस बिंदु से उनके संबंध का बिंदु जहां यह वृत्त को पार करता है, a और b के ज्यामितीय माध्य के समान होता है। समान ज्यामितीय निर्माण समांतर चतुर्भुज और त्रिभुज के चतुर्भुज की समस्याओं का समाधान करता है। | ||
[[File:Quadrature parabole2.png|thumb|[[आर्किमिडीज|आर्किमिडीज़]] ने सिद्ध किया कि परवलयिक खंड का क्षेत्रफल उत्कीर्ण त्रिभुज के क्षेत्रफल का 4/3 है।]]वक्ररेखीय आकृतियों के लिए चतुर्भुज की समस्याएँ अधिक कठिन हैं। 19वीं दशक में कम्पास और स्ट्रेटएज के साथ वृत्त का चतुर्भुज असंभव सिद्ध हुआ था।<ref name=lindemann>{{cite journal |last1=Lindemann |first1=F.|author-link=Ferdinand von Lindemann |title=Über die Zahl π |journal=[[Mathematische Annalen]] |date=1882 |volume=20 |pages=213–225 |url=https://babel.hathitrust.org/cgi/pt?id=hvd.32044102917051;view=1up;seq=237 |trans-title=On the number π |language=de |doi=10.1007/bf01446522|s2cid=120469397}}</ref><ref name=fritsch>{{cite journal | [[File:Quadrature parabole2.png|thumb|[[आर्किमिडीज|आर्किमिडीज़]] ने सिद्ध किया कि परवलयिक खंड का क्षेत्रफल उत्कीर्ण त्रिभुज के क्षेत्रफल का 4/3 है।]]वक्ररेखीय आकृतियों के लिए चतुर्भुज की समस्याएँ अधिक कठिन हैं। 19वीं दशक में कम्पास और स्ट्रेटएज के साथ वृत्त का चतुर्भुज असंभव सिद्ध हुआ था।<ref name=lindemann>{{cite journal |last1=Lindemann |first1=F.|author-link=Ferdinand von Lindemann |title=Über die Zahl π |journal=[[Mathematische Annalen]] |date=1882 |volume=20 |pages=213–225 |url=https://babel.hathitrust.org/cgi/pt?id=hvd.32044102917051;view=1up;seq=237 |trans-title=On the number π |language=de |doi=10.1007/bf01446522|s2cid=120469397}}</ref><ref name=fritsch>{{cite journal | ||
| last = Fritsch | first = Rudolf | | last = Fritsch | first = Rudolf | ||
| Line 56: | Line 56: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 06/12/2023]] | [[Category:Created On 06/12/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 22:01, 18 December 2023
गणित में, विशेष रूप से ज्यामिति में, चतुर्भुज (जिसे स्क्वेरिंग भी कहा जाता है) किसी दिए गए समतल आकृति के समान क्षेत्र के साथ वर्ग बनाने या उस क्षेत्र के संख्यात्मक मान की गणना करने की ऐतिहासिक प्रक्रिया है। शास्त्रीय उदाहरण वृत्त का चतुर्भुज (या वृत्त का वर्ग करना) है। चतुर्भुज समस्याएं कलन के विकास में समस्याओं के मुख्य स्रोतों के रूप में कार्य करती हैं। वे गणितीय विश्लेषण में महत्वपूर्ण विषयों का परिचय देते हैं।
इतिहास
प्राचीनता
ग्रीक गणित ने किसी आकृति के क्षेत्रफल के निर्धारण को ज्यामितीय रूप से समान क्षेत्रफल (वर्गीकरण) वाले वर्ग (ज्यामिति) के निर्माण की प्रक्रिया के रूप में समझा, इस प्रकार इस प्रक्रिया को चतुर्भुज नाम दिया गया। ग्रीक जियोमीटर सदैव सफल नहीं थे (वृत्त का वर्ग करना देखें), किंतु उन्होंने कुछ आकृतियों का चतुर्भुज बनाया, जिनकी भुजाएँ केवल रेखा खंड नहीं थीं, जैसे कि हिप्पोक्रेट्स का लून और परबोला का चतुर्भुज है। निश्चित यूनानी परंपरा के अनुसार, इन निर्माणों को केवल कम्पास और स्ट्रेटएज का उपयोग करके किया जाना था, चूँकि सभी ग्रीक गणितज्ञ इस सिद्धांत का पालन नहीं करते थे।
a और b भुजाओं वाले आयत के चतुर्भुज के लिए भुजा वाले वर्ग का निर्माण करना आवश्यक है (a और b का ज्यामितीय माध्य)। इस प्रयोजन के लिए निम्नलिखित का उपयोग करना संभव है: यदि कोई लंबाई a और b के रेखा खंडों को जोड़ने से बने व्यास के साथ वृत्त खींचता है, तो व्यास से लंबवत खींचे गए रेखा खंड की ऊंचाई (आरेख में बीएच) है। उस बिंदु से उनके संबंध का बिंदु जहां यह वृत्त को पार करता है, a और b के ज्यामितीय माध्य के समान होता है। समान ज्यामितीय निर्माण समांतर चतुर्भुज और त्रिभुज के चतुर्भुज की समस्याओं का समाधान करता है।
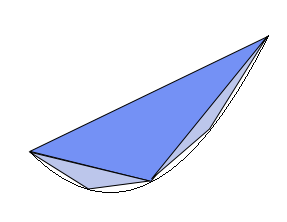
वक्ररेखीय आकृतियों के लिए चतुर्भुज की समस्याएँ अधिक कठिन हैं। 19वीं दशक में कम्पास और स्ट्रेटएज के साथ वृत्त का चतुर्भुज असंभव सिद्ध हुआ था।[1][2] फिर भी, कुछ आकृतियों के लिए चतुर्भुज का प्रदर्शन किया जा सकता है। आर्किमिडीज़ द्वारा अनुसंधान किये गए गोले की सतह के चतुर्भुज और परवलय खंड पुरातनता में विश्लेषण की सर्वोच्च उपलब्धि बन गए।
- किसी गोले की सतह का क्षेत्रफल गोले के बड़े वृत्त द्वारा बने वृत्त के क्षेत्रफल के चार गुना के समान होता है।
- परवलय के एक खंड का क्षेत्रफल इसे विभक्त करने वाली सीधी रेखा द्वारा निर्धारित किया जाता है जो इस खंड में अंकित त्रिभुज के क्षेत्रफल का 4/3 है।
इन परिणामों के प्रमाण के लिए, आर्किमिडीज़ ने यूडोक्सस से संबंधित एक्सहॉस्टिव की विधि का उपयोग किया।[3]
मध्यकालीन गणित
मध्ययुगीन यूरोप में, चतुर्भुज का अर्थ किसी भी विधि द्वारा क्षेत्रफल की गणना करना था। बहुधा अविभाज्य विधि का प्रयोग किया जाता था; यह यूनानियों के ज्यामितीय निर्माणों की तुलना में कम कठोर था, किंतु यह सरल और अधिक शक्तिशाली था। इसकी सहायता से, गैलीलियो गैलीली और गाइल्स डी रोबरवाल ने साइक्लोइड आर्क का क्षेत्र प्राप्त किया, ग्रेगोइरे डी सेंट-विंसेंट ने अतिशयोक्ति के (ओपस जियोमेट्रिकम, 1647) के अनुसार क्षेत्र का परीक्षण किया,[3]: 491 और अल्फोंस एंटोनियो डी सारासा डी सेंट- विंसेंट के शिष्य और टिप्पणीकार ने इस क्षेत्र का लघुगणक से संबंध नोट किया।[3]: 492 [4]
जॉन वालिस ने इस पद्धति का बीजगणित किया; उन्होंने अपने अरिथमेटिका इन्फिनिटोरम (1656) में कुछ श्रृंखलाएँ लिखीं जो कि अब निश्चित अभिन्न अंग कहलाती हैं, और उन्होंने उनके मानों की गणना की। इसहाक बैरो और जेम्स ग्रेगरी (गणितज्ञ) ने और प्रगति की: कुछ बीजगणितीय वक्रों और सर्पिलों के लिए चतुर्भुज है। क्रिस्टियान ह्यूजेन्स ने क्रांति के कुछ ठोस पदार्थों के सतह क्षेत्र का सफलतापूर्वक चतुर्भुज निष्पादित किया।
सेंट-विंसेंट और डी सारासा द्वारा हाइपरबोला के चतुर्भुज ने महत्वपूर्ण महत्व का नया फलन (गणित), प्राकृतिक लघुगणक प्रदान किया। इंटीग्रल कैलकुलस के आविष्कार के साथ क्षेत्र गणना के लिए सार्वभौमिक विधि आई। प्रतिक्रिया में, चतुर्भुज शब्द पारंपरिक हो गया है, और इसके अतिरिक्त क्षेत्र अनुसंधान करने वाले आधुनिक वाक्यांश का उपयोग सामान्यतः तकनीकी रूप से अविभाज्य निश्चित अभिन्न अंग की गणना के लिए किया जाता है।
यह भी देखें
- गाऊसी चतुर्भुज
- अतिपरवलयिक कोण
- संख्यात्मक एकीकरण
- क्वाड्राट्रिक्स
- तन्ह-सिंह चतुर्भुज
टिप्पणियाँ
- ↑ Lindemann, F. (1882). "Über die Zahl π" [On the number π]. Mathematische Annalen (in Deutsch). 20: 213–225. doi:10.1007/bf01446522. S2CID 120469397.
- ↑ Fritsch, Rudolf (1984). "The transcendence of π has been known for about a century—but who was the man who discovered it?". Results in Mathematics. 7 (2): 164–183. doi:10.1007/BF03322501. MR 0774394. S2CID 119986449.
- ↑ 3.0 3.1 3.2 Katz, Victor J. (1998). A History of Mathematics: An Introduction (2nd ed.). Addison Wesley Longman. ISBN 0-321-01618-1.
- ↑ Enrique A. Gonzales-Velasco (2011) Journey through Mathematics, § 2.4 Hyperbolic Logarithms, page 117
संदर्भ
- Boyer, C. B. (1989) A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7).
- Eves, Howard (1990) An Introduction to the History of Mathematics, Saunders, ISBN 0-03-029558-0,
- Christiaan Huygens (1651) Theoremata de Quadratura Hyperboles, Ellipsis et Circuli
- Jean-Etienne Montucla (1873) History of the Quadrature of the Circle, J. Babin translator, William Alexander Myers editor, link from HathiTrust.
- Christoph Scriba (1983) "Gregory's Converging Double Sequence: a new look at the controversy between Huygens and Gregory over the 'analytical' quadrature of the circle", Historia Mathematica 10:274–85.

