सक्रियण ऊर्जा: Difference between revisions
No edit summary |
|||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Energy that must be input to a system to undergo a reaction or process}} | {{Short description|Energy that must be input to a system to undergo a reaction or process}} | ||
[[Image:Incandescence.jpg|thumb|upright|[[ फेरोसेरियम ]] के एक टुकड़े के खिलाफ हड़ताली स्टील द्वारा बनाई गई चिंगारी इस [[ लेम्प बर्नर ]] में दहन शुरू करने के लिए सक्रियण ऊर्जा प्रदान करती है। चिंगारियों के रुकने के बाद नीली लौ अपने आप बनी रहती है क्योंकि लौ का निरंतर दहन अब ऊर्जावान रूप से अनुकूल है।]][[ रसायन विज्ञान ]] और भौतिकी में, सक्रियण ऊर्जा ऊर्जा की न्यूनतम मात्रा है जो यौगिकों को [[ रासायनिक प्रतिक्रिया ]] में परिणाम के लिए प्रदान की जानी चाहिए।<ref>{{Cite web|url=http://www.chem.fsu.edu/chemlab/chm1046course/activation|title=सक्रियण ऊर्जा|website=www.chem.fsu.edu|access-date=2017-01-13|archive-url=https://web.archive.org/web/20161207175516/http://www.chem.fsu.edu/chemlab/chm1046course/activation|archive-date=2016-12-07|url-status=dead}}</ref> सक्रियण ऊर्जा ( | [[Image:Incandescence.jpg|thumb|upright|[[ फेरोसेरियम ]] के एक टुकड़े के खिलाफ हड़ताली स्टील द्वारा बनाई गई चिंगारी इस [[ लेम्प बर्नर ]] में दहन शुरू करने के लिए सक्रियण ऊर्जा प्रदान करती है। चिंगारियों के रुकने के बाद नीली लौ अपने आप बनी रहती है क्योंकि लौ का निरंतर दहन अब ऊर्जावान रूप से अनुकूल है।]][[ रसायन विज्ञान ]] और भौतिकी में, सक्रियण ऊर्जा ऊर्जा की न्यूनतम मात्रा है जो यौगिकों को [[ रासायनिक प्रतिक्रिया | रासायनिक अभिक्रिया]] में परिणाम के लिए प्रदान की जानी चाहिए।<ref>{{Cite web|url=http://www.chem.fsu.edu/chemlab/chm1046course/activation|title=सक्रियण ऊर्जा|website=www.chem.fsu.edu|access-date=2017-01-13|archive-url=https://web.archive.org/web/20161207175516/http://www.chem.fsu.edu/chemlab/chm1046course/activation|archive-date=2016-12-07|url-status=dead}}</ref> सक्रियण ऊर्जा (''E''<sub>a</sub>) अभिक्रिया का माप [[ जूल प्रति मोल ]] (J/mol), या [[ किलोकलरीज प्रति मोल ]] (kcal/mol) में मापा जाता है।<ref>{{cite book |last1=Espenson |first1=James |title=रासायनिक कैनेटीक्स और प्रतिक्रिया तंत्र|date=1995 |publisher=McGraw-Hill |isbn=0070202605}}</ref> सक्रियण ऊर्जा को प्रारंभिक और अंतिम [[ थर्मोडायनामिक अवस्था | ऊष्मागतिक अवस्था]] से संबंधित [[ संभावित ऊर्जा ]] पृष्ठ के [[ न्यूनतम ]] को अलग करने वाले संभावित अवरोध (कभी-कभी ऊर्जा अवरोध कहा जाता है) के परिमाण के रूप में माना जा सकता है। एक रासायनिक अभिक्रिया के लिए एक उचित दर पर आगे बढ़ने के लिए, तंत्र का तापमान इतना अधिक होना चाहिए कि सक्रियण ऊर्जा के बराबर या उससे अधिक की स्थानांतरीय ऊर्जा वाले अणुओं की एक पर्याप्त संख्या उपस्थित हो। सक्रियण ऊर्जा शब्द की शुरुआत 1889 में स्वीडिश वैज्ञानिक [[ स्वंते अरहेनियस ]] ने की थी।<ref>{{Cite web|url=https://opentextbc.ca/introductorychemistry/chapter/activation-energy-and-the-arrhenius-equation-2/|title=सक्रियण ऊर्जा और अरहेनियस समीकरण - परिचयात्मक रसायन विज्ञान- पहला कनाडाई संस्करण|website=opentextbc.ca|language=en-US|access-date=2018-04-05|archive-date=2017-07-08|archive-url=https://web.archive.org/web/20170708223846/https://opentextbc.ca/introductorychemistry/chapter/activation-energy-and-the-arrhenius-equation-2/|url-status=dead}}</ref> | ||
== अन्य उपयोग == | == अन्य उपयोग == | ||
चूँकि यह सामान्यतः कम उपयोग किया जाता है, सक्रियण ऊर्जा [[ परमाणु प्रतिक्रिया | परमाणु अभिक्रियाओ]] पर भी लागू होती है<ref>{{Cite web|url=https://www.asc.ohio-state.edu/kagan.1/phy367/Lectures/P367_lec_14.html |publisher=Ohio State University |access-date=15 October 2021 |last1=Kagan |first1=Harris |last2=Barrett |first2=Tom |title=आधुनिक समाज में ऊर्जा: XIV। परमाणु ऊर्जा|type=Course}}</ref> और विभिन्न अन्य भौतिक घटनाओ में भी लागू होती है।<ref>Pratt, Thomas H. "Electrostatic Ignitions of Fires and Explosions" Wiley-AIChE (July 15, 1997) Center for Chemical Process Safety</ref>{{failed verification|date=October 2021}}<ref>{{cite journal |doi=10.1111/j.1151-2916.1990.tb05175.x |title=शुद्ध एल्यूमिना की दर-नियंत्रित सिंटरिंग से सीमा प्रसार के लिए सक्रियण ऊर्जा का अनुमान, और ज़िरकोनिया या टाइटेनिया के साथ एल्युमिना डोप किया गया|journal=Journal of the American Ceramic Society |volume=73 |issue=5 |pages=1172 |year=1990 |last1=Wang |first1=Jenqdaw |last2=Raj |first2=Rishi }}</ref><ref>{{cite journal |doi=10.1080/00150193.2012.707592 |title=फेरोइलेक्ट्रिक बेरियम टाइटेनेट में रमन फ्रीक्वेंसी, डंपिंग कॉन्स्टेंट और सॉफ्ट-ऑप्टिक मोड की एक्टिवेशन एनर्जी की तापमान निर्भरता|journal=Ferroelectrics |volume=432 |pages=14–21 |year=2012 |last1=Kiraci |first1=A |last2=Yurtseven |first2=H |s2cid=121142463 }}</ref><ref>{{cite journal |doi=10.1016/j.combustflame.2017.02.019 |title=उत्प्रेरक रूप से सक्रिय Ce 0.8 Gd 0.2 O 1.9 कोटिंग का प्रभाव MgO के भीतर मीथेन के विषम दहन पर ZrO 2 झरझरा सिरेमिक को स्थिर करता है|journal=Combustion and Flame |volume=180 |pages=32–39 |year=2017 |last1=Terracciano |first1=Anthony C |last2=De Oliveira |first2=Samuel |last3=Vazquez-Molina |first3=Demetrius |last4=Uribe-Romo |first4=Fernando J |last5=Vasu |first5=Subith S |last6=Orlovskaya |first6=Nina }}</ref> | |||
== तापमान पर निर्भरता और अरहेनियस समीकरण से संबंध == | == तापमान पर निर्भरता और अरहेनियस समीकरण से संबंध == | ||
{{Main| | {{Main|अरहेनियस समीकरण}} | ||
[[ अरहेनियस समीकरण ]] सक्रियण ऊर्जा और उस दर के बीच संबंध का मात्रात्मक आधार देता है जिस पर | [[ अरहेनियस समीकरण ]] सक्रियण ऊर्जा और उस दर के बीच संबंध का मात्रात्मक आधार देता है जिस पर अभिक्रिया आगे बढ़ती है। समीकरण से, सक्रियण ऊर्जा संबंध के माध्यम से पाई जा सकती है | ||
<math display="block">k = A e^{{-E_\textrm{a}}/{(RT)}}</math> | <math display="block">k = A e^{{-E_\textrm{a}}/{(RT)}}</math> | ||
जहां | जहां A अभिक्रिया के लिए [[ पूर्व-घातीय कारक ]] है, आर सार्वभौमिक [[ गैस स्थिरांक ]] है, T पूर्ण तापमान है (सामान्यतः [[ केल्विन ]] में), और k [[ प्रतिक्रिया दर स्थिर | अभिक्रिया दर स्थिरांक]] है। ''A'', ''E''<sub>a</sub>. को जाने बिना भी तापमान के एक फलन के रूप में अभिक्रिया दर गुणांक में भिन्नता से मूल्यांकन किया जा सकता है (अरहेनियस समीकरण की वैधता के भीतर)। | ||
अधिक | अधिक विकसित स्तर पर, अरहेनियस समीकरण से शुद्ध अरहेनियस सक्रियण ऊर्जा शब्द को प्रयोगात्मक रूप से निर्धारित पैरामीटर के रूप में सबसे अच्छा माना जाता है जो तापमान के प्रति अभिक्रिया दर की संवेदनशीलता को दर्शाता है। इस सक्रियण ऊर्जा को प्राथमिक अभिक्रिया के लिए प्रारम्भ अवरोध के साथ जोड़ने पर दो आपत्तियां हैं। सबसे पहले, यह अधिकांश स्पष्ट नहीं होता है कि अभिक्रिया एक चरण में आगे बढ़ती है या नहीं; प्रारम्भ अवरोध जो सभी प्रारंभिक चरणों में औसत होते हैं, उनका सैद्धांतिक मूल्य बहुत कम होता है। दूसरा, भले ही अध्ययन की जा रही अभिक्रिया प्राथमिक हो, व्यक्तिगत टकरावों का एक स्पेक्ट्रम अरबों अणुओं से जुड़े थोक ('बल्ब') प्रयोगों से प्राप्त दर स्थिरांक में योगदान देता है, जिसमें कई अलग-अलग अभिक्रिया शील टक्कर ज्यामिति और कोण, अलग-अलग अनुवाद और (संभवतः) कंपन होते हैं। ऊर्जाएँ - जिनमें से सभी विभिन्न सूक्ष्म अभिक्रिया दरों को जन्म दे सकती हैं।{{citation needed|date=May 2018}} | ||
== उत्प्रेरक == | == उत्प्रेरक == | ||
{{Main| | {{Main|उत्प्रेरण}} | ||
[[File:Activation2 updated.svg|left|thumb|एंजाइम-उत्प्रेरित एक्ज़ोथिर्मिक | [[File:Activation2 updated.svg|left|thumb|एंजाइम-उत्प्रेरित एक्ज़ोथिर्मिक अभिक्रिया अभिक्रिया का उदाहरण]] | ||
[[Image:Activation energy.svg|thumb|240x240px|सक्रियण ऊर्जा के बीच संबंध (<math>E_\textrm{a}</math>) और एक उत्प्रेरक के साथ और बिना | [[Image:Activation energy.svg|thumb|240x240px|सक्रियण ऊर्जा के बीच संबंध (<math>E_\textrm{a}</math>) और एक उत्प्रेरक के साथ और बिना अभिक्रिया के मानक थैलेपी (ΔH), [[ प्रतिक्रिया समन्वय | अभिक्रिया समन्वय]] के खिलाफ प्लॉट किए गए। उच्चतम ऊर्जा स्थिति (शिखर स्थिति) संक्रमण अवस्था का प्रतिनिधित्व करती है। उत्प्रेरक के साथ, संक्रमण अवस्था में प्रवेश करने के लिए आवश्यक ऊर्जा कम हो जाती है, जिससे अभिक्रिया शुरू करने के लिए आवश्यक ऊर्जा कम हो जाती है]]एक पदार्थ जो सक्रियण ऊर्जा को कम करने के लिए संक्रमण अवस्था को संशोधित करता है उसे [[ उत्प्रेरक ]] कहा जाता है; एक उत्प्रेरक जो केवल प्रोटीन से बना होता है और (यदि लागू हो) छोटे अणु सहकारकों को [[ एंजाइम ]] कहा जाता है। एक उत्प्रेरक अभिक्रिया में बिना बदले अभिक्रिया की दर को बढ़ाता है।<ref>{{Cite web|url=http://antoine.frostburg.edu/chem/senese/101/reactions/faq/examples-of-catalysts.shtml|title=सामान्य रसायन विज्ञान ऑनलाइन: अक्सर पूछे जाने वाले प्रश्न: रासायनिक परिवर्तन: उत्प्रेरकों को शामिल करने वाली प्रतिक्रियाओं के कुछ उदाहरण क्या हैं?|website=antoine.frostburg.edu|access-date=2017-01-13}}</ref> इसके अतिरिक्त, उत्प्रेरक सक्रियण ऊर्जा को कम करता है, लेकिन यह मूल अभिकारकों या उत्पादों की ऊर्जा को नहीं बदलता है, और इसलिए संतुलन नहीं बदलता है।<ref>{{cite web|last1=Bui|first1=Matthew|title=अरहेनियस कानून: सक्रियण ऊर्जा|url=https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Kinetics/Modeling_Reaction_Kinetics/Temperature_Dependence_of_Reaction_Rates/The_Arrhenius_Law/The_Arrhenius_Law%3A_Activation_Energies|website=Chemistry LibreTexts|publisher=UC Davis|access-date=February 17, 2017}}</ref> बल्कि, अभिक्रिया शील ऊर्जा और उत्पाद ऊर्जा समान रहती है और केवल सक्रियण ऊर्जा बदल जाती है (कम)। | ||
एक उत्प्रेरक अधिक अनुकूल | एक उत्प्रेरक अधिक अनुकूल विधि से एक संक्रमण अवस्था बनाकर सक्रियण ऊर्जा को कम करने में सक्षम है। उत्प्रेरक, स्वभाव से, एक संक्रमण अवस्था में प्रगति की अभिक्रिया के अवस्तर के लिए अधिक आरामदायक के अनुरूप बनाते हैं। यह ऊर्जा के निकलने के कारण संभव है जो तब होता है जब क्रियाधार उत्प्रेरक की [[ सक्रिय साइट | सक्रिय स्थान]] से जुड़ जाता है। इस ऊर्जा को बंधन ऊर्जा के रूप में जाना जाता है। एक उत्प्रेरक के लिए बाध्य होने पर, सक्रिय स्थान (यानी [[ हाइड्रोजन बंध ]], [[ वैन डेर वाल्स फोर्स ]]) के भीतर क्रियाधार कई स्थिर बलों में भाग लेते हैं। सक्रिय स्थल के भीतर विशिष्ट और अनुकूल बंधन तब तक होता है जब तक क्रियाधार उच्च ऊर्जा संक्रमण अवस्था बनने के लिए नहीं बनता है। संक्रमण अवस्था का निर्माण उत्प्रेरक के साथ अधिक अनुकूल है क्योंकि सक्रिय स्थल के भीतर अनुकूल स्थिर बातचीत ऊर्जा जारी करती है। एक उत्प्रेरक की सक्रिय स्थान के भीतर एक स्थिर फिट होने पर एक रासायनिक अभिक्रिया एक उच्च-ऊर्जा संक्रमण अवस्था अणु को अधिक आसानी से बनाने में सक्षम होती है। एक अभिक्रिया की बाध्यकारी ऊर्जा वह ऊर्जा है जो तब निकलती है जब क्रियाधार और उत्प्रेरक के बीच अनुकूल बातचीत होती है। जारी की गई बाध्यकारी ऊर्जा अस्थिर संक्रमण अवस्था को प्राप्त करने में सहायता करती है। अन्यथा उत्प्रेरक के बिना अभिक्रियाओ को संक्रमण अवस्था को प्राप्त करने के लिए ऊर्जा के उच्च निवेश की आवश्यकता होती है। गैर-उत्प्रेरित अभिक्रियाओ में सक्रिय स्थल से मुक्त ऊर्जा उपलब्ध नहीं होती है, जैसे कि उत्प्रेरक एंजाइम अभिक्रिया में होती है।<ref>{{Cite book|title=जैव रसायन - नौवां संस्करण|last=Berg|first=Jeremy |publisher=WH Freeman and Company|year=2019|isbn=978-1-319-11467-1|location=New York, NY|pages=240–244}}</ref> | ||
== सक्रियण की गिब्स ऊर्जा के साथ संबंध == | == सक्रियण की गिब्स ऊर्जा के साथ संबंध == | ||
{{Main| | {{Main|संक्रमण अवस्था सिद्धांत}} | ||
E | अरहेनियस समीकरण में, सक्रियण ऊर्जा शब्द (E<sub>a</sub>) का उपयोग संक्रमण अवस्था तक पहुँचने के लिए आवश्यक ऊर्जा का वर्णन करने के लिए किया जाता है, और घातीय संबंध {{math|1=''k'' = ''A'' exp(−''E''<sub>a</sub>/''RT'')}} धारण करता है। संक्रमण अवस्था सिद्धांत में, अभिक्रिया दर और संक्रमण राज्य के बीच संबंधों का एक अधिक परिष्कृत मॉडल, एक सतही रूप से समान गणितीय संबंध, आइरिंग समीकरण, का उपयोग अभिक्रिया की दर स्थिरांक का वर्णन करने के लिए किया जाता है: {{math|1=''k'' = (''k''<sub>B</sub>''T'' / ''h'') exp(−Δ''G''<sup>‡</sup> / ''RT'')}}. लेकिन, घटनात्मक रूप से अभिक्रिया दर की तापमान निर्भरता को नमूना लेने के अतिरिक्त , आइरिंग समीकरण एक अभिक्रिया के व्यक्तिगत प्राथमिक चरणों को नमूना बानाता है। इस प्रकार, एक बहु-चरणीय प्रक्रिया के लिए, दो नमूनों के बीच कोई सीधा संबंध नहीं है। फिर भी, अरहेनियस और आईरिंग समीकरणों के कार्यात्मक रूप समान हैं, और एक-चरणीय प्रक्रिया के लिए, अरहेनियस और आईरिंग मापदंडों के बीच सरल और रासायनिक रूप से सार्थक पत्राचार तैयार किया जा सकता है। | ||
सक्रियण की एन्थैल्पी | E<sub>a</sub> .का उपयोग करने के अतिरिक्त, आईरिंग समीकरण [[ गिब्स ऊर्जा ]] की अवधारणा और प्रतीक ΔG . का उपयोग करता है संक्रमण अवस्था को प्राप्त करने के लिए सक्रियता की गिब्स ऊर्जा को निरूपित करने के लिए। समीकरण में, k<sub>B</sub> और H क्रमशः बोल्ट्जमान और प्लैंक स्थिरांक हैं। चूकी समीकरण समान दिखते हैं, यह ध्यान रखना महत्वपूर्ण है कि गिब्स ऊर्जा में एन्थैल्पिक के अतिरिक्त एक एन्ट्रॉपी शब्द भी होता है। अरहेनियस समीकरण में, इस [[ एन्ट्रापी ]] शब्द का पूर्व-घातीय कारक a द्वारा अनुमान लगाया जाता है। अधिक विशेष रूप से, हम सक्रियण की एन्थैल्पी और एन्ट्रॉपी के संदर्भ में सक्रियता की गिब्स मुक्त ऊर्जा लिख सकते हैं: {{math|1=Δ''G''<sup>‡</sup> = Δ''H''<sup>‡</sup> − ''T'' Δ''S''<sup>‡</sup>}}. फिर, एक गैर-आणविक, एक-चरणीय अभिक्रिया के लिए, अनुमानित संबंध {{math|1=''E''<sub>a</sub> = Δ''H''<sup>‡</sup> + ''RT''}} तथा {{math|1=''A'' = (''k''<sub>B</sub>''T''/''h'') exp(1 + Δ''S''<sup>‡</sup>/''R'')}} लिख सकते है। ध्यान दें, क्यूकि, अरहेनियस सिद्धांत में उचित है, a तापमान स्वतंत्र है, जबकि यहां, T पर एक रैखिक निर्भरता है। एक-चरणीय गैर-आणविक प्रक्रिया के लिए जिसका आधा जीवन कमरे के तापमान पर लगभग 2 घंटे है, ΔG<sup>‡</sup> लगभग 23 किलो कैलोरी/मोल है। यह भी मोटे तौर पर E<sub>a</sub> का परिमाण है एक अभिक्रिया के लिए जो कमरे के तापमान पर कई घंटों तक चलती है। ''T''Δ''S''<sup>‡</sup> के अपेक्षाकृत छोटे परिमाण के कारण और सामान्य तापमान पर RT अधिकांश अभिक्रियाओ ं के लिए, मैला प्रवचन में, E<sub>a</sub>, Δ''G''<sup>‡</sup>, और Δ''H''<sup>‡</sup> अधिकांश मिश्रित होते हैं और सभी को सक्रियण ऊर्जा के रूप में संदर्भित किया जाता है। | ||
सक्रियण की एन्थैल्पी, एन्ट्रापी और गिब्स ऊर्जा को Δ<sup>‡</sup>''H''<sup>o</sup>, Δ<sup>‡</sup>''S''<sup>o</sup> and Δ<sup>‡</sup>''G''<sup>o</sup> के रूप में अधिक सही विधि से लिखा जाता है, जहां o मानक अवस्थाओ के बीच मूल्यांकन की गई मात्रा को दर्शाता है।<ref>{{cite web |title=सक्रियण की एन्थैल्पी|url=http://goldbook.iupac.org/terms/view/E02142 |website=IUPAC Gold Book (2nd edition, on-line version) |publisher=IUPAC (International Union of Pure and Applied Chemistry) |access-date=10 May 2020 |date=2019}}</ref><ref>{{cite book |last1=Steinfeld |first1=Jeffrey I. |last2=Francisco |first2=Joseph S.|last3=Hase |first3=William L.|title=रासायनिक कैनेटीक्स और गतिशीलता|date=1999 |publisher=Prentice Hall |isbn=0-13-737123-3 |page=301 |edition=2nd}}</ref> लेकिन , कुछ लेखक अंकन को सरल बनाने के लिए o को छोड़ देते हैं।<ref>{{cite book |last1=Atkins |first1=Peter |last2=de Paula |first2=Julio |title=एटकिंस 'भौतिक रसायन विज्ञान|url=https://archive.org/details/physicalchemistr00atki_572 |url-access=limited |date=2006 |publisher=W.H.Freeman |isbn=0-7167-8759-8 |page=[https://archive.org/details/physicalchemistr00atki_572/page/n914 883] |edition=8th |quote=... लेकिन हम नोटेशन पर अधिक बोझ से बचने के लिए मानक राज्य चिह्न को छोड़ देंगे।}}</ref><ref>{{cite book |last1=Laidler |first1=Keith J. |last2=Meiser |first2=John H.|title=भौतिक रसायन|date=1982 |publisher=Benjamin/Cummings |isbn=0-8053-5682-7 |page=381}}</ref> | |||
लेकिन, अभिक्रिया का कुल मुक्त ऊर्जा परिवर्तन सक्रियण ऊर्जा से स्वतंत्र होता है। भौतिक और रासायनिक अभिक्रिया एं या तो [[ एक्सर्जोनिक प्रतिक्रिया | एक्सर्जोनिक अभिक्रिया]] या एंडर्जोनिक अभिक्रिया हो सकती हैं, लेकिन सक्रियण ऊर्जा अभिक्रिया की [[ सहज प्रक्रिया | सहज प्रक्रिया]] से संबंधित नहीं है। समग्र अभिक्रिया ऊर्जा परिवर्तन सक्रियण ऊर्जा द्वारा परिवर्तित नहीं होता है। | |||
== नकारात्मक सक्रियण ऊर्जा == | == नकारात्मक सक्रियण ऊर्जा == | ||
कुछ | कुछ स्थितियो में, बढ़ते तापमान के साथ अभिक्रिया की दर कम हो जाती है। लगभग घातीय संबंध का पालन करते समय दर स्थिरांक अभी भी एक अरहेनियस अभिव्यक्ति के लिए फिट हो सकता है, इसका परिणाम E<sub>a</sub> के नकारात्मक मान होता है. | ||
नकारात्मक सक्रियण ऊर्जाओं को प्रदर्शित करने वाली प्राथमिक अभिक्रिया एं सामान्यतः बाधा रहित अभिक्रिया एं होती हैं, जिसमें अभिक्रिया की प्रक्रिया संभावित कुएं में अणुओं के कब्जे पर निर्भर करती है। तापमान में वृद्धि से टकराने वाले अणुओं की एक दूसरे पर कब्जा करने की संभावना कम हो जाती है (अधिक चमकदार टक्करों के साथ अभिक्रिया नहीं होती है क्योंकि उच्च गति संभावित कुएं से टकराने वाले कणों को बाहर ले जाती है), एक अभिक्रिया [[ क्रॉस सेक्शन (भौतिकी) ]] के रूप में व्यक्त की जाती है बढ़ते तापमान के साथ जो घट जाती है । ऐसी स्थिति अब संभावित अवरोध की ऊंचाई के रूप में प्रत्यक्ष व्याख्या की ओर नहीं ले जाती है।<ref>{{cite journal|journal=J. Phys. Chem.|title=नकारात्मक सक्रियण ऊर्जा और घुमावदार अरहेनियस प्लॉट। 1. संभावित कुओं पर प्रतिक्रियाओं का सिद्धांत|year=1984|pages=6429–6435| first1=Michael |last1=Mozurkewich |first2=Sidney|last2=Benson|volume=88 |issue=25 |doi=10.1021/j150669a073 }}</ref> | |||
कुछ बहु-चरणीय अभिक्रियाओ ं में स्पष्ट नकारात्मक सक्रियण ऊर्जाएँ भी हो सकती हैं। उदाहरण के लिए, दो-चरणीय अभिक्रिया A . के लिए समग्र दर स्थिरांक k {{eqm}} B, B → C k = k<sub>2</sub>K<sub>1</sub> . द्वारा दिया गया है, जहां K<sub>2</sub> दर-सीमित धीमी दूसरे चरण की दर स्थिरांक है और K<sub>1</sub> तीव्र प्रथम चरण का संतुलन स्थिरांक है। कुछ अभिक्रियाओ ं में, K<sub>1</sub> बढ़ने की तुलना में तापमान के साथ k<sub>2</sub> से अधिक तेजी से घटता है, जिससे k वास्तव में नकारात्मक प्रेक्षित सक्रियण ऊर्जा के अनुरूप तापमान के साथ घटता है।<ref>{{cite book |last1=Espenson |first1=James H. |title=रासायनिक गतिकी और प्रतिक्रिया तंत्र|date=1981 |publisher=McGraw-Hill |isbn=0-07-019667-2 |page=121}}</ref><ref>{{cite book |last1=Atkins |first1=Peter |last2=de Paula |first2=Julio |title=एटकिंस 'भौतिक रसायन विज्ञान|date=2006 |publisher=W. H. Freeman |isbn=0-7167-8759-8 |page=822 |edition=8th}}</ref><ref>{{cite web |last1=Kadir |first1=Tamara |title=3.2.2: पूर्व-संतुलन सन्निकटन|url=https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Kinetics/03%3A_Rate_Laws/3.02%3A_Reaction_Mechanisms/3.2.02%3A_Pre-equilibrium_Approximation |website=Chem Libre Texts |access-date=23 January 2022 |date=10 September 2020 |quote=यदि Ea<sub>1</sub> + Ea<sub>2</sub> <Ea<sub>−1</sub>}}</ref> हो तो समग्र सक्रियण ऊर्जा ऋणात्मक होती है | |||
एक उदाहरण [[ नाइट्रिक ऑक्साइड | नाइट्रिक ऑक्साइड]] का ऑक्सीकरण है जो एक टर्मोलेक्यूलर अभिक्रिया है <math>2 NO + O_2 \rightarrow 2 NO_2</math>. दर कानून है <math>v = k \, \left[ {\rm NO} \right]^2 \, \left[ {\rm O_2} \right]</math> एक नकारात्मक सक्रियण ऊर्जा के साथ।<ref>{{cite book |last1=Moore |first1=John W. |last2=Pearson |first2=Ralph G. |title=काइनेटिक्स और तंत्र|date=1981 |publisher=John Wiley and Sons |isbn=0-471-03558-0 |page=316 |edition=3rd}}</ref><ref>{{cite book |last1=Engel |first1=Thomas |last2=Reid |first2=Philip |title=भौतिक रसायन|date=2006 |publisher=Pearson. Benjamin-Cummings. |isbn=0-8053-3842-X |page=*34}}</ref> यह दो-चरणीय तंत्र द्वारा समझाया गया है: <math>2 NO \rightleftarrows N_2O_2</math> तथा <math>N_2O_2 + O_2 \rightarrow 2 NO_2</math>. | |||
कुछ धनायनी बहुलकीकरण अभिक्रियाओं में ऋणात्मक सक्रियण ऊर्जाएँ होती हैं जिससे तापमान के साथ दर घटती जाती है। श्रृंखला-वृद्धि | कुछ धनायनी बहुलकीकरण अभिक्रियाओं में ऋणात्मक सक्रियण ऊर्जाएँ होती हैं जिससे तापमान के साथ दर घटती जाती है। श्रृंखला-वृद्धि बहुलकीकरण के लिए, समग्र सक्रियण ऊर्जा है <math>\textstyle E = E_i + E_p - E_t</math>, जहां i, p और t क्रमशः दीक्षा, प्रसार और समाप्ति चरणों को संदर्भित करते हैं। प्रसार चरण में सामान्य रूप से एक बहुत छोटी सक्रियण ऊर्जा होती है, जिससे कि समग्र मूल्य नकारात्मक होता है यदि समाप्ति के लिए सक्रियण ऊर्जा दीक्षा के लिए उससे बड़ी है। धनायनी बहुलकीकरण के लिए समग्र सक्रियण ऊर्जा की सामान्य सीमा = 40 से +60 kJ/mol तक भिन्न होती है।<ref>{{cite book|last=Cowie|first=J. M. G.|title=पॉलिमर: आधुनिक सामग्री के रसायन विज्ञान और भौतिकी|year=1991|publisher=Blackie (USA: Chapman & Hall+)|page=88|isbn=0-216-92980-6|edition=2nd}}</ref> | ||
== 2D संभावित ऊर्जा सतह में सक्रियण ऊर्जा == | |||
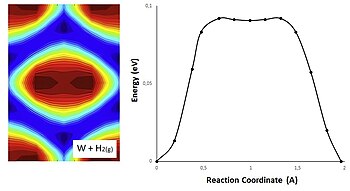
[[File:Comparative between 1D and 2D PES for tungsten and hydrogen gas reaction.jpg|thumb|350x350px|ये हाइड्रोजन गैस और टंगस्टन की अभिक्रिया के लिए PES प्रोफाइल हैं। बाईं ओर अभिक्रिया प्रोफ़ाइल प्रक्रिया का 2 आयामी मार्ग दिखाती है। दाईं ओर इसे उसी प्रक्षेपवक्र का 1 आयाम वाला परिप्रेक्ष्य दिखाया गया है।]]सक्रियण ऊर्जा को 2D [[ संभावित ऊर्जा सतह ]] ((PES) में दर्शाया जा सकता है, जहां अभिकारकों की ज्यामिति और सम्मालित ऊर्जा के बीच संबंध को स्थलाकृतिक मानचित्र के रूप में दर्शाया जाता है। | |||
निम्नलिखित ग्राफिक में गैस चरण और धातु में हाइड्रोजन के बीच एक अभिक्रिया का प्रतिनिधित्व टंगस्टन है। संभावित ऊर्जा PES गणनाओं के साथ प्राप्त की जाती है और ऊर्जा न्यूनीकरण#नज्ड इलास्टिक बैंड गणना से H की स्थिति के अनुरूप होती है। इन पदों पर संभावित ऊर्जा का मूल्यांकन करने के लिए [[ तख़्ता प्रक्षेप ]] के साथ 2-आयामी अंतःक्षेप का उपयोग किया जा सकता है।<ref>{{Cite journal|last=Kristinsdóttir|first=Lilja| last2=Skúlason |first2=Egill| date=2012-09-01|title=संक्रमण धातु सतहों पर हाइड्रोजन प्रसार का एक व्यवस्थित डीएफटी अध्ययन| url=http://www.sciencedirect.com/science/article/pii/S0039602812001604|journal=Surface Science| language=en| volume=606| issue=17 |pages=1400–1404|doi=10.1016/j.susc.2012.04.028|issn=0039-6028}}</ref> उत्पादों और अभिकारकों को नीली सतह में पाया जा सकता है, चूकी लाल सतह [[ स्थिर अवस्था (रसायन विज्ञान) ]] | स्थिर-अवस्था सन्निकटन से मेल खाती है। | |||
ऊर्जा मिनिमा के बीच की सतह जितनी धुंधली होगी, ऊर्जा | चित्र{{Definition needed|date=September 2022}} प्रक्षेपवक्र के अनुरूप। सतह जितनी नीली होगी, हाइड्रोजन बन्ध उतना ही मजबूत होगा, इसलिए नीले रंग मिनिमा ऊर्जा का प्रतिनिधित्व करते हैं और लाल रंग मैक्सिमा ऊर्जा का प्रतिनिधित्व करता हैं। टंगस्टन का PES एक सा है, और पुल स्थल पर एक डुबकी है, यह डुबकी चित्रण के केंद्र में रंग परिवर्तन से मेल खाती है | ||
ऊर्जा मिनिमा के बीच की सतह जितनी अधिक धुंधली होगी, ऊर्जा अवरोधक उतने ही कम होंगे, और इसलिए अधिक आसानी से हाइड्रोजन सतहों के साथ यात्रा करेगी। | |||
== यह भी देखें == | == यह भी देखें == | ||
| Line 69: | Line 75: | ||
{{Firelighting}} | {{Firelighting}} | ||
{{Authority control}} | {{Authority control}} | ||
[[Category: | [[Category:AC with 0 elements]] | ||
[[Category:All articles with failed verification]] | |||
[[Category:All articles with unsourced statements]] | |||
[[Category:Articles with failed verification from October 2021]] | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with invalid date parameter in template]] | |||
[[Category:Articles with short description]] | |||
[[Category:Articles with unsourced statements from May 2018]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:CS1 maint]] | |||
[[Category:CS1 Ελληνικά-language sources (el)]] | |||
[[Category:Citation Style 1 templates|W]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 02/11/2022]] | [[Category:Created On 02/11/2022]] | ||
[[Category:Exclude in print]] | |||
[[Category:Interwiki category linking templates]] | |||
[[Category:Interwiki link templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite web]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikimedia Commons templates]] | |||
[[Category:Wikipedia fully protected templates|Cite web]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:कटैलिसीस]] | |||
[[Category:दहन]] | |||
[[Category:प्रतिक्रिया तंत्र]] | |||
[[Category:रासायनिक गतिकी]] | |||
Latest revision as of 15:32, 4 December 2022

रसायन विज्ञान और भौतिकी में, सक्रियण ऊर्जा ऊर्जा की न्यूनतम मात्रा है जो यौगिकों को रासायनिक अभिक्रिया में परिणाम के लिए प्रदान की जानी चाहिए।[1] सक्रियण ऊर्जा (Ea) अभिक्रिया का माप जूल प्रति मोल (J/mol), या किलोकलरीज प्रति मोल (kcal/mol) में मापा जाता है।[2] सक्रियण ऊर्जा को प्रारंभिक और अंतिम ऊष्मागतिक अवस्था से संबंधित संभावित ऊर्जा पृष्ठ के न्यूनतम को अलग करने वाले संभावित अवरोध (कभी-कभी ऊर्जा अवरोध कहा जाता है) के परिमाण के रूप में माना जा सकता है। एक रासायनिक अभिक्रिया के लिए एक उचित दर पर आगे बढ़ने के लिए, तंत्र का तापमान इतना अधिक होना चाहिए कि सक्रियण ऊर्जा के बराबर या उससे अधिक की स्थानांतरीय ऊर्जा वाले अणुओं की एक पर्याप्त संख्या उपस्थित हो। सक्रियण ऊर्जा शब्द की शुरुआत 1889 में स्वीडिश वैज्ञानिक स्वंते अरहेनियस ने की थी।[3]
अन्य उपयोग
चूँकि यह सामान्यतः कम उपयोग किया जाता है, सक्रियण ऊर्जा परमाणु अभिक्रियाओ पर भी लागू होती है[4] और विभिन्न अन्य भौतिक घटनाओ में भी लागू होती है।[5][failed verification][6][7][8]
तापमान पर निर्भरता और अरहेनियस समीकरण से संबंध
अरहेनियस समीकरण सक्रियण ऊर्जा और उस दर के बीच संबंध का मात्रात्मक आधार देता है जिस पर अभिक्रिया आगे बढ़ती है। समीकरण से, सक्रियण ऊर्जा संबंध के माध्यम से पाई जा सकती है
अधिक विकसित स्तर पर, अरहेनियस समीकरण से शुद्ध अरहेनियस सक्रियण ऊर्जा शब्द को प्रयोगात्मक रूप से निर्धारित पैरामीटर के रूप में सबसे अच्छा माना जाता है जो तापमान के प्रति अभिक्रिया दर की संवेदनशीलता को दर्शाता है। इस सक्रियण ऊर्जा को प्राथमिक अभिक्रिया के लिए प्रारम्भ अवरोध के साथ जोड़ने पर दो आपत्तियां हैं। सबसे पहले, यह अधिकांश स्पष्ट नहीं होता है कि अभिक्रिया एक चरण में आगे बढ़ती है या नहीं; प्रारम्भ अवरोध जो सभी प्रारंभिक चरणों में औसत होते हैं, उनका सैद्धांतिक मूल्य बहुत कम होता है। दूसरा, भले ही अध्ययन की जा रही अभिक्रिया प्राथमिक हो, व्यक्तिगत टकरावों का एक स्पेक्ट्रम अरबों अणुओं से जुड़े थोक ('बल्ब') प्रयोगों से प्राप्त दर स्थिरांक में योगदान देता है, जिसमें कई अलग-अलग अभिक्रिया शील टक्कर ज्यामिति और कोण, अलग-अलग अनुवाद और (संभवतः) कंपन होते हैं। ऊर्जाएँ - जिनमें से सभी विभिन्न सूक्ष्म अभिक्रिया दरों को जन्म दे सकती हैं।[citation needed]
उत्प्रेरक

एक पदार्थ जो सक्रियण ऊर्जा को कम करने के लिए संक्रमण अवस्था को संशोधित करता है उसे उत्प्रेरक कहा जाता है; एक उत्प्रेरक जो केवल प्रोटीन से बना होता है और (यदि लागू हो) छोटे अणु सहकारकों को एंजाइम कहा जाता है। एक उत्प्रेरक अभिक्रिया में बिना बदले अभिक्रिया की दर को बढ़ाता है।[9] इसके अतिरिक्त, उत्प्रेरक सक्रियण ऊर्जा को कम करता है, लेकिन यह मूल अभिकारकों या उत्पादों की ऊर्जा को नहीं बदलता है, और इसलिए संतुलन नहीं बदलता है।[10] बल्कि, अभिक्रिया शील ऊर्जा और उत्पाद ऊर्जा समान रहती है और केवल सक्रियण ऊर्जा बदल जाती है (कम)।
एक उत्प्रेरक अधिक अनुकूल विधि से एक संक्रमण अवस्था बनाकर सक्रियण ऊर्जा को कम करने में सक्षम है। उत्प्रेरक, स्वभाव से, एक संक्रमण अवस्था में प्रगति की अभिक्रिया के अवस्तर के लिए अधिक आरामदायक के अनुरूप बनाते हैं। यह ऊर्जा के निकलने के कारण संभव है जो तब होता है जब क्रियाधार उत्प्रेरक की सक्रिय स्थान से जुड़ जाता है। इस ऊर्जा को बंधन ऊर्जा के रूप में जाना जाता है। एक उत्प्रेरक के लिए बाध्य होने पर, सक्रिय स्थान (यानी हाइड्रोजन बंध , वैन डेर वाल्स फोर्स ) के भीतर क्रियाधार कई स्थिर बलों में भाग लेते हैं। सक्रिय स्थल के भीतर विशिष्ट और अनुकूल बंधन तब तक होता है जब तक क्रियाधार उच्च ऊर्जा संक्रमण अवस्था बनने के लिए नहीं बनता है। संक्रमण अवस्था का निर्माण उत्प्रेरक के साथ अधिक अनुकूल है क्योंकि सक्रिय स्थल के भीतर अनुकूल स्थिर बातचीत ऊर्जा जारी करती है। एक उत्प्रेरक की सक्रिय स्थान के भीतर एक स्थिर फिट होने पर एक रासायनिक अभिक्रिया एक उच्च-ऊर्जा संक्रमण अवस्था अणु को अधिक आसानी से बनाने में सक्षम होती है। एक अभिक्रिया की बाध्यकारी ऊर्जा वह ऊर्जा है जो तब निकलती है जब क्रियाधार और उत्प्रेरक के बीच अनुकूल बातचीत होती है। जारी की गई बाध्यकारी ऊर्जा अस्थिर संक्रमण अवस्था को प्राप्त करने में सहायता करती है। अन्यथा उत्प्रेरक के बिना अभिक्रियाओ को संक्रमण अवस्था को प्राप्त करने के लिए ऊर्जा के उच्च निवेश की आवश्यकता होती है। गैर-उत्प्रेरित अभिक्रियाओ में सक्रिय स्थल से मुक्त ऊर्जा उपलब्ध नहीं होती है, जैसे कि उत्प्रेरक एंजाइम अभिक्रिया में होती है।[11]
सक्रियण की गिब्स ऊर्जा के साथ संबंध
अरहेनियस समीकरण में, सक्रियण ऊर्जा शब्द (Ea) का उपयोग संक्रमण अवस्था तक पहुँचने के लिए आवश्यक ऊर्जा का वर्णन करने के लिए किया जाता है, और घातीय संबंध k = A exp(−Ea/RT) धारण करता है। संक्रमण अवस्था सिद्धांत में, अभिक्रिया दर और संक्रमण राज्य के बीच संबंधों का एक अधिक परिष्कृत मॉडल, एक सतही रूप से समान गणितीय संबंध, आइरिंग समीकरण, का उपयोग अभिक्रिया की दर स्थिरांक का वर्णन करने के लिए किया जाता है: k = (kBT / h) exp(−ΔG‡ / RT). लेकिन, घटनात्मक रूप से अभिक्रिया दर की तापमान निर्भरता को नमूना लेने के अतिरिक्त , आइरिंग समीकरण एक अभिक्रिया के व्यक्तिगत प्राथमिक चरणों को नमूना बानाता है। इस प्रकार, एक बहु-चरणीय प्रक्रिया के लिए, दो नमूनों के बीच कोई सीधा संबंध नहीं है। फिर भी, अरहेनियस और आईरिंग समीकरणों के कार्यात्मक रूप समान हैं, और एक-चरणीय प्रक्रिया के लिए, अरहेनियस और आईरिंग मापदंडों के बीच सरल और रासायनिक रूप से सार्थक पत्राचार तैयार किया जा सकता है।
Ea .का उपयोग करने के अतिरिक्त, आईरिंग समीकरण गिब्स ऊर्जा की अवधारणा और प्रतीक ΔG . का उपयोग करता है संक्रमण अवस्था को प्राप्त करने के लिए सक्रियता की गिब्स ऊर्जा को निरूपित करने के लिए। समीकरण में, kB और H क्रमशः बोल्ट्जमान और प्लैंक स्थिरांक हैं। चूकी समीकरण समान दिखते हैं, यह ध्यान रखना महत्वपूर्ण है कि गिब्स ऊर्जा में एन्थैल्पिक के अतिरिक्त एक एन्ट्रॉपी शब्द भी होता है। अरहेनियस समीकरण में, इस एन्ट्रापी शब्द का पूर्व-घातीय कारक a द्वारा अनुमान लगाया जाता है। अधिक विशेष रूप से, हम सक्रियण की एन्थैल्पी और एन्ट्रॉपी के संदर्भ में सक्रियता की गिब्स मुक्त ऊर्जा लिख सकते हैं: ΔG‡ = ΔH‡ − T ΔS‡. फिर, एक गैर-आणविक, एक-चरणीय अभिक्रिया के लिए, अनुमानित संबंध Ea = ΔH‡ + RT तथा A = (kBT/h) exp(1 + ΔS‡/R) लिख सकते है। ध्यान दें, क्यूकि, अरहेनियस सिद्धांत में उचित है, a तापमान स्वतंत्र है, जबकि यहां, T पर एक रैखिक निर्भरता है। एक-चरणीय गैर-आणविक प्रक्रिया के लिए जिसका आधा जीवन कमरे के तापमान पर लगभग 2 घंटे है, ΔG‡ लगभग 23 किलो कैलोरी/मोल है। यह भी मोटे तौर पर Ea का परिमाण है एक अभिक्रिया के लिए जो कमरे के तापमान पर कई घंटों तक चलती है। TΔS‡ के अपेक्षाकृत छोटे परिमाण के कारण और सामान्य तापमान पर RT अधिकांश अभिक्रियाओ ं के लिए, मैला प्रवचन में, Ea, ΔG‡, और ΔH‡ अधिकांश मिश्रित होते हैं और सभी को सक्रियण ऊर्जा के रूप में संदर्भित किया जाता है।
सक्रियण की एन्थैल्पी, एन्ट्रापी और गिब्स ऊर्जा को Δ‡Ho, Δ‡So and Δ‡Go के रूप में अधिक सही विधि से लिखा जाता है, जहां o मानक अवस्थाओ के बीच मूल्यांकन की गई मात्रा को दर्शाता है।[12][13] लेकिन , कुछ लेखक अंकन को सरल बनाने के लिए o को छोड़ देते हैं।[14][15]
लेकिन, अभिक्रिया का कुल मुक्त ऊर्जा परिवर्तन सक्रियण ऊर्जा से स्वतंत्र होता है। भौतिक और रासायनिक अभिक्रिया एं या तो एक्सर्जोनिक अभिक्रिया या एंडर्जोनिक अभिक्रिया हो सकती हैं, लेकिन सक्रियण ऊर्जा अभिक्रिया की सहज प्रक्रिया से संबंधित नहीं है। समग्र अभिक्रिया ऊर्जा परिवर्तन सक्रियण ऊर्जा द्वारा परिवर्तित नहीं होता है।
नकारात्मक सक्रियण ऊर्जा
कुछ स्थितियो में, बढ़ते तापमान के साथ अभिक्रिया की दर कम हो जाती है। लगभग घातीय संबंध का पालन करते समय दर स्थिरांक अभी भी एक अरहेनियस अभिव्यक्ति के लिए फिट हो सकता है, इसका परिणाम Ea के नकारात्मक मान होता है.
नकारात्मक सक्रियण ऊर्जाओं को प्रदर्शित करने वाली प्राथमिक अभिक्रिया एं सामान्यतः बाधा रहित अभिक्रिया एं होती हैं, जिसमें अभिक्रिया की प्रक्रिया संभावित कुएं में अणुओं के कब्जे पर निर्भर करती है। तापमान में वृद्धि से टकराने वाले अणुओं की एक दूसरे पर कब्जा करने की संभावना कम हो जाती है (अधिक चमकदार टक्करों के साथ अभिक्रिया नहीं होती है क्योंकि उच्च गति संभावित कुएं से टकराने वाले कणों को बाहर ले जाती है), एक अभिक्रिया क्रॉस सेक्शन (भौतिकी) के रूप में व्यक्त की जाती है बढ़ते तापमान के साथ जो घट जाती है । ऐसी स्थिति अब संभावित अवरोध की ऊंचाई के रूप में प्रत्यक्ष व्याख्या की ओर नहीं ले जाती है।[16]
कुछ बहु-चरणीय अभिक्रियाओ ं में स्पष्ट नकारात्मक सक्रियण ऊर्जाएँ भी हो सकती हैं। उदाहरण के लिए, दो-चरणीय अभिक्रिया A . के लिए समग्र दर स्थिरांक k ⇌ B, B → C k = k2K1 . द्वारा दिया गया है, जहां K2 दर-सीमित धीमी दूसरे चरण की दर स्थिरांक है और K1 तीव्र प्रथम चरण का संतुलन स्थिरांक है। कुछ अभिक्रियाओ ं में, K1 बढ़ने की तुलना में तापमान के साथ k2 से अधिक तेजी से घटता है, जिससे k वास्तव में नकारात्मक प्रेक्षित सक्रियण ऊर्जा के अनुरूप तापमान के साथ घटता है।[17][18][19] हो तो समग्र सक्रियण ऊर्जा ऋणात्मक होती है
एक उदाहरण नाइट्रिक ऑक्साइड का ऑक्सीकरण है जो एक टर्मोलेक्यूलर अभिक्रिया है . दर कानून है एक नकारात्मक सक्रियण ऊर्जा के साथ।[20][21] यह दो-चरणीय तंत्र द्वारा समझाया गया है: तथा .
कुछ धनायनी बहुलकीकरण अभिक्रियाओं में ऋणात्मक सक्रियण ऊर्जाएँ होती हैं जिससे तापमान के साथ दर घटती जाती है। श्रृंखला-वृद्धि बहुलकीकरण के लिए, समग्र सक्रियण ऊर्जा है , जहां i, p और t क्रमशः दीक्षा, प्रसार और समाप्ति चरणों को संदर्भित करते हैं। प्रसार चरण में सामान्य रूप से एक बहुत छोटी सक्रियण ऊर्जा होती है, जिससे कि समग्र मूल्य नकारात्मक होता है यदि समाप्ति के लिए सक्रियण ऊर्जा दीक्षा के लिए उससे बड़ी है। धनायनी बहुलकीकरण के लिए समग्र सक्रियण ऊर्जा की सामान्य सीमा = 40 से +60 kJ/mol तक भिन्न होती है।[22]
2D संभावित ऊर्जा सतह में सक्रियण ऊर्जा
सक्रियण ऊर्जा को 2D संभावित ऊर्जा सतह ((PES) में दर्शाया जा सकता है, जहां अभिकारकों की ज्यामिति और सम्मालित ऊर्जा के बीच संबंध को स्थलाकृतिक मानचित्र के रूप में दर्शाया जाता है।
निम्नलिखित ग्राफिक में गैस चरण और धातु में हाइड्रोजन के बीच एक अभिक्रिया का प्रतिनिधित्व टंगस्टन है। संभावित ऊर्जा PES गणनाओं के साथ प्राप्त की जाती है और ऊर्जा न्यूनीकरण#नज्ड इलास्टिक बैंड गणना से H की स्थिति के अनुरूप होती है। इन पदों पर संभावित ऊर्जा का मूल्यांकन करने के लिए तख़्ता प्रक्षेप के साथ 2-आयामी अंतःक्षेप का उपयोग किया जा सकता है।[23] उत्पादों और अभिकारकों को नीली सतह में पाया जा सकता है, चूकी लाल सतह स्थिर अवस्था (रसायन विज्ञान) | स्थिर-अवस्था सन्निकटन से मेल खाती है।
चित्र[definition needed] प्रक्षेपवक्र के अनुरूप। सतह जितनी नीली होगी, हाइड्रोजन बन्ध उतना ही मजबूत होगा, इसलिए नीले रंग मिनिमा ऊर्जा का प्रतिनिधित्व करते हैं और लाल रंग मैक्सिमा ऊर्जा का प्रतिनिधित्व करता हैं। टंगस्टन का PES एक सा है, और पुल स्थल पर एक डुबकी है, यह डुबकी चित्रण के केंद्र में रंग परिवर्तन से मेल खाती है
ऊर्जा मिनिमा के बीच की सतह जितनी अधिक धुंधली होगी, ऊर्जा अवरोधक उतने ही कम होंगे, और इसलिए अधिक आसानी से हाइड्रोजन सतहों के साथ यात्रा करेगी।
यह भी देखें
- सक्रियण ऊर्जा एसिम्प्टोटिक्स
- रासायनिक गतिकी
- अग्नि बिंदु
- माध्य गतिज तापमान
- क्वांटम टनलिंग
- हाइड्रोजन सुरक्षा
- धूल विस्फोट
- स्पार्क प्लग
संदर्भ
- ↑ "सक्रियण ऊर्जा". www.chem.fsu.edu. Archived from the original on 2016-12-07. Retrieved 2017-01-13.
- ↑ Espenson, James (1995). रासायनिक कैनेटीक्स और प्रतिक्रिया तंत्र. McGraw-Hill. ISBN 0070202605.
- ↑ "सक्रियण ऊर्जा और अरहेनियस समीकरण - परिचयात्मक रसायन विज्ञान- पहला कनाडाई संस्करण". opentextbc.ca (in English). Archived from the original on 2017-07-08. Retrieved 2018-04-05.
- ↑ Kagan, Harris; Barrett, Tom. "आधुनिक समाज में ऊर्जा: XIV। परमाणु ऊर्जा" (Course). Ohio State University. Retrieved 15 October 2021.
- ↑ Pratt, Thomas H. "Electrostatic Ignitions of Fires and Explosions" Wiley-AIChE (July 15, 1997) Center for Chemical Process Safety
- ↑ Wang, Jenqdaw; Raj, Rishi (1990). "शुद्ध एल्यूमिना की दर-नियंत्रित सिंटरिंग से सीमा प्रसार के लिए सक्रियण ऊर्जा का अनुमान, और ज़िरकोनिया या टाइटेनिया के साथ एल्युमिना डोप किया गया". Journal of the American Ceramic Society. 73 (5): 1172. doi:10.1111/j.1151-2916.1990.tb05175.x.
- ↑ Kiraci, A; Yurtseven, H (2012). "फेरोइलेक्ट्रिक बेरियम टाइटेनेट में रमन फ्रीक्वेंसी, डंपिंग कॉन्स्टेंट और सॉफ्ट-ऑप्टिक मोड की एक्टिवेशन एनर्जी की तापमान निर्भरता". Ferroelectrics. 432: 14–21. doi:10.1080/00150193.2012.707592. S2CID 121142463.
- ↑ Terracciano, Anthony C; De Oliveira, Samuel; Vazquez-Molina, Demetrius; Uribe-Romo, Fernando J; Vasu, Subith S; Orlovskaya, Nina (2017). "उत्प्रेरक रूप से सक्रिय Ce 0.8 Gd 0.2 O 1.9 कोटिंग का प्रभाव MgO के भीतर मीथेन के विषम दहन पर ZrO 2 झरझरा सिरेमिक को स्थिर करता है". Combustion and Flame. 180: 32–39. doi:10.1016/j.combustflame.2017.02.019.
- ↑ "सामान्य रसायन विज्ञान ऑनलाइन: अक्सर पूछे जाने वाले प्रश्न: रासायनिक परिवर्तन: उत्प्रेरकों को शामिल करने वाली प्रतिक्रियाओं के कुछ उदाहरण क्या हैं?". antoine.frostburg.edu. Retrieved 2017-01-13.
- ↑ Bui, Matthew. "अरहेनियस कानून: सक्रियण ऊर्जा". Chemistry LibreTexts. UC Davis. Retrieved February 17, 2017.
- ↑ Berg, Jeremy (2019). जैव रसायन - नौवां संस्करण. New York, NY: WH Freeman and Company. pp. 240–244. ISBN 978-1-319-11467-1.
- ↑ "सक्रियण की एन्थैल्पी". IUPAC Gold Book (2nd edition, on-line version). IUPAC (International Union of Pure and Applied Chemistry). 2019. Retrieved 10 May 2020.
- ↑ Steinfeld, Jeffrey I.; Francisco, Joseph S.; Hase, William L. (1999). रासायनिक कैनेटीक्स और गतिशीलता (2nd ed.). Prentice Hall. p. 301. ISBN 0-13-737123-3.
- ↑ Atkins, Peter; de Paula, Julio (2006). एटकिंस 'भौतिक रसायन विज्ञान (8th ed.). W.H.Freeman. p. 883. ISBN 0-7167-8759-8.
... लेकिन हम नोटेशन पर अधिक बोझ से बचने के लिए मानक राज्य चिह्न को छोड़ देंगे।
- ↑ Laidler, Keith J.; Meiser, John H. (1982). भौतिक रसायन. Benjamin/Cummings. p. 381. ISBN 0-8053-5682-7.
- ↑ Mozurkewich, Michael; Benson, Sidney (1984). "नकारात्मक सक्रियण ऊर्जा और घुमावदार अरहेनियस प्लॉट। 1. संभावित कुओं पर प्रतिक्रियाओं का सिद्धांत". J. Phys. Chem. 88 (25): 6429–6435. doi:10.1021/j150669a073.
- ↑ Espenson, James H. (1981). रासायनिक गतिकी और प्रतिक्रिया तंत्र. McGraw-Hill. p. 121. ISBN 0-07-019667-2.
- ↑ Atkins, Peter; de Paula, Julio (2006). एटकिंस 'भौतिक रसायन विज्ञान (8th ed.). W. H. Freeman. p. 822. ISBN 0-7167-8759-8.
- ↑ Kadir, Tamara (10 September 2020). "3.2.2: पूर्व-संतुलन सन्निकटन". Chem Libre Texts. Retrieved 23 January 2022.
यदि Ea1 + Ea2 <Ea−1
- ↑ Moore, John W.; Pearson, Ralph G. (1981). काइनेटिक्स और तंत्र (3rd ed.). John Wiley and Sons. p. 316. ISBN 0-471-03558-0.
- ↑ Engel, Thomas; Reid, Philip (2006). भौतिक रसायन. Pearson. Benjamin-Cummings. p. *34. ISBN 0-8053-3842-X.
- ↑ Cowie, J. M. G. (1991). पॉलिमर: आधुनिक सामग्री के रसायन विज्ञान और भौतिकी (2nd ed.). Blackie (USA: Chapman & Hall+). p. 88. ISBN 0-216-92980-6.
- ↑ Kristinsdóttir, Lilja; Skúlason, Egill (2012-09-01). "संक्रमण धातु सतहों पर हाइड्रोजन प्रसार का एक व्यवस्थित डीएफटी अध्ययन". Surface Science (in English). 606 (17): 1400–1404. doi:10.1016/j.susc.2012.04.028. ISSN 0039-6028.