चतुर्भुज

This article is about four-sided mathematical shapes. For other uses, see चतुर्भुज (disambiguation).

"Tetragon" redirects here. For the edible plant, see Tetragonia tetragonoides.

Quadrilateral
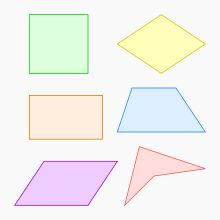Some types of quadrilaterals
किनारेs और कोने	4
स्लीपी सिंबल	{4} (for square)
क्षेत्र	various methods; see below
आंतरिक कोण (डिग्री)	90° (for square and rectangle)

यूक्लिडियन ज्यामिति में एक चतुर्भुज एक चार भुजाओं वाला बहुभुज होता है, जिसमें चार किनारे (ज्यामिति) (भुजाएँ) और चार वर्टेक्स (ज्यामिति) (कोने) होते हैं। यह शब्द लैटिन शब्द क्वाड्री, जो चार का एक प्रकार है, और लैटस, जिसका अर्थ पक्ष है, से लिया गया है। इसे टेट्रागोन भी कहा जाता है, जो ग्रीक टेट्रा से लिया गया है जिसका अर्थ है चार और गॉन का अर्थ कोने या कोण है, जो अन्य बहुभुजों (जैसे पंचकोण) के अनुरूप है। चूँकि गोन का अर्थ कोण होता है, इसे समान रूप से चतुर्भुज, या 4-कोण कहा जाता है। शीर्षों वाला एक चतुर्भुज $A$, $B$, $C$ तथा $D$ कभी-कभी के रूप में दर्शाया जाता है $\square ABCD$. चतुर्भुज या तो साधारण बहुभुज (स्वप्रतिच्छेदी नहीं) या जटिल बहुभुज (स्वप्रतिच्छेदी, या क्रॉस) होते हैं। सरल चतुर्भुज या तो उत्तल बहुभुज या अवतल बहुभुज होते हैं।

एक सरल (और समतल (ज्यामिति)) चतुर्भुज ABCD के आंतरिक और बाह्य कोण 360 डिग्री चाप तक जोड़ते हैं, अर्थात:$\angle A+\angle B+\angle C+\angle D=360^{\circ }.$ यह n-गॉन आंतरिक कोण योग सूत्र का एक विशेष स्थिति है: S = (n - 2) × 180°। सभी गैर-स्व-क्रॉसिंग चतुर्भुज चौकोर, उनके किनारों के मध्य बिंदुओं के चारों ओर बार-बार घूमने से।

सरल चतुर्भुज

कोई भी चतुर्भुज जो स्व-प्रतिच्छेदी नहीं है, एक सरल चतुर्भुज है।

उत्तल चतुर्भुज

कुछ प्रकार के सरल चतुर्भुजों का यूलर आरेख। (यूके) ब्रिटिश अंग्रेजी को दर्शाता है और (यूएस) अमेरिकी अंग्रेजी को दर्शाता है।

सममिति द्वारा उत्तल चतुर्भुज, एक हस्से आरेख के साथ दर्शाया गया है।

एक उत्तल चतुर्भुज में सभी आंतरिक कोण 180° से कम होते हैं, और दोनों विकर्ण चतुर्भुज के अंदर स्थित होते हैं।

• अनियमित चतुर्भुज (ब्रिटिश अंग्रेजी) या ट्रेपेज़ियम (उत्तरी अमेरिकी अंग्रेजी): कोई पक्ष समानांतर नहीं हैं। (ब्रिटिश अंग्रेजी में, इसे एक बार ट्रेपेज़ॉइड कहा जाता था। अधिक जानकारी के लिए, देखें Trapezoid § Trapezium vs Trapezoid)
• ट्रेपेज़ॉइड (यूके) या ट्रेपेज़ॉइड (यूएस): कम से कम एक जोड़ी विपरीत भुजाएँ समानांतर (ज्यामिति) हैं। ट्रेपेज़िया (यूके) और ट्रेपेज़ोइड्स (यूएस) में समांतर चतुर्भुज सम्मिलित हैं।
• समद्विबाहु ट्रेपेज़ियम (यूके) या [[समद्विबाहु ट्रेपेज़ॉइड]] (यूएस): विपरीत भुजाओं का एक जोड़ा समानांतर होता है और आधार कोण माप में बराबर होते हैं। वैकल्पिक परिभाषाएँ समरूपता के अक्ष के साथ एक चतुर्भुज हैं जो विपरीत पक्षों के एक जोड़े को द्विभाजित करती हैं, या समान लंबाई के विकर्णों के साथ एक चतुर्भुज हैं।
• समांतर चतुर्भुज: समानांतर भुजाओं के दो युग्मों वाला चतुर्भुज। समतुल्य स्थितियाँ हैं कि विपरीत भुजाएँ समान लंबाई की हों; सम्मुख कोण बराबर होते हैं; या यह कि विकर्ण एक दूसरे को समद्विभाजित करते हैं। समांतर चतुर्भुजों में सम्मिलित हैं rhombi (उन आयतों सहित जिन्हें वर्ग कहा जाता है) और rhomboids (उन आयतों सहित जिन्हें आयताकार कहा जाता है)। दूसरे शब्दों में, समांतर चतुर्भुज में सभी समचतुर्भुज और सभी समचतुर्भुज सम्मिलित होते हैं, और इस प्रकार इसमें सभी आयत भी सम्मिलित होते हैं।
• समचतुर्भुज, समचतुर्भुज:चारों भुजाएँ समान लंबाई (समबाहु) की हैं। समतुल्य स्थिति यह है कि विकर्ण एक दूसरे को समद्विभाजित करते हैं। अनौपचारिक रूप से: एक पुश-ओवर वर्ग (लेकिन सख्ती से एक वर्ग भी सम्मिलित है)।
• समचतुर्भुज: एक समांतर चतुर्भुज जिसमें आसन्न भुजाएँ असमान लंबाई की होती हैं, और कुछ कोण कोण # कोण के प्रकार होते हैं (समतुल्य, कोई समकोण नहीं होता है)। अनौपचारिक रूप से: एक धक्का दिया हुआ आयताकार। सभी संदर्भ सहमत नहीं हैं, कुछ एक समचतुर्भुज को समांतर चतुर्भुज के रूप में परिभाषित करते हैं जो एक समचतुर्भुज नहीं है।
• आयत: चारों कोण समकोण (समकोणीय) होते हैं। समतुल्य स्थिति यह है कि विकर्ण एक दूसरे को समद्विभाजित करते हैं और लंबाई में बराबर होते हैं। आयतों में वर्ग और आयताकार सम्मिलित हैं। अनौपचारिक रूप से: एक बॉक्स या आयताकार (एक वर्ग सहित)।
• वर्ग (ज्यामिति) (नियमित चतुर्भुज): चारों भुजाएँ समान लंबाई (समबाहु) की होती हैं, और चारों कोण समकोण होते हैं। एक समतुल्य स्थिति यह है कि विपरीत भुजाएं समानांतर होती हैं (एक वर्ग एक समांतर चतुर्भुज होता है), और यह कि विकर्ण लंबवत रूप से एक दूसरे को समद्विभाजित करते हैं और समान लंबाई के होते हैं। एक चतुर्भुज एक वर्ग है यदि और केवल यदि यह एक समचतुर्भुज और एक आयत दोनों है (अर्थात्, चार समान भुजाएँ और चार समान कोण)।
• wikt:आयताकार: चौड़े से लंबा, या लंबे से चौड़ा (यानी, एक आयत जो वर्ग नहीं है)।
• काइट (ज्यामिति): आसन्न भुजाओं के दो जोड़े समान लंबाई के होते हैं। इसका तात्पर्य यह है कि एक विकर्ण पतंग को सर्वांगसम त्रिभुजों में विभाजित करता है, और इसलिए समान भुजाओं के दो युग्मों के बीच के कोण माप में बराबर होते हैं। इसका तात्पर्य यह भी है कि विकर्ण लंबवत हैं। पतंग में रोम्बी सम्मिलित है।

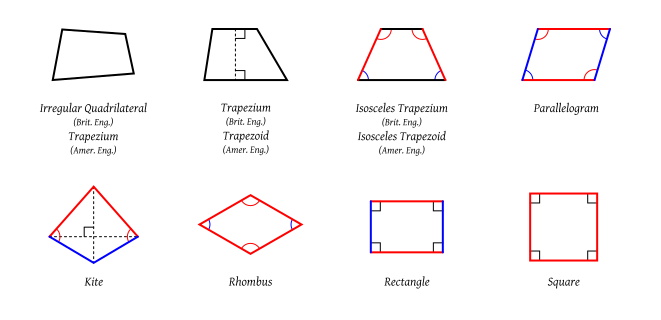* स्पर्शरेखा चतुर्भुज: चार भुजाएँ एक खुदे हुए वृत्त की स्पर्शरेखाएँ हैं। एक उत्तल चतुर्भुज स्पर्शरेखीय होता है यदि और केवल यदि विपरीत भुजाओं का योग बराबर हो।

• स्पर्शरेखा ट्रेपेज़ॉइड: एक ट्रेपेज़ॉइड जहाँ चारों भुजाएँ एक खुदे हुए वृत्त की स्पर्शरेखाएँ होती हैं।
• चक्रीय चतुर्भुज: चारों शीर्ष एक परिबद्ध वृत्त पर स्थित होते हैं। एक उत्तल चतुर्भुज चक्रीय होता है यदि और केवल यदि सम्मुख कोणों का योग 180° हो।
• दाहिनी पतंग: दो विपरीत समकोण वाली पतंग। यह एक प्रकार का चक्रीय चतुर्भुज है।
• हारमोनिक चतुर्भुज: विरोधी पक्षों की लंबाई के गुणनफल बराबर होते हैं। यह एक प्रकार का चक्रीय चतुर्भुज है।
• द्विकेंद्रित चतुर्भुज: यह स्पर्शरेखा और चक्रीय दोनों है।
• ओर्थोडायगोनल चतुर्भुज: विकर्ण समकोण पर काटते हैं।
• समबाहु चतुर्भुज: विकर्ण समान लंबाई के होते हैं।
• Ex-tangential चतुर्भुज: पक्षों के चार विस्तार एक बहिर्वृत्त के स्पर्शरेखा हैं।
• समबाहु चतुर्भुज की दो विपरीत समान भुजाएँ होती हैं जिन्हें बढ़ाने पर वे 60° पर मिलती हैं।
• वाट चतुर्भुज एक ऐसा चतुर्भुज है जिसमें समान लंबाई की विपरीत भुजाओं का युग्म होता है।
• चतुर्भुज एक उत्तल चतुर्भुज होता है जिसके चारों शीर्ष एक वर्ग की परिधि पर स्थित होते हैं।
• व्यासयुक्त चतुर्भुज एक चक्रीय चतुर्भुज होता है जिसकी एक भुजा परिवृत्त के व्यास के रूप में होती है।
• जेल्म्सलेव चतुर्भुज एक ऐसा चतुर्भुज होता है जिसके दो समकोण विपरीत शीर्षों पर होते हैं।

अवतल चतुर्भुज

अवतल चतुर्भुज में, एक आंतरिक कोण 180° से बड़ा होता है, और दो विकर्णों में से एक चतुर्भुज के बाहर स्थित होता है।

• एक डार्ट (या तीर का सिरा) एक पतंग की तरह द्विपक्षीय समरूपता के साथ एक अवतल बहुभुज चतुर्भुज है, लेकिन जहां एक आंतरिक कोण प्रतिवर्त होता है। पतंग (ज्यामिति) देखें।

जटिल चतुर्भुज

एक प्रतिसमांतर चतुर्भुज

स्वयं-प्रतिच्छेदी बहुभुजों की एक सूची|स्व-प्रतिच्छेदी चतुर्भुज को विभिन्न प्रकार से एक क्रॉस-चतुर्भुज, क्रॉस्ड चतुर्भुज, तितली चतुर्भुज या बो टाई चतुर्भुज कहा जाता है। एक क्रॉस किए गए चतुर्भुज में, क्रॉसिंग के दोनों तरफ चार आंतरिक कोण (दो न्यून कोण और दो पलट कोण, सभी बाईं ओर या सभी दाईं ओर जैसा कि आकृति का पता लगाया गया है) 720 डिग्री तक जोड़ते हैं।

• समद्विबाहु ट्रेपेज़ॉइड#स्व-चौराहे (यूएस) या ट्रेपेज़ियम (कॉमनवेल्थ): एक पार किया हुआ चतुर्भुज जिसमें एक जोड़ी असन्निकट भुजाएँ समानांतर होती हैं (एक ट्रेपेज़ॉइड की तरह)
• प्रतिसमांतर चतुर्भुज: एक पार किया हुआ चतुर्भुज जिसमें असन्निकट भुजाओं के प्रत्येक जोड़े की लंबाई समान होती है (एक समांतर चतुर्भुज की तरह)
• पार किया हुआ आयत: एक प्रतिसमांतर चतुर्भुज जिसकी भुजाएँ दो विपरीत भुजाएँ होती हैं और एक आयत के दो विकर्ण होते हैं, इसलिए समानांतर विपरीत भुजाओं का एक युग्म होता है
• स्क्वायर#क्रॉस्ड स्क्वायर: एक क्रास्ड आयत का एक विशेष स्थिति जहां दो पक्ष समकोण पर प्रतिच्छेद करते हैं

विशेष रेखा खंड

उत्तल चतुर्भुज के दो विकर्ण रेखा खंड होते हैं जो विपरीत शीर्षों को जोड़ते हैं।

एक उत्तल चतुर्भुज की दो द्विमाध्यिकाएं वे रेखाखंड होते हैं जो विपरीत भुजाओं के मध्यबिंदुओं को जोड़ते हैं। वे चतुर्भुज के शीर्ष केन्द्रक पर प्रतिच्छेद करते हैं (देखें § Remarkable points and lines in a convex quadrilateral नीचे)।

एक उत्तल चतुर्भुज के चार कोण एक तरफ के लंबवत होते हैं - विपरीत दिशा के मध्य बिंदु के माध्यम से।

एक उत्तल चतुर्भुज का क्षेत्रफल

क्षेत्र के लिए विभिन्न सामान्य सूत्र हैं K पक्षों के साथ एक उत्तल चतुर्भुज ABCD का a = AB, b = BC, c = CD and d = DA.

त्रिकोणमितीय सूत्र

क्षेत्र को त्रिकोणमितीय शब्दों में व्यक्त किया जा सकता है

$K={\frac {pq}{2}}\sin \theta ,$

जहां विकर्णों की लंबाई हैं p तथा q और उनके बीच का कोण है θ. एक ऑर्थोडायगोनल चतुर्भुज (जैसे समचतुर्भुज, वर्ग और पतंग) के मामले में, यह सूत्र कम हो जाता है $K={\tfrac {pq}{2}}$ जबसे θ है 90°.

क्षेत्र को द्विमाध्यकों के रूप में भी व्यक्त किया जा सकता है:$K=mn\sin \varphi ,$ जहां बिमेडियन की लंबाई हैं m तथा n और उनके बीच का कोण है φ.

Bretschneider का सूत्रभुजाओं और दो विपरीत कोणों के संदर्भ में क्षेत्र को व्यक्त करता है:

${\begin{aligned}K&={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{2}}abcd\;[1+\cos(A+C)]}}\\&={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\left[\cos ^{2}\left({\frac {A+C}{2}}\right)\right]}}\end{aligned}}$

जहाँ क्रम में भुजाएँ हैं a, b, c, d, कहाँ पे s अर्धपरिधि है, और A तथा C दो (वास्तव में, कोई भी दो) विपरीत कोण हैं। यह चक्रीय चतुर्भुज के क्षेत्र के लिए ब्रह्मगुप्त के सूत्र को कम करता है - जब A + C = 180° .

कोण के साथ भुजाओं और कोणों के संदर्भ में एक अन्य क्षेत्र सूत्र C पक्षों के बीच होना b तथा c, तथा A पक्षों के बीच होना a तथा d, है

$K={\frac {ad}{2}}\sin {A}+{\frac {bc}{2}}\sin {C}.$

चक्रीय चतुर्भुज के मामले में, बाद वाला सूत्र बन जाता है $K={\frac {ad+bc}{2}}\sin {A}.$ समांतर चतुर्भुज में, जहाँ विपरीत भुजाओं और कोणों के दोनों युग्म बराबर होते हैं, यह सूत्र कम हो जाता है $K=ab\cdot \sin {A}.$ वैकल्पिक रूप से, हम क्षेत्रफल को भुजाओं और प्रतिच्छेदन कोण के रूप में लिख सकते हैं θ विकर्णों की, जितनी लंबी θ नहीं है 90°:

$K={\frac {\left|\tan \theta \right|}{4}}\cdot \left|a^{2}+c^{2}-b^{2}-d^{2}\right|.$

समांतर चतुर्भुज के मामले में, बाद वाला सूत्र बन जाता है $K={\frac {\left|\tan \theta \right|}{2}}\cdot \left|a^{2}-b^{2}\right|.$ पक्षों सहित एक अन्य क्षेत्र सूत्र a, b, c, d है

$K={\frac {\sqrt {((a^{2}+c^{2})-2x^{2})((b^{2}+d^{2})-2x^{2})}}{2}}\sin {\varphi }$

कहाँ पे x विकर्णों के मध्य बिंदुओं के बीच की दूरी है, और φ चतुर्भुज#विशेष रेखाखंडों के बीच का कोण है। पक्षों सहित अंतिम त्रिकोणमिति क्षेत्र सूत्र a, b, c, d और कोण α (के बीच a तथा b) है:

$K={\frac {ab}{2}}\sin {\alpha }+{\frac {\sqrt {4c^{2}d^{2}-(c^{2}+d^{2}-a^{2}-b^{2}+2ab\cdot \cos {\alpha })^{2}}}{4}},$

जिसका उपयोग अवतल चतुर्भुज के क्षेत्र के लिए भी किया जा सकता है (अवतल भाग कोण के विपरीत होता है α), केवल पहला चिह्न बदलकर + प्रति -.

गैर-त्रिकोणमितीय सूत्र

निम्नलिखित दो सूत्र पक्षों के संदर्भ में क्षेत्र को व्यक्त करते हैं a, b, c तथा d, अर्धपरिधि#चतुर्भुज s, और विकर्ण p, q:

$K={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{4}}(ac+bd+pq)(ac+bd-pq)}},$

$K={\frac {\sqrt {4p^{2}q^{2}-\left(a^{2}+c^{2}-b^{2}-d^{2}\right)^{2}}}{4}}.$

तब से चक्रीय चतुर्भुज मामले में पहला ब्रह्मगुप्त के सूत्र को कम करता है pq = ac + bd.

क्षेत्र को द्विमाध्यकों के संदर्भ में भी व्यक्त किया जा सकता है m, n और विकर्ण p, q:

$K={\frac {\sqrt {(m+n+p)(m+n-p)(m+n+q)(m+n-q)}}{2}},$

$K={\frac {\sqrt {p^{2}q^{2}-(m^{2}-n^{2})^{2}}}{2}}.$

वास्तव में, चार मूल्यों में से कोई तीन m, n, p, तथा q क्षेत्र के निर्धारण के लिए पर्याप्त है, क्योंकि किसी भी चतुर्भुज में चार मान इससे संबंधित होते हैं $p^{2}+q^{2}=2(m^{2}+n^{2}).$ संगत भाव हैं:

$K={\frac {\sqrt {[(m+n)^{2}-p^{2}]\cdot [p^{2}-(m-n)^{2}]}}{2}},$ यदि दो द्विमाध्यिकाओं और एक विकर्ण की लंबाई दी गई हो, और

$K={\frac {\sqrt {[(p+q)^{2}-4m^{2}]\cdot [4m^{2}-(p-q)^{2}]}}{4}},$ यदि दो विकर्णों और एक द्विमाध्यिका की लंबाई दी गई हो।

वेक्टर सूत्र

एक चतुर्भुज का क्षेत्रफल ABCD वेक्टर (ज्यामितीय) का उपयोग करके गणना की जा सकती है। चलो वैक्टर AC तथा BD से विकर्ण बनाएँ A प्रति C और यहां ये B प्रति D. तब चतुर्भुज का क्षेत्रफल है

$K={\frac {|\mathbf {AC} \times \mathbf {BD} |}{2}},$

जो सदिशों के क्रॉस उत्पाद का आधा परिमाण है AC तथा BD. द्वि-आयामी यूक्लिडियन अंतरिक्ष में, वेक्टर व्यक्त करना AC एक यूक्लिडियन वेक्टर के रूप में # कार्टेशियन अंतरिक्ष में बराबर (x₁,y₁) तथा BD जैसा (x₂,y₂), इसे फिर से लिखा जा सकता है:

$K={\frac {|x_{1}y_{2}-x_{2}y_{1}|}{2}}.$

विकर्ण

चतुर्भुज में विकर्णों के गुण

निम्न तालिका में यह सूचीबद्ध है कि क्या कुछ अधिकांश मूल रूप से चतुर्भुजों में विकर्ण एक दूसरे को द्विभाजित करते हैं, यदि उनके विकर्ण लंबवत हैं, और यदि उनके विकर्णों की लंबाई समान है। सूची सबसे सामान्य स्थितियो पर लागू होती है, और नामित उप-समुच्चय को बाहर करती है।

चतुर्भुज	समद्विभाजक विकर्ण	लम्बवत्त विकर्ण	समान विकर्ण
समलंब	नहीं	नोट 1 देखें	नहीं
समद्विबाहु समलंब	नहीं	नोट 1 देखें	हाँ
समांतर चतुर्भुज	हाँ	नहीं	नहीं
पतंग	नोट 2 देखें	हाँ	नोट 2 देखें
आयात	हाँ	नहीं	हाँ
समचतुर्भुज	हाँ	हाँ	नहीं
वर्ग	हाँ	हाँ	हाँ

नोट 1: सबसे सामान्य समलंब चतुर्भुज और समद्विबाहु समलम्ब चतुर्भुज में लंबवत विकर्ण नहीं होते हैं, लेकिन अनंत संख्या में (गैर-समान) समलंब और समद्विबाहु समलम्बाकार होते हैं जिनमें लंबवत विकर्ण होते हैं और कोई अन्य नामित चतुर्भुज नहीं होते हैं।

नोट 2: एक पतंग में, एक विकर्ण दूसरे को समद्विभाजित करता है। सबसे सामान्य पतंग में असमान विकर्ण होते हैं, लेकिन अनंत संख्या में (गैर-समान) पतंगें होती हैं जिनमें विकर्ण लंबाई में समान होते हैं (और पतंग कोई अन्य नामित चतुर्भुज नहीं होते हैं)।

विकर्णों की लंबाई

उत्तल चतुर्भुज ABCD में विकर्णों की लंबाई की गणना चतुर्भुज के एक विकर्ण और दो भुजाओं द्वारा निर्मित प्रत्येक त्रिभुज पर कोसाइन के नियम का उपयोग करके की जा सकती है। इस प्रकार

$p={\sqrt {a^{2}+b^{2}-2ab\cos {B}}}={\sqrt {c^{2}+d^{2}-2cd\cos {D}}}$

तथा

$q={\sqrt {a^{2}+d^{2}-2ad\cos {A}}}={\sqrt {b^{2}+c^{2}-2bc\cos {C}}}.$

अन्य, विकर्णों की लंबाई के लिए अधिक सममित सूत्र हैं

$p={\sqrt {\frac {(ac+bd)(ad+bc)-2abcd(\cos {B}+\cos {D})}{ab+cd}}}$

तथा

$q={\sqrt {\frac {(ab+cd)(ac+bd)-2abcd(\cos {A}+\cos {C})}{ad+bc}}}.$

समांतर चतुर्भुज कानून और टॉलेमी के प्रमेय का सामान्यीकरण

किसी भी उत्तल चतुर्भुज ABCD में, चारों भुजाओं के वर्गों का योग दो विकर्णों के वर्गों के योग के बराबर होता है और विकर्णों के मध्य बिंदुओं को जोड़ने वाले रेखा खंड के वर्ग का चार गुना होता है। इस प्रकार

$a^{2}+b^{2}+c^{2}+d^{2}=p^{2}+q^{2}+4x^{2}$

जहाँ x विकर्णों के मध्य बिन्दुओं के बीच की दूरी है। इसे कभी-कभी यूलर के चतुर्भुज प्रमेय के रूप में जाना जाता है और यह समांतर चतुर्भुज नियम का सामान्यीकरण है।

जर्मन गणितज्ञ कार्ल एंटोन Bretschneider ने 1842 में उत्तल चतुर्भुज में विकर्णों के उत्पाद के संबंध में टॉलेमी के प्रमेय के निम्नलिखित सामान्यीकरण को व्युत्पन्न किया।

$p^{2}q^{2}=a^{2}c^{2}+b^{2}d^{2}-2abcd\cos {(A+C)}.$

इस संबंध को एक चतुर्भुज के लिए कोसाइन का नियम माना जा सकता है। एक चक्रीय चतुर्भुज में, जहाँ A + C = 180°, यह घटकर pq = ac + bd हो जाता है। चूँकि cos (A + C) ≥ −1, यह टॉलेमी की असमानता का प्रमाण भी देता है।

अन्य मीट्रिक संबंध

यदि X और Y एक उत्तल चतुर्भुज abcd में b और d से विकर्ण ac = p के मानक के पैर हैं a = ab, b = bc, c = cd , d = da , फिर

$XY={\frac {|a^{2}+c^{2}-b^{2}-d^{2}|}{2p}}.$

एक उत्तल चतुर्भुज ABCD में जिसकी भुजाएँ a = AB, b = BC, c = CD, d = DA है, और जहाँ विकर्ण E पर प्रतिच्छेद करते हैं,

$efgh(a+c+b+d)(a+c-b-d)=(agh+cef+beh+dfg)(agh+cef-beh-dfg)$

जहां e = fe, af = be, g = ce, और h = de।

एक उत्तल चतुर्भुज का आकार और आकार पूरी तरह से क्रम में इसकी भुजाओं की लंबाई और दो निर्दिष्ट शीर्षों के बीच एक विकर्ण द्वारा निर्धारित किया जाता है। एक चतुर्भुज के दो विकर्ण p, q और चारों भुजाओं की लंबाई a, b, c, d संबंधित हैंदूरी ज्यामिति द्वारा#केली.E2.80.93मेंजर निर्धारक|केली-मेंजर निर्धारक, इस प्रकार है:

$\det {\begin{bmatrix}0&a^{2}&p^{2}&d^{2}&1\\a^{2}&0&b^{2}&q^{2}&1\\p^{2}&b^{2}&0&c^{2}&1\\d^{2}&q^{2}&c^{2}&0&1\\1&1&1&1&0\end{bmatrix}}=0.$

कोण द्विभाजक

उत्तल चतुर्भुज के आंतरिक कोण समद्विभाजक या तो एक चक्रीय चतुर्भुज बनाते हैं (अर्थात, आसन्न कोण समद्विभाजक के चार प्रतिच्छेदन बिंदु समवर्ती बिंदु हैं) या वे समवर्ती रेखाएँ हैं। बाद के मामले में चतुर्भुज एक स्पर्शरेखा चतुर्भुज है।

चतुर्भुज ABCD में, यदि A और C के कोणों का समद्विभाजक # विकर्ण BD पर मिलता है, तो B और D के कोण समद्विभाजक विकर्ण AC पर मिलते हैं।

बिमेडियंस

See also: Varignon's theorem

वैरिग्नन समांतरोग्राम ईएफजीएच

चतुर्भुज#चतुर्भुज के विशेष रेखाखंड विपरीत भुजाओं के मध्यबिंदुओं को जोड़ने वाले रेखाखंड होते हैं। द्विमाध्यिकाओं का प्रतिच्छेदन चतुर्भुज के शीर्षों का केन्द्रक होता है।

किसी भी चतुर्भुज (उत्तल, अवतल या पार) की भुजाओं के मध्य बिंदु एक समांतर चतुर्भुज के शीर्ष होते हैं जिन्हें वेरिग्नॉन प्रमेय कहा जाता है। इसके निम्नलिखित गुण हैं:

• वैरिग्नॉन समांतरोग्राम के विपरीत पक्षों की प्रत्येक जोड़ी मूल चतुर्भुज में एक विकर्ण के समानांतर होती है।
• वरिग्नन समांतर चतुर्भुज का एक किनारा मूल चतुर्भुज में विकर्ण के बराबर लंबा होता है, जिसके समानांतर होता है।
• वैरिग्नन समांतर चतुर्भुज का क्षेत्रफल मूल चतुर्भुज के आधे क्षेत्रफल के बराबर होता है। यह उत्तल, अवतल और पार चतुर्भुज के लिए सही है, बशर्ते बाद वाले का क्षेत्रफल दो त्रिभुजों के क्षेत्रों के अंतर के रूप में परिभाषित किया गया हो।
• वैरिग्नन समांतर चतुर्भुज का परिमाप मूल चतुर्भुज के विकर्णों के योग के बराबर होता है।
• वैरिग्नन समांतर चतुर्भुज के विकर्ण मूल चतुर्भुज के द्विमाध्यक हैं।

किसी चतुर्भुज में दो द्विमाध्यिकाएँ और उस चतुर्भुज में विकर्णों के मध्यबिंदुओं को मिलाने वाला रेखाखंड समवर्ती रेखाएँ होती हैं और सभी अपने प्रतिच्छेदन बिंदु द्वारा द्विभाजित होती हैं। पक्षों ए, बी, सी और d के साथ एक उत्तल चतुर्भुज में, बिमेडियन की लंबाई जो पक्षों के मध्य बिंदुओं को जोड़ती है और सी है

$m={\tfrac {1}{2}}{\sqrt {-a^{2}+b^{2}-c^{2}+d^{2}+p^{2}+q^{2}}}$

जहाँ p और q विकर्णों की लंबाई हैं। भुजाओं b और d के मध्यबिंदुओं को जोड़ने वाली द्विमाध्यिका की लंबाई है

$n={\tfrac {1}{2}}{\sqrt {a^{2}-b^{2}+c^{2}-d^{2}+p^{2}+q^{2}}}.$

अत

$\displaystyle p^{2}+q^{2}=2(m^{2}+n^{2}).$

यह वैरिग्नन समांतर चतुर्भुज में लागू समांतर चतुर्भुज कानून का एक परिणाम भी है।

द्विमाध्यकों की लंबाई को दो विपरीत भुजाओं और विकर्णों के मध्यबिंदुओं के बीच की दूरी x के रूप में भी व्यक्त किया जा सकता है। उपरोक्त सूत्रों में यूलर के चतुर्भुज प्रमेय का उपयोग करते समय यह संभव है। जहां से:$m={\tfrac {1}{2}}{\sqrt {2(b^{2}+d^{2})-4x^{2}}}$ तथा

$n={\tfrac {1}{2}}{\sqrt {2(a^{2}+c^{2})-4x^{2}}}.$

ध्यान दें कि इन सूत्रों में दो विपरीत पक्ष वे दो नहीं हैं जिन्हें द्विमाध्यिका जोड़ती है।

एक उत्तल चतुर्भुज में, द्विमाध्यकों और विकर्णों के बीच निम्नलिखित द्वैत (गणित) संबंध होता है:

• दो द्विमाध्यकों की लंबाई समान होती है यदि और केवल यदि दो विकर्ण लंबवत हों।
• दो द्विमाध्यम लंबवत होते हैं यदि और केवल यदि दो विकर्णों की लंबाई समान हो।

त्रिकोणमितीय पहचान

एक सरल चतुर्भुज ABCD के चारों कोण निम्नलिखित सर्वसमिकाओं को संतुष्ट करते हैं:

$\sin {A}+\sin {B}+\sin {C}+\sin {D}=4\sin {\frac {A+B}{2}}\sin {\frac {A+C}{2}}\sin {\frac {A+D}{2}}$

तथा

${\frac {\tan {A}\tan {B}-\tan {C}\tan {D}}{\tan {A}\tan {C}-\tan {B}\tan {D}}}={\frac {\tan {(A+C)}}{\tan {(A+B)}}}.$

भी,

${\frac {\tan {A}+\tan {B}+\tan {C}+\tan {D}}{\cot {A}+\cot {B}+\cot {C}+\cot {D}}}=\tan {A}\tan {B}\tan {C}\tan {D}.$

अंतिम दो सूत्रों में, किसी भी कोण को समकोण होने की अनुमति नहीं है, क्योंकि tan 90° परिभाषित नहीं है।

होने देना $a$, $b$, $c$, $d$ उत्तल चतुर्भुज की भुजाएँ हों, $s$ अर्द्धपरिधि है,

तथा $A$ तथा $C$ विपरीत कोण हैं, तो

$ad\sin ^{2}{\frac {A}{2}}+bc\cos ^{2}{\frac {C}{2}}=(s-a)(s-d)$

तथा

$bc\sin ^{2}{\frac {C}{2}}+ad\cos ^{2}{\frac {A}{2}}=(s-b)(s-c)$.

हम इन सर्वसमिकाओं का उपयोग Bretschneider के सूत्र को व्युत्पन्न करने के लिए कर सकते हैं।

असमानताएं

क्षेत्र

यदि एक उत्तल चतुर्भुज की लगातार भुजाएँ a, b, c, d और विकर्ण p, q हैं, तो इसका क्षेत्रफल K संतुष्ट करता है

$K\leq {\tfrac {1}{4}}(a+c)(b+d)$ समानता के साथ केवल एक आयत के लिए।

$K\leq {\tfrac {1}{4}}(a^{2}+b^{2}+c^{2}+d^{2})$ समानता के साथ केवल एक वर्ग के लिए।

$K\leq {\tfrac {1}{4}}(p^{2}+q^{2})$ समानता के साथ केवल तभी जब विकर्ण लंबवत और समान हों।

$K\leq {\tfrac {1}{2}}{\sqrt {(a^{2}+c^{2})(b^{2}+d^{2})}}$ समानता के साथ केवल एक आयत के लिए।

Bretschneider के सूत्र से यह सीधे तौर पर पता चलता है कि एक चतुर्भुज का क्षेत्रफल संतुष्ट करता है

$K\leq {\sqrt {(s-a)(s-b)(s-c)(s-d)}}$

समानता के साथ अगर और केवल अगर चतुर्भुज चक्रीय चतुर्भुज है या ऐसा पतित है कि एक पक्ष अन्य तीन के योग के बराबर है (यह एक रेखा खंड में ढह गया है, इसलिए क्षेत्र शून्य है)।

किसी चतुर्भुज का क्षेत्रफल भी असमानता को संतुष्ट करता है

$\displaystyle K\leq {\tfrac {1}{2}}{\sqrt[{3}]{(ab+cd)(ac+bd)(ad+bc)}}.$

परिधि को L के रूप में नकारते हुए, हमारे पास है

$K\leq {\tfrac {1}{16}}L^{2},$

समानता के साथ केवल एक वर्ग के मामले में।

एक उत्तल चतुर्भुज का क्षेत्रफल भी संतुष्ट करता है

$K\leq {\tfrac {1}{2}}pq$

विकर्ण लंबाई पी और क्यू के लिए, समानता के साथ अगर और केवल अगर विकर्ण लंबवत हैं।

माना a, b, c, d एक उत्तल चतुर्भुज ABCD की भुजाओं की लंबाई है जिसका क्षेत्रफल K है और विकर्ण AC = p, BD = q है। फिर

$K\leq {\frac {a^{2}+b^{2}+c^{2}+d^{2}+p^{2}+q^{2}+pq-ac-bd}{8}}$ समानता के साथ केवल एक वर्ग के लिए।

माना a, b, c, d एक उत्तल चतुर्भुज ABCD की भुजाओं की लंबाई है जिसका क्षेत्रफल K है, तो निम्नलिखित असमिका धारण करती है:

$K\leq {\frac {1}{3+{\sqrt {3}}}}(ab+ac+ad+bc+bd+cd)-{\frac {1}{2(1+{\sqrt {3}})^{2}}}(a^{2}+b^{2}+c^{2}+d^{2})$ समानता के साथ केवल एक वर्ग के लिए।

विकर्ण और द्विमाध्यिका

असमानता यूलर के चतुर्भुज प्रमेय का परिणाम है

$a^{2}+b^{2}+c^{2}+d^{2}\geq p^{2}+q^{2}$

जहां समानता धारण करती है यदि और केवल यदि चतुर्भुज एक समांतर चतुर्भुज है।

लियोनहार्ड यूलर ने टॉलेमी के प्रमेय को भी सामान्यीकृत किया, जो चक्रीय चतुर्भुज में एक समानता है, एक उत्तल चतुर्भुज के लिए एक असमानता में। यह प्रकट करता है कि

$pq\leq ac+bd$

जहां समता है यदि और केवल यदि चतुर्भुज चक्रीय है। इसे प्रायः टॉलेमी की असमानता कहा जाता है।

किसी भी उत्तल चतुर्भुज में द्विमाध्यिकाएँ m, n और विकर्ण p, q असमानता द्वारा संबंधित हैं

$pq\leq m^{2}+n^{2},$

समानता धारण के साथ यदि और केवल यदि विकर्ण समान हैं। यह चतुर्भुज तत्समक से सीधे अनुसरण करता है $m^{2}+n^{2}={\tfrac {1}{2}}(p^{2}+q^{2}).$

भुजाएँ

किसी भी चतुर्भुज की भुजाएँ a, b, c और d संतुष्ट करती हैं

$a^{2}+b^{2}+c^{2}>{\frac {d^{2}}{3}}$

तथा

$a^{4}+b^{4}+c^{4}\geq {\frac {d^{4}}{27}}.$

अधिकतम और न्यूनतम गुण

दी गई परिधि वाले सभी चतुर्भुजों में, सबसे बड़े क्षेत्रफल वाला चतुर्भुज वर्ग (ज्यामिति) है। इसे चतुर्भुजों के लिए समपरिमितीय असमानता कहा जाता है। यह क्षेत्र असमानता का प्रत्यक्ष परिणाम है

$K\leq {\tfrac {1}{16}}L^{2}$

जहां K परिमाप L के साथ एक उत्तल चतुर्भुज का क्षेत्रफल है। समानता तब और केवल तभी होती है जब चतुर्भुज एक वर्ग हो। दोहरे प्रमेय में कहा गया है कि किसी दिए गए क्षेत्रफल वाले सभी चतुर्भुजों में, वर्ग की परिधि सबसे छोटी होती है।

दी गई भुजाओं की लंबाई वाला चतुर्भुज जिसमें मैक्सिमा और मिनिमा क्षेत्र होते हैं, चक्रीय चतुर्भुज होता है।

दिए गए विकर्णों वाले सभी उत्तल चतुर्भुजों में से, ऑर्थोडायगोनल चतुर्भुज का क्षेत्रफल सबसे बड़ा होता है। यह इस तथ्य का प्रत्यक्ष परिणाम है कि एक उत्तल चतुर्भुज का क्षेत्रफल संतुष्ट करता है

$K={\tfrac {1}{2}}pq\sin {\theta }\leq {\tfrac {1}{2}}pq,$

जहाँ θ विकर्णों p और q के बीच का कोण है। समानता धारण करती है यदि और केवल यदि θ = 90°।

यदि पी उत्तल चतुर्भुज abcd में एक आंतरिक बिंदु है, तो

$AP+BP+CP+DP\geq AC+BD.$

इस असमानता से यह पता चलता है कि एक चतुर्भुज के अंदर बिंदु जो कि मैक्सिमा और मिनिमा वर्टेक्स (ज्यामिति) की दूरियों का योग है, विकर्णों का प्रतिच्छेदन है। इसलिए वह बिंदु एक उत्तल चतुर्भुज का फर्मेट बिंदु है।

== उत्तल चतुर्भुज == में उल्लेखनीय बिंदु और रेखाएँ चतुर्भुज के केंद्र को कई अलग-अलग तरीकों से परिभाषित किया जा सकता है। वर्टेक्स सेंट्रोइड चतुर्भुज को खाली मानने से आता है, लेकिन इसके शीर्षों पर समान द्रव्यमान होता है। पक्ष केन्द्रक पक्षों पर विचार करने से प्रति इकाई लंबाई में निरंतर द्रव्यमान होता है। सामान्य केंद्र, जिसे सिर्फ केन्द्रक (क्षेत्र का केंद्र) कहा जाता है, चतुर्भुज की सतह को निरंतर घनत्व के रूप में मानने से आता है। ये तीन बिंदु सामान्य रूप से एक ही बिंदु नहीं हैं। शीर्ष केन्द्रक दो चतुर्भुज#विशेष रेखा खंडों का प्रतिच्छेदन है। किसी भी बहुभुज की तरह, वर्टेक्स सेंट्रोइड के x और y निर्देशांक शीर्षों के x और y निर्देशांक के अंकगणितीय साधन हैं।

चतुर्भुज ABCD के क्षेत्रफल केन्द्रक की रचना निम्न प्रकार से की जा सकती है। चलो जी_a, जी_b, जी_c, जी_dक्रमशः त्रिभुजों BCD, ACD, ABD, ABC के केन्द्रक बनें। तब क्षेत्र केन्द्रक रेखाओं G का प्रतिच्छेदन है_aG_cऔर जी_bG_d. एक सामान्य उत्तल चतुर्भुज ABCD में, त्रिभुज के परिकेन्द्र और लंबकेन्द्र के लिए कोई प्राकृतिक अनुरूपता नहीं होती है। लेकिन ऐसे दो बिंदुओं का निर्माण निम्नलिखित तरीके से किया जा सकता है। चलो ओ_a, ओ_b, ओ_c, ओ_dत्रिभुजों BCD, ACD, ABD, ABC के परिकेन्द्र क्रमशः हों; और एच द्वारा निरूपित करें_a, एच_b, एच_c, एच_dसमान त्रिभुजों में ऑर्थोसेंटर। फिर रेखाओं का चौराहा O_aO_cऔर ओ_bO_dद्रव्यमान का परिकेंद्र कहा जाता है, और रेखाओं का प्रतिच्छेदन H_aH_cऔर वह_bH_dउत्तल चतुर्भुज का क्वासियोर्थोसेंटर कहा जाता है।इन बिंदुओं का उपयोग चतुर्भुज की यूलर रेखा को परिभाषित करने के लिए किया जा सकता है। एक उत्तल चतुर्भुज में, क्वासिऑर्थोसेंटर एच, क्षेत्र सेंट्रोइड जी, और क्वासिकिरकमसेंटर ओ इस क्रम में संरेख हैं, और एचजी = 2GO।

लाइनों ई के चौराहे के रूप में एक क्वासिनिन-बिंदु केंद्र ई को भी परिभाषित किया जा सकता है_aE_cऔर ई_bE_d, जहां ई_a, तथा_b, तथा_c, तथा_dक्रमशः नौ-बिंदु वृत्त हैं | त्रिभुज BCD, ACD, ABD, ABC के नौ-बिंदु केंद्र हैं। तब E, OH का मध्यबिंदु है।

उत्तल गैर-समांतर चतुर्भुज में एक और उल्लेखनीय रेखा न्यूटन रेखा है, जो विकर्णों के मध्यबिंदुओं को जोड़ती है, इन बिंदुओं को जोड़ने वाले खंड को वर्टेक्स सेंट्रोइड द्वारा द्विभाजित किया जाता है। एक और दिलचस्प रेखा (कुछ अर्थों में न्यूटन रेखा से दोहरी | न्यूटन की एक) वह रेखा है जो विकर्णों के प्रतिच्छेदन बिंदु को शीर्ष केन्द्रक से जोड़ती है। रेखा इस तथ्य से उल्लेखनीय है कि इसमें (क्षेत्र) केन्द्रक सम्मिलित है। वर्टेक्स सेंट्रॉइड विकर्णों के प्रतिच्छेदन और (क्षेत्र) सेंट्रोइड को 3:1 के अनुपात में जोड़ने वाले खंड को विभाजित करता है। बिंदु P और Q वाले किसी भी चतुर्भुज ABCD के लिए क्रमशः AD और BC और AB और CD के चौराहे, वृत्त (PAB), (PCD), (QAD), और (QBC) एक सामान्य बिंदु M से होकर गुजरते हैं, जिसे Miquel कहा जाता है। बिंदु। उत्तल चतुर्भुज ABCD के लिए जिसमें E विकर्णों का प्रतिच्छेदन बिंदु है और F भुजाओं BC और AD के विस्तार का प्रतिच्छेदन बिंदु है, मान लीजिए ω E और F से होकर जाने वाला एक वृत्त है जो CB को आंतरिक रूप से M और DA पर मिलता है N पर CA को फिर से L पर मिलने दें और DB को फिर से K पर मिलने दें। फिर वहाँ पकड़: सीधी रेखाएँ NK और ML बिंदु P पर प्रतिच्छेद करती हैं जो भुजा AB पर स्थित है; सीधी रेखाएँ NL और KM बिंदु Q पर प्रतिच्छेद करती हैं जो भुजा CD पर स्थित है। बिंदुओं P और Q को भुजाओं AB और CD पर वृत्त ω द्वारा निर्मित "पास्कल बिंदु" कहा जाता है।

उत्तल चतुर्भुजों के अन्य गुण

• चलो चतुर्भुज के सभी पक्षों पर बाहरी वर्ग बनाए जाते हैं। केंद्र (ज्यामिति) को जोड़ने वाले खंड # विपरीत वर्गों की सममित वस्तुएं (ए) लंबाई में बराबर हैं, और (बी) लंबवत हैं। इस प्रकार ये केंद्र एक समकोणीय चतुर्भुज के शीर्ष हैं। इसे वैन औबेल प्रमेय कहा जाता है।
• दिए गए किनारे की लंबाई के साथ किसी भी सरल चतुर्भुज के लिए, समान किनारे की लंबाई के साथ एक चक्रीय चतुर्भुज होता है।
• एक उत्तल चतुर्भुज के विकर्णों और भुजाओं से बने चार छोटे त्रिभुजों में यह गुण होता है कि दो विपरीत त्रिभुजों के क्षेत्रफलों का गुणनफल अन्य दो त्रिभुजों के क्षेत्रफलों के गुणनफल के बराबर होता है।

टैक्सोनॉमी

चतुर्भुजों की एक वर्गीकरण, हस्से आरेख का उपयोग करते हुए।

चतुर्भुजों का एक पदानुक्रमित वर्गीकरण (सामान्य) दाईं ओर की आकृति द्वारा चित्रित किया गया है। निम्न वर्ग उच्च वर्गों के विशेष मामले हैं जिनसे वे जुड़े हुए हैं। ध्यान दें कि यहाँ ट्रेपेज़ॉइड उत्तर अमेरिकी परिभाषा (ब्रिटिश समतुल्य एक ट्रेपेज़ियम) की बात कर रहा है। समावेशी परिभाषाओं का उपयोग पूरे समय किया जाता है।

तिरछा चतुर्भुज

See also: Skew polygon

चतुर्भुज डिफेनोइड के (लाल) पार्श्व किनारे एक नियमित ज़िग-ज़ैग तिरछा चतुर्भुज का प्रतिनिधित्व करते हैं

एक गैर-तलीय चतुर्भुज को तिरछा चतुर्भुज कहा जाता है। किनारों की लंबाई से इसके डायहेड्रल कोणों की गणना करने के सूत्र और दो आसन्न किनारों के बीच के कोण को अणुओं के गुणों पर काम करने के लिए प्राप्त किया गया था जैसे कि साइक्लोब्यूटेन जिसमें चार परमाणुओं की एक सिकुड़ी हुई अंगूठी होती है। ऐतिहासिक रूप से गौचे चतुर्भुज शब्द का उपयोग तिरछा चतुर्भुज के लिए भी किया जाता था। एक तिरछा चतुर्भुज अपने विकर्णों के साथ एक (संभवतः गैर-नियमित) चतुर्पाश्वीय बनाता है, और इसके विपरीत प्रत्येक तिरछा चतुर्भुज एक टेट्राहेड्रॉन से आता है जहां विपरीत किनारों (ज्यामिति) की एक जोड़ी को हटा दिया जाता है।

यह भी देखें

• पूर्ण चतुर्भुज
• चतुर्भुज का लम्ब द्विभाजक निर्माण
• सचेरी चतुर्भुज
• Types of mesh § Quadrilateral
• चतुर्भुज (भूगोल)

बाहरी संबंध

• "Quadrangle, complete", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Quadrilaterals Formed by Perpendicular Bisectors, Projective Collinearity and Interactive Classification of Quadrilaterals from cut-the-knot
• Definitions and examples of quadrilaterals and Definition and properties of tetragons from Mathopenref
• A (dynamic) Hierarchical Quadrilateral Tree at Dynamic Geometry Sketches
• An extended classification of quadrilaterals Archived 2019-12-30 at the Wayback Machine at Dynamic Math Learning Homepage Archived 2018-08-25 at the Wayback Machine
• The role and function of a hierarchical classification of quadrilaterals by Michael de Villiers