घनमूल: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Number whose cube is a given number}} | {{Short description|Number whose cube is a given number}} | ||
{{Use dmy dates|date=July 2013}} | {{Use dmy dates|date=July 2013}} | ||
[[File:Cube-root function.svg|thumb|का प्लॉट {{math|1=''y'' = {{radic|''x''|3}}}}. कथानक उत्पत्ति के संबंध में सममित है, क्योंकि यह एक विषम | [[File:Cube-root function.svg|thumb|का प्लॉट {{math|1=''y'' = {{radic|''x''|3}}}}. कथानक उत्पत्ति के संबंध में सममित है, क्योंकि यह एक विषम फलन है। पर {{math|1=''x'' = 0}} इस ग्राफ में एक लंबवत स्पर्शरेखा है।]] | ||
[[File:Cube and doubled cube.svg|thumb|एक इकाई घन (भुजा = 1) और एक घन जिसका आयतन दोगुना (भुजा = {{radic|2|3}} = 1.2599... {{OEIS2C|A002580}}).]]गणित में, किसी संख्या '''''x''''' का घनमूल | [[File:Cube and doubled cube.svg|thumb|एक इकाई घन(भुजा = 1) और एक घन जिसका आयतन दोगुना(भुजा = {{radic|2|3}} = 1.2599... {{OEIS2C|A002580}}).]]गणित में, किसी संख्या '''''x''''' का घनमूल एक संख्या '''''y,''''' {{math|1=''y''<sup>3</sup> = ''x''}} इस प्रकार है कि सभी गैर-शून्य [[वास्तविक संख्या]]ओं में एक वास्तविक घनमूल और जटिल संयुग्मी घनमूलों की एक जोड़ी होती है, और सभी गैर-शून्य [[जटिल संख्या]]ओं में तीन अलग-अलग जटिल घनमूल होते हैं। उदाहरण के लिए, '''8''' का वास्तविक घनमूल 2 है, जिसे इस प्रकार <math>\sqrt[3]8</math> निरूपित किया जाता है, क्योकि {{math|1=2<sup>3</sup> = 8}}, जबकि '''8''' का अन्य घनमूल <math>-1+i\sqrt 3</math> तथा <math>-1-i\sqrt 3</math> '''है । −27''i''''' के तीन घनमूल | ||
:<math>3i, \quad \frac{3\sqrt{3}}{2}-\frac{3}{2}i, \quad \text{and} \quad -\frac{3\sqrt{3}}{2}-\frac{3}{2}i. </math>हैं | :<math>3i, \quad \frac{3\sqrt{3}}{2}-\frac{3}{2}i, \quad \text{and} \quad -\frac{3\sqrt{3}}{2}-\frac{3}{2}i. </math>हैं | ||
कुछ संदर्भों में, विशेष रूप से जब कोई संख्या जिसका घनमूल लिया जाना है, यदि एक वास्तविक संख्या है, तो घनमूलों में से एक (इस विशेष | कुछ संदर्भों में, विशेष रूप से जब कोई संख्या जिसका घनमूल लिया जाना है, यदि एक वास्तविक संख्या है, तो घनमूलों में से एक(इस विशेष परिस्थिति में वास्तविक) को मूल घनमूल के रूप में संदर्भित किया जाता है, जिसे मूल चिह्न <math>\sqrt[3]{~^~}</math> के साथ दर्शाया जाता है। घनमूल, केवल वास्तविक संख्याओं पर विचार करने पर [[घन (बीजगणित)|घन(बीजगणित)]] का व्युत्क्रम फलन है, जिसमे जटिल संख्याओं पर भी विचार नहीं किया जाता है। हालांकि एक संख्या के पास सदैव<math>\left(\sqrt[3]x\right)^3 =x,</math>होता है, एक शून्येतर संख्या के घन में एक से अधिक सम्मिश्र घनमूल होते हैं और इसका मुख्य घनमूल वह संख्या नहीं हो सकती है जिसका घनीकरण किया गया था। उदाहरण के लिए <math>(-1+i\sqrt 3)^3=8</math>, लेकिन <math>-1+i\sqrt 3 \ne \sqrt[3]8=2.</math>। | ||
| Line 16: | Line 16: | ||
=== वास्तविक संख्या === | === वास्तविक संख्या === | ||
किसी भी वास्तविक संख्या x के लिए, एक वास्तविक संख्या y, y<sup>3</sup> = x इस प्रकार होती | किसी भी वास्तविक संख्या x के लिए, एक वास्तविक संख्या y, y<sup>3</sup> = x इस प्रकार होती है। घन फलन(बीजगणित) बढ़ रहा है, इसलिए दो अलग-अलग आगत के लिए समान परिणाम नहीं देता है, और यह सभी वास्तविक संख्याओं को सम्मिलित करता है। दूसरे शब्दों में, यह एक आक्षेप है, या एक के बाद एक है। फिर हम एक विपरीत फलन परिभाषित कर सकते हैं जो एक के बाद भी एक है। सभी वास्तविक संख्याओं के लिए, हम सभी वास्तविक संख्याओं के एक अद्वितीय घनमूल को परिभाषित कर सकते हैं। यदि इस परिभाषा का उपयोग किया जाता है, तो एक ऋणात्मक संख्या का घनमूल एक ऋणात्मक संख्या होती है। | ||
[[Image:3rd roots of unity.svg|thumb|right|1 के तीन घनमूल]]यदि x(यदि x गैर-शून्य है) और y सम्मिश्र संख्या है, तो इसके तीन समाधान हैं, | [[Image:3rd roots of unity.svg|thumb|right|1 के तीन घनमूल]]यदि x(यदि x गैर-शून्य है) और y सम्मिश्र संख्या है, तो इसके तीन समाधान हैं, इसलिए x के तीन घनमूल हैं। एक वास्तविक संख्या में एक वास्तविक घनमूल और इसके अतिरिक्त दो घनमूल होते हैं जो एक जटिल संयुग्म जोड़ी बनाते हैं। उदाहरण के लिए [[1]] का घनमूल हैं: | ||
:<math> 1, \quad -\frac{1}{2}+\frac{\sqrt{3}}{2}i, \quad -\frac{1}{2}-\frac{\sqrt{3}}{2}i. </math> | :<math> 1, \quad -\frac{1}{2}+\frac{\sqrt{3}}{2}i, \quad -\frac{1}{2}-\frac{\sqrt{3}}{2}i. </math> | ||
इनमें से अंतिम दो मूल किसी भी वास्तविक या सम्मिश्र संख्या के सभी मूलों के बीच संबंध को दर्शाते | इनमें से अंतिम दो मूल किसी भी वास्तविक या सम्मिश्र संख्या के सभी मूलों के बीच संबंध को दर्शाते हैं। यदि कोई संख्या किसी विशेष वास्तविक या सम्मिश्र संख्या का एक घनमूल है, तो अन्य दो घनमूल उस घनमूल को 1 के दो जटिल घनमूलों में से एक या दूसरे से गुणा करके प्राप्त किया जा सकता है। | ||
=== जटिल संख्या === | === जटिल संख्या === | ||
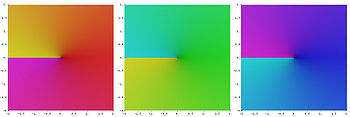
[[Image:Complex cube root.jpg|right|thumb|350px|इसके दो अतिरिक्त पत्तों के साथ जटिल घनमूल का प्लॉट। पहली छवि मुख्य शाखा को दिखाती है, जिसका वर्णन पाठ में किया गया है।]] | [[Image:Complex cube root.jpg|right|thumb|350px|इसके दो अतिरिक्त पत्तों के साथ जटिल घनमूल का प्लॉट। पहली छवि मुख्य शाखा को दिखाती है, जिसका वर्णन पाठ में किया गया है।]] | ||
[[Image:Riemann surface cube root.svg|right|thumb|200px|घनमूल की [[रीमैन सतह]]। कोई देख सकता है कि तीनों पत्ते एक साथ कैसे फिट होते हैं।]]सम्मिश्र संख्याओं के लिए, मुख्य घनमूल को | [[Image:Riemann surface cube root.svg|right|thumb|200px|घनमूल की [[रीमैन सतह]]। कोई देख सकता है कि तीनों पत्ते एक साथ कैसे फिट होते हैं।]]सम्मिश्र संख्याओं के लिए, मुख्य घनमूल को सामान्यतः उस घनमूल के रूप में परिभाषित किया जाता है जिसका सबसे बड़ा [[वास्तविक भाग]] होता है, या समकक्ष रूप से, वह घनमूल जिसका [[तर्क (जटिल विश्लेषण)|तर्क(जटिल विश्लेषण)]] सबसे कम निरपेक्ष मान रखता है। यह सूत्र द्वारा [[प्राकृतिक]] लघुगणक के प्रमुख मान से संबंधित है | ||
:<math>x^{\frac13} = \exp \left( \frac13 \ln{x} \right).</math> | :<math>x^{\frac13} = \exp \left( \frac13 \ln{x} \right).</math> | ||
| Line 38: | Line 38: | ||
:<math>\sqrt[3]{x} = \sqrt[3]{r}\exp \left(\frac {i\theta}{3} \right).</math> | :<math>\sqrt[3]{x} = \sqrt[3]{r}\exp \left(\frac {i\theta}{3} \right).</math> | ||
इसका मतलब है कि ध्रुवीय निर्देशांक में, हम घनमूल को परिभाषित करने के लिए त्रिज्या का घनमूल ले रहे हैं और ध्रुवीय कोण को तीन से विभाजित कर रहे हैं। इस परिभाषा के साथ, एक ऋणात्मक संख्या का मुख्य घनमूल एक सम्मिश्र संख्या है, और उदाहरण के लिए {{radic|−8|3}} | इसका मतलब है कि ध्रुवीय निर्देशांक में, हम घनमूल को परिभाषित करने के लिए त्रिज्या का घनमूल ले रहे हैं और ध्रुवीय कोण को तीन से विभाजित कर रहे हैं। इस परिभाषा के साथ, एक ऋणात्मक संख्या का मुख्य घनमूल एक सम्मिश्र संख्या है, और उदाहरण के लिए {{radic|−8|3}} -2 नहीं होगा, बल्कि {{nowrap|1 + ''i''{{sqrt|3}}}} होगा। | ||
घनमूल को बहु-मूल्यवान फलन के रूप में मानकर इस कठिनाई को भी हल किया जा सकता है: यदि हम मूल जटिल संख्या x को तीन समतुल्य रूपों में लिखते हैं, अर्थात् | घनमूल को बहु-मूल्यवान फलन के रूप में मानकर इस कठिनाई को भी हल किया जा सकता है: यदि हम मूल जटिल संख्या x को तीन समतुल्य रूपों में लिखते हैं, अर्थात् | ||
| Line 51: | Line 51: | ||
\\ \sqrt[3]{r}\exp \left(\frac{i\theta}{3} + \frac{2i \pi}{3} \right), | \\ \sqrt[3]{r}\exp \left(\frac{i\theta}{3} + \frac{2i \pi}{3} \right), | ||
\\ \sqrt[3]{r}\exp \left(\frac{i\theta}{3} - \frac{2i \pi}{3} \right). \end{cases} </math> | \\ \sqrt[3]{r}\exp \left(\frac{i\theta}{3} - \frac{2i \pi}{3} \right). \end{cases} </math> | ||
जब तक {{nowrap|1=''x'' = 0}}, ये तीन सम्मिश्र संख्याएँ अलग-अलग हैं, | जब तक {{nowrap|1=''x'' = 0}}, ये तीन सम्मिश्र संख्याएँ अलग-अलग हैं, यद्यपि x के तीन निरूपण समतुल्य थे। उदाहरण के लिए, {{radic|−8|3}} तब इसकी गणना -2 , {{nowrap|1 + ''i''{{sqrt|3}}}}, या {{nowrap|1 − ''i''{{sqrt|3}}}}.की जा सकती है | ||
यह [[मोनोड्रोमी]] की अवधारणा से संबंधित है: यदि कोई निरंतर फलन घनमूल को शून्य के चारों ओर एक बंद पथ के साथ अनुसरण करता है, तो एक | यह [[मोनोड्रोमी|एकसूत्रीय]] की अवधारणा से संबंधित है: यदि कोई निरंतर फलन घनमूल को शून्य के चारों ओर एक बंद पथ के साथ अनुसरण करता है, तो एक वक्र के बाद घनमूल के मान को <math>e^{2i\pi/3}</math>से गुणा(या विभाजित) किया जाता है। | ||
== [[कम्पास-एंड-सीधा निर्माण]] की असंभवता == | == [[कम्पास-एंड-सीधा निर्माण|सीमा तथा रेखीय निर्माण]] की असंभवता == | ||
घनमूल द्वारा एक ऐसे कोण को खोजने में समस्या | घनमूल द्वारा एक ऐसे कोण को खोजने में समस्या उत्पन्न हुई जिसका माप एक दिए गए कोण(त्रिभुज) का एक तिहाई है और एक घन के किनारे को खोजने में समस्या उत्पन्न हुई जिसका आयतन किसी दिए गए घन के किनारे(घन को दुगुना करने पर) से दोगुना है । 1837 में [[पियरे वांजेल]] ने प्रमाणित किया कि इनमें से कोई भी [[कम्पास-एंड-सीधा निर्माण|सीमा तथा रेखीय]] निर्माण के साथ प्रयोग नहीं किया जा सकता है। | ||
== संख्यात्मक तरीके == | == संख्यात्मक तरीके == | ||
न्यूटन की विधि एक पुनरावृत्त विधि है जिसका उपयोग घनमूल की गणना के लिए किया जा सकता है। वास्तविक [[तैरनेवाला स्थल]] | न्यूटन की विधि एक पुनरावृत्त विधि है जिसका उपयोग घनमूल की गणना के लिए किया जा सकता है। वास्तविक [[तैरनेवाला स्थल|चल बिन्दु]] के लिए यह विधि निम्नलिखित पुनरावृत्त एल्गोरिथम को कम कर देती है ताकि घनमूल के क्रमिक रूप से बेहतर अनुमान लगाया जा सके: | ||
:<math>x_{n+1} = \frac{1}{3} \left(\frac{a}{x_n^2} + 2x_n\right).</math> | :<math>x_{n+1} = \frac{1}{3} \left(\frac{a}{x_n^2} + 2x_n\right).</math> | ||
यह विधि केवल ऐसे चुने गए तीन कारकों का औसत है जो इस प्रकार है | यह विधि केवल ऐसे चुने गए तीन कारकों का औसत है जो इस प्रकार है | ||
:<math> x_n \times x_n \times \frac{a}{x_n^2}=a </math> | :<math> x_n \times x_n \times \frac{a}{x_n^2}=a </math> | ||
हैली की इस विधि पर एक एल्गोरिदम के साथ सुधार करती है जो प्रत्येक पुनरावृत्ति के साथ, यद्यपि प्रति पुनरावृत्ति फलन के साथ अधिक तेज़ी से अभिसरण करती | |||
हैली की इस विधि पर एक एल्गोरिदम के साथ सुधार करती है जो प्रत्येक पुनरावृत्ति के साथ, यद्यपि प्रति पुनरावृत्ति फलन के साथ अधिक तेज़ी से अभिसरण करती है। | |||
:<math>x_{n+1} = x_n \left(\frac{x_n^3 + 2a}{2x_n^3 + a}\right).</math> | :<math>x_{n+1} = x_n \left(\frac{x_n^3 + 2a}{2x_n^3 + a}\right).</math> | ||
| Line 79: | Line 79: | ||
|archive-url=https://web.archive.org/web/20131227144655/http://metamerist.com/cbrt/cbrt.htm | |archive-url=https://web.archive.org/web/20131227144655/http://metamerist.com/cbrt/cbrt.htm | ||
|archive-date=2013-12-27 |url-status=dead | |archive-date=2013-12-27 |url-status=dead | ||
}}</ref> इसलिए दो पुनरावृत्तियों की लागत छह गुणा, छह जोड़ और दो विभाजन हैं। इस प्रकार, हैली की विधि की तेजी से होने की संभावना है यदि एक विभाजन तीन परिवर्धन से अधिक | }}</ref> इसलिए दो पुनरावृत्तियों की लागत छह गुणा, छह जोड़ और दो विभाजन हैं। इस प्रकार, हैली की विधि की तेजी से होने की संभावना है यदि एक विभाजन तीन परिवर्धन से अधिक संकीर्ण है।<!--It's not certain because it depends on how many iteration you need. If you need two Newton's iterations but not three, one of Halley's may not be enough, and two will cost too much.--> | ||
किसी भी विधि के साथ एक निम्न प्रारंभिक सन्निकटन {{math|''x''{{sub|0}}}} बहुत निम्न एल्गोरिथम प्रदर्शन दे सकता है, और एक अच्छा प्रारंभिक सन्निकटन कुछ | किसी भी विधि के साथ एक निम्न प्रारंभिक सन्निकटन {{math|''x''{{sub|0}}}} बहुत निम्न एल्गोरिथम प्रदर्शन दे सकता है, और एक अच्छा प्रारंभिक सन्निकटन कुछ सीमा तक एक कलन प्रवृत्ति है। कुछ कार्यान्वयन अस्थिर -बिंदु संख्या के प्रतिपादक बिट्स में हेरफेर करते हैं; अर्थात वे घातांक को 3 से विभाजित करके प्रारंभिक सन्निकटन पर पहुंचते हैं।{{r|metamerist}} | ||
यह भी उपयोगी है कि यह सामान्यीकृत निरंतर अंश, धनात्मक संख्याओं | यह भी उपयोगी है कि यह सामान्यीकृत निरंतर अंश, धनात्मक संख्याओं के मूल nवें मूल पर मुख्य मूलों की गणना विधि पर आधारित है। | ||
यदि x, a और y = a - x के घनमूल का एक अच्छा प्रथम सन्निकटन है<sup>3</sup>,तब | यदि x, a और y = a - x के घनमूल का एक अच्छा प्रथम सन्निकटन है<sup>3</sup>,तब: | ||
:<math>\sqrt[3]{a} = \sqrt[3]{x^3+y} = x+\cfrac{y} {3x^2+\cfrac{2y} {2x+\cfrac{4y} {9x^2+\cfrac{5y} {2x+\cfrac{7y} {15x^2+\cfrac{8y} {2x+\ddots}}}}}}</math> | :<math>\sqrt[3]{a} = \sqrt[3]{x^3+y} = x+\cfrac{y} {3x^2+\cfrac{2y} {2x+\cfrac{4y} {9x^2+\cfrac{5y} {2x+\cfrac{7y} {15x^2+\cfrac{8y} {2x+\ddots}}}}}}</math> | ||
| Line 92: | Line 92: | ||
== तीसरी और चौथी डिग्री के समीकरणों के समाधान में उपस्थिति == | == तीसरी और चौथी डिग्री के समीकरणों के समाधान में उपस्थिति == | ||
[[घन समीकरण]], जो तीसरी डिग्री के [[बहुपद समीकरण]] हैं (जिसका अर्थ है कि अज्ञात की उच्चतम शक्ति 3 है) को | [[घन समीकरण]], जो तीसरी डिग्री के [[बहुपद समीकरण]] हैं(जिसका अर्थ है कि अज्ञात की उच्चतम शक्ति 3 है) को सदैव घनमूल और वर्गमूल के संदर्भ में उनके तीन समाधानों के लिए हल किया जा सकता है(हालाँकि केवल वर्गमूल के संदर्भ में सरल अभिव्यक्तियाँ उपस्थित हैं) सभी तीन समाधान, यदि उनमें से कम से कम एक [[परिमेय संख्या]] है)। यदि दो समाधान जटिल संख्याएं हैं, तो सभी तीन समाधान अभिव्यक्तियों में एक वास्तविक संख्या का वास्तविक घनमूल सम्मिलित होता है, जबकि यदि सभी तीन समाधान वास्तविक संख्याएं हैं, तो उन्हें [[एक अपूरणीय मामला|एक अपूरणीय परिस्थिति]] के संदर्भ में व्यक्त किया जा सकता है। | ||
कार्तीय समीकरणों को घनमूल और वर्गमूल के रूप में भी हल किया जा सकता है। | |||
== इतिहास == | == इतिहास == | ||
घनमूलों की गणना का पता 1800 ईसा पूर्व से ही [[बेबीलोनियन गणित]] में लगाया जा सकता है।<ref name="cbgr">{{cite book|last=Saggs|first=H. W. F.|title=ग्रीस और रोम से पहले की सभ्यता|url=https://archive.org/details/isbn_9780300050318|url-access=registration|year=1989|publisher=Yale University Press|isbn=978-0-300-05031-8|page=[https://archive.org/details/isbn_9780300050318/page/227 227]}}</ref> चौथी शताब्दी ईसा पूर्व में [[प्लेटो]] ने घन इतिहास को दोगुना करने की समस्या पेश की, जिसके लिए एक दिए गए घन के दोगुने आयतन के साथ एक [[घन (ज्यामिति)]] के किनारे के | घनमूलों की गणना का पता 1800 ईसा पूर्व से ही [[बेबीलोनियन गणित]] में लगाया जा सकता है।<ref name="cbgr">{{cite book|last=Saggs|first=H. W. F.|title=ग्रीस और रोम से पहले की सभ्यता|url=https://archive.org/details/isbn_9780300050318|url-access=registration|year=1989|publisher=Yale University Press|isbn=978-0-300-05031-8|page=[https://archive.org/details/isbn_9780300050318/page/227 227]}}</ref> चौथी शताब्दी ईसा पूर्व में [[प्लेटो]] ने घन इतिहास को दोगुना करने की समस्या पेश की, जिसके लिए एक दिए गए घन के दोगुने आयतन के साथ एक [[घन (ज्यामिति)|घन(ज्यामिति)]] के किनारे के सीमा तथा रेखीय निर्माण की आवश्यकता थी, इसके लिए लंबाई 3√2 के निर्माण की आवश्यकता थी, जिसे अब असंभव माना जाता है। | ||
[[गणितीय कला पर नौ अध्याय]] | [[गणितीय कला पर नौ अध्याय]] में घनमूलों को निकालने की एक विधि दिखाई देती है, एक [[चीनी गणित]] का पाठ दूसरी शताब्दी ईसा पूर्व के आसपास संकलित किया गया था और तीसरी शताब्दी ''CE'' में [[एल आईयू हुई|एलआईयू हुई]] द्वारा टिप्पणी की गई थी।<ref name="oxf">{{cite book|last=Crossley|first=John|last2=W.-C. Lun|first2=Anthony|title=गणितीय कला पर नौ अध्याय: सहयोगी और टिप्पणी|url=https://books.google.com/books?id=eiTJHRGTG6YC&pg=PA213|year=1999|publisher=Oxford University Press|isbn=978-0-19-853936-0|page=213}}</ref> अलेक्जेंड्रिया के [[ग्रीक गणित]] नायक ने पहली शताब्दी ''CE'' में घनमूल की गणना के लिए एक विधि तैयार की। [[आर्किमिडीज]] पर एक टिप्पणी में यूटोकियोस द्वारा उनके सूत्र का फिर से उल्लेख किया गया है।<ref>{{cite journal|last=Smyly|first=J. Gilbart|title=घनमूल के लिए बगुले का सूत्र|journal=Hermathena|year=1920|volume=19|issue=42|pages=64–67|publisher=Trinity College Dublin|jstor=23037103}}</ref> 499 CE में, [[भारतीय गणित]] और [[भारतीय खगोल विज्ञान]] के शास्त्रीय युग के एक [[गणितज्ञ]]-खगोलविद, [[आर्यभट]] ने [[आर्यभटीय]](खंड 2.5) में कई अंकों वाली संख्याओं के घनमूल को खोजने के लिए एक विधि दी।<ref>''[http://www.flipkart.com/aryabhatiya-mohan-apte-book-8174344802 Aryabhatiya] {{Webarchive|url=https://archive.today/20110815204559/http://www.flipkart.com/aryabhatiya-mohan-apte-book-8174344802 |date=15 August 2011 }} {{lang-mr|आर्यभटीय}}'', Mohan Apte, Pune, India, Rajhans Publications, 2009, p.62, {{ISBN|978-81-7434-480-9}}</ref> | ||
| Line 110: | Line 110: | ||
* [[नेस्टेड कट्टरपंथी]] | * [[नेस्टेड कट्टरपंथी]] | ||
* [[एकता की जड़]] | * [[एकता की जड़]] | ||
* [[nth-रूट एल्गोरिथम को स्थानांतरित करना]] | * [[nth-रूट एल्गोरिथम को स्थानांतरित करना|nth-मूल एल्गोरिथम को स्थानांतरित करना]] | ||
==संदर्भ== | ==संदर्भ== | ||
Revision as of 19:18, 10 December 2022
गणित में, किसी संख्या x का घनमूल एक संख्या y, y3 = x इस प्रकार है कि सभी गैर-शून्य वास्तविक संख्याओं में एक वास्तविक घनमूल और जटिल संयुग्मी घनमूलों की एक जोड़ी होती है, और सभी गैर-शून्य जटिल संख्याओं में तीन अलग-अलग जटिल घनमूल होते हैं। उदाहरण के लिए, 8 का वास्तविक घनमूल 2 है, जिसे इस प्रकार निरूपित किया जाता है, क्योकि 23 = 8, जबकि 8 का अन्य घनमूल तथा है । −27i के तीन घनमूल
- हैं
कुछ संदर्भों में, विशेष रूप से जब कोई संख्या जिसका घनमूल लिया जाना है, यदि एक वास्तविक संख्या है, तो घनमूलों में से एक(इस विशेष परिस्थिति में वास्तविक) को मूल घनमूल के रूप में संदर्भित किया जाता है, जिसे मूल चिह्न के साथ दर्शाया जाता है। घनमूल, केवल वास्तविक संख्याओं पर विचार करने पर घन(बीजगणित) का व्युत्क्रम फलन है, जिसमे जटिल संख्याओं पर भी विचार नहीं किया जाता है। हालांकि एक संख्या के पास सदैवहोता है, एक शून्येतर संख्या के घन में एक से अधिक सम्मिश्र घनमूल होते हैं और इसका मुख्य घनमूल वह संख्या नहीं हो सकती है जिसका घनीकरण किया गया था। उदाहरण के लिए , लेकिन ।
औपचारिक परिभाषा
किसी संख्या x का घनमूल संख्या y है जो समीकरण को संतुष्ट करती है
गुण
वास्तविक संख्या
किसी भी वास्तविक संख्या x के लिए, एक वास्तविक संख्या y, y3 = x इस प्रकार होती है। घन फलन(बीजगणित) बढ़ रहा है, इसलिए दो अलग-अलग आगत के लिए समान परिणाम नहीं देता है, और यह सभी वास्तविक संख्याओं को सम्मिलित करता है। दूसरे शब्दों में, यह एक आक्षेप है, या एक के बाद एक है। फिर हम एक विपरीत फलन परिभाषित कर सकते हैं जो एक के बाद भी एक है। सभी वास्तविक संख्याओं के लिए, हम सभी वास्तविक संख्याओं के एक अद्वितीय घनमूल को परिभाषित कर सकते हैं। यदि इस परिभाषा का उपयोग किया जाता है, तो एक ऋणात्मक संख्या का घनमूल एक ऋणात्मक संख्या होती है।
यदि x(यदि x गैर-शून्य है) और y सम्मिश्र संख्या है, तो इसके तीन समाधान हैं, इसलिए x के तीन घनमूल हैं। एक वास्तविक संख्या में एक वास्तविक घनमूल और इसके अतिरिक्त दो घनमूल होते हैं जो एक जटिल संयुग्म जोड़ी बनाते हैं। उदाहरण के लिए 1 का घनमूल हैं:
इनमें से अंतिम दो मूल किसी भी वास्तविक या सम्मिश्र संख्या के सभी मूलों के बीच संबंध को दर्शाते हैं। यदि कोई संख्या किसी विशेष वास्तविक या सम्मिश्र संख्या का एक घनमूल है, तो अन्य दो घनमूल उस घनमूल को 1 के दो जटिल घनमूलों में से एक या दूसरे से गुणा करके प्राप्त किया जा सकता है।
जटिल संख्या

सम्मिश्र संख्याओं के लिए, मुख्य घनमूल को सामान्यतः उस घनमूल के रूप में परिभाषित किया जाता है जिसका सबसे बड़ा वास्तविक भाग होता है, या समकक्ष रूप से, वह घनमूल जिसका तर्क(जटिल विश्लेषण) सबसे कम निरपेक्ष मान रखता है। यह सूत्र द्वारा प्राकृतिक लघुगणक के प्रमुख मान से संबंधित है
यदि हम x को इस रूप में लिखते हैं
जहाँ r एक गैर-ऋणात्मक वास्तविक संख्या है और θ परिसर में स्थित है
- ,
तो मुख्य जटिल घनमूल है
इसका मतलब है कि ध्रुवीय निर्देशांक में, हम घनमूल को परिभाषित करने के लिए त्रिज्या का घनमूल ले रहे हैं और ध्रुवीय कोण को तीन से विभाजित कर रहे हैं। इस परिभाषा के साथ, एक ऋणात्मक संख्या का मुख्य घनमूल एक सम्मिश्र संख्या है, और उदाहरण के लिए 3√−8 -2 नहीं होगा, बल्कि 1 + i√3 होगा।
घनमूल को बहु-मूल्यवान फलन के रूप में मानकर इस कठिनाई को भी हल किया जा सकता है: यदि हम मूल जटिल संख्या x को तीन समतुल्य रूपों में लिखते हैं, अर्थात्
इन तीन रूपों के प्रमुख जटिल घनमूल क्रमशः हैं
जब तक x = 0, ये तीन सम्मिश्र संख्याएँ अलग-अलग हैं, यद्यपि x के तीन निरूपण समतुल्य थे। उदाहरण के लिए, 3√−8 तब इसकी गणना -2 , 1 + i√3, या 1 − i√3.की जा सकती है
यह एकसूत्रीय की अवधारणा से संबंधित है: यदि कोई निरंतर फलन घनमूल को शून्य के चारों ओर एक बंद पथ के साथ अनुसरण करता है, तो एक वक्र के बाद घनमूल के मान को से गुणा(या विभाजित) किया जाता है।
सीमा तथा रेखीय निर्माण की असंभवता
घनमूल द्वारा एक ऐसे कोण को खोजने में समस्या उत्पन्न हुई जिसका माप एक दिए गए कोण(त्रिभुज) का एक तिहाई है और एक घन के किनारे को खोजने में समस्या उत्पन्न हुई जिसका आयतन किसी दिए गए घन के किनारे(घन को दुगुना करने पर) से दोगुना है । 1837 में पियरे वांजेल ने प्रमाणित किया कि इनमें से कोई भी सीमा तथा रेखीय निर्माण के साथ प्रयोग नहीं किया जा सकता है।
संख्यात्मक तरीके
न्यूटन की विधि एक पुनरावृत्त विधि है जिसका उपयोग घनमूल की गणना के लिए किया जा सकता है। वास्तविक चल बिन्दु के लिए यह विधि निम्नलिखित पुनरावृत्त एल्गोरिथम को कम कर देती है ताकि घनमूल के क्रमिक रूप से बेहतर अनुमान लगाया जा सके:
यह विधि केवल ऐसे चुने गए तीन कारकों का औसत है जो इस प्रकार है
हैली की इस विधि पर एक एल्गोरिदम के साथ सुधार करती है जो प्रत्येक पुनरावृत्ति के साथ, यद्यपि प्रति पुनरावृत्ति फलन के साथ अधिक तेज़ी से अभिसरण करती है।
यह अभिसरण की दर से,ऐसी दो पुनरावृत्तियाँ न्यूटन की विधि के तीन पुनरावृत्तियों जितना काम करती हैं। न्यूटन की विधि के प्रत्येक पुनरावृत्ति में दो गुणन, एक जोड़ और एक विभाजन होता है, यह मानते हुए 1/3a पूर्व-गणना की जाती है, इसलिए तीन पुनरावृत्तियों और पूर्व-गणना के लिए सात गुणन, तीन जोड़ और तीन विभाजन की आवश्यकता होती है।
हैली की विधि के प्रत्येक पुनरावृत्ति में तीन गुणा, तीन जोड़ और एक विभाजन की आवश्यकता होती है,[1] इसलिए दो पुनरावृत्तियों की लागत छह गुणा, छह जोड़ और दो विभाजन हैं। इस प्रकार, हैली की विधि की तेजी से होने की संभावना है यदि एक विभाजन तीन परिवर्धन से अधिक संकीर्ण है।
किसी भी विधि के साथ एक निम्न प्रारंभिक सन्निकटन x0 बहुत निम्न एल्गोरिथम प्रदर्शन दे सकता है, और एक अच्छा प्रारंभिक सन्निकटन कुछ सीमा तक एक कलन प्रवृत्ति है। कुछ कार्यान्वयन अस्थिर -बिंदु संख्या के प्रतिपादक बिट्स में हेरफेर करते हैं; अर्थात वे घातांक को 3 से विभाजित करके प्रारंभिक सन्निकटन पर पहुंचते हैं।[1] यह भी उपयोगी है कि यह सामान्यीकृत निरंतर अंश, धनात्मक संख्याओं के मूल nवें मूल पर मुख्य मूलों की गणना विधि पर आधारित है।
यदि x, a और y = a - x के घनमूल का एक अच्छा प्रथम सन्निकटन है3,तब:
दूसरा समीकरण पहले भाग के प्रत्येक युग्म को एक भाग में जोड़ता है, इस प्रकार अभिसरण की गति को दोगुना करता है।
तीसरी और चौथी डिग्री के समीकरणों के समाधान में उपस्थिति
घन समीकरण, जो तीसरी डिग्री के बहुपद समीकरण हैं(जिसका अर्थ है कि अज्ञात की उच्चतम शक्ति 3 है) को सदैव घनमूल और वर्गमूल के संदर्भ में उनके तीन समाधानों के लिए हल किया जा सकता है(हालाँकि केवल वर्गमूल के संदर्भ में सरल अभिव्यक्तियाँ उपस्थित हैं) सभी तीन समाधान, यदि उनमें से कम से कम एक परिमेय संख्या है)। यदि दो समाधान जटिल संख्याएं हैं, तो सभी तीन समाधान अभिव्यक्तियों में एक वास्तविक संख्या का वास्तविक घनमूल सम्मिलित होता है, जबकि यदि सभी तीन समाधान वास्तविक संख्याएं हैं, तो उन्हें एक अपूरणीय परिस्थिति के संदर्भ में व्यक्त किया जा सकता है।
कार्तीय समीकरणों को घनमूल और वर्गमूल के रूप में भी हल किया जा सकता है।
इतिहास
घनमूलों की गणना का पता 1800 ईसा पूर्व से ही बेबीलोनियन गणित में लगाया जा सकता है।[2] चौथी शताब्दी ईसा पूर्व में प्लेटो ने घन इतिहास को दोगुना करने की समस्या पेश की, जिसके लिए एक दिए गए घन के दोगुने आयतन के साथ एक घन(ज्यामिति) के किनारे के सीमा तथा रेखीय निर्माण की आवश्यकता थी, इसके लिए लंबाई 3√2 के निर्माण की आवश्यकता थी, जिसे अब असंभव माना जाता है।
गणितीय कला पर नौ अध्याय में घनमूलों को निकालने की एक विधि दिखाई देती है, एक चीनी गणित का पाठ दूसरी शताब्दी ईसा पूर्व के आसपास संकलित किया गया था और तीसरी शताब्दी CE में एलआईयू हुई द्वारा टिप्पणी की गई थी।[3] अलेक्जेंड्रिया के ग्रीक गणित नायक ने पहली शताब्दी CE में घनमूल की गणना के लिए एक विधि तैयार की। आर्किमिडीज पर एक टिप्पणी में यूटोकियोस द्वारा उनके सूत्र का फिर से उल्लेख किया गया है।[4] 499 CE में, भारतीय गणित और भारतीय खगोल विज्ञान के शास्त्रीय युग के एक गणितज्ञ-खगोलविद, आर्यभट ने आर्यभटीय(खंड 2.5) में कई अंकों वाली संख्याओं के घनमूल को खोजने के लिए एक विधि दी।[5]
यह भी देखें
- वर्गमूल की गणना करने की विधियाँ
- बहुपद विषयों की सूची
- नवीं जड़
- वर्गमूल
- नेस्टेड कट्टरपंथी
- एकता की जड़
- nth-मूल एल्गोरिथम को स्थानांतरित करना
संदर्भ
- ↑ 1.0 1.1 "फास्ट क्यूब रूट की तलाश में". metamerist.com. 2008. Archived from the original on 27 December 2013.
- ↑ Saggs, H. W. F. (1989). ग्रीस और रोम से पहले की सभ्यता. Yale University Press. p. 227. ISBN 978-0-300-05031-8.
- ↑ Crossley, John; W.-C. Lun, Anthony (1999). गणितीय कला पर नौ अध्याय: सहयोगी और टिप्पणी. Oxford University Press. p. 213. ISBN 978-0-19-853936-0.
- ↑ Smyly, J. Gilbart (1920). "घनमूल के लिए बगुले का सूत्र". Hermathena. Trinity College Dublin. 19 (42): 64–67. JSTOR 23037103.
- ↑ Aryabhatiya Archived 15 August 2011 at archive.today Marathi: आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.62, ISBN 978-81-7434-480-9
इस पेज में लापता आंतरिक लिंक की सूची
- पुराना फंक्शन
- ऊर्ध्वाधर स्पर्शरेखा
- अंक शास्त्र
- जटिल सन्युग्म
- कट्टरपंथी संकेत
- उलटा काम करना
- निरपेक्ष मूल्य
- धुवीय निर्देशांक
- बहुविकल्पी समारोह
- निरंतर कार्य
- घन को दोगुना करना
- कोण तिरछा
- पुनरावर्ती विधि
- अभिसरण की दर
- चतुर्थांश समीकरण
- अलेक्जेंड्रिया के हीरो
- खगोल विज्ञानी
- वर्गमूल की गणना के तरीके