यंत्र के सिद्धांत: Difference between revisions
(Content Modified) |
No edit summary |
||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 19: | Line 19: | ||
=== शुद्धगतिक युगल (काइनेमेटिक पेयर) === | === शुद्धगतिक युगल (काइनेमेटिक पेयर) === | ||
शुद्धगतिक युगल को यंत्र के दो कड़ियों या तत्वों के रूप में परिभाषित किया जाता है, जब एक दूसरे के संपर्क में एक जोड़ी बनाने के लिए कहा जाता है। यदि उनके बीच सापेक्ष गति पूरी तरह से या सफलतापूर्वक एक निश्चित दिशा में बाधित है, | शुद्धगतिक युगल को यंत्र के दो कड़ियों या तत्वों के रूप में परिभाषित किया जाता है, जब एक दूसरे के संपर्क में एक जोड़ी बनाने के लिए कहा जाता है। यदि उनके बीच सापेक्ष गति पूरी तरह से या सफलतापूर्वक एक निश्चित दिशा में बाधित होती है तब, जोड़ी को शुद्धगतिक युगल के रूप में जाना जाता है।<ref>शुद्धगतिक युगल (काइनेमेटिक पेयर)([https://learnmechanical.com/kinematic-pair/ "Kinematic-pair]")</ref> | ||
चित्र-1 में दिखाए गए एक स्लाइडर क्रैंक तंत्र में , यहाँ शुद्धगतिक युगल हैं। | चित्र-1 में दिखाए गए एक स्लाइडर क्रैंक तंत्र में , यहाँ शुद्धगतिक युगल हैं। | ||
* कड़ी 2 कड़ी 1 के सापेक्ष घूमता है और इसलिए कड़ी 1 और 2 एक शुद्धगतिक युगल है। | * कड़ी 2 कड़ी 1 के सापेक्ष घूमता है और इसलिए कड़ी 1 और 2 एक शुद्धगतिक युगल है। | ||
* कड़ी 2 कड़ी 3 के सापेक्ष गति कर रहा है और इसलिए कड़ी 2 और कड़ी 3 एक शुद्धगतिक युगल है | * कड़ी 2 कड़ी 3 के सापेक्ष गति कर रहा है, और इसलिए कड़ी 2 और कड़ी 3 एक शुद्धगतिक युगल है | ||
* कड़ी 3 में कड़ी 4 के सापेक्ष गति हो रही है | * कड़ी 3 में कड़ी 4 के सापेक्ष गति हो रही है | ||
* कड़ी 4 कड़ी 1 के सापेक्ष गति कर रहा है। इसलिए कड़ी 3,4 और 4, 1 शुद्धगतिक युगल का गठन करते हैं। | * कड़ी 4 कड़ी 1 के सापेक्ष गति कर रहा है। इसलिए कड़ी 3,4 और 4, 1 शुद्धगतिक युगल का गठन करते हैं। | ||
| Line 30: | Line 30: | ||
शुद्धगतिक युगल का वर्गीकरण | शुद्धगतिक युगल का वर्गीकरण | ||
1. कड़ियों के बीच संपर्क की | 1. कड़ियों के बीच संपर्क की स्वभाव के अनुसार। | ||
* | * निम्नतर युगल (लोअर पेयर) - दो कड़ियों के बीच सतह संपर्क या क्षेत्र संपर्क होता है। उदाहरण: शाफ्ट एक बेयरिंग में घूमता है, नट एक स्क्रू पर घूमता है। | ||
* | * उच्चतर युगल (हायर पेयर) - दो कड़ियों के बीच एक बिंदु या संपर्क रेखा होती है। उदाहरण: एक सतह पर पहिया लुढ़कना और कैम और अनुयायी | ||
[[File:Screw Pair.jpg|thumb|201x201px|चित्र-3 स्क्रू पेयर]]2. दो कड़ियों के बीच सापेक्ष गति के प्रकार के अनुसार | [[File:Screw Pair.jpg|thumb|201x201px|चित्र-3 स्क्रू पेयर]]2. दो कड़ियों के बीच सापेक्ष गति के प्रकार के अनुसार | ||
* स्लाइडिंग पेयर- शुद्धगतिक युगल, जहां दो कड़ी एक दूसरे के सापेक्ष एक सर्पी गति(स्लाइडिंग मोशन) रखते हैं। उदाहरण: एक आयताकार छेद में आयत रॉड जैसा कि चित्र-2 में दिखाया गया है। | * स्लाइडिंग पेयर- शुद्धगतिक युगल, जहां दो कड़ी एक दूसरे के सापेक्ष एक सर्पी गति(स्लाइडिंग मोशन) रखते हैं। उदाहरण: एक आयताकार छेद में आयत रॉड जैसा कि चित्र-2 में दिखाया गया है। | ||
| Line 49: | Line 49: | ||
एक पिंड में जितनी स्वतंत्र गतियाँ (स्थानांतरण और घूर्णी) हो सकती हैं, उन्हें स्वतंत्रता कोटि के रूप में जाना जाता है।<ref>" प्रतिबंधित कठोर निकायों के मूल किनेमेटिक्स"([https://www.cs.cmu.edu/~rapidproto/mechanisms/chpt4.html "Basic Kinematics of constrained rigid bodies"])</ref> | एक पिंड में जितनी स्वतंत्र गतियाँ (स्थानांतरण और घूर्णी) हो सकती हैं, उन्हें स्वतंत्रता कोटि के रूप में जाना जाता है।<ref>" प्रतिबंधित कठोर निकायों के मूल किनेमेटिक्स"([https://www.cs.cmu.edu/~rapidproto/mechanisms/chpt4.html "Basic Kinematics of constrained rigid bodies"])</ref> | ||
चित्र 6. अंतरिक्ष में एक कठोर पिंड को दर्शाता है। यदि पिंड पर कोई बाधा नहीं है तो निम्नलिखित स्वतंत्र गति का वर्णन किया जा सकता है। | चित्र 6. अंतरिक्ष में एक कठोर पिंड को दर्शाता है। यदि पिंड पर कोई बाधा नहीं है, तो निम्नलिखित स्वतंत्र गति का वर्णन किया जा सकता है। | ||
x, y, और z अक्षों के अनुदिश स्थानांतरण गति | x, y, और z अक्षों के अनुदिश स्थानांतरण गति | ||
| Line 55: | Line 55: | ||
x, y, और z अक्ष के आस पास में घूर्णन गति। | x, y, और z अक्ष के आस पास में घूर्णन गति। | ||
इसलिए पिंड में छह स्वतंत्र गति हो सकती | इसलिए पिंड में छह स्वतंत्र गति हो सकती हैं। कहा जाता है कि इस पिंड में छह स्वतंत्रता कोटि हैं । | ||
स्वतंत्रता कोटि = 6 - बाधाओं की संख्या यदि बाधाओं की संख्या चार है तो, स्वतंत्रता कोटि = 6 - 4 = 2 | स्वतंत्रता कोटि = 6 - बाधाओं की संख्या, यदि बाधाओं की संख्या चार है तो, स्वतंत्रता कोटि = 6 - 4 = 2 | ||
=== शुद्धगतिक श्रृंखला === | === शुद्धगतिक श्रृंखला === | ||
शुद्धगतिक श्रृंखला को शुद्धगतिक युगल के संयोजन के रूप में परिभाषित किया जाता है, जो इस तरह से जुड़ते हैं कि प्रत्येक कड़ी दो पेयर(जोड़े) का एक हिस्सा बनाती है और एक-दूसरे के सापेक्ष की गति निश्चित होती है। या जब शुद्धगतिक युगल को इस प्रकार जोड़ा जाता है कि निश्चित गति को संचारित करने के लिए अंतिम कड़ी पहली कड़ी से जुड़ जाती है, तो इसे शुद्धगतिक श्रृंखला कहा जाता है।[[File:Degrees of Freedom.jpg|thumb|197x197px|चित्र-6 स्वतंत्रता कोटि]] | शुद्धगतिक श्रृंखला को शुद्धगतिक युगल के संयोजन के रूप में परिभाषित किया जाता है, जो इस तरह से जुड़ते हैं कि प्रत्येक कड़ी दो पेयर(जोड़े) का एक हिस्सा बनाती है और एक-दूसरे के सापेक्ष की गति निश्चित होती है। या जब शुद्धगतिक युगल को इस प्रकार जोड़ा जाता है कि निश्चित गति को संचारित करने के लिए अंतिम कड़ी पहली कड़ी से जुड़ जाती है, तो इसे शुद्धगतिक श्रृंखला कहा जाता है।[[File:Degrees of Freedom.jpg|thumb|197x197px|चित्र-6 स्वतंत्रता कोटि]] | ||
चित्र-1 में, स्लाइडर क्रैंक यंत्रावली कड़ी 1 कड़ी 2 से जुड़ी है और कड़ी 4 से भी जुड़ी | चित्र-1 में, स्लाइडर क्रैंक यंत्रावली कड़ी 1 कड़ी 2 से जुड़ी है और कड़ी 4 से भी जुड़ी है। कड़ी 1 और 2 काइनेमेटिक जोड़ी है, कड़ी 1 और 4 एक काइनेमेटिक जोड़ी है। इसलिए कड़ी 1 दो शुद्धगतिक युगल का हिस्सा है। इसी प्रकार कड़ी 2 दो जोड़ियों का एक भाग बनाता है (कड़ी 2 और 1 की शुद्धगतिक युगल और कड़ी 2 और 3 की शुद्धगतिक युगल)। इसी तरह कड़ी 3 और 4 प्रत्येक दो जोड़े का एक हिस्सा बनाते हैं। इसलिए एक स्लाइडर क्रैंक तंत्र में, प्रत्येक कड़ी दो जोड़े का एक हिस्सा बनाता है, और प्रत्येक के सापेक्ष दूसरे की गति निश्चित है। तो इन कड़ियों का कुल संयोजन एक शुद्धगतिक श्रृंखला है। | ||
पेयर(जोड़े) की संख्या (p) और चार कड़ीओं की शुद्धगतिक श्रृंखला में कड़ीओं की संख्या (L) के बीच संबंध का उल्लेख इस प्रकार से किया गया है | |||
<math>L = 2p - 4</math> ........... (1.1) | <math>L = 2p - 4</math> ........... (1.1) | ||
कड़ीओं की संख्या (L) और जोड़ों की संख्या (j) के बीच संबंध चार कड़ीओं की शुद्धगतिक श्रृंखला में बनाने के द्वारा इस प्रकार दिया जाता है | |||
<math>j = \frac{3}{2} L -2</math> ...........(1.2) | <math>j = \frac{3}{2} L -2</math> ...........(1.2) | ||
समीकरण (1.1) और (1.2) केवल | समीकरण (1.1) और (1.2) केवल निम्नतर युगल वाली शुद्धगतिक श्रृंखलाओं पर लागू होते हैं। यदि उन्हें उच्चतर युगल वाली शुद्धगतिक श्रृंखलाओं पर लागू किया जाता है, तो प्रत्येक उच्चतर युगल को दो निम्नतर युगल और एक अतिरिक्त कड़ी के बराबर लिया जाना चाहिए। | ||
समीकरणों (1.1) और (1.2) में यदि | समीकरणों (1.1) और (1.2) में यदि | ||
| Line 90: | Line 90: | ||
== संदर्भ == | == संदर्भ == | ||
<references /> | <references /> | ||
[[Category:Organic Articles]] | |||
Latest revision as of 10:00, 16 December 2022
परिभाषा
यंत्र के सिद्धांत(थ्योरी ऑफ़ मशीन्स), विज्ञान की एक शाखा है जो यंत्र(मशीन) के विभिन्न भागों और उन पर कार्य करने वाले बलों के बीच सापेक्ष गति के अध्ययन से संबंधित है।[1] थ्योरी ऑफ़ मशीन्स की दो उप शाखाएँ हैं, अर्थात् काइनेमेटिक्स और डायनेमिक्स ।
काइनेमेटिक्स, मशीन के विभिन्न भागों के बीच सापेक्ष गति के अध्ययन से संबंधित है। उन पर कार्य करने वाला बल स्वभाव से स्थिर होगा।
डायनेमिक्स, एक मशीन के विभिन्न भागों के बीच सापेक्ष गति के अध्ययन से संबंधित है। उन पर कार्य करने वाला बल स्वभाव से स्थिर या गतिशील होगा। डायनेमिक्स की दो उप शाखाएँ हैं जिनका नाम काइनेटिक्स और स्टैटिक्स है।
काइनेटिक्स, यंत्र के सिद्धांत की एक शाखा है जो पिंडों के गतिमान होने पर विभिन्न बलों से संबंधित है जबकि स्टेटिक्स, यंत्र के सिद्धांत की एक शाखा है जो पिंडों के स्थिर होने पर विभिन्न बलों से संबंधित है।
क्रियाविधि/ यंत्रावली
यंत्रावली, कठोर या अवरोधक पिंडों का एक संयोजन है, जो इस प्रकार रूपित और जुड़े हुए हैं कि वे एक-दूसरे पर निश्चित सापेक्ष गति के साथ आगे बढ़ते हैं।
यंत्र
यंत्र, एक तंत्र या तंत्र का एक संयोजन[2] है, जो न केवल भागों को निश्चित गति प्रदान करता है, बल्कि उपलब्ध यांत्रिक ऊर्जा को किसी प्रकार की उपयोगी ऊर्जा में प्रसारित और संशोधित करता है। यह उपयोगी ऊर्जा किसी वांछित कार्य के रूप में हो सकती है। स्लाइडर-क्रैंक तंत्र(slider-crank mechanism), एक यंत्र बन जाता है जब इसे ऑटोमोबाइल इंजन में वाल्व तंत्र जोड़कर इस्तेमाल किया जाता है । यहां इस उपलब्ध ऊर्जा को, जो पिस्टन पर बल है, वांछित ऊर्जा में परिवर्तित कर देता है, जो अरालदंड(क्रैंकशाफ्ट) पर आघूर्ण बल(टॉर्क) है। यह टॉर्क, वाहन की गति को सक्षम करता है।
कड़ी
कड़ी/लिंक को एक सदस्य या सदस्यों के संयोजन के रूप में परिभाषित किया जाता है, जो अन्य सदस्यों को जोड़ता है और उनके सापेक्ष गति रखता है। एक स्लाइडर क्रैंक तंत्र में निम्नलिखित चार लिंक होते हैं। 1. फ्रेम, 2. क्रैंक, 3. कनेक्टिंग रॉड, 4. स्लाइडर
शुद्धगतिक युगल (काइनेमेटिक पेयर)
शुद्धगतिक युगल को यंत्र के दो कड़ियों या तत्वों के रूप में परिभाषित किया जाता है, जब एक दूसरे के संपर्क में एक जोड़ी बनाने के लिए कहा जाता है। यदि उनके बीच सापेक्ष गति पूरी तरह से या सफलतापूर्वक एक निश्चित दिशा में बाधित होती है तब, जोड़ी को शुद्धगतिक युगल के रूप में जाना जाता है।[3]
चित्र-1 में दिखाए गए एक स्लाइडर क्रैंक तंत्र में , यहाँ शुद्धगतिक युगल हैं।
- कड़ी 2 कड़ी 1 के सापेक्ष घूमता है और इसलिए कड़ी 1 और 2 एक शुद्धगतिक युगल है।
- कड़ी 2 कड़ी 3 के सापेक्ष गति कर रहा है, और इसलिए कड़ी 2 और कड़ी 3 एक शुद्धगतिक युगल है
- कड़ी 3 में कड़ी 4 के सापेक्ष गति हो रही है
- कड़ी 4 कड़ी 1 के सापेक्ष गति कर रहा है। इसलिए कड़ी 3,4 और 4, 1 शुद्धगतिक युगल का गठन करते हैं।
शुद्धगतिक युगल का वर्गीकरण
1. कड़ियों के बीच संपर्क की स्वभाव के अनुसार।
- निम्नतर युगल (लोअर पेयर) - दो कड़ियों के बीच सतह संपर्क या क्षेत्र संपर्क होता है। उदाहरण: शाफ्ट एक बेयरिंग में घूमता है, नट एक स्क्रू पर घूमता है।
- उच्चतर युगल (हायर पेयर) - दो कड़ियों के बीच एक बिंदु या संपर्क रेखा होती है। उदाहरण: एक सतह पर पहिया लुढ़कना और कैम और अनुयायी
2. दो कड़ियों के बीच सापेक्ष गति के प्रकार के अनुसार
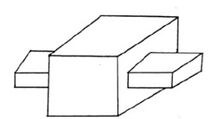
- स्लाइडिंग पेयर- शुद्धगतिक युगल, जहां दो कड़ी एक दूसरे के सापेक्ष एक सर्पी गति(स्लाइडिंग मोशन) रखते हैं। उदाहरण: एक आयताकार छेद में आयत रॉड जैसा कि चित्र-2 में दिखाया गया है।
- टर्निंग पेयर- शुद्धगतिक युगल, जहां एक कड़ी में दूसरे के सापेक्ष एक मोड़ गति(टर्निंग मोशन) होती है। चित्र-1 में, कड़ी 2 में कड़ी 1 के सापेक्ष एक मोड़ गति(टर्निंग मोशन) है, इसलिए कड़ी 2 और 1 से टर्निंग पेयर बनती है। इसी तरह 3 और 4 और 2 और 3 , टर्निंग पेयर का उत्पादन करते हैं ।
- रोलिंग पेयर- शुद्धगतिक युगल, जहाँ एक कड़ी में दूसरे के सापेक्ष लुढ़कने(रोलिंग) की गति होती है। उदाहरण: एक सपाट सतह पर एक रोलिंग व्हील, एक रोलिंग पेयर बनाती है। बॉल बेयरिंग में, बॉल और बेयरिंग एक रोलिंग पेयर बनाते हैं और दूसरी रोलिंग पेयर, बॉल और शाफ्ट होती हैं ।
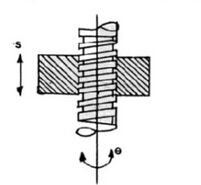
- स्क्रू पेयर(हेलिकल पेयर)- शुद्धगतिक युगल, जहां दो कड़ी के बीच एक मोड़(टर्निंग) और साथ ही सर्पी गति(स्लाइडिंग मोशन) होती है। अग्रग पेंच(लेड स्क्रू) और लेथ का नट एक स्क्रू पेयर है। चित्र-3 स्क्रू पेयर दिखाता है।
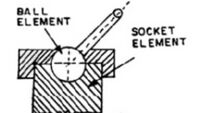
- स्फेरिकल पेयर- शुद्धगतिक युगल, जहाँ गोले(स्फेरिकल) के रूप में एक कड़ी, एक निश्चित कड़ी के अंदर मुड़ जाती है। चित्र-4 में दिखाया गया कन्दुक खल्लिका संधि(बॉल और सॉकेट जॉइन्ट) एक स्फेरिकल पेयर है।
3. दो कड़ियों के बीच यांत्रिक बाधा के गुण के अनुसार
- क्लोज्ड पेयर - पेयर के दो तत्व यांत्रिक रूप से एक साथ जुड़े होते हैं
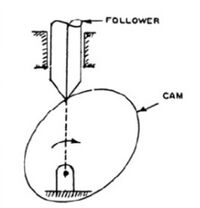
- अंक्लोज्ड पेयर - पेयर के दो तत्व गुरुत्वाकर्षण बल के कारण या किसी स्प्रिंग एक्शन(कमानी क्रिया) के कारण संपर्क में होते हैं। उदाहरण ; कैम और अनुयायी चित्र-5 में क्योंकि इसे स्प्रिंग और गुरुत्वाकर्षण द्वारा लगाए गए बलों द्वारा संपर्क में रखा जाता है।
स्वतंत्रता कोटि
एक पिंड में जितनी स्वतंत्र गतियाँ (स्थानांतरण और घूर्णी) हो सकती हैं, उन्हें स्वतंत्रता कोटि के रूप में जाना जाता है।[4]
चित्र 6. अंतरिक्ष में एक कठोर पिंड को दर्शाता है। यदि पिंड पर कोई बाधा नहीं है, तो निम्नलिखित स्वतंत्र गति का वर्णन किया जा सकता है।
x, y, और z अक्षों के अनुदिश स्थानांतरण गति
x, y, और z अक्ष के आस पास में घूर्णन गति।
इसलिए पिंड में छह स्वतंत्र गति हो सकती हैं। कहा जाता है कि इस पिंड में छह स्वतंत्रता कोटि हैं ।
स्वतंत्रता कोटि = 6 - बाधाओं की संख्या, यदि बाधाओं की संख्या चार है तो, स्वतंत्रता कोटि = 6 - 4 = 2
शुद्धगतिक श्रृंखला
शुद्धगतिक श्रृंखला को शुद्धगतिक युगल के संयोजन के रूप में परिभाषित किया जाता है, जो इस तरह से जुड़ते हैं कि प्रत्येक कड़ी दो पेयर(जोड़े) का एक हिस्सा बनाती है और एक-दूसरे के सापेक्ष की गति निश्चित होती है। या जब शुद्धगतिक युगल को इस प्रकार जोड़ा जाता है कि निश्चित गति को संचारित करने के लिए अंतिम कड़ी पहली कड़ी से जुड़ जाती है, तो इसे शुद्धगतिक श्रृंखला कहा जाता है।
चित्र-1 में, स्लाइडर क्रैंक यंत्रावली कड़ी 1 कड़ी 2 से जुड़ी है और कड़ी 4 से भी जुड़ी है। कड़ी 1 और 2 काइनेमेटिक जोड़ी है, कड़ी 1 और 4 एक काइनेमेटिक जोड़ी है। इसलिए कड़ी 1 दो शुद्धगतिक युगल का हिस्सा है। इसी प्रकार कड़ी 2 दो जोड़ियों का एक भाग बनाता है (कड़ी 2 और 1 की शुद्धगतिक युगल और कड़ी 2 और 3 की शुद्धगतिक युगल)। इसी तरह कड़ी 3 और 4 प्रत्येक दो जोड़े का एक हिस्सा बनाते हैं। इसलिए एक स्लाइडर क्रैंक तंत्र में, प्रत्येक कड़ी दो जोड़े का एक हिस्सा बनाता है, और प्रत्येक के सापेक्ष दूसरे की गति निश्चित है। तो इन कड़ियों का कुल संयोजन एक शुद्धगतिक श्रृंखला है।
पेयर(जोड़े) की संख्या (p) और चार कड़ीओं की शुद्धगतिक श्रृंखला में कड़ीओं की संख्या (L) के बीच संबंध का उल्लेख इस प्रकार से किया गया है
........... (1.1)
कड़ीओं की संख्या (L) और जोड़ों की संख्या (j) के बीच संबंध चार कड़ीओं की शुद्धगतिक श्रृंखला में बनाने के द्वारा इस प्रकार दिया जाता है
...........(1.2)
समीकरण (1.1) और (1.2) केवल निम्नतर युगल वाली शुद्धगतिक श्रृंखलाओं पर लागू होते हैं। यदि उन्हें उच्चतर युगल वाली शुद्धगतिक श्रृंखलाओं पर लागू किया जाता है, तो प्रत्येक उच्चतर युगल को दो निम्नतर युगल और एक अतिरिक्त कड़ी के बराबर लिया जाना चाहिए।
समीकरणों (1.1) और (1.2) में यदि
L.H.S > R.H.S तो श्रृंखला अभिबद्ध(लॉक) है
L.H.S = R.H.S तो श्रृंखला प्रतिबंधित(कन्स्ट्रैन्ड) है
L.H.S < R.H.S तो श्रृंखला अप्रतिबंधित(अनकन्स्ट्रैन्ड) है
बाहरी संबंध
Fundamental_of_Kinematics_&_Mechanism
यह सभी देखें
संदर्भ
- ↑ बंसल, डॉ. आर. के. थ्योरी ऑफ मशीन्स। पृष्ठ। 1.(Bansal, Dr. R. K. Theory of Machines. p. 1.)
- ↑ मैके, रॉब.एफ. (1915) मशीनों का सिद्धांत। लंडन। पृष्ठ 2(McKAY, ROBT.F. (1915). The theory of Machines. LONDON. p. 2.)
- ↑ शुद्धगतिक युगल (काइनेमेटिक पेयर)("Kinematic-pair")
- ↑ " प्रतिबंधित कठोर निकायों के मूल किनेमेटिक्स"("Basic Kinematics of constrained rigid bodies")