कतारबद्ध सिद्धांत

कतार नेटवर्क ऐसे सिस्टम हैं जिनमें सिंगल कतारें एक रूटिंग नेटवर्क द्वारा जुड़ी होती हैं।इस छवि में, सर्वर को मंडलियों द्वारा, आयतों की एक श्रृंखला द्वारा कतारों और तीर द्वारा रूटिंग नेटवर्क द्वारा दर्शाया जाता है।कतार नेटवर्क के अध्ययन में एक आमतौर पर नेटवर्क के संतुलन वितरण को प्राप्त करने की कोशिश करता है, हालांकि कई अनुप्रयोगों में क्षणिक राज्य का अध्ययन मौलिक है।

कतारबद्ध सिद्धांत प्रतीक्षा रेखाओं या कतारों का गणितीय अध्ययन है। कतार की लंबाई और प्रतीक्षा समय का कतारबद्ध मॉडल के द्वारा अनुमान लगाया जा सकता है। कतारबद्ध सिद्धांत को आमतौर पर संचालन अनुसंधान की एक शाखा माना जाता है क्योंकि परिणाम अक्सर उपयोग किए जाते हैं जब एक सेवा प्रदान करने के लिए आवश्यक संसाधनों के बारे में व्यावसायिक निर्णय लेते हैं।

कतारबद्ध सिद्धांत की उत्पत्ति एगनेर क्रूप एर्लंग द्वारा शोध में हुई है जब उन्होंने कोपेनहेगन टेलीफोन एक्सचेंज कंपनी, एक डेनिश कंपनी की प्रणाली का वर्णन करने के लिए मॉडल बनाए। विचारों ने तब से दूरसंचार, यातायात अभियांत्रिकी, अभिकलन, और विशेष रूप से औद्योगिक अभियांत्रिकी में, कारखानों, दुकानों, कार्यालयों और अस्पतालों के प्रारुप के साथ-साथ परियोजना प्रबंधन में अनुप्रयोगों को देखा है।

वर्तनी

"कतार" की वर्तनी आमतौर पर सैद्धांतिक शोध क्षेत्र में "कतार" ही होती है। वास्तव में, क्षेत्र की प्रमुख पत्रिकाओं में से एक कतारबद्ध प्रणाली है।

एकल कतारबद्ध नोड्स

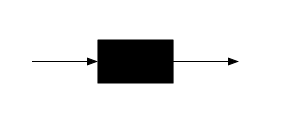
एक कतार, या कतारबद्ध नोड को लगभग एक ब्लैक बॉक्स माना जा सकता है। नौकरियां या "ग्राहक" कतार में आते हैं, संभवतः कुछ समय प्रतीक्षा करते हैं, संसाधित होने में कुछ समय लेते हैं, और फिर कतार से प्रस्थान करते हैं।

एक ब्लैक बॉक्स।नौकरियां कतार में पहुंचती हैं, और प्रस्थान करती हैं।

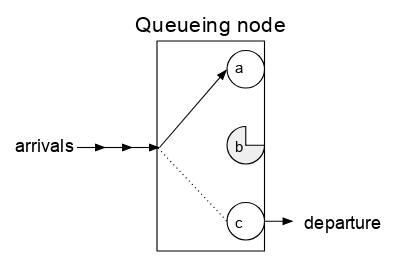
कतारबद्ध नोड बहुत शुद्ध ब्लैक बॉक्स नहीं है, हालांकि, चूंकि कतारबद्ध नोड के भीतर की कुछ जानकारी की आवश्यकता है। कतार में एक या एक से अधिक सर्वर होते हैं, जिनमें से प्रत्येक को आने वाली नौकरी के साथ जोड़ा जा सकता है, जब तक कि यह प्रस्थान नहीं करता है, जिसके बाद वह सर्वर किसी अन्य आने वाली नौकरी के साथ जोड़े जाने के लिए स्वतंत्र होगा।

3 सर्वर के साथ एक कतारबद्ध नोड।सर्वर ए निष्क्रिय है, और इस प्रकार इसे संसाधित करने के लिए एक आगमन दिया जाता है।सर्वर बी वर्तमान में व्यस्त है और अपनी नौकरी की सेवा पूरी करने से पहले कुछ समय लेगा।सर्वर सी ने अभी नौकरी की सेवा पूरी कर ली है और इस तरह एक आगमन नौकरी प्राप्त करने के लिए बगल में होगा।

सुपरमार्केट में श्रोता प्रायः सादृश्य का उपयोग करता है। अन्य मॉडल हैं, लेकिन यह सामान्यतः साहित्य में पाया जाता है। ग्राहक आते हैं, श्रोता द्वारा संसाधित होते हैं, और प्रस्थान करते हैं। प्रत्येक श्रोता एक समय में एक ग्राहक को संसाधित करता है, और इसलिए यह केवल एक सर्वर के साथ एक कतारबद्ध नोड है। एक परिस्थिति जहां ग्राहक के आने पर, श्रोता व्यस्त होने पर, ग्राहक शीघ्र निकल जाएगा, जिसे बिना किसी प्रतिरोध (या कोई प्रतीक्षा क्षेत्र, या इसी तरह की शर्तों) के साथ कतार के रूप में संदर्भित किया जाता है। अधिकतम n ग्राहकों के लिए प्रतीक्षा क्षेत्र वाली परिस्थिति को n विस्तार के प्रतिरोध वाली कतार कहा जाता है।

जन्म-मृत्यु प्रक्रिया

एक एकल कतार के व्यवहार (जिसे एक कतारबद्ध नोड भी कहा जाता है) का वर्णन एक जन्म -मृत्यु प्रक्रिया द्वारा किया जा सकता है, जो कतार से आगमन और प्रस्थान का वर्णन करता है, साथ ही नौकरियों की संख्या (जिसे "ग्राहक" या "अनुरोध" भी कहा जाता है, या अन्य वस्तुओं की कोई संख्या, क्षेत्र के आधार पर) वर्तमान में प्रणाली में हैं। एक आगमन से नौकरियों की संख्या को 1 से बढ़ती है, और एक प्रस्थान (अपनी सेवा को पूरा करने वाली नौकरी) k को 1 से घटाता है।

एक जन्म -मृत्यु प्रक्रिया।हलकों में मूल्य जन्म-मृत्यु प्रक्रिया की स्थिति का प्रतिनिधित्व करते हैं।एक कतार प्रणाली के लिए, k सिस्टम में नौकरियों की संख्या है (या तो सेवित किया जा रहा है या प्रतीक्षा कर रहा है यदि कतार में प्रतीक्षा नौकरियों का एक बफर है)।जन्म और मौतों द्वारा K के मूल्यों के बीच सिस्टम संक्रमण होता है जो क्रमशः λ <सब> i और μ <सब> i के विभिन्न मूल्यों द्वारा दी गई दरों पर होता है।इसके अतिरिक्त, एक कतार के लिए, आगमन की दर और प्रस्थान दर को आमतौर पर कतार में नौकरियों की संख्या के साथ भिन्न नहीं माना जाता है, इसलिए कतार में प्रति यूनिट समय के लिए आगमन/प्रस्थान की एक ही औसत दर मान ली जाती है।इस धारणा के तहत, इस प्रक्रिया में λ = λ <सब> 1 , λ <सब> 2 , ..., λ <सब> k और एक प्रस्थान दर का आगमन दर है।μ = μ <सब> 1 , μ <ub> 2 , ..., μ <सब> k (अगला आंकड़ा देखें)।

1 सर्वर के साथ एक कतार, आगमन दर λ और प्रस्थान दर μ।

संतुलन समीकरण

जन्म-मृत्यु प्रक्रिया के लिए स्थिर अवस्था समीकरण, जिसे संतुलन समीकरण कहा जाता है, निम्नलिखित है। यहां $P_{n}$ अवस्था n में होने की स्थिर अवस्था प्रायिकता है।

$\mu _{1}P_{1}=\lambda _{0}P_{0}$

$\lambda _{0}P_{0}+\mu _{2}P_{2}=(\lambda _{1}+\mu _{1})P_{1}$

$\lambda _{n-1}P_{n-1}+\mu _{n+1}P_{n+1}=(\lambda _{n}+\mu _{n})P_{n}$

पहले दो समीकरणों का तात्पर्य,

$P_{1}={\frac {\lambda _{0}}{\mu _{1}}}P_{0}$

तथा

$P_{2}={\frac {\lambda _{1}}{\mu _{2}}}P_{1}+{\frac {1}{\mu _{2}}}(\mu _{1}P_{1}-\lambda _{0}P_{0})={\frac {\lambda _{1}}{\mu _{2}}}P_{1}={\frac {\lambda _{1}\lambda _{0}}{\mu _{2}\mu _{1}}}P_{0}.$

गणितीय अनुगम द्वारा,

$P_{n}={\frac {\lambda _{n-1}\lambda _{n-2}\cdots \lambda _{0}}{\mu _{n}\mu _{n-1}\cdots \mu _{1}}}P_{0}=P_{0}\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}.$

स्थिति $\sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1$ फलस्वरूप,

$P_{0}={\frac {1}{1+\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}}},$

जो, साथ में समीकरण के साथ $P_{n}$ $(n\geq 1)$, पूरी तरह से आवश्यक स्थिर अवस्था प्रायिकताओं का वर्णन करता है।

केंडल का अंकन

एकल कतारबद्ध नोड्स को सामान्यतः ए/एस/सी (A/S/c) के रूप में केंडल के अंकन का उपयोग करके वर्णित किया जाता है, जहां ए (A) कतार में प्रत्येक आगमन के बीच अवधि के वितरण का वर्णन करता है, एस (S) नौकरियों के लिए सेवा समय का वितरण और सी (c) नोड पर सर्वर की संख्या वर्णन करता है। अंकन के एक उदाहरण के लिए, एम/एम/1 (M/M/1) कतार एक सरल मॉडल है जहां एक एकल सर्वर पॉइसन प्रक्रिया (जहां अंतर-आगमन अवधि को तेजी से वितरित किया जाता है) के अनुसार आने वाली नौकरियों पर काम करता है और तेजी से वितरित सेवा समय (एम एक मार्कोव प्रक्रिया को दर्शाता है) होता है। एम/जी/1 (M/G/1) कतार में, जी (G) "सामान्य", और सेवा समय के लिए स्वेच्छाचारी प्रायिकता वितरण को इंगित करता है।

एम/एम/1 कतार का उदाहरण विश्लेषण

एक सर्वर और निम्नलिखित विशेषताओं के साथ एक कतार पर विचार करें:

• λ: आगमन दर (आने वाले प्रत्येक ग्राहक के बीच अपेक्षित समय का पारस्परिक, उदाहरण के लिए प्रति सेकंड 10 ग्राहक)
• μ: औसत सेवा समय का व्युत्क्रम (एक ही इकाई समय में लगातार सेवा पूर्ण होने की अपेक्षित संख्या, उदाहरण के लिए प्रति 30 सेकंड)
• n: प्रणाली में ग्राहकों की संख्या को चिह्नित करने वाला पैरामीटर
• $P_{n}$: स्थिर अवस्था में प्रणाली में n ग्राहक होने की प्रायिकता।

इसके अतिरिक्त, E_n को प्रणाली द्वारा अवस्था n में प्रवेश करने की संख्या का प्रतिनिधित्व करने दें, और Ln प्रणाली द्वारा अवस्था n को छोड़ने की संख्या का प्रतिनिधित्व करता है। तब सभी n के लिए, |E_n − L_n| ∈ {0, 1}। अर्थात्, प्रणाली द्वारा किसी अवस्था को छोड़ने की संख्या उस अवस्था में प्रवेश करने की संख्या से अधिकतम 1 से भिन्न होती है, क्योंकि यह या तो भविष्य में किसी समय उस स्थिति में वापस आ जाएगी (E_n = L_n) या नहीं (E_n − L_n = 1)।

जब सिस्टम स्थिर स्थिति में आता है, तो आगमन दर प्रस्थान दर के बराबर होनी चाहिए।

इस प्रकार संतुलन समीकरण,

$\mu P_{1}=\lambda P_{0}$

$\lambda P_{0}+\mu P_{2}=(\lambda +\mu )P_{1}$

$\lambda P_{n-1}+\mu P_{n+1}=(\lambda +\mu )P_{n}$

अर्थातl,

$P_{n}={\frac {\lambda }{\mu }}P_{n-1},\ n=1,2,\ldots$

यह तथ्य कि $P_{0}+P_{1}+\cdots =1$ ज्यामितीय वितरण सूत्र की ओर ले जाता है

$P_{n}=(1-\rho )\rho ^{n}$

जहां $\rho ={\frac {\lambda }{\mu }}<1.$

सरल दो-समीकरण कतार

एक सामान्य मूलभूत कतार प्रणाली का श्रेय एरलांग को दिया जाता है, और लिटिल के नियम का एक संशोधन है। आगमन दर λ, निर्गामी दर σ, और प्रस्थान दर μ, कतार की लंबाई L हो तो,

$L={\frac {\lambda -\sigma }{\mu }}.$

दरों के लिए एक घातीय वितरण को मानते हुए, प्रतीक्षा समय W को आगमन के अनुपात के रूप में परिभाषित किया जा सकता है। यह उन लोगों की घातीय उत्तरजीविता दर के बराबर है जो प्रतीक्षा अवधि के दौरान बाहर नहीं निकलते हैं।

${\frac {\mu }{\lambda }}=e^{-W{\mu }}$

दूसरा समीकरण सामान्यतः पुनः लिखा जाता है,

$W={\frac {1}{\mu }}\mathrm {ln} {\frac {\lambda }{\mu }}$

जानपदिक रोग विज्ञान में दो-चरण एकल-बॉक्स मॉडल सामान्य है।

सिद्धांत के विकास का अवलोकन

1909 में, कोपेनहेगन टेलीफोन एक्सचेंज के लिए काम करने वाले डेनिश अभियांत्रिक एग्नेर क्रारुप एरलांग ने पहला पेपर प्रकाशित किया, जिसे अब कतारबद्ध सिद्धांत कहा जाता है। उन्होंने एक पॉइसन प्रक्रिया द्वारा एक दूरभाष केंद्र में आने वाले टेलीफोन कॉल की संख्या को मॉडल तैयार किया और 1917 में एम/डी/1 (M/D/1) कतार को हल किया और 1920 में एम/डी/के (M/D/K ) कतारबद्ध मॉडल को हल किया। केंडल के संकेतन में

• एम (M) मार्कोव या स्मृतिहीन को दर्शाता है और इसका अर्थ है कि एक पॉइसन प्रक्रिया के अनुसार आगमन होता है
• डी (D) नियतात्मक को दर्शाता है और इसका अर्थ है कि कतार में आने वाली नौकरियां जिन्हें एक निश्चित मात्रा में सेवा की आवश्यकता होती है
• k कतार नोड पर सर्वर की संख्या (k = 1, 2, ....) का वर्णन करता है।

यदि सर्वर की तुलना में नोड पर अधिक नौकरियां हैं, तो नौकरियां कतारबद्ध होंगी और सेवा की प्रतीक्षा करेंगी।

एम/जी/1 (M/G/1) कतार को 1930 में फेलिक्स पोलाकज़ेक द्वारा हल किया गया था, अलेक्जेंड्र खिनचिन द्वारा एक हल बाद में संभाव्यता शब्दों में पुनः दिया गया, जिसे पोलाकज़ेक-खिनचीन सूत्र के रूप में जाना जाता है।

1940 के दशक के बाद कतारबद्ध सिद्धांत गणितज्ञों के लिए अनुसंधान रुचि का एक क्षेत्र बन गया। 1953 में डेविड जॉर्ज केंडल ने जीआई/एम/के (GI/M/k) कतार को हल किया और कतारों के लिए आधुनिक संकेतन प्रस्तुत किया, जिसे केंडल के संकेतन के रूप में जाना जाता है। 1957 में पोलाकज़ेक ने एक अभिन्न समीकरण का उपयोग करके जीआई/जी/1 (GI/G1) का अध्ययन किया। जॉन किंगमैन ने जी/जी/1 (G/G/1) कतार में औसत प्रतीक्षा समय के लिए एक सूत्र दिया, जिसे किंगमैन सूत्र कहा जाता है।

लियोनार्ड क्लेनक्रॉक ने 1960 के दशक की शुरुआत में संदेश स्विचन और 1970 के दशक की शुरुआत में पैकेट स्विचन के लिए कतारबद्ध सिद्धांत के अनुप्रयोग पर कार्या किया। इस क्षेत्र में उनका प्रारंभिक योगदान 1962 में मैसाचुसेट्स प्रौद्योगिकी संस्थान में उनकी डॉक्टरेट थीसिस थी, जो 1964 में पुस्तक रूप में प्रकाशित हुई। 1970 के दशक की शुरुआत में प्रकाशित उनके सैद्धांतिक कार्य ने इंटरनेट पर एक अग्रदूत अरपनेट (ARPANET) में पैकेट स्विचन के उपयोग को रेखांकित किया।

आव्यूह ज्यामितीय विधि और आव्यूह विश्लेषणात्मक विधियों ने कतारों को चरण-प्रकार के वितरित अंतर-आगमन और सेवा समय वितरण पर विचार करने की अनुमति दी है।

वायरलेस नेटवर्क और सिग्नल प्रोसेसिंग के अनुप्रयोग में कतारबद्ध सिद्धांत में युग्मित कक्षाओं के साथ प्रणाली का एक महत्वपूर्ण हिस्सा हैं। एम/जी/के (M/G/k) कतार के लिए प्रदर्शन आव्यूह जैसी समस्याएं एक खुली समस्या बनी हुई हैं।

सेवा अनुशासन

पहले पहले बाहर (FIFO) कतार उदाहरण।

कतारबद्ध नोड्स पर विभिन्न समय-सारणी नीतियों का उपयोग किया जा सकता है।

पेहले आये पेहलॆ गये

इसे पहले आओ, पहले पाओ (FCFS) भी कहा जाता है, इस सिद्धांत में कहा गया है कि ग्राहकों को एक समय में एक सेवा दी जाती है और जो ग्राहक सबसे लंबे समय से प्रतीक्षा कर रहा है उसे पहले सेवा दी जाती है।

अंतिम अंदर प्रथम बाहर

यह सिद्धांत ग्राहकों को सेवा प्रदान करने के साथ साथ उन ग्राहकों को पहले सेवा प्रदान करता है जिनके पास प्रतीक्षा समय कम होता है। एक स्टैक के रूप में भी जाना जाता है।

प्रोसेसर सहभाजन

सेवा सामर्थ्य ग्राहकों के बीच समान रूप से साझा की जाती है।

प्राथमिकता

उच्च प्राथमिकता वाले ग्राहकों को पहले सेवा दी जाती है। प्राथमिकता कतारें दो प्रकार की हो सकती हैं, अपूर्व-निर्धारित (जहां सेवा में एक नौकरी बाधित नहीं की जा सकती है) और पूर्व-निर्धारित (जहां सेवा में नौकरी को उच्च प्राथमिकता वाली नौकरी से बाधित किया जा सकता है)। किसी भी मॉडल में कोई काम अदृष्ट नहीं होता है।

सबसे छोटा काम पहले

सेवा की जाने वाली अगली नौकरी सबसे छोटी है।

पूर्व-निर्धारित सबसे छोटी नौकरी पहले

अगली नौकरी जो दी जानी है वह है सबसे छोटे मूल आकार की है।

सबसे कम शेष प्रसंस्करण समय

सेवा करने के लिए अगला काम वह है जिसमें सबसे छोटी शेष प्रसंस्करण आवश्यकता है।

सेवा सुविधा

• एकल सर्वर: ग्राहक कतार बढ़ती है और केवल एक सर्वर होता है।
• कई समानांतर सर्वर-एकल कतार: ग्राहक कतार बढ़ती है और कई सर्वर होते हैं।
• कई सर्वर -व्यक्तिगत कतारें: कई काउंटर हैं और ग्राहक तय कर सकते हैं कि कहाँ जाना है।

अविश्वसनीय सर्वर

सर्वर विफलताएं प्रसंभाव्य प्रक्रिया (प्रायः पॉइसन) के अनुसार होती हैं और इसके बाद व्यवस्थापन अवधि होती है, जिसके दौरान सर्वर अनुपलब्ध है। बाधित ग्राहक सेवा क्षेत्र में तब तक रहता है जब तक कि सर्वर ठीक नहीं हो जाता।

प्रतीक्षा करने का ग्राहक का व्यवहार

• बालक: ग्राहक कतार में शामिल नहीं होने का निर्णय लेते हैं यदि यह बहुत लंबा है
• जॉकी: ग्राहक कतारों के बीच स्विच करते हैं यदि उन्हें लगता है कि वे ऐसा करके तेजी से सेवा करेंगे
• रेनेगिंग: ग्राहक कतार छोड़ देते हैं यदि उन्होंने सेवा के लिए बहुत लंबा इंतजार किया है

आने वाले ग्राहकों की सेवा नहीं की जाती है (या तो कतार के कारण कोई बफर नहीं है, या ग्राहक द्वारा चालाक या पुनर्जीवित होने के कारण) को भी ड्रॉपआउट के रूप में जाना जाता है और ड्रॉपआउट की औसत दर एक महत्वपूर्ण पैरामीटर है जो एक कतार का वर्णन करती है।

कतारबद्ध नेटवर्क

कतारों के नेटवर्क ऐसी प्रणाली है जिनमें कई कतारों को ग्राहक परिसंचरण के रूप में जाना जाता है। जब एक ग्राहक को एक नोड पर सेवित किया जाता है तो यह सेवा के लिए एक और नोड और कतार में शामिल हो सकता है, या नेटवर्क छोड़ सकता है।

एम (m) नोड्स के नेटवर्क के लिए, प्रणाली की स्थिति को एम-विमीय सदिश (x₁, x₂, ...,x_m) द्वारा वर्णित किया जा सकता है जहां x_i प्रत्येक नोड पर ग्राहकों की संख्या का प्रतिनिधित्व करता है।

कतारों के सबसे सरल असाधारण नेटवर्क को अग्रानुक्रम कतार कहा जाता है। इस क्षेत्र में पहले सार्थक परिणाम जैक्सन नेटवर्क था, जिसके लिए कुशल उत्पाद-रूप स्थिर वितरण मौजूद है और औसत मूल्य विश्लेषण है जो औसत आव्यूह जैसे प्रवाह क्षमता और अवस्थान समाय की गणना करने की अनुमति देता है। यदि नेटवर्क में ग्राहकों की कुल संख्या स्थिर रहती है, तो नेटवर्क को बंद नेटवर्क कहा जाता है और इसे गॉर्डन-नेवेल प्रमेय में एक उत्पाद -प्रफुल्ल स्थिर वितरण भी दिखाया गया है। यह परिणाम बीसीएमपी (BCMP) नेटवर्क तक बढ़ाया गया था जहां बहुत सामान्य सेवा समय के साथ नेटवर्क, व्यवस्थाओं और ग्राहक परिसंचरण को एक उत्पाद-रूप स्थिर वितरण को प्रदर्शित करने के लिए दिखाया गया है।सामान्यीकरण स्थिरांक की गणना 1973 में प्रस्तावित बुज़ेन के एल्गोरिथ्म के साथ की जा सकती है।

ग्राहकों के नेटवर्क की भी जांच की गई है, केली नेटवर्क्स जहां विभिन्न वर्गों के ग्राहक विभिन्न सेवा नोड्स पर विभिन्न प्राथमिकता स्तरों का अनुभव करते हैं। एक अन्य प्रकार के नेटवर्क जी-नेटवर्क हैं जो पहले 1993 में एरोल गेलेनबे द्वारा प्रस्तावित हैं ये नेटवर्क आदर्श जैक्सन नेटवर्क की तरह घातीय समय वितरण नहीं मानते हैं।

परिसंचरण कलनविधि

असतत समय नेटवर्क में जहां एक बाधा होती है, जिस पर सेवा नोड किसी भी समय सक्रिय हो सकते हैं, अधिकतम-वजन समय-सारणी एल्गोरिथ्म इस मामले में सर्वोत्कृष्ट प्रवाह क्षमता देने के लिए एक सेवा नीति चुनता है कि प्रत्येक नौकरी केवल एक-व्यक्ति सेवा नोड पर जाती है। अधिक सामान्य स्थिति में जहां नौकरियां एक से अधिक नोड पर जा सकती हैं, वापस दबाव परिसंचरण सर्वोत्कृष्ट प्रवाह क्षमता देता है। एक नेटवर्क समय सारणिक को एक कतारबद्ध एल्गोरिथ्म का चयन करना होगा, जो बड़े नेटवर्क की विशेषताओं को प्रभावित करता है। कतारबद्ध प्रणाली के समय-सारणी के बारे में अधिक जानकारी के लिए प्रसंभाव्य समय-सारणी भी देखें।

औसत-क्षेत्र सीमाएं

औसत-क्षेत्र मॉडल अनुभवजन्य माप (विभिन्न स्थितियो में कतारों का अनुपात) के सीमित व्यवहार पर विचार करते हैं क्योंकि कतारों की संख्या (m से ऊपर) अनंत तक जाती है। नेटवर्क में किसी भी कतार पर अन्य कतारों का प्रभाव एक अंतर समीकरण द्वारा अनुमानित किया जाता है। नियतात्मक मॉडल मूल मॉडल के रूप में एक ही स्थिर वितरण में परिवर्तित होता है।

भारी यातायात/प्रसार सन्निकटन

उच्च अधिभोग दरों के साथ एक प्रणाली में (1 के पास उपयोग) परावर्तित ब्राउनियन गति द्वारा कतार की लंबाई का अनुमान लगाने के लिए एक भारी यातायात सन्निकटन का उपयोग किया जा सकता है, ऑर्नस्टीन -उहलेनबेक प्रक्रिया या अधिक सामान्य प्रसार प्रक्रिया। ब्राउनियन प्रक्रिया के आयामों की संख्या कतारबद्ध नोड्स की संख्या के बराबर है, जिसमें प्रसार सकारात्मक ऑर्थेंट तक सीमित होता है।

द्रव सीमा

द्रव मॉडल कतारबद्ध नेटवर्क के निरंतर नियतात्मक अनुरूप हैं, जो प्रक्रिया को समय और स्थान में बढ़ने पर प्राप्त होते है, जिससे विजातीय वस्तुओं की अनुमति मिलती है। यह बढ़ाया गया प्रक्षेपपथ एक नियतात्मक समीकरण में परिवर्तित हो जाता है जो प्रणाली की स्थिरता को सिद्ध करने की अनुमति देता है। यह ज्ञात है कि एक कतार नेटवर्क स्थिर हो सकता है, लेकिन इसकी एक अस्थिर द्रव सीमा है।

यह भी देखें

• Ehrenfest मॉडल
• एर्लंग यूनिट
• नेटवर्क सिमुलेशन
• प्रोजेक्ट प्रोडक्शन मैनेजमेंट
• कतार क्षेत्र
• कतार में देरी
• कतार प्रबंधन प्रणाली
• अंगूठे का नियम
• यादृच्छिक प्रारंभिक पता लगाना
• नवीकरण सिद्धांत
• थ्रूपुट
• शेड्यूलिंग (कम्प्यूटिंग)
• ट्रैफ़िक जाम
• ट्रैफिक जनरेशन मॉडल
• प्रवाह नेटवर्क

अग्रिम पठन

• Gross, Donald; Carl M. Harris (1998). Fundamentals of Queueing Theory. Wiley. ISBN 978-0-471-32812-4. Online
• Zukerman, Moshe (2013). Introduction to Queueing Theory and Stochastic Teletraffic Models (PDF). arXiv:1307.2968.
• Deitel, Harvey M. (1984) [1982]. An introduction to operating systems (revisited first ed.). Addison-Wesley. p. 673. ISBN 978-0-201-14502-1. chap.15, pp. 380–412
• Gelenbe, Erol; Isi Mitrani (2010). Analysis and Synthesis of Computer Systems. World Scientific 2nd Edition. ISBN 978-1-908978-42-4.
• Newell, Gordron F. (1 June 1971). Applications of Queueing Theory. Chapman and Hall.
• Leonard Kleinrock, Information Flow in Large Communication Nets, (MIT, Cambridge, May 31, 1961) Proposal for a Ph.D. Thesis
• Leonard Kleinrock. Information Flow in Large Communication Nets (RLE Quarterly Progress Report, July 1961)
• Leonard Kleinrock. Communication Nets: Stochastic Message Flow and Delay (McGraw-Hill, New York, 1964)
• Kleinrock, Leonard (2 January 1975). Queueing Systems: Volume I – Theory. New York: Wiley Interscience. pp. 417. ISBN 978-0471491101.
• Kleinrock, Leonard (22 April 1976). Queueing Systems: Volume II – Computer Applications. New York: Wiley Interscience. pp. 576. ISBN 978-0471491118.
• Lazowska, Edward D.; John Zahorjan; G. Scott Graham; Kenneth C. Sevcik (1984). Quantitative System Performance: Computer System Analysis Using Queueing Network Models. Prentice-Hall, Inc. ISBN 978-0-13-746975-8.
• Jon Kleinberg; Éva Tardos (30 June 2013). Algorithm Design. Pearson. ISBN 978-1-292-02394-6.

बाहरी संबंध

• Queueing theory calculator
• Teknomo's Queueing theory tutorial and calculators
• Office Fire Emergency Evacuation Simulation on YouTube
• Virtamo's Queueing Theory Course
• Myron Hlynka's Queueing Theory Page
• Queueing Theory Basics
• A free online tool to solve some classical queueing systems
• JMT: an open source graphical environment for queueing theory
• LINE: a general-purpose engine to solve queueing models
• What You Hate Most About Waiting in Line: (It’s not the length of the wait.), by Seth Stevenson, Slate, 2012 – popular introduction