द्रव्य का संरक्षण: Difference between revisions

Latest revision as of 09:54, 4 August 2022

भौतिकी एवं रसायन विज्ञान में, द्रव्यमान के संरक्षण के सिद्धांत के अनुसार वह बंद निकाय, जिसमे पदार्थ एवं ऊर्जा का स्थानांतरण अनिवार्य नहीं होता तथा इनकी मात्रा न तो जोड़ी जा सकती है और न ही घटाई जा सकती है, अत: निकाय का द्रव्यमान संरक्षित (निकाय का द्रव्यमान समय के साथ स्थिर) रहता है।

इस नियमानुसार, द्रव्यमान को न तो उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है, हालांकि इसे अंतरिक्ष में पुनर्व्यवस्थित किया जा सकता है, या इससे जुड़ी इकाईयों को बदला जा सकता है। उदाहरण के लिए, रासायनिक अभिक्रियाओं में, अभिक्रिया से पहले अभिकारकों का द्रव्यमान अभिक्रिया के बाद के अभिकारकों के द्रव्यमान के बराबर होता है। इस प्रकार, विलगित निकाय में किसी भी रासायनिक अभिक्रिया और कम-ऊर्जा कि उष्मागतिकी प्रक्रियाओं के दौरान, अभिकारकों या उपादान का कुल द्रव्यमान उत्पादों के द्रव्यमान के बराबर होना चाहिए।

रसायन विज्ञान, यांत्रिकी और द्रव गतिकी में द्रव्यमान संरक्षण की अवधारणा का व्यापक रूप से उपयोग किया जाता है। ऐतिहासिक रूप से, रासायनिक अभिक्रियाओं में द्रव्यमान का संरक्षण मिखाइल लोमोनोसोव द्वारा स्वतंत्र रूप से प्रमाणित किया गया था और बाद में 18 वीं शताब्दी के अंत में एंटोनी लावोसियर द्वारा पुनः खोजा गया था। कीमिया से आधुनिक प्राकृतिक रसायन विज्ञान की प्रगति में इस नियम का महत्वपूर्ण महत्व था।

वास्तव में, द्रव्यमान का संरक्षण केवल सन्निकटत धारण करता है और चिरसम्मत यांत्रिकी में पूर्वधारणाओं की श्रृंखला का हिस्सा माना जाता है। द्रव्यमान-ऊर्जा तुल्यता के सिद्धांत के तहत क्वांटम यांत्रिकी और विशेष सापेक्षता के नियमों का पालन करने के लिए नियमो को संशोधित किया जाना है, जिसके अनुसार ऊर्जा और द्रव्यमान एक संरक्षित मात्रा बनाते हैं। अत्याधिक ऊर्जावान प्रणालियों (जैसे परमाणु अभिक्रियाओं और कण भौतिकी में कण-प्रतिकण विनाश) के लिए द्रव्यमान का संरक्षण नहीं होता।

वह निकाय जिसमे ऊर्जा तथा पदर्थ दोनो का ही विनिमय होता है, खुला निकाय कहलाता है तथा खुले निकाय का द्रव्यमान संरक्षित नहीं होता है। हालांकि, जब तक रेडियोधर्मिता या नाभिकीय अभिक्रिया शामिल नहीं होती हैं, ऊर्जा, यांत्रिक कार्य, या विद्युत चुम्बकीय विकिरण, जैसी प्रणालियों से निकलने (या प्रवेश) करने वाली ऊर्जा की मात्रा प्रायः निकाय के द्रव्यमान में कमी (या वृद्धि) के रूप में मापने के लिए बहुत छोटी होती है।

सामान्य सापेक्षता को ध्यान में रखकर, उन प्रणालियों के लिए जिनमें बड़े गुरुत्वाकर्षण क्षेत्र शामिल हैं, इस प्रकार विभिन्न परिभाषाओं के अधीन द्रव्यमान-ऊर्जा संरक्षण एक अधिक जटिल अवधारणा बन जाती है, विशेष सापेक्षता कि तुलना में द्रव्यमान और ऊर्जा उतनी ही सख्ती से और सरलता से संरक्षित नहीं होते है।

मीथेन की दहन प्रतिक्रिया। जहां प्रतिक्रिया से पहले और बाद में हाइड्रोजन के 4 परमाणु, ऑक्सीजन के 4 परमाणु और कार्बन के 1 परमाणु मौजूद होते हैं। प्रतिक्रिया के बाद का कुल द्रव्यमान प्रतिक्रिया के पहले जैसा ही होता है।

सूत्रीकरण और उदाहरण

द्रव्यमान के संरक्षण का नियम केवल चिरसम्मत यांत्रिकी में सूत्रित किया जा सकता है, जिसमें विलगित निकाय से जुड़े ऊर्जा परिमाण $mc^{2}$ से बहुत छोटा होता है, जहां $m$ विरामावस्था में निकाय कि विशिष्ट वस्तु का निर्देश तंत्र में मापा गया द्रव्यमान है, और $c$ प्रकाश की गति है।

द्रव यांत्रिकी और सातत्य यांत्रिकी के क्षेत्र में द्रव्यमान संरक्षण के नियम को सांतत्य समीकरण का उपयोग करके गणित में अवकल रूप में सूत्रित किया जा सकता है।

${\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {v} )=0,$

जहां ${\textstyle \rho }$ घनत्व (द्रव्यमान प्रति इकाई आयतन), ${\textstyle t}$ समय, ${\textstyle \nabla \cdot }$ विचलन, और ${\textstyle \mathbf {v} }$ प्रवाह वेग क्षेत्र है।

द्रव्यमान के लिए सांतत्य समीकरण की व्याख्या निम्नलिखित है। किसी समय अंतराल में निकाय में द्रव्यमान का परिवर्तन, समान समयांतराल में निकाय के पारगमित द्रव्यमान के बराबर होता है। यदि पदार्थ अंदर जाता है तो सकारात्मक और यदि पदार्थ बाहर जाता है तो नकारात्मक। संपूर्ण विलगित निकाय के लिए, इस स्थिति का तात्पर्य है कि कुल द्रव्यमान ${\textstyle M}$ (निकाय में सभी घटकों के द्रव्यमान का योग) समय के साथ परिवर्तित नहीं होता है, अर्थात

${\frac {{\text{d}}M}{{\text{d}}t}}={\frac {\text{d}}{{\text{d}}t}}\int \rho {\text{d}}V=0$

जहां ${\textstyle {\text{d}}V}$ वह अवकलन है जो निकाय के संपूर्ण अयतन पर समकालन को परिभाषित करता है।

द्रव्यमान के लिए सांतत्य समीकरण, द्रव गतिकी के यूलर समीकरणों का हिस्सा है। कई अन्य संवहन-प्रसार समीकरण, निकाय में द्रव्यमान और पदार्थ के संरक्षण और प्रवाह का वर्णन करते हैं।

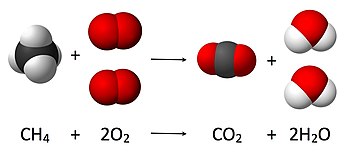
रसायन विज्ञान में, रासायनिक अभिक्रिया, या रससमीकरणमिति (स्टोइकोमेट्री) में अभिकारक और उत्पादों की मात्रा की गणना, द्रव्यमान के संरक्षण के सिद्धांत के आधार पर की जाती है। सिद्धांत का तात्पर्य है कि रासायनिक अभिक्रिया के दौरान अभिकारकों का कुल द्रव्यमान उत्पादों के कुल द्रव्यमान के बराबर होता है। उदाहरण के लिए, निम्नलिखित अभिक्रिया में,

CH₄ + 2O₂ → CO₂ + 2H₂O

जहां मीथेन का एक अणु (CH₄) और दो ऑक्सीजन के अणु (O₂) कार्बन डाइऑक्साइड के एक अणु (CO₂) और दो जल के अणुओं (H₂O) में परिवर्तित हो जाते हैं। अभिक्रिया में शुरू में चार हाइड्रोजन परमाणु, चार ऑक्सीजन परमाणु और एक कार्बन परमाणु मौजूद हैं तथा अभिक्रिया के पश्चात् उत्पाद के अणुओं की संख्या समान है, यह संख्या द्रव्यमान के संरक्षण के सिद्धांत से प्राप्त की जा सकती है।

समय के साथ कई अभियान्त्रिकी समस्याओं को, किसी निकाय के द्रव्यमान वितरण नियम का पालन करके, हल किया जाता है। इस क्रियाविधि द्रव्यमान संतुलन कहलती है।

इतिहास

रूसी वैज्ञानिक मिखाइल लोमोनोसोव ने 1756 में प्रयोगों द्वारा बड़े पैमाने पर संरक्षण के कानून की खोज की, और इस निष्कर्ष पर पहुंचे कि फ्लॉजिस्टन सिद्धांत गलत है। ^[1] ^[2] ^[3]

द्रव्यमान के संरक्षण के नियम की एंटोनी लावोज़ियर की खोज ने 19वीं शताब्दी में कई नए निष्कर्ष निकाले। जोसेफ प्राउस्ट का निश्चित अनुपात का नियम और जॉन डाल्टन का परमाणु सिद्धांत एंटोनी लेवोजियर की खोजों से अलग है। लैवोज़ियर के मात्रात्मक प्रयोगों से पता चला कि दहन में ऑक्सीजन शामिल था, जो पहले फ्लॉजिस्टन माना जाता था।

520 ईसा पूर्व, जैन दर्शनशास्त्र, महावीर की शिक्षाओं पर आधारित एक असृजनवादी दर्शनशास्त्र,^[4] ने कहा कि ब्रह्मांड और उसके घटक जैसे पदार्थ को नष्ट या बनाया नहीं जा सकता है। जैन ग्रंथ तत्त्वार्थसूत्र (दूसरी शताब्दी सीई (CE)) में कहा गया है कि पदार्थ स्थायी है, लेकिन इसकी विधियां निर्माण और विनाश की विशेषता है।^[5] "कुछ भी नहीं से कुछ नहीं आता है", प्राचीन यूनानी दर्शन में एक महत्वपूर्ण विचार था ताकि जो अभी मौजूद है, वह हमेशा अस्तित्व में रहे। कोई भी नया पदार्थ अस्तित्व में नहीं आ सकता, जहां पहले कोई नहीं था। इसका एक स्पष्ट कथन, आगे के सिद्धांत का एक विचार, कुछ भी नहीं में कुछ भी नहीं गुजर सकता है, एम्पेडोकल्स (चौथी शताब्दी ईसा पूर्व) में पाया गया, "क्योंकि कुछ नहीं से कुछ भी आना असंभव है, और जो कुछ है वह पूरी तरह से नष्ट हो जाना चाहिए, यह लाया या सुना नहीं जा सकता है।"

संरक्षण का एक और सिद्धांत तीसरी शताब्दी ईसा पूर्व के आसपास एपिकुरस द्वारा व्यक्त गया था, जिन्होंने ब्रह्मांड की प्रकृति का वर्णन करते हुए लिखा था कि "चीजों की समग्रता हमेशा वैसी ही थी जैसी अब है, और हमेशा रहेगी"।

रसायन विज्ञान में खोजें

18 वीं शताब्दी तक रासायनिक अभिक्रियाओं के दौरान द्रव्यमान के संरक्षण के सिद्धांत का व्यापक रूप से उपयोग किया गया था और प्रयोगों के दौरान एक महत्वपूर्ण धारणा थी, यहां तक कि एक परिभाषा औपचारिक रूप से स्थापित होने से पहले ही,^[6] जैसा कि जोसेफ ब्लैक, हेनरी कैवेन्डिश और जीन रे के कार्यों में देखा जा सकता है।^[7] 1756 में इस सिद्धांत को दर्शाने वाले पहले व्यक्ति मिखाइल लोमोनोसोव थे। उन्होंने इसे प्रयोगों द्वारा प्रदर्शित किया हो सकता है और निःसन्देह 1748 में लियोनहार्ड यूलर के साथ पत्राचार में सिद्धांत पर चर्चा की थी,^[8] हालांकि इस विषय पर उनके दावे को कभी-कभी चुनौती दी जाती है।^[9]^[10] सोवियत भौतिकीविद् याकोव डोर्फ़मैन के अनुसार,

सार्वभौमिक नियम लोमोनोसोव द्वारा सामान्य दार्शनिक भौतिकवादी प्रतिफलो के आधार पर सूत्रबद्ध किया गया था, यह उनके द्वारा कभी भी पूछताछ या परीक्षण नहीं किया गया था, बल्कि इसके विपरीत, उन्हें अपने पूरे जीवन में सभी शोधों में एक ठोस प्रारंभिक स्थिति के रूप में कार्य किया।

प्रयोगों की एक और अधिक परिष्कृत श्रृंखला बाद में एंटोनी लावोज़ियर द्वारा की गई, जिन्होंने 1773 में अपना निष्कर्ष में द्रव्यमान के संरक्षण के सिद्धांत को लोकप्रिय व्यक्त किया। सिद्धांत के प्रदर्शनों ने तत्कालीन लोकप्रिय फ्लॉजिस्टन सिद्धांत को अप्रमाणित कर दिया, जिसके अनुसार दहन और उष्मीय प्रक्रियाओं में द्रव्यमान प्राप्त या अदृश्य (लुप्त) हो सकता है।

द्रव्यमान का संरक्षण, गैसों के भार पर पृथ्वी के वायुमंडल के उत्प्लावन प्रभाव के कारण सदियों तक अस्पष्ट था। उदाहरण के लिए, लकड़ी का एक टुकड़ा जलने के पश्चात् कम वजन का होता है, इस घटना से ऐसा प्रतीत होता है कि इसका कुछ द्रव्यमान लुप्त हो जाता है, या बदल या खो जाता है। यह तब तक अस्वीकृत नहीं था, जब तक कि सावधानीपूर्वक प्रयोग नहीं किए गए थे, जैसे सीलबंद कांच कि शीशियों में, जंग लगने जैसी रासायनिक अभिक्रिया का होना, इस रासायनिक अभिक्रिया में सीलबंद पात्र और उसकी सामग्री के वजन को नहीं बदला। 17वीं शताब्दी में वैक्यूम पंप के आविष्कार तक तराजू का उपयोग करके गैसों को तौलना संभव नहीं था।

कीमिया से आधुनिक रसायन विज्ञान की प्रगति में द्रव्यमान के संरक्षण का बहुत महत्व हैं। एक बार रसायनज्ञों ने संपादित किया कि रासायनिक पदार्थ समान भार वाले अन्य पदार्थों में परिवर्तित हो जाते हैं न कि नष्ट हो जाते हैं, अतः वैज्ञानिको के द्वारा पदार्थों के परिवर्तनों का मात्रात्मक अध्ययन किया जा सकता है। द्रव्यमान संरक्षण का विचार है कि कुछ "तात्विक पदार्थ" भी रासायनिक अभिक्रियाओं द्वारा दूसरे पदार्थो में परिवर्तित नहीं किए जा सकते हैं, जबकि रासायनिक तत्वों की समझ के साथ-साथ यह विचार भी आया कि सभी रासायनिक प्रक्रियाएं और परिवर्तन (जैसे दहन और उपापचयी अभिक्रियाएं) इन रासायनिक तत्वों की अपरिवर्तनीय मात्रा या भार के बीच की प्रतिक्रियाएं हैं।

लैवोज़ियर के अग्रणी कार्य के बाद, जीन स्टास के व्यापक प्रयोगों ने रासायनिक अभिक्रियाओं में इस नियम की स्थिरता का समर्थन किया।^[11] उनके शोध^[12]^[13] के अनुसार अभिक्रियाओं में हानि या लाभ 1,00,000 में 2 से 4 भागों से अधिक नहीं हो सकता था।^[14] एक ओर लवॉज़ियर और दूसरी ओर मॉर्ले और स्टास द्वारा लक्षित और प्राप्त की गई परिशुद्धता में बहुत बड़ा अंतर है।^[15]

आधुनिक भौतिकी

विशेष सापेक्षता के आगमन के साथ द्रव्यमान के संरक्षण के नियम को चुनौती दी गई थी। 1905 में अल्बर्ट आइंस्टीन के एनस मिराबिलिस लिखित प्रमाणों में से एक में, उन्होंने द्रव्यमान और ऊर्जा के बीच समानता का संकेत दिया था। इस सिद्धांत में, निकाय की आंतरिक ऊर्जा पूरे निकाय के द्रव्यमान में योगदान कर सकती है, या उस द्रव्यमान को विद्युत चुम्बकीय विकिरण में परिवर्तित किया जा सकता है, जैसे कई दावे निहित थे। हालाँकि, मैक्स प्लैंक के अनुसार, आइंस्टीन के सिद्धांत द्वारा अनुमानित, रासायनिक ऊर्जा के निष्कर्षण या जोड़ के परिणामस्वरूप द्रव्यमान में परिवर्तन, इतना छोटा होता है कि इसे उपलब्ध उपकरणों से नहीं मापा जा सकता है और इसे विशेष सापेक्षता के परीक्षण के रूप में प्रस्तुत नहीं किया जा सकता है। आइंस्टीन ने अनुमान लगाया कि रेडियोधर्मिता से जुड़ी ऊर्जाएं उन्हें उत्पन्न करने वाले निकाय के द्रव्यमान की तुलना में अत्यधिक महत्वपूर्ण थीं, अभिक्रिया की ऊर्जा को निकाय से हटा दिया गया, ताकि उनके द्रव्यमान के परिवर्तन को मापा जा सके। यह बाद में वास्तव में संभव साबित हुआ, कॉकक्रॉफ्ट और वाल्टन के द्वारा 1932 में पहली कृत्रिम परमाणु रूपांतरण अभिक्रिया प्रदर्शित कि गई, जो ऊर्जा वृद्धि के साथ द्रव्यमान क्षय से संबंधित आइंस्टीन के सिद्धांत का पहला सफल परीक्षण साबित हुआ।

द्रव्यमान संरक्षण और ऊर्जा संरक्षण के नियमो को अंततः द्रव्यमान-ऊर्जा तुल्यता (एक अधिक सामान्य सिद्धांत) द्वारा खारिज कर दिया गया। विशेष सापेक्षता, द्रव्यमान और ऊर्जा की अवधारणा को फिर से परिभाषित करती है, जिसे एक दूसरे के स्थान पर उपयोग किया जा सकता है और निर्देश तंत्र के सापेक्ष परिभाषित किया जाता है। स्थिरता के लिए कई मात्राओं को परिभाषित किया गया, जैसे कि कण का स्थिर द्रव्यमान (कण के विरामस्थ तंत्र में द्रव्यमान) और आपेक्षिकीय द्रव्यमान (दूसरी दशा में)।

सामान्यीकरण

विशेष सापेक्षता

विशेष सापेक्षता में, द्रव्यमान का संरक्षण नियम खुले निकाय पर लागू नहीं होता है, परन्तु यह बंद (पृथक) निकाय पर पूरी तरह से लागू होता है। याद किसी निकाय से ऊर्जा उत्सर्जित नहीं होती, तो इसका द्रव्यमान घट नहीं सकता है। सापेक्षता सिद्धांत में, जब तक किसी निकाय में किसी भी प्रकार की ऊर्जा रहती है, यह ऊर्जा द्रव्यमान प्रदर्शित करती है।

विलगित निकाय में पदार्थ पूरी तरह से संरक्षित नहीं हो सकता है जबकि द्रव्यमान हमेशा संरक्षित होता है, अतः द्रव्यमान को पदार्थ से अलग किया जाना चाहिए। हालांकि, रसायन विज्ञान में पदार्थ अल्प संरक्षित होने के कारण परमाणु युग तक पदार्थ संरक्षण के उल्लंघन को मापा नहीं गया, और पदार्थ संरक्षण की धारणा रसायन विज्ञान और अन्य अध्ययनों में अधिकांश निकायों में एक महत्वपूर्ण उपयोगी अवधारणा है जिसमें उच्च ऊर्जा (रेडियोधर्मिता और परमाणु अभिक्रिया की ऊर्जा) शामिल नहीं है।

ऊर्जा की रासायनिक मात्रा से जुड़ा द्रव्यमान मापने के लिए बहुत छोटा है

19 वीं शताब्दी के दौरान रासायनिक अभिक्रियाओं में ऊष्मीय या विकिरण ऊर्जा की छोटी मात्रा के परिवर्धन या अभाव से द्रव्यमान में परिवर्तन बहुत कम होने के कारण, खुले निकायों के द्रव्यमान में परिवर्तन, जहां परमाणु या बड़े कण बाहर नहीं निकल सकते, लेकिन अन्य प्रकार की ऊर्जाएं (जैसे प्रकाश या ऊष्मा) निकासित या संयोजित हो सकती है, पर किसी का ध्यान नहीं गया। (सैद्धांतिक रूप से, विलगित निकाय में किए गए प्रयोगों के लिए द्रव्यमान बिल्कुल नहीं बदलेगा जहां अंदर या बाहर ऊष्मा और कार्य की अनुमति नहीं।)

ऊर्जा का ह्रास न होने पर जन संरक्षण सही रहता है

सापेक्षतावादी द्रव्यमान के संरक्षण का तात्पर्य एक प्रेक्षक (या एकल जड़त्वीय फ्रेम से दृश्य) के दृष्टिकोण से है क्योंकि जड़त्वीय फ्रेम बदलने से निकाय के लिए कुल ऊर्जा (सापेक्ष ऊर्जा) में परिवर्तन हो सकता है, और यह मात्रा सापेक्षतावादी द्रव्यमान को निर्धारित करती है।

यह सिद्धांत कि चिरसम्मत भौतिकी में कणों के निकाय का द्रव्यमान उनके गतिहीन द्रव्यमानों के योग के बराबर होता है परन्तु विशेष सापेक्षता में नहीं होता। इसका कारण यह है कि गतिहीन द्रव्यमानों को आसानी से नहीं जोड़ा जा सकता है, यह ऊर्जा के अन्य रूपों, जैसे गतिज और स्थितिज ऊर्जा, और बड़े पैमाने पर कणों, जैसे फोटॉन को ध्यान में नहीं रखता है, जो निकाय के कुल द्रव्यमान को प्रभावित कर सकते हैं (या नहीं)।

किसी निकाय में बड़े कणों को स्थानांतरित करने के लिए, विभिन्न कणों के गतिहीन द्रव्यमानों की जांच करना भी कई अलग-अलग जड़त्वीय अवलोकन फ़्रेमों को उत्पन्न करने के बराबर है (जो निकाय कि कुल ऊर्जा और संवेग को संरक्षित करने के लिए प्रतिबंधित है), और यह भी कि जब कण के विरामस्थ तंत्र में, यह प्रक्रिया अन्य कणों के संवेग को उपेक्षित करती है, जो निकाय के द्रव्यमान को प्रभावित करती है यदि अन्य कण इस तंत्र में गति में हैं।

विशेष प्रकार के द्रव्यमान के लिए जिसे अपरिवर्तनीय द्रव्यमान कहा जाता है, पूर्ण बंद निकाय के लिए अवलोकन के जड़त्वीय फ्रेम को बदलने से निकाय के अपरिवर्तनीय द्रव्यमान के माप पर कोई प्रभाव नहीं पड़ता है, जो विभिन्न प्रेक्षक के लिए भी संरक्षित और अपरिवर्तनीय दोनों रहता है। किसी भी प्रेक्षक के लिए, अपरिवर्तनीय द्रव्यमान ऊर्जा और संवेग का एक निकाय संयोजन है, क्योंकि किसी भी जड़त्वीय फ्रेम में, विभिन्न कणों की ऊर्जा और संवेग हमेशा एक ही मात्रा (संवेग नकारात्मक हो सकता है, इसलिए अतिरिक्त मात्रा एक घटाव) में होते है। संवेग फ्रेम के केंद्र में देखे जाने पर अपरिवर्तनीय द्रव्यमान निकाय का सापेक्ष द्रव्यमान होता है। यह न्यूनतम द्रव्यमान है जिसे एक प्रणाली प्रदर्शित कर सकती है, जैसा कि सभी संभावित जड़त्वीय फ्रेम से देखा जाता है।

दोनों सापेक्षतावादी और अपरिवर्तनीय द्रव्यमान का संरक्षण युग्म उत्पादन द्वारा बनाए गए कणों की निकायों पर भी लागू होता है, जहां नए कणों को ऊर्जा अन्य कणों की गतिज ऊर्जा से प्राप्त हो सकती है, या एक या एक से अधिक फोटॉन से एक निकाय के हिस्से के रूप में जिसमें अन्य कण शामिल हैं। पुनः जब नए कण बनते हैं तो सापेक्षतावादी और पूर्ण रूप से बंद (अर्थात विलगित) निकायों का अपरिवर्तनीय द्रव्यमान नही बदलता। हालांकि, विभिन्न जड़त्वीय प्रेक्षक इस संरक्षित द्रव्यमान के मूल्य पर असहमत होंगे, यदि यह सापेक्षतावादी द्रव्यमान है (यानी, सापेक्षतावादी द्रव्यमान संरक्षित है लेकिन अपरिवर्तनीय नहीं है)। हालांकि, सभी प्रेक्षक संरक्षित द्रव्यमान के मूल्य पर सहमत होते हैं यदि मापा जा रहा द्रव्यमान अपरिवर्तनीय द्रव्यमान है (अर्थात, अपरिवर्तनीय द्रव्यमान संरक्षित और अपरिवर्तनीय दोनों है)।

द्रव्यमान-ऊर्जा तुल्यता सूत्र अपृथक निकायों में एक अलग भविष्यवाणी देता है, क्योंकि यदि ऊर्जा को एक निकाय से उत्सर्जित होने की अनुमति दी जाती है, तो सापेक्ष द्रव्यमान और अपरिवर्तनीय द्रव्यमान दोनों भी निकासित हो जाएंगे। इस स्थिति में, द्रव्यमान-ऊर्जा तुल्यता सूत्र भविष्यवाणी करता है कि किसी निकाय के द्रव्यमान में परिवर्तन ऊर्जा के जोड़े या घटाए जाने के कारण उसकी ऊर्जा में परिवर्तन से जुड़ा है, $\Delta m=\Delta E/c^{2}.$ परिवर्तनों को शामिल करने वाला यह रूप वह रूप था जिसमें यह प्रसिद्ध समीकरण मूल रूप से आइंस्टीन द्वारा प्रस्तुत किया गया था। इस अर्थ में, किसी भी निकाय में बड़े पैमाने पर परिवर्तन की व्याख्या केवल तभी की जाती है जब निकाय से जोड़ी या हटाई गई ऊर्जा के द्रव्यमान को ध्यान में रखा जाता है।

सूत्र का तात्पर्य है कि यदि निकाय को बाध्य करने के बाद बंधन ऊर्जा को निकाय से उत्सर्जित होने के लिए अनुमत हो, बद्ध निकाय में उनके अवयवों के योग से कम अपरिवर्तनीय द्रव्यमान (निकाय के लिए शेष द्रव्यमान) होता है। यह निकाय स्थितिज ऊर्जा को किसी अन्य प्रकार की सक्रिय ऊर्जा में परिवर्तित (जैसे गतिज ऊर्जा या फोटॉन, जो आसानी से बद्ध निकाय से निकासित हो जाते हैं) करके हो सकता है। निकाय के द्रव्यमान में अंतर, जिसे द्रव्यमान दोष कहा जाता है, बध्य निकाय में बंधन ऊर्जा की मात्रा है, दूसरे शब्दों में, निकाय को अलग करने के लिए आवश्यक ऊर्जा। द्रव्यमान दोष जितना अधिक होगा, बंधन ऊर्जा उतनी ही अधिक होगी। बंधन ऊर्जा (जिसमें स्वयं द्रव्यमान होता है) को जारी किया जाना चाहिए (प्रकाश या गर्मी के रूप में) जब अवयवों को बध्य निकाय बनाने के लिए संयुक्त किया जाता है, तथा इस कारणवश जब ऊर्जा निकाय से उत्सर्जित होती है तो बध्य निकाय का द्रव्यमान कम हो जाता है।^[16] बंधन ऊर्जा का द्रव्यमान जो बच गया है, को ध्यान में रखने पर कुल अपरिवर्तनीय द्रव्यमान वास्तव में संरक्षित होता है।

सामान्य सापेक्षता

सामान्य सापेक्षता में, अभिरक्त विस्थापन के कारण, अंतरिक्ष के विस्तारित आयतन में फोटॉन का कुल अपरिवर्तनीय द्रव्यमान घट जाएगा। बदलती गुरुत्वाकर्षण स्थितिज ऊर्जा के कारण द्रव्यमान और ऊर्जा दोनों का संरक्षण सिद्धांत में ऊर्जा में किए गए विभिन्न संशोधन पर निर्भर करता है।

यह सभी देखें

संदर्भ

↑ Volkenstein, Mikhail V. (2009). Entropy and Information (illustrated ed.). Springer Science & Business Media. p. 20. ISBN 978-3-0346-0078-1. Extract of page 20
↑ Okuň, Lev Borisovič (2009). Energy and Mass in Relativity Theory. World Scientific. p. 253. ISBN 978-981-281-412-8. Extract of page 253
↑ Lewis, David (2012). Early Russian Organic Chemists and Their Legacy (illustrated ed.). Springer Science & Business Media. p. 29. ISBN 978-3-642-28219-5. Extract of page 29
↑ Fr. 12; see pp.291–2 of Kirk, G. S.; J. E. Raven; Malcolm Schofield (1983). The Presocratic Philosophers (2 ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-27455-5.
↑ Long, A. A.; D. N. Sedley (1987). "Epicureanism: The principals of conservation". The Hellenistic Philosophers. Vol 1: Translations of the principal sources with philosophical commentary. Cambridge: Cambridge University Press. pp. 25–26. ISBN 978-0-521-27556-9.
↑ Whitaker, Robert D. (1975-10-01). "An historical note on the conservation of mass". Journal of Chemical Education. 52 (10): 658. Bibcode:1975JChEd..52..658W. doi:10.1021/ed052p658. ISSN 0021-9584.
↑ Robert D. Whitaker, "An Historical Note on the Conservation of Mass", Journal of Chemical Education, 52, 10, 658-659, Oct 75
↑ Pismen, Len (2018). The Swings of Science: From Complexity to Simplicity and Back. Springer. p. 41. ISBN 978-3-319-99777-3.
↑ Pomper, Philip (October 1962). "Lomonosov and the Discovery of the Law of the Conservation of Matter in Chemical Transformations". Ambix. 10 (3): 119–127. doi:10.1179/amb.1962.10.3.119.
↑ Lomonosov, Mikhail Vasil’evich (1970). Mikhail Vasil'evich Lomonosov on the Corpuscular Theory. Henry M. Leicester (trans.). Cambridge, Mass.: Harvard University Press. Introduction, p. 25.
↑ Matthew Moncrieff Pattison Muir, The Elements of Chemistry (1904)
↑ Nouv. Recherches sur les lois des proportions chimiques (1865) 152, 171, 189
↑ "Conservation of Mass in Chemical Changes"Journal - Chemical Society, London, Vol.64, Part 2 Chemical Society (Great Britain)
↑ William Edwards Henderson, A Course in General Chemistry (1921)
↑ Ida Freund, The study of Chemical Composition: an account of its method and historical development, with illustrative quotations (1904)
↑ Kenneth R. Lang, Astrophysical Formulae, Springer (1999), ISBN 3-540-29692-1

[1] Volkenstein, Mikhail V. (2009). Entropy and Information (illustrated ed.). Springer Science & Business Media. p. 20. ISBN 978-3-0346-0078-1. Extract of page 20

[2] Okuň, Lev Borisovič (2009). Energy and Mass in Relativity Theory. World Scientific. p. 253. ISBN 978-981-281-412-8. Extract of page 253

[3] Lewis, David (2012). Early Russian Organic Chemists and Their Legacy (illustrated ed.). Springer Science & Business Media. p. 29. ISBN 978-3-642-28219-5. Extract of page 29

[4] Fr. 12; see pp.291–2 of Kirk, G. S.; J. E. Raven; Malcolm Schofield (1983). The Presocratic Philosophers (2 ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-27455-5.

[5] Long, A. A.; D. N. Sedley (1987). "Epicureanism: The principals of conservation". The Hellenistic Philosophers. Vol 1: Translations of the principal sources with philosophical commentary. Cambridge: Cambridge University Press. pp. 25–26. ISBN 978-0-521-27556-9.

[6] Whitaker, Robert D. (1975-10-01). "An historical note on the conservation of mass". Journal of Chemical Education. 52 (10): 658. Bibcode:1975JChEd..52..658W. doi:10.1021/ed052p658. ISSN 0021-9584.

[7] Robert D. Whitaker, "An Historical Note on the Conservation of Mass", Journal of Chemical Education, 52, 10, 658-659, Oct 75

[8] Pismen, Len (2018). The Swings of Science: From Complexity to Simplicity and Back. Springer. p. 41. ISBN 978-3-319-99777-3.

[9] Pomper, Philip (October 1962). "Lomonosov and the Discovery of the Law of the Conservation of Matter in Chemical Transformations". Ambix. 10 (3): 119–127. doi:10.1179/amb.1962.10.3.119.

[10] Lomonosov, Mikhail Vasil’evich (1970). Mikhail Vasil'evich Lomonosov on the Corpuscular Theory. Henry M. Leicester (trans.). Cambridge, Mass.: Harvard University Press. Introduction, p. 25.

[11] Matthew Moncrieff Pattison Muir, The Elements of Chemistry (1904)

[12] Nouv. Recherches sur les lois des proportions chimiques (1865) 152, 171, 189

[13] "Conservation of Mass in Chemical Changes"Journal - Chemical Society, London, Vol.64, Part 2 Chemical Society (Great Britain)

[14] William Edwards Henderson, A Course in General Chemistry (1921)

[15] Ida Freund, The study of Chemical Composition: an account of its method and historical development, with illustrative quotations (1904)

[KL2-16] Kenneth R. Lang, Astrophysical Formulae, Springer (1999), ISBN 3-540-29692-1

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

@@ Line 1: / Line 1: @@
-[[:hi:भौतिक शास्त्र|भौतिकी]] एवं [[:hi:रसायन विज्ञान|रसायन विज्ञान]] में, '''द्रव्यमान के संरक्षण के नियम''' या '''सिद्धांत''' के अनुसार [[:hi:संवृत तंत्र|वह बंद निकाय]] जिसमे [[:hi:पदार्थ|पदार्थ]] एवं [[:hi:ऊर्जा|ऊर्जा]] का स्थानांतरण अनिवार्य न हो तथा इनकी मात्रा न तो जोड़ी जा सकती है और न ही घटाई जा सकती है, अत: निकाय का [[:hi:द्रव्यमान|द्रव्यमान]] संरक्षित (निकाय का द्रव्यमान समय के साथ स्थिर) रहता है।
+[[भौतिक विज्ञान|भौतिकी]] एवं रसायन विज्ञान में, '''द्रव्यमान के संरक्षण के''' '''सिद्धांत''' के अनुसार वह [[:hi:संवृत तंत्र|बंद निकाय]], जिसमे [[:hi:पदार्थ|पदार्थ]] एवं [[ऊर्जा]] का स्थानांतरण अनिवार्य नहीं होता तथा इनकी मात्रा न तो जोड़ी जा सकती है और न ही घटाई जा सकती है, अत: निकाय का द्रव्यमान संरक्षित (निकाय का द्रव्यमान समय के साथ स्थिर) रहता है।
-इस नियम का तात्पर्य है कि द्रव्यमान को न तो उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है, हालांकि इसे अंतरिक्ष में पुनर्व्यवस्थित किया जा सकता है, या इससे जुड़ी संस्थाओं को रूप में बदला जा सकता है। उदाहरण के लिए, [[:hi:रासायनिक अभिक्रिया|रासायनिक अभिक्रियाओं]] में, अभिक्रिया से पहले [[:hi:अभिकर्मक|अभिकारकों]] का द्रव्यमान अभिक्रिया के बाद के अभिकारकों के द्रव्यमान के बराबर होता है। इस प्रकार, विलगित निकाय में किसी भी रासायनिक अभिक्रिया और कम-ऊर्जा कि [[:hi:थर्मोडायनामिक प्रक्रिया|उष्मागतिकी प्रक्रियाओं]] के दौरान, अभिकारकों या उपादान का कुल द्रव्यमान उत्पादों के द्रव्यमान के बराबर होना चाहिए।
+इस नियमानुसार, द्रव्यमान को न तो उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है, हालांकि इसे अंतरिक्ष में पुनर्व्यवस्थित किया जा सकता है, या इससे जुड़ी इकाईयों को बदला जा सकता है। उदाहरण के लिए, [https://en.wikipedia.org/wiki/Chemical_reaction|'''रासायनिक अभिक्रियाओं'''] में, अभिक्रिया से पहले [[:hi:अभिकर्मक|अभिकारकों]] का द्रव्यमान अभिक्रिया के बाद के अभिकारकों के द्रव्यमान के बराबर होता है। इस प्रकार, विलगित निकाय में किसी भी रासायनिक अभिक्रिया और कम-ऊर्जा कि उष्मागतिकी प्रक्रियाओं के दौरान, अभिकारकों या उपादान का कुल द्रव्यमान उत्पादों के द्रव्यमान के बराबर होना चाहिए।
-[[:hi:रसायन विज्ञान|रसायन विज्ञान]], [[:hi:यांत्रिकी|यांत्रिकी]] और [[:hi:तरल गतिकी|द्रव गतिकी]] में द्रव्यमान संरक्षण की अवधारणा का व्यापक रूप से उपयोग किया जाता है। ऐतिहासिक रूप से, रासायनिक अभिक्रियाओं में द्रव्यमान का संरक्षण [[:hi:मिखाइल लोमोनोसोव|मिखाइल लोमोनोसोव]] द्वारा स्वतंत्र रूप से प्रमाणित किया गया था और बाद में 18 वीं शताब्दी के अंत में [[:hi:एंटोनी लेवोज़ियर|एंटोनी लावोसियर]] द्वारा पुनः खोजा गया था। [[:hi:कीमिया|कीमिया]] से आधुनिक [[:hi:प्राकृतिक विज्ञान|प्राकृतिक रसायन विज्ञान]] की प्रगति में इस नियम का महत्वपूर्ण महत्व था।
+रसायन विज्ञान, [[:hi:यांत्रिकी|यांत्रिकी]] और [[द्रव गतिविज्ञान|द्रव गतिकी]] में द्रव्यमान संरक्षण की अवधारणा का व्यापक रूप से उपयोग किया जाता है। ऐतिहासिक रूप से, रासायनिक अभिक्रियाओं में द्रव्यमान का संरक्षण [[:hi:मिखाइल लोमोनोसोव|मिखाइल लोमोनोसोव]] द्वारा स्वतंत्र रूप से प्रमाणित किया गया था और बाद में 18 वीं शताब्दी के अंत में [[:hi:एंटोनी लेवोज़ियर|एंटोनी लावोसियर]] द्वारा पुनः खोजा गया था। [[:hi:कीमिया|कीमिया]] से आधुनिक [[:hi:प्राकृतिक विज्ञान|प्राकृतिक रसायन विज्ञान]] की प्रगति में इस नियम का महत्वपूर्ण महत्व था।
-वास्तव में, द्रव्यमान का संरक्षण केवल सन्निकटत धारण करता है और [[:hi:चिरसम्मत यांत्रिकी|चिरसम्मत यांत्रिकी]] में पूर्वधारणाओं की श्रृंखला का हिस्सा माना जाता है। [[:hi:द्रव्यमान-ऊर्जा समतुल्यता|द्रव्यमान-ऊर्जा तुल्यता]] के सिद्धांत के तहत [[:hi:प्रमात्रा यान्त्रिकी|क्वांटम यांत्रिकी]] और [[:hi:विशिष्ट आपेक्षिकता|विशेष सापेक्षता]] के नियमों का पालन करने के लिए नियमो को संशोधित किया जाना है, जिसके अनुसार ऊर्जा और द्रव्यमान एक संरक्षित मात्रा बनाते हैं। अत्याधिक ऊर्जावान प्रणालियों (जैसे [[:hi:नाभिकीय अभिक्रिया|परमाणु अभिक्रियाओं]] और [[:hi:कण भौतिकी|कण भौतिकी]] में कण-प्रतिकण [[:hi:परिशून्यन|विनाश]]) के लिए द्रव्यमान का संरक्षण नहीं होता।
+वास्तव में, द्रव्यमान का संरक्षण केवल सन्निकटत धारण करता है और [[:hi:चिरसम्मत यांत्रिकी|चिरसम्मत यांत्रिकी]] में पूर्वधारणाओं की श्रृंखला का हिस्सा माना जाता है। [[:hi:द्रव्यमान-ऊर्जा समतुल्यता|द्रव्यमान-ऊर्जा तुल्यता]] के सिद्धांत के तहत [[क्वांटम यांत्रिकी]] और [[:hi:विशिष्ट आपेक्षिकता|विशेष सापेक्षता]] के नियमों का पालन करने के लिए नियमो को संशोधित किया जाना है, जिसके अनुसार ऊर्जा और द्रव्यमान एक संरक्षित मात्रा बनाते हैं। अत्याधिक ऊर्जावान प्रणालियों (जैसे [[:hi:नाभिकीय अभिक्रिया|परमाणु अभिक्रियाओं]] और [[कण भौतिकी]] में कण-प्रतिकण [[:hi:परिशून्यन|विनाश]]) के लिए द्रव्यमान का संरक्षण नहीं होता।
-वह निकाय जिसमे ऊर्जा तथा पदर्थ दोनो का ही विनिमय होता है, [[:hi:ओपन सिस्टम (ऊष्मप्रवैगिकी)|खुला निकाय]] कैहलाता है तथा खुले निकाय का द्रव्यमान संरक्षित नहीं होता है। हालांकि, जब तक [[:hi:रेडियोसक्रियता|रेडियोधर्मिता]] या नाभिकीय अभिक्रिया शामिल नहीं होती हैं, [[:hi:ऊष्मा|ऊर्जा]], [[:hi:कार्य (भौतिकी)|यांत्रिक कार्य]], या [[:hi:विद्युतचुंबकीय विकिरण|विद्युत चुम्बकीय विकिरण]] जैसी प्रणालियों से निकलने (या प्रवेश) वाली ऊर्जा की मात्रा अक्सर सिस्टम के द्रव्यमान में कमी (या वृद्धि) के रूप में मापने के लिए बहुत छोटी होती है।
+वह निकाय जिसमे ऊर्जा तथा पदर्थ दोनो का ही विनिमय होता है, [[:hi:ओपन सिस्टम (ऊष्मप्रवैगिकी)|खुला निकाय]] कहलाता है तथा खुले निकाय का द्रव्यमान संरक्षित नहीं होता है। हालांकि, जब तक [[:hi:रेडियोसक्रियता|रेडियोधर्मिता]] या नाभिकीय अभिक्रिया शामिल नहीं होती हैं, [[:hi:ऊष्मा|ऊर्जा]], [[:hi:कार्य (भौतिकी)|यांत्रिक कार्य]], या [[:hi:विद्युतचुंबकीय विकिरण|विद्युत चुम्बकीय विकिरण]], जैसी प्रणालियों से निकलने (या प्रवेश) करने वाली ऊर्जा की मात्रा प्रायः निकाय के द्रव्यमान में कमी (या वृद्धि) के रूप में मापने के लिए बहुत छोटी होती है।
 [[:hi:सामान्य आपेक्षिकता|सामान्य सापेक्षता]] को ध्यान में रखकर, उन प्रणालियों के लिए जिनमें बड़े गुरुत्वाकर्षण क्षेत्र शामिल हैं, इस प्रकार विभिन्न परिभाषाओं के अधीन द्रव्यमान-ऊर्जा संरक्षण एक अधिक जटिल अवधारणा बन जाती है, विशेष सापेक्षता कि तुलना में द्रव्यमान और ऊर्जा उतनी ही सख्ती से और सरलता से संरक्षित नहीं होते है।[[File:Combustion reaction of methane.jpg|thumb|350x350px |   [[:hi:मिथेन|मीथेन]] की दहन प्रतिक्रिया। जहां प्रतिक्रिया से पहले और बाद में हाइड्रोजन के 4 परमाणु, ऑक्सीजन के 4 परमाणु और कार्बन के 1 परमाणु मौजूद होते हैं। प्रतिक्रिया के बाद का कुल द्रव्यमान प्रतिक्रिया के पहले जैसा ही होता है। ]]
@@ Line 15: / Line 15: @@
 द्रव्यमान के संरक्षण का नियम केवल [[:hi:चिरसम्मत यांत्रिकी|चिरसम्मत यांत्रिकी]] में सूत्रित किया जा सकता है, जिसमें  विलगित निकाय से जुड़े ऊर्जा परिमाण <math>mc^2</math> से बहुत छोटा होता है, जहां <math>m</math> विरामावस्था में निकाय कि विशिष्ट वस्तु का [[:hi:संदर्भ विन्यास|निर्देश तंत्र]] में मापा गया द्रव्यमान है, और <math>c</math> [[:hi:प्रकाश का वेग|प्रकाश की गति है]]।
-[[:hi:तरल यांत्रिकी|द्रव यांत्रिकी]] और [[:hi:सातत्यक यांत्रिकी|सातत्य यांत्रिकी]] के क्षेत्र में द्रव्यमान संरक्षण के नियम को [[:hi:सातत्य समीकरण|सांतत्य समीकरण]] का उपयोग करके गणित में [[:hi:अवकल समीकरण|अवकल रूप]] में सूत्रित किया जा सकता है।
+[[:hi:तरल यांत्रिकी|द्रव यांत्रिकी]] और सातत्य यांत्रिकी के क्षेत्र में द्रव्यमान संरक्षण के नियम को [[:hi:सातत्य समीकरण|सांतत्य समीकरण]] का उपयोग करके गणित में [[:hi:अवकल समीकरण|अवकल रूप]] में सूत्रित किया जा सकता है।
 <math>\frac{\partial \rho}{\partial t}+\nabla\cdot(\rho \mathbf{v})=0,</math>
@@ Line 21: / Line 21: @@
 जहां <math display="inline">\rho</math> [[:hi:घनत्व|घनत्व]] (द्रव्यमान प्रति इकाई आयतन), <math display="inline">t</math> समय, <math display="inline">\nabla\cdot</math> [[:hi:विचलन|विचलन]], और <math display="inline">\mathbf{v}</math> [[:hi:प्रवाह वेग|प्रवाह वेग]] क्षेत्र है।
-द्रव्यमान के लिए सांतत्य समीकरण की व्याख्या निम्नलिखित है। किसी समय अंतराल में निकाय में द्रव्यमान का परिवर्तन समान समय अंतराल में निकाय के पारगमित द्रव्यमान के बराबर होता है। यदि पदार्थ अंदर जाता है तो सकारात्मक और यदि पदार्थ बाहर जाता है तो नकारात्मक। संपूर्ण विलगित निकाय के लिए, इस स्थिति का तात्पर्य है कि कुल द्रव्यमान <math display="inline">M</math> (निकाय में सभी घटकों के द्रव्यमान का योग) समय के साथ परिवर्तित नहीं होता है, अर्थात
+द्रव्यमान के लिए सांतत्य समीकरण की व्याख्या निम्नलिखित है। किसी समय अंतराल में निकाय में द्रव्यमान का परिवर्तन, समान समयांतराल में निकाय के पारगमित द्रव्यमान के बराबर होता है। यदि पदार्थ अंदर जाता है तो सकारात्मक और यदि पदार्थ बाहर जाता है तो नकारात्मक। संपूर्ण विलगित निकाय के लिए, इस स्थिति का तात्पर्य है कि कुल द्रव्यमान <math display="inline">M</math> (निकाय में सभी घटकों के द्रव्यमान का योग) समय के साथ परिवर्तित नहीं होता है, अर्थात
 <math>\frac{\text{d}M}{\text{d}t}=\frac{\text{d}}{\text{d}t}\int \rho \text{d}V=0</math>
@@ Line 27: / Line 27: @@
 जहां <math display="inline">\text{d}V</math> वह [[:hi:डिफरेंशियल (अनंतिमल)|अवकलन]] है जो निकाय के संपूर्ण अयतन पर [[:hi:समाकलन|समकालन]] को परिभाषित करता है।
-द्रव्यमान के लिए सांतत्य समीकरण द्रव गतिकी के [[:hi:यूलर समीकरण (द्रव गतिकी)|यूलर समीकरणों]] का हिस्सा है। कई अन्य [[:hi:संवहन-प्रसार समीकरण|संवहन-प्रसार समीकरण]] निकाय में द्रव्यमान और पदार्थ के संरक्षण और प्रवाह का वर्णन करते हैं।
+द्रव्यमान के लिए सांतत्य समीकरण, द्रव गतिकी के [[:hi:यूलर समीकरण (द्रव गतिकी)|यूलर समीकरणों]] का हिस्सा है। कई अन्य [[:hi:संवहन-प्रसार समीकरण|संवहन-प्रसार समीकरण]], निकाय में द्रव्यमान और पदार्थ के संरक्षण और प्रवाह का वर्णन करते हैं।
-रसायन विज्ञान में, रासायनिक अभिक्रिया, या  [[:hi:रससमीकरणमिति|रससमीकरणमिति (स्टोइकोमेट्री]]) में [[:hi:अभिकर्मक|अभिकारक]] और [[:hi:उत्पाद (रसायन विज्ञान)|उत्पादों]] की मात्रा की गणना, द्रव्यमान के संरक्षण के सिद्धांत के आधार पर की जाती है। सिद्धांत का तात्पर्य है कि रासायनिक अभिक्रिया के दौरान अभिकारकों का कुल द्रव्यमान उत्पादों के कुल द्रव्यमान के बराबर होता है। उदाहरण के लिए, निम्नलिखित अभिक्रिया में
+रसायन विज्ञान में, रासायनिक अभिक्रिया, या  [[:hi:रससमीकरणमिति|रससमीकरणमिति (स्टोइकोमेट्री]]) में [[:hi:अभिकर्मक|अभिकारक]] और [[:hi:उत्पाद (रसायन विज्ञान)|उत्पादों]] की मात्रा की गणना, द्रव्यमान के संरक्षण के सिद्धांत के आधार पर की जाती है। सिद्धांत का तात्पर्य है कि रासायनिक अभिक्रिया के दौरान अभिकारकों का कुल द्रव्यमान उत्पादों के कुल द्रव्यमान के बराबर होता है। उदाहरण के लिए, निम्नलिखित अभिक्रिया में,
 CH<sub>4</sub> + 2O<sub>2</sub> → CO<sub>2</sub> + 2H<sub>2</sub>O
-जहां [[:hi:मिथेन|मीथेन]] का एक [[:hi:अणु|अणु]] (CH<sub>4</sub>) और दो [[:hi:ऑक्सीजन|ऑक्सीजन]] के अणु (O<sub>2</sub>) [[:hi:कार्बन डाईऑक्साइड|कार्बन डाइऑक्साइड]] के एक अणु (CO<sub>2</sub>) और दो [[:hi:जल|जल]] के अणुओं (H<sub>2</sub>O) में परिवर्तित हो जाते हैं। अभिक्रिया में शुरू में चार [[:hi:हाइड्रोजन|हाइड्रोजन]] परमाणु, चार ऑक्सीजन परमाणु और एक कार्बन परमाणु मौजूद हैं तथा अभिक्रिया पश्चात् उत्पाद के अणुओं की संख्या समान है यह संख्या द्रव्यमान के संरक्षण के सिद्धांत से प्राप्त की जा सकती है।
+जहां [[:hi:मिथेन|मीथेन]] का एक [[:hi:अणु|अणु]] (CH<sub>4</sub>) और दो [[:hi:ऑक्सीजन|ऑक्सीजन]] के अणु (O<sub>2</sub>) [https://en.wikipedia.org/wiki/Carbon_dioxide कार्बन डाइऑक्साइड] के एक अणु (CO<sub>2</sub>) और दो [[:hi:जल|जल]] के अणुओं (H<sub>2</sub>O) में परिवर्तित हो जाते हैं। अभिक्रिया में शुरू में चार [[:hi:हाइड्रोजन|हाइड्रोजन]] परमाणु, चार ऑक्सीजन परमाणु और एक कार्बन परमाणु मौजूद हैं तथा अभिक्रिया के पश्चात् उत्पाद के अणुओं की संख्या समान है, यह संख्या द्रव्यमान के संरक्षण के सिद्धांत से प्राप्त की जा सकती है।
 समय के साथ कई [[:hi:अभियान्त्रिकी|अभियान्त्रिकी]] समस्याओं को, किसी निकाय के द्रव्यमान वितरण नियम का पालन करके, हल किया जाता है। इस क्रियाविधि [[:hi:द्रव्यमान संतुलन|द्रव्यमान संतुलन]] कहलती है।
@@ Line 41: / Line 41: @@
 [[File:Antoine laurent lavoisier.jpg|thumb| द्रव्यमान के संरक्षण के नियम की [[:hi:एंटोनी लेवोज़ियर|एंटोनी लावोज़ियर]] की खोज ने 19वीं शताब्दी में कई नए निष्कर्ष निकाले। [[:hi:जोसेफ प्राउस्ट|जोसेफ प्राउस्ट]] [[:hi:निश्चित अनुपात का नियम|का निश्चित अनुपात का नियम]] और [[:hi:जॉन डाल्टन|जॉन डाल्टन]] का [[:hi:परमाणुवाद|परमाणु सिद्धांत]] एंटोनी लेवोजियर की खोजों से अलग है। लैवोज़ियर के मात्रात्मक प्रयोगों से पता चला कि दहन में [[:hi:ऑक्सीजन|ऑक्सीजन]] शामिल था, जो पहले [[:hi:फ्लॉजिस्टन सिद्धांत|फ्लॉजिस्टन]] माना जाता था। |324x324px]]
-ईसा पूर्व, जैन दर्शनशास्त्र, महावीर की शिक्षाओं पर आधारित एक असृजनवादी दर्शनशास्त्र,<ref>Fr. 12; see pp.291&#x2013;2 of {{Cite book|edition=2|publisher=[[Cambridge University Press]]|isbn=978-0-521-27455-5|last=Kirk|first=G. S.|last2=J. E. Raven|last3=Malcolm Schofield|title=The Presocratic Philosophers|location=Cambridge|year=1983}}</ref> ने कहा कि ब्रह्मांड और उसके घटक जैसे पदार्थ को नष्ट या बनाया नहीं जा सकता है। जैन ग्रंथ तत्त्वार्थसूत्र (दूसरी शताब्दी सीई) में कहा गया है कि एक पदार्थ स्थायी है, लेकिन इसकी विधियां निर्माण और विनाश की विशेषता है।<ref>{{Cite book|publisher=Cambridge University Press|isbn=978-0-521-27556-9|pages=25–26|last=Long|first=A. A.|last2=D. N. Sedley|title=The Hellenistic Philosophers. Vol 1: Translations of the principal sources with philosophical commentary|chapter=Epicureanism: The principals of conservation|location=Cambridge|year=1987}}</ref> [[:hi:यूनानी दर्शन|प्राचीन यूनानी दर्शन]] में "[[:hi:कुछ नहीं से कुछ नहीं आता|कुछ भी नहीं से कुछ नहीं आता है]]" एक महत्वपूर्ण विचार था ताकि जो अभी मौजूद है वह हमेशा अस्तित्व में रहे। कोई भी नया पदार्थ अस्तित्व में नहीं आ सकता, जहां पहले कोई नहीं था। इसका एक स्पष्ट कथन, आगे के सिद्धांत के साथ कि कुछ भी नहीं में कुछ भी नहीं गुजर सकता है, [[:hi:एंपेडोक्लीज़|एम्पेडोकल्स]] (चौथी शताब्दी ईसा पूर्व) में पाया जाता है, "क्योंकि कुछ नहीं से कुछ भी आना असंभव है, और जो कुछ है वह पूरी तरह से नष्ट हो जाना चाहिए, यह लाया या सुना नहीं जा सकता है।"
+ईसा पूर्व, जैन दर्शनशास्त्र, महावीर की शिक्षाओं पर आधारित एक असृजनवादी दर्शनशास्त्र,<ref>Fr. 12; see pp.291&#x2013;2 of {{Cite book|edition=2|publisher=[[Cambridge University Press]]|isbn=978-0-521-27455-5|last=Kirk|first=G. S.|last2=J. E. Raven|last3=Malcolm Schofield|title=The Presocratic Philosophers|location=Cambridge|year=1983}}</ref> ने कहा कि ब्रह्मांड और उसके घटक जैसे पदार्थ को नष्ट या बनाया नहीं जा सकता है। जैन ग्रंथ तत्त्वार्थसूत्र (दूसरी शताब्दी सीई (CE)) में कहा गया है कि पदार्थ स्थायी है, लेकिन इसकी विधियां निर्माण और विनाश की विशेषता है।<ref>{{Cite book|publisher=Cambridge University Press|isbn=978-0-521-27556-9|pages=25–26|last=Long|first=A. A.|last2=D. N. Sedley|title=The Hellenistic Philosophers. Vol 1: Translations of the principal sources with philosophical commentary|chapter=Epicureanism: The principals of conservation|location=Cambridge|year=1987}}</ref> "[[:hi:कुछ नहीं से कुछ नहीं आता|कुछ भी नहीं से कुछ नहीं आता है]]", [[:hi:यूनानी दर्शन|प्राचीन यूनानी दर्शन]] में  एक महत्वपूर्ण विचार था ताकि जो अभी मौजूद है, वह हमेशा अस्तित्व में रहे। कोई भी नया पदार्थ अस्तित्व में नहीं आ सकता, जहां पहले कोई नहीं था। इसका एक स्पष्ट कथन, आगे के सिद्धांत का एक विचार, कुछ भी नहीं में कुछ भी नहीं गुजर सकता है, [[:hi:एंपेडोक्लीज़|एम्पेडोकल्स]] (चौथी शताब्दी ईसा पूर्व) में पाया गया, "क्योंकि कुछ नहीं से कुछ भी आना असंभव है, और जो कुछ है वह पूरी तरह से नष्ट हो जाना चाहिए, यह लाया या सुना नहीं जा सकता है।"
 संरक्षण का एक और सिद्धांत तीसरी शताब्दी ईसा पूर्व के आसपास [[:hi:एपिकुरुस|एपिकुरस]] द्वारा व्यक्त गया था, जिन्होंने ब्रह्मांड की प्रकृति का वर्णन करते हुए लिखा था कि "चीजों की समग्रता हमेशा वैसी ही थी जैसी अब है, और हमेशा रहेगी"।
@@ Line 50: / Line 50: @@
 सार्वभौमिक नियम लोमोनोसोव द्वारा सामान्य दार्शनिक भौतिकवादी प्रतिफलो के आधार पर सूत्रबद्ध किया गया था, यह उनके द्वारा कभी भी पूछताछ या परीक्षण नहीं किया गया था, बल्कि इसके विपरीत, उन्हें अपने पूरे जीवन में सभी शोधों में एक ठोस प्रारंभिक स्थिति के रूप में कार्य किया।
-प्रयोगों की एक और अधिक परिष्कृत श्रृंखला बाद में [[:hi:एंटोनी लेवोज़ियर|एंटोनी लावोज़ियर]] द्वारा की गई जिन्होंने 1773 में अपना निष्कर्ष में द्रव्यमान के संरक्षण के सिद्धांत को लोकप्रिय व्यक्त किया। सिद्धांत के प्रदर्शनों ने तत्कालीन लोकप्रिय [[:hi:फ्लॉजिस्टन सिद्धांत|फ्लॉजिस्टन सिद्धांत]] को अप्रमाणित कर दिया, जिसके अनुसार [[:hi:दहन|दहन]] और उष्मीय प्रक्रियाओं में द्रव्यमान प्राप्त या अदृश्य (लुप्त) हो सकता है।
+प्रयोगों की एक और अधिक परिष्कृत श्रृंखला बाद में [[:hi:एंटोनी लेवोज़ियर|एंटोनी लावोज़ियर]] द्वारा की गई, जिन्होंने 1773 में अपना निष्कर्ष में द्रव्यमान के संरक्षण के सिद्धांत को लोकप्रिय व्यक्त किया। सिद्धांत के प्रदर्शनों ने तत्कालीन लोकप्रिय [[:hi:फ्लॉजिस्टन सिद्धांत|फ्लॉजिस्टन सिद्धांत]] को अप्रमाणित कर दिया, जिसके अनुसार [[:hi:दहन|दहन]] और उष्मीय प्रक्रियाओं में द्रव्यमान प्राप्त या अदृश्य (लुप्त) हो सकता है।
-द्रव्यमान का संरक्षण, गैसों के भार पर पृथ्वी के वायुमंडल के उत्प्लावन प्रभाव के कारण सदियों तक अस्पष्ट था। उदाहरण के लिए, लकड़ी का एक टुकड़ा जलने के पश्चात् कम वजन का होता है, इस घटना से ऐसा प्रतीत होता है कि इसका कुछ द्रव्यमान लुप्त हो जाता है, या बदल या खो जाता है। यह तब तक अस्वीकृत नहीं था जब तक कि सावधानीपूर्वक प्रयोग नहीं किए गए थे जैसे सीलबंद कांच कि शीशियों में, जंग लगने जैसी रासायनिक अभिक्रिया का होना, इस रासायनिक अभिक्रिया में सीलबंद पात्र और उसकी सामग्री के वजन को नहीं बदला। 17वीं शताब्दी में [[:hi:निर्वात पम्प|वैक्यूम पंप]] के आविष्कार तक तराजू का उपयोग करके गैसों को तौलना संभव नहीं था।
+द्रव्यमान का संरक्षण, गैसों के भार पर पृथ्वी के वायुमंडल के उत्प्लावन प्रभाव के कारण सदियों तक अस्पष्ट था। उदाहरण के लिए, लकड़ी का एक टुकड़ा जलने के पश्चात् कम वजन का होता है, इस घटना से ऐसा प्रतीत होता है कि इसका कुछ द्रव्यमान लुप्त हो जाता है, या बदल या खो जाता है। यह तब तक अस्वीकृत नहीं था, जब तक कि सावधानीपूर्वक प्रयोग नहीं किए गए थे, जैसे सीलबंद कांच कि शीशियों में, जंग लगने जैसी रासायनिक अभिक्रिया का होना, इस रासायनिक अभिक्रिया में सीलबंद पात्र और उसकी सामग्री के वजन को नहीं बदला। 17वीं शताब्दी में [[:hi:निर्वात पम्प|वैक्यूम पंप]] के आविष्कार तक तराजू का उपयोग करके गैसों को तौलना संभव नहीं था।
-[[:hi:कीमिया|कीमिया]] से आधुनिक रसायन विज्ञान की प्रगति में द्रव्यमान के संरक्षण का बहुत महत्व हैं। एक बार रसायनज्ञों ने संपादित किया कि रासायनिक पदार्थ समान भार वाले अन्य पदार्थों में परिवर्तित हो जाते हैं न कि नष्ट हो जाते हैं, अतः वैज्ञानिको के द्वारा पदार्थों के परिवर्तनों का मात्रात्मक अध्ययन किया जा सकता है। द्रव्यमान संरक्षण का विचार और एक अनुमान है कि कुछ "तात्विक पदार्थ" भी रासायनिक अभिक्रियाओं द्वारा दूसरे पदार्थो में परिवर्तित नहीं किए जा सकते हैं, जबकि [[:hi:रासायनिक तत्व|रासायनिक तत्वों]] की समझ के साथ-साथ यह विचार भी आया कि सभी रासायनिक प्रक्रियाएं और परिवर्तन (जैसे दहन और उपापचयी अभिक्रियाएं) इन रासायनिक तत्वों की अपरिवर्तनीय मात्रा या भार के बीच की प्रतिक्रियाएं हैं।
+[[:hi:कीमिया|कीमिया]] से आधुनिक रसायन विज्ञान की प्रगति में द्रव्यमान के संरक्षण का बहुत महत्व हैं। एक बार रसायनज्ञों ने संपादित किया कि रासायनिक पदार्थ समान भार वाले अन्य पदार्थों में परिवर्तित हो जाते हैं न कि नष्ट हो जाते हैं, अतः वैज्ञानिको के द्वारा पदार्थों के परिवर्तनों का मात्रात्मक अध्ययन किया जा सकता है। द्रव्यमान संरक्षण का विचार है कि कुछ "तात्विक पदार्थ" भी रासायनिक अभिक्रियाओं द्वारा दूसरे पदार्थो में परिवर्तित नहीं किए जा सकते हैं, जबकि [[:hi:रासायनिक तत्व|रासायनिक तत्वों]] की समझ के साथ-साथ यह विचार भी आया कि सभी रासायनिक प्रक्रियाएं और परिवर्तन (जैसे दहन और उपापचयी अभिक्रियाएं) इन रासायनिक तत्वों की अपरिवर्तनीय मात्रा या भार के बीच की प्रतिक्रियाएं हैं।
-लैवोज़ियर के अग्रणी कार्य के बाद, [[:hi:जीन स्टास|जीन स्टास]] के व्यापक प्रयोगों ने रासायनिक अभिक्रियाओं में इस नियम की स्थिरता का समर्थन किया। <ref>Matthew Moncrieff Pattison Muir, [https://books.google.com/books?id=EwZZAAAAYAAJ ''The Elements of Chemistry''] (1904)</ref> उनके शोध <ref>''Nouv. Recherches sur les lois des proportions chimiques'' (1865) 152, 171, 189</ref><ref>"Conservation of Mass in Chemical Changes"[https://books.google.com/books?id=bhQ3AAAAYAAJ ''Journal - Chemical Society, London'', Vol.64], Part 2 Chemical Society (Great Britain)</ref> के अनुसार अभिक्रियाओं में हानि या लाभ 1,00,000 में 2 से 4 भागों से अधिक नहीं हो सकता था।<ref>William Edwards Henderson, [https://archive.org/details/acourseingenera00hendgoog ''A Course in General Chemistry''] (1921)</ref> एक ओर लवॉज़ियर और दूसरी ओर [[:hi:एडवर्ड मॉर्ले|मॉर्ले]] और स्टास द्वारा लक्षित और प्राप्त की गई परिशुद्धता में बहुत बड़ा अंतर है।<ref>[[Ida Freund]], [https://archive.org/details/studychemicalco01freugoog ''The study of Chemical Composition'': an account of its method and historical development, with illustrative quotations] (1904)</ref>
+लैवोज़ियर के अग्रणी कार्य के बाद, [[:hi:जीन स्टास|जीन स्टास]] के व्यापक प्रयोगों ने रासायनिक अभिक्रियाओं में इस नियम की स्थिरता का समर्थन किया।<ref>Matthew Moncrieff Pattison Muir, [https://books.google.com/books?id=EwZZAAAAYAAJ ''The Elements of Chemistry''] (1904)</ref> उनके शोध<ref>''Nouv. Recherches sur les lois des proportions chimiques'' (1865) 152, 171, 189</ref><ref>"Conservation of Mass in Chemical Changes"[https://books.google.com/books?id=bhQ3AAAAYAAJ ''Journal - Chemical Society, London'', Vol.64], Part 2 Chemical Society (Great Britain)</ref> के अनुसार अभिक्रियाओं में हानि या लाभ 1,00,000 में 2 से 4 भागों से अधिक नहीं हो सकता था।<ref>William Edwards Henderson, [https://archive.org/details/acourseingenera00hendgoog ''A Course in General Chemistry''] (1921)</ref> एक ओर लवॉज़ियर और दूसरी ओर [[:hi:एडवर्ड मॉर्ले|मॉर्ले]] और स्टास द्वारा लक्षित और प्राप्त की गई परिशुद्धता में बहुत बड़ा अंतर है।<ref>[[Ida Freund]], [https://archive.org/details/studychemicalco01freugoog ''The study of Chemical Composition'': an account of its method and historical development, with illustrative quotations] (1904)</ref>
 === आधुनिक भौतिकी ===
@@ Line 73: / Line 73: @@
 ==== ऊर्जा का ह्रास न होने पर जन संरक्षण सही रहता है ====
-[[:hi:सापेक्ष द्रव्यमान|सापेक्षतावादी द्रव्यमान]] के संरक्षण का तात्पर्य एकल पर्यवेक्षक (या एकल जड़त्वीय फ्रेम से दृश्य) के दृष्टिकोण से है क्योंकि जड़त्वीय फ्रेम बदलने से सिस्टम के लिए कुल ऊर्जा (सापेक्ष ऊर्जा) में परिवर्तन हो सकता है, और यह मात्रा सापेक्षतावादी द्रव्यमान को निर्धारित करती है।
+[[:hi:सापेक्ष द्रव्यमान|सापेक्षतावादी द्रव्यमान]] के संरक्षण का तात्पर्य एक प्रेक्षक (या एकल जड़त्वीय फ्रेम से दृश्य) के दृष्टिकोण से है क्योंकि जड़त्वीय फ्रेम बदलने से निकाय के लिए कुल ऊर्जा (सापेक्ष ऊर्जा) में परिवर्तन हो सकता है, और यह मात्रा सापेक्षतावादी द्रव्यमान को निर्धारित करती है।
-यह सिद्धांत कि कणों की एक प्रणाली का द्रव्यमान उनके [[:hi:निश्चर द्रव्यमान|बाकी द्रव्यमानों]] के योग के बराबर होना चाहिए, भले ही शास्त्रीय भौतिकी में सच हो, [[:hi:विशिष्ट आपेक्षिकता|विशेष सापेक्षता]] में गलत हो सकता है। इसका कारण यह है कि बाकी द्रव्यमानों को आसानी से नहीं जोड़ा जा सकता है, यह ऊर्जा के अन्य रूपों, जैसे गतिज और संभावित ऊर्जा, और बड़े पैमाने पर कणों जैसे फोटॉन को ध्यान में नहीं रखता है, जो सभी के कुल द्रव्यमान को प्रभावित कर सकते हैं (या नहीं) सिस्टम
+यह सिद्धांत कि चिरसम्मत भौतिकी में कणों के निकाय का द्रव्यमान उनके [[:hi:निश्चर द्रव्यमान|गतिहीन द्रव्यमानों]] के योग के बराबर होता है परन्तु [[:hi:विशिष्ट आपेक्षिकता|विशेष सापेक्षता]] में नहीं होता। इसका कारण यह है कि गतिहीन द्रव्यमानों को आसानी से नहीं जोड़ा जा सकता है, यह ऊर्जा के अन्य रूपों, जैसे गतिज और स्थितिज ऊर्जा, और बड़े पैमाने पर कणों, जैसे फोटॉन को ध्यान में नहीं रखता है, जो निकाय के कुल द्रव्यमान को प्रभावित कर सकते हैं (या नहीं)।
-एक प्रणाली में बड़े पैमाने पर कणों को स्थानांतरित करने के लिए, विभिन्न कणों के बाकी द्रव्यमानों की जांच करना भी कई अलग-अलग जड़त्वीय अवलोकन फ़्रेमों को पेश करने के बराबर है (जो कि कुल सिस्टम ऊर्जा और गति को संरक्षित करने के लिए निषिद्ध है), और यह भी कि जब एक के बाकी फ्रेम में कण, यह प्रक्रिया अन्य कणों के गति को अनदेखा करती है, जो सिस्टम द्रव्यमान को प्रभावित करती है यदि अन्य कण इस फ्रेम में गति में हैं।
+किसी निकाय में बड़े कणों को स्थानांतरित करने के लिए, विभिन्न कणों के गतिहीन द्रव्यमानों की जांच करना भी कई अलग-अलग जड़त्वीय अवलोकन फ़्रेमों को उत्पन्न करने के बराबर है (जो निकाय कि कुल ऊर्जा और संवेग को संरक्षित करने के लिए प्रतिबंधित है), और यह भी कि जब कण के विरामस्थ तंत्र में, यह प्रक्रिया अन्य कणों के संवेग को उपेक्षित करती है, जो निकाय के द्रव्यमान को प्रभावित करती है यदि अन्य कण इस तंत्र में गति में हैं।
-विशेष प्रकार के द्रव्यमान के लिए जिसे [[:hi:निश्चर द्रव्यमान|अपरिवर्तनीय]] द्रव्यमान कहा जाता है, पूरे बंद सिस्टम के लिए अवलोकन के जड़त्वीय फ्रेम को बदलने से सिस्टम के अपरिवर्तनीय द्रव्यमान के माप पर कोई प्रभाव नहीं पड़ता है, जो विभिन्न पर्यवेक्षकों के लिए भी संरक्षित और अपरिवर्तनीय (अपरिवर्तनीय) दोनों रहता है। पूरी प्रणाली। अपरिवर्तनीय द्रव्यमान ऊर्जा और संवेग का एक प्रणाली संयोजन है, जो किसी भी पर्यवेक्षक के लिए अपरिवर्तनीय है, क्योंकि किसी भी जड़त्वीय फ्रेम में, विभिन्न कणों की ऊर्जा और गति हमेशा एक ही मात्रा में जोड़ते हैं (संवेग नकारात्मक हो सकता है, इसलिए अतिरिक्त मात्रा एक घटाव)। [[:hi:गति फ्रेम का केंद्र|गति फ्रेम के केंद्र]] में देखे जाने पर अपरिवर्तनीय द्रव्यमान प्रणाली का सापेक्ष द्रव्यमान होता है। यह न्यूनतम द्रव्यमान है जिसे एक प्रणाली प्रदर्शित कर सकती है, जैसा कि सभी संभावित जड़त्वीय फ्रेम से देखा जाता है।
+विशेष प्रकार के द्रव्यमान के लिए जिसे [[:hi:निश्चर द्रव्यमान|अपरिवर्तनीय]] द्रव्यमान कहा जाता है, पूर्ण बंद निकाय के लिए अवलोकन के जड़त्वीय फ्रेम को बदलने से निकाय के अपरिवर्तनीय द्रव्यमान के माप पर कोई प्रभाव नहीं पड़ता है, जो विभिन्न प्रेक्षक के लिए भी संरक्षित और अपरिवर्तनीय दोनों रहता है। किसी भी प्रेक्षक के लिए, अपरिवर्तनीय द्रव्यमान ऊर्जा और संवेग का एक निकाय संयोजन है, क्योंकि किसी भी जड़त्वीय फ्रेम में, विभिन्न कणों की ऊर्जा और संवेग हमेशा एक ही मात्रा (संवेग नकारात्मक हो सकता है, इसलिए अतिरिक्त मात्रा एक घटाव) में होते है। [[:hi:गति फ्रेम का केंद्र|संवेग फ्रेम के केंद्र]] में देखे जाने पर अपरिवर्तनीय द्रव्यमान निकाय का सापेक्ष द्रव्यमान होता है। यह न्यूनतम द्रव्यमान है जिसे एक प्रणाली प्रदर्शित कर सकती है, जैसा कि सभी संभावित जड़त्वीय फ्रेम से देखा जाता है।
-दोनों सापेक्षतावादी और अपरिवर्तनीय द्रव्यमान का संरक्षण [[:hi:युग्म उत्पादन|जोड़ी उत्पादन]] द्वारा बनाए गए कणों की प्रणालियों पर भी लागू होता है, जहां नए कणों के लिए ऊर्जा अन्य कणों की गतिज ऊर्जा से आ सकती है, या एक या एक से अधिक फोटॉन से एक प्रणाली के हिस्से के रूप में जिसमें अन्य कण शामिल हैं। फोटान फिर, जब नए कण बनते हैं तो न तो सापेक्षतावादी और न ही पूरी तरह से बंद (अर्थात पृथक) प्रणालियों का अपरिवर्तनीय द्रव्यमान बदलता है। हालांकि, विभिन्न जड़त्वीय पर्यवेक्षक इस संरक्षित द्रव्यमान के मूल्य पर असहमत होंगे, यदि यह सापेक्षतावादी द्रव्यमान है (यानी, सापेक्षतावादी द्रव्यमान संरक्षित है लेकिन अपरिवर्तनीय नहीं है)। हालांकि, सभी पर्यवेक्षक संरक्षित द्रव्यमान के मूल्य पर सहमत होते हैं यदि मापा जा रहा द्रव्यमान अपरिवर्तनीय द्रव्यमान है (यानी, अपरिवर्तनीय द्रव्यमान संरक्षित और अपरिवर्तनीय दोनों है)।
+दोनों सापेक्षतावादी और अपरिवर्तनीय द्रव्यमान का संरक्षण [[:hi:युग्म उत्पादन|युग्म उत्पादन]] द्वारा बनाए गए कणों की निकायों पर भी लागू होता है, जहां नए कणों को ऊर्जा अन्य कणों की गतिज ऊर्जा से प्राप्त हो सकती है, या एक या एक से अधिक फोटॉन से एक निकाय के हिस्से के रूप में जिसमें अन्य कण शामिल हैं। पुनः जब नए कण बनते हैं तो सापेक्षतावादी और पूर्ण रूप से बंद (अर्थात विलगित) निकायों का अपरिवर्तनीय द्रव्यमान नही बदलता। हालांकि, विभिन्न जड़त्वीय प्रेक्षक इस संरक्षित द्रव्यमान के मूल्य पर असहमत होंगे, यदि यह सापेक्षतावादी द्रव्यमान है (यानी, सापेक्षतावादी द्रव्यमान संरक्षित है लेकिन अपरिवर्तनीय नहीं है)। हालांकि, सभी प्रेक्षक संरक्षित द्रव्यमान के मूल्य पर सहमत होते हैं यदि मापा जा रहा द्रव्यमान अपरिवर्तनीय द्रव्यमान है (अर्थात, अपरिवर्तनीय द्रव्यमान संरक्षित और अपरिवर्तनीय दोनों है)।
-द्रव्यमान-ऊर्जा तुल्यता सूत्र गैर- [[:hi:विलगित तंत्र|पृथक प्रणालियों]] में एक अलग भविष्यवाणी देता है, क्योंकि यदि ऊर्जा को एक प्रणाली से बचने की अनुमति दी जाती है, तो [[:hi:सापेक्ष द्रव्यमान|सापेक्ष द्रव्यमान]] और [[:hi:निश्चर द्रव्यमान|अपरिवर्तनीय द्रव्यमान]] दोनों भी बच जाएंगे। इस मामले में, द्रव्यमान-ऊर्जा तुल्यता सूत्र भविष्यवाणी करता है कि किसी प्रणाली के द्रव्यमान में ''परिवर्तन'' ऊर्जा के जोड़े या घटाए जाने के कारण उसकी ऊर्जा में ''परिवर्तन'' से जुड़ा है: <math>\Delta m = \Delta E/c^2.</math> परिवर्तनों को शामिल करने वाला यह रूप वह रूप था जिसमें यह प्रसिद्ध समीकरण मूल रूप से आइंस्टीन द्वारा प्रस्तुत किया गया था। इस अर्थ में, किसी भी प्रणाली में बड़े पैमाने पर परिवर्तन की व्याख्या केवल तभी की जाती है जब सिस्टम से जोड़ी या हटाई गई ऊर्जा के द्रव्यमान को ध्यान में रखा जाता है।
+द्रव्यमान-ऊर्जा तुल्यता सूत्र [[:hi:विलगित तंत्र|अपृथक निकायों]] में एक अलग भविष्यवाणी देता है, क्योंकि यदि ऊर्जा को एक निकाय से उत्सर्जित होने की अनुमति दी जाती है, तो [[:hi:सापेक्ष द्रव्यमान|सापेक्ष द्रव्यमान]] और [[:hi:निश्चर द्रव्यमान|अपरिवर्तनीय द्रव्यमान]] दोनों भी निकासित हो जाएंगे। इस स्थिति में, द्रव्यमान-ऊर्जा तुल्यता सूत्र भविष्यवाणी करता है कि किसी निकाय के द्रव्यमान में परिवर्तन ऊर्जा के जोड़े या घटाए जाने के कारण उसकी ऊर्जा में परिवर्तन से जुड़ा है, <math>\Delta m = \Delta E/c^2.</math> परिवर्तनों को शामिल करने वाला यह रूप वह रूप था जिसमें यह प्रसिद्ध समीकरण मूल रूप से आइंस्टीन द्वारा प्रस्तुत किया गया था। इस अर्थ में, किसी भी निकाय में बड़े पैमाने पर परिवर्तन की व्याख्या केवल तभी की जाती है जब निकाय से जोड़ी या हटाई गई ऊर्जा के द्रव्यमान को ध्यान में रखा जाता है।
 सूत्र का तात्पर्य है कि यदि निकाय को बाध्य करने के बाद बंधन ऊर्जा को निकाय से उत्सर्जित होने के लिए अनुमत हो, बद्ध निकाय में उनके अवयवों के योग से कम अपरिवर्तनीय द्रव्यमान (निकाय के लिए शेष द्रव्यमान) होता है। यह निकाय स्थितिज ऊर्जा को किसी अन्य प्रकार की सक्रिय ऊर्जा में परिवर्तित (जैसे गतिज ऊर्जा या फोटॉन, जो आसानी से बद्ध निकाय से निकासित हो जाते हैं) करके हो सकता है। निकाय के द्रव्यमान में अंतर, जिसे द्रव्यमान दोष कहा जाता है, बध्य निकाय में [[:hi:बाँधने वाली ऊर्जा|बंधन ऊर्जा]] की मात्रा है, दूसरे शब्दों में, निकाय को अलग करने के लिए आवश्यक ऊर्जा। द्रव्यमान दोष जितना अधिक होगा, बंधन ऊर्जा उतनी ही अधिक होगी। बंधन ऊर्जा (जिसमें स्वयं द्रव्यमान होता है) को जारी किया जाना चाहिए (प्रकाश या गर्मी के रूप में) जब अवयवों को बध्य निकाय बनाने के लिए संयुक्त किया जाता है, तथा इस कारणवश जब ऊर्जा निकाय से उत्सर्जित होती है तो बध्य निकाय का द्रव्यमान कम हो जाता है।<ref name="KL2">Kenneth R. Lang, ''Astrophysical Formulae'', Springer (1999), {{ISBN|3-540-29692-1}}</ref> बंधन ऊर्जा का द्रव्यमान जो बच गया है, को ध्यान में रखने पर कुल अपरिवर्तनीय द्रव्यमान वास्तव में संरक्षित होता है।
 === सामान्य सापेक्षता ===
-सामान्य सापेक्षता में, [[:hi:अभिरक्त विस्थापन|अभिरक्त विस्थापन]] के कारण, अंतरिक्ष के विस्तारित आयतन में फोटॉन का कुल [[:hi:निश्चर द्रव्यमान|अपरिवर्तनीय द्रव्यमान]] घट जाएगा। बदलती [[:hi:गुरुत्वाकर्षण ऊर्जा|गुरुत्वाकर्षण स्थितिज ऊर्जा]] के कारण. द्रव्यमान और ऊर्जा दोनों का संरक्षण सिद्धांत में ऊर्जा में किए गए विभिन्न संशोधन पर निर्भर करता है।
+सामान्य सापेक्षता में, [[:hi:अभिरक्त विस्थापन|अभिरक्त विस्थापन]] के कारण, अंतरिक्ष के विस्तारित आयतन में फोटॉन का कुल [[:hi:निश्चर द्रव्यमान|अपरिवर्तनीय द्रव्यमान]] घट जाएगा। बदलती [[:hi:गुरुत्वाकर्षण ऊर्जा|गुरुत्वाकर्षण स्थितिज ऊर्जा]] के कारण द्रव्यमान और ऊर्जा दोनों का संरक्षण सिद्धांत में ऊर्जा में किए गए विभिन्न संशोधन पर निर्भर करता है।
 == यह सभी देखें ==
@@ Line 99: / Line 99: @@
 == संदर्भ ==
+[[Category:Machine Translated Page]]
+[[Category:CS1]]
+[[Category:Pages with template loops]]
+[[Category:Templates using TemplateData]]
+[[Category:Wikipedia pages with incorrect protection templates|Cite book/TemplateData]]

Anonymous

Search

द्रव्य का संरक्षण: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 09:54, 4 August 2022

Contents

सूत्रीकरण और उदाहरण

इतिहास

रसायन विज्ञान में खोजें

आधुनिक भौतिकी

सामान्यीकरण

विशेष सापेक्षता

ऊर्जा की रासायनिक मात्रा से जुड़ा द्रव्यमान मापने के लिए बहुत छोटा है

ऊर्जा का ह्रास न होने पर जन संरक्षण सही रहता है

सामान्य सापेक्षता

यह सभी देखें

संदर्भ

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

द्रव्य का संरक्षण: Difference between revisions

Latest revision as of 09:54, 4 August 2022

सूत्रीकरण और उदाहरण

इतिहास

रसायन विज्ञान में खोजें

आधुनिक भौतिकी

सामान्यीकरण

विशेष सापेक्षता

ऊर्जा की रासायनिक मात्रा से जुड़ा द्रव्यमान मापने के लिए बहुत छोटा है

ऊर्जा का ह्रास न होने पर जन संरक्षण सही रहता है

सामान्य सापेक्षता

यह सभी देखें

संदर्भ

Navigation

Wiki tools

Page tools

Other projects

Hidden categories