ऊष्मा समीकरण: Difference between revisions
No edit summary |
No edit summary |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Partial differential equation describing the evolution of temperature in a region}} | {{Short description|Partial differential equation describing the evolution of temperature in a region}} | ||
[[Image:Heat eqn.gif|thumb|upright=1.8|ऊष्मा समीकरण द्वारा अनुमानित एक वर्ग धातु की प्लेट में तापमान के विकास का एनिमेटेड प्लॉट। ऊंचाई और लाली प्रत्येक बिंदु पर तापमान दर्शाती है। प्रारंभिक अवस्था में समान रूप से गर्म खुर के आकार का क्षेत्र (लाल) होता है जो समान रूप से ठंडे क्षेत्र (पीला) से घिरा होता है। जैसे-जैसे समय बीतता है ऊष्माठंडे क्षेत्र में फैल जाती है।]]गणित और भौतिकी में, ऊष्मा समीकरण एक निश्चित आंशिक अंतर समीकरण है। ऊष्मा समीकरण के समाधान को कभी-कभी कैलोरी फलन के रूप में जाना जाता है। ऊष्मा समीकरण का सिद्धांत पहली बार 1822 में [[जोसेफ फूरियर]] द्वारा मॉडलिंग के उद्देश्य से विकसित किया गया था कि किसी दिए गए क्षेत्र में ऊष्मा जैसी मात्रा कैसे | [[Image:Heat eqn.gif|thumb|upright=1.8|ऊष्मा समीकरण द्वारा अनुमानित एक वर्ग धातु की प्लेट में तापमान के विकास का एनिमेटेड प्लॉट। ऊंचाई और लाली प्रत्येक बिंदु पर तापमान दर्शाती है। प्रारंभिक अवस्था में समान रूप से गर्म खुर के आकार का क्षेत्र (लाल) होता है जो समान रूप से ठंडे क्षेत्र (पीला) से घिरा होता है। जैसे-जैसे समय बीतता है ऊष्माठंडे क्षेत्र में फैल जाती है।]]गणित और भौतिकी में, ऊष्मा समीकरण एक निश्चित आंशिक अंतर समीकरण है। ऊष्मा समीकरण के समाधान को कभी-कभी कैलोरी फलन के रूप में जाना जाता है। ऊष्मा समीकरण का सिद्धांत पहली बार 1822 में [[जोसेफ फूरियर]] द्वारा मॉडलिंग के उद्देश्य से विकसित किया गया था कि किसी दिए गए क्षेत्र में ऊष्मा जैसी मात्रा कैसे विसरित होती है। | ||
प्रोटोटाइपिकल [[परवलयिक आंशिक अंतर समीकरण]] के रूप में, ऊष्मा समीकरण [[शुद्ध गणित]] में सबसे व्यापक रूप से अध्ययन किए जाने वाले विषयों में से एक है, और इसके विश्लेषण को आंशिक अंतर समीकरणों के व्यापक क्षेत्र के लिए मूल सिद्धान्त माना जाता है। [[रीमैनियन कई गुना]] पर ऊष्मा समीकरण पर भी विचार किया जा सकता है, जिससे कई ज्यामितीय अनुप्रयोग हो सकते हैं। [[सुब्बरमा मीनाक्षीसुंदरम]] और एके प्लीजेल के काम के बाद, ऊष्मा समीकरण [[वर्णक्रमीय ज्यामिति]] से घनिष्ठ रूप से संबंधित है। 1964 में [[जेम्स एल्स]] और जोसेफ एच. सैम्पसन द्वारा [[अंतर ज्यामिति]] के लिए एक | प्रोटोटाइपिकल [[परवलयिक आंशिक अंतर समीकरण]] के रूप में, ऊष्मा समीकरण [[शुद्ध गणित]] में सबसे व्यापक रूप से अध्ययन किए जाने वाले विषयों में से एक है, और इसके विश्लेषण को आंशिक अंतर समीकरणों के व्यापक क्षेत्र के लिए मूल सिद्धान्त माना जाता है। [[रीमैनियन कई गुना|रीमैनियन बहुआयामी]] पर ऊष्मा समीकरण पर भी विचार किया जा सकता है, जिससे कई ज्यामितीय अनुप्रयोग हो सकते हैं। [[सुब्बरमा मीनाक्षीसुंदरम]] और एके प्लीजेल के काम के बाद, ऊष्मा समीकरण [[वर्णक्रमीय ज्यामिति]] से घनिष्ठ रूप से संबंधित है। 1964 में [[जेम्स एल्स]] और जोसेफ एच. सैम्पसन द्वारा [[अंतर ज्यामिति]] के लिए एक बीजीय [[हार्मोनिक नक्शा]] प्रस्तुत किया गया था, जो 1982 में रिचर्ड एस हैमिल्टन द्वारा [[रिक्की प्रवाह]] की प्रारम्भ को प्रेरित करता है और 2003 में [[त्वरित पेरेलमैन]] द्वारा पॉइनकेयर अनुमान के प्रमाण में परिणत हुआ। ऊष्मा समीकरण के रूप में जाने वाले ऊष्मा समीकरण के समाधान उस क्षेत्र के बारे में सूक्ष्म जानकारी प्रदान करते हैं, जिस पर उन्हें परिभाषित किया गया है, जैसा कि अतियाह-सिंगर सूचक प्रमेय में उनके आवेदन के माध्यम से उदाहरण दिया गया है।<ref>Berline, Nicole; Getzler, Ezra; Vergne, Michèle. Heat kernels and Dirac operators. Grundlehren der Mathematischen Wissenschaften, 298. Springer-Verlag, Berlin, 1992. viii+369 pp. {{ISBN|3-540-53340-0}}</ref> | ||
ऊष्मा समीकरण, इसके प्रकारों के साथ, विज्ञान और [[व्यावहारिक गणित]] के कई क्षेत्रों में भी महत्वपूर्ण है। संभाव्यता सिद्धांत में, फोकर-प्लैंक समीकरण के माध्यम से ऊष्मा समीकरण अनियमित चलने और [[ब्राउनियन गति]] के अध्ययन से जुड़ा हुआ है। [[वित्तीय गणित]] का काला-स्कोल्स समीकरण ऊष्मा समीकरण का एक | ऊष्मा समीकरण, इसके प्रकारों के साथ, विज्ञान और [[व्यावहारिक गणित]] के कई क्षेत्रों में भी महत्वपूर्ण है। संभाव्यता सिद्धांत में, फोकर-प्लैंक समीकरण के माध्यम से ऊष्मा समीकरण अनियमित चलने और [[ब्राउनियन गति]] के अध्ययन से जुड़ा हुआ है। [[वित्तीय गणित]] का काला-स्कोल्स समीकरण ऊष्मा समीकरण का एक संक्षिप्त रूप है, और [[क्वांटम यांत्रिकी]] के श्रोडिंगर समीकरण को [[काल्पनिक संख्या]] में ऊष्मा समीकरण के रूप में माना जा सकता है। [[छवि विश्लेषण]] में, ऊष्मा समीकरण का उपयोग कभी-कभी पिक्सेलेशन और [[किनारे का पता लगाना|किनारे का पता लगाने की विधि]] को हल करने के लिए किया जाता है। रॉबर्ट डी. रिचटमायर और [[जॉन वॉन न्यूमैन]] द्वारा कृत्रिम श्यानता विधियों के प्रारम्भ के बाद, ऊष्मा समीकरणों के समाधान [[शॉक (द्रव गतिकी)]] के गणितीय सूत्रीकरण में उपयोगी रहे हैं। 1950 के दशक के प्रारम्भ में जिम डगलस, डी.डब्ल्यू. पीसमैन, और हेनरी रैचफोर्ड जूनियर साथ में काम किये थे। | ||
== समीकरण का कथन == | == समीकरण का कथन == | ||
'<nowiki | <nowiki>''''</nowiki>''''''''गणित में, यदि R<sup>''n''</sup> का एक खुला उपसमुच्चय ''U'' दिया जाए और R का एक उपअंतराल {{mvar|I}} , यह कहता है कि एक फलन{{math|''u'' : ''U'' × ''I'' → '''R'''}} ऊष्मा समीकरण का समाधान है अगर'''''''''''' | ||
:<math>\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x_1^2} + \cdots + \frac{\partial^2 u}{\partial x_n^2},</math> | :<math>\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x_1^2} + \cdots + \frac{\partial^2 u}{\partial x_n^2},</math> | ||
जहाँ पर | जहाँ पर {{math|(''x''<sub>1</sub>, …, ''x''<sub>''n''</sub>, ''t'')}} डोमेन के एक सामान्य बिंदु को दर्शाता है संक्षेप संदर्भों में भी जहां ये वाक्यांश अपने सहज अर्थ के लिए विफल होते हैं, यहां पर {{mvar|t}} को समय के रूप में और {{math|''x''<sub>1</sub>, …, ''x''<sub>''n''</sub>}} स्थानिक चर के रूप में निरूपित करना सामान्य है। स्थानिक चरों के संग्रह को प्रायः x बस के रूप में संदर्भित किया जाता है। ''t'' के किसी दिए गए मूल्य के लिए, समीकरण का दाहिना पक्ष फलन {{math|''u''(⋅, ''t'') : ''U'' → '''R'''}} का लाप्लास संकारक है। जैसे, ऊष्मा समीकरण को प्रायः अधिक सघन रूप से इस प्रकार लिखा जाता है | ||
{{Equation box 1 | {{Equation box 1 | ||
|equation=<math>\frac{\partial u}{\partial t}=\Delta u</math>. | |equation=<math>\frac{\partial u}{\partial t}=\Delta u</math>. | ||
| Line 17: | Line 17: | ||
|border colour = #50C878 | |border colour = #50C878 | ||
|background colour=#ECFCF4}} | |background colour=#ECFCF4}} | ||
भौतिकी और इंजीनियरिंग संदर्भों में, विशेष रूप से एक माध्यम से प्रसार के संदर्भ में, कार्टेशियन समन्वय प्रणाली को | भौतिकी और इंजीनियरिंग संदर्भों में, विशेष रूप से एक माध्यम से प्रसार के संदर्भ में, कार्टेशियन समन्वय प्रणाली को निर्धारित करना और फिर किसी फलन (गणित) {{math|''u''(''x'', ''y'', ''z'', ''t'')}} के विशिष्ट सन्दर्भ पर विचार करना अधिक सामान्य है। तीन स्थानिक चर के {{math|(''x'', ''y'', ''z'')}} और [[समय]] {{mvar|t}}.परिवर्तनशील है । इस प्रकार यह कहा जा सकता है {{mvar|u}} ऊष्मा समीकरण का समाधान है यदि | ||
:<math>\frac{\partial u}{\partial t} = \alpha\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}\right)</math> | :<math>\frac{\partial u}{\partial t} = \alpha\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}\right)</math> | ||
जिसमें {{math|''α''}} एक धनात्मक गुणांक है जिसे माध्यम का ऊष्मीय विसारकता कहा जाता है। अन्य भौतिक परिघटनाओं के अतिरिक्त, यह समीकरण एक सजातीय और समदैशिक माध्यम में ऊष्मा के प्रवाह का वर्णन करता है, साथ में {{math|''u''(''x'', ''y'', ''z'', ''t'')}} बिंदु पर तापमान होना {{math|(''x'', ''y'', ''z'')}} और समय {{mvar|t}}. यदि माध्यम सजातीय और समदैशिक नहीं है, तो {{math|α}} एक निश्चित गुणांक नहीं होगा, और इसके अतिरिक्त ( x, y, z ) पर निर्भर करेगा | जिसमें {{math|''α''}} एक धनात्मक गुणांक है जिसे माध्यम का ऊष्मीय विसारकता कहा जाता है। अन्य भौतिक परिघटनाओं के अतिरिक्त, यह समीकरण एक सजातीय और समदैशिक माध्यम में ऊष्मा के प्रवाह का वर्णन करता है, साथ में {{math|''u''(''x'', ''y'', ''z'', ''t'')}} बिंदु पर तापमान होना {{math|(''x'', ''y'', ''z'')}} और समय {{mvar|t}}. यदि माध्यम सजातीय और समदैशिक नहीं है, तो {{math|α}} एक निश्चित गुणांक नहीं होगा, और इसके अतिरिक्त ( x, y, z ) पर निर्भर करेगा, जो समीकरण का कुछ अलग रूप भी होगा। भौतिकी और इंजीनियरिंग साहित्य में अतिरिक्त लाप्लासियन निरूपित करने के लिए {{math|∆}} का {{math|∇<sup>2</sup>}} का प्रयोग सामान्य है। | ||
गणित के साथ-साथ भौतिकी और इंजीनियरिंग में समय व्युत्पन्न के लिए न्यूटन के अंकन का उपयोग करना | गणित के साथ-साथ भौतिकी और इंजीनियरिंग में समय व्युत्पन्न के लिए न्यूटन के अंकन का उपयोग करना साधारण बात है, जहाँ पर <math>\dot u</math> निरूपित करने के लिए {{math|{{sfrac|''∂u''|''∂t''}}}}, प्रयोग किया जाता है इसलिए यह समीकरण इस प्रकार लिखा जा सकता है | ||
{{Equation box 1 | {{Equation box 1 | ||
| Line 30: | Line 30: | ||
|border colour = #50C878 | |border colour = #50C878 | ||
|background colour=#ECFCF4}} | |background colour=#ECFCF4}} | ||
यह भी ध्यान दें कि | यह भी ध्यान दें कि {{math|∆}} या {{math|∇<sup>2</sup>}} उपयोग करने की क्षमता लाप्लासियन को निरूपित करने के लिए, स्थानिक चर के स्पष्ट संदर्भ के बिना''', इस तथ्य''' का प्रतिबिंब है कि लाप्लासियन समन्वय प्रणाली के आकर्षण से स्वतंत्र है। गणितीय शब्दों में, कोई भी यह कहेगा कि लाप्लासियन अनुवादात्मक रूप से रूप से और घूर्णी रूप से अचर है। वास्तव में, यह (शिथिलता से बोलना) सबसे सरल अंतर संचालक है जिसमें ये समरूपताएं हैं। यह लाप्लासियन के उपयोग के एक महत्वपूर्ण (और विशुद्ध रूप से गणितीय) औचित्य के रूप में लिया जा सकता है और किसी भी भौतिक घटना के प्रतिरूपण में ऊष्मा समीकरण के समरूप और समदैशिक हैं, जिनमें से ऊष्मा का प्रसार एक प्रमुख उदाहरण है। | ||
प्रसार स्थिरांक {{math|''α''}} | प्रसार स्थिरांक {{math|''α''}} ऊष्मा समीकरण के गणितीय अध्ययन में प्रायः उपस्थित नहीं होता है, जबकि इंजीनियरिंग में इसका मूल्य बहुत महत्वपूर्ण हो सकता है। निम्नलिखित कारणों से यह एक बड़ा अंतर नहीं है। माना कि {{mvar|u}} एक फलन हो जिसके साथ | ||
:<math>\frac{\partial u}{\partial t}=\alpha\Delta u.</math> | :<math>\frac{\partial u}{\partial t}=\alpha\Delta u.</math> | ||
एक नया | एक नया फलन <math>v(t,x)=u(t/\alpha,x) </math> परिभाषित करें. फिर, शृंखला नियम के अनुसार, किसी एक के पास | ||
{{NumBlk|:|<math> | {{NumBlk|:|<math> | ||
\frac{\partial}{\partial t} v(t,x) | \frac{\partial}{\partial t} v(t,x) | ||
| Line 42: | Line 42: | ||
= \Delta v(t,x) | = \Delta v(t,x) | ||
</math>|{{EquationRef|⁎}}}} | </math>|{{EquationRef|⁎}}}} | ||
इस प्रकार, सामान्य मान के साथ ताप समीकरण के समाधानों के बीच अनुवाद करने का | इस प्रकार, सामान्य मान α के साथ ताप समीकरण के समाधानों के बीच अनुवाद करने का और ऊष्मा समीकरण के समाधान के साथ {{math|1=''α'' = 1}} एक सीधा तरीका है। जैसे, गणितीय विश्लेषण के लिए, प्रायः केवल दशा ''α'' = 1.पर विचार करना ही पर्याप्त होता है। | ||
तब से <math>\alpha>0</math> | तब से <math>\alpha>0</math> पर <math>v</math> परिभाषित करने के लिए एक अन्य विकल्प है। संतुष्टि देने वाला <math display="inline">\frac{\partial}{\partial t} v = \Delta v </math> जैसे की ({{EquationNote|⁎}}) उपर्युक्त समीकरण में परिवर्तन करके <math>v(t,x) = u(t, \alpha^{1/2} x) </math>, ध्यान दें कि नए फलन '''''v''''' को परिभाषित करने के दो संभावित साधन समय की माप की इकाई या लंबाई के माप की इकाई को बदलने के लिए यहाँ पर चर्चा की गई है। | ||
== व्याख्या == | == व्याख्या == | ||
| Line 51: | Line 51: | ||
अनौपचारिक रूप से, लाप्लासियन संचालक {{math|∆}} किसी बिंदु के समीप में किसी फलन के औसत मान और उस बिंदु पर उसके मान के बीच का अंतर देता है। इस प्रकार, यदि {{mvar|u}} तापमान है, {{math|∆}} बताता है कि क्या (और कितना) प्रत्येक बिंदु के आस पास की पदार्थ उस बिंदु पर पदार्थ की तुलना में औसतन अधिक गर्म या ठंडी है। | अनौपचारिक रूप से, लाप्लासियन संचालक {{math|∆}} किसी बिंदु के समीप में किसी फलन के औसत मान और उस बिंदु पर उसके मान के बीच का अंतर देता है। इस प्रकार, यदि {{mvar|u}} तापमान है, {{math|∆}} बताता है कि क्या (और कितना) प्रत्येक बिंदु के आस पास की पदार्थ उस बिंदु पर पदार्थ की तुलना में औसतन अधिक गर्म या ठंडी है। | ||
ऊष्मप्रवैगिकी के दूसरे नियम के अनुसार, तापमान के अंतर और उनके बीच की पदार्थ की तापीय चालकता के अनुपात में ऊष्मा गर्म पिंडों से निकटवर्ती ठंडे पिंडों तक प्रवाहित होगी। जब ऊष्मा किसी पदार्थ में (क्रमशः, बाहर) प्रवाहित होती है, तो इसका तापमान बढ़ जाता है (क्रमशः, घट जाता है), पदार्थ की मात्रा ([[द्रव्यमान]]) द्वारा विभाजित ऊष्मा की मात्रा के अनुपात में, [[आनुपातिकता (गणित)]] के साथ पदार्थ | ऊष्मप्रवैगिकी के दूसरे नियम के अनुसार, तापमान के अंतर और उनके बीच की पदार्थ की तापीय चालकता के अनुपात में ऊष्मा गर्म पिंडों से निकटवर्ती ठंडे पिंडों तक प्रवाहित होगी। जब ऊष्मा किसी पदार्थ में (क्रमशः, बाहर) प्रवाहित होती है, तो इसका तापमान बढ़ जाता है (क्रमशः, घट जाता है), पदार्थ की मात्रा ([[द्रव्यमान]]) द्वारा विभाजित ऊष्मा की मात्रा के अनुपात में, [[आनुपातिकता (गणित)]] के साथ पदार्थ की [[विशिष्ट ऊष्मा क्षमता]] कहलाती है। | ||
इन अवलोकनों के संयोजन से, ताप समीकरण दर | इन अवलोकनों के संयोजन से, ताप समीकरण दर <math>\dot u</math> कहते हैं जिस बिंदु पर पदार्थ गर्म हो जाएगी (या ठंडा हो जाएगी) आस पास की पदार्थ कितनी गर्म (या कूलर) के समानुपाती होगी। गुणांक {{math|α}} समीकरण में पदार्थ की तापीय चालकता, विशिष्ट ऊष्मा और [[घनत्व]] को ध्यान में रखा जाता है। | ||
=== समीकरण की गणितीय व्याख्या === | === समीकरण की गणितीय व्याख्या === | ||
उपरोक्त भौतिकीय सोच के पहले भाग को गणितीय रूप में रखा जा सकता है। कुंजी यह है कि, किसी भी निश्चित {{mvar|x}} के लिए, | उपरोक्त भौतिकीय सोच के पहले भाग को गणितीय रूप में रखा जा सकता है। कुंजी यह है कि, किसी भी निश्चित {{mvar|x}} के लिए, किसी एक के पास | ||
:<math>\begin{align} | :<math>\begin{align} | ||
u_{(x)}(0)&=u(x)\\ | u_{(x)}(0)&=u(x)\\ | ||
| Line 62: | Line 62: | ||
u_{(x)}''(0)&=\frac{1}{n}\Delta u(x) | u_{(x)}''(0)&=\frac{1}{n}\Delta u(x) | ||
\end{align}</math> | \end{align}</math> | ||
जहाँ पर {{math|''u''<sub>(''x'')</sub>(''r'')}} के औसत मान ''u'' को दर्शाने वाला एकल-चर फलन है जो त्रिज्या ''r'' के गोले की सतह ''x'' पर केंद्रित है | जहाँ पर {{math|''u''<sub>(''x'')</sub>(''r'')}} के औसत मान ''u'' को दर्शाने वाला एकल-चर फलन है जो त्रिज्या ''r'' के गोले की सतह ''x'' पर केंद्रित है, यह इसके द्वारा परिभाषित किया जा सकता है | ||
:<math>u_{(x)}(r)=\frac{1}{\omega_{n-1}r^{n-1}}\int_{\{y:|x-y|=r\}}u\,d\mathcal{H}^{n-1},</math> | :<math>u_{(x)}(r)=\frac{1}{\omega_{n-1}r^{n-1}}\int_{\{y:|x-y|=r\}}u\,d\mathcal{H}^{n-1},</math> | ||
जिसमें {{math|ω<sub>''n'' − 1</sub>}} यूनिट बॉल के सतह क्षेत्र {{mvar|n}}-आयामी यूक्लिडियन अंतरिक्ष को दर्शाता | जिसमें {{math|ω<sub>''n'' − 1</sub>}} यूनिट बॉल के सतह क्षेत्र {{mvar|n}}-आयामी यूक्लिडियन अंतरिक्ष को दर्शाता है। यह उपरोक्त कथन को निश्चित रूप देता है कि {{math|∆''u''}} का मूल्य एक बिंदु {{mvar|x}} पर {{math|''u''(''x'')}} के मान के अंतर को मापता है और ''u'' का मूल्य ''x'' के पास के बिंदुओं पर, इस अर्थ में कि उत्तरार्द्ध के मूल्यों द्वारा {{math|''u''<sub>(''x'')</sub>(''r'')}} छोटे सकारात्मक मूल्यों के लिए {{mvar|r}}. कूटबद्ध किया गया है। | ||
इस अवलोकन के बाद, ऊष्मा समीकरण की व्याख्या किसी फलन के अतिसूक्ष्म औसत के रूप में की जा सकती है। ऊष्मा समीकरण के एक हल को देखते हुए, | इस अवलोकन के बाद, ऊष्मा समीकरण की व्याख्या किसी फलन के अतिसूक्ष्म औसत के रूप में की जा सकती है। ऊष्मा समीकरण के एक हल को देखते हुए, {{math|''u''(''x'', ''t'' + τ)}} का मान τ के एक छोटे से सकारात्मक मूल्य के लिए {{math|{{sfrac|1|2''n''}}}} फलन {{math|''u''(⋅, ''t'')}} के औसत मूल्य का गुना पर केंद्रित x पर बहुत छोटे त्रिज्या के एक गोले के.रूप में अनुमानित किया जा सकता है। | ||
=== समाधान की प्रकृति === | === समाधान की प्रकृति === | ||
[[Image:Heatequation exampleB.gif|right|frame|1D ऊष्मा आंशिक अवकल समीकरण का हल। तापमान (<math>u</math>) शुरू में इंसुलेटेड एंडपॉइंट्स के साथ एक-आयामी, एक-इकाई-लंबे अंतराल (x = [0,1]) पर वितरित किया जाता है। वितरण समय के साथ संतुलन तक पहुंचता है।]] | [[Image:Heatequation exampleB.gif|right|frame|1D ऊष्मा आंशिक अवकल समीकरण का हल। तापमान (<math>u</math>) शुरू में इंसुलेटेड एंडपॉइंट्स के साथ एक-आयामी, एक-इकाई-लंबे अंतराल (x = [0,1]) पर वितरित किया जाता है। वितरण समय के साथ संतुलन तक पहुंचता है।]] | ||
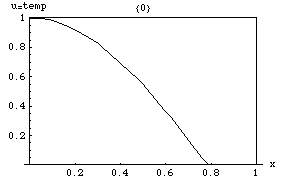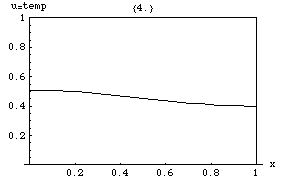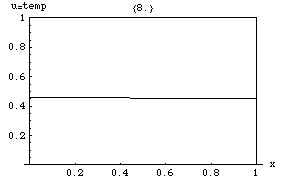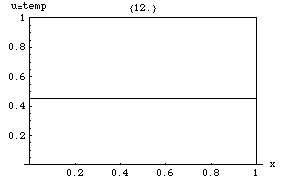
[[File:Heat Transfer.gif|thumb|तापमान का व्यवहार जब 1डी रॉड के किनारे निश्चित तापमान पर होते हैं (इस | [[File:Heat Transfer.gif|thumb|तापमान का व्यवहार जब 1डी रॉड के किनारे निश्चित तापमान पर होते हैं (इस सन्दर्भ में, प्रारंभिक गॉसियन वितरण के साथ 0.8 और 0)। तापमान एक रेखीय कार्य तक पहुंचता है क्योंकि यह समीकरण का स्थिर समाधान है: जहां भी तापमान में गैर-शून्य दूसरा स्थानिक व्युत्पन्न होता है, समय व्युत्पन्न गैर-शून्य भी होता है।]]ऊष्मा समीकरण का तात्पर्य है कि चोटियों ([[स्थानीय अधिकतम]]) <math>u</math> धीरे-धीरे कम हो जाएगा, जबकि अवसाद ([[स्थानीय न्यूनतम]]) भर जाएगा। किसी बिंदु पर मूल्य केवल तब तक स्थिर रहेगा जब तक कि यह अपने तत्काल परिवेश में औसत मूल्य के बराबर हो। विशेष रूप से, यदि निकटवर्ती में मान एक रेखीय फलन <math>A x + B y + C z + D</math>, के बहुत करीब हैं तो उस समीप के केंद्र में मान उस समय नहीं बदलेगा (अर्थात, व्युत्पन्न <math>\dot u</math> शून्य होगा)। | ||
एक अधिक सूक्ष्म परिणाम [[अधिकतम सिद्धांत]] है, जो कहता है कि ''u'' का अधिकतम मूल्य | एक अधिक सूक्ष्म परिणाम [[अधिकतम सिद्धांत]] है, जो कहता है कि ''u'' का अधिकतम मूल्य किसी भी क्षेत्र में माध्यम <math>R</math> का अधिकतम मान उस अधिकतम मान से अधिक नहीं होगा जो पहले <math>R</math> में हुआ था, जब तक कि यह की '''''R''''' सीमा पर न हो। इसका तात्पर्य यह है कि किसी क्षेत्र में अधिकतम तापमान <math>R</math> तभी बढ़ सकता है जब बाहर '''''R''''' से ऊष्मा आए। यह परवलयिक आंशिक अवकल समीकरणों का एक गुण है और इसे गणितीय रूप से सिद्ध करना कठिन नहीं है (नीचे देखें)। | ||
एक और दिलचस्प विशेषता | एक और दिलचस्प विशेषता यह है कि भले ही <math>u</math> प्रारम्भ में माध्यम के अंदर किसी सतह पर मूल्य की एक तेज प्रवणता (असंतोष) होती है, प्रवणता तुरंत उस सतह के माध्यम से ऊष्मा के प्रवाह की एक क्षणिक, असीम रूप से छोटी लेकिन असीम रूप से बड़ी दर से सुचारू हो जाती है। उदाहरण के लिए, यदि दो अलग-अलग पिंड, शुरू में एक समान लेकिन अलग-अलग तापमान पर <math>u_0</math> तथा <math>u_1</math>, एक दूसरे को संपर्क करने के लिए बने हैं, संपर्क के बिंदु पर तापमान तुरंत कुछ मध्यवर्ती मान ग्रहण करेगा, और उस बिंदु के आसपास एक क्षेत्र विकसित होगा जहां <math>u</math> , <math>u_0</math> तथा <math>u_1</math> के बीच धीरे धीरे परिवर्तित होगा। | ||
यदि माध्यम में एक बिंदु पर अचानक एक निश्चित मात्रा में ऊष्मा लागू की जाती है, तो यह प्रसार तरंग के रूप में सभी दिशाओं में | यदि माध्यम में एक बिंदु पर अचानक एक निश्चित मात्रा में ऊष्मा लागू की जाती है, तो यह प्रसार तरंग के रूप में सभी दिशाओं में प्रसारित हो जाएगी। [[यांत्रिक तरंग]] और [[विद्युत चुम्बकीय तरंग]] के विपरीत, प्रसार तरंग की गति समय के साथ कम हो जाती है: जैसे ही यह एक बड़े क्षेत्र में प्रसारित होती है, तापमान प्रवणता कम हो जाती है, और इसलिए ऊष्मा का प्रवाह भी कम हो जाता है। | ||
== विशिष्ट उदाहरण == | == विशिष्ट उदाहरण == | ||
=== एक समान छड़ में ऊष्मा का प्रवाह === | === एक समान छड़ में ऊष्मा का प्रवाह === | ||
ऊष्मा प्रवाह के लिए, ऊष्मा समीकरण चालन(ऊष्मा) के भौतिक नियमों और ऊर्जा के संरक्षण से अनुसरण करता | ऊष्मा प्रवाह के लिए, ऊष्मा समीकरण चालन(ऊष्मा) के भौतिक नियमों और ऊर्जा के संरक्षण से अनुसरण करता है। {{harv|Cannon|1984}}. | ||
एक समदैशिक माध्यम के लिए फूरियर के नियम से, एक सतह के माध्यम से प्रति इकाई क्षेत्र में ऊष्मा ऊर्जा के प्रवाह की दर इसके सापेक्ष नकारात्मक तापमान प्रवणता के समानुपाती होती है: | |||
:<math>\mathbf{q} = - k \, \nabla u </math> | :<math>\mathbf{q} = - k \, \nabla u </math> | ||
जहाँ पर <math>k</math> पदार्थ की तापीय चालकता है, <math>u=u(\mathbf{x},t)</math> तापमान है, और <math>\mathbf{q} = \mathbf{q}(\mathbf{x},t)</math> एक [[वेक्टर (भौतिकी)]] क्षेत्र है जो अंतरिक्ष और समय t का | जहाँ पर <math>k</math> पदार्थ की तापीय चालकता है, <math>u=u(\mathbf{x},t)</math> तापमान है, और <math>\mathbf{q} = \mathbf{q}(\mathbf{x},t)</math> एक [[वेक्टर (भौतिकी)|सदिश (भौतिकी)]] क्षेत्र है जो अंतरिक्ष और समय t का बिंदु x पर ताप प्रवाह की परिमाण और दिशा का प्रतिनिधित्व करता है। | ||
यदि माध्यम समान खंड और पदार्थ की एक पतली छड़ है, तो स्थिति एकल समन्वय x है, ऊष्मा का प्रवाह | यदि माध्यम समान खंड और पदार्थ की एक पतली छड़ है, तो स्थिति एकल समन्वय x है, ऊष्मा का प्रवाह बढ़ते हुए <math>x</math> की ओर <math>q = q(t,x)</math>अदिश क्षेत्र है, और ढलान के '''''x''''' संबंध में एक सामान्य व्युत्पन्न है। समीकरण बन जाता है | ||
:<math>q = -k \,\frac{\partial u}{\partial x}</math> | :<math>q = -k \,\frac{\partial u}{\partial x}</math> | ||
माना की | माना की <math>Q=Q(x,t)</math> प्रत्येक बिंदु और समय पर बार की प्रति इकाई आयतन आंतरिक '''ऊ'''ष्मा ऊर्जा हो। बाहरी या आंतरिक स्रोतों से ऊष्मा ऊर्जा उत्पादन की अनुपस्थिति में, पदार्थ में प्रति इकाई आयतन में आंतरिक ऊष्मा ऊर्जा में परिवर्तन की दर, <math>\partial Q/\partial t</math>, इसके तापमान के परिवर्तन की दर <math>\partial u/\partial t</math> के समानुपाती होता है, वह है, | ||
:<math>\frac{\partial Q}{\partial t} = c \, \rho \, \frac{\partial u}{\partial t}</math> | :<math>\frac{\partial Q}{\partial t} = c \, \rho \, \frac{\partial u}{\partial t}</math> | ||
जहाँ पर | जहाँ पर <math>c</math> विशिष्ट ताप क्षमता है (स्थिर दबाव में, गैस के सन्दर्भ में) और <math>\rho</math> पदार्थ का घनत्व (द्रव्यमान प्रति इकाई आयतन) है। यह व्युत्पत्ति मानती है कि पदार्थ में अंतरिक्ष के साथ-साथ समय के माध्यम से निरंतर द्रव्यमान घनत्व और ताप क्षमता स्थिर होती है। | ||
केंद्रित माध्यम x पर एक छोटे से तत्व के लिए ऊर्जा के संरक्षण के नियम को लागू करने पर, कोई यह निष्कर्ष निकालता है कि किसी दिए गए बिंदु x पर जिस दर से ऊष्मा एकत्रित होती है उस बिंदु पर ऊष्मा प्रवाह के व्युत्पन्न नगण्य के बराबर है। वह इस प्रकार है, | |||
:<math>\frac{\partial Q}{\partial t} = - \frac{\partial q}{\partial x}</math> | :<math>\frac{\partial Q}{\partial t} = - \frac{\partial q}{\partial x}</math> | ||
उपरोक्त समीकरणों से यह इस प्रकार है | उपरोक्त समीकरणों से यह इस प्रकार दिया गया है | ||
:<math>\frac{\partial u}{\partial t} \;=\; - \frac{1}{c \rho} \frac{\partial q}{\partial x} | :<math>\frac{\partial u}{\partial t} \;=\; - \frac{1}{c \rho} \frac{\partial q}{\partial x} | ||
| Line 111: | Line 111: | ||
==== विकिरण हानि के लिए लेखांकन ==== | ==== विकिरण हानि के लिए लेखांकन ==== | ||
ऊष्मा के विकिरण संबंधी अभाव के लिए समीकरण में एक अतिरिक्त शब्द प्रस्तुत | ऊष्मा के विकिरण संबंधी अभाव के लिए समीकरण में एक अतिरिक्त शब्द प्रस्तुत किया जा सकता है। स्टीफन-बोल्ट्जमैन नियम के अनुसार, वह शब्द <math>\mu \left(u^4 - v^4\right)</math>है , जहाँ पर <math>v=v(x,t)</math> निकटवर्ती तापमान है, और <math>\mu</math> एक गुणांक है जो पदार्थ के भौतिक गुणों पर निर्भर करता है। आंतरिक ऊर्जा में परिवर्तन की दर रूपांतरित हो जाती है | ||
:<math>\frac{\partial Q}{\partial t} = - \frac{\partial q}{\partial x} - \mu \left(u^4 - v^4\right)</math> | :<math>\frac{\partial Q}{\partial t} = - \frac{\partial q}{\partial x} - \mu \left(u^4 - v^4\right)</math> | ||
और u के | और u के विमोचन के लिए समीकरण हो जाता है | ||
:<math>\frac{\partial u}{\partial t} = \frac{k}{c \rho} \frac{\partial^2 u}{\partial x^2} - \frac{\mu}{c \rho}\left(u^4 - v^4\right).</math> | :<math>\frac{\partial u}{\partial t} = \frac{k}{c \rho} \frac{\partial^2 u}{\partial x^2} - \frac{\mu}{c \rho}\left(u^4 - v^4\right).</math> | ||
| Line 120: | Line 120: | ||
====गैर-समान समदैशिक माध्यम==== | ====गैर-समान समदैशिक माध्यम==== | ||
ध्यान दें कि ऊष्मप्रवैगिकी के पहले नियम ( | ध्यान दें कि ऊष्मप्रवैगिकी के पहले नियम (अर्थात ऊर्जा के संरक्षण) द्वारा दिए गए दशीय समीकरण को निम्नलिखित रूप में लिखा गया है (बिना द्रव्यमान स्थानांतरण या विकिरण के)। यह रूप अधिक सरल है और यह पहचानने के लिए विशेष रूप से उपयोगी है कि कौन सी विशेषता(जैसे सी<sub>p</sub>या<math>\rho</math>) किस पद को प्रभावित करता है। | ||
:<math>\rho c_p \frac{\partial T}{\partial t} - \nabla \cdot \left( k \nabla T \right) = \dot q_V </math> | :<math>\rho c_p \frac{\partial T}{\partial t} - \nabla \cdot \left( k \nabla T \right) = \dot q_V </math> | ||
जहाँ पर <math>\dot q_V </math> | जहाँ पर <math>\dot q_V </math> आयतनमितीय ऊष्मा श्रोत है। | ||
=== त्रि-[[आयाम]] | === त्रि-[[आयाम]] समस्या === | ||
[[समदैशिक]] और सजातीय में ऊष्मा के प्रसार के विशेष | [[समदैशिक]] और सजातीय में ऊष्मा के प्रसार के विशेष सन्दर्भ में: 3-आयामी अंतरिक्ष में सजातीय माध्यम, यह समीकरण है | ||
:<math> \frac{\partial u}{\partial t} = \alpha \nabla^2 u = | :<math> \frac{\partial u}{\partial t} = \alpha \nabla^2 u = | ||
| Line 133: | Line 133: | ||
\frac{\partial^2 u}{\partial z^2 }\right) </math>: | \frac{\partial^2 u}{\partial z^2 }\right) </math>: | ||
जहाँ पर, | जहाँ पर, | ||
* <math> u = u(x, y, z, t) </math> अंतरिक्ष और समय के | * <math> u = u(x, y, z, t) </math> अंतरिक्ष और समय के फलन के रूप में तापमान है; | ||
* <math> \tfrac{\partial u}{\partial t} </math> समय के साथ एक बिंदु पर तापमान के परिवर्तन की दर है; | * <math> \tfrac{\partial u}{\partial t} </math> समय के साथ एक बिंदु पर तापमान के परिवर्तन की दर है; | ||
* <math> u_{xx} </math>, <math> u_{yy} </math>, तथा <math> u_{zz} </math> में तापमान के दूसरे स्थानिक [[यौगिक]] (तापीय चालन) | * <math> u_{xx} </math>, <math> u_{yy} </math>, तथा <math> u_{zz} </math> क्रमशः x, y, z दिशा में तापमान के दूसरे स्थानिक [[यौगिक]] (तापीय चालन) हैं। | ||
* <math>\alpha \equiv \tfrac{k}{c_p\rho}</math> तापीय प्रसार | * <math>\alpha \equiv \tfrac{k}{c_p\rho}</math> तापीय प्रसार, तापीय चालकता के आधार पर एक सामग्री-विशिष्ट मात्रा <math> k </math>, विशिष्ट ताप क्षमता <math> c_p </math>, और [[द्रव्यमान घनत्व]] <math> \rho </math> है। | ||
ऊष्मा समीकरण फूरियर के चालन के नियम का परिणाम है ([[गर्मी चालन|ऊष्माचालन]] देखें)। | ऊष्मा समीकरण फूरियर के चालन के नियम का परिणाम है ([[गर्मी चालन|ऊष्माचालन]] देखें)। | ||
यदि माध्यम संपूर्ण स्थान नहीं है, तो विशिष्ट रूप से ऊष्मा समीकरण को हल करने के लिए हमें u के लिए सीमा शर्तों को भी निर्दिष्ट करने की आवश्यकता है। पूरे अंतरिक्ष में समाधानों की विशिष्टता निर्धारित करने के लिए अतिरिक्त शर्तों को | यदि माध्यम संपूर्ण स्थान नहीं है, तो विशिष्ट रूप से ऊष्मा समीकरण को हल करने के लिए हमें u के लिए सीमा शर्तों को भी निर्दिष्ट करने की आवश्यकता है। पूरे अंतरिक्ष में समाधानों की विशिष्टता निर्धारित करने के लिए अतिरिक्त शर्तों को मानना आवश्यक है, उदाहरण के लिए समाधान के विकास पर एक घातीय बाध्यता<ref>{{citation|title=Computational Financial Mathematics using MATHEMATICA®: Optimal Trading in Stocks and Options|first=Srdjan|last=Stojanovic|publisher=Springer|year=2003|isbn=9780817641979|pages=112–114|url=https://books.google.com/books?id=ERYzXjt3iYkC&pg=PA112|contribution=3.3.1.3 Uniqueness for heat PDE with exponential growth at infinity}}</ref> या एक सांकेतिक स्थिति ([[डेविड मेष]] के परिणामस्वरूप गैर-नकारात्मक समाधान अद्वितीय हैं)।<ref>{{Cite book |last=John |first=Fritz |url=https://books.google.com/books?id=cBib_bsGGLYC&q=fritz+john+partial |title=आंशिक अंतर समीकरण|date=1991-11-20 |publisher=Springer Science & Business Media |isbn=978-0-387-90609-6 |pages=222 |language=en}}</ref> | ||
ऊष्मा समीकरण के समाधान को किसी वस्तु के गर्म से ठंडे क्षेत्रों में ऊष्मा के प्रवाह द्वारा प्रारंभिक तापमान वितरण के क्रमिक चौरसाई द्वारा चित्रित किया जाता है। सामान्यतः, कई अलग-अलग स्थिति और प्रारम्भी स्थितियां एक ही स्थिर [[थर्मोडायनामिक संतुलन]] की ओर बढ़ती हैं। परिणाम स्वरुप, समाधान को विपरीत करने के लिए और वर्तमान ताप वितरण से पहले के समय या प्रारंभिक स्थितियों के बारे में कुछ निष्कर्ष निकालने के लिए सबसे कम समय अवधि को छोड़कर बहुत अशुद्ध है। | |||
लाप्लास संचालक का उपयोग करके, | ऊष्मा समीकरण एक परवलयिक आंशिक अवकल समीकरण का प्रोटोटाइपिकल उदाहरण है। | ||
लाप्लास संचालक का उपयोग करके, ऊष्मा समीकरण को सरलीकृत किया जा सकता है, और अनियमित तरीके से आयामों की संख्या के समान समीकरणों के लिए सामान्यीकृत किया जा सकता है, जैसा कि | |||
:<math>u_t = \alpha \nabla^2 u = \alpha \Delta u, </math> | :<math>u_t = \alpha \nabla^2 u = \alpha \Delta u, </math> | ||
जहां लाप्लास ऑपरेटर, Δ या ∇<sup>2</sup>, ग्रेडिएंट का विचलन, स्थानिक चरों में लिया जाता है। | जहां लाप्लास ऑपरेटर, Δ या ∇<sup>2</sup>, ग्रेडिएंट का विचलन, स्थानिक चरों में लिया जाता है। | ||
ऊष्मा समीकरण ऊष्मा प्रसार, साथ ही साथ अन्य विसारक प्रक्रियाओं को नियंत्रित करता है, जैसे कि [[कण प्रसार]] या तंत्रिका कोशिकाओं में क्रिया क्षमता का | ऊष्मा समीकरण ऊष्मा प्रसार, साथ ही साथ अन्य विसारक प्रक्रियाओं को नियंत्रित करता है, जैसे कि [[कण प्रसार]] या तंत्रिका कोशिकाओं में क्रिया क्षमता का प्रसार है। हालांकि वे प्रकृति में विसारक नहीं हैं, कुछ क्वांटम यांत्रिकी समस्याएं भी ऊष्मा समीकरण के गणितीय अनुरूप (नीचे देखें) द्वारा नियंत्रित होती हैं। इसका उपयोग [[वित्त]] में उत्पन्न होने वाली कुछ घटनाओं को मॉडल करने के लिए भी किया जा सकता है, जैसे काला-स्कोल्स या ऑर्स्टीन-उहलेनबेक प्रक्रियाएं। छवि विश्लेषण में समीकरण और विभिन्न गैर-रेखीय एनालॉग्स का भी उपयोग किया गया है। | ||
ऊष्मा समीकरण, तकनीकी रूप से, [[विशेष सापेक्षता]] के उल्लंघन में है, क्योंकि इसके समाधान में बाधा का तात्कालिक प्रसार सम्मिलित है। अग्रिम [[प्रकाश शंकु]] के बाहर अशांति का हिस्सा सामान्यतः सुरक्षित रूप से उपेक्षित किया जा सकता है, लेकिन अगर ऊष्मा के संचरण के लिए एक उचित गति विकसित करना आवश्यक है, तो इसके अतिरिक्त एक [[अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण]] पर विचार किया जाना चाहिए - जैसे आंशिक अंतर समीकरण जिसमें एक दूसरा समय व्युत्पन्न सम्मिलित है। अरेखीय ऊष्मा चालन के कुछ मॉडल (जो परवलयिक समीकरण भी हैं) में परिमित ताप संचरण गति के साथ समाधान होते हैं।<ref>The [http://mathworld.wolfram.com/PorousMediumEquation.html Mathworld: Porous Medium Equation] and the other related models have solutions with finite wave propagation speed.</ref><ref name="pme">{{Citation | isbn=978-0-19-856903-9|title=The Porous Medium Equation: Mathematical Theory | author=Juan Luis Vazquez|publisher=Oxford University Press, USA|date=2006-12-28}}</ref> | |||
'''<big>आंतरिक ताप उत्पादन</big>''' | |||
मान लीजिए कि एक पिंड ऊष्मा समीकरण का पालन करता है और, इसके अलावा, प्रति इकाई आयतन (जैसे, वाट/लीटर - W/L में) अपनी स्वयं की ऊष्मा उत्पन्न करता है, जो एक ज्ञात | उपरोक्त फलन '''''U''''' एक शरीर के तापमान का प्रतिनिधित्व करता है। वैकल्पिक रूप से, कभी-कभी इकाइयों को बदलना और एक माध्यम के ताप घनत्व के रूप में यू का प्रतिनिधित्व करना सुविधाजनक होता है। चूंकि ऊष्माघनत्व एक सजातीय माध्यम में तापमान के समानुपाती होता है, इसलिए नई इकाइयों में अभी भी ऊष्मासमीकरण का पालन किया जाता है। | ||
मान लीजिए कि एक पिंड ऊष्मा समीकरण का पालन करता है और, इसके अलावा, प्रति इकाई आयतन (जैसे, वाट/लीटर - W/L में) अपनी स्वयं की ऊष्मा उत्पन्न करता है, जो एक ज्ञात फलन q द्वारा दी गई दर से होती है, जो अंतरिक्ष और समय में भिन्न होती है।<ref>Note that the units of ''u'' must be selected in a manner compatible with those of ''q''. Thus instead of being for thermodynamic temperature ([[Kelvin]] - K), units of ''u'' should be J/L.</ref> तब ऊष्माप्रति इकाई आयतन u एक समीकरण को संतुष्ट करता है, | |||
: <math>\frac{1}{\alpha} \frac{\partial u}{\partial t} = \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right) + \frac{1}{k}q.</math> | : <math>\frac{1}{\alpha} \frac{\partial u}{\partial t} = \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right) + \frac{1}{k}q.</math> | ||
| Line 180: | Line 182: | ||
{{NumBlk|:|<math>u(0,t) = 0 = u(L,t) \quad \forall t > 0 </math>.|{{EqRef|3}}}} | {{NumBlk|:|<math>u(0,t) = 0 = u(L,t) \quad \forall t > 0 </math>.|{{EqRef|3}}}} | ||
आइए इसका समाधान खोजने का प्रयास करते हैं {{EqNote|1}} यह समान रूप से शून्य नहीं है जो सीमा शर्तों को संतुष्ट करता है {{EqNote|3}} लेकिन निम्नलिखित संपत्ति के साथ: यू एक उत्पाद है जिसमें एक्स, टी पर यू की निर्भरता अलग हो जाती है, | आइए इसका समाधान खोजने का प्रयास करते हैं {{EqNote|1}} यह समान रूप से शून्य नहीं है जो सीमा शर्तों को संतुष्ट करता है {{EqNote|3}} लेकिन निम्नलिखित संपत्ति के साथ: यू एक उत्पाद है जिसमें एक्स, टी पर यू की निर्भरता अलग हो जाती है, अर्थात: | ||
{{NumBlk|:|<math> u(x,t) = X(x) T(t).</math>|{{EqRef|4}}}} | {{NumBlk|:|<math> u(x,t) = X(x) T(t).</math>|{{EqRef|4}}}} | ||
| Line 197: | Line 199: | ||
अब हम इसके लिए गैर-तुच्छ समाधान दिखाएंगे {{EqNote|6}} λ ≤ 0 के मानों के लिए नहीं हो सकता: | अब हम इसके लिए गैर-तुच्छ समाधान दिखाएंगे {{EqNote|6}} λ ≤ 0 के मानों के लिए नहीं हो सकता: | ||
# मान लीजिए कि λ < 0. तो वास्तविक संख्याएं बी, सी | # मान लीजिए कि λ < 0. तो वास्तविक संख्याएं बी, सी उपस्थित हैं जैसे कि <math display="block">X(x) = B e^{\sqrt{-\lambda} \, x} + C e^{-\sqrt{-\lambda} \, x}.</math> से {{EqNote|3}} हमें X(0) = 0 = X(L) मिलता है और इसलिए B = 0 = C जिसका अर्थ है कि आप समान रूप से 0 हैं। | ||
# मान लीजिए कि λ = 0. तब वास्तविक संख्याएँ B, C | # मान लीजिए कि λ = 0. तब वास्तविक संख्याएँ B, C उपस्थित हैं जैसे कि X(x) = Bx + C. समीकरण से {{EqNote|3}} हम उसी तरह से निष्कर्ष निकालते हैं जैसे 1 में कि यू समान रूप से 0 है। | ||
# इसलिए, यह मामला होना चाहिए कि λ > 0. फिर वास्तविक संख्याएं ए, बी, सी | # इसलिए, यह मामला होना चाहिए कि λ > 0. फिर वास्तविक संख्याएं ए, बी, सी उपस्थित हैं जैसे कि <math display="block">T(t) = A e^{-\lambda \alpha t}</math> तथा <math display="block">X(x) = B \sin\left(\sqrt{\lambda} \, x\right) + C \cos\left(\sqrt{\lambda} \, x\right).</math> से {{EqNote|3}} हमें C = 0 मिलता है और वह भी किसी धनात्मक पूर्णांक n के लिए, <math display="block">\sqrt{\lambda} = n \frac{\pi}{L}.</math> | ||
यह | यह ऊष्मासमीकरण को विशेष सन्दर्भ में हल करता है कि यू की निर्भरता का विशेष रूप है {{EqNote|4}}. | ||
सामान्यतः, समाधान का योग {{EqNote|1}} जो सीमा शर्तों को पूरा करते हैं {{EqNote|3}} संतुष्ट भी करता है {{EqNote|1}} तथा {{EqNote|3}}. हम दिखा सकते हैं कि इसका समाधान {{EqNote|1}}, {{EqNote|2}} तथा {{EqNote|3}} द्वारा दिया गया है | |||
:<math>u(x,t) = \sum_{n = 1}^{\infty} D_n \sin \left(\frac{n\pi x}{L}\right) e^{-\frac{n^2 \pi^2 \alpha t}{L^2}}</math> | :<math>u(x,t) = \sum_{n = 1}^{\infty} D_n \sin \left(\frac{n\pi x}{L}\right) e^{-\frac{n^2 \pi^2 \alpha t}{L^2}}</math> | ||
जहाँ पे | |||
:<math>D_n = \frac{2}{L} \int_0^L f(x) \sin \left(\frac{n\pi x}{L}\right ) \, dx.</math> | :<math>D_n = \frac{2}{L} \int_0^L f(x) \sin \left(\frac{n\pi x}{L}\right ) \, dx.</math> | ||
| Line 211: | Line 213: | ||
=== समाधान तकनीक का सामान्यीकरण === | === समाधान तकनीक का सामान्यीकरण === | ||
ऊपर उपयोग की गई समाधान तकनीक को कई अन्य प्रकार के समीकरणों तक विस्तृत किया जा सकता है। विचार यह है कि संचालक यू<sub>xx</sub>शून्य सीमा शर्तों के साथ इसके [[eigenfunction]]s के संदर्भ में प्रतिनिधित्व किया जा सकता है। यह स्वाभाविक रूप से रैखिक [[स्व-आसन्न ऑपरेटर]] | ऊपर उपयोग की गई समाधान तकनीक को कई अन्य प्रकार के समीकरणों तक विस्तृत किया जा सकता है। विचार यह है कि संचालक यू<sub>xx</sub>शून्य सीमा शर्तों के साथ इसके [[eigenfunction]]s के संदर्भ में प्रतिनिधित्व किया जा सकता है। यह स्वाभाविक रूप से रैखिक [[स्व-आसन्न ऑपरेटर]] के [[वर्णक्रमीय सिद्धांत]] के मूल विचारों में से एक की ओर जाता है। | ||
रैखिक संकारक Δu = u पर विचार करें<sub>xx</sub>. कार्यों का अनंत क्रम | रैखिक संकारक Δu = u पर विचार करें<sub>xx</sub>. कार्यों का अनंत क्रम | ||
| Line 226: | Line 228: | ||
== गैर-सजातीय अनिसोट्रोपिक मीडिया में ऊष्मा चालन == | == गैर-सजातीय अनिसोट्रोपिक मीडिया में ऊष्मा चालन == | ||
सामान्यतः, ऊष्मा चालन का अध्ययन कई सिद्धांतों पर आधारित होता है। ऊष्मा प्रवाह [[ऊर्जा]] प्रवाह का एक रूप है, और इस तरह अंतरिक्ष के एक क्षेत्र में ऊष्माके प्रवाह की समय दर की बात करना सार्थक है। | |||
* एक क्षेत्र वी में ऊष्माप्रवाह की समय दर समय-निर्भर मात्रा | * एक क्षेत्र वी में ऊष्माप्रवाह की समय दर समय-निर्भर मात्रा q द्वारा दी जाती है<sub>''t''</sub>(वी)। हम मानते हैं कि q में [[रैडॉन-निकोडिम डेरिवेटिव]] q है, ताकि <math display="block"> q_t(V) = \int_V Q(x,t)\,d x \quad </math> | ||
* | * ऊष्मा फ्लो एक टाइम-डिपेंडेंट वेक्टर फलन H(''x'') है जिसकी विशेषता निम्नानुसार है: एरिया ''dS'' और यूनिट नॉर्मल वेक्टर n के साथ एक इनफिनिटिमल सरफेस एलिमेंट के माध्यम से बहने वाली ऊष्मा की समय दर है <math display="block"> \mathbf{H}(x) \cdot \mathbf{n}(x) \, dS .</math> इस प्रकार वी में ऊष्माके प्रवाह की दर भी सतह अभिन्न द्वारा दी गई है <math display="block"> q_t(V)= - \int_{\partial V} \mathbf{H}(x) \cdot \mathbf{n}(x) \, dS </math> जहाँ n(''x'') ''x'' पर बाहर की ओर इंगित करने वाला सामान्य वेक्टर है। | ||
* [[ऊष्मा चालन का नियम]] कहता है कि ऊष्मा ऊर्जा प्रवाह का तापमान प्रवणता पर निम्नलिखित रैखिक निर्भरता है <math display="block"> \mathbf{H}(x) = -\mathbf{A}(x) \cdot \nabla u (x) </math> जहां A(''x'') एक 3 × 3 वास्तविक [[मैट्रिक्स (गणित)]] है जो [[सममित]] और [[सकारात्मक-निश्चित मैट्रिक्स]] है। | * [[ऊष्मा चालन का नियम]] कहता है कि ऊष्मा ऊर्जा प्रवाह का तापमान प्रवणता पर निम्नलिखित रैखिक निर्भरता है <math display="block"> \mathbf{H}(x) = -\mathbf{A}(x) \cdot \nabla u (x) </math> जहां A(''x'') एक 3 × 3 वास्तविक [[मैट्रिक्स (गणित)]] है जो [[सममित]] और [[सकारात्मक-निश्चित मैट्रिक्स]] है। | ||
* [[विचलन प्रमेय]] द्वारा, 'वी' में ऊष्माप्रवाह के लिए पिछली सतह अभिन्न मात्रा अभिन्न में परिवर्तित हो सकती है <math display="block">\begin{align} | * [[विचलन प्रमेय]] द्वारा, 'वी' में ऊष्माप्रवाह के लिए पिछली सतह अभिन्न मात्रा अभिन्न में परिवर्तित हो सकती है <math display="block">\begin{align} | ||
| Line 243: | Line 245: | ||
* गुणांक ''κ''(''x'') ''x'' पर पदार्थ की [[विशिष्ट ऊष्मा]] का व्युत्क्रम ''x'' पर पदार्थ का घनत्व है: <math>\kappa = 1/(\rho c_p)</math>. | * गुणांक ''κ''(''x'') ''x'' पर पदार्थ की [[विशिष्ट ऊष्मा]] का व्युत्क्रम ''x'' पर पदार्थ का घनत्व है: <math>\kappa = 1/(\rho c_p)</math>. | ||
* एक समदैशिक माध्यम के | * एक समदैशिक माध्यम के सन्दर्भ में, मैट्रिक्स a तापीय चालकता 'के' के बराबर एक स्केलर मैट्रिक्स है। | ||
* अनिसोट्रोपिक | * अनिसोट्रोपिक सन्दर्भ में जहां गुणांक मैट्रिक्स ए स्केलर नहीं है और/या यदि यह 'x'' पर निर्भर करता है, तो ऊष्मासमीकरण के समाधान के लिए एक स्पष्ट सूत्र अनुमानतः ही कभी लिखा जा सकता है, हालांकि सामान्यतः विचार करना संभव है संबंधित अमूर्त [[कॉची समस्या]] और यह दिखाएं कि यह एक अच्छी तरह से प्रस्तुत समस्या है और/या कुछ गुणात्मक गुणों को दिखाने के लिए (जैसे सकारात्मक प्रारंभिक डेटा का संरक्षण, प्रसार की अनंत गति, एक संतुलन की ओर अभिसरण, गुणों को चिकना करना)। यह सामान्यतः [[एक-पैरामीटर सेमीग्रुप]] सिद्धांत द्वारा किया जाता है: उदाहरण के लिए, यदि 'a' एक सममित मैट्रिक्स है, तो वक्राकार संचालक द्वारा परिभाषित <math display="block">Au(x):=\sum_{i, j} \partial_{x_i} a_{i j}(x) \partial_{x_j} u (x)</math> स्व-संलग्न और अपव्यय है, इस प्रकार [[वर्णक्रमीय प्रमेय]] द्वारा यह एक-पैरामीटर सेमीग्रुप उत्पन्न करता है।'' | ||
== [[मौलिक समाधान]] == | == [[मौलिक समाधान]] == | ||
| Line 255: | Line 257: | ||
u(x,0)=\delta(x)& | u(x,0)=\delta(x)& | ||
\end{cases}</math> | \end{cases}</math> | ||
जहाँ पे<math>\delta</math>[[डिराक डेल्टा समारोह|डिराक डेल्टा]] फलनहै। इस समस्या का समाधान मौलिक समाधान (ऊष्मा कर्नेल) है | |||
:<math>\Phi(x,t)=\frac{1}{\sqrt{4\pi kt}}\exp\left(-\frac{x^2}{4kt}\right).</math> | :<math>\Phi(x,t)=\frac{1}{\sqrt{4\pi kt}}\exp\left(-\frac{x^2}{4kt}\right).</math> | ||
| Line 270: | Line 272: | ||
:<math>\Phi(\mathbf{x},t) = \Phi(x_1,t) \Phi(x_2,t) \cdots \Phi(x_n,t) = \frac{1}{\sqrt{(4\pi k t)^n}} \exp \left (-\frac{\mathbf{x}\cdot\mathbf{x}}{4kt} \right).</math> | :<math>\Phi(\mathbf{x},t) = \Phi(x_1,t) \Phi(x_2,t) \cdots \Phi(x_n,t) = \frac{1}{\sqrt{(4\pi k t)^n}} \exp \left (-\frac{\mathbf{x}\cdot\mathbf{x}}{4kt} \right).</math> | ||
R पर ऊष्मा समीकरण का सामान्य हल<sup>n </sup> तब कनवल्शन द्वारा प्राप्त किया जाता है, ताकि u('x', 0) = g('x') के साथ प्रारंभिक मूल्य समस्या को हल करने के लिए, एक के पास | R पर ऊष्मा समीकरण का सामान्य हल<sup>n</sup> तब कनवल्शन द्वारा प्राप्त किया जाता है, ताकि u('x', 0) = g('x') के साथ प्रारंभिक मूल्य समस्या को हल करने के लिए, एक के पास | ||
:<math>u(\mathbf{x},t) = \int_{\R^n}\Phi(\mathbf{x}-\mathbf{y},t)g(\mathbf{y})d\mathbf{y}.</math> | :<math>u(\mathbf{x},t) = \int_{\R^n}\Phi(\mathbf{x}-\mathbf{y},t)g(\mathbf{y})d\mathbf{y}.</math> | ||
| Line 279: | Line 281: | ||
u(\mathbf{x},0)=g(\mathbf{x})&\mathbf{x}\in\Omega | u(\mathbf{x},0)=g(\mathbf{x})&\mathbf{x}\in\Omega | ||
\end{cases}</math> | \end{cases}</math> | ||
[[डिरिचलेट समस्या]] या [[न्यूमैन समस्या]] सीमा डेटा के साथ। एक ग्रीन का कार्य | [[डिरिचलेट समस्या]] या [[न्यूमैन समस्या]] सीमा डेटा के साथ। एक ग्रीन का कार्य सदैव उपलब्ध होता है, लेकिन जब तक डोमेन Ω को एक-चर समस्याओं (नीचे देखें) में आसानी से विघटित नहीं किया जा सकता है, तब तक इसे स्पष्ट रूप से लिखना संभव नहीं हो सकता है। ग्रीन के कार्यों को प्राप्त करने के अन्य तरीकों में [[छवियों की विधि]], चरों का पृथक्करण और [[लाप्लास रूपांतरण]] (कोल, 2011) सम्मिलित हैं। {{see also|वेइरस्ट्रास रूपांतरण}} | ||
| Line 309: | Line 311: | ||
:<math>\Phi(x,t)=\frac{1}{\sqrt{t}}\,\Phi\left(\frac{x}{\sqrt{t}},1\right)</math> | :<math>\Phi(x,t)=\frac{1}{\sqrt{t}}\,\Phi\left(\frac{x}{\sqrt{t}},1\right)</math> | ||
:<math>\int_{-\infty}^{\infty}\Phi(x,t)\,dx=1,</math> | :<math>\int_{-\infty}^{\infty}\Phi(x,t)\,dx=1,</math> | ||
ताकि, [[शमन करनेवाला]] के बारे में सामान्य तथ्यों से, Φ(⋅, t) ∗ g → g as t → 0 विभिन्न अर्थों में, विशिष्ट g के | ताकि, [[शमन करनेवाला|कार्यफलन]] के बारे में सामान्य तथ्यों से, Φ(⋅, t) ∗ g → g as t → 0 विभिन्न अर्थों में, विशिष्ट g के अनुसार उदाहरण के लिए, यदि g को 'R' पर परिबद्ध और सतत मान लिया जाए तो {{nowrap|Φ(⋅, ''t'') ∗ ''g''}} t → 0 के रूप में समान रूप से g में परिवर्तित हो जाता है, जिसका अर्थ है कि u(x, t) निरंतर चालू है {{nowrap|'''R''' × [0, ∞)}} साथ {{nowrap|1=''u''(''x'', 0) = ''g''(''x'').}} | ||
;प्रारंभिक मूल्य समस्या (0,∞) सजातीय डिरिचलेट सीमा शर्तों के साथ | ;प्रारंभिक मूल्य समस्या (0,∞) सजातीय डिरिचलेट सीमा शर्तों के साथ | ||
| Line 318: | Line 320: | ||
\end{cases} </math> | \end{cases} </math> | ||
:<math>u(x,t)=\frac{1}{\sqrt{4\pi kt}} \int_{0}^{\infty} \left[\exp\left(-\frac{(x-y)^2}{4kt}\right)-\exp\left(-\frac{(x+y)^2}{4kt}\right)\right] g(y)\,dy </math> | :<math>u(x,t)=\frac{1}{\sqrt{4\pi kt}} \int_{0}^{\infty} \left[\exp\left(-\frac{(x-y)^2}{4kt}\right)-\exp\left(-\frac{(x+y)^2}{4kt}\right)\right] g(y)\,dy </math> | ||
टिप्पणी। यह समाधान पूर्ववर्ती सूत्र से प्राप्त किया गया है जैसा कि डेटा g(x) पर लागू किया गया है, जिसे उपयुक्त रूप से 'R' तक बढ़ाया गया है, ताकि यह एक विषम फलन बन सके, | टिप्पणी। यह समाधान पूर्ववर्ती सूत्र से प्राप्त किया गया है जैसा कि डेटा g(x) पर लागू किया गया है, जिसे उपयुक्त रूप से 'R' तक बढ़ाया गया है, ताकि यह एक विषम फलन बन सके, अर्थात g(−x) := −g(x) सभी के लिए एक्स। इसके अनुरूप, (−∞,∞) पर आरंभिक मूल्य समस्या का समाधान, टी के सभी मानों के लिए चर x के संबंध में एक विषम कार्य है, और विशेष रूप से यह सजातीय डिरिचलेट सीमा शर्तों u(0, t) = 0 को संतुष्ट करता है . | ||
इस समाधान की ग्रीन की कार्य संख्या X10 है। | इस समाधान की ग्रीन की कार्य संख्या X10 है। | ||
| Line 329: | Line 331: | ||
\end{cases} </math> | \end{cases} </math> | ||
:<math>u(x,t)=\frac{1}{\sqrt{4\pi kt}} \int_{0}^{\infty} \left[\exp\left(-\frac{(x-y)^2}{4kt}\right)+\exp\left(-\frac{(x+y)^2}{4kt}\right)\right]g(y)\,dy </math> | :<math>u(x,t)=\frac{1}{\sqrt{4\pi kt}} \int_{0}^{\infty} \left[\exp\left(-\frac{(x-y)^2}{4kt}\right)+\exp\left(-\frac{(x+y)^2}{4kt}\right)\right]g(y)\,dy </math> | ||
टिप्पणी, यह पहले समाधान सूत्र से प्राप्त किया गया है जैसा कि डेटा g(x) पर लागू किया गया है, जिसे उपयुक्त रूप से 'R' तक विस्तारित किया गया है, ताकि यह एक सम फलन बन सके, अर्थात, सभी x के लिए g(−x):= g(x) . इसके अनुरूप, 'R' पर प्रारंभिक मूल्य समस्या का समाधान t > 0 के सभी मानों के लिए चर x के संबंध में एक सम फलन है, और विशेष रूप से, सहज होने के कारण, यह सजातीय न्यूमैन सीमा स्थितियों u को संतुष्ट करता है<sub>x</sub>(0, t) = 0. इस समाधान की ग्रीन की फलन संख्या X20 है। | |||
;समस्या (0,∞) सजातीय प्रारंभिक स्थितियों और गैर-सजातीय डिरिचलेट सीमा स्थितियों के साथ | ;समस्या (0,∞) सजातीय प्रारंभिक स्थितियों और गैर-सजातीय डिरिचलेट सीमा स्थितियों के साथ | ||
| Line 339: | Line 341: | ||
\end{cases} </math> | \end{cases} </math> | ||
:<math>u(x,t)=\int_{0}^{t} \frac{x}{\sqrt{4\pi k(t-s)^3}} \exp\left(-\frac{x^2}{4k(t-s)}\right)h(s)\,ds, \qquad\forall x>0</math> | :<math>u(x,t)=\int_{0}^{t} \frac{x}{\sqrt{4\pi k(t-s)^3}} \exp\left(-\frac{x^2}{4k(t-s)}\right)h(s)\,ds, \qquad\forall x>0</math> | ||
टिप्पणी, यह हल चर t के संबंध में कनवल्शन है | |||
:<math>\psi(x,t):=-2k \partial_x \Phi(x,t) = \frac{x}{\sqrt{4\pi kt^3}} \exp\left(-\frac{x^2}{4kt}\right)</math> | :<math>\psi(x,t):=-2k \partial_x \Phi(x,t) = \frac{x}{\sqrt{4\pi kt^3}} \exp\left(-\frac{x^2}{4kt}\right)</math> | ||
और | और फलन h (t), चूँकि Φ(x, t) का मूल हल है | ||
:<math>\partial_t-k\partial^2_x,</math> | :<math>\partial_t-k\partial^2_x,</math> | ||
फलन ψ(x, t) भी उसी ऊष्मा समीकरण का एक हल है, और ऐसा ही u भी है := ψ ∗ h, अवकलन के संबंध में कनवल्शन के सामान्य गुणों के | फलन ψ(x, t) भी उसी ऊष्मा समीकरण का एक हल है, और ऐसा ही u भी है:= ψ ∗ h, अवकलन के संबंध में कनवल्शन के सामान्य गुणों के कारण इसके अतिरिक्त, | ||
:<math>\psi(x,t)=\frac{1}{x^2}\,\psi\left(1,\frac{t}{x^2}\right)</math> | :<math>\psi(x,t)=\frac{1}{x^2}\,\psi\left(1,\frac{t}{x^2}\right)</math> | ||
:<math>\int_0^{\infty}\psi(x,t)\,dt=1,</math> | :<math>\int_0^{\infty}\psi(x,t)\,dt=1,</math> | ||
ताकि, मोलिफायर के बारे में सामान्य तथ्यों से, ψ(x, ⋅) ∗ h → h as x → 0 विभिन्न अर्थों में, विशिष्ट h के | ताकि, मोलिफायर के बारे में सामान्य तथ्यों से, ψ(x, ⋅) ∗ h → h as x → 0 विभिन्न अर्थों में, विशिष्ट h के अनुसार उदाहरण के लिए, यदि h को [0, ∞) में समर्थन के साथ 'R' पर निरंतर माना जाता है, तो ψ(x, ⋅) ∗ h कॉम्पेक्टा पर समान रूप से x → 0 के रूप में परिवर्तित होता है, जिसका अर्थ है कि u(x, t) निरंतर है पर {{nowrap|[0, ∞) × [0, ∞)}} साथ {{nowrap|1=''u''(0, ''t'') = ''h''(''t'').}} | ||
[[File:2D Nonhomogeneous heat equation .gif|thumb|चित्रित गैर-सजातीय ऊष्मासमीकरण का एक संख्यात्मक समाधान है। समीकरण को 0 प्रारंभिक और सीमा शर्तों और एक स्टोव टॉप बर्नर का प्रतिनिधित्व करने वाले स्रोत शब्द के साथ हल किया गया है।]] | [[File:2D Nonhomogeneous heat equation .gif|thumb|चित्रित गैर-सजातीय ऊष्मासमीकरण का एक संख्यात्मक समाधान है। समीकरण को 0 प्रारंभिक और सीमा शर्तों और एक स्टोव टॉप बर्नर का प्रतिनिधित्व करने वाले स्रोत शब्द के साथ हल किया गया है।]] | ||
| Line 358: | Line 360: | ||
: | : | ||
टिप्पणी, यह हल 'R' में कनवल्शन है<sup>2</sup>, जो मूल समाधान के चर x और t दोनों के संबंध में है | |||
:<math>\Phi(x,t) := \frac{1}{\sqrt{4\pi kt}} \exp\left(-\frac{x^2}{4 kt}\right)</math> | :<math>\Phi(x,t) := \frac{1}{\sqrt{4\pi kt}} \exp\left(-\frac{x^2}{4 kt}\right)</math> | ||
और फलन f(x, t), दोनों का मतलब संपूर्ण 'R' पर परिभाषित है<sup>2</sup> और समान रूप से 0 सभी t → 0 के | और फलन f(x, t), दोनों का मतलब संपूर्ण 'R' पर परिभाषित है<sup>2</sup> और समान रूप से 0 सभी t → 0 के लिए एक इसे सत्यापित करता है | ||
:<math>\left (\partial_t-k \partial_x^2 \right )(\Phi*f)=f,</math> | :<math>\left (\partial_t-k \partial_x^2 \right )(\Phi*f)=f,</math> | ||
| Line 378: | Line 380: | ||
:<math>u(x,t)=\int_{0}^{t}\int_{0}^{\infty} \frac{1}{\sqrt{4\pi k(t-s)}} \left(\exp\left(-\frac{(x-y)^2}{4k(t-s)}\right)-\exp\left(-\frac{(x+y)^2}{4k(t-s)}\right)\right) | :<math>u(x,t)=\int_{0}^{t}\int_{0}^{\infty} \frac{1}{\sqrt{4\pi k(t-s)}} \left(\exp\left(-\frac{(x-y)^2}{4k(t-s)}\right)-\exp\left(-\frac{(x+y)^2}{4k(t-s)}\right)\right) | ||
f(y,s)\,dy\,ds </math> | f(y,s)\,dy\,ds </math> | ||
टिप्पणी। यह समाधान पूर्ववर्ती सूत्र से प्राप्त किया गया है जैसा कि डेटा f(x, t) पर लागू किया गया है, जिसे उपयुक्त रूप से 'R' × [0,∞) तक बढ़ाया गया है, ताकि वेरिएबल x का एक विषम कार्य हो सके, | टिप्पणी। यह समाधान पूर्ववर्ती सूत्र से प्राप्त किया गया है जैसा कि डेटा f(x, t) पर लागू किया गया है, जिसे उपयुक्त रूप से 'R' × [0,∞) तक बढ़ाया गया है, ताकि वेरिएबल x का एक विषम कार्य हो सके, अर्थात f( −x, t):= −f(x, t) सभी x और t के लिए इसके अनुरूप, (−∞,∞) पर विषम समस्या का समाधान टी के सभी मूल्यों के लिए चर x के संबंध में एक विषम कार्य है, और विशेष रूप से यह सजातीय डिरिचलेट सीमा शर्तों u(0, t) = 0 को संतुष्ट करता है। | ||
समसामयिक न्यूमैन सीमा स्थितियों और प्रारंभिक स्थितियों के साथ (0,∞) पर समस्या | समसामयिक न्यूमैन सीमा स्थितियों और प्रारंभिक स्थितियों के साथ (0,∞) पर समस्या | ||
| Line 389: | Line 391: | ||
:<math>u(x,t)=\int_{0}^{t}\int_{0}^{\infty} \frac{1}{\sqrt{4\pi k(t-s)}} \left(\exp\left(-\frac{(x-y)^2}{4k(t-s)}\right)+\exp\left(-\frac{(x+y)^2}{4k(t-s)}\right)\right) | :<math>u(x,t)=\int_{0}^{t}\int_{0}^{\infty} \frac{1}{\sqrt{4\pi k(t-s)}} \left(\exp\left(-\frac{(x-y)^2}{4k(t-s)}\right)+\exp\left(-\frac{(x+y)^2}{4k(t-s)}\right)\right) | ||
f(y,s)\,dy\,ds </math> | f(y,s)\,dy\,ds </math> | ||
टिप्पणी। यह समाधान पहले सूत्र से प्राप्त किया जाता है जैसा कि डेटा f(x, t) पर लागू होता है जिसे उपयुक्त रूप से 'R' × [0,∞) तक बढ़ाया जाता है, ताकि वेरिएबल x का एक समान कार्य हो सके, | टिप्पणी। यह समाधान पहले सूत्र से प्राप्त किया जाता है जैसा कि डेटा f(x, t) पर लागू होता है जिसे उपयुक्त रूप से 'R' × [0,∞) तक बढ़ाया जाता है, ताकि वेरिएबल x का एक समान कार्य हो सके, अर्थात f( −x, t) := f(x, t) सभी x और t के लिए इसके अनुरूप, (−∞,∞) पर विषम समस्या का समाधान, t के सभी मूल्यों के लिए चर x के संबंध में एक समान कार्य है, और विशेष रूप से, एक सहज कार्य होने के नाते, यह सजातीय न्यूमैन सीमा शर्तों U को संतुष्ट करता है<sub>x</sub>(0, t) = 0। | ||
==== उदाहरण ==== | ==== उदाहरण ==== | ||
चूंकि ऊष्मासमीकरण रैखिक है, उपरोक्त ग्रीन के | चूंकि ऊष्मासमीकरण रैखिक है, उपरोक्त ग्रीन के फलन समाधानों के उचित [[रैखिक संयोजन]] को ले कर सीमा शर्तों के अन्य संयोजनों, अमानवीय अवधि और प्रारंभिक स्थितियों के समाधान प्राप्त किए जा सकते हैं। | ||
उदाहरण के लिए, हल करना | उदाहरण के लिए, हल करना | ||
| Line 413: | Line 415: | ||
u(0,t)=h(t) & \text{BC} | u(0,t)=h(t) & \text{BC} | ||
\end{cases} </math> | \end{cases} </math> | ||
U = w + v + r जहां w, v, और r समस्याओं को हल करते हैं | |||
:<math>\begin{cases} | :<math>\begin{cases} | ||
| Line 427: | Line 429: | ||
[[हार्मोनिक फ़ंक्शन|हार्मोनिक]] फलनके माध्य-मूल्य गुणों के अनुरूप माध्य-मूल्य संपत्ति को संतुष्ट करें, के समाधान | [[हार्मोनिक फ़ंक्शन|हार्मोनिक]] फलनके माध्य-मूल्य गुणों के अनुरूप माध्य-मूल्य संपत्ति को संतुष्ट करें, के समाधान | ||
:<math>\Delta u = 0,</math> | :<math>\Delta u = 0,</math> | ||
हालांकि | हालांकि कुछ और जटिल है, अगर आप हल करते हैं | ||
:<math>(\partial_t -\Delta)u=0</math> | :<math>(\partial_t -\Delta)u=0</math> | ||
तथा | तथा | ||
| Line 441: | Line 443: | ||
== स्थिर-अवस्था ऊष्मा समीकरण == | == स्थिर-अवस्था ऊष्मा समीकरण == | ||
स्थिर-अवस्था ऊष्मा समीकरण परिभाषा के अनुसार समय पर निर्भर नहीं है। दूसरे शब्दों में, यह माना जाता है कि ऐसी स्थितियाँ | स्थिर-अवस्था ऊष्मा समीकरण परिभाषा के अनुसार समय पर निर्भर नहीं है। दूसरे शब्दों में, यह माना जाता है कि ऐसी स्थितियाँ उपस्थित हैं: | ||
:<math>\frac{\partial u}{\partial t} = 0</math> | :<math>\frac{\partial u}{\partial t} = 0</math> | ||
यह स्थिति समय स्थिरांक और सीमा शर्तों को लागू किए जाने के बाद से बीत चुके समय पर निर्भर करती है। इस प्रकार, स्थिति उन स्थितियों में पूरी होती है जिनमें समय संतुलन स्थिरांक काफी तेज होता है कि अधिक जटिल समय-निर्भर ऊष्मासमीकरण को स्थिर-अवस्था के | यह स्थिति समय स्थिरांक और सीमा शर्तों को लागू किए जाने के बाद से बीत चुके समय पर निर्भर करती है। इस प्रकार, स्थिति उन स्थितियों में पूरी होती है जिनमें समय संतुलन स्थिरांक काफी तेज होता है कि अधिक जटिल समय-निर्भर ऊष्मासमीकरण को स्थिर-अवस्था के सन्दर्भ में अनुमानित किया जा सकता है। समतुल्य रूप से, सभी सन्दर्भ के लिए स्थिर-स्थिति की स्थिति उपस्थित है जिसमें पर्याप्त समय बीत चुका है कि ऊष्मीय क्षेत्र 'U' अब समय पर विकसित नहीं होता है। | ||
स्थिर-स्थिति के | स्थिर-स्थिति के सन्दर्भ में, एक स्थानिक तापीय प्रवणता उपस्थित हो सकती है (या नहीं भी हो सकती है), लेकिन यदि ऐसा होता है, तो यह समय के साथ नहीं बदलता है। इसलिए यह समीकरण उन सभी तापीय समस्याओं के अंतिम परिणाम का वर्णन करता है जिसमें एक स्रोत को चालू किया जाता है (उदाहरण के लिए, एक ऑटोमोबाइल में एक इंजन चालू होता है), और सभी स्थायी तापमान प्रवणता के लिए अंतरिक्ष में स्वयं को स्थापित करने के लिए पर्याप्त समय बीत चुका होता है, जिसके बाद ये स्थानिक ढाल अब समय में नहीं बदलते (फिर से, एक ऑटोमोबाइल के साथ जिसमें इंजन काफी लंबे समय से चल रहा है)। अन्य (तुच्छ) समाधान सभी स्थानिक तापमान प्रवणताओं के साथ-साथ गायब होने के लिए है, जिस स्थिति में तापमान अंतरिक्ष में भी समान हो जाता है। | ||
समीकरण बहुत सरल है और ऊष्मापरिवहन प्रक्रिया की गतिशीलता पर ध्यान केंद्रित किए बिना सामग्रियों के भौतिकी को बेहतर ढंग से समझने में मदद कर सकता है। यह व्यापक रूप से सरल इंजीनियरिंग समस्याओं के लिए उपयोग किया जाता है, यह मानते हुए कि समय के साथ तापमान क्षेत्र और ताप परिवहन का संतुलन है। | समीकरण बहुत सरल है और ऊष्मापरिवहन प्रक्रिया की गतिशीलता पर ध्यान केंद्रित किए बिना सामग्रियों के भौतिकी को बेहतर ढंग से समझने में मदद कर सकता है। यह व्यापक रूप से सरल इंजीनियरिंग समस्याओं के लिए उपयोग किया जाता है, यह मानते हुए कि समय के साथ तापमान क्षेत्र और ताप परिवहन का संतुलन है। | ||
| Line 458: | Line 460: | ||
जहाँ u [[थर्मोडायनामिक तापमान]] है, k तापीय चालकता है और q प्रति इकाई आयतन में ऊष्मा उत्पादन की दर है। | जहाँ u [[थर्मोडायनामिक तापमान]] है, k तापीय चालकता है और q प्रति इकाई आयतन में ऊष्मा उत्पादन की दर है। | ||
[[इलेक्ट्रोस्टाटिक्स]] में, यह उस | [[इलेक्ट्रोस्टाटिक्स]] में, यह उस सन्दर्भ के बराबर है जहां विचाराधीन स्थान में विद्युत आवेश होता है। | ||
वॉल्यूम के भीतर ऊष्मास्रोत के बिना स्थिर-अवस्था ऊष्मासमीकरण (सजातीय मामला) इलेक्ट्रोस्टैटिक्स में मुक्त स्थान की मात्रा के लिए समीकरण है जिसमें चार्ज नहीं होता है। यह लाप्लास के समीकरण द्वारा वर्णित है: | वॉल्यूम के भीतर ऊष्मास्रोत के बिना स्थिर-अवस्था ऊष्मासमीकरण (सजातीय मामला) इलेक्ट्रोस्टैटिक्स में मुक्त स्थान की मात्रा के लिए समीकरण है जिसमें चार्ज नहीं होता है। यह लाप्लास के समीकरण द्वारा वर्णित है: | ||
| Line 468: | Line 470: | ||
=== कण प्रसार === | === कण प्रसार === | ||
{{main| | {{main|प्रसार समीकरण}} | ||
कोई भी एक समीकरण द्वारा कण [[प्रसार]] को मॉडल कर सकता है: | कोई भी एक समीकरण द्वारा कण [[प्रसार]] को मॉडल कर सकता है: | ||
* बड़ी संख्या में कणों के [[सामूहिक प्रसार]] के | * बड़ी संख्या में कणों के [[सामूहिक प्रसार]] के सन्दर्भ में कणों की वॉल्यूमेट्रिक सांद्रता, निरूपित C, या | ||
* एक कण की स्थिति से जुड़ा प्रायिकता घनत्व फलन, जिसे P निरूपित किया गया है। | * एक कण की स्थिति से जुड़ा प्रायिकता घनत्व फलन, जिसे P निरूपित किया गया है। | ||
किसी भी | किसी भी सन्दर्भ में, कोई ऊष्मा समीकरण का उपयोग करता है | ||
:<math>c_t = D \Delta c, </math> | :<math>c_t = D \Delta c, </math> | ||
या | या | ||
:<math>P_t = D \Delta P. </math> | :<math>P_t = D \Delta P. </math> | ||
सी और | सी और P दोनों स्थिति और समय के कार्य हैं। d प्रसार गुणांक है जो प्रसार प्रक्रिया की गति को नियंत्रित करता है, और सामान्यतः सेकंड से अधिक वर्ग मीटर में व्यक्त किया जाता है। यदि प्रसार गुणांक d स्थिर नहीं है, लेकिन एकाग्रता C (या दूसरे सन्दर्भ में P) पर निर्भर करता है, तो [[प्रसार समीकरण]] प्राप्त होता है। | ||
=== ब्राउनियन गति === | === ब्राउनियन गति === | ||
| Line 486: | Line 488: | ||
X_0=0 | X_0=0 | ||
\end{cases}</math> | \end{cases}</math> | ||
जहाँ पे <math>B</math> [[वीनर प्रक्रिया]] (मानक ब्राउनियन गति) है, फिर की संभावना घनत्व फलन<math>X</math> किसी भी समय दिया जाता है <math>t</math> द्वारा | |||
: <math>\frac{1}{\sqrt{4\pi kt}}\exp\left(-\frac{x^2}{4kt}\right)</math> | : <math>\frac{1}{\sqrt{4\pi kt}}\exp\left(-\frac{x^2}{4kt}\right)</math> | ||
| Line 495: | Line 497: | ||
u(x,0)=\delta(x) | u(x,0)=\delta(x) | ||
\end{cases}</math> | \end{cases}</math> | ||
जहाँ पे <math>\delta</math> डिराक डेल्टा फलनहै। | |||
=== एक मुक्त कण के लिए श्रोडिंगर समीकरण === | === एक मुक्त कण के लिए श्रोडिंगर समीकरण === | ||
{{main| | {{main|श्रोडिंगर समीकरण}} | ||
एक साधारण विभाजन के साथ, किसी लागू बल क्षेत्र की अनुपस्थिति में द्रव्यमान m के एक कण के लिए श्रोडिंगर समीकरण को निम्नलिखित तरीके से फिर से लिखा जा सकता है: | एक साधारण विभाजन के साथ, किसी लागू बल क्षेत्र की अनुपस्थिति में द्रव्यमान m के एक कण के लिए श्रोडिंगर समीकरण को निम्नलिखित तरीके से फिर से लिखा जा सकता है: | ||
| Line 510: | Line 512: | ||
D &\to \frac{i \hbar}{2m} | D &\to \frac{i \hbar}{2m} | ||
\end{align}</math> | \end{align}</math> | ||
कण प्रसार के | कण प्रसार के सन्दर्भ में निर्धारित ग्रीन फलन की अभिव्यक्तियों में इस परिवर्तन को लागू करने से श्रोडिंगर समीकरण के ग्रीन फलनप्राप्त होते हैं, जो बदले में किसी भी समय लहर फलन को t =0: तरंग फलन पर एक अभिन्न के माध्यम से प्राप्त करने के लिए उपयोग किया जा सकता है। | ||
: <math>\psi(\mathbf R, t) = \int \psi\left(\mathbf R^0,t=0\right) G\left(\mathbf R - \mathbf R^0,t\right) dR_x^0 \, dR_y^0 \, dR_z^0,</math> | : <math>\psi(\mathbf R, t) = \int \psi\left(\mathbf R^0,t=0\right) G\left(\mathbf R - \mathbf R^0,t\right) dR_x^0 \, dR_y^0 \, dR_z^0,</math> | ||
साथ | साथ | ||
| Line 516: | Line 518: | ||
टिप्पणी: क्वांटम यांत्रिकी और प्रसार के बीच यह सादृश्य विशुद्ध रूप से औपचारिक है। भौतिक रूप से, श्रोडिंगर के समीकरण को संतुष्ट करने वाले तरंग प्रकार्य के विकास का प्रसार के अलावा अन्य कोई मूल हो सकता है। | टिप्पणी: क्वांटम यांत्रिकी और प्रसार के बीच यह सादृश्य विशुद्ध रूप से औपचारिक है। भौतिक रूप से, श्रोडिंगर के समीकरण को संतुष्ट करने वाले तरंग प्रकार्य के विकास का प्रसार के अलावा अन्य कोई मूल हो सकता है। | ||
=== [[पॉलिमर]] में | === [[पॉलिमर]] में ऊष्मीय विसरणशीलता === | ||
गोलाकार निर्देशांक में [[फूरियर सिद्धांत]] के संयोजन के साथ ऊष्मासमीकरण का प्रत्यक्ष व्यावहारिक अनुप्रयोग, | गोलाकार निर्देशांक में [[फूरियर सिद्धांत]] के संयोजन के साथ ऊष्मासमीकरण का प्रत्यक्ष व्यावहारिक अनुप्रयोग, ऊष्मीय ट्रांसफर प्रोफाइल की भविष्यवाणी और पॉलिमर (अन्सवर्थ और एफजे डुआर्टे) में ऊष्मीय डिफ्यूसिविटी का माप है। यह दोहरी सैद्धांतिक-प्रायोगिक विधि रबर, व्यावहारिक रुचि के विभिन्न अन्य बहुलक पदार्थ और माइक्रोफ्लुइड्स पर लागू होती है। इन लेखकों ने एक गोले के केंद्र में तापमान के लिए एक व्यंजक निकाला {{mvar|T<sub>C</sub>}} | ||
:<math>\frac{T_C - T_S}{T_0 - T_S} =2 \sum_{n = 1}^{\infty} (-1)^{n+1} \exp\left({-\frac{n^2 \pi^2 \alpha t}{L^2}}\right)</math> | :<math>\frac{T_C - T_S}{T_0 - T_S} =2 \sum_{n = 1}^{\infty} (-1)^{n+1} \exp\left({-\frac{n^2 \pi^2 \alpha t}{L^2}}\right)</math> | ||
जहाँ पे {{math|''T''<sub>0</sub>}} गोले का प्रारंभिक तापमान है और {{mvar|T<sub>S</sub>}} त्रिज्या के गोले की सतह पर तापमान {{mvar|L}}. इस समीकरण को बायोफिजिक्स में प्रोटीन ऊर्जा हस्तांतरण और ऊष्मीय मॉडलिंग में भी आवेदन मिला है। | |||
=== | === अग्रिम आवेदन === | ||
ऊष्मा समीकरण कई परिघटनाओं के गणितीय मॉडल में उत्पन्न होता है और प्रायः [[विकल्प (वित्त)]] के मॉडलिंग में वित्तीय गणित में उपयोग किया जाता है। काला-स्कोल्स ऑप्शन प्राइसिंग मॉडल के [[अंतर समीकरण]] को | ऊष्मा समीकरण कई परिघटनाओं के गणितीय मॉडल में उत्पन्न होता है और प्रायः [[विकल्प (वित्त)]] के मॉडलिंग में वित्तीय गणित में उपयोग किया जाता है। काला-स्कोल्स ऑप्शन प्राइसिंग मॉडल के [[अंतर समीकरण]] को ऊष्मा समीकरण में तब्दील किया जा सकता है, जिससे गणित के परिचित निकाय से अपेक्षाकृत आसान समाधान मिलते हैं। सरल विकल्प मॉडल के कई एक्सटेंशन में बंद फॉर्म समाधान नहीं होते हैं और इस प्रकार एक मॉडल विकल्प मूल्य प्राप्त करने के लिए संख्यात्मक रूप से हल किया जाना चाहिए। अंतरित माध्यम में दबाव प्रसार का वर्णन करने वाला समीकरण ऊष्मासमीकरण के रूप में समान है। डिरिचलेट सीमा स्थितियों, न्यूमैन सीमा स्थितियों और रॉबिन सीमा स्थितियों से निपटने वाली प्रसार समस्याओं ने विश्लेषणात्मक समाधानों को बंद कर दिया है {{harv|थम्बिनायगम|2011}}. | ||
छवि विश्लेषण में ऊष्मा समीकरण का भी व्यापक रूप से उपयोग किया जाता है {{harv| | छवि विश्लेषण में ऊष्मा समीकरण का और मशीन-लर्निंग में [[स्केल स्पेस]] भी व्यापक रूप से उपयोग किया जाता है {{harv|पेरोना|मलिक|1990}}। स्केल-स्पेस या [[ग्राफ लाप्लासियन]] विधियों के पीछे ड्राइविंग सिद्धांत के रूप में निहित क्रैंक-निकोलसन विधि का उपयोग करके ऊष्मासमीकरण को संख्यात्मक रूप से कुशलतापूर्वक हल किया जा सकता है {{harv|क्रैंक|निकोल्सन|1947}}. इस विधि को बिना किसी बंद फॉर्म समाधान वाले कई मॉडलों तक बढ़ाया जा सकता है, उदाहरण के लिए देखें {{harv|विल्मट|होइसन|ड्वेन|1995}}. | ||
[[विविध]] पर ऊष्मासमीकरण का एक अमूर्त रूप अतियाह-सिंगर इंडेक्स प्रमेय के लिए एक प्रमुख दृष्टिकोण प्रदान करता है, और रीमैनियन ज्यामिति में ऊष्मासमीकरणों पर और अधिक काम करने के लिए प्रेरित किया है। | [[विविध]] पर ऊष्मासमीकरण का एक अमूर्त रूप अतियाह-सिंगर इंडेक्स प्रमेय के लिए एक प्रमुख दृष्टिकोण प्रदान करता है, और रीमैनियन ज्यामिति में ऊष्मासमीकरणों पर और अधिक काम करने के लिए प्रेरित किया है। | ||
| Line 531: | Line 533: | ||
* [[कैलोरी बहुपद]] | * [[कैलोरी बहुपद]] | ||
* [[वक्र-छोटा प्रवाह]] | * [[वक्र-छोटा प्रवाह|वक्र-संक्षिप्त प्रवाह]] | ||
* प्रसार समीकरण | * प्रसार समीकरण | ||
* [[सापेक्षतावादी ऊष्मा चालन]] | * [[सापेक्षतावादी ऊष्मा चालन]] | ||
| Line 589: | Line 591: | ||
*अण्डाकार ऑपरेटर | *अण्डाकार ऑपरेटर | ||
*स्वयं adjoint | *स्वयं adjoint | ||
*पुराना | *पुराना फलन | ||
*यहां तक कि समारोह | *यहां तक कि समारोह | ||
*संभाव्यता घनत्व कार्य | *संभाव्यता घनत्व कार्य | ||
| Line 607: | Line 609: | ||
* [http://eqworld.ipmnet.ru/en/solutions/lpde/heat-toc.pdf Linear heat equations]: Particular solutions and boundary value problems - from EqWorld | * [http://eqworld.ipmnet.ru/en/solutions/lpde/heat-toc.pdf Linear heat equations]: Particular solutions and boundary value problems - from EqWorld | ||
* {{cite web |title=The Heat Equation |work=[[PBS Infinite Series]] |date=November 17, 2017 |url=https://www.youtube.com/watch?v=NHucpzbD600 |archive-url=https://ghostarchive.org/varchive/youtube/20211211/NHucpzbD600| archive-date=2021-12-11 |url-status=live|via=[[YouTube]] }}{{cbignore}} | * {{cite web |title=The Heat Equation |work=[[PBS Infinite Series]] |date=November 17, 2017 |url=https://www.youtube.com/watch?v=NHucpzbD600 |archive-url=https://ghostarchive.org/varchive/youtube/20211211/NHucpzbD600| archive-date=2021-12-11 |url-status=live|via=[[YouTube]] }}{{cbignore}} | ||
[[Category: | |||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:Articles with short description]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:CS1 maint]] | |||
[[Category:CS1 Ελληνικά-language sources (el)]] | |||
[[Category:Citation Style 1 templates|W]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 29/11/2022]] | |||
[[Category:Exclude in print]] | |||
[[Category:Interwiki category linking templates]] | |||
[[Category:Interwiki link templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages that use a deprecated format of the math tags]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite web]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikimedia Commons templates]] | |||
[[Category:Wikipedia fully protected templates|Cite web]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:ऊष्मा चालन|समीकरण]] | [[Category:ऊष्मा चालन|समीकरण]] | ||
[[Category:गर्मी हस्तांतरण]] | |||
[[Category:परवलयिक आंशिक अवकल समीकरण]] | [[Category:परवलयिक आंशिक अवकल समीकरण]] | ||
[[Category:गर्मी | [[Category:प्रसार|गर्मी समीकरण]] | ||
Latest revision as of 10:28, 28 December 2022

गणित और भौतिकी में, ऊष्मा समीकरण एक निश्चित आंशिक अंतर समीकरण है। ऊष्मा समीकरण के समाधान को कभी-कभी कैलोरी फलन के रूप में जाना जाता है। ऊष्मा समीकरण का सिद्धांत पहली बार 1822 में जोसेफ फूरियर द्वारा मॉडलिंग के उद्देश्य से विकसित किया गया था कि किसी दिए गए क्षेत्र में ऊष्मा जैसी मात्रा कैसे विसरित होती है।
प्रोटोटाइपिकल परवलयिक आंशिक अंतर समीकरण के रूप में, ऊष्मा समीकरण शुद्ध गणित में सबसे व्यापक रूप से अध्ययन किए जाने वाले विषयों में से एक है, और इसके विश्लेषण को आंशिक अंतर समीकरणों के व्यापक क्षेत्र के लिए मूल सिद्धान्त माना जाता है। रीमैनियन बहुआयामी पर ऊष्मा समीकरण पर भी विचार किया जा सकता है, जिससे कई ज्यामितीय अनुप्रयोग हो सकते हैं। सुब्बरमा मीनाक्षीसुंदरम और एके प्लीजेल के काम के बाद, ऊष्मा समीकरण वर्णक्रमीय ज्यामिति से घनिष्ठ रूप से संबंधित है। 1964 में जेम्स एल्स और जोसेफ एच. सैम्पसन द्वारा अंतर ज्यामिति के लिए एक बीजीय हार्मोनिक नक्शा प्रस्तुत किया गया था, जो 1982 में रिचर्ड एस हैमिल्टन द्वारा रिक्की प्रवाह की प्रारम्भ को प्रेरित करता है और 2003 में त्वरित पेरेलमैन द्वारा पॉइनकेयर अनुमान के प्रमाण में परिणत हुआ। ऊष्मा समीकरण के रूप में जाने वाले ऊष्मा समीकरण के समाधान उस क्षेत्र के बारे में सूक्ष्म जानकारी प्रदान करते हैं, जिस पर उन्हें परिभाषित किया गया है, जैसा कि अतियाह-सिंगर सूचक प्रमेय में उनके आवेदन के माध्यम से उदाहरण दिया गया है।[1]
ऊष्मा समीकरण, इसके प्रकारों के साथ, विज्ञान और व्यावहारिक गणित के कई क्षेत्रों में भी महत्वपूर्ण है। संभाव्यता सिद्धांत में, फोकर-प्लैंक समीकरण के माध्यम से ऊष्मा समीकरण अनियमित चलने और ब्राउनियन गति के अध्ययन से जुड़ा हुआ है। वित्तीय गणित का काला-स्कोल्स समीकरण ऊष्मा समीकरण का एक संक्षिप्त रूप है, और क्वांटम यांत्रिकी के श्रोडिंगर समीकरण को काल्पनिक संख्या में ऊष्मा समीकरण के रूप में माना जा सकता है। छवि विश्लेषण में, ऊष्मा समीकरण का उपयोग कभी-कभी पिक्सेलेशन और किनारे का पता लगाने की विधि को हल करने के लिए किया जाता है। रॉबर्ट डी. रिचटमायर और जॉन वॉन न्यूमैन द्वारा कृत्रिम श्यानता विधियों के प्रारम्भ के बाद, ऊष्मा समीकरणों के समाधान शॉक (द्रव गतिकी) के गणितीय सूत्रीकरण में उपयोगी रहे हैं। 1950 के दशक के प्रारम्भ में जिम डगलस, डी.डब्ल्यू. पीसमैन, और हेनरी रैचफोर्ड जूनियर साथ में काम किये थे।
समीकरण का कथन
'''''''गणित में, यदि Rn का एक खुला उपसमुच्चय U दिया जाए और R का एक उपअंतराल I , यह कहता है कि एक फलनu : U × I → R ऊष्मा समीकरण का समाधान है अगर'''''''
जहाँ पर (x1, …, xn, t) डोमेन के एक सामान्य बिंदु को दर्शाता है संक्षेप संदर्भों में भी जहां ये वाक्यांश अपने सहज अर्थ के लिए विफल होते हैं, यहां पर t को समय के रूप में और x1, …, xn स्थानिक चर के रूप में निरूपित करना सामान्य है। स्थानिक चरों के संग्रह को प्रायः x बस के रूप में संदर्भित किया जाता है। t के किसी दिए गए मूल्य के लिए, समीकरण का दाहिना पक्ष फलन u(⋅, t) : U → R का लाप्लास संकारक है। जैसे, ऊष्मा समीकरण को प्रायः अधिक सघन रूप से इस प्रकार लिखा जाता है
.
भौतिकी और इंजीनियरिंग संदर्भों में, विशेष रूप से एक माध्यम से प्रसार के संदर्भ में, कार्टेशियन समन्वय प्रणाली को निर्धारित करना और फिर किसी फलन (गणित) u(x, y, z, t) के विशिष्ट सन्दर्भ पर विचार करना अधिक सामान्य है। तीन स्थानिक चर के (x, y, z) और समय t.परिवर्तनशील है । इस प्रकार यह कहा जा सकता है u ऊष्मा समीकरण का समाधान है यदि
जिसमें α एक धनात्मक गुणांक है जिसे माध्यम का ऊष्मीय विसारकता कहा जाता है। अन्य भौतिक परिघटनाओं के अतिरिक्त, यह समीकरण एक सजातीय और समदैशिक माध्यम में ऊष्मा के प्रवाह का वर्णन करता है, साथ में u(x, y, z, t) बिंदु पर तापमान होना (x, y, z) और समय t. यदि माध्यम सजातीय और समदैशिक नहीं है, तो α एक निश्चित गुणांक नहीं होगा, और इसके अतिरिक्त ( x, y, z ) पर निर्भर करेगा, जो समीकरण का कुछ अलग रूप भी होगा। भौतिकी और इंजीनियरिंग साहित्य में अतिरिक्त लाप्लासियन निरूपित करने के लिए ∆ का ∇2 का प्रयोग सामान्य है।
गणित के साथ-साथ भौतिकी और इंजीनियरिंग में समय व्युत्पन्न के लिए न्यूटन के अंकन का उपयोग करना साधारण बात है, जहाँ पर निरूपित करने के लिए ∂u/∂t, प्रयोग किया जाता है इसलिए यह समीकरण इस प्रकार लिखा जा सकता है
.
यह भी ध्यान दें कि ∆ या ∇2 उपयोग करने की क्षमता लाप्लासियन को निरूपित करने के लिए, स्थानिक चर के स्पष्ट संदर्भ के बिना, इस तथ्य का प्रतिबिंब है कि लाप्लासियन समन्वय प्रणाली के आकर्षण से स्वतंत्र है। गणितीय शब्दों में, कोई भी यह कहेगा कि लाप्लासियन अनुवादात्मक रूप से रूप से और घूर्णी रूप से अचर है। वास्तव में, यह (शिथिलता से बोलना) सबसे सरल अंतर संचालक है जिसमें ये समरूपताएं हैं। यह लाप्लासियन के उपयोग के एक महत्वपूर्ण (और विशुद्ध रूप से गणितीय) औचित्य के रूप में लिया जा सकता है और किसी भी भौतिक घटना के प्रतिरूपण में ऊष्मा समीकरण के समरूप और समदैशिक हैं, जिनमें से ऊष्मा का प्रसार एक प्रमुख उदाहरण है।
प्रसार स्थिरांक α ऊष्मा समीकरण के गणितीय अध्ययन में प्रायः उपस्थित नहीं होता है, जबकि इंजीनियरिंग में इसका मूल्य बहुत महत्वपूर्ण हो सकता है। निम्नलिखित कारणों से यह एक बड़ा अंतर नहीं है। माना कि u एक फलन हो जिसके साथ
एक नया फलन परिभाषित करें. फिर, शृंखला नियम के अनुसार, किसी एक के पास
-
(⁎)
इस प्रकार, सामान्य मान α के साथ ताप समीकरण के समाधानों के बीच अनुवाद करने का और ऊष्मा समीकरण के समाधान के साथ α = 1 एक सीधा तरीका है। जैसे, गणितीय विश्लेषण के लिए, प्रायः केवल दशा α = 1.पर विचार करना ही पर्याप्त होता है।
तब से पर परिभाषित करने के लिए एक अन्य विकल्प है। संतुष्टि देने वाला जैसे की (⁎) उपर्युक्त समीकरण में परिवर्तन करके , ध्यान दें कि नए फलन v को परिभाषित करने के दो संभावित साधन समय की माप की इकाई या लंबाई के माप की इकाई को बदलने के लिए यहाँ पर चर्चा की गई है।
व्याख्या
समीकरण की भौतिक व्याख्या
अनौपचारिक रूप से, लाप्लासियन संचालक ∆ किसी बिंदु के समीप में किसी फलन के औसत मान और उस बिंदु पर उसके मान के बीच का अंतर देता है। इस प्रकार, यदि u तापमान है, ∆ बताता है कि क्या (और कितना) प्रत्येक बिंदु के आस पास की पदार्थ उस बिंदु पर पदार्थ की तुलना में औसतन अधिक गर्म या ठंडी है।
ऊष्मप्रवैगिकी के दूसरे नियम के अनुसार, तापमान के अंतर और उनके बीच की पदार्थ की तापीय चालकता के अनुपात में ऊष्मा गर्म पिंडों से निकटवर्ती ठंडे पिंडों तक प्रवाहित होगी। जब ऊष्मा किसी पदार्थ में (क्रमशः, बाहर) प्रवाहित होती है, तो इसका तापमान बढ़ जाता है (क्रमशः, घट जाता है), पदार्थ की मात्रा (द्रव्यमान) द्वारा विभाजित ऊष्मा की मात्रा के अनुपात में, आनुपातिकता (गणित) के साथ पदार्थ की विशिष्ट ऊष्मा क्षमता कहलाती है।
इन अवलोकनों के संयोजन से, ताप समीकरण दर कहते हैं जिस बिंदु पर पदार्थ गर्म हो जाएगी (या ठंडा हो जाएगी) आस पास की पदार्थ कितनी गर्म (या कूलर) के समानुपाती होगी। गुणांक α समीकरण में पदार्थ की तापीय चालकता, विशिष्ट ऊष्मा और घनत्व को ध्यान में रखा जाता है।
समीकरण की गणितीय व्याख्या
उपरोक्त भौतिकीय सोच के पहले भाग को गणितीय रूप में रखा जा सकता है। कुंजी यह है कि, किसी भी निश्चित x के लिए, किसी एक के पास
जहाँ पर u(x)(r) के औसत मान u को दर्शाने वाला एकल-चर फलन है जो त्रिज्या r के गोले की सतह x पर केंद्रित है, यह इसके द्वारा परिभाषित किया जा सकता है
जिसमें ωn − 1 यूनिट बॉल के सतह क्षेत्र n-आयामी यूक्लिडियन अंतरिक्ष को दर्शाता है। यह उपरोक्त कथन को निश्चित रूप देता है कि ∆u का मूल्य एक बिंदु x पर u(x) के मान के अंतर को मापता है और u का मूल्य x के पास के बिंदुओं पर, इस अर्थ में कि उत्तरार्द्ध के मूल्यों द्वारा u(x)(r) छोटे सकारात्मक मूल्यों के लिए r. कूटबद्ध किया गया है।
इस अवलोकन के बाद, ऊष्मा समीकरण की व्याख्या किसी फलन के अतिसूक्ष्म औसत के रूप में की जा सकती है। ऊष्मा समीकरण के एक हल को देखते हुए, u(x, t + τ) का मान τ के एक छोटे से सकारात्मक मूल्य के लिए 1/2n फलन u(⋅, t) के औसत मूल्य का गुना पर केंद्रित x पर बहुत छोटे त्रिज्या के एक गोले के.रूप में अनुमानित किया जा सकता है।
समाधान की प्रकृति
ऊष्मा समीकरण का तात्पर्य है कि चोटियों (स्थानीय अधिकतम) धीरे-धीरे कम हो जाएगा, जबकि अवसाद (स्थानीय न्यूनतम) भर जाएगा। किसी बिंदु पर मूल्य केवल तब तक स्थिर रहेगा जब तक कि यह अपने तत्काल परिवेश में औसत मूल्य के बराबर हो। विशेष रूप से, यदि निकटवर्ती में मान एक रेखीय फलन , के बहुत करीब हैं तो उस समीप के केंद्र में मान उस समय नहीं बदलेगा (अर्थात, व्युत्पन्न शून्य होगा)।
एक अधिक सूक्ष्म परिणाम अधिकतम सिद्धांत है, जो कहता है कि u का अधिकतम मूल्य किसी भी क्षेत्र में माध्यम का अधिकतम मान उस अधिकतम मान से अधिक नहीं होगा जो पहले में हुआ था, जब तक कि यह की R सीमा पर न हो। इसका तात्पर्य यह है कि किसी क्षेत्र में अधिकतम तापमान तभी बढ़ सकता है जब बाहर R से ऊष्मा आए। यह परवलयिक आंशिक अवकल समीकरणों का एक गुण है और इसे गणितीय रूप से सिद्ध करना कठिन नहीं है (नीचे देखें)।
एक और दिलचस्प विशेषता यह है कि भले ही प्रारम्भ में माध्यम के अंदर किसी सतह पर मूल्य की एक तेज प्रवणता (असंतोष) होती है, प्रवणता तुरंत उस सतह के माध्यम से ऊष्मा के प्रवाह की एक क्षणिक, असीम रूप से छोटी लेकिन असीम रूप से बड़ी दर से सुचारू हो जाती है। उदाहरण के लिए, यदि दो अलग-अलग पिंड, शुरू में एक समान लेकिन अलग-अलग तापमान पर तथा , एक दूसरे को संपर्क करने के लिए बने हैं, संपर्क के बिंदु पर तापमान तुरंत कुछ मध्यवर्ती मान ग्रहण करेगा, और उस बिंदु के आसपास एक क्षेत्र विकसित होगा जहां , तथा के बीच धीरे धीरे परिवर्तित होगा।
यदि माध्यम में एक बिंदु पर अचानक एक निश्चित मात्रा में ऊष्मा लागू की जाती है, तो यह प्रसार तरंग के रूप में सभी दिशाओं में प्रसारित हो जाएगी। यांत्रिक तरंग और विद्युत चुम्बकीय तरंग के विपरीत, प्रसार तरंग की गति समय के साथ कम हो जाती है: जैसे ही यह एक बड़े क्षेत्र में प्रसारित होती है, तापमान प्रवणता कम हो जाती है, और इसलिए ऊष्मा का प्रवाह भी कम हो जाता है।
विशिष्ट उदाहरण
एक समान छड़ में ऊष्मा का प्रवाह
ऊष्मा प्रवाह के लिए, ऊष्मा समीकरण चालन(ऊष्मा) के भौतिक नियमों और ऊर्जा के संरक्षण से अनुसरण करता है। (Cannon 1984).
एक समदैशिक माध्यम के लिए फूरियर के नियम से, एक सतह के माध्यम से प्रति इकाई क्षेत्र में ऊष्मा ऊर्जा के प्रवाह की दर इसके सापेक्ष नकारात्मक तापमान प्रवणता के समानुपाती होती है:
जहाँ पर पदार्थ की तापीय चालकता है, तापमान है, और एक सदिश (भौतिकी) क्षेत्र है जो अंतरिक्ष और समय t का बिंदु x पर ताप प्रवाह की परिमाण और दिशा का प्रतिनिधित्व करता है।
यदि माध्यम समान खंड और पदार्थ की एक पतली छड़ है, तो स्थिति एकल समन्वय x है, ऊष्मा का प्रवाह बढ़ते हुए की ओर अदिश क्षेत्र है, और ढलान के x संबंध में एक सामान्य व्युत्पन्न है। समीकरण बन जाता है
माना की प्रत्येक बिंदु और समय पर बार की प्रति इकाई आयतन आंतरिक ऊष्मा ऊर्जा हो। बाहरी या आंतरिक स्रोतों से ऊष्मा ऊर्जा उत्पादन की अनुपस्थिति में, पदार्थ में प्रति इकाई आयतन में आंतरिक ऊष्मा ऊर्जा में परिवर्तन की दर, , इसके तापमान के परिवर्तन की दर के समानुपाती होता है, वह है,
जहाँ पर विशिष्ट ताप क्षमता है (स्थिर दबाव में, गैस के सन्दर्भ में) और पदार्थ का घनत्व (द्रव्यमान प्रति इकाई आयतन) है। यह व्युत्पत्ति मानती है कि पदार्थ में अंतरिक्ष के साथ-साथ समय के माध्यम से निरंतर द्रव्यमान घनत्व और ताप क्षमता स्थिर होती है।
केंद्रित माध्यम x पर एक छोटे से तत्व के लिए ऊर्जा के संरक्षण के नियम को लागू करने पर, कोई यह निष्कर्ष निकालता है कि किसी दिए गए बिंदु x पर जिस दर से ऊष्मा एकत्रित होती है उस बिंदु पर ऊष्मा प्रवाह के व्युत्पन्न नगण्य के बराबर है। वह इस प्रकार है,
उपरोक्त समीकरणों से यह इस प्रकार दिया गया है
जो विसरण गुणांक के साथ एक आयाम में ऊष्मा समीकरण है
इस मात्रा को माध्यम का तापीय विसरण कहते हैं।
विकिरण हानि के लिए लेखांकन
ऊष्मा के विकिरण संबंधी अभाव के लिए समीकरण में एक अतिरिक्त शब्द प्रस्तुत किया जा सकता है। स्टीफन-बोल्ट्जमैन नियम के अनुसार, वह शब्द है , जहाँ पर निकटवर्ती तापमान है, और एक गुणांक है जो पदार्थ के भौतिक गुणों पर निर्भर करता है। आंतरिक ऊर्जा में परिवर्तन की दर रूपांतरित हो जाती है
और u के विमोचन के लिए समीकरण हो जाता है
गैर-समान समदैशिक माध्यम
ध्यान दें कि ऊष्मप्रवैगिकी के पहले नियम (अर्थात ऊर्जा के संरक्षण) द्वारा दिए गए दशीय समीकरण को निम्नलिखित रूप में लिखा गया है (बिना द्रव्यमान स्थानांतरण या विकिरण के)। यह रूप अधिक सरल है और यह पहचानने के लिए विशेष रूप से उपयोगी है कि कौन सी विशेषता(जैसे सीpया) किस पद को प्रभावित करता है।
जहाँ पर आयतनमितीय ऊष्मा श्रोत है।
त्रि-आयाम समस्या
समदैशिक और सजातीय में ऊष्मा के प्रसार के विशेष सन्दर्भ में: 3-आयामी अंतरिक्ष में सजातीय माध्यम, यह समीकरण है
- :
जहाँ पर,
- अंतरिक्ष और समय के फलन के रूप में तापमान है;
- समय के साथ एक बिंदु पर तापमान के परिवर्तन की दर है;
- , , तथा क्रमशः x, y, z दिशा में तापमान के दूसरे स्थानिक यौगिक (तापीय चालन) हैं।
- तापीय प्रसार, तापीय चालकता के आधार पर एक सामग्री-विशिष्ट मात्रा , विशिष्ट ताप क्षमता , और द्रव्यमान घनत्व है।
ऊष्मा समीकरण फूरियर के चालन के नियम का परिणाम है (ऊष्माचालन देखें)।
यदि माध्यम संपूर्ण स्थान नहीं है, तो विशिष्ट रूप से ऊष्मा समीकरण को हल करने के लिए हमें u के लिए सीमा शर्तों को भी निर्दिष्ट करने की आवश्यकता है। पूरे अंतरिक्ष में समाधानों की विशिष्टता निर्धारित करने के लिए अतिरिक्त शर्तों को मानना आवश्यक है, उदाहरण के लिए समाधान के विकास पर एक घातीय बाध्यता[2] या एक सांकेतिक स्थिति (डेविड मेष के परिणामस्वरूप गैर-नकारात्मक समाधान अद्वितीय हैं)।[3]
ऊष्मा समीकरण के समाधान को किसी वस्तु के गर्म से ठंडे क्षेत्रों में ऊष्मा के प्रवाह द्वारा प्रारंभिक तापमान वितरण के क्रमिक चौरसाई द्वारा चित्रित किया जाता है। सामान्यतः, कई अलग-अलग स्थिति और प्रारम्भी स्थितियां एक ही स्थिर थर्मोडायनामिक संतुलन की ओर बढ़ती हैं। परिणाम स्वरुप, समाधान को विपरीत करने के लिए और वर्तमान ताप वितरण से पहले के समय या प्रारंभिक स्थितियों के बारे में कुछ निष्कर्ष निकालने के लिए सबसे कम समय अवधि को छोड़कर बहुत अशुद्ध है।
ऊष्मा समीकरण एक परवलयिक आंशिक अवकल समीकरण का प्रोटोटाइपिकल उदाहरण है।
लाप्लास संचालक का उपयोग करके, ऊष्मा समीकरण को सरलीकृत किया जा सकता है, और अनियमित तरीके से आयामों की संख्या के समान समीकरणों के लिए सामान्यीकृत किया जा सकता है, जैसा कि
जहां लाप्लास ऑपरेटर, Δ या ∇2, ग्रेडिएंट का विचलन, स्थानिक चरों में लिया जाता है।
ऊष्मा समीकरण ऊष्मा प्रसार, साथ ही साथ अन्य विसारक प्रक्रियाओं को नियंत्रित करता है, जैसे कि कण प्रसार या तंत्रिका कोशिकाओं में क्रिया क्षमता का प्रसार है। हालांकि वे प्रकृति में विसारक नहीं हैं, कुछ क्वांटम यांत्रिकी समस्याएं भी ऊष्मा समीकरण के गणितीय अनुरूप (नीचे देखें) द्वारा नियंत्रित होती हैं। इसका उपयोग वित्त में उत्पन्न होने वाली कुछ घटनाओं को मॉडल करने के लिए भी किया जा सकता है, जैसे काला-स्कोल्स या ऑर्स्टीन-उहलेनबेक प्रक्रियाएं। छवि विश्लेषण में समीकरण और विभिन्न गैर-रेखीय एनालॉग्स का भी उपयोग किया गया है।
ऊष्मा समीकरण, तकनीकी रूप से, विशेष सापेक्षता के उल्लंघन में है, क्योंकि इसके समाधान में बाधा का तात्कालिक प्रसार सम्मिलित है। अग्रिम प्रकाश शंकु के बाहर अशांति का हिस्सा सामान्यतः सुरक्षित रूप से उपेक्षित किया जा सकता है, लेकिन अगर ऊष्मा के संचरण के लिए एक उचित गति विकसित करना आवश्यक है, तो इसके अतिरिक्त एक अतिशयोक्तिपूर्ण आंशिक अंतर समीकरण पर विचार किया जाना चाहिए - जैसे आंशिक अंतर समीकरण जिसमें एक दूसरा समय व्युत्पन्न सम्मिलित है। अरेखीय ऊष्मा चालन के कुछ मॉडल (जो परवलयिक समीकरण भी हैं) में परिमित ताप संचरण गति के साथ समाधान होते हैं।[4][5]
आंतरिक ताप उत्पादन
उपरोक्त फलन U एक शरीर के तापमान का प्रतिनिधित्व करता है। वैकल्पिक रूप से, कभी-कभी इकाइयों को बदलना और एक माध्यम के ताप घनत्व के रूप में यू का प्रतिनिधित्व करना सुविधाजनक होता है। चूंकि ऊष्माघनत्व एक सजातीय माध्यम में तापमान के समानुपाती होता है, इसलिए नई इकाइयों में अभी भी ऊष्मासमीकरण का पालन किया जाता है।
मान लीजिए कि एक पिंड ऊष्मा समीकरण का पालन करता है और, इसके अलावा, प्रति इकाई आयतन (जैसे, वाट/लीटर - W/L में) अपनी स्वयं की ऊष्मा उत्पन्न करता है, जो एक ज्ञात फलन q द्वारा दी गई दर से होती है, जो अंतरिक्ष और समय में भिन्न होती है।[6] तब ऊष्माप्रति इकाई आयतन u एक समीकरण को संतुष्ट करता है,
उदाहरण के लिए, एक टंगस्टन लाइट बल्ब फिलामेंट ऊष्माउत्पन्न करता है, इसलिए इसे चालू करने पर q के लिए धनात्मक अशून्य मान होगा। जबकि प्रकाश बंद है, टंगस्टन फिलामेंट के लिए q का मान शून्य होगा।
== फूरियर श्रृंखला == का उपयोग करके ऊष्मासमीकरण को हल करना
ऊष्मा समीकरण के लिए निम्नलिखित समाधान तकनीक जोसेफ फूरियर द्वारा 1822 में प्रकाशित अपने ग्रंथ थ्योरी एनालिटिक डे ला चालेर द्वारा प्रस्तावित की गई थी। एक अंतरिक्ष चर के लिए ऊष्मासमीकरण पर विचार करें। इसका उपयोग रॉड में ऊष्माचालन के मॉडल के लिए किया जा सकता है। समीकरण है
-
(1)
जहाँ u = u(x, t) दो चर x और t का फलन है। यहां
- x स्पेस वेरिएबल है, इसलिए x ∈ [0, L], जहाँ L रॉड की लंबाई है।
- टी समय चर है, इसलिए टी ≥ 0।
हम प्रारंभिक स्थिति मानते हैं
-
(2)
जहां फलनएफ दिया गया है, और सीमा की स्थिति
-
.
(3)
आइए इसका समाधान खोजने का प्रयास करते हैं (1) यह समान रूप से शून्य नहीं है जो सीमा शर्तों को संतुष्ट करता है (3) लेकिन निम्नलिखित संपत्ति के साथ: यू एक उत्पाद है जिसमें एक्स, टी पर यू की निर्भरता अलग हो जाती है, अर्थात:
-
(4)
इस समाधान तकनीक को चरों का पृथक्करण कहा जाता है। u को वापस समीकरण में प्रतिस्थापित करना (1),
चूंकि दाहिना पक्ष केवल x पर निर्भर करता है और बायां पक्ष केवल t पर निर्भर करता है, दोनों पक्ष किसी स्थिर मान -λ के बराबर होते हैं। इस प्रकार:
-
(5)
तथा
-
(6)
अब हम इसके लिए गैर-तुच्छ समाधान दिखाएंगे (6) λ ≤ 0 के मानों के लिए नहीं हो सकता:
- मान लीजिए कि λ < 0. तो वास्तविक संख्याएं बी, सी उपस्थित हैं जैसे कि से (3) हमें X(0) = 0 = X(L) मिलता है और इसलिए B = 0 = C जिसका अर्थ है कि आप समान रूप से 0 हैं।
- मान लीजिए कि λ = 0. तब वास्तविक संख्याएँ B, C उपस्थित हैं जैसे कि X(x) = Bx + C. समीकरण से (3) हम उसी तरह से निष्कर्ष निकालते हैं जैसे 1 में कि यू समान रूप से 0 है।
- इसलिए, यह मामला होना चाहिए कि λ > 0. फिर वास्तविक संख्याएं ए, बी, सी उपस्थित हैं जैसे कि तथासे (3) हमें C = 0 मिलता है और वह भी किसी धनात्मक पूर्णांक n के लिए,
यह ऊष्मासमीकरण को विशेष सन्दर्भ में हल करता है कि यू की निर्भरता का विशेष रूप है (4).
सामान्यतः, समाधान का योग (1) जो सीमा शर्तों को पूरा करते हैं (3) संतुष्ट भी करता है (1) तथा (3). हम दिखा सकते हैं कि इसका समाधान (1), (2) तथा (3) द्वारा दिया गया है
जहाँ पे
समाधान तकनीक का सामान्यीकरण
ऊपर उपयोग की गई समाधान तकनीक को कई अन्य प्रकार के समीकरणों तक विस्तृत किया जा सकता है। विचार यह है कि संचालक यूxxशून्य सीमा शर्तों के साथ इसके eigenfunctions के संदर्भ में प्रतिनिधित्व किया जा सकता है। यह स्वाभाविक रूप से रैखिक स्व-आसन्न ऑपरेटर के वर्णक्रमीय सिद्धांत के मूल विचारों में से एक की ओर जाता है।
रैखिक संकारक Δu = u पर विचार करेंxx. कार्यों का अनंत क्रम
n ≥ 1 के लिए Δ के eigenfunctions हैं। वास्तव में,
- : : : : : : : : : : : : : : : : : : : : : : : :
इसके अलावा, सीमा शर्तों f(0) = f(L) = 0 के साथ Δ का कोई भी eigenfunction f फॉर्म का हैn कुछ n ≥ 1 के लिए। कार्य ईn n ≥ 1 के लिए [0, L] पर वास्तविक-मूल्यवान कार्यों के स्थान पर एक निश्चित आंतरिक उत्पाद के संबंध में एक ऑर्थोनॉर्मल अनुक्रम बनाते हैं। इसका मतलब है की
अंत में, अनुक्रम {ईn}n ∈ N एल के एक घने रैखिक उप-स्थान को फैलाता है2((0, एल))। इससे पता चलता है कि असल में हमारे पास विकर्ण मैट्रिक्स संचालक Δ है।
गैर-सजातीय अनिसोट्रोपिक मीडिया में ऊष्मा चालन
सामान्यतः, ऊष्मा चालन का अध्ययन कई सिद्धांतों पर आधारित होता है। ऊष्मा प्रवाह ऊर्जा प्रवाह का एक रूप है, और इस तरह अंतरिक्ष के एक क्षेत्र में ऊष्माके प्रवाह की समय दर की बात करना सार्थक है।
- एक क्षेत्र वी में ऊष्माप्रवाह की समय दर समय-निर्भर मात्रा q द्वारा दी जाती हैt(वी)। हम मानते हैं कि q में रैडॉन-निकोडिम डेरिवेटिव q है, ताकि
- ऊष्मा फ्लो एक टाइम-डिपेंडेंट वेक्टर फलन H(x) है जिसकी विशेषता निम्नानुसार है: एरिया dS और यूनिट नॉर्मल वेक्टर n के साथ एक इनफिनिटिमल सरफेस एलिमेंट के माध्यम से बहने वाली ऊष्मा की समय दर है इस प्रकार वी में ऊष्माके प्रवाह की दर भी सतह अभिन्न द्वारा दी गई हैजहाँ n(x) x पर बाहर की ओर इंगित करने वाला सामान्य वेक्टर है।
- ऊष्मा चालन का नियम कहता है कि ऊष्मा ऊर्जा प्रवाह का तापमान प्रवणता पर निम्नलिखित रैखिक निर्भरता है जहां A(x) एक 3 × 3 वास्तविक मैट्रिक्स (गणित) है जो सममित और सकारात्मक-निश्चित मैट्रिक्स है।
- विचलन प्रमेय द्वारा, 'वी' में ऊष्माप्रवाह के लिए पिछली सतह अभिन्न मात्रा अभिन्न में परिवर्तित हो सकती है
- x पर तापमान परिवर्तन की समय दर एक अतिसूक्ष्म आयतन तत्व में प्रवाहित होने वाली ऊष्मा के समानुपाती होती है, जहाँ आनुपातिकता का स्थिरांक एक स्थिर κ पर निर्भर होता है
इन समीकरणों को एक साथ रखने से ऊष्मा प्रवाह का सामान्य समीकरण मिलता है:
टिप्पणियां।
- गुणांक κ(x) x पर पदार्थ की विशिष्ट ऊष्मा का व्युत्क्रम x पर पदार्थ का घनत्व है: .
- एक समदैशिक माध्यम के सन्दर्भ में, मैट्रिक्स a तापीय चालकता 'के' के बराबर एक स्केलर मैट्रिक्स है।
- अनिसोट्रोपिक सन्दर्भ में जहां गुणांक मैट्रिक्स ए स्केलर नहीं है और/या यदि यह 'x पर निर्भर करता है, तो ऊष्मासमीकरण के समाधान के लिए एक स्पष्ट सूत्र अनुमानतः ही कभी लिखा जा सकता है, हालांकि सामान्यतः विचार करना संभव है संबंधित अमूर्त कॉची समस्या और यह दिखाएं कि यह एक अच्छी तरह से प्रस्तुत समस्या है और/या कुछ गुणात्मक गुणों को दिखाने के लिए (जैसे सकारात्मक प्रारंभिक डेटा का संरक्षण, प्रसार की अनंत गति, एक संतुलन की ओर अभिसरण, गुणों को चिकना करना)। यह सामान्यतः एक-पैरामीटर सेमीग्रुप सिद्धांत द्वारा किया जाता है: उदाहरण के लिए, यदि 'a' एक सममित मैट्रिक्स है, तो वक्राकार संचालक द्वारा परिभाषित स्व-संलग्न और अपव्यय है, इस प्रकार वर्णक्रमीय प्रमेय द्वारा यह एक-पैरामीटर सेमीग्रुप उत्पन्न करता है।
मौलिक समाधान
एक मौलिक समाधान, जिसे ऊष्मा कर्नेल भी कहा जाता है, एक ज्ञात स्थिति में ऊष्मा के प्रारंभिक बिंदु स्रोत की प्रारंभिक स्थिति के अनुरूप ऊष्मा समीकरण का एक समाधान है। इनका उपयोग कुछ डोमेन पर ताप समीकरण का सामान्य समाधान खोजने के लिए किया जा सकता है; देखें, उदाहरण के लिए, (Evans 2010) एक प्रारंभिक उपचार के लिए।
एक चर में, ग्रीन का कार्य प्रारंभिक मूल्य समस्या का समाधान है (ड्यूहमेल के सिद्धांत द्वारा, पहले समीकरण के समाधान के रूप में डेल्टा फलनके साथ एक के रूप में ग्रीन के कार्य की परिभाषा के बराबर)
जहाँ पेडिराक डेल्टा फलनहै। इस समस्या का समाधान मौलिक समाधान (ऊष्मा कर्नेल) है
कोई घुमाव लगाकर −∞ < x < ∞ और 0 < t < ∞ के लिए प्रारंभिक स्थिति u(x, 0) = g(x) के साथ एक चर ऊष्मा समीकरण का सामान्य समाधान प्राप्त कर सकता है:
कई स्थानिक चरों में, मौलिक समाधान समान समस्या को हल करता है
एन-वैरिएबल मौलिक समाधान प्रत्येक चर में मौलिक समाधान का उत्पाद है; अर्थात।,
R पर ऊष्मा समीकरण का सामान्य हलn तब कनवल्शन द्वारा प्राप्त किया जाता है, ताकि u('x', 0) = g('x') के साथ प्रारंभिक मूल्य समस्या को हल करने के लिए, एक के पास
R में एक डोमेन Ω पर सामान्य समस्याएन है
डिरिचलेट समस्या या न्यूमैन समस्या सीमा डेटा के साथ। एक ग्रीन का कार्य सदैव उपलब्ध होता है, लेकिन जब तक डोमेन Ω को एक-चर समस्याओं (नीचे देखें) में आसानी से विघटित नहीं किया जा सकता है, तब तक इसे स्पष्ट रूप से लिखना संभव नहीं हो सकता है। ग्रीन के कार्यों को प्राप्त करने के अन्य तरीकों में छवियों की विधि, चरों का पृथक्करण और लाप्लास रूपांतरण (कोल, 2011) सम्मिलित हैं।
=== 1D === में कुछ ग्रीन के कार्य समाधान
एक-आयाम में विभिन्न प्रकार के प्राथमिक ग्रीन के कार्य समाधान यहां दर्ज किए गए हैं; कई अन्य कहीं और उपलब्ध हैं।[7] इनमें से कुछ में स्थानिक डोमेन (−∞,∞) है। दूसरों में, यह अर्ध-अनंत अंतराल (0,∞) है जिसमें या तो न्यूमैन समस्या या डिरिचलेट समस्या सीमा स्थितियां हैं। एक और भिन्नता यह है कि इनमें से कुछ विषम समीकरण को हल करते हैं
जहाँ f, x और t का दिया हुआ फलन है।
सजातीय ताप समीकरण
- प्रारंभिक मूल्य समस्या (−∞,∞) पर

इंटरएक्टिव संस्करण।
टिप्पणी। यह हल मौलिक हल के चर x के संबंध में कनवल्शन है
और फलनजी (एक्स)। (मौलिक हल की ग्रीन की फलन संख्या X00 है।)
इसलिए, भेदभाव के संबंध में संकल्प के सामान्य गुणों के अनुसार, यू = जी ∗ Φ समान ऊष्मासमीकरण का समाधान है, के लिए
इसके अतिरिक्त,
ताकि, कार्यफलन के बारे में सामान्य तथ्यों से, Φ(⋅, t) ∗ g → g as t → 0 विभिन्न अर्थों में, विशिष्ट g के अनुसार उदाहरण के लिए, यदि g को 'R' पर परिबद्ध और सतत मान लिया जाए तो Φ(⋅, t) ∗ g t → 0 के रूप में समान रूप से g में परिवर्तित हो जाता है, जिसका अर्थ है कि u(x, t) निरंतर चालू है R × [0, ∞) साथ u(x, 0) = g(x).
- प्रारंभिक मूल्य समस्या (0,∞) सजातीय डिरिचलेट सीमा शर्तों के साथ
टिप्पणी। यह समाधान पूर्ववर्ती सूत्र से प्राप्त किया गया है जैसा कि डेटा g(x) पर लागू किया गया है, जिसे उपयुक्त रूप से 'R' तक बढ़ाया गया है, ताकि यह एक विषम फलन बन सके, अर्थात g(−x) := −g(x) सभी के लिए एक्स। इसके अनुरूप, (−∞,∞) पर आरंभिक मूल्य समस्या का समाधान, टी के सभी मानों के लिए चर x के संबंध में एक विषम कार्य है, और विशेष रूप से यह सजातीय डिरिचलेट सीमा शर्तों u(0, t) = 0 को संतुष्ट करता है . इस समाधान की ग्रीन की कार्य संख्या X10 है।
सजातीय न्यूमैन सीमा स्थितियों के साथ (0,∞) पर प्रारंभिक मूल्य समस्या
टिप्पणी, यह पहले समाधान सूत्र से प्राप्त किया गया है जैसा कि डेटा g(x) पर लागू किया गया है, जिसे उपयुक्त रूप से 'R' तक विस्तारित किया गया है, ताकि यह एक सम फलन बन सके, अर्थात, सभी x के लिए g(−x):= g(x) . इसके अनुरूप, 'R' पर प्रारंभिक मूल्य समस्या का समाधान t > 0 के सभी मानों के लिए चर x के संबंध में एक सम फलन है, और विशेष रूप से, सहज होने के कारण, यह सजातीय न्यूमैन सीमा स्थितियों u को संतुष्ट करता हैx(0, t) = 0. इस समाधान की ग्रीन की फलन संख्या X20 है।
- समस्या (0,∞) सजातीय प्रारंभिक स्थितियों और गैर-सजातीय डिरिचलेट सीमा स्थितियों के साथ
टिप्पणी, यह हल चर t के संबंध में कनवल्शन है
और फलन h (t), चूँकि Φ(x, t) का मूल हल है
फलन ψ(x, t) भी उसी ऊष्मा समीकरण का एक हल है, और ऐसा ही u भी है:= ψ ∗ h, अवकलन के संबंध में कनवल्शन के सामान्य गुणों के कारण इसके अतिरिक्त,
ताकि, मोलिफायर के बारे में सामान्य तथ्यों से, ψ(x, ⋅) ∗ h → h as x → 0 विभिन्न अर्थों में, विशिष्ट h के अनुसार उदाहरण के लिए, यदि h को [0, ∞) में समर्थन के साथ 'R' पर निरंतर माना जाता है, तो ψ(x, ⋅) ∗ h कॉम्पेक्टा पर समान रूप से x → 0 के रूप में परिवर्तित होता है, जिसका अर्थ है कि u(x, t) निरंतर है पर [0, ∞) × [0, ∞) साथ u(0, t) = h(t).
अमानवीय ऊष्मा समीकरण
- समस्या पर (-∞,∞) सजातीय प्रारंभिक स्थितियां
टिप्पणी, यह हल 'R' में कनवल्शन है2, जो मूल समाधान के चर x और t दोनों के संबंध में है
और फलन f(x, t), दोनों का मतलब संपूर्ण 'R' पर परिभाषित है2 और समान रूप से 0 सभी t → 0 के लिए एक इसे सत्यापित करता है
जो वितरण की भाषा में व्यक्त हो जाता है
जहां वितरण δ डिराक का डेल्टा फलनहै, वह 0 पर मूल्यांकन है।
समसामयिक डिरिचलेट सीमा स्थितियों और प्रारंभिक स्थितियों के साथ (0,∞) पर समस्या
टिप्पणी। यह समाधान पूर्ववर्ती सूत्र से प्राप्त किया गया है जैसा कि डेटा f(x, t) पर लागू किया गया है, जिसे उपयुक्त रूप से 'R' × [0,∞) तक बढ़ाया गया है, ताकि वेरिएबल x का एक विषम कार्य हो सके, अर्थात f( −x, t):= −f(x, t) सभी x और t के लिए इसके अनुरूप, (−∞,∞) पर विषम समस्या का समाधान टी के सभी मूल्यों के लिए चर x के संबंध में एक विषम कार्य है, और विशेष रूप से यह सजातीय डिरिचलेट सीमा शर्तों u(0, t) = 0 को संतुष्ट करता है।
समसामयिक न्यूमैन सीमा स्थितियों और प्रारंभिक स्थितियों के साथ (0,∞) पर समस्या
टिप्पणी। यह समाधान पहले सूत्र से प्राप्त किया जाता है जैसा कि डेटा f(x, t) पर लागू होता है जिसे उपयुक्त रूप से 'R' × [0,∞) तक बढ़ाया जाता है, ताकि वेरिएबल x का एक समान कार्य हो सके, अर्थात f( −x, t) := f(x, t) सभी x और t के लिए इसके अनुरूप, (−∞,∞) पर विषम समस्या का समाधान, t के सभी मूल्यों के लिए चर x के संबंध में एक समान कार्य है, और विशेष रूप से, एक सहज कार्य होने के नाते, यह सजातीय न्यूमैन सीमा शर्तों U को संतुष्ट करता हैx(0, t) = 0।
उदाहरण
चूंकि ऊष्मासमीकरण रैखिक है, उपरोक्त ग्रीन के फलन समाधानों के उचित रैखिक संयोजन को ले कर सीमा शर्तों के अन्य संयोजनों, अमानवीय अवधि और प्रारंभिक स्थितियों के समाधान प्राप्त किए जा सकते हैं।
उदाहरण के लिए, हल करना
मान लीजिए u = w + v जहाँ w और v समस्याएँ हल करते हैं
इसी प्रकार हल करना
U = w + v + r जहां w, v, और r समस्याओं को हल करते हैं
ऊष्मा समीकरण के लिए माध्य-मूल्य गुण
ऊष्मा समीकरणों के हल
हार्मोनिक फलनके माध्य-मूल्य गुणों के अनुरूप माध्य-मूल्य संपत्ति को संतुष्ट करें, के समाधान
हालांकि कुछ और जटिल है, अगर आप हल करते हैं
तथा
फिर
जहां ईλएक ऊष्मा-गेंद है, जो ऊष्मा समीकरण के मूलभूत समाधान का एक उच्च-स्तरीय समुच्चय है:
नोटिस जो
λ → ∞ के रूप में इसलिए उपरोक्त सूत्र किसी भी (x, t) के लिए (खुले) सेट डोम (यू) में λ के लिए काफी बड़ा है।[8] यह हार्मोनिक कार्यों के लिए समान तर्क के समान एक तर्क द्वारा दिखाया जा सकता है # औसत मूल्य संपत्ति।
स्थिर-अवस्था ऊष्मा समीकरण
स्थिर-अवस्था ऊष्मा समीकरण परिभाषा के अनुसार समय पर निर्भर नहीं है। दूसरे शब्दों में, यह माना जाता है कि ऐसी स्थितियाँ उपस्थित हैं:
यह स्थिति समय स्थिरांक और सीमा शर्तों को लागू किए जाने के बाद से बीत चुके समय पर निर्भर करती है। इस प्रकार, स्थिति उन स्थितियों में पूरी होती है जिनमें समय संतुलन स्थिरांक काफी तेज होता है कि अधिक जटिल समय-निर्भर ऊष्मासमीकरण को स्थिर-अवस्था के सन्दर्भ में अनुमानित किया जा सकता है। समतुल्य रूप से, सभी सन्दर्भ के लिए स्थिर-स्थिति की स्थिति उपस्थित है जिसमें पर्याप्त समय बीत चुका है कि ऊष्मीय क्षेत्र 'U' अब समय पर विकसित नहीं होता है।
स्थिर-स्थिति के सन्दर्भ में, एक स्थानिक तापीय प्रवणता उपस्थित हो सकती है (या नहीं भी हो सकती है), लेकिन यदि ऐसा होता है, तो यह समय के साथ नहीं बदलता है। इसलिए यह समीकरण उन सभी तापीय समस्याओं के अंतिम परिणाम का वर्णन करता है जिसमें एक स्रोत को चालू किया जाता है (उदाहरण के लिए, एक ऑटोमोबाइल में एक इंजन चालू होता है), और सभी स्थायी तापमान प्रवणता के लिए अंतरिक्ष में स्वयं को स्थापित करने के लिए पर्याप्त समय बीत चुका होता है, जिसके बाद ये स्थानिक ढाल अब समय में नहीं बदलते (फिर से, एक ऑटोमोबाइल के साथ जिसमें इंजन काफी लंबे समय से चल रहा है)। अन्य (तुच्छ) समाधान सभी स्थानिक तापमान प्रवणताओं के साथ-साथ गायब होने के लिए है, जिस स्थिति में तापमान अंतरिक्ष में भी समान हो जाता है।
समीकरण बहुत सरल है और ऊष्मापरिवहन प्रक्रिया की गतिशीलता पर ध्यान केंद्रित किए बिना सामग्रियों के भौतिकी को बेहतर ढंग से समझने में मदद कर सकता है। यह व्यापक रूप से सरल इंजीनियरिंग समस्याओं के लिए उपयोग किया जाता है, यह मानते हुए कि समय के साथ तापमान क्षेत्र और ताप परिवहन का संतुलन है।
स्थिर स्थिति:
एक आयतन के लिए स्थिर-अवस्था ऊष्मा समीकरण जिसमें ऊष्मा स्रोत (असमान स्थिति) होता है, पॉसों का समीकरण है:
जहाँ u थर्मोडायनामिक तापमान है, k तापीय चालकता है और q प्रति इकाई आयतन में ऊष्मा उत्पादन की दर है।
इलेक्ट्रोस्टाटिक्स में, यह उस सन्दर्भ के बराबर है जहां विचाराधीन स्थान में विद्युत आवेश होता है।
वॉल्यूम के भीतर ऊष्मास्रोत के बिना स्थिर-अवस्था ऊष्मासमीकरण (सजातीय मामला) इलेक्ट्रोस्टैटिक्स में मुक्त स्थान की मात्रा के लिए समीकरण है जिसमें चार्ज नहीं होता है। यह लाप्लास के समीकरण द्वारा वर्णित है:
अनुप्रयोग
कण प्रसार
कोई भी एक समीकरण द्वारा कण प्रसार को मॉडल कर सकता है:
- बड़ी संख्या में कणों के सामूहिक प्रसार के सन्दर्भ में कणों की वॉल्यूमेट्रिक सांद्रता, निरूपित C, या
- एक कण की स्थिति से जुड़ा प्रायिकता घनत्व फलन, जिसे P निरूपित किया गया है।
किसी भी सन्दर्भ में, कोई ऊष्मा समीकरण का उपयोग करता है
या
सी और P दोनों स्थिति और समय के कार्य हैं। d प्रसार गुणांक है जो प्रसार प्रक्रिया की गति को नियंत्रित करता है, और सामान्यतः सेकंड से अधिक वर्ग मीटर में व्यक्त किया जाता है। यदि प्रसार गुणांक d स्थिर नहीं है, लेकिन एकाग्रता C (या दूसरे सन्दर्भ में P) पर निर्भर करता है, तो प्रसार समीकरण प्राप्त होता है।
ब्राउनियन गति
स्टोकेस्टिक प्रक्रिया होने दें स्टोकास्टिक अंतर समीकरण का समाधान बनें
जहाँ पे वीनर प्रक्रिया (मानक ब्राउनियन गति) है, फिर की संभावना घनत्व फलन किसी भी समय दिया जाता है द्वारा
जो प्रारंभिक मूल्य समस्या का समाधान है
जहाँ पे डिराक डेल्टा फलनहै।
एक मुक्त कण के लिए श्रोडिंगर समीकरण
एक साधारण विभाजन के साथ, किसी लागू बल क्षेत्र की अनुपस्थिति में द्रव्यमान m के एक कण के लिए श्रोडिंगर समीकरण को निम्नलिखित तरीके से फिर से लिखा जा सकता है:
- ,
जहां i काल्पनिक इकाई है, ħ घटी हुई प्लांक नियतांक है, और ψ कण की तरंग क्रिया है।
यह समीकरण औपचारिक रूप से कण प्रसार समीकरण के समान है, जो निम्नलिखित परिवर्तन के माध्यम से प्राप्त होता है:
कण प्रसार के सन्दर्भ में निर्धारित ग्रीन फलन की अभिव्यक्तियों में इस परिवर्तन को लागू करने से श्रोडिंगर समीकरण के ग्रीन फलनप्राप्त होते हैं, जो बदले में किसी भी समय लहर फलन को t =0: तरंग फलन पर एक अभिन्न के माध्यम से प्राप्त करने के लिए उपयोग किया जा सकता है।
साथ
टिप्पणी: क्वांटम यांत्रिकी और प्रसार के बीच यह सादृश्य विशुद्ध रूप से औपचारिक है। भौतिक रूप से, श्रोडिंगर के समीकरण को संतुष्ट करने वाले तरंग प्रकार्य के विकास का प्रसार के अलावा अन्य कोई मूल हो सकता है।
पॉलिमर में ऊष्मीय विसरणशीलता
गोलाकार निर्देशांक में फूरियर सिद्धांत के संयोजन के साथ ऊष्मासमीकरण का प्रत्यक्ष व्यावहारिक अनुप्रयोग, ऊष्मीय ट्रांसफर प्रोफाइल की भविष्यवाणी और पॉलिमर (अन्सवर्थ और एफजे डुआर्टे) में ऊष्मीय डिफ्यूसिविटी का माप है। यह दोहरी सैद्धांतिक-प्रायोगिक विधि रबर, व्यावहारिक रुचि के विभिन्न अन्य बहुलक पदार्थ और माइक्रोफ्लुइड्स पर लागू होती है। इन लेखकों ने एक गोले के केंद्र में तापमान के लिए एक व्यंजक निकाला TC
जहाँ पे T0 गोले का प्रारंभिक तापमान है और TS त्रिज्या के गोले की सतह पर तापमान L. इस समीकरण को बायोफिजिक्स में प्रोटीन ऊर्जा हस्तांतरण और ऊष्मीय मॉडलिंग में भी आवेदन मिला है।
अग्रिम आवेदन
ऊष्मा समीकरण कई परिघटनाओं के गणितीय मॉडल में उत्पन्न होता है और प्रायः विकल्प (वित्त) के मॉडलिंग में वित्तीय गणित में उपयोग किया जाता है। काला-स्कोल्स ऑप्शन प्राइसिंग मॉडल के अंतर समीकरण को ऊष्मा समीकरण में तब्दील किया जा सकता है, जिससे गणित के परिचित निकाय से अपेक्षाकृत आसान समाधान मिलते हैं। सरल विकल्प मॉडल के कई एक्सटेंशन में बंद फॉर्म समाधान नहीं होते हैं और इस प्रकार एक मॉडल विकल्प मूल्य प्राप्त करने के लिए संख्यात्मक रूप से हल किया जाना चाहिए। अंतरित माध्यम में दबाव प्रसार का वर्णन करने वाला समीकरण ऊष्मासमीकरण के रूप में समान है। डिरिचलेट सीमा स्थितियों, न्यूमैन सीमा स्थितियों और रॉबिन सीमा स्थितियों से निपटने वाली प्रसार समस्याओं ने विश्लेषणात्मक समाधानों को बंद कर दिया है (थम्बिनायगम 2011). छवि विश्लेषण में ऊष्मा समीकरण का और मशीन-लर्निंग में स्केल स्पेस भी व्यापक रूप से उपयोग किया जाता है (पेरोना & मलिक 1990)। स्केल-स्पेस या ग्राफ लाप्लासियन विधियों के पीछे ड्राइविंग सिद्धांत के रूप में निहित क्रैंक-निकोलसन विधि का उपयोग करके ऊष्मासमीकरण को संख्यात्मक रूप से कुशलतापूर्वक हल किया जा सकता है (क्रैंक & निकोल्सन 1947). इस विधि को बिना किसी बंद फॉर्म समाधान वाले कई मॉडलों तक बढ़ाया जा सकता है, उदाहरण के लिए देखें (विल्मट, होइसन & ड्वेन 1995).
विविध पर ऊष्मासमीकरण का एक अमूर्त रूप अतियाह-सिंगर इंडेक्स प्रमेय के लिए एक प्रमुख दृष्टिकोण प्रदान करता है, और रीमैनियन ज्यामिति में ऊष्मासमीकरणों पर और अधिक काम करने के लिए प्रेरित किया है।
यह भी देखें
- कैलोरी बहुपद
- वक्र-संक्षिप्त प्रवाह
- प्रसार समीकरण
- सापेक्षतावादी ऊष्मा चालन
- श्रोडिंगर समीकरण
- वीयरस्ट्रास रूपांतरण
टिप्पणियाँ
- ↑ Berline, Nicole; Getzler, Ezra; Vergne, Michèle. Heat kernels and Dirac operators. Grundlehren der Mathematischen Wissenschaften, 298. Springer-Verlag, Berlin, 1992. viii+369 pp. ISBN 3-540-53340-0
- ↑ Stojanovic, Srdjan (2003), "3.3.1.3 Uniqueness for heat PDE with exponential growth at infinity", Computational Financial Mathematics using MATHEMATICA®: Optimal Trading in Stocks and Options, Springer, pp. 112–114, ISBN 9780817641979
- ↑ John, Fritz (1991-11-20). आंशिक अंतर समीकरण (in English). Springer Science & Business Media. p. 222. ISBN 978-0-387-90609-6.
- ↑ The Mathworld: Porous Medium Equation and the other related models have solutions with finite wave propagation speed.
- ↑ Juan Luis Vazquez (2006-12-28), The Porous Medium Equation: Mathematical Theory, Oxford University Press, USA, ISBN 978-0-19-856903-9
- ↑ Note that the units of u must be selected in a manner compatible with those of q. Thus instead of being for thermodynamic temperature (Kelvin - K), units of u should be J/L.
- ↑ The Green's Function Library contains a variety of fundamental solutions to the heat equation.
- ↑ Conversely, any function u satisfying the above mean-value property on an open domain of Rn × R is a solution of the heat equation
संदर्भ
- Cannon, John Rozier (1984), The one–dimensional heat equation, Encyclopedia of Mathematics and its Applications, vol. 23, Reading, MA: Addison-Wesley Publishing Company, Advanced Book Program, ISBN 0-201-13522-1, MR 0747979, Zbl 0567.35001
- Crank, J.; Nicolson, P. (1947), "A Practical Method for Numerical Evaluation of Solutions of Partial Differential Equations of the Heat-Conduction Type", Proceedings of the Cambridge Philosophical Society, 43 (1): 50–67, Bibcode:1947PCPS...43...50C, doi:10.1017/S0305004100023197, S2CID 16676040
- Evans, Lawrence C. (2010), Partial Differential Equations, Graduate Studies in Mathematics, vol. 19 (2nd ed.), Providence, RI: American Mathematical Society, ISBN 978-0-8218-4974-3
- Perona, P; Malik, J. (1990), "Scale-Space and Edge Detection Using Anisotropic Diffusion" (PDF), IEEE Transactions on Pattern Analysis and Machine Intelligence, 12 (7): 629–639, doi:10.1109/34.56205, S2CID 14502908
- Thambynayagam, R. K. M. (2011), The Diffusion Handbook: Applied Solutions for Engineers, McGraw-Hill Professional, ISBN 978-0-07-175184-1
- Wilmott, Paul; Howison, Sam; Dewynne, Jeff (1995), The mathematics of financial derivatives. A student introduction, Cambridge: Cambridge University Press, ISBN 0-521-49699-3
अग्रिम पठन
- Carslaw, H.S.; Jaeger, J.C. (1988), Conduction of heat in solids, Oxford Science Publications (2nd ed.), New York: The Clarendon Press, Oxford University Press, ISBN 978-0-19-853368-9
- Cole, Kevin D.; Beck, James V.; Haji-Sheikh, A.; Litkouhi, Bahan (2011), Heat conduction using Green's functions, Series in Computational and Physical Processes in Mechanics and Thermal Sciences (2nd ed.), Boca Raton, FL: CRC Press, ISBN 978-1-43-981354-6
- Einstein, Albert (1905), "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen", Annalen der Physik, 322 (8): 549–560, Bibcode:1905AnP...322..549E, doi:10.1002/andp.19053220806
- Friedman, Avner (1964), Partial differential equations of parabolic type, Englewood Cliffs, N.J.: Prentice-Hall
- Unsworth, J.; Duarte, F. J. (1979), "Heat diffusion in a solid sphere and Fourier Theory", Am. J. Phys., 47 (11): 891–893, Bibcode:1979AmJPh..47..981U, doi:10.1119/1.11601
- Widder, D.V. (1975), The heat equation, Pure and Applied Mathematics, vol. 67, New York-London: Academic Press [Harcourt Brace Jovanovich, Publishers]
इस पेज में लापता आंतरिक लिंक की सूची
- अंक शास्त्र
- भौतिक विज्ञान
- आंशिक विभेदक समीकरण
- गर्म गिरी
- संख्यात्मक विश्लेषण
- सिद्धांत संभावना
- यादृच्छिक चाल
- लाप्लास ऑपरेटर
- कार्तीय समन्वय प्रणाली
- फलन(गणित)
- ऊष्मीय विसरणशीलता
- गुणक
- श्रृंखला नियम
- ऊष्मप्रवैगिकी का दूसरा नियम
- ऊष्मीय चालकता
- प्रसार लहर
- चालन (गर्मी)
- ऊर्जा संरक्षण
- ऊष्मप्रवैगिकी का पहला नियम
- सीमारेखा की हालत
- ऑर्नस्टीन-उहलेनबेक प्रक्रिया
- क्रिया सामर्थ्य
- रैखिक ऑपरेटर
- अंदरूनी प्रोडक्ट
- अच्छी तरह से उत्पन्न समस्या
- अण्डाकार ऑपरेटर
- स्वयं adjoint
- पुराना फलन
- यहां तक कि समारोह
- संभाव्यता घनत्व कार्य
- एकाग्रता
- अनेक संभावनाओं में से चुनी हूई प्रक्रिया
- स्टोचैस्टिक अंतर समीकरण
- रॉबिन सीमा की स्थिति
- गणित का मॉडल
- डिरिचलेट सीमा की स्थिति
- न्यूमैन सीमा की स्थिति
- रिमानियन ज्यामिति
- वेइरस्ट्रास रूपांतरण
बाहरी संबंध
- Derivation of the heat equation
- Linear heat equations: Particular solutions and boundary value problems - from EqWorld
- "The Heat Equation". PBS Infinite Series. November 17, 2017. Archived from the original on 2021-12-11 – via YouTube.