लिपशिट्ज निरंतरता: Difference between revisions
(Created page with "{{short description|Strong form of uniform continuity}} File:Lipschitz Visualisierung.gif|thumb|right|लिपशित्ज़ निरंतर कार्य के...") |
No edit summary |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Strong form of uniform continuity}} | {{short description|Strong form of uniform continuity}} | ||
[[File:Lipschitz Visualisierung.gif|thumb|right|लिपशित्ज़ निरंतर कार्य के लिए, एक डबल शंकु (सफेद) | [[File:Lipschitz Visualisierung.gif|thumb|right|लिपशित्ज़ निरंतर कार्य के लिए, एक डबल शंकु (सफेद) उपस्थित है जिसका मूल ग्राफ के साथ स्थानांतरित किया जा सकता है ताकि पूरा ग्राफ हमेशा डबल शंकु के बाहर रहे]]गणितीय विश्लेषण में, जर्मनी के गणितज्ञ रुडोल्फ लिप्सचित्ज़ के नाम पर लिप्सचिट्ज़ निरंतरता, फलन (गणित) के लिए समान निरंतरता का एक मजबूत रूप है। सहज रूप से, एक लिपशिट्ज निरंतर कार्य सीमित है कि यह कितनी तेजी से बदल सकता है: एक वास्तविक संख्या उपस्थित है, जैसे कि इस फलन के लेखाचित्र पर प्रत्येक जोड़ी के लिए, उन्हें जोड़ने वाली रेखा के ढलान का पूर्ण मूल्य इससे अधिक नहीं है यह वास्तविक संख्या; इस तरह की सबसे छोटी सीमा को फलन (या '' निरंतरता का मापांक '') का ''लिप्सचिट्ज़ स्थिरांक '' कहा जाता है। उदाहरण के लिए, प्रत्येक कार्य जो पहले यौगिक को सीमित करता है, वह लिप्सचिट्ज़ निरंतर है।<ref>{{cite book |url=https://www.google.com/books/edition/_/gBPI_oYZoMMC?hl=en&gbpv=1&pg=PA142 |last=Sohrab |first=H. H. |year=2003 |title=बुनियादी वास्तविक विश्लेषण|volume=231 |publisher=Birkhäuser |page=142 |isbn=0-8176-4211-0 }}</ref> | ||
विभेदक समीकरणों के सिद्धांत में, लिपशिट्ज निरंतरता पिकार्ड-लिंडेलोफ प्रमेय की केंद्रीय स्थिति है जो प्रारंभिक मूल्य समस्या के समाधान के अस्तित्व और विशिष्टता की गारंटी देती है। एक विशेष प्रकार की लिप्सचिट्ज़ निरंतरता, जिसे संकुचन मानचित्रण कहा जाता है, का उपयोग बानाच फिक्स्ड-पॉइंट प्रमेय में किया जाता है।<ref>{{cite book |first=Brian S. |last=Thomson |first2=Judith B. |last2=Bruckner |first3=Andrew M. |last3=Bruckner |title=प्राथमिक वास्तविक विश्लेषण|publisher=Prentice-Hall |year=2001 |page=623 |url=https://www.google.com/books/edition/Elementary_Real_Analysis/6l_E9OTFaK0C?hl=en&gbpv=1&pg=PA623 }}</ref> | विभेदक समीकरणों के सिद्धांत में, लिपशिट्ज निरंतरता पिकार्ड-लिंडेलोफ प्रमेय की केंद्रीय स्थिति है जो प्रारंभिक मूल्य समस्या के समाधान के अस्तित्व और विशिष्टता की गारंटी देती है। एक विशेष प्रकार की लिप्सचिट्ज़ निरंतरता, जिसे संकुचन मानचित्रण कहा जाता है, का उपयोग बानाच फिक्स्ड-पॉइंट प्रमेय में किया जाता है।<ref>{{cite book |first=Brian S. |last=Thomson |first2=Judith B. |last2=Bruckner |first3=Andrew M. |last3=Bruckner |title=प्राथमिक वास्तविक विश्लेषण|publisher=Prentice-Hall |year=2001 |page=623 |url=https://www.google.com/books/edition/Elementary_Real_Analysis/6l_E9OTFaK0C?hl=en&gbpv=1&pg=PA623 }}</ref> | ||
हमारे पास वास्तविक रेखा के | हमारे पास वास्तविक रेखा के एक बंद और परिबद्ध गैर-तुच्छ अंतराल पर कार्यों के लिए सख्त समावेशन की निम्नलिखित श्रृंखला है: | ||
: निरंतर अवकलनीय ⊂ लिप्सचिट्ज़ निरंतर ⊂ <math>\alpha</math>-होल्डर निरंतर, | : निरंतर अवकलनीय ⊂ लिप्सचिट्ज़ निरंतर ⊂ <math>\alpha</math>-होल्डर निरंतर, | ||
| Line 11: | Line 11: | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
दो | दो मापीय रिक्त स्थान दिए गए हैं (एक्स, डी<sub>''X''</sub>) और (वाई, डी<sub>''Y''</sub>), जहां घ<sub>''X''</sub> समूह एक्स और डी पर मापीय (गणित) को दर्शाता है<sub>''Y''</sub> समूह वाई पर मीट्रिक है, एक फलन एफ: एक्स → वाई को 'लिप्सचिट्ज़ निरंतर' कहा जाता है यदि वास्तविक निरंतर के ≥ 0 उपस्थित है, तो सभी एक्स के लिए<sub>1</sub> और एक्स<sub>2</sub> एक्स में, | ||
:<math> d_Y(f(x_1), f(x_2)) \le K d_X(x_1, x_2).</math><ref>{{Citation | last1=Searcóid | first1=Mícheál Ó | title=Metric Spaces |chapter-url=https://www.google.com/books/edition/_/aP37I4QWFRcC?hl=en&gbpv=1&pg=PA154 | publisher=[[Springer-Verlag]] | location=Berlin, New York | series=Springer undergraduate mathematics series | isbn=978-1-84628-369-7 | year=2006 |chapter=Lipschitz Functions }}</ref> | :<math> d_Y(f(x_1), f(x_2)) \le K d_X(x_1, x_2).</math><ref>{{Citation | last1=Searcóid | first1=Mícheál Ó | title=Metric Spaces |chapter-url=https://www.google.com/books/edition/_/aP37I4QWFRcC?hl=en&gbpv=1&pg=PA154 | publisher=[[Springer-Verlag]] | location=Berlin, New York | series=Springer undergraduate mathematics series | isbn=978-1-84628-369-7 | year=2006 |chapter=Lipschitz Functions }}</ref> | ||
ऐसे किसी भी K को फलन f के लिए 'a | ऐसे किसी भी K को फलन f के लिए 'a लिप्सचिट्ज़ स्थिरांक' कहा जाता है और f को 'K-लिप्सचिट्ज़' भी कहा जा सकता है। सबसे छोटे स्थिरांक को कभी-कभी '(सर्वश्रेष्ठ) लिप्सचिट्ज़ स्थिरांक' कहा जाता है<ref>{{cite book |last1=Benyamini |first1=Yoav |last2=Lindenstrauss |first2=Joram |title=ज्यामितीय गैर रेखीय कार्यात्मक विश्लेषण|date=2000 |publisher=American Mathematical Society |isbn=0-8218-0835-4 |page=11}}</ref> च या 'फैलाव' या 'फैलाव' की<ref>{{cite book |last1=Burago |first1=Dmitri |last2=Burago |first2=Yuri |last3=Ivanov |first3=Sergei |title=मीट्रिक ज्यामिति में एक कोर्स|date=2001 |publisher=American Mathematical Society |isbn=0-8218-2129-6}}</ref>{{rp|at=p. 9, Definition 1.4.1}}<ref>{{cite journal |last1=Mahroo |first1=Omar A |last2=Shalchi |first2=Zaid |last3=Hammond |first3=Christopher J |title='Dilatation' और 'dilation': अटलांटिक के दोनों किनारों पर उपयोग में रुझान|journal=British Journal of Ophthalmology |date=2014 |volume=98 |issue=6 |pages=845-846 |doi=10.1136/bjophthalmol-2014-304986 |url=https://bjo.bmj.com/content/98/6/845}}</ref><ref>{{cite book |last1=Gromov |first1=Mikhael |author1-link=Mikhael Gromov (mathematician) |editor1-last=Rossi |editor1-first=Hugo |title=गणित में संभावनाएँ: प्रिंसटन विश्वविद्यालय की 250वीं वर्षगांठ के अवसर पर आमंत्रित वार्ता, 17-21 मार्च, 1996, प्रिंसटन विश्वविद्यालय|chapter=Quantitative Homotopy Theory |date=1999 |publisher=American Mathematical Society |isbn=0-8218-0975-X |page=46}}</ref> बंद। यदि K = 1 फलन को 'लघु मानचित्र' कहा जाता है, और यदि 0 ≤ K <1 और f स्वयं के लिए एक मापीय स्थान मानचित्र करता है, तो फलन को 'संकुचन मानचित्रण' कहा जाता है। | ||
विशेष रूप से, एक वास्तविक-मूल्यवान फलन f : R → R को लिप्सचिट्ज़ निरंतर कहा जाता है यदि वहाँ एक सकारात्मक वास्तविक स्थिरांक K | विशेष रूप से, एक वास्तविक-मूल्यवान फलन f : R → R को लिप्सचिट्ज़ निरंतर कहा जाता है यदि वहाँ एक सकारात्मक वास्तविक स्थिरांक K उपस्थित है जैसे कि, सभी वास्तविक x के लिए<sub>1</sub> और एक्स<sub>2</sub>, | ||
:<math> |f(x_1) - f(x_2)| \le K |x_1 - x_2|.</math> | :<math> |f(x_1) - f(x_2)| \le K |x_1 - x_2|.</math> | ||
इस मामले में, वाई मानक मीट्रिक डी के साथ वास्तविक संख्या 'आर' का | इस मामले में, वाई मानक मीट्रिक डी के साथ वास्तविक संख्या 'आर' का समूह है<sub>''Y''</sub>(वाई<sub>1</sub>, वाई<sub>2</sub>) = |वाई<sub>1</sub>- और<sub>2</sub>|, और X 'R' का उपसमुच्चय है। | ||
सामान्य तौर पर, असमानता (तुच्छ रूप से) संतुष्ट होती है यदि x<sub>1</sub> = एक्स<sub>2</sub>. अन्यथा, कोई समतुल्य रूप से एक | सामान्य तौर पर, असमानता (तुच्छ रूप से) संतुष्ट होती है यदि x<sub>1</sub> = एक्स<sub>2</sub>. अन्यथा, कोई समतुल्य रूप से एक फलन को लिप्सचिट्ज़ निरंतर होने के लिए परिभाषित कर सकता है यदि और केवल यदि एक स्थिर K ≥ 0 उपस्थित है जैसे कि, सभी x के लिए<sub>1</sub> ≠ एक्स<sub>2</sub>, | ||
:<math>\frac{d_Y(f(x_1),f(x_2))}{d_X(x_1,x_2)}\le K.</math> | :<math>\frac{d_Y(f(x_1),f(x_2))}{d_X(x_1,x_2)}\le K.</math> | ||
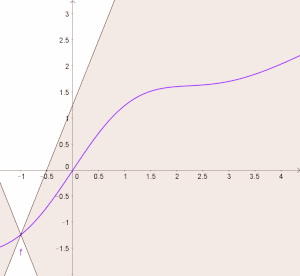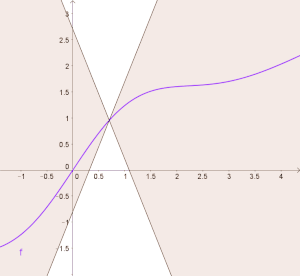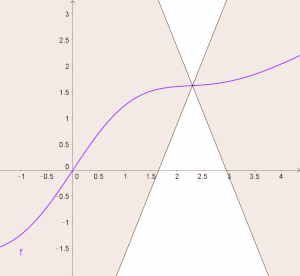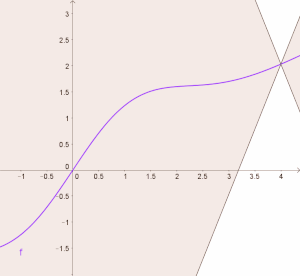
कई वास्तविक चरों के वास्तविक-मूल्यवान कार्यों के लिए, यह तभी और केवल तभी होता है जब सभी छेदक रेखाओं के ढलानों का निरपेक्ष मान K से घिरा | कई वास्तविक चरों के वास्तविक-मूल्यवान कार्यों के लिए, यह तभी और केवल तभी होता है जब सभी छेदक रेखाओं के ढलानों का निरपेक्ष मान K से घिरा हो।और ढलान K की रेखाओं का समूह फलन के लेखाचित्र पर एक बिंदु से होकर निकलता है। गोलाकार शंकु,और एक फलन लिपशिट्ज है यदि और केवल अगर फलन का लेखाचित्र हर जगह इस शंकु के बाहर पूरी तरह से स्थित है (आंकड़ा देखें)। | ||
एक | एक फलन को 'स्थानीय रूप से लिप्सचिट्ज़ निरंतर' कहा जाता है और यदि एक्स में प्रत्येक एक्स के लिए एक्स का पड़ोस (गणित) यू उपस्थित है जैसे कि यू तक सीमित एफ लिप्सचिट्ज़ निरंतर है। समतुल्य रूप से, यदि X एक स्थानीय रूप से सघन मापीय स्थान है, तो f स्थानीय रूप से लिप्सचिट्ज़ है यदि और केवल यदि यह X के प्रत्येक सघन उपसमुच्चय पर लिप्सचिट्ज़ निरंतर है। उन स्थानों में जो स्थानीय रूप से सघन नहीं हैं, यह एक आवश्यक है लेकिन पर्याप्त स्थिति नहीं है। | ||
अधिक | अधिक सामान्यतः, एक्स पर परिभाषित एक फलन एफ को 'होल्डर निरंतर' कहा जाता है या एक्स पर अनुक्रम α > 0 की 'धारक की स्थिति ' को पूरा करने के लिए कहा जाता है यदि निरंतर एम ≥ 0 उपस्थित है जैसे कि | ||
:<math>d_Y(f(x), f(y)) \leq M d_X(x, y)^{\alpha}</math> X में सभी x और y के लिए। कभी-कभी | :<math>d_Y(f(x), f(y)) \leq M d_X(x, y)^{\alpha}</math> X में सभी x और y के लिए। कभी-कभी अनुक्रम α की धारक की स्थिति को 'अनुक्रम की यूनिफॉर्म लिप्सचिट्ज़ स्थिति' α> 0 भी कहा जाता है। | ||
{{anchor|Bilipschitz function|Bilipschitz map}}वास्तविक संख्या K ≥ 1 के लिए, यदि | {{anchor|Bilipschitz function|Bilipschitz map}}वास्तविक संख्या K ≥ 1 के लिए, यदि | ||
:<math>\frac{1}{K}d_X(x_1,x_2) \le d_Y(f(x_1), f(x_2)) \le K d_X(x_1, x_2)\quad\text{ for all }x_1,x_2\in X,</math> | :<math>\frac{1}{K}d_X(x_1,x_2) \le d_Y(f(x_1), f(x_2)) \le K d_X(x_1, x_2)\quad\text{ for all }x_1,x_2\in X,</math> | ||
तब f को 'K-bilipschitz' कहा जाता है ('K-bi- | तब f को 'K-bilipschitz' कहा जाता है ('K-bi-लिप्सचिट्ज़' भी लिखा जाता है)। हम कहते हैं कि f 'bilipschitz' या 'bi-लिप्सचिट्ज़' है, जिसका अर्थ है कि ऐसा K उपस्थित है। एक bilipschitz मानचित्रण अंतः क्षेपण फलन है, और वास्तव में इसकी छवि पर एक होमोमोर्फिज्म है। एक बाइलिप्सिट्ज़ फलन एक एकैकी लिप्सचिट्ज़ फलन के समान है जिसका व्युत्क्रम फलन भी लिप्सचिट्ज़ है। | ||
== उदाहरण == | == उदाहरण == | ||
Lipschitz निरंतर कार्य:{{unordered list | Lipschitz निरंतर कार्य:{{unordered list | ||
| | |फ़ंक्शन <math>f(x)=\sqrt{x^2+5}</math> सभी वास्तविक संख्याओं के लिए परिभाषित लिप्सचिट्ज़ निरंतर लिप्सचिट्ज़ स्थिरांक ''K'' {{=}} 1 के साथ है , क्योंकि यह हर जगह है [[डिफरेंशिएबल फंक्शन|अंतर ]] और यौगिक का निरपेक्ष मान 1 से ऊपर है।|इसी तरह, [[sine]] फलन लिप्सचिट्ज़ निरंतर है क्योंकि इसका व्युत्पन्न, कोज्या फलन, निरपेक्ष मान में 1 से ऊपर परिबद्ध है।|फ़ंक्शन ''f''(''x'') {{=}} {{!}}''x''{{!}} वास्तविक पर परिभाषित लिप्सचिट्ज़ निरंतर लिप्सचिट्ज़ निरंतर बराबर है [[रिवर्स त्रिकोण असमानता]] द्वारा 1 तक। यह एक लिपशिट्ज निरंतर कार्य का एक उदाहरण है जो भिन्न-भिन्न नहीं है। अधिक सामान्यतः , एक सदिश स्थान पर एक [[मानक (गणित)|मानदंड]] संबंधित मापीय के संबंध में लिप्सचिट्ज़ निरंतर है, जिसमें लिप्सचिट्ज़ स्थिरांक 1 के बराबर है।}} | ||
}} | |||
लिप्सचिट्ज़ निरंतर कार्य जो हर जगह भिन्न नहीं होते हैं:{{unordered list | लिप्सचिट्ज़ निरंतर कार्य जो हर जगह भिन्न नहीं होते हैं:{{unordered list | ||
| | |फ़ंक्शन <math>f(x) = |x|</math>}} | ||
लिपशिट्ज निरंतर कार्य जो हर जगह | लिपशिट्ज निरंतर कार्य जो हर जगह भिन्न -भिन्न होते हैं लेकिन लगातार भिन्न -भिन्न नहीं होते हैं:{{unordered list | ||
| | | फ़ंक्शन <math>f(x) \;=\; \begin{cases} x^2\sin (1/x) & \text{if }x \ne 0 \\ 0 & \text{if }x=0\end{cases}</math>, जिसका व्युत्पत्ति मौजूद है लेकिन इसमें एक आवश्यक विच्छिन्नता है<math>x=0</math>. | ||
}} | }} | ||
निरंतर कार्य जो (विश्व स्तर पर) लिप्सचिट्ज़ निरंतर नहीं हैं:{{unordered list | निरंतर कार्य जो (विश्व स्तर पर) लिप्सचिट्ज़ निरंतर नहीं हैं:{{unordered list | ||
| | |1=फलन f(x) = √x [0, 1] पर परिभाषित लिप्सचिट्ज़ निरंतर नहीं है। जैसे-जैसे x 0 की ओर बढ़ता है, यह फलन असीम रूप से तीव्र हो जाता है क्योंकि इसका व्युत्पन्न अनंत हो जाता है। यद्यपि , यह समान रूप से निरंतर है, और दोनों होल्डर निरंतर वर्ग C0, α के लिए α ≤ 1/2 और [0, 1] पर भी बिल्कुल निरंतर (दोनों जिनमें से पूर्व का अर्थ है)।}} | ||
}} | |||
अलग-अलग कार्य जो (स्थानीय रूप से) लिप्सचिट्ज़ निरंतर नहीं हैं:{{unordered list | अलग-अलग कार्य जो (स्थानीय रूप से) लिप्सचिट्ज़ निरंतर नहीं हैं:{{unordered list | ||
| | |1=0<x≤1 के लिए f(0) = 0 और f(x) = x3/2sin(1/x) द्वारा परिभाषित फलन f एक ऐसे फलन का उदाहरण देता है जो कॉम्पैक्ट समूह पर अलग-अलग होता है, जबकि स्थानीय रूप से लिप्सचिट्ज़ नहीं व्युत्पन्न कार्य बाध्य नहीं है। नीचे पहली संपत्ति भी देखें।}} | ||
}} | |||
विश्लेषणात्मक कार्य जो (विश्व स्तर पर) लिप्सचिट्ज़ निरंतर नहीं हैं:{{unordered list | विश्लेषणात्मक कार्य जो (विश्व स्तर पर) लिप्सचिट्ज़ निरंतर नहीं हैं:{{unordered list | ||
| | |घातीय फलन x → ∞ के रूप में मनमाने ढंग से तीव्र हो जाता है, और इसलिए एक विश्लेषणात्मक कार्य होने के अतिरिक्त विश्व स्तर पर लिप्सचिट्ज़ निरंतर नहीं है|2=सभी वास्तविक संख्याओं वाले डोमेन के साथ फलन f(x) =x2 लिप्सचिट्ज़ निरंतर नहीं है। जैसे ही x अनंत तक पहुंचता है, यह फलन मनमाने ढंग से खड़ी हो जाती है। यद्यपि यह स्थानीय रूप से लिप्सचिट्ज़ निरंतर है।}} | ||
}} | |||
== गुण == | == गुण == | ||
*एक हर जगह भिन्न होने वाला | *एक हर जगह भिन्न होने वाला फलन g : 'R' → 'R' लिप्सचिट्ज़ निरंतर है (K = sup |g′(x)|) अगर और केवल अगर यह पहले यौगिक से घिरा हुआ है; माध्य मान प्रमेय से एक दिशा का अनुसरण होता है। विशेष रूप से, कोई भी लगातार भिन्न होने वाला कार्य स्थानीय रूप से लिप्सचिट्ज़ है, क्योंकि निरंतर कार्य स्थानीय रूप से बंधे हुए हैं, इसलिए इसकी ढाल स्थानीय रूप से भी बंधी हुई है। | ||
*ए लिपशिट्ज | *ए लिपशिट्ज फलन g : 'R' → 'R' पूरी तरह से निरंतर है और इसलिए लगभग हर जगह अंतर है, यानी, लेबेस्ग माप शून्य के समूह के बाहर हर बिंदु पर अंतर है। इसका व्युत्पन्न अनिवार्य रूप से लिप्सचिट्ज़ स्थिरांक द्वारा परिमाण में बंधा हुआ है, और a < b के लिए, अंतर g(b) − g(a) अंतराल [a, b] पर व्युत्पन्न g′ के अभिन्न के बराबर है। | ||
** इसके विपरीत, यदि f : I → 'R' बिल्कुल निरंतर है और इस प्रकार लगभग हर जगह | ** इसके विपरीत, यदि f : I → 'R' बिल्कुल निरंतर है और इस प्रकार लगभग हर जगह भिन्न-भिन्न है, और संतुष्ट करता है |f′(x)| I में लगभग सभी x के लिए ≤ K, फिर f लिप्सचिट्ज़ निरंतर लिप्सचिट्ज़ स्थिरांक के साथ अधिकांश K पर है। | ||
** | **सामान्यतः, रैडेमाकर का प्रमेय यूक्लिडियन रिक्त स्थान के बीच लिप्सचिट्ज़ मानचित्रण के लिए विभेदीकरण परिणाम का विस्तार करता है: एक लिपशिट्ज मानचित्र f : U → 'R'<sup>m</sup>, जहां U 'R' में एक विवृत समुच्चय है<sup>n</sup>, लगभग हर जगह व्युत्पन्न है। और इसके अतिरिक्त, अगर K f का सबसे अच्छा लिप्सचिट्ज़ स्थिरांक है, तो <math>\|Df(x)\|\le K</math> जब भी कुल व्युत्पन्न डीएफ उपस्थित होता है। | ||
* एक भिन्न लिप्सचिट्ज़ मानचित्र के लिए <math>f: U \to \R^m</math> असमानता <math>\|Df\|_{W^{1,\infty}(U)}\le K</math> सबसे अच्छा लिपशिट्ज स्थिरांक रखता है <math>K</math> का <math>f</math>. यदि डोमेन <math>U</math> वास्तव में उत्तल है <math>\|Df\|_{W^{1,\infty}(U)}= K</math>.{{Explain|date=November 2019}} | * एक भिन्न लिप्सचिट्ज़ मानचित्र के लिए <math>f: U \to \R^m</math> असमानता <math>\|Df\|_{W^{1,\infty}(U)}\le K</math> सबसे अच्छा लिपशिट्ज स्थिरांक रखता है <math>K</math> का <math>f</math>. यदि डोमेन <math>U</math> वास्तव में उत्तल है <math>\|Df\|_{W^{1,\infty}(U)}= K</math>.{{Explain|date=November 2019}} | ||
*मान लीजिए कि {एफ<sub>n</sub>} दो | *मान लीजिए कि {एफ<sub>n</sub>} दो मापीय रिक्त स्थान के बीच लिप्सचिट्ज़ निरंतर मानचित्रण का अनुक्रम है, और यह कि सभी f<sub>n</sub>लिप्सचिट्ज़ स्थिरांक कुछ K द्वारा परिबद्ध है। यदि f<sub>n</sub>मानचित्रण f एक समान अभिसरण में अभिसरण करता है, फिर f भी लिप्सचिट्ज़ है, जिसमें लिप्सचिट्ज़ स्थिरांक उसी K से घिरा होता है। विशेष रूप से, इसका तात्पर्य यह है कि लिप्सचिट्ज़ स्थिरांक के लिए एक विशेष सीमा के साथ एक सघन मापीय स्थान पर वास्तविक-मूल्यवान कार्यों का समूह है निरंतर कार्यों के बनच स्थान का एक बंद और उत्तल उपसमुच्चय। यद्यपि , यह परिणाम उन अनुक्रमों के लिए नहीं है जिनमें फ़ंक्शंस में अबाध लिप्सचिट्ज़ स्थिरांक हो सकते हैं। वास्तव में, सघन मेट्रिक स्पेस पर सभी लिप्सचिट्ज़ फ़ंक्शंस का स्थान निरंतर कार्यों के बानाच स्पेस का एक सबलजेब्रा है, और इस प्रकार इसमें घना है, जो स्टोन-वीयरस्ट्रैस प्रमेय का एक प्रारंभिक परिणाम है (या वेइरस्ट्रास सन्निकटन प्रमेय के परिणामस्वरूप, क्योंकि हर बहुपद स्थानीय रूप से लिप्सचिट्ज़ निरंतर है)। | ||
* प्रत्येक लिपशित्ज़ निरंतर मानचित्र समान रूप से निरंतर है, और इसलिए एक फ़ोर्टियोरी निरंतर कार्य करता है। अधिक | * प्रत्येक लिपशित्ज़ निरंतर मानचित्र समान रूप से निरंतर है, और इसलिए एक फ़ोर्टियोरी निरंतर कार्य करता है। अधिक सामान्यतः, परिबद्ध लिप्सचिट्ज़ स्थिरांक वाले कार्यों का एक समूह एक सम-सतत समूह बनाता है। अरज़ेला-एस्कोली प्रमेय का अर्थ यह है कि यदि {f<sub>n</sub>} परिबद्ध लिप्सचिट्ज़ स्थिरांक के साथ कार्यों का एक समान रूप से बंधा हुआ अनुक्रम है, तो इसका एक अभिसरण अनुवर्ती है। पिछले अनुच्छेद के परिणाम से, सीमा फंक्शन भी लिप्सचिट्ज़ है, लिप्सचिट्ज़ स्थिरांक के लिए समान बाउंड के साथ। विशेष रूप से सघन मेट्रिक स्पेस एक्स पर लिप्सचिट्ज़ स्थिरांक ≤ के वाले सभी वास्तविक-मूल्यवान लिप्सचिट्ज़ फ़ंक्शंस का समूह बानाच स्पेस सी (एक्स) का स्थानीय रूप से सघन स्पेस उत्तल सबसमूह है। | ||
* | *लिप्सचिट्ज़ के एक परिवार के लिए निरंतर कार्य f<sub>α</sub> सामान्य स्थिरांक के साथ, फलन <math>\sup_\alpha f_\alpha</math> (तथा <math>\inf_\alpha f_\alpha</math>) लिप्सचिट्ज़ निरंतर भी है, समान लिप्सचिट्ज़ स्थिरांक के साथ, बशर्ते कि यह कम से कम एक बिंदु पर एक परिमित मान ग्रहण करे। | ||
*यदि U | *यदि U मापीय स्थान M का एक उपसमुच्चय है और f : U → 'R' एक लिप्सचिट्ज़ निरंतर कार्य है, तो सर्वदा लिप्सचिट्ज़ निरंतर मानचित्र M → 'R' उपस्थित होते हैं जो f का विस्तार करते हैं और f के समान लिप्सचिट्ज़ स्थिरांक रखते हैं (यह भी देखें किर्स्ज़ब्रौन प्रमेय)। द्वारा एक विस्तार प्रदान किया जाता है | ||
::<math>\tilde f(x):=\inf_{u\in U}\{ f(u)+k\, d(x,u)\},</math> : जहाँ k, U पर f के लिए लिप्सचिट्ज़ स्थिरांक है। | ::<math>\tilde f(x):=\inf_{u\in U}\{ f(u)+k\, d(x,u)\},</math> : जहाँ k, U पर f के लिए लिप्सचिट्ज़ स्थिरांक है। | ||
== लिप्सचिट्ज़ मैनिफोल्ड्स == | == लिप्सचिट्ज़ मैनिफोल्ड्स == | ||
एक टोपोलॉजिकल मैनिफोल्ड पर एक लिप्सचिट्ज़ संरचना को एक एटलस (टोपोलॉजी) का उपयोग करके परिभाषित किया गया है, जिसके संक्रमण मानचित्र बाइलिप्सचिट्ज़ हैं; यह संभव है क्योंकि बाइलिप्सचिट्ज़ मानचित्र एक | एक टोपोलॉजिकल मैनिफोल्ड पर एक लिप्सचिट्ज़ संरचना को एक एटलस (टोपोलॉजी) का उपयोग करके परिभाषित किया गया है, जिसके संक्रमण मानचित्र बाइलिप्सचिट्ज़ हैं; और यह संभव है क्योंकि बाइलिप्सचिट्ज़ मानचित्र एक छद्मसमूह बनाते हैं। इस तरह की संरचना किसी को इस तरह के मैनिफोल्ड्स के बीच स्थानीय रूप से लिप्सचिट्ज़ मानचित्रों को परिभाषित करने की अनुमति देती है, इसी तरह चिकनी मैनिफोल्ड्स के बीच चिकने नक्शों को कैसे परिभाषित किया जाता है: यदि {{mvar|M}} तथा {{mvar|N}} लिप्सचिट्ज़ मैनिफोल्ड्स हैं, फिर एक फलन <math>f:M \to N</math> स्थानीय रूप से लिप्सचिट्ज़ है अगर और केवल अगर समन्वय चार्ट के प्रत्येक जोड़े के लिए <math>\phi:U \to M</math> तथा <math>\psi:V \to N</math>, कहाँ पे {{mvar|U}} तथा {{mvar|V}} इसी यूक्लिडियन रिक्त स्थान, संरचना में खुले समूह हैं | ||
<math display="block">\psi^{-1} \circ f \circ \phi:U \cap (f \circ \phi)^{-1}(\psi(V)) \to N</math> | <math display="block">\psi^{-1} \circ f \circ \phi:U \cap (f \circ \phi)^{-1}(\psi(V)) \to N</math> | ||
स्थानीय रूप से लिप्सचिट्ज़ है। यह परिभाषा किसी | स्थानीय रूप से लिप्सचिट्ज़ है। यह परिभाषा किसी मापीय को परिभाषित करने पर निर्भर नहीं करती है {{mvar|M}} या {{mvar|N}}.<ref name="Rosenberg">{{cite conference |first=Jonathan |last=Rosenberg |author-link=Jonathan Rosenberg (mathematician) |book-title=Miniconferences on harmonic analysis and operator algebras (Canberra, 1987) |title=लिपशिट्ज मैनिफोल्ड्स पर विश्लेषण के अनुप्रयोग|year=1988 |publisher=[[Australian National University]] |location=Canberra |pages=269–283 |url=https://projecteuclid.org/proceedings/proceedings-of-the-centre-for-mathematics-and-its-applications/Miniconference-on-Harmonic-Analysis-and-Operator-Algebras/Chapter/Applications-of-analysis-on-Lipschitz-manifolds/pcma/1416336222}} {{MathSciNet|id=954004}}</ref> | ||
यह संरचना एक टुकड़ा-रेखीय कई गुना और एक स्थलीय कई गुना के बीच मध्यवर्ती है: एक पीएल संरचना एक अद्वितीय लिप्सचिट्ज़ संरचना को जन्म देती है।<ref>{{SpringerEOM|title=Topology of manifolds}}</ref> जबकि लिप्सचिट्ज़ मैनिफोल्ड्स टोपोलॉजिकल मैनिफोल्ड्स से निकटता से संबंधित हैं, रेडमाकर का प्रमेय किसी को विश्लेषण करने की अनुमति देता है, विभिन्न अनुप्रयोगों को उत्पन्न करता है।<ref name="Rosenberg"/> | यह संरचना एक टुकड़ा-रेखीय कई गुना और एक स्थलीय कई गुना के बीच मध्यवर्ती है: एक पीएल संरचना एक अद्वितीय लिप्सचिट्ज़ संरचना को जन्म देती है।<ref>{{SpringerEOM|title=Topology of manifolds}}</ref> जबकि लिप्सचिट्ज़ मैनिफोल्ड्स टोपोलॉजिकल मैनिफोल्ड्स से निकटता से संबंधित हैं, रेडमाकर का प्रमेय किसी को विश्लेषण करने की अनुमति देता है, और विभिन्न अनुप्रयोगों को उत्पन्न करता है।<ref name="Rosenberg"/> | ||
== एक तरफा लिपशिट्ज == | == एक तरफा लिपशिट्ज == | ||
चलो F(x) | चलो F(x) एकअर्ध-निरंतर का ऊपरी अर्ध-निरंतर कार्य x हो, और यह कि F(x) सभी x के लिए एक बंद, उत्तल समूह है। तब F एक तरफा लिपशिट्ज है<ref>{{cite journal |last=Donchev |first=Tzanko |last2=Farkhi |first2=Elza |year=1998 |title=स्थिरता और यूलर सन्निकटन एक तरफा लिपशित्ज़ विभेदक समावेशन|journal=SIAM Journal on Control and Optimization |volume=36 |issue=2 |pages=780–796 |doi=10.1137/S0363012995293694 }}</ref> यदि | ||
:<math>(x_1-x_2)^T(F(x_1)-F(x_2))\leq C\Vert x_1-x_2\Vert^2</math> कुछ सी के लिए और सभी एक्स के लिए<sub>1</sub> और एक्स<sub>2</sub>. | :<math>(x_1-x_2)^T(F(x_1)-F(x_2))\leq C\Vert x_1-x_2\Vert^2</math> कुछ सी के लिए और सभी एक्स के लिए<sub>1</sub> और एक्स<sub>2</sub>. | ||
यह संभव है कि | यह संभव है कि फलन F में एक बहुत बड़ा लिप्सचिट्ज़ स्थिरांक हो सकता है, लेकिन एक मध्यम आकार का, या नकारात्मक, एक ओर लिप्सचिट्ज़ स्थिरांक भी हो सकता है। उदाहरण के लिए, समारोह | ||
:<math>\begin{cases} | :<math>\begin{cases} | ||
| Line 88: | Line 81: | ||
== यह भी देखें == | == यह भी देखें == | ||
* {{annotated link| | * {{annotated link|संकुचन मानचित्रण}} | ||
* दीनी निरंतरता | * दीनी निरंतरता | ||
* निरंतरता का मापांक | * निरंतरता का मापांक | ||
* क्वासी-आइसोमेट्री | * क्वासी-आइसोमेट्री | ||
* जॉनसन-लिंडनस्ट्रॉस लेम्मा - किसी पूर्णांक n≥0 के लिए, कोई परिमित उपसमुच्चय X⊆'R'<sup>n</sup>, और कोई वास्तविक संख्या 0<ε<1, एक (1+ε)-bi- | * जॉनसन-लिंडनस्ट्रॉस लेम्मा - किसी पूर्णांक n≥0 के लिए, कोई परिमित उपसमुच्चय X⊆'R'<sup>n</sup>, और कोई वास्तविक संख्या 0<ε<1, एक (1+ε)-bi-लिप्सचिट्ज़ फलन उपस्थित है <math>f:\mathbb R^n\to\mathbb R^d,</math> कहाँ पे <math>d=\lceil15(\ln|X|)/\varepsilon^2\rceil.</math> | ||
| Line 100: | Line 93: | ||
==संदर्भ== | ==संदर्भ== | ||
{{reflist}} | {{reflist}} | ||
[[Category:Articles with short description]] | |||
[[Category: | |||
[[Category:Created On 25/11/2022]] | [[Category:Created On 25/11/2022]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Wikipedia articles needing clarification from November 2019]] | |||
[[Category:कई गुना संरचनाएं]] | |||
[[Category:लिप्सचिट्ज़ मानचित्र| ]] | |||
Latest revision as of 10:12, 4 January 2023
गणितीय विश्लेषण में, जर्मनी के गणितज्ञ रुडोल्फ लिप्सचित्ज़ के नाम पर लिप्सचिट्ज़ निरंतरता, फलन (गणित) के लिए समान निरंतरता का एक मजबूत रूप है। सहज रूप से, एक लिपशिट्ज निरंतर कार्य सीमित है कि यह कितनी तेजी से बदल सकता है: एक वास्तविक संख्या उपस्थित है, जैसे कि इस फलन के लेखाचित्र पर प्रत्येक जोड़ी के लिए, उन्हें जोड़ने वाली रेखा के ढलान का पूर्ण मूल्य इससे अधिक नहीं है यह वास्तविक संख्या; इस तरह की सबसे छोटी सीमा को फलन (या निरंतरता का मापांक ) का लिप्सचिट्ज़ स्थिरांक कहा जाता है। उदाहरण के लिए, प्रत्येक कार्य जो पहले यौगिक को सीमित करता है, वह लिप्सचिट्ज़ निरंतर है।[1]
विभेदक समीकरणों के सिद्धांत में, लिपशिट्ज निरंतरता पिकार्ड-लिंडेलोफ प्रमेय की केंद्रीय स्थिति है जो प्रारंभिक मूल्य समस्या के समाधान के अस्तित्व और विशिष्टता की गारंटी देती है। एक विशेष प्रकार की लिप्सचिट्ज़ निरंतरता, जिसे संकुचन मानचित्रण कहा जाता है, का उपयोग बानाच फिक्स्ड-पॉइंट प्रमेय में किया जाता है।[2] हमारे पास वास्तविक रेखा के एक बंद और परिबद्ध गैर-तुच्छ अंतराल पर कार्यों के लिए सख्त समावेशन की निम्नलिखित श्रृंखला है:
- निरंतर अवकलनीय ⊂ लिप्सचिट्ज़ निरंतर ⊂ -होल्डर निरंतर,
कहाँ पे . हमारे पास भी है
- लिपशिट्ज निरंतर ⊂ बिल्कुल निरंतर ⊂ समान रूप से निरंतर।
परिभाषाएँ
दो मापीय रिक्त स्थान दिए गए हैं (एक्स, डीX) और (वाई, डीY), जहां घX समूह एक्स और डी पर मापीय (गणित) को दर्शाता हैY समूह वाई पर मीट्रिक है, एक फलन एफ: एक्स → वाई को 'लिप्सचिट्ज़ निरंतर' कहा जाता है यदि वास्तविक निरंतर के ≥ 0 उपस्थित है, तो सभी एक्स के लिए1 और एक्स2 एक्स में,
ऐसे किसी भी K को फलन f के लिए 'a लिप्सचिट्ज़ स्थिरांक' कहा जाता है और f को 'K-लिप्सचिट्ज़' भी कहा जा सकता है। सबसे छोटे स्थिरांक को कभी-कभी '(सर्वश्रेष्ठ) लिप्सचिट्ज़ स्थिरांक' कहा जाता है[4] च या 'फैलाव' या 'फैलाव' की[5]: p. 9, Definition 1.4.1 [6][7] बंद। यदि K = 1 फलन को 'लघु मानचित्र' कहा जाता है, और यदि 0 ≤ K <1 और f स्वयं के लिए एक मापीय स्थान मानचित्र करता है, तो फलन को 'संकुचन मानचित्रण' कहा जाता है।
विशेष रूप से, एक वास्तविक-मूल्यवान फलन f : R → R को लिप्सचिट्ज़ निरंतर कहा जाता है यदि वहाँ एक सकारात्मक वास्तविक स्थिरांक K उपस्थित है जैसे कि, सभी वास्तविक x के लिए1 और एक्स2,
इस मामले में, वाई मानक मीट्रिक डी के साथ वास्तविक संख्या 'आर' का समूह हैY(वाई1, वाई2) = |वाई1- और2|, और X 'R' का उपसमुच्चय है।
सामान्य तौर पर, असमानता (तुच्छ रूप से) संतुष्ट होती है यदि x1 = एक्स2. अन्यथा, कोई समतुल्य रूप से एक फलन को लिप्सचिट्ज़ निरंतर होने के लिए परिभाषित कर सकता है यदि और केवल यदि एक स्थिर K ≥ 0 उपस्थित है जैसे कि, सभी x के लिए1 ≠ एक्स2,
कई वास्तविक चरों के वास्तविक-मूल्यवान कार्यों के लिए, यह तभी और केवल तभी होता है जब सभी छेदक रेखाओं के ढलानों का निरपेक्ष मान K से घिरा हो।और ढलान K की रेखाओं का समूह फलन के लेखाचित्र पर एक बिंदु से होकर निकलता है। गोलाकार शंकु,और एक फलन लिपशिट्ज है यदि और केवल अगर फलन का लेखाचित्र हर जगह इस शंकु के बाहर पूरी तरह से स्थित है (आंकड़ा देखें)।
एक फलन को 'स्थानीय रूप से लिप्सचिट्ज़ निरंतर' कहा जाता है और यदि एक्स में प्रत्येक एक्स के लिए एक्स का पड़ोस (गणित) यू उपस्थित है जैसे कि यू तक सीमित एफ लिप्सचिट्ज़ निरंतर है। समतुल्य रूप से, यदि X एक स्थानीय रूप से सघन मापीय स्थान है, तो f स्थानीय रूप से लिप्सचिट्ज़ है यदि और केवल यदि यह X के प्रत्येक सघन उपसमुच्चय पर लिप्सचिट्ज़ निरंतर है। उन स्थानों में जो स्थानीय रूप से सघन नहीं हैं, यह एक आवश्यक है लेकिन पर्याप्त स्थिति नहीं है।
अधिक सामान्यतः, एक्स पर परिभाषित एक फलन एफ को 'होल्डर निरंतर' कहा जाता है या एक्स पर अनुक्रम α > 0 की 'धारक की स्थिति ' को पूरा करने के लिए कहा जाता है यदि निरंतर एम ≥ 0 उपस्थित है जैसे कि
- X में सभी x और y के लिए। कभी-कभी अनुक्रम α की धारक की स्थिति को 'अनुक्रम की यूनिफॉर्म लिप्सचिट्ज़ स्थिति' α> 0 भी कहा जाता है।
वास्तविक संख्या K ≥ 1 के लिए, यदि
तब f को 'K-bilipschitz' कहा जाता है ('K-bi-लिप्सचिट्ज़' भी लिखा जाता है)। हम कहते हैं कि f 'bilipschitz' या 'bi-लिप्सचिट्ज़' है, जिसका अर्थ है कि ऐसा K उपस्थित है। एक bilipschitz मानचित्रण अंतः क्षेपण फलन है, और वास्तव में इसकी छवि पर एक होमोमोर्फिज्म है। एक बाइलिप्सिट्ज़ फलन एक एकैकी लिप्सचिट्ज़ फलन के समान है जिसका व्युत्क्रम फलन भी लिप्सचिट्ज़ है।
उदाहरण
Lipschitz निरंतर कार्य:
- फ़ंक्शन सभी वास्तविक संख्याओं के लिए परिभाषित लिप्सचिट्ज़ निरंतर लिप्सचिट्ज़ स्थिरांक K = 1 के साथ है , क्योंकि यह हर जगह है अंतर और यौगिक का निरपेक्ष मान 1 से ऊपर है।
- इसी तरह, sine फलन लिप्सचिट्ज़ निरंतर है क्योंकि इसका व्युत्पन्न, कोज्या फलन, निरपेक्ष मान में 1 से ऊपर परिबद्ध है।
- फ़ंक्शन f(x) = |x| वास्तविक पर परिभाषित लिप्सचिट्ज़ निरंतर लिप्सचिट्ज़ निरंतर बराबर है रिवर्स त्रिकोण असमानता द्वारा 1 तक। यह एक लिपशिट्ज निरंतर कार्य का एक उदाहरण है जो भिन्न-भिन्न नहीं है। अधिक सामान्यतः , एक सदिश स्थान पर एक मानदंड संबंधित मापीय के संबंध में लिप्सचिट्ज़ निरंतर है, जिसमें लिप्सचिट्ज़ स्थिरांक 1 के बराबर है।
लिप्सचिट्ज़ निरंतर कार्य जो हर जगह भिन्न नहीं होते हैं:
- फ़ंक्शन
लिपशिट्ज निरंतर कार्य जो हर जगह भिन्न -भिन्न होते हैं लेकिन लगातार भिन्न -भिन्न नहीं होते हैं:
- फ़ंक्शन , जिसका व्युत्पत्ति मौजूद है लेकिन इसमें एक आवश्यक विच्छिन्नता है.
निरंतर कार्य जो (विश्व स्तर पर) लिप्सचिट्ज़ निरंतर नहीं हैं:
- फलन f(x) = √x [0, 1] पर परिभाषित लिप्सचिट्ज़ निरंतर नहीं है। जैसे-जैसे x 0 की ओर बढ़ता है, यह फलन असीम रूप से तीव्र हो जाता है क्योंकि इसका व्युत्पन्न अनंत हो जाता है। यद्यपि , यह समान रूप से निरंतर है, और दोनों होल्डर निरंतर वर्ग C0, α के लिए α ≤ 1/2 और [0, 1] पर भी बिल्कुल निरंतर (दोनों जिनमें से पूर्व का अर्थ है)।
अलग-अलग कार्य जो (स्थानीय रूप से) लिप्सचिट्ज़ निरंतर नहीं हैं:
- 0<x≤1 के लिए f(0) = 0 और f(x) = x3/2sin(1/x) द्वारा परिभाषित फलन f एक ऐसे फलन का उदाहरण देता है जो कॉम्पैक्ट समूह पर अलग-अलग होता है, जबकि स्थानीय रूप से लिप्सचिट्ज़ नहीं व्युत्पन्न कार्य बाध्य नहीं है। नीचे पहली संपत्ति भी देखें।
विश्लेषणात्मक कार्य जो (विश्व स्तर पर) लिप्सचिट्ज़ निरंतर नहीं हैं:
- घातीय फलन x → ∞ के रूप में मनमाने ढंग से तीव्र हो जाता है, और इसलिए एक विश्लेषणात्मक कार्य होने के अतिरिक्त विश्व स्तर पर लिप्सचिट्ज़ निरंतर नहीं है
- सभी वास्तविक संख्याओं वाले डोमेन के साथ फलन f(x) =x2 लिप्सचिट्ज़ निरंतर नहीं है। जैसे ही x अनंत तक पहुंचता है, यह फलन मनमाने ढंग से खड़ी हो जाती है। यद्यपि यह स्थानीय रूप से लिप्सचिट्ज़ निरंतर है।
गुण
- एक हर जगह भिन्न होने वाला फलन g : 'R' → 'R' लिप्सचिट्ज़ निरंतर है (K = sup |g′(x)|) अगर और केवल अगर यह पहले यौगिक से घिरा हुआ है; माध्य मान प्रमेय से एक दिशा का अनुसरण होता है। विशेष रूप से, कोई भी लगातार भिन्न होने वाला कार्य स्थानीय रूप से लिप्सचिट्ज़ है, क्योंकि निरंतर कार्य स्थानीय रूप से बंधे हुए हैं, इसलिए इसकी ढाल स्थानीय रूप से भी बंधी हुई है।
- ए लिपशिट्ज फलन g : 'R' → 'R' पूरी तरह से निरंतर है और इसलिए लगभग हर जगह अंतर है, यानी, लेबेस्ग माप शून्य के समूह के बाहर हर बिंदु पर अंतर है। इसका व्युत्पन्न अनिवार्य रूप से लिप्सचिट्ज़ स्थिरांक द्वारा परिमाण में बंधा हुआ है, और a < b के लिए, अंतर g(b) − g(a) अंतराल [a, b] पर व्युत्पन्न g′ के अभिन्न के बराबर है।
- इसके विपरीत, यदि f : I → 'R' बिल्कुल निरंतर है और इस प्रकार लगभग हर जगह भिन्न-भिन्न है, और संतुष्ट करता है |f′(x)| I में लगभग सभी x के लिए ≤ K, फिर f लिप्सचिट्ज़ निरंतर लिप्सचिट्ज़ स्थिरांक के साथ अधिकांश K पर है।
- सामान्यतः, रैडेमाकर का प्रमेय यूक्लिडियन रिक्त स्थान के बीच लिप्सचिट्ज़ मानचित्रण के लिए विभेदीकरण परिणाम का विस्तार करता है: एक लिपशिट्ज मानचित्र f : U → 'R'm, जहां U 'R' में एक विवृत समुच्चय हैn, लगभग हर जगह व्युत्पन्न है। और इसके अतिरिक्त, अगर K f का सबसे अच्छा लिप्सचिट्ज़ स्थिरांक है, तो जब भी कुल व्युत्पन्न डीएफ उपस्थित होता है।
- एक भिन्न लिप्सचिट्ज़ मानचित्र के लिए असमानता सबसे अच्छा लिपशिट्ज स्थिरांक रखता है का . यदि डोमेन वास्तव में उत्तल है .[further explanation needed]
- मान लीजिए कि {एफn} दो मापीय रिक्त स्थान के बीच लिप्सचिट्ज़ निरंतर मानचित्रण का अनुक्रम है, और यह कि सभी fnलिप्सचिट्ज़ स्थिरांक कुछ K द्वारा परिबद्ध है। यदि fnमानचित्रण f एक समान अभिसरण में अभिसरण करता है, फिर f भी लिप्सचिट्ज़ है, जिसमें लिप्सचिट्ज़ स्थिरांक उसी K से घिरा होता है। विशेष रूप से, इसका तात्पर्य यह है कि लिप्सचिट्ज़ स्थिरांक के लिए एक विशेष सीमा के साथ एक सघन मापीय स्थान पर वास्तविक-मूल्यवान कार्यों का समूह है निरंतर कार्यों के बनच स्थान का एक बंद और उत्तल उपसमुच्चय। यद्यपि , यह परिणाम उन अनुक्रमों के लिए नहीं है जिनमें फ़ंक्शंस में अबाध लिप्सचिट्ज़ स्थिरांक हो सकते हैं। वास्तव में, सघन मेट्रिक स्पेस पर सभी लिप्सचिट्ज़ फ़ंक्शंस का स्थान निरंतर कार्यों के बानाच स्पेस का एक सबलजेब्रा है, और इस प्रकार इसमें घना है, जो स्टोन-वीयरस्ट्रैस प्रमेय का एक प्रारंभिक परिणाम है (या वेइरस्ट्रास सन्निकटन प्रमेय के परिणामस्वरूप, क्योंकि हर बहुपद स्थानीय रूप से लिप्सचिट्ज़ निरंतर है)।
- प्रत्येक लिपशित्ज़ निरंतर मानचित्र समान रूप से निरंतर है, और इसलिए एक फ़ोर्टियोरी निरंतर कार्य करता है। अधिक सामान्यतः, परिबद्ध लिप्सचिट्ज़ स्थिरांक वाले कार्यों का एक समूह एक सम-सतत समूह बनाता है। अरज़ेला-एस्कोली प्रमेय का अर्थ यह है कि यदि {fn} परिबद्ध लिप्सचिट्ज़ स्थिरांक के साथ कार्यों का एक समान रूप से बंधा हुआ अनुक्रम है, तो इसका एक अभिसरण अनुवर्ती है। पिछले अनुच्छेद के परिणाम से, सीमा फंक्शन भी लिप्सचिट्ज़ है, लिप्सचिट्ज़ स्थिरांक के लिए समान बाउंड के साथ। विशेष रूप से सघन मेट्रिक स्पेस एक्स पर लिप्सचिट्ज़ स्थिरांक ≤ के वाले सभी वास्तविक-मूल्यवान लिप्सचिट्ज़ फ़ंक्शंस का समूह बानाच स्पेस सी (एक्स) का स्थानीय रूप से सघन स्पेस उत्तल सबसमूह है।
- लिप्सचिट्ज़ के एक परिवार के लिए निरंतर कार्य fα सामान्य स्थिरांक के साथ, फलन (तथा ) लिप्सचिट्ज़ निरंतर भी है, समान लिप्सचिट्ज़ स्थिरांक के साथ, बशर्ते कि यह कम से कम एक बिंदु पर एक परिमित मान ग्रहण करे।
- यदि U मापीय स्थान M का एक उपसमुच्चय है और f : U → 'R' एक लिप्सचिट्ज़ निरंतर कार्य है, तो सर्वदा लिप्सचिट्ज़ निरंतर मानचित्र M → 'R' उपस्थित होते हैं जो f का विस्तार करते हैं और f के समान लिप्सचिट्ज़ स्थिरांक रखते हैं (यह भी देखें किर्स्ज़ब्रौन प्रमेय)। द्वारा एक विस्तार प्रदान किया जाता है
- : जहाँ k, U पर f के लिए लिप्सचिट्ज़ स्थिरांक है।
लिप्सचिट्ज़ मैनिफोल्ड्स
एक टोपोलॉजिकल मैनिफोल्ड पर एक लिप्सचिट्ज़ संरचना को एक एटलस (टोपोलॉजी) का उपयोग करके परिभाषित किया गया है, जिसके संक्रमण मानचित्र बाइलिप्सचिट्ज़ हैं; और यह संभव है क्योंकि बाइलिप्सचिट्ज़ मानचित्र एक छद्मसमूह बनाते हैं। इस तरह की संरचना किसी को इस तरह के मैनिफोल्ड्स के बीच स्थानीय रूप से लिप्सचिट्ज़ मानचित्रों को परिभाषित करने की अनुमति देती है, इसी तरह चिकनी मैनिफोल्ड्स के बीच चिकने नक्शों को कैसे परिभाषित किया जाता है: यदि M तथा N लिप्सचिट्ज़ मैनिफोल्ड्स हैं, फिर एक फलन स्थानीय रूप से लिप्सचिट्ज़ है अगर और केवल अगर समन्वय चार्ट के प्रत्येक जोड़े के लिए तथा , कहाँ पे U तथा V इसी यूक्लिडियन रिक्त स्थान, संरचना में खुले समूह हैं
एक तरफा लिपशिट्ज
चलो F(x) एकअर्ध-निरंतर का ऊपरी अर्ध-निरंतर कार्य x हो, और यह कि F(x) सभी x के लिए एक बंद, उत्तल समूह है। तब F एक तरफा लिपशिट्ज है[10] यदि
- कुछ सी के लिए और सभी एक्स के लिए1 और एक्स2.
यह संभव है कि फलन F में एक बहुत बड़ा लिप्सचिट्ज़ स्थिरांक हो सकता है, लेकिन एक मध्यम आकार का, या नकारात्मक, एक ओर लिप्सचिट्ज़ स्थिरांक भी हो सकता है। उदाहरण के लिए, समारोह
लिप्सचिट्ज़ स्थिरांक K = 50 और एक तरफा लिप्सचिट्ज़ स्थिरांक C = 0 है। एक उदाहरण जो एक तरफा लिप्सचिट्ज़ है लेकिन लिप्सचिट्ज़ निरंतर नहीं है F(x) = e−x, C = 0 के साथ।
यह भी देखें
- संकुचन मानचित्रण – Function reducing distance between all points
- दीनी निरंतरता
- निरंतरता का मापांक
- क्वासी-आइसोमेट्री
- जॉनसन-लिंडनस्ट्रॉस लेम्मा - किसी पूर्णांक n≥0 के लिए, कोई परिमित उपसमुच्चय X⊆'R'n, और कोई वास्तविक संख्या 0<ε<1, एक (1+ε)-bi-लिप्सचिट्ज़ फलन उपस्थित है कहाँ पे
इस पेज में लापता आंतरिक लिंक की सूची
संदर्भ
- ↑ Sohrab, H. H. (2003). बुनियादी वास्तविक विश्लेषण. Vol. 231. Birkhäuser. p. 142. ISBN 0-8176-4211-0.
- ↑ Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2001). प्राथमिक वास्तविक विश्लेषण. Prentice-Hall. p. 623.
- ↑ Searcóid, Mícheál Ó (2006), "Lipschitz Functions", Metric Spaces, Springer undergraduate mathematics series, Berlin, New York: Springer-Verlag, ISBN 978-1-84628-369-7
- ↑ Benyamini, Yoav; Lindenstrauss, Joram (2000). ज्यामितीय गैर रेखीय कार्यात्मक विश्लेषण. American Mathematical Society. p. 11. ISBN 0-8218-0835-4.
- ↑ Burago, Dmitri; Burago, Yuri; Ivanov, Sergei (2001). मीट्रिक ज्यामिति में एक कोर्स. American Mathematical Society. ISBN 0-8218-2129-6.
- ↑ Mahroo, Omar A; Shalchi, Zaid; Hammond, Christopher J (2014). "'Dilatation' और 'dilation': अटलांटिक के दोनों किनारों पर उपयोग में रुझान". British Journal of Ophthalmology. 98 (6): 845–846. doi:10.1136/bjophthalmol-2014-304986.
- ↑ Gromov, Mikhael (1999). "Quantitative Homotopy Theory". In Rossi, Hugo (ed.). गणित में संभावनाएँ: प्रिंसटन विश्वविद्यालय की 250वीं वर्षगांठ के अवसर पर आमंत्रित वार्ता, 17-21 मार्च, 1996, प्रिंसटन विश्वविद्यालय. American Mathematical Society. p. 46. ISBN 0-8218-0975-X.
- ↑ 8.0 8.1 Rosenberg, Jonathan (1988). "लिपशिट्ज मैनिफोल्ड्स पर विश्लेषण के अनुप्रयोग". Miniconferences on harmonic analysis and operator algebras (Canberra, 1987). Canberra: Australian National University. pp. 269–283. MR954004
- ↑ "Topology of manifolds", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- ↑ Donchev, Tzanko; Farkhi, Elza (1998). "स्थिरता और यूलर सन्निकटन एक तरफा लिपशित्ज़ विभेदक समावेशन". SIAM Journal on Control and Optimization. 36 (2): 780–796. doi:10.1137/S0363012995293694.