समानांतर (ज्यामिति)

समानांतर लाइनों और घटता की लाइन आर्ट ड्राइंग। Alt ==

ज्यामिति में, समानांतर रेखाएँ ही समतलीय सीधी रेखाएँ होती हैं जो किसी भी बिंदु पर प्रतिच्छेद नहीं करती हैं। समानांतर समतल एक ही त्रिविम समष्टि में समतल हैं जो कभी नहीं मिलते हैं। समानांतर वक्र वे वक्र होते हैं जो एक दूसरे को स्पर्श नहीं करते हैं या प्रतिच्छेद नहीं करते हैं और एक निश्चित न्यूनतम दूरी रखते हैं। त्रिविम यूक्लिडियन समष्टि में, रेखा और समतल जो एक बिंदु साझा नहीं करते हैं, उन्हें भी समानांतर कहा जाता है। हालाँकि, दो गैर समतलीय रेखाएँ तिरछी रेखाएँ कहलाती हैं।

समानांतर रेखाएं यूक्लिड की समानांतर अभिधारणा का विषय हैं समानांतर रेखाएं यूक्लिड की समानांतर अभिधारणा का विषय हैं.[1] समानांतरवाद प्राथमिक रूप से एफ़िन ज्यामिति का एक गुण है और यूक्लिडियन ज्यामिति  इसका एक विशेष उदाहरण है। कुछ अन्य ज्यामिति में, जैसे अतिपरवलयिक ज्यामिति, रेखाओं में समान गुण हो सकते हैं जिन्हें समांतरता कहा जाता है।

प्रतीक

समानांतर का $\parallel$ प्रतीक है.उदाहरण, $AB\parallel CD$ इंगित करता है कि रेखा AB, रेखा CD के समानांतर है।

यूनिकोड वर्ण समुच्चय में, "समानांतर" और "समानांतर नहीं" संकेतों में क्रमशः U 2225 (∥) और U 2226 (∦) कोडपॉइंट होते हैं। इसके अलावा, U 22D5 (⋕) "बराबर और समानांतर" संबंध का प्रतिनिधित्व करता है।

विद्युत् इंजीनियरी (समानांतर सक्रियक) में  द्विआधारी फ़ंक्शन के लिए एक ही प्रतीक का उपयोग किया जाता है। यह दोहरी-ऊर्ध्वाधर-रेखा कोष्ठक से अलग है जो एक मानदंड को इंगित करता है, साथ ही कई प्रोग्रामिंग भाषाओं में तार्किक या सक्रियक (||) से भी अलग है।

यूक्लिडियन समानांतरवाद

एक समतल में दो रेखाएं

समानांतरवाद के लिए शर्तें

जैसा कि टिक के निशान द्वारा दिखाया गया है, लाइन ए और बी समानांतर हैं।यह साबित किया जा सकता है क्योंकि ट्रांसवर्सल टी बधाई संगत कोणों का उत्पादन करता है $\theta$, यहाँ दोनों को ट्रांसवर्सल के दाईं ओर दिखाया गया है, एक ऊपर और लाइन ए और दूसरे के ऊपर और ऊपर और लाइन बी से सटे।

यूक्लिडियन समष्टि में समानांतर सीधी रेखाएं एल और एम को देखते हुए, निम्नलिखित गुण समतुल्य हैं:

1. रेखा m पर प्रत्येक बिंदु रेखा (समतुल्य रेखा) से ठीक उसी (न्यूनतम) दूरी पर स्थित है।
2. रेखा m, रेखा l के समान तल में है, लेकिन l को नहीं काटती है (याद रखें कि रेखाएँ किसी भी दिशा में अनंत तक जाती हैं)।
3. जब रेखाएँ m और l दोनों को एक ही तल में एक तीसरी सीधी रेखा (एक तिर्यक रेखा) द्वारा प्रतिच्छेदित किया जाता है, तो अनुप्रस्थ के साथ प्रतिच्छेदन के संगत कोण सर्वांगसम होते हैं।

चूंकि ये समतुल्य गुण हैं, इनमें से किसी एक को यूक्लिडियन समष्टि में समानांतर रेखाओं की परिभाषा के रूप में लिया जा सकता है, लेकिन पहले और तीसरे गुणों में माप शामिल है और इसलिए, दूसरे की तुलना में  ये "अधिक जटिल" हैं। इस प्रकार, दूसरी विशेषता है जिसे आमतौर पर यूक्लिडियन ज्यामिति में समानांतर रेखाओं की परिभाषित संपत्ति के रूप में चुना जाता है।एक अन्य गुण जिसमें मापन भी शामिल है वह यह है कि एक दूसरे के समानांतर रेखाओं में समान ढाल (ढलान) होती है।

इतिहास

समतल में सीधी रेखाओं के एक जोड़े के रूप में समानांतर रेखाओं की परिभाषा जो यूक्लिड के तत्वों की पुस्तक I में परिभाषा 23 के रूप में नहीं मिलते हैं। यूनानियों द्वारा वैकल्पिक परिभाषाओं पर अक्सर समानांतर अभिधारणा को साबित करने के प्रयास के हिस्से के रूप में चर्चा की गई। प्रोक्लस समानांतर रेखाओं की परिभाषा को पॉसिडोनियस के समान दूरी के रूप में परिभाषित करता है और इसी तरह की नस में जेमिनस को उद्धृत करता है। सिम्पलिसियस ने पोसिडोनियस की परिभाषा के साथ-साथ दार्शनिक एगनिस द्वारा इसके संशोधन का भी उल्लेख किया है।

उन्नीसवीं शताब्दी के अंत में, इंग्लैंड में, यूक्लिड के तत्व अभी भी माध्यमिक विद्यालयों में मानक पाठ्यपुस्तक थे। प्रक्षेप्य ज्यामिति और अयूक्लिडीय ज्यामिति में नए विकास से ज्यामिति के पारंपरिक व्यवहार को बदलने के लिए दबाव डाला जा रहा था, इसलिए इस समय ज्यामिति के शिक्षण के लिए कई नई पाठ्यपुस्तकें लिखी गईं। समानांतर रेखाओं का उपचार  ही इन सुधार ग्रंथों के बीच एक बड़ा अंतर, दोनों के बीच और उनके और यूक्लिड के बीच है। ये सुधार ग्रंथ उनके आलोचकों के बिना नहीं थे और उनमें से एक, चार्ल्स डोडसन (उर्फ लुईस कैरोल) ने एक नाटक, यूक्लिड एंड हिज मॉडर्न राइवल्स लिखा, जिसमें इन ग्रंथों को आलोचना की है।

प्रारंभिक सुधार पाठ्यपुस्तकों में से एक 1868 की जेम्स मौरिस विल्सन की प्राथमिक ज्यामिति थी। विल्सन ने दिशा की आदिम धारणा पर समानांतर रेखाओं की अपनी परिभाषा को आधारित किया था। विल्हेम किलिंग के अनुसार इस विचार का पता लाइबनिज से लगाया जा सकता है। विल्सन, दिशा को परिभाषित किए बिना,अन्य परिभाषाओं में इस शब्द का उपयोग करता है जैसे कि उनकी छठी परिभाषा, "दो सीधी रेखाएं जो एक दूसरे से मिलती हैं, उनकी अलग-अलग दिशाएं होती हैं, और उनकी दिशाओं का अंतर उनके बीच का कोण होता है। विल्सन (1868, पृ. 2) परिभाषा 15 में उन्होंने इस प्रकार समानांतर रेखाओं का परिचय दिया  "सीधी रेखाएँ जिनकी दिशा समान होती है, लेकिन वे एक ही सीधी रेखा के भाग नहीं होते हैं, समानांतर रेखाएँ कहलाती हैं।" विल्सन (1868, पृष्ठ 12) ऑगस्टस डी मॉर्गन ने मुख्य रूप से इस परिभाषा के आधार पर और जिस तरह से विल्सन ने समानांतर रेखाओं के बारे में चीजों को साबित करने के लिए इसका इस्तेमाल किया, इसे विफल घोषित किया था। डोडसन ने अपने नाटक का एक बड़ा हिस्सा (एक्ट II, सीन VI § 1) भी समर्पित किया, जिसमें विल्सन के समानांतर व्यवहार की निंदा की गई थी। विल्सन ने इस अवधारणा को अपने पाठ के तीसरे और उच्चतर संस्करणों से संपादित किया था।

सुधारकों द्वारा प्रस्तावित अन्य विशेषताएं , समानांतर रेखाओं की परिभाषा के लिए प्रतिस्थापन के रूप में उपयोग की जाती हैं, उनका प्रदर्शन बहुत बेहतर नहीं था। डोडसन द्वारा इंगित की गई मुख्य कठिनाई यह थी कि उन्हें इस तरह से उपयोग करने के लिए प्रणाली में अतिरिक्त स्वयंसिद्धों को जोड़ने की आवश्यकता थी। पोसिडोनियस की समदूरस्थ रेखा परिभाषा, जिसे फ्रांसिस कथबर्टसन ने अपने 1874 के पाठ यूक्लिडियन ज्योमेट्री में प्रतिपादित किया था, इस समस्या से ग्रस्त है कि एक सीधी रेखा के एक तरफ एक निश्चित दूरी पर पाए जाने वाले बिंदुओं को एक सीधी रेखा बनाने के लिए दिखाया जाना चाहिए था। इसे सच माना जाना चाहिए यह साबित नहीं किया जा सकता है। डब्लू डी कूली द्वारा अपने 1860 के पाठ, ज्यामिति के तत्व में इस्तेमाल किए गए एक अनुप्रस्थ विशेषता द्वारा बनाए गए संगत कोणों को सरलीकृत और समझाया गया है, इस तथ्य के प्रमाण की आवश्यकता है कि यदि एक अनुप्रस्थ संगत कोणों में लाइनों की एक जोड़ी से मिलता है तो सभी अनुप्रस्थ को करना चाहिए। फिर से, इस कथन को सही ठहराने के लिए एक नए स्वयंसिद्ध की आवश्यकता है।

निर्माण

समानांतर रेखाओं की ऊपर के तीन गुण निर्माण के तीन अलग -अलग तरीकों की ओर ले जाते हैं।

समस्या: एल के समानांतर के माध्यम से एक रेखा खींचें।

• 

  गुण 1: रेखा m की हर जगह रेखा l से समान दूरी है।

• 

  गुण 2: a से होकर जाने वाली एक यादृच्छिक रेखा लीजिए जो l को x में काटती है। बिंदु x को अनंत तक ले जाएँ।

• 

  गुण 3: l और m दोनों a से होकर एक तिर्यक रेखा साझा करते हैं जो उन्हें 90° पर प्रतिच्छेद करती है।

दो समानांतर रेखाओं के बीच की दूरी

चूंकि यूक्लिडियन तल में समानांतर रेखाएं समान दूरी पर होती हैं, इसलिए दो समानांतर रेखाओं के बीच एक अद्वितीय दूरी होती है। दो गैर-ऊर्ध्वाधर, गैर-क्षैतिज समानांतर रेखाओं के समीकरण निश्चित हुये  है,

$y=mx+b_{1}\,$

$y=mx+b_{2}\,,$

दो रेखाओं के बीच की दूरी को दो बिंदुओं (प्रत्येक पंक्ति पर एक) का पता लगाकर पाया जा सकता है जो समानांतर रेखाओं के एक सामान्य लंबवत पर स्थित हैं और उनके बीच की दूरी की गणना करते हैं। चूँकि रेखाओं का ढलान m है, एक उभयनिष्ठ लंबवत का ढलान −1/m होगा और हम समीकरण y = −x/m वाली रेखा को एक उभयनिष्ठ लंब के रूप में ले सकते हैं। रैखिक प्रणालियों को हल करें

${\begin{cases}y=mx+b_{1}\\y=-x/m\end{cases}}$

तथा

${\begin{cases}y=mx+b_{2}\\y=-x/m\end{cases}}$

अंकों के निर्देशांक प्राप्त करने के लिए।रैखिक प्रणालियों के समाधान अंक हैं

$\left(x_{1},y_{1}\right)\ =\left({\frac {-b_{1}m}{m^{2}+1}},{\frac {b_{1}}{m^{2}+1}}\right)\,$

तथा

$\left(x_{2},y_{2}\right)\ =\left({\frac {-b_{2}m}{m^{2}+1}},{\frac {b_{2}}{m^{2}+1}}\right).$

ये सूत्र अभी भी सही बिंदु निर्देशांक देते हैं, भले ही समानांतर रेखाएं क्षैतिज हों (यानी, एम = 0)।बिंदुओं के बीच की दूरी है

$d={\sqrt {\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}}={\sqrt {\left({\frac {b_{1}m-b_{2}m}{m^{2}+1}}\right)^{2}+\left({\frac {b_{2}-b_{1}}{m^{2}+1}}\right)^{2}}}\,,$

जो कम कर देता है

$d={\frac {|b_{2}-b_{1}|}{\sqrt {m^{2}+1}}}\,.$

जब लाइनें एक लाइन के समीकरण के सामान्य रूप द्वारा दी जाती हैं (क्षैतिज और ऊर्ध्वाधर रेखाएं शामिल हैं):

$ax+by+c_{1}=0\,$

$ax+by+c_{2}=0,\,$

उनकी दूरी को व्यक्त किया जा सकता है

$d={\frac {|c_{2}-c_{1}|}{\sqrt {a^{2}+b^{2}}}}.$

त्रिविम समष्टि में दो रेखाये

दो रेखाएं जो एक ही त्रिविम समष्टि में प्रतिच्छेद नहीं करती हैं, समानांतर होने की आवश्यकता नहीं है। अगर वे एक सामान्य समतल में हैं तो उन्हें समानांतर कहा जाता है; अन्यथा वे तिरछी रेखाएँ कहलाती हैं।

त्रिविम समष्टि में दो अलग-अलग रेखाएं l और m समानांतर हैं यदि केवल  रेखा m पर एक बिंदु P से रेखा l पर निकटतम बिंदु तक की दूरी रेखा m पर P के स्थान से स्वतंत्र है। यह तिरछी रेखाओं के लिए कभी नहीं रहता है।

रेखा और समतल

त्रिविम समष्टि में एक रेखा m और एक समतल q है, वह रेखा जो उस तल में नहीं  है, समानांतर हैं यदि वे प्रतिच्छेद नहीं करते हैं।

समान रूप से, वे समानांतर होते हैं यदि और केवल यदि रेखा m पर एक बिंदु P से समष्टि q में निकटतम बिंदु की दूरी रेखा m पर P के स्थान से स्वतंत्र होती है।

दो समतल

इस तथ्य के समान समानांतर रेखाएँ एक ही तल में स्थित होनी चाहिए, समानांतर तल समान त्रिविम समष्टि में स्थित होने चाहिए और उनमें कोई भी बिंदु उभयनिष्ठ नहीं होना चाहिए।

दो अलग-अलग समतल q और r समानांतर हैं यदि और केवल यदि तल q में एक बिंदु P से तल r में निकटतम बिंदु तक की दूरी विमान q में P के स्थान से स्वतंत्र है। यदि दो तल एक ही त्रिविम समष्टि में नहीं हैं तो यह कभी भी धारण नहीं कर सकता है।

अयूक्लिडीय ज्यामिति के लिए विस्तार

अयूक्लिडीय ज्यामिति ज्यामिति में, (सीधी) रेखाओं की तुलना में अल्पांतरी के बारे में बात करना अधिक सामान्य है। किसी दिए गए ज्यामिति में दो बिंदुओं के बीच एक अल्पांतरी सबसे छोटा पथ है। भौतिकी में इसकी व्याख्या उस पथ के रूप में की जा सकती है जिस पर कोई बल लागू नहीं होता है। अयूक्लिडीय ज्यामिति (अण्डाकार या अतिपरवलयिक ज्यामिति) में ऊपर वर्णित तीन यूक्लिडियन गुण समतुल्य नहीं हैं और केवल दूसरा गुण है, (रेखा m, रेखा l के समान तल में है लेकिन l को प्रतिच्छेद नहीं करती है) क्योंकि इसमें कोई माप शामिल नहीं है, गैर-यूक्लिडियन ज्यामिति में उपयोगी नहीं है। सामान्य ज्यामिति में उपरोक्त तीन गुण क्रमशः तीन अलग-अलग प्रकार के वक्र, समदूरस्थ वक्र, समानांतर अल्पांतरी और अल्पांतरी एक सामान्य लंबवत साझा करते हैं।

अतिपरवलयिक ज्यामिति

हाइपरबोलिक विमान में एल के संबंध में ए के माध्यम से समानांतर, समानांतर और अल्ट्रा समानांतर रेखाएं।समानांतर लाइनें छवि से दूर l को चौराहे पर दिखाई देती हैं।यह केवल दृश्य की एक कलाकृति है।एक वास्तविक हाइपरबोलिक विमान पर लाइनें एक -दूसरे के करीब पहुंचेंगी और अनंत में 'मिलते हैं'।

जबकि यूक्लिडियन ज्यामिति में दो भूगणित या तो प्रतिच्छेद कर सकते हैं या समानांतर हो सकते हैं, अतिपरवलयिक ज्यामिति में, तीन संभावनाएं हैं। एक ही तल से संबंधित दो भूगणित या तो हो सकते हैं:

1. प्रतिच्छेद करना, यदि वे समतल में एक उभयनिष्ठ बिंदु पर प्रतिच्छेद करते हैं,
2. समानांतर, यदि वे समतल में प्रतिच्छेद नहीं करते हैं, लेकिन अनंत (आदर्श बिंदु) पर एक सामान्य सीमा बिंदु पर अभिसरण करते हैं, या
3. अतिवादी समानांतर, अगर उनके पास अनंत पर एक सामान्य सीमा बिंदु नहीं है।

साहित्य में अतिवादी समानांतर अल्पांतरी को अक्सर गैर-प्रतिच्छेदन कहा जाता है। अनंत पर प्रतिच्छेद करने वाले अल्पांतरी को सीमित समानांतर कहा जाता है।

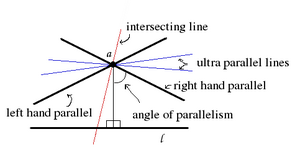
जैसा कि एक बिंदु के माध्यम से चित्रण में है जो लाइन l पर नहीं है, दो सीमित समानांतर रेखाएं हैं, प्रत्येक दिशा के लिए एक रेखा l के आदर्श बिंदु है। वे उन रेखाओं को अलग करते हैं जो रेखा l को काटती हैं और जो रेखा l के अति समानांतर हैं।

अतिवादी समानांतर रेखाओं में एक समान लंबवत (अति समानांतर प्रमेय) होता है, और इस सामान्य लंबवत के दोनों किनारों पर विचलन होता है।

गोलाकार या अण्डाकार ज्यामिति

गोले पर एक समानांतर रेखा जैसी कोई चीज नहीं है।लाइन ए एक महान सर्कल है, जो गोलाकार ज्यामिति में एक सीधी रेखा के बराबर है।लाइन सी लाइन ए के बराबर है, लेकिन एक महान सर्कल नहीं है।यह अक्षांश का एक समानांतर है।लाइन बी एक और जियोडेसिक है जो दो एंटीपोडल बिंदुओं में ए को इंटरसेक्ट करता है।वे दो सामान्य लंबवत (नीले रंग में दिखाया गया) साझा करते हैं।

गोलाकार ज्यामिति में, सभी अल्पांतरी बड़े वृत्त होते हैं। बड़े वृत्त गोले को दो बराबर गोलार्द्धों में विभाजित करते हैं और सभी बड़े वृत्त एक दूसरे को काटते हैं। इस प्रकार, किसी दिए गए अल्पांतरी के समानांतर अल्पांतरी नहीं हैं, क्योंकि सभी अल्पांतरी एक दूसरे को काटते हैं। गोले पर समदूरस्थ वक्रों को ग्लोब पर अक्षांश रेखाओं के अनुरूप अक्षांश के समानांतर कहा जाता है। अक्षांश के समांतर गोले के केंद्र के माध्यम से एक विमान के समानांतर एक विमान के साथ गोले के चौराहे से उत्पन्न हो सकते हैं।

प्रतिवर्त परिवर्ती

यदि l, m, n तीन अलग-अलग रेखाएँ हैं, तो $l\parallel m\ \land \ m\parallel n\ \implies \ l\parallel n.$

इस मामले में, समानता एक सकर्मक संबंध है। हालाँकि, l = n के मामले में, यूक्लिडियन ज्यामिति में अध्यारोपित रेखाओं को समानांतर नहीं माना जाता है। समानांतर रेखाओं के बीच द्विआधारी संबंध स्पष्ट रूप से एक सममित संबंध है। यूक्लिड के सिद्धांतों के अनुसार, समांतरता एक प्रतिवर्त संबंध नहीं है और इस प्रकार एक तुल्यता संबंध बनने में विफल रहता है। फिर भी, एफ़िन ज्यामिति में समानांतर रेखाओं की एक पेंसिल को रेखाओं के समूह में एक तुल्यता वर्ग के रूप में लिया जाता है जहाँ समानता एक तुल्यता संबंध है।

इस उद्देश्य के लिए, एमिल आर्टिन (1957) ने समानांतरवाद की परिभाषा को अपनाया, जहां दो रेखाएं समानांतर होती हैं यदि उनके सभी या कोई भी बिंदु समान नहीं हैं। फिर एक रेखा अपने आप के समानांतर होती है ताकि प्रतिवर्त और संक्रमणीय गुण इस प्रकार के समानांतरवाद से संबंधित हों, जो रेखाओं के सेट पर एक तुल्यता संबंध बनाते हैं। आपतन ज्यामिति के अध्ययन में, समांतरता के इस प्रकार का उपयोग एफ़िन प्लेन में किया जाता है।

यह भी देखें

• क्लिफोर्ड समानांतर
• समवर्ती लाइनें
• समानांतर को सीमित करना
• समानांतर वक्र
• अल्ट्रापारल प्रमेय

संदर्भ

• Heath, Thomas L. (1956), The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.), New York: Dover Publications

(3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3). Heath's authoritative translation plus extensive historical research and detailed commentary throughout the text.

• Richards, Joan L. (1988), Mathematical Visions: The Pursuit of Geometry in Victorian England, Boston: Academic Press, ISBN 0-12-587445-6
• Wilson, James Maurice (1868), Elementary Geometry (1st ed.), London: Macmillan and Co.
• Wylie Jr., C. R. (1964), Foundations of Geometry, McGraw–Hill

अग्रिम पठन

• Papadopoulos, Athanase; Théret, Guillaume (2014), La théorie des parallèles de Johann Heinrich Lambert : Présentation, traduction et commentaires, Paris: Collection Sciences dans l'histoire, Librairie Albert Blanchard, ISBN 978-2-85367-266-5

बाहरी संबंध

• Constructing a parallel line through a given point with compass and straightedge