यूक्लिडियन प्लेन आइसोमेट्री: Difference between revisions
No edit summary |
|||
| (17 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
[[ ज्यामिति ]] में, | [[ज्यामिति]] में, '''यूक्लिडियन समतल [[आइसोमेट्री]]''' यूक्लिडियन समतल का एक आइसोमेट्री है, या अधिक अनौपचारिक रूप से, समतल को रूपांतरित करने का एक तरीका है जो ज्यामितीय गुणों जैसे कि लंबाई को संरक्षित करता है। चार प्रकार हैं: [[ट्रांसलेशन|अंतरण]] (गणित में), घूर्णन, परावर्तन और ग्लाइड परावर्तन (नीचे यूक्लिडियन समतल सममितियों के वर्गीकरण के अंतर्गत देखें)। | ||
[[ यूक्लिडियन | [[यूक्लिडियन प्लेन|यूक्लिडियन समतल]] आइसोमेट्री का सम्मुचय संरचना के अंतर्गत [[ समूह (गणित) |समूह (गणित)]] बनाता है: [[यूक्लिडियन समूह]] दो आयामों में। यह रेखाओं में परावर्तनों द्वारा उत्पन्न होता है, और यूक्लिडियन समूह का प्रत्येक तत्व तीन अलग-अलग परावर्तनों का सम्मिश्रण है। | ||
== अनौपचारिक चर्चा == | == अनौपचारिक चर्चा == | ||
अनौपचारिक रूप से, | अनौपचारिक रूप से, यूक्लिडियन समतल आइसोमेट्री समतल को "विरूपित" किए बिना परिवर्तित करने का कोई तरीका है। उदाहरण के लिए, मान लीजिए कि यूक्लिडियन समतल को डेस्क पर रखे पारदर्शी प्लास्टिक की शीट द्वारा दर्शाया गया है। आइसोमेट्री के उदाहरणों में सम्मिलित हैं: | ||
* शीट को एक इंच दाईं ओर खिसकाने पर। | |||
* किसी चिन्हित बिंदु (जो गतिहीन रहता है) के चारों ओर शीट को दस डिग्री घुमाने पर। | |||
* pछे से देखने के लिए शीट को पलट दें और ध्यान दें कि यदि शीट के एक तरफ कोई चित्र बनाया जाता है, तो शीट को पलटने के बाद, हमें चित्र का दर्पण प्रतिबिम्ब दिखाई देता है। | |||
ये क्रमशः अंतरण, घूर्णन और परावर्तन के उदाहरण हैं। एक और प्रकार की आइसोमेट्री है, जिसे ग्लाइड रिफ्लेक्शन कहा जाता है (नीचे यूक्लिडियन समतल सममिति के वर्गीकरण के अंतर्गत देखें)। | |||
यद्यपि, शीट को मोड़ने, काटने या पिघलाने को आइसोमेट्री नहीं माना जाता है। बंकन, प्रसार या मरोड़ना जैसे कम कठोर परिवर्तन भी नहीं हैं। | |||
== औपचारिक परिभाषा == | == औपचारिक परिभाषा == | ||
यूक्लिडियन | यूक्लिडियन समतल आइसोमेट्री समतल का दूरी-संरक्षण परिवर्तन है। अर्थात, यह एक [[ नक्शा (गणित) |आलेख्यपत्र (मैप गणित)]] है | ||
:<math> M : \textbf{R}^2 \to \textbf{R}^2 </math> | :<math> M : \textbf{R}^2 \to \textbf{R}^2 </math> | ||
इस प्रकार | इस प्रकार, समतल में किसी बिंदु p और q के लिए, | ||
:<math>d(p, q) = d(M(p), M(q)),</math> | :<math>d(p, q) = d(M(p), M(q)),</math> | ||
जहाँ d(p, q) p और q के बीच सामान्य [[ यूक्लिडियन दूरी ]] है। | जहाँ d(p, q) p और q के बीच सामान्य [[ यूक्लिडियन दूरी |यूक्लिडियन दूरी]] है। | ||
== वर्गीकरण == | == वर्गीकरण == | ||
यह | यह दर्शाया जा सकता है कि चार प्रकार के यूक्लिडियन समतल सममिति़ हैं। (ध्यान दें: नीचे सूचीबद्ध सममिति़ के प्रकार के लिए संकेतन पूरी तरह से मानकीकृत नहीं हैं।) | ||
=== | === परावर्तन === | ||
[[Image:Euclidean plane isometry reflection.png|right|frame| | [[Image:Euclidean plane isometry reflection.png|right|frame|Reflection]] | ||
परावर्तन (गणित) या मिरर आइसोमेट्री, जिसे ''F<sub>c,v</sub>,'' द्वारा दर्शाया जाता है जहाँ c समतल में एक बिंदु है और 'R<sup>2</sup>' में v एक इकाई सदिश है। (''F'' फ्लिपको दर्शाता है।) रेखा L में बिंदु P को परावर्तनित करने का प्रभाव है जो v के लंबवत है और जो c के माध्यम से गुजरता है। रेखा L को 'परावर्तन अक्ष' या संबंधित 'दर्पण' कहा जाता है। F<sub>''c'',''v''</sub>, के लिए सूत्र खोजने के लिए हम v दिशा में p - c के घटक t को खोजने के लिए सबसे पहले[[ डॉट उत्पाद |डॉट प्रोडक्ट]] का उपयोग करते हैं, | |||
:<math>t = (p-c) \cdot v = (p_x - c_x)v_x + (p_y - c_y)v_y,</math> | :<math>t = (p-c) \cdot v = (p_x - c_x)v_x + (p_y - c_y)v_y,</math> | ||
: और फिर हम घटाव द्वारा | : और फिर हम घटाव द्वारा p का परावर्तन प्राप्त करते हैं, | ||
:<math>F_{c,v}(p) = p - 2tv.</math> | :<math>F_{c,v}(p) = p - 2tv.</math> | ||
मूल के बारे में | मूल के बारे में घूर्णनों का संयोजन और मूल के माध्यम से एक रेखा के बारे में परावर्तन सभी आयतीय आव्यूह (अर्थात सारणिक 1 और -1 के साथ) के साथ प्राप्त किया जाता है जो आयतीय समूह ओ (2) बनाते हैं। -1 के सारणिक की स्थिति में हमारे पास है: | ||
::<math>R_{0,\theta}(p) = | ::<math>R_{0,\theta}(p) = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 38: | Line 40: | ||
\end{pmatrix} | \end{pmatrix} | ||
\begin{bmatrix} p_x \\ p_y \end{bmatrix}.</math> | \begin{bmatrix} p_x \\ p_y \end{bmatrix}.</math> | ||
जो x-अक्ष में एक | जो x-अक्ष में एक परावर्तन है जिसके बाद कोण θ द्वारा घूर्णन होता है, या समकक्ष रूप से, x-अक्ष के साथ θ/2 का कोण बनाने वाली रेखा में परावर्तन होता है। समानांतर रेखा में परावर्तन इसके लिए एक सदिश लम्ब जोड़ने पर सामान लगता है। | ||
=== | === अंतरण === | ||
अंतरण (गणित) द्वारा ''T<sub>v</sub>'', जहाँ 'R<sup>2</sup>' में v एक [[ वेक्टर (ज्यामितीय) |सदिश (ज्यामितीय)]] है यह तल को v की दिशा में स्थानांतरित करने का प्रभाव होता है। अर्थात, तल में किसी बिंदु p के लिए, | |||
::<math>T_v(p) = p + v,</math> | ::<math>T_v(p) = p + v,</math> | ||
:या (x, y) निर्देशांक के संदर्भ में, | :या (x, y) निर्देशांक के संदर्भ में, | ||
::<math> T_v(p) = \begin{bmatrix} p_x + v_x \\ p_y + v_y \end{bmatrix}. </math> | ::<math> T_v(p) = \begin{bmatrix} p_x + v_x \\ p_y + v_y \end{bmatrix}. </math> | ||
अंतरण को दो समांतर परावर्तनों के संयोजन के रूप में देखा जा सकता है। | |||
=== | === घूर्णन === | ||
[[Image:Euclidean plane isometry | [[Image:Euclidean plane isometry translation.png|right|frame|Translation]] | ||
[[ रोटेशन (गणित) | घूर्णन (गणित)]] , R<sub>c,θ</sub>, द्वारा निरूपित जहाँ c समतल (घूर्णन का केंद्र) में एक बिंदु है, और θ घूर्णन का कोण है। निर्देशांक के संदर्भ में, घूर्णन को दो संक्रियाओं में तोड़कर सबसे आसानी से व्यक्त किया जाता है। सबसे पहले, मूलबिंदु के चारों ओर एक घूर्णन किसके द्वारा दिया जाता है | |||
::<math>R_{0,\theta}(p) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} | ::<math>R_{0,\theta}(p) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} | ||
\begin{bmatrix} p_x \\ p_y \end{bmatrix}.</math> | \begin{bmatrix} p_x \\ p_y \end{bmatrix}.</math> | ||
: ये मैट्रिसेस [[ ऑर्थोगोनल मैट्रिक्स ]] हैं (अर्थात प्रत्येक | : ये मैट्रिसेस [[ ऑर्थोगोनल मैट्रिक्स |आयतीय मैट्रिक्स]] हैं (अर्थात प्रत्येक [[ स्क्वायर मैट्रिक्स |स्क्वायर मैट्रिक्स]] <var>G</var> है जिसका स्थानान्तरण इसका व्युत्क्रम मैट्रिक्स है, अर्थात <math>GG^T=G^T G=I_2.</math>) सारणिक 1 के साथ (आयतीय आव्यूह के लिए दूसरी संभावना -1 है, जो एक दर्पण छवि देता है, नीचे देखें)। वे विशेष लांबिक समूह SO(2) बनाते हैं। | ||
: | |||
: c के चारों ओर | :c के चारों ओर घूर्णन को पहले c को मूल में अंतरण करके, फिर मूल के चारों ओर घुमाकर, और अंत में मूल को वापस c में अंतरण करके पूरा किया जा सकता है। वह है, | ||
::<math>R_{c,\theta} = T_c \circ R_{0,\theta} \circ T_{-c},</math> | ::<math>R_{c,\theta} = T_c \circ R_{0,\theta} \circ T_{-c},</math> | ||
:या दूसरे शब्दों में, | :या दूसरे शब्दों में, | ||
::<math>R_{c,\theta}(p) = c + R_{0,\theta}(p - c).</math> | ::<math>R_{c,\theta}(p) = c + R_{0,\theta}(p - c).</math> | ||
: वैकल्पिक रूप से, मूल के चारों ओर | : वैकल्पिक रूप से, मूल के चारों ओर घूर्णन किया जाता है, उसके बाद अंतरण किया जाता है: | ||
::<math>R_{c,\theta}(p) = c-R_{0,\theta} c + R_{0,\theta}(p).</math> | ::<math>R_{c,\theta}(p) = c-R_{0,\theta} c + R_{0,\theta}(p).</math> | ||
एक | एक घूर्णन को दो असमानांतर परावर्तनों के सम्मिश्रण के रूप में देखा जा सकता है। | ||
=== | |||
=== रिजिड रूपांतरण === | |||
{{main|रिजिड रूपांतरण}} | |||
अंतरण और घूर्णन का सम्मुचय एक साथ रिजिड गति या रिजिड विस्थापन का निर्माण करता है। यह सम्मुचय रचना के अंतर्गत समूह (गणित) बनाता है,''कठोर गतियों का समूह '', यूक्लिडियन सममिति़ के पूर्ण समूह का एक उपसमूह। | |||
=== ग्लाइड परावर्तन === | |||
ग्लाइड परावर्तन, ''G<sub>c,v,w</sub>,'' द्वारा निरूपित जहाँ c समतल में एक बिंदु है, 'R<sup>2</sup>' में v एक इकाई सदिश है, और w नॉन-रिक्त एक सदिश है जो v के लंबवत है, c और v द्वारा वर्णित रेखा में परावर्तन का संयोजन है, जिसके बाद w के साथ अंतरण होता है। वह है, | |||
::<math>G_{c,v,w} = T_w \circ F_{c,v},</math> | ::<math>G_{c,v,w} = T_w \circ F_{c,v},</math> | ||
:या दूसरे शब्दों में, | :या दूसरे शब्दों में, | ||
::<math>G_{c,v,w}(p) = w + F_{c,v}(p).</math> | ::<math>G_{c,v,w}(p) = w + F_{c,v}(p).</math> | ||
: | :यह भी सच है | ||
::<math>G_{c,v,w}(p) = F_{c,v}(p + w);</math> | ::<math>G_{c,v,w}(p) = F_{c,v}(p + w);</math> | ||
अर्थात, यदि हम अंतरण और परावर्तन को विपरीत क्रम में करते हैं तो हमें वही परिणाम मिलता है।) वैकल्पिक रूप से हम आयतीय मैट्रिक्स द्वारा सारणिक -1 (मूल के माध्यम से एक पंक्ति में एक परावर्तन के अनुरूप) के साथ गुणा करते हैं, जिसके बाद अंतरण होता है। यह एक ग्लाइड परावर्तन है, विशेष स्थिति को छोड़कर कि अंतरण परावर्तन की रेखा के लंबवत है, इस स्थिति में संयोजन स्वयं समानांतर रेखा में एक परावर्तन है। | |||
सभी बिंदुओं के लिए I (p) = p द्वारा परिभाषित [[ पहचान (गणित) |पहचान (गणित)]]आइसोमेट्री एक अंतरण का एक विशेष मामला है, और एक घूर्णन का एक विशेष मामला भी है। यह एकमात्र आइसोमेट्री है जो ऊपर वर्णित एक से अधिक प्रकारों से संबंधित है। | |||
सभी स्थितियों में हम स्थिति सदिश को आयतीय मैट्रिक्स से गुणा करते हैं और एक सदिश जोड़ते हैं; यदि सारणिक 1 है तो हमारे पास एक घूर्णन, एक अंतरण या पहचान है, और यदि यह -1 है तो हमारे पास ग्लाइड परावर्तन या परावर्तन है। | |||
यादृच्छिक आइसोमेट्री, जैसे मेज से कागज की शीट लेना और इसे बेतरतीब ढंग से वापस रखना, [[ लगभग निश्चित रूप से |लगभग निश्चित रूप से]] घूर्णन या ग्लाइड परावर्तन है (उनके पास स्वतंत्रता की तीन डिग्री (भौतिकी और रसायन विज्ञान) है)। यह संभाव्यता वितरण के विवरण की परवाह किए बिना लागू होता है, जब तक कि θ और जोड़े गए सदिश की दिशा [[ सांख्यिकीय स्वतंत्रता |सांख्यिकीय स्वतंत्रता]] और [[ समान वितरण (निरंतर) |समान वितरण (निरंतर)]]है और जोड़े गए सदिश की लंबाई में निरंतर वितरण होता है। एक शुद्ध अंतरण और शुद्ध परावर्तन स्वतंत्रता की केवल दो डिग्री के साथ विशेष स्थिति हैं, जबकि पहचान और भी विशेष है, स्वतंत्रता की कोई डिग्री नहीं है। | |||
किसी भी आइसोमेट्री का उत्पादन करने के लिए | |||
== [[ प्रतिबिंब समूह | परावर्तन समूह]] के रूप में आइसोमेट्री == | |||
किसी भी आइसोमेट्री का उत्पादन करने के लिए परावर्तन, या दर्पण सममिति़ को जोड़ा जा सकता है। इस प्रकार आइसोमेट्री परावर्तन समूह का उदाहरण है। | |||
=== दर्पण संयोजन === | === दर्पण संयोजन === | ||
यूक्लिडियन | यूक्लिडियन समतल में, हमारे पास निम्नलिखित संभावनाएँ हैं। | ||
[[Image:Mirrors make isometries 2005-07-08.png|right|320px|दर्पण के रूप में आइसोमेट्री]] | [[Image:Mirrors make isometries 2005-07-08.png|right|320px|दर्पण के रूप में आइसोमेट्री]] | ||
*; [<span style="color:gray;">d</span> ] पहचान | *; [<span style="color:gray;">d</span> ] पहचान | ||
: एक ही दर्पण में दो | : एक ही दर्पण में दो परावर्तन प्रत्येक बिंदु को उसकी मूल स्थिति में पुनर्स्थापित करते हैं। सभी बिंदुओं को स्थिर छोड़ दिया गया है। समान दर्पणों की किसी भी युग्म का प्रभाव समान होता है। | ||
*; [<span style="color:gray;"> | *; [<span style="color:gray;">db</span>] परावर्तन | ||
: जैसा कि ऐलिस ने लुकिंग-ग्लास के माध्यम से पाया | लुकिंग-ग्लास के माध्यम से, एक दर्पण बाएं और दाएं हाथों को स्विच करने का कारण बनता है। (औपचारिक शब्दों में, टोपोलॉजिकल ओरिएंटेशन उलट जाता है।) दर्पण पर बिंदुओं को स्थिर छोड़ दिया जाता है। प्रत्येक दर्पण का | : जैसा कि ऐलिस ने लुकिंग-ग्लास के माध्यम से पाया | लुकिंग-ग्लास के माध्यम से, एक दर्पण बाएं और दाएं हाथों को स्विच करने का कारण बनता है। (औपचारिक शब्दों में, टोपोलॉजिकल ओरिएंटेशन उलट जाता है।) दर्पण पर बिंदुओं को स्थिर छोड़ दिया जाता है। प्रत्येक दर्पण का अनूठा प्रभाव होता है। | ||
*; [<span style="color:gray;">d</span><span style= color:green; >p</span>] | *; [<span style="color:gray;">d</span><span style= color:green; >p</span>] घूर्णन | ||
: दो अलग-अलग प्रतिच्छेदी दर्पणों में | : दो अलग-अलग प्रतिच्छेदी दर्पणों में सामान्य बिंदु होता है, जो स्थिर रहता है। अन्य सभी बिंदु इसके चारों ओर दर्पणों के बीच के कोण के दोगुने से घूमते हैं। समान निश्चित बिंदु और समान कोण वाले कोई भी दो दर्पण समान घूर्णन देते हैं, जब तक कि उनका उपयोग सही क्रम में किया जाता है। | ||
*; [<span style="color:gray;"> | *; [<span style="color:gray;">dg</span>] अंतरण | ||
:दो अलग-अलग दर्पण जो प्रतिच्छेद नहीं करते हैं उन्हें समानांतर होना चाहिए। प्रत्येक बिंदु समान मात्रा में, दर्पणों के बीच की दुगुनी दूरी पर और एक ही दिशा में गति करता है। कोई अंक निश्चित नहीं छोड़ा गया है। समान समानांतर दिशा और समान दूरी वाले कोई भी दो दर्पण समान | :दो अलग-अलग दर्पण जो प्रतिच्छेद नहीं करते हैं उन्हें समानांतर होना चाहिए। प्रत्येक बिंदु समान मात्रा में, दर्पणों के बीच की दुगुनी दूरी पर और एक ही दिशा में गति करता है। कोई अंक निश्चित नहीं छोड़ा गया है। समान समानांतर दिशा और समान दूरी वाले कोई भी दो दर्पण समान अंतरण देते हैं, जब तक कि उनका सही क्रम में उपयोग किया जाता है। | ||
*; [<span style="color:gray;">d</span><span style= color:green; >q</span>] | *; [<span style="color:gray;">d</span><span style= color:green; >q</span>] ग्लाइड परावर्तन | ||
: तीन दर्पण। यदि वे सभी समानांतर हैं, तो प्रभाव एकल दर्पण के समान होता है (तीसरे को | : तीन दर्पण। यदि वे सभी समानांतर हैं, तो प्रभाव एकल दर्पण के समान होता है (तीसरे को अस्वीकृत करने के लिए एक युग्म को स्लाइड करें)। अन्यथा हम एक समतुल्य व्यवस्था प्राप्त कर सकते हैं जहां दो समानांतर हैं और तीसरा उनके लिए लंबवत है। प्रभाव दर्पण के समानांतर अंतरण के साथ संयुक्त परावर्तन है। कोई अंक निश्चित नहीं छोड़ा गया है। | ||
=== तीन दर्पण पर्याप्त === | === तीन दर्पण पर्याप्त === | ||
अधिक दर्पण जोड़ने से अधिक संभावनाएँ ( | अधिक दर्पण जोड़ने से अधिक संभावनाएँ ( समतल में) नहीं जुड़ती हैं, क्योंकि अस्वीकृतीकरण का कारण बनने के लिए उन्हें हमेशा पुनर्व्यवस्थित किया जा सकता है। | ||
:सबूत। एक आइसोमेट्री पूरी तरह से तीन स्वतंत्र (संरेखित नहीं) बिंदुओं पर इसके प्रभाव से निर्धारित होती है। तो मान लीजिए '' | :सबूत। एक आइसोमेट्री पूरी तरह से तीन स्वतंत्र (संरेखित नहीं) बिंदुओं पर इसके प्रभाव से निर्धारित होती है। तो मान लीजिए ''p''<sub>1</sub>, p<sub>2</sub>, p<sub>3</sub> q के लिए नक्शा<sub>1</sub>, q<sub>2</sub>, q<sub>3</sub>; हम इसे निम्नानुसार प्राप्त करने के लिए दर्पणों का एक क्रम उत्पन्न कर सकते हैं। यदि प<sub>1</sub> और q<sub>1</sub> भिन्न हैं, उनके लंब समद्विभाजक को दर्पण के रूप में चुनें। अब p<sub>1</sub> q के नक्शे<sub>1</sub>; और हम आगे के सभी दर्पणों को q से गुजारेंगे<sub>1</sub>, इसे ठीक करके छोड़ दें। p की छवियों को कॉल करें<sub>2</sub> और p<sub>3</sub> इस परावर्तन के अंतर्गत p<sub>2</sub>' और p<sub>3</sub> ,यदि q<sub>2</sub> p<sub>2</sub> से भिन्न है, कोण को q<sub>1</sub> पर समद्विभाजित करें एक नए आईने के साथ। p<sub>1</sub> के साथ और p<sub>2</sub> अब जगह में, p<sub>3</sub> p<sub>3</sub> पर है; और यदि यह जगह में नहीं है, q<sub>1</sub> के माध्यम से एक अंतिम दर्पण और q<sub>2</sub> इसे q<sub>3</sub> पर फ़्लिप करेंगे इस प्रकार किसी भी समतल आइसोमेट्री को पुन: उत्पन्न करने के लिए अधिकतम तीन परावर्तन पर्याप्त हैं। | ||
=== मान्यता === | === मान्यता === | ||
हम पहचान सकते हैं कि इनमें से कौन सी आइसोमेट्री हमारे पास है या नहीं यह हाथों को संरक्षित करता है या उन्हें | हम पहचान सकते हैं कि इनमें से कौन सी आइसोमेट्री हमारे पास है या नहीं, इसके अनुसार यह हाथों को संरक्षित करता है या उन्हें विनिमय करता है, और क्या इसमें कम से कम एक निश्चित बिंदु है या नहीं, जैसा कि निम्नलिखित तालिका में दिखाया गया है (पहचान को छोड़ कर)। | ||
{| class=wikitable | {| class=wikitable | ||
| colspan=2 rowspan=2| | | colspan=2 rowspan=2| | ||
! colspan="2" | Preserves hands? | ! colspan="2" | Preserves hands? | ||
|- align="center" | |- align="center" | ||
| ''Yes'' || '' | | ''Yes'' || ''नहीं'' | ||
|- align="center" | |- align="center" | ||
! rowspan="2" | | ! rowspan="2" | नियत बिन्दु? | ||
| align="right" | '' | | align="right" | ''हाँ'' || घूर्णन || परावर्तन | ||
|- align="center" | |- align="center" | ||
| align="right" | '' | | align="right" | ''नहीं'' || अंतरण || ग्लाइड परावर्तन | ||
|} | |} | ||
=== समूह संरचना === | === समूह संरचना === | ||
विषम संख्या में दर्पणों की आवश्यकता वाले | विषम संख्या में दर्पणों की आवश्यकता वाले सममिति़ - परावर्तन और ग्लाइड परावर्तन - हमेशा बाएँ और दाएँ परिवर्तित होते हैं। यहां तक कि सममिति़ - पहचान, घूर्णन और अंतरण - कभी नहीं करते; वे कठोर गतियों के अनुरूप हैं, और सममिति़ के पूर्ण यूक्लिडियन समूह का एक [[ सामान्य उपसमूह |सामान्य उपसमूह]] बनाते हैं। न तो पूरा समूह और न ही उपसमूह [[ एबेलियन समूह |एबेलियन समूह]] हैं; उदाहरण के लिए, दो समानांतर दर्पणों की रचना के क्रम को परिवर्तित करने से उनके द्वारा उत्पन्न अंतरण की दिशा परिवर्तित हो जाती है। | ||
:' | :'प्रमाण'। पहचान एक आइसोमेट्री है; इसलिए दूरी नहीं बदल सकती। और यदि एक आइसोमेट्री दूरी नहीं बदल सकती है, न ही दो (या तीन, या अधिक) उत्तराधिकार में; इस प्रकार दो आइसोमेट्री की संरचना फिर से एक आइसोमेट्री है, और आइसोमेट्री का सम्मुचय रचना के अंतर्गत बंद है। पहचान [[ समरूपता |आइसोमेट्री]] भी रचना के लिए एक पहचान है, और रचना साहचर्य है; इसलिए आइसोमेट्री एक [[ semigroup |अर्धसमूह]] के लिए स्वयंसिद्धों को संतुष्ट करती है। एक समूह (गणित) के लिए, हमारे पास प्रत्येक तत्व के लिए व्युत्क्रम भी होना चाहिए। एक परावर्तन को अस्वीकृत करने के लिए, हम केवल इसे स्वयं के साथ बनाते हैं (परावर्तन इनवॉल्यूशन (गणित) हैं)। और चूंकि प्रत्येक आइसोमेट्री को परावर्तनों के अनुक्रम के रूप में व्यक्त किया जा सकता है, इसके व्युत्क्रम को उस क्रम के परिवर्तित होने के रूप में व्यक्त किया जा सकता है। ध्यान दें कि समान परावर्तनों की एक युग्म को अस्वीकृत करने से अनुक्रम की समता को संरक्षित करते हुए परावर्तनों की संख्या एक सम संख्या से कम हो जाती है; यह भी ध्यान दें कि सर्वसमिका में सम समानता है। इसलिए सभी आइसोमेट्री एक समूह बनाते हैं, और आइसोमेट्री भी एक उपसमूह बनाते हैं। (विषम आइसोमेट्री में पहचान शामिल नहीं है, इसलिए उपसमूह नहीं हैं)। यह उपसमूह एक सामान्य उपसमूह है, क्योंकि दो विषम समूहों के बीच एक समान आइसोमेट्री को सैंडविचिंग करने से एक समान आइसोमेट्री प्राप्त होती है। | ||
चूँकि सम उपसमूह सामान्य है, यह [[ भागफल समूह ]] के लिए | चूँकि सम उपसमूह सामान्य है, यह [[ भागफल समूह |भागफल समूह]] के लिए आइसोमेट्री का कर्नेल (बीजगणित) है, जहाँ भागफल परावर्तन और पहचान वाले समूह के लिए समरूप है। यद्यपि पूरा समूह [[ समूहों का प्रत्यक्ष उत्पाद |समूहों का प्रत्यक्ष उत्पाद]] नहीं है, बल्कि केवल उपसमूह और भागफल समूह का एक [[ अर्ध-प्रत्यक्ष उत्पाद |अर्ध-प्रत्यक्ष उत्पाद]] है। | ||
=== रचना === | === रचना === | ||
आइसोमेट्री की संरचना विभिन्न प्रकार से मिश्रित होती है। हम पहचान को या तो दो दर्पणों के रूप में सोच सकते हैं या कोई नहीं; किसी भी तरह से, रचना में इसका कोई प्रभाव नहीं है। और दो | आइसोमेट्री की संरचना विभिन्न प्रकार से मिश्रित होती है। हम पहचान को या तो दो दर्पणों के रूप में सोच सकते हैं या कोई नहीं; किसी भी तरह से, रचना में इसका कोई प्रभाव नहीं है। और दो परावर्तन या तो अंतरण या घूर्णन, या पहचान देते हैं (जो दोनों निरर्थक तरीके से है)। इनमें से किसी के साथ बना परावर्तन एक ही परावर्तन को अस्वीकृत कर सकता है; अन्यथा यह केवल उपलब्ध तीन-दर्पण आइसोमेट्री, एक ग्लाइड परावर्तन देता है। अंतरणों की युग्म हमेशा एक ही अंतरण में घट जाती है; इसलिए चुनौतीपूर्ण स्थितियों में घूर्णन शामिल है। हम जानते हैं कि एक घूर्णन या तो एक घूर्णन या एक अंतरण से बना एक घूर्णन एक समान आइसोमेट्री का उत्पादन करना चाहिए। अंतरण के साथ संरचना एक और घूर्णन उत्पन्न करती है (उसी राशि से, स्थानांतरित निश्चित बिंदु के साथ), लेकिन घूर्णन के साथ संरचना या तो अंतरण या घूर्णन उत्पन्न कर सकती है। यह अक्सर कहा जाता है कि दो घूर्णनों की संरचना घूर्णन उत्पन्न करती है, और [[ यूलर |यूलर]] ने 3D में उस प्रभाव के लिए एक प्रमेय सिद्ध किया; यद्यपि, यह केवल एक निश्चित बिंदु साझा करने वाले घूर्णनों के लिए सही है। | ||
=== | === अंतरण, घूर्णन, और आयतीय उपसमूह === | ||
इस प्रकार हमारे पास दो नए प्रकार के आइसोमेट्री उपसमूह हैं: सभी | इस प्रकार हमारे पास दो नए प्रकार के आइसोमेट्री उपसमूह हैं: सभी अंतरण, और घूर्णन एक निश्चित बिंदु साझा करते हैं। दोनों समान उपसमूह के उपसमूह हैं, जिसके भीतर अंतरण सामान्य हैं। क्योंकि अंतरण एक सामान्य उपसमूह हैं, हम आइसोमेट्री के उपसमूह को एक निश्चित बिंदु, ओर्थोगोनल समूह के साथ छोड़कर उन्हें कारक बना सकते हैं। | ||
[[Image:Translations combine as mirrors 2005-07-08.png|right|400px|दर्पण के साथ | [[Image:Translations combine as mirrors 2005-07-08.png|right|400px|दर्पण के साथ अंतरण जोड़]]:सबूत। यदि दो घूर्णन निश्चित बिंदु साझा करते हैं, तो हम केवल बाहरी युग्म को छोड़कर, चार (दो और दो) के अनुक्रम के आंतरिक दर्पणों को अस्वीकृत करने के लिए दूसरे घूर्णन के दर्पण जोड़े को घुमा सकते हैं। इस प्रकार सामान्य निश्चित बिंदु के साथ दो घूर्णनों की संरचना एक ही निश्चित बिंदु के कोणों के योग से एक घूर्णन उत्पन्न करती है। | ||
: यदि दो | : यदि दो अंतरण समानांतर हैं, तो हम दूसरे अंतरण के दर्पण जोड़े को चार के अनुक्रम के आंतरिक दर्पण को अस्वीकृत करने के लिए स्लाइड कर सकते हैं, जितना कि घूर्णन स्थिति में। इस प्रकार दो समानांतर अंतरणों की रचना एक ही दिशा में दूरियों के योग द्वारा अंतरण उत्पन्न करती है। अब मान लीजिए कि अंतरण समानांतर नहीं हैं, और दर्पण अनुक्रम A<sub>1</sub> है, A<sub>2</sub> (पहला अंतरण) उसके बाद B<sub>1</sub>, B<sub>2</sub> (द्वितीय)। फिर A<sub>2</sub> और B<sub>1</sub> पार करना होगा, c पर कहें; और, पुन: संबद्ध करते हुए, हम इस आंतरिक युग्म को c के आसपास पिवट करने के लिए स्वतंत्र हैं। यदि हम 90° को पिवोट करते हैं, तो रोचक बात घटित होती है: अब A<sub>1</sub> और A<sub>2</sub> 90° के कोण पर प्रतिच्छेद करता है, मान लीजिए p पर, और इसी प्रकार B<sub>1</sub> पर भी' और B<sub>2</sub>, q पर कहें। पुन: संबद्ध करते हुए, हम बी बनाने के लिए p<sub>2</sub> के चारों ओर पहली युग्म को पिवोट करते हैं″ q से गुजरें, और दूसरी युग्म को q के चारों ओर A<sub>1</sub> बनाने के लिए पिवोट करें″ p के माध्यम से पारित करें। आंतरिक दर्पण अब सन्निपतित हैं और अस्वीकृत हो जाते हैं, और बाहरी दर्पण समानांतर रह जाते हैं। इस प्रकार दो नॉन-समानांतर अंतरणों की रचना भी अंतरण उत्पन्न करती है। साथ ही, तीन धुरी बिंदु एक त्रिभुज बनाते हैं, जिसके किनारे सदिश योग का हेड-टू-टेल नियम देते हैं: 2(p c) + 2(c q) = 2(p q)। | ||
{{clear}} | {{clear}} | ||
=== नेस्टेड समूह निर्माण === | === नेस्टेड समूह निर्माण === | ||
उपसमूह संरचना एक | उपसमूह संरचना एक एकपक्षीय आइसोमेट्री बनाने का एक और तरीका सुझाती है: | ||
: एक निश्चित बिंदु चुनें, और इसके माध्यम से | : एक निश्चित बिंदु चुनें, और इसके माध्यम से दर्पण चुनें। | ||
# यदि आइसोमेट्री विषम है, तो दर्पण का उपयोग करें; अन्यथा नहीं। | # यदि आइसोमेट्री विषम है, तो दर्पण का उपयोग करें; अन्यथा नहीं। | ||
# यदि आवश्यक हो, तो निश्चित बिंदु के चारों ओर घुमाएँ। | # यदि आवश्यक हो, तो निश्चित बिंदु के चारों ओर घुमाएँ। | ||
# यदि आवश्यक हो, | # यदि आवश्यक हो, अंतरण करें। | ||
यह काम करता है क्योंकि | यह काम करता है क्योंकि अंतरण आइसोमेट्री के पूर्ण समूह का सामान्य उपसमूह है, भागफल के साथ ओर्थोगोनल समूह; और एक निश्चित बिंदु के बारे में घूर्णन आयतीय समूह का एक सामान्य उपसमूह है, जिसमें भागफल एक परावर्तन होता है। | ||
=== असतत उपसमूह === | === असतत उपसमूह === | ||
[[Image:Pentagon symmetry as mirrors 2005-07-08.png|right|140px|नियमित पेंटागन | [[Image:Pentagon symmetry as mirrors 2005-07-08.png|right|140px|नियमित पेंटागन आइसोमेट्री का डायहेड्रल समूह]]अब तक जिन उपसमूहों की चर्चा की गई है, वे न केवल अनंत हैं, वे निरंतर भी हैं (लाई समूह)। कम से कम एक नॉन-जीरो अंतरण वाला कोई भी उपसमूह अनंत होना चाहिए, लेकिन आयतीय समूह के उपसमूह परिमित हो सकते हैं। उदाहरण के लिए, एक नियमित[[ पंचकोण |पंचकोण]]की[[ समरूपता |आइसोमेट्री]]में 72° (360° / 5) के पूर्णांक गुणकों द्वारा घूर्णनों के साथ-साथ पाँच दर्पणों में परावर्तन होते हैं जो किनारों को लंबवत रूप से विभाजित करते हैं। यह एक समूह है, D<sub>5</sub>, 10 तत्वों के साथ। इसका उपसमूह है, C<sub>5</sub>, आधे आकार का, परावर्तनों को छोड़ते हुए। ये दो समूह दो परिवारों के सदस्य हैं, D<sub>''n''</sub> और C<sub>''n''</sub>, किसी भी n> 1 के लिए। साथ में, ये परिवार [[ बिंदु समूह |बिंदु समूह]] बनाते हैं। | ||
अंतरण स्वयं पर वापस नहीं आते हैं, लेकिन हम उपसमूह के रूप में किसी भी परिमित अंतरण के पूर्णांक गुणक, या ऐसे दो स्वतंत्र अंतरणों के गुणकों का योग ले सकते हैं। ये समतल के आवधिक [[ चौकोर |चौकोर]] की [[ जाली (समूह) |जाली (समूह)]] उत्पन्न करते हैं। | |||
हम इन दो प्रकार के असतत समूहों को भी जोड़ सकते हैं - एक निश्चित बिंदु के चारों ओर असतत | हम इन दो प्रकार के असतत समूहों को भी जोड़ सकते हैं - एक निश्चित बिंदु के चारों ओर असतत घूर्णन और परावर्तन और असतत अंतरण - फ्रिजी समूह और [[ वॉलपेपर समूह |वॉलपेपर समूह]] उत्पन्न करने के लिए। विचित्र रूप से, निश्चित-बिंदु समूहों में से केवल कुछ ही असतत अंतरणों के साथ [[ क्रिस्टलोग्राफिक प्रतिबंध प्रमेय |क्रिस्टलोग्राफिक प्रतिबंध प्रमेय]] पाए जाते हैं। वास्तव में, लैटिस अनुकूलन इतने कड़े प्रतिबंध लगाता है कि [[ समाकृतिकता |समाकृतिकता]] तक, हमारे पास केवल 7 अलग-अलग फ्रिज़ समूह और 17 अलग-अलग वॉलपेपर समूह हैं। उदाहरण के लिए, पेंटागन आइसोमेट्री, D<sub>5</sub>, अंतरणों के असतत जाली के साथ असंगत हैं। (प्रत्येक उच्च आयाम में ऐसे [[ क्रिस्टलोग्राफिक समूह |क्रिस्टलोग्राफिक समूह]] की केवल एक सीमित संख्या होती है, लेकिन संख्या तेजी से बढ़ती है; उदाहरण के लिए, 3D में 230 समूह हैं और 4D में 4783 हैं।) | ||
== [[ जटिल आंकड़े ]] में | == [[ जटिल आंकड़े | जटिल समतल]] में सममिति == | ||
सम्मिश्र संख्याओं के संदर्भ में, समतल की सममितियाँ या तो किसी रूप की होती हैं | सम्मिश्र संख्याओं के संदर्भ में, समतल की सममितियाँ या तो किसी रूप की होती हैं | ||
:<math>\begin{array}{ccc}\mathbb{C}&\longrightarrow&\mathbb{C}\\ z&\mapsto&a+\omega z\end{array}</math> | :<math>\begin{array}{ccc}\mathbb{C}&\longrightarrow&\mathbb{C}\\ z&\mapsto&a+\omega z\end{array}</math> | ||
| Line 183: | Line 195: | ||
कुछ सम्मिश्र संख्याओं के लिए a और ω के साथ |ω| = 1. यह सिद्ध करना आसान है: यदि a = f(0) और ω = f(1) − f(0) और यदि कोई परिभाषित करता है | कुछ सम्मिश्र संख्याओं के लिए a और ω के साथ |ω| = 1. यह सिद्ध करना आसान है: यदि a = f(0) और ω = f(1) − f(0) और यदि कोई परिभाषित करता है | ||
:<math>\begin{array}{rccc}g\colon&\mathbb{C}&\longrightarrow&\mathbb{C}\\ &z&\mapsto&\frac{f(z)-a}{\omega}\mbox{,}\end{array}</math> | :<math>\begin{array}{rccc}g\colon&\mathbb{C}&\longrightarrow&\mathbb{C}\\ &z&\mapsto&\frac{f(z)-a}{\omega}\mbox{,}\end{array}</math> | ||
तो | तो g एक आइसोमेट्री है, जी (0) = 0, और जी (1) = 1। फिर यह देखना आसान है कि g या तो पहचान या संयुग्मन है, और सिद्ध किया जा रहा कथन, इससे और इस तथ्य से है कि f(z) = a + ωg(z). | ||
यह स्पष्ट रूप से समतल आइसोमेट्री के पिछले वर्गीकरण से संबंधित है, क्योंकि: | यह स्पष्ट रूप से समतल आइसोमेट्री के पिछले वर्गीकरण से संबंधित है, क्योंकि: | ||
* z → a + z प्रकार के कार्य | * z → a + z प्रकार के कार्य अंतरण हैं; | ||
* z → ωz प्रकार के कार्य घूर्णन हैं (जब |ω| = 1); | * z → ωz प्रकार के कार्य घूर्णन हैं (जब |ω| = 1); | ||
*संयुग्मन प्रतिबिम्ब है। | *संयुग्मन प्रतिबिम्ब है। | ||
ध्यान दें कि जटिल बिंदु | ध्यान दें कि जटिल बिंदु p के बारे में एक घूर्णन जटिल अंकगणित द्वारा प्राप्त किया जाता है | ||
:<math>z \mapsto \omega (z - p) + p = \omega z + p(1 - \omega)</math> | :<math>z \mapsto \omega (z - p) + p = \omega z + p(1 - \omega)</math> | ||
जहां अंतिम अभिव्यक्ति 0 और एक | जहां अंतिम अभिव्यक्ति 0 और एक अंतरण पर घूर्णन के बराबर मैपिंग दिखाती है। | ||
इसलिए, प्रत्यक्ष आइसोमेट्री दी गई है <math>z \mapsto \omega z + a,</math> कोई हल कर सकता है | |||
<math>p(1 - \omega) = a</math> प्राप्त करने के लिए <math>p = a/(1 - \omega)</math> समतुल्य घूर्णन के केंद्र के रूप में, परंतु <math>\omega \ne 1</math>, परंतु प्रत्यक्ष आइसोमेट्री शुद्ध अंतरण न हो। जैसा कि सीडरबर्ग ने कहा है, एक प्रत्यक्ष आइसोमेट्री या तो एक घूर्णन या एक अंतरण है।<ref>{{cite book|last=Cederberg|first=Judith N.|year=2001|title=आधुनिक ज्यामिति में एक कोर्स|url=https://archive.org/details/coursemoderngeom00cede|url-access=limited|pages=[https://archive.org/details/coursemoderngeom00cede/page/n153 136]–164|isbn=978-0-387-98972-3}}, quote from page 151</ref> | |||
== यह भी देखें == | == यह भी देखें == | ||
* बेकमैन-क्वार्ल्स प्रमेय, रूपांतरण के रूप में आइसोमेट्री का लक्षण वर्णन जो इकाई दूरी को संरक्षित करता है | * बेकमैन-क्वार्ल्स प्रमेय, रूपांतरण के रूप में आइसोमेट्री का लक्षण वर्णन जो इकाई दूरी को संरक्षित करता है | ||
* [[ सर्वांगसमता (ज्यामिति) ]] | * [[ सर्वांगसमता (ज्यामिति) ]] | ||
* समन्वय घूर्णन और | * समन्वय घूर्णन और परावर्तन | ||
* ह्जेल्म्सलेव प्रमेय, यह कथन कि रेखाओं की | * ह्जेल्म्सलेव प्रमेय, यह कथन कि रेखाओं की सममिति में बिंदुओं के संगत युग्मों के मध्य बिंदु संरेखी होते हैं | ||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist}} | {{Reflist}} | ||
==बाहरी कड़ियाँ== | ==बाहरी कड़ियाँ== | ||
* [http://www.cut-the-knot.org/pythagoras/Transforms/index.shtml Plane Isometries] | * [http://www.cut-the-knot.org/pythagoras/Transforms/index.shtml Plane Isometries] | ||
[[श्रेणी: क्रिस्टलोग्राफी]] | [[श्रेणी: क्रिस्टलोग्राफी]] | ||
[[श्रेणी:यूक्लिडियन समतल ज्यामिति]] | [[श्रेणी:यूक्लिडियन समतल ज्यामिति]] | ||
[[श्रेणी: यूक्लिडियन समरूपता]] | [[श्रेणी: यूक्लिडियन समरूपता|श्रेणी: यूक्लिडियन आइसोमेट्री]] | ||
[[श्रेणी: समूह सिद्धांत]] | [[श्रेणी: समूह सिद्धांत]] | ||
[[श्रेणी:साक्ष्य युक्त लेख]] | [[श्रेणी:साक्ष्य युक्त लेख]] | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category: | |||
[[Category:Created On 27/12/2022]] | [[Category:Created On 27/12/2022]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with broken file links]] | |||
[[Category:Pages with script errors]] | |||
Latest revision as of 09:38, 10 January 2023
ज्यामिति में, यूक्लिडियन समतल आइसोमेट्री यूक्लिडियन समतल का एक आइसोमेट्री है, या अधिक अनौपचारिक रूप से, समतल को रूपांतरित करने का एक तरीका है जो ज्यामितीय गुणों जैसे कि लंबाई को संरक्षित करता है। चार प्रकार हैं: अंतरण (गणित में), घूर्णन, परावर्तन और ग्लाइड परावर्तन (नीचे यूक्लिडियन समतल सममितियों के वर्गीकरण के अंतर्गत देखें)।
यूक्लिडियन समतल आइसोमेट्री का सम्मुचय संरचना के अंतर्गत समूह (गणित) बनाता है: यूक्लिडियन समूह दो आयामों में। यह रेखाओं में परावर्तनों द्वारा उत्पन्न होता है, और यूक्लिडियन समूह का प्रत्येक तत्व तीन अलग-अलग परावर्तनों का सम्मिश्रण है।
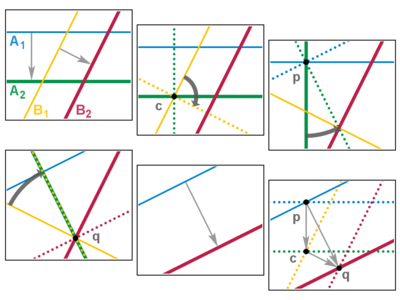
अनौपचारिक चर्चा
अनौपचारिक रूप से, यूक्लिडियन समतल आइसोमेट्री समतल को "विरूपित" किए बिना परिवर्तित करने का कोई तरीका है। उदाहरण के लिए, मान लीजिए कि यूक्लिडियन समतल को डेस्क पर रखे पारदर्शी प्लास्टिक की शीट द्वारा दर्शाया गया है। आइसोमेट्री के उदाहरणों में सम्मिलित हैं:
- शीट को एक इंच दाईं ओर खिसकाने पर।
- किसी चिन्हित बिंदु (जो गतिहीन रहता है) के चारों ओर शीट को दस डिग्री घुमाने पर।
- pछे से देखने के लिए शीट को पलट दें और ध्यान दें कि यदि शीट के एक तरफ कोई चित्र बनाया जाता है, तो शीट को पलटने के बाद, हमें चित्र का दर्पण प्रतिबिम्ब दिखाई देता है।
ये क्रमशः अंतरण, घूर्णन और परावर्तन के उदाहरण हैं। एक और प्रकार की आइसोमेट्री है, जिसे ग्लाइड रिफ्लेक्शन कहा जाता है (नीचे यूक्लिडियन समतल सममिति के वर्गीकरण के अंतर्गत देखें)।
यद्यपि, शीट को मोड़ने, काटने या पिघलाने को आइसोमेट्री नहीं माना जाता है। बंकन, प्रसार या मरोड़ना जैसे कम कठोर परिवर्तन भी नहीं हैं।
औपचारिक परिभाषा
यूक्लिडियन समतल आइसोमेट्री समतल का दूरी-संरक्षण परिवर्तन है। अर्थात, यह एक आलेख्यपत्र (मैप गणित) है
इस प्रकार, समतल में किसी बिंदु p और q के लिए,
जहाँ d(p, q) p और q के बीच सामान्य यूक्लिडियन दूरी है।
वर्गीकरण
यह दर्शाया जा सकता है कि चार प्रकार के यूक्लिडियन समतल सममिति़ हैं। (ध्यान दें: नीचे सूचीबद्ध सममिति़ के प्रकार के लिए संकेतन पूरी तरह से मानकीकृत नहीं हैं।)
परावर्तन
परावर्तन (गणित) या मिरर आइसोमेट्री, जिसे Fc,v, द्वारा दर्शाया जाता है जहाँ c समतल में एक बिंदु है और 'R2' में v एक इकाई सदिश है। (F फ्लिपको दर्शाता है।) रेखा L में बिंदु P को परावर्तनित करने का प्रभाव है जो v के लंबवत है और जो c के माध्यम से गुजरता है। रेखा L को 'परावर्तन अक्ष' या संबंधित 'दर्पण' कहा जाता है। Fc,v, के लिए सूत्र खोजने के लिए हम v दिशा में p - c के घटक t को खोजने के लिए सबसे पहलेडॉट प्रोडक्ट का उपयोग करते हैं,
- और फिर हम घटाव द्वारा p का परावर्तन प्राप्त करते हैं,
मूल के बारे में घूर्णनों का संयोजन और मूल के माध्यम से एक रेखा के बारे में परावर्तन सभी आयतीय आव्यूह (अर्थात सारणिक 1 और -1 के साथ) के साथ प्राप्त किया जाता है जो आयतीय समूह ओ (2) बनाते हैं। -1 के सारणिक की स्थिति में हमारे पास है:
जो x-अक्ष में एक परावर्तन है जिसके बाद कोण θ द्वारा घूर्णन होता है, या समकक्ष रूप से, x-अक्ष के साथ θ/2 का कोण बनाने वाली रेखा में परावर्तन होता है। समानांतर रेखा में परावर्तन इसके लिए एक सदिश लम्ब जोड़ने पर सामान लगता है।
अंतरण
अंतरण (गणित) द्वारा Tv, जहाँ 'R2' में v एक सदिश (ज्यामितीय) है यह तल को v की दिशा में स्थानांतरित करने का प्रभाव होता है। अर्थात, तल में किसी बिंदु p के लिए,
- या (x, y) निर्देशांक के संदर्भ में,
अंतरण को दो समांतर परावर्तनों के संयोजन के रूप में देखा जा सकता है।
घूर्णन
घूर्णन (गणित) , Rc,θ, द्वारा निरूपित जहाँ c समतल (घूर्णन का केंद्र) में एक बिंदु है, और θ घूर्णन का कोण है। निर्देशांक के संदर्भ में, घूर्णन को दो संक्रियाओं में तोड़कर सबसे आसानी से व्यक्त किया जाता है। सबसे पहले, मूलबिंदु के चारों ओर एक घूर्णन किसके द्वारा दिया जाता है
- ये मैट्रिसेस आयतीय मैट्रिक्स हैं (अर्थात प्रत्येक स्क्वायर मैट्रिक्स G है जिसका स्थानान्तरण इसका व्युत्क्रम मैट्रिक्स है, अर्थात ) सारणिक 1 के साथ (आयतीय आव्यूह के लिए दूसरी संभावना -1 है, जो एक दर्पण छवि देता है, नीचे देखें)। वे विशेष लांबिक समूह SO(2) बनाते हैं।
- c के चारों ओर घूर्णन को पहले c को मूल में अंतरण करके, फिर मूल के चारों ओर घुमाकर, और अंत में मूल को वापस c में अंतरण करके पूरा किया जा सकता है। वह है,
- या दूसरे शब्दों में,
- वैकल्पिक रूप से, मूल के चारों ओर घूर्णन किया जाता है, उसके बाद अंतरण किया जाता है:
एक घूर्णन को दो असमानांतर परावर्तनों के सम्मिश्रण के रूप में देखा जा सकता है।
रिजिड रूपांतरण
अंतरण और घूर्णन का सम्मुचय एक साथ रिजिड गति या रिजिड विस्थापन का निर्माण करता है। यह सम्मुचय रचना के अंतर्गत समूह (गणित) बनाता है,कठोर गतियों का समूह , यूक्लिडियन सममिति़ के पूर्ण समूह का एक उपसमूह।
ग्लाइड परावर्तन
ग्लाइड परावर्तन, Gc,v,w, द्वारा निरूपित जहाँ c समतल में एक बिंदु है, 'R2' में v एक इकाई सदिश है, और w नॉन-रिक्त एक सदिश है जो v के लंबवत है, c और v द्वारा वर्णित रेखा में परावर्तन का संयोजन है, जिसके बाद w के साथ अंतरण होता है। वह है,
- या दूसरे शब्दों में,
- यह भी सच है
अर्थात, यदि हम अंतरण और परावर्तन को विपरीत क्रम में करते हैं तो हमें वही परिणाम मिलता है।) वैकल्पिक रूप से हम आयतीय मैट्रिक्स द्वारा सारणिक -1 (मूल के माध्यम से एक पंक्ति में एक परावर्तन के अनुरूप) के साथ गुणा करते हैं, जिसके बाद अंतरण होता है। यह एक ग्लाइड परावर्तन है, विशेष स्थिति को छोड़कर कि अंतरण परावर्तन की रेखा के लंबवत है, इस स्थिति में संयोजन स्वयं समानांतर रेखा में एक परावर्तन है।
सभी बिंदुओं के लिए I (p) = p द्वारा परिभाषित पहचान (गणित)आइसोमेट्री एक अंतरण का एक विशेष मामला है, और एक घूर्णन का एक विशेष मामला भी है। यह एकमात्र आइसोमेट्री है जो ऊपर वर्णित एक से अधिक प्रकारों से संबंधित है।
सभी स्थितियों में हम स्थिति सदिश को आयतीय मैट्रिक्स से गुणा करते हैं और एक सदिश जोड़ते हैं; यदि सारणिक 1 है तो हमारे पास एक घूर्णन, एक अंतरण या पहचान है, और यदि यह -1 है तो हमारे पास ग्लाइड परावर्तन या परावर्तन है।
यादृच्छिक आइसोमेट्री, जैसे मेज से कागज की शीट लेना और इसे बेतरतीब ढंग से वापस रखना, लगभग निश्चित रूप से घूर्णन या ग्लाइड परावर्तन है (उनके पास स्वतंत्रता की तीन डिग्री (भौतिकी और रसायन विज्ञान) है)। यह संभाव्यता वितरण के विवरण की परवाह किए बिना लागू होता है, जब तक कि θ और जोड़े गए सदिश की दिशा सांख्यिकीय स्वतंत्रता और समान वितरण (निरंतर)है और जोड़े गए सदिश की लंबाई में निरंतर वितरण होता है। एक शुद्ध अंतरण और शुद्ध परावर्तन स्वतंत्रता की केवल दो डिग्री के साथ विशेष स्थिति हैं, जबकि पहचान और भी विशेष है, स्वतंत्रता की कोई डिग्री नहीं है।
परावर्तन समूह के रूप में आइसोमेट्री
किसी भी आइसोमेट्री का उत्पादन करने के लिए परावर्तन, या दर्पण सममिति़ को जोड़ा जा सकता है। इस प्रकार आइसोमेट्री परावर्तन समूह का उदाहरण है।
दर्पण संयोजन
यूक्लिडियन समतल में, हमारे पास निम्नलिखित संभावनाएँ हैं।
- [d ] पहचान
- एक ही दर्पण में दो परावर्तन प्रत्येक बिंदु को उसकी मूल स्थिति में पुनर्स्थापित करते हैं। सभी बिंदुओं को स्थिर छोड़ दिया गया है। समान दर्पणों की किसी भी युग्म का प्रभाव समान होता है।
- [db] परावर्तन
- जैसा कि ऐलिस ने लुकिंग-ग्लास के माध्यम से पाया | लुकिंग-ग्लास के माध्यम से, एक दर्पण बाएं और दाएं हाथों को स्विच करने का कारण बनता है। (औपचारिक शब्दों में, टोपोलॉजिकल ओरिएंटेशन उलट जाता है।) दर्पण पर बिंदुओं को स्थिर छोड़ दिया जाता है। प्रत्येक दर्पण का अनूठा प्रभाव होता है।
- [dp] घूर्णन
- दो अलग-अलग प्रतिच्छेदी दर्पणों में सामान्य बिंदु होता है, जो स्थिर रहता है। अन्य सभी बिंदु इसके चारों ओर दर्पणों के बीच के कोण के दोगुने से घूमते हैं। समान निश्चित बिंदु और समान कोण वाले कोई भी दो दर्पण समान घूर्णन देते हैं, जब तक कि उनका उपयोग सही क्रम में किया जाता है।
- [dg] अंतरण
- दो अलग-अलग दर्पण जो प्रतिच्छेद नहीं करते हैं उन्हें समानांतर होना चाहिए। प्रत्येक बिंदु समान मात्रा में, दर्पणों के बीच की दुगुनी दूरी पर और एक ही दिशा में गति करता है। कोई अंक निश्चित नहीं छोड़ा गया है। समान समानांतर दिशा और समान दूरी वाले कोई भी दो दर्पण समान अंतरण देते हैं, जब तक कि उनका सही क्रम में उपयोग किया जाता है।
- [dq] ग्लाइड परावर्तन
- तीन दर्पण। यदि वे सभी समानांतर हैं, तो प्रभाव एकल दर्पण के समान होता है (तीसरे को अस्वीकृत करने के लिए एक युग्म को स्लाइड करें)। अन्यथा हम एक समतुल्य व्यवस्था प्राप्त कर सकते हैं जहां दो समानांतर हैं और तीसरा उनके लिए लंबवत है। प्रभाव दर्पण के समानांतर अंतरण के साथ संयुक्त परावर्तन है। कोई अंक निश्चित नहीं छोड़ा गया है।
तीन दर्पण पर्याप्त
अधिक दर्पण जोड़ने से अधिक संभावनाएँ ( समतल में) नहीं जुड़ती हैं, क्योंकि अस्वीकृतीकरण का कारण बनने के लिए उन्हें हमेशा पुनर्व्यवस्थित किया जा सकता है।
- सबूत। एक आइसोमेट्री पूरी तरह से तीन स्वतंत्र (संरेखित नहीं) बिंदुओं पर इसके प्रभाव से निर्धारित होती है। तो मान लीजिए p1, p2, p3 q के लिए नक्शा1, q2, q3; हम इसे निम्नानुसार प्राप्त करने के लिए दर्पणों का एक क्रम उत्पन्न कर सकते हैं। यदि प1 और q1 भिन्न हैं, उनके लंब समद्विभाजक को दर्पण के रूप में चुनें। अब p1 q के नक्शे1; और हम आगे के सभी दर्पणों को q से गुजारेंगे1, इसे ठीक करके छोड़ दें। p की छवियों को कॉल करें2 और p3 इस परावर्तन के अंतर्गत p2' और p3 ,यदि q2 p2 से भिन्न है, कोण को q1 पर समद्विभाजित करें एक नए आईने के साथ। p1 के साथ और p2 अब जगह में, p3 p3 पर है; और यदि यह जगह में नहीं है, q1 के माध्यम से एक अंतिम दर्पण और q2 इसे q3 पर फ़्लिप करेंगे इस प्रकार किसी भी समतल आइसोमेट्री को पुन: उत्पन्न करने के लिए अधिकतम तीन परावर्तन पर्याप्त हैं।
मान्यता
हम पहचान सकते हैं कि इनमें से कौन सी आइसोमेट्री हमारे पास है या नहीं, इसके अनुसार यह हाथों को संरक्षित करता है या उन्हें विनिमय करता है, और क्या इसमें कम से कम एक निश्चित बिंदु है या नहीं, जैसा कि निम्नलिखित तालिका में दिखाया गया है (पहचान को छोड़ कर)।
| Preserves hands? | |||
|---|---|---|---|
| Yes | नहीं | ||
| नियत बिन्दु? | हाँ | घूर्णन | परावर्तन |
| नहीं | अंतरण | ग्लाइड परावर्तन | |
समूह संरचना
विषम संख्या में दर्पणों की आवश्यकता वाले सममिति़ - परावर्तन और ग्लाइड परावर्तन - हमेशा बाएँ और दाएँ परिवर्तित होते हैं। यहां तक कि सममिति़ - पहचान, घूर्णन और अंतरण - कभी नहीं करते; वे कठोर गतियों के अनुरूप हैं, और सममिति़ के पूर्ण यूक्लिडियन समूह का एक सामान्य उपसमूह बनाते हैं। न तो पूरा समूह और न ही उपसमूह एबेलियन समूह हैं; उदाहरण के लिए, दो समानांतर दर्पणों की रचना के क्रम को परिवर्तित करने से उनके द्वारा उत्पन्न अंतरण की दिशा परिवर्तित हो जाती है।
- 'प्रमाण'। पहचान एक आइसोमेट्री है; इसलिए दूरी नहीं बदल सकती। और यदि एक आइसोमेट्री दूरी नहीं बदल सकती है, न ही दो (या तीन, या अधिक) उत्तराधिकार में; इस प्रकार दो आइसोमेट्री की संरचना फिर से एक आइसोमेट्री है, और आइसोमेट्री का सम्मुचय रचना के अंतर्गत बंद है। पहचान आइसोमेट्री भी रचना के लिए एक पहचान है, और रचना साहचर्य है; इसलिए आइसोमेट्री एक अर्धसमूह के लिए स्वयंसिद्धों को संतुष्ट करती है। एक समूह (गणित) के लिए, हमारे पास प्रत्येक तत्व के लिए व्युत्क्रम भी होना चाहिए। एक परावर्तन को अस्वीकृत करने के लिए, हम केवल इसे स्वयं के साथ बनाते हैं (परावर्तन इनवॉल्यूशन (गणित) हैं)। और चूंकि प्रत्येक आइसोमेट्री को परावर्तनों के अनुक्रम के रूप में व्यक्त किया जा सकता है, इसके व्युत्क्रम को उस क्रम के परिवर्तित होने के रूप में व्यक्त किया जा सकता है। ध्यान दें कि समान परावर्तनों की एक युग्म को अस्वीकृत करने से अनुक्रम की समता को संरक्षित करते हुए परावर्तनों की संख्या एक सम संख्या से कम हो जाती है; यह भी ध्यान दें कि सर्वसमिका में सम समानता है। इसलिए सभी आइसोमेट्री एक समूह बनाते हैं, और आइसोमेट्री भी एक उपसमूह बनाते हैं। (विषम आइसोमेट्री में पहचान शामिल नहीं है, इसलिए उपसमूह नहीं हैं)। यह उपसमूह एक सामान्य उपसमूह है, क्योंकि दो विषम समूहों के बीच एक समान आइसोमेट्री को सैंडविचिंग करने से एक समान आइसोमेट्री प्राप्त होती है।
चूँकि सम उपसमूह सामान्य है, यह भागफल समूह के लिए आइसोमेट्री का कर्नेल (बीजगणित) है, जहाँ भागफल परावर्तन और पहचान वाले समूह के लिए समरूप है। यद्यपि पूरा समूह समूहों का प्रत्यक्ष उत्पाद नहीं है, बल्कि केवल उपसमूह और भागफल समूह का एक अर्ध-प्रत्यक्ष उत्पाद है।
रचना
आइसोमेट्री की संरचना विभिन्न प्रकार से मिश्रित होती है। हम पहचान को या तो दो दर्पणों के रूप में सोच सकते हैं या कोई नहीं; किसी भी तरह से, रचना में इसका कोई प्रभाव नहीं है। और दो परावर्तन या तो अंतरण या घूर्णन, या पहचान देते हैं (जो दोनों निरर्थक तरीके से है)। इनमें से किसी के साथ बना परावर्तन एक ही परावर्तन को अस्वीकृत कर सकता है; अन्यथा यह केवल उपलब्ध तीन-दर्पण आइसोमेट्री, एक ग्लाइड परावर्तन देता है। अंतरणों की युग्म हमेशा एक ही अंतरण में घट जाती है; इसलिए चुनौतीपूर्ण स्थितियों में घूर्णन शामिल है। हम जानते हैं कि एक घूर्णन या तो एक घूर्णन या एक अंतरण से बना एक घूर्णन एक समान आइसोमेट्री का उत्पादन करना चाहिए। अंतरण के साथ संरचना एक और घूर्णन उत्पन्न करती है (उसी राशि से, स्थानांतरित निश्चित बिंदु के साथ), लेकिन घूर्णन के साथ संरचना या तो अंतरण या घूर्णन उत्पन्न कर सकती है। यह अक्सर कहा जाता है कि दो घूर्णनों की संरचना घूर्णन उत्पन्न करती है, और यूलर ने 3D में उस प्रभाव के लिए एक प्रमेय सिद्ध किया; यद्यपि, यह केवल एक निश्चित बिंदु साझा करने वाले घूर्णनों के लिए सही है।
अंतरण, घूर्णन, और आयतीय उपसमूह
इस प्रकार हमारे पास दो नए प्रकार के आइसोमेट्री उपसमूह हैं: सभी अंतरण, और घूर्णन एक निश्चित बिंदु साझा करते हैं। दोनों समान उपसमूह के उपसमूह हैं, जिसके भीतर अंतरण सामान्य हैं। क्योंकि अंतरण एक सामान्य उपसमूह हैं, हम आइसोमेट्री के उपसमूह को एक निश्चित बिंदु, ओर्थोगोनल समूह के साथ छोड़कर उन्हें कारक बना सकते हैं।
:सबूत। यदि दो घूर्णन निश्चित बिंदु साझा करते हैं, तो हम केवल बाहरी युग्म को छोड़कर, चार (दो और दो) के अनुक्रम के आंतरिक दर्पणों को अस्वीकृत करने के लिए दूसरे घूर्णन के दर्पण जोड़े को घुमा सकते हैं। इस प्रकार सामान्य निश्चित बिंदु के साथ दो घूर्णनों की संरचना एक ही निश्चित बिंदु के कोणों के योग से एक घूर्णन उत्पन्न करती है।
- यदि दो अंतरण समानांतर हैं, तो हम दूसरे अंतरण के दर्पण जोड़े को चार के अनुक्रम के आंतरिक दर्पण को अस्वीकृत करने के लिए स्लाइड कर सकते हैं, जितना कि घूर्णन स्थिति में। इस प्रकार दो समानांतर अंतरणों की रचना एक ही दिशा में दूरियों के योग द्वारा अंतरण उत्पन्न करती है। अब मान लीजिए कि अंतरण समानांतर नहीं हैं, और दर्पण अनुक्रम A1 है, A2 (पहला अंतरण) उसके बाद B1, B2 (द्वितीय)। फिर A2 और B1 पार करना होगा, c पर कहें; और, पुन: संबद्ध करते हुए, हम इस आंतरिक युग्म को c के आसपास पिवट करने के लिए स्वतंत्र हैं। यदि हम 90° को पिवोट करते हैं, तो रोचक बात घटित होती है: अब A1 और A2 90° के कोण पर प्रतिच्छेद करता है, मान लीजिए p पर, और इसी प्रकार B1 पर भी' और B2, q पर कहें। पुन: संबद्ध करते हुए, हम बी बनाने के लिए p2 के चारों ओर पहली युग्म को पिवोट करते हैं″ q से गुजरें, और दूसरी युग्म को q के चारों ओर A1 बनाने के लिए पिवोट करें″ p के माध्यम से पारित करें। आंतरिक दर्पण अब सन्निपतित हैं और अस्वीकृत हो जाते हैं, और बाहरी दर्पण समानांतर रह जाते हैं। इस प्रकार दो नॉन-समानांतर अंतरणों की रचना भी अंतरण उत्पन्न करती है। साथ ही, तीन धुरी बिंदु एक त्रिभुज बनाते हैं, जिसके किनारे सदिश योग का हेड-टू-टेल नियम देते हैं: 2(p c) + 2(c q) = 2(p q)।
नेस्टेड समूह निर्माण
उपसमूह संरचना एक एकपक्षीय आइसोमेट्री बनाने का एक और तरीका सुझाती है:
- एक निश्चित बिंदु चुनें, और इसके माध्यम से दर्पण चुनें।
- यदि आइसोमेट्री विषम है, तो दर्पण का उपयोग करें; अन्यथा नहीं।
- यदि आवश्यक हो, तो निश्चित बिंदु के चारों ओर घुमाएँ।
- यदि आवश्यक हो, अंतरण करें।
यह काम करता है क्योंकि अंतरण आइसोमेट्री के पूर्ण समूह का सामान्य उपसमूह है, भागफल के साथ ओर्थोगोनल समूह; और एक निश्चित बिंदु के बारे में घूर्णन आयतीय समूह का एक सामान्य उपसमूह है, जिसमें भागफल एक परावर्तन होता है।
असतत उपसमूह
अब तक जिन उपसमूहों की चर्चा की गई है, वे न केवल अनंत हैं, वे निरंतर भी हैं (लाई समूह)। कम से कम एक नॉन-जीरो अंतरण वाला कोई भी उपसमूह अनंत होना चाहिए, लेकिन आयतीय समूह के उपसमूह परिमित हो सकते हैं। उदाहरण के लिए, एक नियमितपंचकोणकीआइसोमेट्रीमें 72° (360° / 5) के पूर्णांक गुणकों द्वारा घूर्णनों के साथ-साथ पाँच दर्पणों में परावर्तन होते हैं जो किनारों को लंबवत रूप से विभाजित करते हैं। यह एक समूह है, D5, 10 तत्वों के साथ। इसका उपसमूह है, C5, आधे आकार का, परावर्तनों को छोड़ते हुए। ये दो समूह दो परिवारों के सदस्य हैं, Dn और Cn, किसी भी n> 1 के लिए। साथ में, ये परिवार बिंदु समूह बनाते हैं।
अंतरण स्वयं पर वापस नहीं आते हैं, लेकिन हम उपसमूह के रूप में किसी भी परिमित अंतरण के पूर्णांक गुणक, या ऐसे दो स्वतंत्र अंतरणों के गुणकों का योग ले सकते हैं। ये समतल के आवधिक चौकोर की जाली (समूह) उत्पन्न करते हैं।
हम इन दो प्रकार के असतत समूहों को भी जोड़ सकते हैं - एक निश्चित बिंदु के चारों ओर असतत घूर्णन और परावर्तन और असतत अंतरण - फ्रिजी समूह और वॉलपेपर समूह उत्पन्न करने के लिए। विचित्र रूप से, निश्चित-बिंदु समूहों में से केवल कुछ ही असतत अंतरणों के साथ क्रिस्टलोग्राफिक प्रतिबंध प्रमेय पाए जाते हैं। वास्तव में, लैटिस अनुकूलन इतने कड़े प्रतिबंध लगाता है कि समाकृतिकता तक, हमारे पास केवल 7 अलग-अलग फ्रिज़ समूह और 17 अलग-अलग वॉलपेपर समूह हैं। उदाहरण के लिए, पेंटागन आइसोमेट्री, D5, अंतरणों के असतत जाली के साथ असंगत हैं। (प्रत्येक उच्च आयाम में ऐसे क्रिस्टलोग्राफिक समूह की केवल एक सीमित संख्या होती है, लेकिन संख्या तेजी से बढ़ती है; उदाहरण के लिए, 3D में 230 समूह हैं और 4D में 4783 हैं।)
जटिल समतल में सममिति
सम्मिश्र संख्याओं के संदर्भ में, समतल की सममितियाँ या तो किसी रूप की होती हैं
या रूप का
कुछ सम्मिश्र संख्याओं के लिए a और ω के साथ |ω| = 1. यह सिद्ध करना आसान है: यदि a = f(0) और ω = f(1) − f(0) और यदि कोई परिभाषित करता है
तो g एक आइसोमेट्री है, जी (0) = 0, और जी (1) = 1। फिर यह देखना आसान है कि g या तो पहचान या संयुग्मन है, और सिद्ध किया जा रहा कथन, इससे और इस तथ्य से है कि f(z) = a + ωg(z).
यह स्पष्ट रूप से समतल आइसोमेट्री के पिछले वर्गीकरण से संबंधित है, क्योंकि:
- z → a + z प्रकार के कार्य अंतरण हैं;
- z → ωz प्रकार के कार्य घूर्णन हैं (जब |ω| = 1);
- संयुग्मन प्रतिबिम्ब है।
ध्यान दें कि जटिल बिंदु p के बारे में एक घूर्णन जटिल अंकगणित द्वारा प्राप्त किया जाता है
जहां अंतिम अभिव्यक्ति 0 और एक अंतरण पर घूर्णन के बराबर मैपिंग दिखाती है।
इसलिए, प्रत्यक्ष आइसोमेट्री दी गई है कोई हल कर सकता है
प्राप्त करने के लिए समतुल्य घूर्णन के केंद्र के रूप में, परंतु , परंतु प्रत्यक्ष आइसोमेट्री शुद्ध अंतरण न हो। जैसा कि सीडरबर्ग ने कहा है, एक प्रत्यक्ष आइसोमेट्री या तो एक घूर्णन या एक अंतरण है।[1]
यह भी देखें
- बेकमैन-क्वार्ल्स प्रमेय, रूपांतरण के रूप में आइसोमेट्री का लक्षण वर्णन जो इकाई दूरी को संरक्षित करता है
- सर्वांगसमता (ज्यामिति)
- समन्वय घूर्णन और परावर्तन
- ह्जेल्म्सलेव प्रमेय, यह कथन कि रेखाओं की सममिति में बिंदुओं के संगत युग्मों के मध्य बिंदु संरेखी होते हैं
संदर्भ
- ↑ Cederberg, Judith N. (2001). आधुनिक ज्यामिति में एक कोर्स. pp. 136–164. ISBN 978-0-387-98972-3., quote from page 151
बाहरी कड़ियाँ
श्रेणी: क्रिस्टलोग्राफी श्रेणी:यूक्लिडियन समतल ज्यामिति श्रेणी: यूक्लिडियन आइसोमेट्री श्रेणी: समूह सिद्धांत श्रेणी:साक्ष्य युक्त लेख