ग्रेडिएंट नेटवर्क: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Primary sources|date=October 2021}}{{Confusing|date=October 2021}} | {{Primary sources|date=October 2021}}{{Confusing|date=October 2021}} | ||
[[नेटवर्क विज्ञान]] में, एक | [[नेटवर्क विज्ञान]] में, एक ग्रेडिएंट नेटवर्क एक अप्रत्यक्ष [[कंप्यूटर नेटवर्क|"सब्सट्रेट" नेटवर्क]] का एक निर्देशित [[subnetwork|सबनेटवर्क]] है जहां प्रत्येक [[नोड (नेटवर्किंग)]] में एक संबंधित स्केलर क्षमता होती है और एक आउट-लिंक होता है जो नोड को उसके निकट में सबसे छोटी (या सबसे बड़ी) क्षमता के रूप में परिभाषित करता है। सब्सट्रेट नेटवर्क पर स्वयं और उसके [[पड़ोस (ग्राफ सिद्धांत)|निकट (ग्राफ सिद्धांत)]] के संघ के रूप में परिभाषित किया गया है।<ref name="grad2">{{cite journal | last1=Danila | first1=Bogdan | last2=Yu | first2=Yong | last3=Earl | first3=Samuel | last4=Marsh | first4=John A. | last5=Toroczkai | first5=Zoltán | last6=Bassler | first6=Kevin E. | title=जटिल नेटवर्क पर कंजेशन-ग्रेडिएंट संचालित परिवहन| journal=Physical Review E | volume=74 | issue=4 | date=2006-10-19 | issn=1539-3755 | doi=10.1103/physreve.74.046114 | page=046114| pmid=17155140 | arxiv=cond-mat/0603861 | bibcode=2006PhRvE..74d6114D | s2cid=16009613 }}</ref> | ||
== परिभाषा == | == परिभाषा == | ||
परिवहन एक निश्चित नेटवर्क <math>G = G(V,E) </math> पर होता है। सब्सट्रेट ग्राफ कहा जाता है। इसमें N नोड्स हैं, <math>V = \{0, 1, ...,N-1\} </math> और सेट किनारों की <math>E = \{(i,j) | i,j\in V\} </math> एक नोड i दिए जाने पर, द्वारा इसके निकटतम के समुच्चय को G में S<sub>i</sub><sup>(1)</sup> = {j ∈ V | (i,j)∈ E} द्वारा परिभाषित कर सकते हैं। | परिवहन एक निश्चित नेटवर्क <math>G = G(V,E) </math> पर होता है। सब्सट्रेट ग्राफ कहा जाता है। इसमें N नोड्स हैं, <math>V = \{0, 1, ...,N-1\} </math> और सेट किनारों की <math>E = \{(i,j) | i,j\in V\} </math> एक नोड i दिए जाने पर, द्वारा इसके निकटतम के समुच्चय को G में S<sub>i</sub><sup>(1)</sup> = {j ∈ V | (i,j)∈ E} द्वारा परिभाषित कर सकते हैं। | ||
[[File:Gradient network (sample diagram).jpg|thumb|250px|right| | [[File:Gradient network (sample diagram).jpg|thumb|250px|right|ग्रेडिएंट नेटवर्क का एक उदाहरण।<ref name=toro/>]]आइए हम नोड्स V के सेट पर परिभाषित एक स्केलर फ़ील्ड, h = {h0, .., hN−1} पर भी विचार करें, ताकि प्रत्येक नोड i का एक स्केलर मान hi से जुड़ा हो। | ||
एक नेटवर्क पर | एक नेटवर्क पर ग्रेडिएंट: '''∇h'''''<sub>i</sub>'''(i, μ(i))''''' | ||
अर्थात् ''i'' से ''μ(i)'' तक निर्देशित किनारा, जहां ''μ''(''i'') ∈S<sub>i</sub><sup>(1)</sup> ∪ {i}, और h<sub>μ</sub> में अधिकतम मान <math>{ h_j | j \in S_i^{(1)} \cup {i}}</math> है. | अर्थात् ''i'' से ''μ(i)'' तक निर्देशित किनारा, जहां ''μ''(''i'') ∈S<sub>i</sub><sup>(1)</sup> ∪ {i}, और h<sub>μ</sub> में अधिकतम मान <math>{ h_j | j \in S_i^{(1)} \cup {i}}</math> है. | ||
'' | ''ग्रेडिएंट नेटवर्क'': ''∇<math>G = </math> ∇<math>G </math> <math> (V, F) </math>'' | ||
जहां F G पर | जहां F G पर ग्रेडिएंट किनारों का सेट है। | ||
सामान्य तौर पर, स्केलर क्षेत्र प्रवाह, बाहरी स्रोतों और नेटवर्क पर डूबने के कारण समय पर निर्भर करता है। इसलिए, | सामान्य तौर पर, स्केलर क्षेत्र प्रवाह, बाहरी स्रोतों और नेटवर्क पर डूबने के कारण समय पर निर्भर करता है। इसलिए, ग्रेडिएंट नेटवर्क ∇<math>G </math> गतिशील होगा।<ref name="grad">{{cite journal|last1=Toroczkai|first1=Zoltán|last2=Kozma|first2=Balázs|last3=Bassler|first3=Kevin E|last4=Hengartner|first4=N W|last5=Korniss|first5=G|date=2008-04-02|title=धीरे-धीरे नेटवर्क|journal=Journal of Physics A: Mathematical and Theoretical|publisher=IOP Publishing|volume=41|issue=15|page=155103|arxiv=cond-mat/0408262|doi=10.1088/1751-8113/41/15/155103|bibcode=2008JPhA...41o5103T|s2cid=118983053|issn=1751-8113}}</ref> | ||
| Line 21: | Line 21: | ||
== प्रेरणा और इतिहास == | == प्रेरणा और इतिहास == | ||
ग्रेडिएंट नेटवर्क की अवधारणा को सबसे पहले तोरोज्काई और बैस्लर (2004) द्वारा पेश किया गया था।<ref>{{Cite journal|last1=Niu|first1=Rui-Wu|last2=Pan|first2=Gui-Jun|date=2016-04-01|title=जटिल ढाल नेटवर्क पर परिवहन अनुकूलन|url=https://www.sciencedirect.com/science/article/pii/S0577907316301654|journal=Chinese Journal of Physics|language=en|volume=54|issue=2|pages=278–284|doi=10.1016/j.cjph.2016.04.014|bibcode=2016ChJPh..54..278N|issn=0577-9073}}</ref><ref>{{Cite journal|last1=Toroczkai|first1=Zoltán|last2=Bassler|first2=Kevin E.|date=2004|title=जैमिंग स्केल-फ्री सिस्टम में सीमित है|url=https://www.nature.com/articles/428716a|journal=Nature|language=en|volume=428|issue=6984|pages=716|doi=10.1038/428716a|pmid=15085122|s2cid=2839066|issn=1476-4687}}</ref> | |||
सामान्यतः, वास्तविक विश्व नेटवर्क (जैसे [[उद्धरण ग्राफ]], [[इंटरनेट]], सेलुलर चयापचय नेटवर्क, विश्वव्यापी हवाईअड्डा नेटवर्क), जो अधिकांश सूचना, कारों, बिजली, पानी, बलों आदि जैसे परिवहन संस्थाओं के लिए विकसित होते हैं, यह विश्व स्तर पर डिज़ाइन नहीं किए गए हैं; इसके अतिरिक्त, यह स्थानीय परिवर्तनों के माध्यम से विकसित होते हैं। उदाहरण के लिए, यदि इंटरनेट पर एक [[राउटर (कंप्यूटिंग)]] अधिकांश भीड़भाड़ वाला होता है और उसके कारण पैकेट खो जाते हैं या विलंबित हो जाते हैं, तो इसे कई परस्पर जुड़े नए राउटर से बदल दिया जाएगा।<ref name="toro" /> | सामान्यतः, वास्तविक विश्व नेटवर्क (जैसे [[उद्धरण ग्राफ]], [[इंटरनेट]], सेलुलर चयापचय नेटवर्क, विश्वव्यापी हवाईअड्डा नेटवर्क), जो अधिकांश सूचना, कारों, बिजली, पानी, बलों आदि जैसे परिवहन संस्थाओं के लिए विकसित होते हैं, यह विश्व स्तर पर डिज़ाइन नहीं किए गए हैं; इसके अतिरिक्त, यह स्थानीय परिवर्तनों के माध्यम से विकसित होते हैं। उदाहरण के लिए, यदि इंटरनेट पर एक [[राउटर (कंप्यूटिंग)]] अधिकांश भीड़भाड़ वाला होता है और उसके कारण पैकेट खो जाते हैं या विलंबित हो जाते हैं, तो इसे कई परस्पर जुड़े नए राउटर से बदल दिया जाएगा।<ref name="toro" /> | ||
इसके अतिरिक्त, यह प्रवाह अधिकांश स्केलर के स्थानीय | इसके अतिरिक्त, यह प्रवाह अधिकांश स्केलर के स्थानीय ग्रेडिएंट द्वारा उत्पन्न या प्रभावित होता है। उदाहरण के लिए: विद्युत प्रवाह विद्युत क्षमता के ग्रेडिएंट द्वारा संचालित होता है। सूचना नेटवर्क में, नोड्स के गुण नोड से उसके पड़ोसियों को सूचना प्रसारित करने के तरीके में एक पूर्वाग्रह उत्पन्न करेंगे। इस विचार ने ग्रेडिएंट नेटवर्क का उपयोग करके नेटवर्क की प्रवाह दक्षता का अध्ययन करने के दृष्टिकोण को प्रेरित किया, जब प्रवाह नेटवर्क पर वितरित [[अदिश क्षेत्र]] के ग्रेडिएंट द्वारा संचालित होता है।<ref name="toro" /><ref name="grad" /> | ||
हाल ही में किए गए शोध{{Which|date=October 2021}}{{Update inline|date=October 2021}} [[नेटवर्क टोपोलॉजी]] और परिवहन की प्रवाह दक्षता के बीच संबंध की जांच करता है।<ref name="toro">{{cite web|title=ग्रेडियेंट नेटवर्क|url=http://cnls.lanl.gov/External/people/highlights/Toroczkai_net.pdf|url-status=live|archive-url=https://web.archive.org/web/20061004090327/https://cnls.lanl.gov/External/people/highlights/Toroczkai_net.pdf|archive-date=4 October 2006|access-date=19 March 2021|website=cnls.lanl.gov}}</ref> | हाल ही में किए गए शोध{{Which|date=October 2021}}{{Update inline|date=October 2021}} [[नेटवर्क टोपोलॉजी]] और परिवहन की प्रवाह दक्षता के बीच संबंध की जांच करता है।<ref name="toro">{{cite web|title=ग्रेडियेंट नेटवर्क|url=http://cnls.lanl.gov/External/people/highlights/Toroczkai_net.pdf|url-status=live|archive-url=https://web.archive.org/web/20061004090327/https://cnls.lanl.gov/External/people/highlights/Toroczkai_net.pdf|archive-date=4 October 2006|access-date=19 March 2021|website=cnls.lanl.gov}}</ref> | ||
[[File:Gradient network with node pointing to largest increase.jpg|thumb|300px|left|नोड I पर | [[File:Gradient network with node pointing to largest increase.jpg|thumb|300px|left|नोड I पर ग्रेडिएंट एक निर्देशित किनारा है जो नोड के निकट में अदिश क्षमता की सबसे बड़ी वृद्धि की ओर संकेत करता है।<ref name="toro" />]] | ||
== | == ग्रेडिएंट नेटवर्क का [[इन-डिग्री]] वितरण == | ||
ग्रेडिएंट नेटवर्क में, नोड i, ''k<sub>i</sub> <sup>(in)</sup>''-डिग्री की ग्रेडिएंट किनारों की संख्या i है, और इन-डिग्री वितरण <math>R(l)= P\{k_i^{(in)}=l\}</math> है. | |||
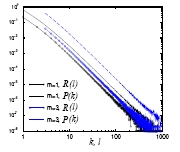
[[File:Degree distributions of gradient network and substrate (BA model).jpg|thumb|200px|left| | [[File:Degree distributions of gradient network and substrate (BA model).jpg|thumb|200px|left|ग्रेडिएंट नेटवर्क का डिग्री वितरण औरसब्सट्रेट ([[बीए मॉडल]])।<ref name="grad" />]]जब सब्सट्रेट G एक यादृच्छिक ग्राफ होता है और नोड्स की प्रत्येक जोड़ी प्रायिकता P (अर्थात् एक एर्दो-रेनी यादृच्छिक ग्राफ) से जुड़ी होती है, तो स्केलर ''h<sub>i</sub>'' i.i.d. होते हैं। (स्वतंत्र समान रूप से वितरित) '''''R(l)''''' के लिए सटीक अभिव्यक्ति द्वारा दिया गया है | ||
{{center|1=<math>R(l)=\frac{1}{N}\sum_{n=0}^{N-1}\mathrm{C}^{N-1-n}_l[1-p(1-p)]^{N-1-n-l}[p(1-p)^n]^l]</math><ref name="grad" />}} | {{center|1=<math>R(l)=\frac{1}{N}\sum_{n=0}^{N-1}\mathrm{C}^{N-1-n}_l[1-p(1-p)]^{N-1-n-l}[p(1-p)^n]^l]</math><ref name="grad" />}} | ||
सीमा में <math>N\to\infty </math> तथा <math>P\to 0 </math>, डिग्री वितरण शक्ति कानून बन जाता है | सीमा में <math>N\to\infty </math> तथा <math>P\to 0 </math>, डिग्री वितरण शक्ति कानून बन जाता है | ||
{{center|1=<math> R(l) \approx l^{-1} </math>}} | {{center|1=<math> R(l) \approx l^{-1} </math>}} | ||
यह इस सीमा में दिखाता है, यादृच्छिक नेटवर्क का | यह इस सीमा में दिखाता है, यादृच्छिक नेटवर्क का ग्रेडिएंट नेटवर्क स्केल-फ्री है।<ref name="grad" /> | ||
इसके अतिरिक्त, यदि सब्सट्रेट नेटवर्क जी स्केल-फ्री है, जैसे कि बारबासी-अल्बर्ट मॉडल में, तो | इसके अतिरिक्त, यदि सब्सट्रेट नेटवर्क जी स्केल-फ्री है, जैसे कि बारबासी-अल्बर्ट मॉडल में, तो ग्रेडिएंट नेटवर्क भी जी के समान प्रतिनिधि के साथ शक्ति नियम का पालन करता है।<ref name="toro" /> | ||
| Line 45: | Line 45: | ||
तथ्य यह है कि सब्सट्रेट नेटवर्क की टोपोलॉजी [[नेटवर्क संकुलन]] के स्तर को प्रभावित करती है, इसे एक सरल उदाहरण द्वारा स्पष्ट किया जा सकता है: यदि नेटवर्क में स्टार जैसी संरचना है, तो केंद्रीय नोड पर, प्रवाह संकुलित हो जाएगा क्योंकि केंद्रीय नोड को अन्य नोड्स से सभी प्रवाह को संभालना चाहिए। चूंकि, यदि नेटवर्क में रिंग जैसी संरचना है, क्योंकि प्रत्येक नोड समान भूमिका निभाता है, तो कोई प्रवाह संकुलन नहीं होता है। | तथ्य यह है कि सब्सट्रेट नेटवर्क की टोपोलॉजी [[नेटवर्क संकुलन]] के स्तर को प्रभावित करती है, इसे एक सरल उदाहरण द्वारा स्पष्ट किया जा सकता है: यदि नेटवर्क में स्टार जैसी संरचना है, तो केंद्रीय नोड पर, प्रवाह संकुलित हो जाएगा क्योंकि केंद्रीय नोड को अन्य नोड्स से सभी प्रवाह को संभालना चाहिए। चूंकि, यदि नेटवर्क में रिंग जैसी संरचना है, क्योंकि प्रत्येक नोड समान भूमिका निभाता है, तो कोई प्रवाह संकुलन नहीं होता है। | ||
[[File:Star network vs ring network.jpg|thumb|200px|left|प्रवाह पर संरचना के प्रभाव का चित्रण।<ref name=grad/>]]इस धारणा के अनुसार कि प्रवाह नेटवर्क में | [[File:Star network vs ring network.jpg|thumb|200px|left|प्रवाह पर संरचना के प्रभाव का चित्रण।<ref name=grad/>]]इस धारणा के अनुसार कि प्रवाह नेटवर्क में ग्रेडिएंट द्वारा उत्पन्न होता है, नेटवर्क पर प्रवाह दक्षता को जैमिंग कारक (या संकुलन कारक) के माध्यम से वर्णित किया जा सकता है, जिसे निम्नानुसार परिभाषित किया गया है: | ||
: <math> J = 1 - \langle \langle \frac{N_\text{receive}}{N_\text{send}} \rangle_h \rangle_\text{network} = R(0)</math> | : <math> J = 1 - \langle \langle \frac{N_\text{receive}}{N_\text{send}} \rangle_h \rangle_\text{network} = R(0)</math> | ||
जहां N<sub>receive</sub> | जहां N<sub>receive</sub> ग्रेडिएंट प्रवाह प्राप्त करने वाले नोड्स की संख्या है और N<sub>send</sub> ग्रेडिएंट प्रवाह भेजने वाले नोड्स की संख्या है। | ||
J का मान 0 और 1 के बीच है; <math>J=0</math> अर्थ कोई भीड़ नहीं, और <math>J=1</math> अधिकतम भीड़ के समान है। | J का मान 0 और 1 के बीच है; <math>J=0</math> अर्थ कोई भीड़ नहीं, और <math>J=1</math> अधिकतम भीड़ के समान है। | ||
Revision as of 19:01, 20 December 2022
This article relies excessively on references to primary sources. (October 2021) (Learn how and when to remove this template message) |
This article may be confusing or unclear to readers. (October 2021) (Learn how and when to remove this template message) |
नेटवर्क विज्ञान में, एक ग्रेडिएंट नेटवर्क एक अप्रत्यक्ष "सब्सट्रेट" नेटवर्क का एक निर्देशित सबनेटवर्क है जहां प्रत्येक नोड (नेटवर्किंग) में एक संबंधित स्केलर क्षमता होती है और एक आउट-लिंक होता है जो नोड को उसके निकट में सबसे छोटी (या सबसे बड़ी) क्षमता के रूप में परिभाषित करता है। सब्सट्रेट नेटवर्क पर स्वयं और उसके निकट (ग्राफ सिद्धांत) के संघ के रूप में परिभाषित किया गया है।[1]
परिभाषा
परिवहन एक निश्चित नेटवर्क पर होता है। सब्सट्रेट ग्राफ कहा जाता है। इसमें N नोड्स हैं, और सेट किनारों की एक नोड i दिए जाने पर, द्वारा इसके निकटतम के समुच्चय को G में Si(1) = {j ∈ V | (i,j)∈ E} द्वारा परिभाषित कर सकते हैं।
आइए हम नोड्स V के सेट पर परिभाषित एक स्केलर फ़ील्ड, h = {h0, .., hN−1} पर भी विचार करें, ताकि प्रत्येक नोड i का एक स्केलर मान hi से जुड़ा हो।
एक नेटवर्क पर ग्रेडिएंट: ∇hi(i, μ(i))
अर्थात् i से μ(i) तक निर्देशित किनारा, जहां μ(i) ∈Si(1) ∪ {i}, और hμ में अधिकतम मान है.
ग्रेडिएंट नेटवर्क: ∇ ∇
जहां F G पर ग्रेडिएंट किनारों का सेट है।
सामान्य तौर पर, स्केलर क्षेत्र प्रवाह, बाहरी स्रोतों और नेटवर्क पर डूबने के कारण समय पर निर्भर करता है। इसलिए, ग्रेडिएंट नेटवर्क ∇ गतिशील होगा।[3]
प्रेरणा और इतिहास
ग्रेडिएंट नेटवर्क की अवधारणा को सबसे पहले तोरोज्काई और बैस्लर (2004) द्वारा पेश किया गया था।[4][5]
सामान्यतः, वास्तविक विश्व नेटवर्क (जैसे उद्धरण ग्राफ, इंटरनेट, सेलुलर चयापचय नेटवर्क, विश्वव्यापी हवाईअड्डा नेटवर्क), जो अधिकांश सूचना, कारों, बिजली, पानी, बलों आदि जैसे परिवहन संस्थाओं के लिए विकसित होते हैं, यह विश्व स्तर पर डिज़ाइन नहीं किए गए हैं; इसके अतिरिक्त, यह स्थानीय परिवर्तनों के माध्यम से विकसित होते हैं। उदाहरण के लिए, यदि इंटरनेट पर एक राउटर (कंप्यूटिंग) अधिकांश भीड़भाड़ वाला होता है और उसके कारण पैकेट खो जाते हैं या विलंबित हो जाते हैं, तो इसे कई परस्पर जुड़े नए राउटर से बदल दिया जाएगा।[2]
इसके अतिरिक्त, यह प्रवाह अधिकांश स्केलर के स्थानीय ग्रेडिएंट द्वारा उत्पन्न या प्रभावित होता है। उदाहरण के लिए: विद्युत प्रवाह विद्युत क्षमता के ग्रेडिएंट द्वारा संचालित होता है। सूचना नेटवर्क में, नोड्स के गुण नोड से उसके पड़ोसियों को सूचना प्रसारित करने के तरीके में एक पूर्वाग्रह उत्पन्न करेंगे। इस विचार ने ग्रेडिएंट नेटवर्क का उपयोग करके नेटवर्क की प्रवाह दक्षता का अध्ययन करने के दृष्टिकोण को प्रेरित किया, जब प्रवाह नेटवर्क पर वितरित अदिश क्षेत्र के ग्रेडिएंट द्वारा संचालित होता है।[2][3]
हाल ही में किए गए शोध[which?][needs update] नेटवर्क टोपोलॉजी और परिवहन की प्रवाह दक्षता के बीच संबंध की जांच करता है।[2]
ग्रेडिएंट नेटवर्क का इन-डिग्री वितरण
ग्रेडिएंट नेटवर्क में, नोड i, ki (in)-डिग्री की ग्रेडिएंट किनारों की संख्या i है, और इन-डिग्री वितरण है.
जब सब्सट्रेट G एक यादृच्छिक ग्राफ होता है और नोड्स की प्रत्येक जोड़ी प्रायिकता P (अर्थात् एक एर्दो-रेनी यादृच्छिक ग्राफ) से जुड़ी होती है, तो स्केलर hi i.i.d. होते हैं। (स्वतंत्र समान रूप से वितरित) R(l) के लिए सटीक अभिव्यक्ति द्वारा दिया गया है
सीमा में तथा , डिग्री वितरण शक्ति कानून बन जाता है
यह इस सीमा में दिखाता है, यादृच्छिक नेटवर्क का ग्रेडिएंट नेटवर्क स्केल-फ्री है।[3]
इसके अतिरिक्त, यदि सब्सट्रेट नेटवर्क जी स्केल-फ्री है, जैसे कि बारबासी-अल्बर्ट मॉडल में, तो ग्रेडिएंट नेटवर्क भी जी के समान प्रतिनिधि के साथ शक्ति नियम का पालन करता है।[2]
नेटवर्क पर भीड़
तथ्य यह है कि सब्सट्रेट नेटवर्क की टोपोलॉजी नेटवर्क संकुलन के स्तर को प्रभावित करती है, इसे एक सरल उदाहरण द्वारा स्पष्ट किया जा सकता है: यदि नेटवर्क में स्टार जैसी संरचना है, तो केंद्रीय नोड पर, प्रवाह संकुलित हो जाएगा क्योंकि केंद्रीय नोड को अन्य नोड्स से सभी प्रवाह को संभालना चाहिए। चूंकि, यदि नेटवर्क में रिंग जैसी संरचना है, क्योंकि प्रत्येक नोड समान भूमिका निभाता है, तो कोई प्रवाह संकुलन नहीं होता है।
इस धारणा के अनुसार कि प्रवाह नेटवर्क में ग्रेडिएंट द्वारा उत्पन्न होता है, नेटवर्क पर प्रवाह दक्षता को जैमिंग कारक (या संकुलन कारक) के माध्यम से वर्णित किया जा सकता है, जिसे निम्नानुसार परिभाषित किया गया है:
जहां Nreceive ग्रेडिएंट प्रवाह प्राप्त करने वाले नोड्स की संख्या है और Nsend ग्रेडिएंट प्रवाह भेजने वाले नोड्स की संख्या है।
J का मान 0 और 1 के बीच है; अर्थ कोई भीड़ नहीं, और अधिकतम भीड़ के समान है।
की सीमा में, एर्डोस-रेनी रैंडम ग्राफ़ के लिए, भीड़ कारक बन जाता है है
इस परिणाम से पता चलता है कि यादृच्छिक नेटवर्क उस सीमा में अधिकतम भीड़भाड़ वाले होते हैं।
इसके विपरीत, स्केल-फ्री नेटवर्क के लिए, जे किसी भी एन के लिए स्थिर है, जिसका अर्थ है कि स्केल-फ्री नेटवर्क अधिकतम जैमिंग के लिए प्रवण नहीं हैं।[6]
भीड़भाड़ को नियंत्रित करने के उपाय
संचार नेटवर्क में एक समस्या यह समझ रही है कि भीड़भाड़ को कैसे नियंत्रित किया जाए और सामान्य और कुशल नेटवर्क कार्य को कैसे बनाए रखा जाए।[7] ज़ोंगहुआ लियू एट अल (2006) ने दिखाया कि नेटवर्क में उच्च डिग्री वाले नोड्स पर भीड़ होने की संभावना अधिक होती है, और नोड्स के एक छोटे अंश (जैसे 3%) की संदेश-प्रक्रिया क्षमता को चुनिंदा रूप से बढ़ाने का एक कुशल दृष्टिकोण सभी नोड्स की क्षमता को बढ़ाने के साथ-साथ प्रदर्शन करने के लिए दिखाया गया है।[7]
एना एल पास्टर वाई पियोन्ती एट अल (2008) ने दिखाया कि विश्राम संबंधी गतिशीलता[clarification needed] नेटवर्क की भीड़ को कम कर सकते हैं।[8]
पान एट अल। (2011) ने एक योजना में जैमिंग गुणों का अध्ययन किया जहां किनारों को नोड क्षमता के बीच स्केलर अंतर की शक्ति का भार दिया जाता है।[9][clarification needed]
नीयू और पान (2016) ने दिखाया कि ग्रेडिएंट फील्ड और स्थानीय नेटवर्क टोपोलॉजी के बीच संबंध स्थापित करके भीड़भाड़ को कम किया जा सकता है।[10][clarification needed]

यह भी देखें
- नेटवर्क गतिकी
- नेटवर्क टोपोलॉजी
- क्वांटम जटिल नेटवर्क
संदर्भ
- ↑ Danila, Bogdan; Yu, Yong; Earl, Samuel; Marsh, John A.; Toroczkai, Zoltán; Bassler, Kevin E. (2006-10-19). "जटिल नेटवर्क पर कंजेशन-ग्रेडिएंट संचालित परिवहन". Physical Review E. 74 (4): 046114. arXiv:cond-mat/0603861. Bibcode:2006PhRvE..74d6114D. doi:10.1103/physreve.74.046114. ISSN 1539-3755. PMID 17155140. S2CID 16009613.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 "ग्रेडियेंट नेटवर्क" (PDF). cnls.lanl.gov. Archived (PDF) from the original on 4 October 2006. Retrieved 19 March 2021.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Toroczkai, Zoltán; Kozma, Balázs; Bassler, Kevin E; Hengartner, N W; Korniss, G (2008-04-02). "धीरे-धीरे नेटवर्क". Journal of Physics A: Mathematical and Theoretical. IOP Publishing. 41 (15): 155103. arXiv:cond-mat/0408262. Bibcode:2008JPhA...41o5103T. doi:10.1088/1751-8113/41/15/155103. ISSN 1751-8113. S2CID 118983053.
- ↑ Niu, Rui-Wu; Pan, Gui-Jun (2016-04-01). "जटिल ढाल नेटवर्क पर परिवहन अनुकूलन". Chinese Journal of Physics (in English). 54 (2): 278–284. Bibcode:2016ChJPh..54..278N. doi:10.1016/j.cjph.2016.04.014. ISSN 0577-9073.
- ↑ Toroczkai, Zoltán; Bassler, Kevin E. (2004). "जैमिंग स्केल-फ्री सिस्टम में सीमित है". Nature (in English). 428 (6984): 716. doi:10.1038/428716a. ISSN 1476-4687. PMID 15085122. S2CID 2839066.
- ↑ Toroczkai, Zoltán; Bassler, Kevin E. (2004). "जैमिंग स्केल-फ्री सिस्टम में सीमित है". Nature. Springer Science and Business Media LLC. 428 (6984): 716. doi:10.1038/428716a. ISSN 0028-0836. PMID 15085122. S2CID 2839066.
- ↑ 7.0 7.1 7.2 7.3 Liu, Zonghua; Ma, Weichuan; Zhang, Huan; Sun, Yin; Hui, P.M. (2006). "स्केल-फ्री नेटवर्क में ट्रैफिक भीड़ को नियंत्रित करने का एक कुशल तरीका". Physica A: Statistical Mechanics and Its Applications. Elsevier BV. 370 (2): 843–853. arXiv:0806.1845. Bibcode:2006PhyA..370..843L. doi:10.1016/j.physa.2006.02.021. ISSN 0378-4371. S2CID 17324268.
- ↑ L Pastore y Piontti, Ana; E La Rocca, Cristian; Toroczkai, Zoltán; A Braunstein, Lidia; A Macri, Pablo; López, Eduardo (14 May 2008). "नेटवर्क कंजेशन को कम करने के लिए रिलैक्सेशनल डायनेमिक्स का उपयोग करना". New Journal of Physics (in English) (published 5 September 2008). 10 (9): 093007. Bibcode:2008NJPh...10i3007P. doi:10.1088/1367-2630/10/9/093007. S2CID 11842310.
- ↑ Pan, Gui-Jun; Liu, Sheng-Hong; Li, Mei (2011-09-15). "वेटेड ग्रेडिएंट नेटवर्क में जैमिंग". Physica A: Statistical Mechanics and Its Applications (in English). 390 (18): 3178–3182. Bibcode:2011PhyA..390.3178P. doi:10.1016/j.physa.2011.03.018. ISSN 0378-4371.
- ↑ Niu, Rui-Wu; Pan, Gui-Jun (2016-04-01). "जटिल ढाल नेटवर्क पर परिवहन अनुकूलन". Chinese Journal of Physics (in English). 54 (2): 278–284. Bibcode:2016ChJPh..54..278N. doi:10.1016/j.cjph.2016.04.014. ISSN 0577-9073.