किरण अनुरेखण (भौतिकी): Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 2: | Line 2: | ||
{{Distinguish|किरण कास्टिंग|किरण अनुरेखण (ग्राफिक्स)}} | {{Distinguish|किरण कास्टिंग|किरण अनुरेखण (ग्राफिक्स)}} | ||
भौतिकी में किरण अनुरेखण विभिन्न प्रसार [[ वेग ]] अवशोषण विशेषताओं और सतहों को परावर्तित करने वाले क्षेत्रों के साथ प्रणाली के माध्यम से तरंगों या उप-परमाणु कणों के मार्ग की गणना करने की एक विधि है। इन परिस्थितियों में तरंगाग्र झुक सकती है दिशा बदल सकती है और सतहों को प्रतिबिंबित कर सकती है जिससे जटिल विश्लेषण कर सकती है। किरण अनुरेखण असतत मात्रा में | भौतिकी में किरण अनुरेखण विभिन्न प्रसार [[ वेग |वेग]] अवशोषण विशेषताओं और सतहों को परावर्तित करने वाले क्षेत्रों के साथ प्रणाली के माध्यम से तरंगों या उप-परमाणु कणों के मार्ग की गणना करने की एक विधि है। इन परिस्थितियों में तरंगाग्र झुक सकती है दिशा बदल सकती है और सतहों को प्रतिबिंबित कर सकती है जिससे जटिल विश्लेषण कर सकती है। किरण अनुरेखण असतत मात्रा में एक माध्यम से किरण (ऑप्टिक्स)' नामक आदर्श पुंज को बार बार आगे बढ़ाकर समस्या को हल करती है। सरल गणितके माध्यम से कुछ किरणों का प्रसार करके सरल समस्याओं का विश्लेषण किया जा सकता है। अधिक विस्तृत विश्लेषण अनेक किरणों के प्रसार हेतु कंप्यूटर का प्रयोग कर किया जाता है। | ||
जब [[ विद्युत चुम्बकीय विकिरण ]] की समस्याओं पर लागू किया जाता है, तो किरण अनुरेखण अधिकांशतः | जब[[ विद्युत चुम्बकीय विकिरण | विद्युत चुम्बकीय विकिरण]] की समस्याओं पर लागू किया जाता है, तो किरण अनुरेखण अधिकांशतः मैक्सवेल के समीकरणों के अनुमानित समाधानों पर निर्भर करता है जो तब तक मान्य होते हैं जब तक कि [[ प्रकाश तरंग |प्रकाश तरंग]] के माध्यम से उन वस्तुओं के आसपास फैल जाती हैं जिनके आयाम प्रकाश की[[ तरंग दैर्ध्य ]]से बहुत अधिक होते हैं। किरण सिद्धांत तरंग प्रसार और [[ विवर्तन |विवर्तन]] जैसी घटनाओं का वर्णन नहीं करता है, जिसके लिए [[ तरंग प्रकाशिकी |तरंग प्रकाशिकी]] की आवश्यकता होती है। जिसमें तरंग की प्रावस्था सम्मिलित होती है। | ||
== तकनीक == | == तकनीक == | ||
[[File:Raytrace changing refractive index.svg|thumb|right|300px|बदलते [[ अपवर्तक सूचकांक ]] के साथ एक माध्यम से गुजरने वाली प्रकाश की किरण का किरण अनुरेखण। किरण को एक छोटी राशि से आगे बढ़ाया जाता है | [[File:Raytrace changing refractive index.svg|thumb|right|300px|बदलते [[ अपवर्तक सूचकांक |अपवर्तक सूचकांक]] के साथ एक माध्यम से गुजरने वाली प्रकाश की किरण का किरण अनुरेखण। किरण को एक छोटी राशि से आगे बढ़ाया जाता है और दिशा की फिर से गणना की जाती है।]]किरण अनुरेखण यह मानकर काम करती है कि कण या तरंग को बड़ी संख्या में बहुत संकीर्ण पुंज किरणों के रूप में तैयार किया जाता है और इसमें कुछ दूरी बहुत कम होती है जिस पर एक किरण स्थानीय रूप से सीधी होती है। किरण अनुरेखक इस दूरी पर किरण को आगे बढ़ाता है और फिर किरण की नई दिशा की गणना करने के लिए माध्यम के व्युत्पन्न का उपयोग करता है। इस स्थान से एक नई किरण भेजी जाती है और प्रक्रिया तब तक दोहराई जाती है जब तक कि एक पूर्ण पथ उत्पन्न नहीं हो जाता। यदि सिमुलेशन में ठोस वस्तुएं के रूप में सम्मलित होती है तो प्रत्येक चरण में उनके साथ प्रतिच्छेदन के लिए किरण का परीक्षण किया जा सकता है और यदि टक्कर मिलती है तो किरण की दिशा में समायोजन किया जा सकता है। जैसे जैसे[[ तीव्रता (भौतिकी) | तीव्रता (भौतिकी)]] तरंगदैर्घ्य या[[ ध्रुवीकरण (लहरें) ]]का अनुकार आगे बढ़ता है किरण के अन्य गुणों में भी परिवर्तन हो सकता है। इस प्रक्रिया को उतनी ही किरणों के साथ दोहराया जाता है जितनी व्यवस्था के व्यवहार को समझने के लिए आवश्यक होती हैं। | ||
== उपयोग करता है == | == उपयोग करता है == | ||
=== खगोल विज्ञान === | === खगोल विज्ञान === | ||
{{further| | {{further|वायु द्रव्यमान (खगोल विज्ञान)}} | ||
आकाश की वास्तविक छवियों को अनुकरण करने के लिए खगोल विज्ञान में किरण अनुरेखण का तेजी से उपयोग किया जाता है। पारंपरिक सिमुलेशन के विपरीत किरण अनुरेखण दूरबीन के संभावित या गणना किए गए पीएसएफ का उपयोग नहीं करता है और इसके अतिरिक्त प्रत्येक फोटॉन के ऊपरी वायुमंडल में डिटेक्टर के लिए प्रवेश की यात्रा का पता लगाता है।<ref>{{Cite journal |doi = 10.1088/0067-0049/218/1/14|title = एक व्यापक फोटॉन मोंटे कार्लो दृष्टिकोण का उपयोग करके ऑप्टिकल सर्वेक्षण टेलीस्कोप से खगोलीय छवियों का अनुकरण|journal = The Astrophysical Journal Supplement Series|volume = 218|pages = 14|year = 2015|last1 = Peterson|first1 = J. R.|last2 = Jernigan|first2 = J. G.|last3 = Kahn|first3 = S. M.|last4 = Rasmussen|first4 = A. P.|last5 = Peng|first5 = E.|last6 = Ahmad|first6 = Z.|last7 = Bankert|first7 = J.|last8 = Chang|first8 = C.|last9 = Claver|first9 = C.|last10 = Gilmore|first10 = D. K.|last11 = Grace|first11 = E.|last12 = Hannel|first12 = M.|last13 = Hodge|first13 = M.|last14 = Lorenz|first14 = S.|last15 = Lupu|first15 = A.|last16 = Meert|first16 = A.|last17 = Nagarajan|first17 = S.|last18 = Todd|first18 = N.|last19 = Winans|first19 = A.|last20 = Young|first20 = M.|issue = 1|arxiv = 1504.06570|bibcode = 2015ApJS..218...14P|doi-access = free}}</ref> मुख्य रूप से वायुमंडल प्रकाशिकी और डिटेक्टर से उत्पन्न होने वाले प्रकीर्णन और विकृति को ध्यान में रखा जाता है। जबकि छवियों का अनुकरण करने की यह विधि स्वाभाविक रूप से धीमी होती है परंतु सीपीयू तथा जीपीयू क्षमताओं में प्रगति ने इस समस्या को कुछ हद तक कम कर दिया है। इसका उपयोग दूरबीन डिजाइन करने में भी किया जा सकता है। उल्लेखनीय उदाहरणों में[[ लार्ज सिनॉप्टिक सर्वे टेलीस्कोप | लार्ज सिनॉप्टिक सर्वे दूरबीन]] का प्रयोग किया जा रहा है जहां इस तरह की किरण अनुरेखण का उपयोग पहली बार फोसिम के साथ किया जाता था<ref>{{Cite web|url=https://bitbucket.org/phosim/phosim_release/wiki/Home|title = फ़ोसिम / फ़ोसिम_रिलीज़ / विकी / होम — बिटबकेट}}</ref> ताकि नकली छवियां बनाई जा सकें.।<ref>{{Cite web|url=https://www.lsst.org/scientists/simulations/phosim|title = फोटॉन सिम्युलेटर (फोसिम)|date = 19 September 2015}}</ref> | |||
=== रेडियो सिग्नल === | === रेडियो सिग्नल === | ||
{{See also| | {{See also|रेडियो प्रचार}} | ||
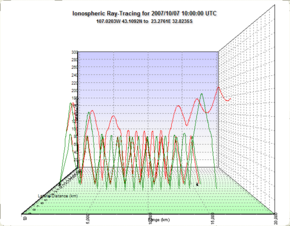
[[File:3D Ionospheric Ray Example.png|right|290px|thumb|बाईं ओर के ट्रांसमीटर से दाईं ओर रिसीवर तक रेडियो | [[File:3D Ionospheric Ray Example.png|right|290px|thumb|बाईं ओर के ट्रांसमीटर से दाईं ओर रिसीवर तक रेडियो संकेत 3 डी ग्रिड के आधार पर त्रिकोण का पता लगाया गया है।]]किरण अनुरेखण का एक विशेष रूप [[ रेडियो |रेडियो]] संकेत किरण अनुरेखण के रूप में होता है जो [[आयनमंडल]] के माध्यम से रेडियो संकेतों को किरणों के रूप में रेखांकित करता है और पृथ्वी पर वापस परावर्तित होता है। किरण अनुरेखण के इस रूप में विभेदक समीकरणों का एकीकरण सम्मलित होता है जो आवेशित तथा[[ असमदिग्वर्ती होने की दशा | असमदिग्वर्ती होने की दशा]] में मीडिया के माध्यम से विद्युत चुम्बकीय विकिरण के प्रसार का वर्णन करता है। भौतिकी आधारित रेडियो संकेत किरण अनुरेखण का एक उदाहरण दाईं ओर दिखाया गया है। रेडियो संचारक रेडियो संकेतों के सटीक व्यवहार को निर्धारित करने में मदद करने के लिए किरण अनुरेखण का उपयोग करते हैं क्योंकि वे आयनमंडल के माध्यम से प्रसारित होते हैं। | ||
दाईं ओर की छवि स्थिति | दाईं ओर की छवि स्थिति जटिलता को दर्शाती है। ऑप्टिकल किरण अनुरेखण के विपरीत होता है जहां वस्तुओं के बीच के माध्यम में सामान्यतः एक निरंतर अपवर्तक सूचकांक होता है जो संकेत किरण अनुरेखण को स्थानिक रूप से भिन्न अपवर्तक सूचकांक की जटिलताओं से निपटना चाहिए जहां आयनमंडली प्रभाव[[ इलेक्ट्रॉन ]]घनत्व में परिवर्तन अपवर्तक सूचकांक को प्रभावित करते हैं और इसलिए किरण प्रक्षेपवक्र संकेतों के दो सेट अलग-अलग उन्नयन कोणों पर प्रसारित होते हैं। जब मुख्य संकेत आयनमंडल में प्रवेश करता है तो चुंबकीय क्षेत्र संकेत को दो घटक तरंगों में विभाजित करता है जो आयनमंडल के माध्यम से अलग अलग किरणों का पता लगाती हैं।[[ Birefringence | द्वि अपवर्तन]] लाल घटक द्वि अपवर्तन हरा घटक से पूरी तरह से स्वतंत्र पथ का अनुसरण करता है। | ||
{{see also| | {{see also|वायुमंडल में रेडियो तरंग क्षीणन की गणना}} | ||
=== महासागर ध्वनिकी === | === महासागर ध्वनिकी === | ||
{{See also| | {{See also|पानी के नीचे ध्वनिकी}} | ||
समुद्र में ध्वनि का वेग [[ घनत्व ]] और [[ तापमान ]] में परिवर्तन के कारण गहराई के साथ बदलता रहता है | समुद्र में ध्वनि का वेग[[ घनत्व | घनत्व]] और [[ तापमान |तापमान]] में परिवर्तन के कारण गहराई के साथ बदलता रहता है जो 800-1000 मीटर की गहराई के निकट[[ स्थानीय न्यूनतम | स्थानीय न्यूनतम]] तक पहुंचता है। यह स्थानीय न्यूनतम जिसे सोफर चैनल कहा जाता है और ये [[ वेवगाइड |तरंग पथक]] के रूप में कार्य करता है क्योंकि ध्वनि इसकी ओर झुकती है। किरण अनुरेखण का उपयोग समुद्र के माध्यम से बहुत बड़ी दूरी तक ध्वनि के पथ की गणना करने के लिए किया जा सकता है जिसमें सोफर चैनल के प्रभावों के साथ साथ प्रतिबिंब (भौतिकी) और समुद्र की सतह और तल से[[ अपवर्तन ]]होता हैं। इससे उच्च और निम्न संकेत तीव्रता के स्थानों की गणना की जा सकती है जो[[ ध्वनिक समुद्र विज्ञान | ध्वनिक समुद्र विज्ञान]], [[पानी के नीचे ध्वनिक संचार]] और[[ ध्वनिक थर्मोमेट्री | ध्वनिक थर्मोमेट्री]] के क्षेत्र में उपयोगी होते हैं। | ||
[[File:Rays test.gif|thumb|center|436px|समुद्र के अलग | [[File:Rays test.gif|thumb|center|436px|समुद्र के अलग अलग घनत्व के माध्यम से फैलने वाले ध्वनिक तरंगाग्र की किरण अनुरेखण के रूप में है। ये सोफर चैनल के बारे में दोलन करने के लिए देखा जा सकता है।]] | ||
=== ऑप्टिकल डिजाइन === | === ऑप्टिकल डिजाइन === | ||
{{See also| | {{See also|ऑप्टिकल लेंस डिजाइन}} | ||
किरण अनुरेखण का उपयोग [[ लेज़र ]] (ऑप्टिक्स) और [[ ऑप्टिकल प्रणाली ]] के डिजाइन में किया जा सकता है | किरण अनुरेखण का उपयोग [[ लेज़र |लेज़र]] (ऑप्टिक्स) और[[ ऑप्टिकल प्रणाली ]]के डिजाइन में किया जा सकता है जैसे कि कैमरे सूक्ष्मदर्शी[[ ऑप्टिकल टेलीस्कोप | ऑप्टिकल दूरबीन]] और[[ दूरबीन ]]के रूप में होता है और इस क्षेत्र में इसका अनुप्रयोग 1900 के दशक से पहले का है। जियोमेट्रिक किरण अनुरेखण का उपयोग लेंस प्रणाली या ऑप्टिक्स उपकरण के माध्यम से प्रकाश किरणों के प्रसार का वर्णन करने के लिए किया जाता है, जिससे प्रणाली के छवि बनाने वाले गुणों को मॉडल किया जा सके। निम्नलिखित प्रभावों को सीधे तरीके से किरण अनुरेखक में एकीकृत किया जा सकता है | ||
* | * फैलाव [[ प्रकाशिकी |प्रकाशिकी]] से रंगीन विपथन होता है | ||
* ध्रुवीकरण (लहरें) | * ध्रुवीकरण (लहरें) | ||
** [[ क्रिस्टल प्रकाशिकी ]] | ** [[ क्रिस्टल प्रकाशिकी ]] | ||
** [[ फ्रेस्नेल समीकरण ]] | ** [[ फ्रेस्नेल समीकरण ]] | ||
* लेजर | * लेजर प्रकाश प्रभाव | ||
* सतह की परावर्तकता की गणना करने के लिए [[ पतली फिल्म प्रकाशिकी ]] | * सतह की परावर्तकता की गणना करने के लिए[[ पतली फिल्म प्रकाशिकी ]][[ ऑप्टिकल कोटिंग |ऑप्टिकल कोटिंग]] [[ साबुन का बुलबुला |साबुन का बुलबुला]] का उपयोग किया जा सकता है। | ||
लेंस डिजाइन के | लेंस डिजाइन के अनुप्रयोग के लिए तरंग व्यतिकरण के दो विशेष स्थितियो को ध्यान में रखना महत्वपूर्ण है। फोकस (प्रकाशिकी) बिंदु में प्रकाश स्रोत से किरणें फिर से मिलती हैं और रचनात्मक या विनाशकारी रूप से एक दूसरे के साथ हस्तक्षेप कर सकती हैं। इस बिंदु के निकट एक बहुत ही छोटे क्षेत्र के भीतर आने वाली रोशनी को समतल तरंगों द्वारा अनुमानित किया जा सकता है जो किरणों से उनकी दिशा प्राप्त करते हैं। चरण तरंगों की गणना करने के लिए प्रकाश स्रोत से[[ ऑप्टिकल पथ की लंबाई | ऑप्टिकल पथ की लंबाई]] का उपयोग किया जाता है। स्रोत स्थिति पर फोकल क्षेत्र में किरण की स्थिति के व्युत्पन्न का उपयोग किरण की चौड़ाई प्राप्त करने के लिए किया जाता है और इससे समतल तरंग का[[ आयाम | आयाम]] प्राप्त होता है। परिणाम स्वरुप[[ बिंदु फैलाव समारोह | बिंदु प्रसार फलन]] के रूप में है जिसका[[ फूरियर रूपांतरण | फूरियर रूपांतरण,]][[ ऑप्टिकल स्थानांतरण समारोह | ऑप्टिकल स्थानांतरण फलन]] के रूप में होता है। इससे स्ट्रील अनुपात की गणना की जा सकती है। | ||
अन्य विशेष स्थिति पर विचार करने के लिए तरंगाग्र के हस्तक्षेप की है जो समतल के रूप में अनुमानित हैं। परंतु जब किरणें एक-दूसरे के पास आती हैं या एक-दूसरे को काटती हैं तो तरंगाग्र सन्निकटन टूट जाती है। गोलीय तरंगों के व्यतिकरण को सामान्यतः किरण अनुरेखण के साथ संयोजित नहीं किया जाता है, इस प्रकार छिद्र में विवर्तन की गणना नहीं की जा सकती। चूंकि इन सीमाओं को [[ फील्ड ट्रेसिंग |फील्ड अनुरेखण]] नामक एक उन्नत मॉडलिंग तकनीक द्वारा हल किया जा सकता है। फील्ड अनुरेखण एक मॉडलिंग तकनीक है जिसमें ज्यामितीय प्रकाशिकी के साथ भौतिक प्रकाशिकी का संयोजन किया जाता है जो डिजाइन में हस्तक्षेप और विवर्तन की सीमाओं को दूर करता है। | |||
[[ पराबैंगनी |पराबैंगनी]] और[[ एक्स-रे | एक्स-रे]] प्रकाशिकी जैसी छोटी तरंग दैर्ध्य अनुप्रयोगों तथा माइक्रोवेव अथवा रेडियो प्रणालियों के विचलन को छोड़कर यंत्र की डिजाइन को अनुकूलतम बनाने के लिए किरण अनुरेखण तकनीकों का उपयोग किया जाता है। | |||
[[ कंप्यूटर |कंप्यूटर]] के आगमन से पूर्व किरण अनुरेखण गणना हाथ से[[ त्रिकोणमिति | त्रिकोणमिति]] और लघुगणक तालिकाओं का उपयोग करके की जाती थी। कई क्लासिक फ़ोटोग्राफ़ी लेंसों के ऑप्टिकल फ़ार्मुलों को लोगों के बीच में ही अनुकूलित किया गया था जिनमें से हरेक ने बड़ी गणना का एक छोटा सा हिस्सा संभाला था। अब वे[[ ऑप्टिकल लेंस डिजाइन | ऑप्टिकल लेंस डिजाइन सॉफ्टवेयर]] में काम कर रहे थे। [[ रे ट्रांसफर मैट्रिक्स विश्लेषण |किरण अनुरेखण मैट्रिक्स]] का एक सरल संस्करण जिसे किरण अंतरण मैट्रिक्स विश्लेषण के रूप में जाना जाता है अधिकांशतः लेजर में प्रयुक्त[[ ऑप्टिकल गुहा | ऑप्टिकल गुंजयमान यंत्र]] के डिजाइन में उपयोग किया जाता है। सबसे अधिक उपयोग किए जाने वाले कलन विधि के मूल सिद्धांत स्पेंसर तथा मुर्ति के मूल लेख सामान्यतः किरण अनुरेखण प्रक्रिया में पाए जाते हैं।<ref>{{cite journal |doi=10.1364/JOSA.52.000672 |title=सामान्य रे-ट्रेसिंग प्रक्रिया†|journal=Journal of the Optical Society of America |volume=52 |issue=6 |pages=672 |year=1962 |last1=Spencer |first1=G. H |last2=Murty |first2=M. V. R. K }}</ref> | |||
=== भूकंप विज्ञान === | === भूकंप विज्ञान === | ||
[[File:Earthquake wave shadow zone.svg|thumb|right|150px|पृथ्वी के आंतरिक भाग के माध्यम से भूकंपीय तरंगों के इस किरण अनुरेखण से पता चलता है कि रास्ते काफी जटिल हो सकते हैं, और [[ पृथ्वी की संरचना ]] के बारे में जानकारी देने वाली जानकारी प्रकट करते हैं।]][[ भूकंप विज्ञान ]] में | [[File:Earthquake wave shadow zone.svg|thumb|right|150px|पृथ्वी के आंतरिक भाग के माध्यम से भूकंपीय तरंगों के इस किरण अनुरेखण से पता चलता है कि रास्ते काफी जटिल हो सकते हैं, और [[ पृथ्वी की संरचना |पृथ्वी की संरचना]] के बारे में जानकारी देने वाली जानकारी प्रकट करते हैं।]][[ भूकंप विज्ञान |भूकंप विज्ञान]] में भूभौतिकीविद भूकंप के स्थान और पृथ्वी की संरचना के [[ टोमोग्राफी |टोमोग्राफी]] पुनर्निर्माण में सहायता करने के लिए किरण अनुरेखण का उपयोग करते हैं। तथा पृथ्वी के आंतरिक भाग को परिष्कृत करने में मदद करते हैं।<ref>{{Cite book|doi=10.1016/S0065-2687(07)49003-3 |chapter=Seismic ray tracing and wavefront tracking in laterally heterogeneous media |title=भूभौतिकी खंड 49 में अग्रिम|volume=49 |pages=203–273 |series=Advances in Geophysics |year=2008 |last1=Rawlinson |first1=N |last2=Hauser |first2=J |last3=Sambridge |first3=M |isbn=9780123742315 }}</ref><ref>{{cite book | ||
| title=भूकंपीय किरण सिद्धांत| author=Cerveny, V. | | title=भूकंपीय किरण सिद्धांत| author=Cerveny, V. | ||
| year=2001 | | year=2001 | ||
| isbn=978-0-521-36671-7 | | isbn=978-0-521-36671-7 | ||
}}</ref> भूकंपीय तरंग वेग पृथ्वी | }}</ref> भूकंपीय तरंग वेग पृथ्वी के [[भूपृष्ठ]][[ पपड़ी (भूविज्ञान) | (भूविज्ञान)]] के भीतर और नीचे बदलता रहता है जिसके कारण ये तरंगें झुकती और प्रतिबिंबित होती हैं। किरण अनुरेखण का उपयोग एक भूभौतिकीय मॉडल के माध्यम से पथों की गणना करने के लिए किया जाता है जो उन्हें बाद में अपने स्रोत जैसे कि भूकंप या हस्तक्षेप करने वाली सामग्री के गुणों को कम कर सकता है।<ref>[http://web.ics.purdue.edu/~nowack/geos557/lecture14c-dir/lecture14c.htm Purdue University<!-- Bot generated title -->]</ref> विशेष रूप से भूकंपीय छाया क्षेत्र की खोज से वैज्ञानिकों को पृथ्वी के पिघले हुए कोर की उपस्थिति का अनुमान लगाया जा सकता है। जैसे दाएं चित्र में दिखाया गया है। | ||
=== [[ सामान्य सापेक्षता |सामान्य सापेक्षता]] === | |||
सामान्य सापेक्षता में जहां[[ गुरुत्वाकर्षण लेंस | गुरुत्वाकर्षण लेंस]] हो सकते हैं प्रेक्षक पर प्राप्त होने वाली प्रकाश किरणों के भूगर्भ विज्ञान को समय के साथ पीछे की ओर एकीकृत किया जाता है जब तक कि वे रुचि के क्षेत्र से प्रभावित न हो जाएं। इस तकनीक के अंतर्गत प्रतिबिंब संश्लेषण को कंप्यूटर ग्राफिक्स में सामान्य किरण अनुरेखण के विस्तार के रूप में देखा जा सकता है।<ref>{{cite journal |doi=10.1016/j.cpc.2012.04.030 |title=जीपीयू-आधारित चार-आयामी सामान्य-सापेक्षिक किरण अनुरेखण|journal=Computer Physics Communications |volume=183 |issue=10 |pages=2282–2290 |year=2012 |last1=Kuchelmeister |first1=Daniel |last2=Müller |first2=Thomas |last3=Ament |first3=Marco |last4=Wunner |first4=Günter |last5=Weiskopf |first5=Daniel |bibcode=2012CoPhC.183.2282K }}</ref><ref>{{cite journal |doi=10.1016/j.cpc.2014.04.013 |title=GeoViS—चार आयामी दिक्-काल में आपेक्षिक किरण अनुरेखण|journal=Computer Physics Communications |volume=185 |issue=8 |pages=2301–2308 |year=2014 |last1=Müller |first1=Thomas |bibcode=2014CoPhC.185.2301M }}</ref> इस तरह के संश्लेषण का एक उदाहरण 2014 फिल्म के अंतरराज्यीय फिल्म में पाया जाता है।<ref name="wired">{{cite news|url=https://www.wired.com/2014/10/astrophysics-interstellar-black-hole/|title=रिंकल्स इन स्पेसटाइम: द वॉर्प्ड एस्ट्रोफिजिक्स ऑफ इंटरस्टेलर|first=Adam|last=Rogers|date=October 23, 2014|work=[[Wired (magazine)|Wired]]|access-date=October 25, 2014|url-status=live|archive-url=https://web.archive.org/web/20141025002411/http://www.wired.com/2014/10/astrophysics-interstellar-black-hole/|archive-date=October 25, 2014}}</ref> | |||
== यह भी देखें == | == यह भी देखें == | ||
* [[ वायुमंडलीय प्रकाशिकी रे-ट्रेसिंग कोड | वायुमंडलीय प्रकाशिकी रे-अनुरेखण कोड]] | * [[ वायुमंडलीय प्रकाशिकी रे-ट्रेसिंग कोड | वायुमंडलीय प्रकाशिकी रे-अनुरेखण कोड]] | ||
| Line 76: | Line 73: | ||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist}} | {{Reflist}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Created On 02/01/2023]] | [[Category:Created On 02/01/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
Latest revision as of 10:00, 20 January 2023
भौतिकी में किरण अनुरेखण विभिन्न प्रसार वेग अवशोषण विशेषताओं और सतहों को परावर्तित करने वाले क्षेत्रों के साथ प्रणाली के माध्यम से तरंगों या उप-परमाणु कणों के मार्ग की गणना करने की एक विधि है। इन परिस्थितियों में तरंगाग्र झुक सकती है दिशा बदल सकती है और सतहों को प्रतिबिंबित कर सकती है जिससे जटिल विश्लेषण कर सकती है। किरण अनुरेखण असतत मात्रा में एक माध्यम से किरण (ऑप्टिक्स)' नामक आदर्श पुंज को बार बार आगे बढ़ाकर समस्या को हल करती है। सरल गणितके माध्यम से कुछ किरणों का प्रसार करके सरल समस्याओं का विश्लेषण किया जा सकता है। अधिक विस्तृत विश्लेषण अनेक किरणों के प्रसार हेतु कंप्यूटर का प्रयोग कर किया जाता है।
जब विद्युत चुम्बकीय विकिरण की समस्याओं पर लागू किया जाता है, तो किरण अनुरेखण अधिकांशतः मैक्सवेल के समीकरणों के अनुमानित समाधानों पर निर्भर करता है जो तब तक मान्य होते हैं जब तक कि प्रकाश तरंग के माध्यम से उन वस्तुओं के आसपास फैल जाती हैं जिनके आयाम प्रकाश कीतरंग दैर्ध्य से बहुत अधिक होते हैं। किरण सिद्धांत तरंग प्रसार और विवर्तन जैसी घटनाओं का वर्णन नहीं करता है, जिसके लिए तरंग प्रकाशिकी की आवश्यकता होती है। जिसमें तरंग की प्रावस्था सम्मिलित होती है।
तकनीक

किरण अनुरेखण यह मानकर काम करती है कि कण या तरंग को बड़ी संख्या में बहुत संकीर्ण पुंज किरणों के रूप में तैयार किया जाता है और इसमें कुछ दूरी बहुत कम होती है जिस पर एक किरण स्थानीय रूप से सीधी होती है। किरण अनुरेखक इस दूरी पर किरण को आगे बढ़ाता है और फिर किरण की नई दिशा की गणना करने के लिए माध्यम के व्युत्पन्न का उपयोग करता है। इस स्थान से एक नई किरण भेजी जाती है और प्रक्रिया तब तक दोहराई जाती है जब तक कि एक पूर्ण पथ उत्पन्न नहीं हो जाता। यदि सिमुलेशन में ठोस वस्तुएं के रूप में सम्मलित होती है तो प्रत्येक चरण में उनके साथ प्रतिच्छेदन के लिए किरण का परीक्षण किया जा सकता है और यदि टक्कर मिलती है तो किरण की दिशा में समायोजन किया जा सकता है। जैसे जैसे तीव्रता (भौतिकी) तरंगदैर्घ्य याध्रुवीकरण (लहरें) का अनुकार आगे बढ़ता है किरण के अन्य गुणों में भी परिवर्तन हो सकता है। इस प्रक्रिया को उतनी ही किरणों के साथ दोहराया जाता है जितनी व्यवस्था के व्यवहार को समझने के लिए आवश्यक होती हैं।
उपयोग करता है
खगोल विज्ञान
आकाश की वास्तविक छवियों को अनुकरण करने के लिए खगोल विज्ञान में किरण अनुरेखण का तेजी से उपयोग किया जाता है। पारंपरिक सिमुलेशन के विपरीत किरण अनुरेखण दूरबीन के संभावित या गणना किए गए पीएसएफ का उपयोग नहीं करता है और इसके अतिरिक्त प्रत्येक फोटॉन के ऊपरी वायुमंडल में डिटेक्टर के लिए प्रवेश की यात्रा का पता लगाता है।[1] मुख्य रूप से वायुमंडल प्रकाशिकी और डिटेक्टर से उत्पन्न होने वाले प्रकीर्णन और विकृति को ध्यान में रखा जाता है। जबकि छवियों का अनुकरण करने की यह विधि स्वाभाविक रूप से धीमी होती है परंतु सीपीयू तथा जीपीयू क्षमताओं में प्रगति ने इस समस्या को कुछ हद तक कम कर दिया है। इसका उपयोग दूरबीन डिजाइन करने में भी किया जा सकता है। उल्लेखनीय उदाहरणों में लार्ज सिनॉप्टिक सर्वे दूरबीन का प्रयोग किया जा रहा है जहां इस तरह की किरण अनुरेखण का उपयोग पहली बार फोसिम के साथ किया जाता था[2] ताकि नकली छवियां बनाई जा सकें.।[3]
रेडियो सिग्नल
किरण अनुरेखण का एक विशेष रूप रेडियो संकेत किरण अनुरेखण के रूप में होता है जो आयनमंडल के माध्यम से रेडियो संकेतों को किरणों के रूप में रेखांकित करता है और पृथ्वी पर वापस परावर्तित होता है। किरण अनुरेखण के इस रूप में विभेदक समीकरणों का एकीकरण सम्मलित होता है जो आवेशित तथा असमदिग्वर्ती होने की दशा में मीडिया के माध्यम से विद्युत चुम्बकीय विकिरण के प्रसार का वर्णन करता है। भौतिकी आधारित रेडियो संकेत किरण अनुरेखण का एक उदाहरण दाईं ओर दिखाया गया है। रेडियो संचारक रेडियो संकेतों के सटीक व्यवहार को निर्धारित करने में मदद करने के लिए किरण अनुरेखण का उपयोग करते हैं क्योंकि वे आयनमंडल के माध्यम से प्रसारित होते हैं।
दाईं ओर की छवि स्थिति जटिलता को दर्शाती है। ऑप्टिकल किरण अनुरेखण के विपरीत होता है जहां वस्तुओं के बीच के माध्यम में सामान्यतः एक निरंतर अपवर्तक सूचकांक होता है जो संकेत किरण अनुरेखण को स्थानिक रूप से भिन्न अपवर्तक सूचकांक की जटिलताओं से निपटना चाहिए जहां आयनमंडली प्रभावइलेक्ट्रॉन घनत्व में परिवर्तन अपवर्तक सूचकांक को प्रभावित करते हैं और इसलिए किरण प्रक्षेपवक्र संकेतों के दो सेट अलग-अलग उन्नयन कोणों पर प्रसारित होते हैं। जब मुख्य संकेत आयनमंडल में प्रवेश करता है तो चुंबकीय क्षेत्र संकेत को दो घटक तरंगों में विभाजित करता है जो आयनमंडल के माध्यम से अलग अलग किरणों का पता लगाती हैं। द्वि अपवर्तन लाल घटक द्वि अपवर्तन हरा घटक से पूरी तरह से स्वतंत्र पथ का अनुसरण करता है।
महासागर ध्वनिकी
समुद्र में ध्वनि का वेग घनत्व और तापमान में परिवर्तन के कारण गहराई के साथ बदलता रहता है जो 800-1000 मीटर की गहराई के निकट स्थानीय न्यूनतम तक पहुंचता है। यह स्थानीय न्यूनतम जिसे सोफर चैनल कहा जाता है और ये तरंग पथक के रूप में कार्य करता है क्योंकि ध्वनि इसकी ओर झुकती है। किरण अनुरेखण का उपयोग समुद्र के माध्यम से बहुत बड़ी दूरी तक ध्वनि के पथ की गणना करने के लिए किया जा सकता है जिसमें सोफर चैनल के प्रभावों के साथ साथ प्रतिबिंब (भौतिकी) और समुद्र की सतह और तल सेअपवर्तन होता हैं। इससे उच्च और निम्न संकेत तीव्रता के स्थानों की गणना की जा सकती है जो ध्वनिक समुद्र विज्ञान, पानी के नीचे ध्वनिक संचार और ध्वनिक थर्मोमेट्री के क्षेत्र में उपयोगी होते हैं।
ऑप्टिकल डिजाइन
किरण अनुरेखण का उपयोग लेज़र (ऑप्टिक्स) औरऑप्टिकल प्रणाली के डिजाइन में किया जा सकता है जैसे कि कैमरे सूक्ष्मदर्शी ऑप्टिकल दूरबीन औरदूरबीन के रूप में होता है और इस क्षेत्र में इसका अनुप्रयोग 1900 के दशक से पहले का है। जियोमेट्रिक किरण अनुरेखण का उपयोग लेंस प्रणाली या ऑप्टिक्स उपकरण के माध्यम से प्रकाश किरणों के प्रसार का वर्णन करने के लिए किया जाता है, जिससे प्रणाली के छवि बनाने वाले गुणों को मॉडल किया जा सके। निम्नलिखित प्रभावों को सीधे तरीके से किरण अनुरेखक में एकीकृत किया जा सकता है
- फैलाव प्रकाशिकी से रंगीन विपथन होता है
- ध्रुवीकरण (लहरें)
- लेजर प्रकाश प्रभाव
- सतह की परावर्तकता की गणना करने के लिएपतली फिल्म प्रकाशिकी ऑप्टिकल कोटिंग साबुन का बुलबुला का उपयोग किया जा सकता है।
लेंस डिजाइन के अनुप्रयोग के लिए तरंग व्यतिकरण के दो विशेष स्थितियो को ध्यान में रखना महत्वपूर्ण है। फोकस (प्रकाशिकी) बिंदु में प्रकाश स्रोत से किरणें फिर से मिलती हैं और रचनात्मक या विनाशकारी रूप से एक दूसरे के साथ हस्तक्षेप कर सकती हैं। इस बिंदु के निकट एक बहुत ही छोटे क्षेत्र के भीतर आने वाली रोशनी को समतल तरंगों द्वारा अनुमानित किया जा सकता है जो किरणों से उनकी दिशा प्राप्त करते हैं। चरण तरंगों की गणना करने के लिए प्रकाश स्रोत से ऑप्टिकल पथ की लंबाई का उपयोग किया जाता है। स्रोत स्थिति पर फोकल क्षेत्र में किरण की स्थिति के व्युत्पन्न का उपयोग किरण की चौड़ाई प्राप्त करने के लिए किया जाता है और इससे समतल तरंग का आयाम प्राप्त होता है। परिणाम स्वरुप बिंदु प्रसार फलन के रूप में है जिसका फूरियर रूपांतरण, ऑप्टिकल स्थानांतरण फलन के रूप में होता है। इससे स्ट्रील अनुपात की गणना की जा सकती है।
अन्य विशेष स्थिति पर विचार करने के लिए तरंगाग्र के हस्तक्षेप की है जो समतल के रूप में अनुमानित हैं। परंतु जब किरणें एक-दूसरे के पास आती हैं या एक-दूसरे को काटती हैं तो तरंगाग्र सन्निकटन टूट जाती है। गोलीय तरंगों के व्यतिकरण को सामान्यतः किरण अनुरेखण के साथ संयोजित नहीं किया जाता है, इस प्रकार छिद्र में विवर्तन की गणना नहीं की जा सकती। चूंकि इन सीमाओं को फील्ड अनुरेखण नामक एक उन्नत मॉडलिंग तकनीक द्वारा हल किया जा सकता है। फील्ड अनुरेखण एक मॉडलिंग तकनीक है जिसमें ज्यामितीय प्रकाशिकी के साथ भौतिक प्रकाशिकी का संयोजन किया जाता है जो डिजाइन में हस्तक्षेप और विवर्तन की सीमाओं को दूर करता है।
पराबैंगनी और एक्स-रे प्रकाशिकी जैसी छोटी तरंग दैर्ध्य अनुप्रयोगों तथा माइक्रोवेव अथवा रेडियो प्रणालियों के विचलन को छोड़कर यंत्र की डिजाइन को अनुकूलतम बनाने के लिए किरण अनुरेखण तकनीकों का उपयोग किया जाता है।
कंप्यूटर के आगमन से पूर्व किरण अनुरेखण गणना हाथ से त्रिकोणमिति और लघुगणक तालिकाओं का उपयोग करके की जाती थी। कई क्लासिक फ़ोटोग्राफ़ी लेंसों के ऑप्टिकल फ़ार्मुलों को लोगों के बीच में ही अनुकूलित किया गया था जिनमें से हरेक ने बड़ी गणना का एक छोटा सा हिस्सा संभाला था। अब वे ऑप्टिकल लेंस डिजाइन सॉफ्टवेयर में काम कर रहे थे। किरण अनुरेखण मैट्रिक्स का एक सरल संस्करण जिसे किरण अंतरण मैट्रिक्स विश्लेषण के रूप में जाना जाता है अधिकांशतः लेजर में प्रयुक्त ऑप्टिकल गुंजयमान यंत्र के डिजाइन में उपयोग किया जाता है। सबसे अधिक उपयोग किए जाने वाले कलन विधि के मूल सिद्धांत स्पेंसर तथा मुर्ति के मूल लेख सामान्यतः किरण अनुरेखण प्रक्रिया में पाए जाते हैं।[4]
भूकंप विज्ञान

भूकंप विज्ञान में भूभौतिकीविद भूकंप के स्थान और पृथ्वी की संरचना के टोमोग्राफी पुनर्निर्माण में सहायता करने के लिए किरण अनुरेखण का उपयोग करते हैं। तथा पृथ्वी के आंतरिक भाग को परिष्कृत करने में मदद करते हैं।[5][6] भूकंपीय तरंग वेग पृथ्वी के भूपृष्ठ (भूविज्ञान) के भीतर और नीचे बदलता रहता है जिसके कारण ये तरंगें झुकती और प्रतिबिंबित होती हैं। किरण अनुरेखण का उपयोग एक भूभौतिकीय मॉडल के माध्यम से पथों की गणना करने के लिए किया जाता है जो उन्हें बाद में अपने स्रोत जैसे कि भूकंप या हस्तक्षेप करने वाली सामग्री के गुणों को कम कर सकता है।[7] विशेष रूप से भूकंपीय छाया क्षेत्र की खोज से वैज्ञानिकों को पृथ्वी के पिघले हुए कोर की उपस्थिति का अनुमान लगाया जा सकता है। जैसे दाएं चित्र में दिखाया गया है।
सामान्य सापेक्षता
सामान्य सापेक्षता में जहां गुरुत्वाकर्षण लेंस हो सकते हैं प्रेक्षक पर प्राप्त होने वाली प्रकाश किरणों के भूगर्भ विज्ञान को समय के साथ पीछे की ओर एकीकृत किया जाता है जब तक कि वे रुचि के क्षेत्र से प्रभावित न हो जाएं। इस तकनीक के अंतर्गत प्रतिबिंब संश्लेषण को कंप्यूटर ग्राफिक्स में सामान्य किरण अनुरेखण के विस्तार के रूप में देखा जा सकता है।[8][9] इस तरह के संश्लेषण का एक उदाहरण 2014 फिल्म के अंतरराज्यीय फिल्म में पाया जाता है।[10]
यह भी देखें
- वायुमंडलीय प्रकाशिकी रे-अनुरेखण कोड
- वायुमंडलीय अपवर्तन
- ग्रेडिएंट-इंडेक्स ऑप्टिक्स
- किरण अनुरेखण सॉफ्टवेयर की सूची
- महासागर ध्वनिक टोमोग्राफी
- किरण अनुरेखण (ग्राफिक्स)
- किरण ट्रांसफर मैट्रिक्स विश्लेषण
संदर्भ
- ↑ Peterson, J. R.; Jernigan, J. G.; Kahn, S. M.; Rasmussen, A. P.; Peng, E.; Ahmad, Z.; Bankert, J.; Chang, C.; Claver, C.; Gilmore, D. K.; Grace, E.; Hannel, M.; Hodge, M.; Lorenz, S.; Lupu, A.; Meert, A.; Nagarajan, S.; Todd, N.; Winans, A.; Young, M. (2015). "एक व्यापक फोटॉन मोंटे कार्लो दृष्टिकोण का उपयोग करके ऑप्टिकल सर्वेक्षण टेलीस्कोप से खगोलीय छवियों का अनुकरण". The Astrophysical Journal Supplement Series. 218 (1): 14. arXiv:1504.06570. Bibcode:2015ApJS..218...14P. doi:10.1088/0067-0049/218/1/14.
- ↑ "फ़ोसिम / फ़ोसिम_रिलीज़ / विकी / होम — बिटबकेट".
- ↑ "फोटॉन सिम्युलेटर (फोसिम)". 19 September 2015.
- ↑ Spencer, G. H; Murty, M. V. R. K (1962). "सामान्य रे-ट्रेसिंग प्रक्रिया†". Journal of the Optical Society of America. 52 (6): 672. doi:10.1364/JOSA.52.000672.
- ↑ Rawlinson, N; Hauser, J; Sambridge, M (2008). "Seismic ray tracing and wavefront tracking in laterally heterogeneous media". भूभौतिकी खंड 49 में अग्रिम. Advances in Geophysics. Vol. 49. pp. 203–273. doi:10.1016/S0065-2687(07)49003-3. ISBN 9780123742315.
- ↑ Cerveny, V. (2001). भूकंपीय किरण सिद्धांत. ISBN 978-0-521-36671-7.
- ↑ Purdue University
- ↑ Kuchelmeister, Daniel; Müller, Thomas; Ament, Marco; Wunner, Günter; Weiskopf, Daniel (2012). "जीपीयू-आधारित चार-आयामी सामान्य-सापेक्षिक किरण अनुरेखण". Computer Physics Communications. 183 (10): 2282–2290. Bibcode:2012CoPhC.183.2282K. doi:10.1016/j.cpc.2012.04.030.
- ↑ Müller, Thomas (2014). "GeoViS—चार आयामी दिक्-काल में आपेक्षिक किरण अनुरेखण". Computer Physics Communications. 185 (8): 2301–2308. Bibcode:2014CoPhC.185.2301M. doi:10.1016/j.cpc.2014.04.013.
- ↑ Rogers, Adam (October 23, 2014). "रिंकल्स इन स्पेसटाइम: द वॉर्प्ड एस्ट्रोफिजिक्स ऑफ इंटरस्टेलर". Wired. Archived from the original on October 25, 2014. Retrieved October 25, 2014.