रिसाव प्रेरकत्व

क्षरण(लीकेज या रिसाव) प्रेरकत्व एक अपूर्ण रूप से युग्मित ट्रांसफार्मर की विद्युत संपत्ति से प्राप्त होता है जिससे प्रत्येक कुंडली संबंधित ओमिक प्रतिरोध स्थिरांक के साथ श्रृंखला में स्व-प्रेरकत्व के रूप में व्यवहार करता है। यह चार कुंडली स्थिरांक ट्रांसफार्मर के पारस्परिक प्रेरकत्व के साथ भी संपर्क करते हैं। कुंडली क्षरण प्रेरकत्व क्षरण प्रवाह के कारण होता है जो प्रत्येक अपूर्ण रूप से युग्मित कुंडली के सभी घुमावों से नहीं जुड़ता है।

क्षरण प्रतिक्रिया सामान्यतः ऊर्जा घटक, वोल्टेज घटाव, प्रतिक्रियाशील विद्युत उपभोग और स्तरभ्रंश धारा विचार के कारण धारा प्रणाली ट्रांसफॉर्मर का सबसे महत्वपूर्ण तत्व है।

क्षरण प्रेरकत्व और कुंडली अंतर्भाग की ज्यामिति पर निर्भर करता है। क्षरण प्रतिक्रिया के परिणाम में वोल्टेज का पतन प्रायः ट्रांसफॉर्मर विद्युत भार के साथ अवांछनीय आपूर्ति विनियमन में होती है। लेकिन यह कुछ भारों के हार्मोनिक् (विद्युत शक्ति) पृथक्रकरण (उच्च आवृत्तियों को क्षीण करने) के लिए भी उपयोगी हो सकता है।

क्षरण प्रेरकत्व विद्युत मोटर सहित किसी भी अपूर्ण-युग्मित चुंबकीय सर्किट उपकरणों पर अनप्रयुक्‍त होता है।

क्षरण प्रेरकत्व और आगमनात्मक युग्मन कारक

अंजीर। 1एल_P^{और मैं_Sσ आगमनात्मक युग्मन गुणांक के रूप में व्यक्त प्राथमिक और द्वितीयक रिसाव प्रेरकत्व हैं $k$खुले परिचालित परिस्थितियों में।}

चुंबकीय सर्किट का प्रवाह जो दोनों कुंडलियों को अंतराबंध नहीं करता है, प्राथमिक क्षरण प्रेरकत्व LPσ और द्वितीयक क्षरण प्रेरकत्व LSσ के अनुरूप है।

चित्र 1 को दर्शाते हुए, इन क्षरण प्रेरकत्व को ट्रांसफॉर्मर कुंडली ओपन-सर्किट प्रेरकत्व और संबंधित युग्मक गुणांक या युग्मक घटक $k$ के संदर्भ में परिभाषित किया गया है। .

प्राथमिक ओपन-सर्किट स्व-प्रेरकत्व जिसके द्वारा दिया जाता है

$L_{oc}^{pri}=L_{P}=L_{M}+L_{P}^{\sigma }$ ------ (समीकरण 1.1क)

जहाँ

$L_{P}^{\sigma }=L_{P}\cdot {(1-k)}$ ------ (समीकरण 1.1बी)

$L_{M}=L_{P}\cdot {k}$ ------ (समीकरण 1.1ग)

और

• $L_{oc}^{pri}=L_{P}$ प्राथमिक स्व-प्रेरकत्व है
• $L_{P}^{\sigma }$ प्राथमिक क्षरण प्रेरकत्व है
• $L_{M}$ चुंबकीय प्रेरण है
• $k$ आगमनात्मक युग्मन गुणांक है

आधारिक ट्रांसफार्मर प्रेरकत्व और युग्मन कारक को मापना

ट्रांसफार्मर स्व-प्रेरकत्व $L_{P}$ & $L_{S}$ और पारस्परिक प्रेरण $M$ द्वारा दिए गए दो कुंडलियों के धनात्मक और ऋणात्मक सम्बंधित श्रृंखला में हैं,

धनात्मक संबंध में,

$L_{ser}^{+}=L_{P}+L_{S}+2M$, और,

ऋणात्मक संबंध में,

$L_{ser}^{-}=L_{P}+L_{S}-2M$

जैसे कि इन ट्रांसफॉर्मर प्रेरकत्व को निम्नलिखित तीन समीकरणों से निर्धारित किया जा सकता है:

$L_{ser}^{+}-L_{ser}^{-}=4M$

$L_{ser}^{+}+L_{ser}^{-}=2\cdot (L_{P}+L_{S})$ ::

$L_{P}=a^{2}.L_{S}$.

युग्मक घटक एक कुंडली में मापे गए उपपादन मान से लिया गया है, जो निम्न के अनुसार दूसरे कुंडली में शॉर्ट-सर्किट के साथ जुड़ा है:

प्रति समीकरण 2.7,

$L_{sc}^{pri}=L_{S}\cdot {(1-k^{2})}$ और $L_{sc}^{sec}=L_{P}\cdot {(1-k^{2})}$ :::ऐसा है कि

$k={\sqrt {1-{\frac {L_{sc}^{pri}}{L_{S}}}}}={\sqrt {1-{\frac {L_{sc}^{sec}}{L_{P}}}}}$

कैंपबेल ब्रिज सर्किट का उपयोग ट्रांसफॉर्मर स्व-प्रेरकत्व और पारस्परिक प्रेरकत्व को निर्धारित करने के लिए भी किया जा सकता है, जो पुल पक्षों में से एक के लिए एक चर मानक पारस्परिक प्रारंभ करने वाली जोड़ी का उपयोग करता है।

इसलिए यह ओपन-सर्किट स्व-प्रेरकत्व और प्रेरकत्व युग्मक घटक $k$ द्वारा अनुसरण करता है

$L_{oc}^{sec}=L_{S}=L_{M2}+L_{S}^{\sigma }$ ------ (समीकरण 1.2), और,

$k={\frac {\left|M\right|}{\sqrt {L_{P}L_{S}}}}$, 0 <के साथ $k$ <1 ------ (समीकरण 1.3)

जहाँ

$L_{S}^{\sigma }=L_{S}\cdot {(1-k)}$

$L_{M2}=L_{S}\cdot {k}$

और

• $M$ पारस्परिक प्रेरकत्व है
• $L_{oc}^{sec}=L_{S}$ द्वितीयक स्व-प्रेरकत्व है
• $L_{S}^{\sigma }$ द्वितीयक क्षरण प्रेरकत्व है
• $L_{M2}=L_{M}/a^{2}$ द्वितीयक को संदर्भित चुंबकन प्रेरकत्व है
• $k$ आगमनात्मक युग्मन गुणांक है
• $a\equiv {\sqrt {\frac {L_{p}}{L_{s}}}}\approx N_{P}/N_{S}$ अनुमानित मोड़ अनुपात है

चित्र 1 में ट्रांसफॉर्मर आरेख की विद्युत वैधता विचार किए गए संबंधित कुंडली प्रेरकत्व के लिए ओपन-सर्किट स्थितियों पर सख़्ती से निर्भर करती है। अधिक सामान्यीकृत सर्किट स्थितियां अगले दो खंडों में विकसित की गई हैं।

आगमनात्मक रिसाव कारक और अधिष्ठापन

See also: Inductance § Mutual inductance

एक गैर-आदर्श रैखिक दो-कुंडली ट्रांसफॉर्मर को ट्रांसफॉर्मर के पांच आसन्नता (विद्युत) स्थिरांक को जोड़ने वाले दो पारस्परिक प्रेरकत्व-युग्मित सर्किट परिपथ द्वारा दर्शाया जा सकता है जैसा कि चित्र 2 में दिखाया गया है।

अंजीर। 2 गैर-आदर्श ट्रांसफार्मर सर्किट आरेख

जहाँ

* एम पारस्परिक प्रेरण है

• $R_{P}$ & $R_{S}$ प्राथमिक और द्वितीयक कुंडली प्रतिरोध हैं

* स्थिरांक $M$, $L_{P}$, $L_{S}$, $R_{P}$ & $R_{S}$ ट्रांसफार्मर के अंतिम सिरे पर मापने योग्य हैं

* युग्मन कारक $k$ परिभाषित किया जाता है

$k=\left|M\right|/{\sqrt {L_{P}L_{S}}}$, जहां 0 < $k$ <1 ------ (समीकरण 2.1)

घुमावदार अनुपात बदल जाता है $a$ व्यवहार में दिया जाता है

$a={\sqrt {L_{P}/L_{S}}}=N_{P}/N_{S}\approx v_{P}/v_{S}\approx i_{S}/i_{P}=$ ------ (समीकरण 2.2)।

जहाँ

• एन_P & एन_S प्राथमिक और द्वितीयक कुंडली हैं
• वि_P & में_S और मैं_P & मैं_S प्राथमिक और द्वितीयक कुंडली वोल्टेज और धाराएं हैं।

गैर-आदर्श ट्रांसफार्मर के पाश समीकरणों को निम्नलिखित वोल्टेज और प्रवाह संयोजन समीकरणों द्वारा व्यक्त किया जा सकता है,

$v_{P}=R_{P}\cdot i_{P}+{\frac {d\Psi {_{P}}}{dt}}$ ------ (समीकरण 2.3)

$v_{S}=-R_{S}\cdot i_{S}-{\frac {d\Psi {_{S}}}{dt}}$ ------ (समीकरण 2.4)

$\Psi _{P}=L_{P}\cdot i_{P}-M\cdot i_{S}$ ------ (समीकरण 2.5)

$\Psi _{S}=L_{S}\cdot i_{S}-M\cdot i_{P}$ ------ (समीकरण 2.6),

जहाँ

• $\Psi$ प्रवाह संयोजन है
• ${\frac {d\Psi }{dt}}$ समय के संबंध में प्रवाह संयोजन का व्युत्पन्न है।

इन समीकरणों को यह दिखाने के लिए विकसित किया जा सकता है कि संबंधित वाइंडिंग प्रतिरोधों की उपेक्षा करते हुए, एक वाइंडिंग सर्किट के अधिष्ठापन और अन्य वाइंडिंग शॉर्ट-सर्किट परीक्षण के साथ धाराओं का अनुपात | शॉर्ट-सर्किट और ओपन-सर्किट परीक्षण इस प्रकार है,

$\sigma =1-{\frac {M^{2}}{L_{P}L_{S}}}=1-k^{2}\approx {\frac {L_{sc}}{L_{oc}}}\approx {\frac {L_{sc}^{sec}}{L_{P}}}\approx {\frac {L_{sc}^{pri}}{L_{S}}}\approx {\frac {i_{oc}}{i_{sc}}}$ ------ (समीकरण 2.7),

कहाँ पे,

• मैं_oc & मैं_sc ओपन-सर्किट और शॉर्ट-सर्किट धाराएँ हैं
• ल_oc और एल_sc ओपन-सर्किट और शॉर्ट-सर्किट इंडक्शन हैं।
• $\sigma$ आगमनात्मक रिसाव कारक या हेलैंड कारक है
• $L_{sc}^{pri}$ & $L_{sc}^{sec}$ प्राथमिक और द्वितीयक शॉर्ट-सर्किट लीकेज इंडक्शन हैं।

ट्रांसफॉर्मर अधिष्ठापन को तीन अधिष्ठापन स्थिरांक के रूप में वर्णित किया जा सकता है,

$L_{M}=a{M}$ ------ (समीकरण 2.8)

$L_{P}^{\sigma }=L_{P}-a{M}$ ------ (समीकरण 2.9)

$L_{S}^{\sigma }=L_{S}-{M}/a$ ------ (समीकरण 2.10) ,

कहाँ,

अंजीर। 3 गैर-आदर्श ट्रांसफार्मर समकक्ष सर्किट

:*ल_M मैग्नेटाइजिंग इंडक्शन है, जो मैग्नेटाइजिंग रिएक्शन एक्स के अनुरूप है_M

• ल_P^एस और एल_S^σ प्राइमरी और सेकेंडरी लीकेज इंडक्शन हैं, जो प्राइमरी और सेकेंडरी लीकेज रिएक्शन X के अनुरूप हैं_P^एस और एक्स_S^{σ</सुप>.}

ट्रांसफॉर्मर को चित्र 3 में समतुल्य सर्किट के रूप में अधिक आसानी से व्यक्त किया जा सकता है, जिसमें द्वितीयक स्थिरांक (अर्थात, प्राइम सुपरस्क्रिप्ट नोटेशन के साथ) प्राथमिक को संदर्भित किया जाता है,:$L_{S}^{\sigma \prime }=a^{2}L_{S}-aM$

$R_{S}^{\prime }=a^{2}R_{S}$

$V_{S}^{\prime }=aV_{S}$

$I_{S}^{\prime }=I_{S}/a$.

अंजीर। युग्मन गुणांक k के संदर्भ में 4 गैर-आदर्श ट्रांसफार्मर समकक्ष सर्किट

तब से

$k=M/{\sqrt {L_{P}L_{S}}}$ ------ (समीकरण 2.11)

और

$a={\sqrt {L_{P}/L_{S}}}$ ------ (समीकरण 2.12),

अपने पास

$aM={\sqrt {L_{P}/L_{S}}}\cdot k\cdot {\sqrt {L_{P}L_{S}}}=kL_{P}$ ------ (समीकरण 2.13),

जो वाइंडिंग लीकेज और मैग्नेटाइजिंग इंडक्शन स्थिरांक के संदर्भ में चित्र 4 में समतुल्य सर्किट की अभिव्यक्ति की अनुमति देता है, जैसा कि निम्नानुसार है,

अंजीर। 5 सरलीकृत गैर-आदर्श ट्रांसफार्मर समकक्ष सर्किट

:$L_{P}^{\sigma }=L_{S}^{\sigma \prime }=L_{P}\cdot (1-k)$ ------ (समीकरण 2.14 $\equiv$ सम। 1.1बी)

$L_{M}=kL_{P}$ ------ (समीकरण 2.15 $\equiv$ सम। 1.1 सी)।

चित्र 4 में गैर-आदर्श ट्रांसफार्मर को चित्र 5 में सरलीकृत समतुल्य परिपथ के रूप में दिखाया जा सकता है, जिसमें द्वितीयक स्थिरांक को प्राथमिक और आदर्श ट्रांसफार्मर अलगाव के बिना संदर्भित किया जाता है, जहां,

$i_{M}=i_{P}-i_{S}^{'}$ ------ (समीकरण 2.16)

• $i_{M}$ फ्लक्स Φ द्वारा उत्तेजित धारा को चुम्बकित कर रहा है_M जो प्राथमिक और द्वितीयक वाइंडिंग दोनों को जोड़ता है
• $i_{P}$ प्राथमिक धारा है
• $i_{S}'$ ट्रांसफार्मर के प्राथमिक पक्ष को संदर्भित द्वितीयक धारा है।

परिष्कृत आगमनात्मक रिसाव कारक

परिष्कृत आगमनात्मक रिसाव कारक व्युत्पत्ति

एक। प्रति समीकरण। 2.1 और IEC IEV 131-12-41 आगमनात्मक युग्मन कारक $k$ द्वारा दिया गया है

$k=\left|M\right|/{\sqrt {L_{P}L_{S}}}$ --------------------- (समीकरण 2.1):

बी। प्रति समीकरण। 2.7 और IEC IEV 131-12-42 आगमनात्मक रिसाव कारक $\sigma$ द्वारा दिया गया है

$\sigma =1-k^{2}=1-{\frac {M^{2}}{L_{P}L_{S}}}$ ------ (समीकरण 2.7) और (समीकरण 3.7क)

सी। ${\frac {M^{2}}{L_{P}L_{S}}}$ से गुणा ${\frac {a^{2}}{a^{2}}}$ देता है

$\sigma =1-{\frac {a^{2}M^{2}}{L_{P}a^{2}L_{S}}}$ ----------------- (समीकरण 3.7बी)

डी। प्रति समीकरण। 2-8 और यह जानकर $a^{2}L_{S}=L_{S}^{\prime }$

$\sigma =1-{\frac {L_{M}^{2}}{L_{P}L_{S}^{\prime }}}$ ------------------------------------- (समीकरण 3.7ग)

इ। ${\frac {L_{M}^{2}}{L_{P}L_{S}^{\prime }}}$ से गुणा ${\frac {L_{M}.L_{M}}{L_{M}^{2}}}$ देता है

$\sigma =1-{\frac {1}{{\frac {L_{P}}{L_{M}}}.{\frac {L_{S}^{\prime }}{L_{M}}}}}$ ------------------ (समीकरण 3.7d)

एफ। प्रति समीकरण। 3.5 $\approx$ सम। 1.1बी और समीकरण। 2.14 और समीकरण। 3.6 $\approx$ सम। 1.1बी और समीकरण। 2.14:

$\sigma =1-{\frac {1}{(1+\sigma _{P})(1+\sigma _{S})}}$ --- (समीकरण 3.7e)

इस लेख में सभी समीकरण स्थिर-अवस्था स्थिर-आवृत्ति तरंग स्थितियों को मानते हैं $k$ & $\sigma$ जिनके मान आयाम रहित, निश्चित, परिमित और सकारात्मक हैं लेकिन 1 से कम हैं।

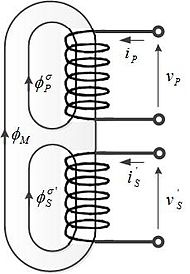
चित्र 6 में फ्लक्स आरेख का संदर्भ देते हुए, निम्नलिखित समीकरण धारण करते हैं:

fig.1। एक चुंबकीय सर्किट में चुंबकीयकरण और रिसाव प्रवाह

एस_P = एफ_P^{स/एफ़_M = एल_Pσ/एल_M ------ (समीकरण 3.1 $\approx$ सम। 2.7)}

उसी तरह से,

σ_S = एफ_S^σ/एफ_M = एल_S^σ/एल_M ------ (समीकरण 3.2 $\approx$ सम। 2.7)

और इसीलिए,

Φ_P = एफ_M + एफ_P^σ = Φ_M + पी_PΦ_M = (1 + पृ_P) पीएचआई_M ------ (समीकरण 3.3)

पीएचआई_S^' = एफ_M + एफ_S^σ' = Φ_M + पी_SΦ_M = (1 + पृ_S) पीएचआई_M ------ (समीकरण 3.4)

एल_P = एल_M + एल_P^σ = एल_M + पी_PL_M = (1 + पृ_P) एल_M ------ (समीकरण 3.5 $\approx$ सम। 1.1बी और समीकरण। 2.14)

एल_S^'=एल_M + एल_S^σ' = एल_M + पी_SL_M = (1 + पृ_S) एल_M ------ (समीकरण 3.6 $\approx$ सम। 1.1बी और समीकरण। 2.14),

कहाँ पे

• σ_P & पी_S क्रमशः, प्राथमिक रिसाव कारक और द्वितीयक रिसाव कारक हैं

• Φ_M और एल_M क्रमशः, पारस्परिक प्रवाह और चुंबकत्व अधिष्ठापन हैं
• Φ_P^एस और एल_P^σ क्रमशः, प्राथमिक रिसाव प्रवाह और प्राथमिक रिसाव अधिष्ठापन हैं

• Φ_S^σ' और एल_S^σ' क्रमशः द्वितीयक रिसाव प्रवाह और द्वितीयक रिसाव अधिष्ठापन दोनों प्राथमिक को संदर्भित हैं।

रिसाव अनुपात σ इस प्रकार उपरोक्त वाइंडिंग-विशिष्ट अधिष्ठापन और आगमनात्मक रिसाव कारक समीकरणों के अंतर्संबंध के संदर्भ में निम्नानुसार परिष्कृत किया जा सकता है:

$\sigma =1-{\frac {M^{2}}{L_{P}L_{S}}}=1-{\frac {a^{2}M^{2}}{L_{P}a^{2}L_{S}}}=1-{\frac {L_{M}^{2}}{L_{P}L_{S}{^{'}}}}=1-{\frac {1}{{\frac {L_{P}}{L_{M}}}.{\frac {L_{S}^{'}}{L_{M}}}}}=1-{\frac {1}{(1+\sigma _{P})(1+\sigma _{S})}}$ ------ (समीकरण 3.7क से 3.7e).

अनुप्रयोग

रिसाव अधिष्ठापन एक अवांछनीय गुण हो सकता है, क्योंकि यह लोडिंग के साथ वोल्टेज को बदलने का कारण बनता है।

उच्च रिसाव ट्रांसफार्मर

कई मामलों में यह उपयोगी होता है। रिसाव अधिष्ठापन में एक ट्रांसफॉर्मर (और लोड) में मौजूदा प्रवाह को सीमित करने का उपयोगी प्रभाव होता है, बिना स्वयं को नष्ट करने वाली शक्ति (सामान्य गैर-आदर्श ट्रांसफॉर्मर नुकसान को छोड़कर)। ट्रांसफॉर्मर आम तौर पर रिसाव अधिष्ठापन के एक विशिष्ट मूल्य के लिए डिज़ाइन किए जाते हैं जैसे कि इस अधिष्ठापन द्वारा बनाई गई रिसाव प्रतिक्रिया ऑपरेशन की वांछित आवृत्ति पर एक विशिष्ट मूल्य है। इस मामले में, वास्तव में काम करने वाला उपयोगी पैरामीटर लीकेज इंडक्शन वैल्यू नहीं है, बल्कि शॉर्ट-सर्किट इंडक्शन वैल्यू है।

2,500 केवीए तक रेट किए गए वाणिज्यिक और वितरण ट्रांसफॉर्मर आमतौर पर लगभग 3% और 6% के बीच के शॉर्ट-सर्किट प्रतिबाधा के साथ और संबंधित के साथ डिज़ाइन किए जाते हैं $X/R$ लगभग 3 और 6 के बीच अनुपात (वाइंडिंग रिएक्शन/वाइंडिंग प्रतिरोध अनुपात), जो नो-लोड और पूर्ण लोड के बीच प्रतिशत माध्यमिक वोल्टेज भिन्नता को परिभाषित करता है। इस प्रकार विशुद्ध रूप से प्रतिरोधक भार के लिए, ऐसे ट्रांसफॉर्मर का पूर्ण-टू-नो-लोड वोल्टेज विनियमन लगभग 1% और 2% के बीच होगा।

कुछ नकारात्मक प्रतिरोध अनुप्रयोगों के लिए उच्च रिसाव रिएक्शन ट्रांसफॉर्मर का उपयोग किया जाता है, जैसे कि नियॉन संकेत, जहां वोल्टेज प्रवर्धन (ट्रांसफार्मर क्रिया) के साथ-साथ वर्तमान सीमित करने की आवश्यकता होती है। इस मामले में रिसाव प्रतिघात आमतौर पर पूर्ण लोड प्रतिबाधा का 100% होता है, इसलिए भले ही ट्रांसफॉर्मर को छोटा कर दिया जाए, यह क्षतिग्रस्त नहीं होगा। रिसाव अधिष्ठापन के बिना, इन गैस निर्वहन लैंपों की नकारात्मक प्रतिरोध विशेषता उन्हें अत्यधिक वर्तमान का संचालन करने और नष्ट करने का कारण बनती है।

चाप वेल्डिंग सेट में करंट को नियंत्रित करने के लिए वेरिएबल लीकेज इंडक्शन वाले ट्रांसफॉर्मर का उपयोग किया जाता है। इन मामलों में, रिसाव अधिष्ठापन विद्युत प्रवाह प्रवाह को वांछित परिमाण तक सीमित करता है। पावर सिस्टम में अधिकतम स्वीकार्य मूल्य के भीतर सर्किट फॉल्ट करंट को सीमित करने में ट्रांसफार्मर लीकेज रिएक्शन की बड़ी भूमिका होती है।

इसके अलावा, एक एचएफ-ट्रांसफार्मर का रिसाव अधिष्ठापन एक गुंजयमान कनवर्टर में एक श्रृंखला प्रारंभ करनेवाला को बदल सकता है। इसके विपरीत, एक पारंपरिक ट्रांसफार्मर और एक प्रारंभ करनेवाला को श्रृंखला में जोड़ने से एक रिसाव ट्रांसफार्मर के समान विद्युत व्यवहार होता है, लेकिन यह आवारा क्षेत्र के कारण ट्रांसफार्मर वाइंडिंग में एड़ी की धारा को कम करने के लिए फायदेमंद हो सकता है।

यह भी देखें

• अवरुद्ध रोटर परीक्षण
• सर्किल आरेख
• अधिष्ठापन#म्यूचुअल अधिष्ठापन
• इंडक्शन मोटर # स्टेनमेट्ज़ समतुल्य सर्किट
• शॉर्ट-सर्किट इंडक्शन
• शॉर्ट-सर्किट परीक्षण
• वोल्टेज अधिनियम

बाहरी कड़ियाँ

IEC Electropedia links:

• Linked flux
• Ideal voltage source
• Inductance
• Ideal current source
• Coupling
• Inductive coupling
• Inductive coupling factor
• Inductive leakage factor
• Ideal transformer
• Magnetic leakage factor
• Self-inductance
• Mutual inductance

ग्रन्थसूची

• Brenner, Egon; Javid, Mansour (1959). "Chapter 18 – Circuits with Magnetic Coupling". Analysis of Electric Circuits. McGraw-Hill. pp. esp. 586–617.
• Didenko, V.; Sirotin, D. (2012). "Accurate Measurement of Resistance and Inductance of Transformer Windings" (PDF). XX IMEKO World Congress – Metrology for Green Growth. Busan, Republic of Korea, September 9−14, 2012.{{cite conference}}: CS1 maint: location (link)
• Erickson, Robert W.; Maksimovic, Dragan (2001). "Chapter 12: Basic Magnetics Theory (Instructor slides only for book)" (PDF). Fundamentals of Power Electronics (2nd ed.). Boulder: University of Colorado (slides) / Springer (book). pp. 72 slides. ISBN 978-0-7923-7270-7.
• "Electropedia: The World's Online Electrotechnical Vocabulary". IEC 60050 (Publication date: 1990-10). Archived from the original on 2015-04-27.
• Hameyer, Kay (2001). Electrical Machines I: Basics, Design, Function, Operation (PDF). RWTH Aachen University Institute of Electrical Machines. Archived from the original (PDF) on 2013-02-10.
• Harris, Forest K. (1952). Electrical Measurements (5th printing (1962) ed.). New York, London: John Wiley & Sons.
• Heyland, A. (1894). "A Graphical Method for the Prediction of Power Transformers and Polyphase Motors". ETZ. 15: 561–564.
• Heyland, A. (1906). A Graphical Treatment of the Induction Motor. Translated by George Herbert Rowe; Rudolf Emil Hellmund. McGraw-Hill. pp. 48 pages.
• Irwin, J. D. (1997). The Industrial Electronics Handbook. A CRC handbook. Taylor & Francis. ISBN 978-0-8493-8343-4.
• Khurana, Rohit (2015). Electronic Instrumentation and Measurement. Vikas Publishing House. ISBN 9789325990203.
• Kim, Joong Chung (1963). The Determination of Transformer Leakage Reactance by Using an Inpulse Driving Function. University of Oregon.
• Knowlton, A.E., ed. (1949). Standard Handbook for Electrical Engineers (8th ed.). McGraw-Hill. p. 802, § 8–67: The Leakage Factor.
• MIT-Press (1977). "Self- and Mutual Inductances". Magnetic circuits and transformers a first course for power and communication engineers. Cambridge, Mass.: MIT-Press. pp. 433–466. ISBN 978-0-262-31082-6.
• Pyrhönen, J.; Jokinen, T.; Hrabovcová, V. (2008). Design of Rotating Electrical Machines. p. Chapter 4 Flux Leakage.
• "Mutual Inductance" (PDF). Rhombus Industries Inc. 1998. Retrieved 4 August 2018.
• Saarbafi, Karim; Mclean, Pamela (2014). "AESO Transformer Modelling Guide" (PDF). Calgary: AESO - Alberta Electric System Operator (prepared by Teshmont Consultants LP). pp. 304 pages. Retrieved August 6, 2018.
• Singh, Mahendra (2016). "Mutual Inductance". Electronics Tutorials. Retrieved 6 January 2017.
• "Measuring Leakage Inductance" (PDF). Voltech Instruments. 2016. Retrieved 5 August 2018.