घन फलन

Not to be confused with Cubic equation.

एक फ़ंक्शन के 3 वास्तविक संख्या रूट के साथ एक क्यूबिक फ़ंक्शन का ग्राफ (जहां वक्र क्षैतिज अक्ष को पार करता है - जहां y = 0)।दिखाए गए मामले में दो महत्वपूर्ण बिंदु (गणित) हैं।यहाँ कार्य है f(x) = (x³ + 3x² − 6x − 8)/4।

गणित में, एक घन फलन रूप का एक फलन है $f(x)=ax^{3}+bx^{2}+cx+d$

जहाँ गुणांक a, b, c और d सम्मिश्र संख्याएँ हैं, और चर x वास्तविक मान लेता है, और $a\neq 0$। दूसरे शब्दों में, यह डिग्री तीन का बहुपद फलन और वास्तविक फलन दोनों है।विशेष रूप से, डोमेन और कोडोमेन वास्तविक संख्याओं का समुच्चय हैं।

f(x) = 0 स्थापन करना प्रपत्र का घन समीकरण उत्पन्न करता है

$ax^{3}+bx^{2}+cx+d=0,$

जिनके हल फलन के रूट्स कहलाते हैं।

एक घन फलन के या तो एक या तीन वास्तविक रूट्स होते हैं (जो भिन्न नहीं हो सकते हैं); सभी विषम-डिग्री बहुपद का कम से कम एक वास्तविक रूट होता है।

घन फलन के लेखाचित्र (ग्राफ़) में हमेशा एक ही विभक्ति बिंदु होता है। इसके दो महत्वपूर्ण बिंदु हो सकते हैं, एक स्थानीय न्यूनतम और एक स्थानीय अधिकतम। अन्यथा, एक घन फलन एकदिष्ट (मोनोटोनिक) है। एक घन फलन का लेखाचित्र इसके विभक्ति बिंदु के संबंध में सममित है; यही है, अर्थात्, यह इस बिंदु के चारों ओर एक आधे चक्कर के घूर्णन के तहत अपरिवर्तनीय है। एक अफ़िन परिवर्तन तक, घन फलन के लिए केवल तीन संभावित लेखाचित्र हैं।

घन प्रक्षेप के लिए घन फलन मौलिक हैं।

इतिहास

Main article: घन समीकरण § इतिहास

महत्वपूर्ण और विभक्ति अंक

The roots, stationary points, inflection point and concavity of a cubic polynomial x³ − 3x² − 144x + 432 (black line) and its first and second derivatives (red and blue).

घन फलन के महत्वपूर्ण बिंदु इसके स्थिर बिंदु हैं, अर्थात वे बिंदु जहां फलन का ढलान शून्य है। इस प्रकार घन फलन f के महत्वपूर्ण बिंदु द्वारा परिभाषित किया गया है

f(x) = ax³ + bx² + cx + d,

x के मानों पर होता है जैसे कि व्युत्पन्न

$3ax^{2}+2bx+c=0$

घन फलन का शून्य है।

इस समीकरण के समाधान महत्वपूर्ण बिंदुओं के x-मान हैं और द्विघात सूत्र का उपयोग करके दिए गए हैं।

$x_{\text{critical}}={\frac {-b\pm {\sqrt {b^{2}-3ac}}}{3a}}.$

वर्गमूल के अंदर अभिव्यक्ति का संकेत महत्वपूर्ण बिंदुओं की संख्या निर्धारित करता है। यदि यह सकारात्मक है, तो दो महत्वपूर्ण बिंदु हैं, एक स्थानीय अधिकतम और दूसरा स्थानीय न्यूनतम है। यदि b² – 3ac = 0, फिर केवल एक महत्वपूर्ण बिंदु है, जो एक विभक्ति बिंदु है। यदि b² – 3ac < 0, है, तो कोई (वास्तविक) महत्वपूर्ण बिंदु नहीं हैं। बाद के दो मामलों में, यानी, अगर b² – 3ac गैर-सकारात्मक है, तो घन फलन सख्ती से एकदिष्ट है। केस Δ0 > 0 के उदाहरण के लिए चित्र देखें।

किसी फलन का विभक्ति बिंदु वह होता है जहां वह फलन अवतलता को बदलता है। एक विभक्ति बिंदु तब होता है जब दूसरा व्युत्पन्न होता है $f''(x)=6ax+2b,$ शून्य है, और तीसरा व्युत्पन्न अशून्य है। इस प्रकार एक घन फलन में हमेशा एक ही विभक्ति बिंदु होता है, जो पर होता है

$x_{\text{inflection}}=-{\frac {b}{3a}}.$

वर्गीकरण

रूप के घन कार्य $y=x^{3}+cx.$
किसी भी क्यूबिक फ़ंक्शन का ग्राफ इस तरह के वक्र के लिए समानता (ज्यामिति) है।

घन फलन का लेखाचित्र एक घन वक्र है, हालांकि कई घन वक्र फलन के लेखाचित्र नहीं हैं।

यद्यपि घन फलन चार मापदंडों पर निर्भर करते हैं, उनके लेखाचित्र में केवल बहुत कम आकार हो सकते हैं। वास्तव में, एक घन फलन का लेखाचित्र हमेशा प्रपत्र के फ़ंक्शन के लेखाचित्र के समान होता है

$y=x^{3}+px.$

इस समानता को निर्देशांक अक्षों के समानांतर अनुवादों की रचना के रूप में बनाया जा सकता है, एक समरूपता (समान स्केलिंग), और, संभवतः, y-अक्ष के संबंध में एक प्रतिबिंब (दर्पण छवि)। एक और गैर-समान स्केलिंग लेखाचित्र को तीन घन फलन में से एक के लेखाचित्र में बदल सकती है

${\begin{aligned}y&=x^{3}+x\\y&=x^{3}\\y&=x^{3}-x.\end{aligned}}$

इसका मतलब यह है कि अफ़िन परिवर्तन तक घन फलन के केवल तीन लेखाचित्र हैं।

सामान्य घन फलन से शुरू होने पर उपरोक्त ज्यामितीय परिवर्तनों को निम्न तरीके से बनाया जा सकता है

$y=ax^{3}+bx^{2}+cx+d.$

सबसे पहले, यदि कोई < 0 है, तो चर x →-x का परिवर्तन एक > 0 मान लेने की अनुमति देता है। चर के इस परिवर्तन के बाद, नया लेखाचित्र y-अक्ष के संबंध में पिछले वाले की दर्पण छवि है।

तब, चर x का परिवर्तन x = x₁ – b/3a प्रपत्र का एक कार्य प्रदान करता है

$y=ax_{1}^{3}+px_{1}+q.$

यह x-अक्ष के समानांतर अनुवाद के अनुरूप है।

चर y = y1 + q का परिवर्तन y-अक्ष के संबंध में अनुवाद के अनुरूप है, और प्रपत्र का एक फलन देता है

$y_{1}=ax_{1}^{3}+px_{1}.$

चर $\textstyle x_{1}={\frac {x_{2}}{\sqrt {a}}},y_{1}={\frac {y_{2}}{\sqrt {a}}}$ का परिवर्तन एक समान स्केलिंग से मेल खाता है, और ${\sqrt {a}},$ द्वारा गुणन के बाद प्रपत्र का एक फलन देता है

$y_{2}=x_{2}^{3}+px_{2},$

जो सरलतम रूप है जो एक समानता द्वारा प्राप्त किया जा सकता है।

फिर, यदि p ≠ 0, असमान स्केलिंग $\textstyle x_{2}=x_{3}{\sqrt {|p|}},\quad y_{2}=y_{3}{\sqrt {|p|^{3}}}$ देता है, $\textstyle {\sqrt {|p|^{3}}},$ से विभाजन देने के बाद

$y_{3}=x_{3}^{3}+x_{3}\operatorname {sgn}(p),$

जहां p के संकेत के आधार पर $\operatorname {sgn}(p)$ का मान 1 या -1 है। यदि कोई $\operatorname {sgn}(0)=0,$ परिभाषित करता है तो फलन के बाद वाला रूप सभी मामलों पर लागू होता है $x_{2}=x_{3}$ तथा $y_{2}=y_{3}$)।

समरूपता

फॉर्म $y=x^{3}+px,$ के घन फलन के लिए विभक्ति बिंदु इस प्रकार मूल है। जैसा कि ऐसा फलन एक विषम फलन है, इसका लेखाचित्र विभक्ति बिंदु के संबंध में सममित है, और विभक्ति बिंदु के चारों ओर आधे मोड़ के रोटेशन के तहत अपरिवर्तनीय है।

एक घन फलन का लेखाचित्र अपने विभक्ति बिंदु के संबंध में सममित है, और विभक्ति बिंदु के चारों ओर एक आधे मोड़ के घूर्णन के तहत अपरिवर्तनीय है।

समरैखिकता

बिंदु P₁, P₂, तथा P₃ (नीले रंग में) कोलेनियर हैं और के ग्राफ से संबंधित हैं x³ + 3/2x² − 5/2x + 5/4।बिंदु T₁, T₂, तथा T₃ (लाल रंग में) ग्राफ के साथ इन बिंदुओं पर ग्राफ के लिए (बिंदीदार) स्पर्शरेखा लाइनों के चौराहे हैं।वे कोलेनियर भी हैं।

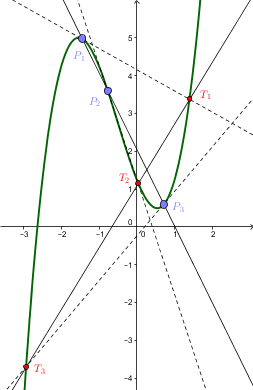
तीन समरेख बिंदुओं पर घन फलन के लेखाचित्र की स्पर्श रेखाएँ घन को फिर से संरेख बिंदुओं पर रोकती हैं। इस प्रकार इसे देखा जा सकता है।

जैसा कि यह संपत्ति एक कठोर गति के तहत अपरिवर्तनीय है, कोई यह मान सकता है कि फलन का रूप है

$f(x)=x^{3}+px.$

यदि α एक वास्तविक संख्या है, तो बिंदु (α, f(α)) पर f के ग्राफ की स्पर्शरेखा रेखा है

{(x, f(α) + (x − α)f ′(α)) : x ∈ R}।

तो, इस रेखा और f के ग्राफ के बीच का प्रतिच्छेदन बिंदु समीकरण को हल करके प्राप्त किया जा सकता है f(x) = f(α) + (x − α)f ′(α), वह है

$x^{3}+px=\alpha ^{3}+p\alpha +(x-\alpha )(3\alpha ^{2}+p),$

जिसे फिर से लिखा जा सकता है

$x^{3}-3\alpha ^{2}x+2\alpha ^{3}=0,$

और गुणनखंडित किया जा सकता है

$(x-\alpha )^{2}(x+2\alpha )=0.$

तो, स्पर्शरेखा घन का अवरोधन करती है

$(-2\alpha ,-8\alpha ^{3}-2p\alpha )=(-2\alpha ,-8f(\alpha )+6p\alpha ).$

तो, फलन जो लेखाचित्र के एक बिंदु (x, y) को दूसरे बिंदु पर मानचित्र करता है जहां स्पर्शरेखा लेखाचित्र का अवरोधन करती है

$(x,y)\mapsto (-2x,-8y+6px).$

यह एक एफिन परिवर्तन है जो समरेख बिंदुओं को समरेख बिंदुओं में बदल देता है। यह दावा किए गए परिणाम को साबित करता है।

घन प्रक्षेप

Main article: Spline interpolation

किसी फलन के मान और दो बिंदुओं पर उसके व्युत्पन्न को देखते हुए, ठीक एक घन फलन होता है जिसमें समान चार मान होते हैं, जिसे घन हर्मिट स्पलाइन कहा जाता है।

इस तथ्य का उपयोग करने के दो मानक तरीके हैं। सबसे पहले, यदि कोई जानता है, उदाहरण के लिए भौतिक माप द्वारा, एक फलन के मान और कुछ नमूने बिंदुओं पर इसके व्युत्पन्न, एक निरंतर भिन्न फलन के साथ फलन को प्रक्षेपित कर सकता है, जो कि एक टुकड़े-टुकड़े घन फलन है।

यदि किसी फलन का मान कई बिंदुओं पर जाना जाता है, तो फलन प्रक्षेप में निरंतर भिन्न होने वाले फलन द्वारा फलन का अनुमान लगाया जाता है, जो कि टुकड़े-टुकड़े घन होता है। एक विशिष्ट रूप से परिभाषित प्रक्षेप होने के लिए, दो और बाधाओं को जोड़ा जाना चाहिए, जैसे कि समापन बिंदु पर व्युत्पन्न के मान, या समापन बिंदु पर शून्य वक्रता।

इस पृष्ठ में गुम आंतरिक लिंक की सूची

• एक समारोह की जड़
• आलोचनात्मक बिंदु (गणित)
• अंक शास्त्र
• समारोह (गणित)
• एक फ़ंक्शन का डोमेन
• बहुपदीय फलन
• एक फ़ंक्शन का ग्राफ
• असंबद्ध परिवर्तन
• संक्रमण का बिन्दु
• घन प्रक्षेप
• यौगिक
• द्वितीय व्युत्पन्न
• दर्पण छवि
• पुराना फंक्शन
• कोलेनियर पॉइंट्स
• लगातार अलग -अलग कार्य
• खंड अनुसार

बाहरी संबंध

• "Cardano formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• History of quadratic, cubic and quartic equations on MacTutor archive.