थर्मल रेज़िज़टेंस: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 169: | Line 169: | ||
=== विद्युत प्रतिरोध समानता के साथ समस्या === | === विद्युत प्रतिरोध समानता के साथ समस्या === | ||
फिलिप्स के शोधकर्ता क्लेमेंस जे. एम. लसांस द्वारा लिखित 2008 के एक समीक्षा पत्र में कहा गया है कि:"चूंकि चालकता (फूरियर का नियम) और विद्युत प्रवाह (ओम का नियम) के प्रवाह के बीच एक समानता है, तापीय चालकता और विद्युत के संबंधित भौतिक गुण चालकता सामान्य परिस्थितियों में बिजली के प्रवाह के बिल्कुल विपरीत ऊष्मा प्रवाह के व्यवहार को बनाने के लिए षड्यंत्र करती है। दुर्भाग्य से, चूंकि विद्युत और तापीय अंतर समीकरण समान हैं,यह निष्कर्ष निकालना गलत है कि विद्युत और के बीच कोई व्यावहारिक सादृश्य है थर्मल प्रतिरोध। ऐसा इसलिए है चूंकि एक सामग्री जिसे विद्युत शब्दों में एक अवरोधक माना जाता है, वह एक सामग्री की तुलना में कम प्रवाहकीय परिमाण लगभग 20 है, जिसे एक | फिलिप्स के शोधकर्ता क्लेमेंस जे. एम. लसांस द्वारा लिखित 2008 के एक समीक्षा पत्र में कहा गया है कि:"चूंकि चालकता (फूरियर का नियम) और विद्युत प्रवाह (ओम का नियम) के प्रवाह के बीच एक समानता है, तापीय चालकता और विद्युत के संबंधित भौतिक गुण चालकता सामान्य परिस्थितियों में बिजली के प्रवाह के बिल्कुल विपरीत ऊष्मा प्रवाह के व्यवहार को बनाने के लिए षड्यंत्र करती है। दुर्भाग्य से, चूंकि विद्युत और तापीय अंतर समीकरण समान हैं,यह निष्कर्ष निकालना गलत है कि विद्युत और के बीच कोई व्यावहारिक सादृश्य है थर्मल प्रतिरोध। ऐसा इसलिए है चूंकि एक सामग्री जिसे विद्युत शब्दों में एक अवरोधक माना जाता है, वह एक सामग्री की तुलना में कम प्रवाहकीय परिमाण लगभग 20 है, जिसे एक अर्धचालक माना जाता है, जबकि, थर्मल शब्दों में, "ऊष्मारोधी" और "अर्धचालक" के बीच का अंतर "परिमाण के एकमात्र तीन आदेशों के बारे में है। तापीय चालकता की पूरी श्रृंखला तब विद्युत चालकता में अंतर के बराबर होती है।" <ref name="Lasance"/> | ||
== मापन मानक == | == मापन मानक == | ||
जंक्शन-से-परिवेश थर्मल प्रतिरोध परिवेश स्थितियों के आधार पर पर्याप्त भिन्नता हो सकती है।<ref name="TongLai2013">{{cite book|author1=Ho-Ming Tong|author2=Yi-Shao Lai|author3=C.P. Wong|title=Advanced Flip Chip Packaging|url=https://archive.org/details/advancedflipchip00lanz|url-access=limited|year=2013|publisher=Springer Science & Business Media|isbn=978-1-4419-5768-9|pages=[https://archive.org/details/advancedflipchip00lanz/page/n463 460]–461}}</ref> (उसी तथ्य को व्यक्त करने का एक अधिक परिष्कृत नियम यह कह रहा है कि जंक्शन-से-परिवेश थर्मल प्रतिरोध सीमा-स्थिति स्वतंत्र (बीसीआई) नहीं है।<ref name="Lasance">{{Cite journal | doi = 10.1080/01457630701673188| title = Ten Years of Boundary-Condition- Independent Compact Thermal Modeling of Electronic Parts: A Review| journal = Heat Transfer Engineering| volume = 29| issue = 2| pages = 149–168| year = 2008| last1 = Lasance | first1 = C. J. M. |bibcode = 2008HTrEn..29..149L | s2cid = 121803741}}</ref>) [[JEDEC]] के पास [[प्राकृतिक संवहन]] के तहत इलेक्ट्रॉनिक्स पैकेजों का वायु तापीय प्रतिरोध और [[मजबूर संवहन]] के तहत माप के लिए एक अन्य मानक (संख्या JESD51-6) है। | |||
परिवेश स्थितियों के आधार पर | |||
जंक्शन- | जंक्शन-दर-स्थिति थर्मल रेजिस्टेंस (JESD51-14) को मापने के लिए एक JEDEC मानक अपेक्षाकृत नवागंतुक है, जो 2010 के अंत में प्रकाशित हुआ था; यह एकमात्र एकल ताप प्रवाह और खुली शीतलन सतह वाले पैकेजों से संबंधित है।<ref name="LasancePoppe2013">{{cite book|author1=Clemens J.M. Lasance|author2=András Poppe|title=Thermal Management for LED Applications|year=2013|publisher=Springer Science & Business Media|isbn=978-1-4614-5091-7|page=247}}</ref><ref>{{Cite web | url=http://www.electronics-cooling.com/2013/02/experiment-vs-simulation-part-3-jesd51-14/ | title=Experiment vs. Simulation, Part 3: JESD51-14| date=2013-02-22}}</ref><ref>{{Cite conference | doi = 10.1109/STHERM.2011.5767204| chapter = Transient dual interface measurement — A new JEDEC standard for the measurement of the junction-to-case thermal resistance| title = 2011 27th Annual IEEE Semiconductor Thermal Measurement and Management Symposium| pages = 222| year = 2011| last1 = Schweitzer | first1 = D. | last2 = Pape | first2 = H. | last3 = Chen | first3 = L. | last4 = Kutscherauer | first4 = R. | last5 = Walder | first5 = M. | isbn = 978-1-61284-740-5}}</ref> | ||
== समग्र | == समग्र में प्रतिरोध == | ||
=== समानांतर थर्मल प्रतिरोध === | === समानांतर थर्मल प्रतिरोध === | ||
| Line 197: | Line 195: | ||
=== श्रृंखला और समानांतर में प्रतिरोध === | === श्रृंखला और समानांतर में प्रतिरोध === | ||
[[File:Equivalent thermal circuits for series-parallel composite wall.jpg|thumb|श्रृंखला-समानांतर समग्र दीवार के लिए समतुल्य थर्मल सर्किट]]यह | [[File:Equivalent thermal circuits for series-parallel composite wall.jpg|thumb|श्रृंखला-समानांतर समग्र दीवार के लिए समतुल्य थर्मल सर्किट]]यह अधिकांशतः एक-आयामी स्थितियों को ग्रहण करने के लिए उपयुक्त होता है, चूंकि ऊष्मा का प्रवाह बहुआयामी होता है। अब, इस स्थिति के लिए दो भिन्न परिपथों का उपयोग किया जा सकता है। केस (ए) के लिए, हम एक्स-दिशा के समानांतर [[Index.php?title=आइसोथर्मल|आइसोथर्मल]] सतहों को मानते हैं, जबकि केस (बी) के लिए हम एक्स-दिशा के समानांतर [[Index.php?title=एडियाबेटिक|एडियाबेटिक]] सतहों को मानते हैं। हम कुल प्रतिरोध के लिए अलग-अलग परिणाम प्राप्त कर सकते हैं <math> {R_{tot} }</math> और ऊष्मा हस्तांतरण के वास्तविक संगत मूल्यों को ब्रैकेट में रखा गया है <math> {q} </math>. जब बहुआयामी प्रभाव अधिक महत्वपूर्ण हो जाते हैं, तो ये अंतर बढ़ने के साथ बढ़ जाते हैं <math> {| k_f - k_g |} </math>.<ref name="Incropera, Dewitt, Bergman, Lavine 2013">{{cite book |last=Incropera, Dewitt, Bergman, Lavine |first= Frank P., David P., Theodore L., Adrienne S.|date=2013 |title=Principles of Heat and Mass Transfer|publisher=John Wiley & Sons; 7th Edition, Interna edition|isbn=978-0470646151}}</ref> | ||
=== रेडियल सिस्टम === | === रेडियल सिस्टम === | ||
रेडियल दिशा में [[तापमान प्रवणता]] के कारण गोलाकार और बेलनाकार प्रणालियों को एक आयामी माना जा सकता है। मानक विधि का उपयोग स्थिर अवस्था स्थितियों के तहत रेडियल सिस्टम के विश्लेषण के लिए किया जा सकता है, | रेडियल दिशा में [[तापमान प्रवणता]] के कारण गोलाकार और बेलनाकार प्रणालियों को एक आयामी माना जा सकता है। मानक विधि का उपयोग स्थिर अवस्था स्थितियों के तहत रेडियल सिस्टम के विश्लेषण के लिए किया जा सकता है, ऊष्मा समीकरण के उचित रूप से आरंभ होता है, या वैकल्पिक विधि, फूरियर के नियम के उपयुक्त रूप से आरंभ होता है। अतिरिक्त ऊष्मा उत्पादन वाली स्थिर स्थिति में एक खोखले सिलिंडर के लिए, ऊष्मा समीकरण का उपयुक्त रूप है <ref name="Incropera, Dewitt, Bergman, Lavine 2013"/> | ||
<math>{ {1 \over r}{d\over dr} \left(kr{dT \over dr} \right) = 0 }</math> (4) | <math>{ {1 \over r}{d\over dr} \left(kr{dT \over dr} \right) = 0 }</math> (4) | ||
जहाँ <math> {k} </math> एक चर के रूप में माना जाता है। फूरियर के नियम के उपयुक्त रूप को ध्यान में रखते हुए, उपचार का भौतिक महत्व <math> {k} </math> एक चर के रूप में स्पष्ट हो जाता है जब एक बेलनाकार सतह पर जिस दर से ऊर्जा प्रवाहित होती है, उसे इस रूप में दर्शाया जाता है | |||
<math>{ q_r = -kA {dT \over dr} = -k(2\pi rL){dT \over dr}}</math> (5) | <math>{ q_r = -kA {dT \over dr} = -k(2\pi rL){dT \over dr}}</math> (5) | ||
जहाँ <math> {A = 2\pi rL} </math> वह क्षेत्र है जो उस दिशा के सामान्य है जहां ऊष्मा हस्तांतरण होता है। समीकरण 1 का अर्थ है कि मात्रा <math> {kr(dT/dr)} </math> त्रिज्या पर निर्भर नहीं है <math> {r} </math>, यह समीकरण 5 से अनुसरण करता है कि ऊष्मा हस्तांतरण दर, <math> {q_r} </math> रेडियल दिशा में एक स्थिरांक है। | |||
[[File:Hollow cylinder with convective surface conditions.jpg|thumb|थर्मल चालन में संवहन सतह की स्थिति के साथ खोखले सिलेंडर]]सिलेंडर में तापमान वितरण का निर्धारण करने के लिए, उपयुक्त सीमा स्थितियों को लागू करते हुए समीकरण 4 को हल किया जा सकता है। इस धारणा के साथ कि <math> {k } </math> स्थिर है | [[File:Hollow cylinder with convective surface conditions.jpg|thumb|थर्मल चालन में संवहन सतह की स्थिति के साथ खोखले सिलेंडर]]थर्मल चालन में संवहन सतह की स्थिति के साथ खोखले सिलेंडर में तापमान वितरण का निर्धारण करने के लिए, उपयुक्त सीमा स्थितियों को लागू करते हुए समीकरण 4 को हल किया जा सकता है। इस धारणा के साथ कि <math> {k } </math> स्थिर है | ||
<math> { T(r) = C_1\ln r + C_2 } </math> (6) | <math> { T(r) = C_1\ln r + C_2 } </math> (6) | ||
| Line 222: | Line 220: | ||
थंबनेल चित्र के इनसेट में तापमान का लघुगणकीय वितरण आरेखित किया गया है। | थंबनेल चित्र के इनसेट में तापमान का लघुगणकीय वितरण आरेखित किया गया है। | ||
यह मानते हुए कि तापमान वितरण, समीकरण 7, समीकरण 5 में फूरियर के नियम के साथ प्रयोग किया जाता है, | यह मानते हुए कि तापमान वितरण, समीकरण 7, समीकरण 5 में फूरियर के नियम के साथ प्रयोग किया जाता है, ऊष्मा हस्तांतरण दर को निम्न रूप में व्यक्त किया जा सकता है | ||
<math> {\dot{Q}_r = {2\pi Lk (T_{s,1} - T_{s,2}) \over \ln(r_2/r_1)} } </math> | <math> {\dot{Q}_r = {2\pi Lk (T_{s,1} - T_{s,2}) \over \ln(r_2/r_1)} } </math> | ||
अंत में, एक बेलनाकार दीवार में रेडियल चालन के लिए, थर्मल प्रतिरोध का रूप है | अंत में, एक बेलनाकार दीवार में रेडियल चालन के लिए, थर्मल प्रतिरोध का रूप है | ||
<math> { R_{t,\mathrm{cond}} = {\ln(r_2/r_1) \over 2\pi Lk} }</math> | <math> { R_{t,\mathrm{cond}} = {\ln(r_2/r_1) \over 2\pi Lk} }</math> <math> {r_2 > r_1} </math> | ||
| Line 241: | Line 239: | ||
== अग्रिम पठन == | == अग्रिम पठन == | ||
इस विषय पर बड़ी मात्रा में साहित्य है। सामान्य तौर पर, "थर्मल रेजिस्टेंस" शब्द का उपयोग करने वाले कार्य अधिक इंजीनियरिंग-उन्मुख होते हैं, जबकि शब्द का उपयोग करने वाले कार्य [[Index.php?title=ऊष्मीय चालकता|ऊष्मीय चालकता]] अधिक [शुद्ध-] भौतिकी-उन्मुख हैं। निम्नलिखित पुस्तकें प्रतिनिधि हैं, लेकिन आसानी से प्रतिस्थापित की जा सकती हैं। | |||
* {{cite book|editor= | * {{cite book|editor=टेरी एम. ट्रिट|title=तापीय चालकता: सिद्धांत, गुण और अनुप्रयोग|year=2004|publisher=स्प्रिंगर साइंस एंड बिजनेस मीडिया|isbn=978-0-306-48327-1}} | ||
* {{cite book|author= | * {{cite book|author=यूनुस शबानी|title=हीट ट्रांसफर: इलेक्ट्रॉनिक्स का थर्मल प्रबंधन|year=2011|publisher=सीआरसी प्रेस|isbn=978-1-4398-1468-0}} | ||
* {{cite book|author= | * {{cite book|author=ज़िंगकुन कॉलिन टोंग|title=इलेक्ट्रॉनिक पैकेजिंग के थर्मल प्रबंधन के लिए उन्नत सामग्री|year=2011|publisher=स्प्रिंगर साइंस एंड बिजनेस मीडिया|isbn=978-1-4419-7759-5}} | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* | * गुओपिंग जू (2006), [https://cseweb.ucsd.edu/classes/wi06/cse291-b/slide/let9/thermal.pdf Thermal Management for Electronic Packaging], सन माइक्रोसिस्टम्स | ||
* http://www.electronics-cooling.com/2012/09/update-on-jedec-thermal-standards/ | * http://www.electronics-cooling.com/2012/09/update-on-jedec-thermal-standards/ | ||
*The importance of [https://web.archive.org/web/20141202091212/http://tempsand.com.au/services/tempsand-soil-test-soil-thermal-conductivity-resistivity/ Soil Thermal Resistivity] for power companies | *The importance of [https://web.archive.org/web/20141202091212/http://tempsand.com.au/services/tempsand-soil-test-soil-thermal-conductivity-resistivity/ Soil Thermal Resistivity] for power companies | ||
[[Category:All Wikipedia articles written in American English]] | |||
[[Category:All articles with unsourced statements]] | |||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Articles with unsourced statements from January 2015]] | |||
[[Category:CS1 maint]] | |||
[[Category:Created On 15/02/2023]] | [[Category:Created On 15/02/2023]] | ||
[[Category:Lua-based templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Use American English from January 2019]] | |||
[[Category:इलेक्ट्रॉनिक यन्त्रशास्त्र]] | |||
[[Category:गर्मी चालन]] | |||
Latest revision as of 10:53, 21 February 2023
थर्मल प्रतिरोध एक ऊष्मा संपत्ति है और तापमान अंतर का माप है जिसके द्वारा कोई वस्तु या संपत्ति ऊष्मा प्रवाह का विरोध करती है। तापीय प्रतिरोध तापीय चालकता का व्युत्क्रम है।
- (निरपेक्ष) थर्मल प्रतिरोध आर केल्विन प्रति वाट (के/डब्ल्यू) में एक विशेष घटक की एक संपत्ति है। उदाहरण के लिए, ऊष्माशोषी की एक विशेषता है।
- विशिष्ट तापीय प्रतिरोध या तापीय प्रतिरोधकता Rλकेल्विन-मीटर प्रति वाट (K⋅m/W) में, एक भौतिक स्थिरांक है।
- 'थर्मल प्रतिरोध' में SI इकाइयों में वर्ग मीटर केल्विन प्रति वाट (m2⋅K/W) या इंपीरियल इकाइयों मेंया वर्ग फुट डिग्री फारेनहाइट-घंटे प्रति ब्रिटिश थर्मल यूनिट (ft2⋅°F⋅h/Btu) होता है। यह एक सामग्री के इकाई क्षेत्र का थर्मल प्रतिरोध है। रोधन के संदर्भ में, इसे आर-वैल्यू द्वारा मापा जाता है।
पूर्ण तापीय प्रतिरोध
निरपेक्ष ऊष्मीय प्रतिरोध एक संरचना में तापमान का अंतर है जब इकाई समय में ऊष्मा ऊर्जा की एक इकाई इसके माध्यम से प्रवाहित होती है। यह तापीय चालकता का व्युत्क्रम है। पूर्ण तापीय प्रतिरोध की SI इकाई केल्विन प्रति वाट (K/W) या समतुल्य डिग्री सेल्सियस प्रति वाट (°C/W) है - दोनों समान हैं चूंकि अंतराल समान हैं: ΔT = 1 K = 1 °C।
इलेक्ट्रॉनिक अभियान्तों के लिए सामग्रियों का थर्मल प्रतिरोध बहुत महत्व रखता है चूंकि अधिकांश विद्युत घटक ऊष्मा उत्पन्न करते हैं और उन्हें ठंडा करने की आवश्यकता होती है। ज़्यादा गरम होने पर इलेक्ट्रॉनिक घटक खराब हो जाते हैं या विफल हो जाते हैं, और इसे रोकने के लिए कुछ भागों को नियमित रूप से डिज़ाइन चरण में उपाय करने की आवश्यकता होती है।
उपमा और नामकरण
इलेक्ट्रिकल अभियान्ता ओम के नियम से प्रचलित हैं और इसलिए थर्मल प्रतिरोध से जुड़ी गणना करते समय अधिकांशतः इसे एक सादृश्य के रूप में उपयोग करते हैं। मैकेनिकल और संरचनात्मक अभियान्ता हुक के नियम से अधिक प्रचलित हैं और इसलिए थर्मल प्रतिरोध से जुड़े गणना करते समय अधिकांशतः इसे एक सादृश्य के रूप में उपयोग करते हैं।
| प्रकार | संरचनात्मक सादृश्य | हाइड्रोलिक सादृश्य | थर्मल | विद्युत सादृश्य |
|---|---|---|---|---|
| मात्रा | आवेग [N·s] | आयतन [m3] | ऊष्मा [J] | विद्युत आवेग [C] |
| संभावना | विस्थापन [m] | दबाव [N/m2] | तापमान [K] | विद्युतीय संभाव्यता [V = J/C] |
| प्रवाह | भार या बल [N] | प्रवाह दर [m3/s] | ऊष्मा हस्तांतरण दर [W = J/s] | धारा विद्युत् [A = C/s] |
| प्रवाह का घनत्व | दबाव [Pa = N/m2] | वेग [m/s] | ऊष्मा का प्रवाह [W/m2] | वर्तमान घनत्व [C/(m2·s) = A/m2] |
| प्रतिरोध | फ्लेक्सीबिलिटी (रियोलॉजी परिभाषित) [1/Pa] | द्रव प्रतिरोध [...] | थर्मल रेज़िज़टेंस [K/W] | विद्युतीय प्रतिरोध [Ω] |
| प्रवाहकत्त्व | ... [Pa] | द्रव चालन [...] | ऊष्मीय चालकता [W/K] | विद्युत चालन [S] |
| प्रतिरोधकता | फ्लेक्सीबिलिटी [m/N] | द्रव प्रतिरोधकता | थर्मल प्रतिरोधकता [(m·K)/W] | विद्युत प्रतिरोधकता [Ω·m] |
| चालकता | कठोरता [N/m] | द्रव चालकता | ऊष्मीय चालकता [W/(m·K)] | इलेक्ट्रिकल कंडक्टीविटी [S/m] |
| गांठदार तत्व रैखिक मॉडल | हुक का नियम | हेगन-पॉइज़्यूइल समीकरण | न्यूटन का शीतलन का नियम | ओम लोह |
| वितरित रैखिक मॉडल | ... | ... | फूरियर का नियम | ओम लोह |
इलेक्ट्रॉनिक्स के दृष्टिकोण से स्पष्टीकरण
समतुल्य थर्मल सर्किट
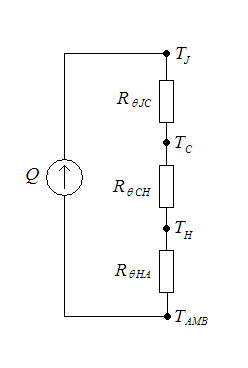
- डिवाइस द्वारा छितरी हुई शक्ति है।
- डिवाइस में जंक्शन तापमान है।
- इस स्थिति में तापमान है।
- वह तापमान है जहां हीट सिंक जुड़ा होता है।
- परिवेशी वायु तापमान है।
- जंक्शन से केस तक डिवाइस का पूर्ण थर्मल प्रतिरोध है।
- केस से हीटसिंक तक पूर्ण तापीय प्रतिरोध है।
- हीट सिंक का पूर्ण तापीय प्रतिरोध है।
ऊष्मा प्रवाह को एक विद्युत परिपथ के सादृश्य द्वारा प्रतिरूपित किया जा सकता है जहाँ ऊष्मा प्रवाह को धारा द्वारा दर्शाया जाता है, तापमान को वोल्टेज द्वारा दर्शाया जाता है, ऊष्मा स्रोतों को निरंतर वर्तमान स्रोतों द्वारा दर्शाया जाता है, पूर्ण तापीय प्रतिरोधों को और तापीय धारिता द्वारा संधारित्र द्वारा दर्शाया जाता है।
आरेख एक अर्धचालक उपकरण के लिए ऊष्माशोषी के साथ एक समतुल्य थर्मल सर्किट दिखाता है।
उदाहरण गणना
| उदाहरण |
|---|
|
Consider a component such as a silicon transistor that is bolted to the metal frame of a piece of equipment. The transistor's manufacturer will specify parameters in the datasheet called the absolute thermal resistance from junction to case (symbol: ), and the maximum allowable temperature of the semiconductor junction (symbol: ). The specification for the design should include a maximum temperature at which the circuit should function correctly. Finally, the designer should consider how the heat from the transistor will escape to the environment: this might be by convection into the air, with or without the aid of a heat sink, or by conduction through the printed circuit board. For simplicity, let us assume that the designer decides to bolt the transistor to a metal surface (or heat sink) that is guaranteed to be less than above the ambient temperature. Note: THS appears to be undefined. Given all this information, the designer can construct a model of the heat flow from the semiconductor junction, where the heat is generated, to the outside world. In our example, the heat has to flow from the junction to the case of the transistor, then from the case to the metalwork. We do not need to consider where the heat goes after that, because we are told that the metalwork will conduct heat fast enough to keep the temperature less than above ambient: this is all we need to know. Suppose the engineer wishes to know how much power can be put into the transistor before it overheats. The calculations are as follows.
where is the absolute thermal resistance of the bond between the transistor's case and the metalwork. This figure depends on the nature of the bond - for example, a thermal bonding pad or thermal transfer grease might be used to reduce the absolute thermal resistance.
We use the general principle that the temperature drop across a given absolute thermal resistance with a given heat flow through it is:
Substituting our own symbols into this formula gives:
and, rearranging, The designer now knows , the maximum power that the transistor can be allowed to dissipate, so they can design the circuit to limit the temperature of the transistor to a safe level. Let us substitute some sample numbers:
The result is then: This means that the transistor can dissipate about 18 watts before it overheats. A cautious designer would operate the transistor at a lower power level to increase its reliability. This method can be generalized to include any number of layers of heat-conducting materials, simply by adding together the absolute thermal resistances of the layers and the temperature drops across the layers. |
ऊष्मा चालन के लिए फूरियर के नियम से व्युत्पन्न
ऊष्मा चालन के लिए फूरियर के नियम से, निम्नलिखित समीकरण प्राप्त किया जा सकता है, और यह तब तक मान्य है जब तक कि सभी पैरामीटर (x और k) प्रतिरूप में स्थिर हैं।
जहाँ:
- प्रतिरूप के घनत्व में पूर्ण तापीय प्रतिरोध (K/W) है,
- प्रतिरूप का घनत्व (एम) है (ऊष्मा प्रवाह के समानांतर पथ पर मापा जाता है),
- प्रतिरूप में तापीय चालकता (W/(K·m)) है,
- प्रतिरूप की तापीय प्रतिरोधकता (K·m/W) है,
- क्रॉस-अनुभागीय क्षेत्र (एम2) ऊष्मा प्रवाह के पथ के लंबवत है।
प्रतिरूप में तापमान ढाल और प्रतिरूप के माध्यम से ऊष्मा प्रवाह के संदर्भ में, संबंध है:
जहाँ:
- प्रतिरूप के घनत्व में पूर्ण तापीय प्रतिरोध (K/W) है,
- प्रतिरूप का घनत्व (एम) है (ऊष्मा प्रवाह के समानांतर पथ पर मापा जाता है),
- प्रतिरूप के माध्यम से ऊष्मा प्रवाह है (वाट·एम-2),
- प्रतिरूप में तापमान प्रवणता है (केल्विन·एम−1),
- प्रतिरूप के माध्यम से ऊष्मा प्रवाह के पथ के लंबवत पार-अनुभागीय क्षेत्र (एम 2) है,
- प्रतिरूप में तापमान अंतर (केल्विन) है,
- प्रतिरूप के माध्यम से ऊष्मा प्रवाह (वाट) की दर है।
विद्युत प्रतिरोध समानता के साथ समस्या
फिलिप्स के शोधकर्ता क्लेमेंस जे. एम. लसांस द्वारा लिखित 2008 के एक समीक्षा पत्र में कहा गया है कि:"चूंकि चालकता (फूरियर का नियम) और विद्युत प्रवाह (ओम का नियम) के प्रवाह के बीच एक समानता है, तापीय चालकता और विद्युत के संबंधित भौतिक गुण चालकता सामान्य परिस्थितियों में बिजली के प्रवाह के बिल्कुल विपरीत ऊष्मा प्रवाह के व्यवहार को बनाने के लिए षड्यंत्र करती है। दुर्भाग्य से, चूंकि विद्युत और तापीय अंतर समीकरण समान हैं,यह निष्कर्ष निकालना गलत है कि विद्युत और के बीच कोई व्यावहारिक सादृश्य है थर्मल प्रतिरोध। ऐसा इसलिए है चूंकि एक सामग्री जिसे विद्युत शब्दों में एक अवरोधक माना जाता है, वह एक सामग्री की तुलना में कम प्रवाहकीय परिमाण लगभग 20 है, जिसे एक अर्धचालक माना जाता है, जबकि, थर्मल शब्दों में, "ऊष्मारोधी" और "अर्धचालक" के बीच का अंतर "परिमाण के एकमात्र तीन आदेशों के बारे में है। तापीय चालकता की पूरी श्रृंखला तब विद्युत चालकता में अंतर के बराबर होती है।" [1]
मापन मानक
जंक्शन-से-परिवेश थर्मल प्रतिरोध परिवेश स्थितियों के आधार पर पर्याप्त भिन्नता हो सकती है।[2] (उसी तथ्य को व्यक्त करने का एक अधिक परिष्कृत नियम यह कह रहा है कि जंक्शन-से-परिवेश थर्मल प्रतिरोध सीमा-स्थिति स्वतंत्र (बीसीआई) नहीं है।[1]) JEDEC के पास प्राकृतिक संवहन के तहत इलेक्ट्रॉनिक्स पैकेजों का वायु तापीय प्रतिरोध और मजबूर संवहन के तहत माप के लिए एक अन्य मानक (संख्या JESD51-6) है।
जंक्शन-दर-स्थिति थर्मल रेजिस्टेंस (JESD51-14) को मापने के लिए एक JEDEC मानक अपेक्षाकृत नवागंतुक है, जो 2010 के अंत में प्रकाशित हुआ था; यह एकमात्र एकल ताप प्रवाह और खुली शीतलन सतह वाले पैकेजों से संबंधित है।[3][4][5]
समग्र में प्रतिरोध
समानांतर थर्मल प्रतिरोध
विद्युत परिपथों के समान, स्थिर अवस्था स्थितियों के लिए कुल तापीय प्रतिरोध की गणना निम्नानुसार की जा सकती है।
कुल थर्मल प्रतिरोध
(1)
समीकरण को सरल करने पर, हम प्राप्त करते हैं
(2) चालन के लिए तापीय प्रतिरोध की शर्तों के साथ, हम प्राप्त करते हैं
(3)
श्रृंखला और समानांतर में प्रतिरोध
यह अधिकांशतः एक-आयामी स्थितियों को ग्रहण करने के लिए उपयुक्त होता है, चूंकि ऊष्मा का प्रवाह बहुआयामी होता है। अब, इस स्थिति के लिए दो भिन्न परिपथों का उपयोग किया जा सकता है। केस (ए) के लिए, हम एक्स-दिशा के समानांतर आइसोथर्मल सतहों को मानते हैं, जबकि केस (बी) के लिए हम एक्स-दिशा के समानांतर एडियाबेटिक सतहों को मानते हैं। हम कुल प्रतिरोध के लिए अलग-अलग परिणाम प्राप्त कर सकते हैं और ऊष्मा हस्तांतरण के वास्तविक संगत मूल्यों को ब्रैकेट में रखा गया है . जब बहुआयामी प्रभाव अधिक महत्वपूर्ण हो जाते हैं, तो ये अंतर बढ़ने के साथ बढ़ जाते हैं .[6]
रेडियल सिस्टम
रेडियल दिशा में तापमान प्रवणता के कारण गोलाकार और बेलनाकार प्रणालियों को एक आयामी माना जा सकता है। मानक विधि का उपयोग स्थिर अवस्था स्थितियों के तहत रेडियल सिस्टम के विश्लेषण के लिए किया जा सकता है, ऊष्मा समीकरण के उचित रूप से आरंभ होता है, या वैकल्पिक विधि, फूरियर के नियम के उपयुक्त रूप से आरंभ होता है। अतिरिक्त ऊष्मा उत्पादन वाली स्थिर स्थिति में एक खोखले सिलिंडर के लिए, ऊष्मा समीकरण का उपयुक्त रूप है [6]
(4)
जहाँ एक चर के रूप में माना जाता है। फूरियर के नियम के उपयुक्त रूप को ध्यान में रखते हुए, उपचार का भौतिक महत्व एक चर के रूप में स्पष्ट हो जाता है जब एक बेलनाकार सतह पर जिस दर से ऊर्जा प्रवाहित होती है, उसे इस रूप में दर्शाया जाता है
(5)
जहाँ वह क्षेत्र है जो उस दिशा के सामान्य है जहां ऊष्मा हस्तांतरण होता है। समीकरण 1 का अर्थ है कि मात्रा त्रिज्या पर निर्भर नहीं है , यह समीकरण 5 से अनुसरण करता है कि ऊष्मा हस्तांतरण दर, रेडियल दिशा में एक स्थिरांक है।
थर्मल चालन में संवहन सतह की स्थिति के साथ खोखले सिलेंडर में तापमान वितरण का निर्धारण करने के लिए, उपयुक्त सीमा स्थितियों को लागू करते हुए समीकरण 4 को हल किया जा सकता है। इस धारणा के साथ कि स्थिर है
(6) निम्नलिखित सीमा स्थितियों का उपयोग करते हुए, स्थिरांक और गणना की जा सकती है और सामान्य समाधान हमें देता है
और के लिए हल करना और और सामान्य समाधान में प्रतिस्थापित करते हुए, हम प्राप्त करते हैं (7)
थंबनेल चित्र के इनसेट में तापमान का लघुगणकीय वितरण आरेखित किया गया है। यह मानते हुए कि तापमान वितरण, समीकरण 7, समीकरण 5 में फूरियर के नियम के साथ प्रयोग किया जाता है, ऊष्मा हस्तांतरण दर को निम्न रूप में व्यक्त किया जा सकता है
अंत में, एक बेलनाकार दीवार में रेडियल चालन के लिए, थर्मल प्रतिरोध का रूप है
यह भी देखें
संदर्भ
- ↑ Jump up to: 1.0 1.1 Lasance, C. J. M. (2008). "Ten Years of Boundary-Condition- Independent Compact Thermal Modeling of Electronic Parts: A Review". Heat Transfer Engineering. 29 (2): 149–168. Bibcode:2008HTrEn..29..149L. doi:10.1080/01457630701673188. S2CID 121803741.
- ↑ Ho-Ming Tong; Yi-Shao Lai; C.P. Wong (2013). Advanced Flip Chip Packaging. Springer Science & Business Media. pp. 460–461. ISBN 978-1-4419-5768-9.
- ↑ Clemens J.M. Lasance; András Poppe (2013). Thermal Management for LED Applications. Springer Science & Business Media. p. 247. ISBN 978-1-4614-5091-7.
- ↑ "Experiment vs. Simulation, Part 3: JESD51-14". 2013-02-22.
- ↑ Schweitzer, D.; Pape, H.; Chen, L.; Kutscherauer, R.; Walder, M. (2011). "Transient dual interface measurement — A new JEDEC standard for the measurement of the junction-to-case thermal resistance". 2011 27th Annual IEEE Semiconductor Thermal Measurement and Management Symposium. p. 222. doi:10.1109/STHERM.2011.5767204. ISBN 978-1-61284-740-5.
- ↑ Jump up to: 6.0 6.1 Incropera, Dewitt, Bergman, Lavine, Frank P., David P., Theodore L., Adrienne S. (2013). Principles of Heat and Mass Transfer. John Wiley & Sons; 7th Edition, Interna edition. ISBN 978-0470646151.
{{cite book}}: CS1 maint: multiple names: authors list (link)
10. K Einalipour, S. Sadeghzadeh, F. Molaei. “Interfacial thermal resistance engineering for polyaniline (C3N)-graphene heterostructure”, The Journal of Physical Chemistry, 2020. DOI:10.1021/acs.jpcc.0c02051
- Michael Lenz, Günther Striedl, Ulrich Fröhler (January 2000) Thermal Resistance, Theory and Practice. Infineon Technologies AG, Munich, Germany.
- Directed Energy, Inc./IXYSRF (March 31, 2003) R Theta And Power Dissipation Technical Note. Ixys RF, Fort Collins, Colorado. Example thermal resistance and power dissipation calculation in semiconductors.
अग्रिम पठन
इस विषय पर बड़ी मात्रा में साहित्य है। सामान्य तौर पर, "थर्मल रेजिस्टेंस" शब्द का उपयोग करने वाले कार्य अधिक इंजीनियरिंग-उन्मुख होते हैं, जबकि शब्द का उपयोग करने वाले कार्य ऊष्मीय चालकता अधिक [शुद्ध-] भौतिकी-उन्मुख हैं। निम्नलिखित पुस्तकें प्रतिनिधि हैं, लेकिन आसानी से प्रतिस्थापित की जा सकती हैं।
- टेरी एम. ट्रिट, ed. (2004). तापीय चालकता: सिद्धांत, गुण और अनुप्रयोग. स्प्रिंगर साइंस एंड बिजनेस मीडिया. ISBN 978-0-306-48327-1.
- यूनुस शबानी (2011). हीट ट्रांसफर: इलेक्ट्रॉनिक्स का थर्मल प्रबंधन. सीआरसी प्रेस. ISBN 978-1-4398-1468-0.
- ज़िंगकुन कॉलिन टोंग (2011). इलेक्ट्रॉनिक पैकेजिंग के थर्मल प्रबंधन के लिए उन्नत सामग्री. स्प्रिंगर साइंस एंड बिजनेस मीडिया. ISBN 978-1-4419-7759-5.
बाहरी संबंध
- गुओपिंग जू (2006), Thermal Management for Electronic Packaging, सन माइक्रोसिस्टम्स
- http://www.electronics-cooling.com/2012/09/update-on-jedec-thermal-standards/
- The importance of Soil Thermal Resistivity for power companies


