नेटवर्क विश्लेषण: Difference between revisions

Revision as of 12:47, 26 August 2022

इलेक्ट्रिकल इंजीनियरिंग और इलेक्ट्रॉनिक्स के संदर्भ में एक नेटवर्क, परस्पर जुड़े घटकों का एक संग्रह है।नेटवर्क विश्लेषण (network analysis) उस प्रक्रिया को कहते हैं जिसमें वोल्टास (voltages) का पता लगाया जाता है। इन मूल्यों की गणना के लिए कई तकनीकें हैं। हालांकि, अधिकांश भाग के लिए, तकनीक रैखिक घटकों को मान लेती है। जहां कहा गया है, इस आलेख में वर्णित विधियां केवल रैखिक नेटवर्क विश्लेषण पर लागू होती हैं।

परिभाषाएँ

{३३३३

      घटक   दो या अधिक टर्मिनल के साथ एक उपकरण जिसमें से धारा प्रवाहित हो सकती है।

     नोड  एक बिंदु जिस पर दो से अधिक घटकों के टर्मिनल जुड़ते हैं। पर्याप्त शून्य प्रतिरोध वाले कंडक्टर को विश्लेषण के उद्देश्य के लिए एक नोड माना जाता है।

    शाखा   दो नोड्स में शामिल होने वाले घटक।

  मेष   एक नेटवर्क के भीतर शाखाओं का एक समूह एक पूर्ण लूप बनाने के लिए शामिल हो गया, जैसे कि इसके अंदर कोई अन्य लूप नहीं है।

  पोर्ट  दो टर्मिनल जहां एक में करंट दूसरे से करंट के समान होता है।

   विद्युत परिपथ (सर्किट)  जनरेटर के एक टर्मिनल से लोड घटक के माध्यम से करंट दूसरे टर्मिनल में वापस होता है। इस अर्थ में, सर्किट एक पोर्ट नेटवर्क है और विश्लेषण करने के लिए छोटा कारक है। यदि किसी अन्य सर्किट से कोई संबंध है तो एक गैर ट्रिपियल नेटवर्क बनाया गया है और कम से कम दो पोर्ट मौजूद होने चाहिए। अक्सर, "विद्युत परिपथ" और "नेटवर्क" का एक-दूसरे के स्थान पर उपयोग किया जाता है, लेकिन कई विश्लेषक "नेटवर्क" को आदर्श घटकों से युक्त एक आदर्श मॉडल के रूप में सुरक्षित रखते हैं।^[1]

    ट्रांसफर फ़ंक्शन  दो पोर्ट के बीच धाराओं और वोल्टेज के संबंध। अक्सर, एक इनपुट पोर्ट और एक आउटपुट पोर्ट पर चर्चा की जाती है और ट्रांसफर फ़ंक्शन को लाभ या सत्यापन के रूप में वर्णित किया जाता है।

 घटक ट्रांसफर फ़ंक्शन दो-टर्मिनल कंपोनेंट (यानी वन-पोर्ट कंपोनेंट) के लिए, करंट और वोल्टेज को इनपुट और आउटपुट के रूप में लिया जाता है और ट्रांसफर फंक्शन में प्रतिबाधा या प्रवेश की इकाइयाँ होंगी (यह आमतौर पर मनमानी सुविधा का मामला है चाहे वोल्टेज हो या करंट को इनपुट माना जाता है)। एक तीन (या अधिक) टर्मिनल घटक में प्रभावी रूप से दो (या अधिक) पोर्ट होते हैं और ट्रांसफर फ़ंक्शन को एकल प्रतिबाधा के रूप में व्यक्त नहीं किया जा सकता है। सामान्य दृष्टिकोण ट्रांसफर फंक्शन को मापदंडों के मैट्रिक्स के रूप में व्यक्त करना है। ये पैरामीटर प्रतिबाधा हो सकते हैं, लेकिन बड़ी संख्या में अन्य दृष्टिकोण हैं (देखें दो-पोर्ट नेटवर्क )।

समकक्ष सर्किट

नेटवर्क विश्लेषण में एक उपयोगी प्रक्रिया घटकों की संख्या को कम करके नेटवर्क को सरल बनाना है। यह एक ही प्रभाव वाले अन्य काल्पनिक घटकों के साथ भौतिक घटकों को प्रतिस्थापित करके किया जा सकता है। एक विशेष तकनीक सीधे घटकों की संख्या को कम कर सकती है, उदाहरण के लिए श्रृंखला में प्रतिबाधाओं को मिलाकर। दूसरी ओर, यह केवल उस रूप को बदल सकता है जिसमें बाद के ऑपरेशन में घटकों को कम किया जा सकता है। उदाहरण के लिए, नॉर्टन के प्रमेय का उपयोग करके एक वोल्टेज जनरेटर को वर्तमान जनरेटर में बदल सकता है ताकि बाद में समानांतर प्रतिबाधा भार के साथ जनरेटर के आंतरिक प्रतिरोध को संयोजित करने में सक्षम हो सके।

एक प्रतिरोधक सर्किट एक सर्किट है जिसमें केवलप्रतिरोध , अनुकूल धारा स्रोत और अनुकूल वोल्टेज स्रोत होते है। यदि स्रोत स्थिर ( DC ) स्रोत हैं, तो परिणाम DC सर्किट है। एक सर्किट के विश्लेषण में सर्किट में मौजूद वोल्टेज और धाराओं को हल करना शामिल है। यहां उल्लिखित समाधान सिद्धांत AC सर्किट के चरण विश्लेषण पर भी लागू होते हैं।

दो सर्किट को टर्मिनलों की एक जोड़ी के संबंध में समकक्ष कहा जाता है, यदि नेटवर्क के लिए टर्मिनलों के माध्यम सेवोल्टेज और धारा का संबंध दूसरे नेटवर्क के टर्मिनलों पर वोल्टेज और करंट के समान होता है।

अगर $V_{2}=V_{1}$ implies $I_{2}=I_{1}$ for all (real) values of $V_{1}$ , फिर टर्मिनलों ab और xy के संबंध में सर्किट 1 और सर्किट 2 बराबर हैं।

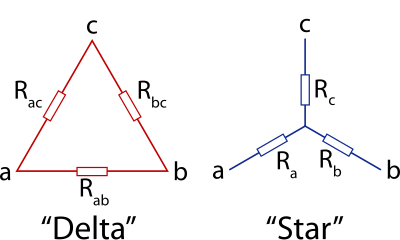
उपरोक्तएक-पोर्ट नेटवर्क के लिए पर्याप्त परिभाषा है। एक से अधिक पोर्ट के लिए, यह परिभाषित किया जाना चाहिए कि संबंधित पोर्ट के सभी जोड़े के बीच धाराओं और वोल्टेज में समान संबंध होना चाहिए। उदाहरण के लिए, स्टार (star) और डेल्टा (delta) नेटवर्क प्रभावी रूप से तीन पोर्ट नेटवर्क हैं और इसलिए उनकी तुल्यता को पूरी तरह से निर्दिष्ट करने के लिए एक साथ तीन समीकरणों की आवश्यकता होती है।

श्रृंखला और समानांतर में प्रतिबाधा

कुछ दो टर्मिनल नेटवर्क के प्रतिबाधा अंततः श्रृंखला में प्रतिबाधा या समानांतर में प्रतिबाधा के लगातार अनुप्रयोगों द्वारा कम किया जा सकता है।

  श्रृंखला  में बाधाएं:  $Z_{\mathrm {eq} }=Z_{1}+Z_{2}+\,\cdots \,+Z_{n}.$

  समानांतर  में बाधाएं:  ${\frac {1}{Z_{\mathrm {eq} }}}={\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}+\,\cdots \,+{\frac {1}{Z_{n}}}.$

समानांतर में केवल दो बाधाओं के लिए उपरोक्त सरल:

Z_{\mathrm {eq} }={\frac {Z_{1}Z_{2}}{Z_{1}+Z_{2}}}.

डेल्टा-वी परिवर्तन

दो से अधिक टर्मिनलों के साथ प्रतिबाधा के एक नेटवर्क को एकल प्रतिबाधा समकक्ष सर्किट में कम नहीं किया जा सकता है। n-टर्मिनल नेटवर्क, सबसे अच्छा, n प्रतिबाधाओं (सबसे खराब nC2) तक कम किया जा सकता है। तीन टर्मिनल नेटवर्क के लिए, तीन बाधाओं को तीन नोड डेल्टा (Δ) नेटवर्क या चार नोड स्टार (वाई) नेटवर्क के रूप में व्यक्त किया जा सकता है। ये दो नेटवर्क समान हैं और उनके बीच परिवर्तन नीचे दिए गए हैं। नोड्स की मनमानी संख्या के साथ एक सामान्य नेटवर्क को केवल श्रृंखला और समानांतर संयोजन का उपयोग करके प्रतिबाधा की न्यूनतम संख्या तक कम नहीं किया जा सकता है। सामान्य तौर पर, Y-Δ और Δ-Y परिवर्तनों का भी उपयोग किया जाना चाहिए। कुछ नेटवर्क के लिए Y-Δ से स्टार-बहुभुज (STAR-POLYGON) परिवर्तनों के विस्तार की भी आवश्यकता हो सकती है।

तुल्यता के लिए, किसी भी जोड़ी टर्मिनलों के बीच प्रतिबाधा दोनों नेटवर्क के लिए समान होना चाहिए, जिसके परिणामस्वरूप तीन एक साथ समीकरणों का एक सेट होता है। नीचे दिए गए समीकरणों को प्रतिरोध के रूप में व्यक्त किया गया है, लेकिन प्रतिबाधा के साथ सामान्य मामले पर समान रूप से लागू होता है।

==== डेल्टा-टू-स्टार परिवर्तन समीकरण ==== $R_{a}={\frac {R_{\mathrm {ac} }R_{\mathrm {ab} }}{R_{\mathrm {ac} }+R_{\mathrm {ab} }+R_{\mathrm {bc} }}}$

$R_{b}={\frac {R_{\mathrm {ab} }R_{\mathrm {bc} }}{R_{\mathrm {ac} }+R_{\mathrm {ab} }+R_{\mathrm {bc} }}}$

$R_{c}={\frac {R_{\mathrm {bc} }R_{\mathrm {ac} }}{R_{\mathrm {ac} }+R_{\mathrm {ab} }+R_{\mathrm {bc} }}}$

==== स्टार-टू-डेल्टा परिवर्तन समीकरण ==== $R_{\mathrm {ac} }={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{b}}}$

$R_{\mathrm {ab} }={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{c}}}$

$R_{\mathrm {bc} }={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{a}}}$

==== डेल्टा-टू-स्टार परिवर्तन समीकरण ==== $R_{a}={\frac {R_{\mathrm {ac} }R_{\mathrm {ab} }}{R_{\mathrm {ac} }+R_{\mathrm {ab} }+R_{\mathrm {bc} }}}$

$R_{b}={\frac {R_{\mathrm {ab} }R_{\mathrm {bc} }}{R_{\mathrm {ac} }+R_{\mathrm {ab} }+R_{\mathrm {bc} }}}$

$R_{c}={\frac {R_{\mathrm {bc} }R_{\mathrm {ac} }}{R_{\mathrm {ac} }+R_{\mathrm {ab} }+R_{\mathrm {bc} }}}$

==== स्टार-टू-डेल्टा परिवर्तन समीकरण ==== $R_{\mathrm {ac} }={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{b}}}$

$R_{\mathrm {ab} }={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{c}}}$

$R_{\mathrm {bc} }={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{a}}}$

नेटवर्क नोड उन्मूलन का सामान्य रूप

स्टार-टू-डेल्टा और सीरीज़-रिजर्वॉटर ट्रांसफॉर्मेशन जनरल रेसिस्टर नेटवर्क नोड एलिमिनेशन एल्गोरिथ्म के विशेष मामले हैं। किसी भी नोड द्वारा जुड़ा हुआ है $N$ रेसिस्टर्स ( $R_{1}$ .. $R_{N}$ ) से नोड 1 से जुड़ा है। N को ${N \choose 2}$ से बदला जा सकता है। रेसिस्टर्स शेष $N$ नोड्स को आपस में जोड़ते हैं। किन्हीं दो नोड्स $x$ और $y$ द्वारा दिया गया है: $R_{\mathrm {xy} }=R_{x}R_{y}\sum _{i=1}^{N}{\frac {1}{R_{i}}}$

एक स्टार-टू-डेल्टा के लिए $N=3$ ) यह कम कर देता है:

$R_{\mathrm {ab} }=R_{a}R_{b}({\frac {1}{R}}_{a}+{\frac {1}{R}}_{b}+{\frac {1}{R}}_{c})={\frac {R_{a}R_{b}(R_{a}R_{b}+R_{a}R_{c}+R_{b}R_{c})}{R_{a}R_{b}R_{c}}}={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{c}}}$

एक श्रृंखला में कमी के लिए $N=2$ ) यह कम कर देता है:

$R_{\mathrm {ab} }=R_{a}R_{b}({\frac {1}{R}}_{a}+{\frac {1}{R}}_{b})={\frac {R_{a}R_{b}(R_{a}+R_{b})}{R_{a}R_{b}}}=R_{a}+R_{b}$ एक झूलने वाले रोकनेवाला के लिए $N=1$ ) it results in the elimination of the resistor because ${1 \choose 2}=0$ ।

स्रोत परिवर्तन

एक आंतरिक प्रतिबाधा (यानी गैर-आदर्श जनरेटर) के साथ एक जनरेटर को एक आदर्श वोल्टेज जनरेटर या एक आदर्श वर्तमान जनरेटर और प्रतिबाधा के रूप में दर्शाया जा सकता है।ये दो रूप समतुल्य हैं और परिवर्तन नीचे दिए गए हैं।यदि दो नेटवर्क टर्मिनलों एबी के संबंध में बराबर हैं, तो वी और मुझे दोनों नेटवर्क के लिए समान होना चाहिए।इस प्रकार, $V_{\mathrm {s} }=RI_{\mathrm {s} }\,\!$ or $I_{\mathrm {s} }={\frac {V_{\mathrm {s} }}{R}}$

नॉर्टन के प्रमेय में कहा गया है कि किसी भी दो-टर्मिनल रैखिक नेटवर्क को एक आदर्श वर्तमान जनरेटर और एक समानांतर प्रतिबाधा में कम किया जा सकता है।
Thévenin के प्रमेय में कहा गया है कि किसी भी दो-टर्मिनल रैखिक नेटवर्क को एक आदर्श वोल्टेज जनरेटर और एक श्रृंखला प्रतिबाधा में कम किया जा सकता है।

सरल नेटवर्क

कुछ बहुत ही सरल नेटवर्क का विश्लेषण अधिक व्यवस्थित दृष्टिकोण को लागू करने की आवश्यकता के बिना किया जा सकता है।

वोल्टेज डिवीजन ऑफ सीरीज़ कंपोनेंट्स

N पर विचार करें जो श्रृंखला में जुड़े हुए हैं।वोल्टेज $V_{i}$ across any impedance $Z_{i}$ है $V_{i}=Z_{i}I=\left({\frac {Z_{i}}{Z_{1}+Z_{2}+\cdots +Z_{n}}}\right)V$

समानांतर घटकों का वर्तमान विभाजन

N प्रवेश पर विचार करें जो समानांतर में जुड़े हुए हैं।द करेंट $I_{i}$ through any admittance $Y_{i}$ है $I_{i}=Y_{i}V=\left({\frac {Y_{i}}{Y_{1}+Y_{2}+\cdots +Y_{n}}}\right)I$

के लिए $i=1,2,...,n.$

==== विशेष मामला: दो समानांतर घटकों का वर्तमान विभाजन ==== $I_{1}=\left({\frac {Z_{2}}{Z_{1}+Z_{2}}}\right)I$

$I_{2}=\left({\frac {Z_{1}}{Z_{1}+Z_{2}}}\right)I$

==== विशेष मामला: दो समानांतर घटकों का वर्तमान विभाजन ==== $I_{1}=\left({\frac {Z_{2}}{Z_{1}+Z_{2}}}\right)I$

$I_{2}=\left({\frac {Z_{1}}{Z_{1}+Z_{2}}}\right)I$

नोडल विश्लेषण

1. सर्किट में सभी नोड्स को लेबल करें। संदर्भ में अव्यवस्थित रूप से किसी भी नोड का चयन करें।

2. संदर्भ के लिए प्रत्येक शेष नोड से परिवर्ती वोल्टेज को परिभाषित करें। इन परिवर्ती वोल्टेज को परिभाषित किया जाना चाहिए क्योंकि संदर्भ नोड के संबंध में वोल्टेज बढ़ता है।

3. संदर्भ को छोड़कर प्रत्येक नोड के लिए KCL समीकरण लिखें।

4. समीकरणों की परिणामी प्रणाली को हल करें।

जाल (Mesh) विश्लेषण

 जाल - एक लूप जिसमें आंतरिक लूप नहीं होता है।

1. सर्किट में "विंडो पैन" की संख्या की गणना करें। प्रत्येक विंडो पैन में एक जाल धारा आबंटित करें।

2. प्रत्येक जाल के लिए KVL समीकरण लिखें जिसकी धारा अज्ञात है।

3. परिणामी समीकरणों को हल करें।

अधिस्थापन

इस पद्धति में, प्रत्येक जनरेटर के प्रभाव की गणना की जाती है। एक के अलावा अन्य सभी जनरेटर को हटा दिया जाता है और या तो वोल्टेज जनरेटर के मामले में शॉर्ट सर्किट या वर्तमान जनरेटर के मामले में सर्किट शुरु किया जाता है। किसी विशेष शाखा के माध्यम से कुल वर्तमान या कुल वोल्टेज की गणना सभी व्यक्तिगत धाराओं या वोल्टेज को जोड़कर की जाती है।

इस पद्धति के लिए एक अंतर्निहित धारणा है कि कुल धारा या वोल्टेज इसके भागों का एक रैखिक अधिस्थापन है। इसलिए, गैर-रैखिक घटक मौजूद होने पर विधि का उपयोग नहीं किया जा सकता है।^[2] रेखीय परिपथों में भी तत्वों द्वारा उपयोग की गई कुल शक्ति का पता लगाने के लिए शक्तियों के अधिस्थापन का उपयोग नहीं किया जा सकता है। कुल वोल्टेज या करंट के वर्ग के अनुसार शक्ति भिन्न होती है और योग का वर्ग आमतौर पर वर्गों के योग के बराबर नहीं होता है। एक तत्व में कुल शक्ति को वोल्टेज और वर्तमान में स्वतंत्र रूप से अधिस्थापन लागू करके और फिर कुल वोल्टेज और वर्तमान से शक्ति की गणना करके पाया जा सकता है।

विधि का चुनाव

विधि का चुनाव^[3] कुछ हद तक अनुभव की बात है। यदि नेटवर्क विशेष रूप से सरल है या केवल एक विशिष्ट धारा या वोल्टेज की आवश्यकता है तो कुछ सरल समकक्ष सर्किटों की पुनरावृत्ति के बिना उत्तर प्राप्त कर सकते हैं।

नोडल विश्लेषण : वोल्टेज चर की संख्या, और इसलिए समीकरणों को हल करने के लिए, नोड्स की संख्या घटा के बराबर है।संदर्भ नोड से जुड़ा प्रत्येक वोल्टेज स्रोत अज्ञात और समीकरणों की संख्या को कम करता है।
मेष विश्लेषण : वर्तमान चर की संख्या, और इसलिए एक साथ समीकरणों को हल करने के लिए, मेषों की संख्या के बराबर है।एक जाल में प्रत्येक वर्तमान स्रोत अज्ञात की संख्या को कम कर देता है।मेष विश्लेषण केवल नेटवर्क के साथ उपयोग किया जा सकता है जिसे प्लानर नेटवर्क के रूप में खींचा जा सकता है, यानी कोई क्रॉसिंग घटकों के साथ^[4]
सुपरपोज़िशन संभवतः सबसे वैचारिक रूप से सरल विधि है, लेकिन तेजी से बड़ी संख्या में समीकरणों और गन्दी प्रतिबाधा संयोजनों की ओर जाता है क्योंकि नेटवर्क बड़ा हो जाता है।
प्रभावी मध्यम अनुमान : यादृच्छिक प्रतिरोधों के उच्च घनत्व से युक्त एक नेटवर्क के लिए, प्रत्येक व्यक्तिगत तत्व के लिए एक सटीक समाधान अव्यावहारिक या असंभव हो सकता है।इसके बजाय, प्रभावी प्रतिरोध और वर्तमान वितरण गुणों को ग्राफ उपायों और नेटवर्क के ज्यामितीय गुणों के संदर्भ में मॉडल किया जा सकता है^[5]

स्थानांतरण समारोह

ट्रांसफर फ़ंक्शन  एक इनपुट और नेटवर्क के आउटपुट के बीच संबंध को व्यक्त करता है। प्रतिरोधक नेटवर्क के लिए, यह हमेशा एक साधारण वास्तविक संख्या या एक अभिव्यक्ति होगी जो एक वास्तविक संख्या तक उबालती है। प्रतिरोधक नेटवर्क को एक साथ बीजगणितीय समीकरणों की एक प्रणाली द्वारा दर्शाया जाता है। हालांकि, रैखिक नेटवर्क के सामान्य मामले में, नेटवर्क को एक साथ रैखिक अंतर समीकरणों की एक प्रणाली द्वारा दर्शाया जाता है। नेटवर्क विश्लेषण में, सीधे अंतर समीकरणों का उपयोग करने के बजाय, यह सामान्य अभ्यास है कि वे पहले  लाप्लास को  ट्रांसफॉर्म करें और फिर लाप्लास पैरामीटर एस के संदर्भ में परिणाम व्यक्त करें, जो सामान्य रूप से    कॉम्प्लेक्स  है । इसे  एस-डोमेन  में काम करने के रूप में वर्णित किया गया है। समीकरणों के साथ काम करना सीधे समय (या टी) डोमेन में काम करने के रूप में वर्णित किया जाएगा क्योंकि परिणाम अलग -अलग मात्राओं के रूप में व्यक्त किए जाएंगे। लाप्लास रूपांतरण एस-डोमेन और टी-डोमेन के बीच बदलने की गणितीय विधि है।

यह दृष्टिकोण नियंत्रण सिद्धांत में मानक है और एक प्रणाली के स्थिरता का निर्धारण करने के लिए उपयोगी है, उदाहरण के लिए, प्रतिक्रिया के साथ एक एम्पलीफायर में।

दो टर्मिनल घटक हस्तांतरण कार्य

दो टर्मिनल घटकों के लिए स्थानांतरण फ़ंक्शन, या अधिक आम तौर पर गैर-रैखिक तत्वों के लिए, संवैधानिक समीकरण , डिवाइस के वर्तमान इनपुट और इसके पार परिणामी वोल्टेज के बीच संबंध है।ट्रांसफर फ़ंक्शन, z (s), इस प्रकार प्रतिबाधा & nbsp; - ओम्स की इकाइयाँ होंगी।विद्युत नेटवर्क में पाए जाने वाले तीन निष्क्रिय घटकों के लिए, स्थानांतरण कार्य हैं; {३३३३

|  -
|  रोकनेवाला |  $Z(s)=R\,\!$

| -

|  प्रारंभ करनेवाला |  $Z(s)=sL\,\!$

| -

|  कैपेसिटर |  $Z(s)={\frac {1}{sC}}$

| }

एक नेटवर्क के लिए, जिसमें केवल स्थिर एसी सिग्नल लागू होते हैं, एस को J and और AC नेटवर्क सिद्धांत परिणाम से अधिक परिचित मानों से बदल दिया जाता है।

{३३३३

|  -
|  रोकनेवाला |  $Z(j\omega )=R\,\!$

| -

|  प्रारंभ करनेवाला |  $Z(j\omega )=j\omega L\,\!$

| -

|  कैपेसिटर |  $Z(j\omega )={\frac {1}{j\omega C}}$

| }

अंत में, एक नेटवर्क के लिए जिसमें केवल स्थिर डीसी लागू किया जाता है, एस को शून्य से बदल दिया जाता है और डीसी नेटवर्क सिद्धांत लागू होता है।

{३३३३

|  -
|  रोकनेवाला |  $Z=R\,\!$

| -

|  प्रारंभ करनेवाला |  $Z=0\,\!$

| -

|  कैपेसिटर |  $Z=\infty \,\!$

| }

दो पोर्ट नेटवर्क ट्रांसफर फ़ंक्शन =

ट्रांसफर फ़ंक्शंस, सामान्य रूप से, नियंत्रण सिद्धांत में प्रतीक H (s) दिया जाता है।आमतौर पर इलेक्ट्रॉनिक्स में, ट्रांसफर फ़ंक्शन को इनपुट वोल्टेज के आउटपुट वोल्टेज के अनुपात के रूप में परिभाषित किया जाता है और प्रतीक A (s), या अधिक सामान्यतः दिया जाता है (क्योंकि विश्लेषण साइन वेव प्रतिक्रिया के संदर्भ में हमेशा किया जाता है), a (jω), इसलिएवह;

$A(j\omega )={\frac {V_{o}}{V_{i}}}$

संदर्भ के आधार पर क्षीणन, या प्रवर्धन के लिए ए स्टैंडिंग।सामान्य तौर पर, यह J ‘ का एक जटिल कार्य होगा, जिसे नेटवर्क में बाधाओं के विश्लेषण और उनके व्यक्तिगत हस्तांतरण कार्यों से प्राप्त किया जा सकता है।कभी -कभी विश्लेषक केवल लाभ के परिमाण में रुचि रखते हैं न कि चरण कोण।इस मामले में जटिल संख्याओं को स्थानांतरण फ़ंक्शन से समाप्त किया जा सकता है और इसे तब लिखा जा सकता है;

$A(\omega )=\left|{\frac {V_{o}}{V_{i}}}\right|$

दो पोर्ट पैरामीटर

दो-पोर्ट नेटवर्क की अवधारणा नेटवर्क विश्लेषण में ब्लैक बॉक्स के विश्लेषण के लिए उपयोगी हो सकती है। एक बड़े नेटवर्क में दो-पोर्ट नेटवर्क के व्यवहार को पूरी तरह से आंतरिक संरचना के बारे में कुछ भी बताए बिना पूरी तरह से चित्रित किया जा सकता है। हालांकि, ऐसा करने के लिए ऊपर वर्णित A (J and) की तुलना में अधिक जानकारी होना आवश्यक है। यह दिखाया जा सकता है कि दो-पोर्ट नेटवर्क को पूरी तरह से चिह्नित करने के लिए ऐसे चार मापदंडों की आवश्यकता होती है। ये फॉरवर्ड ट्रांसफर फ़ंक्शन हो सकते हैं, इनपुट प्रतिबाधा, रिवर्स ट्रांसफर फ़ंक्शन (यानी, इनपुट पर दिखाई देने वाला वोल्टेज जब आउटपुट पर एक वोल्टेज लागू होता है) और आउटपुट प्रतिबाधा। कई अन्य हैं (एक पूर्ण सूची के लिए मुख्य लेख देखें), इनमें से एक सभी चार मापदंडों को प्रतिबाधा के रूप में व्यक्त करता है। मैट्रिक्स के रूप में चार मापदंडों को व्यक्त करना सामान्य है;

<गणित> \ {bmatrix} शुरू करें

 V_1 \\
 V_0

\ अंत {bmatrix} = \ {bmatrix} शुरू करें

 z (j \ omega) _ {11} & z (j \ omega) _ {12} \\
 z (j \ omega) _ {21} & z (j \ omega) _ {22}

\ अंत {bmatrix} \ {bmatrix} शुरू करें

 I_1 \\
 I_0

\ अंत {bmatrix} </गणित>

मैट्रिक्स को एक प्रतिनिधि तत्व के लिए संक्षिप्त किया जा सकता है;

$\left[z(j\omega )\right]$ or just $\left[z\right]$

ये अवधारणाएं दो से अधिक बंदरगाहों के नेटवर्क तक बढ़ाने में सक्षम हैं। हालांकि, यह वास्तव में शायद ही कभी किया जाता है, क्योंकि कई व्यावहारिक मामलों में, बंदरगाहों को विशुद्ध रूप से इनपुट या विशुद्ध रूप से आउटपुट माना जाता है। यदि रिवर्स दिशा हस्तांतरण कार्यों को नजरअंदाज कर दिया जाता है, तो एक मल्टी-पोर्ट नेटवर्क को हमेशा दो-पोर्ट नेटवर्क की संख्या में विघटित किया जा सकता है।

वितरित घटक =

जहां एक नेटवर्क असतत घटकों से बना है, दो-पोर्ट नेटवर्क का उपयोग करके विश्लेषण पसंद का मामला है, आवश्यक नहीं है। नेटवर्क को हमेशा वैकल्पिक रूप से इसके व्यक्तिगत घटक हस्तांतरण कार्यों के संदर्भ में विश्लेषण किया जा सकता है। हालांकि, यदि किसी नेटवर्क में डिस्ट्रिब्यूटेड घटक होते हैं, जैसे कि ट्रांसमिशन लाइन के मामले में, तो व्यक्तिगत घटकों के संदर्भ में विश्लेषण करना संभव नहीं है क्योंकि वे मौजूद नहीं हैं। इसके लिए सबसे आम दृष्टिकोण लाइन को दो-पोर्ट नेटवर्क के रूप में मॉडल करना है और इसे दो-पोर्ट मापदंडों (या उनके बराबर कुछ) का उपयोग करके चिह्नित करना है। इस तकनीक का एक और उदाहरण एक उच्च आवृत्ति ट्रांजिस्टर में आधार क्षेत्र को पार करने वाले वाहक को मॉडलिंग कर रहा है। आधार क्षेत्र को गांठ वाले घटकों के बजाय वितरित प्रतिरोध और समाई के रूप में तैयार किया जाना है।

छवि विश्लेषण =

ट्रांसमिशन लाइनें और कुछ प्रकार के फ़िल्टर डिज़ाइन उनके स्थानांतरण मापदंडों को निर्धारित करने के लिए छवि विधि का उपयोग करते हैं।इस पद्धति में, समान नेटवर्क की एक असीम रूप से लंबे कैस्केड कनेक्टेड श्रृंखला के व्यवहार पर विचार किया जाता है।इनपुट और आउटपुट प्रतिबाधा और आगे और रिवर्स ट्रांसमिशन फ़ंक्शंस की गणना इस असीम रूप से लंबी श्रृंखला के लिए की जाती है।हालांकि प्राप्त किए गए सैद्धांतिक मूल्यों को कभी भी महसूस नहीं किया जा सकता हैव्यवहार में, कई मामलों में वे एक परिमित श्रृंखला के व्यवहार के लिए एक बहुत अच्छे सन्निकटन के रूप में काम करते हैं जब तक कि यह बहुत छोटा नहीं है।

दो पोर्ट पैरामीटर

दो-पोर्ट नेटवर्क की अवधारणा नेटवर्क विश्लेषण में ब्लैक बॉक्स के विश्लेषण के लिए उपयोगी हो सकती है। एक बड़े नेटवर्क में दो-पोर्ट नेटवर्क के व्यवहार को पूरी तरह से आंतरिक संरचना के बारे में कुछ भी बताए बिना पूरी तरह से चित्रित किया जा सकता है। हालांकि, ऐसा करने के लिए ऊपर वर्णित A (J and) की तुलना में अधिक जानकारी होना आवश्यक है। यह दिखाया जा सकता है कि दो-पोर्ट नेटवर्क को पूरी तरह से चिह्नित करने के लिए ऐसे चार मापदंडों की आवश्यकता होती है। ये फॉरवर्ड ट्रांसफर फ़ंक्शन हो सकते हैं, इनपुट प्रतिबाधा, रिवर्स ट्रांसफर फ़ंक्शन (यानी, इनपुट पर दिखाई देने वाला वोल्टेज जब आउटपुट पर एक वोल्टेज लागू होता है) और आउटपुट प्रतिबाधा। कई अन्य हैं (एक पूर्ण सूची के लिए मुख्य लेख देखें), इनमें से एक सभी चार मापदंडों को प्रतिबाधा के रूप में व्यक्त करता है। मैट्रिक्स के रूप में चार मापदंडों को व्यक्त करना सामान्य है;

<गणित> \ {bmatrix} शुरू करें

 V_1 \\
 V_0

\ अंत {bmatrix} = \ {bmatrix} शुरू करें

 z (j \ omega) _ {11} & z (j \ omega) _ {12} \\
 z (j \ omega) _ {21} & z (j \ omega) _ {22}

\ अंत {bmatrix} \ {bmatrix} शुरू करें

 I_1 \\
 I_0

\ अंत {bmatrix} </गणित>

मैट्रिक्स को एक प्रतिनिधि तत्व के लिए संक्षिप्त किया जा सकता है;

$\left[z(j\omega )\right]$ or just $\left[z\right]$

ये अवधारणाएं दो से अधिक बंदरगाहों के नेटवर्क तक बढ़ाने में सक्षम हैं।हालांकि, यह वास्तव में शायद ही कभी किया जाता है, क्योंकि कई व्यावहारिक मामलों में, बंदरगाहों को विशुद्ध रूप से इनपुट या विशुद्ध रूप से आउटपुट माना जाता है।यदि रिवर्स दिशा हस्तांतरण कार्यों को नजरअंदाज कर दिया जाता है, तो एक मल्टी-पोर्ट नेटवर्क को हमेशा दो-पोर्ट नेटवर्क की संख्या में विघटित किया जा सकता है।

वितरित घटक =

जहां एक नेटवर्क असतत घटकों से बना है, दो-पोर्ट नेटवर्क का उपयोग करके विश्लेषण पसंद का मामला है, आवश्यक नहीं है।नेटवर्क को हमेशा वैकल्पिक रूप से इसके व्यक्तिगत घटक हस्तांतरण कार्यों के संदर्भ में विश्लेषण किया जा सकता है।हालांकि, यदि किसी नेटवर्क में डिस्ट्रिब्यूटेड घटक होते हैं, जैसे कि ट्रांसमिशन लाइन के मामले में, तो व्यक्तिगत घटकों के संदर्भ में विश्लेषण करना संभव नहीं है क्योंकि वे मौजूद नहीं हैं।इसके लिए सबसे आम दृष्टिकोण लाइन को दो-पोर्ट नेटवर्क के रूप में मॉडल करना है और इसे दो-पोर्ट मापदंडों (या उनके बराबर कुछ) का उपयोग करके चिह्नित करना है।इस तकनीक का एक और उदाहरण एक उच्च आवृत्ति ट्रांजिस्टर में आधार क्षेत्र को पार करने वाले वाहक को मॉडलिंग कर रहा है।आधार क्षेत्र को गांठ वाले घटकों के बजाय वितरित प्रतिरोध और समाई के रूप में तैयार किया जाना है।

छवि विश्लेषण =

ट्रांसमिशन लाइनें और कुछ प्रकार के फ़िल्टर डिज़ाइन उनके स्थानांतरण मापदंडों को निर्धारित करने के लिए छवि विधि का उपयोग करते हैं।इस पद्धति में, समान नेटवर्क की एक असीम रूप से लंबे कैस्केड कनेक्टेड श्रृंखला के व्यवहार पर विचार किया जाता है।इनपुट और आउटपुट प्रतिबाधा और आगे और रिवर्स ट्रांसमिशन फ़ंक्शंस की गणना इस असीम रूप से लंबी श्रृंखला के लिए की जाती है।यद्यपि प्राप्त किए गए सैद्धांतिक मूल्यों को कभी भी व्यवहार में वास्तव में महसूस नहीं किया जा सकता है, कई मामलों में वे एक परिमित श्रृंखला के व्यवहार के लिए एक बहुत अच्छे सन्निकटन के रूप में काम करते हैं जब तक कि यह बहुत छोटा नहीं है।

गैर-रैखिक नेटवर्क

अधिकांश इलेक्ट्रॉनिक डिजाइन वास्तव में, गैर-रैखिक हैं।बहुत कम हैं जिनमें कुछ अर्धचालक उपकरण शामिल नहीं हैं।ये हमेशा गैर-रैखिक हैं, एक आदर्श अर्धचालक पी-एन जंक्शन का स्थानांतरण कार्य बहुत गैर-रैखिक संबंध द्वारा दिया गया है; $i=I_{o}(e^{\frac {v}{V_{T}}}-1)$

कहाँ पे;

I और V तात्कालिक वर्तमान और वोल्टेज हैं।
I <सब> o एक मनमाना पैरामीटर है जिसे रिवर्स लीकेज करंट कहा जाता है जिसका मूल्य डिवाइस के निर्माण पर निर्भर करता है।
V <सब> t तापमान के लिए एक पैरामीटर आनुपातिक है जिसे थर्मल वोल्टेज कहा जाता है और कमरे के तापमान पर लगभग 25mv के बराबर होता है।

कई अन्य तरीके हैं जो एक नेटवर्क में गैर-रैखिकता दिखाई दे सकते हैं।रैखिक सुपरपोजिशन का उपयोग करने वाले सभी तरीके विफल हो जाएंगे जब गैर-रैखिक घटक मौजूद होंगे।गैर-रैखिकता से निपटने के लिए कई विकल्प हैं जो सर्किट के प्रकार के आधार पर और विश्लेषक प्राप्त करना चाहते हैं।

संवैधानिक समीकरण

उपरोक्त डायोड समीकरण एक तत्व संवैधानिक समीकरण सामान्य रूप का एक उदाहरण है, $f(v,i)=0\,$

यह एक गैर-रैखिक अवरोधक के रूप में सोचा जा सकता है।गैर-रैखिक इंडिक्टर और कैपेसिटर के लिए संबंधित संवैधानिक समीकरण क्रमशः हैं; $f(v,\varphi )=0\,$ $f(v,q)=0\,$

जहां f कोई मनमाना कार्य है, 'संग्रहीत चुंबकीय प्रवाह है और' 'q' 'संग्रहीत आवेश है।

अस्तित्व, विशिष्टता और स्थिरता

गैर-रैखिक विश्लेषण में एक महत्वपूर्ण विचार विशिष्टता का सवाल है। रैखिक घटकों से बना एक नेटवर्क के लिए हमेशा एक होगा, और केवल एक, सीमा स्थितियों के दिए गए सेट के लिए अद्वितीय समाधान होगा। यह हमेशा गैर-रैखिक सर्किट में मामला नहीं है। उदाहरण के लिए, एक निश्चित वर्तमान के साथ एक रैखिक अवरोधक उस पर लागू होता है, इसके पार वोल्टेज के लिए केवल एक समाधान होता है। दूसरी ओर, गैर-रैखिक टनल डायोड में किसी दिए गए करंट के लिए वोल्टेज के लिए तीन समाधान हैं। यही है, डायोड के माध्यम से वर्तमान के लिए एक विशेष समाधान अद्वितीय नहीं है, अन्य हो सकते हैं, समान रूप से मान्य हो सकते हैं। कुछ मामलों में कोई समाधान नहीं हो सकता है: समाधान के अस्तित्व के प्रश्न पर विचार किया जाना चाहिए।

एक और महत्वपूर्ण विचार स्थिरता का सवाल है। एक विशेष समाधान मौजूद हो सकता है, लेकिन यह स्थिर नहीं हो सकता है, तेजी से उस बिंदु से थोड़ी सी उत्तेजना पर प्रस्थान कर सकता है। यह दिखाया जा सकता है कि एक नेटवर्क जो सभी स्थितियों के लिए बिल्कुल स्थिर है, में एक होना चाहिए, और केवल एक, शर्तों के प्रत्येक सेट के लिए समाधान^[6]

तरीके

स्विचिंग नेटवर्क का बूलियन विश्लेषण

एक स्विचिंग डिवाइस वह है जहां दो विपरीत राज्यों का उत्पादन करने के लिए गैर-रैखिकता का उपयोग किया जाता है। उदाहरण के लिए, डिजिटल सर्किट में सीएमओएस डिवाइस, उनके आउटपुट को सकारात्मक या नकारात्मक आपूर्ति रेल से जुड़े होते हैं और डिवाइस स्विच करने पर एक क्षणिक अवधि के दौरान बीच में कभी भी कुछ भी नहीं पाया जाता है। यहां गैर-रैखिकता को चरम पर डिज़ाइन किया गया है, और विश्लेषक उस तथ्य का लाभ उठा सकते हैं। इस प्रकार के नेटवर्क का विश्लेषण बूलियन बीजगणित का उपयोग करके दो राज्यों (ऑन / ऑफ, पॉजिटिव / नेगेटिव या जो कुछ भी राज्यों का उपयोग किया जा रहा है) का उपयोग करके किया जा सकता है।

इस विश्लेषण में संक्रमणों को नजरअंदाज कर दिया जाता है, साथ ही डिवाइस की स्थिति और नाममात्र की स्थिति के बीच किसी भी मामूली विसंगति के साथ एक बूलियन मूल्य को सौंपा गया है। उदाहरण के लिए, बूलियन 1 को +5V की स्थिति में सौंपा जा सकता है। डिवाइस का आउटपुट +4.5V हो सकता है लेकिन विश्लेषक अभी भी इसे बूलियन 1 मानता है। डिवाइस निर्माता आमतौर पर अपनी डेटा शीट में मानों की एक श्रृंखला को निर्दिष्ट करेंगे जिन्हें अपरिभाषित माना जाता है (यानी परिणाम अप्रत्याशित होगा)।

संक्रमण पूरी तरह से विश्लेषक के लिए निर्बाध नहीं हैं। स्विचिंग की अधिकतम दर एक राज्य से दूसरे राज्य में संक्रमण की गति से निर्धारित होती है। विश्लेषक के लिए खुशी की बात है, कई उपकरणों के लिए अधिकांश संक्रमण उपकरणों के रैखिक भाग में होता है, ट्रांसफर फ़ंक्शन और रैखिक विश्लेषण को कम से कम अनुमानित उत्तर प्राप्त करने के लिए लागू किया जा सकता है।

यह गणितीय रूप से बूलियन बीजगणित एस प्राप्त करना संभव है, जिनमें दो से अधिक राज्य हैं। इलेक्ट्रॉनिक्स में इन के लिए बहुत अधिक उपयोग नहीं किया गया है, हालांकि तीन-राज्य उपकरणों को सामान्य रूप से आम है।

पूर्वाग्रह और संकेत विश्लेषण का पृथक्करण

इस तकनीक का उपयोग किया जाता है जहां सर्किट का संचालन अनिवार्य रूप से रैखिक होना है, लेकिन इसे लागू करने के लिए उपयोग किए जाने वाले उपकरण गैर-रैखिक हैं। एक ट्रांजिस्टर एम्पलीफायर इस तरह के नेटवर्क का एक उदाहरण है। इस तकनीक का सार विश्लेषण को दो भागों में अलग करना है। सबसे पहले, डीसी पूर्वाग्रह का विश्लेषण कुछ गैर-रैखिक विधि का उपयोग करके किया जाता है। यह सर्किट के quiescent ऑपरेटिंग बिंदु स्थापित करता है। दूसरे, सर्किट के छोटे सिग्नल विशेषताओं का रेखीय नेटवर्क विश्लेषण का उपयोग करके विश्लेषण किया जाता है। इन दोनों चरणों के लिए उपयोग किए जा सकने वाले तरीकों के उदाहरण नीचे दिए गए हैं।

डीसी विश्लेषण की ग्राफिकल विधि =

एक महान कई सर्किट डिजाइनों में, डीसी पूर्वाग्रह को एक अवरोधक (या संभवतः प्रतिरोधों का एक नेटवर्क) के माध्यम से एक गैर-रैखिक घटक को खिलाया जाता है। चूंकि प्रतिरोध रैखिक घटक हैं, इसलिए इसके स्थानांतरण फ़ंक्शन के एक ग्राफ से गैर-रैखिक डिवाइस के quiescent ऑपरेटिंग बिंदु को निर्धारित करना विशेष रूप से आसान है। विधि निम्नानुसार है: रैखिक नेटवर्क विश्लेषण से आउटपुट ट्रांसफर फ़ंक्शन (जो आउटपुट करंट के खिलाफ आउटपुट वोल्टेज है) की गणना रोकनेवाला (एस) के नेटवर्क के लिए की जाती है और उन्हें ड्राइविंग करने वाले जनरेटर। यह एक सीधी रेखा होगी (जिसे लोड लाइन कहा जाता है) और गैर-रेखीय डिवाइस के ट्रांसफर फ़ंक्शन प्लॉट पर आसानी से सुपरिम्पोज किया जा सकता है। वह बिंदु जहां लाइन्स क्रॉस क्विसेस ऑपरेटिंग पॉइंट है।

शायद सबसे आसान व्यावहारिक विधि (रैखिक) नेटवर्क ओपन सर्किट वोल्टेज और शॉर्ट सर्किट करंट की गणना करना है और इन्हें गैर-रैखिक डिवाइस के ट्रांसफर फ़ंक्शन पर प्लॉट करना है। इन दो बिंदुओं में शामिल होने वाली सीधी रेखा नेटवर्क का स्थानांतरण फ़ंक्शन है।

वास्तव में, सर्किट का डिजाइनर उस वर्णित के लिए रिवर्स दिशा में आगे बढ़ेगा। गैर-रैखिक डिवाइस के लिए निर्माताओं डेटा शीट में प्रदान किए गए एक भूखंड से शुरू, डिजाइनर वांछित ऑपरेटिंग बिंदु का चयन करेगा और फिर इसे प्राप्त करने के लिए आवश्यक रैखिक घटक मानों की गणना करेगा।

इस पद्धति का उपयोग करना अभी भी संभव है यदिडिवाइस के पक्षपाती होने के कारण इसका पूर्वाग्रह एक अन्य डिवाइस के माध्यम से खिलाया जाता है जो स्वयं गैर-रैखिक & nbsp;-उदाहरण के लिए एक डायोड है।हालांकि इस मामले में, डिवाइस पर नेटवर्क ट्रांसफर फ़ंक्शन का प्लॉट अब एक सीधी रेखा नहीं होगी और परिणामस्वरूप करने के लिए अधिक थकाऊ है।

छोटा सिग्नल समकक्ष सर्किट

इस विधि का उपयोग किया जा सकता है, जहां एक नेटवर्क में इनपुट और आउटपुट सिग्नल का विचलन गैर-रेखीय उपकरणों के स्थानांतरण फ़ंक्शन के एक पर्याप्त रैखिक हिस्से के भीतर रहता है, या फिर इतने छोटे होते हैं कि स्थानांतरण फ़ंक्शन के वक्र को रैखिक माना जा सकता है। इन विशिष्ट स्थितियों के एक सेट के तहत, गैर-रैखिक उपकरण को एक समान रैखिक नेटवर्क द्वारा दर्शाया जा सकता है। यह याद रखना चाहिए कि यह समकक्ष सर्किट पूरी तरह से उल्लेखनीय है और केवल छोटे सिग्नल विचलन के लिए मान्य है। यह डिवाइस के डीसी बायसिंग के लिए पूरी तरह से अनुचित है।

एक साधारण दो-टर्मिनल डिवाइस के लिए, छोटे सिग्नल समतुल्य सर्किट दो घटकों से अधिक नहीं हो सकते हैं। ऑपरेटिंग पॉइंट (जिसे डायनेमिक रेजिस्टेंस कहा जाता है) पर V/I वक्र के ढलान के बराबर एक प्रतिरोध, और वक्र के लिए स्पर्शरेखा। एक जनरेटर, क्योंकि यह स्पर्शरेखा, सामान्य रूप से, मूल से गुजरती नहीं होगी। अधिक टर्मिनलों के साथ, अधिक जटिल समकक्ष सर्किट की आवश्यकता होती है।

ट्रांजिस्टर निर्माताओं के बीच छोटे सिग्नल समतुल्य सर्किट को निर्दिष्ट करने का एक लोकप्रिय रूप दो-पोर्ट नेटवर्क मापदंडों का उपयोग करना है, जिन्हें [एच] पैरामीटर के रूप में जाना जाता है। ये [z] मापदंडों के साथ चार मापदंडों का एक मैट्रिक्स है, लेकिन [एच] मापदंडों के मामले में वे बाधाओं, प्रवेश, वर्तमान लाभ और वोल्टेज लाभ का एक संकर मिश्रण हैं। इस मॉडल में तीन टर्मिनल ट्रांजिस्टर को दो पोर्ट नेटवर्क माना जाता है, इसका एक टर्मिनल दोनों बंदरगाहों के लिए आम है। [एच] पैरामीटर काफी अलग हैं, जिसके आधार पर टर्मिनल को आम के रूप में चुना जाता है। ट्रांजिस्टर के लिए सबसे महत्वपूर्ण पैरामीटर आमतौर पर कॉमन एमिटर कॉन्फ़िगरेशन में आगे वर्तमान लाभ, एच <सब> 21 है। यह डेटा शीट पर H _Fe नामित किया गया है।

दो-पोर्ट मापदंडों के संदर्भ में छोटे सिग्नल समतुल्य सर्किट पर निर्भर जनरेटर की अवधारणा की ओर जाता है। यही है, एक वोल्टेज या वर्तमान जनरेटर का मान सर्किट में एक वोल्टेज या वर्तमान में अन्य जगह पर रैखिक रूप से निर्भर करता है। उदाहरण के लिए [z] पैरामीटर मॉडल इस आरेख में दिखाए गए अनुसार वोल्टेज जनरेटर पर निर्भर करता है;

दिखा रहा है

हमेशा दो-पोर्ट पैरामीटर समतुल्य सर्किट में निर्भर जनरेटर होंगे। यह [एच] मापदंडों के साथ -साथ [z] और किसी अन्य प्रकार पर भी लागू होता है। बड़े रैखिक नेटवर्क विश्लेषण में समीकरणों को विकसित करते समय इन निर्भरता को संरक्षित किया जाना चाहिए।

टुकड़े टुकड़े रैखिक विधि

इस विधि में, गैर-रैखिक डिवाइस का स्थानांतरण फ़ंक्शन क्षेत्रों में टूट गया है। इनमें से प्रत्येक क्षेत्र एक सीधी रेखा द्वारा अनुमानित है। इस प्रकार, स्थानांतरण फ़ंक्शन एक विशेष बिंदु तक रैखिक होगा जहां एक असंतोष होगा। इस बिंदु से पहले स्थानांतरण फ़ंक्शन फिर से रैखिक होगा लेकिन एक अलग ढलान के साथ।

इस पद्धति का एक प्रसिद्ध अनुप्रयोग एक पीएन जंक्शन डायोड के स्थानांतरण फ़ंक्शन का अनुमान है। एक आदर्श डायोड का स्थानांतरण फ़ंक्शन इस (गैर-रैखिक) अनुभाग के शीर्ष पर दिया गया है। हालांकि, इस सूत्र का उपयोग शायद ही कभी नेटवर्क विश्लेषण में किया जाता है, इसके बजाय एक टुकड़े -टुकड़े सन्निकटन का उपयोग किया जा रहा है। यह देखा जा सकता है कि डायोड वर्तमान तेजी से कम हो जाता है -i <सब> o जैसा कि वोल्टेज गिरता है। यह वर्तमान, अधिकांश उद्देश्यों के लिए, इतना छोटा है कि इसे नजरअंदाज किया जा सकता है। बढ़ते वोल्टेज के साथ, वर्तमान तेजी से बढ़ता है। डायोड को घातीय वक्र के घुटने तक एक खुले सर्किट के रूप में तैयार किया गया है, फिर इस बिंदु के रूप में पिछलेअर्धचालक सामग्री के बल्क प्रतिरोध के बराबर एक अवरोधक।

संक्रमण बिंदु वोल्टेज के लिए आमतौर पर स्वीकृत मान सिलिकॉन उपकरणों के लिए 0.7V और जर्मेनियम उपकरणों के लिए 0.3V हैं। डायोड का एक और भी सरल मॉडल, जिसे कभी -कभी स्विचिंग एप्लिकेशन में उपयोग किया जाता है, आगे के वोल्टेज के लिए शॉर्ट सर्किट है और रिवर्स वोल्टेज के लिए ओपन सर्किट है।

एक आगे के पक्षपाती पीएन जंक्शन का मॉडल लगभग निरंतर 0.7V है, जो एम्पलीफायर डिजाइन में ट्रांजिस्टर बेस-एमिटर जंक्शन वोल्टेज के लिए एक बहुत उपयोग किया जाता है।

टुकड़े टुकड़े विधि उस रैखिक नेटवर्क विश्लेषण तकनीकों में छोटे सिग्नल विधि के समान है, केवल तभी लागू किया जा सकता है जब सिग्नल कुछ सीमाओं के भीतर रहता है। यदि सिग्नल एक असंतोष बिंदु को पार करता है तो मॉडल अब रैखिक विश्लेषण उद्देश्यों के लिए मान्य नहीं है। मॉडल को छोटे सिग्नल पर लाभ होता है, हालांकि, यह सिग्नल और डीसी पूर्वाग्रह के लिए समान रूप से लागू होता है। इसलिए इन दोनों का एक ही संचालन में विश्लेषण किया जा सकता है और रैखिक रूप से सुपरइम्पोज़ेबल होगा।

स्विचिंग नेटवर्क का बूलियन विश्लेषण

एक स्विचिंग डिवाइस वह है जहां दो विपरीत राज्यों का उत्पादन करने के लिए गैर-रैखिकता का उपयोग किया जाता है। उदाहरण के लिए, डिजिटल सर्किट में सीएमओएस डिवाइस, उनके आउटपुट को सकारात्मक या नकारात्मक आपूर्ति रेल से जुड़े होते हैं और डिवाइस स्विच करने पर एक क्षणिक अवधि के दौरान बीच में कभी भी कुछ भी नहीं पाया जाता है। यहां गैर-रैखिकता को चरम पर डिज़ाइन किया गया है, और विश्लेषक उस तथ्य का लाभ उठा सकते हैं। इस प्रकार के नेटवर्क का विश्लेषण बूलियन बीजगणित का उपयोग करके दो राज्यों (ऑन / ऑफ, पॉजिटिव / नेगेटिव या जो कुछ भी राज्यों का उपयोग किया जा रहा है) का उपयोग करके किया जा सकता है।

इस विश्लेषण में संक्रमणों को नजरअंदाज कर दिया जाता है, साथ ही डिवाइस की स्थिति और नाममात्र की स्थिति के बीच किसी भी मामूली विसंगति के साथ एक बूलियन मूल्य को सौंपा गया है। उदाहरण के लिए, बूलियन 1 को +5V की स्थिति में सौंपा जा सकता है। डिवाइस का आउटपुट +4.5V हो सकता है लेकिन विश्लेषक अभी भी इसे बूलियन 1 मानता है। डिवाइस निर्माता आमतौर पर अपनी डेटा शीट में मानों की एक श्रृंखला को निर्दिष्ट करेंगे जिन्हें अपरिभाषित माना जाता है (यानी परिणाम अप्रत्याशित होगा)।

संक्रमण पूरी तरह से विश्लेषक के लिए निर्बाध नहीं हैं। स्विचिंग की अधिकतम दर एक राज्य से दूसरे राज्य में संक्रमण की गति से निर्धारित होती है। विश्लेषक के लिए खुशी की बात है, कई उपकरणों के लिए अधिकांश संक्रमण उपकरणों के रैखिक भाग में होता है, ट्रांसफर फ़ंक्शन और रैखिक विश्लेषण को कम से कम अनुमानित उत्तर प्राप्त करने के लिए लागू किया जा सकता है।

यह गणितीय रूप से बूलियन बीजगणित एस प्राप्त करना संभव है, जिनमें दो से अधिक राज्य हैं। इलेक्ट्रॉनिक्स में इन के लिए बहुत अधिक उपयोग नहीं किया गया है, हालांकि तीन-राज्य उपकरणों को सामान्य रूप से आम है।

पूर्वाग्रह और संकेत विश्लेषण का पृथक्करण

इस तकनीक का उपयोग किया जाता है जहां सर्किट का संचालन अनिवार्य रूप से रैखिक होना है, लेकिन इसे लागू करने के लिए उपयोग किए जाने वाले उपकरण गैर-रैखिक हैं।एक ट्रांजिस्टर एम्पलीफायर इस तरह के नेटवर्क का एक उदाहरण है।इस तकनीक का सार विश्लेषण को दो भागों में अलग करना है।सबसे पहले, डीसी पूर्वाग्रह का विश्लेषण कुछ गैर-रैखिक विधि का उपयोग करके किया जाता है।यह सर्किट के quiescent ऑपरेटिंग बिंदु स्थापित करता है।दूसरे, सर्किट के छोटे सिग्नल विशेषताओं का रेखीय नेटवर्क विश्लेषण का उपयोग करके विश्लेषण किया जाता है।इन दोनों चरणों के लिए उपयोग किए जा सकने वाले तरीकों के उदाहरण नीचे दिए गए हैं।

डीसी विश्लेषण की ग्राफिकल विधि =

एक महान कई सर्किट डिजाइनों में, डीसी पूर्वाग्रह को एक अवरोधक (या संभवतः प्रतिरोधों का एक नेटवर्क) के माध्यम से एक गैर-रैखिक घटक को खिलाया जाता है। चूंकि प्रतिरोध रैखिक घटक हैं, इसलिए इसके स्थानांतरण फ़ंक्शन के एक ग्राफ से गैर-रैखिक डिवाइस के quiescent ऑपरेटिंग बिंदु को निर्धारित करना विशेष रूप से आसान है। विधि निम्नानुसार है: रैखिक नेटवर्क विश्लेषण से आउटपुट ट्रांसफर फ़ंक्शन (जो आउटपुट करंट के खिलाफ आउटपुट वोल्टेज है) की गणना रोकनेवाला (एस) के नेटवर्क के लिए की जाती है और उन्हें ड्राइविंग करने वाले जनरेटर। यह एक सीधी रेखा होगी (जिसे लोड लाइन कहा जाता है) और गैर-रेखीय डिवाइस के ट्रांसफर फ़ंक्शन प्लॉट पर आसानी से सुपरिम्पोज किया जा सकता है। वह बिंदु जहां लाइन्स क्रॉस क्विसेस ऑपरेटिंग पॉइंट है।

शायद सबसे आसान व्यावहारिक विधि (रैखिक) नेटवर्क ओपन सर्किट वोल्टेज और शॉर्ट सर्किट करंट की गणना करना है और इन्हें गैर-रैखिक डिवाइस के ट्रांसफर फ़ंक्शन पर प्लॉट करना है। इन दो बिंदुओं में शामिल होने वाली सीधी रेखा नेटवर्क का स्थानांतरण फ़ंक्शन है।

वास्तव में, सर्किट का डिजाइनर उस वर्णित के लिए रिवर्स दिशा में आगे बढ़ेगा। गैर-रैखिक डिवाइस के लिए निर्माताओं डेटा शीट में प्रदान किए गए एक भूखंड से शुरू, डिजाइनर वांछित ऑपरेटिंग बिंदु का चयन करेगा और फिर इसे प्राप्त करने के लिए आवश्यक रैखिक घटक मानों की गणना करेगा।

इस पद्धति का उपयोग करना अभी भी संभव है यदि डिवाइस को पक्षपाती किया जा रहा है, तो इसके पूर्वाग्रह को किसी अन्य डिवाइस के माध्यम से खिलाया गया है जो स्वयं गैर-रैखिक & nbsp;-उदाहरण के लिए एक डायोड है। हालांकि इस मामले में, डिवाइस पर नेटवर्क ट्रांसफर फ़ंक्शन का प्लॉट अब एक सीधी रेखा नहीं होगी और परिणामस्वरूप करने के लिए अधिक थकाऊ है।

छोटा सिग्नल समकक्ष सर्किट

इस विधि का उपयोग किया जा सकता है, जहां एक नेटवर्क में इनपुट और आउटपुट सिग्नल का विचलन गैर-रेखीय उपकरणों के स्थानांतरण फ़ंक्शन के एक पर्याप्त रैखिक हिस्से के भीतर रहता है, या फिर इतने छोटे होते हैं कि स्थानांतरण फ़ंक्शन के वक्र को रैखिक माना जा सकता है। इन विशिष्ट स्थितियों के एक सेट के तहत, गैर-रैखिक उपकरण को एक समान रैखिक नेटवर्क द्वारा दर्शाया जा सकता है। यह याद रखना चाहिए कि यह समकक्ष सर्किट पूरी तरह से उल्लेखनीय है और केवल छोटे सिग्नल विचलन के लिए मान्य है। यह डिवाइस के डीसी बायसिंग के लिए पूरी तरह से अनुचित है।

एक साधारण दो-टर्मिनल डिवाइस के लिए, छोटे सिग्नल समतुल्य सर्किट दो घटकों से अधिक नहीं हो सकते हैं। ऑपरेटिंग पॉइंट (जिसे डायनेमिक रेजिस्टेंस कहा जाता है) पर V/I वक्र के ढलान के बराबर एक प्रतिरोध, और वक्र के लिए स्पर्शरेखा। एक जनरेटर, क्योंकि यह स्पर्शरेखा, सामान्य रूप से, मूल से गुजरती नहीं होगी। अधिक टर्मिनलों के साथ, अधिक जटिल समकक्ष सर्किट की आवश्यकता होती है।

ट्रांजिस्टर निर्माताओं के बीच छोटे सिग्नल समतुल्य सर्किट को निर्दिष्ट करने का एक लोकप्रिय रूप दो-पोर्ट नेटवर्क मापदंडों का उपयोग करना है, जिन्हें [एच] पैरामीटर के रूप में जाना जाता है। ये [z] मापदंडों के साथ चार मापदंडों का एक मैट्रिक्स है, लेकिन [एच] मापदंडों के मामले में वे बाधाओं, प्रवेश, वर्तमान लाभ और वोल्टेज लाभ का एक संकर मिश्रण हैं। इस मॉडल में तीन टर्मिनल ट्रांजिस्टर को दो पोर्ट नेटवर्क माना जाता है, इसका एक टर्मिनल दोनों बंदरगाहों के लिए आम है। [एच] पैरामीटर काफी अलग हैं, जिसके आधार पर टर्मिनल को आम के रूप में चुना जाता है। ट्रांजिस्टर के लिए सबसे महत्वपूर्ण पैरामीटर आमतौर पर कॉमन एमिटर कॉन्फ़िगरेशन में आगे वर्तमान लाभ, एच <सब> 21 है। यह डेटा शीट पर H _Fe नामित किया गया है।

दो-पोर्ट मापदंडों के संदर्भ में छोटे सिग्नल समतुल्य सर्किट पर निर्भर जनरेटर की अवधारणा की ओर जाता है। यही है, एक वोल्टेज या वर्तमान जनरेटर का मान सर्किट में एक वोल्टेज या वर्तमान में अन्य जगह पर रैखिक रूप से निर्भर करता है। उदाहरण के लिए [z] पैरामीटर मॉडल इस आरेख में दिखाए गए अनुसार वोल्टेज जनरेटर पर निर्भर करता है;

दिखा रहा है

हमेशा दो-पोर्ट पैरामीटर समतुल्य सर्किट में निर्भर जनरेटर होंगे।यह [एच] मापदंडों के साथ -साथ [z] और किसी अन्य प्रकार पर भी लागू होता है।बड़े रैखिक नेटवर्क विश्लेषण में समीकरणों को विकसित करते समय इन निर्भरता को संरक्षित किया जाना चाहिए।

टुकड़े टुकड़े रैखिक विधि

इस विधि में, गैर-रैखिक डिवाइस का स्थानांतरण फ़ंक्शन क्षेत्रों में टूट गया है। इनमें से प्रत्येक क्षेत्र एक सीधी रेखा द्वारा अनुमानित है। इस प्रकार, स्थानांतरण फ़ंक्शन एक विशेष बिंदु तक रैखिक होगा जहां एक असंतोष होगा। इस बिंदु से पहले स्थानांतरण फ़ंक्शन फिर से रैखिक होगा लेकिन एक अलग ढलान के साथ।

इस पद्धति का एक प्रसिद्ध अनुप्रयोग एक पीएन जंक्शन डायोड के स्थानांतरण फ़ंक्शन का अनुमान है। एक आदर्श डायोड का स्थानांतरण फ़ंक्शन इस (गैर-रैखिक) अनुभाग के शीर्ष पर दिया गया है। हालांकि, इस सूत्र का उपयोग शायद ही कभी नेटवर्क विश्लेषण में किया जाता है, इसके बजाय एक टुकड़े -टुकड़े सन्निकटन का उपयोग किया जा रहा है। यह देखा जा सकता है कि डायोड वर्तमान तेजी से कम हो जाता है -i <सब> o जैसा कि वोल्टेज गिरता है। यह वर्तमान, अधिकांश उद्देश्यों के लिए, इतना छोटा है कि इसे नजरअंदाज किया जा सकता है। बढ़ते वोल्टेज के साथ, वर्तमान तेजी से बढ़ता है। डायोड को घातीय वक्र के घुटने तक एक खुले सर्किट के रूप में तैयार किया गया है, फिर इस बिंदु को सेमीकंडक्टिंग सामग्री के बल्क प्रतिरोध के बराबर एक रोकनेवाला के रूप में पिछले।

संक्रमण बिंदु वोल्टेज के लिए आमतौर पर स्वीकृत मान सिलिकॉन उपकरणों के लिए 0.7V और जर्मेनियम उपकरणों के लिए 0.3V हैं। डायोड का एक और भी सरल मॉडल, जिसे कभी -कभी स्विचिंग एप्लिकेशन में उपयोग किया जाता है, आगे के वोल्टेज के लिए शॉर्ट सर्किट है और रिवर्स वोल्टेज के लिए ओपन सर्किट है।

एक आगे के पक्षपाती पीएन जंक्शन का मॉडल लगभग निरंतर 0.7V है, जो एम्पलीफायर डिजाइन में ट्रांजिस्टर बेस-एमिटर जंक्शन वोल्टेज के लिए एक बहुत उपयोग किया जाता है।

टुकड़े टुकड़े विधि उस रैखिक नेटवर्क विश्लेषण तकनीकों में छोटे सिग्नल विधि के समान है, केवल तभी लागू किया जा सकता है जब सिग्नल कुछ सीमाओं के भीतर रहता है। यदि सिग्नल एक असंतोष बिंदु को पार करता है तो मॉडल अब रैखिक विश्लेषण उद्देश्यों के लिए मान्य नहीं है। मॉडल को छोटे सिग्नल पर लाभ होता है, हालांकि, यह सिग्नल और डीसी पूर्वाग्रह के लिए समान रूप से लागू होता है। इसलिए इन दोनों का एक ही संचालन में विश्लेषण किया जा सकता है और रैखिक रूप से सुपरइम्पोज़ेबल होगा।

समय-अलग-अलग घटक

रैखिक विश्लेषण में, नेटवर्क के घटकों को अपरिवर्तनीय माना जाता है, लेकिन कुछ सर्किटों में यह लागू नहीं होता है, जैसे कि स्वीप ऑसिलेटर, वोल्टेज नियंत्रित एम्पलीफायर एस, और चर इक्वाइज़र ।कई परिस्थितियों में घटक मूल्य में परिवर्तन आवधिक है।उदाहरण के लिए, एक आवधिक संकेत के साथ उत्साहित एक गैर-रैखिक घटक, समय-समय पर रैखिक घटक के रूप में दर्शाया जा सकता है। सिडनी डार्लिंगटन ने ऐसे आवधिक समय अलग -अलग सर्किटों का विश्लेषण करने की एक विधि का खुलासा किया।उन्होंने विहित सर्किट रूपों को विकसित किया जो रोनाल्ड एम। फोस्टर और विल्हेम कॉयर के विहित रूपों के अनुरूप हैं।^[7]

वेक्टर सर्किट सिद्धांत =

वेक्टरल धाराओं के लिए स्केलर मात्रा के आधार पर सर्किट सिद्धांत का सामान्यीकरण स्पिन सर्किट जैसे नए विकसित सर्किट के लिए एक आवश्यकता है^{[clarification needed]} सामान्यीकृत सर्किट चर में चार घटक होते हैं: स्केलर करंट और वेक्टर स्पिन करंट एक्स, वाई और जेड दिशाओं में।वोल्टेज और धाराएं प्रत्येक वेक्टर मात्रा बन जाती हैं, जिसमें 4x4 स्पिन चालन मैट्रिक्स के रूप में वर्णित चालन के साथ वेक्टर मात्रा बन जाती है^{[citation needed]}

References

↑ Belevitch V (May 1962). "Summary of the history of circuit theory". Proceedings of the IRE. 50 (5): 849. doi:10.1109/JRPROC.1962.288301. S2CID 51666316. का हवाला देते "IRE Standards on Circuits: Definitions of Terms for Linear Passive Reciprocal Time Invariant Networks, 1960". Proceedings of the IRE. 48 (9): 1609. September 1960. doi:10.1109/JRPROC.1960.287676.इस परिभाषा को सही ठहराने के लिए।
सिडनी डार्लिंगटन Darlington S (1984). "A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors". IEEE Trans. Circuits and Systems. 31 (1): 4. doi:10.1109/TCS.1984.1085415.
Belevitch का अनुसरण करता है, लेकिन नोट्स अब नेटवर्क के कई बोलचाल के उपयोग भी हैं
↑ वाई-काई चेन, सर्किट विश्लेषण और प्रतिक्रिया एम्पलीफायर थ्योरी , पी।6-14, सीआरसी प्रेस, 2005 ISBN 1420037277
↑ Nilsson, J W, Riedel, S A (2007). Electric Circuits (8th ed.). Pearson Prentice Hall. pp. 112–113. ISBN 978-0-13-198925-2.{{cite book}}: CS1 maint: multiple names: authors list (link)
↑ Nilsson, J W, Riedel, S A (2007). Electric Circuits (8th ed.). Pearson Prentice Hall. p. 94. ISBN 978-0-13-198925-2.{{cite book}}: CS1 maint: multiple names: authors list (link)
↑ Kumar, Ankush; Vidhyadhiraja, N. S.; Kulkarni, G. U . (2017). "Current distribution in conducting nanowire networks". Journal of Applied Physics. 122 (4): 045101. Bibcode:2017JAP...122d5101K. doi:10.1063/1.4985792.
↑ Ljiljana Trajković, Nonlinear सर्किट, द इलेक्ट्रिकल इंजीनियरिंग हैंडबुक (एड: वाई-काई चेन), पीपी। 79-81, अकादमिक प्रेस, 2005 ISBN 0-12-170960-4
↑ US patent 3265973, Sidney Darlington, Irwin W. Sandberg, "Synthesis of two-port networks having periodically time-varying elements", issued 1966-08-09

External links

Circuit Analysis Techniques — includes node/mesh analysis, superposition, and thevenin/norton transformation

[1] Belevitch V (May 1962). "Summary of the history of circuit theory". Proceedings of the IRE. 50 (5): 849. doi:10.1109/JRPROC.1962.288301. S2CID 51666316. का हवाला देते "IRE Standards on Circuits: Definitions of Terms for Linear Passive Reciprocal Time Invariant Networks, 1960". Proceedings of the IRE. 48 (9): 1609. September 1960. doi:10.1109/JRPROC.1960.287676.इस परिभाषा को सही ठहराने के लिए।
सिडनी डार्लिंगटन Darlington S (1984). "A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors". IEEE Trans. Circuits and Systems. 31 (1): 4. doi:10.1109/TCS.1984.1085415.
Belevitch का अनुसरण करता है, लेकिन नोट्स अब नेटवर्क के कई बोलचाल के उपयोग भी हैं

[2] वाई-काई चेन, सर्किट विश्लेषण और प्रतिक्रिया एम्पलीफायर थ्योरी , पी।6-14, सीआरसी प्रेस, 2005 ISBN 1420037277

[3] Nilsson, J W, Riedel, S A (2007). Electric Circuits (8th ed.). Pearson Prentice Hall. pp. 112–113. ISBN 978-0-13-198925-2.{{cite book}}: CS1 maint: multiple names: authors list (link)

[4] Nilsson, J W, Riedel, S A (2007). Electric Circuits (8th ed.). Pearson Prentice Hall. p. 94. ISBN 978-0-13-198925-2.{{cite book}}: CS1 maint: multiple names: authors list (link)

[5] Kumar, Ankush; Vidhyadhiraja, N. S.; Kulkarni, G. U . (2017). "Current distribution in conducting nanowire networks". Journal of Applied Physics. 122 (4): 045101. Bibcode:2017JAP...122d5101K. doi:10.1063/1.4985792.

[6] Ljiljana Trajković, Nonlinear सर्किट, द इलेक्ट्रिकल इंजीनियरिंग हैंडबुक (एड: वाई-काई चेन), पीपी। 79-81, अकादमिक प्रेस, 2005 ISBN 0-12-170960-4

[7] US patent 3265973, Sidney Darlington, Irwin W. Sandberg, "Synthesis of two-port networks having periodically time-varying elements", issued 1966-08-09

[1]

[2]

[3]

[4]

[5]

[6]

[7]

@@ Line 145: / Line 145: @@
 इस पद्धति के लिए एक अंतर्निहित धारणा है कि कुल धारा या वोल्टेज इसके भागों का एक रैखिक अधिस्थापन है। इसलिए, गैर-रैखिक घटक मौजूद होने पर विधि का उपयोग नहीं किया जा सकता है।<ref>वाई-काई चेन, '' सर्किट विश्लेषण और प्रतिक्रिया एम्पलीफायर थ्योरी '', पी।6-14, सीआरसी प्रेस, 2005 {{ISBN|1420037277}}</ref>  रेखीय परिपथों में भी तत्वों द्वारा उपयोग की गई कुल शक्ति का पता लगाने के लिए शक्तियों के अधिस्थापन का उपयोग नहीं किया जा सकता है। कुल वोल्टेज या करंट के वर्ग के अनुसार शक्ति भिन्न होती है और योग का वर्ग आमतौर पर वर्गों के योग के बराबर नहीं होता है। एक तत्व में कुल शक्ति को वोल्टेज और वर्तमान में स्वतंत्र रूप से अधिस्थापन लागू करके और फिर कुल वोल्टेज और वर्तमान से शक्ति की गणना करके पाया जा सकता है।
-== विधि की पसंद ==
+== विधि का चुनाव ==
-विधि की पसंद<ref>{{cite book |author=Nilsson, J W, Riedel, S A |title=Electric Circuits |publisher=Pearson Prentice Hall  |year=2007 |isbn=978-0-13-198925-2 |edition=8th |pages=112–113 |url=https://books.google.com/books?id=sxmM8RFL99wC&q=112&pg=PA112 }}</ref> कुछ हद तक स्वाद की बात है।यदि नेटवर्क विशेष रूप से सरल है या केवल एक विशिष्ट वर्तमान या वोल्टेज की आवश्यकता है, तो कुछ सरल समकक्ष सर्किटों के तदर्थ अनुप्रयोग अधिक व्यवस्थित तरीकों के लिए पुनरावृत्ति के बिना उत्तर प्राप्त कर सकते हैं।
+विधि का चुनाव<ref>{{cite book |author=Nilsson, J W, Riedel, S A |title=Electric Circuits |publisher=Pearson Prentice Hall  |year=2007 |isbn=978-0-13-198925-2 |edition=8th |pages=112–113 |url=https://books.google.com/books?id=sxmM8RFL99wC&q=112&pg=PA112 }}</ref> कुछ हद तक अनुभव की बात है। यदि नेटवर्क विशेष रूप से सरल है या केवल एक विशिष्ट धारा या वोल्टेज की आवश्यकता है तो कुछ सरल समकक्ष सर्किटों की पुनरावृत्ति के बिना उत्तर प्राप्त कर सकते हैं।
-*  [[ नोडल विश्लेषण ]]: वोल्टेज चर की संख्या, और इसलिए एक साथ समीकरणों को हल करने के लिए, नोड्स माइनस की संख्या के बराबर है।संदर्भ नोड से जुड़ा प्रत्येक वोल्टेज स्रोत अज्ञात और समीकरणों की संख्या को कम करता है।
+*  [[ नोडल विश्लेषण ]]: वोल्टेज चर की संख्या, और इसलिए समीकरणों को हल करने के लिए, नोड्स की संख्या घटा के बराबर है।संदर्भ नोड से जुड़ा प्रत्येक वोल्टेज स्रोत अज्ञात और समीकरणों की संख्या को कम करता है।
 *  [[ मेष विश्लेषण ]]: वर्तमान चर की संख्या, और इसलिए एक साथ समीकरणों को हल करने के लिए, मेषों की संख्या के बराबर है।एक जाल में प्रत्येक वर्तमान स्रोत अज्ञात की संख्या को कम कर देता है।मेष विश्लेषण केवल नेटवर्क के साथ उपयोग किया जा सकता है जिसे  [[ प्लानर ग्राफ |  प्लानर ]] नेटवर्क के रूप में खींचा जा सकता है, यानी कोई क्रॉसिंग घटकों के साथ<ref>{{cite book |author=Nilsson, J W, Riedel, S A |title=Electric Circuits |publisher=Pearson Prentice Hall  |year=2007 |isbn=978-0-13-198925-2 |edition=8th |page=94 |url=https://books.google.com/books?id=sxmM8RFL99wC&pg=PA94 }}</ref>
 *  [[ सुपरपोजिशन प्रमेय |  सुपरपोज़िशन ]] संभवतः सबसे वैचारिक रूप से सरल विधि है, लेकिन तेजी से बड़ी संख्या में समीकरणों और गन्दी प्रतिबाधा संयोजनों की ओर जाता है क्योंकि नेटवर्क बड़ा हो जाता है।

Anonymous

Search

नेटवर्क विश्लेषण: Difference between revisions

Revision as of 12:47, 26 August 2022

परिभाषाएँ

समकक्ष सर्किट

श्रृंखला और समानांतर में प्रतिबाधा

डेल्टा-वी परिवर्तन

नेटवर्क नोड उन्मूलन का सामान्य रूप

स्रोत परिवर्तन

सरल नेटवर्क

वोल्टेज डिवीजन ऑफ सीरीज़ कंपोनेंट्स

समानांतर घटकों का वर्तमान विभाजन

नोडल विश्लेषण

जाल (Mesh) विश्लेषण

अधिस्थापन

विधि का चुनाव

स्थानांतरण समारोह

दो टर्मिनल घटक हस्तांतरण कार्य

दो पोर्ट नेटवर्क ट्रांसफर फ़ंक्शन =

दो पोर्ट पैरामीटर

वितरित घटक =

छवि विश्लेषण =

दो पोर्ट पैरामीटर

वितरित घटक =

छवि विश्लेषण =

गैर-रैखिक नेटवर्क

संवैधानिक समीकरण

अस्तित्व, विशिष्टता और स्थिरता

तरीके

स्विचिंग नेटवर्क का बूलियन विश्लेषण

पूर्वाग्रह और संकेत विश्लेषण का पृथक्करण

डीसी विश्लेषण की ग्राफिकल विधि =

छोटा सिग्नल समकक्ष सर्किट

टुकड़े टुकड़े रैखिक विधि

स्विचिंग नेटवर्क का बूलियन विश्लेषण

पूर्वाग्रह और संकेत विश्लेषण का पृथक्करण

डीसी विश्लेषण की ग्राफिकल विधि =

छोटा सिग्नल समकक्ष सर्किट

टुकड़े टुकड़े रैखिक विधि

समय-अलग-अलग घटक

वेक्टर सर्किट सिद्धांत =

See also

References

External links

Navigation

Wiki tools

Page tools

Other projects

Categories